0 引言
在传统Terzaghi[1]固结理论中,为便于求得解析解,黏土层上下两侧的砂层常被处理为完全透水或完全不透水的边界,但实际应为处于这两种极端情况之间的半透水边界。例如,砂垫层会由于黏土颗粒排水拥堵而变为部分排水砂垫层。最早研究半透水边界问题的专家是Gray[2],随后Schiffman等[3]和Mesri等[4]对这一问题进行了初步研究。为了更合理地分析边界透水性对地基固结进程的影响,国内已有学者[5-6]将半透水边界引入到Terzaghi一维固结理论中,发现半透水边界对地基的固结过程具有显著的影响,但这些研究是基于达西渗流假定之上的。
饱和黏土具有显著的流变特性,这应该是导致基于线弹性变形假定的传统固结理论常常不能很好地描述软土地基固结问题的原因。为此,有学者[7-8]在固结分析中先后引入了由弹簧和黏壶元件串联或并联而成的黏弹性模型。但试验表明,有时需要较多的元件组合才能较好地模拟某些土体的流变特性,但此时的方程由于阶数太高而不易求解。随着分数阶微积分的推广应用,这一问题得到较大改观,比如,Gemant等[9]经过对一系列流变模型实验的分析后认为,采用分数阶导数模型描述材料的本构关系更为合适。随后,一些学者开始用基于分数阶导数修正的Kelvin模型[10]和Merchant模型[11]等来描述软黏土的流变固结特性。
综上所述,目前关于半透水边界条件下固结分析时同时考虑分数阶黏弹性土体和非Darcy渗流影响的研究还很少。因此,为进一步揭示饱和黏性土的流变固结机制,本文引入基于Caputo分数定义的分数阶Merchant模型来描述饱和黏弹性土体的本构关系,并采用非牛顿指数渗流方程描述其中的非Darcy渗流,重新推导半透水边界条件下一维固结方程,并给出了方程的隐式有限差分格式,最后讨论相关模型参数对流变固结的影响。
1 分数阶Merchant模型
分数阶Merchant模型(图1)是由分数阶Kelvin模型串联一个弹簧组成。其中的弹簧元件描述固体的弹性行为,而Koeller弹壶元件描述的是性质处于固体和流体之间的材料。与分数阶Kelvin模型相比,分数阶Merchant模型能体现加载瞬间的变形,因此它的应用范围更为广泛。
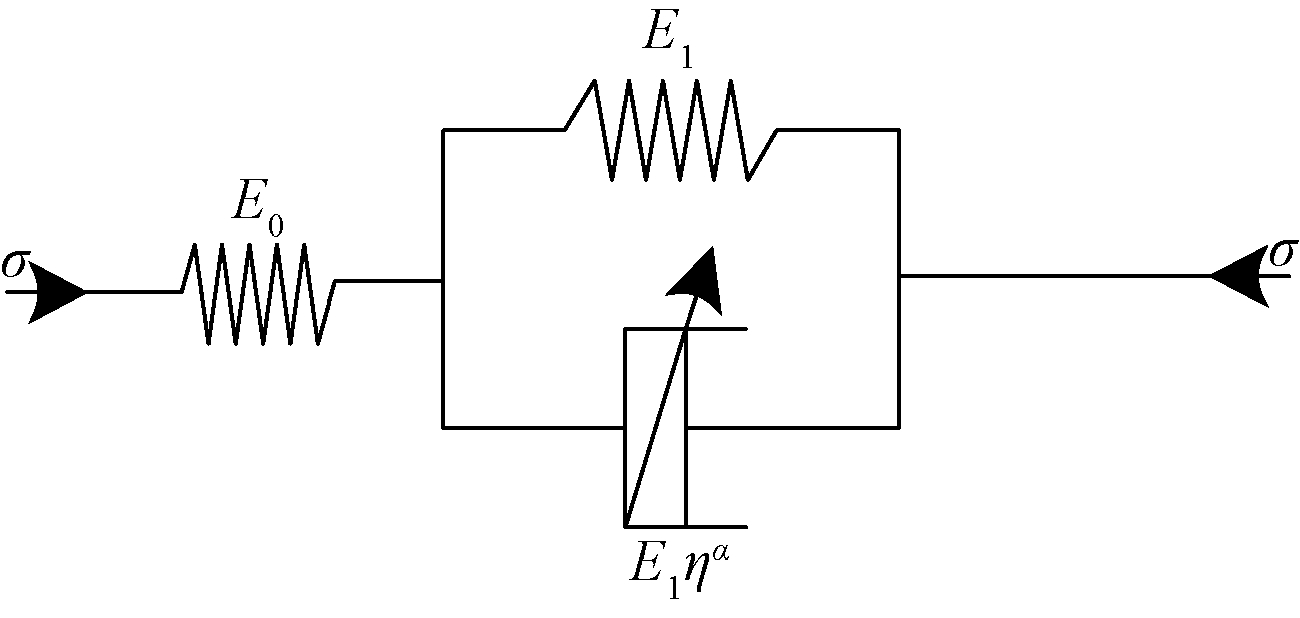
图1 分数阶Merchant模型
Figure 1 Fractional-order Merchant model
刘忠玉等[11]曾给出了该分数阶Merchant模型的蠕变柔量J(t)为
(1)
式中:η=F/E1为黏滞时间,F为黏滞系数;E0和E1分别为独立弹簧和Kelvin体的弹性模量;α为分数导数阶数;t为时间;![]() 为Mittag-Leffler函数。
为Mittag-Leffler函数。
当α=1时,Eα(x)=ex,式(1)退化为![]() 此即整数阶Merchant模型的蠕变柔量表达式。这样,低应变情况下黏弹性体的本构方程为
此即整数阶Merchant模型的蠕变柔量表达式。这样,低应变情况下黏弹性体的本构方程为
ε(t)=![]() J(t-τ)dσ′(τ)。
J(t-τ)dσ′(τ)。
(2)
式中:σ′为有效应力。
2 一维黏弹性固结方程及求解
如图2所示,设某厚度为H的均质饱和黏性土地基在自重应力作用下已完全固结,其上半透水边界厚度为L1,相应的渗透系数为k1,下半透水边界厚度为L2,相应的渗透系数为k2。现于顶面一次骤然施加无限均布荷载p0 ,假定固结过程中的渗流可用非牛顿指数渗流方程描述[11,15-16]:
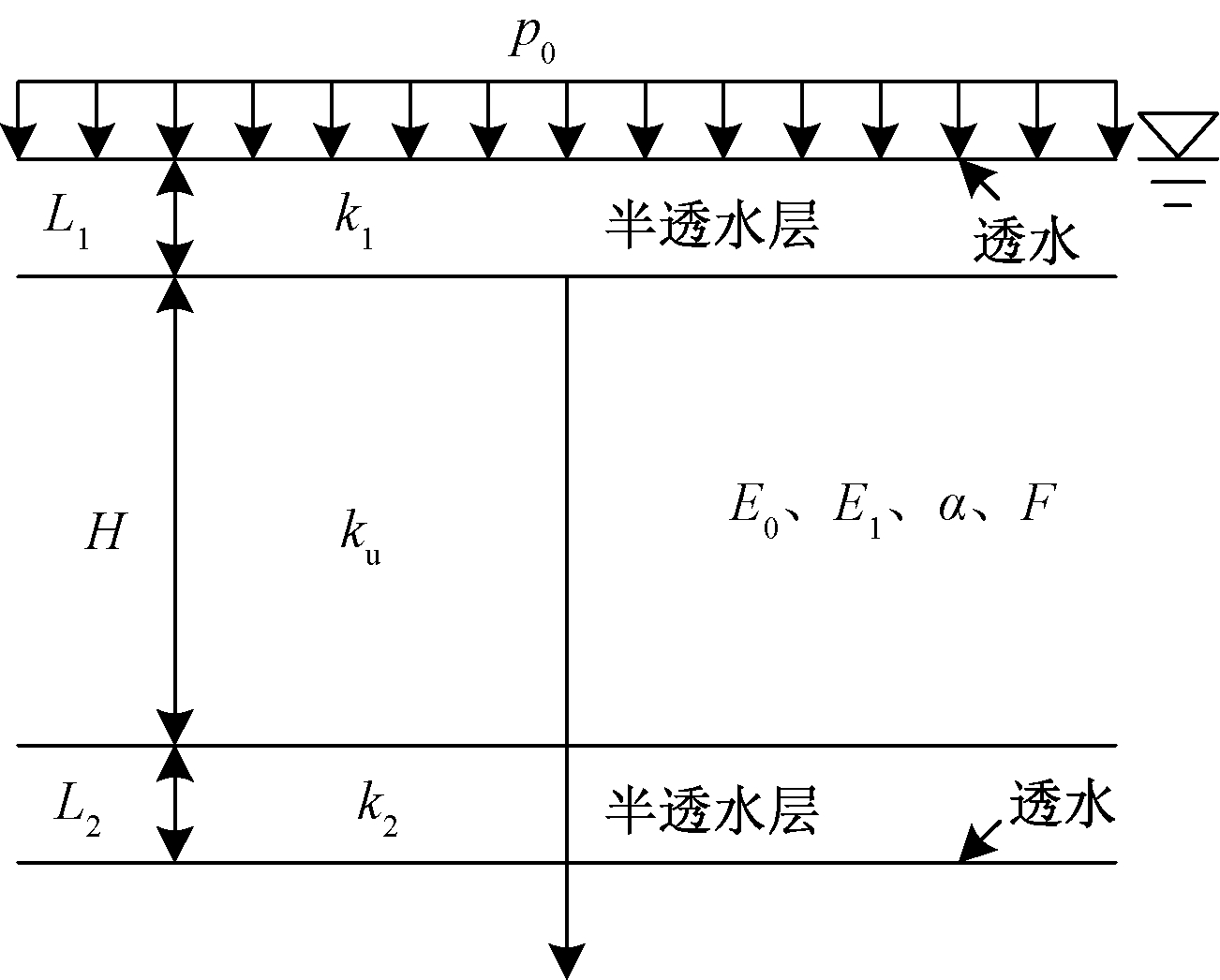
图2 半透水边界下均质饱和黏土地基的
黏弹性固结过程
Figure 2 Viscoelastic consolidation process of homogeneous saturated clay foundation under semi-permeable boundary
v=-ku[i-i0(1-e-i/i0)]。
(3)
式中:v为渗流速度;i为水力坡降;ku和i0分别为v-i曲线渐近线的斜率和截距,ku类似于达西渗流的渗透系数,i0为非牛顿指数,当i0=0时,式(3)退化为达西定律。
土骨架的黏弹性变形可用式 (2) 描述,且各模型参数为常量,其他基本假设同Terzaghi一维固结理论。设时刻t、深度z处的超静孔隙水压力为u(z,t),由渗流连续性条件可得控制方程为[11]
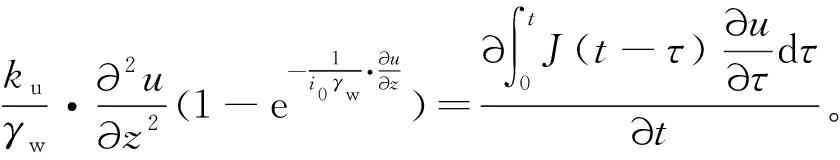
(4)
与图2所示相对应的初始条件为
u(z,0)=p0, 0<z<H。
(5)
边界条件为
(6)
(7)
式中:![]() 易见,当R1=∞、R2=0和当R1=R2=∞,求解条件式(6)和式(7)即转化为一维黏弹性固结问题中常见的单面排水和双面排水条件。
易见,当R1=∞、R2=0和当R1=R2=∞,求解条件式(6)和式(7)即转化为一维黏弹性固结问题中常见的单面排水和双面排水条件。
为了便于分析,对以下参数进行无量纲化处理:
这样,控制方程(4)和定解条件式(5)~(7)可变为
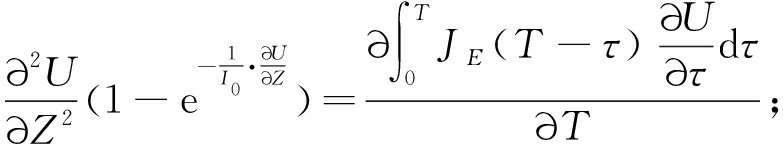
(8)
U(Z,0)=1, 0<Z<1;
(9)
(10)
(11)
式中:![]()
3 方程有限差分格式
3.1 离散方程
类似文献[11],引入隐式有限差分法来求解式(8) 。这里分别以ΔT和ΔZ为时间步长和空间步长,并分别用j、i′表示空间离散点和时间离散点。其中地基离散为K-1层,节点从1到K编号。
对式(8)等号左边关于Z的偏导采用中心差分近似,等号右边关于T的偏导采用向前差分近似,则式(8)可离散为
γj,i′Uj-1,i′+1-bj,i′Uj,i′+1+γj,i′Uj+1,i′+1=
Gj,i′-JE(ΔT/2)Uj,i′。
(12)
式中:bj,i′=[2γj,i′+JE(ΔT/2)];
初始条件式(9)可离散为
Uj,0=1。
(13)
采用泰勒展开的方法对边界条件式(10)、式(11)进行处理,并忽略3次及更高阶项,可得:
(3+2R1ΔZ)U1,i′+1-4U2,i′+1+U3,i′+1=0;
(14)
(3+2R2ΔZ)Uk,i′+1-4Uk-1,i′+1+Uk-2,i′+1=0。
(15)
这样,式(12)~(14)组成封闭的方程组,但其系数是与孔压相关的函数,所以可采用迭代法进行求解。
3.2 平均固结度
分别引入按孔压和变形定义的固结度UP和Us来分析地基中孔压的整体消散情况和沉降规律:
(16)
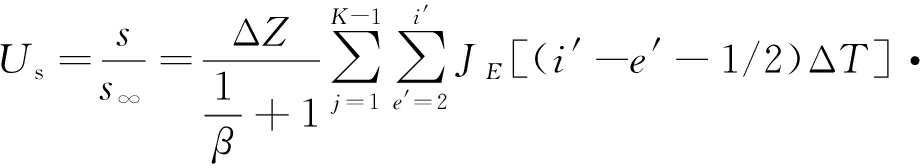
![]()
(17)
式中:s和s∞分别为地基在时刻t的沉降量和最终沉降量。
3.3 解法验证
根据上述解,利用MATLAB编写了相应的算法程序。为验证算法的正确性,选取两种情况进行比较。首先,考虑刘忠玉等[7]基于Darcy渗流和整数阶Merchant模型的算例。由于文献[7]考虑的是完全透水或不透水边界,所以这里令α=1、R1=∞、R2=0。图3(a)给出了本文和该文献中两种固结度UP和Us与无量纲时间T的关系曲线的对比结果。可见,Darcy渗流条件下的整数阶Merchant模型是本文的一个特例。
其次,选取文献[11]同时考虑非牛顿指数渗流和分数阶Merchant模型的算例。由于该文献考虑的仍为传统边界条件,因此,这里仍需令R1=∞、R2=0。其他参数与该文献一致,即取α=0.35、V=1、β=1。关于I0=0和I0=1两种情况下的对比结果如图3(b)所示。很明显,两者吻合良好。
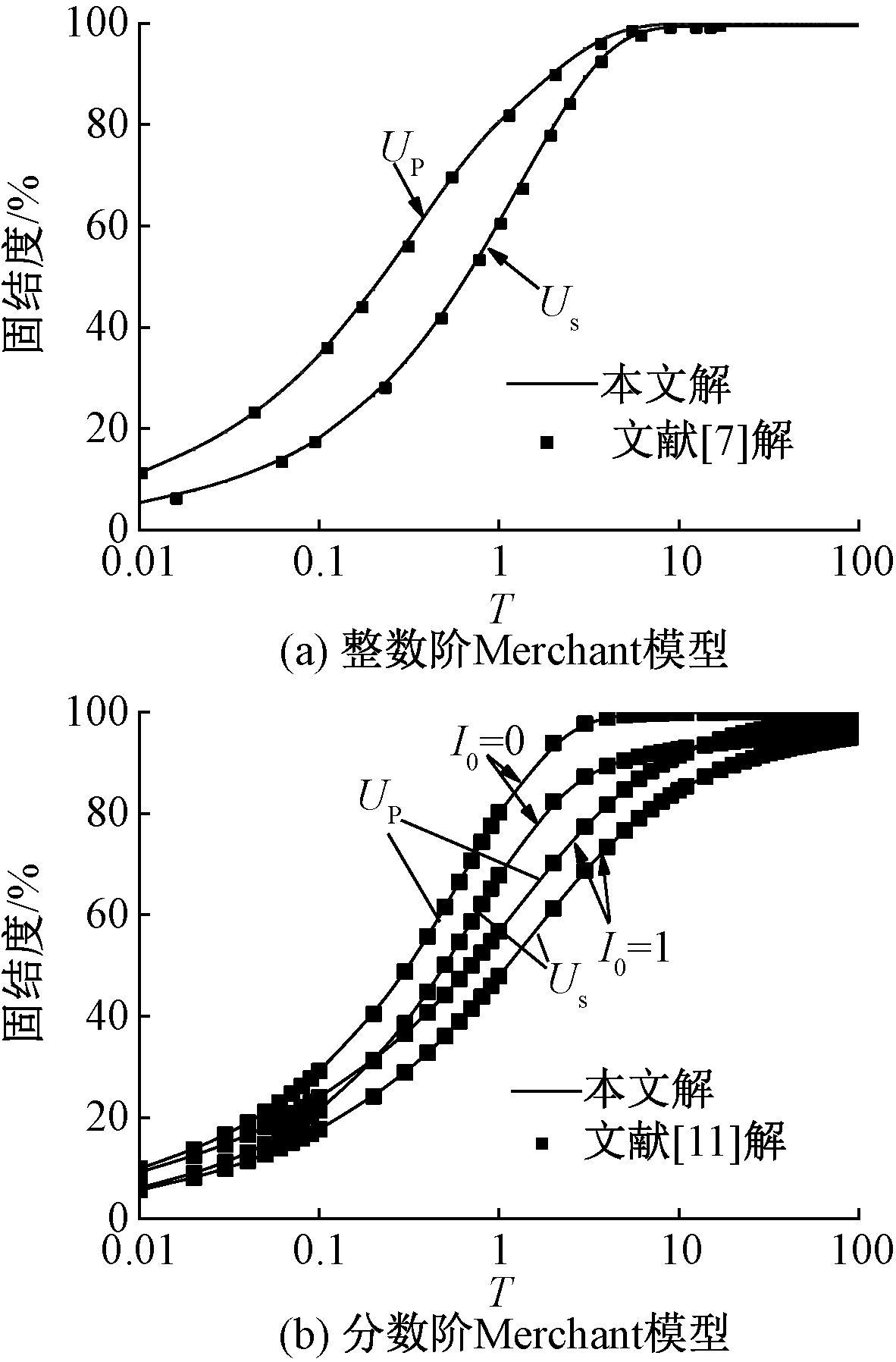
图3 单面完全透水时的固结度
Figure 3 Degree of consolidation of soil with single drainage boundary
4 参数分析
4.1 半透水边界参数对固结过程的影响
考虑到上下边界透水性能对固结过程的影响相似[5],这里只考虑上边界半透水参数R1对固结过程的影响。取α=0.35、β=1、V=0.1、R2=1、I0=1,结果如图4所示。其中,图4(a)为上半透水边界参数R1对固结度UP的影响曲线。可以看出,当R1=0时,其边界退化为不透水边界,其固结速率是最慢的;随着R1的增大,地基内孔压的消散速度随边界透水条件的改善而逐渐加快,即增大半透水边界参数能够加快地基的固结进程,这与文献[5]考虑流变效应和文献[10]基于分数阶Kelvin-Voigt模型的结论类似。但不同的是,本文考虑了非Darcy渗流,达到相同固结度所需的时间更长。
图4(b)为R1对固结度Us的影响曲线。很明显,该参数对地基沉降速率的影响与对孔压消散的影响相似,即随着半透水边界参数的增大,地基沉降速率逐渐加快。同时从图4可以看出,当R1达到50后,进一步增大R1,上述两个固结度变化很小,这说明当半透水边界参数大于50时,半透水边界参数对地基的固结几乎没有影响。
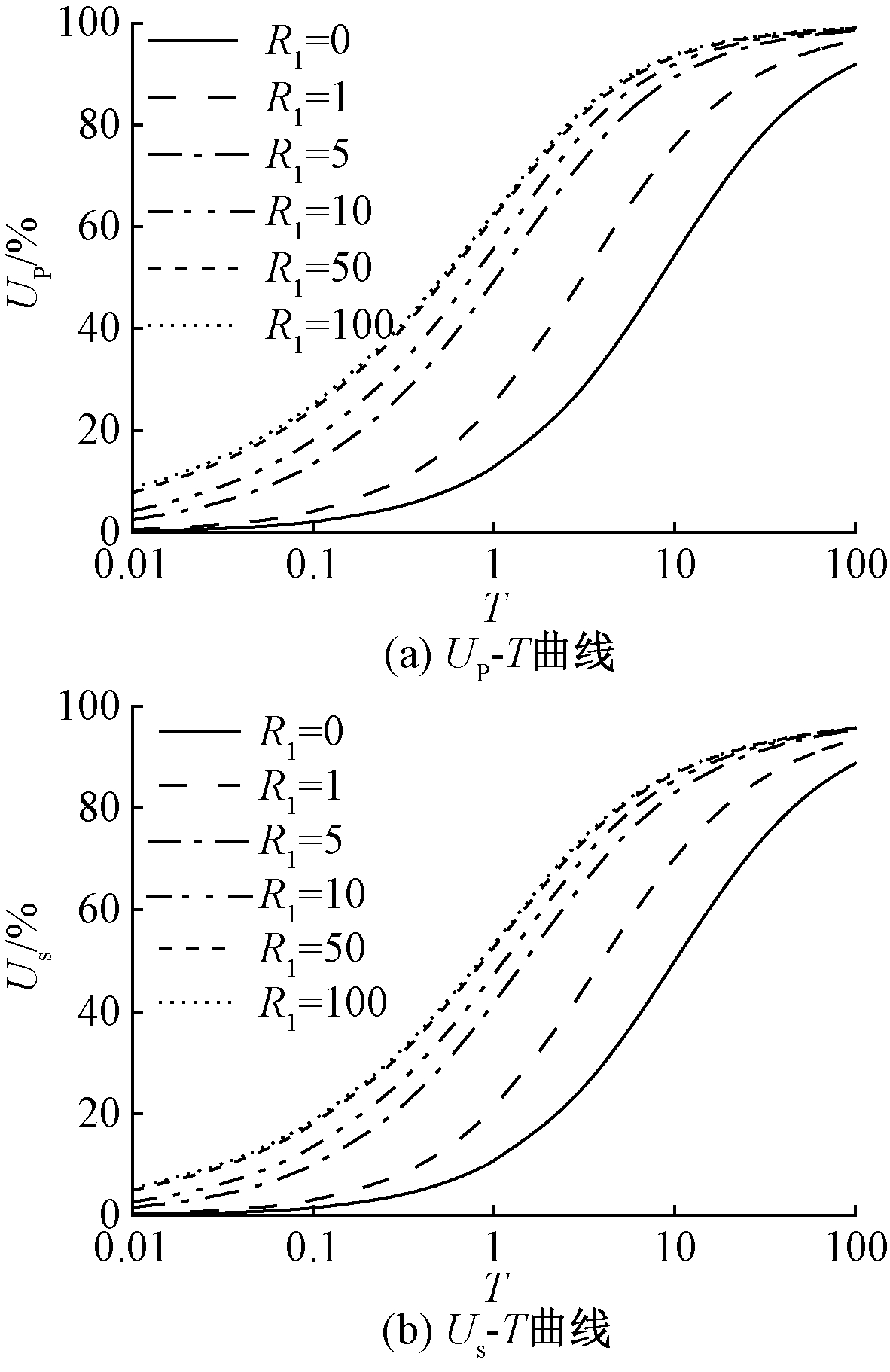
图4 半透水边界参数R1对固结度的影响
Figure 4 Influence of semi-permeable boundary parameters R1 on degree of consolidation
4.2 非牛顿指数I0对固结进程的影响
已有研究表明,非Darcy渗流对固结过程有显著影响。为此,本文讨论了非牛顿指数I0对半渗透边界下固结过程的影响。I0参数取值如图5所示,其他参数取值同4.1节。图5(a)表明,当I0=0时,土中渗流退化为Darcy渗流,地基的固结速率最快,且随着I0的增大,地基固结逐渐变慢。所以,如果忽略非Darcy渗流的影响,地基的孔压消散速率将会被高估。
从图5(b)可以看出,非牛顿指数越大,地基的沉降就越慢。同时,对比图5(a)和5(b)可以看出,固结度Us总是小于固结度UP。如当I0=0.5,T=1时,固结度Us为33.37%,固结度UP为39.49%,所以,地基的沉降总是滞后于地基中孔压的整体消散,这与李传勋等[16]和刘忠玉等[11]的研究结论类似。值得注意的是,上述结果与经典Terzaghi固结理论的结论不同,这是因为Terzaghi固结理论假定变形是线弹性的。
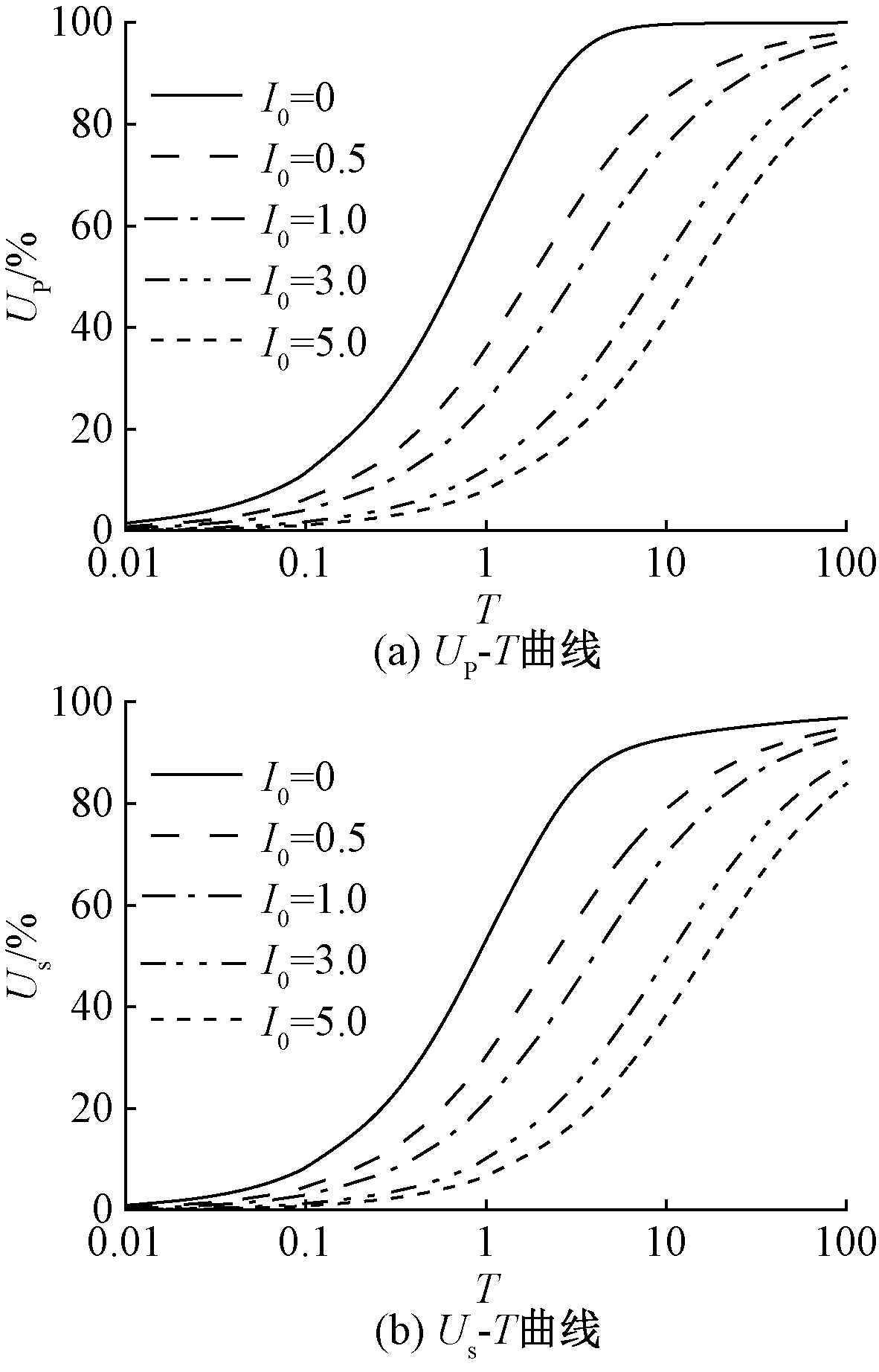
图5 I0对固结度的影响
Figure 5 Influence of I0 on degree of consolidation
4.3 分数导数阶数α对固结进程的影响
图6为分数导数阶数α取不同值时固结度UP和Us随无量纲时间T的变化曲线。由图6(a)可以看出,α对固结度UP的影响主要集中在固结的中期。在固结中期,随着α的增大,固结度UP变小,即增大分数阶数会减缓地基中孔压的整体消散。这与刘忠玉等[11]基于非牛顿指数渗流和分数阶的Merchant模型的结论存在差异。后者认为在固结初期分数阶数α越大,其固结也越快,这应该是由于边界条件不同而导致的,后者考虑的是单面完全透水边界。
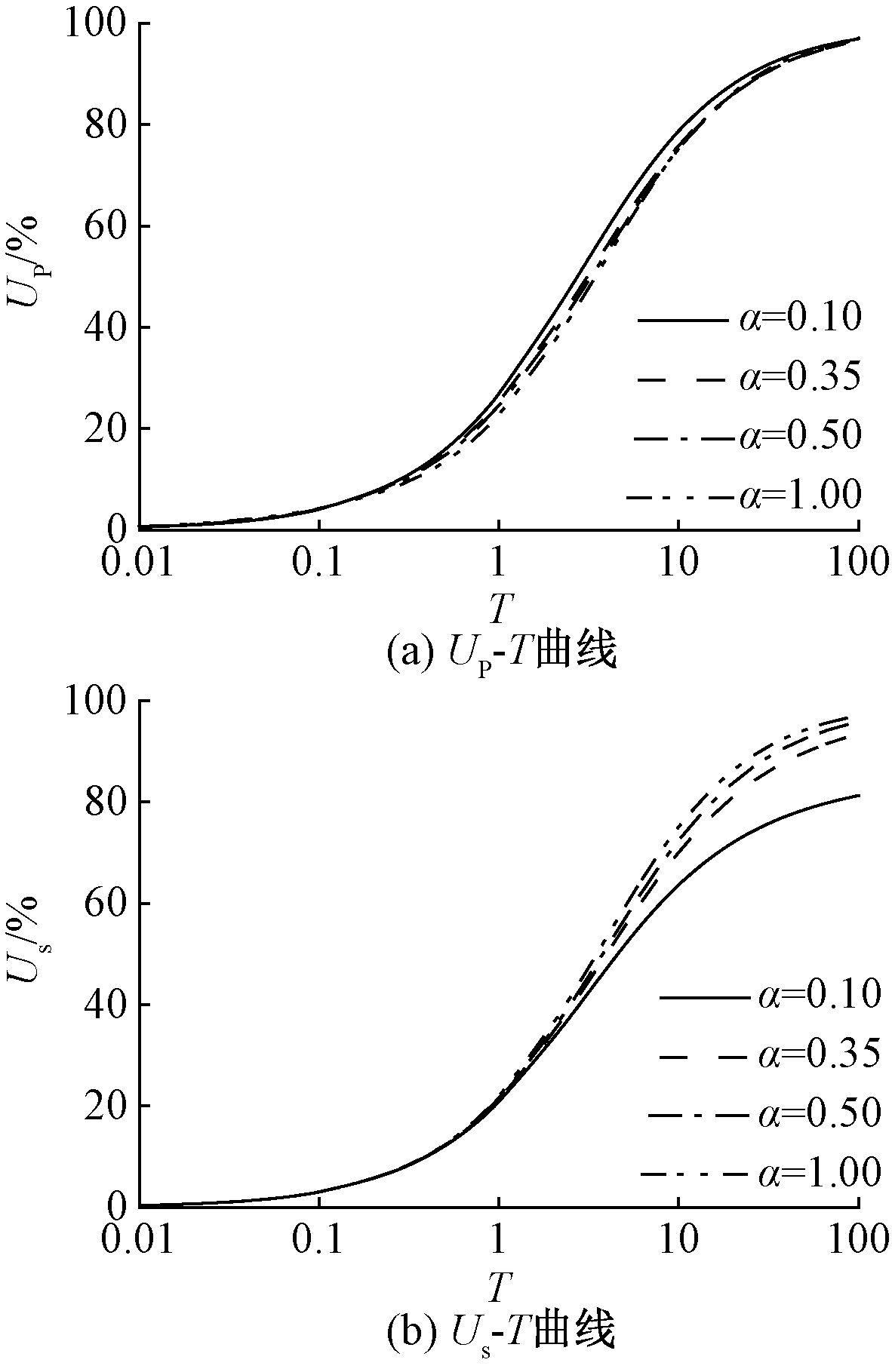
图6 分数阶α对固结度的影响
Figure 6 Influence of the fractional order α on degree of consolidation
由图6(b)可知,与图6(a)不同,α对固结度Us的影响主要集中在中后期阶段。在固结初期,α对地基的沉降几乎没有影响或影响较小。随着α的增大,地面沉降逐渐加快。通过对比图6(a)和6(b),发现α对固结度Us的影响更为显著。
4.4 模量比β对固结进程的影响
β=E1/E0为分数阶Kelvin体中并联弹簧与独立弹簧的模量比。图7表示β对2个固结度UP和Us的影响。相关参数取值见图7。当β=∞时,即E1→∞,此时分数阶Merchant模型退化为Hooke弹簧模型,即不考虑土体的流变特性。如图7所示,随着β的增大,两种固结度UP和Us的固结进程逐渐加快。即模量比越大,地基的孔压消散速率和地基沉降速率越快。这似乎与刘忠玉等[11]得出的结论有所不同。后者认为模量比越大,孔隙水压力消散速率和地基沉降速率越慢。事实上,这是因为本文定义的模量比与后者不同。此外,因为本文考虑的是半透水边界,所以达到相同固结度所用的时间比单面透水边界[11]要长。
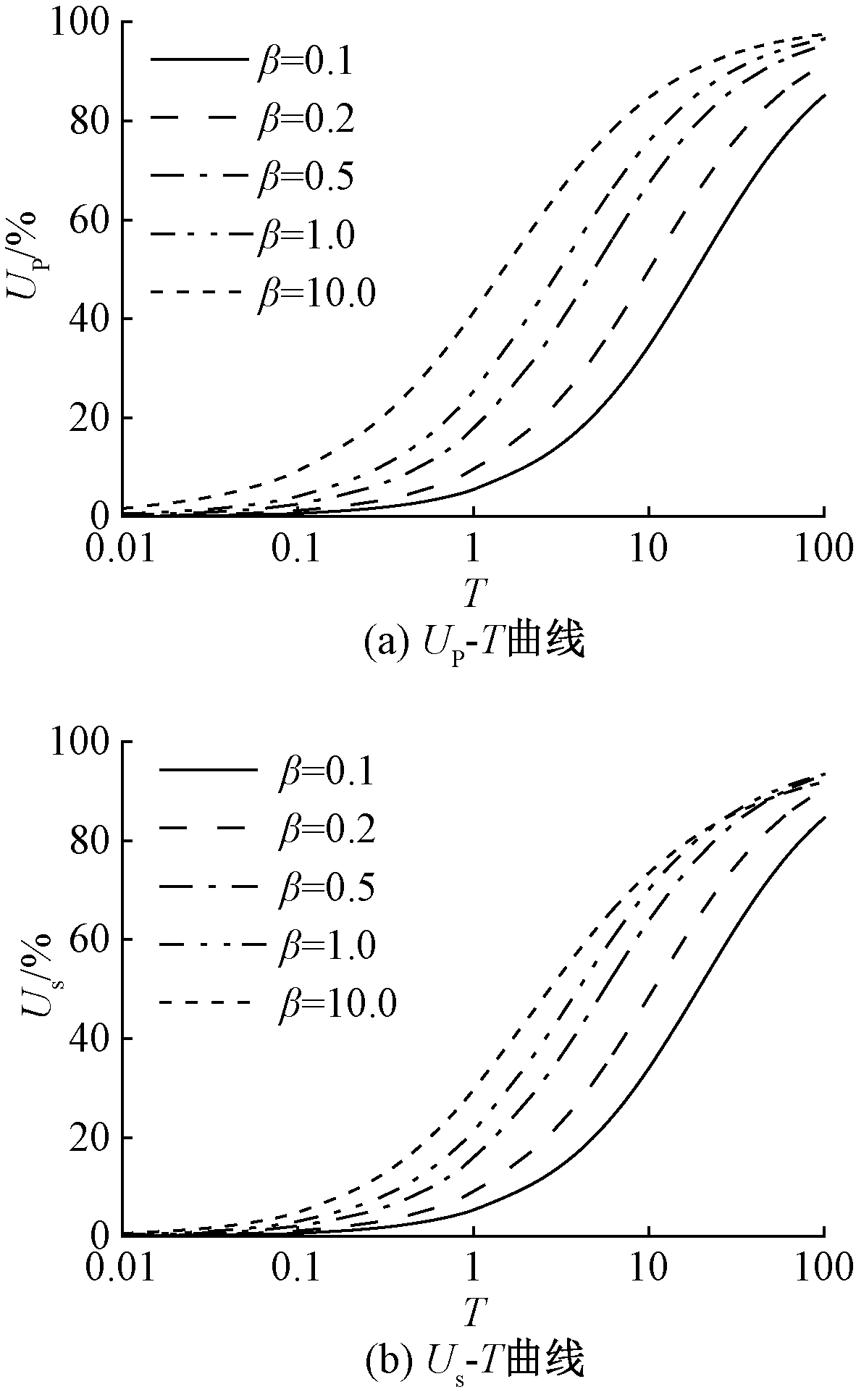
图7 β对固结度的影响
Figure 7 Influence of β on degree of consolidation
4.5 黏滞系数V对固结进程的影响
V=KuF/(H2γw),它可视为无量纲的黏滞系数。为考察半透水边界条件下V对固结过程的影响,图8给出了两个固结度UP和Us随无量纲时间T的变化曲线。图8 (a)表明,在固结的前期和中期,随着V的增大,固结度UP变大,即整体孔压消散将加快。在固结的后期,4条曲线已基本重合,这说明V对固结后期孔压消散的影响很弱。
从图8(b)可以看出,在固结初期,V的变化对固结度Us没有影响,即在固结初期,黏滞系数对地基沉降没有影响。但在T>0.6后,固结度Us随着V的增大而变小,即无量纲黏滞系数越大,地基沉降就越慢。由此可见,土体的黏滞性会减缓地基的沉降,且主要体现在固结的中后期。这与刘忠玉等[11]和汪磊等[10]的研究结论是一致的。
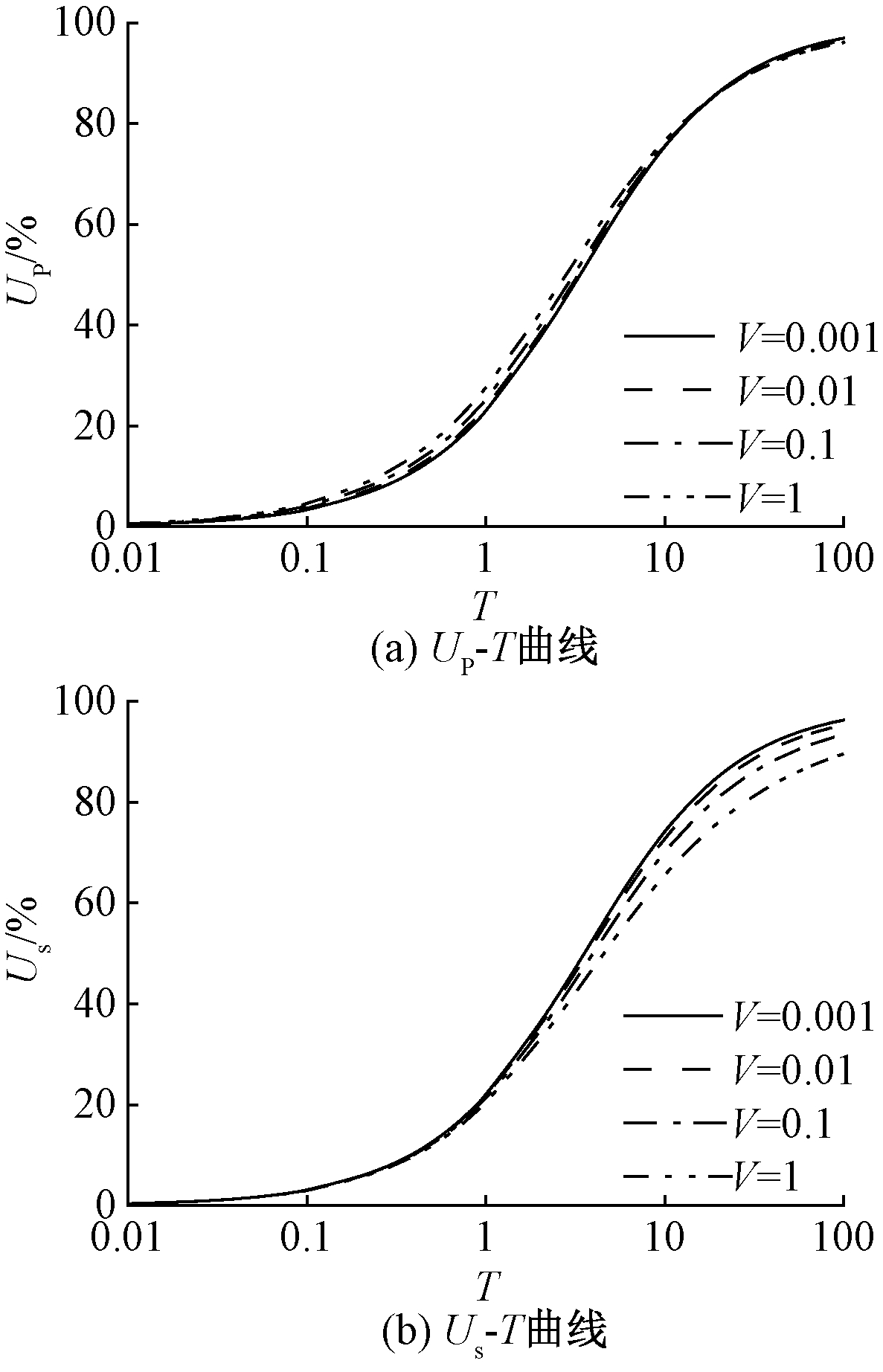
图8 V对固结度的影响
Figure 8 Influence of V on degree of consolidation
5 结论
基于半透水边界,考虑用非牛顿指数表示的非Darcy渗流和分数阶Merchant模型,重新推导了一维流变固结方程,并采用隐式有限差分法进行了数值求解。通过参数分析,得出以下结论:
(1)随着半透水边界参数的增大,饱和黏土层的固结过程将加快。而当半透水边界参数大于50后,半透水边界可视为完全透水边界。
(2)地基的固结过程会随着非牛顿指数的增大而减缓,且非牛顿指数越大,该现象越明显。因此忽略非Darcy渗流的影响,地基的孔压消散速率和沉降速率将会被高估。
(3)分数阶Merchant流变模型参数对两种固结度UP和Us的影响存在明显差异。分数导数阶数越小或无量纲黏滞系数越大,固结度Us就越小。但它们对固结度UP的影响相对较小。随着Kelvin体与独立弹簧的模量之比β的增大,土层的固结过程也加快,但其作用主要体现在固结中期。
[1] TERZAGHI K. Theoretical soil mechanics[M]. New York: John Wiley and Sons Inc., 1943.
[2] GRAY H. Simultaneous consolidation contiguous layers of unlike compressible soil[J]. Trans ASCE, 1945, 110:1327-1356.
[3] SCHIFFMAN R L, STEIN J R. One-dimensional consolidation of layered systems[J]. Journal of soil mechanics & foundations Div, 1970, 96(4): 1499-1504.
[4] MESRI G. One-dimensional consolidation of a clay layer with impeded drainage boundaries[J]. Water resources research, 1973, 9(4):1090-1093.
[5] 王奎华,谢康和,曾国熙. 双面半透水边界的一维粘弹性固结理论[J].岩土工程学报,1998,20(2):34-36.
WANG K H, XIE K H, ZENG G X. A study on 1D consolidation of soils exhibiting rheological characteristics with impeded boundaries[J]. Chinese journal of geotechnical engineering, 1998, 20(2): 34-36.
[6] XIE K H, XIE X Y, GAO X. Theory of one dimensional consolidation of two-layered soil with partially drained boundaries[J]. Computers and geotechnics, 1999, 24(4): 265-278.
[7] 刘忠玉,闫富有,王喜军. 基于非达西渗流的饱和黏土一维流变固结分析[J] .岩石力学与工程学报, 2013 ,32 (9) :1937-1944.
LIU Z Y, YAN F Y, WANG X J. One-dimensional rheological consolidation analysis of saturated clay considering non-Darcy flow[J]. Chinese journal of rock mechanics and engineering, 2013, 32(9): 1937-1944.
[8] 李传勋,马浩天,周恩全,等. 考虑初始孔压非均布及起始坡降的黏土流变固结解[J].岩石力学与工程学报, 2019, 38(增刊2):3859-3869.
LI C X, MA H T, ZHOU E Q, et al. Analytical solutions for rheological consolidation of soft clays with consideration of threshold hydraulic gradients and nonuniform distribution of initial excess pore water pressure[J]. Chinese journal of rock mechanics and engineering, 2019, 38(S2):3859-3869.
[9] GEMANT A . A method of analyzing experimental results obtained from elasto-viscous bodies[J]. Physics, 1936, 7(8): 311-317.
[10] 汪磊,李林忠,徐永福, 等.半透水边界下分数阶黏弹性饱和土一维固结特性分析[J].岩土力学, 2018, 39(11): 4142-4148.
WANG L, LI L Z, XU Y F, et al. Analysis of one-dimensional consolidation of fractional viscoelastic saturated soils with semi-permeable boundary[J]. Rock and soil mechanics,.
[11] 刘忠玉,崔鹏陆,郑占垒,等. 基于非牛顿指数渗流和分数阶Merchant模型的一维流变固结分析[J].岩土力学, 2019, 40(6): 2029-2038.
LIU Z Y, CUI P L, ZHENG Z L, et al. Analysis of one-dimensional rheological consolidation with flow described by non-Newtonian index and fractional-order Merchant′s model[J]. Rock and soil mechanics, 2019, 40(6): 2029-2038.
[12] HANSBO S. Deviation from Darcy′s law observed in one-dimensional consolidation[J]. Geotechnique, 2003, 53(6): 601-605.
[13] 孙丽云,乐金朝,张杰. 饱和黏土非达西渗透特性试验研究[J].郑州大学学报(工学版), 2010, 31(6): 31-34 .
SUN L Y, YUE J C, ZHANG J. Experimental study on non-darcy permeability characteristics of saturated clays[J]. Journal of Zhengzhou university (engineering science), 2010, 31(6): 31-34.
[14] LIU Z Y, ZHANG J C, DUAN S Q, et al. A consolidation modelling algorithm based on the unified hardening constitutive relation and Hansbo′s flow rule[J]. Computers and geotechnics, 2020, 117:103233.
[15] SWARTZENDRUBER D. Modification of Darcy′s law for the flow of water in soils[J]. Soil science, 1962, 93(1): 22-29.
[16] 李传勋,谢康和,卢萌盟,等.基于非牛顿指数描述的非达西渗流一维固结分析[J].岩土力学, 2011, 32 (1): 281-287.
LI C X, XIE K H, LU M M, et al. Analysis of one-dimensional consolidation with non-Darcy flow described by non-Newtonian index[J]. Rock and soil mechanics, 2011, 32(1): 281-287.