降水趋势分析是开展变化环境下水循环演变模拟[1]、水资源动态评估、防涝减灾等研究的重要基础。传统的趋势分析方法如线性回归法[2]、滑动平均法[3]、累积距平法[4]、Spearman秩次相关检验法、Mann-Kendall趋势检验法[5]等依赖序列平稳性、独立性等强假设,难以适应降水过程的高度不确定性,且仅能识别整体单调趋势,无法量化序列内部结构变异[6]。为了克服传统趋势分析方法的局限性,
en[7-8]首先提出了创新趋势分析(innovative trend analysis,ITA),并据此优化出了创新多边形趋势分析(innovative polygon trend analysis,IPTA)[9];Ceribasi等[10]又在IPTA的基础上提出了创新趋势枢轴分析(innovative trend pivot analysis method,ITPAM)。其中,ITA从归纳和演绎的角度对时间序列进行趋势识别,对序列分布、样本大小、数据中的相关性等均无特定要求,且保证了对趋势存在性进行直观检查的可能性[11];IPTA在ITA的基础上通过多边形的形式描述时间序列内部(如年内不同月份、不同季节之间)的变化趋势;ITPAM是IPTA的延伸,通过风险区域划分建立被分析数据之间的关系。目前创新趋势分析体系已被广泛应用于降水[12]、径流[13]等水文气象变量的趋势分析,在全球典型区域验证了其有效性及合理性,例如Sonali等[14]采用了11种方法来分析印度的年、月最高和最低温度变化,发现ITA的分析结果与其他方法总体趋势是匹配的,且ITA还用图形直接表征出序列的变化趋势;an等[15]对越南Vu Gia-Thu Bon河谷地区15个站点的月降雨量进行趋势分析,与其他方法相比,ITA和IPTA在趋势识别方面更敏感,且IPTA还提供了系列时段内部的变异性;Ceribasi等[10]将其提出的ITPAM在土耳其Susurluk盆地进行应用。在中国,聚焦黄河流域关键枢纽三门峡库区的多尺度降水变异研究仍较为匮乏[16]。已有的研究多局限于单一尺度或传统方法,忽视了库区降水“强度-历时-风险”协同演变机制,缺乏对“高值降水主导年际变异”的精细化诊断。因此,急需系统、全面的研究方法填补库区精细化降水趋势研究的空白。
三门峡库区洪水多为暴雨洪水,以三门峡库区国家基本气象站三门峡站为例,系统组合应用ITA、IPTA和ITPAM开展1957—2020年降水量年、月、日不同时间尺度的趋势变异分析,并与传统趋势检验方法进行比较。本文在时间尺度、多值区段、风险识别等方面实现了从趋势检验到机制解释的综合分析,以期为三门峡水库优化、联合调度,流域防灾减灾,水资源管理提供依据。
1 研究区域与数据来源
1.1 研究区概况
如图1所示,三门峡水库位于黄河干流中游,在陕西、山西、河南三省交界地区,担负着防洪、防凌、减淤和供水等任务,是黄河下游防洪减淤工程体系的重要组成部分[17]。三门峡气象站位于34°48′N、111°18′E,高程389.9 m,在三门峡水库库区中段,是度量三门峡库区降水的重要站点。库区范围属于典型的暖温带大陆性季风气候,多年(1957—2020年)平均降水量为558.1 mm,降水年际年内变化较大,7—9月份是降水集中期,降水量占全年的51%。
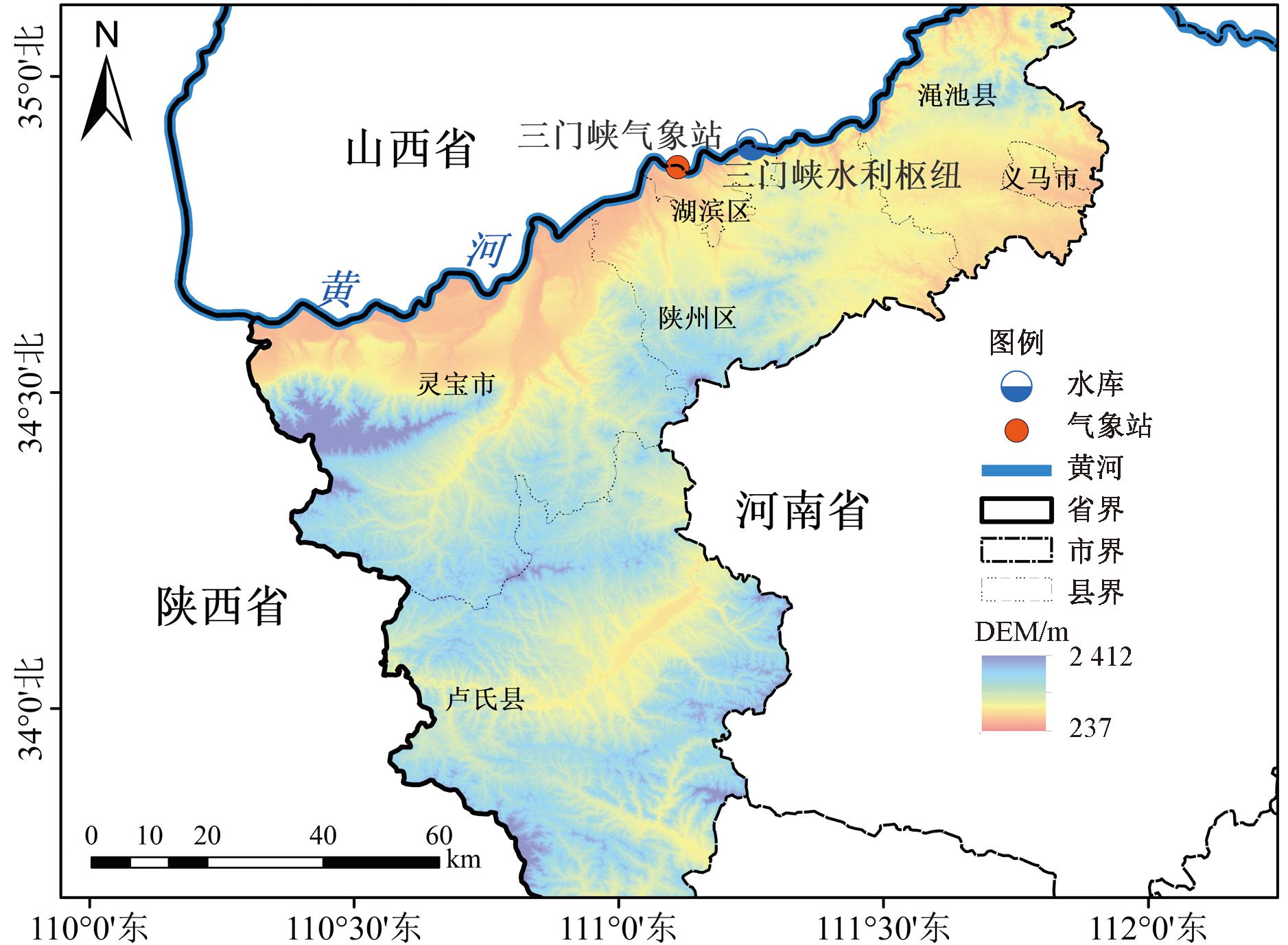
注:该图基于自然资源部标准地图服务网站下载的标准地图,底图无修改(审图号为GS(2022)4309)。
图1 研究区域及气象站位置
Figure 1 Study area and location of weather station
1.2 数据来源
从国家气象信息中心-中国气象数据网(https:∥data.cma.cn/)获取三门峡气象站点1957—2020年逐日降水数据,并将原始数据中微量降雨(量级)视为零降雨。年、月、日不同时间尺度选取的降水指标见表1。
表1 降水指标
Table 1 Precipitation indices defined
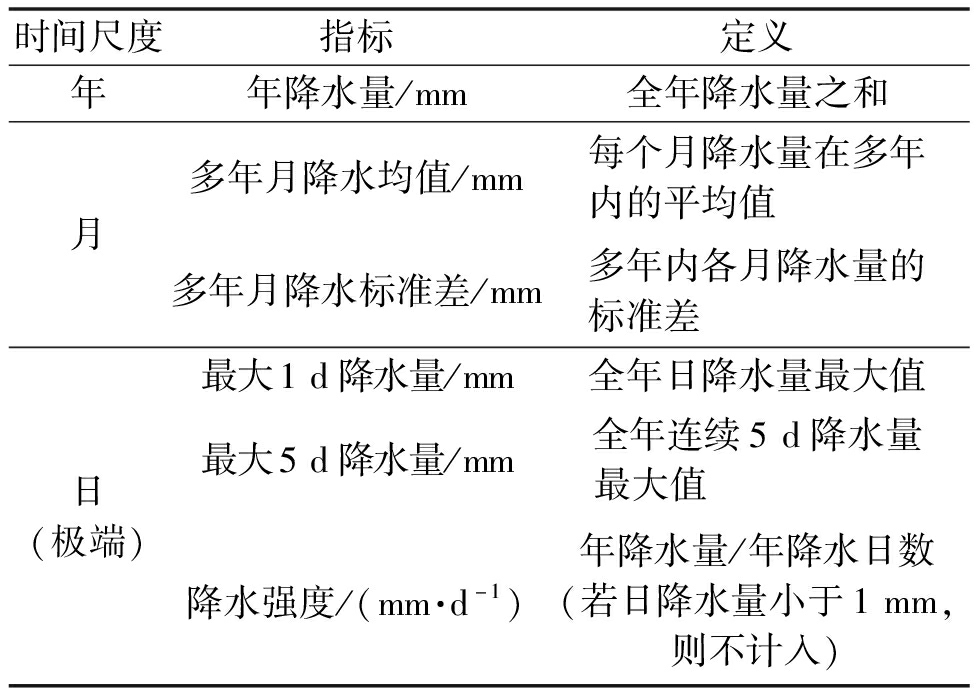
时间尺度指标定义年年降水量/mm全年降水量之和月多年月降水均值/mm每个月降水量在多年内的平均值 多年月降水标准差/mm多年内各月降水量的标准差 日(极端)最大1d降水量/mm全年日降水量最大值最大5d降水量/mm全年连续5d降水量最大值 降水强度/(mm·d-1)年降水量/年降水日数(若日降水量小于1mm,则不计入)
2 研究方法
2.1 研究思路
如图2所示,从年、月、日不同时间尺度选定降水指标,基于方法适宜性,采用ITA对年、日降水指标进行趋势分析,采用IPTA、ITPAM分别对月降水指标进行趋势分析,将ITA计算结果与Spearman秩次相关检验法、Kendall秩次相关检验法、Mann-Kendall趋势检验法进行对比分析。
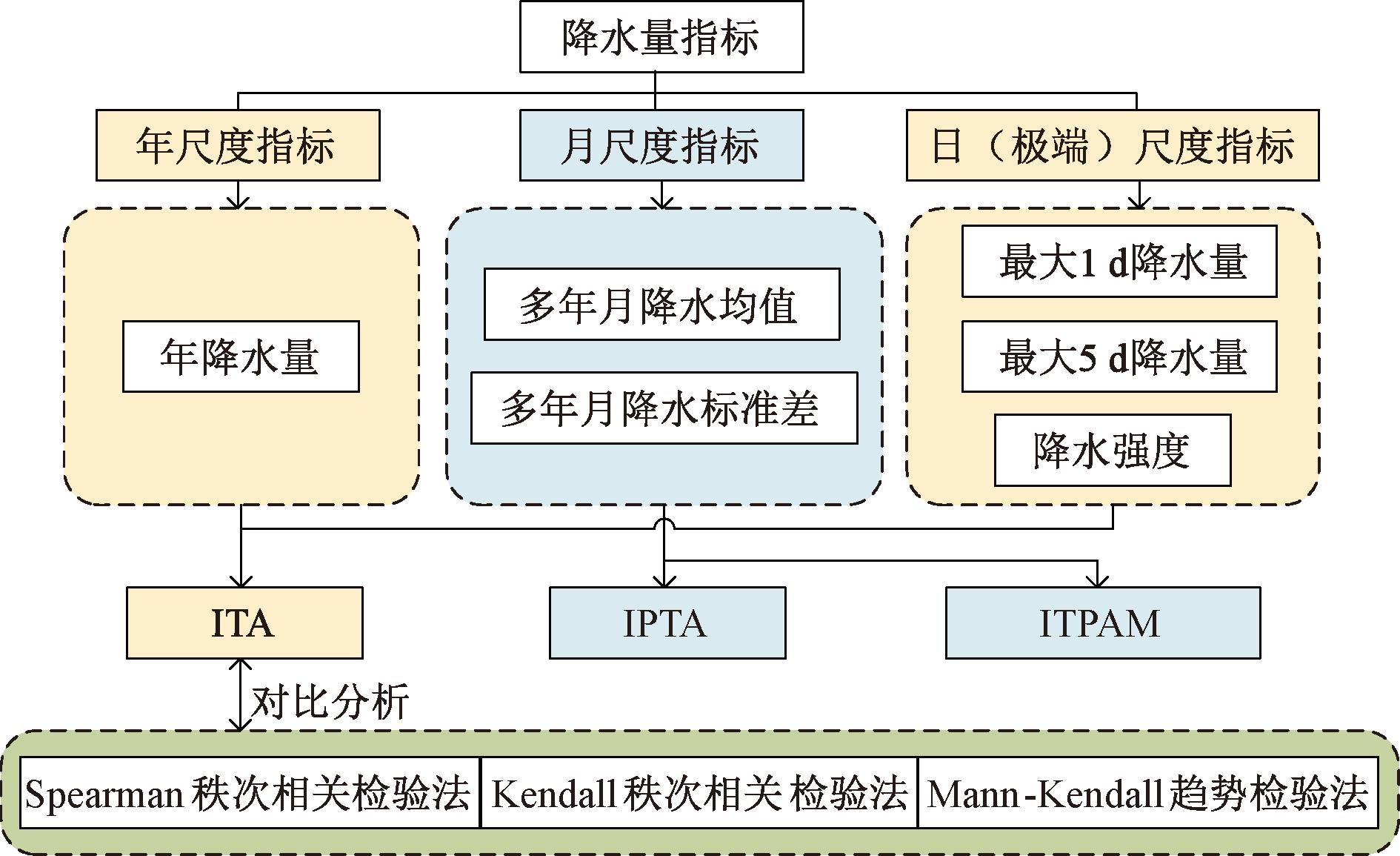
图2 多尺度降水变异分析研究思路
Figure 2 Research ideas on multi-scale precipitation variation analysis
2.2 创新趋势分析方法
2.2.1 创新趋势分析(ITA)
作为一种非参数统计检验方法,ITA通过对数据点进行分区域和分组,从而能直观判别变量整体及不同量级的变化趋势[7-8]。此外,ITA还可以用数值表征趋势增减性和变化的显著程度,ITA示意图如图3所示。具体分析步骤如下。
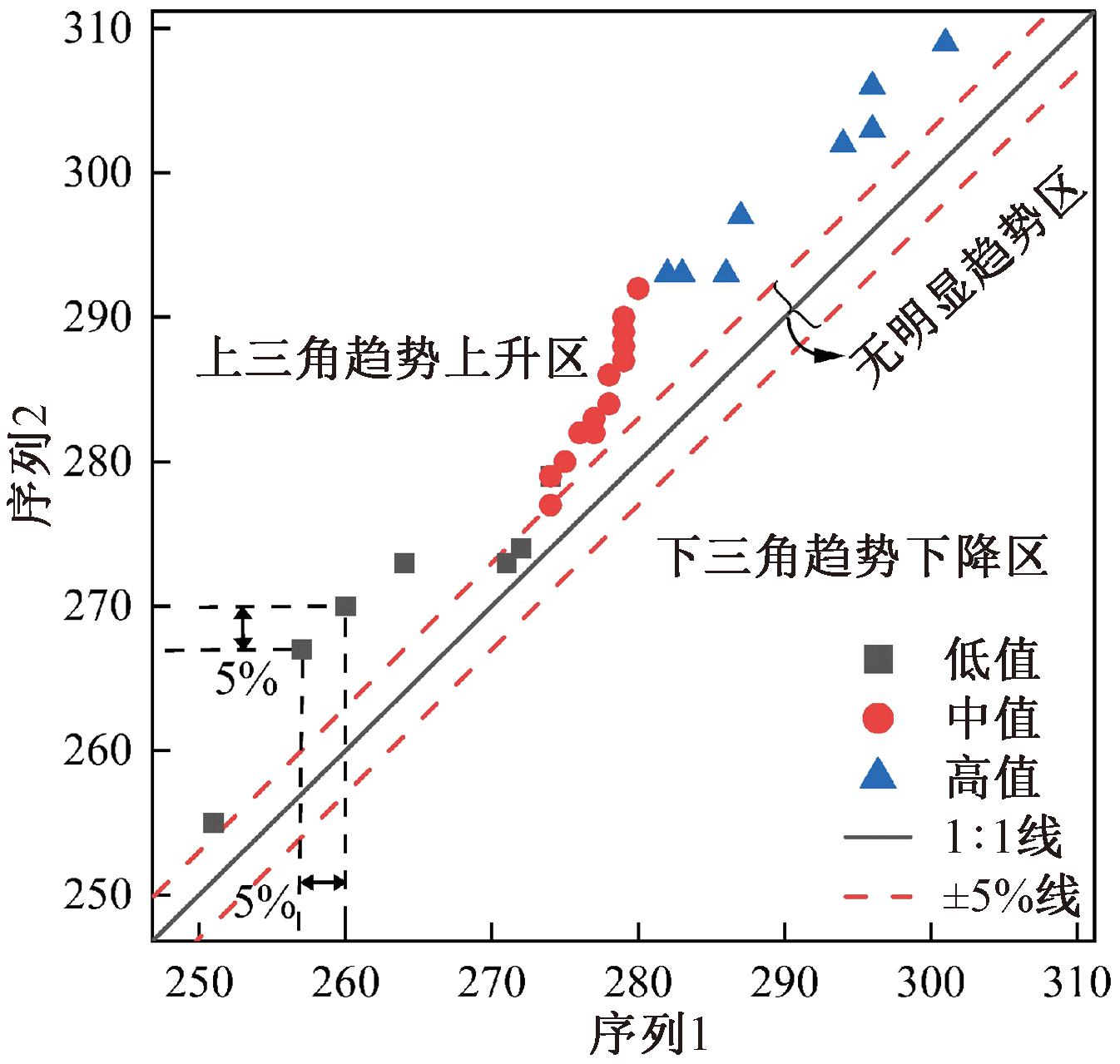
图3 ITA示意图
Figure 3 ITA schematic diagram
(1)将变量的时间序列划分成两个等时间长度的子序列(序列1、序列2),分别按照升序排列,然后以序列1为横坐标、序列2为纵坐标,绘制数据散点在笛卡尔坐标系中。
(2)对数据散点进行分区域和分组。利用1∶1线及±5%线(与1∶1线水平距离为横坐标总长度的5%,以及与1∶1线垂直距离为纵坐标轴总长度的5%的平行线)作为识别趋势显著性的阈值,将区域划分为上三角趋势上升区、无明显趋势区和下三角趋势下降区。根据数据散点在序列中的位置,基于排位顺序按百分比将变量划分为低值(≤25%)、中值(25%～75%)和高值(≥75%)[11]。
(3)根据散点位置进行趋势分析,如果散点分布位于1∶1线附近区域(±5%线内),则认为该序列没有显著变化趋势;落在上三角趋势上升区,表明该序列具有上升趋势;落在下三角趋势下降区,则表明具有下降趋势[7]。低、中、高不同分组数值序列在ITA图中的增减趋势同样反映指标中该分组数值的变化情况,其中降水指标中的低值具体可理解为轻微降水事件,中、高值可分别指代中等强度降水事件、强烈降水事件。
(4)为进一步定量描述趋势及其显著性,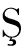en[18]提出了统计量S,计算公式为
(1)
式中:
和
分别为序列1、序列2的均值;n为时间序列的总数。
S服从均值为零、标准差为σS的正态分布。如果S大于0,则表示系列呈上升趋势;S小于0,则序列呈下降趋势。若序列的统计量S在置信区间CL之外(即|S|≥|CL|),则说明具有显著的变化趋势。统计量S显著性的置信区间计算公式如下所示:
CL(1-α)=0±scri·σS;
(2)
(3)
(4)
式中:α为显著性水平;scri为标准正态分布对应于α的置信区间(本文取α=5%,此时scri值为1.96);σ为原时间序列的标准差;
为相关系数。
2.2.2 创新多边形趋势分析(IPTA)
IPTA在ITA基础上以多边形的形式分析序列的变化趋势,可以分析序列中两个连续部分之间的趋势转换,也可在多个时间尺度(季、月、周等)上进行应用[9]。本文考虑了月尺度降水指标,其中序列划分与散点绘制的步骤与ITA相同,将绘制好的图内各点按月份顺序首尾相接,可得到创新多边形(图4)。多边形中连续月份点间直线的长度和斜率即为相邻月份变量的趋势长度和趋势斜率:
(5)
(6)
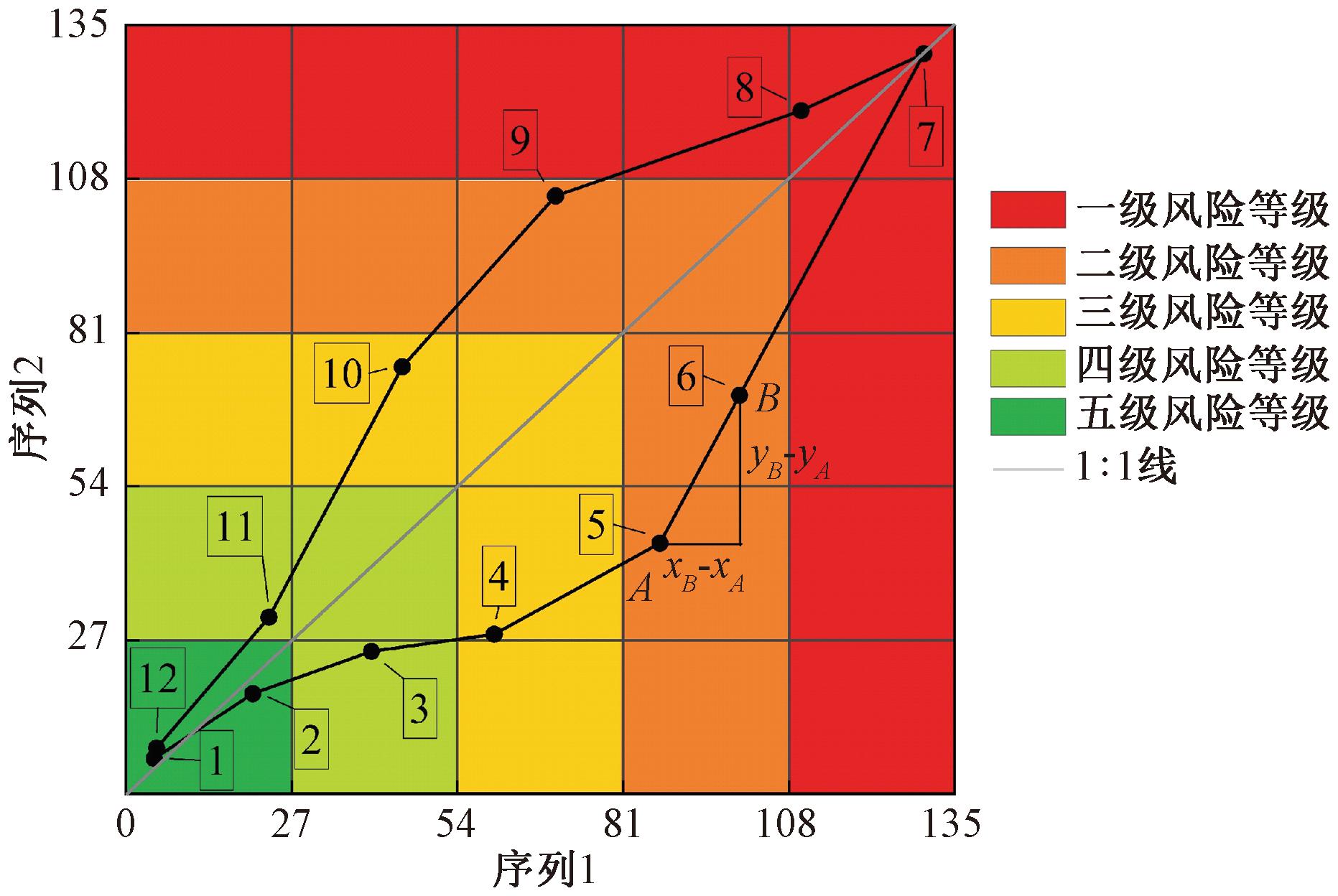
图4 IPTA、ITPAM示意图
Figure 4 IPTA,ITPAM schematic diagram
式中:A、B为连续的两点;|AB|为趋势长度;k为趋势斜率。
多边形形状越规则,面积越狭窄,则表明水文气象变化越稳定;反之则表示系统变化越剧烈,随机性越强。趋势长度反映相邻两月份间变量值的变化幅度,长度大表示相邻月份变量值差异显著;反之则表示变量值变化平缓,趋势稳定。趋势斜率反映趋势变化的方向与强度,若趋势线位于1∶1线以上,则表示序列呈上升趋势,反之则呈下降趋势;若趋势斜率的绝对值越大,表示数值变化强度越高(如陡增或骤减),反之表示变化平缓或接近无变化趋势。
2.2.3 创新趋势枢轴分析法(ITPAM)
ITPAM在IPTA基础上通过划分数据位置来确定风险等级[10](图4),具体步骤如下。
(1)将IPTA检验结果图的X轴、Y轴分别划分为5等份,划分出的区域被识别为5种不同的颜色。
(2)对不同颜色的区域进行风险分类,分为一至五级风险等级。
对比ITPAM风险图和IPTA检验结果图,可以挖掘到序列1与序列2之间是否存在显著变化的点。
2.3 Spearman秩次相关检验法
Spearman秩次相关检验法[19-20]通过研究两组变量之间秩的关系来判断变量是否具有同步性。在对水文时间序列进行检验时,将长度为n的序列xt用秩次Rt代替(t为时间),对Rt和t的相关性r进行分析,计算统计r的检验统计量T,判断序列趋势变化的显著性。
2.4 Kendall秩次相关检验法
Kendall秩次相关检验法[21]是反映分类变量相关性的指标,适用于两个分类变量均为有序分类的情况,可以对相关的有序变量进行非参数相关检验。计算统计量τ和标准变量M,研究序列变化趋势以及趋势显著性。
2.5 Mann-Kendall趋势检验法
Mann-Kendall趋势检验法[22]是一种非参数检验方法,通常用于判断时间序列是否存在变化趋势以及确定变化的显著性。对于时间序列,求解标准化统计量Z,Z>0和Z<0分别表示序列存在上升和下降趋势,|Z|值越大,意味着变化趋势越显著。
3 研究结果与分析
3.1 年降水趋势分析
1957—2020年三门峡气象站年均降水量为558.1 mm,线性回归显示总体呈下降趋势(图5)。年降水量ITA检验结果如图6所示,其中S=-1.031<0,CL=±0.004,年降水整体呈显著的下降趋势。从分组来看,低值类和中值类无显著变化趋势,大部分位于±5%线内,少部分呈现下降趋势;高值类绝大部分位于下三角趋势下降区,说明多年来三门峡库区整体高值类降水呈显著下降趋势。
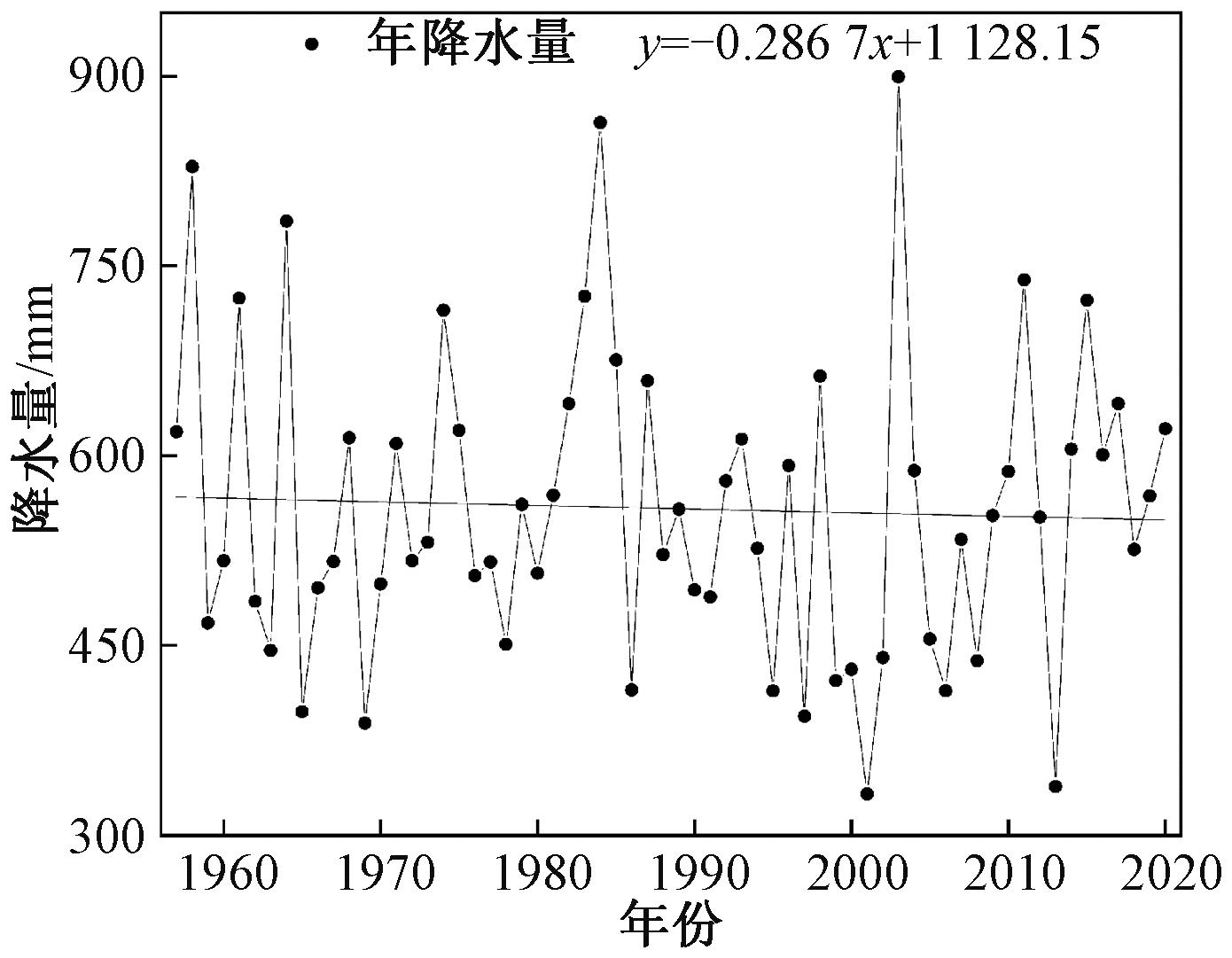
图5 1957—2020年三门峡站年降水量
Figure 5 Precipitation of Sanmenxia weather station from 1957 to 2020
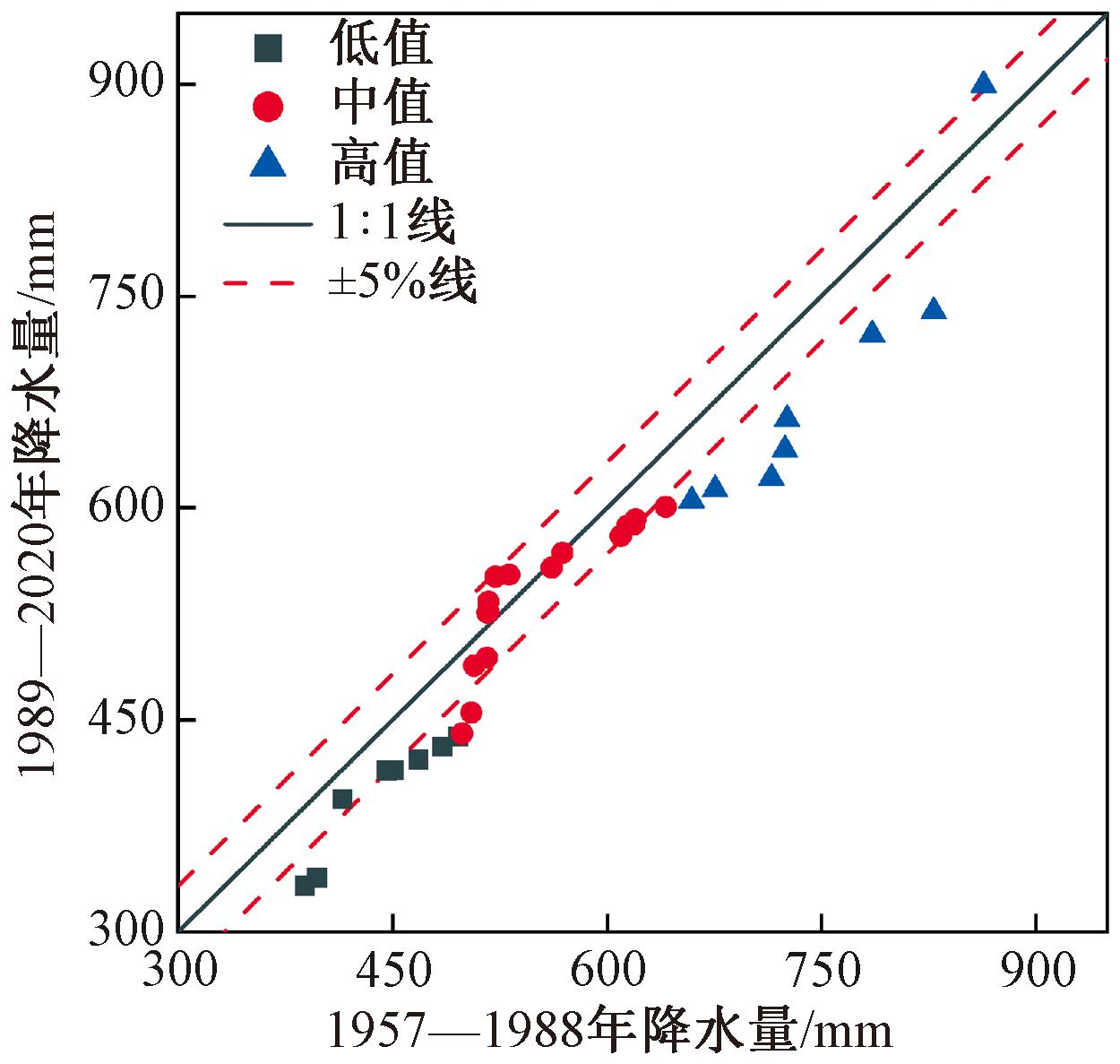
图6 年降水量ITA检验结果
Figure 6 ITA test results of annual precipitation
3.2 月降水趋势分析
用IPTA和ITPAM分别对三门峡气象站月尺度降水指标(多年月降水均值、多年月降水标准差)进行分析,得到检验结果见图7和表2。
表2 多年月降水均值和标准差的IPTA统计值
Table 2 Monthly precipitation mean and standard deviation of IPTA statistics
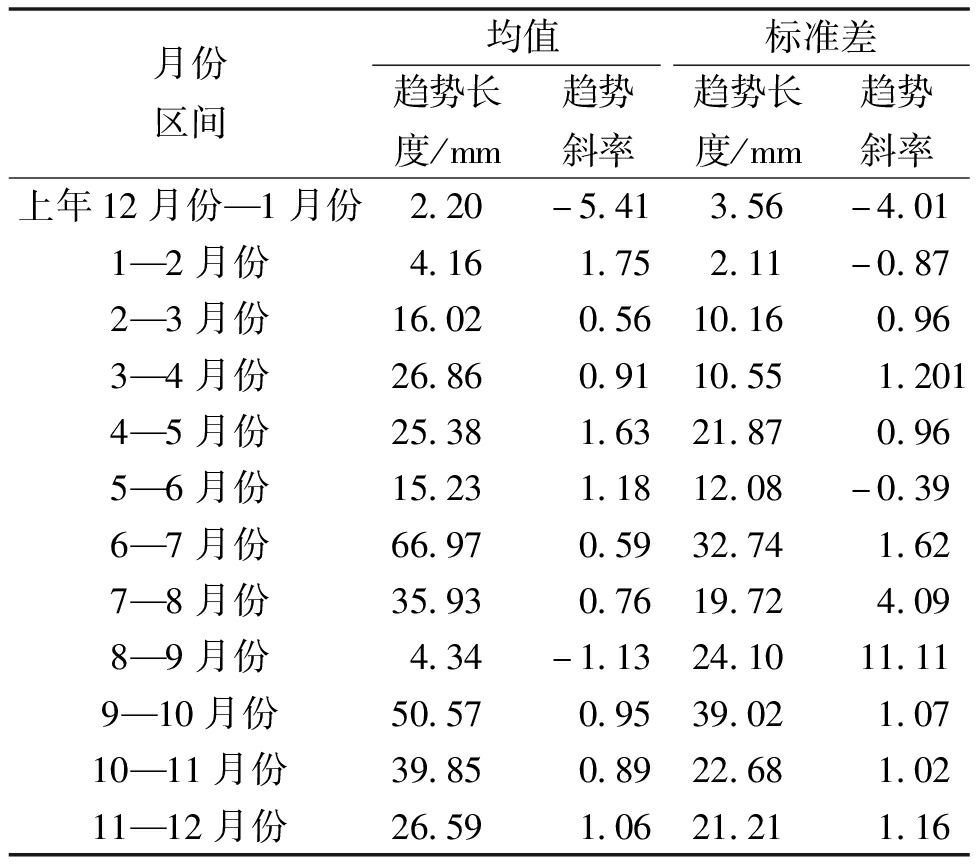
月份区间均值标准差趋势长度/mm趋势斜率趋势长度/mm趋势斜率上年12月份—1月份2.20-5.413.56-4.011—2月份4.161.752.11-0.872—3月份16.020.5610.160.963—4月份26.860.9110.551.2014—5月份25.381.6321.870.965—6月份15.231.1812.08-0.396—7月份66.970.5932.741.627—8月份35.930.7619.724.098—9月份4.34-1.1324.1011.119—10月份50.570.9539.021.0710—11月份39.850.8922.681.0211—12月份26.591.0621.211.16
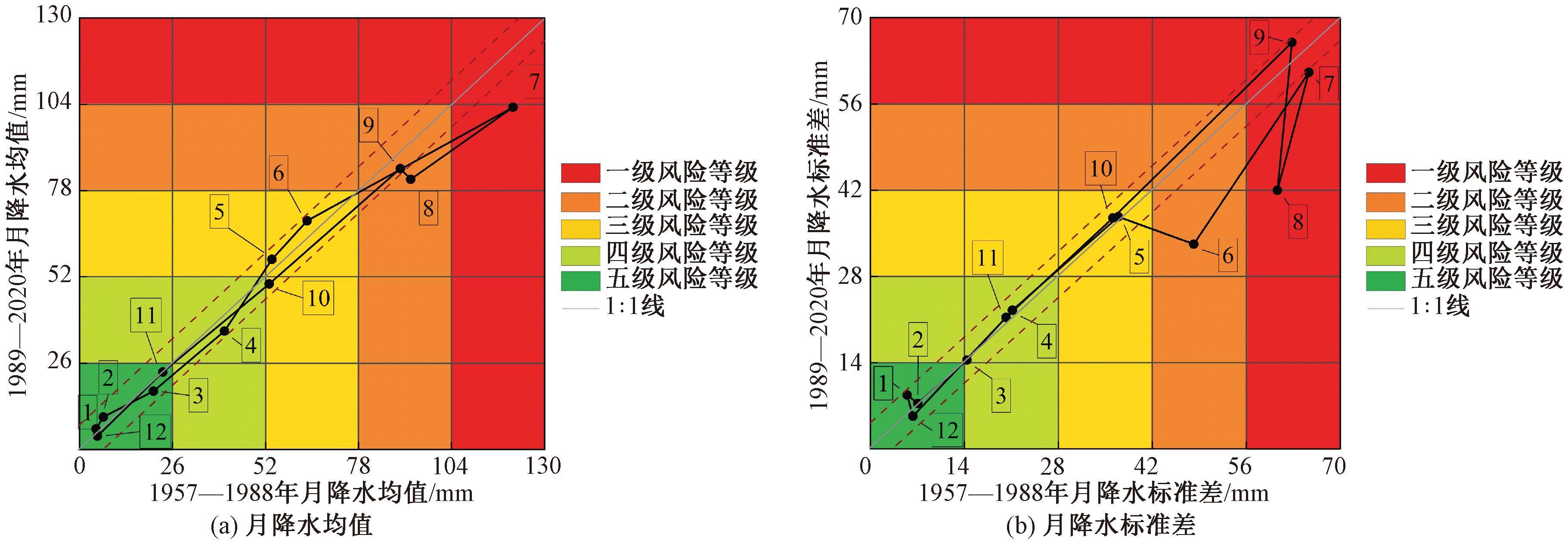
图7 IPTA和ITPAM检验结果
Figure 7 IPTA and ITPAM test results
3.2.1 多年月降水均值
从图7(a)可以看出,IPTA多边形为不规则的非单一多边形,面积狭长,整体围绕1∶1线波动,表明多年来各月降水整体无明显变化趋势,其中7月份、8月份低于1∶1线,表明这两个月的降水量均值呈下降趋势。
如表2所示,均值的趋势长度最小值出现在上年12月份至2月份,表明多年该连续月份的降水量均值变化小,符合冬季气候稳定的特征;最大值出现在6—7月份,反映汛期降水量变化剧烈。斜率绝对值最大出现在上年12月份至1月份,表明期间降水均值变化不大,但由于本身降水量小,使得较小的扰动也会显现较强的变化率;其余月份斜率绝对值大多接近1,反映月份间变化基本稳定。
从图7(a)可以看出,12,1,2月份处于五级风险区,表明这些月份可能加剧干旱风险;而7,8,9月份位于一级和二级风险区,表明这些月份极端降水事件的发生概率较高。
3.2.2 多年月降水标准差
从图7(b)可以看出,多边形整体面积小且重叠度高,说明年际间月均降水量整体变化一致性较强,未出现显著偏移;其中6—8月份显著低于1∶1线,说明这两个月份区间的多年降水年际间波动性下降,降水过程呈现均匀化。
如表2所示,标准差的趋势长度在6—7月份、9—10月份显著增大,表明夏秋季降水波动性加剧,极端事件(如短时强降雨)频发;上年12月至2月份趋势长度最小,印证冬季降水过程的均匀性。斜率绝对值最大出现在8—9月份,表明该时段降水波动性急剧增强,降水变得不稳定;1—3月份标准差斜率绝对值较小,反映冬季降水模式稳定。
从图7(b)可以看出,7,8,9月份的多年月降水标准差风险等级较高,预示着降水波动性加剧;而12,1,2月份的风险等级较低,降水较为稳定。
可见,三门峡多年月降水整体变化较为均匀,无明显长期趋势,但各月份间细分来看存在显著差异。7—9月份的月降水呈现出“趋势下降-变幅较大-风险等级高”的复合模式,预示着极端降水事件发生概率提升;6—7月份和9—10月份为过渡阶段,显示出较强的季节转换特征;上年12月份至2月份总体稳定,风险等级较低,显示出冬季降水较为稳定。总体来看,虽然多年月降水量总体均衡,但在季节性交替时,部分月份表现出较为突出的局部变化趋势。
3.3 日降水趋势分析
极端降水选用最大1 d降水量(a)、最大5 d降水量(b)、降水强度(c)的指标来衡量。ITA计算结果显示:Sa=-0.387<0,CLa=±0.001;Sb=-0.637<0,CLb=±0.001;Sc=0.069>0,CLc=±5.369×10-5。可见,三门峡库区最大1 d降水量、最大5 d降水量均呈现显著下降趋势,降水强度呈现显著上升趋势。
如图8所示,最大1 d降水量低值类的变化不明显;中值类和高值类降水则远低于1∶1线,呈现出显著下降趋势,且随着降水量的增加,偏移也增大,说明大量级降水发生的趋势不断下降。最大5 d降水量整体变化不明显,大部分位于±5%线内;
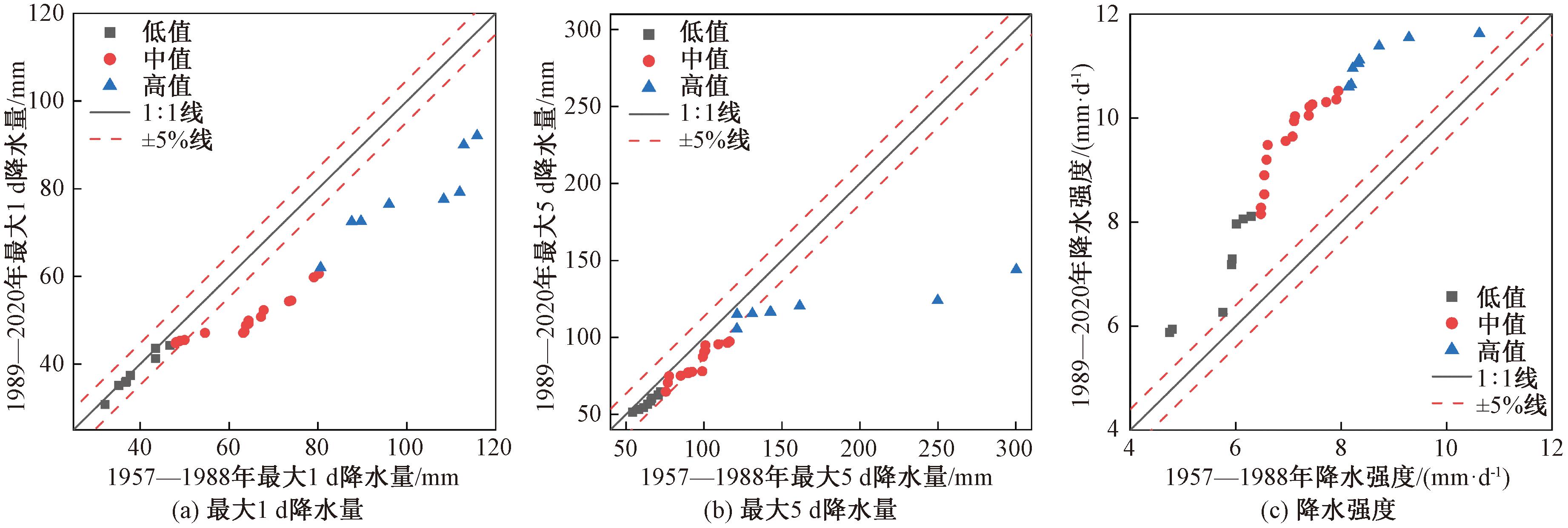
图8 日(极端)降水ITA检验结果
Figure 8 ITA test results of daily (extreme) precipitation
但在高值中可以观察到两个严重离群点出现在下三角趋势下降区,说明三门峡库区发生连续5 d特大降雨的趋势显著下降。降水强度低、中、高值类均呈现显著上升趋势,尤其是中、高值类降水偏离1∶1线较远。结合年、月、日不同尺度降水指标分析结果可知,三门峡库区降水量多年年际间整体处于下降趋势,尤以高值类降水减少最为明显。尽管多年月均降水量整体变化相对均匀,但季节性差异突出,夏季至初秋降水变幅增大,极端降水事件风险提升;而冬季降水稳定、风险较低,体现气候系统的周期性规律。特大连续性降雨趋势减弱,但降水强度却普遍增强。研究结果通过了内部一致性检验且符合物理机制,确保了研究方法的可信度。
综上,三门峡库区降水变化表现为“年总量减少、季节波动加剧、连续日降水总量减少,极端暴雨事件低频-高强度”的综合趋势,需特别关注夏季高风险期短期强降水的影响。
3.4 多种趋势检验方法对比分析
分别用Spearman秩次相关检验法、Kendall秩次相关检验法以及Mann-Kendall趋势检验法计算了三门峡气象站点降水时间序列的趋势性和显著性,并将计算结果与基于创新趋势分析的年、日降水检验结果进行比较,如表3所示。
表3 多种方法下各降水量指标的趋势检验结果表
Table 3 Trend test results of various methods for each precipitation index
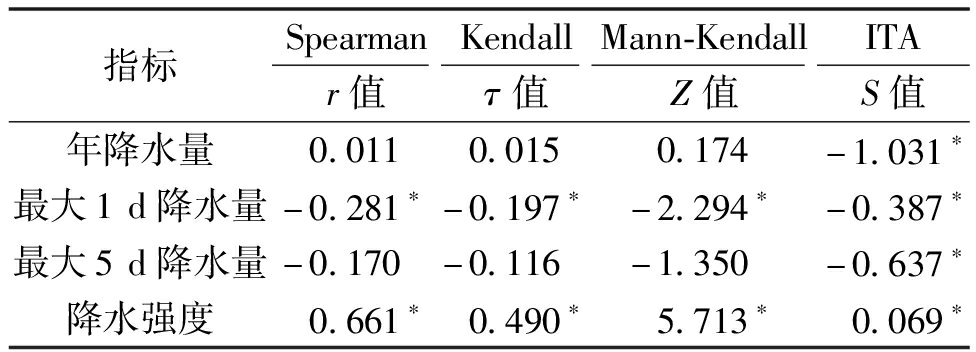
指标SpearmanKendallMann-KendallITAr值τ值Z值S值年降水量0.0110.0150.174-1.031∗最大1d降水量-0.281∗-0.197∗-2.294∗-0.387∗最大5d降水量-0.170-0.116-1.350-0.637∗降水强度0.661∗0.490∗5.713∗0.069∗
注:*表示通过了95%置信水平检验。
Spearman秩次相关检验法、Kendall秩次相关检验法以及Mann-Kendall趋势检验法对年降水量的趋势结果均显示上升,但未通过95%显著性检验;而ITA结果为显著下降趋势。主要原因是传统方法对极端降水敏感性不足,计算结果易受数据分布影响,表现出均化效应;而在极值主导变化的情形下,ITA通过分区分析,有效识别出高值区降水的显著下降趋势,具有更强的敏感性和适用性。在最大5 d降水量的趋势分析结果中,Spearman秩次相关检验法、Kendall相关检验法和Mann-Kendal趋势检验法呈现下降趋势,但并未通过显著性检验;ITA显示出显著的下降趋势。4种方法最大1 d降水量和降水强度的检验结论均一致,均分别呈现显著下降和显著上升的趋势。
综合对比3种传统趋势分析法与ITA可知,传统方法更关注长期的单调趋势,未能有效捕捉到降水数据内部的变化模式;而ITA可以得到整体以及不同组别(低、中、高值区)的序列趋势变化。因此,在实际应用中,建议采用多种方法综合判断:传统方法提供整体判断,创新方法识别异常时段与高风险等级区域,从而实现由宏观到微观的多层次决策支持。
4 结论
基于改进创新趋势分析方法(ITA、IPTA、ITPAM)开展了三门峡库区1957—2020年降水的趋势特征分析,并与传统非参数检验方法进行对比分析。结果表明,年尺度上降水量呈下降趋势;月尺度降水无显著趋势,但夏季降水变幅增大,年内分配不均;日尺度上呈现高值类明显下降,但强度增大的特征。与传统方法相比,ITA可以得到整体及低、中、高值区的降水趋势变化,IPTA可以识别连续月份间的变化特征,ITPAM有助于确定极端事件的灾害风险等级。综合使用创新趋势分析系列方法实现了降水“值域-时段-风险”三维解析;在气象水文序列趋势变异分析中具有独特优势,揭示了传统方法在显著性检验中的滞后性和敏感度不足。基于多维度分析结果,识别出三门峡库区的降水演变“低频-高强度”的新模式,为黄河流域水库调度与水资源综合管理提供了更精细的依据。
[1] 甘容,马超鑫,高勇,等.基于二次分解和支持向量机的月径流预测方法[J].郑州大学学报(工学版),2024,45(6):32-39.GAN R,MA C X,GAO Y,et al.Monthly runoff prediction method based on secondary decomposition and support vector machine[J].Journal of Zhengzhou University (Engineering Science),2024,45(6):32-39.
[2] 任建成,谷山青,冯存峨,等.气候变化背景下山东省气温与降水时空变化特征分析[J].水利水电技术(中英文),2023,54(5):27-37.REN J C,GU S Q,FENG C E,et al.Analysis of the temporal and spatial variation characteristics of temperature and precipitation in Shandong Province under the background of climate change[J].Water Resources and Hydropower Engineering,2023,54(5):27-37.
[3] 张文浩,瞿思敏,徐瑶,等.泼河水库对潢河径流过程及水文情势的影响[J].水资源保护,2021,37(3):61-65.ZHANG W H,QU S M,XU Y,et al.Influence of Pohe Reservoir on runoff process and hydrological regime of Huanghe River[J].Water Resources Protection,2021,37(3):61-65.
[4] 姜瑶,徐宗学,王静.基于年径流序列的五种趋势检测方法性能对比[J].水利学报,2020,51(7):845-857.JIANG Y,XU Z X,WANG J.Comparison among five methods of trend detection for annual runoff series[J].Journal of Hydraulic Engineering,2020,51(7):845-857.
[5] 邹磊,夏军,张印,等.海河流域降水时空演变特征及其驱动力分析[J].水资源保护,2021,37(1):53-60.ZOU L,XIA J,ZHANG Y,et al.Spatial-temporal change characteristics and driving forces of precipitation in the Haihe River Basin[J].Water Resources Protection,2021,37(1):53-60.
[6] 王霞雨,贾文豪,王森,等.基于创新趋势分析方法的珠江流域降水径流变化趋势研究[J].水利水电技术(中英文),2025,56(4):52-69.WANG X Y,JIA W H,WANG S,et al.Research on the variation trends of precipitation and runoff in the Pearl River Basin based on innovative trend analysis method[J].Water Resources and Hydropower Engineering,2025,56(4):52-69.
[7] 
EN Z.Innovative trend analysis methodology[J].Journal of Hydrologic Engineering,2012,17(9):1042-1046.
[8] EN Z.Trend identification simulation and application[J].Journal of Hydrologic Engineering,2014,19(3):635-642.
[9] ZEK
I ,EYÜP ,DABANLI I.Innovative polygon trend analysis (IPTA) and applications[J].Journal of Hydrology,2019,575:202-210.
[10] CERIBASI G,CEYHUNLU A I,AHMED N.Innovative trend pivot analysis method (ITPAM):a case study for precipitation data of Susurluk Basin in Turkey[J].Acta Geophysica,2021,69(4):1465-1480.
[11] WU H,QIAN H.Innovative trend analysis of annual and seasonal rainfall and extreme values in Shaanxi,China,since the 1950s[J].International Journal of Climatology,2017,37(5):2582-2592.
[12] 李昕阳,杜军凯,胡新功,等.基于多种趋势分析方法的降水演变趋势分析[J].水电能源科学,2023,41(10):14-18.LI X Y,DU J K,HU X G,et al.Analysis of precipitation evolution trend based on various trend analysis methods[J].Water Resources and Power,2023,41(10):14-18.
[13] 可灏,贾本有,王文卓,等.基于IPTA的黄河流域天然月径流趋势分析[J].水文,2021,41(6):18-25.KE H,JIA B Y,WANG W Z,et al.Natural runoff trend analysis of the Yellow River Basin based on IPTA[J].Journal of China Hydrology,2021,41(6):18-25.
[14] SONALI P,KUMAR D N.Review of trend detection methods and their application to detect temperature changes in India[J].Journal of Hydrology,2013,476:212-227.
[15] AN M,AKÇAY F,LINH N T T,et al.Innovative and polygonal trend analyses applications for rainfall data in Vietnam[J].Theoretical and Applied Climatology,2021,144(3):809-822.
[16] 郑珊,吴保生,侯素珍,等.三门峡水库时空冲淤与滞后响应[J].水利学报,2019,50(12):1433-1445.ZHENG S,WU B S,HOU S Z,et al.Spatial and temporal erosion and deposition processes and the delayed response of the Sanmenxia reservoir[J].Journal of Hydraulic Engineering,2019,50(12):1433-1445.
[17] 沈逸,郑珊,吴保生.基于滞后响应模型的三门峡水库冲淤计算方法[J].水利学报,2022,53(10):1207-1217.SHEN Y,ZHENG S,WU B S.Calculation method for erosion and deposition processes in the Sanmenxia reservoir based on delayed response model[J].Journal of Hydraulic Engineering,2022,53(10):1207-1217.
[18] EN Z.Innovative trend significance test and applications[J].Theoretical and Applied Climatology,2017,127(3):939-947.
[19] ALSAQR A M.Remarks on the use of Pearson′s and Spearman′s correlation coefficients in assessing relationships in ophthalmic data[J].African Vision and Eye Health,2021,80(1):1-10.
[20] EDEN S K,LI C,SHEPHERD B E.Nonparametric estimation of Spearman′s rank correlation with bivariate survival data[J].Biometrics,2022,78(2):421-434.
[21] 张殷钦,胡伟,刘俊民.基于R/S分析法的地下水位动态变化趋势分析[J].中南大学学报(自然科学版),2012,43(12):4912-4916.ZHANG Y Q,HU W,LIU J M.Groundwater level regime variation trend on basis of rescaled range analysis[J].Journal of Central South University (Science and Technology),2012,43(12):4912-4916.
[22] 许钦,叶鸣,蔡晶,等.1956—2018年太湖流域降水统计特征及演变趋势[J].水资源保护,2023,39(1):127-132,173.XU Q,YE M,CAI J,et al.Precipitation statistical characteristics and evolution trend in Taihu Lake Basin from 1956 to 2018[J].Water Resources Protection,2023,39(1):127-132,173.