生理信号能够真实刻画个体的生理变化,在情感识别中展现出独特优势。其中,脑电(electroencephalogram,EEG)信号因直接关联大脑活动而更具情感相关性,采自左、右颞区和额叶区的脑电信号已被广泛用于表征情感状态[1],体现出较高的客观性和可靠性,成为情感识别研究的重要手段。
传统的脑电情感识别研究通常包括特征提取和分类模型构建两个阶段。常用特征主要包括时域、频域以及时频域等。经典机器学习分类器包括决策树(decision tree,DT)[2]、多层感知机(multi-layer perceptron,MLP)[3]、k邻近(k-nearest neighbor,KNN)[4]、随机森林(random forest,RF)[5]以及支持向量机(support vector machine,SVM)[6]。传统的情感识别方法特征提取过程复杂,分类器依赖反复调优,对复杂情境下的情感分类能力有限。
深度学习的发展使其在脑电情感识别中的应用已成为研究的重点方向。总体而言,基于深度学习的情感识别主要分为两大类。一类是先提取EEG特征,再利用深度学习模型完成分类。魏琛等[7]基于6级小波包变换提取特征,集成6个不同深度的卷积神经网络(convolutional neural networks,CNN)进行分类;Song等[8]提出动态图卷积神经网络(dynamical graph convolutional neural networks,DGCNN)模型对微分熵、功率谱、不对称差、不对称商以及微分因果这5类特征进行分类;Yang等[9]构建时域卷积网络(temporal convolutional network,TCN)对固定长度、多个频带的微分熵(differential entropy,DE)特征进行分类。另一类是通过时频谱图将EEG转化为高维特征矩阵,采用二维CNN、三维CNN或GCNN等不同结构的网络完成分类。Salama等[10]先将多通道脑电信号处理为二维矩阵,再将多个二维矩阵组成三维矩阵,构建3D-CNN对其进行分类。Ramzan等[11]通过集成CNN和长短期记忆递归神经网络实现情感分类。
尽管基于深度学习的脑电情感识别在分类精度方面取得了显著提升,但仍面临诸多问题与挑战。第一类方法仅将深度学习模型作为分类器,难以充分发挥其端到端学习的优势,且与传统方法类似,在最优特征选择上存在较大的不确定性。而第二类方法则依赖多种时频分析方法,缺乏统一的标准,不同实验对象往往需要针对性地调整分析方法和参数设置。此外,部分基于图卷积的网络在构建中高度依赖专业知识,尤其是在图结构设计和节点特征定义方面,对领域经验要求较高。
为了充分利用情感脑电信号中的丰富信息,降低特征提取和模型构建的复杂度,本文提出基于时间序列成像(time series imaging,TSI)的多任务学习驱动方法。首先,一维脑电信号通过3种不同的时间序列成像算法转换为二维图像;其次,为实现不同成像算法之间的优势互补,基于多任务学习,设计多任务特征融合框架,构建多个并行ResNet18骨干网络和融合模块,提高情感识别的准确性;最后,本文在DEAP和AMIGOS数据集上对基于时间序列成像的多任务学习驱动情感识别方法开展情感识别二分类、四分类和八分类任务的性能评估,并系统分析了不同频带、时间尺度、特征融合策略以及数据增强方式的影响。
1 时间序列成像
时间序列成像将时间序列数据划分为多个窗口,并将每个窗口数据转换为图像,最终将这些图像合并成一个整体图像,从而直观展示时间序列数据的演变趋势、周期性和异常情况。本文以时间序列成像在标准时间序列数据集的分类性能作为选取依据,采用格拉姆角场、马尔可夫转移场、模式差分场3种算法将脑电信号转化为图像。
1.1 格拉姆角场
格拉姆角场(Gramian angular field,GAF)变换是一种将时间序列通过极坐标映射为角度,利用角度和余弦与角度差正弦分别生成对称与反对称矩阵的图像编码方法。该变换在保留数据时序相关性的同时,能够捕捉序列的空间连续性。GAF编码的步骤如下。
(1)最小-最大归一化。将时间序列
缩放到[-1,1],归一化后的时间序列
其中,
(1)
(2)极坐标转换。
(2)
式中:φ为转换后的角度;α为正则化极坐标跨度的常数因子;ti为xi的时间戳。
(3)三角和差。通过角度和余弦与角度差正弦分别得到格拉姆角和场(Gramian angular summation field,GASF)矩阵O∈Rn×n与格拉姆角差场(Gramian angular difference field,GADF)矩阵H∈Rn×n,其元素分别为
(3)
式中:φi和φj分别为时刻i和时刻j处的归一化信号值通过式(2)转换的角度。
GASF为对称图像,反映了相邻时刻信号的相似性;GADF为反对称图像,强调相邻时刻信号的趋势差异。GAF变换的运算过程如图1所示。
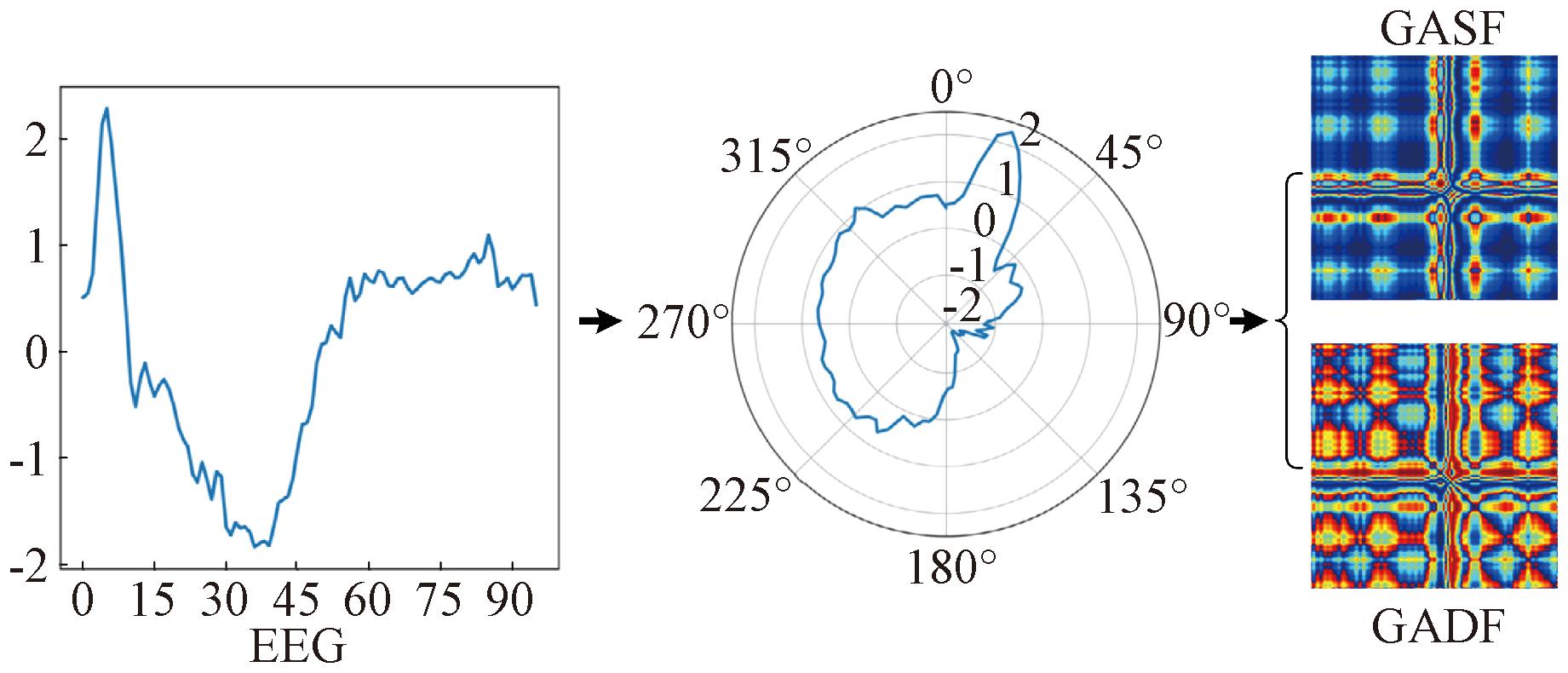
图1 基于GAF的脑电信号图像编码
Figure 1 EEG signal image encoding with GAF
1.2 马尔可夫转移场
马尔可夫转移场(Markov transition field,MTF)借助马尔可夫转移概率来捕捉时间序列的动态变化,将一维时间序列转换为二维的转移概率图像。MTF的图像编码步骤如下。
(1)分位离散化。将时间序列的值域范围通过Q分位离散化为状态空间
分配xi到其对应的qk构造新的状态序列
(2)计算转移概率。根据状态序列S,基于一阶马尔可夫链,计算从状态qk转移到状态ql的转移概率p(qk→ql):
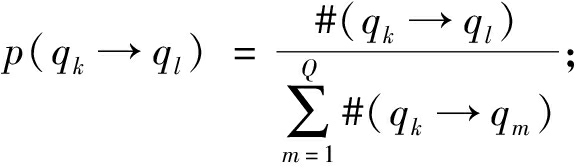
(4)
且si+1=ql}。
(5)
式中:#(qk→ql)为状态从qk转移到ql的转移次数;1≤k;l≤Q。
(3)构造MTF矩阵Φ∈RQ×Q,其元素为
Φkl=p(qk→ql)。
(6)
4分位MTF变换的运算过程如图2所示。
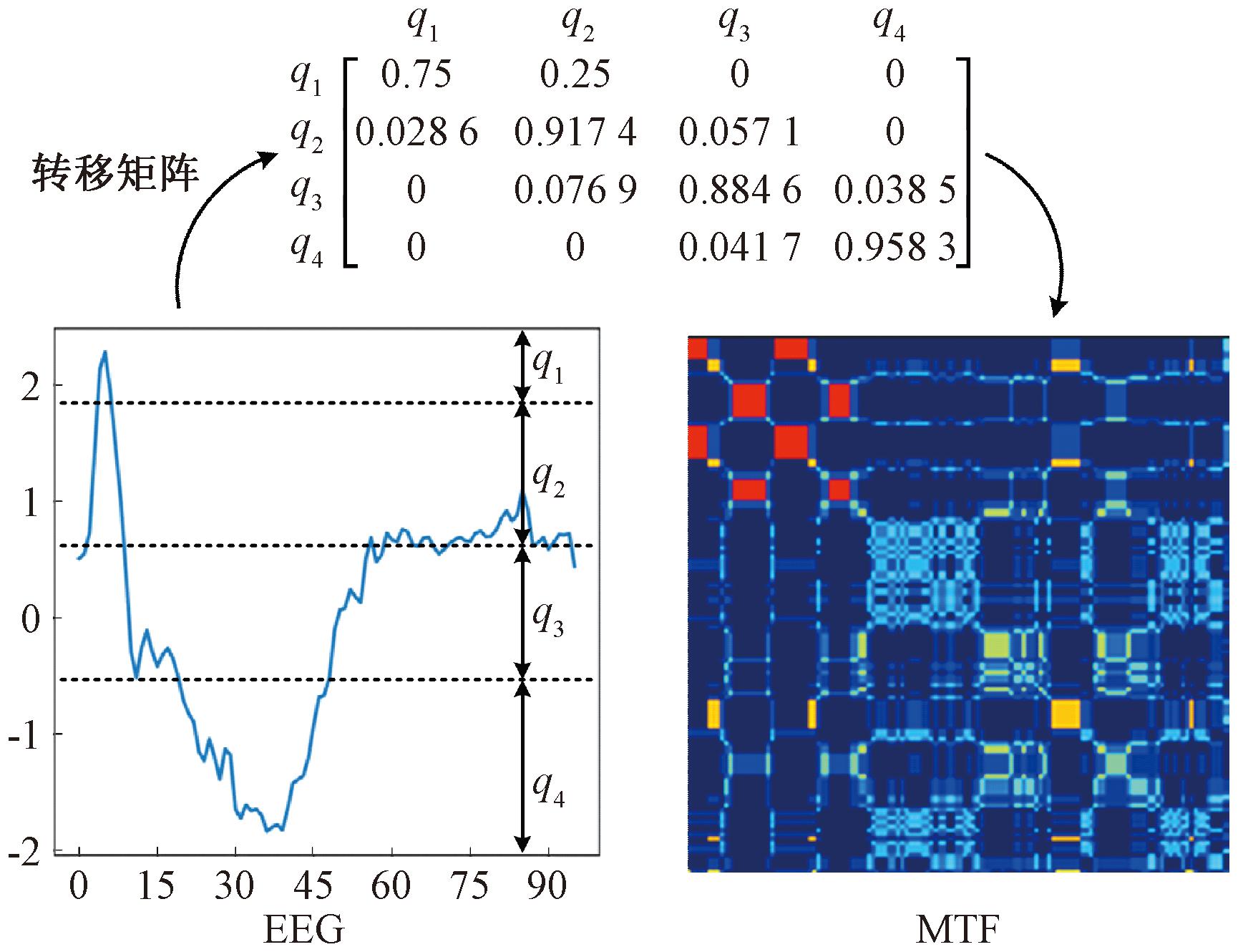
图2 基于MTF的脑电信号图像编码
Figure 2 EEG signal image encoding with MTF
1.3 模式差分场
模式差分场(motif difference field,MDF)划分时间序列为相同长度的重叠子序列,通过计算子序列中相邻点的欧氏距离生成差分矩阵,并按相邻点的时间间隔维度堆叠,构造多幅图像。该方法的主要优点在于能够捕捉时间序列中的局部模式和重复性,并且不需要先验知识或模型。MDF的图像编码步骤如下。
(1)差分子序列。基于时间序列
构造起始点为s,步长为d,长度为m的子序列
Rm:
(7)
式中:1<m≤n;s=1,2,…,n-(m-1)d,1≤d≤dmax;dmax=⎣(n-1)/(m-1)」。
通过将
按行堆叠,可得步长为d的子序列矩阵
(8)
对
进行相邻点差分,可得差分子序列矩阵
(9)
式中:
的第i(i=1,2,…,m-1)个元素为xs+id-xs+(i-1)d。
(2)零填充。由于
中子序列的个数为n-(m-1)d,最多为n-(m-1),为了使得中子序列的维度相同,均为(n-(m-1))(m-1),构造新序列
满足以下条件:
(10)
相对应的,新的差分矩阵为
(11)
将不同步长的新差分矩阵堆叠,可得模式差分场:
(12)
(3)图像修正。由以上分析可知,长度为m的差分子序列
有m-1个元素,所以Jm可以生成m-1个通道图像。第k个通道图像矩阵可以表示为
(13)
式中:
为了修正填充的0元素,k通道的图像矩阵可更改为
(14)
式中:⊙为Hadamard积;G′mk由
旋转180°后得到;Km为掩码矩阵,其元素表示为
(15)
子序列长度为3的MDF变换的运算过程如图3所示。
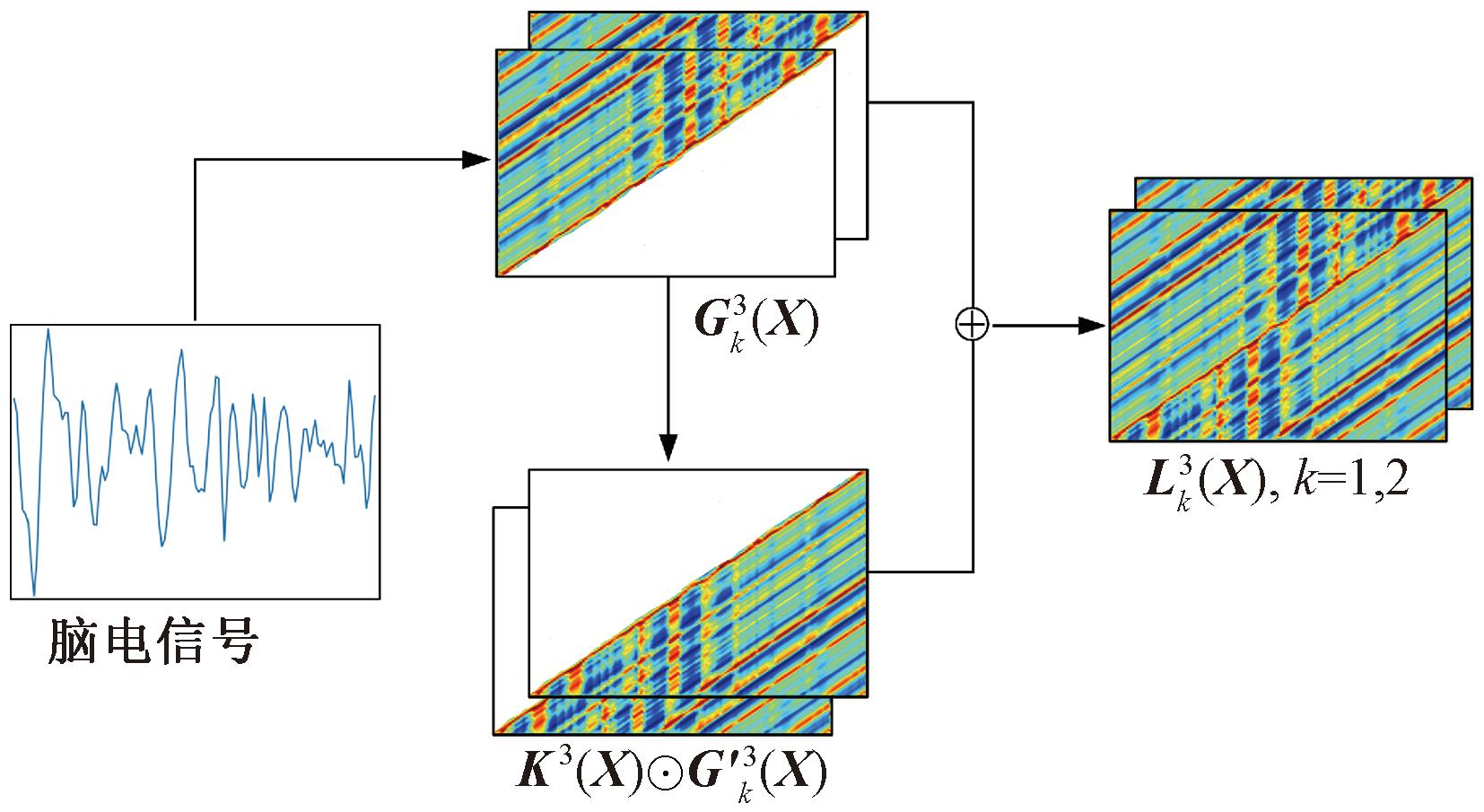
图3 基于MDF的脑电信号图像编码
Figure 3 EEG signal image encoding with MDF
2 多任务特征融合
GAF通过极坐标映射,衡量数据点之间的相关性和连续性;MTF利用各离散状态间的转移概率描述脑电信号整体变化趋势;MDF通过求相邻脑电片段的差值来判断相邻脑电序列的相似性。不同的TSI算法侧重于刻画脑电信号的不同特征,生成的图像具有互补性。
为充分融合不同TSI算法编码图像的特征,进一步提高模型的分类能力,设计多任务特征融合框架,如图4所示。
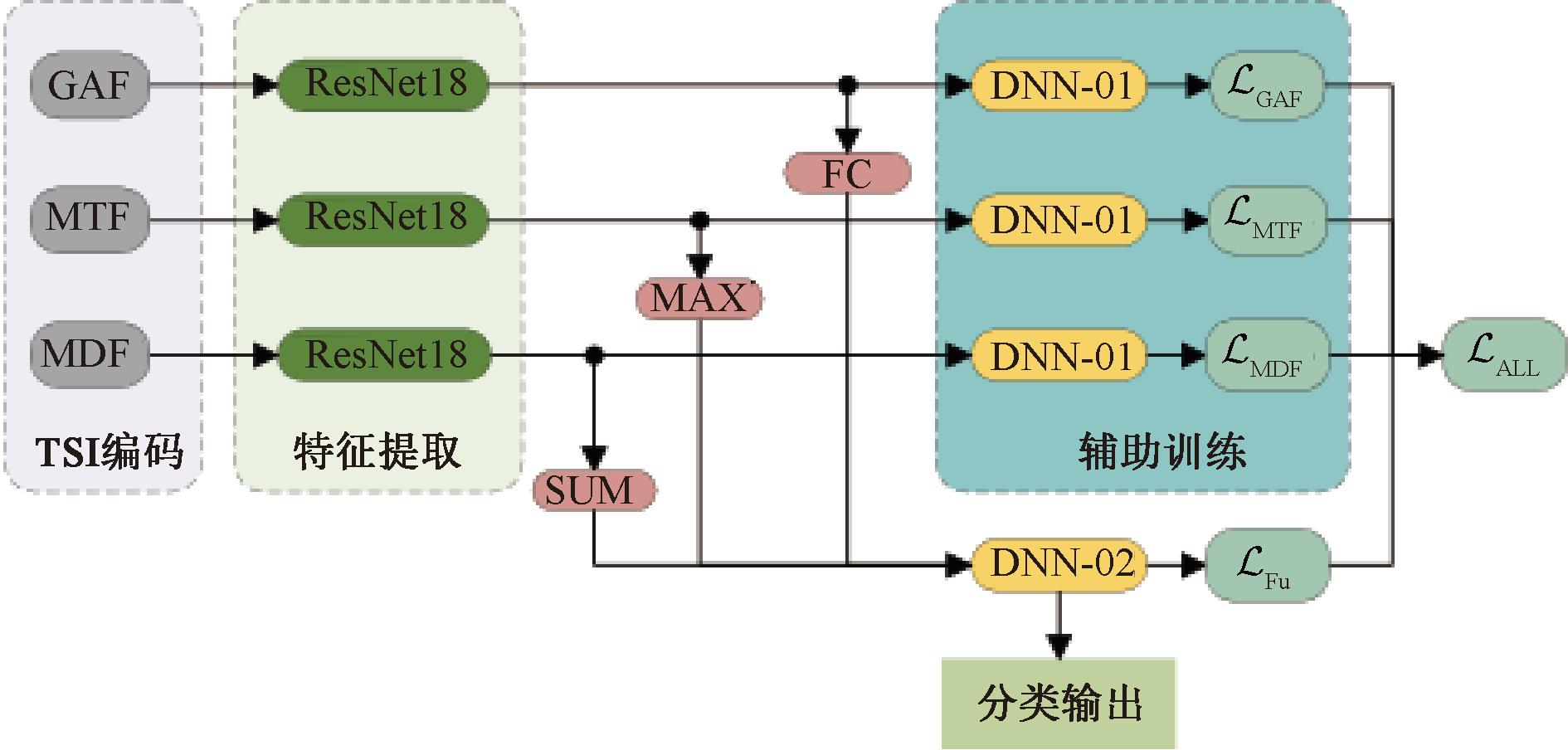
图4 基于TSI的多任务特征融合网络
Figure 4 Multi-task feature fusion network based on TSI
借助多任务学习的思想,3类TSI编码的脑电图像分别送入ResNet18特征提取网络抽取图像特征,提取到的图像特征在经过特征融合模块后送入下层DNN-02网络的同时,分别通过DNN-01网络进行辅助训练,最终由DNN-02输出分类结果。DNN-01和DNN-02的网络结构如图5所示。
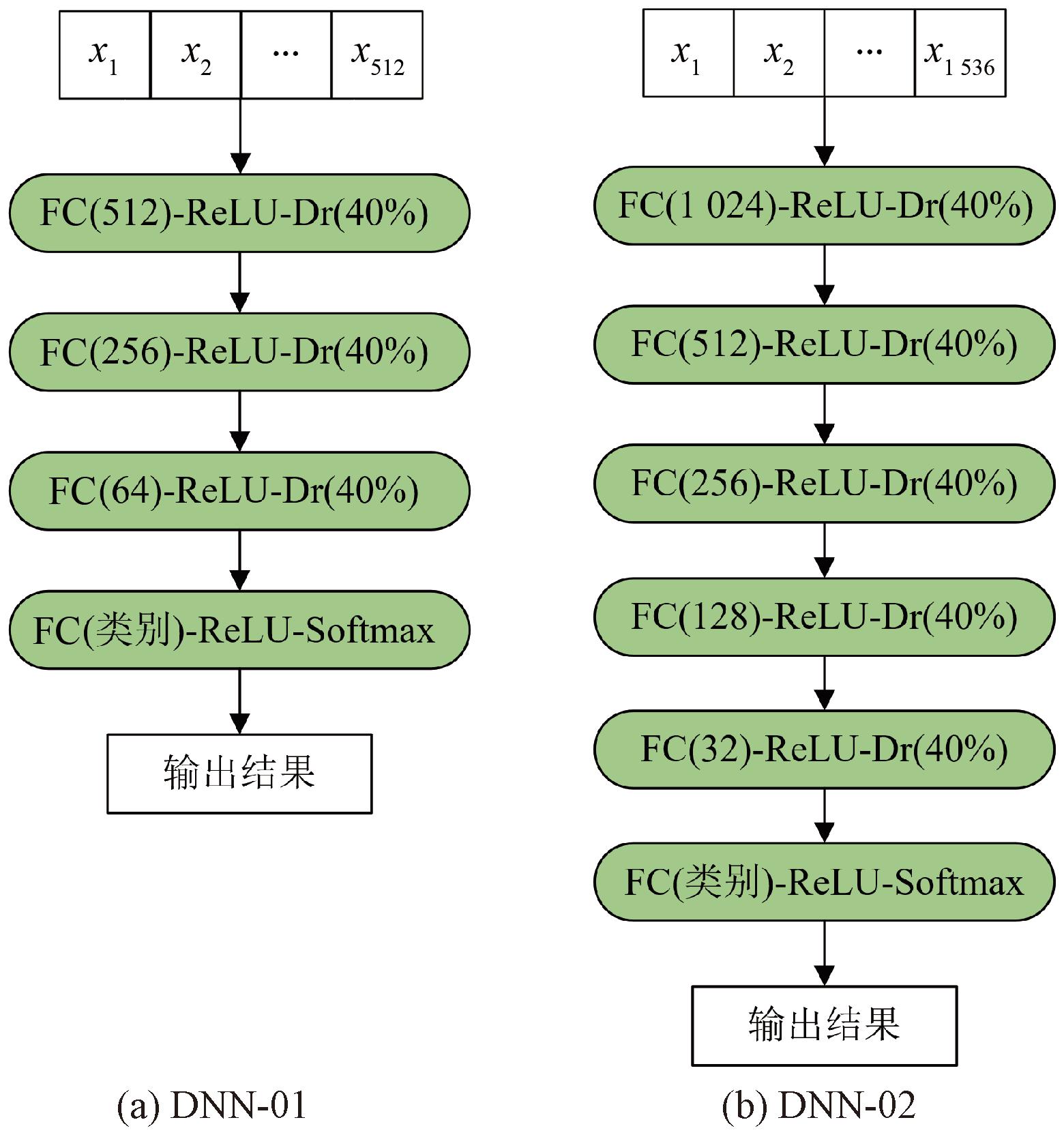
图5 DNN-01和DNN-02的网络结构
Figure 5 Network structure of DNN-01 and DNN-02
特征融合模块采用3种方式:特征叠加(SUM)、特征最大化(MAX)以及特征全连接(FC)。其中,SUM融合假设不同TSI编码的重要性一致,在不改变特征向量大小的同时,能够减轻网络特征选择的压力;MAX融合从高级特征向量中选择最重要的特征,以减少特征维度,突出关键特征,避免噪声和非关键特征对模型的不良影响;FC融合通过全连接层学习特征之间的非线性关系,动态分配不同特征的权重,增强重要特征的表达能力。3种融合方式如下所示:
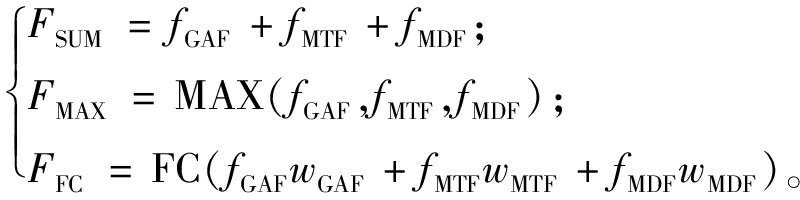
(16)
式中:fGAF、fMTF、fMDF为分别从使用GAF、MTF、MDF编码后的图像中提取到的特征;wGAF、wMTF、wMDF分别为对应全连接层中的权重;FSUM、FMAX、FFC均为融合后的特征。
为了让单个特征和融合后的特征之间保持平衡,设计了一个总损失函数
ALL:
ALL=a(GAF+MTF+MDF)+bFu。
(17)
式中:a和b为平衡权重,此处分别设为1/3和1.0,使它们在训练时对网络参数的优化贡献相等;GAF、MTF、MDF分别为GAF、MTF、MDF各自训练时的损失函数,用来辅助优化各自对应的训练模型;Fu为特征融合后的损失函数;整个特征融合网络由ALL优化。
3 实验设置
3.1 情感识别数据集
DEAP数据集共有32名被试者参与,男女各半。实验中采集40通道生理信号,其中前32个通道为脑电信号,采集位置按照10-20系统选择。原始采样率512 Hz的信号经降采样预处理至128 Hz。观看完每段视频后,被试者按9点评分量表,从Valence、Arousal、Dominance、Liking这4个情感维度进行自我评分。
AMIGOS数据集包含短视频与长视频两类实验,分别有40名和37名被试者参与。每位被试者在10-20系统电极位置布置14个电极。观看每段视频后,被试者按9点评分量表从Valence、Arousal、Dominance、Familiarity、Liking这5个维度评分。
DEAP和AMIGOS数据集的数据格式及内容如表1所示。
表1 数据集格式
Table 1 Dataset format
数据集名称形状描述DEAP生理信号40×40×8064视频/通道/长度标签40×4视频/标签AMIGOS生理信号16×16×(2060～9000)视频/通道/长度标签16×5视频/标签
3.2 数据预处理
为降低低频噪声和个体差异对情感识别的干扰,需要对脑电数据进行基线预处理[12]。DEAP经基线去除和分割处理后,每个样本包含32个通道,128个采样点,每名被试者的采样数据经分割后生成2 400个样本。AMIGOS为14个通道,128个采样点,每名被试者的采样数据生成1 378个样本。实验均基于Valence和Arousal两个情感维度进行,各种情感标签的阈值均为5(≤5表示低,>5表示高)。
3.3 脑电图像拼接
由于不同通道捕捉的神经活动信息存在差异,为了提高情感识别精度,需要将各通道的TSI图像按照对应通道的物理位置进行图像拼接,具体拼接方式如图6所示。
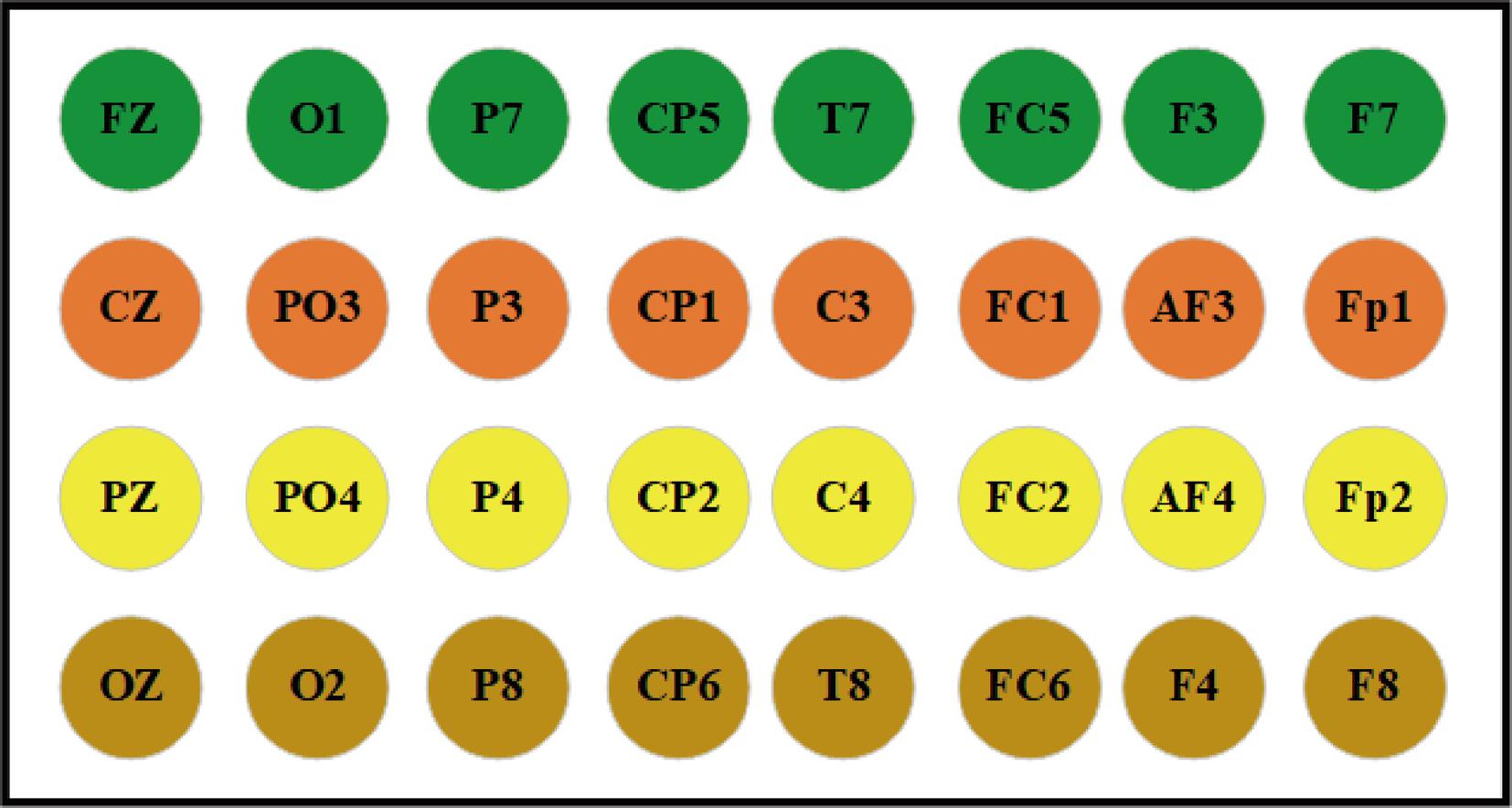
图6 多通道图像拼接方式
Figure 6 Multi-channel image stitching method
研究表明,与情感相关的EEG信号主要分布在额叶、颞叶和顶叶[6],因此,DEAP选取Fp1,Fp2,F3,F4,P3,P4,F7,FC5,FC1,T7,P7,PO3,PZ,FZ,F8,FC6,FC2,T8,P8,PO4共20个通道;AMIGOS选取F7,F3,FC5,T7,P7,P8,T8,FC6,F4,F8共10个通道。
3.4 参数设置
模型训练基于开源深度学习框架Pytorch,使用Adam优化器,学习率设置为10-4,dropout比率设置为0.4。模型评估采用准确率指标,通过十折交叉完成验证。所有实验都在一台运行Ubuntu Linux 21.04的服务器上进行,配置为Intel Xeon(R)Gold 5218 CPU、128 GB RAM和NVIDIA GTX 2080Ti显卡。
4 实验结果与分析
4.1 脑电频带
脑电信号在频域上可划分为多个频带,不同频带反映不同的神经活动。情感状态会引起特定频带的变化,合理选择频带有助于提升情感识别的准确性。全频带下不同时间序列成像脑电情感识别的性能如图7所示,可以看出,GADF整体上优于GASF,MTF优于GAF,MDF在3种时间序列算法中表现最佳,且在子序列长度为4时效果最优。结果表明,时间序列成像算法可提取稳定且显著的情感特征,即使是浅层的识别模型也能有效学习,体现出时间序列成像算法将脑电信号转化为图像进行分类的优势。
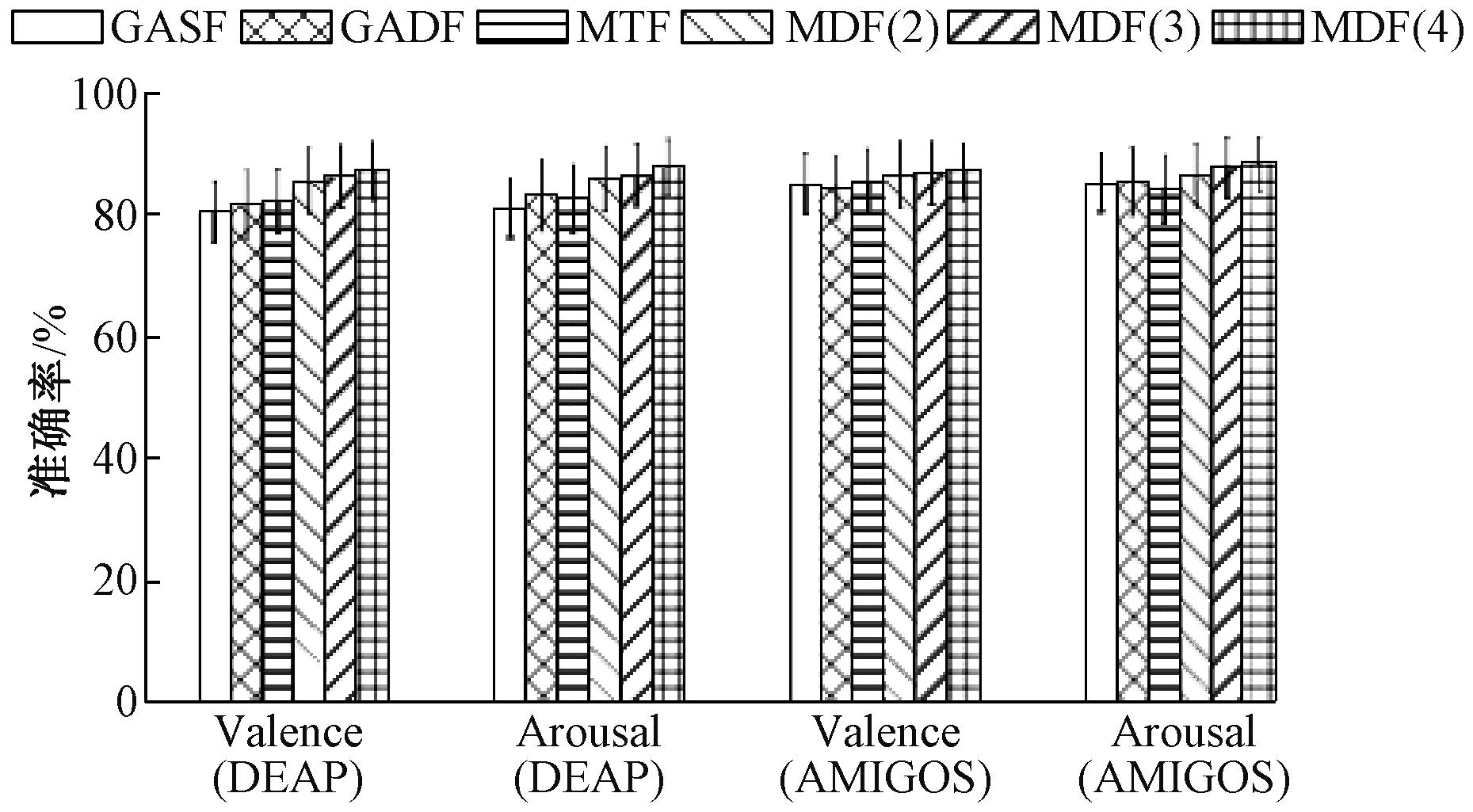
图7 DEAP和AMIGOS数据集上不同时间序列成像的分类准确率
Figure 7 Classification accuracies of different TSI methods with DEAP and AMIGOS datasets
相关研究表明,Theta(4～8 Hz)、Alpha(8～13 Hz)、Beta(13～30 Hz)、Gamma(30～50 Hz)这4个频带更能反映情感特性,但其脑电特征信息存在一定的差异[13],需要进一步确定最适合时间序列成像的脑电频带。实验使用零相位巴特沃斯四阶带通滤波器对DEAP和AMIGOS数据集进行分频,在基线预处理和通道选择的基础上,选用MDF(4)算法将全部通道的脑电数据转化为图像,并用ResNet18进行分类。
图8的频带选择实验结果显示,分类准确率随着频率的增加而提升,使用全频段时的分类效果最佳,在DEAP和AMIGOS数据集上,Valence和Arousal两个维度的平均分类准确率分别为87.52%和87.73%。这表明基于TSI的脑电情感识别需要综合不同频率范围的信息。
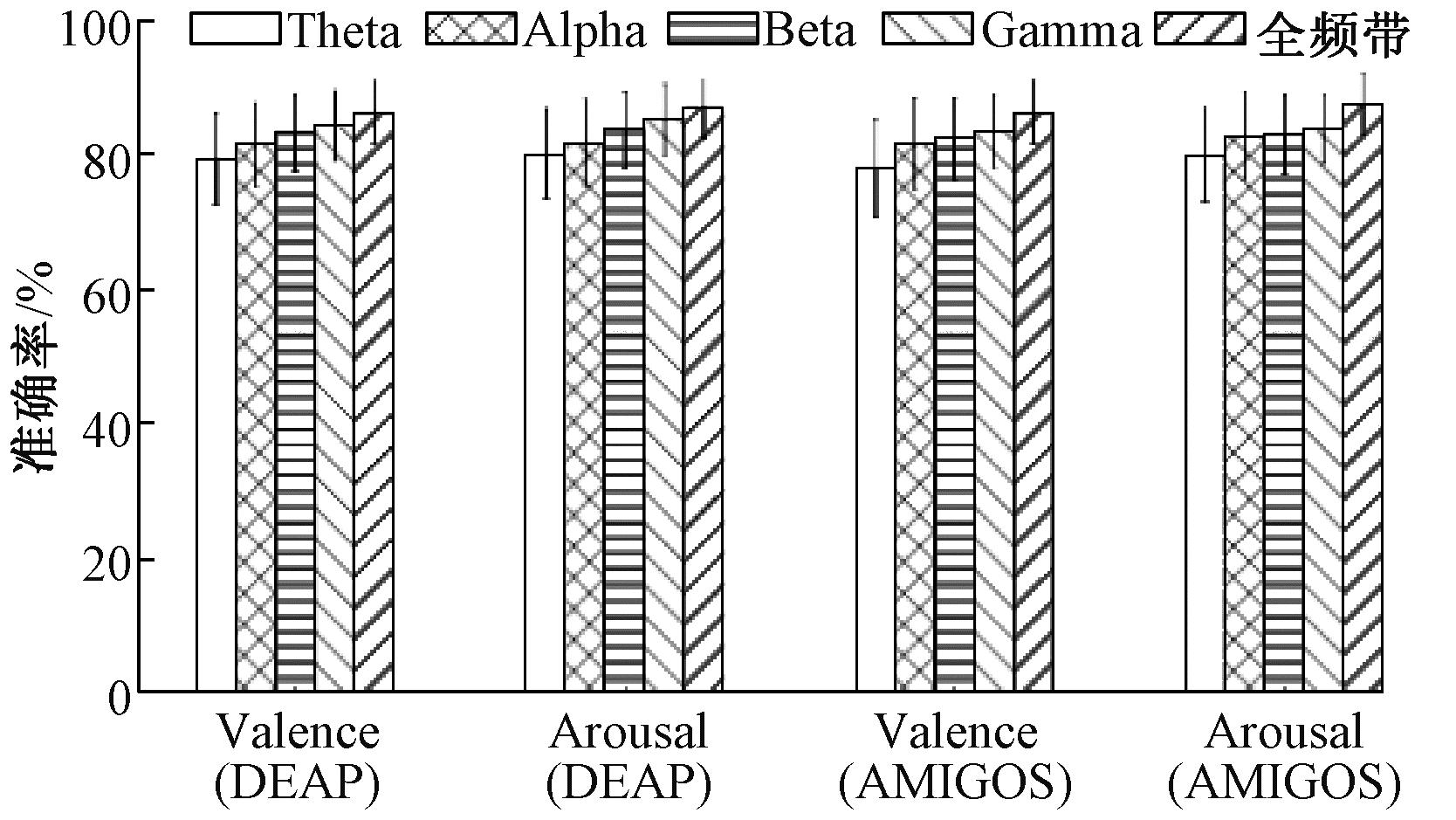
图8 DEAP和AMIGOS数据集上不同频带的分类准确率
Figure 8 Classification accuracies across different frequency bands with DEAP and AMIGOS datasets
4.2 多尺度处理
传统单一尺度的时域和频域分析无法捕获脑电信号的局部特征。对脑电信号进行多尺度处理[14]之后的情感识别结果如图9所示。当时间尺度为2时,分类效果最佳,DEAP数据集上Valence和Arousal两个维度的平均分类准确率分别为89.33%和89.50%;AMIGOS数据集上分别为92.37%和92.87%。随着时间尺度的增大,分类准确率逐渐降低,这是因为时间尺度过大会导致不同尺度上提取的特征出现重叠,造成信息冗余,信号中的噪声也会随之增加,从而影响分类效果。当时间尺度超过4时,分类准确率甚至低于直接使用原始脑电信号,此时局部动态信息被较长的时间尺度所平滑,导致特征信息丢失。
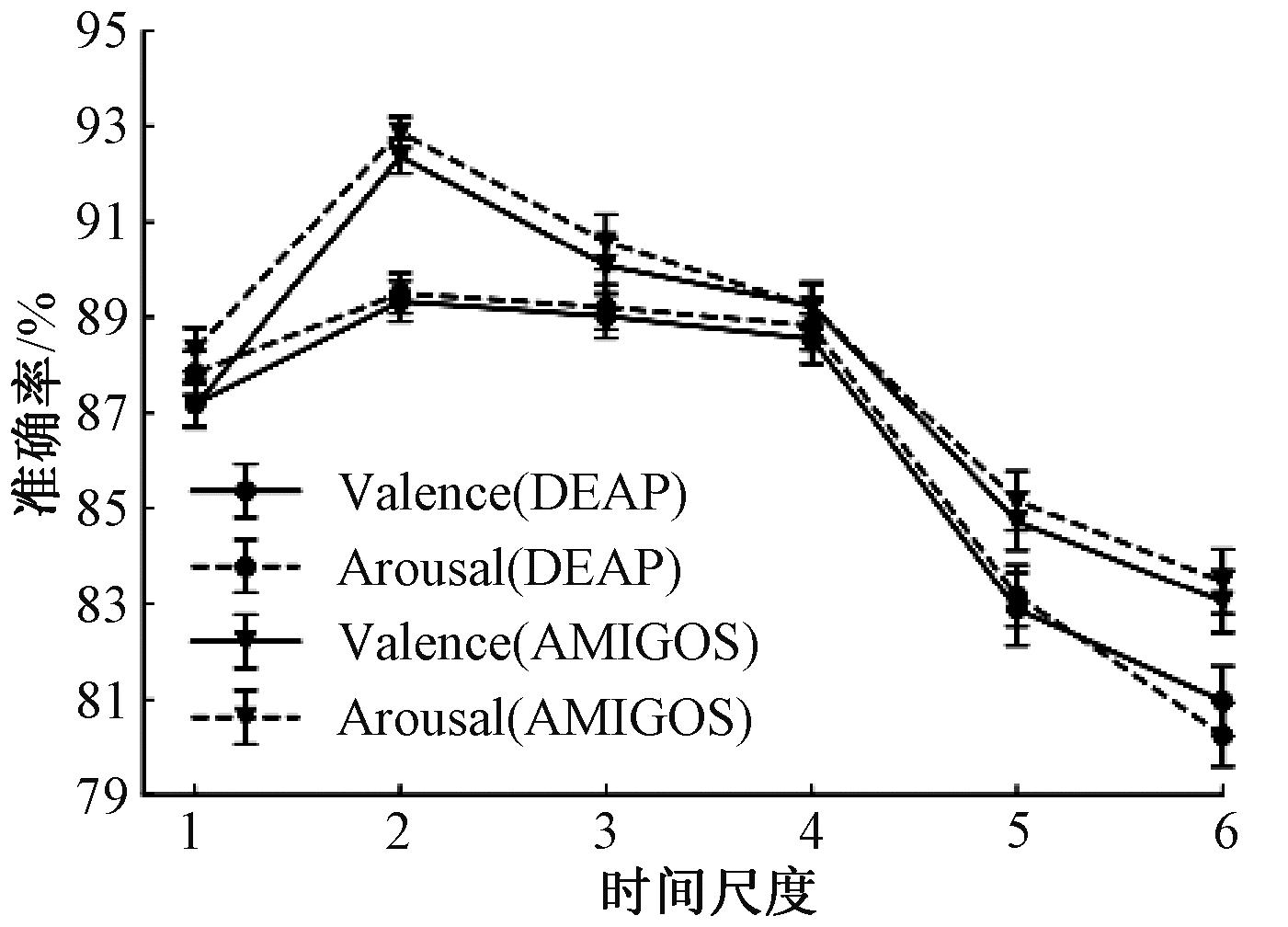
图9 DEAP和AMIGOS数据集上不同时间尺度的分类准确率
Figure 9 Classification accuracies across different time scales with DEAP and AMIGOS datasets
4.3 不同特征融合脑电情感识别结果
为了评估3种特征融合方式对多任务特征融合分类性能的影响,基于4.1节的识别结果,选用GADF、MTF、MDF(4)(记为GMM)和MDF(2)、MDF(3)、MDF(4)(记为MMM)这两种组合进行多任务特征融合实验。通过表2中的分类结果可知,MMM组合优于GMM组合,且无论采用哪种多任务组合方式,使用FC融合进行特征融合的分类效果始终最好。具体来说,在FC融合方式下,GMM组合在DEAP和AMIGOS上的平均分类准确率分别为91.11%和93.03%,而MMM组合的平均分类准确率分别为94.87%和96.66%,分别提升了3.76百分点和3.63百分点。与单模型的最佳分类结果(图8)相比,基于MMM组合的多任务特征融合模型的情感分类在DEAP和AMIGOS上的平均分类准确率分别提高了7.35百分点和8.93百分点。
表2 DEAP和AMIGOS数据集上不同特征融合方式的分类准确率
Table 2 Classification accuracies of different feature fusion methods with DEAP and AMIGOS datasets
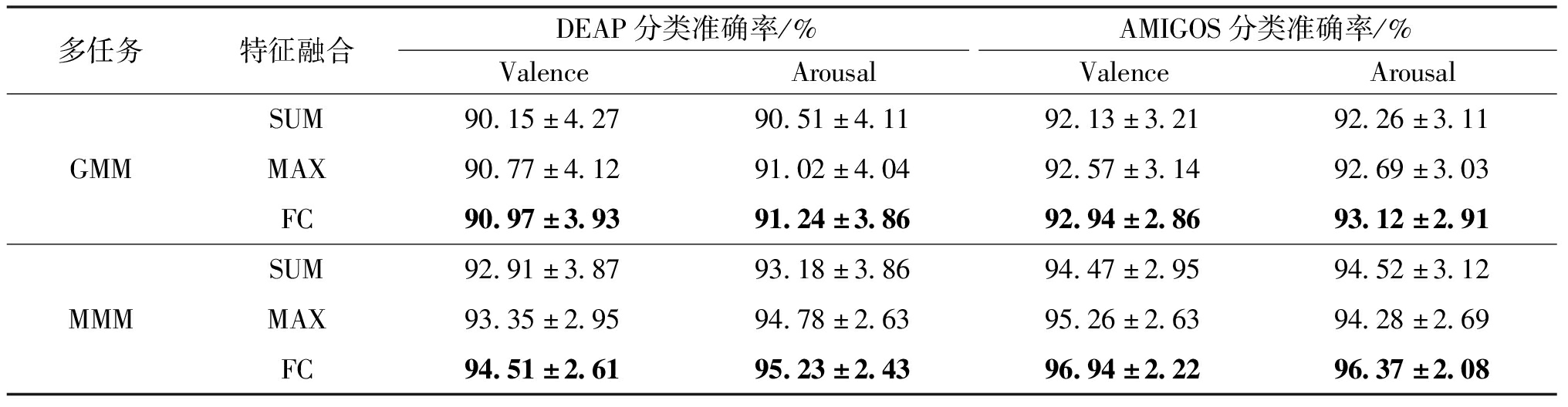
多任务特征融合DEAP分类准确率/%AMIGOS分类准确率/%ValenceArousalValenceArousalGMMSUM90.15±4.2790.51±4.1192.13±3.2192.26±3.11MAX90.77±4.1291.02±4.0492.57±3.1492.69±3.03FC90.97±3.9391.24±3.8692.94±2.8693.12±2.91MMMSUM92.91±3.8793.18±3.8694.47±2.9594.52±3.12MAX93.35±2.9594.78±2.6395.26±2.6394.28±2.69FC94.51±2.6195.23±2.4396.94±2.2296.37±2.08
4.4 数据增强
Mixup数据增强[15]能够将不同的样本以一定的比例进行混合,从而产生新的训练样本。图10所示为经过Mixup数据增强后的MMM+FC融合的分类结果,可以看出,随着混合系数的增加,分类准确率也随之提升,在0.4时最高。
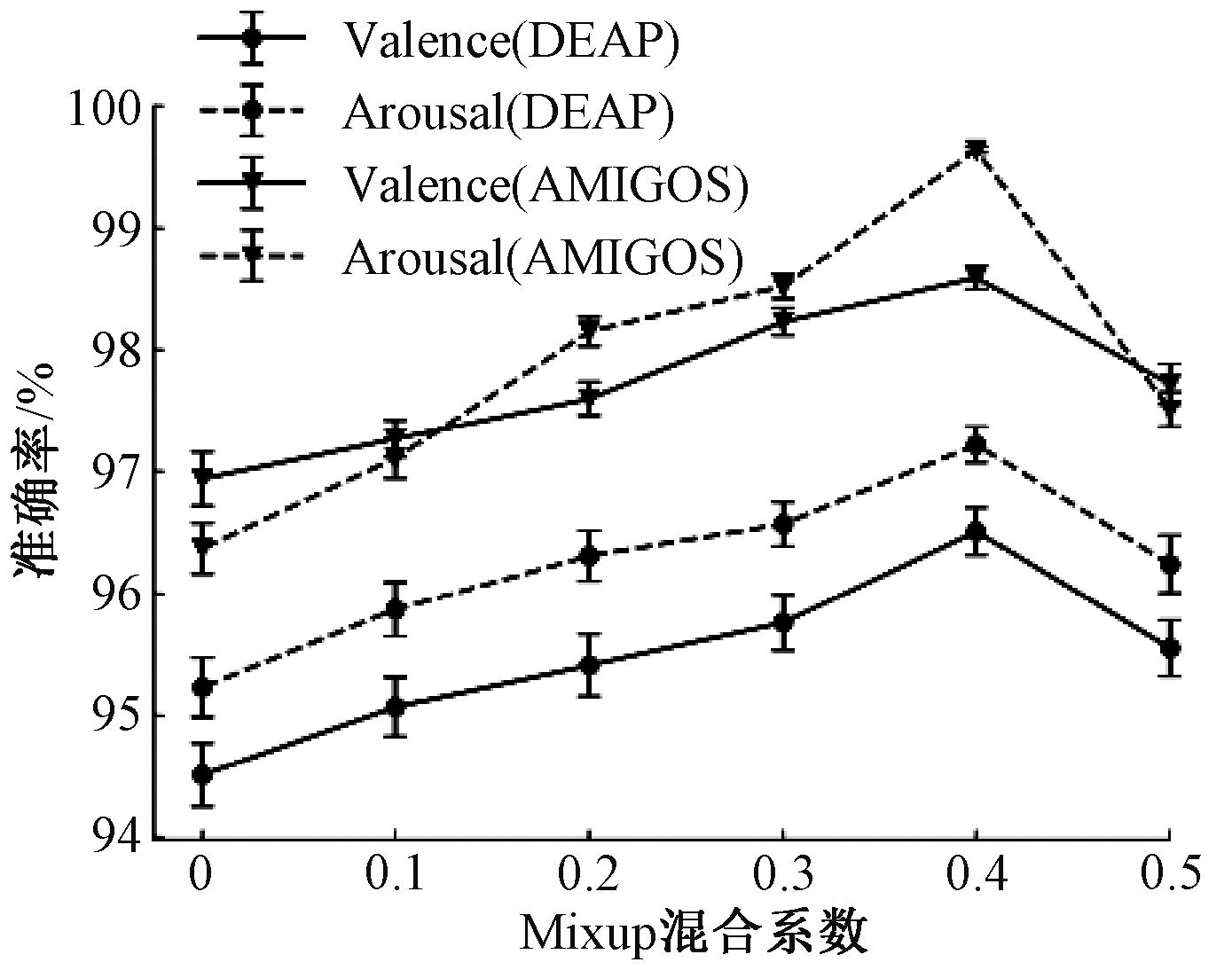
图10 DEAP和AMIGOS数据集上不同Mixup混合系数的分类准确率
Figure 10 Classification accuracies with different Mixup mixing coefficients with DEAP and AMIGOS datasets
4.5 与现有模型方法的二分类结果对比
表3对比了多任务特征融合模型与当前常用的、准确率较高的机器学习和深度学习方法的情感识别分类结果。由表3可知,传统机器学习在DEAP和AMIGOS数据集上的分类准确率普遍低于90%,而结合LSTM、CNN等深度学习模型整体上可有效提升识别性能。
表3 不同方法在DEAP和AMIGOS数据集的平均分类准确率对比
Table 3 Comparison of average classification accuracies of different methods with DEAP and AMIGOS datasets
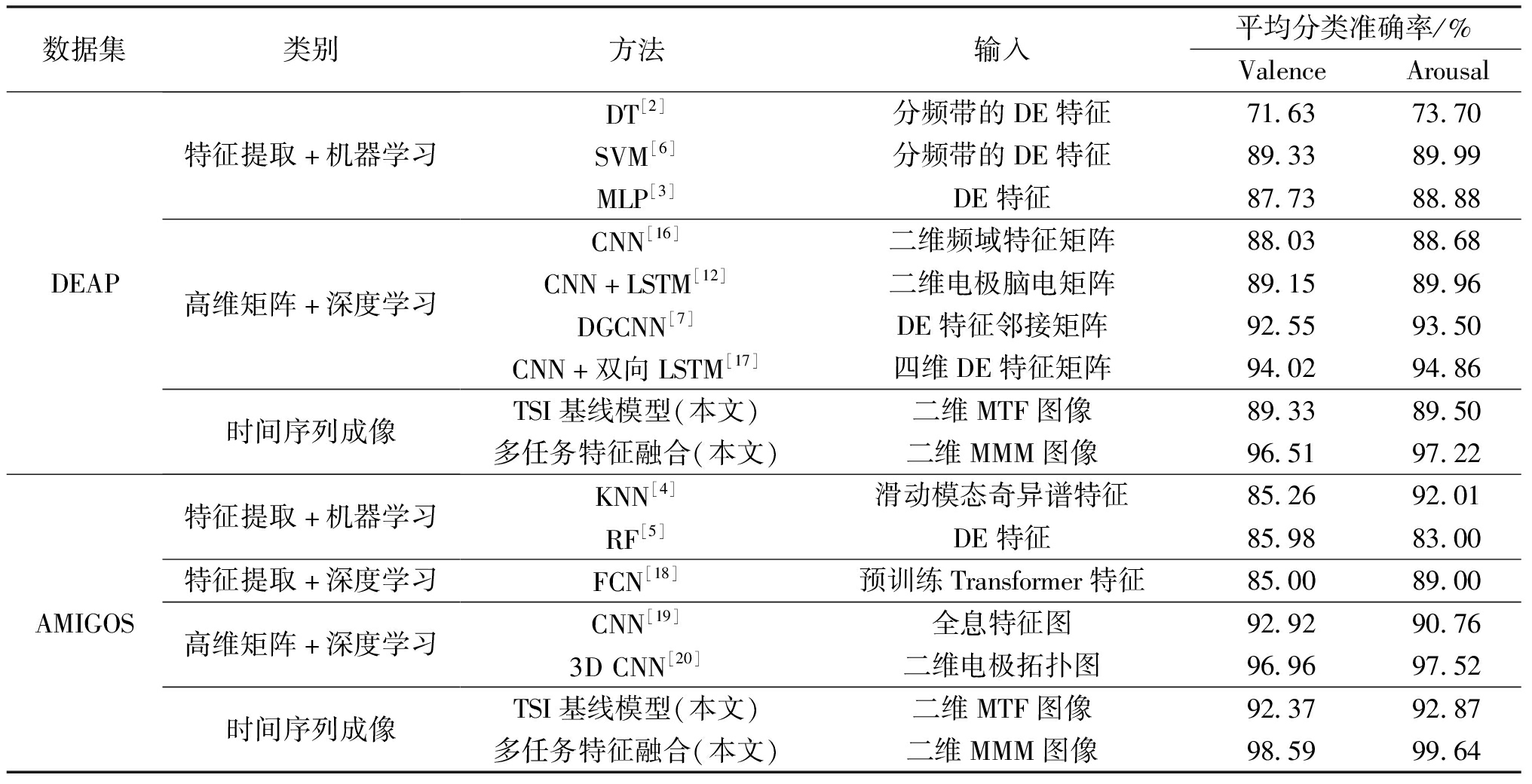
数据集类别方法输入平均分类准确率/%ValenceArousalDEAP特征提取+机器学习高维矩阵+深度学习时间序列成像DT[2]分频带的DE特征71.6373.70SVM[6]分频带的DE特征89.3389.99MLP[3]DE特征87.7388.88CNN[16]二维频域特征矩阵88.0388.68CNN+LSTM[12]二维电极脑电矩阵89.1589.96DGCNN[7]DE特征邻接矩阵92.5593.50CNN+双向LSTM[17]四维DE特征矩阵94.0294.86TSI基线模型(本文)二维MTF图像89.3389.50多任务特征融合(本文)二维MMM图像96.5197.22AMIGOS特征提取+机器学习特征提取+深度学习高维矩阵+深度学习时间序列成像KNN[4]滑动模态奇异谱特征85.2692.01RF[5]DE特征85.9883.00FCN[18]预训练Transformer特征85.0089.00CNN[19]全息特征图92.9290.763DCNN[20]二维电极拓扑图96.9697.52TSI基线模型(本文)二维MTF图像92.3792.87多任务特征融合(本文)二维MMM图像98.5999.64
本文提出的基于时间序列成像的脑电情感识别方法取得了较高的分类准确率,TSI基线模型在DEAP和AMIGOS数据集上的平均分类准确率分别超过了89%和92%,与一些基于时频谱图进行分类的方法相比,性能相当。而利用多任务特征融合的平均分类准确率可分别提升至96%以上和98%以上,充分体现了时间序列成像在脑电情感识别任务中的有效性。
脑电情感识别时频特征提取通常依赖较多参数,如脑电信号分帧长度、帧移等,同时存在较多的二维时频特征可供选取。相比之下,时间序列成像算法不仅能有效捕捉脑电信号复杂的时序特征,并且计算简单、参数设置较少,比如GAF不需要额外参数设置;MTF只需要设置转移概率值域划分范围;MDF仅需要设置子片段长度和时间间隔。
4.6 四分类和八分类实验结果对比
当前基于脑电信号的情感识别研究通常被视为二分类问题,只能判断具有或不具有特定情感状态的类别。为了进一步探究多任务学习特征融合模型的性能,将识别任务扩展到四分类和八分类。由表4可知,不管是四分类任务还是八分类任务,特征融合方式使用FC时效果均最好。四分类的平均分类准确率均在90%以上,但是八分类的平均分类准确率均有一定的降低。这是因为当类别数越多时,单个类别的数据量就越少,此时数据量限制了模型的分类能力。
表4 四分类和八分类的平均分类准确率
Table 4 Average classification accuracies of four-class and eight-class classification
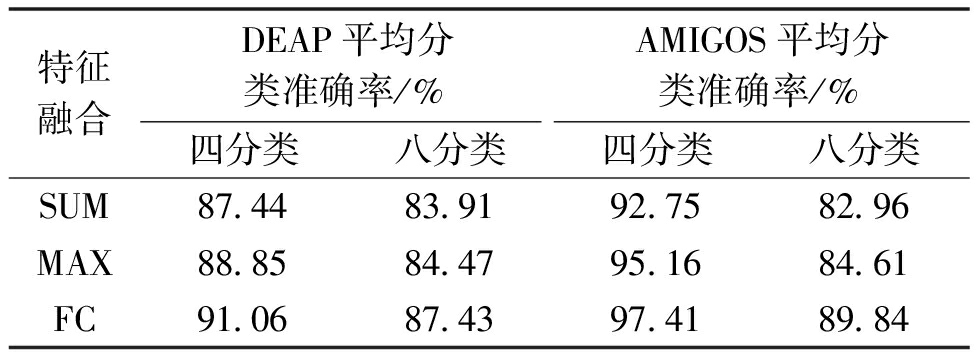
特征融合DEAP平均分类准确率/%AMIGOS平均分类准确率/%四分类八分类四分类八分类SUM87.4483.9192.7582.96MAX88.8584.4795.1684.61FC91.0687.4397.4189.84
5 结论
本文提出基于时间序列成像的脑电情感识别方法,利用相位映射、状态转移以及局部差分3类策略实现原始脑电信号图像编码,具有较高的计算效率和良好的情感特征表达能力,并结合多任务特征融合框架,实现多策略联合建模,进一步增强时间序列成像的脑电情感识别能力。在二分类、四分类和八分类识别任务中,平均分类准确率分别超过96%,91%和87%,验证了时间序列成像应用于脑电情感识别的有效性。下一步研究将考虑扩大样本数量,建立多样化的脑电数据库,引入图像分类更优的Transformer架构,提高多类别情感识别的分类性能。
[1] WANG Y M,ZHANG B,DI L M.Research progress of EEG-based emotion recognition:a survey[J].ACM Computing Surveys,2024,56(11):1-49.
[2] LIU Y,WEI Y,LI C,et al.Bi-CapsNet:a binary capsule network for EEG-based emotion recognition[J].IEEE Journal of Biomedical and Health Informatics,2023,27(3):1319-1330.
[3] YANG Y L,WU Q F,FU Y Z,et al.Continuous convolutional neural network with 3D input for EEG-based emotion recognition[J].Lecture Notes in Computer Science,2018,11307(1):433-443.
[4] SHARMA L D,BHATTACHARYYA A.A computerized approach for automatic human emotion recognition using sliding mode singular spectrum analysis[J].IEEE Sensors Journal,2021,21(23):26931-26940.
[5] GALV
O F,ALARCO S M,FONSECA M J.Predicting exact valence and arousal values from EEG[J].Sensors,2021,21(10):3414.
[6] TAO W,LI C,SONG R C,et al.EEG-based emotion recognition via channel-wise attention and self attention[J].IEEE Transactions on Affective Computing,2023,14(1):382-393.
[7] 魏琛,陈兰岚,张傲.基于集成卷积神经网络的脑电情感识别[J].华东理工大学学报(自然科学版),2019,45(4):614-622.WEI C,CHEN L L,ZHANG A.Emotion recognition of EEG based on ensemble convolutional neural networks[J].Journal of East China University of Science and Technology,2019,45(4):614-622.
[8] SONG T F,ZHENG W M,SONG P,et al.EEG emotion recognition using dynamical graph convolutional neural networks[J].IEEE Transactions on Affective Computing,2020,11(3):532-541.
[9] YANG L Q,LIU J W.EEG-based emotion recognition using temporal convolutional network[C]∥2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS).Piscataway:IEEE,2019:437-442.
[10] SALAMA E S,EL-KHORIBI R A,SHOMAN M E,et al.EEG-based emotion recognition using 3D convolutional neural networks[J].International Journal of Advanced Computer Science and Applications,2018,9(8):329-337.
[11] RAMZAN M,DAWN S.Fused CNN-LSTM deep learning emotion recognition model using electroencephalography signals[J].International Journal of Neuroscience,2023,133(6):587-597.
[12] YANG Y L,WU Q F,QIU M,et al.Emotion recognition from multi-channel EEG through parallel convolutional recurrent neural network[C]∥2018 International Joint Conference on Neural Networks (IJCNN).Piscataway:IEEE,2018:1-7.
[13] LU Y F,ZHENG W L,LI B B,et al.Combining eye movements and EEG to enhance emotion recognition[C]∥International Joint Conference on Artificial Intelligence.Buenos Aires:IJCAI,2015:1170-1176.
[14] BUSA M A,VAN EMMERIK R E A.Multiscale entropy:a tool for understanding the complexity of postural control[J].Journal of Sport and Health Science,2016,5(1):44-51.
[15] ZHANG H Y,CISSE M,DAUPHIN Y N,et al.Mixup:beyond empirical risk minimization[EB/OL].(2018-04-27)[2025-03-30].https:∥arxiv.org/abs/1710.09412.
[16] GAGLIARDI G,ALFEO A L,CATRAMBONE V,et al.Improving emotion recognition systems by exploiting the spatial information of EEG sensors[J].IEEE Access,2023,11:39544-39554.
[17] CUI F C,WANG R Q,DING W W,et al.A novel DE-CNN-BiLSTM multi-fusion model for EEG emotion recognition[J].Mathematics,2022,10(4):582-593.
[18] VAZQUEZ-RODRIGUEZ J,LEFEBVRE G,CUMIN J,et al.Emotion recognition with pre-trained transformers using multimodal signals[C]∥2022 10th International Conference on Affective Computing and Intelligent Interaction (ACII).Piscataway:IEEE,2022:1-8.
[19] TOPIC A,RUSSO M,STELLA M,et al.Emotion recognition using a reduced set of EEG channels based on holographic feature maps[J].Sensors,2022,22(9):3248.
[20] ZHAO Y X,YANG J,LIN J L,et al.A 3D convolutional neural network for emotion recognition based on EEG signals[C]∥2020 International Joint Conference on Neural Networks (IJCNN).Piscataway:IEEE,2020:1-6.