由于组装水轮发电机定子所需的硅钢片排列密集,通常将水轮发电机定子圆度的测量分为上中下3圈,每圈等间隔选取39个测量点。人工驱动的测量方法测量效率低,工作强度大且不利于后续的数据记录和数据处理。为此,设计了一套自动定子圆度测量系统,该测量系统的测量臂采用了轻量化的悬臂梁结构,测量臂到达测量点后末端存在残余振动,且衰减速度较为缓慢,增加了测量过程的无效时间。因此抑制测量臂末端的残余振动对进一步提高测量效率具有积极意义。
目前,振动抑制方法可分为两种:被动控制和主动控制。被动控制通过改善材料和结构来改变机构的质量和刚度,从而改变系统参数,实现对系统振动的抑制[1-2]。郑继周等[3]针对悬臂机构的振动问题提出了一种缓冲型双层颗粒阻尼器,有效降低了悬臂结构末端的振动,使加速度衰减率大于20%。该方法较为容易实现,适用于大多场合,但由于材料和结构的限制,被动控制的抑振效果有限。
主动控制可分为闭环控制和开环控制。闭环控制技术通过对机构运动时的振动状态进行检测来实时调节机构的运动轨迹,实现对振动的抑制[4-5]。Berta等[6]采用PD/模糊控制器使共振衰减时间减少78%;Huang等[7]通过粒子群算法优化压电约束层配置,得到控制器的最优反馈增益;Díaz等[8]提出了一种基于速度反馈的控制算法,控制振动衰减。刘德馨等[9]提出自适应输入整形算法提升柔性负载控制精度。闭环控制可以实现对振动的实时控制,但振动抑制效果主要与振动状态检测的精度有关,当存在一定误差时,抑振效果不够稳定,且很多应用领域存在经济和工程应用方面的限制,导致很难实现振动状态的精准检测。
开环控制技术通过修改输入命令得到最小振动效果的最优运动轨迹。刘卓清等[10]通过利用构造微分平坦输出信号和B样条曲线设计,对塔式吊车的运动轨迹进行优化,实现了多目标最优轨迹规划,提升了防摆性能。卢宁等[11]改进七段式S轨迹控制方法,使防摆效率提升23%。Guo等[12]提出一种双模态输入整形器ZVD-EI,有效抑制Delta机器人运行的残余振动。Sun等[13]结合滤波-曲线方法,对车载混凝土泵臂架的振动进行抑制。Lee等[14]提出卷积S型速度曲线的多模态抑制方案,其抑振效果更加稳定。Baumgart等[15]针对多个输入信号下的振动,开发协作输入整形技术,利用输入协同工作的能力来完成振动抑制。
本文将光滑整形器(smooth input shaper,SIS)应用到水轮发电机定子圆度测量臂的残余振动抑制中。对SIS与传统整形器的抑振效果进行了仿真比较,并通过实验和现场测量对仿真结果进行验证。该方法相比于传统整形器,鲁棒性好,抑振效果稳定;相比于闭环控制,操作简单,无须实时检测振动状态,可以有效减少测量时间,提高测量效率。
1 输入整形方法
1.1 输入整形原理
输入整形是一种开环的前馈控制技术[16-17],结构框图如图1所示。通过将输入信号与一系列根据系统阻尼比和固有频率计算出的脉冲信号进行卷积,使每个脉冲信号引起的振动依次抵消,最终实现残余振动的消除,如图2所示。
图1 输入整形结构图
Figure 1 Input shaping diagram
图2 输入整形原理图
Figure 2 Input shaping schematic diagram
1.2 光滑整形器(SIS)
与传统整形器不同,SIS通过引入一段连续函数与输入信号进行卷积,完成输入信号的光滑处理,避免了引入脉冲信号导致的局部阶跃,使被控对象运动时的瞬态振荡减小,使残余振动得到抑制。
二阶系统可以近似表达任意的线性系统,其传递函数[18]为
(1)
式中:ωn为系统无阻尼固有频率;ξ为系统阻尼比。
其单位脉冲响应为
(2)
式中:tn表示单位脉冲作用的时刻;
为系统有阻尼固有频率。
定义光滑函数为
S(
)=
s()d。
(3)
式中:t1表示光滑函数不为零的时间。
二阶系统关于光滑函数的响应为
)d。
(4)
利用欧拉公式对其进行分解[19]得
(5)
S(ωn,ξ)=
s()eωnξsin (ωn
;
(6)
C(ωn,ξ)=
s()eωnξcos (ωn
。
(7)
取tn=0 s,残余振动响应为
(8)
为了保证残余振动为零,需要满足:S(ωn,ξ)=0,C(ωn,ξ)=0,求得
s(t)=s0e-ξωnt。
(9)
将式(9)代入式(6)和式(7),得
S(ωn,ξ)=
s0sin (ωn
;
(10)
C(ωn,ξ)=
s0cos (ωn
。
(11)
式(10)和式(11)只有在整数个周期时积分为零。为了减小时滞,选取一个周期作为积分区间,得到SIS时域表达式为
s(t)=s0e-ξωnt,0≤t≤T1。
(12)
式中:T1为振动周期。
为了保证信号不失真,需要满足
s(t)dt=1,可得
(13)
2 仿真模拟与实验验证
2.1 系统参数估算
搭建如图3所示的实验平台,测量臂通过连接板和旋转轴固定在三爪卡盘上,跟随三爪卡盘旋转,末端通过钢丝绳拉至水平。测量臂总长为3.1 m,材料为铝合金。使用激光位移传感器对末端振幅进行测量[20],所用传感器型号为基恩士LK-H050,基准距离为50 mm,测量范围为±10 mm,重复精度为0.025 μm,采样频率1 000 Hz。为方便激光位移传感器测量末端的振幅,在测量臂同侧贴上表面光滑的塑料片。由于系统尺寸较大,建立精确模型较为复杂,采用运动测试法对系统参数进行估算,末端振幅测量原理如图4所示。
图3 测量臂振动抑制实验台
Figure 3 Measuring arm vibration suppression test bench
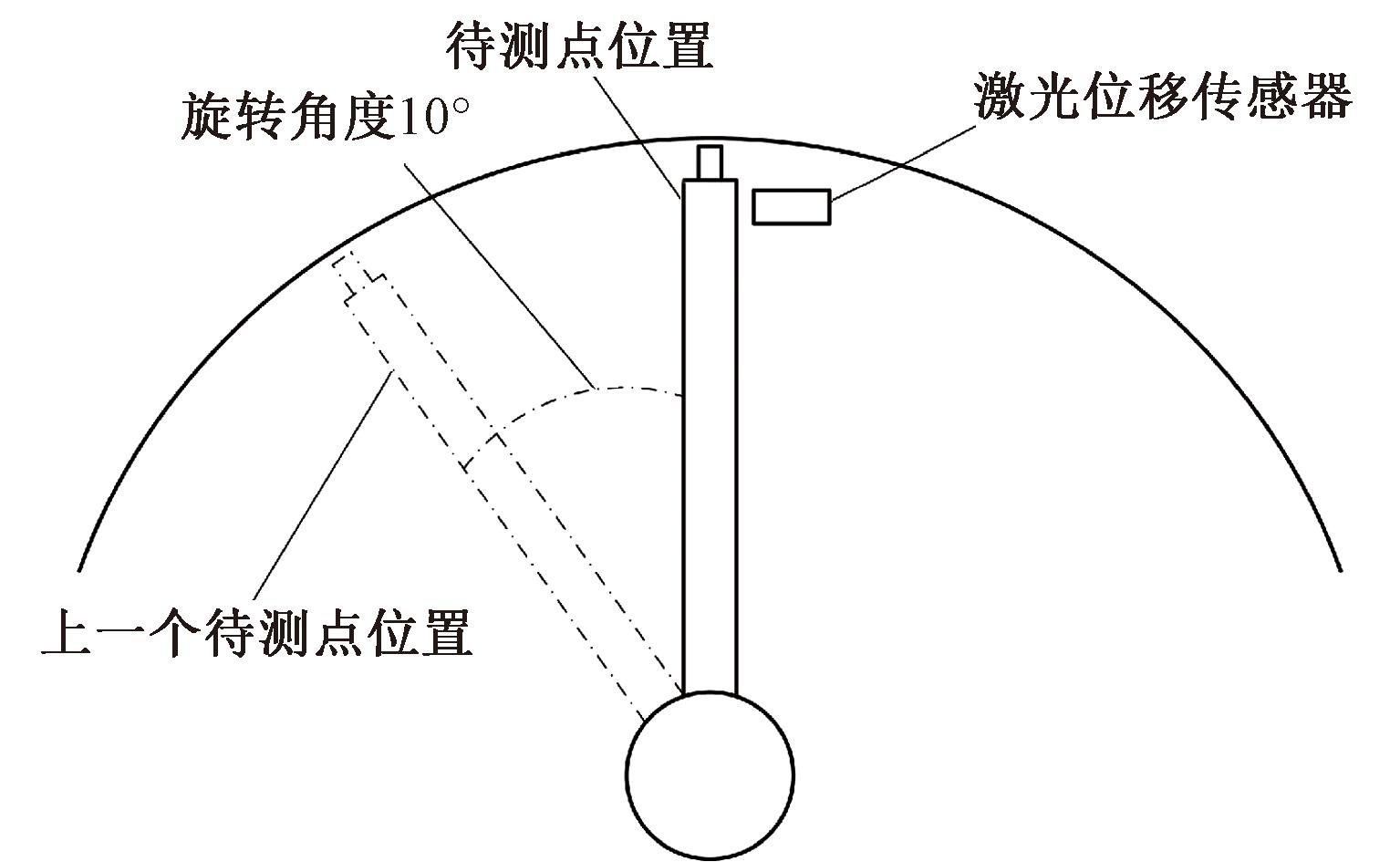
图4 末端振幅测量原理图
Figure 4 End amplitude measurement schematic
测量臂在梯形速度规划,旋转加速度为20°/s2,最大旋转速度为2°/s的条件下,从上一个待测点位置转动10°后到达待测点位置,用位移传感器记录测量臂的残余振动,结果如图5所示。
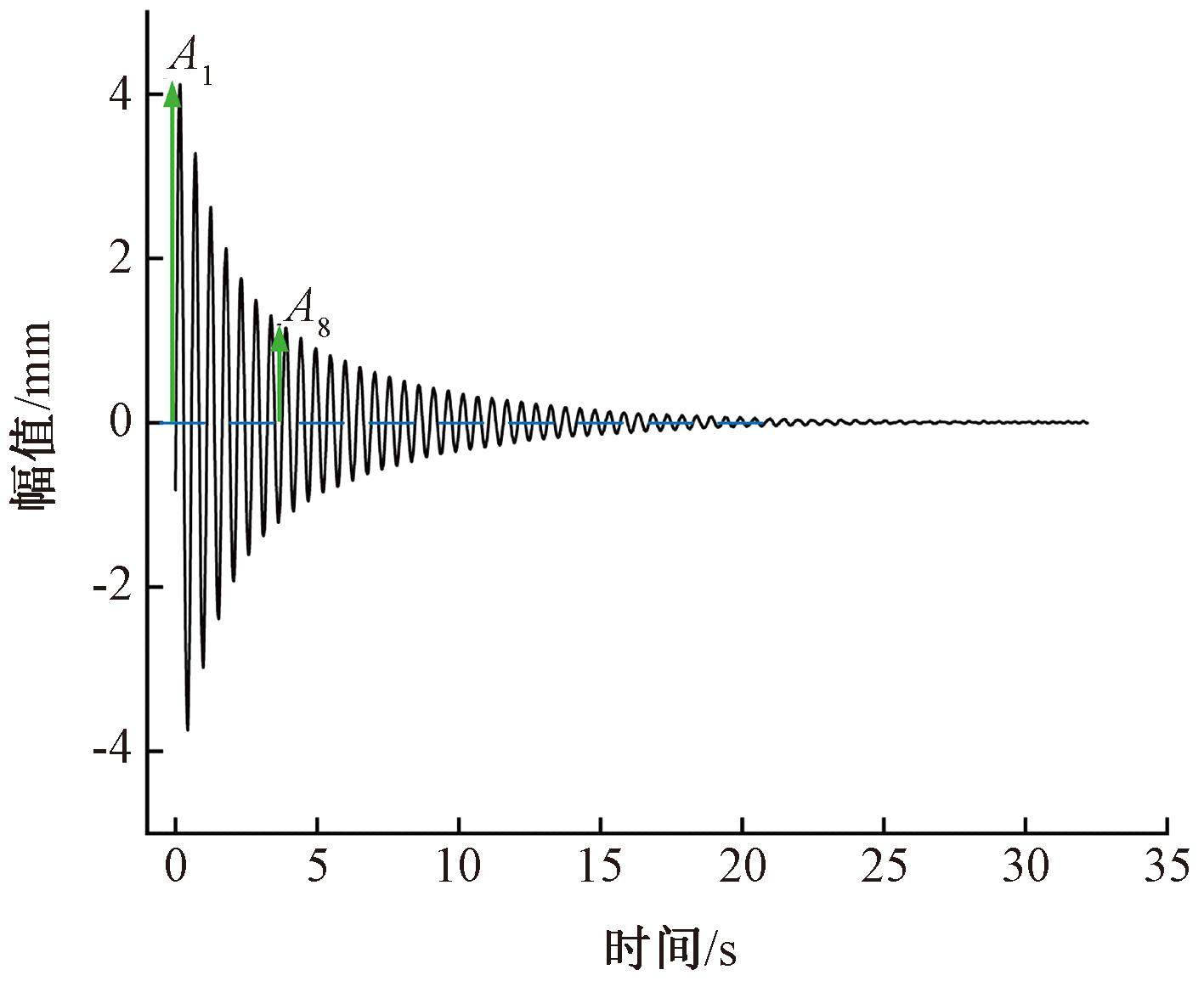
图5 未抑制的残余振动
Figure 5 Unsuppressed residual vibration
由测量结果可知一个振荡周期为0.557 s,由
可近似求出系统固有频率为11.28 Hz。
对于二阶系统,有
η=eξωnT1。
(14)
式中:
为幅值衰减系数。
为减少误差选取前8个幅值进行计算:
(15)
即
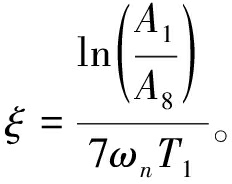
(16)
由测量结果可知A1=4.121 mm,A8=1.152 mm,可得ξ=0.029。
2.2 仿真分析
2.2.1 残余振动分析
利用MATLAB对引入SIS、ZV(zero vibration shaper)、ZVD(zero vibration and derivative shaper)和EI(extra insensitivity shaper)(Vtol=0.05)整形器后的残余振动进行仿真,对不同方法的时滞和抑振效果进行对比,步骤如图6所示。
图6 不同方法残余振动仿真步骤图
Figure 6 Step-by-step diagram of residual vibration simulation with different methods
梯形速度信号经过不同方法整形后的轨迹如图7所示,残余振动如图8所示。当系统固有频率和阻尼比准确时,ZV、ZVD和SIS整形器都可以立刻消除残余振动。
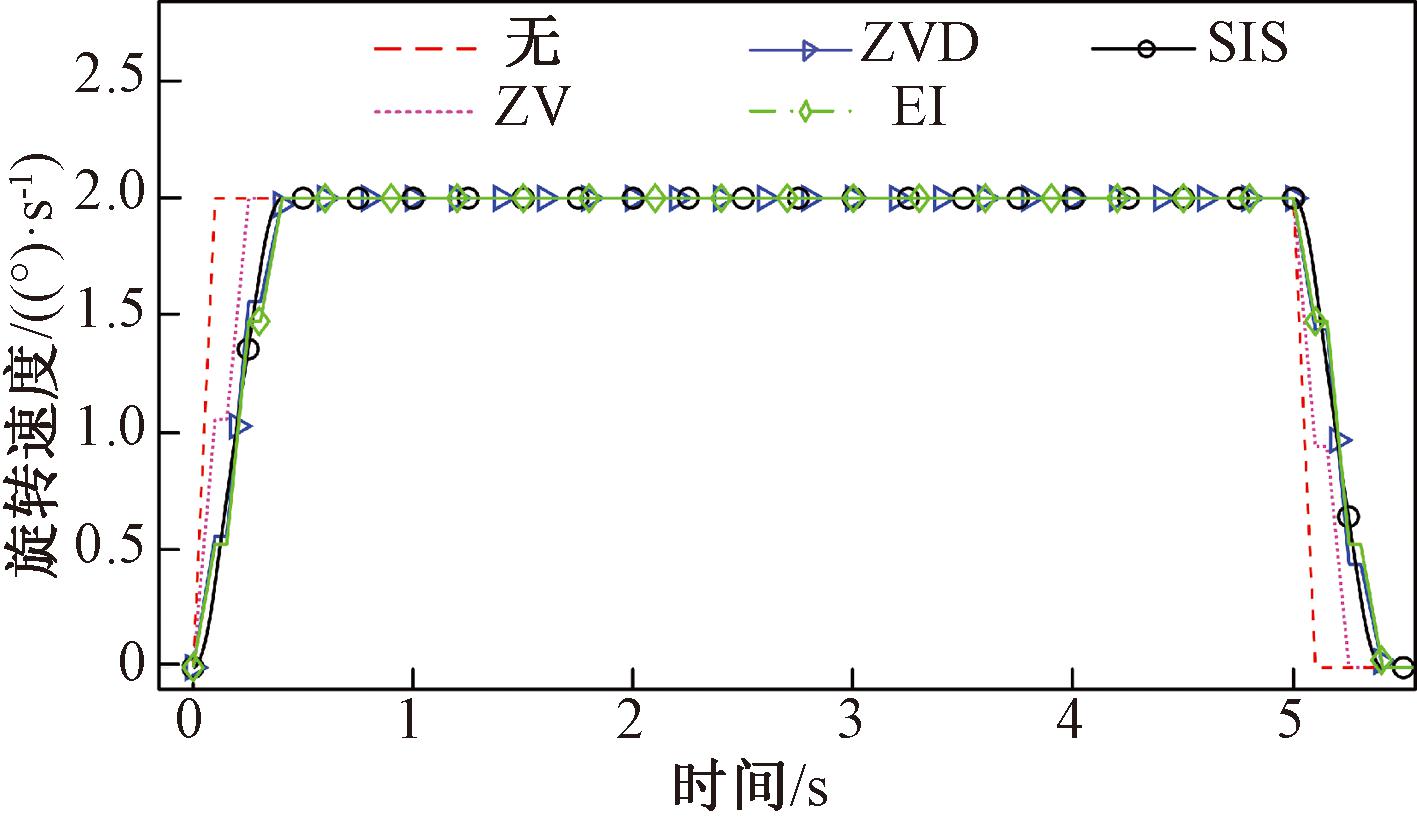
图7 梯形速度曲线经不同方法整形后的速度信号对比
Figure 7 Comparison of velocity signals of trapezoidal velocity profile shaped by different methods
图8 不同整形方法残余振动对比
Figure 8 Comparison of residual vibration of shaped by different methods
不同方案的时滞如表1所示。由表1可以看出,ZV延迟时间最短,为0.5个振动周期,其余方法延迟时间都为1个振动周期。
表1 不同方法引起的时滞表
Table 1 Delay table caused by different methods
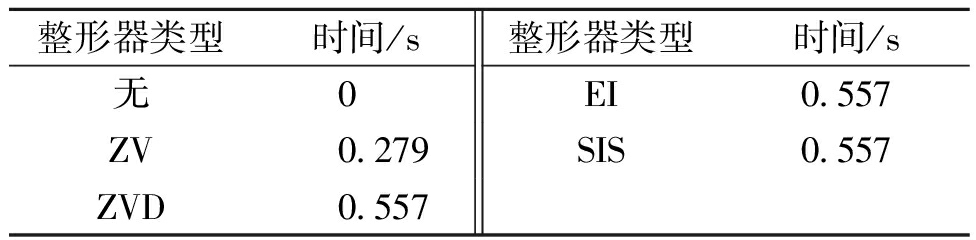
整形器类型时间/s整形器类型时间/s无0 EI0.557ZV0.279SIS0.557ZVD0.557
2.2.2 鲁棒性分析
由于系统实际尺寸较大,无法得到系统参数精确值,需要对整形器的鲁棒性进行分析。以阶跃信号为输入信号,分析比较不同整形器基于频率和阻尼比的灵敏度曲线,如图9所示,选取最大允许残余振动范围内包含的频率宽度和阻尼比宽度为标准,宽度越宽,整形器的鲁棒性越好。
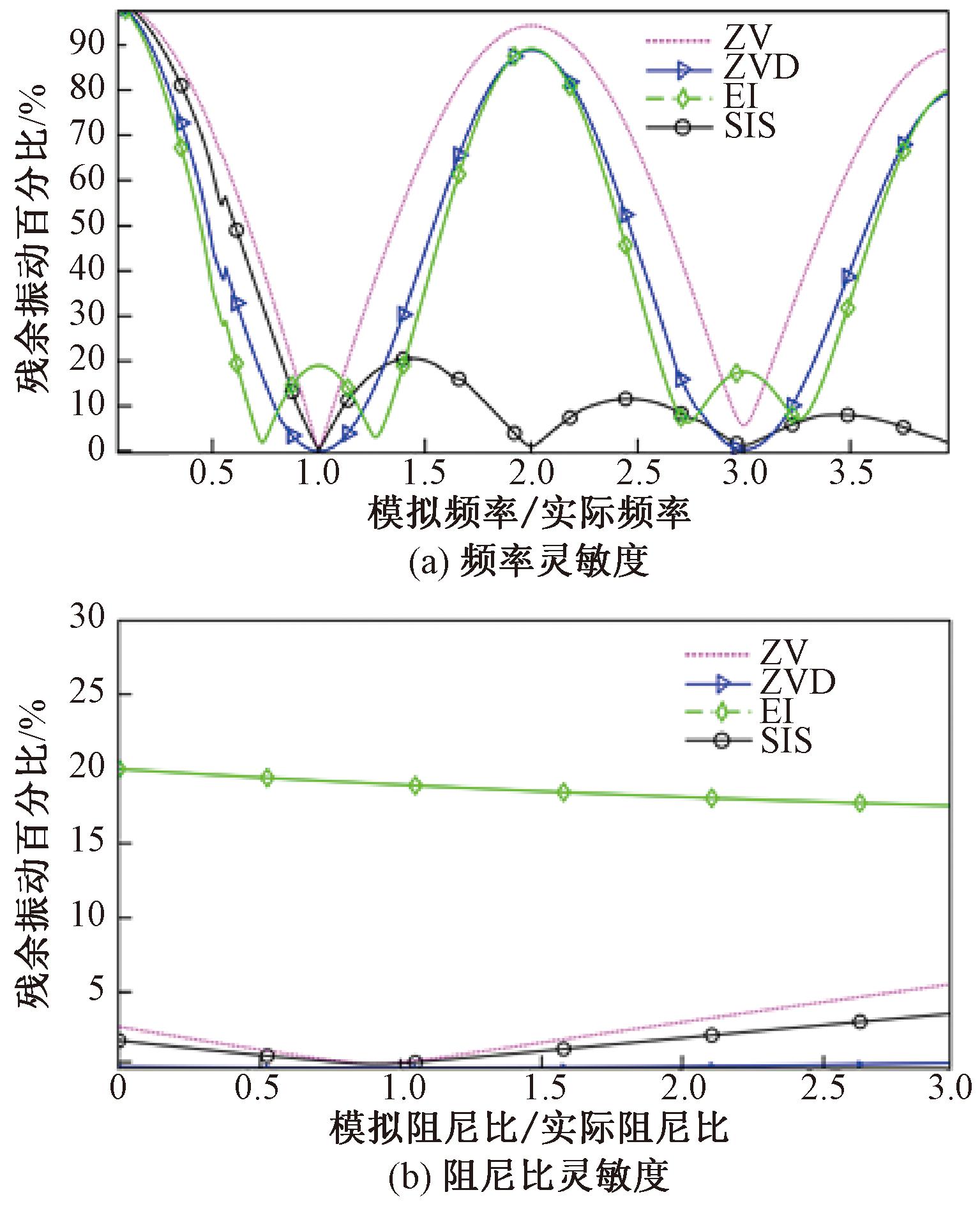
图9 4种方法灵敏度曲线
Figure 9 Sensitivity curves of the four methods
由图9(a)可知,在一定的残余振动百分比以内,SIS包含的频率宽度最宽,鲁棒性最好,之后依次是EI、ZVD、ZV。观察图9(b)可以发现,在一定的残余振动百分比以内,ZVD包含的阻尼比范围最广,鲁棒性最好,之后依次是SIS、ZV、 EI。
2.3 实验结果分析
当测量臂转至10°后,利用激光位移传感器对测量臂末端残余振动进行测量。当测量臂开始从上一个待测点向待测点旋转时,激光位移传感器开始记录数据,当传感器读数波动范围小于0.05 mm时停止记录(0.05 mm低于原始振幅最大峰值的5%),因此,以原始振幅最大峰值的5%为标准,统计不同方法振幅衰减到该标准的时间。
不同整形方法的残余振动如图10所示。由图10可以看出,当系统参数不够准确时,4种整形器对残余振动的峰值抑制效果不同。以原始信号残余振动最大振幅的5%为标准,对不同方法残余振动衰减到达标准所需的时间进行对比,如表2所示。
表2 不同方案残余振动峰值和衰减时间表
Table 2 Residual vibration peak and attenuation schedule of different schemes
整形器类型振动峰值/mm衰减时间/s无4.12113.266ZV1.2568.213ZVD1.2413.821EI0.6082.374SIS0.3451.912
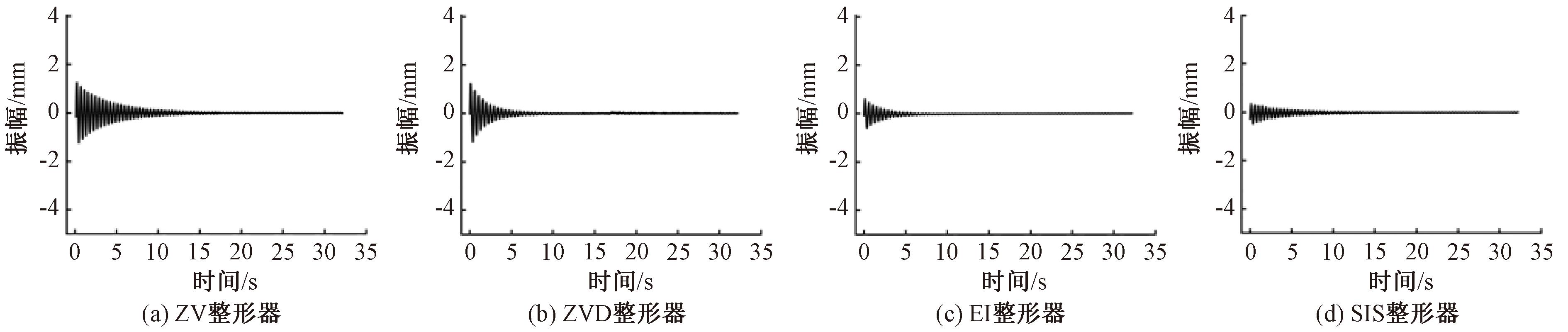
图10 不同整形方法的残余振动图
Figure 10 Residual vibration with different shaping methods
可以看出SIS对振动抑制的效果最好,振动峰值减小了91.6%,SIS的衰减时间减小了85.6%。
在青海羊曲水电站进行了现场测量,如图11所示,考虑到悬臂梁变形的问题,利用拉杆和水平仪使测量臂保持水平,进而消除悬臂梁变形引起的误差。进行定子圆度测量时,测量臂旋转速度为2°/s,两个测量点间距为9.23°,位移传感器测量方向为径向。对39个待测点至中心柱的距离进行测量,并分析测量数据,测量值的最大值与最小值的差值即为圆度,其测量原理如图12所示。
图11 现场测量图
Figure 11 Field measurement diagram
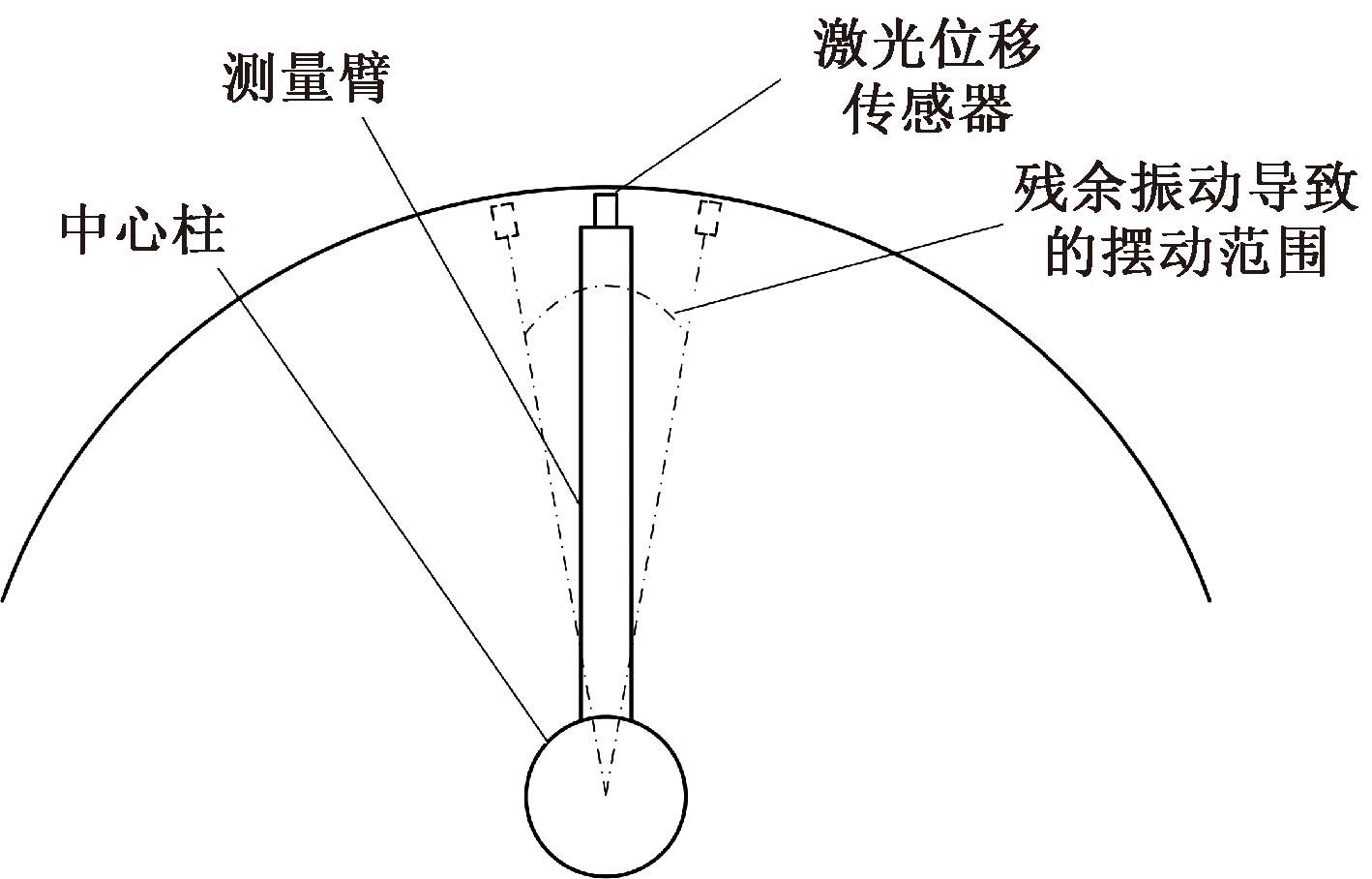
图12 现场圆度测量原理图
Figure 12 Schematic diagram of field roundness measurement
对不同方法下测量臂的振动衰减时间进行计算,记录振幅衰减到未整形时最大振幅的5%的时间,在此基础上增加1 s作为开始测量的时间。分别记录不同方案下,从第1个测量点开始,旋转至下一个测量点并完成测量的时间,如表3所示,可以看出SIS所用时间最短,整体测量时间减小了15.2 s,到达测量点后的振动衰减时间减少了87.9%。
表3 不同方案测量时间对比表
Table 3 Comparison table of measurement times for different programs
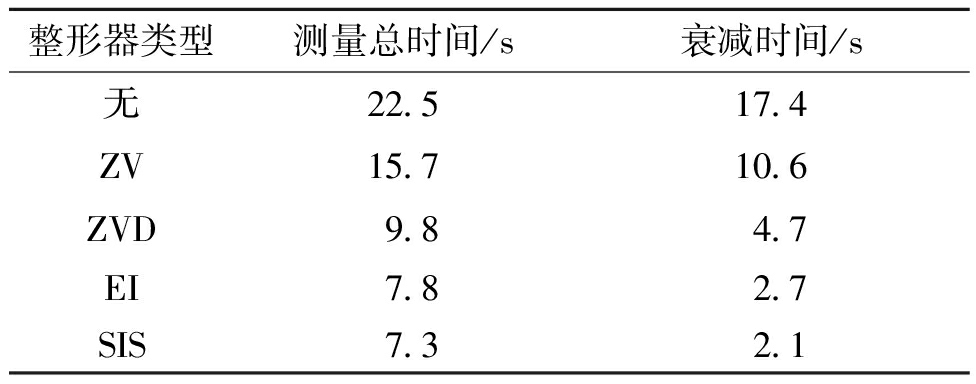
整形器类型测量总时间/s衰减时间/s无22.517.4ZV15.710.6ZVD9.84.7EI7.82.7SIS7.32.1
3 结论
本文针对水轮发电机定子圆度测量臂的残余振动进行了研究,提出采用光滑整形器对测量臂的残余振动进行抑制。
(1)SIS的鲁棒性优于传统整形器ZV、ZVD和EI,当系统参数不够准确时,SIS仍能维持较好的抑振效果,振动峰值减小了91.6%,衰减时间减小了85.6%。
(2)在青海羊曲水电站进行了现场测试,具备SIS整形器的定子测圆系统在保证精度的同时,将定子圆度测量时的振动衰减时间减少了87.9%,完成一个测量点测量的时间减小了15.2 s,完成一圈测量的时间减小了592.8 s,提高了测量效率。
(3)与闭环控制相比,SIS在工程应用方面操作简单,成本低,较为容易实现,可以适用于多数大型测量臂系统。
[1] 李欣业, 高赫远, 郭晓强, 等. 钻柱振动的主被动控制研究进展与展望[J]. 天然气工业, 2024, 44(6): 98-110.
LI X Y, GAO H Y, GUO X Q, et al. Research progress and prospect in active and passive control of drill string vibration[J]. Natural Gas Industry, 2024, 44(6): 98-110.
[2] 李小彭, 尚东阳, 陈仁桢, 等. 基于机械臂位姿变换的柔性负载伺服驱动系统控制策略[J]. 机械工程学报, 2020, 56(21): 56-69.
LI X P, SHANG D Y, CHEN R Z, et al. Control strategy of flexible load servo drive system based on manipulator position and position transformation[J]. Journal of Mechanical Engineering, 2020, 56(21): 56-69.
[3] 郑继周, 韩翔, 郭浩然, 等. 基于颗粒阻尼器的悬臂结构减振试验研究[J]. 农机化研究, 2022, 44(3): 137-141.
ZHENG J Z, HAN X, GUO H R, et al. Experimental study on vibration reduction of cantilever structure based on particle damper[J]. Journal of Agricultural Mechanization Research, 2022, 44(3): 137-141.
[4] 康建云, 毕果, 苏史博. 压电柔性机械臂系统辨识与振动主动控制[J]. 振动、测试与诊断, 2021, 41(1): 90-95, 202.
KANG J Y, BI G, SU S B. Experimental identification and active vibration control of piezoelectric flexible manipulator[J]. Journal of Vibration, Measurement &Diagnosis, 2021, 41(1): 90-95, 202.
[5] 文茜茜, 张弘毅, 陈政清, 等. 基于塔内位移观测器和均衡空间低维控制器的高塔结构振动主动控制系统[J]. 振动工程学报, 2024, 37(7): 1126-1138.
WEN X X, ZHANG H Y, CHEN Z Q, et al. Active control system of high tower based on displacement observer inside tower and low-dimension controller in equilibrium space[J]. Journal of Vibration Engineering, 2024, 37(7): 1126-1138.
[6] BERTA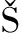 
, GOGA V, 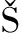ARK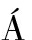
N L, et al. Active vibration damping of aluminum beam using piezoelectric actuator[C]∥Applied Physics of Condensed Matter (Apcom 2022). trbské Pleso: AIP Publishing, 2023: 2778-2787.
[7] HUANG Z C, HUANG F, WANG X G, et al. Active vibration control of composite cantilever beams[J]. Materials, 2022, 16(1): 95.
[8] D
AZ A, BELLO-ROBLES J C, FUENTES-AGUILAR R Q, et al. Control system for vibration attenuation in a flexible beam[C]∥2023 20th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE). Piscataway: IEEE, 2023: 1-6.
[9] 刘德馨, 张建成, 李媛, 等. 采摘机械臂自适应输入整形控制研究[J]. 控制理论与应用, 2022, 39(6): 1043-1050.
LIU D X, ZHANG J C, LI Y, et al. Research on adaptive input shaping control of fruits and vegetable harvesting robot arm[J]. Control Theory &Applications, 2022, 39(6): 1043-1050.
[10] 刘卓清, 孙宁, 吴易鸣, 等. 考虑状态约束的五自由度塔式吊车多目标最优轨迹规划[J]. 中国科学: 信息科学, 2022, 52(3): 521-538.
LIU Z Q, SUN N, WU Y M, et al. Multi-objective trajectory planning for 5-DOF underactuated tower cranes with state constraints[J]. Scientia Sinica (Informationis), 2022, 52(3): 521-538.
[11] 卢宁, 宋鹏程. 基于自适应S速度轨迹的塔式起重机变幅定位与防摆控制研究[J]. 机电工程, 2022, 39(1): 120-127.
LU N, SONG P C. Variable amplitude positioning and anti-swing control of tower crane based on adaptive S speed locus[J]. Journal of Mechanical &Electrical Engineering, 2022, 39(1): 120-127.
[12] GUO Z F, ZHANG J Q, ZHANG P S. Research on the residual vibration suppression of delta robots based on the dual-modal input shaping method[J]. Actuators, 2023, 12(2): 84.
[13] SUN X J, YE H, FEI S M. A closed-loop detection and open-loop control strategy for booms of truck-mounted concrete pump[J]. Automation in Construction, 2013, 31: 265-273.
[14] LEE S, PARK S, LEE W, et al. Input shaping algorithm using the s curve velocity command for gantry stage[C]∥2010 5th IEEE Conference on Industrial Electronics and Applications. Piscataway: IEEE, 2010: 656-661.
[15] BAUMGART M D, PAO L Y. Cooperative multi-input shaping for arbitrary inputs[C]∥Proceedings of the 2001 American Control Conference. Piscataway: IEEE, 2001: 275-280.
[16] FASIH S M, MOHAMED Z, HUSAIN A R, et al. Payload swing control of a tower crane using a neural network-based input shaper[J]. Measurement and Control, 2020, 53(7/8): 1171-1182.
[17] 刘灿. 基于自适应鲁棒控制方法的塔式起重机定位防摆相关研究[D]. 济南: 山东建筑大学, 2024.
LIU C. Research related to positioning and anti-swing of tower cranes based on adaptive robust control methods[D]. Jinan: Shandong Jianzhu University, 2024.
[18] 马瑞. 基于输入整形技术的桥式起重机吊具防摆控制研究[D]. 兰州: 兰州理工大学, 2024.
MA R. Research on anti-swing control of overhead crane spreader based on input shaping technology[D]. Lanzhou: Lanzhou University of Technology, 2024.
[19] BOSCARIOL P, RICHIEDEI D, TAMELLIN I. Residual vibration suppression in uncertain systems: a robust structural modification approach to trajectory planning[J]. Robotics and Computer-Integrated Manufacturing, 2022, 74: 102282.
[20] 梁杰, 孙震伟. 基于线激光的压缩机曲轴圆度和平面度测量[J]. 郑州大学学报(工学版), 2024, 45(4): 133-139.
LIANG J, SUN Z W. Line laser based roundness and flatness measurement of compressor crankshaft[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(4): 133-139.