由于无线信号的广播特性,雷达在感知目标过程中会面临感知安全问题,目标信息可能会被非法雷达窃取。为了使目标对非法雷达隐身,电磁隐身材料得到了广泛关注[1-2]。传统电磁隐身材料可以通过吸收入射信号能量来降低反射信号功率[3-4]。然而,由于涂层厚度、入射角度和材料固有特性的限制,电磁隐身材料在灵活性和适应性方面存在不足。
近年来,智能反射表面(intelligent reflecting surface,IRS)作为一种前景广阔的技术得到了工业界和学术界的广泛关注。IRS能够重塑无线传播环境来提升无线通信系统的容量和可靠性[5]。此外,IRS还可以辅助无线感知以提高对目标的感知精度[6-7]。Wang等[6]、Ma等[7]将IRS视为无线网络中的附加锚节点,以提高基站(base station,BS)的感知精度。但雷达信号在被BS接收机/雷达接收之前需要经过多次反射,存在一定程度的路径损耗,降低了对目标的感知效率和精度。
由于IRS具有增强期望接收端无线信号及抑制非期望接收端无线信号的能力,因此,IRS也可被用于无线感知系统以增强雷达感知[8-9]或削弱雷达感知使目标对雷达隐身[10-11]。相比于电磁隐身材料,IRS的关键优势是实时可重构性,弥补了电磁隐身材料的不足。Xiong等[10]在单个(unauthorized radar station,URS)场景下将IRS安装在目标上并与电磁隐身材料协同工作,提出了最小化非法雷达URS信噪比的优化问题。Zheng等[11]在多个URS场景下提出了最小化URS接收信号功率之和的优化问题。上述研究虽然可以实现目标对URS隐身,但同时也使得目标对合法雷达(legitimate radar station,LRS)隐身。Li等[12]提出了基于近端策略优化的子脉冲捷变方法,利用诱导子脉冲欺骗干扰机以提升雷达的抗干扰性能。Bai等[13]将研究扩展到多雷达对抗多干扰机场景,并采用重要性差异的强化学习方法生成抗干扰策略。Shao等[14]在单个URS和LRS的场景下提出了在保证URS接收信号功率上限约束的前提下,最大化LRS接收信号功率的优化问题。
但是,上述研究考虑的感知场景简单,在LRS和URS同时存在的场景下,随着URS数目的增加,会面临新的技术挑战:①URS之间可能存在协作,增加了IRS反射系数设计的复杂性;②IRS反射系数设计需要同时考虑多个非法雷达信号,导致优化问题求解难度显著增加。针对以上问题,本文提出了一种基于IRS的两阶段感知协议,其中IRS具备感知功能并部署于目标上。在第1阶段,IRS反射元件关闭,感知元件估计所有雷达的角度信息;在第2阶段,根据估计结果设计IRS反射系数。具体地,考虑到感知概率与接收信噪比之间的单调关系,在保证LRS信噪比约束以及IRS反射相移模约束的前提下,构建了一个最小化最大URS信噪比优化问题,并提出了一种基于Dinkelbach和半正定松弛(semidefinite relaxation,SDR)技术的迭代优化算法。首先,引入松弛变量将分数目标函数线性化,并利用Dinkelbach变换将分式约束转换为多项式表达式;其次,采用SDR技术松弛秩一约束,将问题转化为凸优化问题;最后,通过迭代更新辅助变量直至收敛。仿真结果表明:所提方案显著提升了无线感知系统的安全性能,并验证了在多URS场景下的鲁棒性和适应性。
1 系统模型
基于IRS辅助的雷达安全感知系统模型如图1所示,由一个LRS、K-1个URS和一个目标组成。目标表面安装了具有感知功能的IRS,用于反射来自雷达发送至目标的信号。通过设计IRS反射系数,可以分别优化其对LRS和URS的反射效果。此外,目标其余表面被电磁隐身材料覆盖[14],使LRS和URS仅能接收到IRS反射的信号,从而IRS可以对目标接收到的雷达信号进行完全控制。
图1 基于IRS辅助的雷达安全感知系统模型
Figure 1 IRS-based radar security perception system model
假设LRS和URS都是单静态雷达(其发射器和接收器位于同一位置),且均配备了由M=Mx·My根天线组成的均匀平面阵列(uniform planar array,UPA)。IRS配备N=Nx·Ny个反射元件。此外,为了估计雷达信号的到达角(angle of arrival,AoA),将l=lx+ly-1个感知器件集成到IRS中,lx和ly分别表示沿x轴和y轴的感知器件数量[15]。
假设t时刻非法雷达到IRS之间的信道矩阵为
时刻合法雷达到IRS之间的信道矩阵为
不失一般性,本文假设LRS/URS与IRS之间为LoS信道。
首先,将均匀线性阵列(uniform linear array, ULA)的一维导向矢量定义[11]为
(1)
式中:φ为相邻两根天线/单元的信号相移差;
为ULA中天线/单元的个数。
将IRS的AoA/AoD(到达角/离开角)对表示为
将LRS和URS的AoA/AoD对分别表示为
和
令
表示IRS的阵列响应向量;令
和
分别表示URS和LRS的阵列响应向量[11],则有
(2)
(3)
(4)
式中:λ为信号波长,m;Δe为IRS的元件间距,m;Δa为各雷达处的天线间距,m。
假设目标以恒定的速度v运动,并且信道链路受到多普勒频率影响,因此,雷达和IRS之间的远场LoS信道被建模为其两侧阵列响应向量的外积[10],即
(5)
式中: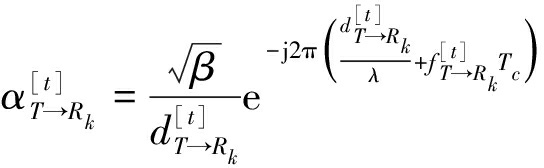
为t时刻对应的路径增益;β表示距离为1 m时的参考路径增益;
表示t时刻两节点之间距离,
为多普勒频率;Tc为信道相干间隔。
假设雷达与IRS之间的信道在相干时间内保持近似恒定,则
时刻的IRS反射系数向量
其中
和
分别表示第n个IRS元件的反射幅度和相移。因此,雷达k接收到的从IRS反射的信号可表示为
。
(6)
式中:Θ[t]=diag(θ[t])为t时刻IRS的相移矩阵;
为t时刻发射雷达波形,满足
且子载波数量P>M;GRk→s∈Cl×M为方差σ2的零均值加性高斯白噪声矩阵。
各信道相干时间内雷达感知过程[10]可表示为二元假设检验问题:
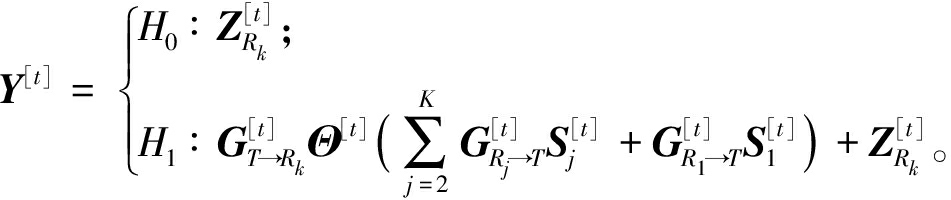
(7)
式中:H0和H1分别表示目标不存在和目标存在。
把感知目标是否存在的问题转化为二元假设问题,用NP准则(给定t时的信噪比ψ[t]和虚警概率
要求探测概率
最大)对此二元假设问题进行最优决策。根据NP准则,探测概率[10]为
(8)
式中:Q(·)为Marcum-Q函数。
对于给定的更高的信噪比将导致更高的目标检测概率。考虑到式(8)中信噪比与探测概率之间的单调关系,将信噪比作为评价系统性能的指标。
本文假设URS之间存在协作,USR和LRS直接非协作,则URS和LRS接收的信噪比可分别表示为
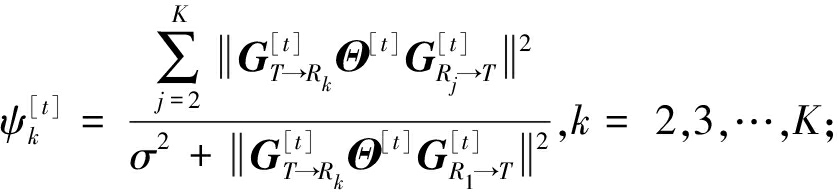
(9)
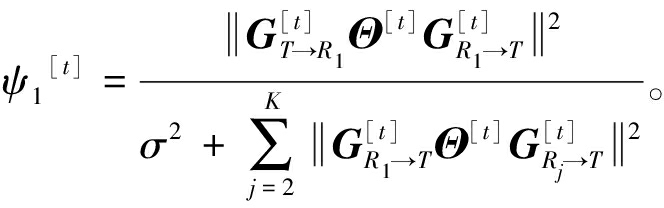
(10)
2 感知协议
本文提出的基于IRS的两阶段感知协议如图2所示,该协议定义了一个相干时间感知块,目标和雷达的位置和方向在信道相干时间感知块内保持恒定,而在不同块内可能发生变化[9]。每个感知块分为两阶段,第1阶段:IRS反射元件关闭,根据IRS感知元件收到的信号估计所有雷达的角度信息;第2阶段:根据估计的信息,设计IRS的反射系数。
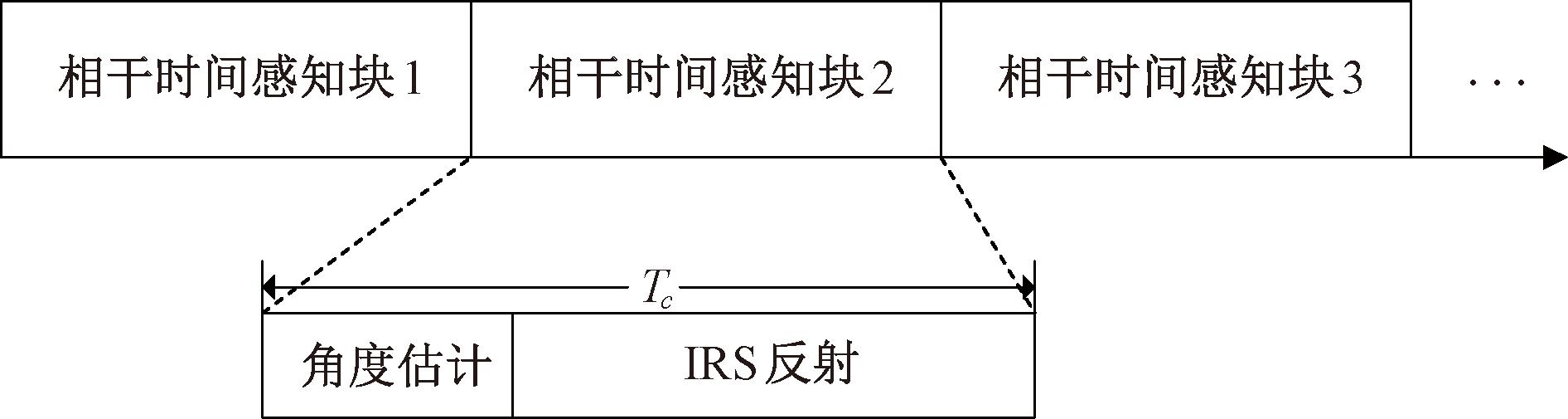
图2 基于IRS的两阶段感知协议
Figure 2 IRS-based two-stage perception protocol
在第1阶段,IRS反射元件关闭,在IRS上嵌入了一个由l=lx+ly-1个感知器件组成的L形阵列,使其用于估计所有雷达的K个角度信息。
表示感知元件的阵列响应向量[16],矢量as,x和as,y分别为
(11)
(12)
L形感知阵列与雷达k之间的信道可表示为GRk→s∈Cl×M,被建模为其两侧阵列响应向量的外积。在信道相干时间内(省去时间索引[t])L形感知阵列接收到的信号为
T→Rk,φT→Rk)S+Zs=
[as(R1→T,φR1→T),…,as(Rk→T,φRk→T)]·
T→Rk,φT→Rk)S]T+Zs=
AsF+Zs。
(13)
式中:
为方差σ2的零均值加性高斯白噪声矩阵;As∈Cl×K为L形感知阵列的阵列响应矩阵;F=[F1,F2,…,FK]T为K个雷达的发射波束形成信号矩阵,
T→Rk,φT→Rk)S,k=1,2,…,K;S=[s1,s2,…,sp]为该时刻的发射雷达波形,满足E[SSH]=IM且P>M。
基于式(13),现有的AoA估计算法如多重信号分类算法[17]可用于AoA对(Rk→T,φRk→T),k=1,2,…,K的估计。
在第2阶段,根据上述估计的角度信息,设计IRS的反射系数,从而增强LRS接收信噪比的同时降低URS接收的信噪比。
3 问题的提出和求解
3.1 问题提出
为提高IRS辅助无线感知系统的安全性,在保证LRS信噪比约束以及IRS反射相移模约束条件下,本文通过优化IRS反射系数,最小化最大URS的信噪比,以尽可能降低URS窃听的信息。此外,本文以感知块为单元进行处理,因此删除时间索引[t],相应的优化问题可以表示为
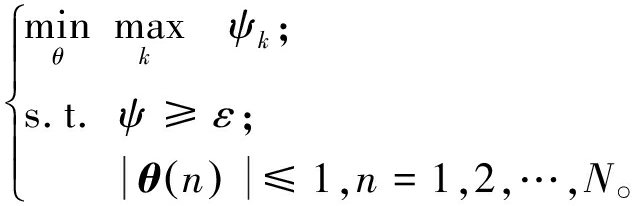
(14)
式中:ε为LRS为实现目标感知性能所需的最小信噪比。利用雷达与目标之间的信道结构可以对式(9)和式(10)中的信噪比表达式进行简化,将式(5)代入式(9)和式(10),则URS和LRS的信噪比分别为
(15)
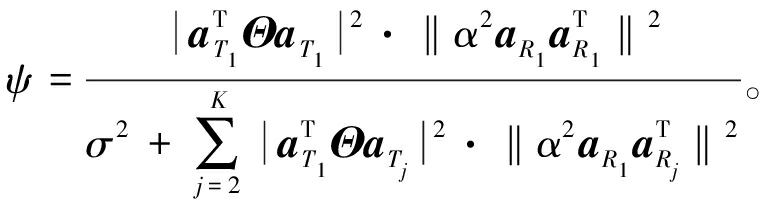
(16)
式中:aR1=aR1(T→R1,φT→R1),aRk=aRk(T→Rk,φT→Rk);aT1=aR1(R1→T,φR1→T),aTk=aRk(Rk→T,φRk→T)且
均为常数,式(14)可化简为
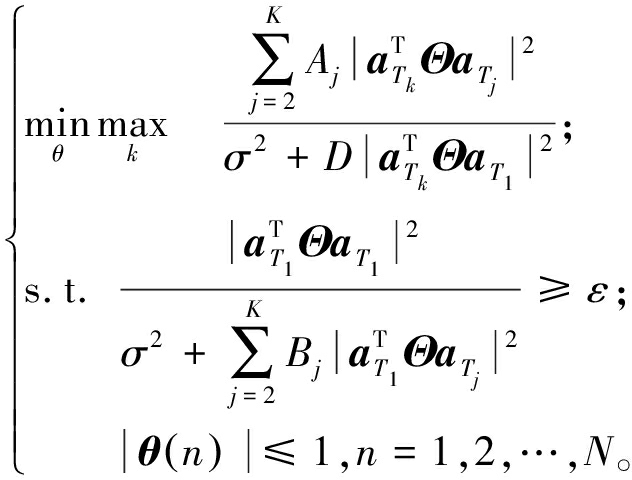
(17)
式(17)为典型的非凸优化问题。为了求解该问题,提出了一种基于Dinkelbach和SDR技术的迭代优化算法进行求解。
3.2 问题求解
式(17)进一步简化为
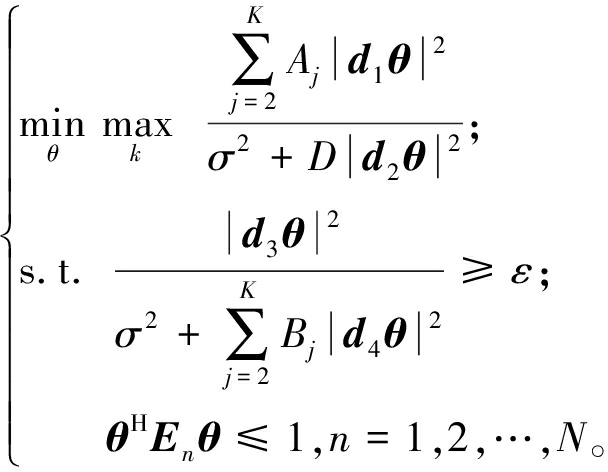
(18)
式中:
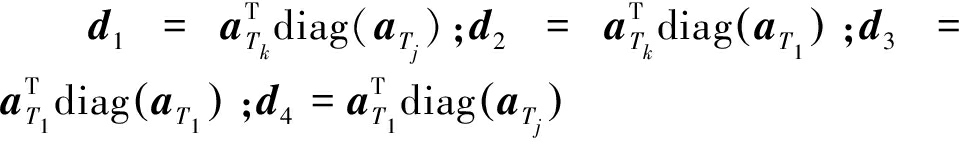
为级联阵列响应;En∈CN×N表示第n个对角线元素为1,其余元素为0的选择矩阵。
引入一个松弛变量z,将问题重新表述为如下形式[18]:
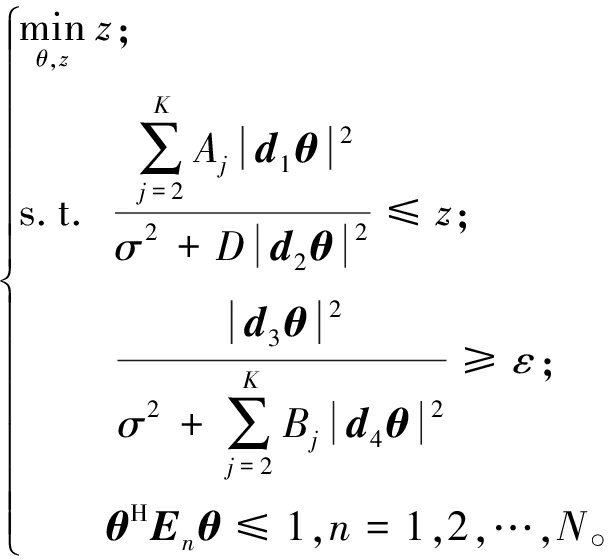
(19)
上述问题仍然难以解决。注意到式(19)与最大-最小比分数规划问题具有相似的形式[19],可以应用Dinkelbach变换将其转化为更易于处理的形式[18]。具体来说,第1个分式约束可以转换成一个多项表达式。通过引入一个辅助变量qk,其本质上表示第k个URS的信噪比ψk,并且可以用反射系数向量θ对其进行更新。qk的最优值为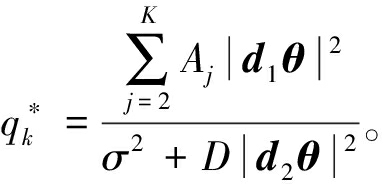
优化问题可以进一步表示为
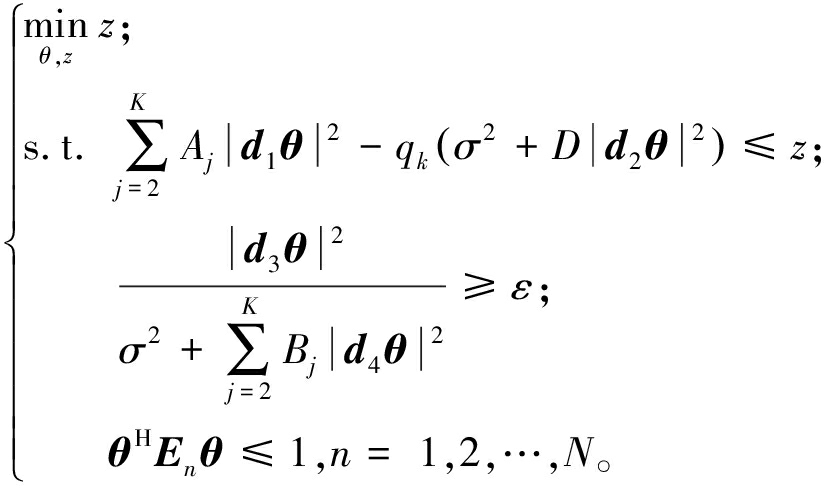
(20)
通过定义X=θθH将二次项θθH转化为主变量X。同时,秩为1的埃尔米特半正定矩阵X满足
(21)
定义所有N×N维埃尔米特半正定矩阵的集合为SN
{S|S=SH,S≥0},将式(20)转化为
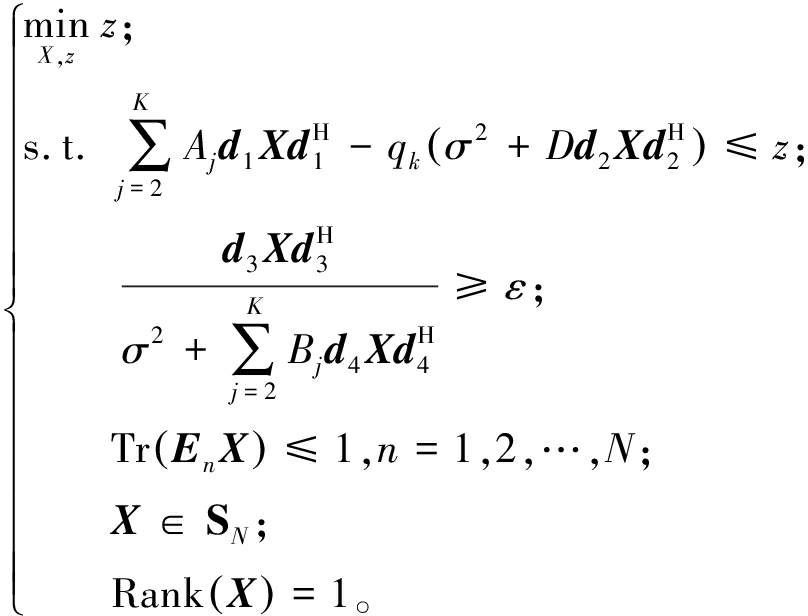
(22)
采用SDR算法,原问题可简化为
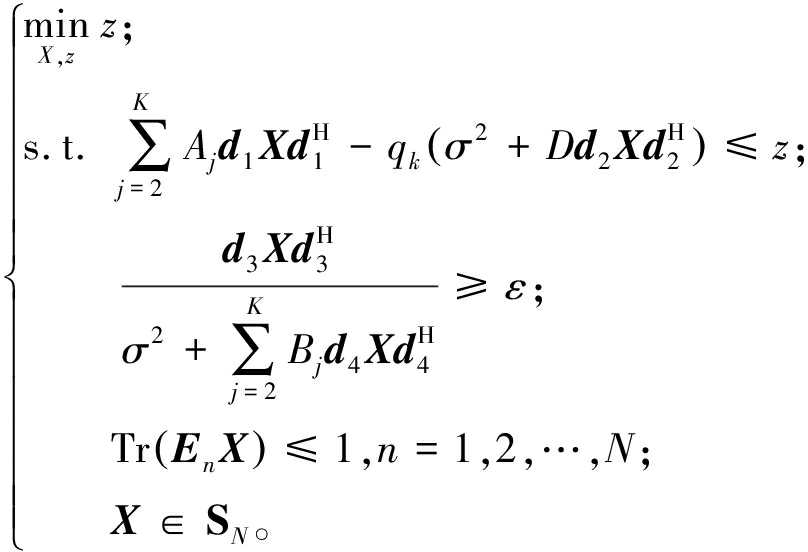
(23)
上述为一个半正定规划问题,可以使用CVX工具箱直接得到最优解X。当X的秩不为1时,通常使用EVD分解或高斯随机化来得到最优解θ*。
基于Dinkelbach和SDR技术的迭代优化算法如算法1所示,上标(·)表示算法的某次迭代。设置收敛阈值参数为ξ,最大迭代次数为Rmax。
算法1 基于Dinkelbach和SDR的迭代优化算法。
输入:Aj,D,Bj,d1,d2,d3,d4,ε;
输出:θ*。
① 初始化
② 迭代次数r=0
③
④
⑤ 由式(23)更新X(r+1)
⑥ 对X(r+1)进行EVD分解得到θ(r+1)
⑦
⑧ r=r+1
⑨ end while
⑩ 得到 θ*=θ(r)
3.3 收敛性和复杂度分析
(1)收敛性。将η(θ)表示为原始问题式(18)的目标值。在IRS反射系数设计中,引入一个辅助变量qk并应用Dinkelbach转换为问题式(20)。由于 Dinkelbach 算法的单调性,辅助变量qk单调递减,很容易证明算法的收敛性[20]。
η(θ(r))≥η(θ(r+1))。
(24)
式(24)表明式(18)的目标值在算法迭代的过程中递减,又因为式(18)的目标值大于零,所以可以收敛到局部最优点。
(2)复杂度。问题(式(23))是一个凸优化问题,涉及 一个 N×N 维变量需要优化,含K个二阶约束和 N+1 个线性矩阵不等式约束。使用 CVX 求解器时,计算复杂度为
为收敛阈值。更新 qk的计算复杂度为 O(N+K),更新θ的计算复杂度为O(N3)。因此,所提算法的总计算复杂度为 
为迭代次数。
4 仿真结果
本节通过MATLAB软件仿真分析所提方案的性能。为简化仿真,假设LRS、URS和IRS均为均匀线性阵列(ULA)。IRS辅助多雷达的感知模拟场景如图3所示。通用仿真参数如表1所示,其他仿真参数设置如下:URS的个数为3;IRS的反射元件和感知元件个数分别为N=49, l=13;URS与目标的最短距离d_UT=30 m。在所有的仿真中,令URS的信噪比代表3个URSs的信噪比之和。首先,假设IRS感知器件对LRS和URS到目标IRS的AoA进行了完美估计;然后,评估了其他非完美估计对雷达性能的影响。
表1 仿真参数
Table 1 Simulation parameters
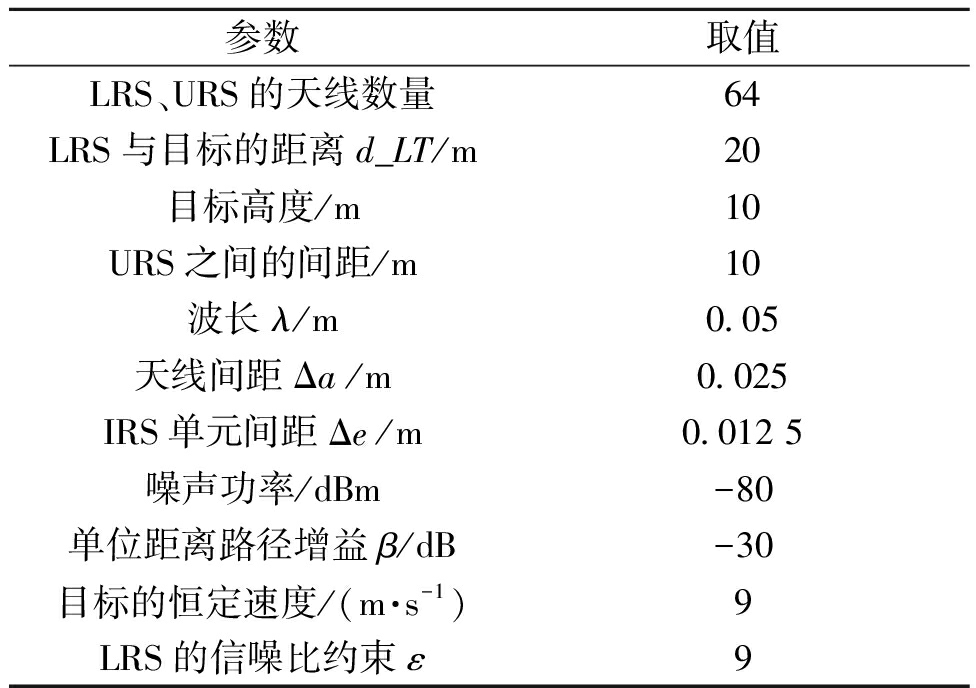
参数取值LRS、URS的天线数量64LRS与目标的距离d_LT/m20目标高度/m10URS之间的间距/m10波长λ/m0.05天线间距Δa/m0.025IRS单元间距Δe/m0.012 5噪声功率/dBm-80单位距离路径增益β/dB-30目标的恒定速度/(m·s-1)9LRS的信噪比约束ε9
图3 IRS辅助多雷达的感知模拟场景(2D视图)
Figure 3 IRS-assisted perception simulation scenarios for multi-radar(2D view)
本文将所提方案与以下两种基准方案进行对比分析:①随机相移,假设每个IRS反射元件独立且均匀分布在[0,2π);②目标未安装IRS,也未安装任何反射元件。
图4描绘了LRS信噪比与反射元件数量N的关系。首先,所提方法随着IRS元件数量增加,LRS接收信噪比也随着增大,这是因为在IRS中安装更多反射元件可以增强被动波束形成增益;其次,该方案在增大接收信噪比方面优于无IRS和随机相移方案;最后,随机相移设计下的信噪比随IRS元件数量的增加而降低。这表明,如果 IRS 反射的信号设计不当,使用 IRS 获得的性能甚至比不使用 IRS 时更差。
图4 LRS信噪比与反射元件数量N的关系
Figure 4 Relationship between the signal-to-noise ratio of LRS and the number of reflecting element N
在图5中,只改变URSs到目标的距离,绘制了LRS/URS信噪比与URSs到目标的最短距离的关系图。由图5可知,在较宽的距离范围内,与目标未安装IRS的情况相比,目标安装IRS可以显著减少URS接收信噪比,同时增加LRS接收信噪比。
图5 LRS/URS 信噪比与URSs到目标的最短距离的关系
Figure 5 Relationship between the LRS/URS signal-to-noise ratio and the shortest distance from the URS to the target
图6为IRS感知元件角度估计误差对LRS/URS信噪比的影响。随着AoA估计误差的增加,LRS信噪比降低,URS信噪比增大。这表明AoA估计误差会降低IRS的信号叠加/抵消能力。但如果角度估计误差低于1°(对应于100 m雷达-目标距离的误差小于1.7 m)时,则性能损失较小。
图6 AoA估计误差对LRS/URS信噪比的影响
Figure 6 Effect of angle estimation error of AoA on LRS/URS signal-to-noise ratio
本文评估了URS数目对LRS/URS信噪比的影响,如图7所示。与目标未安装IRS情况相比,安装IRS能够显著降低URS信噪比,同时提升LRS信噪比。且随着URSs数量增加,所提方案下LRS信噪比和URS信噪比变化较为缓慢。这表明,所提方案能够在多雷达场景下有效提升LRS的感知性能,同时抑制URS的感知能力。随着URS数目增加,系统表现出较强的鲁棒性和适应性。
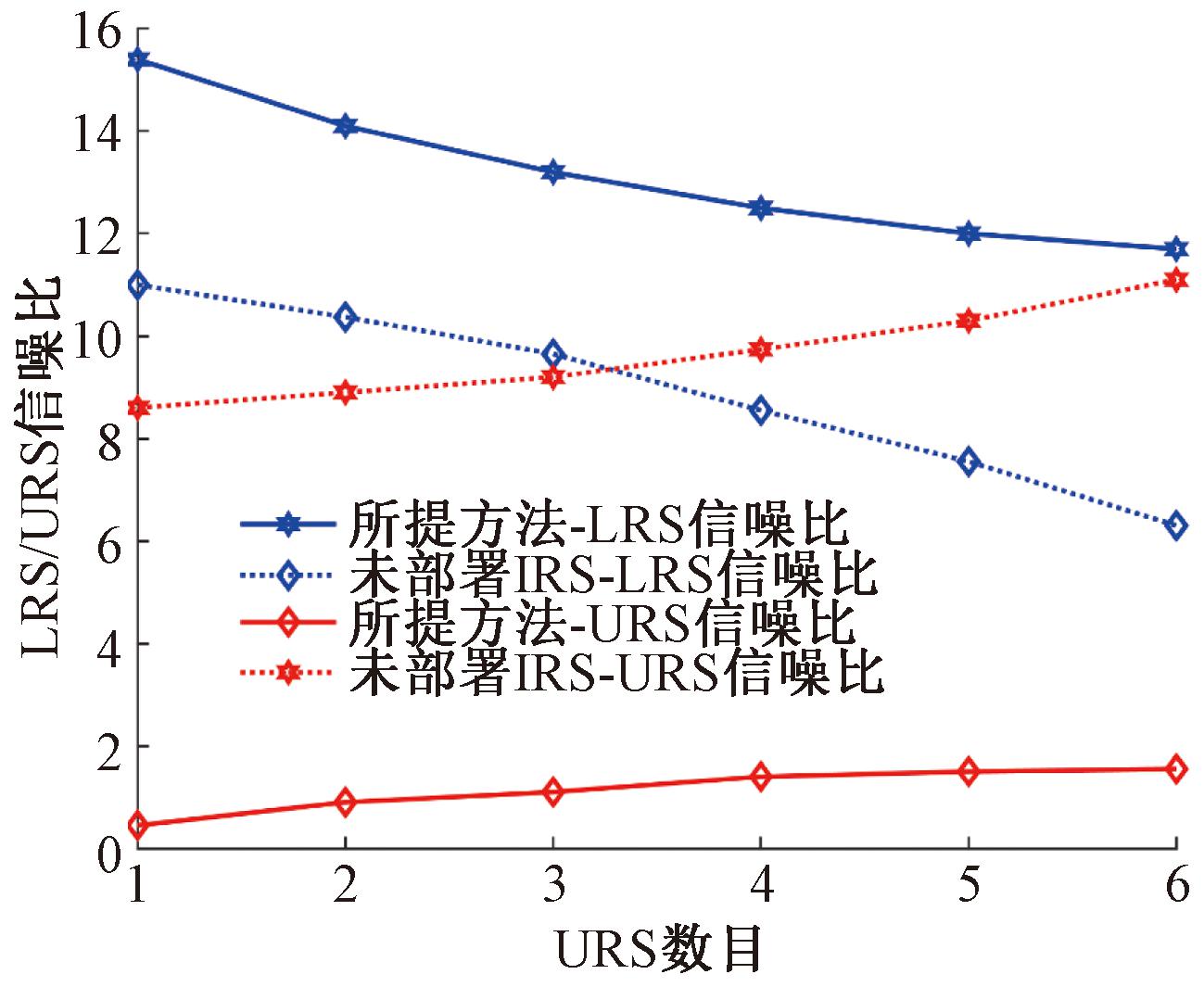
图7 URS数目对LRS/URS信噪比的影响
Figure 7 Effect of URS number on LRS/URS signal-to-noise ratio
5 结论
针对多雷达场景下无线感知系统的安全问题,提出了一个基于IRS辅助的安全无线感知系统,利用IRS增强LRS感知能力的同时减弱URS的感知能力。将具有感知功能的IRS部署于目标上,提出了两阶段感知协议。证明了雷达感知概率与接收信噪比之间的单调关系,将信噪比作为评价系统性能的指标。在保证LRS信噪比约束以及IRS反射相移模约束的条件下,通过优化IRS的反射系数,最小化最大URS信噪比。由于所构建的优化问题非凸,提出一种迭代优化算法进行求解。仿真结果表明所提方案可以极大提高合法雷达感知的安全性。
[1] PATTANAIK B, CHAUHAN A. A study of stealth technology[J]. Materials Today: Proceedings, 2023, 81: 543-546.
[2] AHMAD H, TARIQ A, SHEHZAD A, et al. Stealth technology: methods and composite materials: a review[J]. Polymer Composites, 2019, 40(12): 4457-4472.
[3] KHAN T A, LI J X, CHEN J, et al. Design of a low scattering metasurface for stealth applications[J]. Materials, 2019, 12(18): 3031.
[4] WANG W, LIU D Q, CHENG H F, et al. Structural design and broadband radar absorbing performance of multi-layer patch using carbon black[J]. Advanced Composites and Hybrid Materials, 2022, 5(4): 3137-3145.
[5] 郭歆莹, 刘龙飞, 朱春华. RIS辅助无人机通信系统波束赋形双重循环优化算法[J]. 郑州大学学报(工学版), 2025, 46(2): 67-74.
GUO X Y, LIU L F, ZHU C H. Beamforming dual-loop optimization algorithm for RIS-assisted UAV communication systems[J]. Journal of Zhengzhou University (Engineering Science), 2025, 46(2): 67-74.
[6] WANG F Z, LI H B, FANG J. Joint active and passive beamforming for IRS-assisted radar[J]. IEEE Signal Processing Letters, 2021, 29: 349-353.
[7] MA T, XIAO Y, LEI X, et al. Distributed reconfigurable intelligent surfaces assisted indoor positioning[J]. IEEE Transactions on Wireless Communications, 2023, 22(1): 47-58.
[8] SHAO X D, YOU C S, MA W Y, et al. Target sensing with intelligent reflecting surface: architecture and performance[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(7): 2070-2084.
[9] WANG P L, MEI W D, FANG J, et al. Target-mounted intelligent reflecting surface for joint location and orientation estimation[J]. IEEE Journal on Selected Areas in Communications, 2023, 41(12): 3768-3782.
[10] XIONG X, ZHENG B X, SWINDLEHURST A L, et al. A new intelligent reflecting surface-aided electromagnetic stealth strategy[J]. IEEE Wireless Communications Letters, 2024, 13(5): 1498-1502.
[11] ZHENG B X, XIONG X, TANG J, et al. Intelligent reflecting surface-aided electromagnetic stealth against radar detection[J]. IEEE Transactions on Signal Processing, 2024, 72: 3438-3452.
[12] LI K, JIU B, WANG P H, et al. Radar active antagonism through deep reinforcement learning: a way to address the challenge of mainlobe jamming[J]. Signal Processing, 2021, 186: 108130.
[13] BAI L H, JIU B, LI K, et al. Importance differentiation based coordinated anti-jamming strategy optimization for frequency agile radar[C]∥2023 IEEE International Radar Conference (RADAR). Piscataway: IEEE, 2023: 1-5.
[14] SHAO X D, ZHANG R. Target-mounted intelligent reflecting surface for secure wireless sensing[J]. IEEE Transactions on Wireless Communications, 2024, 23(8): 9745-9758.
[15] WU Q Q, ZHANG S W, ZHENG B X, et al. Intelligent reflecting surface-aided wireless communications: a tutorial[J]. IEEE Transactions on Communications, 2021, 69(5): 3313-3351.
[16] CHEN H F, CHEN W J, WANG Y, et al. A low computational cost lightning mapping algorithm with a nonuniform L-shaped array: principle and verification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 4106410.
[17] CAI J J, ZHANG H Y, LIU W, et al. A derivative-based music algorithm for two-dimensional angle estimation employing an L-shaped array [EB/OL].(2021-04-22)[2025-02-15]. https:∥ieeexplore.ieee.org/document/9408790.
[18] LU W D, DING Y, FENG Y Q, et al. Dinkelbach-guided deep reinforcement learning for secure communication in UAV-aided MEC networks [EB/OL].(2023-01-11)[2025-02-15]. https:∥ieeexplore.ieee.org/document/10001574.
[19] SHEN K M, YU W. Fractional programming for communication systems: part I: power control and beamforming[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2616-2630.
[20] CROUZEIX J P, FERLAND J A. Algorithms for generalized fractional programming[J]. Mathematical Programming, 1991, 52(1): 191-207.