提高新能源在总能源结构中的占比成为实现“双碳”目标的重要手段。其中太阳能因其再生性、环保性及广泛可用性,成为可持续发展的关键能源选择。然而,光伏发电因其自身特性及外部环境影响,表现出显著的随机性、间歇性与波动性,这在并网过程中对电网的稳定性构成了较大挑战。为提高电能质量,光伏发电系统中配置储能已成为行业标准,尤其在可再生能源发电侧有广泛应用。蓄电池具有高能量密度和可以长时间储存电能的优点,但功率密度低、循环寿命短;超级电容器具备高功率密度、长循环寿命以及快速充放电的优点,但能量密度低。所以可将蓄电池与超级电容器混合使用,作为光伏发电系统的储能方案[1],可以有效补偿预测误差和平抑出力波动[2]。
闫群民等[3]采用完全集合经验模态分解和希尔伯特变换初步分配混合储能系统的内部功率,利用均衡管理方法修正其衰减后,再进行修正参考功率的容量配置。马超等[4]为优化配置多个光伏组件组合电站的混合储能容量,提出一种融合统计分析与数学模型的配置方法。李相俊等[5]通过分析日前光伏出力预测误差曲线的置信水平,确定储能的额定功率和容量。余洋等[6]针对电池储能系统进行光伏波动平抑时寿命损耗高及荷电状态一致性差的问题,提出了光伏波动平抑下改进K-means的BESS动态分组控制策略。上述文献多直接使用历史或预测出力数据作为次日调度值,这不仅误差较大,还难以满足并网计划。段俊东等[7]提出了一种基于经验模态分解(empirical mode decomposition,EMD)的储能系统(energy storage systems,ESS)容量优化方法。通过EMD处理DG配网功率样本,结合ESS运行效率和荷电状态约束,确定了ESS的最小容量需求。陈阳等[8]提出了一种针对预测误差补偿和平滑并网功率波动的双层优化模型,但未考虑储能容量成本,仅使用电池作为储能元件,忽视了混合储能系统中超级电容的应用。
为解决这些问题,本文构建了一种双层规划模型,目标是补偿光伏预测误差、平稳并网功率波动,并最小化等年值成本。首先,对光伏出力进行预测;其次,上层模型以等年值成本最小为目标,其由系统的投资成本、设备更换成本、维护成本、碳排放效益成本构成;再次,采用模糊遗传粒子群算法建立不同性质充放电功率分配策略,以补偿光伏预测误差和平滑功率波动;最后,通过模型评估验证策略的有效性,并检验储能容量配置的合理性。
1 储能系统结构及其发电特性
在实际应用中,光伏出力因天气因素(如辐照度、温度、湿度)而波动且不确定[9],因此为了便于提高系统稳定性通常进行短期或超短期预测[10],但预测结果与实际情况经常存在偏差。为此,采用混合储能系统来补偿预测误差[11],并尽量平抑并网功率波动[12]。光伏发电系统如图1所示。
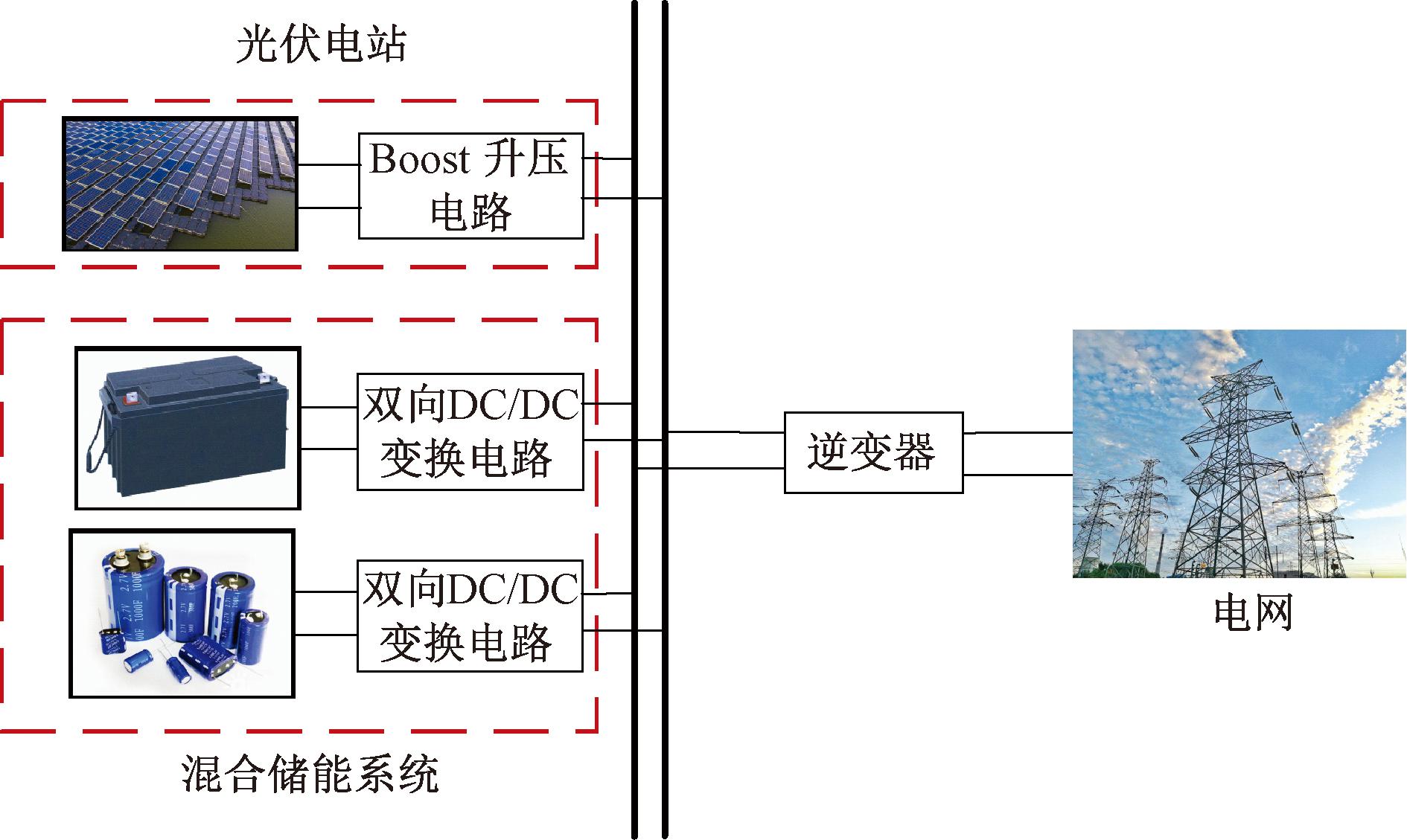
图1 光伏发电系统
Figure 1 Photovoltaic power generation system
由图1可知,光伏发电系统由光伏电站、混合储能系统组成。光伏电站由光伏电池板通过Boost升压电路组成,连接至直流母线;混合储能系统由蓄电池和超级电容与双向DC/DC变换电路组成,接入直流母线,通过逆变器与电网相连。
在多目标规划问题中,双层规划问题最为常见。在双层规划中,上层决策会影响下层行为,并对下层目标的实现产生部分影响,但无法完全控制下层的选择。下层在上层决策的限制下拥有自主权,其结构如图2所示[13]。
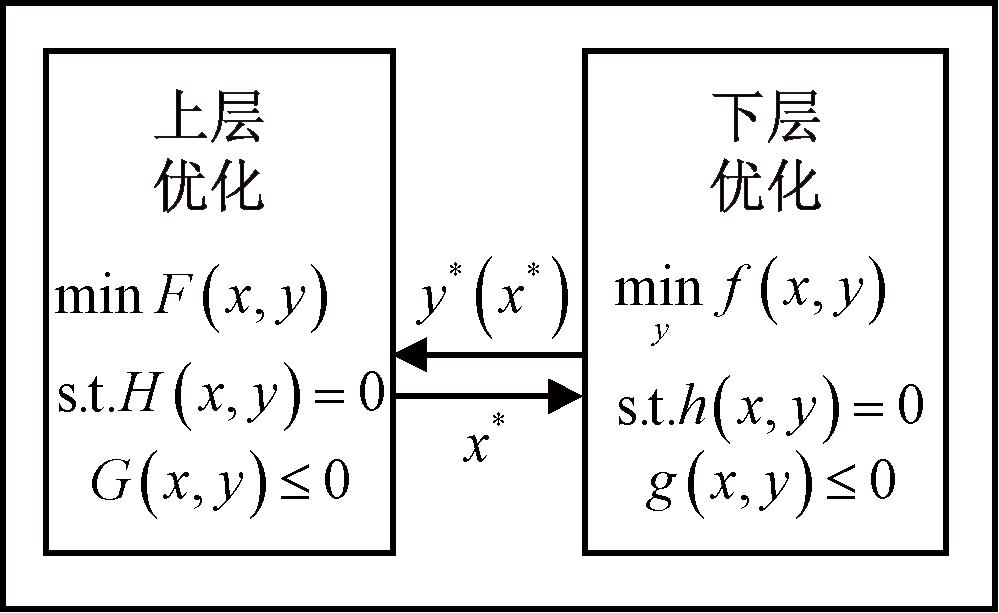
图2 双层优化结构
Figure 2 Double-layer optimized structure
在双层优化模型中,F和f为不同的目标函数,H、G、h和g为约束条件。x和y为上层优化的决策变量,但x在下层中作为参数。因此,双层优化模型是一个由另一个优化问题制约的模型,通常难以确保获得全局最优解,但在满足一定条件下,可以认为达到了全局最优。
2 双层模型控制策略
2.1 双层规划模型
针对光伏出力预测存在误差以及并网波动率高等问题,在等年值成本下优化混合储能容量,以补偿预测误差和平滑功率波动,建立了双层规划模型。上层模型目标是最小化等年值成本,决策变量为超级电容与蓄电池的容量配置;下层模型目标是最小化预测误差和并网波动率,决策变量为超级电容与蓄电池的荷电状态功率。通过考虑5种环境因素(天气温度、天气相对湿度、全球水平辐射、漫反射水平辐射和降雨量),利用基于二次模态分解和核主成分分析双向长短期记忆神经网络的光伏功率预测,预测模型流程图如图3所示。双层模型流程框图如图4所示。
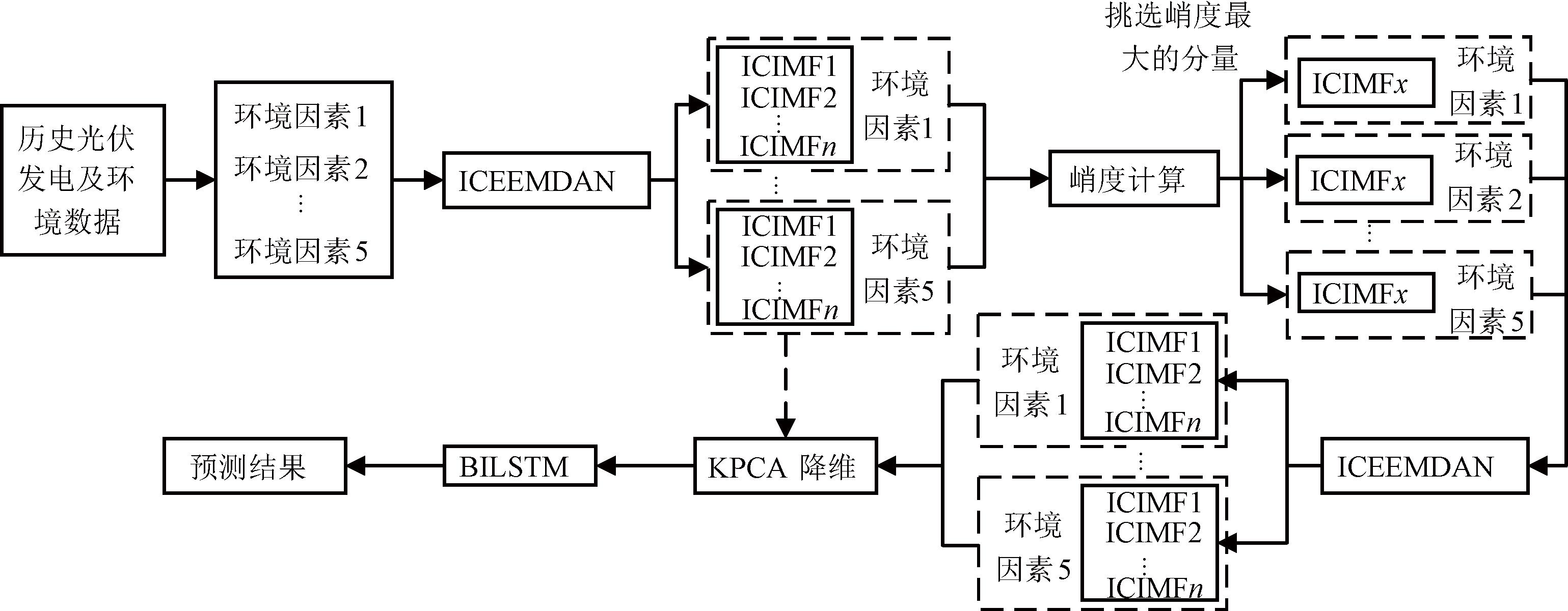
图3 预测模型流程图
Figure 3 Predictive modeling flowchart
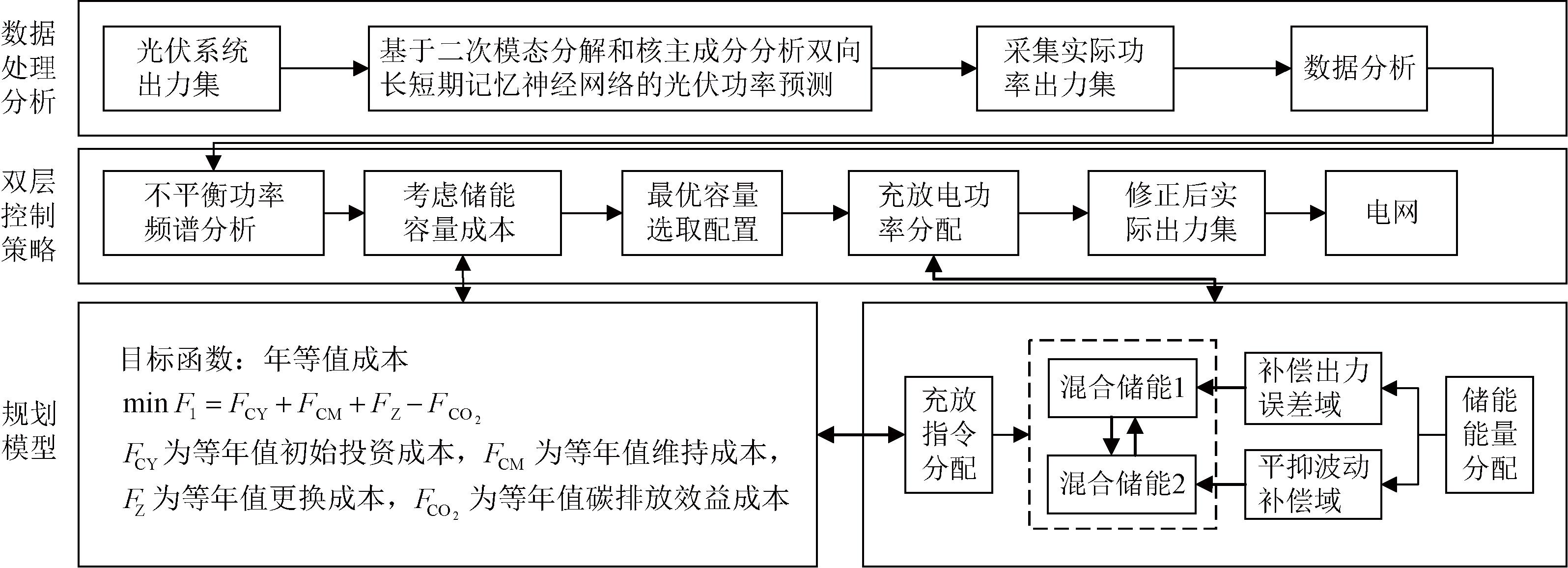
图4 双层模型流程框图
Figure 4 Block diagram of the double-layer model flow
上层等年值成本目标函数[14]为
min F1=FCY+FCM+FZ-FCO2。
(1)
式中:FCY为等年值初始投资成本;FCM为等年值维持成本;FZ为等年值更换成本;FCO2为等年值碳排放成本。
等年值初始投资成本主要由蓄电池和超级电容的购买成本与处置成本之和组成:
FCY=(NbatCbat+NscCsc)fi。
(2)
式中:Nbat、Nsc分别为蓄电池、超级电容数量;Cbat、Csc分别为蓄电池、超级电容年均购买成本和处置成本之和[16];fi为设备的折旧系数。fi公式为
(3)
式中:h为贴现率,此处取值7%[15];Yi为对应设备使用年限。
等年值维持成本为系统在运行过程中产生的安装、损耗、维护、人工费用等成本:
FCM=WbatCbM+WscCsM。
(4)
式中:Wbat、Wsc分别为蓄电池、超级电容使用容量,CbM、CsM分别为蓄电池、超级电容的每千瓦时维修价格。在这里超级电容的维护成本不计[17],即
FCM=WbatCbM。
(5)
等年值更换成本为当系统中的部件达到使用寿命时更换所产生的成本:
(6)
式中:Ni第i种储能数量;Ci为第i种储能的年均购买成本和处置成本之和;Yi为系统生命周期;fri为一个变量因素。fri公式为
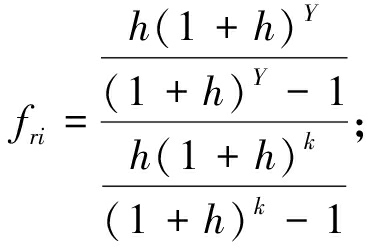
(7)
(8)
等年值碳排放成本为企业可在碳交易市场出售碳排放配额所获取的碳交易收益:
FCO2=PCO2·![]()
![]()
(9)
式中:PCO2为碳排放交易价格,为0.046元/kg;![]() 为单位碳排放量指数,为0.57 kg/(kW·h);PPT(t)为t时刻光伏发电量,t=8 760 h时PPT(t)表示全年发电量。
为单位碳排放量指数,为0.57 kg/(kW·h);PPT(t)为t时刻光伏发电量,t=8 760 h时PPT(t)表示全年发电量。
下层补偿预测误差和平抑波动目标函数分别为:
min P(t)=|Ptr(t)-Ppre(t)|;
(10)
min Δp(t)=(pu(t)-pu(t-1))2。
(11)
式中:P为光伏出力的不平衡功率;Ptr为光伏出力功率;Ppre为光伏预测出力;Δp为并网波动功率;pu为并网功率。
下层约束条件包括光伏预测误差允许范围约束、并网波动率约束、储能系统充放电功率约束和储能系统荷电状态约束。
(1)光伏预测误差允许范围约束:
-10%Ptr≤P≤10%Ptr。
(12)
(2)并网波动率约束:根据文献[18],光伏发电接入电网有功功率在10 min内存在波动率限制,即
r10max<R10;
(13)
(14)
式中:r10、R10分别为10 min内光伏发电波动率和波动限制值;max P10(t)、min P10(t)分别为t时刻光伏发电功率最大值和最小值;PR为光伏电站的额定装机功率。
(3)储能系统充放电功率约束:
(15)
式中:Ebat(t)、Esc(t)分别为t时刻蓄电池、超级电容的充放电功率。
(4)储能系统荷电状态约束[19]:
(16)
式中:SOCbat(t)、SOCsc(t)分别为t时刻蓄电池、超级电容的荷电状态。
2.2 储能系统配置方法
在双层规划模型中,上层在考虑等年值成本的基础上,采用智能优化算法对混合储能系统进行容量配置。
2.2.1 基本粒子群算法
粒子群优化算法(particle swarm optimization,PSO)受到鸟群行为的启发,用于在多维空间中搜索和优化,其中每个粒子代表一个可能的解。通过在搜索空间中移动来寻找最优解,并根据自身及群体经验调整其速度和位置。粒子的速度和位置根据式(17)、式(18)进行更新[20]。
vij(t+1)=ωvij(t)+c1r1(t)[pij(t)-xij(t)]+
c2r2(t)[pgj(t)-xij(t)];
(17)
xij(t+1)=xij(t)+vij(t+1)。
(18)
粒子群算法具有易于实现、强大的全局搜索能力、良好的鲁棒性、高精度和快速收敛等优点。然而,它也存在局限,如容易陷入局部最优和对参数较为敏感。
2.2.2 算法改进
遗传粒子群优化算法(genetic particle swarm optimization,GPSO)融合了粒子群算法与遗传算法的优点,可增加算法的多样性和搜索能力。但对于惯性权重ω、学习因子c1和c2的设定同样也会影响算法的寻优速度以及精度。之前多数都是按照经验将参数设置为定值或依照算法收敛思路设置一个收敛函数,不能按照所处的寻优进度自动设置最优的参数。本文将模糊控制与遗传粒子群算法相结合,使用模糊推理系统来实现参数ω、c1和c2自适应调整,模糊推理结构示意图如图5所示。
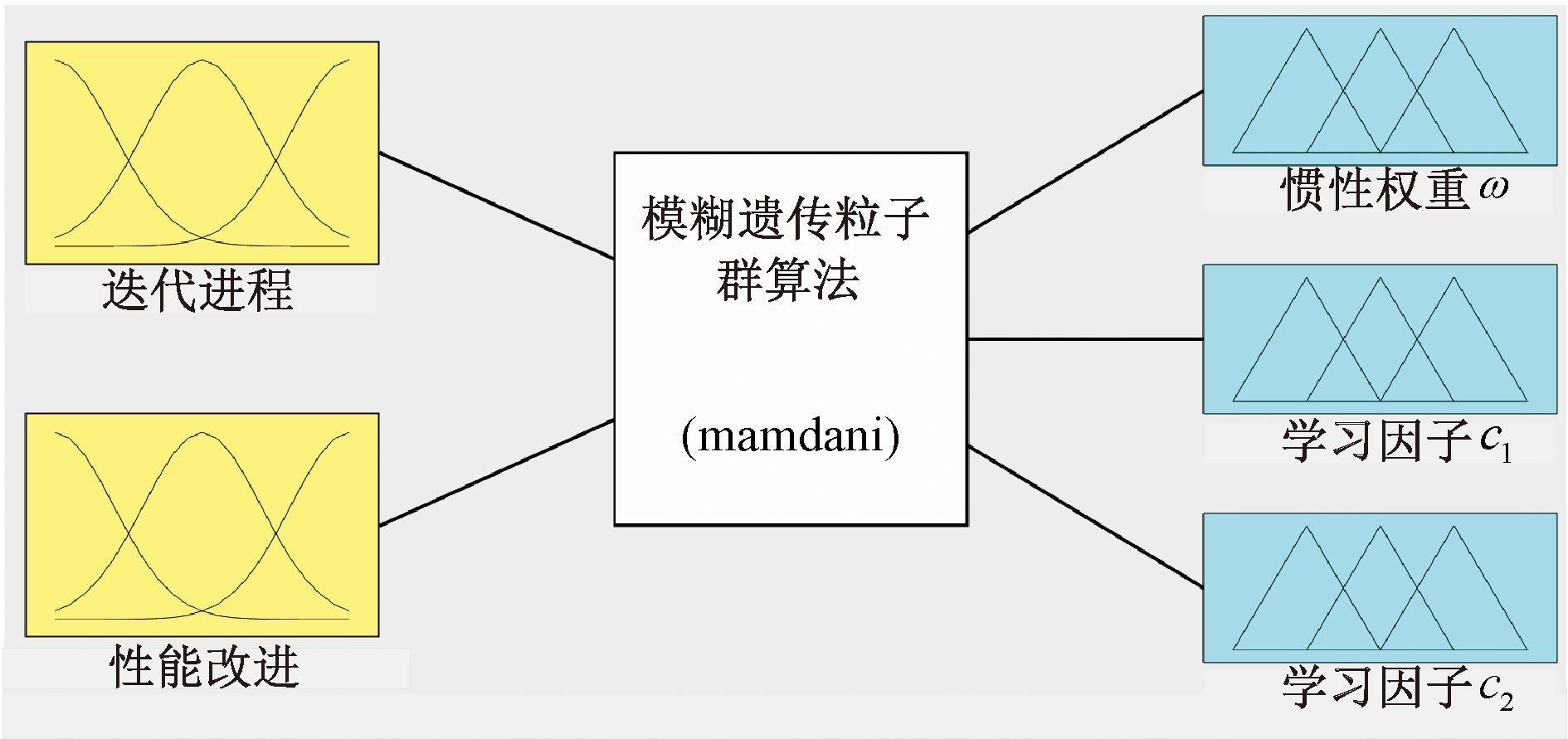
图5 模糊推理结构
Figure 5 Fuzzy inference structure
迭代进程被模糊化为由3个隶属度函数表示的模糊变量,性能改进被模糊化为由4个隶属度函数表示的模糊变量隶属度函数,如图6所示。如图7所示,ω、c1和c2模糊变量被模糊化为3个隶属度函数。
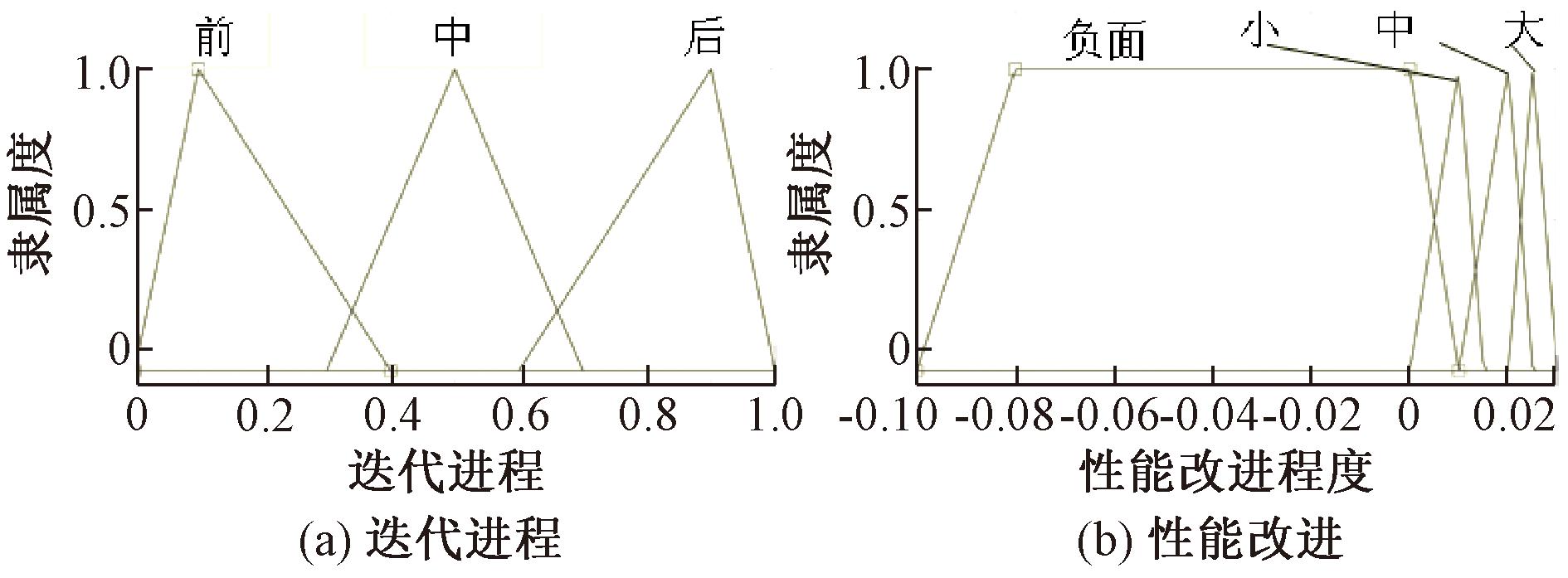
图6 模糊推理输入量的隶属度函数
Figure 6 Affiliation functions for fuzzy inference input quantities

图7 模糊推理输出量的隶属度函数
Figure 7 Affiliation function for fuzzy inference output quantities
模糊系统规则遵循以下规则:惯性权重ω初始设定一个较大的值,逐步减小以促进较早阶段的全局搜索,随着迭代进度的增加,逐渐减小ω的值,以减少粒子在最后阶段的振荡,有利于更精细地搜索局部最优解。学习因子c1和学习因子c2在寻优初期时较大,以增加全局搜索能力,随着迭代进行而逐渐减小,在此基础上进行模糊规则的设计,如表1所示。
表1 模糊规则表
Table 1 Fuzzy rules

负面改进改进较小改进中等改进较大ωc1c2ωc1c2ωc1c2ωc1c2前期高高高中低低高中中高高高中期高高高中低低中中中中中中后期高高高低低低中低高低中中
在这个过程中模糊控制会自动调节ω、c1和c2系数大小,以此达到自适应的效果,步骤如下。
步骤1 初始化粒子位置和速度,计算适应度值。
步骤2 基于模糊逻辑来动态调整权重和学习因子,优化粒子的移动。
步骤3 对粒子更新,依据全局和个体最优位置调整速度和位置。
步骤4 选取粒子进入杂交池,选择父代粒子并生成子代粒子,若子代更优,则更新相应粒子的位置和速度。
步骤5 随机选择部分粒子进行变异操作,改变其位置,若变异后的粒子比原粒子更优,则更新该粒子的位置。
步骤6 判断是否满足终止条件,如未满足,则重新迭代。
2.3 混合储能充放电功率分配策略
运用混合储能补偿光伏预测功率误差,当光伏预测功率小于实际功率,即P(t)=Ptr(t)-Ppre(t)>0时,混合储能系统充电;当光伏预测功率大于实际功率,即P(t)=Ptr(t)-Ppre(t)<0时,混合储能系统放电。考虑到混合储能中蓄电池与超级电容的不同特性,为提高系统响应速度和蓄电池的循环寿命,首先将P(t)利用变分模态分解(variational mode decomposition, VMD)分为频率高、幅值低和频率低、幅值高两部分,再将频率高、幅值低的部分通过超级电容进行补偿,同时将频率低、幅值高的部分通过蓄电池进行补偿。
当使用混合储能平抑并网波动时,将上述进行预测补偿过的功率用VMD分解为高频与低频分量,将满足10 min波动率的低频分量输出到电网中,将剩余高频分量再次分解,高频部分通过超级电容补偿,同时低频部分由蓄电池负责。
蓄电池如果不受保护过度充放电,将造成损耗降低循环寿命。如果蓄电池的SSOC已经达到过充危险区,则应控制蓄电池不再进行充电;反之若蓄电池的SSOC一旦进入过放危险区,应停止蓄电池放电。如果蓄电池突然需要较大功率补偿,它很可能会进入危险区。遇到以上情况,则需要将超出危险区的部分交给超级电容进行补偿。
综上所述,混合储能充放电功率分配策略如图8所示。
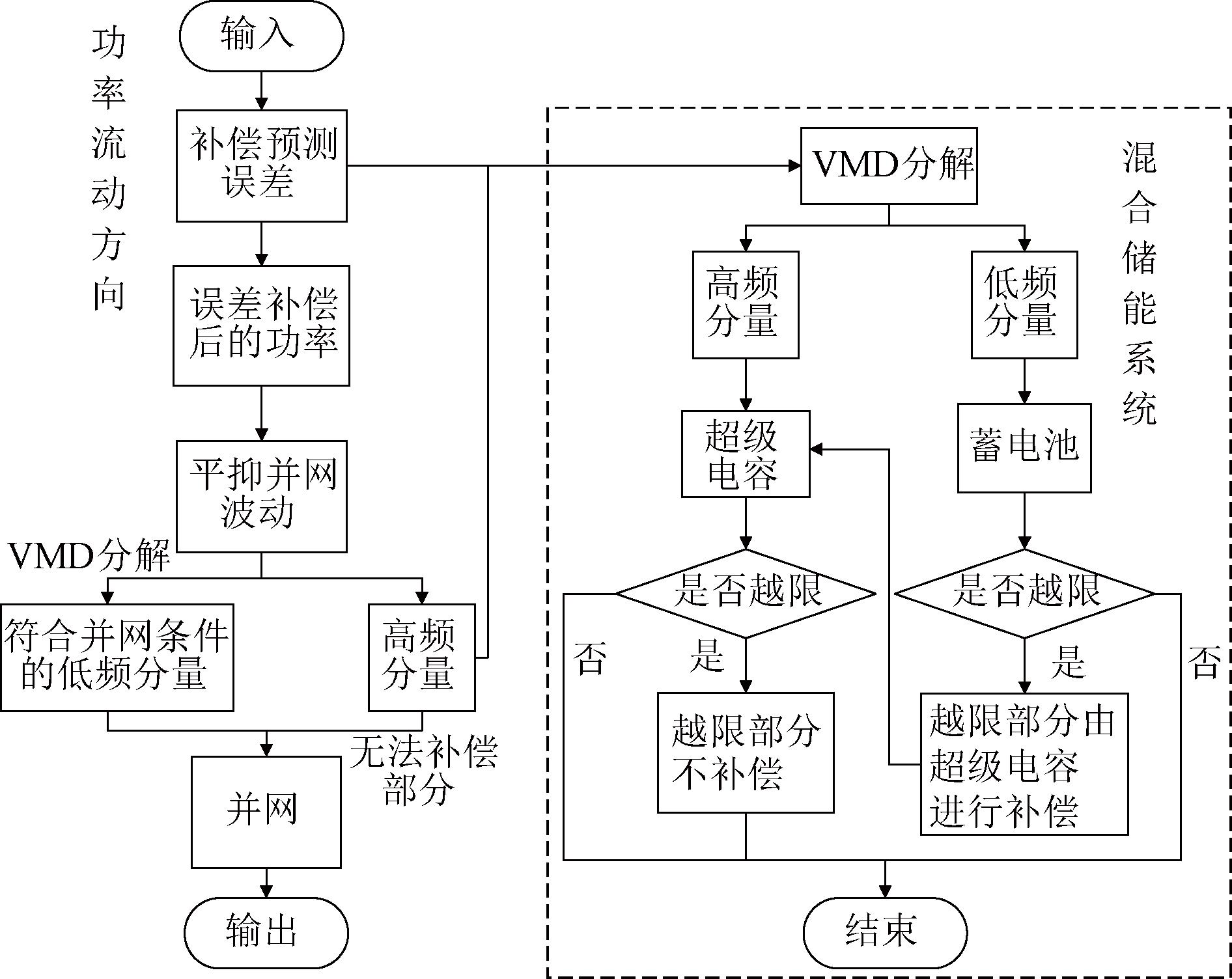
图8 混合储能充放电功率分配策略
Figure 8 Hybrid energy storage charging and discharging power allocation strategy
3 算例仿真
3.1 研究对象与参数的确定
本文选取某光伏电站2022年3月1日至2022年5月31日共3个月的光伏发电功率数据进行光伏预测。为适应不同天气情况下光伏出力特性不同以及预测精准度不同,将测试集中的数据运用K-means++聚类算法进行天气划分。由于K-means++聚类属于无监督算法,超参数K的取值需要人为确定。在此根据评价指标轮廓系数对K值寻优,K值选取3~9的区间,不同K值对应的轮廓系数均值如图9所示。

图9 不同K值对应的轮廓系数均值
Figure 9 The mean of the profile coefficients corresponding to the different K values
由图9可知,K=4时轮廓系数取得最大值,即聚类效果最好,因此确定将天气类型分为4类。然后考虑影响光伏输出功率的5个环境因素,采用基于二次模态分解和核主成分分析双向长短期记忆神经网络进行光伏功率预测。求解后的光伏预测功率曲线如图10所示。

图10 4种典型天气光伏预测功率曲线
Figure 10 Predicted PV power curves for four typical weather conditions
光伏电站数据采集时间尺度5 min,采样数据点为144。蓄电池、超级电容的充放电效率分别设置为90%,98%,二者荷电状态(SOC)范围分别为(20%,80%)、(10%,90%),4种典型日天气的蓄电池、超级电容的初始SOC为0.5,系统生命周期为30 a。
蓄电池、超级电容器的参数如表2所示。
表2 蓄电池、超级电容器参数
Table 2 Parameters of batteries and supercapacitors

设备单机容量/W·h购买与处置成本/元运维成本/(元·kW-1·a-1)使用年限/a蓄电池1 200 45075超级电容3.53 130—
3.2 储能容量的确定
通过上层规划模型的目标函数计算蓄电池和超级电容的容量,以满足补偿预测误差和平抑波动的需求,确保功率预测误差保持在光伏出力指标范围内且控制在5%以内。
为验证本文所提出模糊自适应遗传粒子群算法的收敛性和计算效率,将其与粒子群优化算法、遗传粒子群优化算法进行比较。挑选第1种典型天气数据进行验证,同时设置种群规模5,迭代次数15,杂交概率0.5,变异概率0.05,算法迭代过程如图11所示。
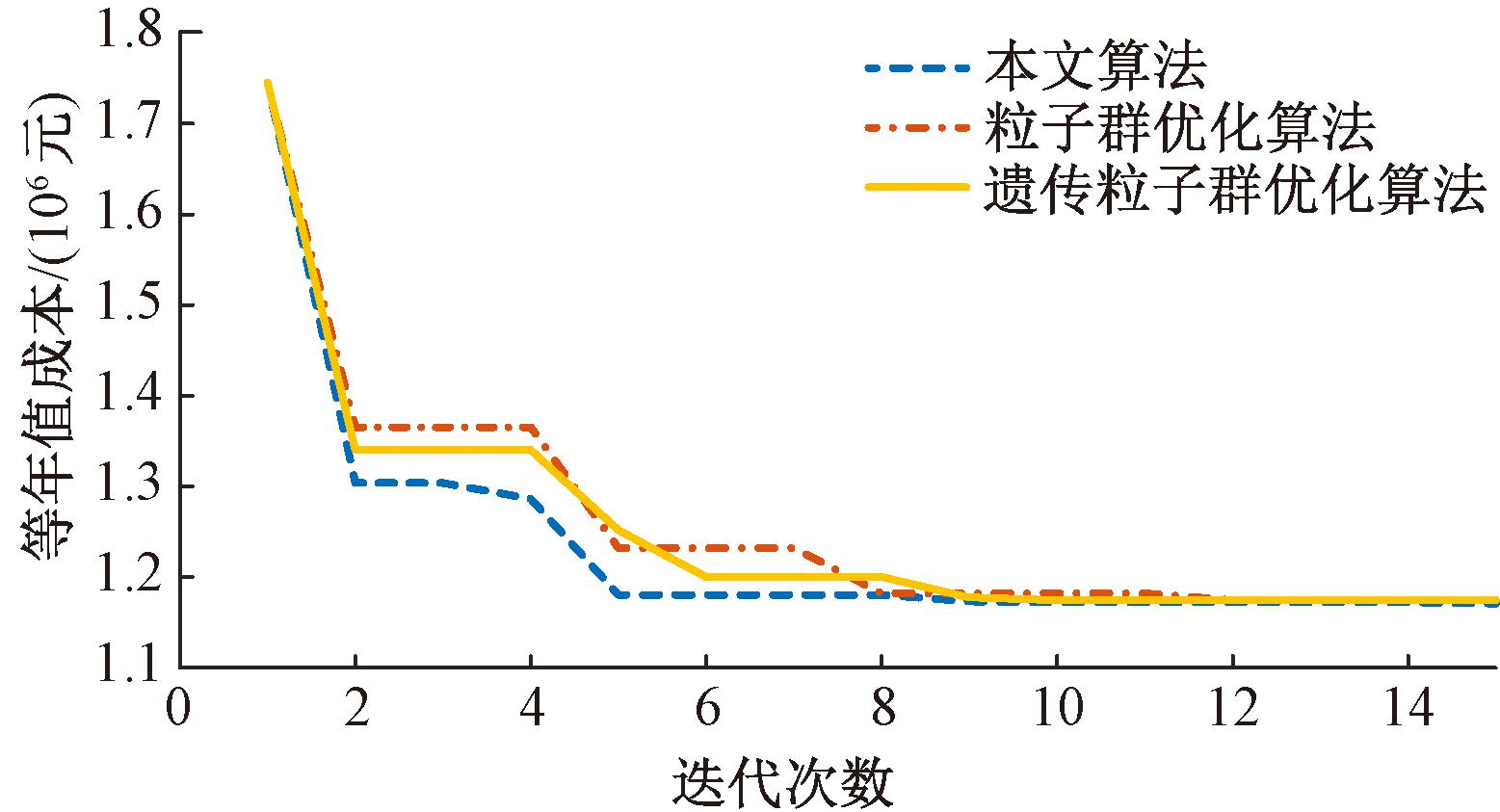
图11 3种算法迭代过程比较
Figure 11 Comparison of the iterative process of the three algorithms
经验证,相较于粒子群优化算法和遗传粒子群优化算法,该算法在迭代速度和优化能力方面表现出显著优势。具体而言,该算法利用自适应机制动态调整遗传操作中的选择、交叉和变异率,相比于固定参数的算法,更能够在不同的优化阶段灵活应对问题的复杂性。此外,模糊逻辑的引入,使得算法在搜索过程中的决策更加智能,能够有效地平衡探索与利用,从而避免了传统算法中常见的早熟收敛问题。将4种典型天气数据带入,迭代过程如图12所示。
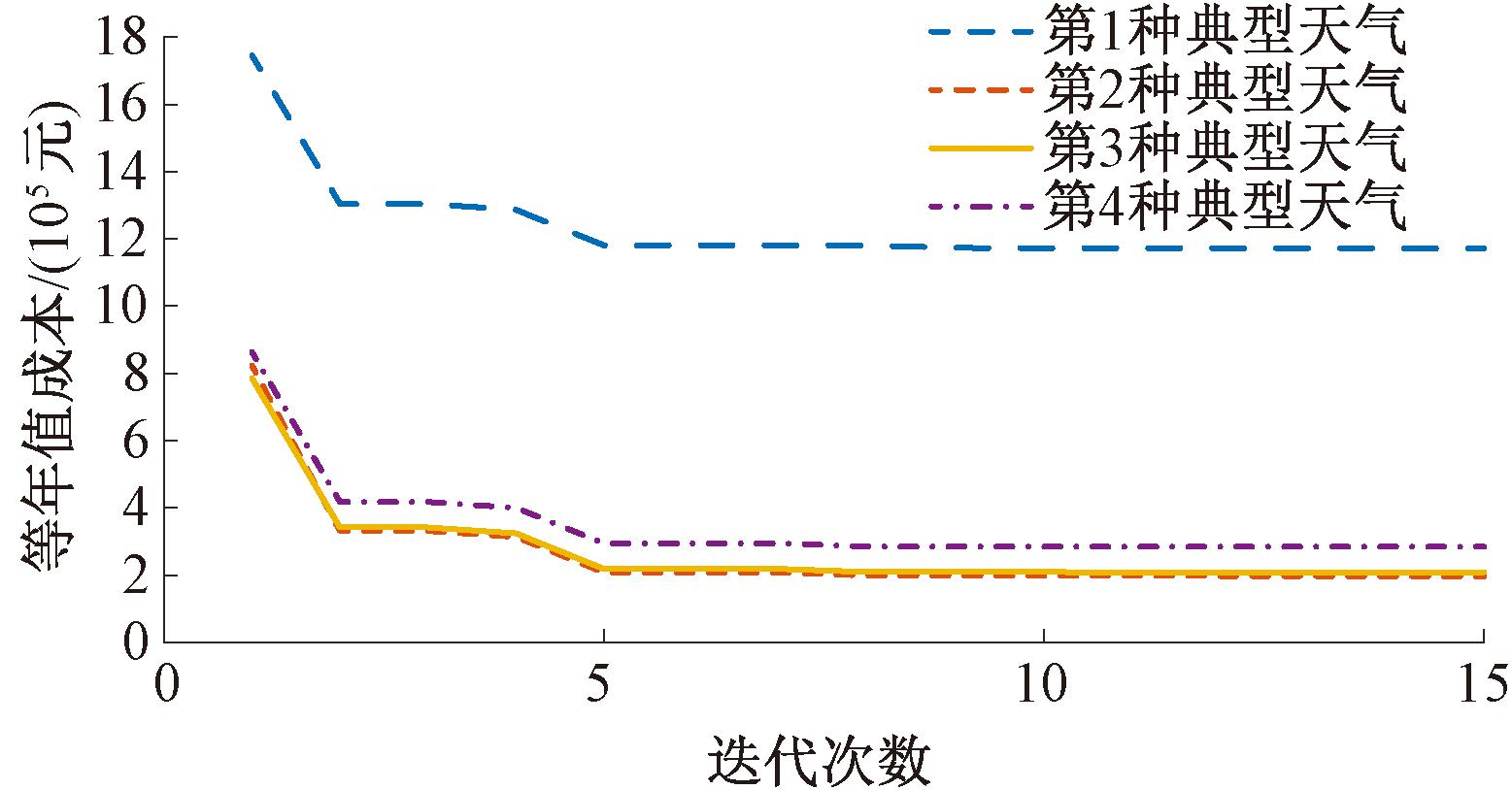
图12 4种典型天气数据迭代过程
Figure 12 Four typical iterative processes for weather data
由图12可得,上层函数迭代到第10步后收敛,根据上层模型,配置的混合储能容量结果见表3。
表3 混合储能容量配置
Table 3 Hybrid energy storage capacity configuration
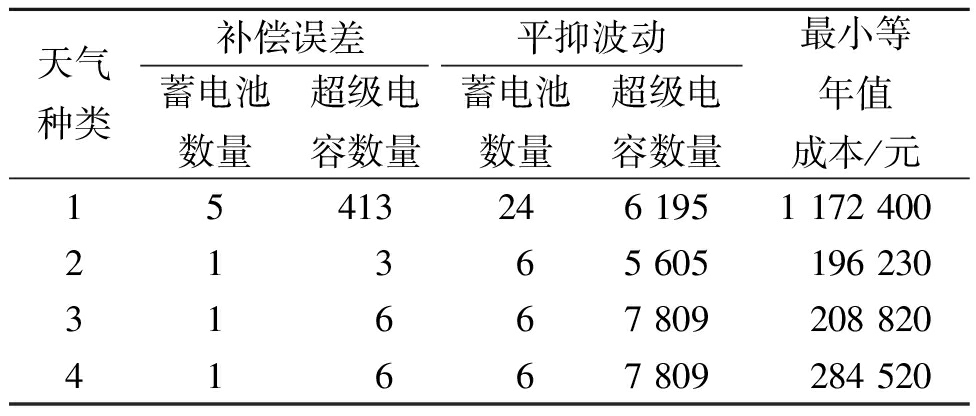
天气种类补偿误差平抑波动蓄电池数量超级电容数量蓄电池数量超级电容数量最小等年值成本/元15413246 1951 172 40021365 605196 23031667 809208 82041667 809284 520
为保证系统在任何天气都能正常运行,选择补偿预测误差的蓄电池数量为5个,超级电容数量为413个;用于平抑波动的蓄电池数量为24个,超级电容数量为7 809个。
按照以上混合储能数量设定,自2022年5月23日至2022年5月29日运行,得出光伏发电系统运行一周的等年值成本,如表4所示。
表4 运行一周等年值成本
Table 4 Equivalent annual operating cost of one week

类型成本/元等年值初始投资成本13 272.00等年值维持成本1 125 900.00等年值更换成本883.26等年值碳排放成本7 687.40等年值总成本1 132 367.86
由表4可知,系统运行一周所需要的最小等年值成本为1 132 367.86元。
3.3 不同场景的仿真分析
上层模型确定了混合储能系统所需要的蓄电池和超级电容的容量配置,下层加入混合储能前后补偿误差的结果如图13所示。
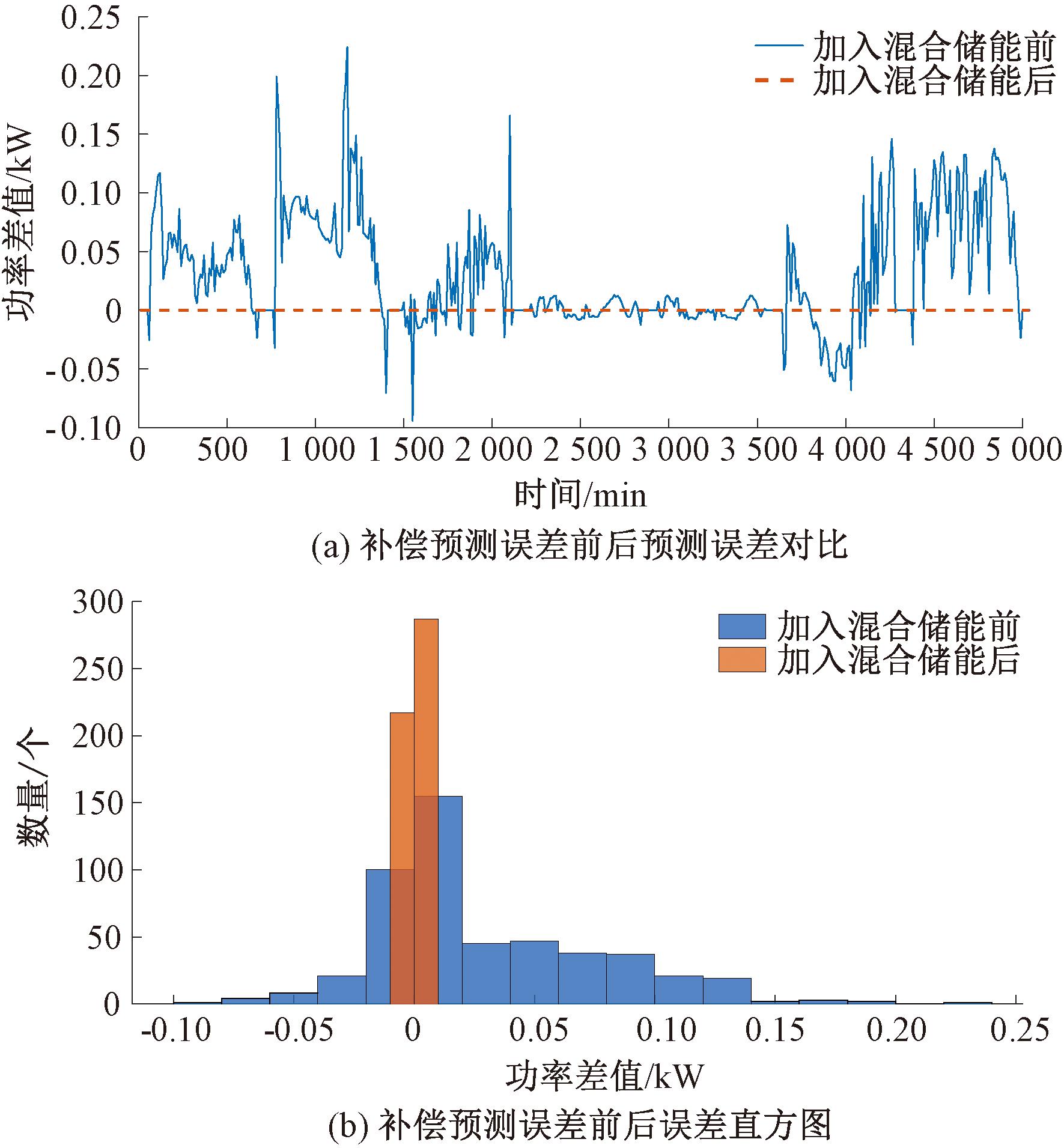
图13 补偿预测误差前后数据对比
Figure 13 Comparison before and after compensating for prediction error
由图13可以看出,在未加入储能前,误差需求的波动较大,在加入混合储能后光伏预测功率和实际功率的误差大幅度减少。补偿预测误差过程中混合储能的运行情况如图14所示。
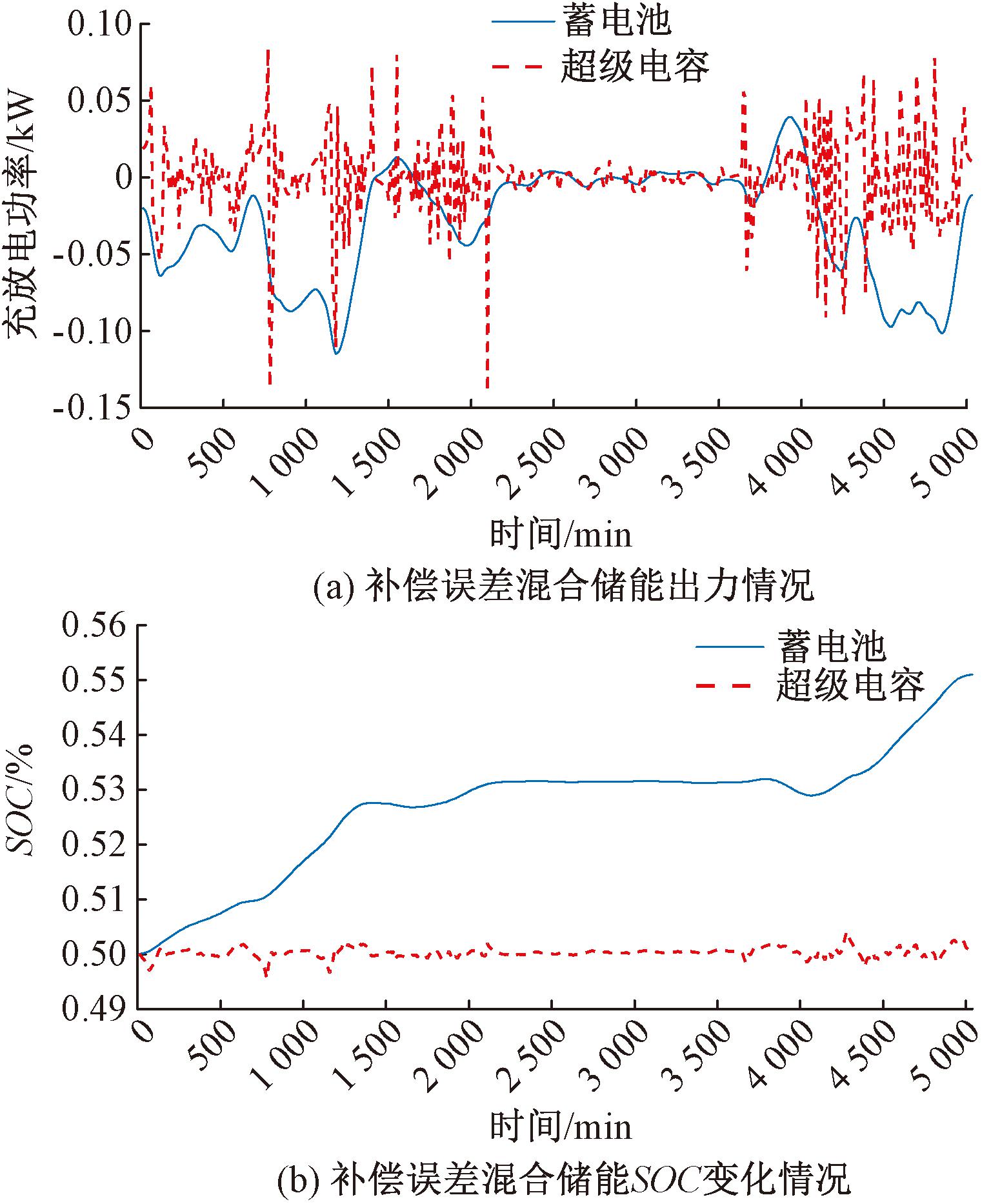
图14 补偿误差过程中混合储能运行情况
Figure 14 Hybrid energy storage operation during compensation of errors
从图14(a)、14(b)中可以看出,蓄电池主要用来处理幅值大且频率低的误差信号,超级电容主要用来处理幅值小且频率高的误差信号,可以大幅度延长蓄电池使用寿命且提高系统响应速度。
为验证控制策略的有效性,引入预测指标函数,包括均方根误差(RMSE)、平均绝对百分比误差(MAPE)。这些指标有效表征了系统的预测效果,模型评价结果见表5。
表5 评价指标
Table 5 Evaluation indicators

补偿前补偿后RMSE/kWMAPE/%RMSE/kWMAPE/%0.055 57.015 70.000 0260.002 07
引入混合储能并采用充放电策略后,预测误差的RMSE、MAPE分别降低了99.95%,99.97%,证明策略和储能容量配置的合理性。加入混合储能前后进行平抑波动的结果如图15所示。
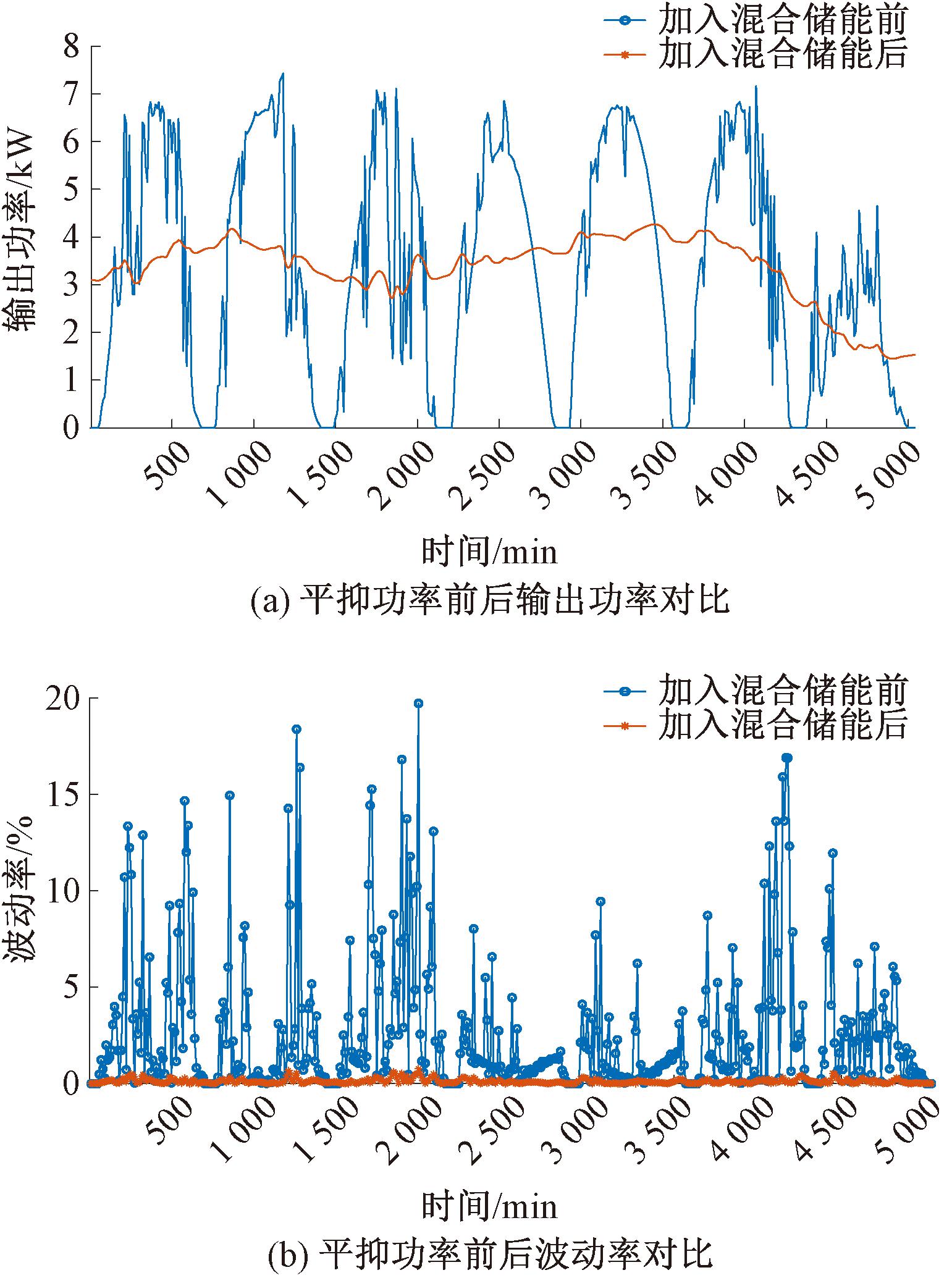
图15 平抑功率前后数据对比
Figure 15 Comparison of data before and after power leveling
由图15(a)可得,混合储能系统将补偿预测误差后的功率低频输出到电网之中。在加入混合储能前光伏发电系统输出功率的波动率最大值为19.732 9%。在加入混合储能后波动率最大为0.773 1%,最大并网波动率降低96.08%,波动均未超过10%的要求,表明VMD在平抑功率波动方面效果良好。
在平抑波动过程中混合储能运行情况如图16所示。
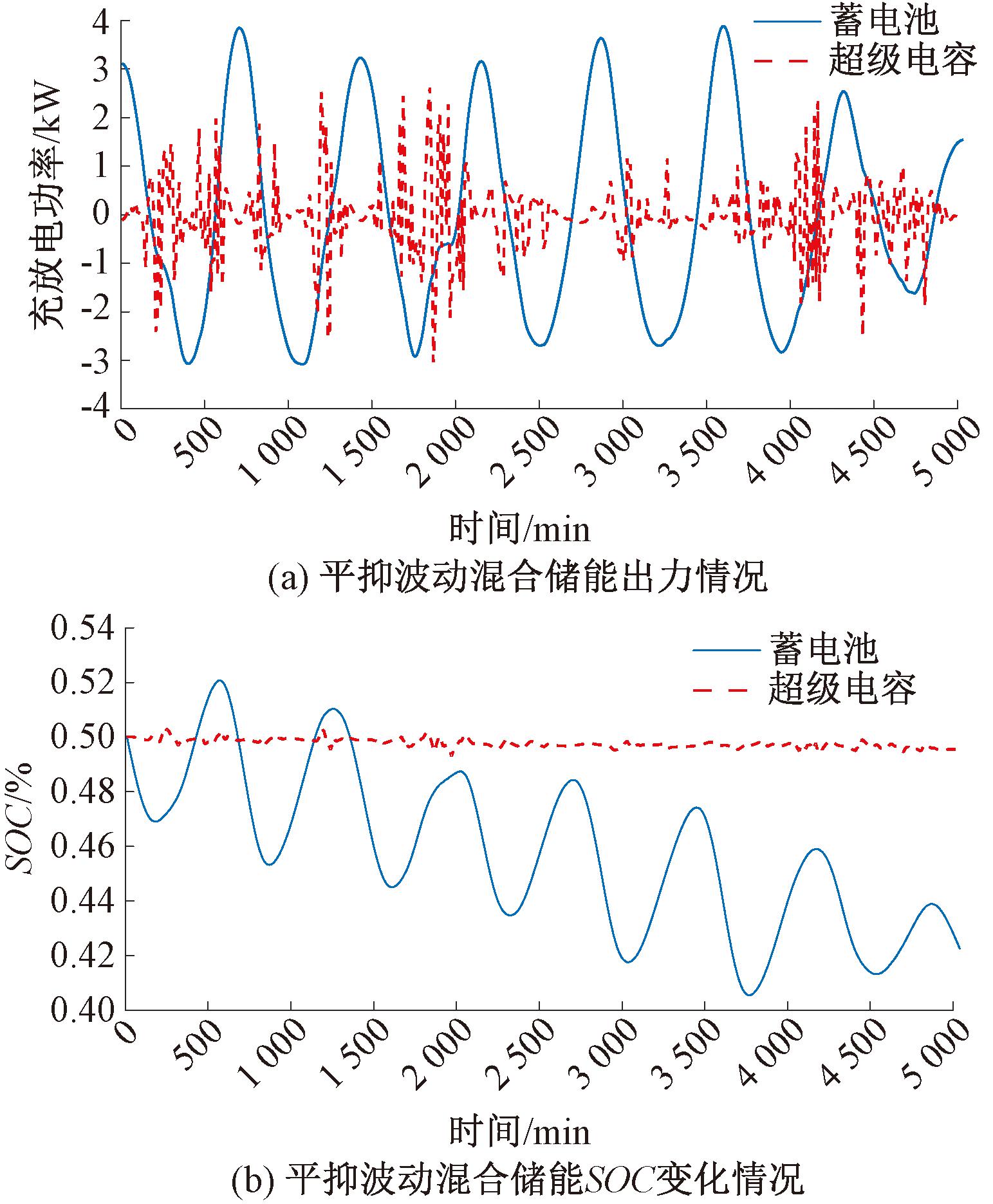
图16 平抑波动过程中混合储能运行情况
Figure 16 Hybrid energy storage operation during smoothing of fluctuations
由图16可知,在平抑波动的过程中,低频功率主要交给蓄电池进行处理,高频功率主要交给超级电容进行处理,这样大幅度提高了蓄电池的使用寿命和系统的响应速度。
4 结论
本文提出了一种双层优化规划模型,旨在解决光伏发电中的预测误差和功率波动问题,同时实现最小等年值成本。上层优化以最小化系统的等年值成本为目标,包括投资、设备更换、维护和碳排放效益成本,采用模糊遗传粒子群算法进行优化。结果显示,补偿预测误差的储能配置为5个蓄电池和413个超级电容器,而平抑功率波动的配置为24个蓄电池和7 809个超级电容器,系统运行一周的最小等年值成本为1 132 367.86元。下层优化则以最小化预测误差和并网波动率为目标,通过制定充放电功率分配策略,提高系统响应速度和蓄电池循环寿命。引入混合储能系统后,光伏发电的预测误差和功率波动率显著降低,为新能源储能的优化利用提供了有价值的参考。
[1] 丁明, 张颖媛, 茆美琴, 等. 包含钠硫电池储能的微网系统经济运行优化[J]. 中国电机工程学报, 2011, 31(4): 7-14.
DING M, ZHANG Y Y, MAO M Q, et al. Economic operation optimization for microgrids including Na/S battery storage[J]. Proceedings of the CSEE, 2011, 31(4): 7-14.
[2] 李建林, 袁晓冬, 郁正纲, 等. 利用储能系统提升电网电能质量研究综述[J].电力系统自动化, 2019, 43(8): 15-24.
LI J L, YUAN X D, YU Z G, et al. Comments on power quality enhancement research for power grid by energy storage system[J]. Automation of Electric Power Systems, 2019, 43(8): 15-24.
[3] 闫群民, 刘语忱, 董新洲, 等. 基于CEEMDAN-HT的平抑光伏出力混合储能容量优化配置[J]. 电力系统保护与控制, 2022, 50(21): 43-53.
YAN Q M, LIU Y C, DONG X Z, et al. Hybrid energy storage capacity optimization configuration for smoothing PV output based on CEEMDAN-HT[J]. Power System Protection and Control, 2022, 50(21): 43-53.
[4] 马超, 董森, 华正操. 多种光伏组件组合光伏电站的混合储能容量优化配置研究[J]. 天津大学学报(自然科学与工程技术版), 2020, 53(11): 1128-1135.
MA C, DONG S, HUA Z C. Capacity configuration of hybrid energy storage system for PV power stations using multiple solar trackers[J]. Journal of Tianjin University (Science and Technology), 2020, 53(11): 1128-1135.
[5] 李相俊, 马会萌, 姜倩. 新能源侧储能配置技术研究综述[J]. 中国电力, 2022, 55(1): 13-25.
LI X J, MA H M, JIANG Q. Review of energy storage configuration technology on renewable energy side[J]. Electric Power, 2022, 55(1): 13-25.
[6] 余洋, 陆文韬, 陈东阳, 等. 光伏波动平抑下改进K-means的电池储能动态分组控制策略[J]. 电力系统保护与控制, 2024, 52(7): 1-11.
YU Y, LU W T, CHEN D Y, et al. Dynamic grouping control strategy for battery energy storage based on improved K-means under photovoltaic fluctuation suppression[J]. Power System Protection and Control, 2024, 52(7): 1-11.
[7] 段俊东, 付子恒, 张普胜, 等. 平滑含DG配网功率波动的储能容量优化研究[J]. 郑州大学学报(工学版), 2020,41(5): 50-54.
DUAN J D, FU Z H, ZHANG P S, et al. Optimized study of energy storage systems capacity for power smoothing of distribution containing DG[J]. Journal of Zhengzhou University (Engineering Science), 2020,41(5): 50-54.
[8] 陈阳, 谢丽蓉, 马兰, 等. 考虑光伏预测误差兼顾平抑波动的双层储能运行策略[J]. 电力工程技术, 2023, 42(1): 70-79.
CHEN Y, XIE L R, MA L, et al. Double-layer energy storage operation strategy that takes into account PV output error and smooths out fluctuations[J]. Electric Power Engineering Technology, 2023, 42(1): 70-79.
[9] 史如新, 王德顺, 余涛, 等. 基于NARX神经网络-小波分解光伏发电功率预测[J]. 郑州大学学报(工学版), 2020,41(6): 79-84.
SHI R X, WANG D S, YU T, et al. Prediction of photovoltaic power generation based on NARX neural network-wavelet decomposition[J]. Journal of Zhengzhou University (Engineering Science), 2020,41(6): 79-84.
[10] 于波, 沈啸轩. 浅谈基于混合储能的光伏发电并网系统的能量管理及协调控制[J]. 中国设备工程, 2021(13): 194-195.
YU B, SHEN X X. An overview of energy management and coordinated control of grid-connected photovoltaic power generation system based on hybrid energy storage[J]. China Plant Engineering, 2021(13): 194-195.
[11] BLUDSZUWEIT H, DOMINGUEZ-NAVARRO J A. A probabilistic method for energy storage sizing based on wind power forecast uncertainty[J]. IEEE Transactions on Power Systems, 2011, 26: 1651-1658.
[12] 程龙, 张方华. 用于混合储能系统平抑功率波动的小波变换方法[J]. 电力自动化设备, 2021, 41(3): 100-104,128.
CHENG L, ZHANG F H. Wavelet transform method for hybrid energy storage system smoothing power fluctuation[J]. Electric Power Automation Equipment, 2021, 41(3): 100-104,128.
[13] 丁逸行, 徐青山, 吕亚娟, 等. 考虑需量管理的用户侧储能优化配置[J]. 电网技术, 2019, 43(4): 1179-1186.
DING Y X, XU Q S, LV Y J, et al. Optimal configuration of user-side energy storage considering power demand management[J]. Power System Technology, 2019, 43(4): 1179-1186.
[14] 陈崇德, 郭强, 宋子秋, 等. 计及碳收益的风电场混合储能容量优化配置[J]. 中国电力, 2022,55(12): 22-33.
CHEN C D, GUO Q, SONG Z Q, et al. Optimal configuration of hybrid energy storage capacity for wind farms considering carbon trading revenue[J]. Electric Power, 2022,55(12): 22-33.
[15] 李雯雯. 多微网混合储能系统的功率协同控制与容量优化配置研究[D]. 成都:西南交通大学, 2021.
LI W W. Research on power cooperative controland capacity optimization configuration ofmulti-microgrid hybrid energy storagesystem[D]. Chengdu:Southwest Jiaotong University, 2021.
[16] 刘慧文. 独立运行风光柴储微电网多目标容量优化配置研究[D]. 呼和浩特:内蒙古工业大学, 2021.
LIU H W. Research on multi-objective optimal capacity configuration for standalone microgrid with WT-PV-DE-BES[D]. Hohhot:Inner Mongolia University of Technology, 2021.
[17] 李双拾. 孤立风/光/储直流微电网配置优化研究[D]. 太原:太原理工大学, 2021.
LI S S. Optimization of isolated wind/solar/storagemicrogrid[D]. Taiyuan:Taiyuan University of Technology, 2021.
[18] 路民辉,孙文文,何国庆.《光伏发电系统接入配电网技术规定》标准解读和修订建议(英文)[J]. 中国标准化(英文版),2022(1):62-65.
LU M H, SUN W W, HE G Q. Interpretation and revision proposals of GB/T 29319—2012, technical require- ments for connecting photovoltaic power system to distribution network[J].China Standardization, 2022(1): 62-65.
[19] 皮晟源,刘牧阳,陈雨田,等.基于IPOA-VMD的风储联合发电系统混合储能容量配置[J/OL].电力系统及其自动化学报,2025:1-10(2025-01-17)[2025-02-18]. https:∥link.cnki.net/doi/10.19635/j.cnki.csu-epsa.00158.
PI S Y, LIU M Y, CHEN Y T, et al. Hybrid Energy Storage Capacity Allocation for Wind-storage Co-generation System Based on IPOA-VMD [J/OL]. Proceedings of the CSU-EPSA,2025:1-10(2025-01-17)[2025-02-18]. https:∥link.cnki.net/doi/10.19635/j.cnki.csu-epsa.00158.
[20] 欧阳海滨, 全永彬, 高立群, 等. 基于混合遗传粒子群优化算法的层次路径规划方法[J]. 郑州大学学报(工学版), 2020,41(4): 34-40.
OUYANG H B, QUAN Y B, GAO L Q, et al. Hierarchical path planning method for mobile robots based on hybrid genetic particle swarm optimization algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2020,41(4): 34-40.