近年来,极端天气频发,严重威胁人民生命财产安全,并引发大规模停电事故,造成巨大经济损失。如:2008年5月,汶川大地震使得川西北电网瘫痪,四川省全网瞬时损失负荷高达31.8%[1];2016年7月,17级超强台风“尼伯特”袭击台湾,造成54万余户电力中断[2];2021年10月,受极端强降雨影响,山西超500条10 kV及以上配电线路停运[3]。根据统计数据[4]表明,由极端灾害引起的配电网大规模停电事故占比约为50%,可见极端灾害对电网造成的影响值得引起重视。
韧性定义为“系统预防、适应扰动并快速恢复的能力”,重点在于系统从受扰动到恢复的动态过程。配电网作为电力系统末端,易受极端灾害破坏,分析其韧性及提升策略具有重要意义。目前,在极端灾害影响机理、韧性指标及韧性评估方法等方面研究已取得一定进展,但多维韧性指标体系、多类型极端灾害的交互影响需进一步研究。林杰欢[5]研究了配电网在冰暴天气下的脆弱性及恢复力;王振浩等[6]基于Batts台风风场模型,分析了暴雨对配电网元件故障的影响;吴勇军等[7]分析了暴雨的致灾机理,从滑坡、山洪等方面建立线路故障率模型。在现实中,配电网常受到多种灾害的影响,而现有研究多聚焦于单一灾害类型的评估,忽略了多灾害情况下的韧性评估,因此,考虑多类型极端灾害影响的配电网韧性评估具有重要理论价值与现实意义。配电网韧性评估指标分为两个方面,即元件的故障概率[8]和电网性能[9]。电力元件的故障率模型是韧性评估的基础,根据故障率模型可以准确分析配电网故障情况,并采取有效的韧性措施。Ma等[10]分析了风速对杆塔、树木以及洪水对地下电缆的影响,构建了配电线路的时变失效概率函数;Ghosh等[11]考虑到不同风速对配电网杆塔、导线的影响,得到各元件在任意风速下的脆弱性曲线。电网性能也可以从多方面评估,王钰山等[12]以台风灾害期间受灾配电网的累积切负荷损失值作为韧性指标;雷霞等[13]将配电网的供电能力作为系统性能指标,通过采取提升措施前后系统性能曲线之间的差额面积来评估配电网的韧性能力;李振坤等[14]基于配电网防灾及减灾两阶段,从配电网防御时间、弹性恢复系数和孤岛可持续时间覆盖率等方面评估了其韧性能力。由此可知,涵盖元件故障概率和电网性能的多维韧性指标体系能够全面评估配电网韧性,而各指标权重大小如何影响评估结果是需要进一步研究的问题。
为此,本文提出了一种多类型极端灾害影响下的配电网元件故障率模型及多维韧性评估方法(multi-dimensional resilience evaluation method,MREM)。首先,提取台风、暴雨及冰暴天气的特征参数,分析多种灾害耦合影响下配电网元件的荷载效应,建立统一的配电网元件故障率模型;其次,根据配电网遭受灾害的不同阶段,考虑指标权重在韧性评估中的作用,从防御力、适应力和恢复力3个维度构建韧性评估指标体系;最后,以IEEE33节点和IEEE69节点系统为例,采用负荷削减量最小为优化目标建立多源协同恢复模型,比较加固线路、分布式电源动态调度和提升移动电源容量3种措施的效果,验证了所提评估方法在多灾害场景下的有效性与优越性。
1 配电网韧性特征以及多类型极端灾害建模
1.1 配电网韧性特征
配电网在极端灾害下的系统功能曲线如图1所示,系统状态大致可分为4个阶段:[0,t1)正常运行阶段、[t1,t2)灾害抵御阶段、[t2,t3)降额运行阶段和[t3,t6)故障恢复阶段。

图1 配电网在极端灾害下的系统功能曲线
Figure 1 System function curve of distribution network with extreme disaster
1.2 台风灾害下配电网元件荷载效应
为分析台风风速和风向对配电网杆塔、导线的影响,本文采用Batts风场模型,并考虑台风移动路径[15]的变化。Batts风场模型如下:
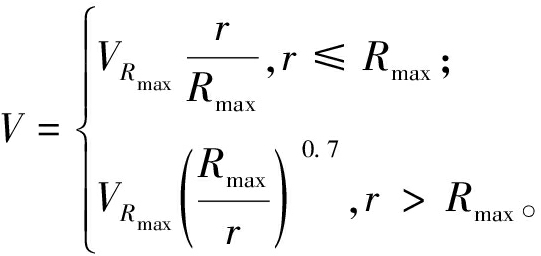
(1)
式中:V为任意位置处时变风速,风向为模拟圆上逆时针切向方向;r为线路距台风中心的距离;Rmax为台风中心到最大风速处的距离即最大风速半径;VRmax为最大风速半径处的风速。
配电网导线单位风荷载与导线所受的风速及风向有关,导线水平方向作用力N1和垂直方向重力N2具体计算公式如下:
(2)
式中:D1为导线外径;β为风向与线路的夹角。
N2=mwireg。
(3)
式中:mwire为导线单位长度的质量;g为重力加速度。
配电网导线在台风天气下的综合荷载为
(4)
(5)
式中:Fl为导线悬挂点沿切线方向的综合荷载;Flz为导线弧垂最低点的张力;N0为导线单位长度的综合张力;dgv为导线悬挂点到导线弧垂最低点的距离;α为高度差角,即导线前后两悬挂点的连线与水平面的夹角。
配电网杆塔风荷载Mt具体计算公式如下:
(6)
式中:ht为杆塔高度;Ot为杆身风压合力作用点到杆根的距离;δtb为杆塔体型系数;Dt1、Dt2分别为杆塔顶部直径与杆根直径;Flk为架空线k的风荷载;Ι为档距;hlk为架空线k到杆塔底部的垂直距离;np,l为杆塔所悬挂导线的根数。
对于架空线路而言,台风天气下树木倒塌造成的线路故障或断开也是停电的主要原因。树木倒塌造成的导线故障率[16]计算公式如下:
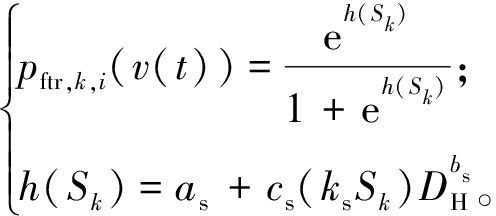
(7)
式中:pftr,k,i(v(t))表示树木倒塌影响导线i的故障概率;Sk为导线k处的风强度(0~1尺度);DH为树胸高处的直径;ks为考虑局部地形效应的因子;as、bs和cs均为与树种相关的参数。
1.3 台风暴雨灾害下配电网元件荷载效应
台风登陆时常伴随暴雨天气,暴雨对配电网元件的影响也不容忽视。暴雨天气下配电网导线水平Fw_h与垂直Fw_v方向荷载[17]暴雨影响导线的荷载、暴雨影响杆塔的荷载分别为
(8)
(9)
(10)
(11)
式中:ρw为雨水密度;R为降雨强度;ρa为空气密度;A为配电杆塔迎风面积;D为雨滴直径;V为线路承受的风速;CD(Vwire,R)为导线在台风暴雨耦合影响下的阻力系数;n(D,R)为雨滴大小分布;kr为预定义的常量;S(γVwire,R)和S(Vterm(D),R)分别为水平和垂直方向下的雨滴冲击力归一化曲线面积;Vterm(D)表示直径为D的雨滴的垂直终端速度;γ为雨滴水平速度与相应风速之比。
1.4 冰暴灾害下配电网元件荷载效应
以配电网某线路i单位长度导线在坐标系的位置(xi,yi)为例,可得到该位置处导线的覆冰荷载为
(12)
式中:Lice为导线覆冰荷载;(xE,yE)表示随时间变化的灾害中心点坐标;Arate表示覆冰增长率;σx、σy分别表示导线在x轴和y轴上的荷载参数,取值与灾害影响半径相关。
杆塔覆冰荷载[20]如下式所示:
(13)
式中:Gice为杆塔覆冰荷载;Gv=0.027 7Lice(Lice+D1)为导线单位垂直荷载;l1、l2分别为杆塔两侧档距;F1、F2分别为杆塔两侧水平张力;h1、h2分别为杆塔两侧悬挂点的高度差,比邻塔高为正,反之则为负。
1.5 多类型极端灾害下配电网元件故障率模型
多类型灾害下导线综合应力为
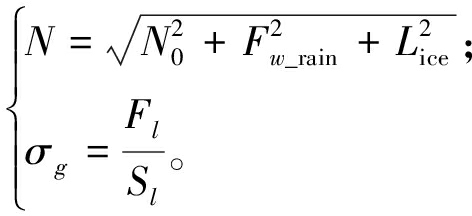
(14)
式中:Sl为导线截面积。
多类型灾害下杆塔综合弯矩为
(15)
架空线路杆塔及导线的故障率均服从正态分布[9],线路正常运行的条件是导线与杆塔均不故障,故考虑多类型极端灾害的影响下的架空线路综合故障率计算公式如下:
(16)
式中:Pi(t)为架空线路i的时变故障率;m1为线路i的导线数;m2为线路i的杆塔数;pmw,k,i表示线路i的第k段导线的时变故障率;pft,c,i表示线路i的第c个杆塔的时变故障率。
2 配电网韧性评估指标与评估方法
2.1 韧性指标计算
2.1.1 防御力
配电网防御力指标包括配电网加权负荷缺失面积R1、加权负荷损失速率Slos。R1定义如下:
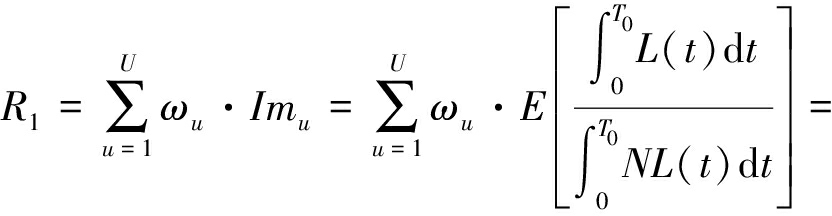
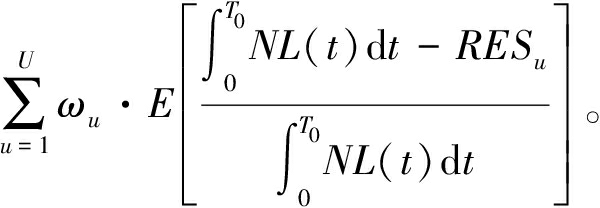
(17)
式中:ωu为场景u的发生概率;U为故障场景数;Imu表示场景u的供电缺失量;T0=t3-t1表示配电网受极端天气影响的时间;L(t)表示极端天气下配电网的实际负荷曲线;NL(t)表示系统正常运行时的目标负荷曲线;RESu表示负荷曲线的缺失面积。
Slos定义如下:
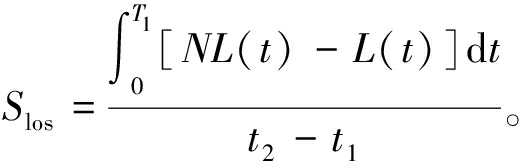
(18)
式中:T1=t2-t1表示配网从正常运行状态过渡到降额运行状态的时间。
2.1.2 适应力
极端灾害可导致配电网停电,配电网通过优化联络开关、柴油发电机和柔性负荷调度,保持降额稳定运行。本文提出用重要负荷支撑率R2和系统平均停电时间SAIDIT作为评估配电网适应灾害韧性的指标[19],具体定义如下:
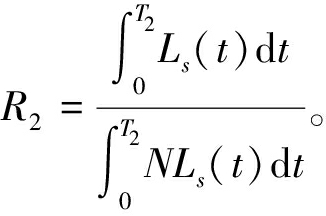
(19)
式中:T2=t3-t2表示处于降额稳定运行的时间;Ls(t)表示极端灾害发生期间配电网实际的重要负荷曲线;NLs(t)表示配电网正常运行时的重要负荷曲线。
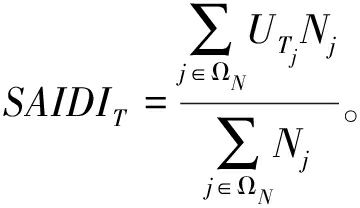
(20)
式中:UTj为极端天气导致的负荷点停运时间;Nj为负荷节点j的用户数。
2.1.3 恢复力
恢复力指标反映配电网灾后恢复能力,包括恢复速率Sre、恢复水平Fad。
Sre反映了配电网在灾后恢复期间单位时间的负荷恢复量,可衡量系统性能恢复的快慢。

(21)
式中:NLre(t)表示灾害恢复后配电系统的实际负荷曲线。
Fad表示系统经过恢复措施所能达到的运行稳定状态比例,即
(22)
式中:Fr表示配电网采取恢复措施后的负荷水平;F0表示未遭受极端灾害的配电网原始负荷水平。
2.2 韧性指标体系赋权
本文采用综合权重法,结合防御力、适应力及恢复力指标,以极端天气下配电网韧性评估为目标层,从灾前、灾中及灾后三阶段考虑配电网的韧性特征,建立如图2所示的极端天气下配电网韧性能力评估体系。该体系通过定性与定量分析,得到韧性指标的主观权重,然后计算指标数据本身的信息熵,根据熵权对指标权重修正后得到其客观权重。
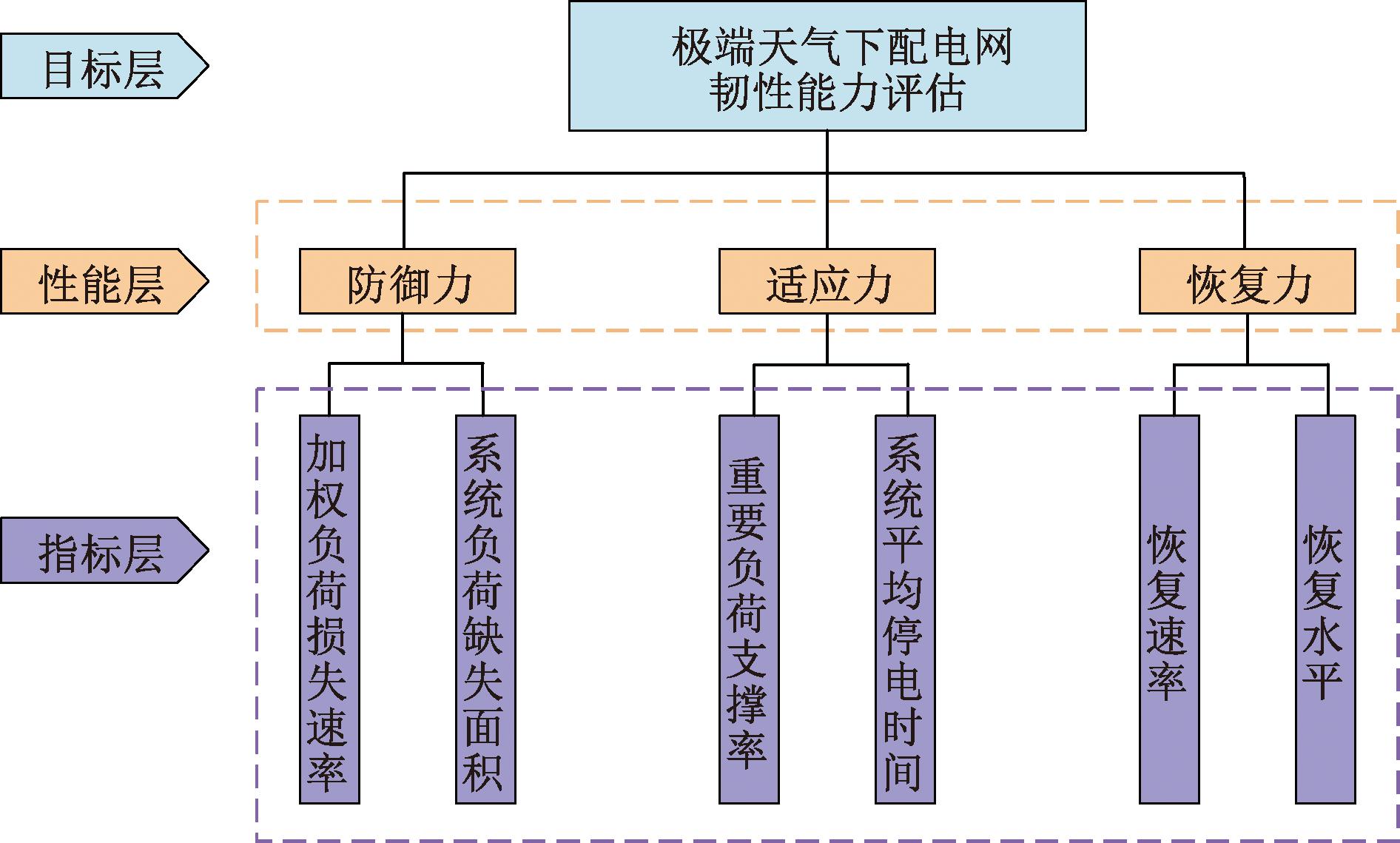
图2 韧性能力评估体系
Figure 2 Resilience capacity assessment system
根据韧性指标的主、客观权重计算指标综合权重Wb,计算公式如下:
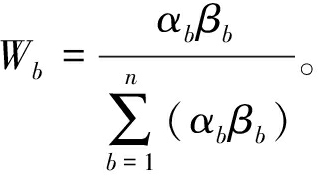
(23)
式中:αb、βb分别为主观、客观权重,其中主观权重根据比例标度表由专家打分计算得到,客观权重由配电网运行数据分析计算得到;n为韧性指标的个数。
2.3 多源协同优化的灾后恢复模型
2.3.1 目标函数
优先恢复重要负荷供电的同时,最大程度减少配电网负荷功率削减,目标函数如式(24)所示。
(24)
式中:wj表示节点j的削负荷成本,根据负荷不同重要程度设置不同的削负荷成本;ΩT为故障时段的集合;ΩN为配电网节点集合;![]() 为t时刻节点j处的负荷有功削减功率。
为t时刻节点j处的负荷有功削减功率。
2.3.2 约束条件
约束条件包括配电网辐射拓扑约束、负荷削减约束、分布式电源出力约束、配电网运行约束、EV及MESS的时空动态调度约束和充放电约束、电动汽车充放电约束,具体公式见文献[20]。
3 算例分析
本文采用IEEE33系统和更大规模的IEEE69节点配电系统算例,验证所提评估方法的有效性。建立的灾后多源协同恢复问题为混合整数二阶锥规划模型,可通过MATLAB R2021a软件调用商业求解器Gurobi求解。使用的仿真环境为Intel i5-8300 H(2.30 GHz),内存8 GB。
3.1 算例设置
本文针对IEEE33和IEEE69节点配电系统建立了直角坐标系,分别以节点1和线路L1为原点和x轴正方向,以垂直L1向上为y轴正方向,线路长度与角度参照文献[21]。线路采用LGJ-240/30架空线,档距50 m,杆塔为G级混凝土电杆,承受最大弯矩48.76 kN/m,线路抗拉强度均值和标准差分别为184.75 N/mm2和21.26 N/mm2。假设两个节点间配电线路被档距分开的不同线段所受的荷载均等于该线路中心处的荷载,该线路的不同杆塔所受荷载由线路中心处杆塔荷载决定。配网区域位于纬度118°58′N~119°2′N和经度28°14′E~28°22′E之间。
本文以2023年某地区台风、暴雨灾害为例,结合历年冰暴灾害数据,台风登陆位置为(70.6 km,-25.91 km),登陆参数为[1.57 rad,16 km/h,7.536×103 Pa],暴雨及冰暴灾害起始位置为(58.6 km,-8.41 km),初始移动速度为10 km/h,影响范围半径为8 km。灾害开始时刻为00:00,即第0 h,持续时间为14 h,灾害开始时刻为仿真起始时刻。
3.2 多维指标体系与单指标的韧性评估分析
为验证多维韧性评估体系的有效性,基于IEEE33节点系统,采用多维韧性指标与单一指标进行评估。通过蒙特卡洛法生成1 000个灾害场景,并利用K-means算法(聚类数为5)筛选出5个代表性故障场景,灾后负荷恢复曲线见图3。
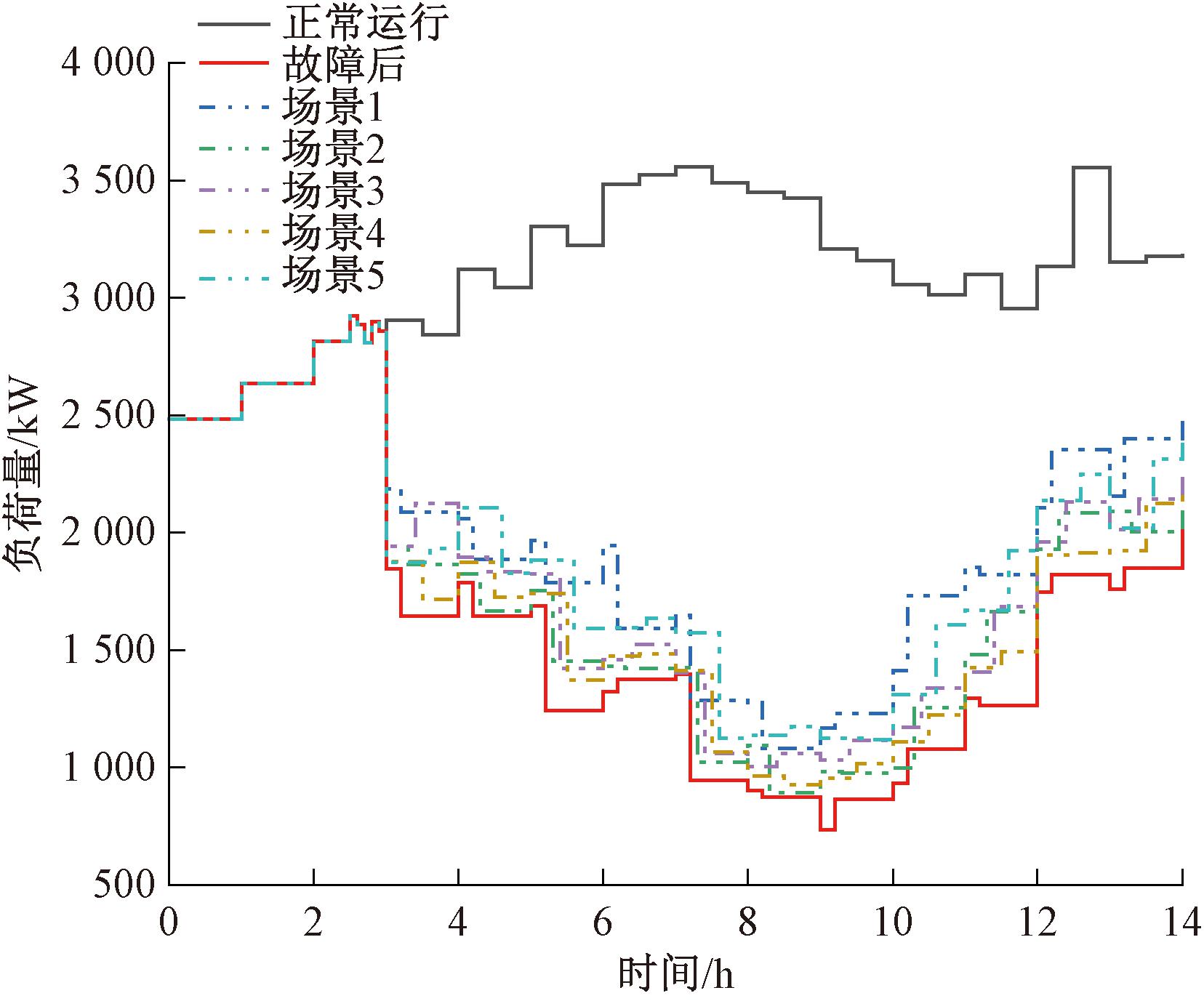
图3 极端灾害下配电网供电恢复负荷曲线
Figure 3 Load recovery curve of distribution network with extreme disaster
选取重要负荷支撑率和梯形面积作为对比指标,与本文提出的MREM方法进行对比,评估结果映射至[0,100][22],结果如表1所示。其中,MREM韧性指标综合权重分别为ψ1=0.251 7,ψ2=0.115 3,ψ3=0.087 2,ψ4=0.133 7,ψ5=0.219 6,ψ6=0.192 5。
表1 聚类后故障场景的韧性评估结果分析
Table 1 Analysis of toughness evaluation results of fault scenarios after clustering

场景R1SlosR2SAIDITSreFad梯形面积重要负荷支撑率RMREM场景10.4370.3310.9180.3260.3510.47952.491.860.0场景20.5380.3350.8960.3380.3140.39749.589.654.7场景30.5370.3330.9060.3340.2370.43150.390.655.1场景40.6190.4250.9220.3450.2280.38847.292.248.1场景50.4390.3790.7910.3320.3360.40451.779.158.4
由表1可知,传统梯形面积法与MREM方法在总体趋势上基本一致。以场景4为例,尽管6个指标较差,两者得分均为最低,但重要负荷支撑率评分却高于场景1;而场景1的6个指标表现较好,3种方法得分均为最高。这表明重要负荷支撑率在评估中存在片面性。
此外,场景2和场景3的分析表明,梯形面积法与重要负荷支撑率得分接近,区分度较低;而MREM方法考虑了负荷损失速率与恢复力,能够有效区分两者差异。
3.3 韧性指标权重对配电网韧性评估的影响
本文采用传统主观赋权法作为IEEE33节点的韧性评估对比方法,基于上述计算结果和评估指标体系,两种方法的评估结果如表2所示。
表2 MREM指标的赋权评分结果
Table 2 Empowerment scores of MREM indicators
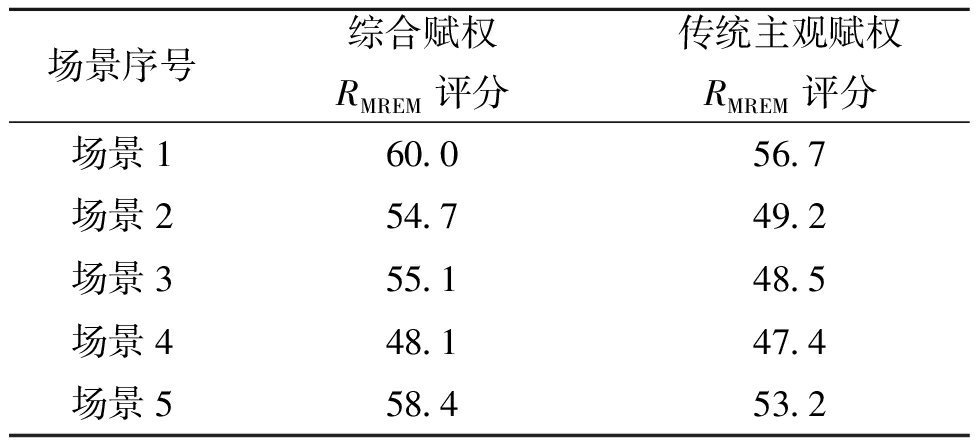
场景序号综合赋权RMREM评分传统主观赋权RMREM评分场景160.056.7场景254.749.2场景355.148.5场景448.147.4场景558.453.2
由表2可知,场景3的综合赋权RMREM评分高于场景2,而传统主观赋权RMREM评分评估结果则相反。这是因为场景3在R1和Fad指标上表现更好,尽管场景2的Slos和SAIDIT指标较高,但其权重较小,因此场景3的综合韧性更强。
此外,表1数据显示,场景1的R1最小且权重最大,指标表现最好;而场景5尽管负荷损失较大,但RMREM综合得分高于场景2,3,4。与主观赋权法相比,综合权重法的评估结果更科学、准确。
3.4 不同场景下配电网韧性评估分析
3.4.1 加固线路对配电网韧性的影响
更换高强度架空线和杆塔可有效降低线路在极端灾害中的故障率。本文以IEEE33和IEEE69节点系统为算例,采用I级杆塔(抗弯力矩58.5 kN·m)与LGJ 240/55架空线(抗拉强度均值195.35 N/mm2,标准差29.52 N/mm2)替换部分线路。
以线路4和线路13为例,通过对以下4种韧性提升措施的对比来验证评估方法的有效性,结果如表3所示。
表3 更换线路元件对配电网韧性的影响
Table 3 Impact of replacing line components on the resilience of distribution networks
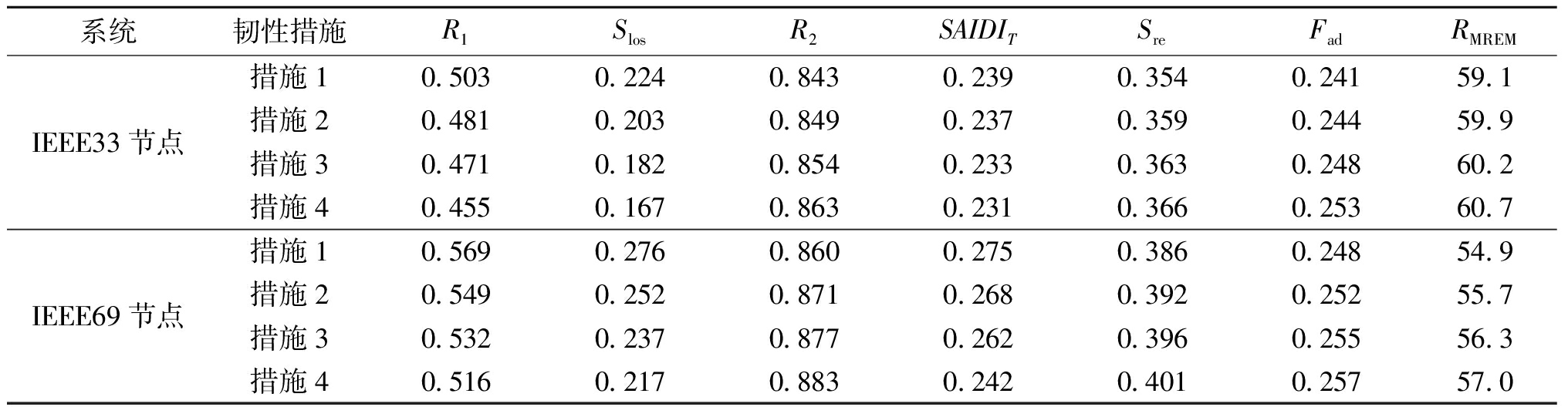
系统韧性措施R1SlosR2SAIDITSreFadRMREM措施10.5030.2240.8430.2390.3540.24159.1IEEE33节点措施20.4810.2030.8490.2370.3590.24459.9措施30.4710.1820.8540.2330.3630.24860.2措施40.4550.1670.8630.2310.3660.25360.7措施10.5690.2760.8600.2750.3860.24854.9IEEE69节点措施20.5490.2520.8710.2680.3920.25255.7措施30.5320.2370.8770.2620.3960.25556.3措施40.5160.2170.8830.2420.4010.25757.0
措施1:G级杆塔和LGJ 240/30架空线;措施2:I级杆塔和LGJ 240/30架空线;措施3:G级杆塔和LGJ 240/55架空线;措施4:I级杆塔和LGJ 240/55架空线。
由表3中韧性指标的变化可知,提升杆塔或导线强度有效增强配电网的韧性,采用高抗拉强度的架空线比采用高抗弯强度的杆塔,韧性提升效果更明显。此外,对比措施4下两个配电系统韧性提升效果发现,IEEE69系统的抵御力提升程度较IEEE33系统高6.7%,RMREM提升程度较IEEE33系统高31.3%,表明评估方法对大规模配电网依然具有良好的适用性。
3.4.2 分布式电源参与调度对配电网韧性水平的影响
以4种故障场景为例,对比不同措施下的负荷恢复情况并计算RMREM,对IEEE33节点和IEEE69节点配电网进行韧性评估。在该场景下,IEEE33节点系统线路3,7,28,35发生故障,IEEE69节点系统线路12,27,46,60发生故障。
基于以下3种情形,IEEE33节点与IEEE69节点系统的故障恢复过程如图4和图5所示,采用本文所提MREM的韧性评估结果见表4所示。
表4 不同分布式电源参与调度的配电网韧性评估结果
Table 4 Resilience assessment results of distribution networks with different distributed power sources participating in scheduling
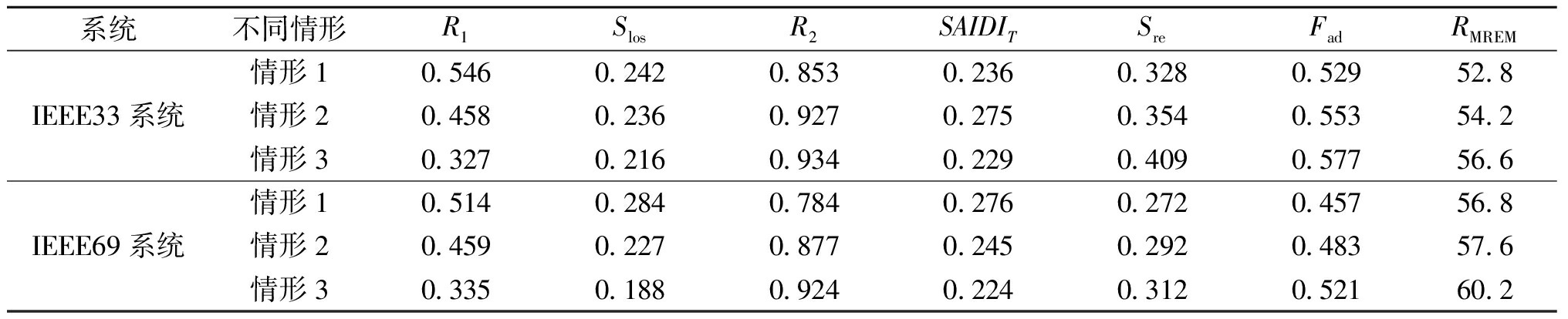
系统不同情形R1SlosR2SAIDITSreFadRMREM情形10.5460.2420.8530.2360.3280.52952.8IEEE33系统情形20.4580.2360.9270.2750.3540.55354.2情形30.3270.2160.9340.2290.4090.57756.6情形10.5140.2840.7840.2760.2720.45756.8IEEE69系统情形20.4590.2270.8770.2450.2920.48357.6情形30.3350.1880.9240.2240.3120.52160.2

图4 不同分布式电源对IEEE33配电网负荷恢复的影响
Figure 4 The impact of different distributed power sources on load recovery of IEEE33 distribution network
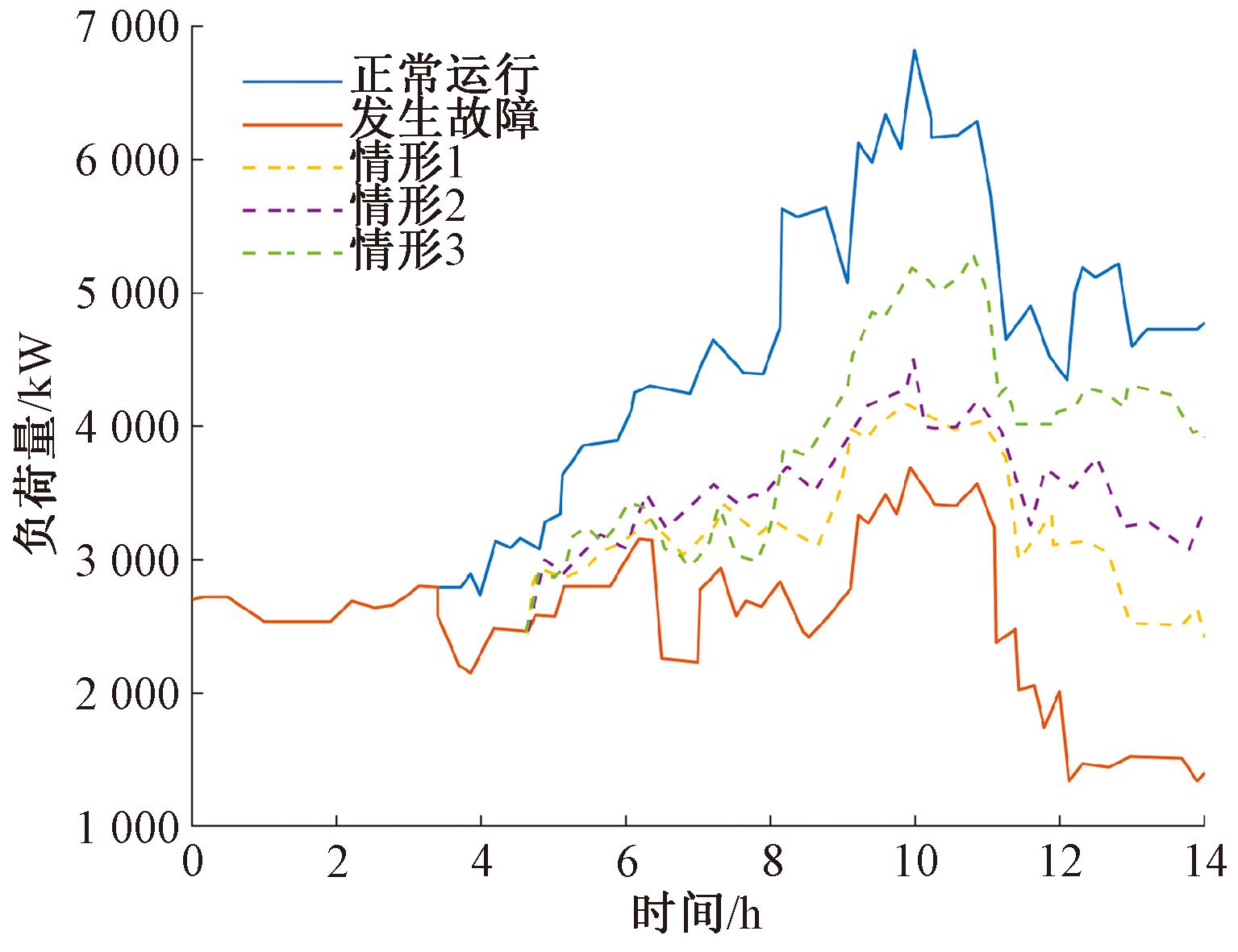
图5 不同分布式电源对IEEE69配电网负荷恢复的影响
Figure 5 The impact of different distributed power sources on load recovery of IEEE69 distribution network
情形1为含移动储能与柴油发电机的动态调度,不含EV调度;情形2为含EV、移动储能与柴油发电机的动态调度;情形3为接入光伏、EV、移动储能与柴油发电机的动态恢复调度。
从表4可以看出,对IEEE33节点配电网而言,相比于情形1,情形2的R1减少16.1%,Slos仅降低2.5%,R2提高8.7%,Fad仅提高4.5%,配电网综合韧性值RMREM提高14%;情形3接入光伏后,系统能够恢复更多负荷供电,且负荷波动幅度变小,配电网综合韧性值RMREM较情形2提高24%。对于规模更大的IEEE69节点系统而言,与情形1相比,情形2的R1减少10.7%,Slos降低20%,R2提高11.9%,Fad提高5.7%,配电网综合韧性值RMREM提高8%;由于IEEE69配电网接入更多的光伏,情形3的RMREM较情形2提高46%,系统韧性提升更加显著。
此外,对比图4的供电负荷曲线可知,第3.2 h时,EV参与负荷恢复,但受灾后交通网络拥堵影响,负荷恢复略有延迟;第5.5 h时,EV到达负荷节点并处于放电状态;7~10 h时段EV处于充电状态;9~11 h时段EV参与负荷供电。情形2的负荷水平高于情形1,同时受EV接入容量的限制,负荷恢复效果有待进一步提高,而情形3接入光伏后,更多负荷得到恢复。
图5表明,IEEE69节点系统故障后负荷波动较大,4.2 h接入EV和移动电源后负荷有所提升,但情形2提升幅度有限。同样情况下,接入光伏不仅负荷恢复更高,且有效平抑了波动。
3.4.3 移动电源可供容量对配电网韧性的影响
通过研究MESS和EV作为移动电源恢复配电网故障节点的效果,提高电源容量,分析其对IEEE33节点配电网韧性的影响,并验证评估方法的有效性,设置表5的3种情形进行分析。
表5 不同容量MESS及EV的配置情景
Table 5 Configuration scenarios of MESS and EV with different capacities

不同情形MESS额定容量/(kW·h)EV额定容量/(kW·h)情形120020情形230030情形340040
3种不同情形的恢复结果见图6;韧性评估结果如表6所示。
表6 提高移动电源可供容量后配电网韧性评估结果
Table 6 Distribution network resilience accessment results after increasing the available capacity of mobile power

不同情形R1SlosR2SAIDITSreFadRMREM情形10.4760.2590.8070.2740.3610.49055.2情形20.4640.2610.8690.2700.3960.51157.8情形30.4550.2570.8710.2620.4450.51458.1

图6 提高移动电源可供容量对配电网负荷恢复的影响
Figure 6 Influence of increasing available capacity of mobile power on load recovery of distribution network
在图6中,对比情形1和情形2可知,随着移动电源容量增加,重要负荷支撑率、恢复速率和恢复水平提高,系统平均停电时间减少,配电网韧性增强;而加权负荷损失速率保持不变,因为该指标仅与灾害强度、电网元件和线路类型相关,受移动电源容量影响较小。
在图6中,比较情形2和情形3的负荷恢复情况,随着移动电源容量的增加,重要负荷支撑率和恢复水平几乎不再提高,综合指标体系因涵盖加权负荷缺失面积和系统平均停电时间,评估范围更广,能够更全面反映配电网不同维度的韧性特征。
4 结论
为全面评估极端灾害下配电网的韧性水平,本文提出了多类型极端天气下配电网元件故障率模型及多维韧性评估方法,得出以下结论。
(1)本文考虑台风、暴雨及冰暴天气参数对配电网元件故障率的影响,提出一种统一的配网元件故障率模型,通过算例验证了模型的有效性,进而为韧性提升措施提供科学指导。
(2)在配电网韧性评估中,基于防御力、适应力和恢复力3个维度,采用综合权重法进行评估,比传统梯形面积和重要负荷支撑率评估方法更加全面、准确。
(3)韧性评估结果表明,加固线路、移动电源动态调度及提高移动电源容量均能有效提升配电网韧性,所提评估方法适用于不同场景、规模的配电系统。
[1] 孙江玉, 刘创, 欧阳敏, 等. 地震灾害下电网性能研究综述: 以弹性视角为主[J]. 自然灾害学报, 2018,27(2): 14-23.
SUN J Y, LIU C, OUYANG M, et al. Review of performance studies on electric power grids under seismic hazards: with a focus on resilience perspective[J]. Journal of Natural Disasters, 2018,27(2): 14-23.
[2] 李天友. 配电网防灾减灾综述[J]. 供用电, 2016,33(9): 2-5.
LI T Y. A review of disaster prevention and mitigationin distribution network[J]. Distribution &Utilization, 2016,33(9): 2-5.
[3] 梁振锋, 闫俊杰, 李江锋, 等. 极端暴雨灾害下城市配电网风险评估方法[J]. 电网技术, 2023,47(10): 4180-4190.
LIANG Z F, YAN J J, LI J F, et al. Risk assessment of urban distribution network underextreme rainstorm disasters[J]. Power System Technology, 2023, 47(10): 4180-4190.
[4] WANG Y Z, CHEN C, WANG J H, et al. Research on resilience of power systems under natural disasters: a review[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1604-1613.
[5] 林杰欢. 强台风条件下配电网可靠性评估建模与预警框架研究[D]. 广州: 广东工业大学, 2019.
LIN J H. Research on reliability evaluation modeling and early warning framework of distribution networkunder strong typhoon conditions[D]. Guangzhou: Guangdong University of Technology, 2019.
[6] 王振浩, 罗剑潇, 成龙, 等. 面向台风天气下主动配电网韧性提升的改进分级减载策略[J]. 电力系统保护与控制, 2023,51(22): 34-48.
WANG Z H, LUO J X, CHENG L, et al. Improved graded load reduction strategy for resilience enhancement of an active distribution network in a typhoon[J]. Power System Protection and Control, 2023,51(22): 34-48.
[7] 吴勇军, 薛禹胜, 谢云云, 等. 台风及暴雨对电网故障率的时空影响[J]. 电力系统自动化, 2016,40(2): 20-29, 83.
WU Y J, XUE Y S, XIE Y Y, et al. Space-time impact of typhoon and rainstorm on power grid fault probability[J]. Automation of Electric Power Systems, 2016, 40(2): 20-29, 83.
[8] 周晓敏, 葛少云, 李腾,等. 极端天气条件下的配电网韧性分析方法及提升措施研究[J]. 中国电机工程学报, 2018,38(2): 505-513, 681.
ZHOU X M, GE S Y, LI T, etal. Assessing and boosting resilience of distribution system under extreme weather[J]. Proceedings of the CSEE, 2018, 38(2): 505-513, 681.
[9] PANTELI M, MANCARELLA P, WILKINSON S, et al. Assessment of the resilience of transmission networks to extreme wind events[C]∥2015 IEEE Eindhoven PowerTech. Piscataway: IEEE, 2015: 1-6.
[10] MA S S, CHEN B K, WANG Z Y. Resilience enhancement strategy for distribution systems under extreme weather events[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1442-1451.
[11] GHOSH P, DEM L. Probabilistic quantification of distribution system resilience for an extreme event[J]. International Transactions on Electrical Energy Systems, 2022, 2022: 3838695.
[12] 王钰山, 邓晖, 王旭, 等. 考虑台风时空演变的配电网移动储能优化配置与运行策略[J]. 电力系统自动化, 2022,46(9): 42-51.
WANG Y S, DENG H, WANG X, et al. Optimal configuration and operation strategy of mobile energy storage in distribution network considering spatial-temporal evolution of typhoon[J]. Automation of Electric Power Systems, 2022, 46(9): 42-51.
[13] 雷霞, 郑国鑫, 胡益. 地震灾害下配电网的脆弱性分析及弹性提升措施[J]. 电网技术, 2021, 45(9): 3674-3680.
LEI X, ZHENG G X, HU Y. Vulnerability analysisand resilience improvement of distribution network under earthquake disasters[J]. Power System Technology, 2021, 45(9): 3674-3680.
[14] 李振坤, 王法顺, 郭维一, 等. 极端天气下智能配电网的弹性评估[J]. 电力系统自动化, 2020,44(9): 60-68.
LI Z K, WANG F S, GUO W Y, et al. Resilience evaluation of smart distribution network in extreme weather[J]. Automation of Electric Power Systems, 2020,44(9): 60-68.
[15] 郭明鑫, 李少岩, 顾雪平. 计及台风灾害全过程模拟的配电网差异化加固规划韧性提升方法[J]. 电力系统保护与控制, 2024,52(3): 62-73.
GUO M X, LI S Y, GU X P. Differentiated reinforcement planning method for a distribution network considering simulation of the whole process of typhoon disasters[J]. Power System Protection and Control, 2024,52(3): 62-73.
[16] CANHAM C D, PAPAIK M J,LATTY E F. Interspecific variation in susceptibility to windthrow as a function of tree size and storm severity for northern temperate tree species[J]. Canadian Journal of Forest Research,2001, 31(1): 1-10.
[17] FU X, LI H N, LI G, et al. Fragility analysis of a transmission tower under combined wind and rain loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 199: 104098.
[18] 王守相, 黄仁山, 潘志新, 等. 极端冰雪天气下配电网弹性恢复力指标的构建及评估方法[J]. 高电压技术, 2020,46(1): 123-132.
WANG S X, HUANG R S, PAN Z X, etal. Construction and evaluation of resilience restoration capability indices for distribution network under extreme ice and snow weather[J]. High Voltage Engineering, 2020, 46(1): 123-132.
[19] 陈根永, 高翔宇, 谭超, 等. 集中式馈线自动化配电网供电可靠性评估[J]. 郑州大学学报(工学版), 2024,45(1): 114-121.
CHEN G Y, GAO X Y, TAN C, et al. Evaluation of power supply reliability of centralized feeder automation distribution network[J]. Journal of Zhengzhou University (Engineering Science), 2024,45(1): 114-121.
[20] 王月汉, 刘文霞, 姚齐, 等. 面向配电网韧性提升的移动储能预布局与动态调度策略[J]. 电力系统自动化, 2022,46(15): 37-45.
WANG Y H, LIU W X, YAO Q, et al. Pre-layout and dynamic scheduling strategy of mobile energy storage for resilience enhancement of distribution network[J]. Automation of Electric Power Systems, 2022, 46(15): 37-45.
[21] 李牧水. 考虑台风对线路荷载可靠度影响的架空线路加固规划[D].重庆: 重庆大学, 2020.
LI M S.Strengtheningplanning of overhead lines considering the influence of typhoon on line load reliability[D].Chongqing: Chongqing University,2020.
[22] 符杨, 顾吉平, 田书欣, 等. 基于地震灾害场景的主动配电网多维韧性评估方法[J]. 电力自动化设备, 2023,43(3): 1-11.
FU Y, GU J P, TIAN S X, et al. Multidimensional resilience evaluation method of active distribution network based on earthquake disaster scene[J]. Electric Power Automation Equipment, 2023,43(3): 1-11.