随着生物技术的迅猛发展,微生物在医学鉴定、疾病诊断和治疗等领域的应用越来越广泛。微生物种类繁多且其在人体内的作用复杂,准确识别和分类微生物对于疾病的诊断和治疗至关重要。然而,微生物数据常存在样本不平衡的问题,影响机器学习模型的训练效果和医学鉴定的准确性[1]。此外,微生物群落数据面临高维数据、类别不平衡和过度稀疏等挑战,尤其在样本数量较少的情况下,OTUs的数量远超样本数量[2]。尽管分类器能实现较高准确性,但误诊可能对患者造成致命影响,因此必须提高阳性样本的召回率,以识别更多患病样本[3]。
目前,微生物数据扩增的研究主要集中在以下方面:①传统数据扩增方法,典型的如合成少数类过采样法[4](synthetic minority over-sampling technique,SMOTE)、自适应合成采样法[5] (adaptive synthetic sampling approach,ADASYN)和欠采样[6]等。这些方法虽然简单易行,但在处理较高IR的数据集时,往往生成的合成样本质量较低。在此基础上,王曦等[7]基于代价敏感和空间划分提出的MFCS(cost-sensitive microbial data augmentation through matrix factorization)和温柳英等[8]基于矩阵分解和改进空间划分提出的MFSP(fusing matrix factorization and space partitioning microbial data augmentation algorithm),虽然在一定程度上改进了传统方法的不足,但在高IR数据集上的表现仍待提升。②基于生成模型的扩增方法,生成对抗网络(generative adversarial networks,GAN)[9]和变分自编码器(variational auto-encoders,VAE)[10]等生成模型对数据扩增的效果显著,如Wen等[11]提出的KGA(integrating kpca and gan for microbial data augmentation)算法等。这些方法通过学习数据的潜在分布生成合成样本,但在高不平衡比IR情况下容易受到模式崩溃的影响,导致生成样本的多样性不足。③集成学习与模型融合,通过多种扩增方法结合的方式以提升微生物数据的分类性能,如Feng等[12]基于集成边界和欠采样技术提出的集成分类算法。该方法更注重构建平衡数据集,但在高IR的微生物数据中,阳性样本过于稀少,欠采样难以达到理想平衡。
鉴于现有的扩增算法在高IR数据集表现不佳和样本多样性不足的局限性,本文提出了一种改进的微生物数据扩增算法。该算法运用主成分分析(principal component analysis,PCA)算法进行特征转换,降低特征维度并保留关键信息,以缓解强稀疏性问题;对少数类聚类后,依据聚类密度、难度及IR和权重比计算权重值,选取合适样本扩增,降低过拟合与欠拟合概率;最后利用局部异常因子(local outlier factor,LOF)算法过滤异常样本,保障合成样本质量与分布合理,提升样本多样性和分类性能。
1 FTMC算法
针对微生物数据的高维、稀疏以及类别不平衡等问题,本文提出了一种基于特征转换和少数类聚类的数据扩增算法(data augmentation algorithmba-sed on feature transformation and minority clustering,FTMC)。该算法由特征转换、少数类聚类、筛选核心聚类和样本扩增过滤4个阶段组成,如图1所示。
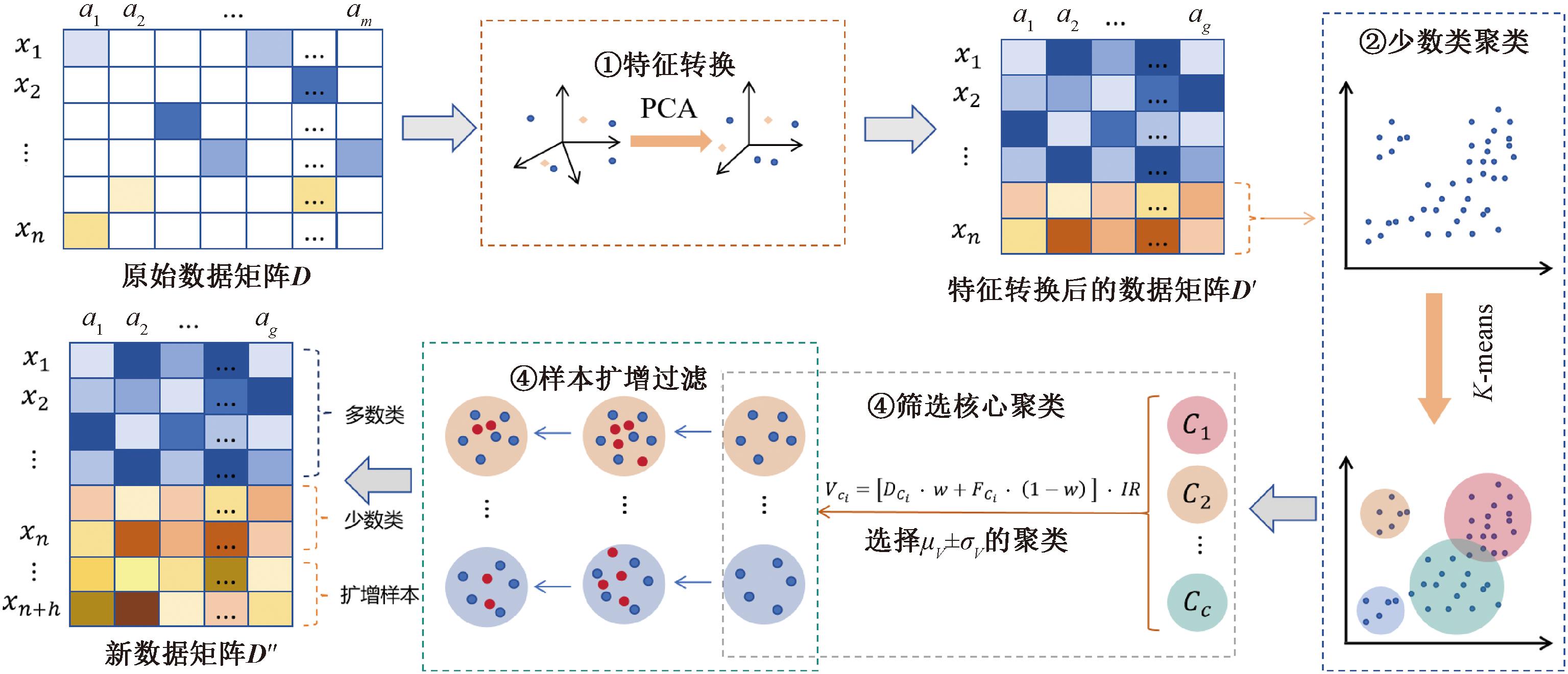
图1 FTMC算法框架
Figure 1 FTMC algorithm framework
(1)特征转换阶段。基于PCA算法对归一化数据特征进行变换降维。该过程可以从原始数据中去除冗余信息,实现数据简化和压缩,增强数据的线性可分性,以缓解其强稀疏性问题。
(2)少数类聚类。对特征转换后矩阵中的少数类样本进行K-means聚类,以捕捉数据的局部特征,同时避免在扩增样本时过度集中在某些特征区域。
(3)筛选核心聚类。该阶段是FTMC算法中的关键步骤,主要目的是计算每个聚类的密度和难度,并结合IR和调整权重比w来计算权重值,然后筛选权重在均值±标准差内的核心聚类进行后续的样本生成及过滤。分配权重和筛选聚类有助于生成更具代表性的合成样本,避免过度集中在某些特征区域,以缓解过拟合和欠拟合,提高数据多样性。
(4)样本扩增过滤。对每个核心聚类通过线性插值生成合成样本,并使用LOF算法检测数据中的异常点进行数据过滤,以确保数据质量,提高模型的鲁棒性。
1.1 特征转换
在此阶段,先将含大量零值的原始数据进行标准化处理,如式(1)所示;再基于PCA 对标准化数据特征变换[13],如式(2)所示。通过选取主成分映射数据,有效降低特征矩阵维数。
(1)
D′=PCA(Z,g)。
(2)
式中:Zij为标准化数据矩阵;Dij为原始数据矩阵;μi为第i个特征的均值;σi为第i个特征的标准差;D′为特征转换后数据矩阵;Z为标准化数据矩阵;g为降维后的维度。
1.2 少数类聚类
该阶段主要针对高维数据中的少数类样本,通过聚类捕捉其分布在不同局部区域的特征,挖掘隐藏特性,识别多种模式,避免局部过度集中,使合成样本更具代表性。
首先,对特征转换后的D′中的少数类样本M+进行K-means聚类[14],聚类的集合表示为
C={Ci|i=1,2,…,c}=K-means(M+,c)。
(3)
其次,计算每个聚类的密度和难度,密度DCi是指在聚类Ci中的样本数量。密度越高,表示该聚类中的样本越多,如式(4)所示:
(4)
式中:NCi表示聚类Ci中样本数量。
难度FCi表示样本到聚类Ci中心的平均距离。距离越大,表示该聚类的样本分布越分散,难度越高,如式(5)所示:
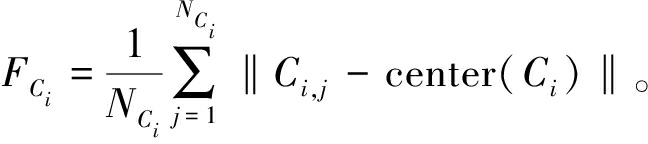
(5)
式中:NCi为聚类Ci中的样本数量;Ci,j为聚类Ci中的样本;center(Ci)为聚类Ci的中心;‖·‖表示欧几里得距离。
1.3 筛选核心聚类
筛选核心聚类是根据聚类的难度和密度信息计算每一个聚类的权重值,以此为基础筛选出核心聚类,用于后续的样本扩增。
聚类Ci的权重值VCi计算公式为
VCi=(DCi·w+FCi(1-w))·IR。
(6)
式中:权重比w介于0和1之间,用于平衡难度和密度的影响;IR为原始矩阵D的不平衡比,即多数类样本数量与少数类样本数量的比值。
该过程引入IR计算权重值,以放大聚类差异。IR高时,少数类样本少,各聚类样本的特征区分度不显著,权重值差异小,难以直接有效比较和筛选;IR低时,少数类样本相对较多,密度DCi和难度FCi能够在一定程度上反映样本的分布及特征,对筛选结果的影响较小。
为了筛选更具代表性的核心聚类集合,需要计算权重值V的均值μV和标准差σV,以此确定聚类筛选的边界。均值和标准差分别为
(7)
(8)
根据均值和标准差,筛选出在上界bupper和下界blower内的聚类,作为核心聚类。
bupper,blower=μV±σV。
(9)
上界bupper外的聚类样本多且分布聚集,分类器对其识别效果相对理想,扩增可能导致过拟合问题;而下界blower外的聚类样本少,含噪声样本,难以代表整体数据特征,扩增易增加欠拟合风险。这种筛选方式能避免聚焦特定区域,以减轻过拟合与欠拟合,提升扩增样本的多样性和代表性。
1.4 样本扩增过滤
样本扩增过滤是通过扩增技术生成合成样本,并通过噪声过滤来增强少数类样本。对于一个少数类xi,使用k近邻法来搜寻与其距离最近的k个少数类样本。此处,样本间的距离定义为n维特征空间里的欧氏距离[3],公式如下:
(10)
式中:xi为某个少数类样本;xj为其他少数类样本(其中j≠i);k为某个少数类样本的某一特征。
将所得距离进行排序,从距离最小的k个近邻中随机选取一个
生成新的样本。扩增公式为
(11)
式中:x′为新生成的样本矩阵;δ为介于0和1之间的随机值。
扩增样本的数量依据数据集中少数类和多数类样本的数量差异来确定。根据不同核心聚类内样本的权重值来决定生成多少个合成样本。首先,将各权重值归一化为相应比例;然后,根据所需生成的样本总量,按此比例对样本进行分配。这种方法可以确保生成的样本数量总量固定,同时不同核心聚类之间的差异性更明显。归一化权重值
和第i个核心聚类扩增样本的数量Ci_num分别为
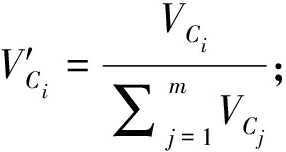
(12)
(13)
式中:h为扩增样本的总数量。
噪声过滤应用LOF算法识别和过滤噪声样本,通过计算每个点的离群因子来判断是否为离群点[15]。若离群因子远大于1,即为离群点;若离群因子接近1,则为正常点。离群因子LOFk(i)为
(14)
式中:ρk(i)为对象i的k最近邻点的局部可达密度;Nk(i)表示与对象i之间距离≤k的对象集合。
经过过滤后保留下的样本矩阵xnew为
xnew=LOF(x′)。
(15)
最后,将扩增过滤得到的样本矩阵与少数类样本矩阵M+相组合得到
再与多数类样本矩阵M-结合,得到新的扩增矩阵D″。
1.5 FTMC 算法
算法1 FTMC算法。
输入:原始数据集D,降维维度g,聚类数量c,权重比w;
输出:扩增后的数据集D″。
① 对原始数据集D标准化得到数据集Z;
② 对Z使用PCA算法,得到维度为g的数据集D′;
③ 划分D′得到多数类样本矩阵M-和少数类样本矩阵M+;
④ 对M+使用K-means算法,划分为c个聚类。记为C={Ci|i=1,2,…,c};
⑤ for each Ci in C do
⑥ 根据式(4)计算密度DCi;
⑦ 根据式(5)计算难度FCi;
⑧ 根据式(6)计算权重值VCi;
⑨ end for
⑩ 初始化扩增样本矩阵x′和扩增过滤后样本矩阵xnew为空集合;
根据式(9)从C中筛选出核心聚类,组成核心聚类集合C′={C1,C2,…,Cm};
for each Cm in C′ do
for each xiin Cm do;
根据式(11)对样本xi进行扩增,得到新的扩增样本,加入x′;
使用LOF算法对x′中的样本进行异常检测和过滤,将过滤后的样本加入xnew;
end for
end for
将xnew与原始少数类样本矩阵M+合并,得到扩增后的少数类样本
将
与多数类样本矩阵M-合并,得到新的扩增数据集D″;
返回扩增后的数据集D″。
1.6 复杂度分析
FTMC算法的实现流程涵盖了特征转换、少数类聚类、核心聚类计算、合成样本生成及噪声处理等关键环节。算法1中各环节复杂度分析如下。
(1)特征转换:先计算协方差矩阵,时间复杂度为O(nm2),其中n为原始样本数,m为原始特征维度;再进行特征值分解,时间复杂度为O(m3)。该环节的时间复杂度为O(nm2)。
(2)K-means聚类:对少数类样本聚类的时间复杂度为O(cpt),其中,c为聚类数量;p为少数类数量;t为迭代次数。
(3)核心聚类计算:该阶段分为两步,一是计算每个聚类的密度和难度,时间复杂度为O(n)和O(nt);二是计算每个聚类的权重值,时间复杂度为O(c)。该环节的时间复杂度为O(nt)。
(4)合成样本生成:首先,根据少数类样本间的距离确定k近邻,时间复杂度为O(p2t);其次,进行排序,时间复杂度为O(pklog p),其中,log p为排序复杂度;最后,通过生成合成样本,时间复杂度为O(hgk),其中,h为合成样本数量。该环节的时间复杂度为O(p2t)。
(5)噪声处理:首先,应用LOF计算生成样本间距离,时间复杂度为O(h2t);其次,排序确定k近邻,时间复杂度为O(hklog h);最后,计算可达密度,时间复杂度为O(hk)。该环节的时间复杂度为O(h2t)。
FTMC算法针对高维微生物数据集所设计,数据维度规模较大,其中特征转换环节的时间复杂度占据主导地位,其时间复杂度为O(nm2)+O(cpt)+O(nt)+O(p2t)+O(h2t)=O(nm2)。
2 实验结果及分析
2.1 实验数据
本文所使用D003015等12个数据集均源自AutoML[16]网站(http:∥39.100.246.211:8050/Dataset),不平衡微生物数据集详细信息见表1。
表1 不平衡微生物数据集
Table 1 Unbalanced microbial datasets
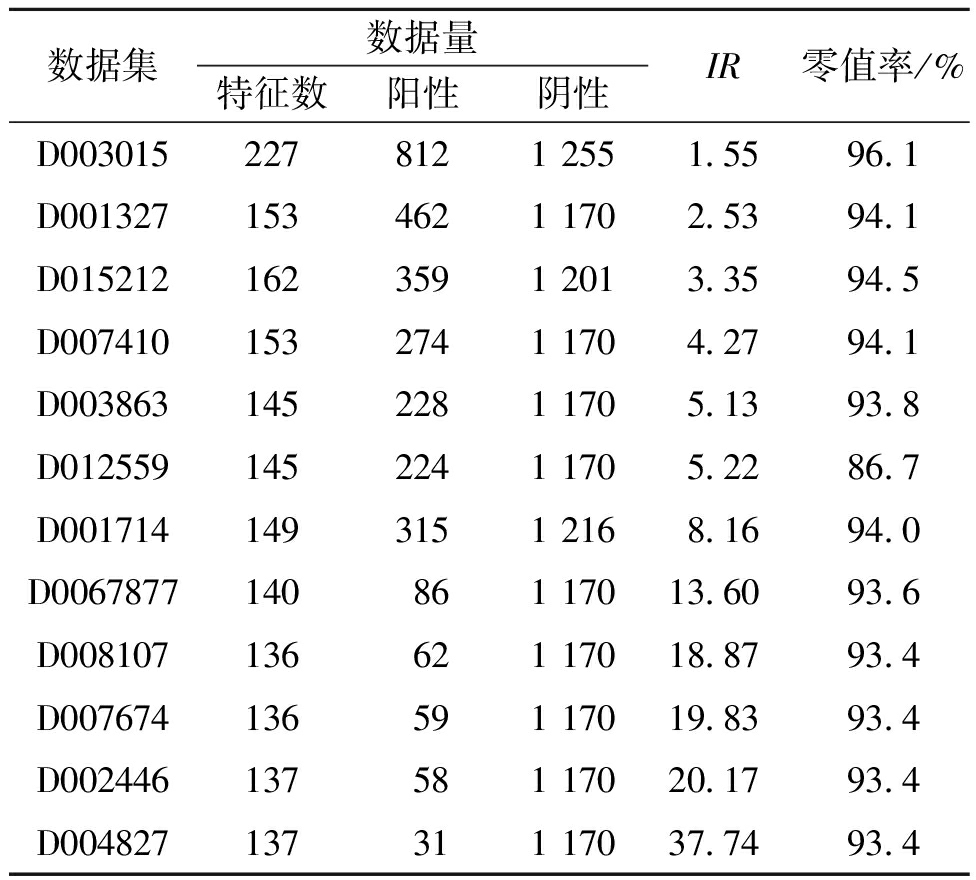
数据集数据量特征数阳性阴性IR零值率/%D0030152278121 2551.5596.1D0013271534621 1702.5394.1D0152121623591 2013.3594.5D0074101532741 1704.2794.1D0038631452281 1705.1393.8D0125591452241 1705.2286.7D0017141493151 2168.1694.0D0067877140861 17013.6093.6D008107136621 17018.8793.4D007674136591 17019.8393.4D002446137581 17020.1793.4D004827137311 17037.7493.4
2.2 对比算法
2.2.1 扩增算法
SMOTE(SMO)通过在少数类样本及其k近邻连线随机生成新样本;根据少数类样本的分布密度,ADASYN(ADA)在较为稀疏的区域生成更多样本;K_means_SMOTE(KSMO)[17]结合K-means与SMOTE,先聚类再在各簇内生成样本;GAN由生成器与判别器对抗生成新样本;VAE是基于变分推断通过学习少数类的潜在分布并采样解码生成新样本;MFCS利用矩阵分解将原始数据分解为对象和特征子空间后进行扩增;KGA通过KPCA映射到低维空间,再用GAN扩增正样本并控制比例;MFSP包括矩阵分解、空间划分及引入代价因子,最后根据类内和类间距离过滤合成样本。
2.2.2 聚类算法
DBSCAN[18]是一种基于密度的聚类算法,通过邻域半径和最小点数识别核心点和噪声点,可发现任意形状的聚类。OPTICS[19]是其改进版,计算可达距离生成有序列表,支持按需截取聚类。AGNES[20]是一种凝聚式层次聚类算法,从各点独立开始,逐步合并最近类形成聚类树,无须预设聚类数。
2.3 评价指标
本文使用表2的混淆矩阵,基于Recall、G-mean和AUC这3个指标来评估不同采样算法的分类性能:
(16)
(17)
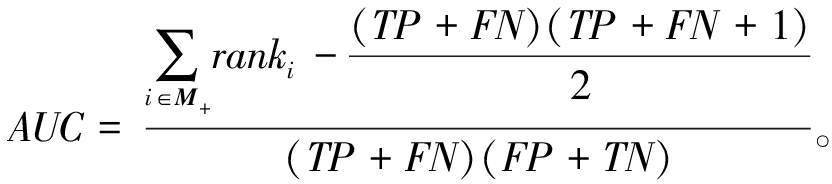
(18)
表2 混淆矩阵
Table 2 Confusion matrix
分类预测正类预测负类真实正类TPFN真实负类FPTN
式中:
为正样本的序号之和。
2.4 扩增结果
本节使用t-SNE算法进行数据可视化。图2为D003863、D007674和D004827经过SMOTE、MFSP和FTMC这3种不同扩增算法的前后对比效果。
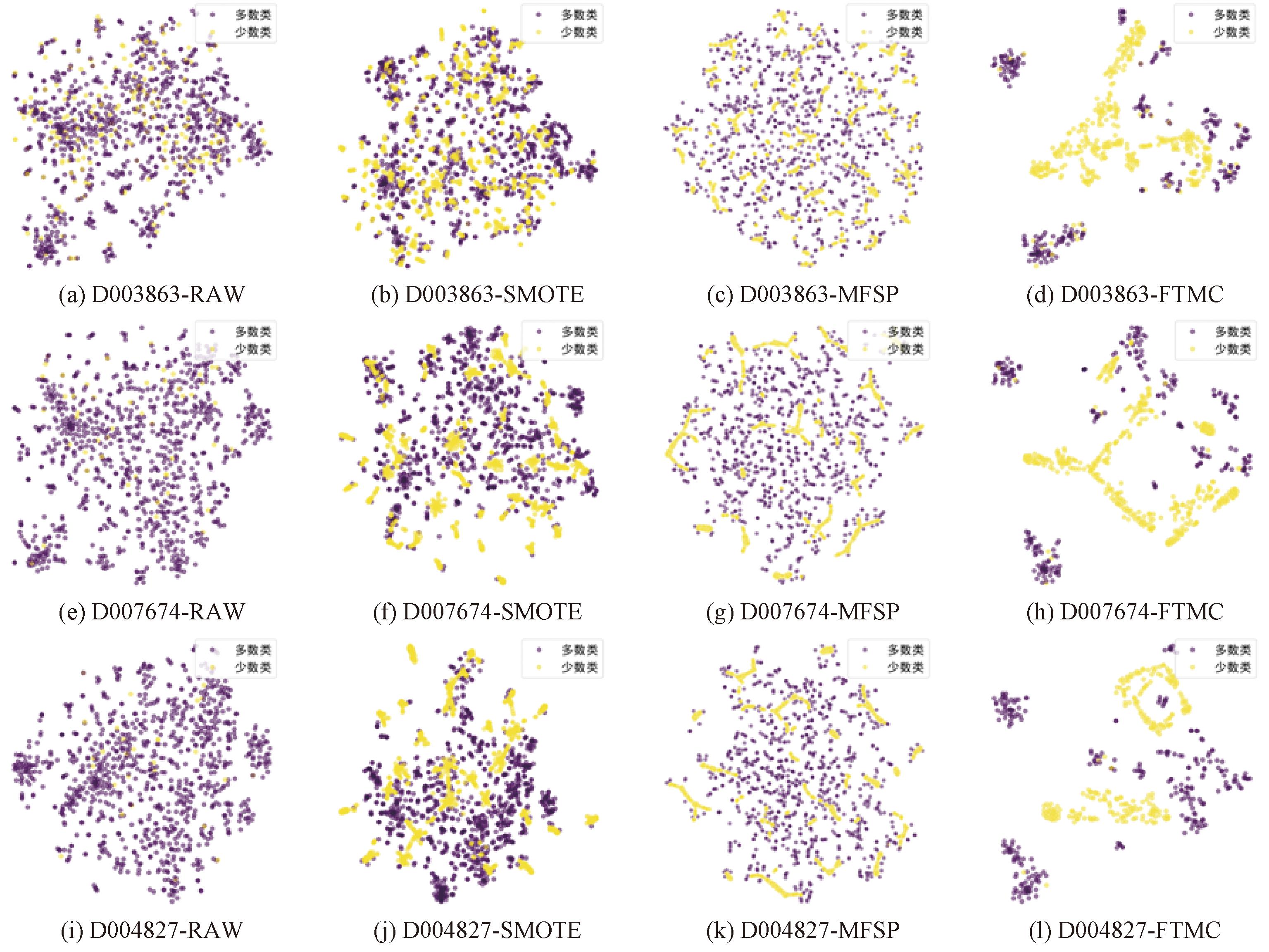
图2 不同算法在数据集D003863、 D007674和D004827上的扩增结果
Figure 2 Augmentation results of different algorithms on datasets D003863, D007674 and D004827
图2显示了D003863原始数据中正负样本随机分布,难以区分的数据经SMOTE与MFSP算法扩增后,虽数量平衡,但样本分布集中甚至重叠。D007674和D004827因IR高,原始数据的正样本稀缺且分布无序,经SMOTE和MFSP算法扩增后虽缓解了数量不平衡,但样本分布仍较为集中。相比之下,FTMC算法扩增后,3个数据集的正负样本分布规律明显,边界清晰,可区分度更高,表明其在数据质量与样本多样性方面具有明显优势,更利于分类器建模与评估。
2.5 分类性能
实验将数据集按8∶2划分为训练集和测试集,保持测试集的不平衡比与原始数据一致。每组实验重复10次,并取均值以减少随机性影响。随后在12个数据集上对比了FTMC与8种扩增方法的分类性能。
图3为各个扩增方法在3种分类器下的分类结果。其中,KNN表示K-nearest neighbour;SVM表示support vector machine;LR表示logistic regression。
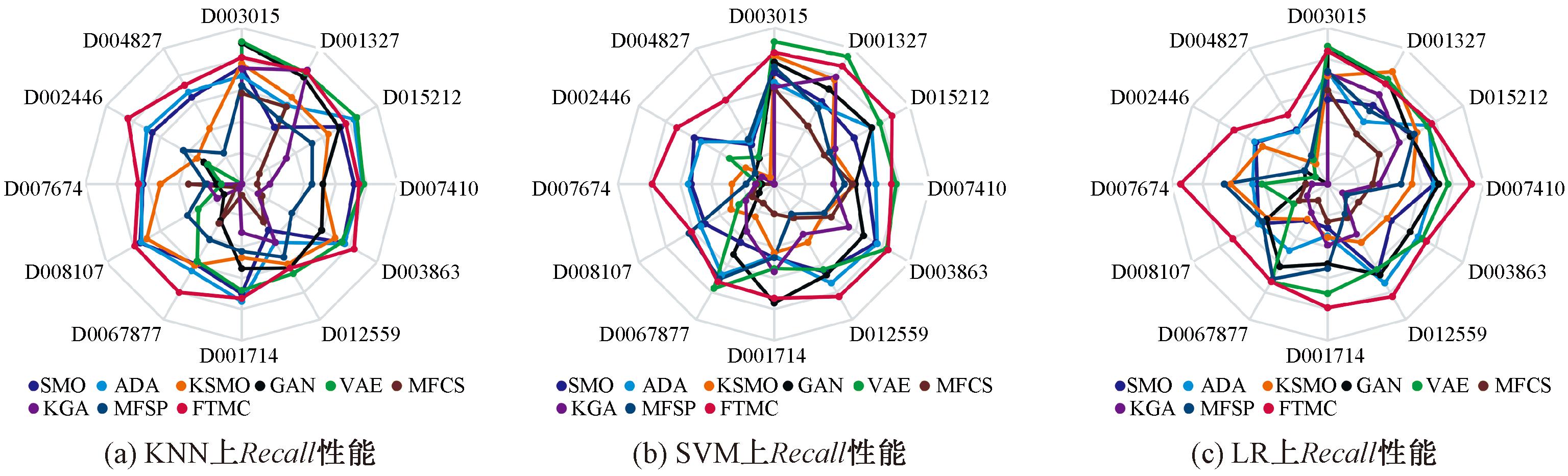
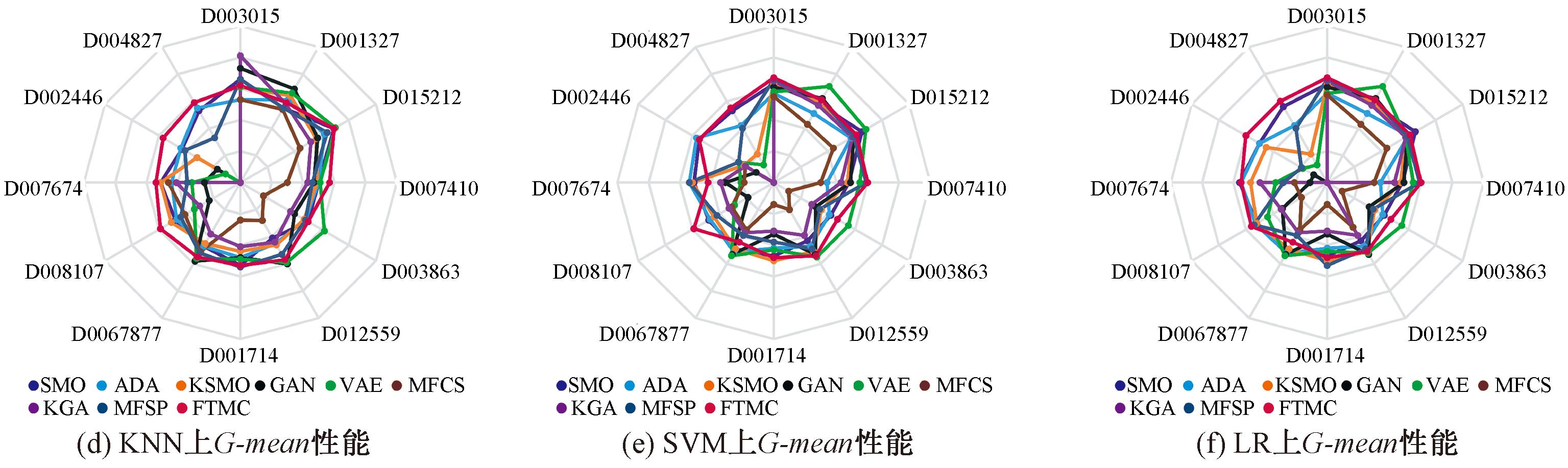
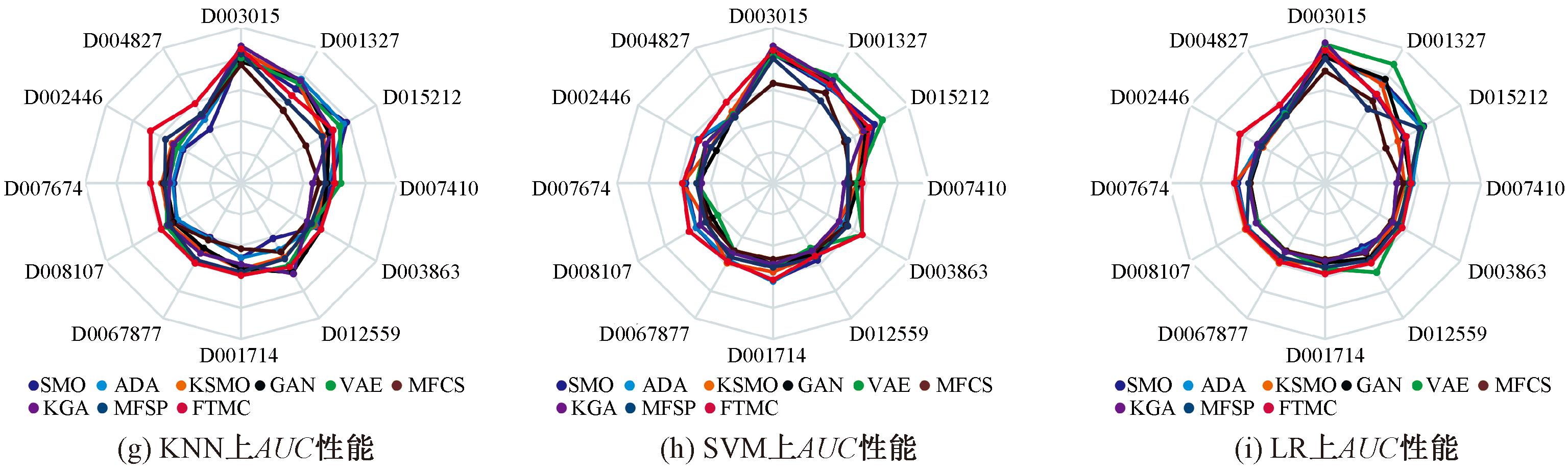
图3 Recall、G-mean和AUC性能对比结果
Figure 3 Comparison results of Recall, G-mean and AUC performance
由图3可知,在12个数据集以及KNN、SVM和LR分类器的实验环境下,FTMC 算法在Recall、G-mean和AUC关键指标上,均展现出超越其他最新采样算法的性能优势,特别在高IR数据集上表现突出,例如在D002446数据集上,FTMC算法的Recall达到0.89,G-mean和AUC分别为0.59和0.74,各项指标不仅稳定且全面超越对比算法,充分体现了FTMC算法在分类性能上的优越性,证明其在识别正样本上优于其他算法。
2.6 消融实验
为探究特征转换阶段、少数类聚类阶段与筛选核心聚类阶段以及应用不同聚类算法对生成样本质量和分类性能的影响,本小节分为算法阶段和聚类阶段两个部分进行消融实验。
2.6.1 算法阶段
本小节选取D003863、D007674和D004827数据集对FTMC算法进行消融实验,实验结果如表3所示。在表3中,FTMC-PCA表示消融特征转换的算法;FTMC-K-means表示消融少数类聚类的算法;FTMC-Screening表示消融筛选核心聚类的算法。
表3 消融实验
Table 3 Ablation experiment
模型D003863D007674D004827Recall G-meanAUCRecall G-meanAUCRecall G-meanAUCFTMC-PCA0.050.210.520.160.380.520.130.310.47FTMC-K-means0.370.170.540.490.210.470.470.140.51FTMC-Screening0.600.440.530.650.450.520.420.450.50FTMC0.73 0.47 0.57 0.72 0.55 0.53 0.51 0.58 0.60
由表3可知,FTMC算法中的特征转换阶段、少数类聚类阶段以及筛选核心聚类阶段均对分类性能的提升起到了重要的作用。特别是特征转换阶段,在Recall和G-mean指标上展现了显著的提升效果,并且在AUC指标上也有一定的提高。说明FTMC算法能够有效解决微生物数据的高维性、稀疏性和类别不平衡问题,使得分类器识别出更多的阳性样本,以验证FTMC算法的可行性和有效性。
2.6.2 聚类阶段
在12个数据集上的聚类阶段应用不同聚类算法(K-means、DBSCAN、OPTICS和AGNES)进行消融实验,如图4所示。
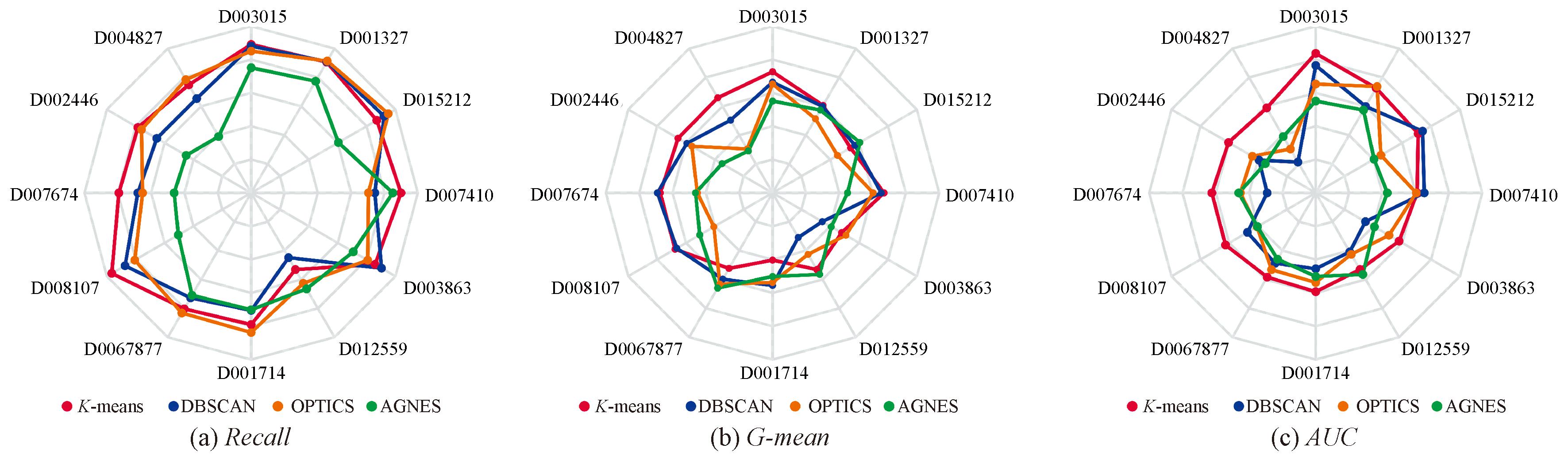
图4 FTMC算法应用不同聚类算法的各指标结果
Figure 4 Results of various indicators for the FTMC algorithm with different clustering algorithms
由图4可知,K-means、DBSCAN和OPTICS 的分类性能良好,且受影响较小,而AGNES却大多表现欠佳;K-means表现优秀,在处理高IR的数据集时,优势明显。综合Recall、G-mean和AUC指标来看,K-means算法的适应性与优势更为显著。
2.7 超参实验
FTMC模型有3个关键的超参数:降维维度g、聚类数量c和权重比w。本节通过D007674数据集在3个分类器上测试不同取值的影响,结果如图5所示。
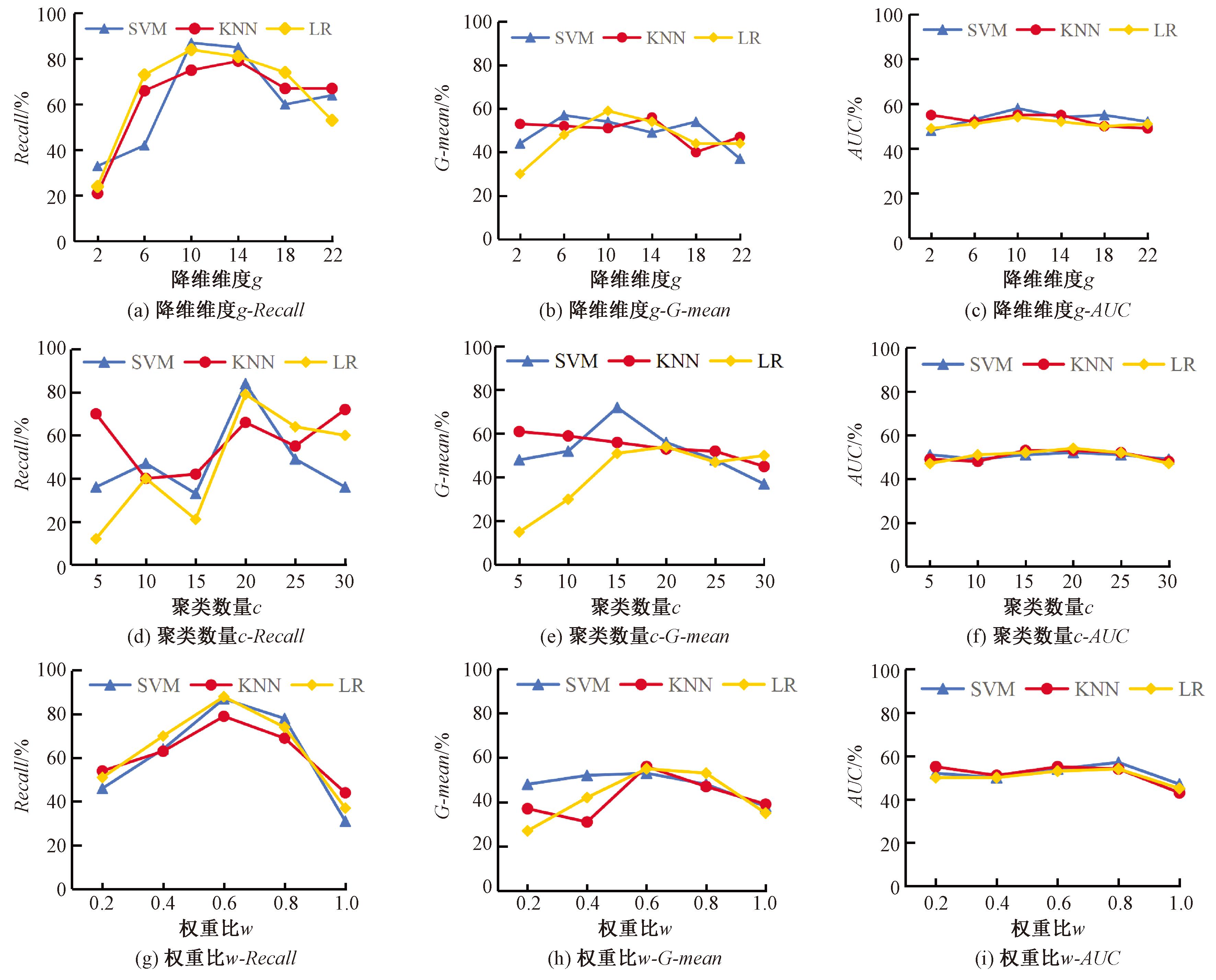
图5 FTMC算法取不同g、c和w值时在3个分类器上的性能
Figure 5 Performance results of the FTMC algorithm on three classifiers with different values of g, c and w
结果表明,10≤g≤14时,Recall稳定且较高,G-mean 波动较小,AUC 相对稳定且小范围浮动;5≤c≤30时,Recall 波动大,20≤c≤25时,G-mean稳定,AUC小范围内浮动;0.2≤w≤1.0时,Recall波动大,w=0.6附近较优,0.6≤w≤0.8时,G-mean 稳定,AUC小范围内浮动,0.8≤w≤1.0时,AUC略有下降。综合来看,不同参数取值对算法性能的影响各异,在实际应用中需根据具体情况选择合适的参数,以优化算法性能。
2.8 FTMC局限性
FTMC算法有效缓解了微生物数据的高维性、稀疏性和类别不平衡问题,在Recall、G-mean和AUC上表现出色,均优于现有采样算法。其各阶段对分类性能的提升均起到重要作用,生成的扩增样本兼具多样性和代表性,但该算法仍存在一定的局限性。
在分类性能方面,虽然FTMC算法在大多数数据集上表现良好,但是处理IR过低的数据集时,FTMC可能不再具有显著的优势。
就参数选择而言,FTMC模型涉及数据维度、聚类数量和权重比等关键超参数。从图5的超参实验的结果来看,不同的参数组合对算法性能影响较大,且在实际应用中很难预先确定最优参数组合,这增加了算法应用的难度与不确定性,参数的调整过程也需要耗费大量计算资源与时间成本。
3 结论
针对微生物数据的高维性、稀疏性以及类别不平衡等问题,本文提出一种基于特征转换和少数类聚类的数据扩增算法FTMC。首先,利用PCA算法进行特征转换,借此降低特征维度、保留重要信息,以缓解强稀疏性问题;其次,通过对少数类进行聚类,分析识别其不同模式,防止样本扩增时过度聚焦特定特征,使扩增样本特征覆盖更全面;随后,综合各聚类的密度、难度,结合IR与权重比调整来计算权重值,选择权重值在均值和标准差范围内核心聚类内的样本进行扩增,降低过拟合与欠拟合概率,有效提升了扩增样本的多样性和代表性;最后,应用LOF算法检测并过滤异常样本,确保合成样本集的数据质量与分布合理性,提高样本多样性及分类性能。实验结果表明,通过FTMC算法生成的扩增样本,在数据质量与分布合理性方面均表现出色,尤其是在处理IR较高数据集时,这种优势更为凸显。这些样本更具多样性和代表性,有效解决了微生物数据的高维性、稀疏性以及类别不平衡等关键问题。
[1] MEGAHED F M, CHEN Y J, MEGAHED A, et al. The class imbalance problem[J]. Nature Methods, 2021,18(11): 1270-1272.
[2] 田鸿朋,张震,张思源,等.复合可靠性分析下的不平衡数据证据分类[J].郑州大学学报(工学版),2023,44(4):22-28.
TIAN H P,ZHANG Z,ZHANG S Y,et al.Imbala-nced data evidential classification with composite reliability[J].Journal of Zhengzhou University (Engine-ering Science),2023,44(4):22-28.
[3] THABTAH F, HAMMOUD S, KAMALOV F, et al. Data imbalance in classification: experimental evaluation[J]. Information Sciences, 2020, 513: 429-441.
[4] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321-357.
[5] HE H B, BAI Y, GARCIA E A, et al. ADASYN: a-daptive synthetic sampling approach for imbalanced le-arning[C]∥2008 IEEE International Joint Conference onNeural Networks. Piscataway: IEEE, 2008: 1322-1328.
[6] MOREO A, ESULI A, SEBASTIANI F. Distributional random oversampling for imbalanced text classification[C]∥Proceedings of the 39th International ACM SIGIR Conference on Research and Development in Informat-ion Retrieval. New York: ACM, 2016: 805-808.
[7] 王曦, 温柳英, 闵帆. 融合矩阵分解和代价敏感的微生物数据扩增算法[J]. 数据采集与处理, 2023, 38(2): 401-412.
WANG X, WEN L Y, MIN F. Fusing matrix factoriz-ation and cost-sensitive microbial data augmentation al-gorithm[J]. Journal of Data Acquisition and Processing,2023, 38(2): 401-412.
[8] 温柳英, 吴俊, 闵帆. 融合矩阵分解和空间划分的微生物数据扩增方法[J]. 山东大学学报(理学版), 2025, 60(1): 14-28,44.
WEN L Y, WU J, MIN F. Fusing matrix factorization and space partition microbial data augmentation algorithm[J]. Journal of Shandong University (Natural Science), 2025, 60(1): 14-28, 44.
[9] LI Y, HUANG C, DING L Z, et al. Deep learning in bioinformatics: introduction, application, and perspective in the big data era[J]. Methods, 2019, 166: 4-21.
[10] LI Y X, CHAI Y, YIN H P, et al. A novel feature learning framework for high-dimensional data classification[J]. International Journal of Machine Learning and Cybernetics, 2021, 12(2): 555-569.
[11] WEN L Y, ZHANG X M, LI Q F, et al. KGA: inte-grating KPCA and GAN for microbial data augmentation[J]. International Journal of Machine Learning and Cybernetics, 2023, 14(4): 1427-1444.
[12] FENG W, HUANG W J, REN J C. Class imbalance ensemble learning based on the margin theory[J]. Applied Sciences, 2018, 8(5): 815.
[13] ABDI H, WILLIAMS L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433-459.
[14] AHMED M, SERAJ R, ISLAM S M S. The k-means algorithm: a comprehensive survey and performance evaluation[J]. Electronics, 2020, 9(8): 1295.
[15] BREUNIG M M, KRIEGEL H P, NG R T, et al. LOF: identifying density-based local outliers[C]∥Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2000: 93-104.
[16] HE X, ZHAO K Y, CHU X W. AutoML: a survey of the state-of-the-art[J]. Knowledge-Based Systems, 2021, 212: 106622.
[17] DOUZAS G, BACAO F, LAST F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE[J]. Information Sciences, 2018, 465: 1-20.
[18] DENG D S. DBSCAN clustering algorithm based on density[C]∥2020 7th International Forum on Electrical Engineering and Automation (IFEEA). Piscataway: IEEE, 2020: 949-953.
[19] ANKERST M, BREUNIG M M, KRIEGEL H P, et al. OPTICS: ordering points to identify the clustering structure[C]∥Proceedings of the 1999 ACM SIGMOD International Conference on Management of Data. New York: ACM, 1999: 49-60.
[20] SCHILT K. The importance of being Agnes[J]. Symbolic Interaction, 2016, 39(2): 287-294.