线性工作台是数控机床的基本运动单元,其精度直接影响数控机床的运动精度和加工精度[1-2]。一维线性工作台常采用双导轨四滑块配置,是典型的并联结构,它的实际运动是零部件加工误差、装配误差、零部件弹性与载荷工况耦合下的六自由度误差运动[3-4],是多种误差协调变形作用下相互耦合的综合结果[5]。
目前,国内外学者针对数控机床和线性工作台误差进行了大量研究。在误差建模方面,以多体系统理论结合齐次坐标变换为基础的误差建模与分析方法最为普遍适用[6-7],但通常以线性工作台整体为研究对象,没有充分考虑导轨直线度误差、两导轨不平行度误差、安装基面加工误差、4个滑块的姿态误差以及弹性协调变形后工作台总体空间位姿的影响[3,7]。在误差耦合机制方面,Tao等[8]、Fan等[9]主要以线性导轨为研究对象,研究集中在滚珠弹性变形、预紧力/外载荷以及导轨轮廓误差等方面,采用有限元与理论分析相结合的方式来探索误差传递规律。在滚珠弹性变形方面,陈汀等[10]假定导轨和滑块为刚体,将滚珠的弹性变形作为误差源,基于赫兹接触理论研究滚珠和滑块裙部变形的影响;吴煜等[5]通过建立滑块-滚珠-导轨的等效弹簧模型,分析滚珠变形量对线性工作台整体空间误差的影响。学者们利用结合面基础特性参数描述了滚珠导轨结合面上各点的相对变形,并用受力平衡方程推导了结合面的相对位移和零件几何尺寸之间的关系[11-15]。同时,外载荷作用下弹性变形、导轨轮廓误差以及多滚动体的误差均化作用都对线性工作台运动产生较大影响[16]。现有耦合机制方面的研究把各部分作为独立单元去研究,只能获得局部影响规律,无法完全揭示不同误差对整体空间误差的影响规律和耦合机制。
在工程实践中,一维线性工作台单个导轨直线度常通过测量滑块运动直线度误差获取。导轨平行度误差既涵盖两导轨在水平面与垂直面内的直线度误差,也包含导轨移动副装配误差[14]。在导轨平行度误差对工作台误差影响方面,何改云等[17]根据多体系统理论和滑块几何结构关系,联合外载荷建立了平行度对工作台误差影响的分析模型,并通过有限元验证了结论;Shi等[18]考虑了导轨之间的平行度误差,建立了准静态分析模型,研究了静压导轨平行度误差对运动精度的影响;Kim等[19]则提出了一种使用传递函数方法计算滑台运动误差的方法,能够计算出由于滑轨导轨平台的直线度引起的运动误差。现有研究将两导轨平行度误差作为单向因素推导最终工作台运动误差,没有考虑安装在导轨上滑块在工作台作用下的协调变形,即没有考虑工作台对滑块和导轨的反作用力。
综上所述,两直线导轨平行度误差是影响一维线性工作台的关键参数,研究其对工作台的运动误差的影响规律非常重要,但是目前在误差建模、误差耦合、影响规律等多个方面的研究依然存在不足。本文以双导轨四滑块线性工作台为研究对象,考虑了滑块在导轨和工作台双重约束下,工作台协调变形的最终位姿状态,建立了两导轨平行度误差与工作台运动误差的映射模型,进而分析了不同种类误差对工作台整体运动误差的影响规律。
1 滑块初始误差映射模型
1.1 一维线性工作台结构
一维线性工作台常采用双导轨四滑块配置如图1所示,主要由基座、导轨、滑块以及工作台构成。两根导轨固定安装在基座上端两侧,每根导轨上安装有两个滑块,滑块内侧和导轨外侧都有滚珠滚道,通过设置于滚道内的滚珠循环滚动实现滑块在导轨上的直线移动,工作台安装在4个滑块上端。
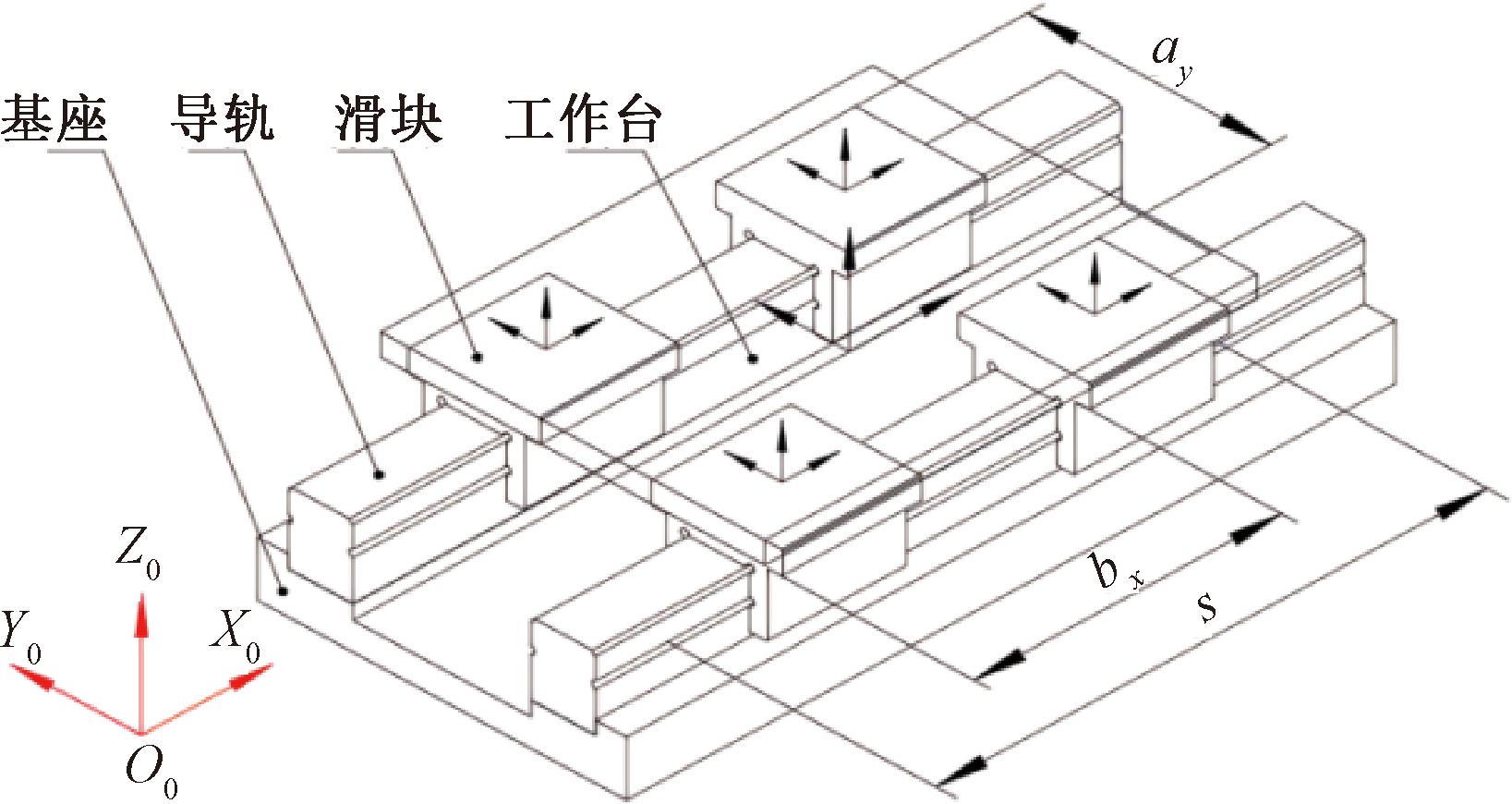
图1 一维线性工作台结构图
Figure 1 One-dimensional linear worktable structure diagram
如图2所示,s为两块在导轨上移动的总行程;bx为同一导轨前后两滑块之间的间距;ay为装配后两导轨的横向跨距。{Oi,xi,yi,xi}(i=1,2,3,4)为4个滑块的运动坐标系,{Ow,xw,yw,zw}为工作台上表面中心运动坐标系,且5个运动坐标系的坐标轴均平行于固定坐标系{O0,x0,y0,z0}。
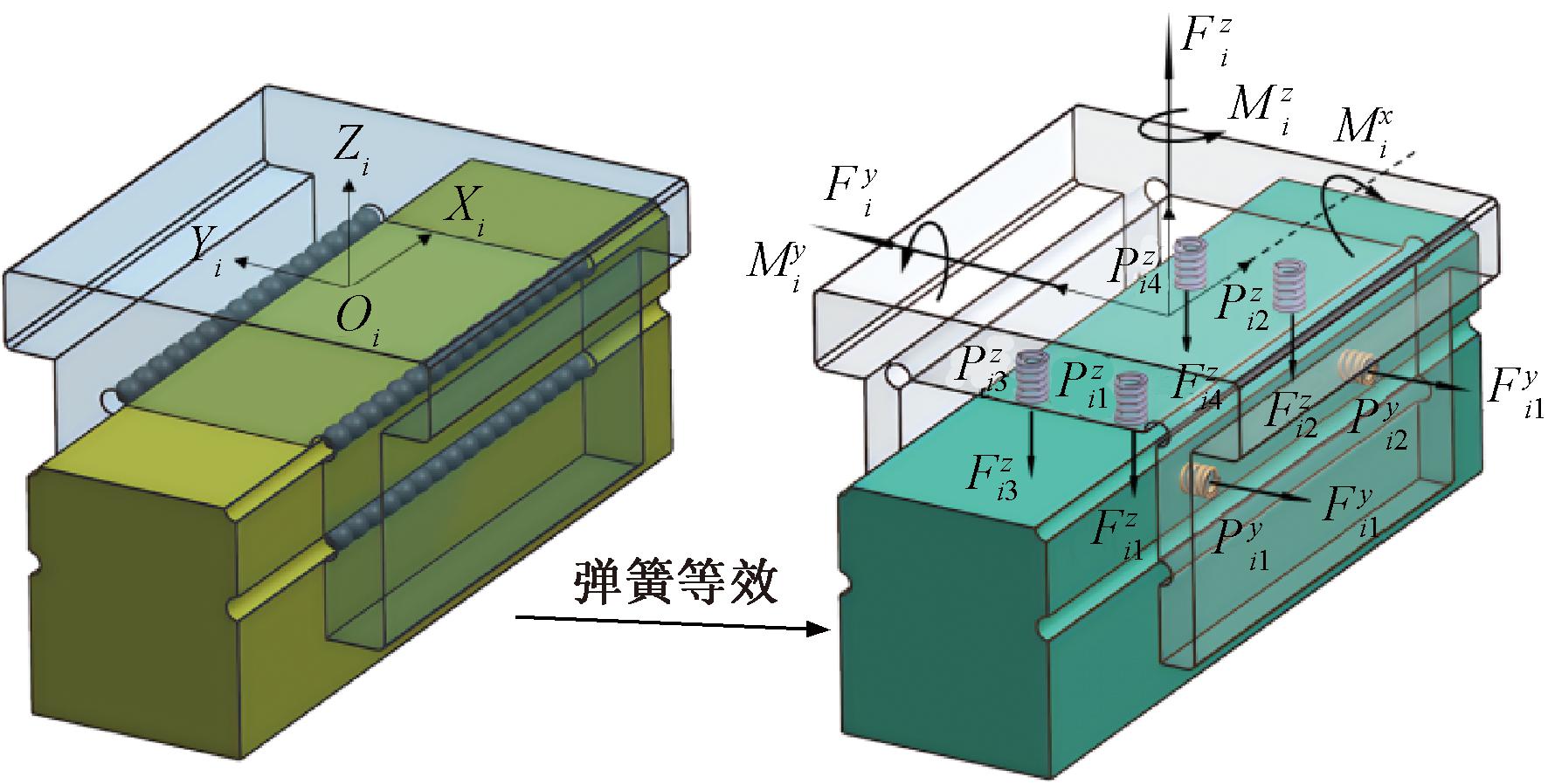
图2 滑块弹簧等效模型与力学模型
Figure 2 Sliding block spring equivalent model and mechanical model
1.2 线性工作台滑块刚度求解
为了求解相对滑块坐标系的五项刚度[5],如图2所示,将4列滚珠用弹簧等效,其中,沿着Z向布置4个弹簧,沿着Y向布置两个弹簧,弹簧的刚度分别为
和
在滑块上的固定端为
和
固定端
和在滑块坐标系{Oi,xi,yi,xi}中的坐标分别为
和
在上述弹簧的各项参数中,上标x、y 代表弹簧放置的方向,i代表滑块的序号,j代表弹簧的序号。滑块的弹簧等效如式(1)所示:
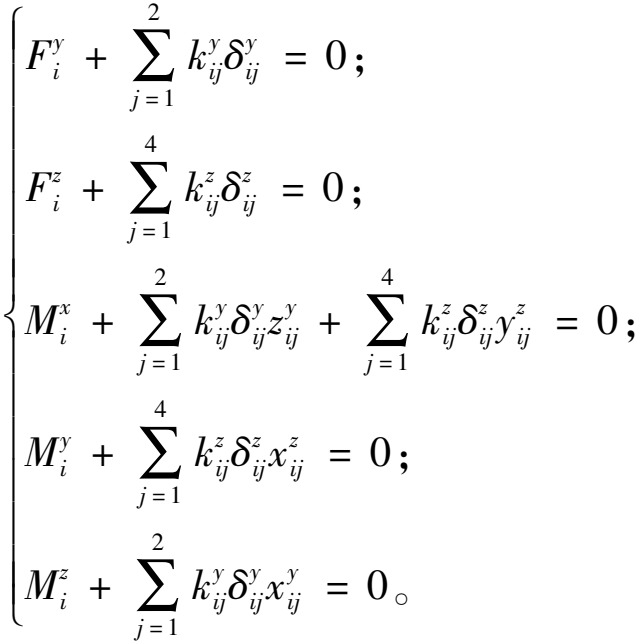
(1)
当外载荷
作用到滑块上时,弹簧由于受力产生变形
与
从而产生约束反力
和
最终滑块在两者的作用下处于平衡状态。并且根据多体系统理论,弹簧的变形量可以由滑块变形产生的误差矢量
求得,其中
(2)
将式(2)代入到式(1)中,可得到外载、滑块误差与等效弹簧刚度间的线性关系式,整理得
Ф。
(3)
式中:
为对滑块坐标系的弹簧等效刚度约束矩阵。
如图3所示,固定端位置的部分参数可以由滑块几何结构求出。而等效弹簧的刚度和其他位置参数可以联合中心位置刚度求出。
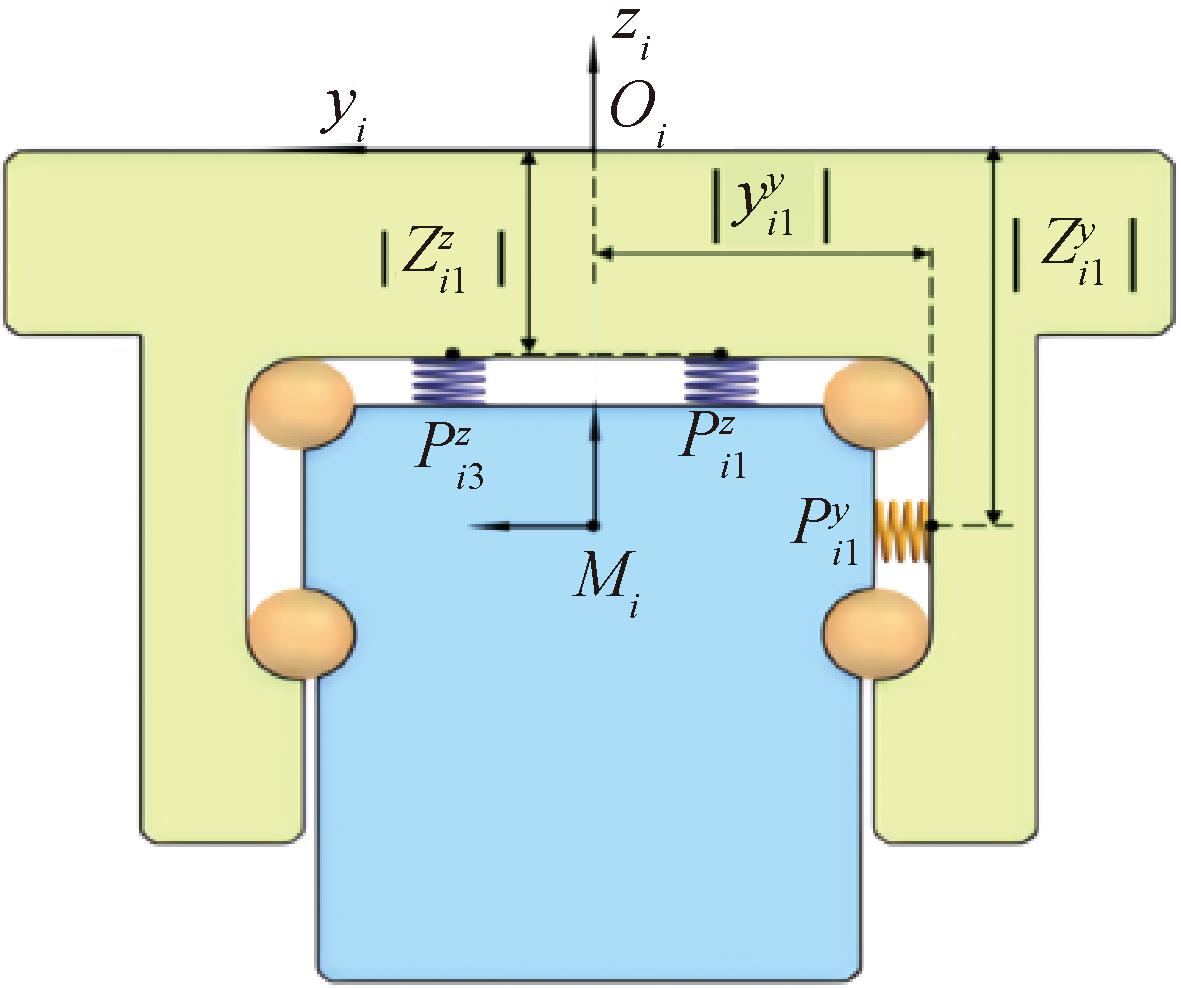
图3 等效弹簧固定端位置参数
Figure 3 Position parameters of fixed end of equivalent spring
如果按照滑块中心坐标系来求解刚度,则Y向弹簧在中心坐标系中的坐标为
向弹簧在中心坐标系的位置为
将坐标代入到滑块刚度矩阵,并根据相对滑块中心位置的五项刚度
可以求出等效弹簧的刚度和其他固定端位置参数:
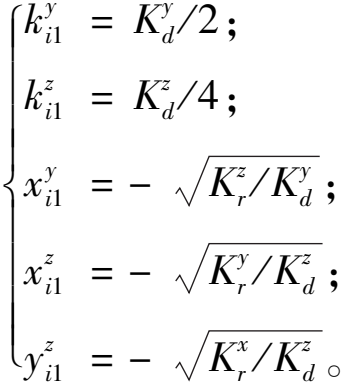
(4)
由图3可得,Y向弹簧固定点的Z轴坐标值为
为了方便表示,将Z轴坐标值用H代替,则求解之后的滑块刚度约束矩阵为
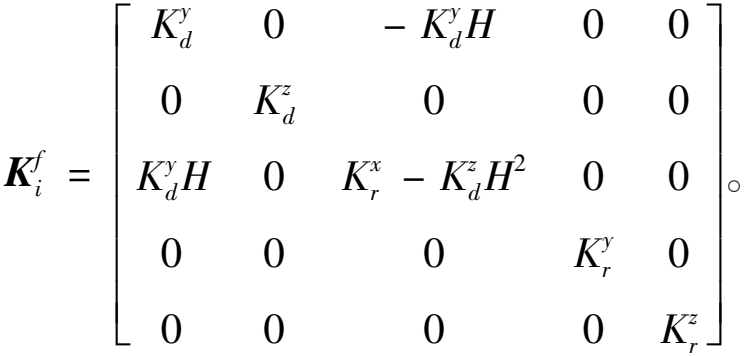
(5)
1.3 线性工作台受力分析
在式(1)中,滑块受到外载荷即为工作台与滑块之间的内力,那么工作台受到与此大小相等,方向相反的反作用力。如图4所示,假设没有外载荷作用,取工作台为研究对象进行整体受力分析,工作台在4个滑块综合作用下保持平衡,用载荷矢量的形式表达为[5]
(6)
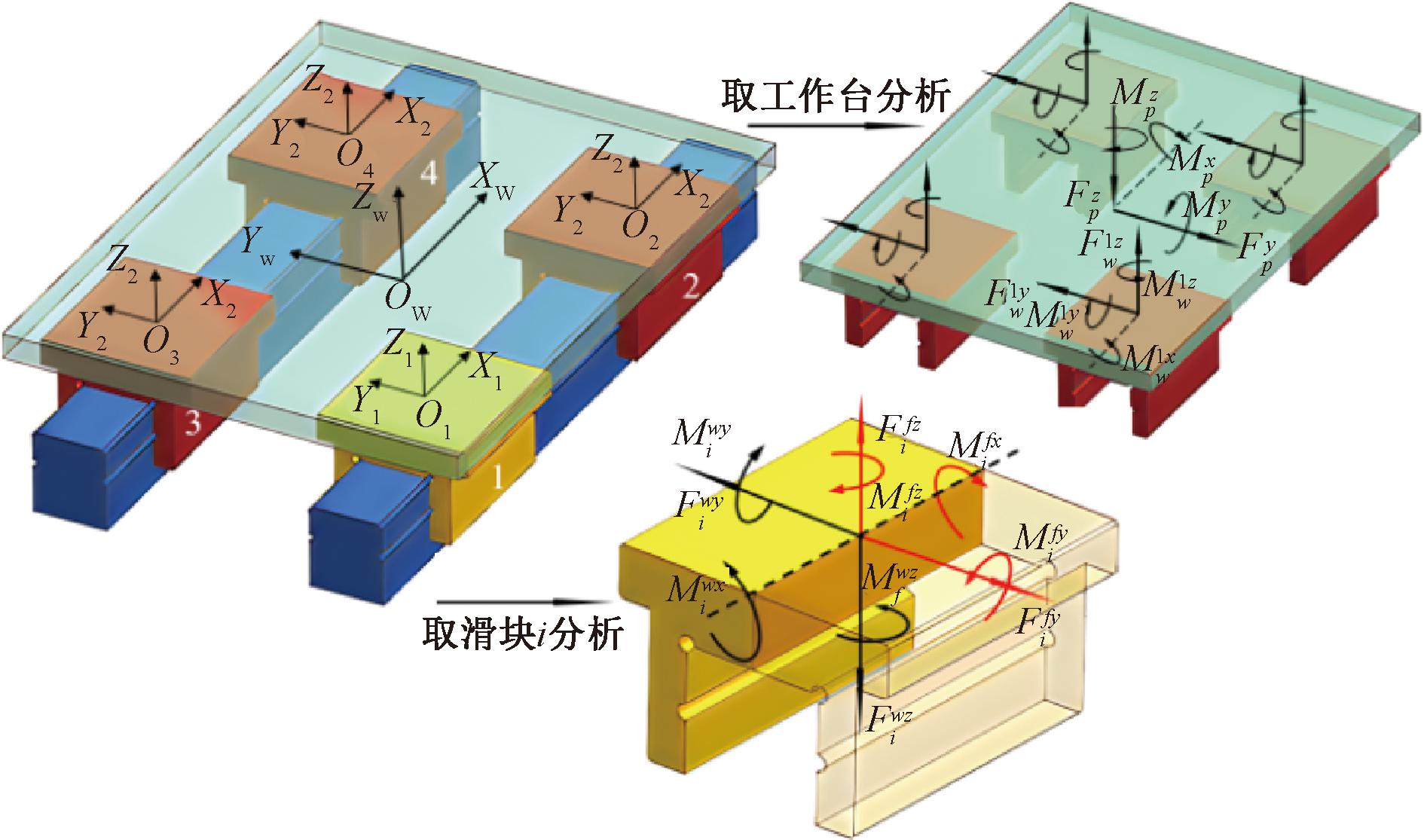
图4 工作台和滑块受力模型
Figure 4 Force model of worktable and slider
在工作台坐标系{Ow,xw,yw,zw}中建立平衡方程:
(7)
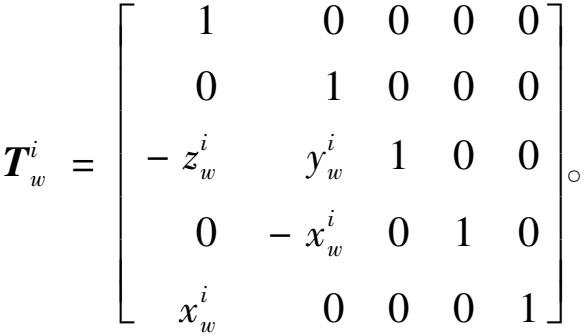
(8)
式中:
表示滑块坐标系{Oi,xi,yi,zi}原点在工作台坐标系{Ow,xw,yw,zw}中的坐标位置。
需要注意的是,工作台对滑块的载荷矢量与滑块对工作台的载荷矢量应该有以下关系:
(9)
1.4 一维线性工作台误差耦合模型
如图5所示,假设4个滑块在装配工作台之前在各自行程内的误差矢量为
假设装配后在整个行程中的误差矢量为Фi(xi)。把工作台给滑块的载荷矢量
视为导轨约束下的外载荷[5],则根据式(3)可得
(10)
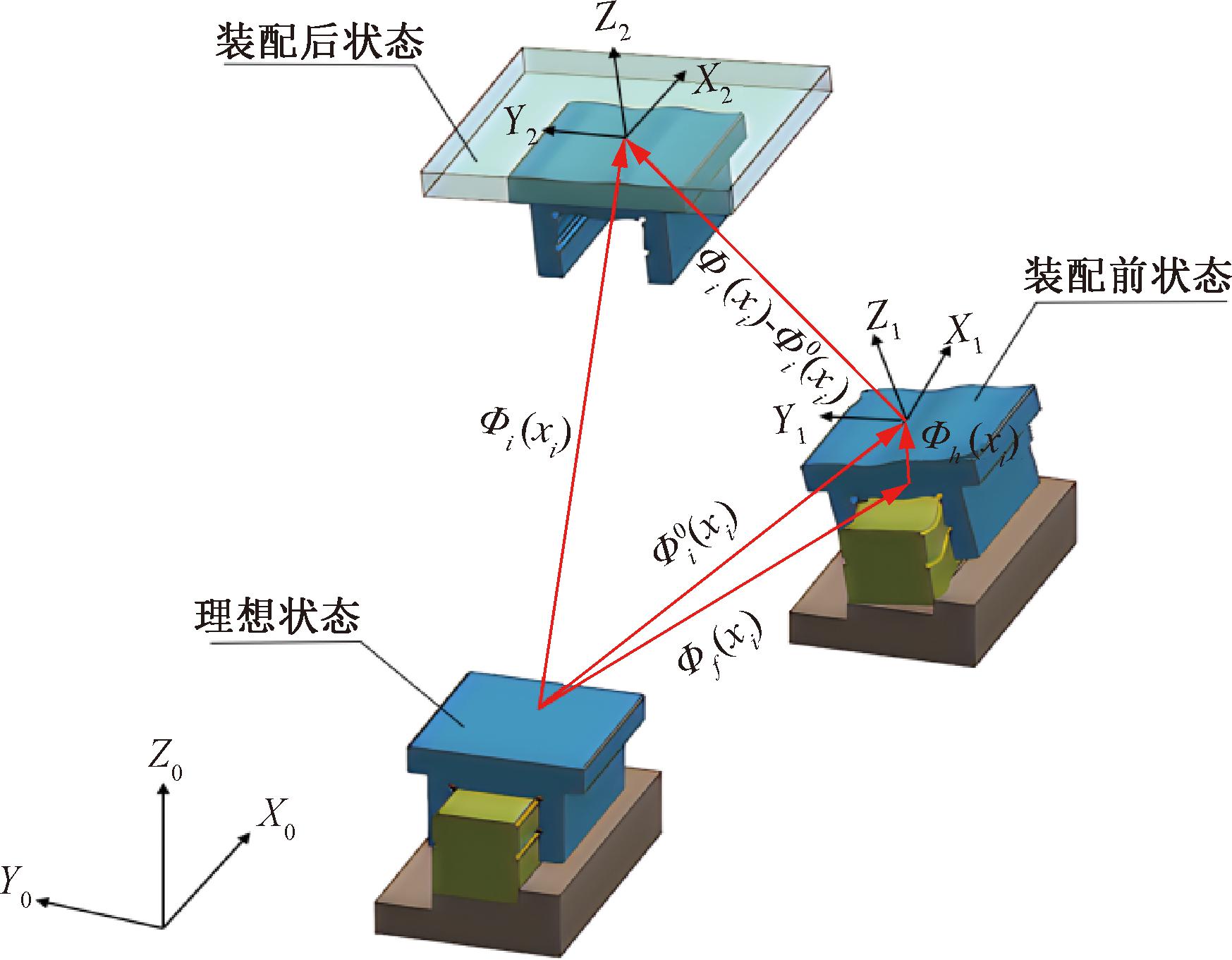
图5 导轨-滑块弹性约束模型
Figure 5 Guide rail-slider elastic constraint model
式中:
如图6所示,一维线性工作台各零部件都装配完成,工作台在行程上任意位置误差矢量为Фw(xw),假设安装一维线性工作台是从上往下装配,将滑块固定在工作台上后,此时滑块只受到工作台的约束,则此时滑块的误差矢量ФiR(xiR)会由工作台的误差矢量Фw(xw)决定:
Фw(xw)。
(11)
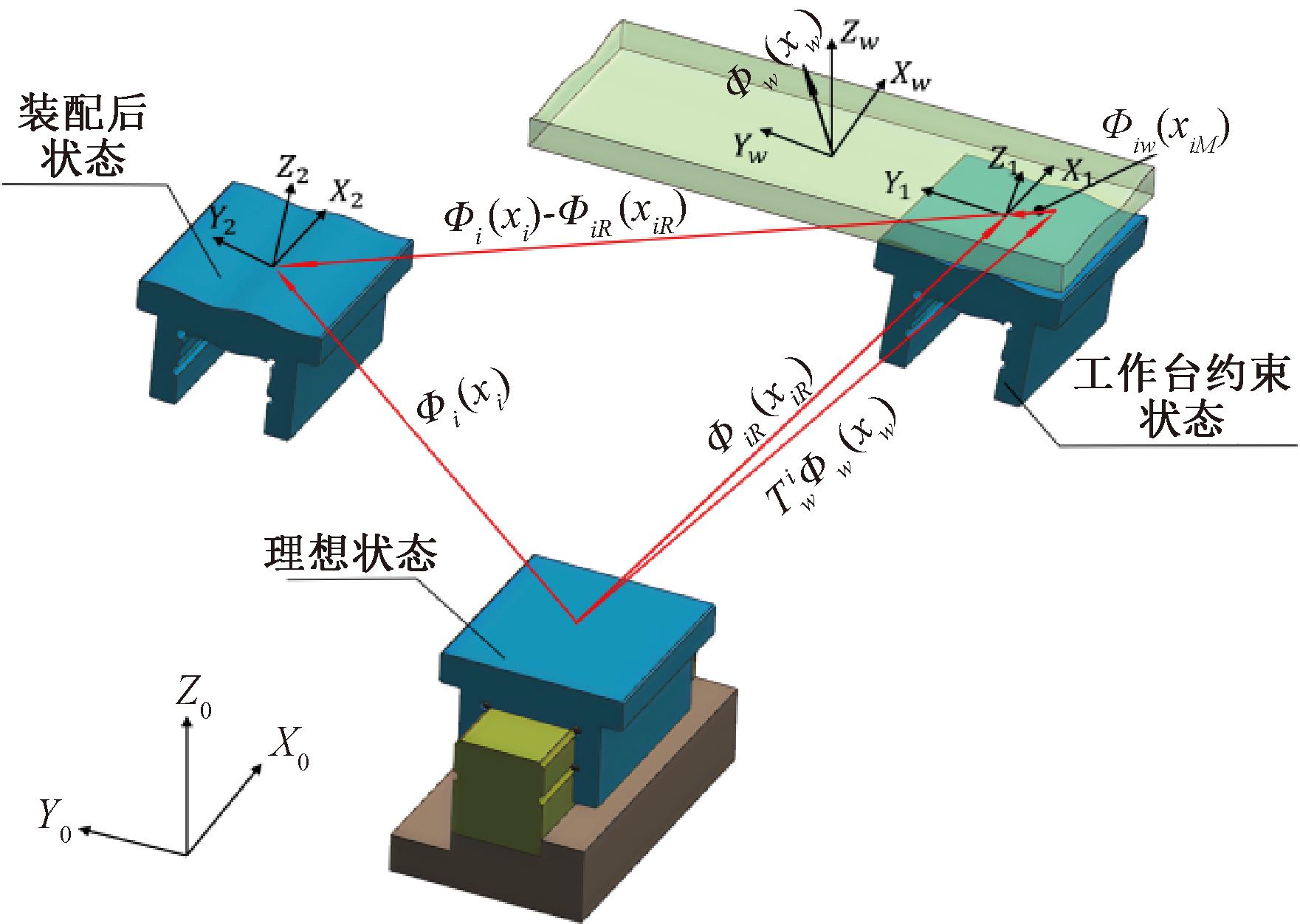
图6 工作台-滑块弹性约束模型
Figure 6 Worktable-slider elastic constraint model
式中:
γw(xw),βw(xw),αw(xw)]T;
βiR(xiR),αiR(xiR)]T。
根据工作台的受力平衡方程,联合式(9)并将式(10)代入到式(7)中可得
(12)
误差矢量Фi(xi)是根据导轨约束从下往上建模推出的滑块误差矢量,同时,误差矢量ФiR(xiR)是根据工作台约束从上往下建模推出的滑块误差矢量,实际上两者相等,因此有
Фi(xi)=ФiR(xiR)。
(13)
根据上式,将式(11)代入到式(12)中变形可得工作台在行程上任意位置误差矢量为
(14)
为滑块初始误差矢量,可通过实验测量滑块初始误差,代入到式(14)中可以求出工作台任意位置误差矢量。
2 两导轨平行度误差映射模型
2.1 两导轨平行度误差
考虑两条导轨间存在平行度误差时,通常认为其中一条导轨位于理想位置,另外一条导轨相对于该导轨存在偏转角度或者偏移位移误差。在本研究中,认为导轨1为理想状态不存在误差,导轨2相对于导轨1有5种偏差,分别为沿着Y轴与Z轴的偏移平行度误差
与
绕着3个轴的旋转平行度γq、βq和αq,分别对应滚转、俯仰、偏摆的误差,如图7所示。
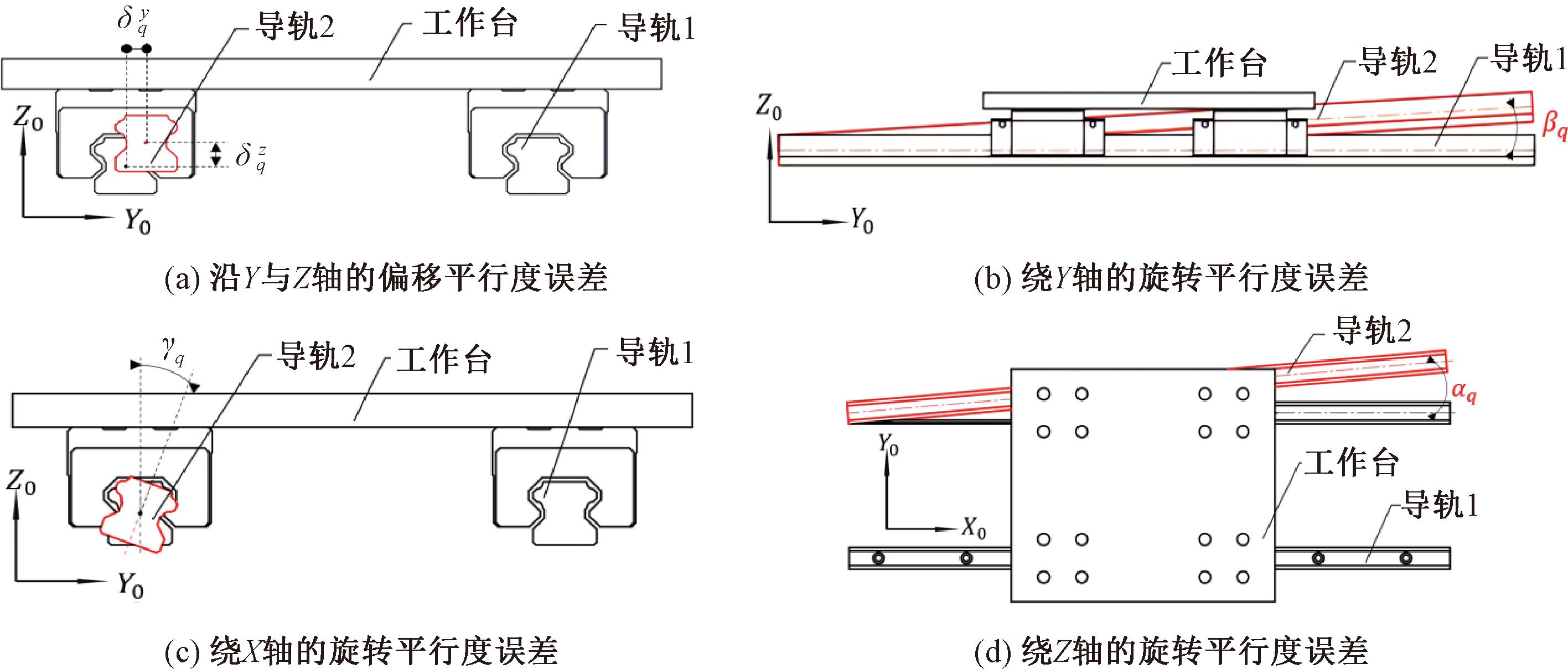
图7 导轨平行度误差
Figure 7 Guide rail parallelism error
2.2 平行度误差与线性工作台误差映射模型
要建立导轨平行度误差到工作台空间误差的映射模型,首先要分析平行度误差对滑块位姿的影响,再通过滑块初始误差映射模型分析平行度误差对工作台误差的影响。
如图8所示,在导轨1与导轨2上分别建立坐标系{Od1,xd1,yd1,zd1}与{Od2,xd2,yd2,zd2},当导轨2相对导轨1有平行度误差
时,把导轨的平行度误差映射到滑块的初始误差上,则导轨2上的滑块3与滑块4有误差,并且两滑块上表面中心位置坐标原点相对导轨2固定坐标系的误差矩阵可以表示为
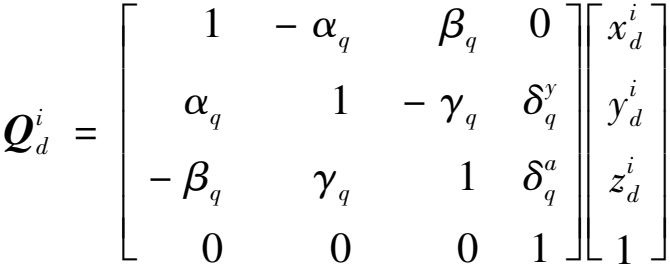
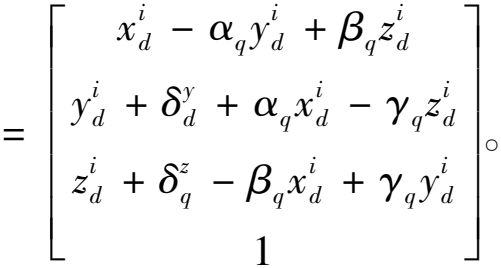
(15)
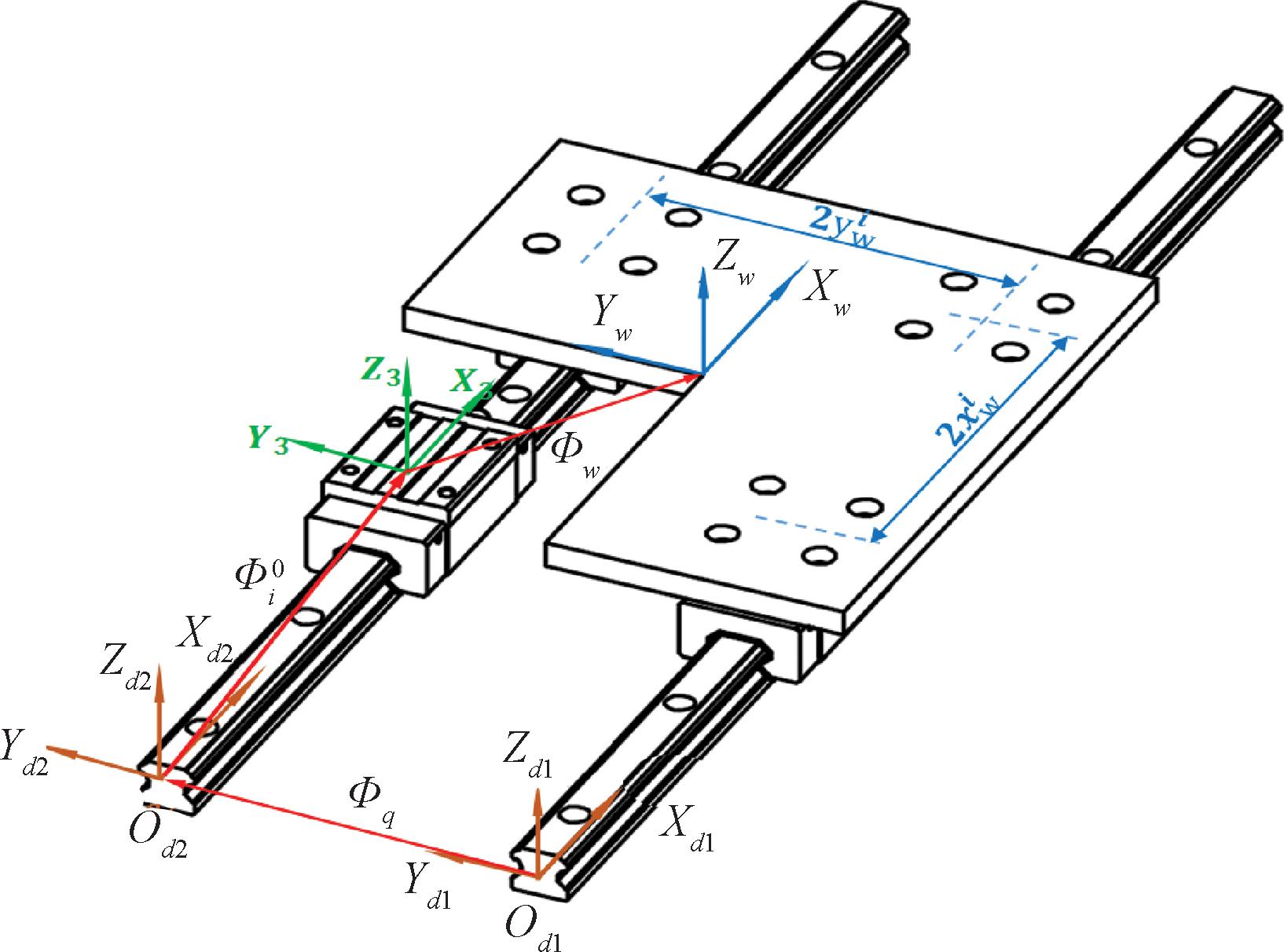
图8 导轨平行度误差映射模型
Figure 8 Guide rail parallelism error mapping model
其中,
表示导轨坐标系在滑块坐标系中的位置,i=3,4。则此时滑块的初始误差
可以描述为
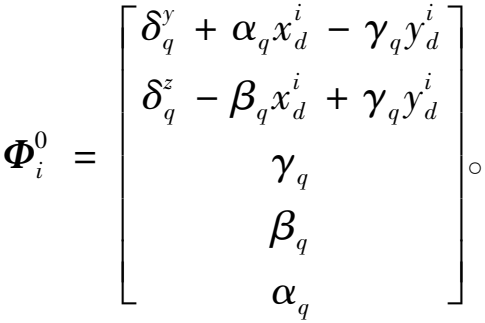
(16)
将式(16)代入到式(14)展开可得
(17)
式中:
式(17)为导轨平行度到工作台误差的映射模型,由模型可以得到以下结论:根据导轨平行度误差可以预测工作台误差,并且五项平行度误差均会影响工作台Y向直线度误差;工作台Z向直线度误差受3项平行度误差影响,工作台的偏摆误差与俯仰误差只由相应的平行度误差决定,且数值大小与导轨平行度误差相同。
2.3 平行度误差影响的数值分析
为了更加清楚地描述导轨平行度误差对工作台误差的影响,选取上银公司型号为HG15型号的滚动导轨,根据平行度误差映射模型,并依据工程中一般机床精度,假设导轨2分别具有五项平行度误差,大小为
通过数值模拟来分析不同平行度误差对空间误差的影响规律。其他所需的参数列于表1。
表1 仿真参数表
Table 1 Simulation parameter
参 数 取 值 参 数 取 值 x iw / m m 7 5 z id / m m 5 y iw / m m 1 1 0 Kyd ( N · m m - 1 ) 1 . 0 4 × 1 0 5 z iw / m m 1 0 Kzd / ( N · m m - 1 ) 1 . 9 6 × 1 0 5 y id / m m 0 Kxr / ( N · m m · r a d - 1 ) 4 . 9 × 1 0 6
根据误差耦合模型可知,当导轨仅具有平行度
和γq时,工作台误差在整个行程上保持不变。结果如表2所示。
表2 数值模拟结果
Table 2 The results of numerical simulation
导轨 平行度 工作台误差 直线度误差 (δ y w ,δ z w ) / μm 角度误差 (γw ,βw ,αw ) / (°) δ y q = 30 μm (15,0) (0,0,0) δ z q = 30 μm ( - 2. 18,15) (7. 81 × 10 - 3 ,0,0) γq = 5. 56 × 10 - 3 ° ( - 0. 43,0) (1. 67 × 10 - 5 ,0,0)
表3 实验数据
Table 3 Experimental data
δ yq / μ m δ zq / μ m γ q / ( ° ) β q / ( ° ) α q / ( ° ) 5 0 5 0 4 . 9 2 × 1 0 - 3 4 . 6 8 × 1 0 - 3 4 . 5 3 × 1 0 - 3
五项平行度误差值分别代入到式(17)中,可获得表2中的数值。如果将其中一个平行度误差值设为变量,将其他参数置为0,简化后的式(17)可得到以下规律。
(1)导轨2仅有误差
的情况下,工作台也仅有Y向直线度误差
数值大小为导轨平行度误差的一半。其余4项的运动误差都为零,并且在整个行程中大小保持不变。
(2)导轨2仅有误差
的情况下,工作台有Z向直线度误差
向直线度误差
以及滚转误差γw,并且此时Y向直线度误差与Z向直线度误差数值大小呈一定的比例关系,比例系数是由滑块刚度与线性工作台结构决定的。
(3)导轨2仅有误差γq的情况下,工作台有Y向直线度误差以及滚转误差γw。但是实际上,此时工作台肯定会有Z向直线度误差,这是由于平行度误差的映射模型中
为零,将此时滚转平行度误差对工作台的影响抵消掉了,但这并不影响结果,因为在导轨具有γq的情况下工作台所具有的运动误差量级很小,几乎可以忽略不计。
当导轨仅有平行度误差βq或αq时,此时工作台运动误差在导轨上位置的变化情况如图9和图10所示。
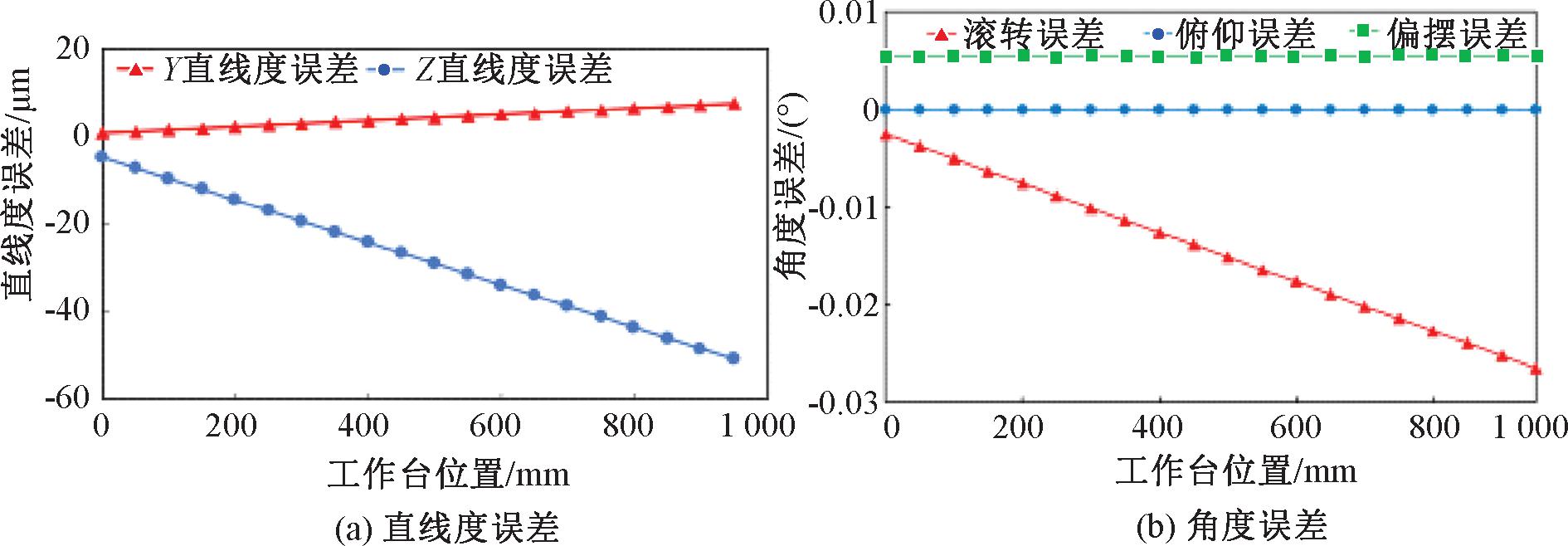
图9 导轨2仅有βq时工作台误差
Figure 9 Worktable error when No. 2 guide rail only has βq
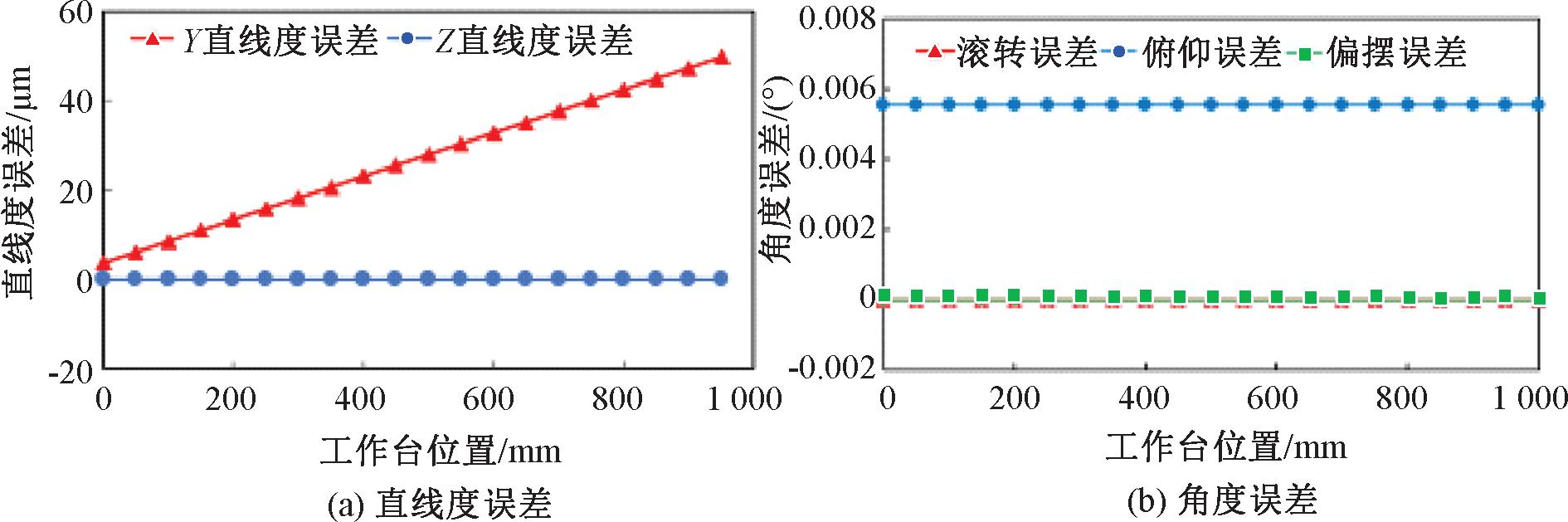
图10 导轨2仅有αq时工作台误差
Figure 10 Worktable error when No. 2 guide rail only has αq
由图9和图10可知,导轨2仅有误差βq的情况下,工作台有直线度误差和
角度误差γw和βw。其中俯仰误差βw在工作台运动过程中保持数值不变,且数值大小与导轨2平行度误差相同,其他误差都随着工作台行程呈一种线性变化。导轨2仅有误差αw的情况下,工作台有直线度误差以及偏摆误差αw。Y向直线度误差随着工作台的行程位置线性增加,而工作台的偏摆误差保持数值不变,并且数值与导轨2平行度误差相同。
在实际工况中,往往有多种平行度误差共同影响工作台运动误差,因此进行当导轨同时具有Y向和Z向平行度误差以及俯仰与偏摆平行度误差的耦合影响分析,结果如图11和图12所示,当同时具有两种平行度误差时,工作台运动误差为两项误差值之和,说明此种情况下,工作台运动误差完全1∶1复映了平行度误差,若要降低平行度误差对工作台误差的影响,就要分别降低各单项误差,从而达到误差之和最小。
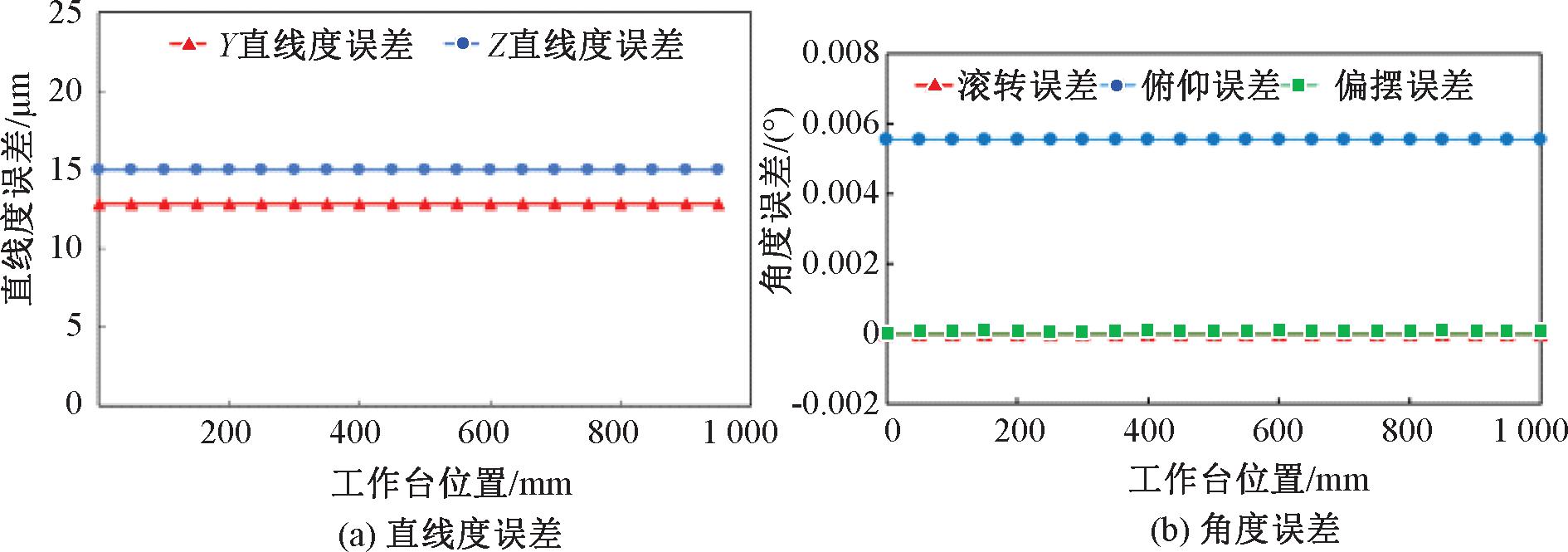
图11 导轨2同时具有
和
时工作台误差
Figure 11 Worktable error when No. 2 guide rail only has 
图12 导轨2同时具有βq和αq时工作台误差
Figure 12 Worktable error when No. 2 guide rail only has βq and αq
3 影响规律的有限元分析
前文基于误差映射模型通过数值分析的方式,研究了导轨平行度误差对工作台误差的影响。下面建立考虑导轨平行度误差影响的工作台有限元模型,通过有限元仿真分析平行度误差的影响规律,同时将有限元计算结果与误差映射模型计算结果进行对比,验证本文建立的误差映射模型的正确性。
3.1 线性工作台有限元模型
在理论建模时,假设导轨与滑块之间的滚珠为弹性体,其他部件为刚体,且弹性变形只发生在滚珠上,因此,通过弹簧单元法将滚动体等效为线性弹簧,在仿真分析中,具有平行度误差的导轨通过调整弹簧的长度来传递误差。
通过Ansys Workbench进行有限元分析,简化的模型如图13所示。
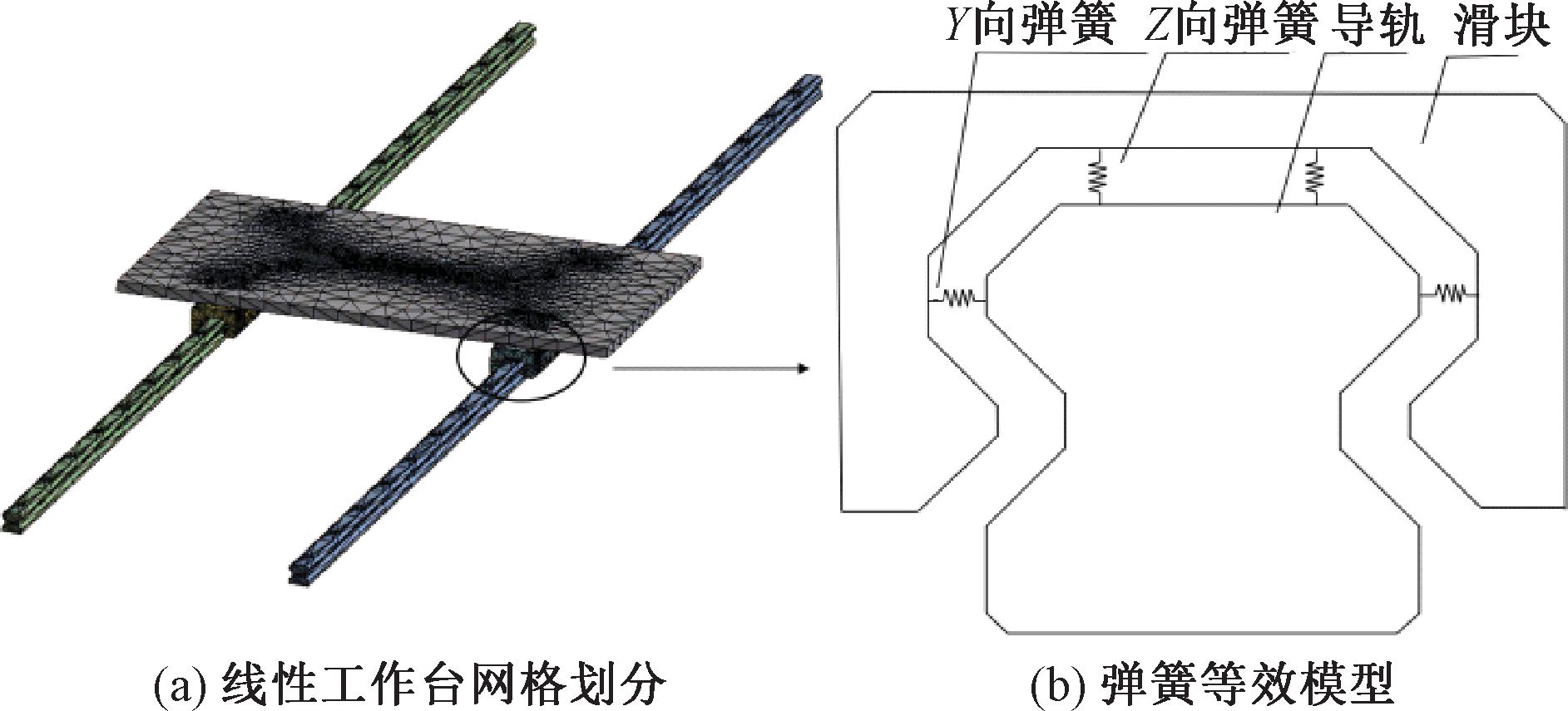
图13 线性工作台有限元模型
Figure 13 Finite element model of linear worktable
本文直线滚动导轨副使用上银公司HG15型号的滚动导轨与滑块,在有限元软件中导入该型号的导轨滑块的有限元模型,导轨滑块材料使用的是马氏体不锈钢,密度为7.75 g/cm3,弹性模量为20 600 MPa,泊松比为0.3,而工作台材料使用的是6063-T6,密度为2.7 g/cm3,弹性模量为71 000 MPa,泊松比为0.33。
3.2 有限元分析
如图14所示,通过线性工作台有限元模型,对导轨2同时施加5种平行度误差,误差大小为
然后与平行度误差映射模型求解结果进行对比,结果如图15所示。
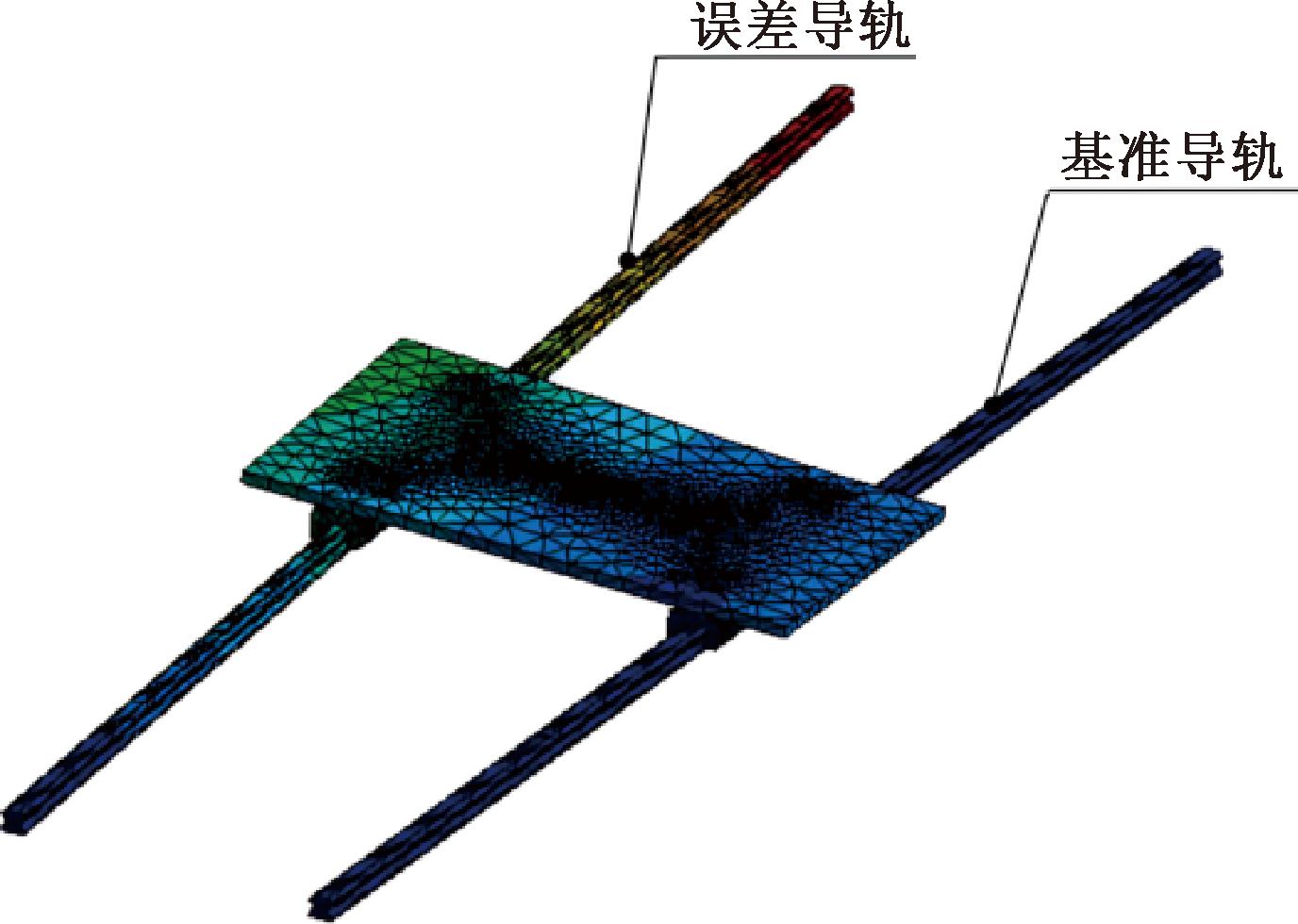
图14 有导轨平行度的有限元模型
Figure 14 The finite element model of the parallelism of guide rail
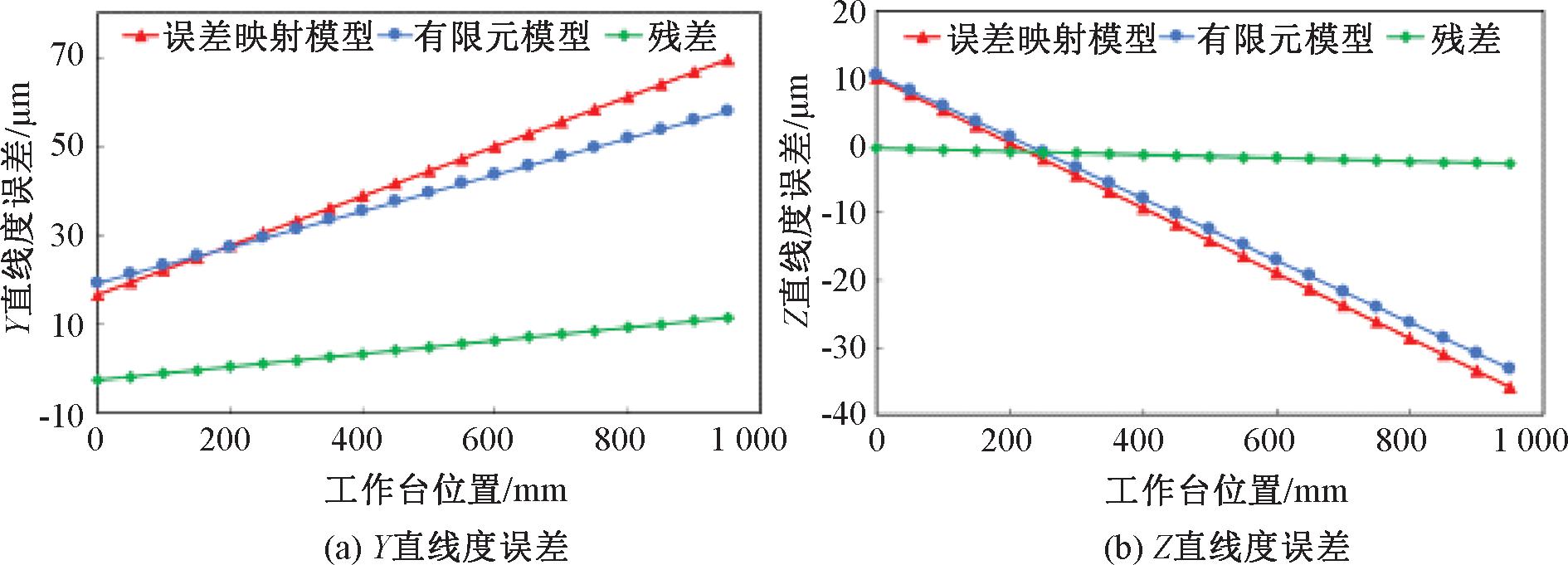
图15 工作台运动误差对比图
Figure 15 Comparison of worktable motion error
从图15中可以看出,数值模拟分析与有限元分析下工作台的运动误差趋势一致。对于工作台Y向直线度误差来说,最大的误差为16.8%,对于Z向直线度误差来说,最大的误差为8%,由此证明了平行度误差映射模型的正确性。通过误差映射模型可以预测平行度误差对工作台误差的影响。其中,对于误差耦合模型和有限元分析结果不一致,原因是有限元模型的简化导致各部件之间的相互作用产生变化,导致无法做到完全理想。
4 实验
前文通过数值模型和有限元的方式分析了平行度误差对工作台误差的影响规律,下面通过实验来验证分析平行度误差的作用规律。
实验平台包括基座、直线导轨、滑块、工作台和滚珠丝杠等核心部件。为了研究不同参数大小的影响规律,核心零件均采用螺钉连接,方便拆卸与组装,具体如图16所示。同时,为了方便对导轨施加平行度误差,设计了分离式基座,当一侧导轨固定时,可以调节另外一侧的基座来调节平行度误差。
图16 实验平台
Figure 16 Experimental platform
实验时,分别对导轨2施加5种平行度误差,具体如图16所示,在平行度误差下,通过实验测量出的工作台曲线可以分析平行度误差的影响规律,也可以再次验证模型的正确性。
装配时,在导轨和基座结合面的位置人为增加不同厚度的铜皮,以改变装配参数,从而达到改变平行度误差的目的。
当导轨分别具有5种平行度误差时,工作台误差如图17所示,其中实心数据标签以左侧纵坐标(直线度误差)为基准,空心数据标签以右侧纵坐标(角度误差)为基准。
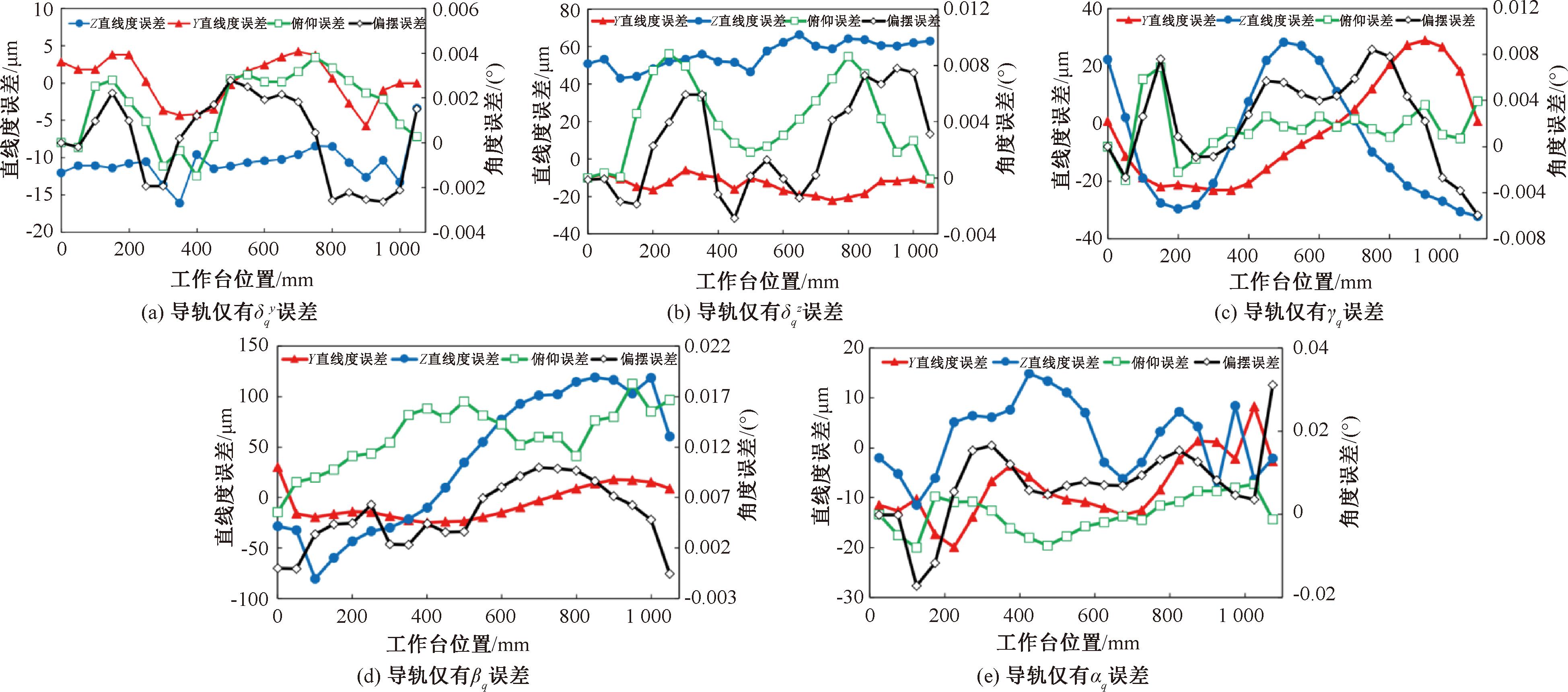
图17 导轨具有5种误差对直线度误差和角度误差的影响
Figure 17 Five guide rail errors affecting straightness and angular errors
从图17可以看出,当导轨具有平行度误差时,工作台会产生5项误差,实验中得到的误差曲线整体趋势与数值模拟的误差曲线趋势整体相近,证明了误差耦合模型的正确性。实验结果与数值模拟结果有区别,主要有两点原因:①实际工况中,工作台各零部件均会产生变形导致均化或者增加一些误差,导致与理论分析有差别;②为了实验更多不同的配置并进行快速组装,本工作台采用了较多的螺栓连接环节,导致误差环节增多,对测量结果产生一定影响。
5 结论
本文建立了误差耦合模型和平行度误差到工作台误差的映射模型,分析了平行度误差对工作台空间误差的影响规律,对于提高线性工作台装配精度有着重要作用,主要结论如下。
(1)建立了一维线性工作台误差耦合模型。模型包含滑块与工作台的力平衡方程以及载荷与变形间的物理方程,研究了导轨几何误差、结合面及零部件刚度等因素对一维线性工作台误差运动的耦合作用。
(2)基于误差耦合模型建立了导轨平行度误差到工作台误差的映射模型,通过数值模拟可以得出:导轨Y向平行度误差只会影响工作台Y向误差;导轨Z向误差影响工作台Y向与Z向的直线度误差、滚转误差与俯仰误差;导轨滚转平行度误差影响工作台Y向直线度与滚转误差,但是差两个数量级,几乎可以忽略;导轨俯仰平行度误差影响工作台Y向与Z向的直线度误差、滚转误差与俯仰误差,且都与工作台行程有关;导轨偏摆平行度误差影响工作台误差的Y向直线度与偏摆误差,且偏摆误差与平行度误差数值相等。
(3)平行度误差映射模型与有限元模型之间的最大误差不超过9.8%,证明了平行度误差映射模型与数值模拟的一致性。
(4)得到了平行度误差对一维线性工作台的影响规律:平行度误差可直接复映至工作台上,若要提高工作台的运行精度,就要降低各个平行度误差值大小。其中俯仰平行度误差和偏摆平行度误差对工作台误差的影响较大,滚转误差几乎可以忽略不计。
(5)为线性工作台误差补偿和精度设计提供了理论依据。对工作台整个行程来说,可以通过人为制造平行度误差来降低工作台整体运动误差,补偿值大小可以由映射模型求出。
[1] FAN K C, CHEN H M, KUO T H. Prediction of machining accuracy degradation of machine tools[J]. Precision Engineering, 2012, 36(2): 288-298.
[2] HE G Y, SHI PP, GUO L Z, et al. A linear model for the machine tool assembly error prediction considering roller guide error and gravity-induced deformation[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234(15): 2939-2950.
[3] 吴煜. 机床移动副精度模型与装配工艺优化研究[D]. 大连: 大连理工大学, 2018.
WU Y. Research on precision model and assembly process optimization of machine tool moving pair[D]. Dalian: Dalian University of Technology,2018.
[4] 马军旭, 赵万华, 张根保. 国产数控机床精度保持性分析及研究现状[J]. 中国机械工程, 2015,26(22): 3108-3115.
MA J X, ZHAO W H, ZHANG G B. Research status and analyses on accuracy retentivity of domestic CNC machine tools[J]. China Mechanical Engineering, 2015, 26(22): 3108-3115.
[5] 吴煜, 申会鹏, 孙璇,等. 机床弹性移动副五维误差预测模型[J]. 华中科技大学学报(自然科学版), 2019,47(11): 121-126.
WU Y, SHEN H P, SUN X, et al. 5D error prediction model for elastic prismatic pair of machine tool[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(11): 121-126.
[6] 王秀山, 杨建国, 闫嘉钰. 基于多体系统理论的五轴机床综合误差建模技术[J]. 上海交通大学学报, 2008,42(5): 761-764, 769.
WANG X S, YANG J G, YAN J Y. Synthesis error modeling of the five-axis machine tools based on multi-body system theory[J]. Journal of Shanghai Jiao Tong University, 2008, 42(5): 761-764, 769.
[7] LI H T, GUOJ J, DENG Y F, et al. Identification of geometric deviations inherent to multi-axis machine tools based on the pose measurement principle[J]. Measurement Science and Technology, 2016, 27(12): 125008.
[8] TAO W J, ZHONG Y, FENG H T, et al. Model for wear prediction of roller linear guides[J]. Wear, 2013, 305(1/2): 260-266.
[9] FAN K C, CHEN M J, HUANG W M. A six-degree-of-freedom measurement system for the motion accuracy of linear stages[J]. International Journal of Machine Tools and Manufacture, 1998, 38(3): 155-164.
[10] 陈汀, 黄其柏. 一种计及滑块裙部变形的滚珠直线导轨副模态分析方法[J]. 中国机械工程, 2012,23(2): 150-154.
CHEN T, HUANG Q B. A modal analysis method of a linear ball guide incorporating flexibility of the carriage[J]. China Mechanical Engineering, 2012, 23(2): 150-154.
[11] 刘耀, 黄玉美. 机床滚珠导轨中圆柱面-球面结合面静特性分析及试验研究[J]. 机械工程学报, 2013,49(21): 25-30.
LIU Y, HUANG Y M. Theoretical analysis and experimental study on static characteristics of the cylindrical-spherical joint surfaces of linear ball guide on machine tool[J]. Journal of Mechanical Engineering, 2013, 49(21): 25-30.
[12] ZHANG W, WANG M, LE B B. Modeling and experiment on contact stiffness and accuracy analysis of ball linear guide feed unit[J]. Journal of Harbin Institute of Technology (New Series), 2019,26(1): 30-41.
[13] ZOU H T, WANG B L. Investigation of the contact stiffness variation of linear rolling guides due to the effects of friction and wear during operation[J]. Tribology International, 2015, 92: 472-484.
[14] TANG H, DUAN J, ZHAO Q C. A systematic approach on analyzing the relationship between straightness &angular errors and guideway surface in precise linear stage[J]. International Journal of Machine Tools and Manufacture, 2017, 120: 12-19.
[15] ZHANG P H, CHEN Y L, ZHANG C Y, et al.Influence of geometric errors of guide rails and table on motion errors of hydrostatic guide ways under quasi-static condition[J].International Journal of Machine Tools &Manufacture2018,125: 55-67.
[16] 马雅丽, 李阳阳. 基于几何误差不确定性的滚动导轨运动误差研究[J]. 机械工程学报, 2019,55(5): 11-18.
MA Y L, LI Y Y. Motion error of rolling guide based on uncertainty of geometric error[J]. Journal of Mechanical Engineering, 2019, 55(5): 11-18.
[17] 何改云, 王凯, 郭龙真, 等. 导轨平行度误差对工作台运动误差影响的建模与分析[J]. 机械科学与技术, 2015, 34(11): 1705-1709.
HE G Y, WANG K, GUO L Z, et al. Influencing modeling and analysis of guide parallelism error on table motion error[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(11): 1705-1709.
[18] SHI C C, WANG Z Z, PENG Y F. Influence of relative difference between paired guide rails on motion accuracy in closed hydrostatic guideways[J]. Journal of Mechanical Science and Technology, 2020, 34(2): 631-648.
[19] KIM G H, HAN J A, LEE S K. Motion error estimation of slide table on the consideration of guide parallelism and pad deflection[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(9): 1935-1946.