随着风力发电装机容量日益扩大,风能发电量的波动性对电力系统的调度和稳定性施加了显著压力[1]。因此,提升风电功率预测的准确性在实际应用中具有举足轻重的意义。
目前,风电功率预测技术已经取得了显著的进步。Wang等[2]提出了CNN-LSTM模型,该模型的预测准确度明显高于单一的CNN模型和单一的LSTM模型,但无法精确地提取风电序列中的时序信息。Liu 等[3]提出了双向长短期记忆(BiLSTM)模型,能够有效提取风电序列中的时序信息,Li等[4]在此基础上将CNN模型与BiLSTM模型融合,构建出CNN-BiLSTM模型,该模型在预测精度上较CNN模型与BiLSTM模型有显著提升,但上述模型依然难以高效精准地提取波动剧烈的气象信息,在极端天气条件下,模型的预测难度大幅度增加。李润金等[5]提出了VMD-CNN-LSTM混合深度学习模型,VMD分解可以将非平稳的功率数据进行平稳化处理,可以有效分析提取风电序列中波动剧烈的气象信息,从而提高短期风电功率预测的准确度,然而该模型中模态分解数K和惩罚因子β难以选取最优值,会在一定程度上影响模型预测的精度。
传统的风电功率预测模型大多为确定性预测,该预测的局限在于只能给出某一时刻的确定性预测结果,对其不确定性难以做出定量分析,将不利于电网调度计划的制定。区间预测解决了这一问题,可以对传统的确定性预测的不确定性给出定量描述。任鹏等[6]提出了一种基于竞争学习机制的LSTM区间预测模型,其区间平均宽度对比最小,然而模型的训练时间较长。陈申等[7]提出了一种AO优化RF并结合KDE的区间预测模型,在3种置信水平下,所提模型的区间预测效果均为最好,然而点预测模型的精度还有较大的提升空间。韩丽等[8]提出了一种波动趋势分段的区间预测方法,保证了较大的区间覆盖率和更小的区间平均宽度,但是未考虑气象数据。崔颢等[9]提出了一种基于灰狼优化算法对BP神经网络进行优化的方法进行风电功率区间预测,相较传统BP神经网络,预测精度大幅提高,然而现有研究中的点预测模型效果尚有提高的需求。
针对上述问题,本文建立了一种组合深度学习的风电功率区间预测模型。首先,采用组合深度学习模型POTDBO-VMD-CNN-BiLSTM对风电功率进行确定性预测;其次,采用非参数核密度估计法(KDE)对组合深度学习模型的预测误差进行拟合,并对风电功率预测值和真实值进行分析,构建了基于不同置信区间的风电功率区间预测模型,并获取相应的预测结果;最后,利用新疆某风电场的实际数据进行验证,以此验证本文方法的有效性。
1 POTDBO-VMD-CNN-BiLSTM模型
1.1 多策略融合改进的蜣螂优化算法
蜣螂优化算法(DBO)的灵感源于蜣螂群体的生活习性,包括滚球、繁育、觅食和偷窃等行为,其中滚球行为可以分为无障碍模式和有障碍模式两类。普通的 DBO 算法具有较强的寻优能力,该算法具备强大的优化能力,然而,它也存在全局寻优与局部探索能力失衡的问题,极易陷入局部最优解[10-11]。针对上述缺点,引入以下3种策略对DBO算法进行改进。
(1)采用Piecewise混沌映射。混沌映射能够提升粒子的多样性,减少寻优时间,从而加速优化过程的收敛。在初始化位置更新过程中,采用Piecewise混沌映射代替DBO算法中的随机分量,表达式如下:

(1)
式中:Q取0.4;Xn为混沌映射的状态变量。
(2)融合鱼鹰优化算法。在原始的DBO算法中,在无障碍模式下,滚球蜣螂的位置更新过于依赖当前种群的最差位置Xworst(t),导致其全局寻优能力欠佳。鱼鹰优化算法[12]具有很强的全局寻优能力,可以弥补DBO算法过于依赖Xworst(t)的不足,采用鱼鹰算法第1阶段的全局寻优策略公式代替无障碍模式下滚球蜣螂的位置更新公式,鱼鹰算法第1阶段的全局寻优策略公式如下:
(2)
式中:![]() 表示第i只鱼鹰在第1阶段时第j维的位置;SFi,j表示鱼鹰选中的鱼;ri,j表示0到1之间的随机数;Ii,j为集合{1,2}中的一个。
表示第i只鱼鹰在第1阶段时第j维的位置;SFi,j表示鱼鹰选中的鱼;ri,j表示0到1之间的随机数;Ii,j为集合{1,2}中的一个。
(3)融合自适应T分布扰动策略。采用以迭代次数变体公式为T分布的自由度参数的T分布变异扰动,对蜣螂个体位置进行扰动。其中,迭代前期t(iter)很小,类似柯西变异,而迭代后期t(iter)偏大,如此能让DBO算法在优化的初期具有较强的全局寻优能力,而在迭代后期则展现出更优的局部探索能力,同时还可以提高DBO算法的收敛速度,具体的位置更新公式如下:
Xi-new=Xi+t(iter)×Xi。
(3)
式中:Xi-new和Xi分别表示变异后和变异前种群中第i个个体的位置;t(iter)表示以迭代次数为自由度的T分布值。
1.2 POTDBO-VMD模型
变分模态分解(VMD)是一种自适应且非递归的信号分解技术,能够高效地处理非平稳的输入信号。采用VMD在对风电功率序列进行分解之前需要预先设定4个参数,包括分解个数K、惩罚因子β、噪声容忍度τ、允许的收敛误差ε。其中,K和β是VMD分解过程中关键的调节参数,对分解效果具有重要影响。若K过大,会造成欠分解,产生虚假模态;若K偏小,则无法有效提取数据的隐含特征。若β偏小,会出现模态混叠;若β较大,会造成局部信息丢失。针对上述问题,采用融合多策略改进的蜣螂优化算法(POTDBO)对VMD的两参数进行寻优处理,以提高VMD的分解性能。
运用优化算法对VMD的参数进行优化处理时,首先应当确定一个适应度值,通过比较适应度值来确定是否要进行位置更新[13],本文采用包络熵作为VMD参数选择的评估标准,熵值越小,对应信号稀疏程度越高。信号Z(i)(i=1,2,…,N)的包络熵Ep为

(4)
式中:a(i)为信号Z(i)(i=1,2,…,N)经Hilbert解调后的包络信号;ui表示a(i)的归一化。
本文选取各个模态分量包络熵的平均值作为适应度函数,计算过程如下:
(5)
1.3 CNN-BiLSTM模型
本节构建了一种用于风电功率预测的混合模型CNN-BiLSTM[5]。在该模型中,CNN层通过卷积层和池化层有效提取气象数据中的空间特征,并将这些特征数据输入到后续的BiLSTM层。BiLSTM层结合了正向LSTM网络和反向LSTM网络,能够充分捕捉数据中的历史信号特征和未来信号特征,从而提高预测的准确性。此外,为了避免过拟合问题,模型引入了Dropout技术对BiLSTM网络的输出进行随机丢弃处理,进一步增强了模型的泛化能力。最终,通过这一系列处理,模型可以输出准确的风电功率预测结果。CNN-BiLSTM的整体网络结构如图1所示,具体实现细节将在后续部分详细阐述。
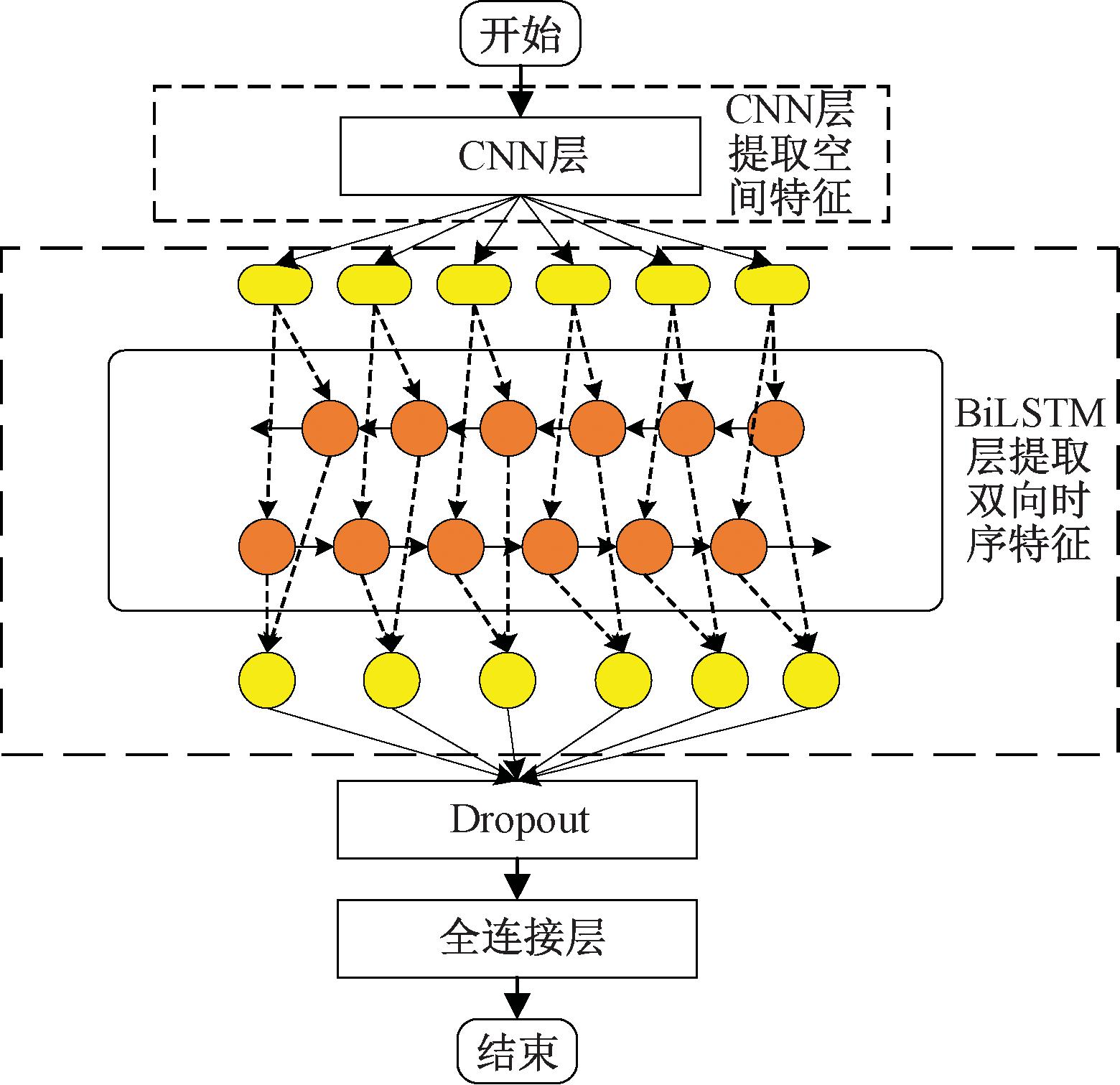
图1 CNN-BiLSTM模型结构图
Figure 1 The model structure diagram of CNN-BiLST
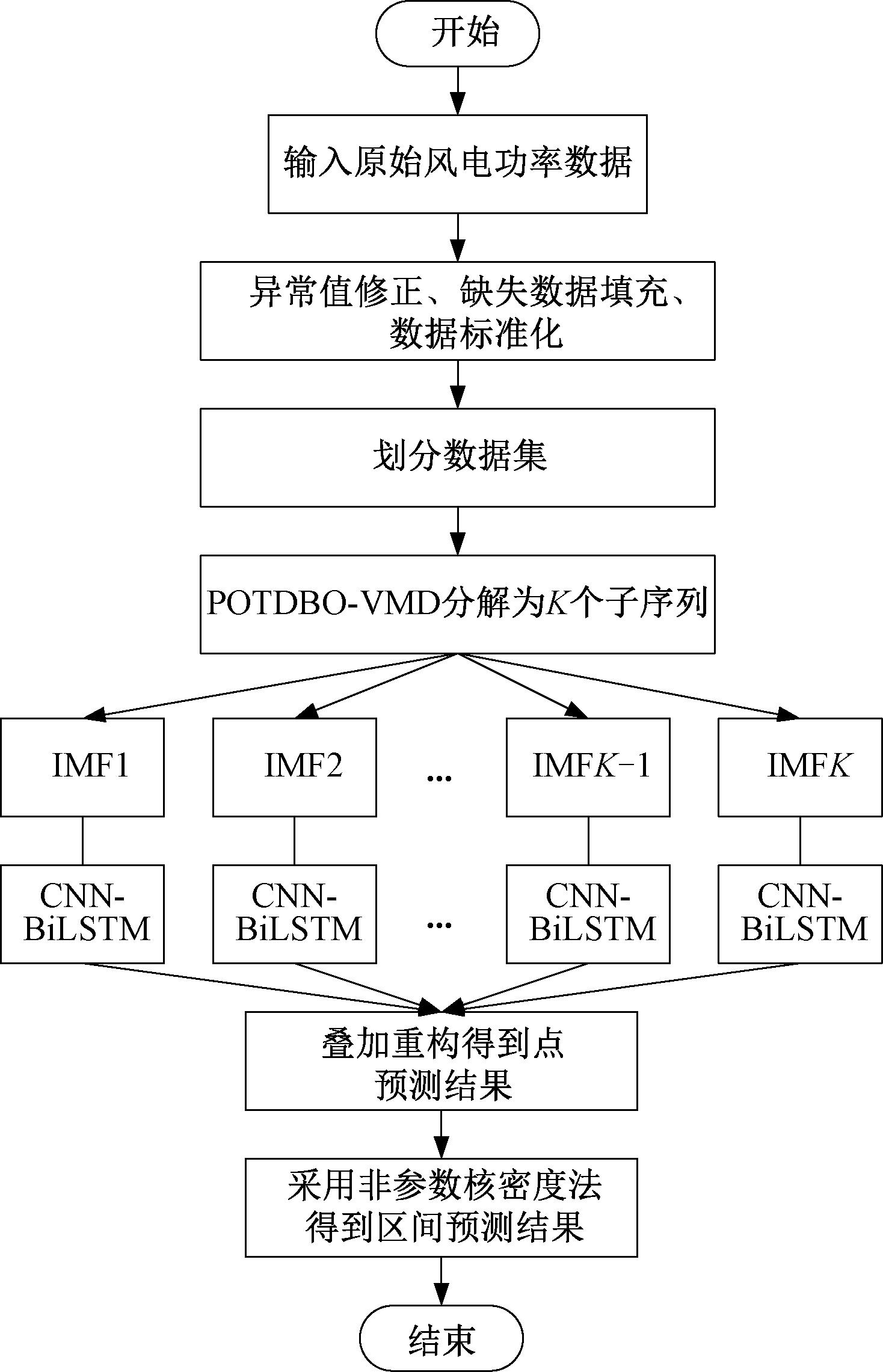
图2 风电功率区间预测模型结构
Figure 2 The structure of wind power interval prediction model
1.4 误差评价指标
评价指标有助于更直观地衡量预测模型的准确度,本文采取RMSE、MAE、MAPE和R2作为误差评价指标。
均方根误差RMSE:
(6)
平均绝对误差MAE:
(7)
平均绝对百分比误差MAPE:
(8)
决定系数R2:

(9)
2 非参数核密度估计模型
2.1 非参数核密度估计
非参数核密度估计法就是采用微分思想[13]将频率直方图的组距逐步缩小,随着组距的减小,矩形宽度会越来越窄,在极限情形下,频率直方图就会变成一条曲线,该曲线即为概率密度曲线。
假设p1,p2,…,pn为有功出力的p在采样周期内采集的n个样本,则p的核密度函数可以表示为[15]
(10)
式中:![]() 表示核密度函数;l表示带宽;pi表示有功出力的第i个样本;
表示核密度函数;l表示带宽;pi表示有功出力的第i个样本;![]() 表示核函数。
表示核函数。
核函数应满足连续性、对称性和非负性,需设置以下约束:
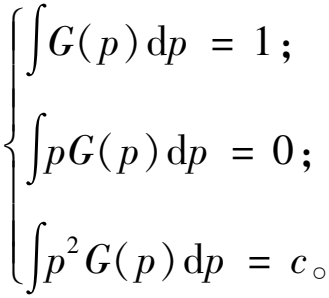
(11)
式中:c为常数。
常用的核函数有Uniform、Triangular、Quartic、Gaussian、Cosine等。其中,Gaussian具有良好的鲁棒性和抗噪声干扰能力[16],故本文选择Gaussian作为核函数,表达式如下:
(12)
此外,带宽l的选择也会影响预测的精度。带宽l过大会使G(p)平滑性过高,从而掩盖有功出力峰值特征,导致较大的预测误差;带宽l过小会使G(p)不稳定性增加,出现过拟合情况。
带宽l的选择过程如下[17]:当n→+∞、l→0、nl→+∞时,核密度估计的偏差B和方差V的表达式为
(13)
(14)
(15)
(16)
由式(13)和式(14)可知,l分别与B、V有正相关和负相关的关系,因此带宽l的选择需要综合考量B、V。
渐进积分均方误差AMISE可以综合考量B、V,当AMISE取最小值时可以得到最优带宽,其计算公式如下:
(17)
(18)
采用正态参考准则将式(17)简化:
(19)
式中:σ表示标准差。
引入散度度量半极差Iqr,用式(20)替换式(19)中的σ:
(20)
式中:Φ(·)表示标准正态累积分布函数。
为了更准确地估计峰值特征,将系数减小至0.9,结合式(18)和式(19),得到最优带宽计算公式:
(21)
2.2 置信区间计算方法
在通过非参数核密度估计得出预测误差的概率密度函数后,便可以通过积分得到累积分布函数:
(22)
根据累积分布函数,在给定的置信水平(1-α)下,有
P(elow<e<eup)=F(eup)-F(elow)=1-α。
(23)
式中:α为显著水平;eup、elow分别为在置信水平(1-α)下误差的上、下界。
通过分析累积概率密度函数的曲线,能够在给定的置信水平上确定误差的上限和下限:
(24)
(25)
结合风电功率的点预测结果,即可实现对风电功率的区间预测:
Plow=P-|eup|;
(26)
Pup=P+|elow|。
(27)
式中:Pup和Plow分别为在给定置信水平下预测的风电功率的上界和下界;P为风电功率点预测值。
2.3 评价指标
为了对区间预测的不确定性进行量化,本文引入以下几种评价指标。
预测区间覆盖率PICP计算公式如下:
(28)
式中:当Pi∈[Pmin,Pmax]时,ci=1,否则ci=0,Pmax和Pmin为第i个Pi的上下界;n为样本个数。
预测区间平均宽度PINAW计算公式如下:
(29)
式中:R为目标值,用于数据归一化。
预测区间覆盖宽度CWC用来综合考量PICP和PINAW,CWC计算公式如下:
CWC=PINAW[1+γe-η(PICP-μ)];
(30)
(31)
式中:η为惩罚系数;μ由置信区间决定,例如当置信水平为80%时,μ=0.8。
3 风电功率区间预测模型的建立
3.1 数据预处理
(1)异常数据的检测。异常数据对预测模型准确度的影响显著,本文通过分析数据特征筛选异常数据,例如,风电数据中每小时风速的平均值不应该超过40 m/s,风向数据应该处于 0°~360°。
此外,各种意外因素也可能导致功率数据出现异常,本文主要排除以下3种情况:①功率序列在某一时间段出现缺失;②当风速、风向等气象因素出现波动,而风电功率值保持不变;③仪器失灵等因素导致测得的功率值明显超出正常范围。
(2)异常数据清洗。四分位法可以分析数据集的分布特性,得到数据的离散程度[18]。本文采用四分位法对风电功率数据进行清洗,剔除异常值。
(3)缺失数据的填补。在用四分位法剔除异常数据之后,为了完整性,采用线性插值法,计算公式如下:
(32)
对于连续出现多位置缺失数据,补全方法如下:

(33)
式中:ρi表示权值;m表示移动窗口数。
(4)数据归一化处理。风电原始数据具有不同的量纲,这会给预测模型的训练带来很大的挑战,影响预测准确度,因此必须对数据进行标准化处理以消除不同气象指标之间的量纲差异,本文选取Max-Min标准化方法[19],其计算公式如下:
(34)
式中:x′为处理后的数据;x为原始数据。
3.2 区间预测步骤
本文提出了一种组合深度学习的风电功率区间预测模型。首先,运用POTDBO 算法优化VMD的参数K和β,旨在探寻VMD 分解风电功率序列的最优参数组合。其次,利用POTDBO-VMD 模型对原始风电功率数据实施平稳化处理,以此避免数据的随机性和波动性对预测精度造成不良影响,随后将处理后的平稳数据输入到 CNN-BiLSTM 模型中,从而得到确定性的预测结果。最后,采用非参数核密度估计法(KDE)对预测误差进行拟合,并针对风电功率的预测值和真实值展开细致分析,在此基础上构建不同置信区间下的风电功率区间预测模型,进而获取不同置信区间下的预测结果,风电功率区间预测模型结构如图 2 所示。具体预测步骤如下。
步骤1 对原始数据开展必要的预处理工作,包括异常值修正、缺失数据填充以及数据标准化等操作,同时依据特定的划分规则将数据划分为训练集和测试集。
步骤2 借助POTDBO-VMD 模型,将训练集和测试集的原始功率数据分解为多个固有模态分量 (IMF),并基于这些分量构建输入信号序列。
步骤3 将训练集的信号序列输入到 CNN-BiLSTM 网络中,通过网络训练过程得到训练好的功率预测模型;接着,将测试集的信号序列输入到已训练好的功率预测模型中,获取各个序列分量的预测结果;最后,对这些分量的预测结果进行整合汇总,得到整体的功率预测值。
步骤4 运用非参数核密度估计法(KDE)对预测误差进行拟合处理,最终得到不同置信区间下的风电功率区间预测结果。
4 算例分析
4.1 基于变分模态法的风电功率分解结果分析
本文选取新疆某地实际风电场2019年5月份的NWP数据和功率数据作为研究对象,数据采集间隔为15 min一个节点,共计2 976组数据。为了验证POTDBO算法的有效性,分别对风电场历史功率序列进行DBO-VMD自适应分解和POTDBO-VMD自适应分解,对比DBO-VMD和POTDBO-VMD的分解结果。在实验设置中,DBO和POTDBO的种群数量设置为10,最大迭代次数设置为50,K的搜索范围为[3,15],β的搜索范围为[100,2 500]。DBO和POTDBO收敛曲线如图3所示。
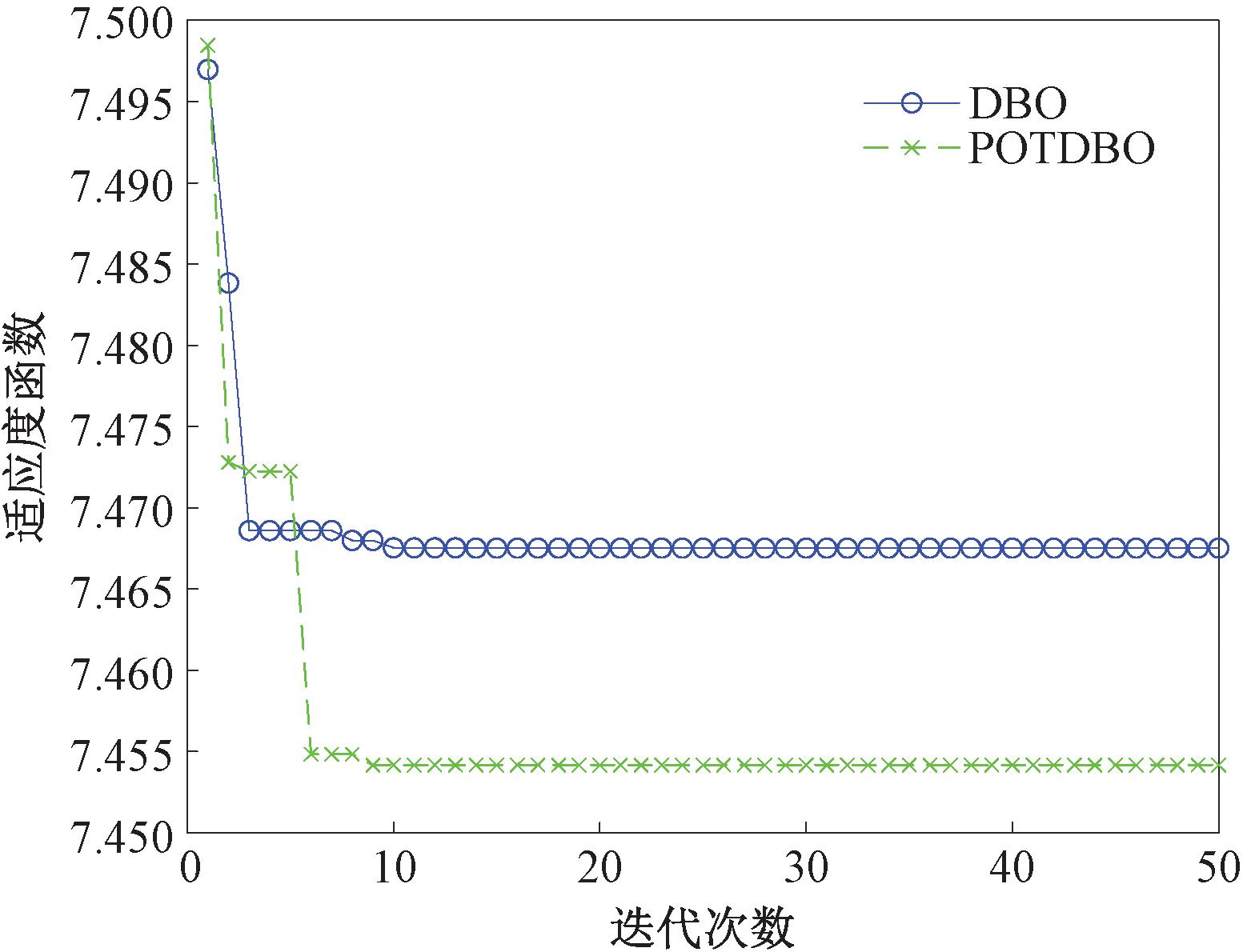
图3 DBO和POTDBO收敛曲线
Figure 3 Convergence curves of DBO and POTDBO
从图3中可以看出,DBO收敛曲线在第10次迭代时收敛至全局最优解,此时适应度值为7.468,VMD最优分解参数为K=6,β=1 144;POTDBO收敛曲线在第9次迭代时收敛至全局最优解,此时适应度值为7.454,VMD最优分解参数为K=5,β=1 252。数据表明,改进的POTDBO算法在风电功率预测的实际应用中要优于普通的DBO算法,有一定的可行性,因此,本文采用POTDBO-VMD模型对风电场历史功率序列进行分解处理。
基于变分模态法的风电功率分解结果如图4、5所示。
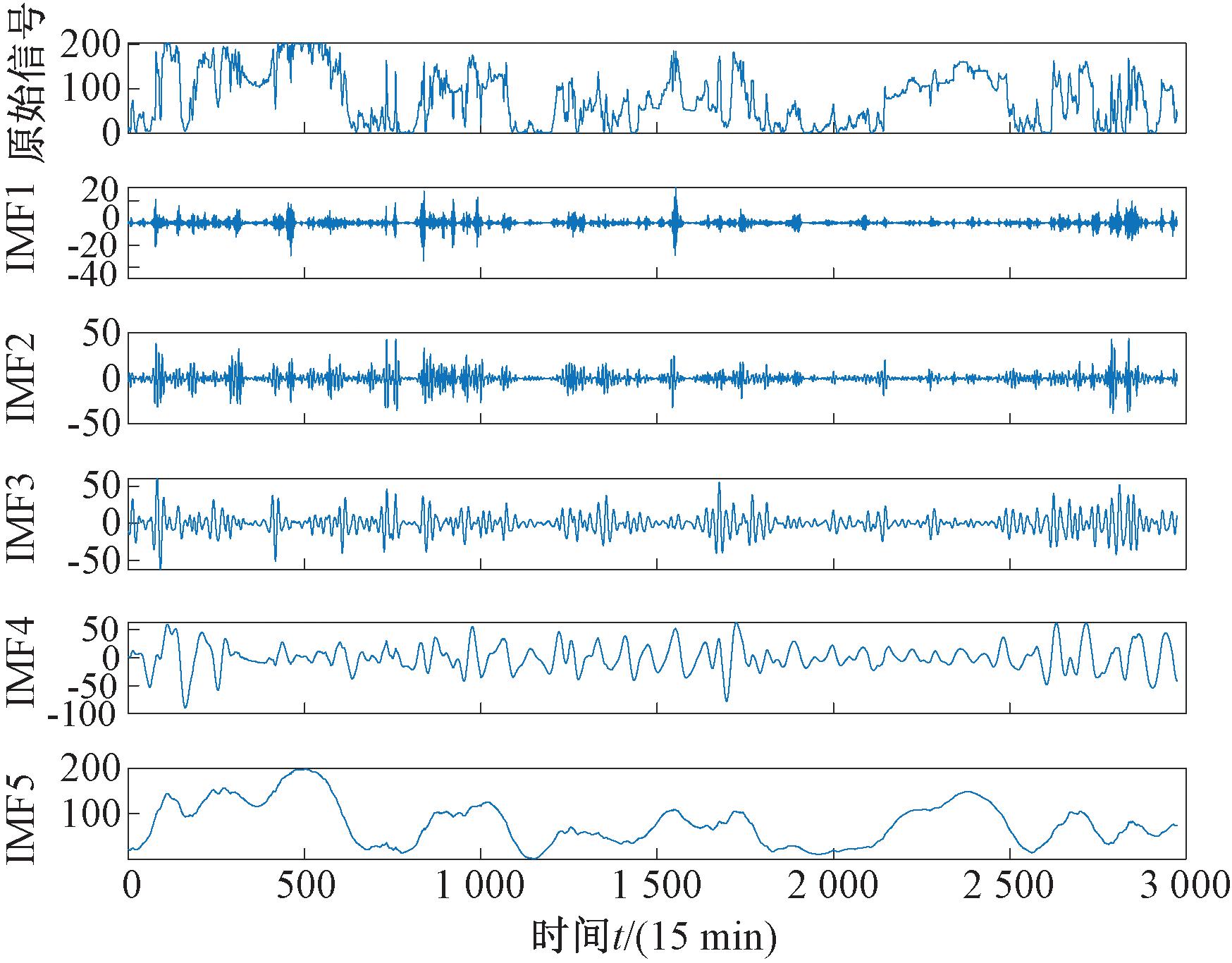
图4 风电场历史功率序列VMD分解图
Figure 4 The exploded view of VMD of historical power series
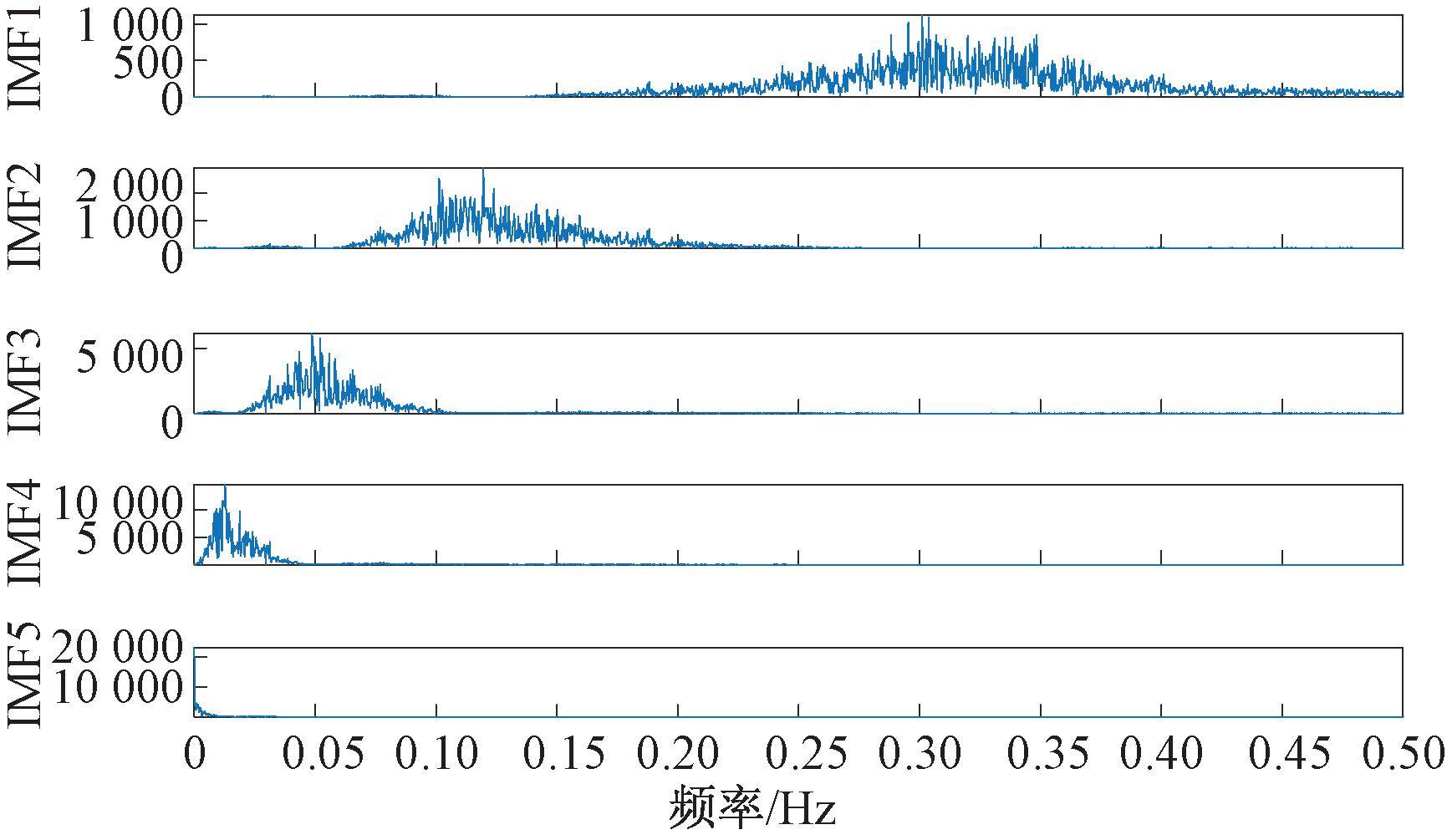
图5 风电场历史功率序列VMD频谱图
Figure 5 The spectrogram of VMD of historical power series
由图4、5可以看出,子序列IMF1至IMF5按照频率依次递减排列。从IMF1到IMF5,数据的波动性呈现出逐渐减弱的趋势,这一现象表明存在随机因素,且这些随机因素会对风电输出功率产生影响;IMF5序列的波动性最小,波形最平缓,可以反映风电输出功率的整体情况。此外,经过VMD分解的5个子序列与原始信号相比,数据的波动性均有不同程度的下降,且每个子序列均未出现明显的模态混叠现象,说明原始风电功率数据经过VMD分解之后数据质量有所提升,进而提高了风电功率预测的准确度,表明VMD分解在提高风电功率预测准确度方面有可行性。
4.2 风电功率确定性预测结果分析
数据中包含风速、风向、温度、湿度等气象因素,通过最大互信息系数法[20]计算每个气象因素与输出功率的相关系数,最终选取相关系数较大的风速(轮毂处)、风向(轮毂处)为功率预测模型的输入,风电输出功率为功率预测模型的输出。为了验证POTDBO-VMD-CNN-BiLSTM模型的先进性,本文引入LSTM、CNN-LSTM、CNN-BiLSTM模型作为对比,CNN层卷积核尺寸为3×1,CNN层步长为[1,1],CNN层卷积核个数为16,BiLSTM神经元数量为[128,32],初始学习率为0.001,风电功率预测结果如图6所示。
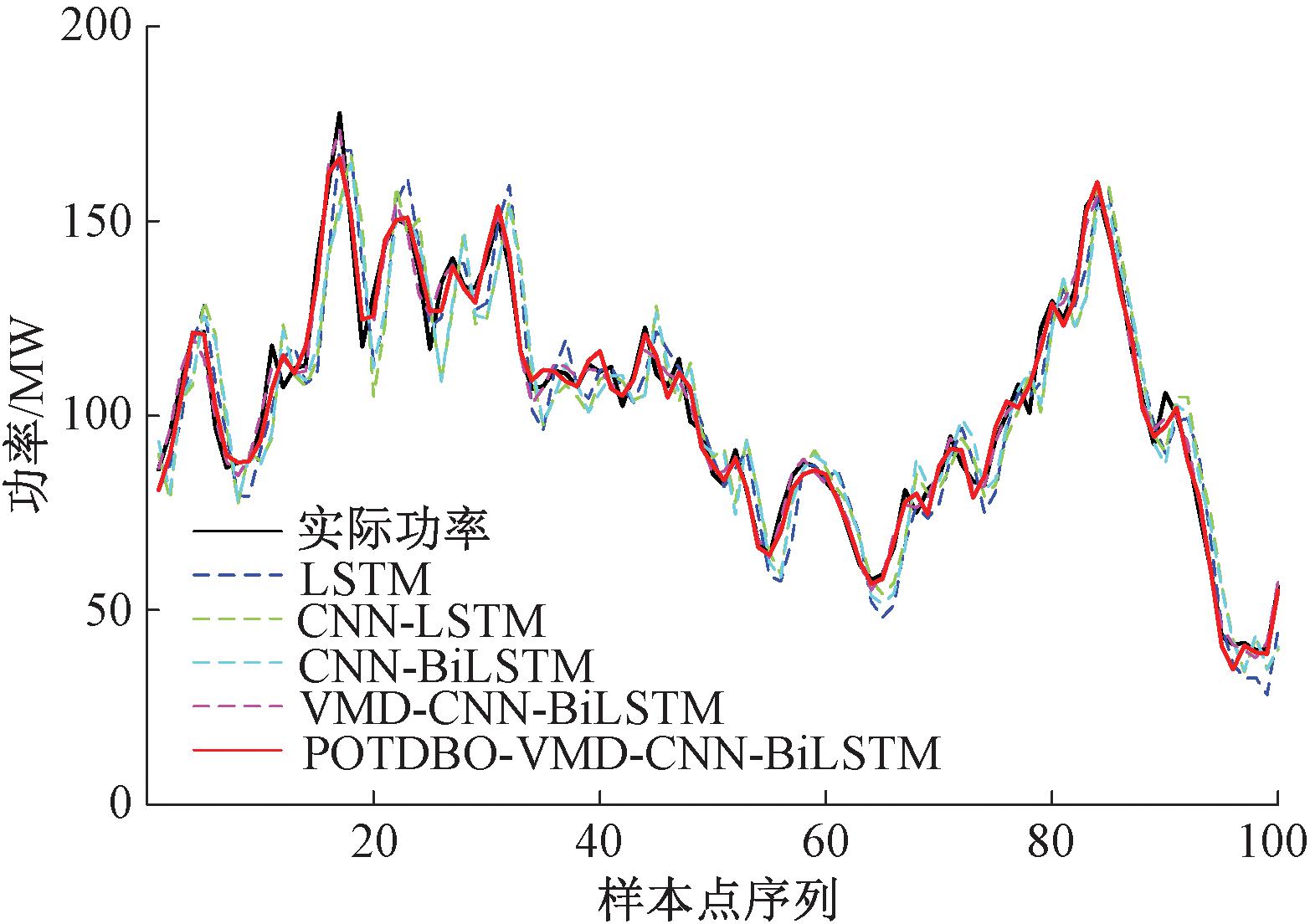
图6 风电功率预测结果对比图
Figure 6 Comparison chart of wind power prediction results
评价指标采取RMSE、MAE、MAPE和R2,本文所用模型与LSTM、CNN-LSTM、CNN-BiLSTM、VMD-CNN-BiLSTM的风电短期功率预测评价指标对比如表1所示。
表1 风电功率预测评价指标对比
Table 1 The comparison of evaluation indicators for wind power prediction

预测模型 RMSE MAE MAPE/ % R 2 LSTM 23. 33 16. 63 16. 59 0. 79 CNN-LSTM 17. 87 12. 14 12. 26 0. 88 CNN-BiLSTM 16. 15 10. 59 11. 35 0. 90 VMD-CNN-BiLSTM 10. 49 8. 12 8. 56 0. 94 本文方法 8. 88 6. 36 6. 57 0. 97
由表1可以看出,经过POTDBO-VMD模型分解之后,风电预测模型的准确度得到了大幅提升。与LSTM、CNN-LSTM、CNN-BiLSTM、VMD-CNN-BiLSTM模型相比,本文模型在RMSE上分别降低了61.94%,50.31%,45.02%,15.35%;MAE分别降低了61.76%,47.61%,39.94%,21.67%;MAPE分别降低了60.40百分点、46.41百分点、42.11百分点、23.24百分点;R2分别提高了22.79%,10.23%,7.78%,3.19%。其性能提升得益于POTDBO-VMD模型能够有效处理非平稳的功率数据,减少风电功率波动性和随机性对预测模型的影响,提高功率预测的准确度。
4.3 风电功率区间预测结果分析
为了验证本文提出的POTDBO-VMD-CNN-BiLSTM结合非参数核密度估计法功率区间预测模型的优越性,选取了T分布估计和高斯分布估计作为对照组,如图7所示。从图7中可以看出,出核密度估计法与真实累积分布函数最为接近,本文模型的精度是最高的。
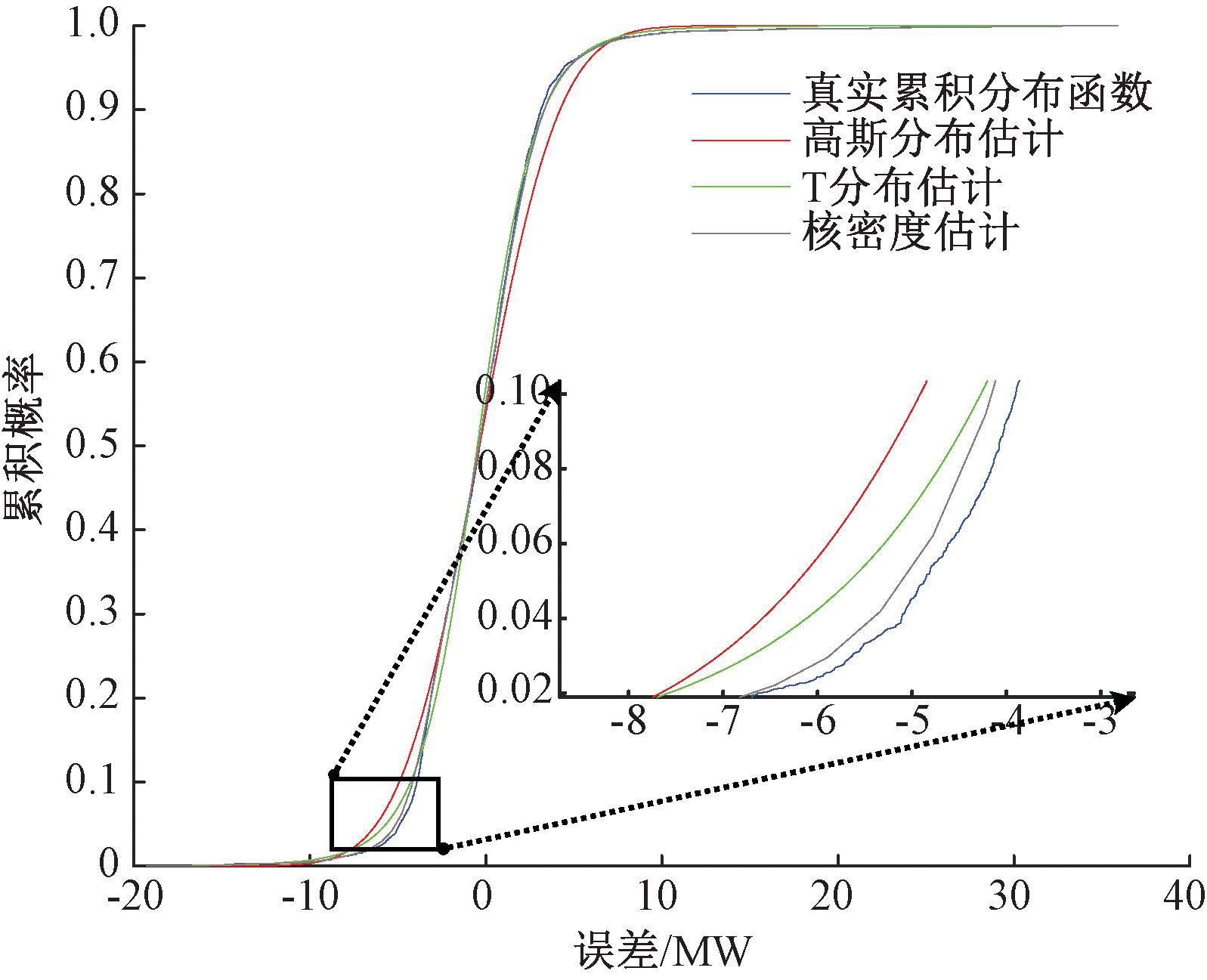
图7 各分布估计方法累积分布函数
Figure 7 Cumulative distribution function of various distribution estimation methods
从POTDBO-VMD-CNN-BiLSTM模型的风电功率预测结果可以看出,传统的确定性预测存在不确定性问题,通过将POTDBO-VMD-CNN-BiLSTM模型的风电功率预测误差通过非参数核密度估计法进行拟合,并对功率预测值和真实值进行分析,得到风电功率区间预测结果如图8所示。
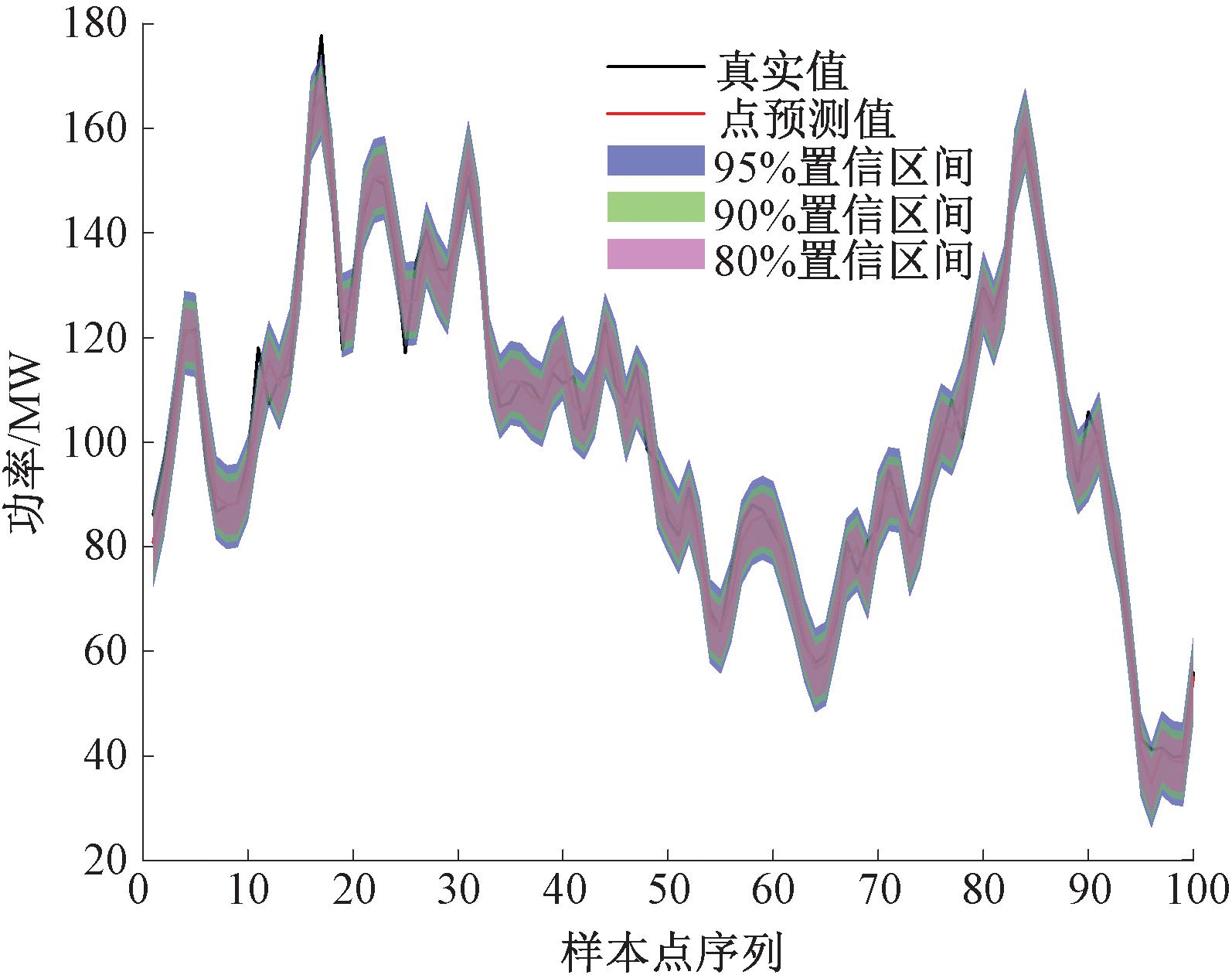
图8 风电功率区间预测结果图
Figure 8 Wind power interval prediction result
评价指标选用PICP、PINAW、CWC,其中在满足工程实践的需求时,PICP的值越接近预设的置信水平,预测效果越好;PINAW值越小,意味着预测区间的宽度越窄,说明预测模型的准确性越高;CWC越小,说明区间预测效果越好。区间预测评价指标如表2所示。
表2 不同置信区间下风电功率区间预测指标对比
Table 2 The comparison of wind power interval prediction indicators with different confidence intervals

预测区间 构建方法 置信水平 95% 置信水平 90% 置信水平 80% PICP PINAW CWC PICP PINAW CWC PICP PINAW CWC 高斯分布 0. 940 5 0. 067 3 0. 175 5 0. 892 9 0. 055 3 0. 134 2 0. 829 4 0. 043 1 0. 043 1 T 分布 0. 930 2 0. 065 9 0. 243 3 0. 884 9 0. 054 4 0. 170 1 0. 823 4 0. 042 0 0. 042 0 本文方法 0. 956 3 0. 071 9 0. 071 9 0. 904 8 0. 058 2 0. 058 2 0. 819 4 0. 040 9 0. 040 9
从图8可以看出,大多数风电功率的真实值落在构建的区间内,表明本文方法进行区间预测的可靠性。从表2可以看出,在置信水平为95%时,与高斯分布、T分布相比,本文方法在CWC上分别降低了0.103 6,0.171 4;在置信水平为90%时,本文方法在CWC上分别降低了0.076,0.111 9;在置信水平为80%时,本文方法在CWC上分别降低了0.002 2,0.001 1。本文所提方法可以提供良好的数据参考,为电力系统的旋转备用调节、调峰调频优化、经济负荷调度等提供理论基础。
5 结论
(1)融合多策略改进的蜣螂优化算法(POTDBO)具备更优的收敛性能,且具有平衡全局寻优和局部探索的能力。
(2)针对气象信息波动剧烈,难以有效提取这一问题,采用 POTDBO-VMD 模型对非平稳的风电功率数据进行处理,与 LSTM、CNN-LSTM、CNN-BiLSTM、VMD-CNN-BiLSTM 模型相比,能够有效减少风电功率波动性和随机性对预测模型的影响,提高功率预测的准确度。
(3)区间预测可以对风电功率预测的不确定性给出定量描述,由实验数据可知,80% 置信水平、90% 置信水平和 95% 置信水平的区间覆盖率均可满足工程实践的需求,能够为电力系统调度决策提供良好的数据参考和坚实的理论基础。
[1] 张文煜, 马可可, 郭振海, 等. 基于灰狼算法和极限学习机的风速多步预测[J]. 郑州大学学报(工学版), 2024, 45(2): 89-96.
ZHANG W Y, MA K K, GUO Z H, et al. Multistep prediction of wind speed based on grey wolf algorithm and extreme learning machine[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(2): 89-96.
[2] WANG S, LI B, LI G Z, et al. Short-term wind power prediction based on multidimensional data cleaning and feature reconfiguration[J]. Applied Energy, 2021, 292: 116851.
[3] LIU W, LIU Y M, FU L, et al. Wind power forecasting method based on bidirectional long short-term memory neural network and error correction[J]. Electric Power Components and Systems, 2021, 49(13/14): 1169-1180.
[4] LI Z, XU R S, LUO X R, et al. Short-term wind power prediction based on modal reconstruction and CNN-BiLSTM[J]. Energy Reports, 2023, 9: 6449-6460.
[5] 李润金, 李丽霞. 基于VMD-CNN-LSTM模型的短期风电功率预测[J]. 沈阳工程学院学报(自然科学版), 2024, 20(1): 6-13.
LI R J, LI L X. Short-term wind power prediction based on VMD-CNN-LSTM model[J]. Journal of Shenyang Institute of Engineering (Natural Science), 2024, 20(1): 6-13.
[6] 任鹏, 付文杰, 申洪涛, 等. 基于竞争学习机制的LSTM风电多目标区间预测[J]. 计算机应用与软件, 2024, 41(6): 305-311, 349.
REN P, FU W J, SHEN H T, et al. Multiple objective interval prediction of LSTM wind power based on competitive learning mechanism[J]. Computer Applications and Software, 2024, 41(6): 305-311, 349.
[7] 陈申, 叶小岭, 熊雄, 等. 基于天鹰优化算法的短期风电功率区间预测[J]. 重庆理工大学学报(自然科学), 2023, 37(4): 304-314.
CHEN S, YE X L, XIONG X, et al. Short-term wind power interval prediction based on Aquila optimization algorithm[J]. Journal of Chongqing University of Technology (Natural Science), 2023, 37(4): 304-314.
[8] 韩丽, 于晓娇, 喻洪波, 等. 基于波动趋势分段的风电功率区间预测[J]. 电力系统自动化, 2023, 47(18): 206-215.
HAN L, YU X J, YU H B, et al. Wind power interval prediction based on fluctuation trend segmentation[J]. Automation of Electric Power Systems, 2023, 47(18): 206-215.
[9] 崔颢, 马平. 基于优化BP神经网络和非参数估计的风功率区间预测[J]. 电子设计工程, 2022, 30(13): 6-10.
CUI H, MA P. Wind power interval prediction based on optimized BP neural network and non-parametric estimation[J]. Electronic Design Engineering, 2022, 30(13): 6-10.
[10] 吴亚钧, 王璐, 张金江. 基于IDBO-LightGBM的光伏阵列故障诊断方法[J/OL]. 电源学报, 2024: 1-15(2024-04-26)[2024-12-13]. http:∥kns.cnki.net/KCMS/detail/detail.aspx? filename=DYXB20240423 01E&dbname=CJFD&dbcode=CJFQ.
WU Y J, WANG L, ZHANG J J. Fault diagnosis method of photovoltaic array based on IDBO-LightGBM[J/OL]. China Industrial Economics, 2024: 1-15(2024-04-26)[2024-12-13]. http:∥kns.cnki.net/KCMS/detail/detail.aspx? filename=DYXB2024042301 E&dbname=CJFD&dbcode=CJFQ.
[11] 郭琴, 郑巧仙. 多策略改进的蜣螂优化算法及其应用[J]. 计算机科学与探索, 2024, 18(4): 930-946.
GUO Q, ZHENG Q X. Multi-strategy improved dung beetle optimizer and its application[J]. Journal of Frontiers of Computer Science and Technology, 2024, 18(4): 930-946.
[12] DEHGHANI M, TROJOVSKY P. Osprey optimization algorithm: a new bio-inspired metaheuristic algorithm for solving engineering optimization problems[J]. Frontiers in Mechanical Engineering, 2023, 8: 1126450.
[13] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81.
TANG G J, WANG X L. Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing[J]. Journal of Xi’an Jiaotong University, 2015, 49(5): 73-81.
[14] 赵志浩. 面向手机部件的目标区域检测算法的设计与实现[D]. 北京: 中国科学院大学(中国科学院沈阳计算技术研究所), 2020.
ZHAO Z H. Design and implementation of target area detection algorithm for mobile phone components[D]. Beijing: Institute of Computing Technology, Chinese Academy of Sciences, 2020.
[15] 饶志, 王科, 谭俊丰, 等. 基于最优带宽的广东海上风电出力非参数核密度估计与分析[J]. 太阳能学报, 2023, 44(12): 274-282.
RAO Z, WANG K, TAN J F, et al. Non-parametric kernel density estimation and analysis of Guangdong offshore wind power output based on optimal bandwidth[J]. Acta Energiae Solaris Sinica, 2023, 44.
[16] 宋绍剑, 姜屹远, 刘斌. 一种TCN的改进模型及其在短期光伏功率区间预测的应用[J]. 计算机应用研究, 2023, 40(10): 3064-3069.
SONG S J, JIANG Y Y, LIU B. Improved TCN model and its application in short-term photovoltaic power interval prediction[J]. Application Research of Computers, 2023, 40(10): 3064-3069.
[17] 饶志, 杨再敏, 蒙文川, 等. 基于改进型非参数核密度估计法的南方区域风电出力特性分析[J]. 电网与清洁能源, 2022, 38(6): 81-88, 97.
RAO Z, YANG Z M, MENG W C, et al. An analysis of wind power output characteristics in Southern China Region based on improved non-parametric kernel density estimation[J]. Power System and Clean Energy, 2022, 38(6): 81-88, 97.
[18] 吴永斌, 张建忠, 邓富金, 等. 基于方差变化率判据-四分位的风电场功率异常数据识别[J]. 电力工程技术, 2023, 42(4): 141-148.
WU Y B, ZHANG J Z, DENG F J, et al. Anomaly data identification of wind power in wind farm with the criterion of variance change rate and quartile[J]. Electric Power Engineering Technology, 2023, 42(4): 141-148.
[19] 孙亚南, 黄越辉, 孙谊媊, 等. 基于运行数据的短期风电功率预测误差互补特性探析[J]. 电力系统自动化, 2021, 45(21): 215-223.
SUN Y N, HUANG Y H, SUN Y Q, et al. Operation data based analysis on complementary characteristics of short-term power prediction error for wind power[J]. Automation of Electric Power Systems, 2021, 45(21): 215-223.
[20] 李津, 史加荣, 张琰妮, 等. 基于最大信息系数的短期太阳辐射协同估计[J]. 太阳能学报, 2023, 44(9): 286-294.
LI J, SHI J R, ZHANG Y N, et al. Short-term solar radiation synergy estimation based on maximum information coefficient[J]. Acta Energiae Solaris Sinica, 2023, 44(9): 286-294.