随着电子商务的迅速发展,越来越多的消费者倾向于网上购物,使得末端配送需求激增,导致传统自营配送模式面临着配送员短缺问题[1]。因此,孟秀丽等[2]提出了一种基于共享经济理念的众包配送模式。该模式通过互联网从社会招募非特定人员(又称众包员)从事配送服务,不仅可以扩展物流运力,而且能提高配送效率。
为充分利用物流运力,学者们针对不同末端配送情景,提出了融合众包配送模式的配送方案优化方法。Archetti等[3]针对自营配送员与众包员共存情景,构建数学规划模型,提出了一种客户指派与车辆路径规划方法。在此基础上,Macrina等[4-5]考虑客户配送时间窗要求、需求可分性以及不同的众包员取货点,提出了客户指派与车辆路径规划方法。杨华龙等[6]考虑一项配送任务可由多个众包员接力完成,提出了客户指派与众包员调度方法。Dayarian等[7]针对客户与配送员随机到达情景,在提出订单推迟处理规则的基础上,基于禁忌搜索算法给出了客户指派与车辆路径规划方法。Schur等[8]考虑众包员随机到达特性以及服务价格对众包员配送任务接收率的影响,基于动态规划提出了一种客户指派与服务价格制定方法,但并未明确车辆配送路径。Dai等[9]基于自营配送员单次仅服务一个顾客的假设,提出了一种配送员调度与客户指派方法。针对纯众包员配送情景,Yildiz等[10]考虑报酬对众包员参与度的影响,基于排队模型确定了最优众包员雇佣数量;Le等[11]考虑众包服务价格对配送需求以及众包员参与度的双重影响,通过构建数学规划模型制定了服务价格与客户指派方案;王会静等[12]考虑众包员具有客户选择权,确定了客户指派方案。
综上可知,在优化采用众包配送模式的末端配送方案时,鲜有研究考虑报酬对众包员参与度的影响[13]。未考虑此影响会导致所得调度方案在实践中会因缺少众包员而不可行,或因向众包员支付报酬过高而导致配送企业利益受损。因此,本文考虑报酬对众包员参与度的影响,同时,考虑众包员供给数量随时间变化的动态特性[14],提出更符合实践需要的自营配送员与众包员共存情景下的末端配送优化方法。其中,自营配送员驾驶卡车进行配送服务,一天可行驶多个行程,每个行程可服务多个客户,即多行程车辆路径问题[15-16]。
为解决该问题,首先,本文根据众包员供给动态特性,基于时空网络[17]构建数学规划模型对问题进行描述;其次,根据模型特征设计局部搜索算子提出求解大规模案例的自适应大邻域搜索算法;最后,通过案例对模型与算法的有效性进行验证,并分析自营配送员与众包员共存的混合配送模式的适用情景以及众包员供给动态性对混合配送模式的影响,为末端配送服务商提供决策参考。
1 问题描述与建模
1.1 问题描述
考虑众包员供给动态性的末端配送优化问题涉及配送中心、客户、自营配送员和众包员4个要素。
(1)配送中心。一个配送中心o为若干个客户i(i∈I)提供配送服务。它的营业时间为[e0,l0]。在营业时间内,自营配送员和众包员都可以来取货,且取货次数不限。配送中心拥有的货物量可以满足所有客户需求。
(2)客户。每个客户所需货物类型相同,所需货量为qi(i∈I),kg;接受配送服务的时间窗为[ei,li];所需服务时间为si,h;客户之间以及与配送中心间的欧氏距离为di,j(i,j∈I∪{o}),km。
(3)自营配送员。自营配送员驾驶卡车从配送中心出发为客户配送货物或将货物交由众包员。卡车固定使用成本为Cf,元;额定载重为Qe,kg;行驶速度为Ve,km/h;单位距离行驶成本为Cd,元/km。在一天的配送过程中,自营配送员可以多次返回配送中心取货。
(4)众包员。为应对配送需求高峰,物流企业会招募一定数量的众包员提供配送服务。愿意执行配送任务的众包员数量随时间变化,因此,将一天平均划分为|T|个时段,每个时段时长为tΔ[18]。时段t∈T愿意执行配送任务的众包员数量(即潜在众包员数量)为![]() 将物流企业在时段t实际招募到的众包员数量Nt与
将物流企业在时段t实际招募到的众包员数量Nt与![]() 的函数关系[19]设为
的函数关系[19]设为

(1)
式中:pt为时段t的众包员报酬,元/单;δ为众包员供给-价格敏感系数;e为常数。
每个众包员驾驶电动摩托车配送货物,最大配送距离为D,km;行驶速度为Vc,km/h。众包员每次仅为一个客户提供服务,其可携带货量能满足任一客户需求,携带的货物来自配送中心或者卡车。物流企业以配送成本最小为目标,制定众包员报酬、指派客户并规划卡车配送路径,如图1所示。
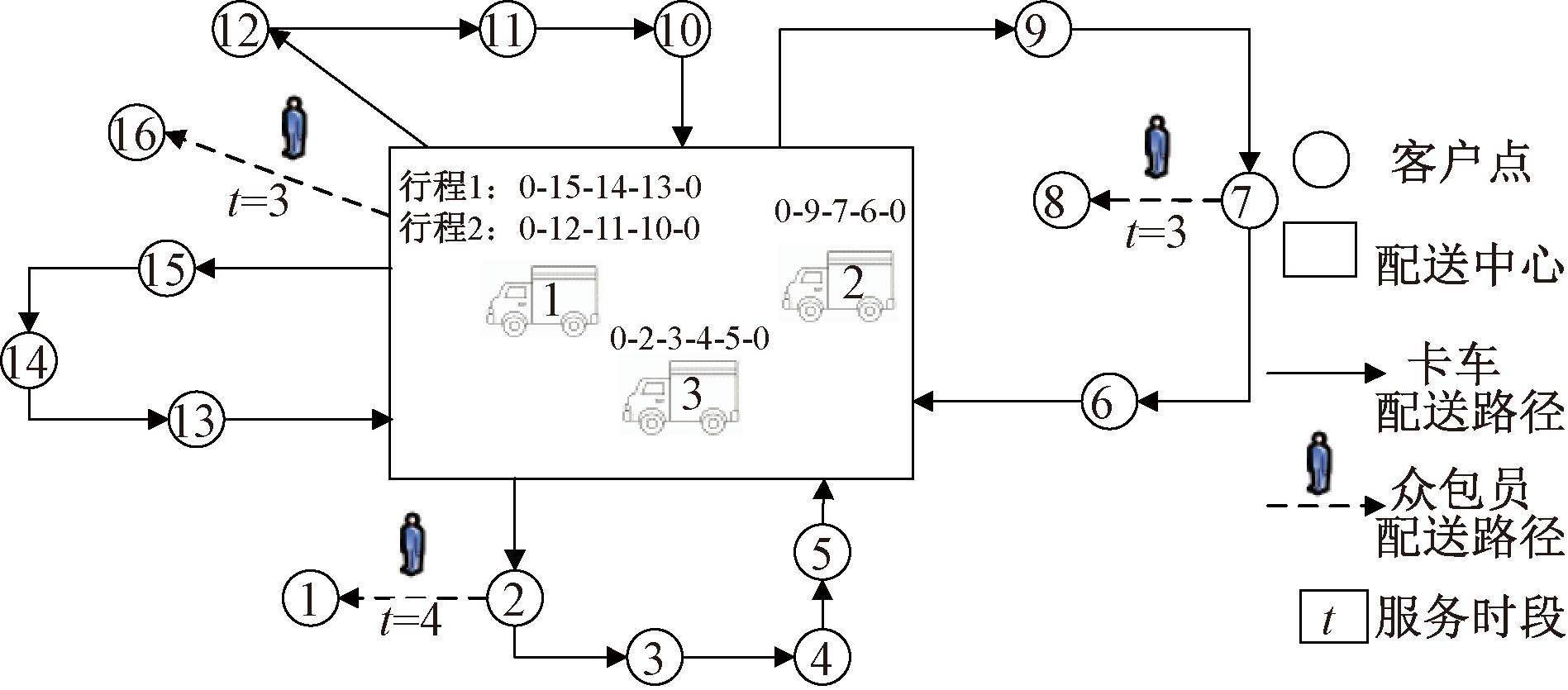
图1 考虑众包员供给动态性的末端配送优化
Figure 1 Last mile delivery optimization considering supply dynamics of crowdsourced personnel
1.2 问题建模
问题建模涉及的决策变量为
(2)
(3)
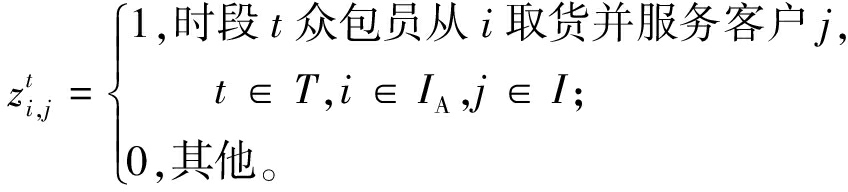
(4)
式中:IA={o}∪I为配送中心(卡车起点)和客户构成的集合;IB={d}∪I为配送中心(卡车终点)和客户构成的集合。
优化模型如式(5)~(25)所示。其中,式(5)是目标函数,最小化卡车行驶成本、固定使用成本和众包员报酬之和;式(6)保证每个客户被服务一次;式(7)~(8)为卡车进出平衡约束;式(9)~(10)为卡车到达节点时刻与配送路径关系;式(11)~(12)为众包员到达节点时刻与其配送服务执行时段以及货物接收点关系;式(13)为到达节点时刻与节点服务开始时刻关系;式(14)为离开节点时刻与节点服务开始时刻关系;式(15)~(16)为时间窗约束;式(17)~(18)描述了卡车到达节点时的载重量与配送路径关系;式(19)为载重量约束;式(20)为众包员配送距离约束;式(21)~(23)为车辆-众包员时空协同约束,确保众包员在客户处接货时,卡车也位于此处;式(24)为众包员可得性约束;式(25)给定了物流企业招募的众包员数量与潜在众包员数量以及众包员报酬关系。
![]()
![]()
(5)
s.t.
(6)
(7)
(8)
(9)
(10)
i∈IA,j∈I,t∈T;
(11)
(12)
ai≤bi,i∈IA;
(13)
ri≥bi+si,i∈I;
(14)
ei≤bi≤li,i∈IA;
(15)
(16)
i∈IA,j∈IB;
(17)
(18)
0≤wi≤Qe,i∈IB;
(19)
(20)
(21)
(22)
(23)
(24)
(25)
式中:ai(i∈IA∪{d})为卡车或众包员到达节点i的时刻;bi(i∈IA)为卡车或众包员开始服务节点i的时刻;ri(i∈IA)为卡车或众包员离开节点i的时刻;wi(i∈IA∪{d})为卡车到达节点i时的载重量。
1.3 线性化
当目标函数达到最小时,式(24)为等式,且![]() 恰好为整数,因此,目标函数项中
恰好为整数,因此,目标函数项中![]() 可以等价为
可以等价为![]() 令
令![]() 引入参数
引入参数![]() 和新决策变量
和新决策变量
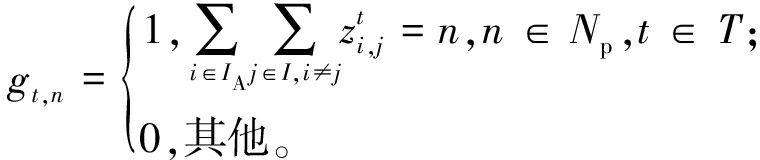
(26)
可将Gt线性化为
(27)
(28)
(29)
综上,模型更新为
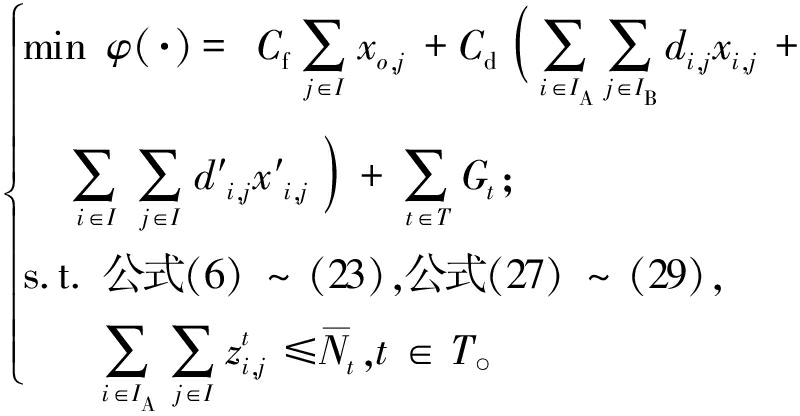
(30)
2 改进自适应大邻域搜索算法
线性化后的模型是一个混合整数线性规划模型,精确算法难以在有限时间内求解其大规模案例[20],因此,本文结合模拟退火算法[21]和自适应大邻域搜索算法[22]设计了一个启发式求解算法,即改进自适应大邻域搜索算法(improved adaptive large neighborhood search, IALNS),如图2所示。该算法根据问题特征改进最小成本插入法生成初始解;利用基于问题领域知识设计的10种破坏算子和改进的最小成本插入法探索解空间;基于模拟退火算法思想接受次优解,避免算法陷入局部最优。

图2 IALNS算法流程
Figure 2 Flowchart of IALNS algorithm
IALNS包括初始解构造阶段和改善阶段。初始解构造阶段利用改进最小成本插入法生成初始解。改进最小成本插入法针对每一个客户,计算卡车和众包员配送成本,并选取配送成本最低的方案。卡车配送成本为新增一条配送路径或将客户加入现有路径所增加成本的最小值,如图3所示,其中,C(·)表示卡车配送成本。众包员配送成本为最低的众包员报酬,如图4所示。在计算众包员报酬时,需判断可行的货物接收地。满足以下3个条件,则一个货物接收地可行:①车辆现有载重加上客户需求量(货物量)后,满足载重量约束;②货物接收地与客户的距离小于众包员最大配送距离;③众包员到达客户时间符合客户时间窗要求。
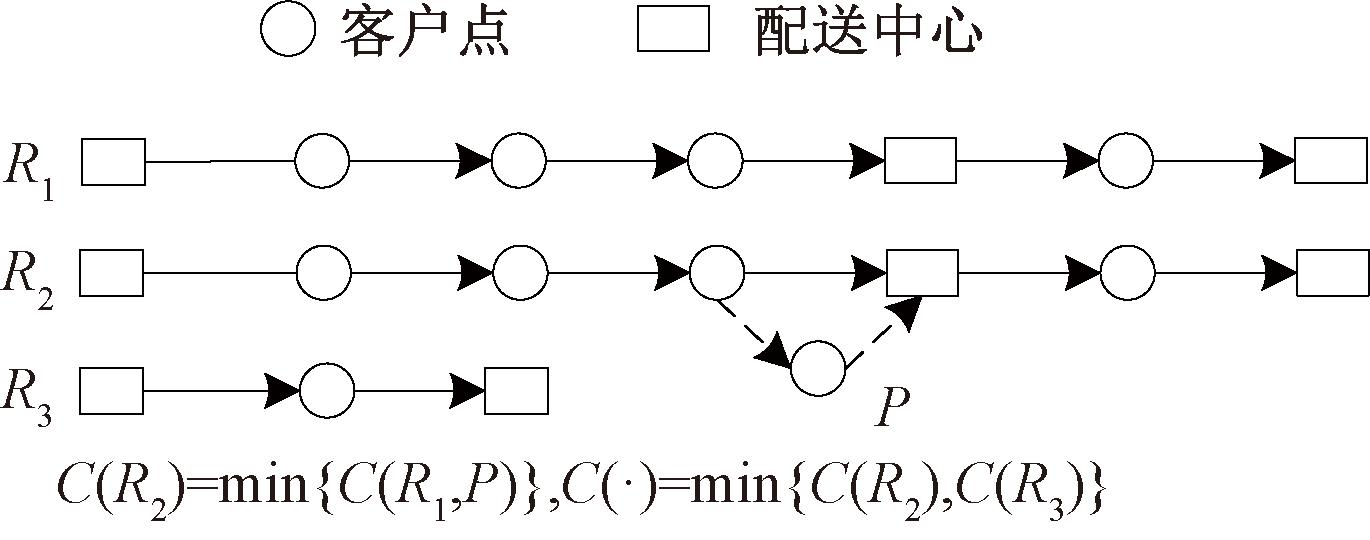
图3 卡车配送成本
Figure 3 Delivery cost of truck
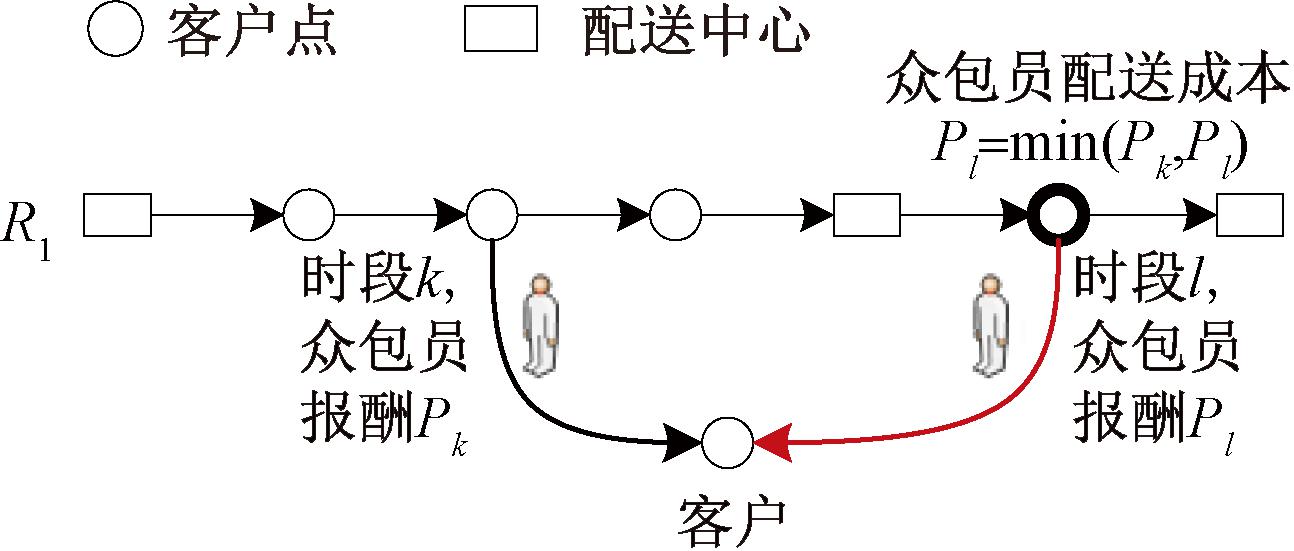
图4 众包员配送成本
Figure 4 Delivery cost of crowdsourced personnel
改善阶段操作步骤如下。
步骤1 初始化参数,包括最大内循环次数![]() 最大外循环次数
最大外循环次数![]() 破坏算子性能增加值
破坏算子性能增加值![]() 温度限值Hmin,降温系数α,0<α<1,客户删除量N。
温度限值Hmin,降温系数α,0<α<1,客户删除量N。
步骤2 根据10种破坏算子性能值,利用轮盘赌规则选择破坏算子,删除当前解中至少N个客户,并用修复算子将其修复成新解Xnew。
步骤3 如果新解优于当前最优解,则更新当前最优解为新解,内循环次数设为0,破坏算子性能值加![]() 否则,如果e(obj-φ(Xnew))/H>random,则更新当前解为新解,内循环次数设为0,破坏算子性能值加
否则,如果e(obj-φ(Xnew))/H>random,则更新当前解为新解,内循环次数设为0,破坏算子性能值加![]() 否则,内循环次数加1,破坏算子性能值加
否则,内循环次数加1,破坏算子性能值加![]()
步骤4 如果内循环次数小于等于![]() 返回步骤2;否则,更新当前解为当前最优解,内循环次数设为0,外循环次数加1,温度降至当前温度的α倍。
返回步骤2;否则,更新当前解为当前最优解,内循环次数设为0,外循环次数加1,温度降至当前温度的α倍。
步骤5 如果外循环次数![]() 或者温度>Hmin,则返回步骤2;否则停止计算,输出结果。
或者温度>Hmin,则返回步骤2;否则停止计算,输出结果。
改善阶段使用的10种破坏算子分别如下:①随机删除路径中的1个客户;②随机删除1名众包员和其服务的客户;③随机选择1条路径,删除引起配送成本增加最多的1个客户[23],如图5所示;④删除报酬最高的1名众包员和其服务的客户,如图6(a)所示;⑤随机选择1条路径,将路径中连续的3个节点删除,如图6(b)所示;⑥随机选择1个行程,将行程中最后3个客户删除,如图6(c)所示;⑦随机删除1辆卡车的配送路径;⑧删除时间窗最接近的客户,时间窗最接近的判断规则为![]() ⑨删除地理位置最接近的客户;⑩随机选择1条路径,删除路径中地理位置最接近的客户。改善阶段使用的修复算子为改进最小成本插入法。
⑨删除地理位置最接近的客户;⑩随机选择1条路径,删除路径中地理位置最接近的客户。改善阶段使用的修复算子为改进最小成本插入法。

图5 导致路径R1配送成本增加最多的客户P
Figure 5 Customer P that added the most delivery cost of route R1
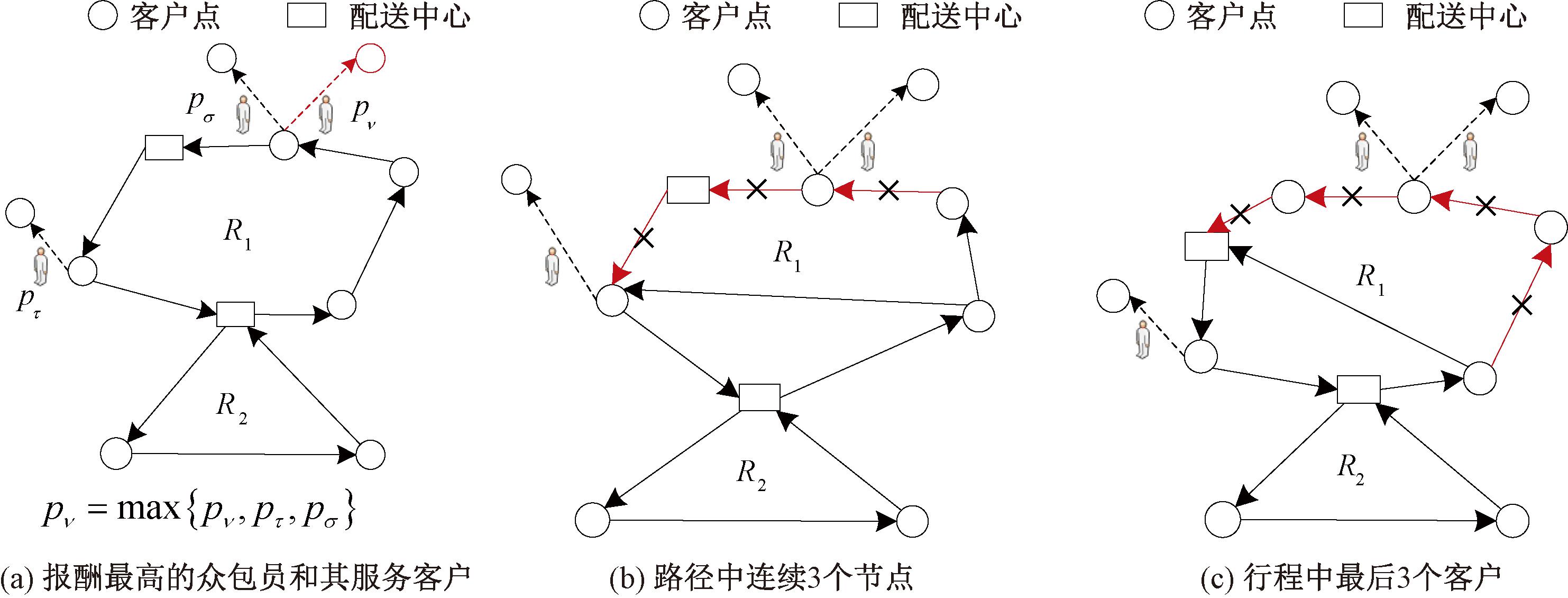
图6 破坏算子4~6的示意图
Figure 6 Schematic diagram of destruction operators No.4 to No.6
3 算例分析
因本研究所考虑问题是VRPTW(vehicle routingproblem withtimewindow)的扩展,故取VRPTW标准算例[25]测试IALNS。VRPTW标准案例根据客户空间分布情况分为C案例集、R案例集和RC案例集。C案例集中,客户集中分布;R案例集中,客户分散分布;RC案例集中,一部分客户集中分布,另一部分客户分散分布。算例参数[26]设置:Cf=519元/辆;Cd=4元/km;Ve=60 km/h;Qe=100 kg;Vc=37.5 km/h;D=20 km;δ=80人/元;![]() 人,t∈T;tΔ与客户服务时间相同。
人,t∈T;tΔ与客户服务时间相同。
算例实验采用的计算机操作系统是Window 10,处理器是Intel(R) Core(TM) i7-10875H CPU @ 2.30 GHz,内存为32 GB,编译软件为C++23。
根据预实验结果,设定IALNS求解参数为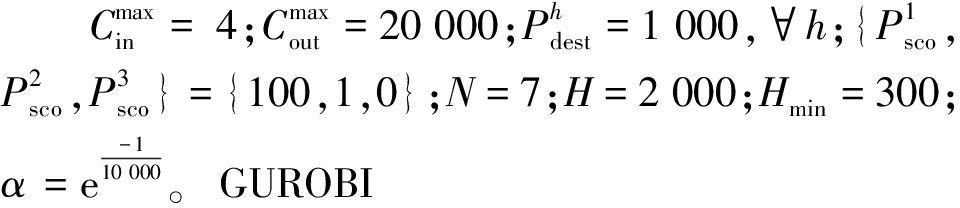 求解时间设定为1 h。
求解时间设定为1 h。
3.1 IALNS求解性能分析
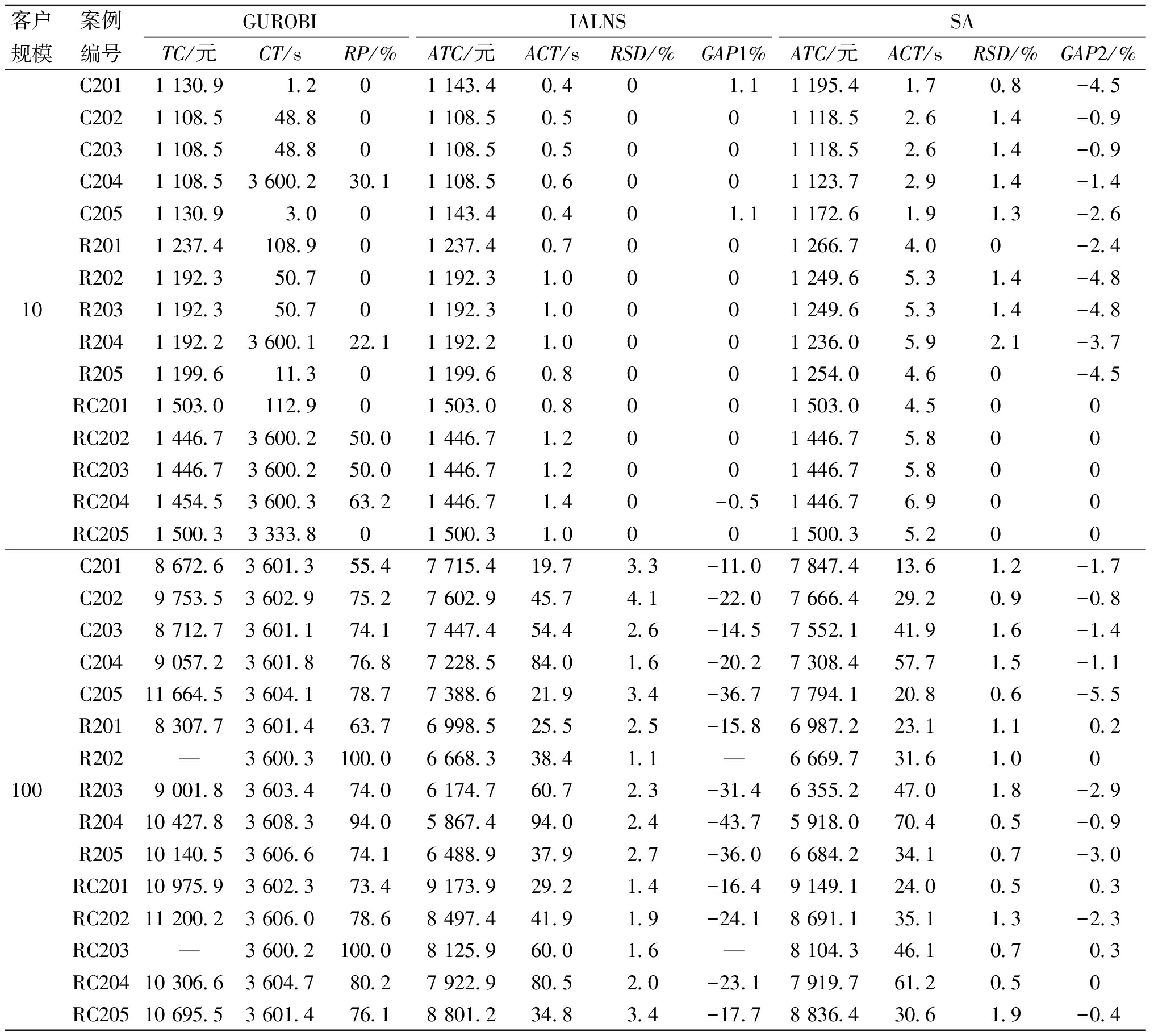
表1为GUROBI、IALNS和模拟退火算法(SA)求解30个算例的结果。
表1 GUROBI、IALNS与SA性能比较
Table 1 Performance comparisons among GUROBI,IALNS and SA
客户规模案例编号GUROBIIALNSSATC/元CT/sRP/%ATC/元ACT/sRSD/%GAP1%ATC/元ACT/sRSD/%GAP2/%10C2011 130.91.20 1 143.40.40 1.11 195.41.70.8-4.5C2021 108.548.801 108.50.5001 118.52.61.4-0.9C2031 108.548.801 108.50.5001 118.52.61.4-0.9C2041 108.53 600.230.11 108.50.6001 123.72.91.4-1.4C2051 130.93.001 143.40.401.11 172.61.91.3-2.6R2011 237.4108.901 237.40.7001 266.74.00-2.4R2021 192.350.701 192.31.0001 249.65.31.4-4.8R2031 192.350.701 192.31.0001 249.65.31.4-4.8R2041 192.23 600.122.11 192.21.0001 236.05.92.1-3.7R2051 199.611.301 199.60.8001 254.04.60-4.5RC2011 503.0112.901 503.00.8001 503.04.500RC2021 446.73 600.250.01 446.71.2001 446.75.800RC2031 446.73 600.250.01 446.71.2001 446.75.800RC2041 454.53 600.363.21 446.71.40-0.51 446.76.900RC2051 500.33 333.801 500.31.0001 500.35.200100C2018 672.63 601.355.47 715.419.73.3-11.07 847.413.61.2-1.7C2029 753.53 602.975.27 602.945.74.1-22.07 666.429.20.9-0.8C2038 712.73 601.174.17 447.454.42.6-14.57 552.141.91.6-1.4C2049 057.23 601.876.87 228.584.01.6-20.27 308.457.71.5-1.1C20511 664.53 604.178.77 388.621.93.4-36.77 794.120.80.6-5.5R2018 307.73 601.463.76 998.525.52.5-15.86 987.223.11.10.2R202—3 600.3100.06 668.338.41.1—6 669.731.61.00R2039 001.83 603.474.06 174.760.72.3-31.46 355.247.01.8-2.9R20410 427.83 608.394.05 867.494.02.4-43.75 918.070.40.5-0.9R20510 140.53 606.674.16 488.937.92.7-36.06 684.234.10.7-3.0RC20110 975.93 602.373.49 173.929.21.4-16.49 149.124.00.50.3RC20211 200.23 606.078.68 497.441.91.9-24.18 691.135.11.3-2.3RC203—3 600.2100.08 125.960.01.6—8 104.346.10.70.3RC20410 306.63 604.780.27 922.980.52.0-23.17 919.761.20.50RC20510 695.53 601.476.18 801.234.83.4-17.78 836.430.61.9-0.4
在表1中,TC为配送成本;CT为求解时间;RP为剩余进度;ATC为平均配送成本;ACT为平均求解时间;RSD为相对标准偏差。
(30)
(31)
(32)
(33)
由表1可以看出,客户规模为10时,GUROBI在10个算例上取得最优配送成本,IALNS稍差于GUROBI,获得了8个算例的最优配送成本,但IALNS求解时间较短,最大耗时仅1.4 s。当客户规模为100时,GUROBI花费1 h无法获得2个算例(R202和RC203)的可行方案;对剩余的13个算例,IALNS的平均配送成本比GUROBI降低了24%。而且,IALNS求解大规模算例所需平均时间为48.5 s,远小于GUROBI所用求解时间。与模拟退火算法相比,IALNS的配送成本也更低,最大降低了5.5%。另外,由IALNS多次求解结果的相对标准偏差小于5%可知,IALNS的求解稳定性较好。综上,本文模型正确,IALNS有效。
3.2 混合配送模式的有效性分析
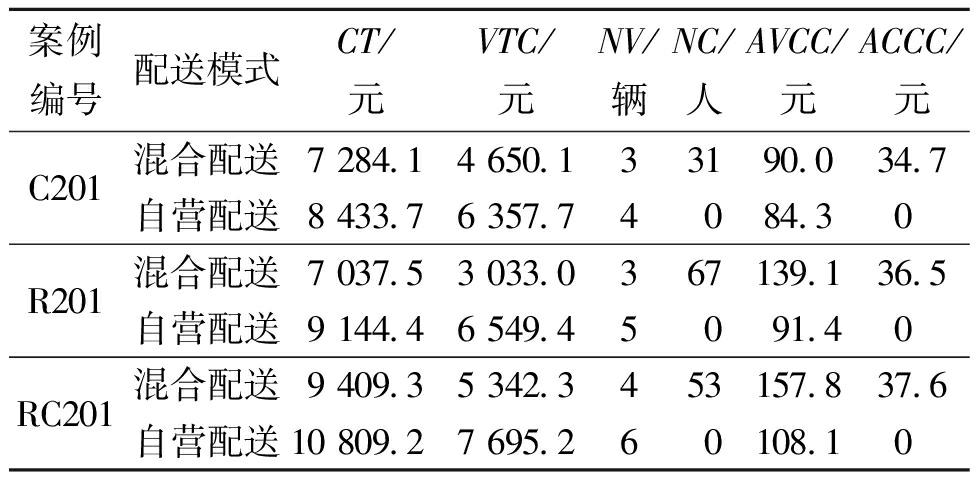
应用100个客户案例,表2比较了自营配送模式与混合配送模式的配送成本,其中,VTC为卡车行驶成本;NV为卡车数;NC为众包员雇佣数;AVCC为卡车服务客户的平均成本;ACCC为众包员服务客户的平均成本。由表2可知,混合配送模式通过减少卡车数量和行驶距离降低了末端配送成本,例如C201案例配送模式从自营配送变成混合配送时,服务相同客户所需卡车数从4辆减少至3辆,节约车辆固定成本519.0元;同时,减少卡车行驶成本1 707.6元;仅因需要众包员,增加众包员雇佣成本1 077.1元,最终减少成本1 149.5元。
表2 自营配送模式与混合配送模式比较
Table 2 Comparison between self-operational delivery mode and hybrid delivery mode
案例编号配送模式CT/元VTC/元NV/辆NC/人AVCC/元ACCC/元C201混合配送 7 284.14 650.1331 90.034.7自营配送 8 433.76 357.74 0 84.3 0R201混合配送 7 037.53 033.0367139.136.5自营配送 9 144.46 549.45 0 91.4 0RC201混合配送 9 409.35 342.3453157.837.6自营配送10 809.27 695.26 0108.1 0
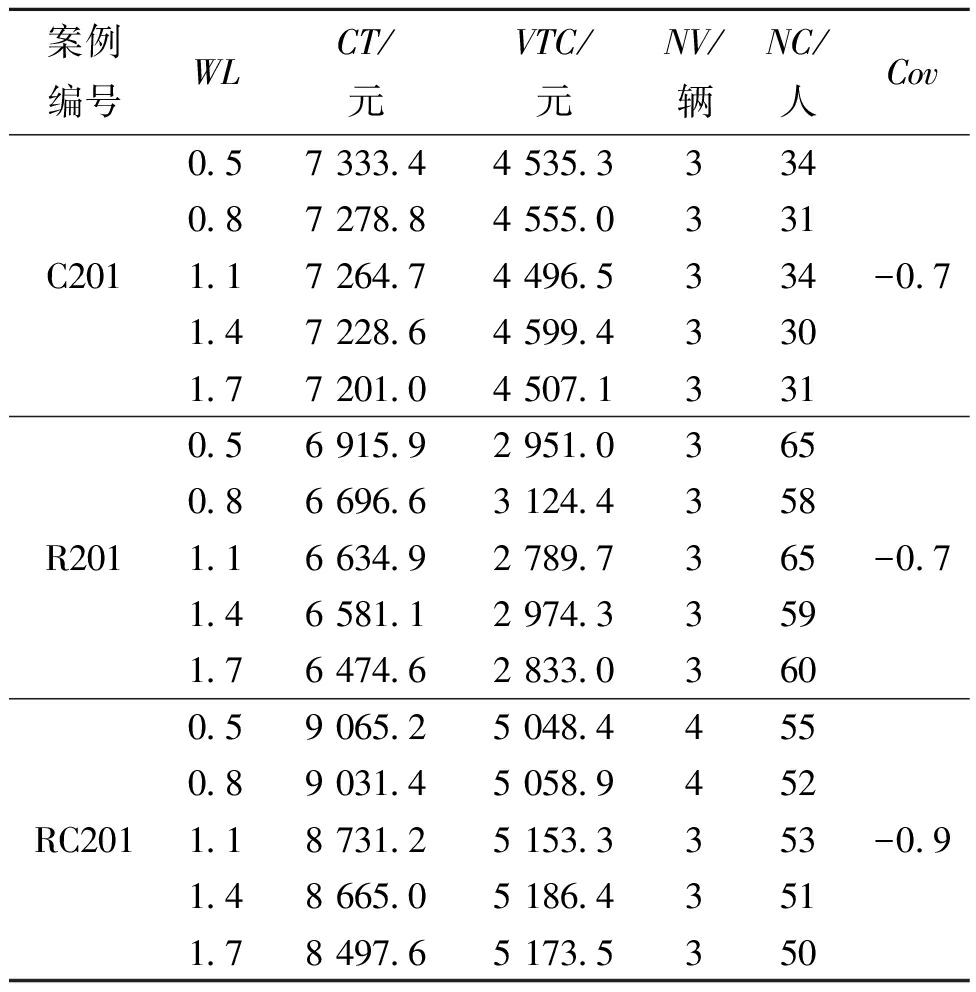
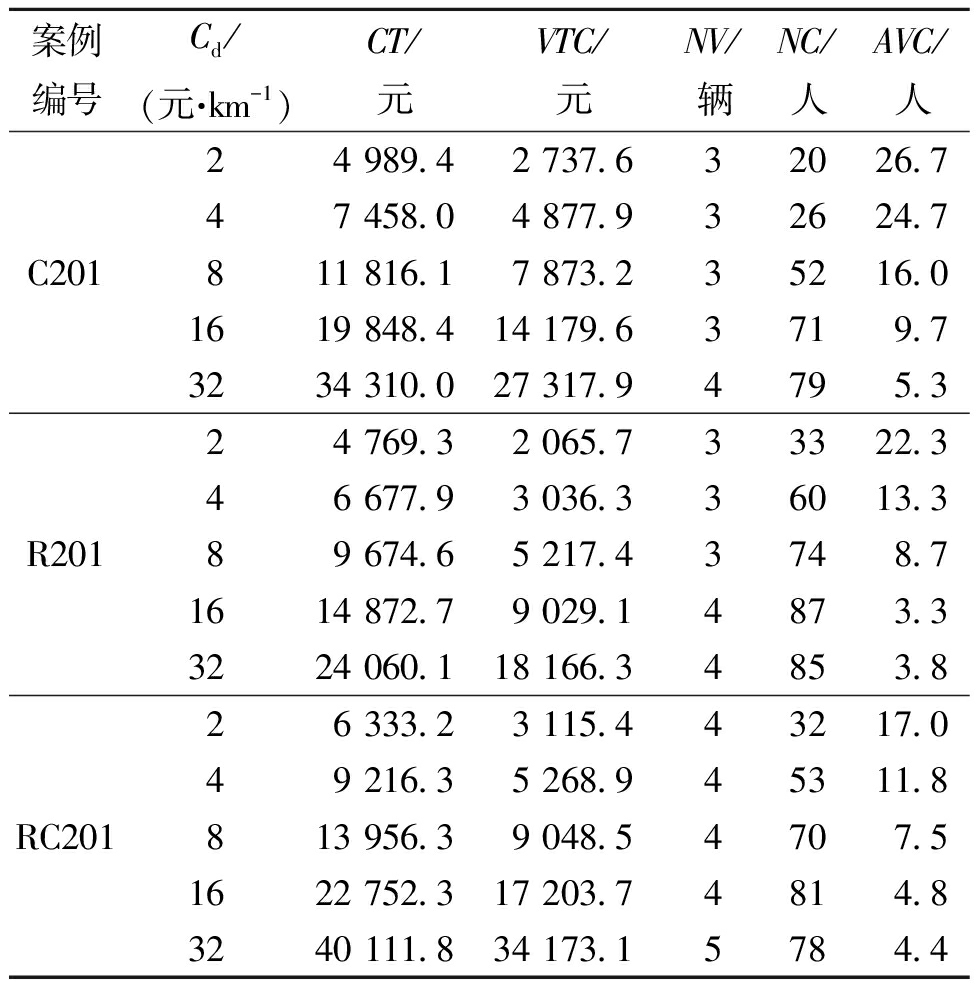
为便于应用,进一步应用100个客户案例分析混合配送模式的适用特性。表3、表4和表5分别为时间窗扩展率WL,卡车单位距离行驶成本Cd以及众包员供给-价格敏感系数δ的影响结果。其中,Cov为Peason相关系数;AVC为平均每辆卡车服务的客户数。由表3~5可知,随WL增加,物流公司雇佣的众包员数量会减少。对于C201、R201和RC201算例,它们间的相关系数分别为-0.7,-0.7和-0.9,相关系数较高。因此,混合配送模式在时间窗紧凑的末端配送中意义显著,如生鲜配送。随Cd增加,物流公司会招募更多的众包员,混合配送模式更有意义。这是因为雇佣众包员可以减少卡车行驶距离,仅需按单支付众包员报酬,因此,混合配送模式适用于卡车行驶成本较高时,如能源价格上涨。物流公司雇佣的众包员数量会随δ的增加而显著下降,表明混合配送模式更适用于就业机会少、众包服务平台少的地区。
表3 时间窗扩展率的影响
Table 3 Effects of time window extend ratio
案例编号WLCT/元VTC/元NV/辆NC/人CovC2010.57 333.44 535.33340.87 278.84 555.03311.17 264.74 496.53341.47 228.64 599.43301.77 201.04 507.1331-0.7R2010.56 915.92 951.03650.86 696.63 124.43581.16 634.92 789.73651.46 581.12 974.33591.76 474.62 833.0360-0.7RC2010.59 065.25 048.44550.89 031.45 058.94521.18 731.25 153.33531.48 665.05 186.43511.78 497.65 173.5350-0.9
表4 卡车单位距离行驶成本的影响
Table 4 Effects of truck′s travel cost per kilometer
案例编号Cd/(元·km-1)CT/元VTC/元NV/辆NC/人AVC/人C2012 4 989.4 2 737.632026.7 4 7 458.0 4 877.932624.7 811 816.1 7 873.235216.01619 848.414 179.6371 9.73234 310.027 317.9479 5.3R201 2 4 769.3 2 065.733322.3 4 6 677.9 3 036.336013.3 8 9 674.6 5 217.4374 8.71614 872.7 9 029.1487 3.33224 060.118 166.3485 3.8RC2012 6 333.2 3 115.443217.0 4 9 216.3 5 268.945311.8 813 956.3 9 048.5470 7.51622 752.317 203.7481 4.83240 111.834 173.1578 4.4
表5 众包员供给-价格敏感系数的影响
Table 5 Effects of supply-price sensitivity factor of crowdsourced personnel
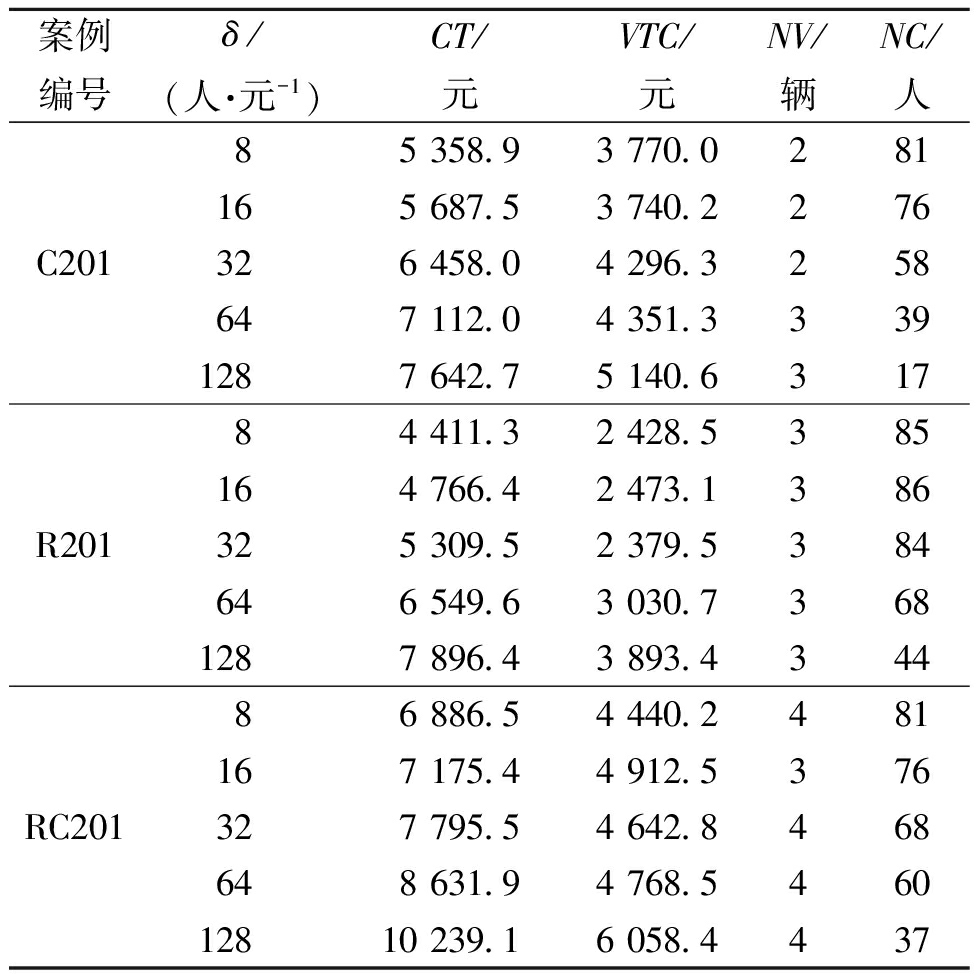
案例编号δ/(人·元-1)CT/元VTC/元NV/辆NC/人C20185 358.93 770.0281 165 687.53 740.2276 326 458.04 296.3258 647 112.04 351.33391287 642.75 140.6317R20184 411.32 428.5385 164 766.42 473.1386 325 309.52 379.5384 646 549.63 030.73681287 896.43 893.4344RC20186 886.54 440.2481 167 175.44 912.5376 327 795.54 642.8468 648 631.94 768.546012810 239.16 058.4437
3.3 众包员供给动态性的影响
为模拟众包员供给动态性,本文利用正态分布生成各时刻的众包员到达概率密度,如图7所示,然后,统计各时段的客户到达概率,将其与一天的众包员供给总量相乘,得到各时段众包员供给量。正态分布均值为配送中心营业时间中点,标准差为σ。σ越小,众包员供给在时间上越集中。
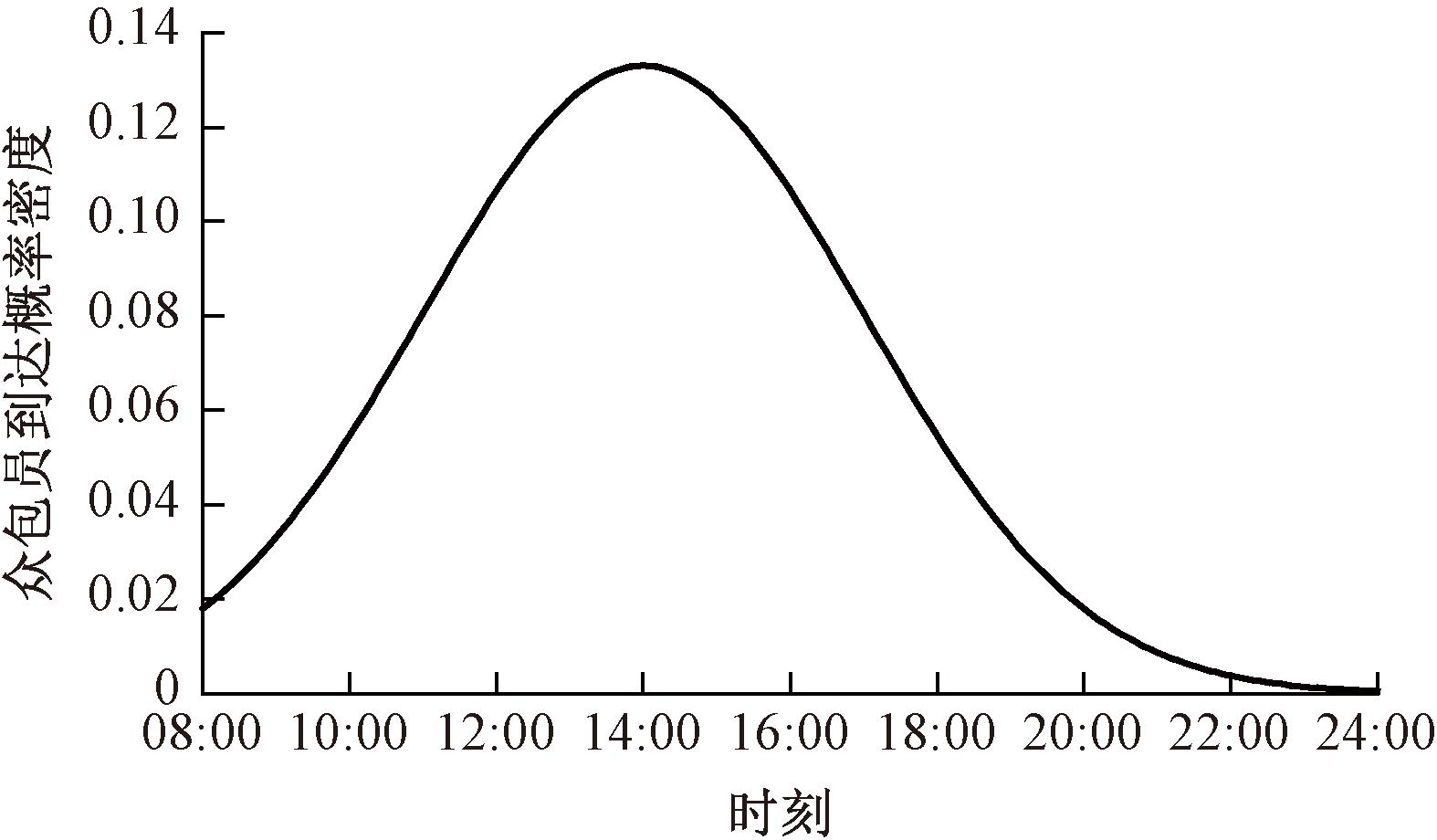
图7 各时刻的众包员到达概率密度
Figure 7 Arriving probability density of crowdsourced personnel at each moment
对100个客户案例,在一天的众包员供给总量为200人、众包员最大配送距离为40 km的条件下,不同众包员供给动态下的求解结果如表6所示。表6中,PC为一个时段的潜在众包员数最大值;NT为雇佣众包员的时段数量;NCPT为一个雇佣时段的众包员平均雇佣量,等于NC/NT;ACP为众包员平均雇佣报酬。可知,众包员供给动态特性显著地影响混合配送模式的配送成本,但影响模式是随机的。这是因为众包员供给动态特性对众包员报酬有双向作用:一方面,它会因增加一部分时段的众包员供给数量而降低众包员报酬;另一方面,它会减少另一些时段的众包员供给数量而导致众包员报酬增加。在雇佣众包员时,物流公司会选择在供给量较多、报酬较低的时段雇佣,因此,可观测到众包员雇佣报酬随σ的减少而降低,而一个雇佣时段的众包员平均雇佣量会随之增加。
表6 众包员供给动态性的影响
Table 6 Effects of supply dynamics of crowdsourced personnel
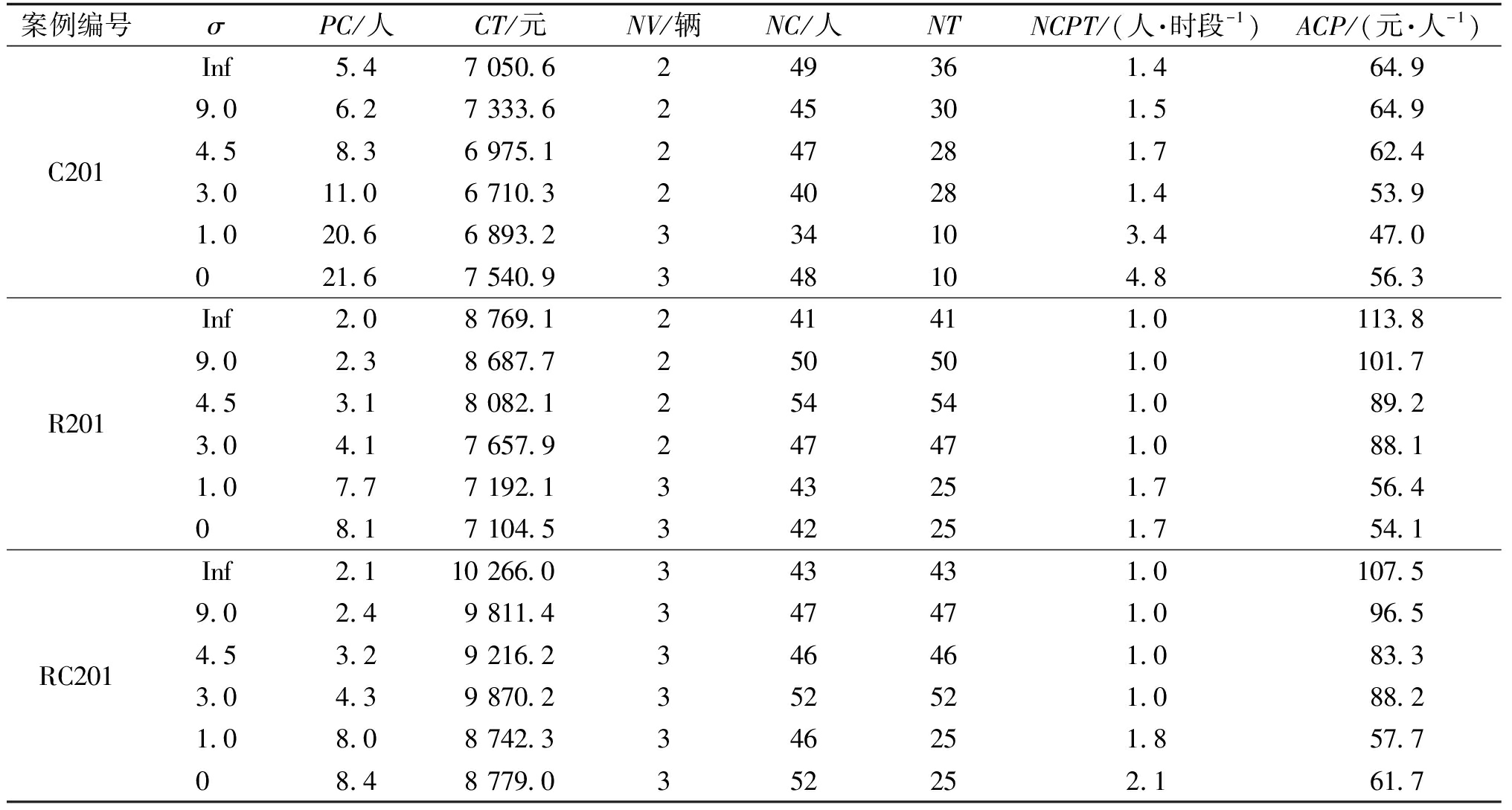
案例编号σPC/人CT/元NV/辆NC/人NTNCPT/(人·时段-1)ACP/(元·人-1)C201Inf 5.4 7 050.6 2 49 36 1.4 64.99.0 6.2 7 333.6 2 45 30 1.5 64.94.5 8.3 6 975.1 2 47 28 1.7 62.43.011.0 6 710.3 2 40 28 1.4 53.91.020.6 6 893.2 3 34 10 3.4 47.00 21.6 7 540.9 3 48 10 4.8 56.3R201Inf 2.0 8 769.12 41 41 1.0 113.89.0 2.3 8 687.72 50 50 1.0 101.74.5 3.1 8 082.12 54 54 1.0 89.23.0 4.1 7 657.92 47 47 1.0 88.11.0 7.7 7 192.13 43 25 1.7 56.40 8.1 7 104.53 42 25 1.7 54.1RC201Inf 2.1 10 266.0 3 43 43 1.0 107.59.0 2.4 9 811.43 47 47 1.0 96.54.5 3.2 9 216.23 46 46 1.0 83.33.0 4.3 9 870.23 52 52 1.0 88.21.0 8.0 8 742.33 46 25 1.8 57.70 8.4 8 779.03 52 25 2.1 61.7
4 结论
(1)所建模型和提出的算法能够有效协同自营配送员和众包员,降低末端配送成本。首先,考虑众包员供给动态性的影响,优化众包员报酬和雇佣数量;然后,以配送成本最小为导向,合理指派客户并安排卡车配送路径。算例结果表明,与自营配送模式相比,协同自营配送员与众包员的混合配送模式通过减少卡车数量和行驶路径,降低了末端配送成本。
(2)采用的模型和算法能够有效解决考虑众包员供给动态性的末端配送优化问题。对于15个客户的小规模案例,直接求解构建的混合整数线性规划模型能够得到66.7%案例的最优配送方案,其余案例的近似最优方案;对于100个客户的大规模问题,设计的IALNS算法能以平均48.5 s获得问题的近似最优方案。
(3)协同自营配送员与众包员的混合配送模式适用于时间窗紧凑、车辆行驶成本较高、就业机会少的场景;众包员供给动态性会显著且随机地影响混合配送模式的配送成本。
本文提供的末端配送优化方法适用于静态需求情景,未来可拓展其至动态需求情景。对于模型求解方法,可结合强化学习提升分支定界算法的求解效率。
[1] 杜子超, 卢福强, 王素欣, 等. 众包物流配送车辆调度模型及优化[J]. 东北大学学报(自然科学版), 2021, 42(8): 1210-1216.
DU Z C, LU F Q, WANG S X, et al. Vehicle scheduling model and optimization of crowdsourcing logistics distribution[J]. Journal of Northeastern University (Natural Science), 2021, 42(8): 1210-1216.
[2] 孟秀丽, 吴一凡, 刘波. 考虑延误险的多期众包物流服务质量优化[J]. 中国管理科学, 2023, 31(12): 87-95.
MENG X L, WU Y F, LIU B. Multi-period crowdsourcing logistics service quality optimization considering delay insurance[J]. Chinese Journal of Management Science, 2023, 31(12): 87-95.
[3] ARCHETTI C, SAVELSBERGH M, SPERANZA M G. The vehicle routing problem with occasional drivers[J]. European Journal of Operational Research, 2016, 254(2): 472-480.
[4] MACRINA G, DIPUGLIAPUGLIESEL, GUERRIERO F, et al. The vehicle routing problem with occasional drivers and time windows[C]∥ Optimization and Decision Science:Methodologiesand Applications. Cham: Springer, 2017: 577-587.
[5] MACRINA G, DIPUGLIAPUGLIESEL, GUERRIERO F, et al. Crowd-shipping with time windows and transshipment nodes[J]. Computers &Operations Research, 2020, 113: 104806.
[6] 杨华龙, 梁晓萍, 王征, 等. 允许中转与绕行的众包同城配送司机包裹匹配优化[J]. 控制与决策, 2024, 39(3): 1021-1029.
YANG H L, LIANG X P, WANG Z, et al. Optimization of driver-parcel matching for crowdsourced intra-city delivery with multi-hop and detour[J]. Control and Decision, 2024, 39(3): 1021-1029.
[7] DAYARIAN I, SAVELSBERGH M. Crowdshipping and same-day delivery: employing in-store customers to deliver online orders[J]. Production and Operations Management, 2020, 29(9): 2153-2174.
[8] SCHUR R, WINHELLER K. Optimizing last-mile delivery: a dynamic compensation strategy for occasional drivers[EB/OL]. (2024-12-26)[2025-02-10]. https:∥doi.org/10.1007/s00291-024-00796-6.
[9] DAI H Y, LIU P. Workforce planning for O2O delivery systems with crowdsourced drivers[J]. Annals of Operations Research, 2020, 291(1): 219-245.
[10] YILDIZ B, SAVELSBERGH M. Service and capacity planning in crowd-sourced delivery[J]. Transportation Research Part C: Emerging Technologies, 2019, 100: 177-199.
[11] LE T V, UKKUSURI S V, XUE J W, et al. Designing pricing and compensation schemes by integrating matching and routing models for crowd-shipping systems[J]. Transportation Research Part E: Logistics and Transportation Review, 2021, 149: 102209.
[12] 王会静,袁鹏程.考虑骑手异质性的众包配送策略优化[J].计算机系统应用,2024,33(12):210-221.
WANG H J, YUAN P C. Optimization of crowdsourcing delivery strategy considering rider heterogeneity[J].Computer Systems &Applications,2024,33(12):210-221.
[13] 张念, 刘志学, 李锋. 考虑服务供应能力和服务质量的众包物流服务定价策略[J]. 管理学报, 2024,21(1): 127-136.
ZHANG N, LIU Z X, LI F. Pricing strategy for crowdsourced logistics services considering service supply capacity and service quality[J]. Chinese Journal of Management, 2024,21(1): 127-136.
[14] 王文杰, 孙中苗, 徐琪. 考虑社会配送供应能力的众包物流服务动态定价模型[J]. 管理学报, 2018, 15(2): 293-300,316.
WANG W J, SUN Z M, XU Q. Dynamic pricing for crowdsourcing logistics services with socialized providers[J]. Chinese Journal of Management, 2018, 15(2): 293-300,316.
[15] 张燕, 李子鑫, 刘进平. 考虑工作量平衡的餐饮垃圾多行程收运路线优化[J]. 交通运输系统工程与信息, 2023, 23(6): 239-249.
ZHANG Y, LI Z X, LIU J P. Multi-trip food waste collection routing optimization with workload balance[J]. Journal of Transportation Systems Engineering and Information Technology, 2023, 23(6): 239-249.
[16] HUANG N, QIN H, XU G Y, et al. An enhanced exact algorithm for the multi-trip vehicle routing problem with time windows and capacitated unloading station[J]. Computers &Operations Research, 2024, 168: 106688.
[17] ZHAO M, LI X P, YIN J T, et al. An integrated framework for electric vehicle rebalancing and staff relocation in one-way carsharing systems: model formulation and Lagrangian relaxation-based solution approach[J]. Transportation Research Part B: Methodological, 2018, 117: 542-572.
[18] XU M, MENG Q, LIU Z Y. Electric vehicle fleet size and trip pricing for one-way carsharing services considering vehicle relocation and personnel assignment[J]. Transportation Research Part B: Methodological, 2018, 111: 60-82.
[19] CHEN X Q, ZHENG H Y, KE J T, et al. Dynamic optimization strategies for on-demand ride services platform: surge pricing, commission rate, and incentives[J]. Transportation Research Part B: Methodological, 2020, 138: 23-45.
[20] YAO C Q, CHEN S B, YANG Z Y. Joint routing and charging problem of multiple electric vehicles: a fast optimization algorithm[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(7): 8184-8193.
[21] 陈可嘉, 司徒腾宽, 方云飞, 等. 灵活车场多类型叫车接送问题的改进模拟退火算法[J/OL]. 控制理论与应用, 2024:1-9. (2024-10-11)[2025-02-18].http:∥kns.cnki.net/kcms/detail/44.1240.TP.20241010.1711.034.html.
CHEN K J, SITU T K, FANG Y F, et al. Improved simulated annealing algorithm for multiple depotsheterogeneous dial-a-ride problem with flexible depots[J/OL]. Control Theory &Applications, 2024:1-9. (2024-10-11)[2025-02-18].http:∥kns.cnki.net/kcms/detail/44.1240.TP.20241010.1711.034.html.
[22] 靳文舟, 邓钦原, 郝小妮, 等. 改进人工蜂群算法的农村DRT路径优化研究[J]. 郑州大学学报(工学版), 2021, 42(4): 84-90.
JIN W Z, DENG Q Y, HAO X N, et al. Research on route optimization of rural DRT based on improved ABC algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(4): 84-90.
[23] 何美玲, 杨梅, 韩珣, 等. 带时间窗的时间依赖型同时取送货车辆路径问题研究[J]. 交通运输系统工程与信息, 2024,24(4): 231-242, 262.
HE M L, YANG M, HAN X, et al. Time-dependent vehicle routing optimization considering simultaneous pickup-delivery and time windows[J]. Journal of Transportation Systems Engineering and Information Technology, 2024,24(4): 231-242, 262.
[24] 李嫚嫚, 孙加辉, 丁楠, 等. 考虑服务定价的选择性众包配送优化[J]. 浙江大学学报(工学版), 2023, 57(8): 1495-1504.
LI M M, SUN J H, DING N, et al. Selective crowdsourcing distribution optimization considering service pricing[J]. Journal of Zhejiang University (Engineering Science), 2023, 57(8): 1495-1504.
[25] SOLOMON M M. Algorithms for the vehicle routing and scheduling problem with time window constraints[J]. Operations Research, 1987, 35(2): 254-265.
[26] 张晓楠, 范厚明. 带时间窗偏好的多行程模糊需求车辆路径优化[J]. 计算机集成制造系统, 2018,24(10): 2461-2477.
ZHANG X N, FAN H M. Optimization for multi-trip vehicle routing problem with fuzzy demands considering time window preference[J]. Computer Integrated Manufacturing Systems, 2018,24(10): 2461-2477.