四轮移动机器人结构简单,被广泛应用于各种工业和生活环境中,带来了很多的便利。基于模型的控制实时性好,但机器人控制中存在着各种各样的不确定性,想要在复杂的、动态的环境中获得一个精确的被控对象模型几乎是不可能的。
在实际研究工作中,将系统未建模动力学、参数不确定性和扰动统一称为集总不确定性。不确定性分为匹配不确定性和非匹配不确定性两类。鲁棒控制是解决这类问题的一种有效方法。滑模控制[1]通过引入切换控制使得控制系统获得一定的鲁棒性[2],即对匹配不确定性不敏感[3],这是解决匹配不确定性问题的一种有效方法。对于非匹配不确定性,往往需要使用观测器对其进行补偿。
滑模控制包括趋近阶段和滑动阶段。在传统的滑模控制中,滑模面被设计成线性,因此在滑动阶段系统状态是渐近收敛到原点的[4]。为了使滑动阶段系统状态能够在有限时间内收敛到原点,终端滑模控制(TSMC)采用了非线性的滑模面设计[5]。与传统滑模相比,终端滑模具有更高的精度[2]。终端滑模不仅要求滑模变量为零,而且要求其导数也为零。目前对终端滑模的研究一方面在于如何更快速地在滑模面上实现收敛[6],另一方面是如何避免奇异[7]。
滑模控制存在抖振现象。抖振对于机器人的传动机构和电机都是有害的。造成抖振的根本原因是在控制律中引入了符号函数[3]。并且,不确定性的存在要求切换控制的增益较大,这也会加剧抖振现象[8]。减小滑模控制的抖振主要有三类方法[9]：一是通过使用饱和函数来替换符号函数[10],这种方法虽然能够减小抖振,但是其付出的代价是牺牲了系统的鲁棒性;二是通过采用高阶滑模技术,将高频控制开关“隐藏”在滑动变量的高阶导数中[11-12],从而显著降低抖振效应;三是对扰动进行估计[13]。
观测器被广泛地应用于扰动的估计。由于滑模控制需要基于非匹配不确定性的界来设计切换增益[12],因此在基于扰动观测器的相关研究中,大量研究在关注扰动的界[14]及其导数的界[15-16]是否已知。例如,Rabiee等[16]提出了一种只需已知扰动的二阶导数上界的阶数的自适应扰动观测器的设计方法;Su等[14]基于系统的先验知识设计了对于定常扰动的观测器。这类方法还是要已知扰动的相关先验知识才能使得扰动观测器有效,这大大限制了观测器的适用范围。一方面,在工程实践中获得扰动的先验知识是非常困难的。系统受到的扰动信号往往是随机的[17],扰动信号的界也经常是随机的、变化的。而且,由于扰动的类型多种多样,并不局限于定常扰动或者斜坡扰动。这类假设在现实环境中并不完全适用。另一方面,扰动观测器描述了扰动信号的具体动力学模型。然而,在使用滑模控制时,人们并不关心扰动信号的具体状态进化轨迹,只需要实现补偿扰动的目标即可。
在控制系统中不可避免地存在着各种未建模因素带来的不确定性。高斯过程回归(GPR)可以用来观测或补偿系统扰动和未建模状态[18]。GPR[19-20]作为一种贝叶斯非参数回归方法,从噪声数据中提供非参数统计学习,能根据训练数据找到输入与输出的关系[21]。这些噪声数据以协方差函数为特征[22],不需要已知系统的先验知识,可以利用有限的数据直接提供对模型不确定性的度量[23]。GPR与迭代学习控制[22]、模型预测控制[23]、滑模控制[24]等相结合,用于主动补偿扰动,可以很好地适应环境和应对建模不确定性的影响。在终端滑模控制中使用GPR对不确定性进行补偿,实际上是将基于模型的滑模控制和数据驱动的GPR相结合。目前,有数据驱动的研究使用神经网络[25]、模糊逻辑[26-27]等方法来逼近不确定性。与这些方法相比,一方面,GPR可以得到估计误差的边界[24];另一方面,GPR更适合应用于随机不确定性的场景。将滑模控制与GPR结合,可以有效减小因提高滑模控制器开关增益保证系统稳定性而产生的抖振,因此,将滑模控制与GPR结合是一项很有意义的研究。
传统方法依赖人为经验选取控制器参数,强化学习算法能够通过最大化累积奖励函数实现对滑模控制器参数的自动调整,使控制器具有更好的适应性。使用强化学习可以实现对于TSMC参数的自适应调优。终端滑模的滑模面和趋近律参数可以通过自适应算法进行调整。近年来,强化学习[28-29]作为一种解决最优决策问题的有效技术应运而生。近端策略优化(PPO)算法 [30]是一种基于策略梯度的强化学习算法,采用Actor-Critic框架进行模型的训练和更新。PPO算法收敛速度较快,实现简单,相比于其他算法更高效,可以有效处理大规模数据[31-32]。通过合理设计奖励函数和Actor的神经网络可以自适应地设置终端滑模控制的滑模面参数。
本文的主要贡献在于:①基于非奇异终端滑模控制理论,提出了一种用于四轮机器人模型的轨迹跟踪控制方法;②将非奇异终端滑模与高斯过程回归相结合,利用高斯过程回归估计外部扰动和模型不确定性;③将滑模面参数和趋近律参数作为PPO算法中Actor神经网络的输出,对终端滑模的参数进行自适应调整。
1 问题描述
1.1 四轮移动机器人的轨迹跟踪误差模型
假设机器人在平面上运动。四轮移动机器人的简化运动学分析[33]如图1所示。图1中点O为车辆起始位置,参考坐标系XOY与地面固定,点A为前轮中心,点B为后轮中心,点C为车辆质心,点D为车辆瞬时旋转中心。机器人的前后轮均可作为转向轮从而调整前进方向。δf和δr分别为前轮和后轮的转向角,lf和lr分别为前轮中心和后轮中心到车辆质心的距离,l=lf+lr为线段AB的长度,v为车辆质心的速度,β为速度v和线段AB间的夹角,φ为线段AB和X轴间的夹角。运动学模型[33]如下所示:
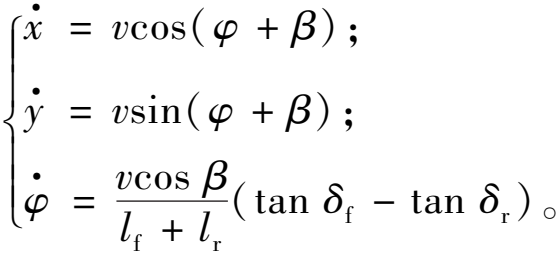
(1)
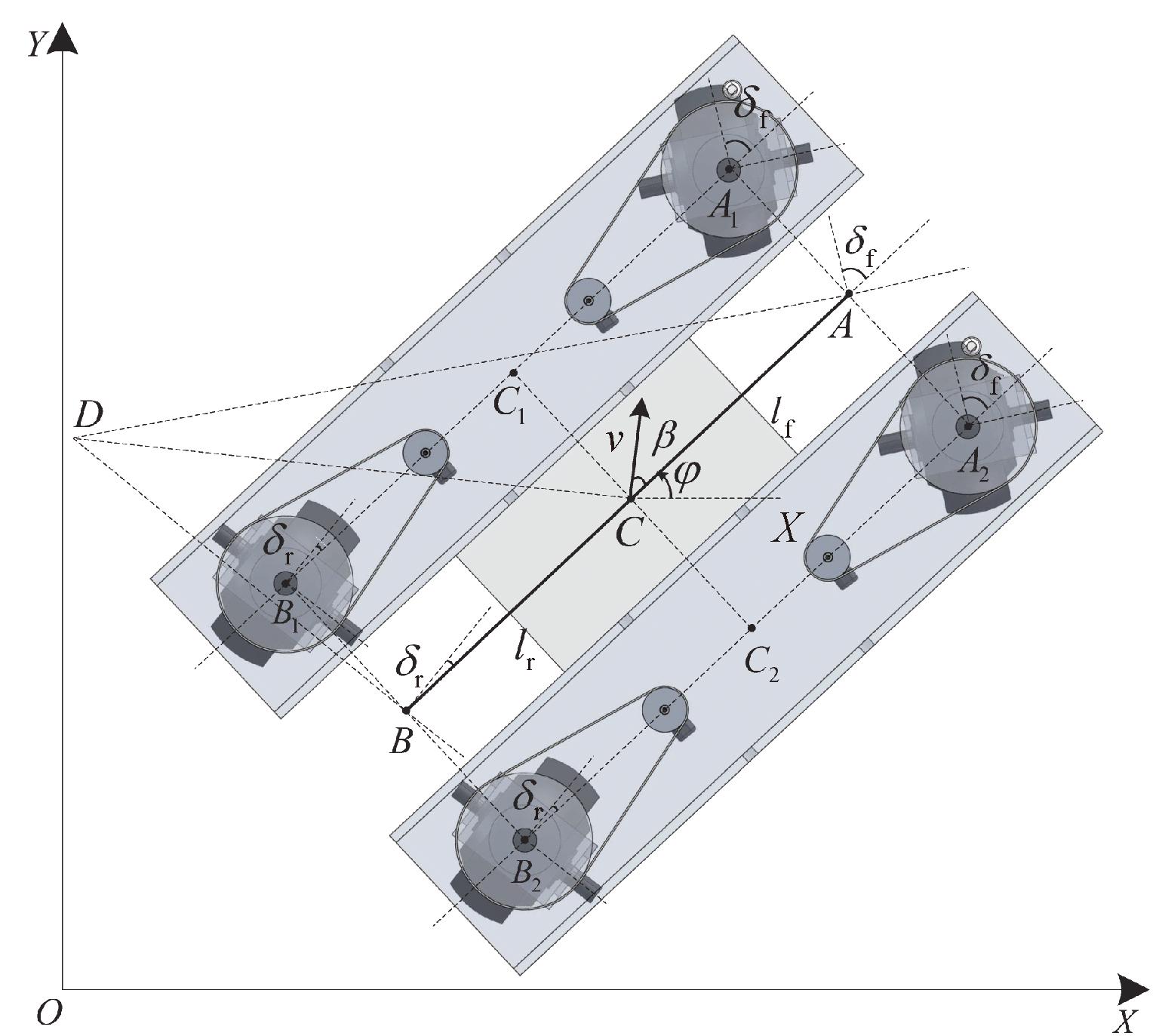
图1 四轮移动机器人运动学模型
Figure 1 Kinematics model of the mobile robot
式中:
研究前轮为转向轮、后轮不转动的情况,即后轮转角δf恒定为零。此时垂直于车身方向上的滑移为零。此时有β=0,得到的简化运动学模型为
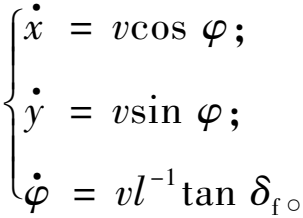
(2)
定义控制量u=tan δf,控制目标为将车辆从初始位置移动到给定路径y=g(x)上。定义误差e=y-g(x),对误差求导,结合式(2)有
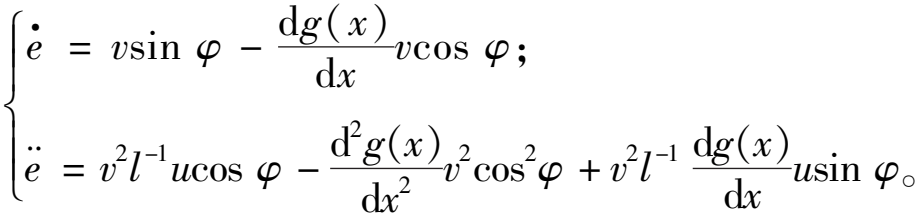
(3)
控制量出现在二阶导数中。为保证能够获得控制输入,需满足以下条件:
(4)
式中:φd为期望路径的切线与X轴的夹角。cos(φ-φd)≠0说明期望路径的切线不能垂直于车身方向。显然,前轮转向的轮式机器人不能直接沿着垂直于车身的方向运动,因此cos(φ-φd)≠0。初始时刻机器人沿着X轴方向运动,cos φd≠0表明此时机器人无法直接沿Y轴方向运动。
1.2 高斯过程回归
高斯过程回归是适合一组点的可能函数的概率分布。多元高斯模型的回归函数[19]为
P(f|X)=
(f| μ,K)。
(5)
式中:X=[x1,x2,…,xn];μ=[m(x1),m(x2),…,m(xn)];Kij=k(xi,xj)。X为观测数据点,m为均值函数,k为核函数。在新的点X*=[x*1,x*2,…,x*n]上对f(X*)进行预测。f和f*的联合先验分布[19]为
(6)
式中:K=K(X,X);K*=K(X,X*);K**=K(X*,X*);(m(X),m(X*))=0。
预测值f*的表达式[19]为
(7)
2 非奇异终端滑模控制器设计
对于给定目标路径为y=g(x)的路径跟踪任务,初始时刻t=0时,x=y=φ=δf=0。对于式(2)所示的运动学模型,考虑不确定性d,有
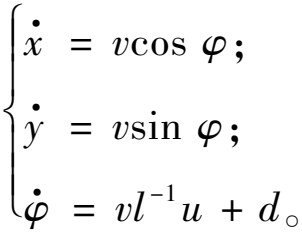
(8)
由于滑模控制对匹配不确定性不敏感,使用高斯过程回归对非匹配不确定性进行补偿。因此,在本文的后续内容中,将d简称为不确定性。基于式(3)设计非奇异滑模面[34]为
(9)
式中:c和α均为滑模面参数,满足c>0,1<α<2。
将滑模面对时间求导并将式(3)代入,可得
(10)
定义趋近律为
(11)
式中:k1和k2均大于0。
将式(11)代入式(10),有控制量:
(12)
式中:
为不确定性d的估计值。
将式(12)代入式(10)中,可得
(13)
(14)
式中:η>0。由于无法获得d的值,式(14)中的
项用估计值的置信区间代替,具体将在第3节中详细介绍。
定理1 如果a1>0,a2>0,0<p<1,且连续函数V(x)>0满足以下不等式[35]：
(15)
那么,系统的沉降时间为
(16)
定理2 如果选择式(9)作为滑模面,控制器设计为式(12),那么系统状态将在有限时间内到达滑模面s=0。
证明 考虑一个李雅普诺夫候选函数:
(17)
式(17)等号两边对时间求导,得
k2s)≤-η|s|-k2
。
(18)
显然,式(18)满足定理1。因此,滑模变量s可以在有限时间收敛到零。
(19)
3 基于高斯过程回归的不确定性估计
在滑模控制器中存在的非匹配不确定性会影响控制律的计算和系统的稳定性。在本节中,使用高斯过程回归对不确定性d进行估计。
本文认为不确定性d与车辆当前转角δn、跟踪误差e及其导数
相关,据此建立如下所示的数据集:
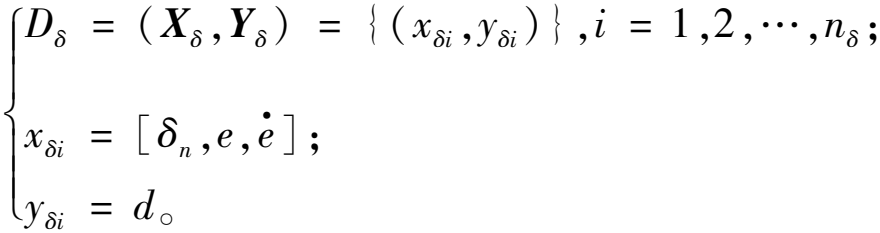
(20)
该数据集满足高斯分布,即
Yδ～(μδ(Xδ),kδ(Xδ,Xδ))。
(21)
数据集的均值μδ(Xδ)和协方差kδ(Xδ,Xδ)均为已知。根据式(7)对点Xδ*进行估计,输出Yδ*的估计值满足如下关系式:
p(Yδ*|Xδ*,Xδ,Yδ)～
(22)
式中:Kδ=Kδ(Xδ,Xδ),Kδ*=Kδ(Xδ,Xδ*),Kδ**=Kδ(Xδ*,Xδ*)。对不确定性的估计
和协方差
为
(23)
显然,不确定性d满足如下不等式:
(24)
式中:z为置信度。式(24)可以等效变换为
(25)
基于不确定性的估计,设计能够保证系统稳定性的滑模控制器,从而得到控制量u和对应的转角δf。由于不确定性的存在,此时车辆的实际转角不一定等于控制量δf,此时实际的车轮转角记为δt。在执行控制量u后根据得到的车辆实际转角δt,按照下式计算不确定性数据:
d=Vl-1(tan δt-u)。
(26)
这样就实现了数据集的更新。在实验中通过建立局部数据集,对系统(式(8))的不确定性进行在线预测估计,避免了昂贵的采样成本。
为了得到数据集Dδ,使用式(26)对d的真实值进行收集,而d的估计值使用式(23)进行计算。在线场景中,数据是实时更新的,使用滑动窗口的方法来收集数据集,即使用大小为nδ的窗口中的数据对系统(式(8))中的不确定性进行在线预测,在线收集每批nδ组数据预测点的不确定性并进行补偿。实际上,窗口数据集是总数据集的一个子集。随着实验的进行,窗口向新数据滑动,新数据被吸收到窗口中,旧数据被丢弃,避免了在采样大量数据时产生的采样成本。
4 自适应滑模控制器设计
终端滑模的参数对控制器的抖振和精度有很大影响,通过自适应算法对滑模面参数和趋近律参数进行调整,以期获得最优的控制器性能指标。因此,本文基于PPO算法设计了一种自适应终端滑模控制器。
在控制器的设计中,首先将GPR技术引入到非奇异终端滑模控制中。用GPR估计外部扰动和模型不确定性,保证了滑模面的存在性。趋近系数主要影响了系统的鲁棒性。由式(14)可知,在用高斯过程回归的方法对不确定性进行补偿后,系统的鲁棒性同时由η和不确定性的估计效果共同决定,从而有效减小了因提高滑模控制器的开关增益k1来保证系统稳定性而产生的抖振。考虑到趋近律参数 k2和滑模面参数c影响滑模变量的到达时间和状态的收敛时间,基于PPO算法对终端滑模参数进行自适应调整。
通过对抖振和控制精度进行加权,在两者之间实现折中。基于跟踪误差及其导数和抖振设计奖励函数为
(27)
式中:ω1、ω2、ω3分别为跟踪误差、跟踪误差导数、控制量抖振的权重。设折扣因子为γ,基于折扣因子计算累积奖励:
(28)
通过奖励函数将PPO算法与滑模控制结合起来。设PPO算法的状态向量为state=[x,y,v,φ,δf]T,动作向量为action=[c,k2]T,两者分别作为Actor网络的输入和输出。Actor网络采用5-64-64-64-64-2的网络结构。即输入层有5个神经元,4个隐含层依次为全连接层、Tanh层、全连接层、Tanh层。每个隐含层有64个神经元,输出层有2个神经元。Critic网络的输入为状态向量state,输出为状态的累积奖励。Critic网络采用5-64-64-64-64-1的网络结构,即输入层有5个神经元,4个隐含层依次为全连接层、Tanh层、全连接层、Tanh层,每个隐含层有64个神经元,输出层有1个神经元。PPO算法将获得使得累积奖励最大的策略。通过PPO算法的策略能够对终端滑模的滑模面参数c和趋近律参数k2进行自适应调整。因此,可以获得能够使累积奖励最大的滑模控制器,并同时减小系统的跟踪误差和控制量抖振。
自适应滑模控制器的整体设计如图2所示。控制器以终端滑模控制为基础,使用高斯过程回归在线估计系统的不确定性,使用PPO算法自适应调节滑模控制器的参数。
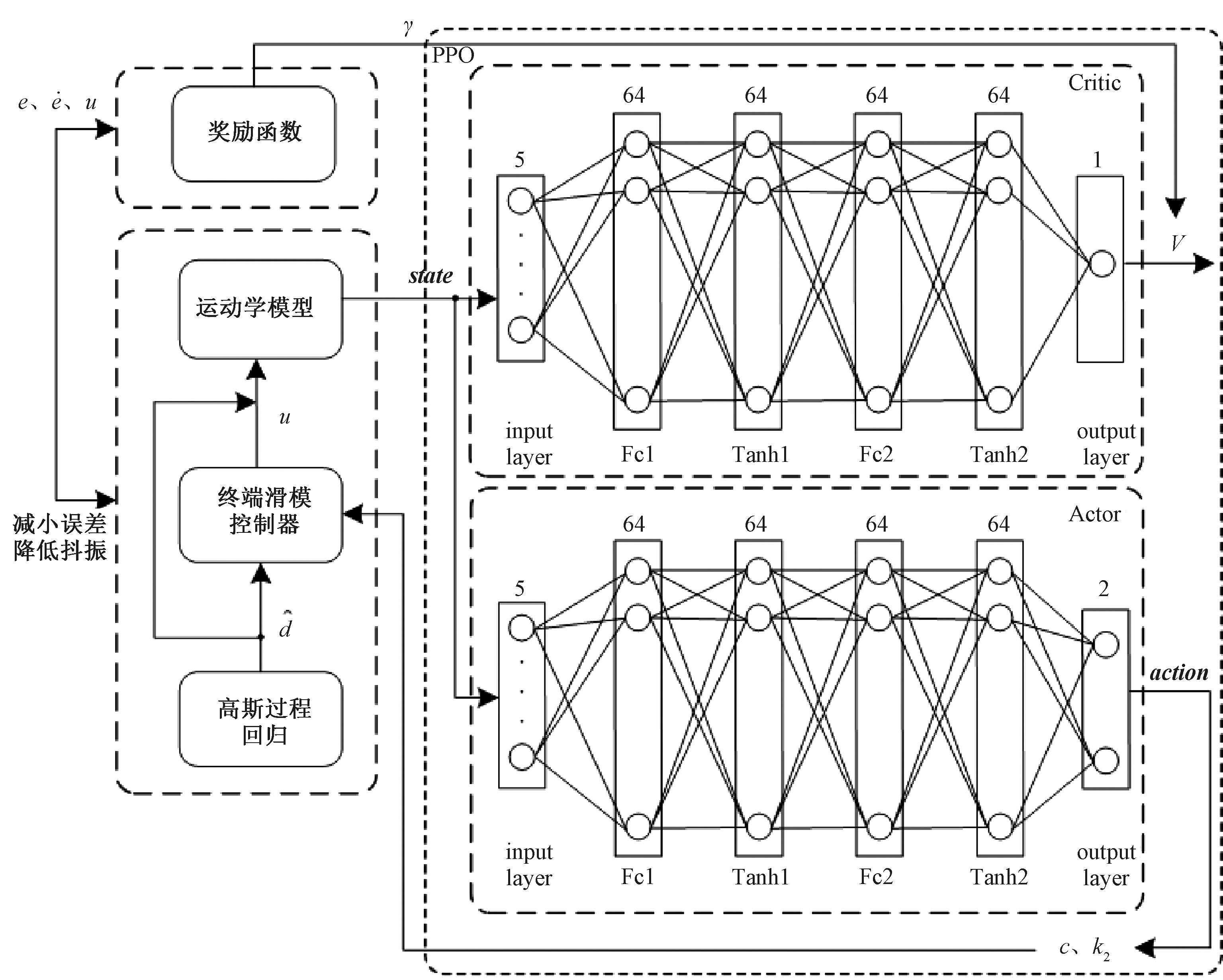
图2 自适应滑模控制器原理图
Figure 2 The schematic diagram of adaptive sliding mode controller
5 数值仿真实验
在本节中,通过数值仿真对终端滑模控制器进行验证。对于给定目标路径为yd=0.5sin(x+0.2)的路径跟踪任务,在系统中引入噪声d=0.05sin t+0.05sin(2t),用这个噪声来模拟非匹配不确定性进行实验。所有实验的时间步长均设置为0.01 s。
在实验1(TSMC)中,使用终端滑模控制器对目标轨迹进行跟踪,设置c=2,α=7/5,k2=1。在没有对不确定性进行补偿时,为保证系统的鲁棒性,需要设定一个较大的增益k1=η=0.1。
在实验2(TSMC+GPR)中,在终端滑模控制器的基础上,使用高斯过程回归对不确定性进行补偿,设置置信度z=2,c=2,α=7/5,k2=1。根据式(14),设置
由η和不确定性的估计值共同决定。此时仅需要设置一个较小的值η=0.005即可保证系统稳定。系统的鲁棒性由k1中不确定性的估计误差项保证。
实验3(TSMC+GPR+RL)中,使用基于PPO算法和高斯过程回归的自适应滑模控制器,PPO算法采用python stable-baseline3的PPO算法[36]。采用的策略是MLP policy,设置α=7/5。根据式(14),设置
由高斯过程回归给出,滑模面参数c和趋近律参数k2由强化学习算法给出。
3组实验的仿真对比图如图3和图4所示。图3(a)是机器人跟踪正弦轨迹的相图。图3(b)是机器人的轨迹跟踪误差及其一阶导数随时间的变化图。图3(c)是滑模变量s随时间的变化图。
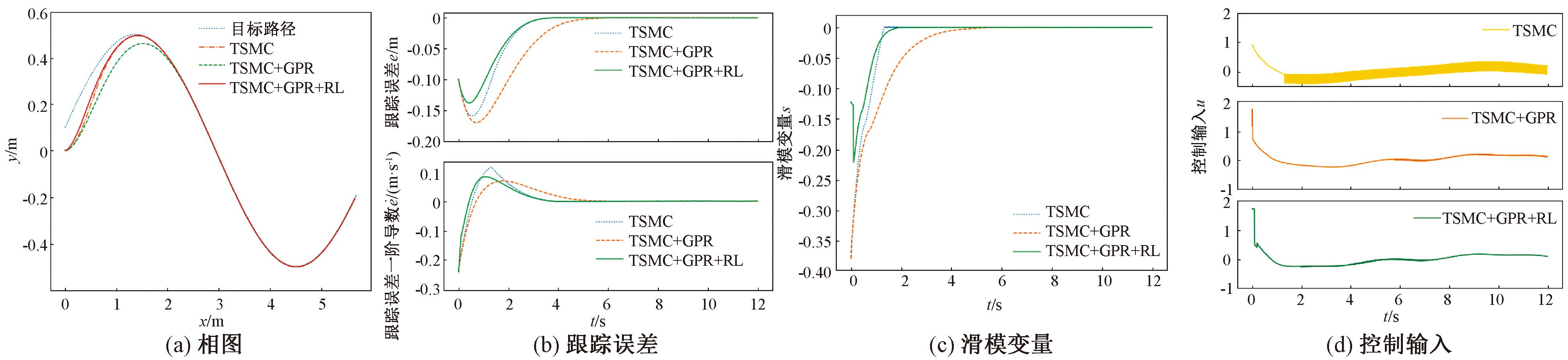
图3 3组实验的相图、跟踪误差、滑模变量和控制输入示意图
Figure 3 Phase diagram, tracking error, sliding mode variable, and control input diagrams for three experimental groups
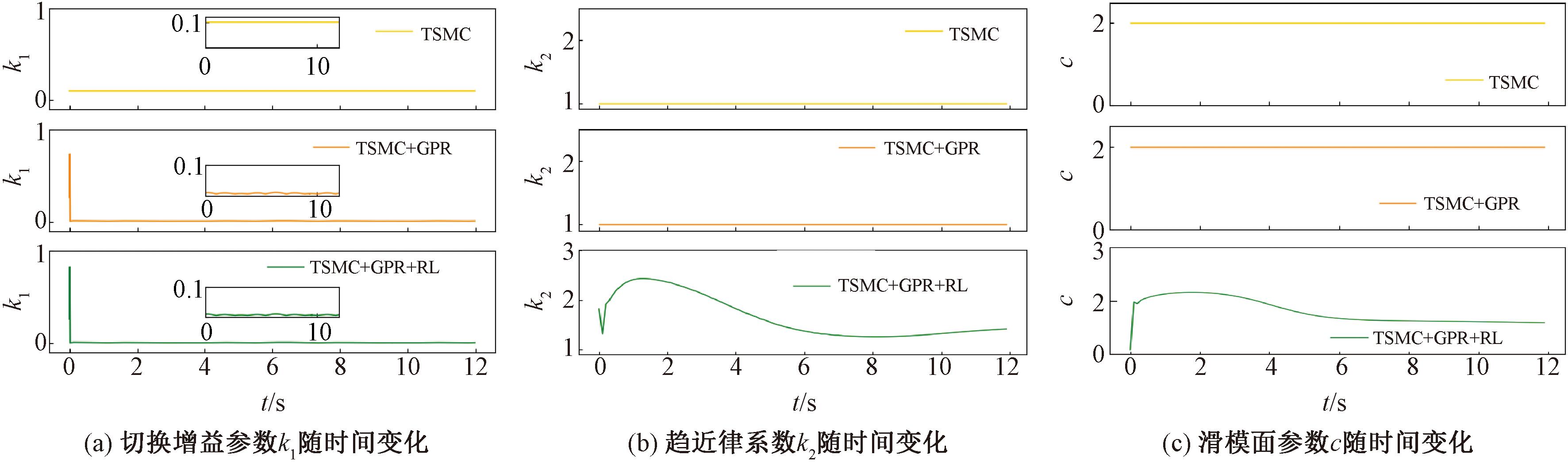
图4 3组实验的参数随时间变化情况
Figure 4 Time variation of parameters for three experimental groups
从图3(a)和3(b)中可以看出,系统的跟踪误差收敛速度较慢,这是由于使用高斯过程回归后,η值变小。由式(19)可知,滑模变量到达滑模面的时间变长,因此跟踪误差收敛时间延长。从3(c)中可以看出,使用了高斯过程回归后,滑模变量到达滑模面的时间变长。图3(d)是机器人的控制输入随时间的变化曲线,可以看出,与实验1方法相比,在实验开始1 s后,实验2和实验3中的控制量抖振振幅减小了90%,这是由于原本的切换增益k1需要保证大于不确定性的界,使用GPR对不确定性进行补偿之后,根据式(14),k1变为和估计误差的界相关,因此减小了k1的值,从而减小了控制量的抖振。
图4为3组实验的参数随时间变化的情况。图3(d)的情况在图4(a)中可以得到验证。图4(b)和图4(c)中主要展示了自适应控制器的趋近律系数k2和滑模面参数c,两者由强化学习算法给出,实现了参数自适应调节。由前面的分析可知,使用高斯过程回归对不确定性进行补偿后,获得的好处是减小了控制输入的抖振,付出的代价是滑模变量到达滑模面的时间变长,从而导致跟踪误差收敛慢。从图3(b)和图3(c)中可以看出,自适应控制器通过使用强化学习算法自适应调节控制器参数,加速了滑模变量到达滑模面的速度,减小了跟踪误差的收敛时间。并且从图3(d)中可以看出,使用强化学习算法并没有对高斯过程回归减小抖振的良好效果产生影响。图5为PPO算法每个训练回合的累积奖励,可以看出,累积奖励随训练回合整体呈上升趋势,最终基本稳定。
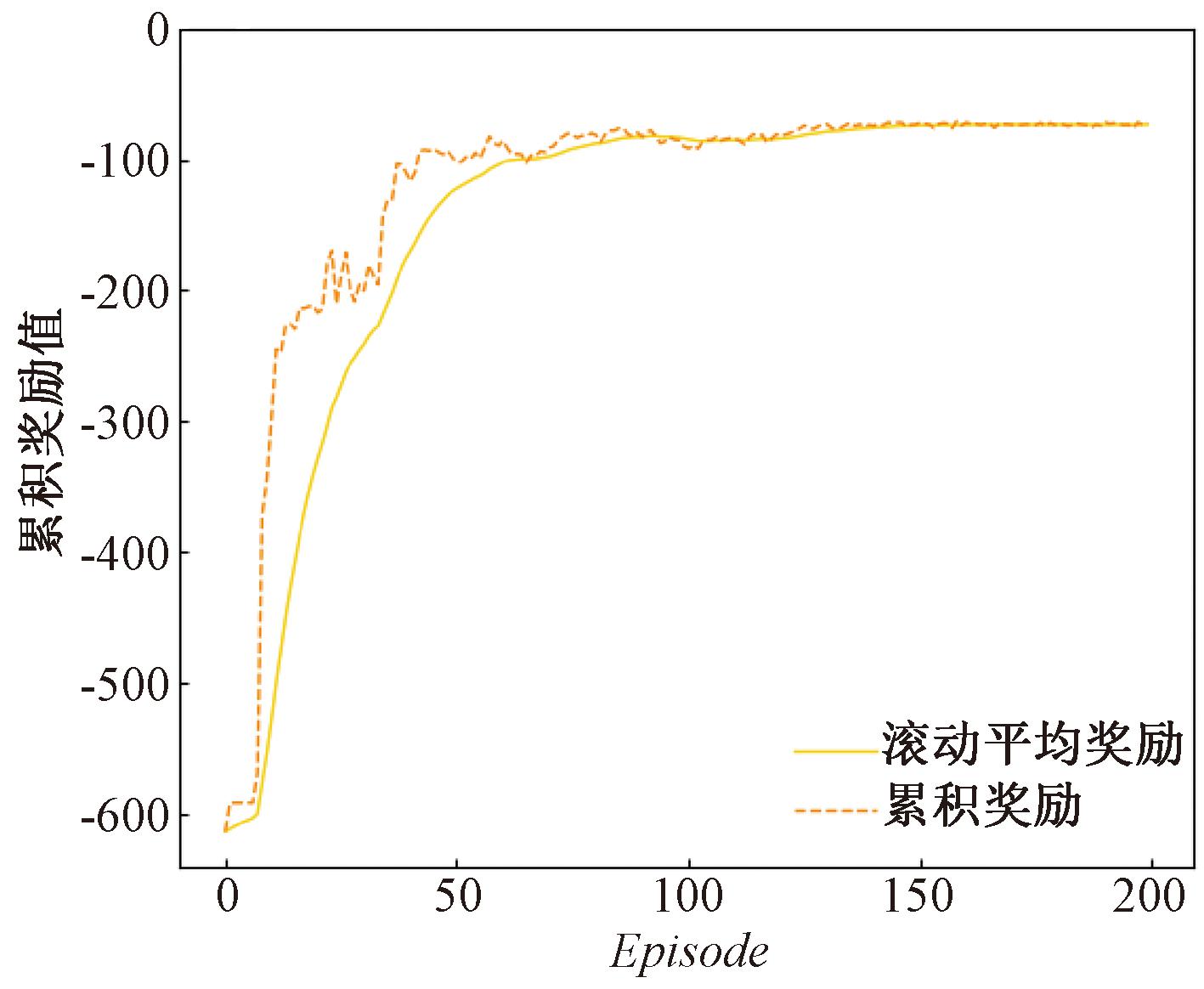
图5 每个训练回合的累积奖励
Figure 5 Cumulative reward trend plot
6 结论
本文基于高斯过程回归对不确定性进行补偿,基于PPO算法设计了一种用于四轮移动机器人的自适应终端滑模控制器,并进行了仿真实验。结果表明,与传统的终端滑模相比,所提出的自适应终端滑模控制器在保持较高控制精度的前提下,控制量抖振振幅减小了90%。下一步将基于SAC、TD3等其他强化算法实现对于终端滑模控制器参数的自适应调整,并开展实物实验对所提出的控制器进行验证。
[1] FRIDMAN L, BARBOT J P, PLESTAN F. Recent trends in sliding mode control[M]. Stevenage, Herts, United Kingdom: The Institute of Engineering and Technology, 2016.
[2] FENG Y, YU X H, HAN F L. On nonsingular terminal sliding-mode control of nonlinear systems[J]. Automatica, 2013, 49(6): 1715-1722.
[3] NGUYEN N P, OH H, MOON J, et al. Multivariable disturbance observer-based finite-time sliding mode attitude control for fixed-wing UAVs under matched and mismatched disturbances[J]. IEEE Control Systems Letters, 2023, 7: 1999-2004.
[4] 王群京, 刘中阳, 李国丽, 等. 基于自适应干扰观测器的永磁球形电机连续非奇异终端滑模控制[J]. 电机与控制学报, 2022, 26(8): 66-78.
WANG Q J, LIU Z Y, LI G L, et al. Adaptive disturbance observer-based continuous nonsingular terminal sliding-mode control for permanent-magnet spherical actuator[J]. Electric Machines and Control, 2022, 26(8): 66-78.
[5] ZEGHLACHE S, GHELLAB M Z, DJERIOUI A, et al. Adaptive fuzzy fast terminal sliding mode control for inverted pendulum-cart system with actuator faults[J]. Mathematics and Computers in Simulation, 2023, 210: 207-234.
[6] GUO X C, WEI G L. Disturbance observer-based fixed-time leader-following consensus control for multiple Euler-Lagrange systems：a non-singular terminal sliding mode scheme[J]. Journal of the Franklin Institute, 2023, 360(9): 6463-6489.
[7] HONG M Q, GU X T, LIU L X, et al. Finite time extended state observer based nonsingular fast terminal sliding mode control of flexible-joint manipulators with unknown disturbance[J]. Journal of the Franklin Institute, 2023, 360(1): 18-37.
[8] MOBAYEN S, BAYAT F, DIN S U, et al. Barrier function-based adaptive nonsingular terminal sliding mode control technique for a class of disturbed nonlinear systems[J]. ISA Transactions, 2023, 134: 481-496.
[9] YAO M, XIAO X, TIAN Y, et al. A fast terminal sliding mode control scheme with time-varying sliding mode surfaces[J]. Journal of the Franklin Institute, 2021, 358(10): 5386-5407.
[10] CUPERTINO F, NASO D, MININNO E, et al. Sliding-mode control with double boundary layer for robust compensation of payload mass and friction in linear motors[J]. IEEE Transactions on Industry Applications, 2009, 45(5): 1688-1696.
[11] CHEN J C, SHUAI Z B, ZHANG H, et al. Path following control of autonomous four-wheel-independent-drive electric vehicles via second-order sliding mode and nonlinear disturbance observer techniques[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2460-2469.
[12] WANG T Q, WANG B, YU Y, et al. Fast high-order terminal sliding-mode current controller for disturbance compensation and rapid convergence in induction motor drives[J]. IEEE Transactions on Power Electronics, 2023, 38(8): 9593-9605.
[13] ZHANG L, NAN H J, ZHAO Z Q, et al. Adaptive disturbance observer-based dual-loop integral-type fast terminal sliding mode control for micro spacecraft and its gimbal tracking device[J]. ISA Transactions, 2022, 130: 121-135.
[14] SU X J, QING F D, CHANG H B, et al. Trajectory tracking control of human support robots via adaptive sliding-mode approach[J]. IEEE Transactions on Cybernetics, 2024, 54(3): 1747-1754.
[15] SUN H L, GAO L L, ZHAO Z X, et al. Adaptive super-twisting fast nonsingular terminal sliding mode control with ESO for high-pressure electro-pneumatic servo valve[J]. Control Engineering Practice, 2023, 134: 105483.
[16] RABIEE H, ATAEI M, EKRAMIAN M. Continuous nonsingular terminal sliding mode control based on adaptive sliding mode disturbance observer for uncertain nonlinear systems[J]. Automatica, 2019, 109: 108515.
[17] YANG J, LI S H, YU X H. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 160-169.
[18] BERNARD P. Observer design for nonlinear systems[M]. Berlin:Springer International Publishing,2019.
[19] RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. Cambridge: The MIT Press, 2005.
[20] WU Q, DU W L. Online detection of model-plant mismatch in closed-loop systems with Gaussian processes[J]. IEEE Transactions on Industrial Informatics, 2022, 18(4): 2213-2222.
[21] ALAKBARI F S, MOHYALDINN M E, AYOUB M A, et al. A robust Gaussian process regression-based model for the determination of static Young’s modulus for sandstone rocks[J]. Neural Computing and Applications, 2023, 35(21): 15693-15707.
[22] BUELTA A, OLIVARES A, STAFFETTI E, et al. A Gaussian process iterative learning control for aircraft trajectory tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3962-3973.
[23] HEWING L, KABZAN J, ZEILINGER M N. Cautious model predictive control using Gaussian process regression[J]. IEEE Transactions on Control Systems Technology, 2020, 28(6): 2736-2743.
[24] LIMA G S, TRIMPE S, BESSA W M. Sliding mode control with Gaussian process regression for underwater robots[J]. Journal of Intelligent &Robotic Systems, 2020, 99(3): 487-498.
[25] SUN Y Z, LIU J X, GAO Y B, et al. Adaptive neural tracking control for manipulators with prescribed performance under input saturation[J]. IEEE/ASME Transactions on Mechatronics, 2023, 28(2): 1037-1046.
[26] ZHAO L, CAO X Y, LI X F. Adaptive sliding-mode control for inertial reference units via adaptive tracking differentiators[J]. IEEE Transactions on Systems, Man, and Cybernetics：Systems, 2023, 53(5): 3208-3218.
[27] ZAARE S, SOLTANPOUR M R. Adaptive fuzzy global coupled nonsingular fast terminal sliding mode control of n-rigid-link elastic-joint robot manipulators in presence of uncertainties[J]. Mechanical Systems and Signal Processing, 2022, 163: 108165.
[28] 王丙琛, 司怀伟, 谭国真. 基于深度强化学习的自动驾驶车控制算法研究[J]. 郑州大学学报(工学版), 2020, 41(4): 41-45, 80.
WANG B C, SI H W, TAN G Z. Research on autopilot control algorithm based on deep reinforcement learning[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(4): 41-45, 80.
[29] 崔建明, 蔺繁荣, 张迪, 等. 基于有向图的强化学习自动驾驶轨迹预测[J]. 郑州大学学报(工学版), 2023, 44(5): 53-61.
CUI J M, LIN F R, ZHANG D, et al. Reinforcement learning autonomous driving trajectory prediction based on directed graph[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 53-61.
[30] SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[EB/OL].(2017-08-28)[2024-07-16]. https：∥doi.org/10.48550/arXiv.1707.06347.
[31] CHENG Y H, HUANG L Y, WANG X S. Authentic boundary proximal policy optimization[J]. IEEE Transactions on Cybernetics, 2022, 52(9): 9428-9438.
[32] SHAKYA A K, PILLAI G, CHAKRABARTY S. Reinforcement learning algorithms：a brief survey[J]. Expert Systems with Applications, 2023, 231: 120495.
[33] RAJAMANI R. Vehicle dynamics and control[M]. Berlin: Springer, 2012.
[34] FENG Y, YU X H, MAN Z H. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167.
[35] DUAN M, JIA J, ITO T. Fast terminal sliding mode control based on speed and disturbance estimation for an active suspension gravity compensation system[J]. Mechanism and Machine Theory, 2021, 155: 104073.
[36] Stable-Baselines3:PPO [EB/OL].[2024-07-16].https：∥stable-baselines3.readthedocs.io/en/master/modules/ppo.html#parameters.