滚动轴承作为工业设备中最常见且极其关键的旋转部件,广泛应用于电机、齿轮箱和涡轮机等旋转机械中,其运行状态的正常与否直接影响到整个设备的性能[1-2]。在运行过程中,滚动轴承由于内部(如退化机理突变)或者外部因素(负荷、工况变化等)的影响,其退化特性也随之改变,经常出现多阶段特征[3-4]。如图1所示,该轴承运行中明显出现了3个典型阶段:早期(缓慢退化期)、中期(中度退化期)、晚期(快速退化期)。
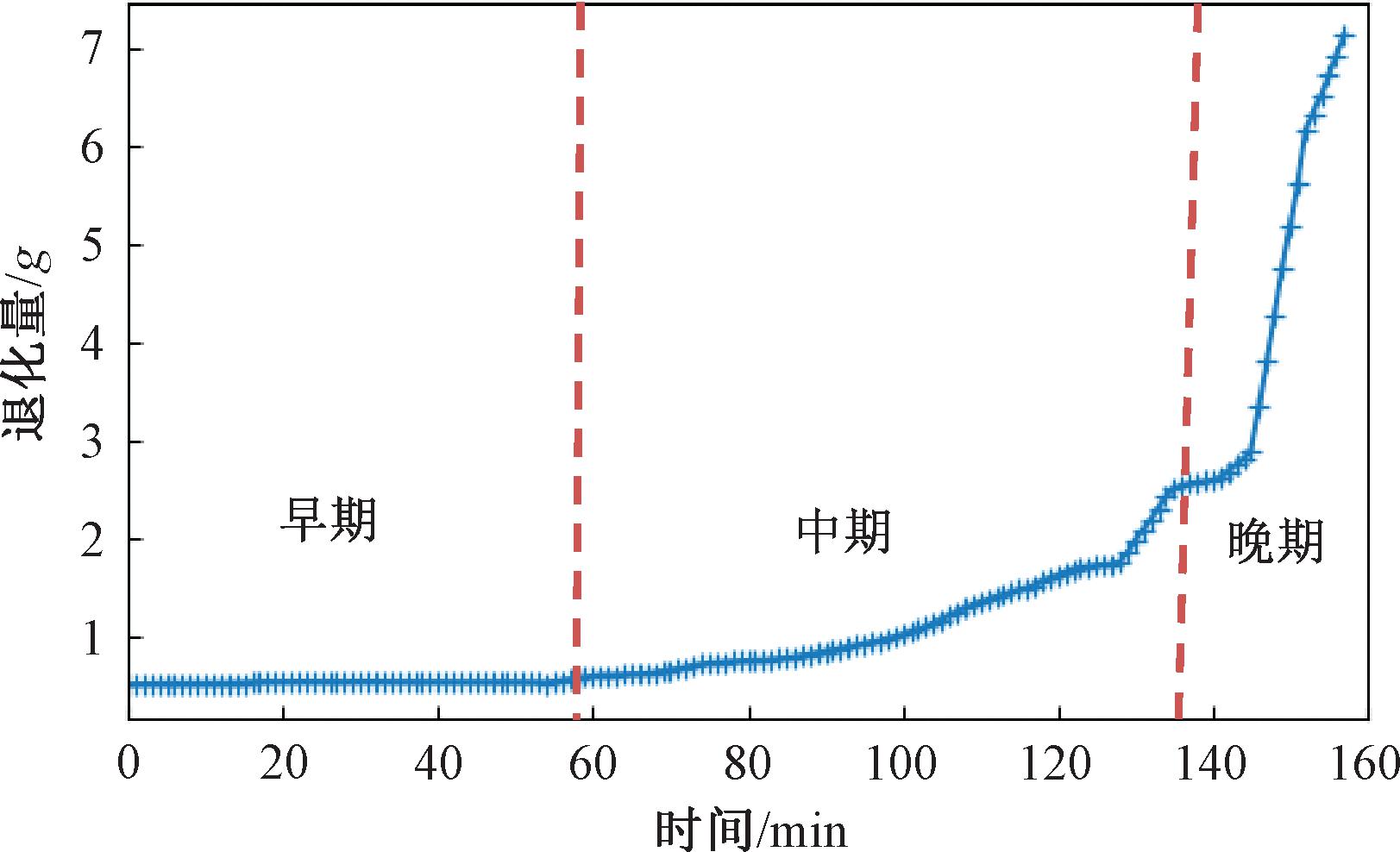
图1 滚动轴承三阶段退化过程
Figure 1 The three-stage degradation process of rolling bearing
Wiener过程是一类具有线性漂移项的扩散过程,由于其良好的数学特性,自20世纪90年代以来被广泛用于设备可靠性预测与寿命分析[5-6]。近年来不断取得新进展,Peng等[7]建立了累积退化模型,在线性框架下对退化建模和预测模型进行研究,推导出了寿命分布的显示解。Lee等[8]提出了改进EM算法估计其退化过程中的参数。Joseph等[9]对非线性退化模型进行了研究,在一定条件下可以将其线性化,并研究了考虑数据相关性的退化建模问题。然而,以上方法均是利用同类设备寿命的历史监测数据,没有利用服役设备运行过程中的监测退化数据。为了解决这一问题,Gebraeel等[10]提出了Bayesian框架下随机退化建模方法,在获取退化监测数据后,采用Bayesian方法对模型的随机参数进行更新,得到其后验估计进而预测剩余寿命的概率分布。史华洁等[11]提出了一种融合先验退化数据和设备自身现场退化数据的剩余寿命预测方法,建立符合非线性Wiener过程描述的设备退化模型。
当前,对于存在典型多阶段退化特征的设备退化建模和寿命预测问题已经有不少研究[12-13]。Ng[14]提出了一种基于单个变点的独立增量两阶段独立增量退化模型。Wang等[15]提出一种结合EM算法和卡尔曼滤波的两阶段轴承的退化建模来进行自适应预测。董青等[16]提出一种基于两阶段自适应Wiener过程的剩余寿命预测方法。对于多阶段过程的退化建模,关键在于准确检测出退化规律发生变化的点,即变点[16-17]。典型三阶段轴承退化过程,一般以第2阶段出现时间点作为初始故障点,也称为首次预测时间点(first prediction time, FPT),以后续两个阶段(中、晚期)为目标进行退化过程建模。图2展示了滚动轴承典型的二阶段退化过程,在确定失效阈值情况下其真实寿命为图2中的M点。目前,对于多阶段退化过程的实时在线寿命预测存在的主要问题是:①若不考虑退化过程的变点,即把该过程认为是单一过程,会导致预测误差非常大,如图2中预测寿命M1点与真实寿命A差距巨大。②在考虑变点将该过程作为二阶段过程时,变点预测精度非常重要,如图2中因变点预测误差导致寿命预测点估计为M2点,带来较大的误差。同时,目前多阶段退化建模和预测均不适合在线寿命预测,不能进行实时的变点检测和实时剩余寿命预测。
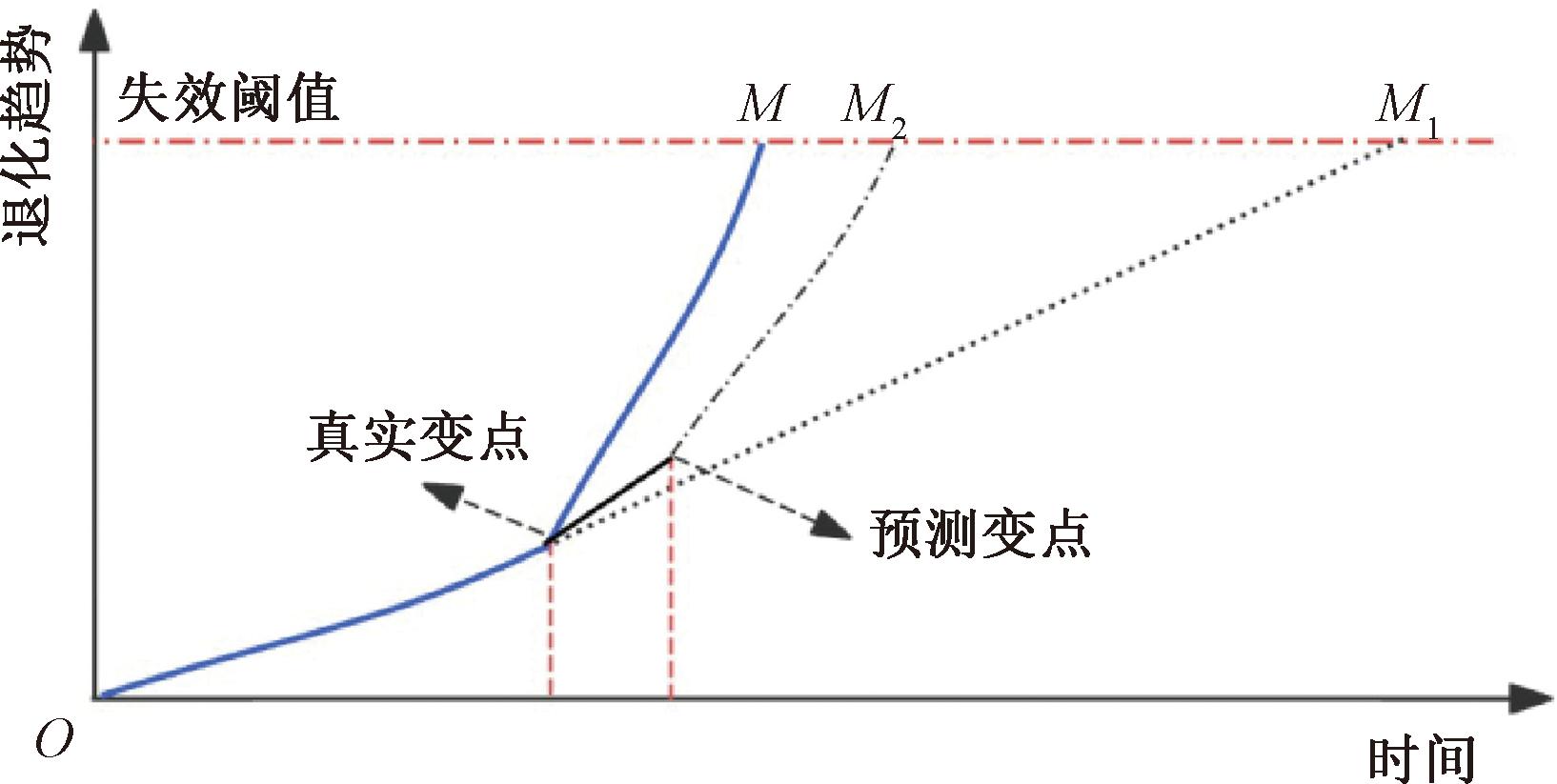
图2 二阶段退化过程寿命预测误差分析
Figure 2 Error analysis of RUL based on two-stage degradation process
变点统计分析理论是研究现实世界中突变现象的非线性统计理论[13,15-16], 近年来在理论和应用上都已经得到较快发展。目前主要的变点检测方法有似然比(LR)检验、贝叶斯检验[18]、累加和(CUSUM)检验[19]等。似然比检验由于需要变点之后的数据计算似然比,因此具有较大的滞后性。累加和检验需要较大的数据量构造检验统计量,当数据量较小时难以得到较为准确的检验结果。相比较而言,贝叶斯变点检测方法在一定的先验条件下,能够比较准确地进行变点检测,同时又能满足实时性检测的要求。
针对以上分析,本文提出了一种新型的自适应变点检测的轴承退化模型的剩余寿命预测方法:首先,根据历史数据进行参数学习以确定变点的分布规律的先验值;其次,估计不同阶段的漂移系数和扩散系数;再次,利用已经采集到的退化观测数据进行变点检测,将观测序列分成多段,以FPT为起点,进行在线寿命预测;最后,通过模拟仿真及实际案例验证了本方法预测的准确性和实用性。
1 问题描述
设X(t)为滚动轴承在t时刻的性能退化量,若退化过程存在变点τ,x0表示退化过程的初值,以变点τ将退化序列分为两个不同阶段
和
对应的退化参数分别为θ(1)和θ(2)(具体参数取决于所建立的模型),设失效阈值为ω,在首达意义下设备寿命Tω定义为[20]
Tω=inf{t:X(t)≥ω|x0<ω}。
(1)
设当前时刻为tk,已经获取的实时退化序列为
则tk时间对应的剩余寿命可记为
Lk=inf{lk:X(lk+tk)≥ω|X(tk)<ω}。
(2)
实时在线寿命预测的任务:①实时估计当前变点τ以及变点前后的模型参数θ(1)和θ(2);②考虑tk≤τ和tk>τ两种情况下,实时估计当前时刻tk的剩余寿命lk。
2 二阶段退化过程模型
对于典型的三阶段滚动轴承退化过程,由于第一阶段运行平稳,一般不进行剩余寿命预测。本文以滚动轴承后两个阶段为研究对象建立二阶段退化过程模型。先作如下假设:①滚动轴承退化过程以FPT为起点,所有预测对象的退化轨迹都具有两个典型退化阶段,即为中度退化阶段(阶段1)和快速退化阶段(阶段2);②每个阶段均为线性的Wiener过程。
2.1 二阶段Wiener线性模型
基于上述假设,研究的退化过程模型表示为
(3)
式中:μ=[μ1,μ2],σ=[σ1,σ2]分别表示1,2阶段的漂移系数与扩散系数;τ和xτ分别表示变点的出现时间以及所对应的退化量;x0为设备初始退化量,一般情况下令其等于0;B(t)为标准的布朗运动,布朗运动的随机性用于反映出剩余寿命预测的不确定性。
2.2 二阶段退化过程寿命分布
基于上述假设,本文研究的二阶段退化过程模型的剩余寿命的概率密度函数(probability density function,PDF)可以表示为[20]
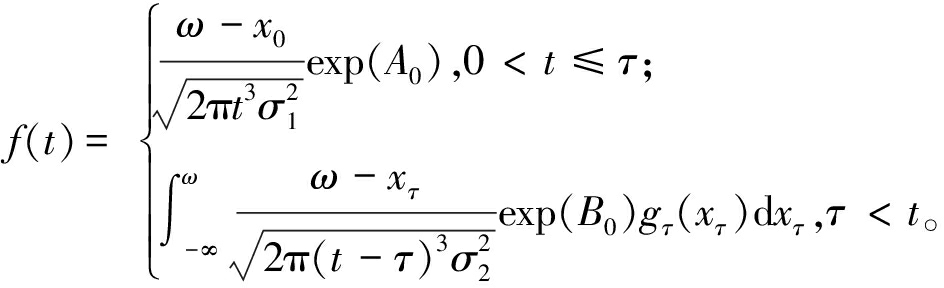
(4)
式中:
gτ(xτ)表示经过时间τ从0转移到xτ的转移概率[20]。
(5)
2.3 剩余寿命PDF分布
tk时刻的寿命PDF分布[20]为
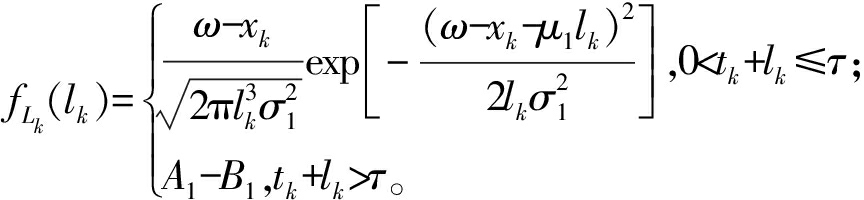
(6)
其中,
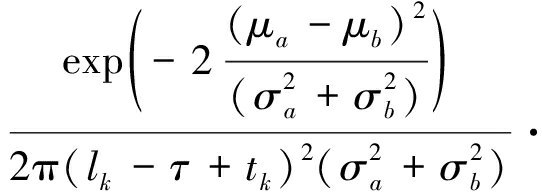
为标准正态分布累积分布函数;φ(·)为标准正态分布的概率密度函数;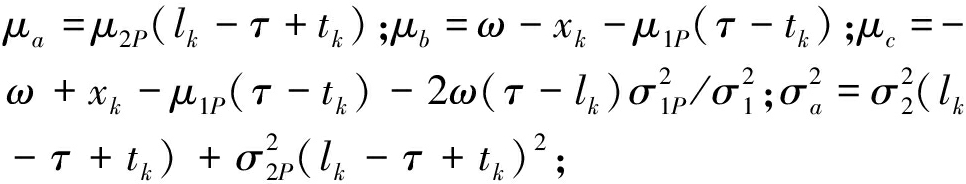
2.4 离线参数估计
考虑到同一批滚动轴承共n个,有n组退化数据,即X=[x1,x2,…,xn],其中,xi=[xi,0,xi,1,xi,2,…,xi,mi]表示第i个轴承在时间[ti,0,ti,1,ti,2,…,ti,mi]上的监测值,mi为第i个轴承的监测值个数。设不同轴承均采用等间隔采集其退化数据,即Δt=ti,j-ti,j-1。设两个阶段的参数μ1和μ2分布服从高斯分布
和
变点τi服从Gamm(α,β)分布,其形状参数和尺度参数分别为α和β。
利用MLE(maximum likelihood estimation)来估计其参数,令τi为设备i的变点,构造似然函数,如式(7)所示:
ln L(μ1,i,σ1,μ2,i,σ2,τi|xi)=
(7)
参数
的最大似然估计[20]为
(8)
利用多个设备的
的值可以得到σ1、σ2、 μ1P、 μ2P、τ的估计值。
3 增量退化量的概率密度分布
对于标准Wiener过程
定义其增量序列
和Δti分别为性能退化增量和时间增量。由Wiener过程的正态性可知Δxi～N(μΔti,σ2Δti),则Δxi的密度分布函数为
(9)
这里,θ=(μ,σ2)的先验分布为正态-逆伽马分布[21],即,θ～N/IGa(m,v,a,B)。
若定义超参数(m,v,a,B),则
(10)
式中:ZNIG(η)=(2π/v)1/2|B|-aΓ(a),Γ(a)为伽马函数。
4 贝叶斯变点检测
贝叶斯变点检测是一种在线变点检测算法[18],通过观察到的数据,生成序列中下一个不可见数据的精确分布来确定是否产生了变点tc。这里采用第3节中的增量退化序列
来进行变点检测。
4.1 变点检测方法
贝叶斯变点检测通过定义从上一变点开始的运行时间长度rt进行建模[18],rt=[r1t,r2t,…,rkt,…,rtt]T,1≤k≤t,rkt=1表示时刻k为变点。给定对于任一时刻(t-1)的运行时长为rt-1,则下一时刻t的运行时长rt只能有两种取值:①当序列按照原有分布规律继续增长,序列的长度rt=rt-1+1;②当t时刻出现变点时,rt=1。
当设备的退化规律发生变化(即出现变点rt=1)的概率为H(rt),当退化规律持续时间服从某一分布时,H(rt)为该分布的冒险率函数[18],则
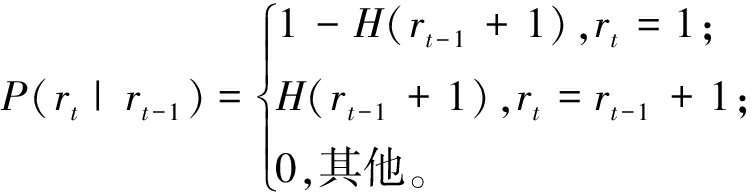
(11)
其中,
为其风险函数[18]。
根据rt,利用边缘概率求和,可知
(12)
其中,
表示在t时刻最近rt(rt=t-k+1)个关联的观测点Δxk,Δxk+1,…,Δxt-1,Δxt。这里的后验概率
为
(13)
联合概率
可以写成递推式
(14)
综合式(13)和式(14)得到rt后验概率的递推公式[18]:
(15)
其中,根据条件独立性性质,预测分布
仅取决于最近的数据
并利用共轭指数分布族的特性来进行简化计算。
根据式(15)可确定当前时间τ对应变点
(16)
4.2 共轭指数分布
为了计算的方便,假设退化增量Δxi由具有共轭先验分布的指数分布族产生[18]。参数θ的先验分布p(θ|η)和后验分布p(θ|Δxi)具有相同的形式,且超参数满足如下关系:
(17)
指数分布的似然函数形式为
(18)
计算出来的边缘分布为T分布,即:Δxi|η～T(Δxi|m,(v+1)B/va,2a)。取φ(θ)=[-u2/2σ2,u/σ2,1/σ2,-log σ2],η=[v,vm,B+vm2/2,a-1/2],φ(θ)和η分别为充分统计量和超参数,且u(Δxi)=[1,Δxi,Δxi2/2,1/2],则得到后验超参数的递推公式为
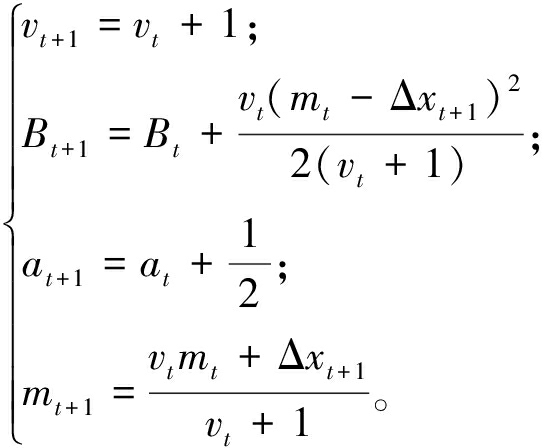
(19)
可得预测分布概率
的递推式:
(20)
式中:
表示依据
计算得到后验分布超参数。
4.3 贝叶斯变点检测算法
算法1 贝叶斯变点检测算法。
步骤1 初始化p(r1)=1,根据离线数据确定利用式(8)来确定其离线参数估计,并利用离线参数估计其超参数值m0、v、a0、B0;
步骤2 获取一组新的退化增量数据Δxt;
步骤3 根据式(20)计算Δxt预测分布概率
步骤4 根据式(15)计算增长rt(rt=rt-1+1)的概率
步骤5 根据式(15)计算变点rt=1的概率
步骤6 根据式(12)利用积分计算证据
步骤7 确定运行时长rt的后验分布
步骤8 根据式(16),确定变点
步骤9 根据式(19)更新超参数,转步骤2。
5 在线参数更新
5.1 在线参数更新
对单个滚动轴承进行实时寿命预测,为了充分利用在线采集数据,可以采用贝叶斯理论进行在线的参数更新,轴承监测当前时间为tk,时间从1到tk获取到的数据为
设Θ0=[μ1,0,σ1,0,μ2,0,σ2,0,τ]为离线学习到的先验信息。设当前设备变点为τ,当tk<τ时,表示设备处于第1退化阶段,且尚无设备第2阶段的退化数据,则此时可以对第1阶段模型参数(μ1P,0,σ1P,0)进行更新。若tk>τ,则变点已经出现,仅需更新第2阶段参数(μ2P,σ2P)。
(1)当
的后验估计
计算如下
(21)
(22)
(2)当tk>τ,仅需要更新
的参数[20]:
(23)
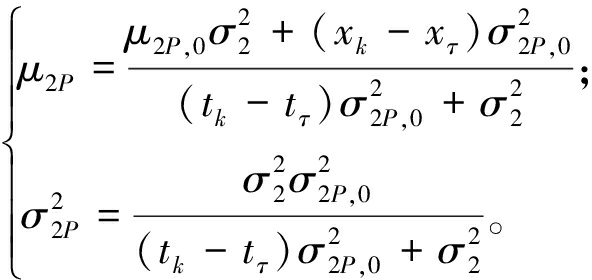
(24)
5.2 多阶段退化寿命预测算法
算法2 多阶段退化寿命预测算法。
步骤1 根据多组的历史数据,利用式(8),确定超参数的先验分布,其中,公共参数(含变点τ)为σ1、σ2、 μ1P、 μ2P、τ的分布为Gamm(α,β)。
步骤2 对于特定某一退化设备,观测到当前时刻tk的时刻的最新数据xk,所有的观测时间序列为
构造差分时间序列
步骤3 利用算法1,计算
判断当前时刻tk是否是最新的变点,根据变点进行处理。
若无变点产生,分两种情况处理,情况1:当tk<τ,以先验信息期望值Eτ作为变点,即为α;情况2:当tk≥τ,则更新变点为tk,按照式(22)利用
序列进行第1阶段的参数更新,计算第1阶段的参数μ1P和σ1。
若当前时间tk产生了变点,则转步骤4。
步骤4 以最新的变点
作为新的退化趋势起点,结合式(24)来更新第2阶段的模型参数(μ2P,σ2)。
步骤5 按照式(23),利用获得的所有参数,计算预测设备的剩余寿命PDF。
步骤6 转到步骤2,直至完成预测过程。
6 仿真验证
数值仿真模型如式(3)所示,其中,μ1,μ2、σ1、σ2分别为第1,2阶段的漂移系数和扩散系数,τ为随机变点。
数值仿真时考虑漂移系数存在随机效应,参数μ1和μ2分布服从高斯分布和其不同阶段的真实参数如表1所示,变点τ也存在随机效应,τ服从Gamm(α,β)分布,且α=100,β=1。扩散系数为定值σ1=0.5,σ2=0.1。设定退化阈值ω=200。
表1 离线参数估计结果
Table 1 Offline parameter estimation results
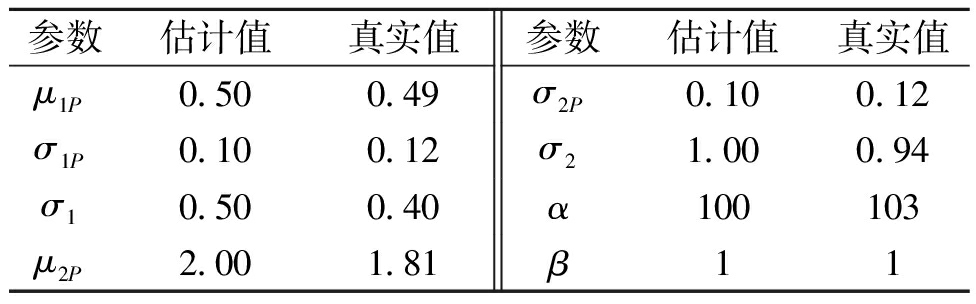
参数估计值真实值参数估计值真实值μ1P0.500.49σ2P0.100.12σ1P0.100.12σ21.000.94σ10.500.40α100103μ2P2.001.81β11
图3显示了样本数n=100时仿真样本轨迹和变点的统计分布情况。
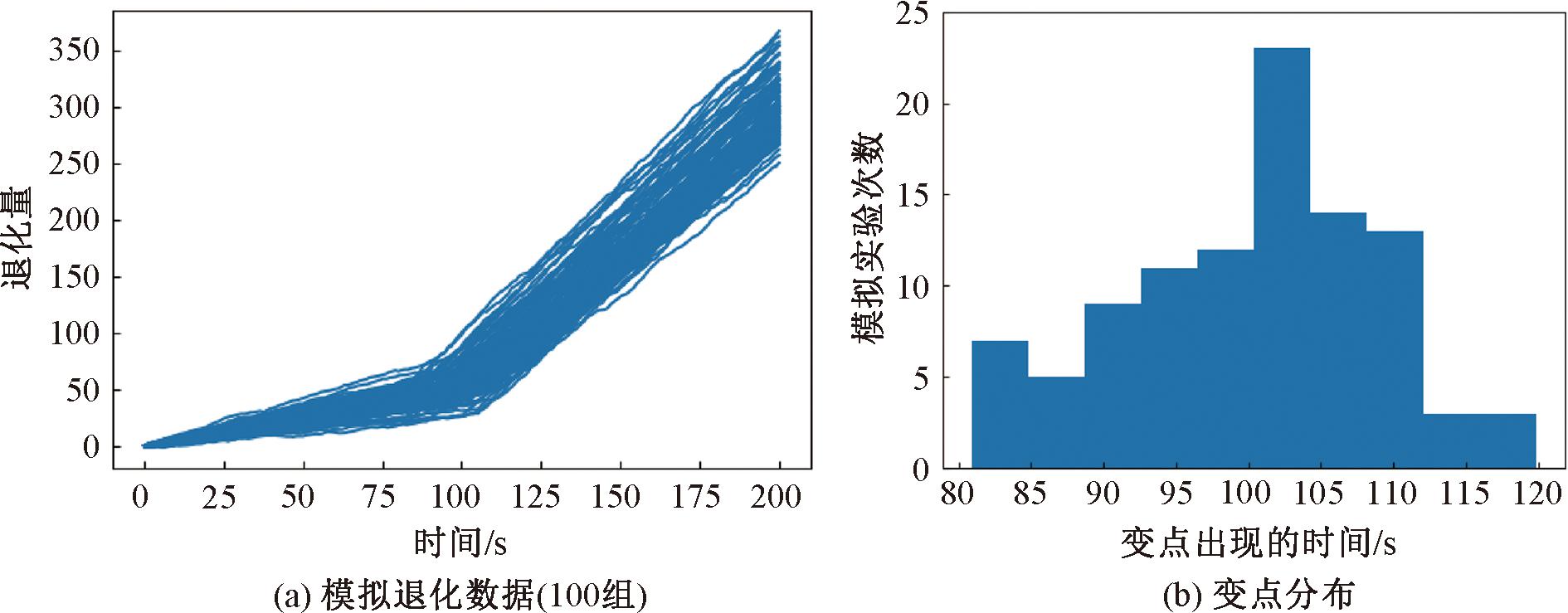
图3 模拟退化数据和变点分布
Figure 3 Simulated degeneration data and distribution of change points
首先,利用除6号样本外的其余99个样本作为离线数据进行先验参数估计,结果如表1所示。图4为样本6的退化趋势和样本6一次差分后得到Δx增量轨迹,采用贝叶斯变点检测方法进行预测,结果如图5所示,其真实变点和预测变点分别为101和104,误差为3。
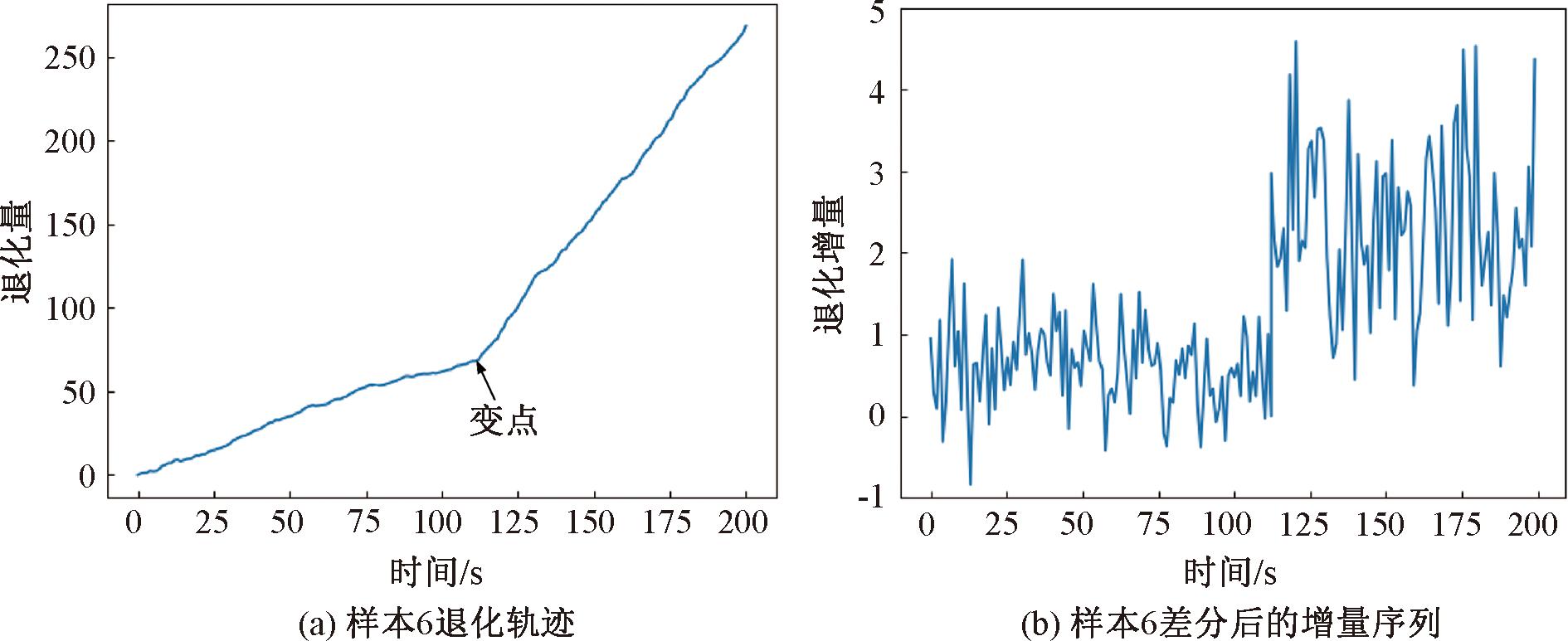
图4 样本6退化轨迹和差分后的增量序列
Figure 4 Trajectory of incremental sequence after differencing of sample 6
图5 样本6变点预测结果[τ′=104 s]
Figure 5 Prediction result of change point for degradation trajectory of sample 6 [τ′=104 s]
图6和图7为采用本文方法与CUSUM变点预测方法[19]的准确性对比。从变点预测的误差值对比情况看,本文方法(贝叶斯变点检测方法)的预测误差值为[-6,0],而CUSUM方法变点预测的误差值为(-20,20)。变点精度提高约85%,同时可见贝叶斯变点预测均为滞后性误差,即预测变点滞后于真实变点,而CUSUM方法预测变点会出现超前和滞后两种情况。
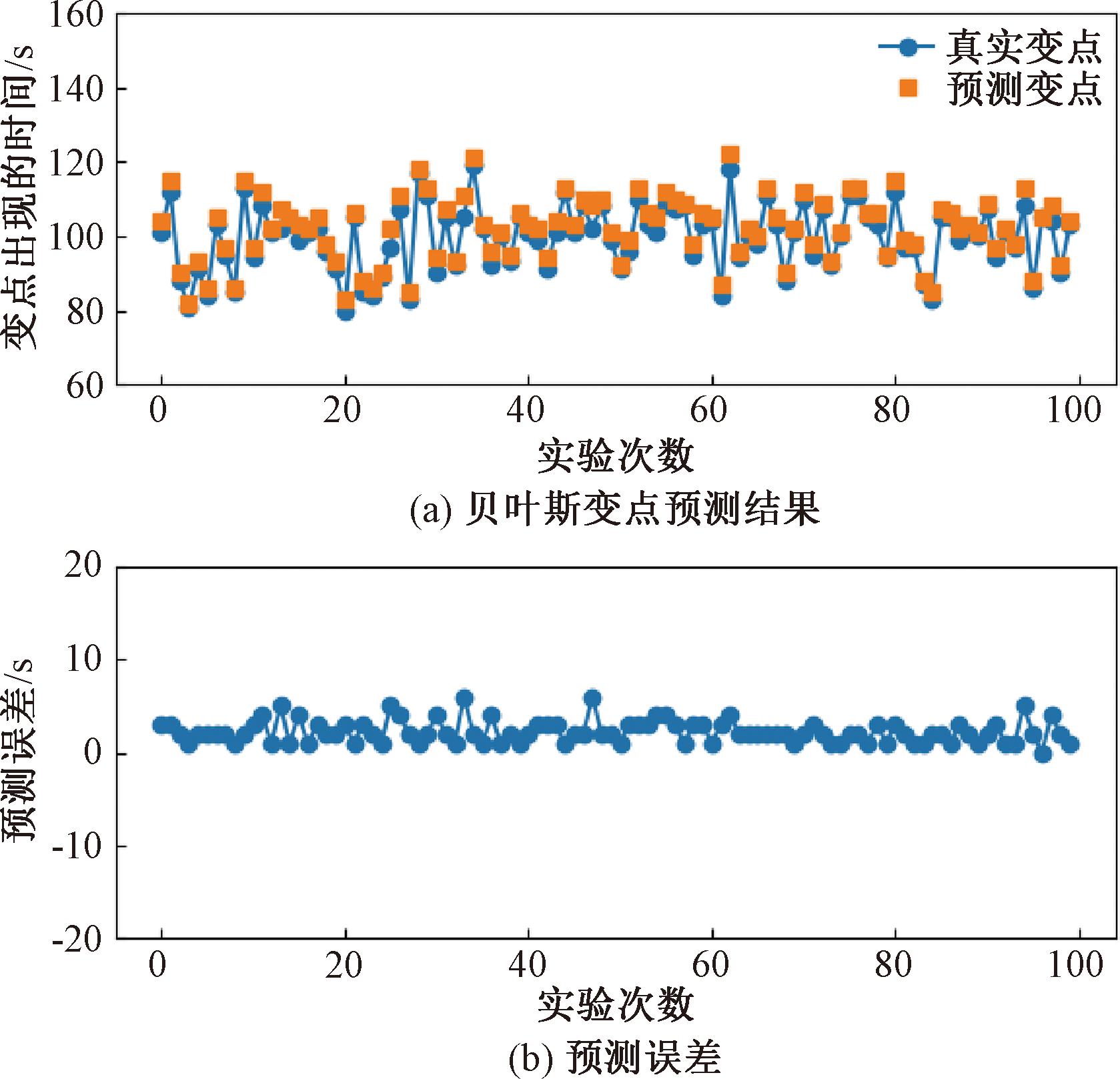
图6 贝叶斯变点检测方法误差分析
Figure 6 Error analysis of Bayesian change-point detection method
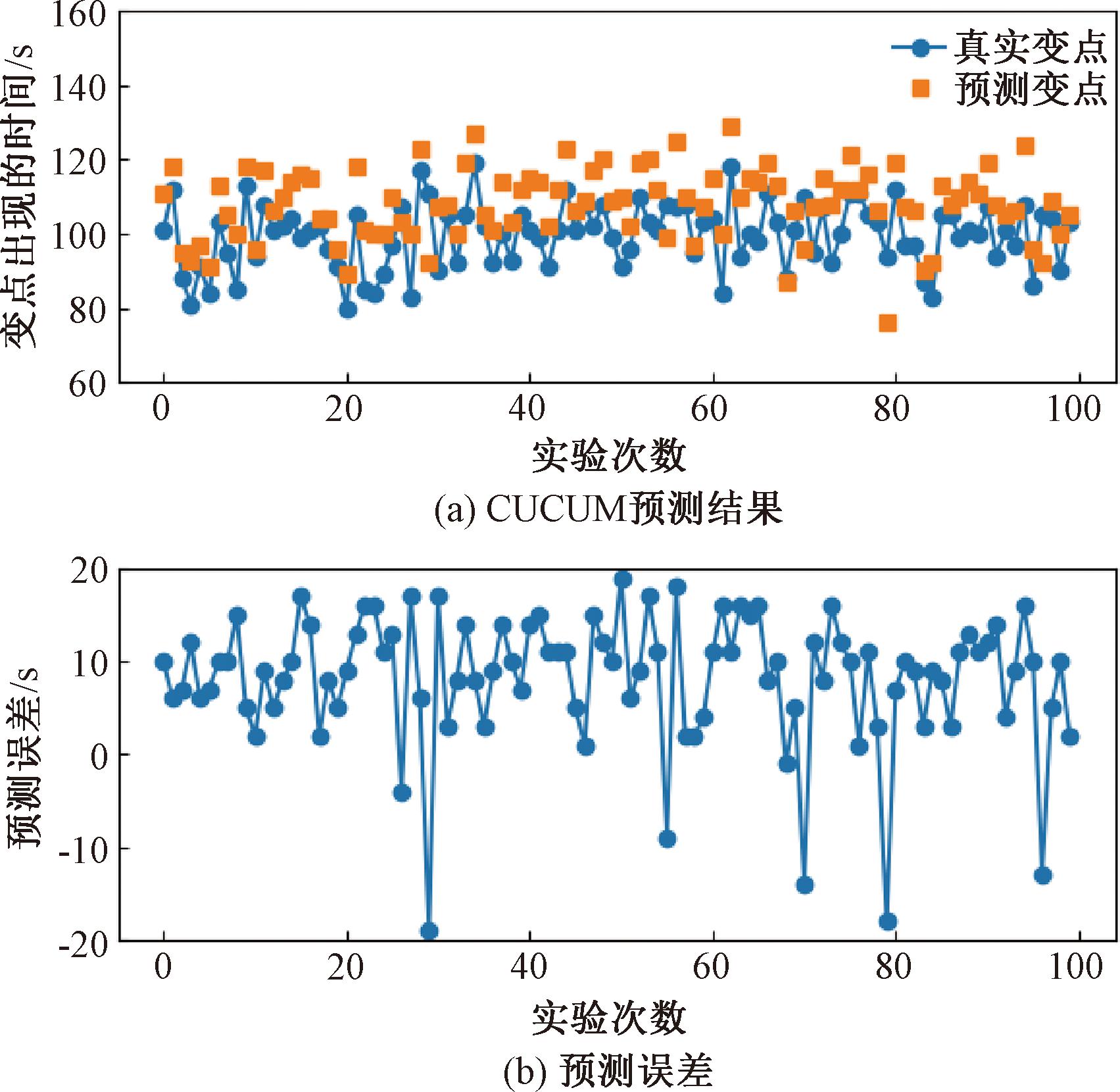
图7 CUSUM方法误差分析
Figure 7 Error analysis of CUSUM method
图8分析了变点预测误差对剩余寿命预测的影响。当预测变点误差为(-12,12)时,①剩余寿命预测误差随变点预测误差增大而增大;②当变点预测误差为负值时(预测变点超前于实际变点),寿命预测的误差更显著。结合图6和图7的分析可知,贝叶斯变点检测方法因其变点误差均为滞后性误差,且误差值较小,因此相对于CUSUM方法,基于贝叶斯变点检测的寿命预测方法有助于提升剩余寿命预测的精度。
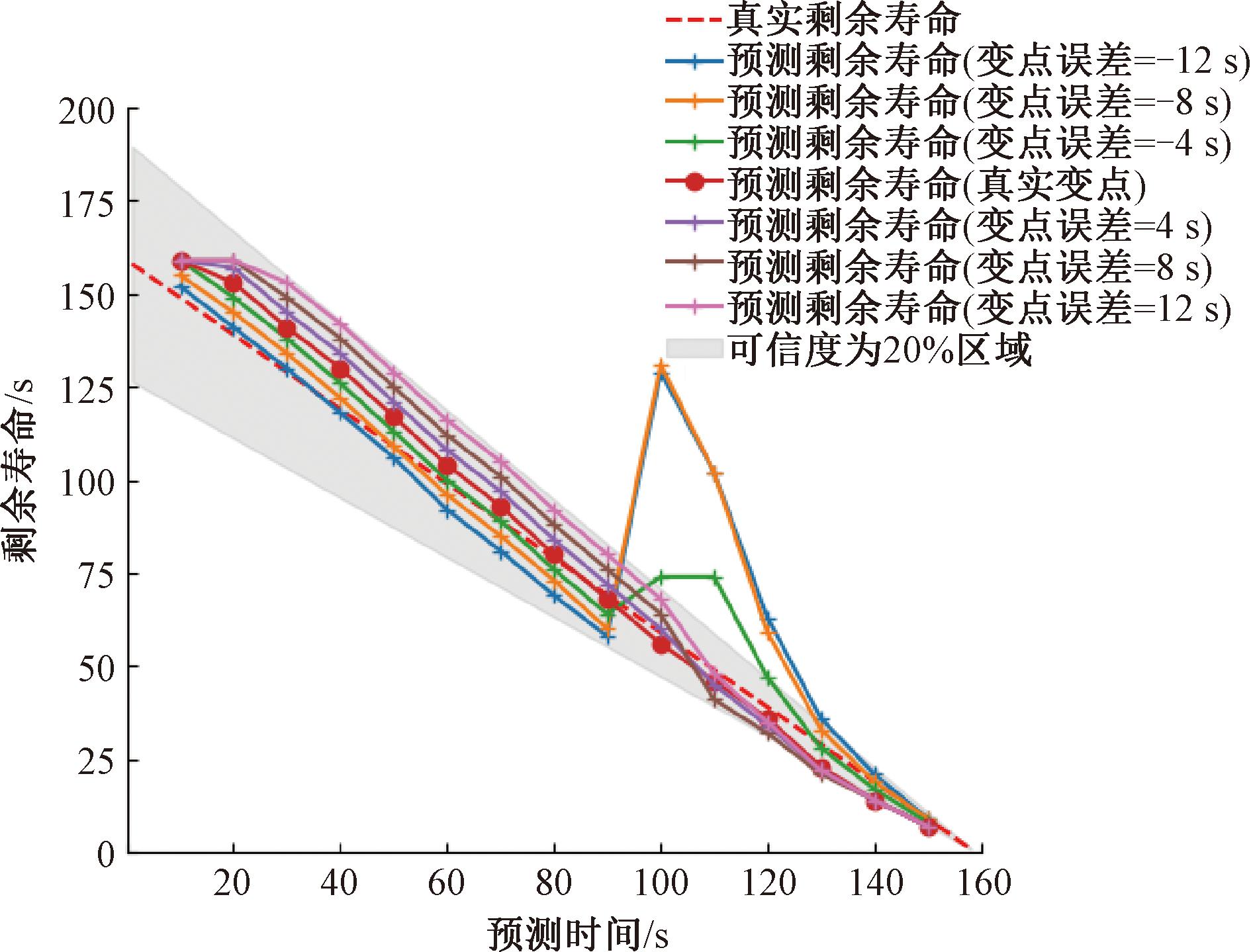
图8 变点误差对剩余寿命预测的影响
Figure 8 The impact of change-point error on remaining life prediction
对于样本6,退化阈值ω=200,根据算法2进行参数实时更新,代入剩余寿命PDF公式,可得到每个时刻剩余寿命结果以及剩余寿命PDF分布情况,分别如图9和图10所示。从结果看,在准确预测变点后,剩余寿命预测取得了较好的效果。
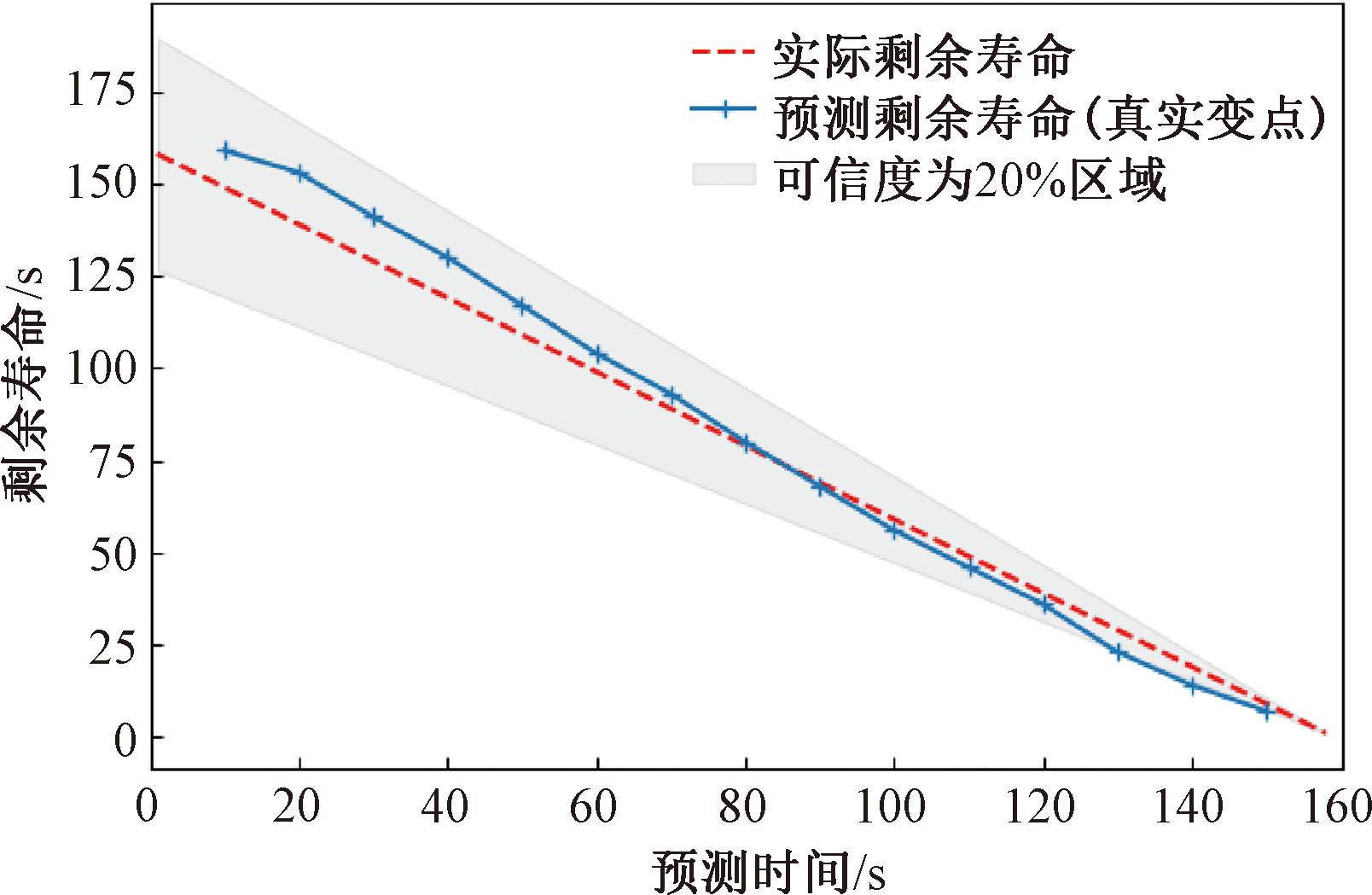
图9 样本6剩余寿命预测结果
Figure 9 Remaining life prediction results of sample 6
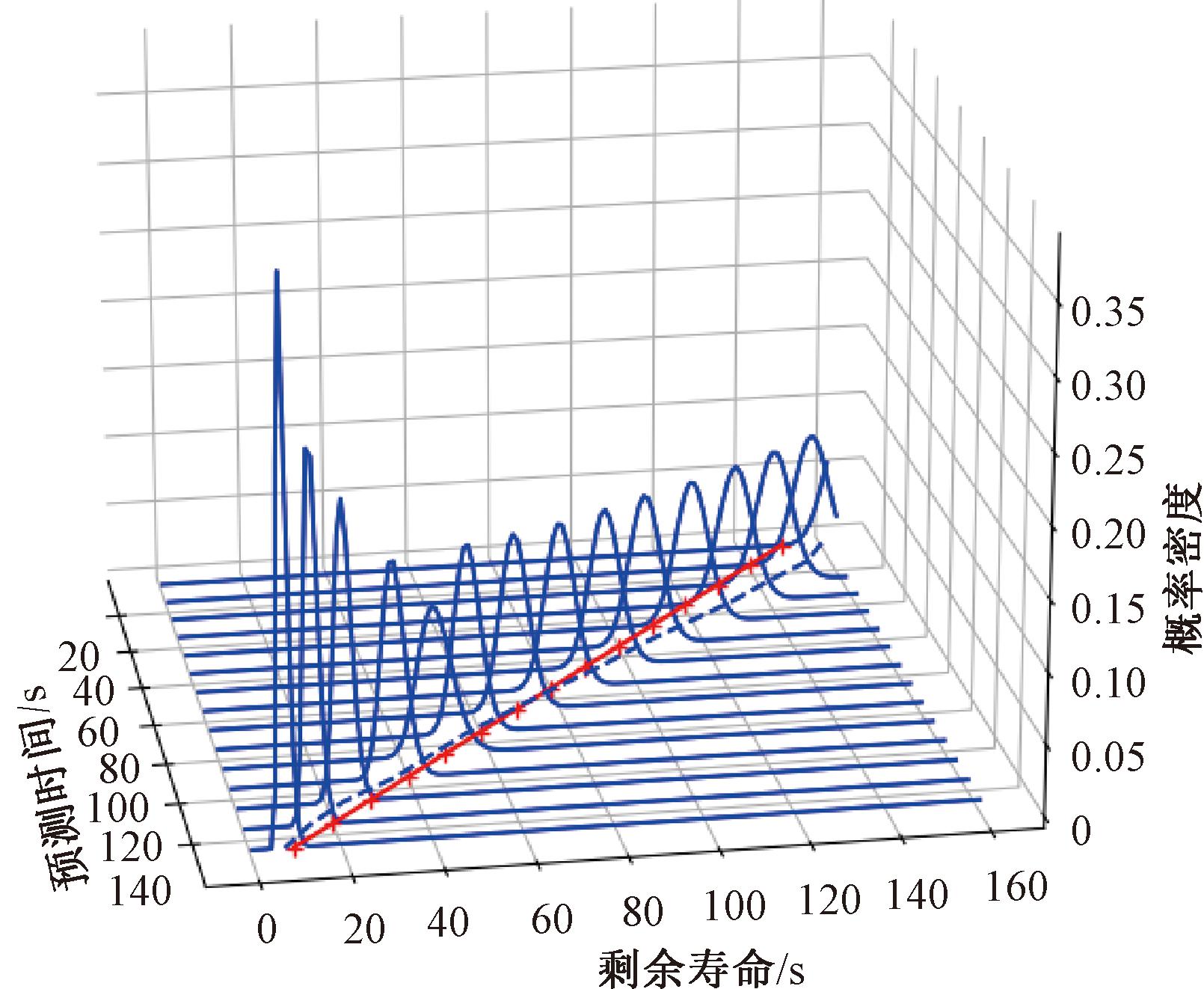
图10 样本6剩余寿命PDF
Figure 10 PDF of remaining useful life of sample 6
7 实例研究
实例数据来自轴承数据集XJTU-SY[22],该数据集包含3种不同工况下15个滚动轴承全寿命周期振动信号数据。其实验台由交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统和测试轴承组成。实验轴承型号为LDK UER204滚动轴承。在实验台中,轴承振动采样频率为25.6 kHz,采样间隔为1 min,每次采样的持续时长为1.28 s。
本实验利用工况1下的4组轴承(Bearing1_1,Bearing1_2,Bearing1_4,Bearing1_5)的退化数据作为离线数据并用于先验参数估计,利用同一工况下的轴承Bearing1_3作为在线运行设备用于在线更新和剩余寿命预测,采用振动的加速度均方根值作为退化指标,退化曲线(去掉了滚动轴承早期缓慢退化期数据)如图11所示,失效阈值为6.5 g。按照2.4节的方法,估计得到模型先验参数μ1=0.005,μ2=0.500,σ1=0.01,σ2=0.05,τ=80 min。
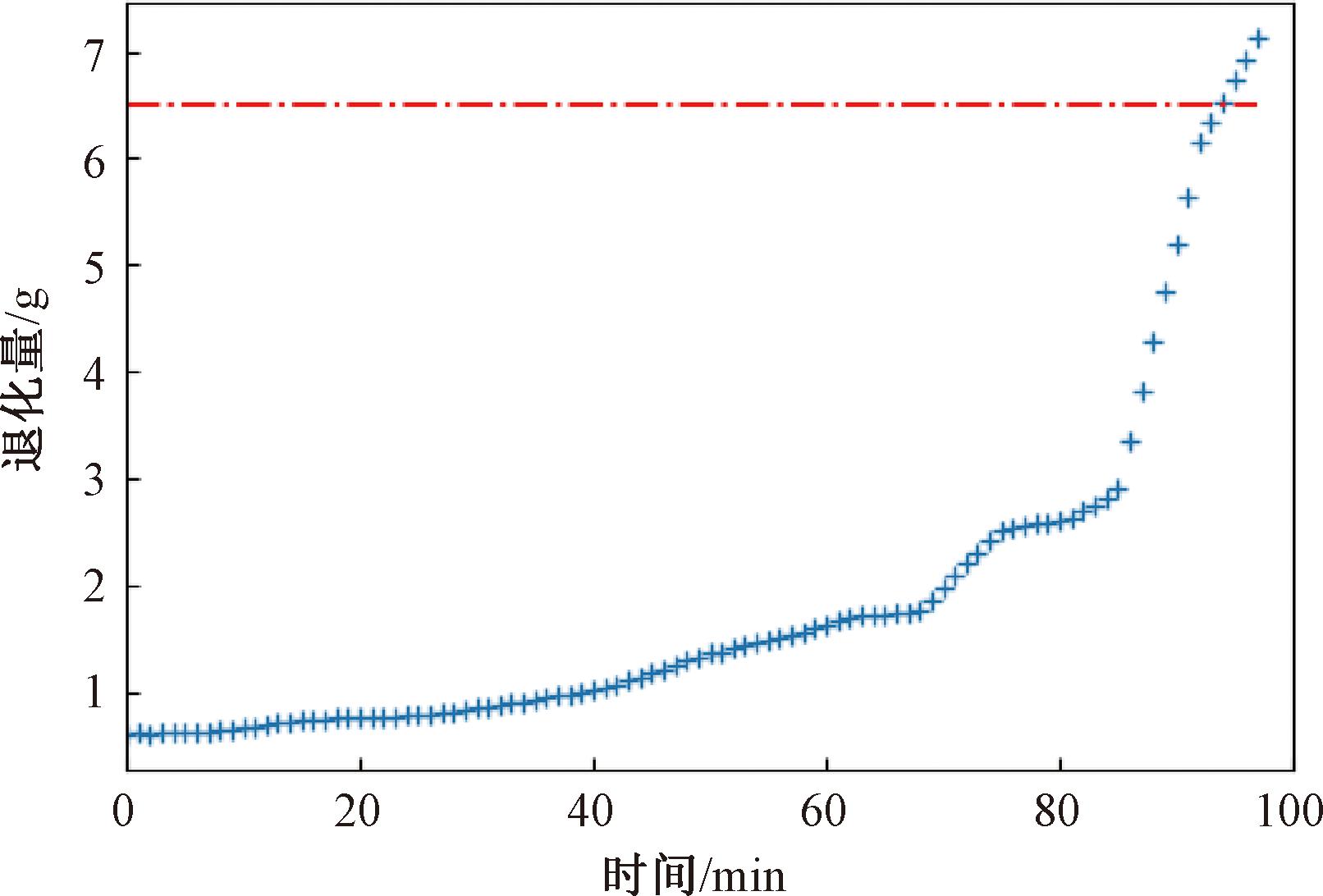
图11 滚动轴承退化趋势(Bearing1_3)
Figure 11 Degradation trend of rolling bearings (Bearing1_3)
利用离线估计的先验参数作为贝叶斯变点检测方法的超参数,分别为m0=0.005,v0=0.1,a0=0.025,B0=0.001 25,其差分后的曲线以及变点概率如图12所示,通过实时变点预测其变点位置为86。对应的剩余寿命预测结果以及PDF分布情况如图13和图14所示,整个生命周期各个预测点上剩余寿命预测均获得比较准确的结果。
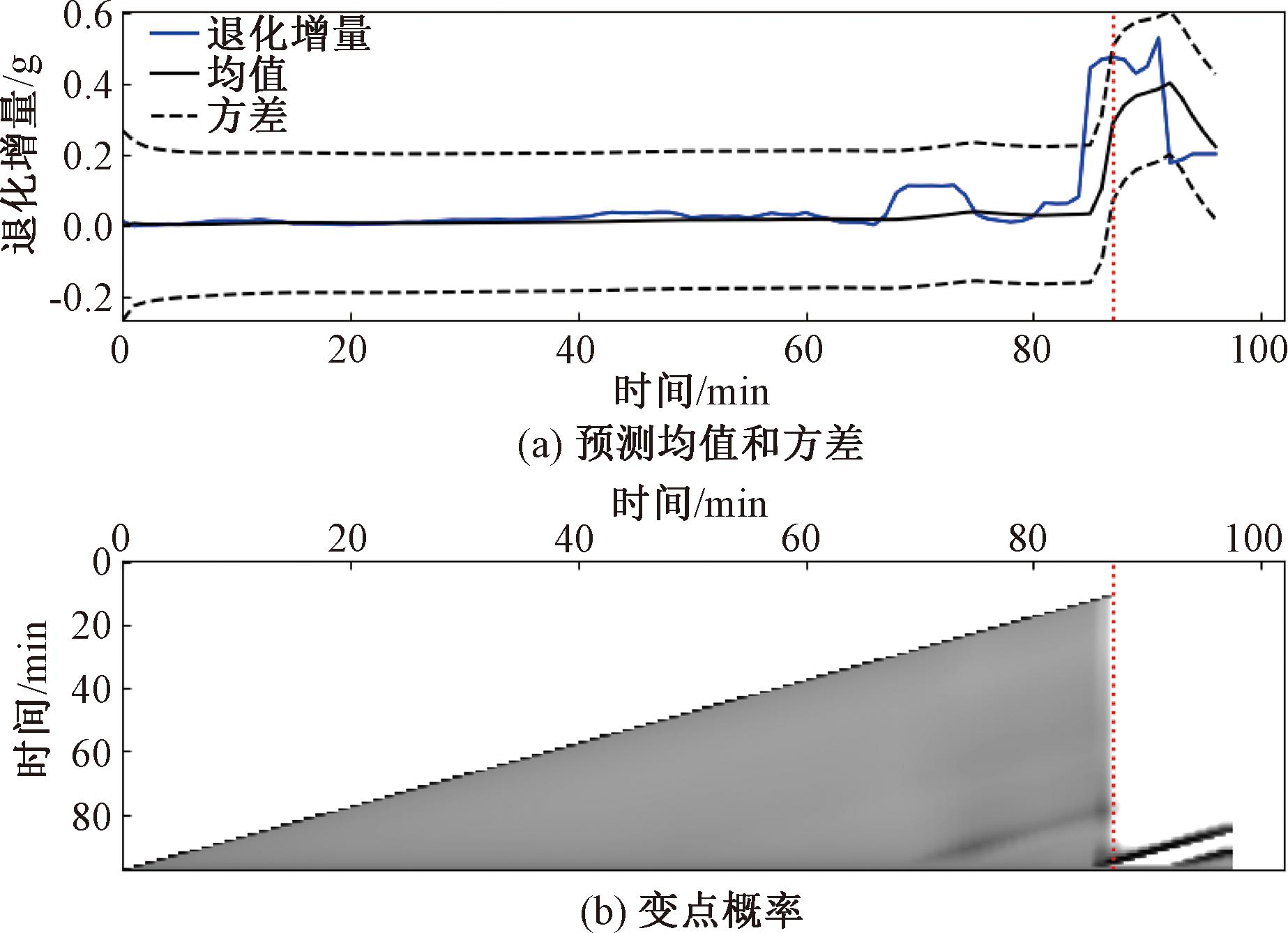
图12 贝叶斯变点检测结果
Figure 12 Bayesian change point detection results
图13 剩余寿命预测结果
Figure 13 Remaining life prediction results
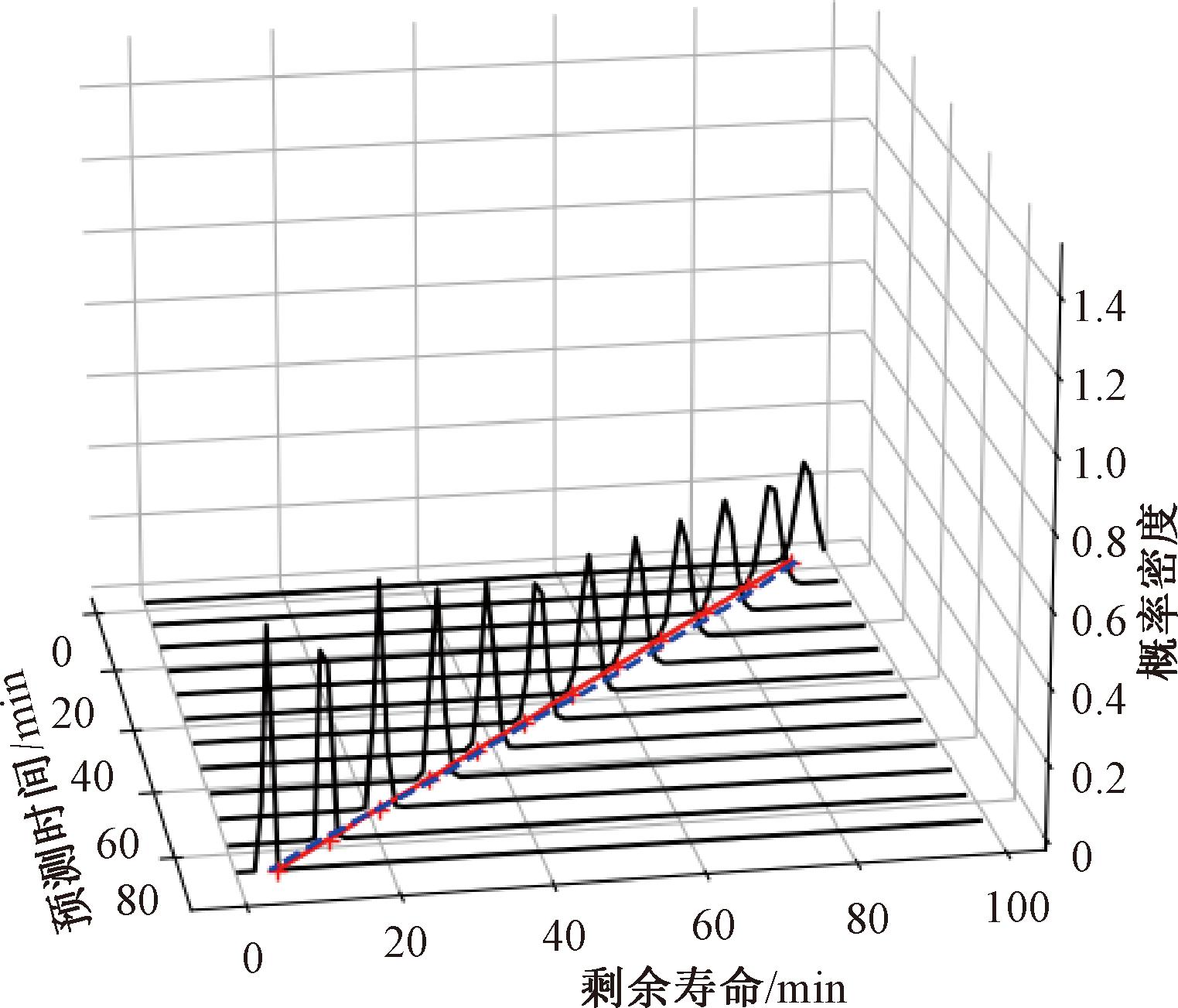
图14 剩余寿命PDF
Figure 14 PDF of remaining life
8 结论
针对滚动轴承运行退化呈现随机变点的多阶段特征,本文提出一种新的基于贝叶斯变点检测的滚动轴承多阶段剩余寿命预测方法,通过分析和实例验证得出如下结论。
(1)本寿命预测方法在变点出现前及出现后均可以完成滚动轴承的寿命预测。特别是在变点出现前的第1阶段,利用离线数据估计的变点以及第2阶段参数的先验值,可以较为准确地预测轴承的剩余寿命。
(2)本寿命预测方法采用了贝叶斯变点检测方法,相对于其他的变点检测方法,可提高变点检测精度(提升85%),进而实现高精度的多阶段剩余寿命预测。
(3)本寿命预测方法是基于在线推理的预测,即通过给定已观察到的数据的情况下,生成序列中下一个未见数据的准确分布的方式进行变点预测,属于在线实时的变点检测,结合在线参数实时更新方法,可以应用于在线实时寿命预测。
[1] 陈远航. 滚动轴承剩余寿命预测算法研究及监测软件开发[D]. 哈尔滨: 哈尔滨工业大学, 2020.
CHEN Y H. Research on prediction algorithm of residual life of rolling bearing and development of monitoring software[D]. Harbin: Harbin Institute of Technology, 2020.
[2] 刘洋, 李凌均, 王宇, 等. 基于FIF-CYCBD的滚动轴承故障特征提取方法研究[J]. 郑州大学学报(工学版), 2022, 43(4): 35-40.
LIU Y, LI L J, WANG Y, et al. Fault feature extraction method of rolling bearings based on FIF-CYCBD[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(4): 35-40.
[3] WEN Y X, WU J G, YUAN Y. Multiple-phase modeling of degradation signal for condition monitoring and remaining useful life prediction[J]. IEEE Transactions on Reliability, 2017, 66(3): 924-938.
[4] WANG W B, ZHANG W J. Early defect identification: application of statistical process control methods[J]. Journal of Quality in Maintenance Engineering, 2008, 14(3): 225-236.
[5] 司小胜, 胡昌华. 数据驱动的设备剩余寿命预测理论及应用[M]. 北京: 国防工业出版社, 2016.
SI X S, HU C H. Data-driven remaining useful life prediction theory and applications for equipment[M]. Beijing: National Defense Industry Press, 2016.
[6] TSENG S T, TANG J, KU I H. Determination of burn-in parameters and residual life for highly reliable products[J]. Naval Research Logistics (NRL), 2003, 50(1):1-14.
[7] PENG C Y, TSENG S T. Mis-specification analysis of linear degradation models[J]. IEEE Transactions on Reliability, 2009, 58(3): 444-455.
[8] LEE M Y, TANG J. A modified EM-algorithm for estimating the parameters of inverse Gaussian distribution based on time-censored Wiener degradation data[J]. Statistica Sinica, 2007,17(3):873.
[9] JOSEPH V R, YU I T. Reliability improvement experiments with degradation data[J]. IEEE Transactions on Reliability, 2006, 55(1): 149-157.
[10] GEBRAEEL N, LAWLEY M, LI R, et al. Residual-life distributions from component degradation signals: a Bayesian approach[J]. IIE Transactions, 2005, 37(6): 543-557.
[11] 史华洁, 薛颂东. 退化数据驱动的设备剩余寿命在线预测[J]. 计算机工程与应用, 2016, 52(23): 249-254.
SHI H J, XUE S D. Degradation data driven online prediction for equipment residual life[J]. Computer Engineering and Applications, 2016, 52(23): 249-254.
[12] WANG Y, PENG Y Z, ZI Y Y, et al. A two-stage data-driven-based prognostic approach for bearing degradation problem[J]. IEEE Transactions on Industrial Informatics, 2016, 12(3): 924-932.
[13] 黄子怡. 基于多退化阶段评估的滚动轴承剩余使用寿命预测方法[D]. 长沙: 中南大学, 2023.
HUANG Z Y. Prediction method of remaining service life of rolling bearing based on multi-degradation stage evaluation[D]. Changsha: Central South University, 2023.
[14] NG T S. An application of the EM algorithm to degradation modeling[J]. IEEE Transactions on Reliability, 2008, 57(1): 2-13.
[15] WANG P P, TANG Y C, BAE S J, et al. Bayesian analysis of two-phase degradation data based on change-point Wiener process[J]. Reliability Engineering &System Safety, 2018, 170: 244-256.
[16] 董青, 郑建飞, 胡昌华, 等. 基于两阶段自适应Wiener过程的剩余寿命预测方法[J]. 自动化学报, 2022, 48(2): 539-553.
DONG Q, ZHENG J F, HU C H, et al. Remaining useful life prognostic method based on two-stage adaptive Wiener process[J]. Acta Automatica Sinica, 2022, 48(2): 539-553.
[17] ARUNAN A, QIN Y, LI X L, et al. A change point detection integrated remaining useful life estimation model under variable operating conditions[J]. Control Engineering Practice, 2024, 144: 105840.
[18] ADAMS R P, MACKAY D J C. Bayesian online changepoint detection[EB/OL].(2007-10-19)(2024-10-09). http://arxiv.org/pdf/0710.3742.
[19] 张正新, 胡昌华, 高迎彬, 等. 多阶段随机退化设备剩余寿命预测方法[J]. 系统工程学报, 2017, 32(1): 1-7.
ZHANG Z X, HU C H, GAO Y B, et al. A residual useful life prediction approach for equipments with multi-state stochastic degradation[J]. Journal of Systems Engineering, 2017, 32(1): 1-7.
[20] ZHANG J X, HU C H, HE X, et al. A novel lifetime estimation method for two-phase degrading systems[J]. IEEE Transactions on Reliability, 2019, 68(2): 689-709.
[21] 胡昌华, 樊红东, 王兆强. 设备剩余寿命预测与最优维修决策[M]. 北京: 国防工业出版社, 2018.
HU C H, FAN H D, WANG Z Q. Residual life prediction and optimal maintenance decision for a piece of equipment[M]. Beijing: National Defense Industry Press, 2018.
[22] 雷亚国, 韩天宇, 王彪, 等. XJTU-SY滚动轴承加速寿命试验数据集解读[J]. 机械工程学报, 2019, 55(16): 1-6.
LEI Y G, HAN T Y, WANG B, et al. XJTU-SY rolling element bearing accelerated life test datasets: a tutorial[J]. Journal of Mechanical Engineering, 2019, 55(16): 1-6.