农业机械设备是提高农业生产效率,推动农业可持续发展的重要工具[1]。随着农机自动导航技术在农业领域的应用,农业生产水平以及资源的利用效率有着显著的提高[2]。农机路径跟踪控制是农机自动导航领域的重要研究方向[3]。其中,提高农机车辆对参考路径的跟踪精度可以更加精准高效地管理农田,有力促进种植业的规模化发展[4]。
近年来,国内外学者针对农机的路径跟踪控制进行了大量的研究,并提出了一些控制算法。美国伊利诺伊州立大学对拖拉机的机械操作系统进行改造,采用FPID控制方法开发出电液操控系统以实现转向动作。该系统可以对小角度转向作出快速准确的反应[5]。黄沛琛等[6]提出了基于BP神经网络实现动态调整农机前视距离改进纯追踪算法,该方法需要对不同种类农机的起始位姿样本进行训练,样本过于庞大,具有一定局限性。唐小涛等[7]提出了一种基于模糊自适应纯追踪模型的农业机械直线路径跟踪方法,以横向误差和速度作为模糊控制器的输入,前视距离作为输出,但该方法忽略了前方目标路径曲度对车辆行驶状态的影响,很难做到快速修正。丁世宏等[8]建立了拖拉机的两轮车动力学模型,采用Kalman滤波有效滤除噪声和重复性测量的影响,实现了输入饱和情况下对农用拖拉机的直线导航控制。张华强等[9]通过粒子群算法,根据实时横向跟踪误差动态确定前视距离,提高了拖拉机自动导航的直线跟踪精度,但并不适合曲线作业。在选择路径跟踪控制方法时,各控制方法具有不同的特点和适用性,比如传统的PID控制具有结构简单、调整方便等特点,在农机路径跟踪控制中被广泛应用。由于其基于反馈的控制方式,控制量滞后输出,系统的鲁棒性不强[10]。非线性自抗扰控制可以通过对扰动的实时估计和补偿,使系统对参数变化和扰动具有很强的鲁棒性,但参数调整的过程较为复杂且对计算资源需求颇高,加大了系统设计和实现的难度[11]。自适应控制的实现过于复杂,且进行简单的模糊处理会降低系统的控制精度与动态品质,当农机系统存在参数不确定性时较难保证系统的稳定性[12]。农机路径跟踪过程本身就是一系列的高维非线性控制问题,在复杂的农田作业环境下,使用的控制算法应具备较强鲁棒性和较好的自适应性才能确保农机对参考路径进行跟踪时取得理想的跟踪精度与稳定性[13]。
本文提出了一种基于全驱控制方法的农机路径跟踪控制。在建模时引入一个未知集总扰动项来表示农机在运动中受到系统的动态变化以及外部干扰的影响,根据农机的运动学特性建立含有未知集总扰动的偏差动力学模型[14]。将建立的农机偏差动力学模型转化为全驱系统,并基于全驱控制方法设计控制器,在所设计出的控制器的作用下,可以使系统状态收敛到任意的椭球区域[15]。最后为说明本文所提出控制方法的合理性与有效性,设置不同实验环境下的不同控制方法的仿真对比[16]。本文创新点总结如下。
(1)将农机车辆的偏差动力学模型转化为全驱系统形式,使控制过程更加简化,为控制设计提供了更多的灵活性。
(2)通过引入参数矩阵的方式求解本文所设计的全驱控制器的未知参数,简化了计算过程,使系统分析更加方便。
(3)采用控制变量法,分别进行了在不同环境下全局控制与PID控制和自抗扰控制的对比仿真实验。
1 农机系统的路径跟踪描述与建模
1.1 建立农机路径跟踪偏差运动学模型
以农田作业中最常见的前轮转向、后轮驱动式的农机车辆为研究对象,根据其低速行驶、小转向角度微调行驶路径的特点,采用二轮车模型推导的方法[17]。以大地坐标系为参考,简化后的农机路径跟踪示意图如图1所示,其中v为车辆纵向行驶速度;A为车辆前轮轮轴的中心;B为车辆后轮轮轴中心;C为后轮轮轴中心B正交投影后到参考路径上的交点;L为车辆的轴距;α为前轮转向角;θt为车辆的航向角;θd为期望航向角;Los为车辆的横向偏差;θos=θd-θt为农机车辆的航向偏差。
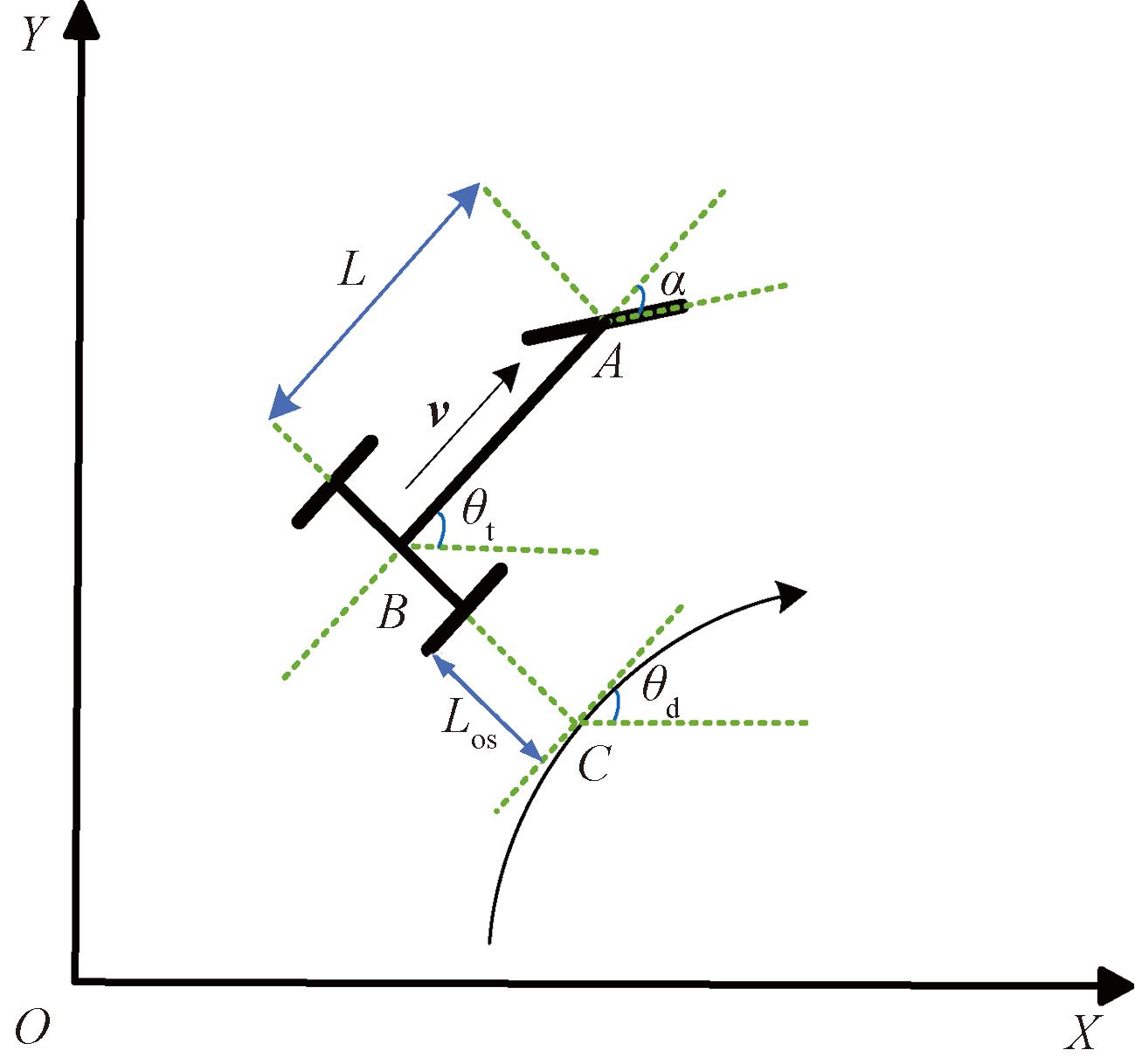
图1 农机路径跟踪示意图
Figure 1 Schematic diagram of agricultural machinery path tracking
考虑到农机在行驶的过程中,由于其本身所具有的复杂性以及在行驶过程中与地面间存在相互作用力,车辆会受到各种因素的影响[18],本文将一个由外部扰动(如路面扰动、侧倾俯仰等影响)和内部扰动(参数不确定、系统未建模动态等因素)构成的未知集总扰动项d引入到系统中。在不考虑车辆所受横向力的前提下,选取图1中横向偏差Los和航向偏差θos为系统状态变量,可得农机路径跟踪偏差动力学模型如下所示:
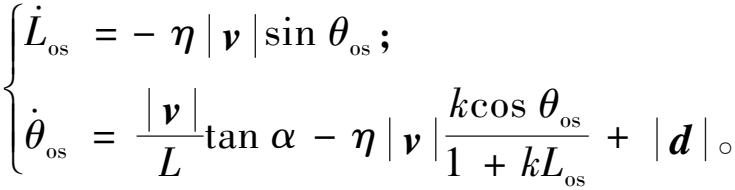
(1)
式中:η为方向系数,用于确定农机车辆是按照顺时针(η=-1)或是逆时针(η=1)方向来进行对参考路径进行跟踪;k为参考路径的曲率;d为农机行驶过程中所受到的未知集总扰动。
1.2 转化农机全驱系统
为方便农机路径跟踪控制器的设计,可以对农机车辆的行驶方向以及对参考路径的跟踪方向进行设定,假定本文中受控的农机车辆为纵向向前行驶的,且按照顺时针方向(η=-1)去跟踪参考路径。首先给出以下定义:
(2)
式中:Los为横向偏差向量。
将式(2)应用于式(1)中,则式(1)的状态空间可以写成以下形式:
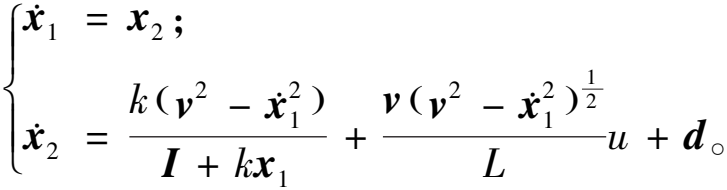
(3)
式中:
为系统的状态向量;u=tan α为虚拟控制量。
假设上述系统受到以下定义的限制[19]：
定义1 未知集扰动项d总是连续可微的,且存在正实常数β,
满足
;
定义2 对于任意存在的x1∈R2,v∈R,都使得矩阵
是非奇异的。
若式(3)满足定义1、定义2的限制,则可以将其转化为全驱系统形式。将式(3)中第1个方程代入到第2个方程中,经过整理可以得到以下全驱系统形式:
(4)
式中: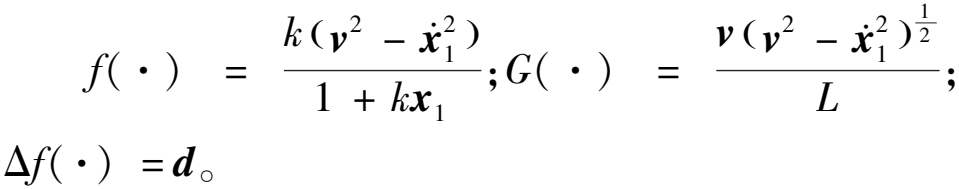
由本文所给出的定义1和定义2可知,在上述系统式(4)中,未知集总扰动项Δf(·)总是连续可微的,且det G(·)≠0。因此系统满足全驱系统的条件,是完全驱动的。
2 控制器的设计与收敛性证明
控制器的设计目标是使系统式(4)在所设计出的全驱控制器的作用下,农机车辆在对参考路径进行跟踪时,所产生的横向偏差和航向偏差在有限时间内能够稳定到原点[20]。下面给出设计过程中所需的几个重要定理。为方便定理的引入与推导,首先给出以下几组符号的定义:
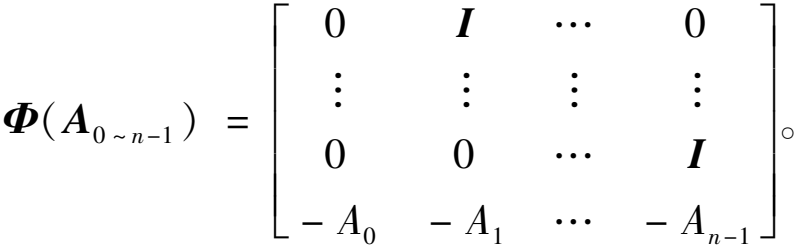
定理1 对于∀μ>0,则∃Ai,i=1,2,满足不等式:
当此条件成立时,则存在一个正定矩阵P,满足以下不等式[21]：
ΦT(A0～1)P(A0～1)+P(A0～1)Φ(A0～1)<
-μP(A0～1)。
(5)
证明 由定理1可知,矩阵
是稳定的,因此存在一个正定矩阵P,满足:
(6)
将上述不等式(6)展开并进行整理,即可得到不等式(5)。证毕。
定理2 当系统模型通过转化能够写成如式(4)形式时,可以通过应用以下控制律进行控制[22]：
(7)
式中:ε为任意给定的正数;ρ为系统不确定性的上界。
此时线性部分的稳定阈值可以收敛到以下的椭球区域:
(8)
式中:μ为任意给定的正数。
在实际应用中,系统状态收敛的椭球区域半径可以通过适当增大线性部分的稳定阈值μ,或者减小ε的值来进行调节。
证明：将控制律式(7)代入系统式(4)中,可以得到以下闭环系统:
(9)
其中:
(10)
将闭环系统式(9)进行整理,可以写成以下状态空间形式:
(11)
为系统式(4)选择以下李雅普诺夫函数:
(12)
结合式(11)与式(12)并整理得
(13)
对不等式(13)的(x(0～1))TPLΨ(x(0～1))部分进行整理可得
(14)
对上述不等式(13)和(14)进行整理后可得
(15)
再由比较定理可得
(16)
由不等式(16)可以看出,当t→∞时得
(17)
由式(17)可以得出,当t→∞时,系统的状态收敛到Θμ,ε(0)的椭球区域。证毕。
3 控制器的求解
根据第2节的定理,并结合农机全驱系统式(4)可以给出如下形式的跟踪控制器:
(18)
为简化计算过程并方便后续的系统分析,可以通过引入参数矩阵F与Z来求解全驱控制器中所涉及的未知矩阵
在对参数矩阵F∈Rnr×nr进行选取时,能满足主对角元素全为负值的对角矩阵这一条件即可。而对参数矩阵Z∈Rr×nr的选取,则可以提供r2n个自由度。对于所引入的参数矩阵F与Z,矩阵A0～n-1以及非奇异矩阵H∈Rnr×nr,则有以下等式成立[23]：
Φ(A0～n-1)=HFH-1。
(19)
其中:
A0～n-1=-ZFnH-1(Z,F);
(20)
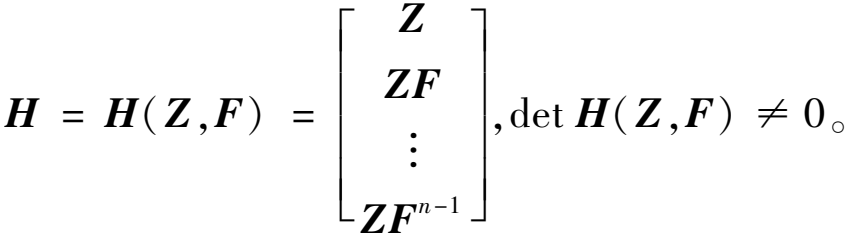
(21)
由以上可知,在对全驱控制器中所涉及的未知参数
进行求解时,可以将参数矩阵F与Z设计为
(22)
(23)
由给出的参数矩阵结合式(20)和式(21)解得以下结果:
(24)
(25)
考虑以下方程式:
(26)
则以下不等式成立:
ΦT(A0～1)P+PΦ(A0～1)≤-5P。
(27)
结合等式(26)与不等式(27),通过求解可得以下结果:
(28)
由
可得
(29)
4 仿真验证
为更好地说明本文所提出的控制方法具有良好的鲁棒性与较强的适应性,分别在标准工况与不确定工况两种不同环境下进行PID控制、自抗扰控制与本文所提出的控制方法的仿真对比实验。引入平均绝对误差(MAE)与均方根误差(RMSE)对不同阶段所产生的横向误差进行统计[24]。通过计算,将PID控制器中的参数选取为KP=100,KI=20,KD=80;自抗扰控制器中参数为b0=0.01,ω0=400,ωc=0.3。
4.1 标准工况下不同控制方法的对比
设定农机的初始位姿坐标与参考路径的起始位置分别为
此时农机的恒定行驶速度为v=3 m/s,车辆的轴距为L=2 m,参考路径的曲率为k=5。将农机的行驶过程分为4个阶段,用每段不同的未知集总扰动项代表农机车辆不同的行驶环境,定义未知集总扰动的表达式[25]为d=vg(t)cos θos,其中:
(30)
图2和图3表示在标准工况下,农机车辆行驶的过程中受到上述4种不同阶段的未知集总扰动时,系统的横向偏差与航向偏差输出响应曲线。
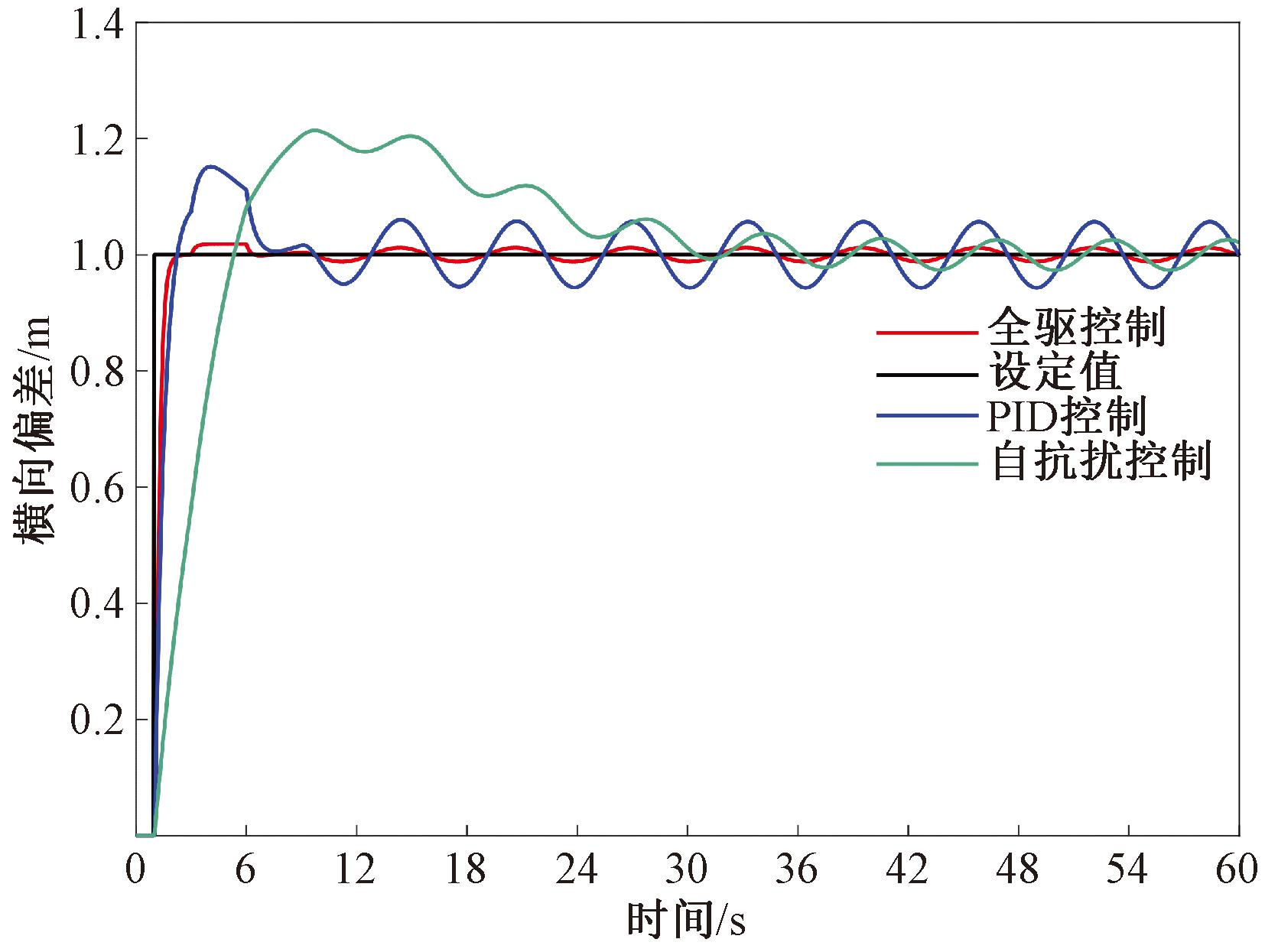
图2 横向偏差响应输出曲线
Figure 2 Output curve of lateral deviation response
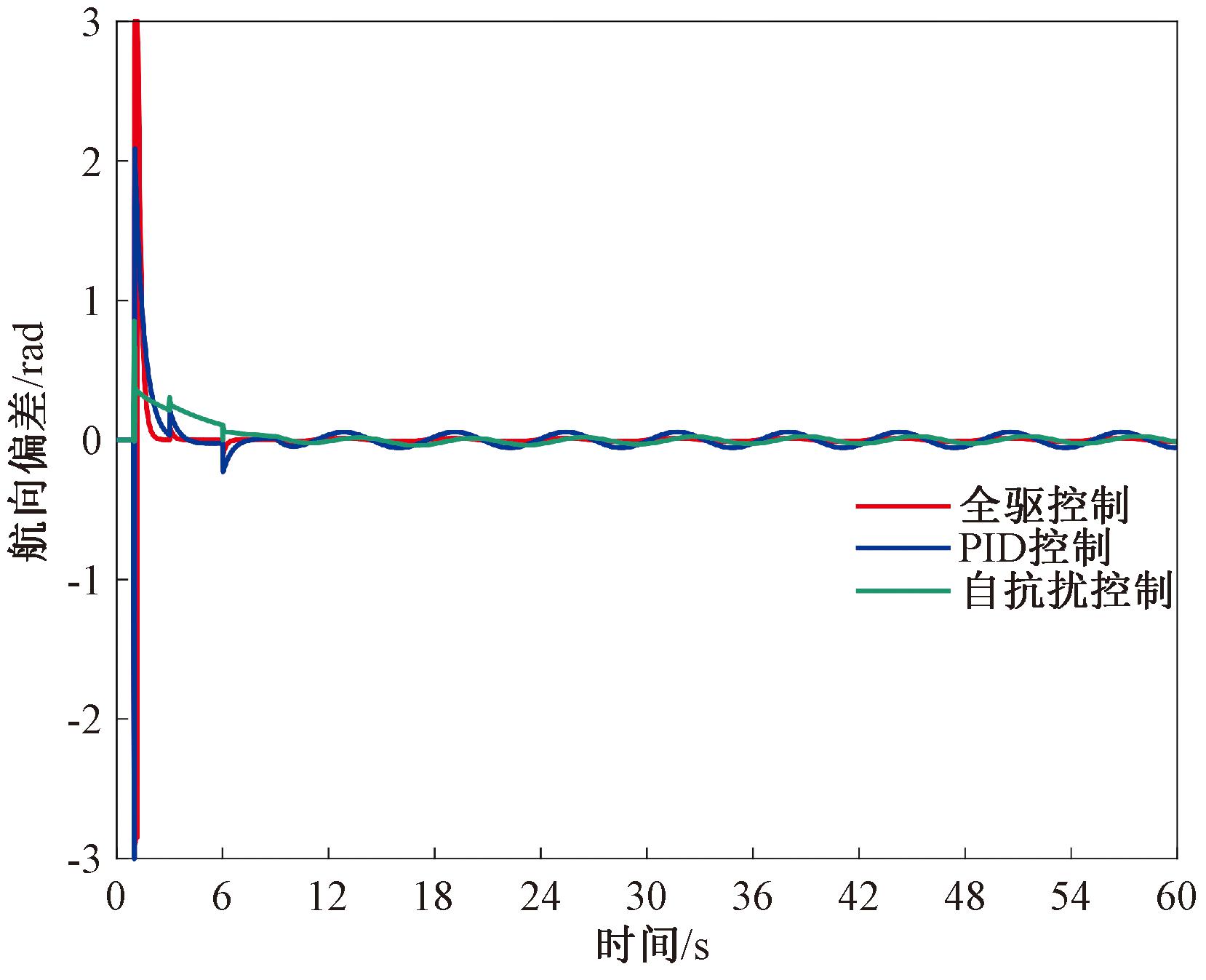
图3 航向偏差响应输出曲线
Figure 3 Output curve of heading deviation response
由图2可以看出,在标准工况下,3种不同的控制方法对农机车辆在4个不同阶段对参考路径进行跟踪控制时,最终系统的横向偏差都能稳定在设定值1 m附近。但是当采用自抗扰控制方法时,系统的超调量过大且上升时间最长。而采用PID控制方法时,虽上升时间减少,但系统的稳态误差较为明显。相比于自抗扰控制与PID控制方法,在本文所提出的全驱控制方法的作用下,农机对不同阶段的参考路径进行跟踪控制时,会受到未知集总扰动变化的影响,农机车辆在短时间内来不及调整自身方向,导致出现了小幅度的超调。但总体上本文所提出的控制方法跟踪误差减小显著,跟踪效果优于PID控制方法与自抗扰控制方法。由图3中可以看出,3种不同的控制方法都可以使得农机车辆在行驶过程中使得航向偏差收敛到原点,但是相较于另外两种控制方法,采用本文提出的控制方法收敛所用的时间最短,收敛效果最好。
通过仿真实验,对农机车辆在不同阶段的行驶过程中所产生的横向误差的数据进行统计,并根据MAE与RMSE的计算公式,得出在标准工况下,采用PID控制、自抗扰控制与本文的全驱控制方法系统横向误差的MAE与RMSE的对比,如表1所示。
表1 3种方法不同阶段下横向误差的统计
Table 1 Statistics of lateral error at different stages of the three methods
控制 方法 MAE/ cm RMSE/ cm 阶段1 阶段2 阶段3 阶段4 阶段1 阶段2 阶段3 阶段4 PID 13 7 5 1 64 25 9 3 自抗扰 50 25 5 1 83 42 9 2 全驱 9 2 1 1 22 2 1 1
由表1中的数据可以看出:农机车辆行驶过程中受到4个不同阶段未知集总扰动的情况下,采用传统的PID控制方法或自抗扰控制方法时,系统横向偏差距离初始设定值1 m处MAE与RMSE的值变化波动范围较大,而采用本文提出的控制方法对参考路径进行跟踪时MAE与RMSE的值变化波动范围较小,且最小值明显小于另外两种控制方法的最小值。这表明基于全驱控制方法的农机路径跟踪控制效果相较于传统的PID控制与自抗扰控制,在面临复杂的农田作业环境以及受到多样的未知因素的影响时,可以更加有效地保证农机车辆对参考路径进行跟踪时的稳定性,能够更好地适应各种复杂的作业环境,满足不同的任务需求。
4.2 不确定工况下控制方法的对比
由于受到驾驶人员技术的差异性以及作业环境的多样性等因素的影响,农机车辆很难以恒定速度行驶,因此在进行不确定工况下的控制方法对比时可以考虑采用控制变量法,通过改变农机的行驶速度或参考路径的曲率来设置不同实验环境,并结合仿真来进一步验证本文所提出的控制方法具有更好的适应性与较强的鲁棒性。给出以下定义的性能评价指标:
(31)
设置农机车辆的初始位姿坐标位置仍为坐标原点处,固定参考路径的曲率为k=5,农机的行驶速度v为1,1.5,3 m/s。固定农机的行驶速度v为实验中最大行驶速度3 m/s,设定参考路径的曲率k为5,15,25,在两种实验前提下参考路径的起始坐标设置为
当参考路径的曲率与农机车辆的行驶速度均发生变化时则可以通过性能评价指标IAEsum的大小来进行判断:若IAEsum的值越小,则说明农机车辆对参考路径的跟踪效果越好;反之则跟踪效果越差。
图4和图5分别为采用PID控制、自抗扰控制与本文所提出的控制方法时系统的横向偏差响应曲线。
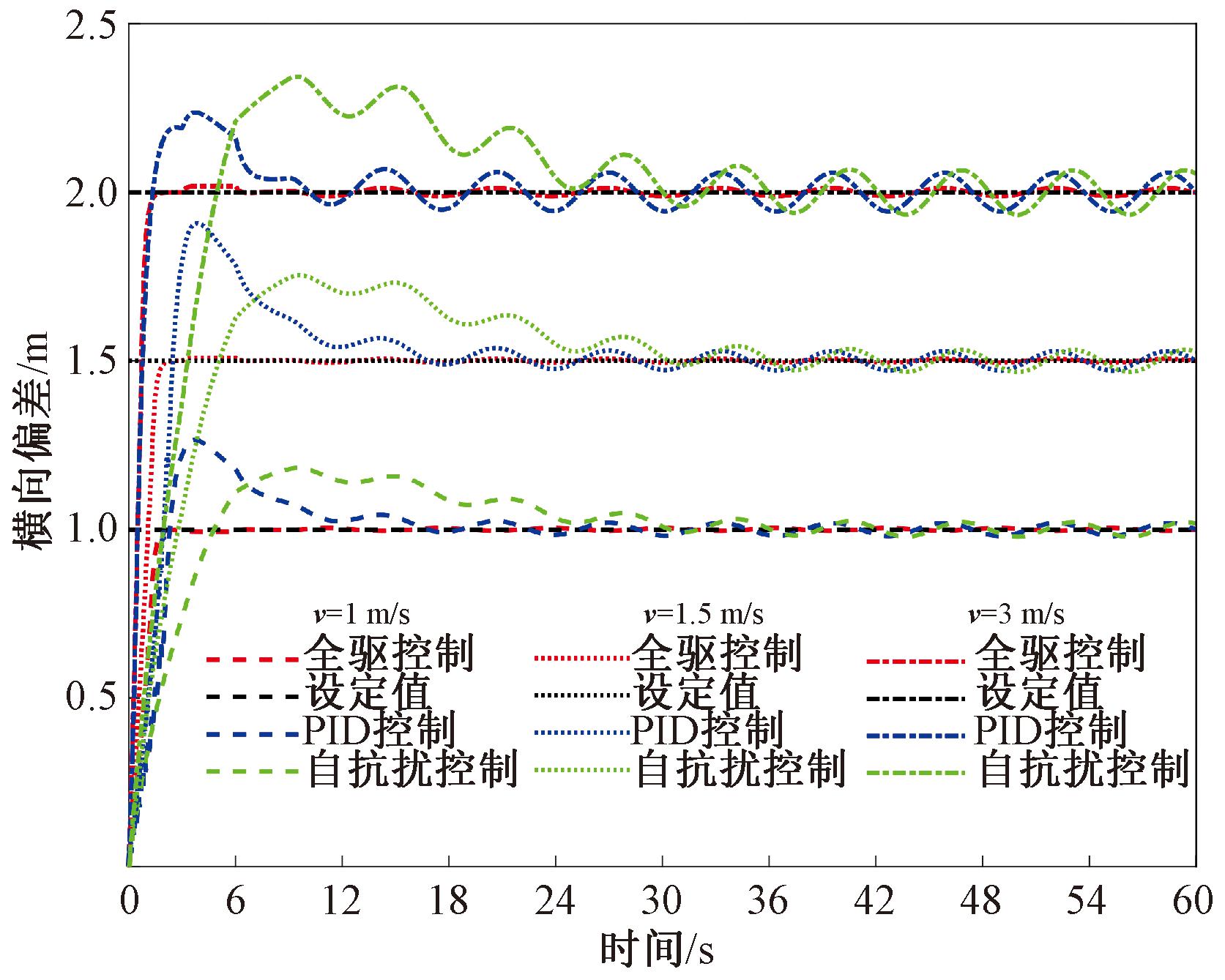
图4 相同参考曲率不同速度下3种方法的横向偏差
Figure 4 Lateral deviation of three methods at different speeds with the same reference curvature
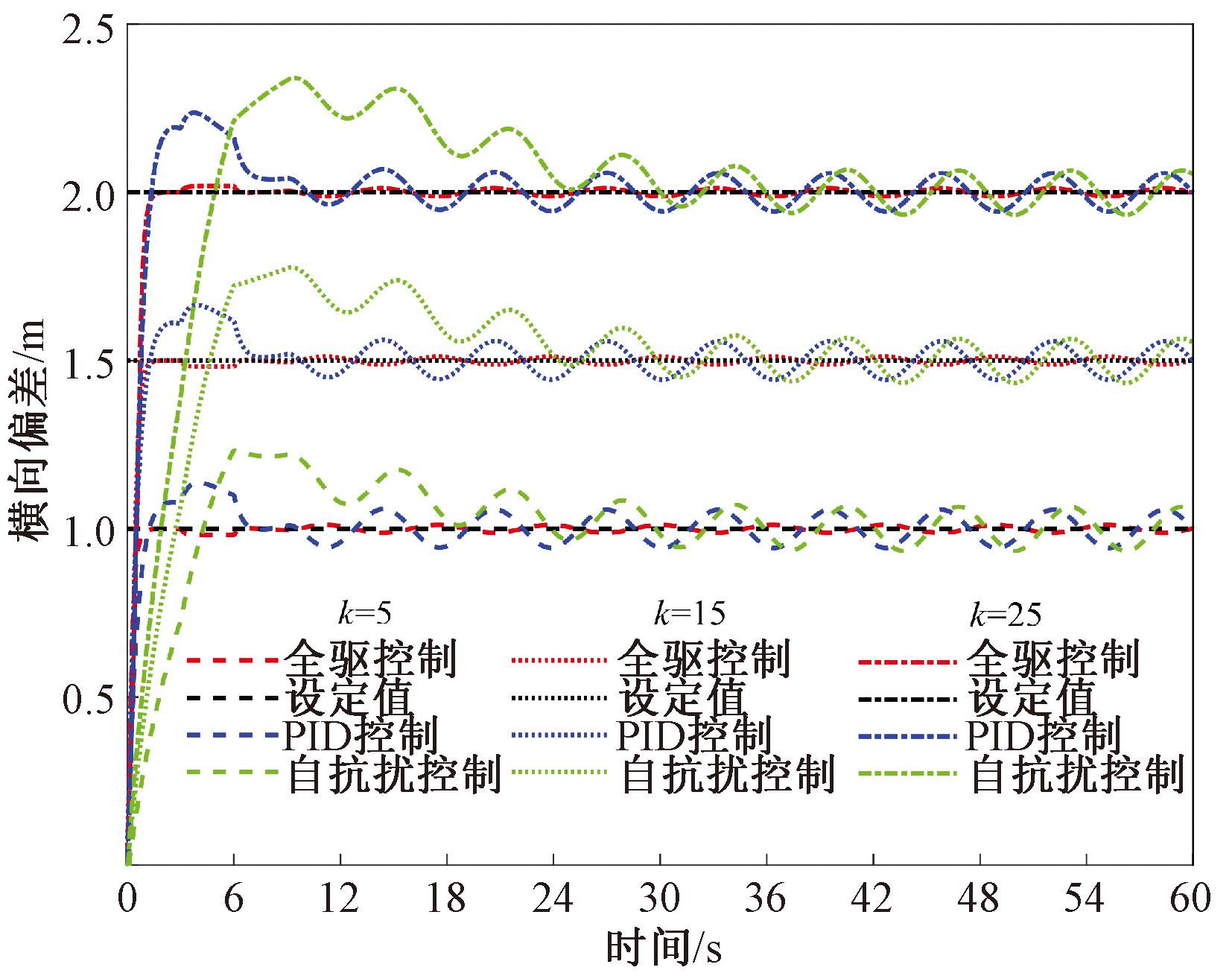
图5 相同速度不同参考曲率下3种方法的横向偏差
Figure 5 Lateral deviation of three methods at different reference curvatures with the same speed
由图4和图5可以看出,当农机行驶速度或者参考路径曲率发生变化时,虽然3种不同的控制方法都能使系统的横向偏差稳定在设定的起始横向偏差附近,但在本文提出的控制方法的作用下,系统在不同阶段所产生的稳态误差明显较小,说明当面对不同的作业环境时,本文提出的控制方法有着更好的适应性。
图6为不同参考路径曲率且不同行驶速度的前提下,农机车辆在行驶的过程中的IAEsum的对比图。从图6中可以看出,当农机车辆的行驶速度与参考路径曲率均发生变化时,采用PID控制或自抗扰控制会导致性能评价指标IAEsum较大,而全驱控制方法的IAEsum从整体来看则较为稳定,并没有产生较大的波动现象。这表明农机车辆在不同的作业任务下进行田间作业时,采用本文所提出控制方法可以使农机车辆更加稳定高效地跟踪参考路径。
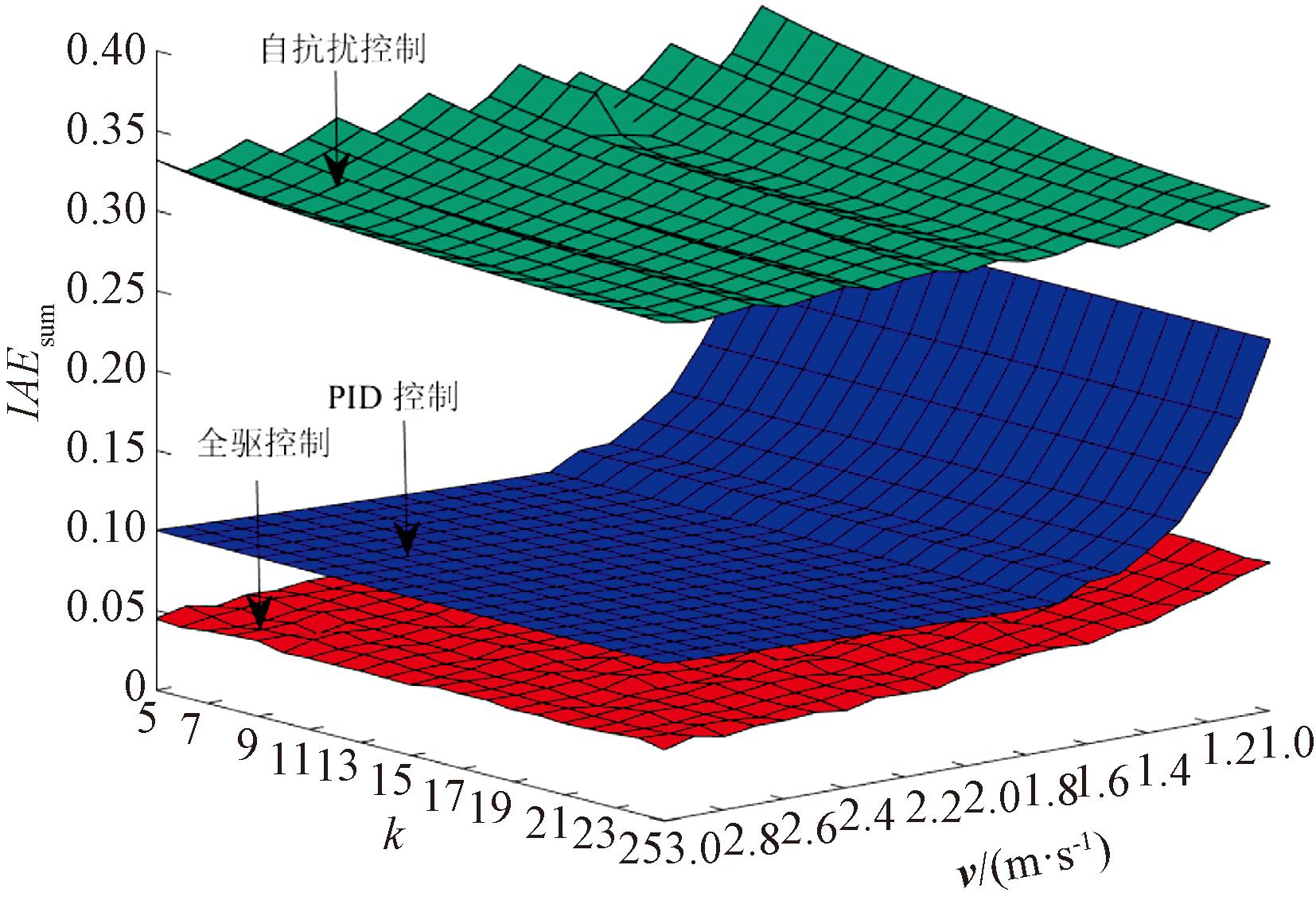
图6 不同速度与不同曲率下的对比仿真
Figure 6 Comparative simulation at different speeds and curvatures
5 结论
针对在未知扰动的影响下农机车辆对参考路径的跟踪控制问题,考虑到农机车辆本身所具有的复杂性以及农机作业环境的多样性等未知不确定因素,本文提出了基于全驱控制方法的农机路径跟踪控制策略,设计了具有不确定性的全驱系统的鲁棒控制器。通过仿真实验表明,在本文所设计控制器的作用下,系统状态可以收敛到任意的椭球区域。相较于PID控制与自抗扰控制方法,具有更高的控制精度与稳定性。下一步将开展农机车辆的实车实验研究工作,通过实车实验验证本文所提方法的有效性。
[1] 万欢, 欧媛珍, 管宪鲁, 等. 无人农机作业环境感知技术综述[J]. 农业工程学报, 2024, 40(8): 1-18.
WAN H, OU Y Z, GUAN X L, et al. Review of the perception technologies for unmanned agricultural machinery operating environment[J]. Transactions of the Chinese Society of Agricultural Engineering, 2024, 40(8): 1-18.
[2] 陈虹, 宫洵, 胡云峰, 等. 汽车控制的研究现状与展望[J]. 自动化学报, 2013, 39(4): 322-346.
CHEN H, GONG X, HU Y F, et al. Automotive control: the state of the art and perspective[J]. Acta Automatica Sinica, 2013, 39(4): 322-346.
[3] 丁幼春, 何志博, 夏中州, 等. 小型履带式油菜播种机导航免疫PID控制器设计[J]. 农业工程学报, 2019, 35(7): 12-20.
DING Y C, HE Z B, XIA Z Z, et al. Design of navigation immune controller of small crawler-type rape seeder[J]. Transactions of the Chinese Society of Agricultural Engineering, 2019, 35(7): 12-20.
[4] 白晓平, 胡静涛, 高雷, 等. 农机导航自校正模型控制方法研究[J]. 农业机械学报, 2015, 46(2): 1-7.
BAI X P, HU J T, GAO L, et al. Self-tuning model control method for farm machine navigation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(2): 1-7.
[5] 连世江, 陈军, 贾海政, 等. 基于PID控制的拖拉机自动转向系统[J]. 农机化研究, 2009, 31(6): 211-213.
LIAN S J, CHEN J, JIA H Z, et al. Automatic turning control system of tractor based on PID control[J]. Journal of Agricultural Mechanization Research, 2009, 31(6): 211-213.
[6] 黄沛琛, 罗锡文, 张智刚. 改进纯追踪模型的农业机械地头转向控制方法[J]. 计算机工程与应用, 2010, 46(21): 216-219.
HUANG P C, LUO X W, ZHANG Z G. Control method of headland turning based on improved pure pursuit model for agricultural machine[J]. Computer Engineering and Applications, 2010, 46(21): 216-219.
[7] 唐小涛, 陶建峰, 李志腾, 等. 自动导航插秧机路径跟踪系统稳定性模糊控制优化方法[J]. 农业机械学报, 2018, 49(1): 29-34.
TANG X T, TAO J F, LI Z T, et al. Fuzzy control optimization method for stability of path tracking system of automatic transplanter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(1): 29-34.
[8] 丁世宏, 姜月霞, 赵德安, 等. 输入饱和情况下农用拖拉机的直线导航控制[J]. 控制理论与应用, 2013, 30(10): 1287-1293.
DING S H, JIANG Y X, ZHAO D A, et al. The straight-line navigation control of an agricultural tractor subject to input saturation[J]. Control Theory &Applications, 2013, 30(10): 1287-1293.
[9] 张华强, 王国栋, 吕云飞, 等. 基于改进纯追踪模型的农机路径跟踪算法研究[J]. 农业机械学报, 2020, 51(9): 18-25.
ZHANG H Q, WANG G D, LYU Y F, et al. Agricultural machinery automatic navigation control system based on improved pure tracking model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(9): 18-25.
[10] 田涛涛, 侯忠生, 刘世达, 等. 基于无模型自适应控制的无人驾驶汽车横向控制方法[J]. 自动化学报, 2017, 43(11): 1931-1940.
TIAN T T, HOU Z S, LIU S D, et al. Model-free adaptive control based lateral control of self-driving car[J]. Acta Automatica Sinica, 2017, 43(11): 1931-1940.
[11] SIAMPIS E, VELENIS E, GARIUOLO S, et al. A real-time nonlinear model predictive control strategy for stabilization of an electric vehicle at the limits of handling[J]. IEEE Transactions on Control Systems Technology, 2018, 26(6): 1982-1994.
[12] TANG L Q, YAN F W, ZOU B, et al. An improved kinematic model predictive control for high-speed path tracking of autonomous vehicles[J]. IEEE Access, 2020, 8: 51400-51413.
[13] TAN Q F, WANG X, TAGHIA J, et al. Force control of two-wheel-steer four-wheel-drive vehicles using model predictive control and sequential quadratic programming for improved path tracking[J]. International Journal of Advanced Robotic Systems, 2017, 14(6): 172988141774629.
[14] 张宏岩, 王伟, 陈仕伟, 等. 基于全驱系统方法的制导控制一体化设计[J]. 航空学报, 2024, 45(1): 137-149.
ZHANG H Y, WANG W, CHEN S W, et al. Integrated guidance and control design based on fully actuated system method[J]. Acta Aeronautica et Astronautica Sinica, 2024, 45(1): 137-149.
[15] LI L, LIU Y H, WU Z L, et al. Controllability, stability and design for high-order fully actuated systems： special cases studies[C]∥2023 2nd Conference on Fully Actuated System Theory and Applications (CFASTA). Piscataway: IEEE, 2023: 851-856.
[16] 崔建明, 蔺繁荣, 张迪, 等. 基于有向图的强化学习自动驾驶轨迹预测[J]. 郑州大学学报(工学版), 2023, 44(5): 53-61.
CUI J M, LIN F R, ZHANG D, et al. Reinforcement learning autonomous driving trajectory prediction based on directed graph[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 53-61.
[17] 刘志强, 张晴. 自适应时域参数MPC的智能车辆轨迹跟踪控制[J]. 郑州大学学报(工学版), 2024, 45(1): 47-53.
LIU Z Q, ZHANG Q. Intelligent vehicle trajectory tracking control based on adaptive time domain parameter MPC[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(1): 47-53.
[18] 李革, 王宇, 郭刘粉, 等. 插秧机导航路径跟踪改进纯追踪算法[J]. 农业机械学报, 2018, 49(5): 21-26.
LI G, WANG Y, GUO L F, et al. Improved pure pursuit algorithm for rice transplanter path tracking[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(5): 21-26.
[19] ASTOLFI A, BOLZERN P, LOCATELLI A. Path-tracking of a tractor-trailer vehicle along rectilinear and circular paths： a Lyapunov-based approach[J]. IEEE Transactions on Robotics and Automation, 2004, 20(1): 154-160.
[20] 孟志军, 刘卉, 王华, 等. 农田作业机械路径优化方法[J]. 农业机械学报, 2012, 43(6): 147-152.
MENG Z J, LIU H, WANG H, et al. Optimal path planning for agricultural machinery[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(6): 147-152.
[21] 丁晨, 魏新华, 梅珂琪. 农用拖拉机的自适应二阶滑模路径跟踪控制[J]. 控制理论与应用, 2023, 40(7): 1287-1295.
DING C, WEI X H, MEI K Q. Adaptive second-order sliding mode path tracking control for agricultural tractors[J]. Control Theory &Applications, 2023, 40(7): 1287-1295.
[22] DUAN G R. High-order fully actuated system approaches： part Ⅰ. Models and basic procedure[J]. International Journal of Systems Science, 2021, 52(2): 422-435.
[23] DUAN G R. High-order fully actuated system approaches： part Ⅱ. Generalized strict-feedback systems[J]. International Journal of Systems Science, 2021, 52(3): 437-454.
[24] DUAN G R. High-order fully actuated system approaches： part Ⅲ. Robust control and high-order backstepping[J]. International Journal of Systems Science, 2021, 52(5): 952-971.
[25] DUAN G R. High-order fully actuated system approaches： part Ⅳ. Adaptive control and high-order backstepping[J]. International Journal of Systems Science, 2021, 52(5): 972-989.