智能制造正引领制造业迈向新纪元,各国都在积极推动这一领域,如德国的“工业4.0计划”、美国的“先进制造业国家战略计划”以及中国出台的“中国制造2025”等[1]。分布式混合流水线(distributed hybrid flowline,DHF)作为新兴制造模式,补充并部分替代了传统的单一车间制造模式[2]。然而,制造过程中由于机器故障对生产调度产生的影响已成为亟待解决的一大难题。同时,我国制造业用电量在第二产业中占比约75%。这不仅凸显了其在国家能源消费中的重要地位,也彰显了节能减排的紧迫需求[3]。
针对机器故障所引发的生产调度中断问题,学者们提出了多种有效的重调度策略,例如完全重调度、右移重调度、部分重调度和插入重调度等。针对混合流水线重调度问题,为最小化最大完工时间,黄家文等[4]与王芊博等[5]分别提出了帝国竞争算法和插值排序算法来结合完全重调度策略。苏建涛等[6]利用非支配排序遗传算法融合右移、右移插入、完全和部分重调度策略求解机器负荷失衡率和最大完工时间同时最小化问题。针对混合作业车间重调度问题,为最小化最大完工时间,李稚等[7]利用基于完全重调度策略的改进头脑风暴算法进行求解;张晓楠等[8]提出了改进遗传算法融合插入和完全重调度策略;周尔民等[9]设计了结合部分、右移和完全重调度策略的遗传变邻域算法。
制造企业调研数据显示,非加工时间在生产周期中占比超过90%[10],同时,全球气候变暖和环境问题的加剧也使节能型生产方式逐步成为行业焦点。因此,将运输时间和节能制造理念融入车间调度问题,不仅具有实际应用价值,也是推动制造业向绿色、高效方向转型的必然要求。对于混合流水线环境,为同时最小化最大完工时间和总能耗,耿凯峰等[11]以及唐艺军等[12]考虑运输时间并分别提出改进的文化基因算法和多目标麻雀搜索算法来解决问题;温廷新等[13]考虑了运输时间、广义能耗以及有限缓冲区约束,设计了狮群算法来求解。
从现有文献来看,关于重调度问题的研究,目标较单一,常为最小化最大完工时间;在计算能耗时多将运输时间忽略或将其与加工时间一起考虑,对其探讨较为有限,这与企业的实际生产存在一定程度的差异。因此,本文提出考虑机器故障和运输时间的分布式混合流水线绿色重调度问题(distributed hybrid flowline green rescheduling problem considering machine breakdown and transportation time, DHFGRP-MT),目标是同时最小化最大完工时间、总能耗和总延期,进而设计了改进灰狼优化算法(improved grey wolf optimization algorithm, IGWO)获取近优解。本文的贡献主要在于在DHF问题中引入机器故障扰动,还考量了运输时间及节能制造的绿色要求,旨在构建一个更贴近现实制造场景的调度模型。
1 问题描述及数学模型
1.1 问题描述
所研究的DHFGRP-MT可概括为对于每个异构工厂f(f∈SF,SF={1, 2,…, F})均内置一条混合流水线,用于处理Q个工件的加工任务。每个工件q(q∈SQ,SQ={1, 2,…, Q})需要在工厂中经过E道生产工序。每道工序e(e∈SE,SE={1, 2,…, E})配置有Kfe台并行机,其中至少有一道工序的机器数Kfe超过1。工件q的第e道工序Oqe在不同的机器k(k∈SKe,SKe={1, 2,…, Kfe})上加工时,其加工时间pfqek会有所不同。期间部分机器可能突发故障,自故障发生时刻BTfek起,该机器停止工作并进入修复状态,经过修复时长RBfek完成修复,这时机器恢复使用。工件q完成一道工序e后到达下一工序e+1进行加工需经一段运输时间te(e+1)。
假设te(e+1)、单位运输能耗PY、各机器单位加工能耗PJfek和单位空闲能耗PKfek已知,调度的目标为①以同时最小化最大完工时间Cmax、总能耗EZ和总延期D为目标,对加工任务进行优化排产;②在机器故障发生的情况下,对所有受影响的工件进行重调度,以减少对生产造成的损失。
1.2 工序集划分
根据故障机器k所在工序e、故障发生时刻BTfek和修复时长RBfek来评估各工序状态,将所有工序划分为完全重调度工序集Π1、并行机重调度工序集Π2、右移重调度工序集Π3和已完工工序集。重调度时无须考虑已完工工序集内工序。
1.3 数学模型
该模型决策变量定义如下:Sqe为重调度方案中工序Oqe的开工时间;
为原调度方案中工序Oqe的开工时间;Cqe为重调度方案中工序Oqe的完工时间;
为原调度方案中工序Oqe的完工时间;Vfqe为0-1决策变量,如果重调度方案中工件q的第e道工序被分配到工厂f,则Vfqe=1,否则Vfqe=0;VVfqek为0-1决策变量,如果重调度方案中工件q被分配到工厂f内工序e的机器k处理,则VVfqek=1,否则
为0-1决策变量,如果工件q的第e道工序在重调度方案和原调度方案被分配的工厂相同,则
否则
为0-1决策变量,如果工件q在重调度方案和原调度方案均被分配至工厂f内工序e的机器k处理,则
否则
为0-1决策变量,如果在工厂f内工序e的机器k上,
是Oqe的紧前工序,则
否则
数学模型表示如下:
min G=ρG1+
G2+(1-ρ-)G3;
(1)
G1=Cmax=max Cj,I;
(2)
G2=EZ=EJ+EY+EK;
(3)
(4)
式中:ρ和 分别为Cmax、EZ和D相关的权重系数;EJ为机器加工能耗;EY为运输能耗;EK为机器空闲能耗;
和
分别为重调度方案和原调度方案中的最大完工时间。采用线性加权的方法将多目标问题转化为单目标问题,可以有效降低问题难度和复杂度。式(1)为所研究问题的目标,即同时最小化最大完工时间、总能耗和总延期,这3部分分别由式(2)～(4)计算得到。
重调度约束条件如下所示。
Sqe≥BTfek,∀f∈SF,k∈SKe,Oqe∈Π1;
(5)
Sqe≥BTfek,∀f∈SF,k∈SKe,Oqe∈Π2;
(6)
∀f∈SF,Oqe∈Π2;
(7)
(8)
(9)
(10)
(11)
(12)
(13)
式中:SF为工厂集;SKe为工厂f内工序e的机器集;k′指故障机器的其他可用并行机。式(5)为集Π1中工序的开工时间限制;式(6)表示集Π2内工序的开工时间是在机器故障发生时刻之后;式(7)为集Π2内工序的开完工时间之间的关系,并规定在并行机重调度中,工序优先选择加工时间最短的可用并行机进行加工;式(8)～(9)表示集Π2内工序是在原调度方案中同一工厂的不同机器上进行加工;式(10)～(11)表示集Π3内工序的开完工时间是原调度方案的开完工时间加上故障机器修复时长;式(12)～(13)确保集Π3内工序仍被分配至原调度方案中的工厂和机器上进行加工。
共有约束条件如下所示。
(14)
(15)
(16)
Cqe+te(e+1)≤Sq(e+1),∀q∈SQ,e∈SE,e≠E;
(17)
(18)
WVfq′qek+WVfqq′ek≤1,∀f∈SF,q′,q∈SQ,
e∈SE,k∈SKe,q′≠q;
(19)
VVfqek-WVfq′qek)≥0,∀q′,q∈SQ,e∈SE,q′≠q;
(20)
(21)
(Sqe-Cq′e)WVfq′qek;
(22)
(23)
(24)
q′,q∈SQ,e∈SE,k∈SKe,q′≠q。
(25)
式中:SQ为工件集合;SE为工序集;M为保持不等式一致性的足够大的正数。式(14)强制每个工件必须分配给确定的一个工厂;式(15)确保一旦一个工件的第一道工序被分配到某个工厂,则该工件的所有后续工序必须在同一工厂中完成;式(16)表示每个工件在其所分配工厂的每一道工序只能由一台机器加工;式(17)定义了工件在完成一道工序后需经一段运输时间到达下一工序才能开始加工;式(18)表示同一工序的完工时间大于或等于开工时间和加工时间之和;式(19)～(20)确保同一台机器上任意两个工件的处理时间不能有重叠,即后一工件的开工时间不得小于前一工件的完工时间;式(21)～(23)分别表示机器加工、空闲能耗和运输能耗;式(24)～(25)为决策变量的取值范围。
1.4 重调度策略
采用干扰事件驱动的重调度策略包括完全重调度、并行机重调度和右移重调度。完全重调度指当机器发生故障时,利用IGWO算法立即对未开工的工序重新调度。并行机重调度是在故障发生时,将加工任务转移到加工时间最短的可用并行机上。右移重调度适用于工件正在故障机器上加工且不存在可用并行机或转移成本过高,即移至其他机器的加工时间超过原机器的加工与修复时间之和,此时将工件的开完工时间向后推移,同时保持原有调度方案的顺序及工厂、机器的分配,直至工序完工。
2 求解DHFGRP-MT的IGWO算法
2.1 编/解码
(1)编码。采用三链式编码方式,包括工序链(记为OS)、工厂链(记为FS)和机器链(记为KS),以解决工序排序、工厂分配以及机器选择这3个高度关联且相互影响的子任务。每部分链长度均为所有工件的工序总数,其中工序链OS内各元素代表工件号,同一工件号重复出现的次数为工件的总工序数E,依次出现时分别对应该工件的第e道工序;工厂链FS说明了OS中相应工件所分配的工厂号;机器链KS中各元素则表示每道工序所使用的机器号。将这3部分的编码链组合,即可形成一个完整的调度解,可表示为X=(OS, FS, KS)。通过该编码方式,可满足式(14)～(16)、式(19)～(20)对于工厂分配和机器占用的资源约束。
(2)解码。为获取式(1)～(4)所定义的最大完工时间、总能耗和总延期,需要通过解码过程将编码转化为实际的加工调度方案。在遵守既定约束的前提下,按照编码链中指定的工序排序,利用插入式贪婪解码将每个工序安排到相应机器的最早可利用时间,以实现机器利用率的最大化和整体时间的最小化。
2.2 生成初始种群
利用NEH启发式法生成50%质量较好的解,剩余解通过完全随机程序产生,以保持种群多样性,避免算法过早收敛。NEH是一种有效解决调度问题的启发式算法,其核心是总加工时间较大的工件应优先安排[14],具体步骤如下所示。
首先,计算每个工件的总加工时间,将它们按照降序排列,得到一个初始序列,即
然后,将初始序列Γ0中前两个工件随机排列得到
和
选择其中最大完工时间最小的加工序列作为当前排列,记作Γ={Γ(1), Γ(2)};最后,从剩余工件中随机选择一个,将其插入到之前工件的最终序列中所有可能位置,来寻找最佳序列,且不更改已分配工件的相对位置,重复该过程,直至所有的工件调度完毕,得到能使最大完工时间最小的工件加工序列。
2.3 领导层狼个体的选择
根据式(26)计算种群内个体的适应度值,从中选择适应度值最大的3个个体作为领导层狼,分别为α、β和γ。其余个体为底层狼ω。
(26)
2.4 捕食行为搜索策略
根据狼群捕食特点,设计了基于跟踪和自主行动的双模式并行搜索方法,即ω狼既可跟随领导层狼进行捕食(交叉操作),又可在捕食行为中积累经验,从而捕食技能发生变化,故也可由其自身进行攻击(变异操作)。这种双模式并行的搜索方法有助于平衡算法的全局与局部搜索能力,避免过早收敛。
2.4.1 跟踪模式
基于领导层狼(α、β、 γ)带领底层狼ω进行捕食的特点,对工序链OS设计了一种基于交叉操作的个体更新策略,即ω狼按照一定的概率与α、β、γ狼内任一个体进行交叉,通过结合不同个体的优秀特征,以生成新个体,即
(27)
式中:rand(·)为在0和1之间服从均匀分布的随机数;OX表示基于顺序的交叉操作,具体操作如图1所示。计算步骤如下:随机选取两个点r1和r2(r1<r2<n)作为交叉点,通过这两点划分出父代个体P1、P2上的子段H1、H2作为交叉保留区域;将H1、H2提取到子代Z1、Z2的相同位置;将P1按顺序删除H2中存在的元素,将余下元素按顺序填入Z2的空位中。同理生成Z1。在上述过程中,OS中各元素变换时,对应的工厂链FS和机器链KS中的元素也随之调整,即不改变各工序所分配的工厂和机器。
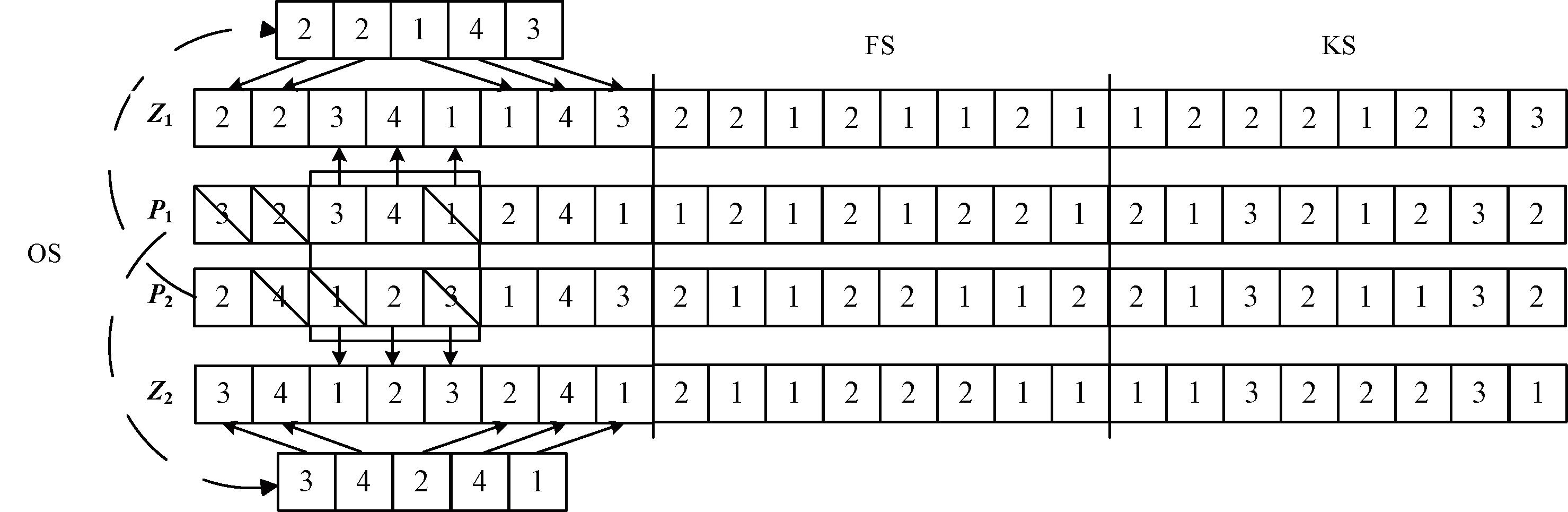
图1 OX交叉
Figure 1 OX crossover
2.4.2 变异算子
为提高算法全局搜索能力,避免陷入局部最优,针对机器链KS引入DE/rand/1差分变异方式,即允许ω狼自主行动,而非完全依赖于领导层狼(α、 β、 γ)的指引进行捕食,公式如下所示:
(28)
式中:
和
分别为种群范围内随机选取的个体;Fr为变异缩放因子。计算步骤如下。
步骤1 差值计算与条件替换。计算Lbg-1和Lcg-1在各维度上的数值差,得到差值序列(Lbg-1-Lcg-1)′。检查(Lbg-1-Lcg-1)′中是否含有非零元素,若存在,则将该元素替换为Lbg-1中对应位置的元素,从而得到一个新的差值序列,即(Lbg-1-Lcg-1)。
步骤2 基于随机数和变异缩放因子的元素调整。随机产生一个与差值序列(Lbg-1-Lcg-1)相同维度的序列,其元素在[0, 1]。遍历(Lbg-1-Lcg-1)内每一个元素,若rand(·)<Fr,则保留该元素不变,否则,将对应位置的元素替换为0,得到新的序列(Lbg-1-Lcg-1)″。
步骤3 基于非零元素的更新。若(Lbg-1-Lcg-1)″中的元素为0,保持Lag-1内相应元素不变。对于非零元素,从[0, 1]中随机生成rand(·),若rand(·)≤0.5,交换Lag-1与Lcg-1相应位置上的元素,若rand(·)>0.5,则将Lag-1中对应元素随机替换为对应工序下其他并行机号。
2.5 禁忌搜索
在禁忌搜索中,应用邻域搜索对工序链OS和机器链KS分别进行探索,以最大迭代数不超过100次为终止条件,以实现全局优化并规避重复低效的搜索路径,同时增加搜索的广度与深度,步骤如下所示。
步骤1 初始化参数并获取初始解。初始化禁忌长度及禁忌表,随机选取一个X作为初始解,将其设置为当前解和最优解。
步骤2 OS邻域搜索。在OS中引入前插变换,随机产生一个位置,将该位置的元素前置到序列的起始处。
步骤3 KS邻域搜索。对KS采用后移操作,随机选取一个子序列段,并将其整体后移至序列末尾,通过此方式探索机器分配的不同组合,以寻找更优的调度方案。
步骤4 适应度评估与更新。更新工序与机器排列,根据式(26)计算新个体的适应度值,选择适应度值最高的个体作为最佳邻域解,记为fit2。最优解的适应度值记为fit1。判断fit2是否大于fit1,若是,则接受新解,并将其设置为最优解和当前解,更新禁忌表;否则,记录未产生有效更新的邻域搜索过程,并尽量避免重复此类搜索,然后继续执行搜索流程。
2.6 算法流程
算法1 IGWO算法。
输入:F, Q等生产参数和种群规模popsize, Fr等算法参数;
输出:最优解。
① t=0
② NEH启发式法和完全随机程序得到初始种群
③ while(t<最大运行时间)do
④ 根据适应度值选择领导层狼α、β和γ,其余个体为ω
⑤ 依照概率使ω与α、β和γ对OS进行交叉操作
⑥ 对ω的KS执行DE/rand/1变异操作
⑦ ∥禁忌搜索
⑧ 在OS中引入前插变换
⑨ 在KS中引入后移操作
⑩ t=算法当前运行时间
end while
输出最优解
3 实验设计与结果分析
3.1 实验设计及数据
由于目前没有可直接用于DHFGRP-MT的基准数据,拓展文献[15]得到本实验所使用的算例规模,以此对IGWO算法的性能进行验证。将其与现有的算法进行对比研究,分别为混合白鲸优化算法[16](HBWO)、混合花朵授粉算法[17](HFPA)、经典灰狼算法(GWO)以及改进飞蛾-火焰优化算法[18](IMFO)。程序编译和运行环境为MATLAB R2021a,并在CPU为AMD R5-6600H,内存为16 GB,主频为3.3 GHz的计算机上进行。
本文实验所使用的算例规模为F∈{2, 3, 4},Q∈{20, 40, 60, 80, 100, 120},E∈{3, 4, 5, 6},Kfe∈{3, 4, 5},故障机器数BK∈{1, 2, 3}。取37种算例组合,每种算例规模随机运行10次,取其平均值作为该算例规模的测试结果,因此本实验共测试了370组算例。假设pfqek～U[10, 20],te(e+1)～U[1, 5],PJfek～U[5, 10],PKfek～U[1, 3],PY～U[1, 5],BTfek～U[10, 80],RBfek～U[15, 25]。
3.2 评价指标
定义ζ1、ζ2、ζ3、ζ4为目标改进率,计算公式为
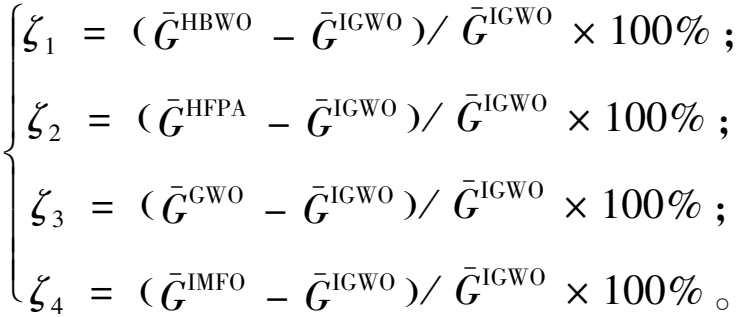
(29)
式中:
和
分别为使用算法IGWO、HBWO、HFPA、GWO和IMFO求解算例的平均目标值。
3.3 算法参数优化
根据正交试验对IGWO算法涉及的主要参数进行最佳设置,取种群规模popsize={80, 100}、跟踪模式概率pd={0.6, 0.8}、变异概率pb={0.2, 0.3}、变异缩放因子Fr={0.3, 0.5}和禁忌长度Tl={3, 5, 7},共取16种参数组合,从前述规模中选取BK=1,F=2,Q=20,E=3作为实验算例进行正交试验,对这16种参数组合进行测试,每种组合随机运行10次,取其平均值作为测试结果,将最大迭代数100次作为停止条件,据此绘制IGWO算法的平均目标值主效应图如图2所示。从图2可知,最佳的参数取值是popsize为100,pd为0.8,pb为0.2,Fr为0.5,Tl为5。
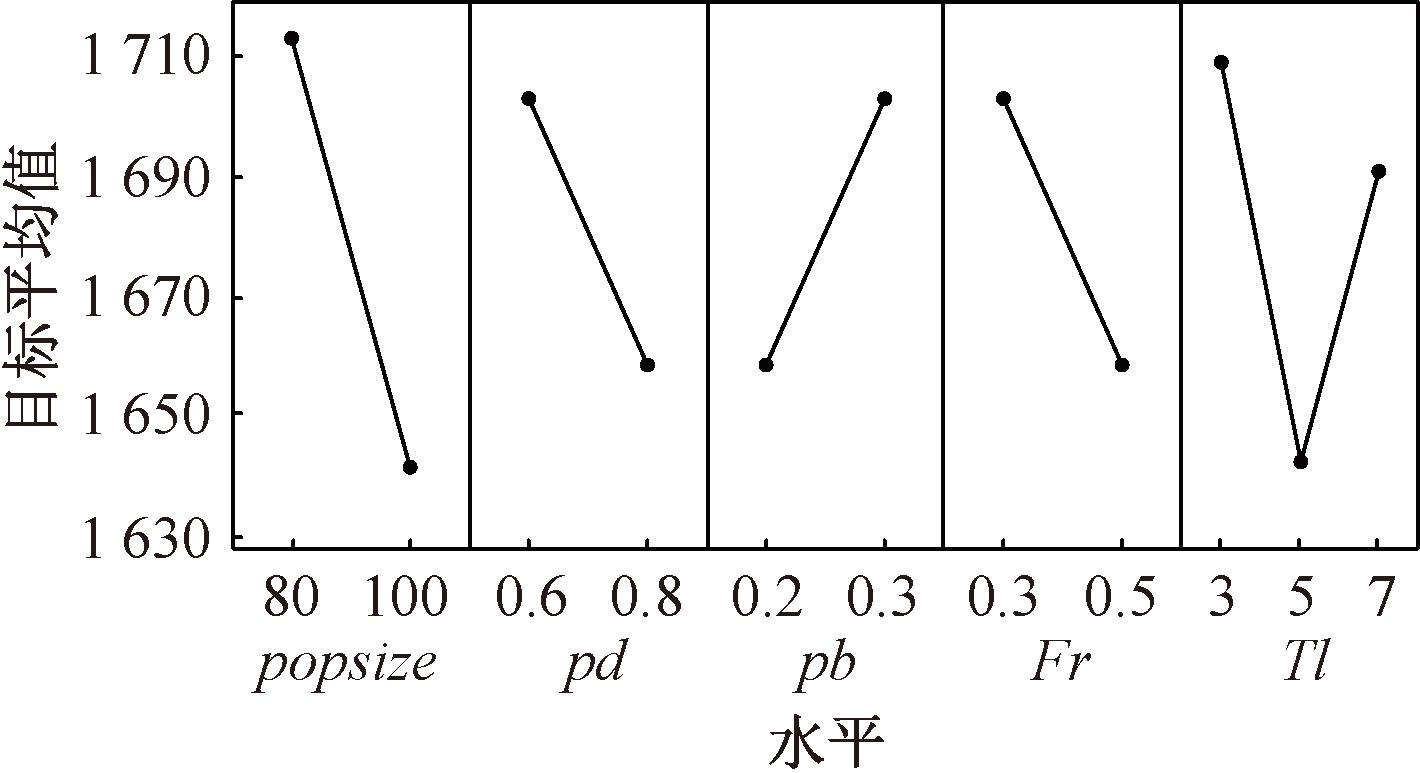
图2 主效应图
Figure 2 Main effect plot
各对比算法的关键参数也依据正交试验进行不同的取值测试,得到最佳参数设置。各算法的popsize均设为100,其他参数设置如下:HBWO中,交叉概率pj和pb均设置为0.5;HFPA中,pj为0.8,转换概率pz为0.85;IMFO中,pj为0.6,pb为0.2。
3.4 改进策略有效性分析
IGWO算法的改进主要体现在种群初始化方法和禁忌搜索。为验证二者对于算法性能的提升效果,从前述37种规模中选择4种规模,每种随机运行10次得到平均目标值,将IGWO算法及其变体算法与其他对比算法进行比较。
(1)初始化方法有效性分析。为验证所引入的基于NEH启发式法和完全随机程序的种群初始化方法的有效性,比较IGWO算法与对比算法HBWO、HFPA、GWO、IMFO在初始解质量上的差异,结果见表1。由表1可知,本文的种群初始化方法得到的初始解目标值优于其对比算法。这说明了基于NEH启发式法和完全随机程序的种群初始化方法对初始解改进的有效性。
表1 初始解目标值
Table 1 Objective values of the initial solutions
BK × F × Q × E 目标值 IGWO HBWO HFPA GWO IMFO 1 ×2 ×20 ×3 1 876. 6 1 952. 5 1 983. 3 2 003. 6 1 984. 8 2 ×3 ×40 ×4 4 285. 3 4 384. 1 4 406. 8 4 421. 6 4 314. 2 2 ×3 ×100 ×510 819. 8 10 972. 9 11 117. 7 11 361. 9 10 980. 2 3 ×4 ×120 ×614 017. 4 14 127. 8 14 351. 9 14 842. 8 14 170. 9
(2)禁忌搜索有效性分析。为验证所引入的禁忌搜索的有效性,在IGWO算法的基础上设计了一种变体算法,即不包含禁忌搜索的IGWO算法(IGWO_nT)。将IGWO算法与IGWO_nT、HBWO、HFPA、GWO和IMFO进行比较,结果见表2。由表2可知,IGWO算法获得了最佳目标值。这说明所引入的禁忌搜索能够较好地跳出局部最优解,规避重复低效的搜索路径。
表2 不同搜索策略所求目标值
Table 2 Objective values of different search strategies
B K × F × Q × E 平 均 目 标 值 I G W O H B W O H F P A G W O I M F O I G W O _ n T 1 × 2 × 2 0 × 3 1 5 3 5 . 3 1 6 4 4 . 2 1 7 1 6 . 7 1 7 0 1 . 6 1 6 9 2 . 5 1 6 6 3 . 4 2 × 3 × 4 0 × 4 3 4 6 9 . 8 3 7 6 4 . 7 3 9 5 6 . 8 4 0 0 8 . 6 3 8 9 4 . 2 3 7 9 8 . 6 2 × 3 × 1 0 0 × 5 9 0 8 2 . 4 9 5 1 3 . 9 1 0 0 1 7 . 7 1 0 0 2 1 . 9 1 0 1 2 0 . 2 9 9 2 3 . 7 3 × 4 × 1 2 0 × 6 1 1 5 2 3 . 9 1 1 9 9 8 . 2 1 2 3 5 1 . 9 1 2 2 3 2 . 8 1 2 3 5 1 . 9 1 2 0 8 4 . 1
3.5 测试结果与分析
为公平起见,以IGWO算法迭代100次且最大不超过1 800 s的运行时间作为所有算法的停止条件。对不同规模问题的测试结果见表3和表4。
表3 中小规模问题的测试结果
Table 3 Test results of small and medium-scale problems
BK F × Q × E IGWO HBWO HFPA GWO IMFO G - G - ζ1 / % G - ζ2 / % G - ζ3 / % G - ζ4 / % 运行时 间/ s 1 2 × 20 × 3 1 489. 4 1 632. 9 9. 63 1 724. 1 15. 76 1 795. 4 20. 55 1 709. 3 14. 76 95. 2 2 × 20 × 4 1 715. 7 1 893. 4 10. 36 1 968. 7 14. 75 1 997. 2 16. 41 1 874. 2 9. 24 118. 4 2 × 20 × 5 2 332. 9 2 474. 5 6. 07 2 738. 4 17. 38 2 698. 9 15. 69 2 693. 8 15. 47 185. 1 2 × 40 × 3 2 803. 7 3 201. 2 14. 18 3 287. 6 17. 26 3 098. 5 10. 51 3 199. 5 14. 12 229. 7 2 × 40 × 4 3 329. 2 3 921. 5 17. 79 4 264. 2 28. 08 4 149. 8 24. 65 4 301. 3 29. 20 290. 0 2 × 40 × 5 3 862. 4 4 286. 3 10. 98 4 451. 6 15. 25 4 353. 6 12. 72 4 273. 1 10. 63 335. 8 2 × 40 × 6 4 178. 8 4 598. 1 10. 03 4 792. 7 14. 69 4 654. 1 11. 37 4 338. 4 3. 82 355. 1 2 × 60 × 3 4 621. 1 4 899. 5 6. 02 5 022. 9 8. 69 5 198. 8 12. 50 4 986. 2 7. 90 281. 7 2 × 60 × 4 4 867. 6 5 482. 7 12. 64 5 479. 4 12. 57 5 142. 3 5. 64 5 567. 9 14. 39 304. 2 2 × 60 × 5 5 194. 3 5 890. 5 13. 40 5 834. 2 12. 32 5 687. 7 9. 50 5 902. 6 13. 64 341. 4 2 × 60 × 6 5 538. 5 6 108. 3 10. 29 6 155. 3 11. 14 6 129. 5 10. 67 6 208. 6 12. 10 402. 3 2 3 × 40 × 3 2 893. 5 3 188. 4 10. 19 3 365. 4 16. 31 3 309. 2 14. 37 3 208. 5 10. 89 210. 5 3 × 40 × 4 3 377. 0 3 797. 0 12. 44 3 966. 7 17. 46 3 948. 8 16. 93 3 857. 2 14. 22 217. 3 3 × 40 × 5 3 747. 4 4 169. 1 11. 25 4 270. 2 13. 95 4 174. 4 11. 39 4 198. 4 12. 04 338. 4 3 × 40 × 6 4 239. 1 4 601. 2 8. 54 4 788. 5 12. 96 4 587. 3 8. 21 4 476. 1 5. 59 389. 5 3 × 60 × 3 4 734. 2 5 322. 9 12. 44 5 274. 1 11. 40 5 145. 9 8. 70 5 098. 3 7. 69 417. 1 3 × 60 × 4 5 287. 9 5 714. 3 8. 06 6 089. 3 15. 16 5 511. 7 4. 23 5 625. 8 6. 39 583. 8 3 × 60 × 5 5 727. 3 6 602. 4 15. 28 6 732. 6 17. 55 6 525. 9 13. 94 6 372. 2 11. 26 671. 4 3 × 60 × 6 6 253. 8 6 827. 2 9. 17 6 972. 6 11. 49 6 867. 1 9. 81 6 693. 9 7. 04 744. 2 平均 4 010. 2 4 453. 2 10. 98 4 588. 3 14. 95 4 472. 4 12. 52 4 451. 9 11. 59 342. 7
表4 大规模问题的测试结果
Table 4 Test results of large-scale problems
BK F × Q × E IGWO HBWO HFPA GWO IMFO G - G - ζ1 / % G - ζ2 / % G - ζ3 / % G - ζ4 / % 运行时 间/ s 2 3 × 80 × 4 7 086. 5 8 193. 1 15. 62 8 229. 4 16. 13 8 211. 2 15. 87 8 235. 4 16. 21 876. 7 3 × 80 × 5 7 372. 4 8 294. 9 12. 51 8 409. 2 14. 06 8 318. 5 12. 83 8 447. 5 14. 58 1 035. 2 3 × 80 × 6 7 556. 1 8 422. 3 11. 46 8 753. 1 15. 84 8 595. 9 13. 76 8 234. 2 8. 97 1 245. 6 3 × 100 × 4 8 712. 9 9 487. 8 8. 89 9 477. 8 8. 78 9 423. 8 8. 16 9 301. 1 6. 75 1 790. 5 3 × 100 × 5 9 031. 6 9 525. 2 5. 47 9 699. 5 7. 40 10 065. 1 11. 44 9 967. 8 10. 37 1 800. 0 3 × 100 × 6 9 402. 8 10 235. 3 8. 85 10 335. 7 9. 92 10 211. 3 8. 60 10 299. 3 9. 53 1 800. 0 4 × 60 × 4 6 024. 2 6 437. 6 6. 86 6 599. 0 9. 54 6 436. 7 6. 85 6 129. 9 1. 75 1 051. 8 4 × 60 × 5 5 991. 4 6 392. 4 6. 69 6 759. 3 12. 82 6 435. 2 7. 41 6 533. 4 9. 05 1 217. 1 4 × 60 × 6 6 058. 2 6 537. 7 7. 91 6 598. 3 8. 92 6 622. 6 9. 32 6 324. 1 4. 39 1 622. 4 3 4 × 80 × 4 7 232. 3 7 726. 3 6. 83 7 765. 9 7. 38 7 926. 7 9. 60 7 742. 6 7. 06 1 255. 9 4 × 80 × 5 7 679. 7 8 160. 5 6. 26 8 326. 8 8. 43 8 195. 2 6. 71 8 211. 3 6. 92 1 318. 3 4 × 80 × 6 8 129. 1 8 713. 7 7. 19 8 966. 5 10. 30 8 512. 3 4. 71 8 531. 6 4. 95 1 390. 0 4 × 100 × 4 8 992. 0 9 321. 9 3. 67 9 433. 3 4. 91 9 938. 4 10. 52 9 547. 5 6. 18 1 638. 1 4 × 100 × 5 9 411. 6 10 134. 2 7. 68 10 192. 1 8. 29 10 012. 1 6. 38 10 129. 7 7. 63 1 800. 0 4 × 100 × 6 9 779. 8 10 398. 1 6. 32 10 488. 2 7. 24 9 984. 8 2. 10 10 633. 8 8. 73 1 800. 0 4 × 120 × 4 10 126. 3 10 748. 4 6. 14 11 237. 7 10. 98 10 537. 5 4. 06 10 625. 2 4. 93 1 800. 0 4 × 120 × 5 10 743. 9 11 232. 6 4. 55 11 121. 2 3. 51 11 267. 8 4. 88 10 963. 1 2. 04 1 800. 0 4 × 120 × 6 11 461. 9 11 901. 8 3. 84 11 966. 6 4. 40 12 013. 2 4. 81 12 045. 4 5. 09 1 800. 0 平均 8 377. 3 8 992. 4 7. 59 9 131. 1 9. 38 9 039. 3 8. 22 8 994. 6 7. 51 1 502. 3
对于中小规模问题,在平均计算时间342.7 s内,IGWO相较于HBWO、HFPA、GWO和IMFO分别改进了10.98%,14.95%,12.52%和11.59%;对于大规模问题,在平均计算时间1 502.3 s内,IGWO相较于HBWO、HFPA、GWO和IMFO分别改进了7.59%,9.38%,8.22%和7.51%。从整体上看,IGWO相较于HBWO、HFPA、GWO和IMFO分别改进了9.33%,12.24%,10.43%和9.61%。IGWO得到的目标值一致优于其他3种算法。
为了检验实验结果在统计学意义上的显著差别,根据表3和4的不同算例测试数据,使用Stata软件对ζ目标改进率进行Wilcoxon符号秩检验,在5%的显著性水平下,P值均小于0.05,由此对于ζ目标改进率指标,IGWO具有显著优势。
4 结论
本文研究了考虑机器故障和运输时间的分布式混合流水线绿色重调度问题,目标为同时最小化最大完工时间、总能耗和总延期。提出了改进灰狼优化算法以有效求解该问题。设计三链式编码和插入式贪婪解码方式,采用NEH启发式法和完全随机程序共同生成初始种群;通过模仿狼群猎食方式对工序链和机器链进行交叉与变异操作;最后,应用禁忌搜索结合多种邻域搜索方式改进解的质量。通过测试不同规模算例进行比较,结果表明了IGWO算法在可接受的时间内得到了较好的近优解,说明了其有效性。
灰狼算法的提出促进了计算机科学和生物学等多个学科的交叉融合,在实际应用中,该算法已经被证明在许多领域中都具有良好的性能。未来还可进一步扩展IGWO算法,将其应用于考虑订单取消或机器恶化时间等情况,也可以使用其他超启发式算法以求解这类问题。
[1] 高艺平, 李新宇, 单杭冠, 等. 5G技术赋能的智能离散制造车间主动调度模式[J]. 机械工程学报, 2023, 59(12): 38-46.
GAO Y P, LI X Y, SHAN H G, et al. Research on proactive scheduling theory and method enabled by 5G technology for intelligent discrete manufacuturing shop[J]. Journal of Mechanical Engineering, 2023, 59(12): 38-46.
[2] LI Y L, LI F, PAN Q K, et al. An artificial bee colony algorithm for the distributed hybrid flowshop scheduling problem[J]. Procedia Manufacturing, 2019, 39: 1158-1166.
[3] 刘欣玥, 王黎明. 数控机床超低待机状态作业车间调度节能研究[J]. 机械设计与制造, 2022(11): 183-187.
LIU X Y, WANG L M. Research on energy saving analysis on job shop scheduling in ultra-low idle state of NC machine tools[J]. Machinery Design &Manufacture, 2022(11): 183-187.
[4] 黄家文, 周昭龙, 陶涛, 等. 基于机器故障下板式定制家具混合流水车间动态调度研究[J]. 林产工业, 2023, 60(11): 66-71, 77.
HUANG J W, ZHOU Z L, TAO T, et al. Research on dynamic scheduling of hybrid flow shop for panel custom furniture based on machine fault[J]. China Forest Products Industry, 2023, 60(11): 66-71, 77.
[5] 王芊博, 张文新, 王柏琳, 等. 基于Agent的混合流水车间动态调度系统[J]. 计算机应用, 2017, 37(10): 2991-2998.
WANG Q B, ZHANG W X, WANG B L, et al. Agent-based dynamic scheduling system for hybrid flow shop[J]. Journal of Computer Applications, 2017, 37(10): 2991-2998.
[6] 苏建涛, 董绍华, 朱诗敏. 多目标混合流水车间机器故障重调度问题研究[J]. 机械工程学报, 2024, 60(4): 438-448.
SU J T, DONG S H, ZHU S M. Research on machine fault rescheduling problem of multi objective hybrid flow shop based on intelligent manufacturing[J]. Journal of Mechanical Engineering, 2024, 60(4): 438-448.
[7] 李稚, 周双牛. 基于GABSO算法的动态柔性作业车间调度问题[J]. 系统工程, 2022, 40(1): 143-151.
LI Z, ZHOU S N. Dynamic flexible job shop scheduling problem based on GABSO algorithm[J]. Systems Engineering, 2022, 40(1): 143-151.
[8] 张晓楠, 龚嘉龙, 姜帅, 等. 考虑模糊质检时间的柔性作业车间动态调度问题[J]. 计算机应用研究, 2024, 41(8): 2351-2359.
ZHANG X N, GONG J L, JIANG S, et al. Flexible job shop dynamic scheduling problem with fuzzy quality control time[J]. Application Research of Computers, 2024, 41(8): 2351-2359.
[9] 周尔民, 马畅, 刘宁. 考虑机器故障的柔性作业车间动态调度[J]. 组合机床与自动化加工技术, 2023(9): 188-192.
ZHOU E M, MA C, LIU N. Dynamic scheduling of flexible job shop considering machine failure[J]. Modular Machine Tool &Automatic Manufacturing Technique, 2023(9): 188-192.
[10] 张峰, 陈乃超, 邢海燕. 柔性车间生产资源与AGV物流资源联合优化调度[J]. 现代制造工程, 2023(10): 1-7.
ZHANG F, CHEN N C, XING H Y. Joint optimal scheduling of flexible workshop production resources and AGV logistics resources[J]. Modern Manufacturing Engineering, 2023(10): 1-7.
[11] 耿凯峰, 叶春明. 考虑多时间因素的绿色可重入混合流水车间调度问题[J]. 计算机集成制造系统, 2023, 29(1): 75-90.
GENG K F, YE C M. Green re-entrant hybrid flow shop scheduling problem considering multiple time factors[J]. Computer Integrated Manufacturing Systems, 2023, 29(1): 75-90.
[12] 唐艺军, 杜纪浩, 李雪. 考虑运输时间的混合流水车间绿色生产调度[J]. 现代制造工程, 2024(5): 23-30.
TANG Y J, DU J H, LI X. Green production scheduling of hybrid flow shop considering transportation time[J]. Modern Manufacturing Engineering, 2024(5): 23-30.
[13] 温廷新, 关婷誉. 考虑能耗和运输的有限缓冲区混合流水车间调度[J]. 系统仿真学报, 2024, 36(6): 1344-1358.
WEN T X, GUAN T Y. Hybrid flow shop scheduling with limited buffers considering energy consumption and transportation[J]. Journal of System Simulation, 2024, 36(6): 1344-1358.
[14] 裴小兵, 李依臻. 应用改进混合进化算法求解零空闲置换流水车间调度问题[J]. 运筹与管理, 2020, 29(11): 204-212.
PEI X B, LI Y Z. Improved hybrid evolutionary algorithm for solving no-idle permutation flow shop scheduling problem[J]. Operations Research and Management Science, 2020, 29(11): 204-212.
[15] 张国辉, 陆熙熙, 胡一凡, 等. 基于改进帝国竞争算法的柔性作业车间机器故障重调度[J]. 计算机应用, 2021, 41(8): 2242-2248.
ZHANG G H, LU X X, HU Y F, et al. Machine breakdown rescheduling of flexible job shop based on improved imperialist competitive algorithm[J]. Journal of Computer Applications, 2021, 41(8): 2242-2248.
[16] 孟冠军, 黄江涛, 魏亚博. 混合白鲸优化算法求解柔性作业车间调度问题[J]. 计算机工程与应用, 2024, 60(12): 325-333.
MENG G J, HUANG J T, WEI Y B. Hybrid beluga whale optimization algorithm for flexible job shop scheduling problem[J]. Computer Engineering and Applications, 2024, 60(12): 325-333.
[17] 唐丽君, 彭石燕. 混合花朵授粉算法在作业车间调度中的应用[J]. 工程数学学报, 2022, 39(6): 997-1004.
TANG L J, PENG S Y. Hybrid flower pollination algorithm for job shop scheduling problem[J]. Chinese Journal of Engineering Mathematics, 2022, 39(6): 997-1004.
[18] XU F, TANG H T, XUN Q N, et al. Research on green reentrant hybrid flow shop scheduling problem based on improved moth-flame optimization algorithm[J]. Processes, 2022, 10(12): 2475.