钢桥的生产方式是典型的定制化生产。作为钢桥的基本组成单元,板单元的生产进度直接制约了桥梁工程的整体建设周期。钢桥板单元生产调度问题本质上属于柔性作业车间调度(flexible job-shop scheduling problem,FJSP)的扩展问题。与普通FJSP相比,钢桥板单元的生产调度更加复杂。虽然不同节段板单元的结构和工艺路线以及加工设备都比较相似,但由于形状和尺寸均不相同,且尺寸规模较大,在同一加工设备上使用的夹具和加工方法无法完全相同;而且作业切换需要使用龙门架或起重机等大型吊装设备,耗费的作业切换时间较长且与作业顺序密切相关;此外,由于加工设备体积庞大,所以通常分布在不同车间或不同区域,物料转运需要借助重型运输设备。因此,作业切换时间和运输时间是生产调度模型中不可忽视的重要因素。
关于钢桥生产调度的相关研究较少,窦金梅[1]提出一种基于工件交叉的改进遗传算法用于求解钢桥单元生产的作业车间问题;Xie等[2]提出基于优势规则的遗传算法用于求解钢桥的批次准时生产调度问题。在其他领域关于作业切换时间和运输时间的FJSP问题的研究中,Kurniady等[3]利用启发式算法求解考虑顺序相关作业切换时间的流水车间问题;Huang等[4]、Zhang等[5]和Li等[6]分别使用改进蚁群算法和改进的Jaya算法求解考虑运输时间和调整时间的柔性作业车间调度问题;Li等[7]使用帝国竞争算法求解具有运输和顺序相关准备时间的节能柔性作业车间调度。
近年来,成组调度也得到了国内外学者的关注,Yuan等[8]提出一种离散差分进化算法求解具有顺序依赖准备时间和运输时间的流水车间成组调度问题;Wang等[9]提出两阶段迭代贪婪算法以求解分布式流水车间成组调度问题;Hosseinzadeh等[10]和Behjat等[11]研究了考虑顺序相关准备时间的成组调度问题。
在上述研究成果的基础上,本文进一步引入成组调度技术,建立了考虑作业切换时间和运输时间的分布式柔性作业车间成组调度(distributed flexible job-shop group scheduling problem with setup &transportation time,DFJGSPST)模型。本文将成组思想与传统遗传算法的编码思想融合,在算法编码中添加成组技术中分组部分,在混合遗传禁忌搜索(genetic algorithm with tabu search,GATS)算法基础上引入短期记忆策略,提出了一种基于三层编码的记忆混合遗传禁忌搜索算法(memory-GATS,MGATS),并通过与其他智能优化算法进行对比,验证算法的有效性和优越性。
1 问题描述
本文以某钢桥标准节段作为研究对象,其结构如图1所示。该节段由顶板、底板、腹板、横隔板和翼缘板等单元组成,球扁钢和U肋板是其中的辅助构件[12]。
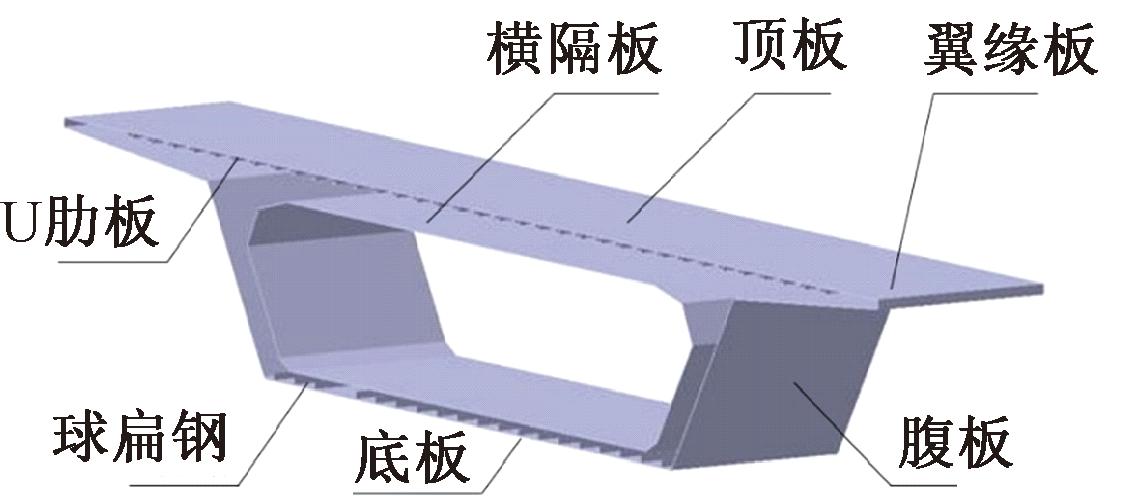
图1 标准节段三维模型
Figure 1 Standard segment 3D model
DFJGSPST问题的描述如下。
(1)根据工件的相似性,t个工件被划分为g个工件组。其中,不同工件组工件的工艺路线均不相同;同一个工件组内工件工艺路线均相同,但工件组内不同工件的相同工序的具体加工参数会有所区别,在调度上主要体现在加工时间不同。
(2)加工机器分布在Q个作业车间中,同一车间内的机器间运输时间短于不同作业车间机器间运输时间。
(3)每道工序有一台或多台并行机器可供选择。
(4)安排在同一机器上加工的不同工件存在一定的作业切换时间,且该切换时间具有顺序相关性。
(5)工件相邻工序之间的传递存在一定的运输时间。
(6)优化目标为最小化所有工件的最大完工时间。
DFJGSPST问题需要解决3个子问题,即加工机器的分配、各机器的工序排序、同一工件组内工件的加工顺序。同时应满足以下假设:①机器加工每道工序的时间确定;②同一机器同一时间只能加工一道工序;③每道工序一旦开始,加工过程不能中断;④工件上一道工序结束后才可以进行工件运输;⑤工件运输到达机器后才可以进行工序加工;⑥机器起始时间都为0;⑦机器间运输时间确定;⑧机器只有加工完当前工序,才可以加工下一道工序;⑨同一机器加工不同的工件需要考虑作业切换时间;⑩同一工件组内的工件具有相同的工序顺序和可选加工机器; 工件的加工批量为1。
工件的加工批量为1。
2 数学模型
2.1 参数定义
对DFJGSPST数学模型涉及的参数进行定义,如表1所示。
表1 参数定义
Table 1 Parameter definition

参数含义g工件组数量m机器数量n(i)工件组Gi中的工件种类数量t工件总数量,t=∑gi=1n(i)Gi工件组编号,i∈[1,g]Je工件编号,e∈[1,t]Ml机器编号,l∈[1,m]p(i)工件组Gi的工序数量pall全部工件组的工序数量总和,pall=∑gi=1p(i)T(i,e,k,l)工件组Gi中工件Je的第k道工序在机器Ml上的加工所需时间CT(e1,e2,l)工件Je1与工件Je2在机器Ml上的作业切换时间TT(l1,l2)工件从机器Ml1运输到机器Ml2的运输时间O(i,k)工件组Gi的第k道工序,k∈[1,p(i)]F(i)工件组Gi中工件编号集合r(i,e)工件Je在工件组Gi中的位置序号,r(i,e)∈[1,n(i)]u(i,k,l)工件组Gi的第k道工序在机器Ml上的作业序号ST(i,e,k,l)工件组Gi中工件Je的第k道工序在机器Ml上加工的开始时间ET(i,e,k,l)工件组Gi中工件Je的第k道工序在机器Ml上加工的结束时间x(i,k,l)决策变量,工件组Gi的第k道工序在机器Ml上加工时为1,否则为0
2.2 目标函数及约束条件
钢桥板单元生产是多品种小批量生产模式,要求交期时间短,因此钢桥板单元生产DFJGSPST以最小化最大完工时间为目标,目标函数为
min f=min ET max=min{max ET(i.e.k,l)}。
(1)
根据柔性作业车间调度和成组技术,构建约束条件如下。
(1)工序约束。工件的后一道工序开始加工时间必须在前一道工序结束运输到位之后:
ST(i,e,k+1,l2)≥ET(i,e,k,l1)+TT(l1,l2),∀i∈[1,g],
Je∈F(i),k∈[1,p(i)-1],
x(i,k,l1)∪x(i,k+1,l2)=1。
(2)
(2)成组约束。同一工件组中在同一工序加工时,后一位置工件的开始加工时间必须在前一位置工件加工结束后:
ST(i,e2,k,l)≥ET(i,e1,k,l)+CT(e1,e2,l),∀i∈[1,g],
Je1∈F(i),Je2∈F(i),r(i,e2)>r(i,e1),x(i,k,l)=1。
(3)
(3)顺序约束。后一分组的第一个工件开始加时间必须在前一分组的最后一个工件加工结束后:
ST(i2,e2,k2,l)≥ET(i1,e1,k1,l)+CT(e1,e2,l),∀i1∈[1,g],
i2∈[1,g],Je1∈F(i1),Je2∈F(i2),
r(i1,e1)=n(i1),r(i2,e2)=1,u(i2,k2,l)>
u(i1,k1,l),x(i1,k1,l)∪x(i2,k2,l)=1。
(4)
(4)机器约束。工件组的工序同一时间只能选择一个机器加工:
(5)
3 基于三层编码的记忆混合遗传禁忌搜索算法
DFJGSPST问题是一种多约束的复杂调度问题,而传统的GATS算法通常使用一维线性编码方式,且后期容易陷入局部最优。因此本文提出一种基于三层编码的记忆混合遗传禁忌搜索算法MGATS求解DFJGSPST问题。对禁忌搜索条件进行改进,记忆每次迭代的最优解和最优解无变化代数,判断其是否陷入局部最优,并对当前最优解进行禁忌搜索,禁忌搜索结果替换当前种群的最劣解,通过这种改进方式可以在保持GATS算法搜索能力的前提下,减少重复搜索,加快算法求解时间。MGATS算法流程如图2所示。
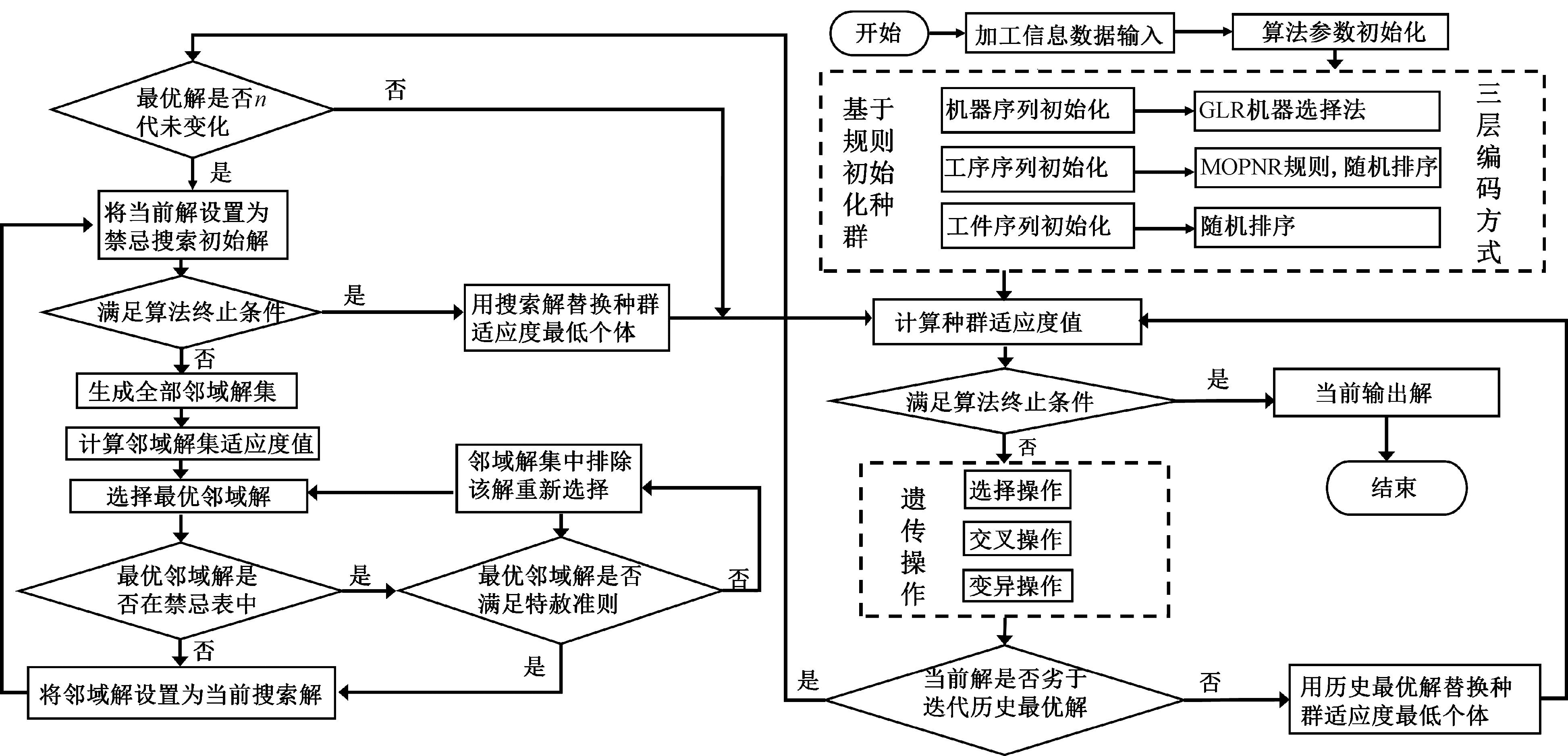
图2 MGATS算法流程
Figure 2 Algorithm flow of MGATS
3.1 染色体编码与解码
3.1.1 三层编码方案
如图3所示,本文采用三层编码方式,染色体由3部分组成:机器选择序列(简称机器序列)、工序排序序列(简称工序序列)和工件组内工件排序序列(简称工件序列)。
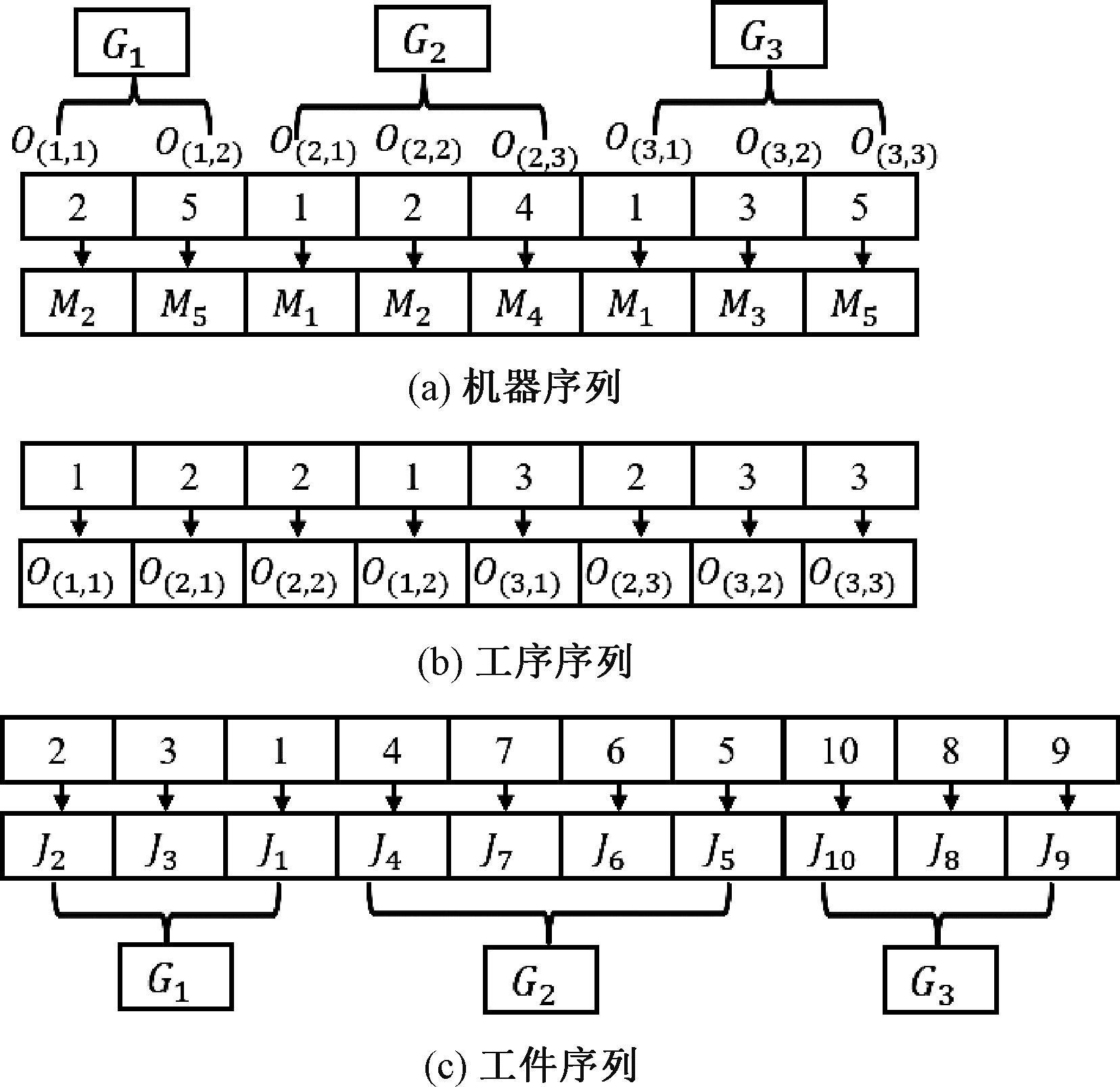
图3 染色体编码示意图
Figure 3 Schematic diagram of chromosome encoding
机器序列分为3个子段,表示工件组中工序选择加工机器的过程,以第一段为例,其含义为G1工件组的工序1选择机器2加工,工序2选择机器5加工。工序序列表示加工顺序为O(1,1)→O(2,1)→O(2,2)→O(1,2)→O(3,1)→O(2,3)→O(3,2)→O(3,3)。工件序列也分为3个子段,表示工件组中组内工件的加工顺序,以第一段为例,其含义为工件组G1在同道工序下组内工件加工排序为J2→J3→J1。
3.1.2 三层解码方案
可将图3所示的机器序列、工序序列和工件序列信息按图4所示的染色体解码示意图解码为各机器加工信息。
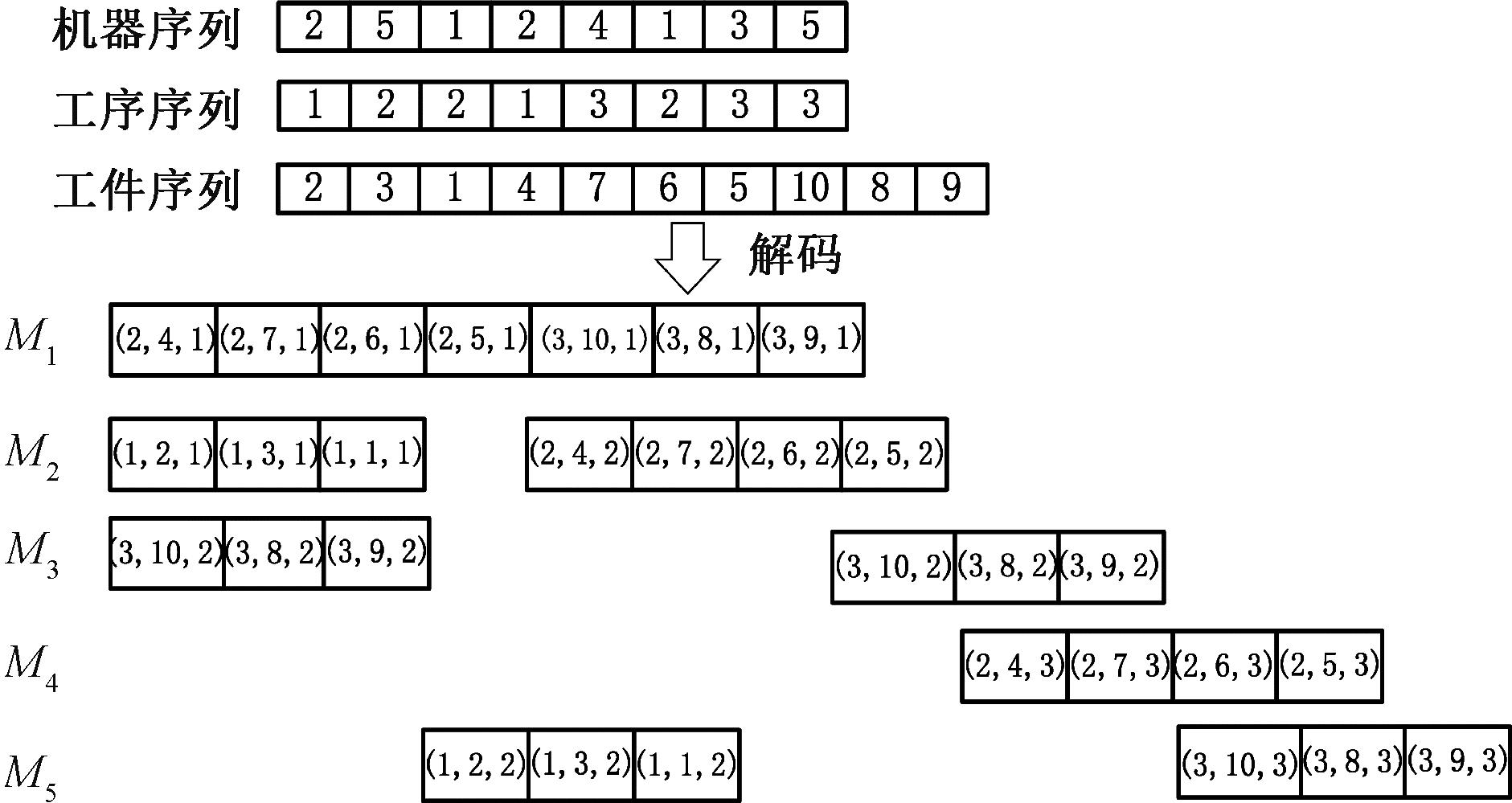
图4 染色体解码示意图
Figure 4 Schematic diagram of chromosome decoding
3.2 算法实现
3.2.1 基于规则的种群初始化
遗传算法在理论上可以进行全局搜索,其收敛结果不依赖于初始解,但随机生成的初始解大概率是劣质解,这要求算法在求解过程中需要增加迭代次数或增大种群规模,使得算法求解效率降低。针对柔性作业车间成组调度问题,本文采用两种种群初始化方法:GLR机器选择法[13]和MOPNR规则[14]。
GLR机器选择法包含全局选择(global selection,GS)、局部选择[15](local selection,LS)和随机选择(random selection,RS)这3种机器选择法,用于机器序列的初始化。本文中GS、LS与RS在初始化机器序列时比例设为3∶3∶4。
MOPNR(most operation remaining)规则优先安排待加工工序数最多的工件,是用于非流水型排序问题的优先规则。本文采用MOPNR规则和随机排序对工序序列进行初始化,两者比例为2∶3,同时使用随机排序对工件序列进行初始化。
3.2.2 算法主要操作
(1)选择操作。本文采用轮盘赌选择方法,按照个体适应度值进行选择。最大完工时间越短,适应度值越高。个体适应度函数为
(6)
(2)交叉操作。本文针对不同序列采用不同的交叉方式:对机器序列采用多点交叉[16](multi-point crossover);对工序序列采用POX[17](precedence order-based crossover)交叉;对工件序列采用工件组交叉。各序列交叉方式如图5所示,其中着色位置为基因交叉位置。
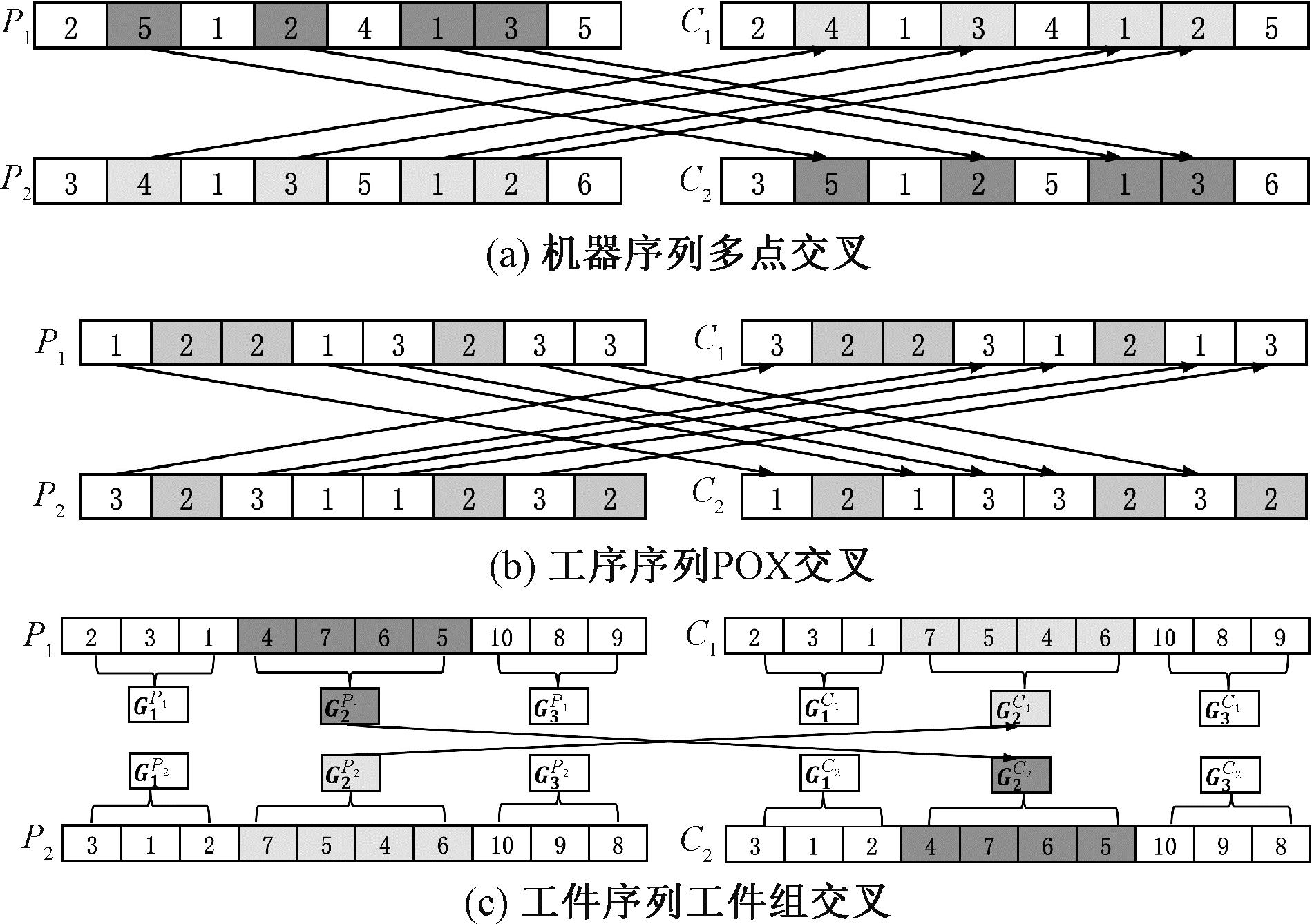
图5 各序列交叉方式
Figure 5 Crossover mode of each sequence
(3)变异操作。本文针对不同序列的结构特点采用不同的变异操作。
机器序列变异操作:机器序列中随机选择部分基因位,根据每个被选基因位代表的工件组工序,在其可选机器集合中随机选择与原机器不同的机器,若可选机器集合为单机器集合,则取消对该基因位的变异操作。
工序序列变异操作:采用两点互换变异,即随机选择工序序列的两个基因位,交换其基因位数值。
工件序列变异操作:随机选择需要变异操作的工件组,重新生成被选工件组的组内工件排序序列。
(4)禁忌搜索操作。在GATS中,禁忌表作为内部记忆策略主要影响禁忌搜索内部操作,但禁忌搜索本身缺乏外部记忆方式,易在收敛阶段重复搜索。为此,本文提出一种宏观记忆方式,在遗传操作结束后,若当前最优解劣于历史最优解,且连续若干代未改进最优解,则触发禁忌搜索,进行记忆操作。通过外部记忆方式和内部记忆策略的结合,有效减少重复搜索,融合了遗传算法与禁忌搜索的优势。为确保操作的可行性,邻域解生成基于工序序列结构,生成策略如图6所示。在固定机器与工件序列的前提下,从左至右依次取出工序序列中一个基因,随机插入至新位置,生成与工序总数相等的邻域解。
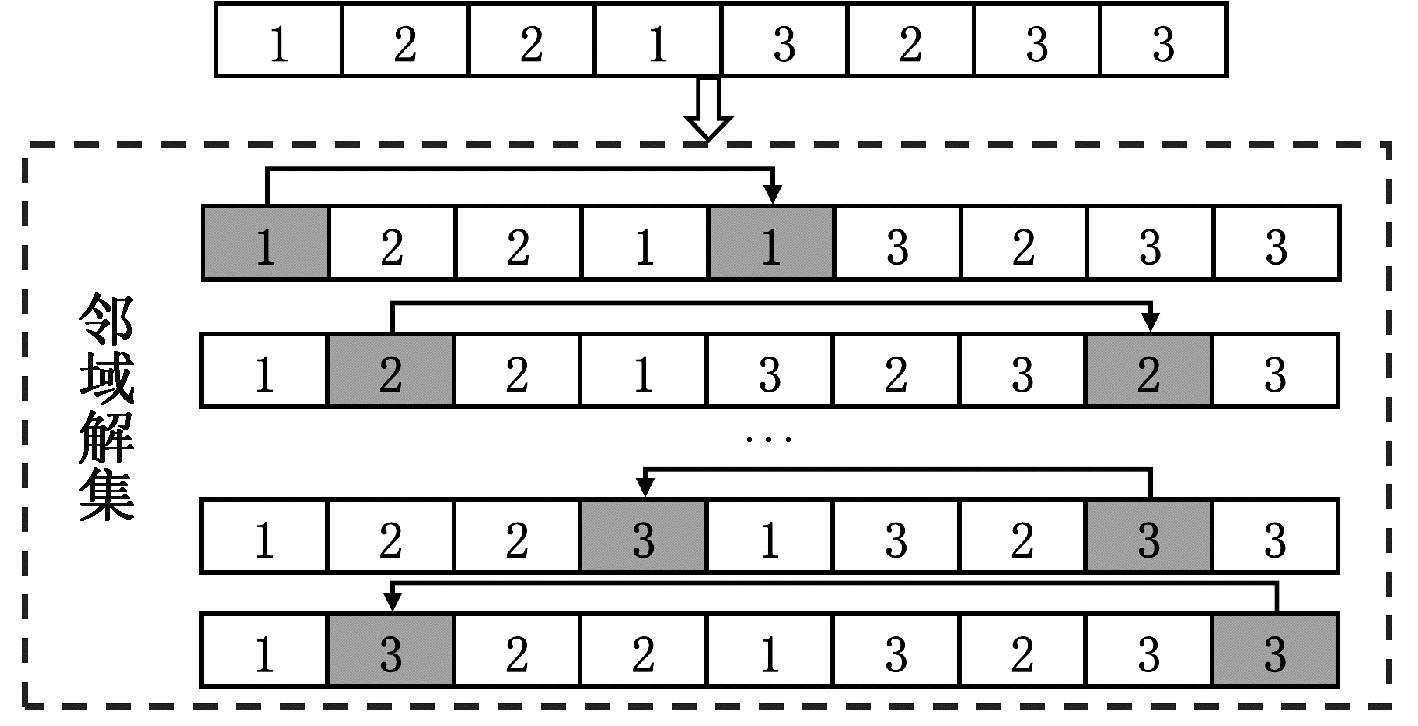
图6 工序序列邻域解生成策略
Figure 6 Strategy of generating neighborhood solutions for sequence of processes
本文采用短期记忆策略(short-term memory strategy,SMS)作为禁忌搜索的禁忌策略[18]。SMS的禁忌表使用一个pall×pall矩阵表示,禁忌表的更新模式是先进先出。当初始解的最优邻域解非禁忌时,将此邻域解设置为当前解,并将其加入禁忌标准;当初始解的最优邻域解已经在禁忌表中,但满足特赦准则时,则将其设置为当前解;当初始解的最优邻域解已经在禁忌表中,但不满足特赦准则时,则它是一个禁忌解,需要重新求得非禁忌最优解;当出现初始解的全部邻域解皆为不满足特赦准则的禁忌解时,则从邻域解集中随机选择一个邻域解作为当前解。
4 算例分析
以某钢桥标准节段板单元生产为例,分别采用GA、GATS和本文提出的MGATS这3种算法进行求解,以验证本文建立的数学模型及求解算法的有效性和实用性。
4.1 加工信息
本实例考虑加工10个工件,分4种板单元组,分别为顶板单元组G1、底板单元组G2、腹板单元组G3和横隔板单元组G4。加工机器包括2台数控下料设备M1、M2,1台折弯机M3,2台铣床M4、M5,2台加劲肋定位组装机M6、M7,1台单元组装反变形胎架M8,1台数控钻床M9,2台船型焊接胎架及半自动焊接机M10、M11,1台焊接机M12,1台探伤仪器M13和2台矫正设备M14、M15。
表2和表3分别表示工件组工序可选机器和各工件工序加工时间。同组工件间作业切换时间为1 min;不同组工件间作业切换时间为10 min;当无前序工件时,作业切换时间为作业准备时间5 min。此时间适用于全部加工机器。在表4中,同车间分布的机器间运输时间较短,而跨车间分布的机器间运输时间较长。
表2 工件组工序可选机器
Table 2 Optional machines for work group processes

工件组工序可选机器O1O2O3O4O5O6O7O8G1M1(M2)M9M4(M5)M6(M7)M10(M11)M13M14(M15)G2M1(M2)M4(M5)M3M6(M7)M10(M11)M13M14(M15)M9G3M1(M2)M8M12M13M14(M15)M4(M5)M9G4M1(M2)M4(M5)M6(M7)M10(M11)M13M14(M15)
表3 各工件工序加工时间
Table 3 Processing time of each unit
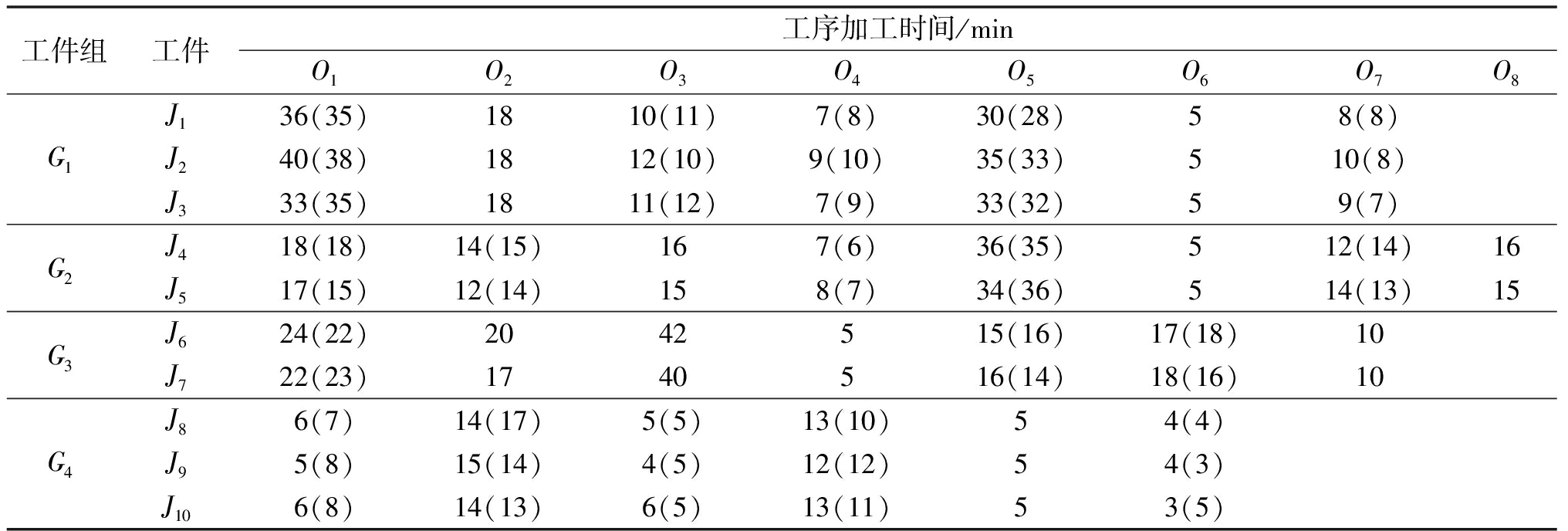
工件组工件工序加工时间/minO1O2O3O4O5O6O7O8J136(35)1810(11)7(8)30(28)58(8)G1J240(38)1812(10)9(10)35(33)510(8)J333(35)1811(12)7(9)33(32)59(7)G2J418(18)14(15)167(6)36(35)512(14)16J517(15)12(14)158(7)34(36)514(13)15G3J624(22)2042515(16)17(18)10J722(23)1740516(14)18(16)10J86(7)14(17)5(5)13(10)54(4)G4J95(8)15(14)4(5)12(12)54(3)J106(8)14(13)6(5)13(11)53(5)
表4 各加工机器间的运输时间
Table 4 Transportation time between processing machines
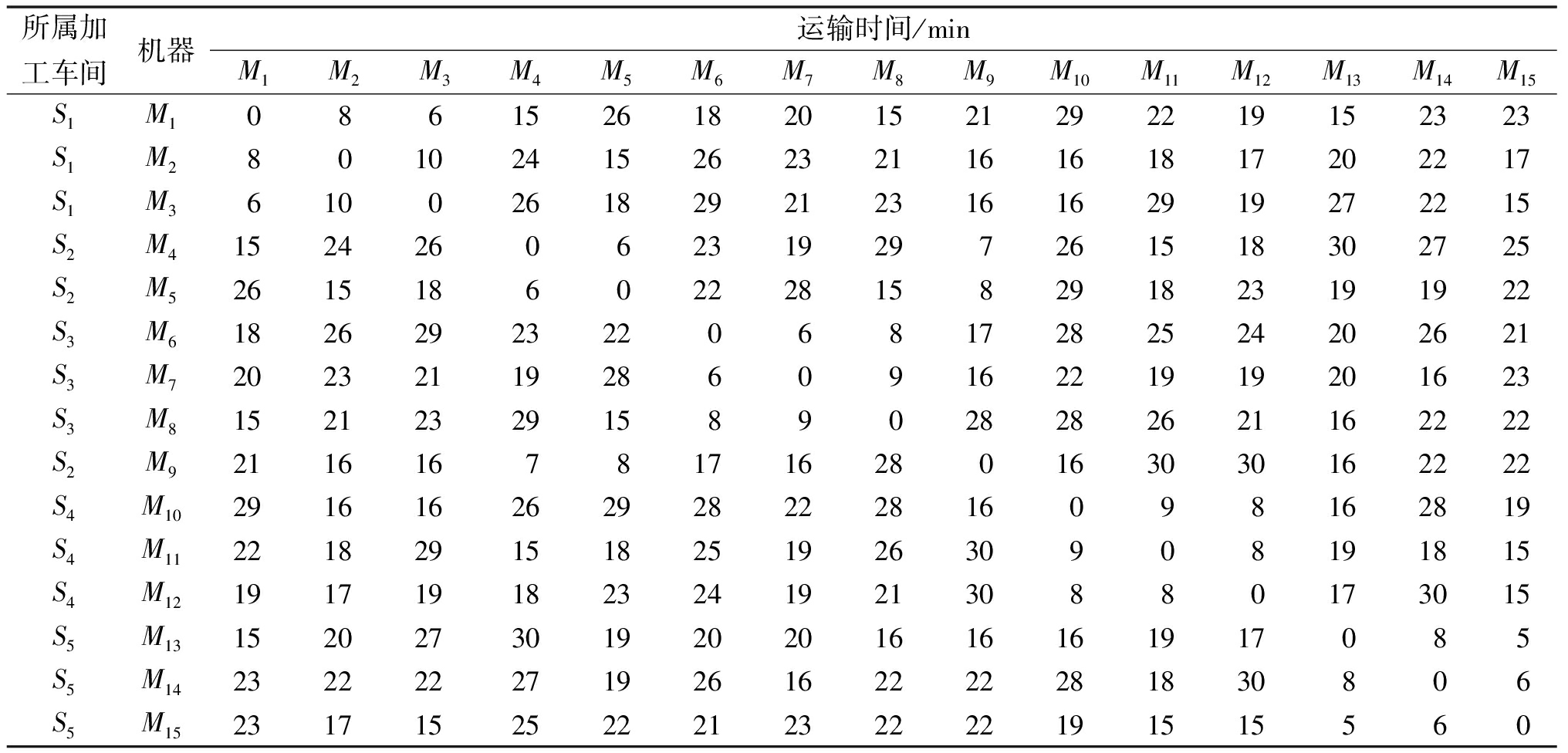
所属加工车间机器运输时间/minM1M2M3M4M5M6M7M8M9M10M11M12M13M14M15S1M1086152618201521292219152323S1M28010241526232116161817202217S1M36100261829212316162919272215S2M4152426062319297261518302725S2M5261518602228158291823191922S3M6182629232206817282524202621S3M7202321192860916221919201623S3M8152123291589028282621162222S2M9211616781716280163030162222S4M10291616262928222816098162819S4M11221829151825192630908191815S4M12191719182324192130880173015S5M13152027301920201616161917085S5M14232222271926162222281830806S5M15231715252221232222191515560
4.2 实验结果处理与分析
本文利用MATLAB R2018a编写算法程序,测试环境为CPU Intel i5-7300HQ 2.50 GHz,运行内存16.0 GB,硬盘128 GB,显卡NVIDIA GeForce GTX 1050 2 GB。由于FJSP问题属于NP难问题[19],因此其扩展问题DFJGSPST也同样属于NP难问题。本文使用的算法为元启发式算法,算法求解时无法保证得到最优解,因此采用相对百分比差异RPD[20]和成功率SR[21]作为算法的性能评价指标,RPD的计算公式为
(7)
式中:ci为算法i得到的最优目标值;cbest为所有算法中的最优目标值。RPD值越低,表示目标值越接近最优值,性能越好。SR表示同一算法实验中得到最优解的实验数量与总实验数量的比值。SR值越大,表示算法成功率越高。算法的参数取值如下:最大遗传代数为100;种群规模为100;代沟为0.9;交叉率为0.8;变异率为0.1;禁忌搜索迭代次数为50;禁忌长度为28;独立求解次数为20。
4.2.1 参数敏感性分析
最大无改进代数限制(maxr)是MGATS优化算法中的关键控制变量,其作用在于设定阈值。当算法的最优解在连续若干代内未发生改进时,输出当前结果作为最优解。在上述的测试环境下,对算法进行参数敏感性分析。选择线性递增的5,10,15,20作为参数maxr的候选取值,每种取值均运行15次。当maxr取值为5时,最小完工时间的平均值和方差均为最小,因此maxr取值为5。
4.2.2 消融实验
在4.2节的测试环境下对算法进行消融实验。设置3种不同的实验配置:交叉、交叉+变异和交叉+变异+禁忌搜索。每组运行10次后取平均值,最终交叉的RPD均值为3.86%;交叉+变异组合的RPD均值为3.36%;交叉+变异+禁忌搜索组合的RPD均值为2.15%。由结果可知,在所有策略组合中,交叉+变异+禁忌搜索组合在RPD均值上表现最佳,相比仅使用交叉策略减小了1.71百分点,相比交叉+变异组合减小了1.21百分点,证明了交叉、变异和禁忌搜索这3种策略的有效性。
4.2.3 结果分析
根据加工信息,建立了钢桥板单元生产DFJGSPST模型,分别采用GA、GATS和本文提出的MGATS这3种算法进行求解,每种算法独立求解20次。所有参与对比的算法均采用与4.2节相同的参数配置,maxr取值为5,运行结果如表5所示。
表5 3种算法的测试结果
Table 5 Test results of 3 algorithms
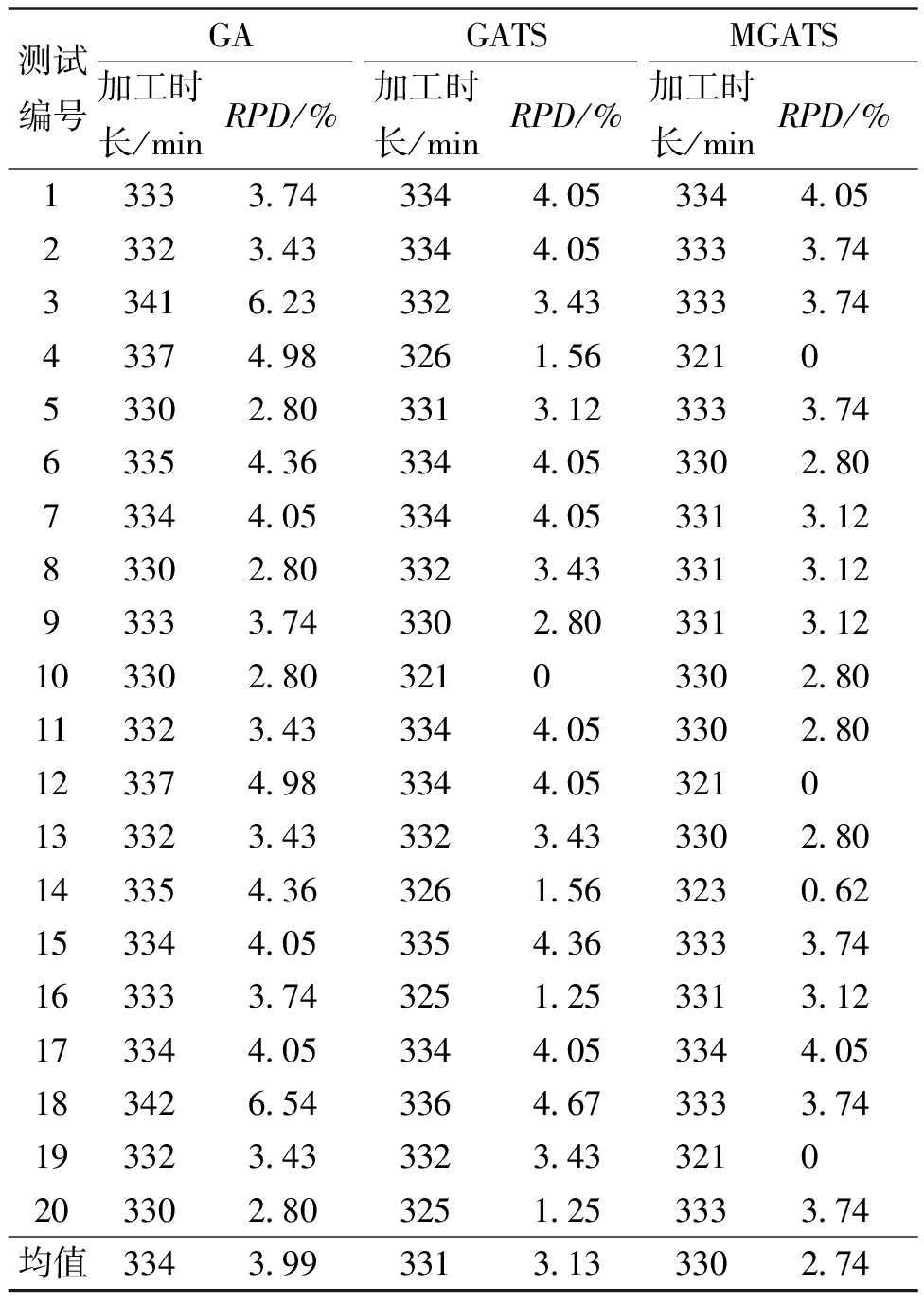
测试编号GAGATSMGATS加工时长/minRPD/%加工时长/minRPD/%加工时长/minRPD/%13333.743344.053344.0523323.433344.053333.7433416.233323.433333.7443374.983261.56321053302.803313.123333.7463354.363344.053302.8073344.053344.053313.1283302.803323.433313.1293333.743302.803313.12103302.8032103302.80113323.433344.053302.80123374.983344.053210133323.433323.433302.80143354.363261.563230.62153344.053354.363333.74163333.743251.253313.12173344.053344.053344.05183426.543364.673333.74193323.433323.433210203302.803251.253333.74均值3343.993313.133302.74
由表5可知,3种对比算法中,MGATS求解出的加工时长的RPD均值最小为2.74%,比GA的RPD均值减小了1.25百分点,比GATS减小了0.39百分点,所以MGATS有更高的算法稳定性。经过计算,GA的SR值为0,表明该算法在独立实验中未达到最优解,而MGATS的SR值为0.15,高于GA的0与GATS的0.05。因此,MGATS具有更高的成功率。
5 结论
针对钢桥板单元生产调度问题,考虑了板单元实际加工中出现的工件在机器间的运输时间,以及工件组间和工件组内顺序相关的作业切换时间,建立了钢桥板单元生产中考虑顺序相关作业切换和运输时间的分布式柔性作业车间成组调度模型。提出一种基于三层染色体编码,以遗传算法为主体,引入种群初始优化、禁忌邻域搜索和记忆策略的混合求解算法。主要结论如下。
(1)建立的数学模型考虑了运输时间、顺序相关作业切换时间、加工设备异地分布和柔性作业车间等因素,与钢桥板单元的实际加工更加贴近。
(2)引入成组技术能有效减少生产准备时间,可为实际的钢桥精细化生产作业提供理论参考。
(3)提出的MGATS求解算法与遗传算法和混合遗传禁忌搜索算法对比结果表明,MGATS加工时长的RPD均值以及SR值均为最优,证明了本文算法具有更好的求解性能。
(4)本文提供的算例为10个板单元工件和15台机器。经实验证明,该算法对求解更大规模算例仍然有效。
[1] 窦金梅.基于遗传算法的钢桥单元制造车间生产优化调度[D].上海:上海交通大学,2013.DOU J M.Optimization of production scheduling in job shop for steel bridge panel fabrication based on genetic algorithm[D].Shanghai:Shanghai Jiao Tong University,2013.
[2] XIE Y,WANG H W,LIU G,et al.Just-in-time precast production scheduling using dominance rule-based genetic algorithm[J].IEEE Transactions on Neural Networks and Learning Systems,2023,34(9):5283-5297.
[3] KURNIADY D,DENIH A,VAGABOV M,et al.Modeling a flexible flow shop scheduling problem without unemployment by considering sequence-dependent preparation times and solving it with a meta-heuristic algorithm[J].Industrial Engineering &Management Systems,2022,21(2):291-302.
[4] HUANG X B,YANG L X.A hybrid genetic algorithm for multi-objective flexible job shop scheduling problem considering transportation time[J].International Journal of Intelligent Computing and Cybernetics,2019,12 (2):154-174.
[5] ZHANG G H,HU Y F,SUN J H,et al.An improved genetic algorithm for the flexible job shop scheduling problem with multiple time constraints[J].Swarm and Evolutionary Computation,2020,54:100664.
[6] LI J Q,DENG J W,LI C Y,et al.An improved Jaya algorithm for solving the flexible job shop scheduling problem with transportation and setup times[J].Knowledge-Based Systems,2020,200:106032.
[7] LI M,LEI D M.An imperialist competitive algorithm with feedback for energy-efficient flexible job shop scheduling with transportation and sequence-dependent setup times[J].Engineering Applications of Artificial Intelligence,2021,103:104307.
[8] YUAN S P,LI T K,WANG B L.A discrete differential evolution algorithm for flow shop group scheduling problem with sequence-dependent setup and transportation times[J].Journal of Intelligent Manufacturing,2021,32(2):427-439.
[9] WANG Z Y,PAN Q K,GAO L,et al.An effective two-stage iterated greedy algorithm to minimize total tardiness for the distributed flowshop group scheduling problem[J].Swarm and Evolutionary Computation,2022,74:101143.
[10] HOSSEINZADEH M R,HEYDARI M,MAHDAVI MAZDEH M.Mathematical modeling and two metaheuristic algorithms for integrated process planning and group scheduling with sequence-dependent setup time[J].Operational Research,2022,22(5):5055-5105.
[11] BEHJAT S,SALMASI N.Total completion time minimisation of no-wait flowshop group scheduling problem with sequence dependent setup times[J].European Journal of Industrial Engineering,2017,11(1):22-48.
[12] 周文博,许凯峰,杨立群,等.大跨径自锚式悬索桥钢箱梁制造技术[J].公路交通科技,2021,38(增刊1):96-100.ZHOU W B,XU K F,YANG L Q,et al.Manufacturing technology of steel box girder of long-span self-anchored suspension bridge[J].Journal of Highway and Transportation Research and Development,2021,38 ( S1 ):96-100.
[13] GU X L,HUANG M,LIANG X.A discrete particle swarm optimization algorithm with adaptive inertia weight for solving multiobjective flexible job-shop scheduling problem[J].IEEE Access,2020,8:33125-33136.
[14] LU M S,ROMANOWSKI R.Multicontextual dispatching rules for job shops with dynamic job arrival[J].The International Journal of Advanced Manufacturing Technology,2013,67(1):19-33.
[15] LI B,XIA X W.A self-adjusting search domain method-based genetic algorithm for solving flexible job shop scheduling problem[J].Computational Intelligence and Neuroscience,2022,2022(1):4212556.
[16] 李长云,谷鹏飞,林多.基于改进遗传算法的多目标柔性作业调度研究[J].制造技术与机床,2022(5):47-52.LI C Y,GU P F,LIN D.Research on multi-objective flexible job scheduling based on improved genetic algorithm[J].Manufacturing Technology &Machine Tool,2022(5):47-52.
[17] 张超勇,饶运清,刘向军,等.基于POX交叉的遗传算法求解Job-Shop调度问题[J].中国机械工程,2004,15(23):2149-2153.ZHANG C Y,RAO Y Q,LIU X J,et al.An improved genetic algorithm for the job shop scheduling problem[J].China Mechanical Engineering,2004,15(23):2149-2153.
[18] XU W X,HU Y W,LUO W,et al.A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission[J].Computers &Industrial Engineering,2021,157:107318.
[19] ![]() J,FINKE G,HAUPT R,et al.New trends in machine scheduling[J].European Journal of Operational Research,1988,37(3):303-317.
J,FINKE G,HAUPT R,et al.New trends in machine scheduling[J].European Journal of Operational Research,1988,37(3):303-317.
[20] WANG B L,HUANG K,LI T K.Permutation flowshop scheduling with time lag constraints and makespan criterion[J].Computers &Industrial Engineering,2018,120:1-14.
[21] 袁帅鹏,李铁克,王柏琳.无关并行机类型混合流水车间成组调度问题的改进候鸟优化算法[J].计算机集成制造系统,2022,28(12):3912-3922.YUAN S P,LI T K,WANG B L.Enhanced migrating birds optimization algorithm for hybrid flowshop group scheduling problem with unrelated parallel machines[J].Computer Integrated Manufacturing Systems,2022,28(12):3912-3922.