混合流水线调度(hybrid flowline scheduling,HFS)在制造业中较为常见,对其进行科学的决策有助于提高企业的生产效率和竞争力。经典HFS假定各工件按同一方向访问所有加工阶段[1],但在实际生产中,出于工艺要求等原因,一些产品的加工可能会忽略或越过某些阶段,如某些钢种需要经过不同的工位,即产生了混合柔性流水线调度(hybrid flexible flowline scheduling,HFFS)。这种跳过阶段的特点提升了调度模型适应实际环境的能力,在包装制造、钢铁生产、半导体制造等行业均可找到其应用[2-4]。
HFFS得到了很多学者的持续关注。针对炼钢-连铸过程,Long等[3]考虑可调处理时间,提出结合质量改进、新精英策略和重启策略的改进遗传算法(genetic algorithm,GA)以最小化makespan、总等待时间、处理时间与其基础处理时间的偏差。Oujana等[5]考虑准备时间和不相关并行机约束,提出了基于线性规划技术的求解方法以最小化总拖期。轩华等[6]考虑恶化效应,提出了一种结合头脑风暴优化算法与候鸟优化算法的启发式算法以最小化makespan与能耗的加权和。Yu等[7]结合基于属性特征的双向量表述提出了改进模因算法,目标是最小化滞留时间和提前/拖期惩罚。黄辉等[8]针对序列设置时间,以最小化makespan和负荷均衡指标为目标,提出了改进的非支配解排序遗传算法。李浩平等[9]针对批量流,结合粒子群算法和GA提出基于双层编码的混合算法最小化makespan和机床负荷平衡。
在HFS中,交货期是常考虑的一个关键因素,对其研究多围绕加权拖期、加权提前/拖期、延迟工件数等开展,旨在缩短产品交付时间与其交货期的差距。然而,当延迟交付对生产线影响巨大或者企业非常重视准时性时,实际生产过程则不允许延迟,即所有产品必须在强制工期内交付使用。上述考虑强制工期的HFFS有着广泛的工业背景[10-11]。例如,在易腐制造领域,由于农产品的易腐性,每个工件有一个无法改变的强制工期。
围绕强制工期约束所开展的研究在车间调度领域已有相关报道。Janaki等[12]研究了带强制工期和均匀分布任务持续时间的单机调度,利用GA来最小化延迟时间。宋存利[13]研究了禁止拖期交付的无等待流水线调度,提出了基于有向无环图的精确搜索算法以及基于该算法的分段迭代搜索算法。Ying等[14]为求解含强制工期的两代理比例流水线调度,提出了两种多项式时间优化算法,分别最小化最大完成时间和总完成时间。对于无拖期作业车间调度,Shi等[15]考虑加班,提出了结合模拟退火的混合GA以最小化总提前库存和加班成本;史双元等[16]考虑加班,提出了多目标金鹰优化算法以最小化总加班时间和makespan;史双元等[17]考虑外协,提出了多目标差分进化-变邻域搜索算法以最小化makespan和总外协成本。
综上所述,本文提出了考虑强制工期约束的HFFS(HFFS with deadline constraints,HFFSDC),由于HFFS是NP-hard问题[5],故所研究的更复杂的HFFSDC也是NP-hard问题。本文的贡献如下。
(1)虽然从不同角度研究HFFS以及带强制工期的生产调度问题已有一些成果,但在HFFS中兼顾强制工期的研究还相对较少。强制工期的引入增加了问题的求解复杂度,若使用常规编码解码策略,可能会产生超出强制工期约束的不可行解。因此,本文结合机器空闲规则、最早完成时间规则以及基于强制工期的前移策略提出两阶段动态解码方案。
(2)在以往研究中,处理HFFS时多假定工件访问所有加工阶段,但将工件在跳过阶段的处理时间视为零,该方式需对工件在所有阶段的机器选择和工件排序进行安排。为了减少工件跳过阶段对其他阶段的安排产生影响且提高运行效率,本文通过设置工件实际加工阶段集的方式,确定工件实际所需访问的阶段。
(3)为有效解决HFFSDC,引入改进GA和邻域搜索提高人工蜂群算法(ABC)的局部搜索能力,引入基于最差解的鲸鱼优化算法(WOA)防止算法过快收敛。因此,结合改进GA、邻域搜索策略提出ABC-WOA混合算法以获取近优解。
1 问题建模
1.1 问题描述
所研究的HFFSDC包含n个工件和o个加工阶段,每个阶段j(j∈{1,2,…,o})有mj(mj≥1)台不相关并行机;工件i(i∈{1,2,…,n})的加工过程可能跳过一些阶段,即它遍历的加工阶段数可能会小于总阶段数。令ui为工件i所经加工阶段的集合,则工件i实际访问的阶段数可表示为|ui|。ui(g)为ui中排在第g个位置的阶段号,g∈{1,2,…,ui}。工件i在相邻两个未缺失阶段ui(g)和ui(g+1)之间的运输时间为![]() 为工件i在阶段j的开始时间,ctji为工件i在阶段j的完成时间,pjki为工件i在阶段j的机器k上的处理时间。设Xjki为二元变量,若工件i在阶段j由机器k加工,Xjki=1,否则Xjki=0。每个工件有对应的强制工期
为工件i在阶段j的开始时间,ctji为工件i在阶段j的完成时间,pjki为工件i在阶段j的机器k上的处理时间。设Xjki为二元变量,若工件i在阶段j由机器k加工,Xjki=1,否则Xjki=0。每个工件有对应的强制工期![]() 这意味着各工件必须在该时间内完成加工,因此在确定工件加工序列时需要核查和调整以满足强制工期要求。当工件i访问阶段j时,由于该阶段的各台机器相互独立,所以不同的机器选择会影响工件在此阶段的处理时间,进而影响它的完成时间。调度的目的是决定工件的加工序列以及各工件的机器选择以使总加权完成时间最小。其他的假设描述包括:①所有工件在零时刻均可用于加工;②每道工序的加工不允许中断;③机器在任何时候都可用,不考虑故障和维护;④每台机器一次只能处理一个工件,每个工件一次只能由一台机器加工。
这意味着各工件必须在该时间内完成加工,因此在确定工件加工序列时需要核查和调整以满足强制工期要求。当工件i访问阶段j时,由于该阶段的各台机器相互独立,所以不同的机器选择会影响工件在此阶段的处理时间,进而影响它的完成时间。调度的目的是决定工件的加工序列以及各工件的机器选择以使总加权完成时间最小。其他的假设描述包括:①所有工件在零时刻均可用于加工;②每道工序的加工不允许中断;③机器在任何时候都可用,不考虑故障和维护;④每台机器一次只能处理一个工件,每个工件一次只能由一台机器加工。
1.2 模型构建
HFFSDC的整数规划模型的构建如下。
优化目标为最小化总加权完成时间:
(1)
式中:wi为工件i的权重。
确保每个工件在任意一个未缺失阶段只能由一台机器加工:
(2)
工件在每个未缺失阶段的开始和完成时间关系为
![]()
(3)
同一阶段分配到同一台机器加工的两个工件之间的加工优先级关系分别为
Zjkli+Zjkil=1,∀i,l,j,k,l≠i;
(4)
sjki+V(3-Xjki-Xjkl-Zjkli)≥cjkl,∀i,l,j,k,l≠i。
(5)
式中:Zjkli为二元变量,若工件l和i均分配到阶段j的机器k且工件l是工件i的紧前工件,Zjkli=1,否则Zjkli=0;sjki和cjki分别为工件i在阶段j的机器k上的开始时间和完成时间;V为一个很大的数。
工件在相邻两个未缺失阶段的工序优先级关系为
stui(g+1)i,∀i,g∈{1,…,|ui|-1}。
(6)
为确保虚拟工件0是安排在每台机器上第一个工件的紧前工件有
(7)
为保证工件i在最后阶段的完成时间不能超过强制工期有
(8)
变量的取值为
Zjkli,Xjki∈{0,1},∀j,k,i,l,l≠i;
(9)
cjki,sjki,stji,ctji≥0,∀j,k,i。
(10)
2 算法设计
2.1 总体流程
ABC-WOA混合算法的具体流程概括如下。
步骤1 参数设置。设置迭代标号q、总迭代数iter、序列集规模Popsize、总累计迭代数lj、累计未改进次数φ=0、迭代次数ik=1。
步骤2 初始化。采用NEH启发式法产生Popsize个工件序列构成初始工件序列集τq。
步骤3 若达到总迭代数,输出最佳解,否则记录当前最佳解,继续步骤4。
步骤4 雇佣蜂阶段。根据轮盘赌规则从工件序列集τq选择Popsize个工件序列执行交叉变异算子,将产生的子代与序列集τq合并。计算所形成的规模为2Popsize的新序列集内每个工件序列的适应度值,按其降序排列工件序列,选取适应度值大的前Popsize个工件序列作为新序列集τq。
步骤5 跟随蜂阶段。针对新序列集τq,应用轮盘赌规则选择Popsize个工件序列,对其执行5种邻域搜索策略。若新工件序列的适应度值较大,则用新工件序列取代序列集τq内对应的工件序列。
步骤6 计算更新后的序列集τq内各工件序列的目标值,选择具有最小总加权完成时间的解作为最佳解,若它优于历史最佳解,令ik=ik+1,φ=0,返回步骤3;否则,令φ=φ+1,若φ<lj,令ik=ik+1,转至步骤3,若φ≥lj,继续步骤7。
步骤7 侦察蜂阶段。将工件序列集τq按照适应度值升序排列,选择前Popsize/2个工件序列,随机利用鲸鱼优化算法的线性包围策略和螺旋包围策略。无论是否产生适应度值更大的新工件序列,都使用新工件序列取代原序列。令ik=ik+1,返回步骤3。
2.2 初始化方法
2.2.1 编码和解码
采用基于工件排序的整数编码方式,取所有工件的工件号组成一个工件序列,其长度等于总工件数n。工件号所处位置即为该工件的加工顺序。根据机器空闲规则、最早完成时间规则以及基于强制工期的前移策略进行两阶段动态解码以确定工件的加工安排。
步骤1 对于虚拟工件0,令ctj0=0(j∈{1,2,…,o});
步骤2 按照给定工件序列依次计算工件i在每个未缺失阶段的机器上的开始时间sui(g)ki、完成时间cui(g)ki以及记录每台机器的负载。计算工件开始时间时,比较该工件在前一个未缺失阶段的完成时间cui(g-1)ki与运输时间![]() 之和(记为CT)和所选机器上工件i的紧前工件的完成时间(记为QT),若CT≥QT,则sui(g)ki=CT;若CT<QT,如果该机器在CT和工件i的紧前工件的开始时间(记为BT)之间存在长度为pui(g)ki的空闲时间段,则将该工件安排至该时间段,记录最早空闲时间段的起点作为sui(g)ki,否则sui(g)ki=QT。进而,得到cui(g)ki,更新该机器在各时刻的负载状态,将工件i记入已安排工件子序列。
之和(记为CT)和所选机器上工件i的紧前工件的完成时间(记为QT),若CT≥QT,则sui(g)ki=CT;若CT<QT,如果该机器在CT和工件i的紧前工件的开始时间(记为BT)之间存在长度为pui(g)ki的空闲时间段,则将该工件安排至该时间段,记录最早空闲时间段的起点作为sui(g)ki,否则sui(g)ki=QT。进而,得到cui(g)ki,更新该机器在各时刻的负载状态,将工件i记入已安排工件子序列。
步骤3 在决定工件i的加工机器时,利用基于最早完成时间规则的机器选择策略,即计算工件i在当前阶段的所有并行机上的完成时间,选取完成时间最早的一台机器作为工件i在该阶段的加工机器。若最早完成时间相同,则选择机器号最小的机器。
步骤4 若工件i的完成时间超过强制工期,则将该工件的加工位置前移,即从{1,2,3}产生随机数rd,将工件i前移rd个位置,根据前述规则确定前移工件i以及后移的rd个工件的开始/完成时间和处理这rd+1个工件的机器;若移动后工件i的完成时间满足强制工期约束,则继续判断已安排工件子序列内下一工件,否则重复该前移过程,直至已安排工件子序列内所有工件满足强制工期约束。返回步骤2,直至完成所有工件。
2.2.2 初始工件序列集
引入NEH启发式法产生Popsize个工件序列以构成初始工件序列集。计算每个工件在所有机器的总处理时间,按照降序排列各工件;选取总处理时间最长的前两个工件作为部分工件序列;随机选取一个未加工工件,插入到部分工件序列的所有可能位置,计算此时该序列的总加权完成时间,选择总加权完成时间最小的序列作为这些工件的当前序列。重复上述步骤直至完成所有工件的插入,形成完整的工件序列。
2.3 雇佣蜂阶段
2.3.1 选择
采用轮盘赌规则从工件序列集中选择Popsize个工件序列,被选中的概率由适应度值决定。由于本文的目标是最小化总加权完成时间,所以第h个工件序列的适应度值和选择概率分别为
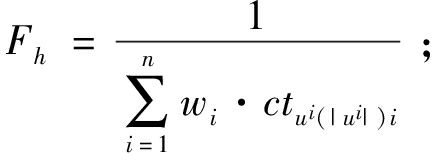
(11)
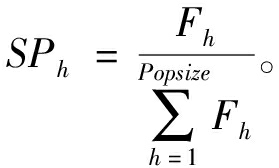
(12)
2.3.2 多点交叉
采取两种基于工件号的多点交叉算子,如图1所示。随机选择两个父代工件序列r1和r2,产生1个[0,1]的随机数rand,若rand<pc(交叉概率),则从两种交叉算子中随机选择一种进行交叉。具体过程如下。

图1 多点交叉算子
Figure 1 Multi-point crossover operator
(1)基于位置的交叉算子。随机产生ε1(ε1<n)个位置,交换被选中位置上的工件号,删除未选中位置上的重复工件号,依次在未选中位置上放入对应父代工件序列内除交换工件号之外的剩余工件号,生成子代工件序列o1和o2。
(2)基于线性次序的交叉算子。随机选择两个位置π1和π2(1≤π1<π2≤n),交换这两个位置之间的工件片段,依次删除未选中位置上的重复工件号,填入对应父代工件序列的除所选工件片段之外的剩余工件号,生成子代工件序列o1和o2。
2.3.3 反转逆序变异
当产生的随机数rand<pm(变异概率)时,利用翻转逆序变异扩大搜索范围,即随机产生两个位置π1和π2(1≤π1<π2≤n),将两个位置之间的工件片段进行翻转。
2.4 跟随蜂阶段
根据HFFSDC的特点,设计了5种产生邻域解的邻域搜索策略,如图2所示。
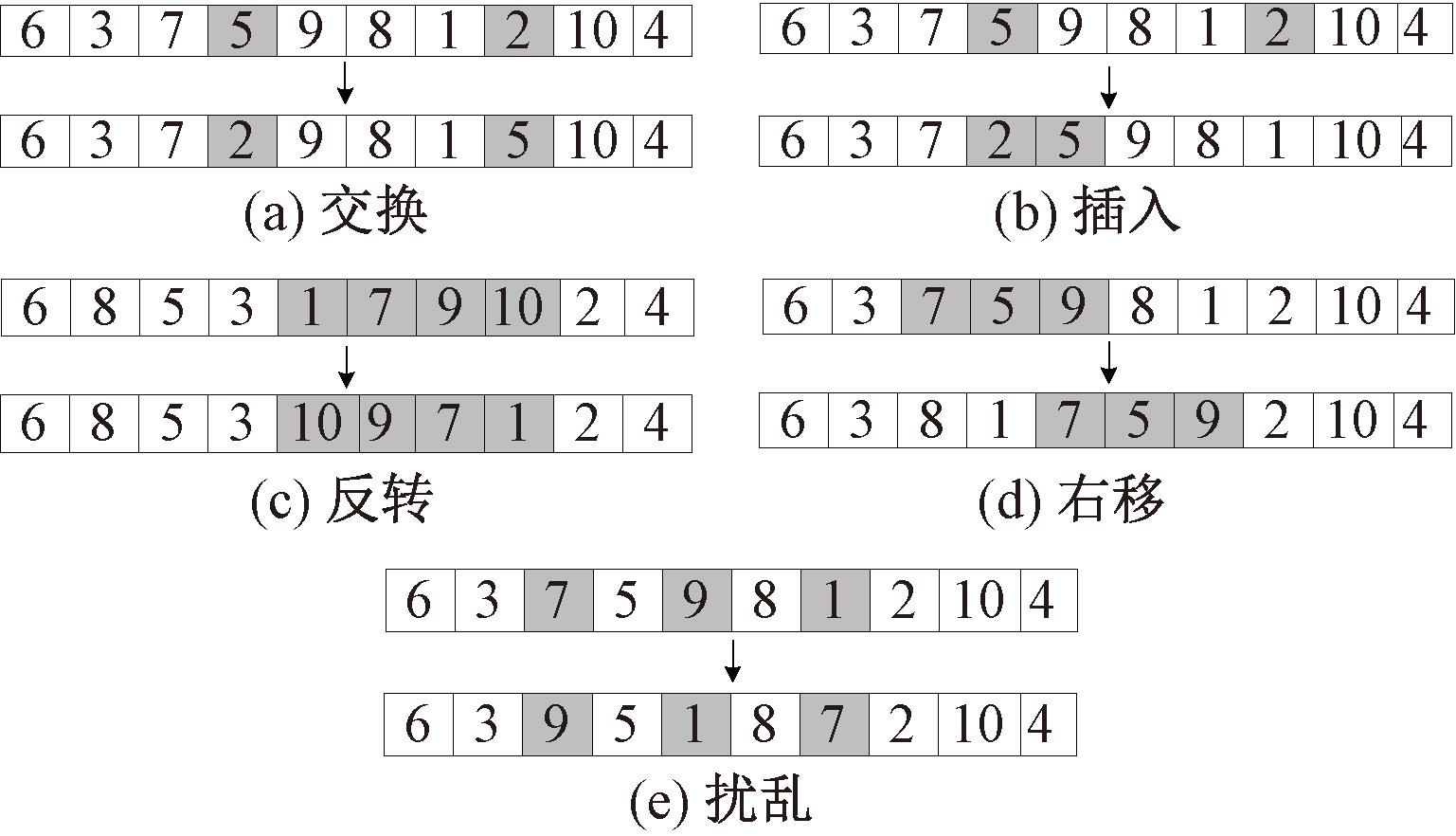
图2 邻域搜索策略
Figure 2 Neighborhood search strategies
对序列集内的工件序列分别进行上述5种邻域搜索,若产生的新序列中最大适应度值超过原序列,则将具有最大适应度值的新序列取代当前序列。
2.5 侦察蜂阶段
WOA具有操作简单、控制参数少及跳出局部最优能力强等特点,因此引入基于最差解的WOA改善解的质量。
(1)线性包围猎物策略Q1。首先,找到当前工件序列集内的最佳工件序列Pbest,若待更新工件序列Pt和Pbest内同一位置上的工件号相同,则保留该位置以及对应的工件号。然后对Pbest内其余位置的工件号进行循环移位。
(2)螺旋包围猎物策略Q2。螺旋包围猎物是在线性包围猎物的基础上,对通过线性包围生成的位置整体进行循环移位来实现的。具体实现过程如图3所示。
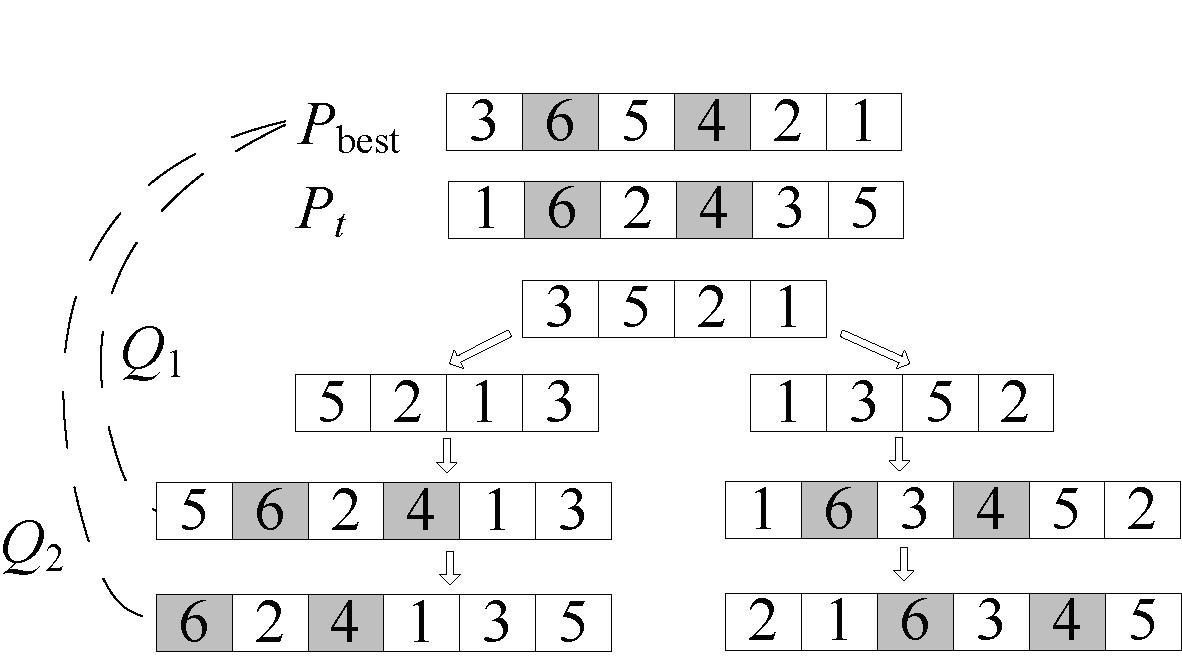
图3 包围猎物策略
Figure 3 Encirclement strategy
3 数值实验与分析
3.1 实验设计
为了验证所提出的ABC-WOA混合算法求解HFFSDC的有效性,将其与结合GA和邻域搜索的人工蜂群算法(ABC&GA),混合变邻域搜索的改进GA[18](IGA&VNS),以及基于邻域搜索的改进离散候鸟优化算法[19](IDMBO)进行对比测试。利用MATLAB R2022b在PC Intel(R) Core i5-13600K/CPU3.5 GHz/RAM32 G的计算机上实现上述算法。实验数据设定如下:n={20,40,60,80,100},o={5,10,15},跳过阶段概![]() 定义各工件的总平均处理时间
定义各工件的总平均处理时间![]() 及总运输时间Tsi:
及总运输时间Tsi:
(13)
(14)
据此产生各工件的强制工期[21]:
(15)
式中:η∈U[0,1]。
为公平比较上述算法,以ABC-WOA混合算法运行100次迭代所需时间为所有算法的最大运行时间。根据正交试验对该算法涉及的主要参数进行最佳设置。pm={0.2,0.3},lj={4,5,6},共得到24种参数组合。选择小规模n=40,o=5,p′=0.2以及大规模n=80,o=10,p′=0.4作为两组实验算例,对这24种参数组合进行测试,每种组合随机运行10次,取平均值作为测试结果,并据此绘制ABC-WOA混合算法的平均目标值主效应图如图4所示。
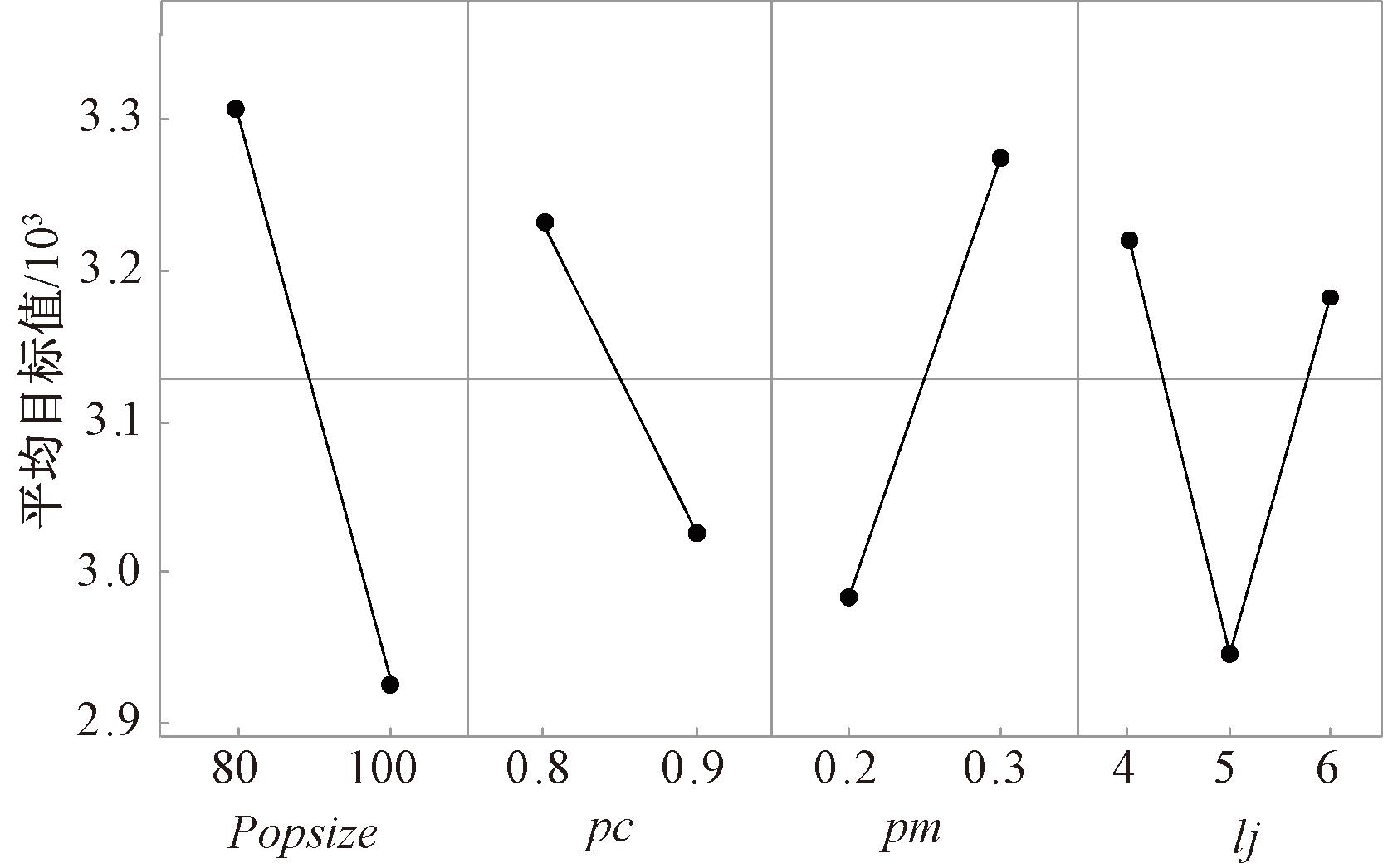
图4 平均目标值的主效应图
Figure 4 Main effect plot of average objective value
各对比算法的关键参数也依据正交试验进行不同的取值测试,得到最佳参数设置,如表1所示。
表1 各算法的参数设置
Table 1 Parameter settings for each algorithm

算法参数ABC&GAPopsize=100,pc=0.8,pm=0.2IGA&VNSPopsize=100,pc=0.9,pm=0.2,变邻域搜索循环次数P=100IDMBOPopsize=101,最大巡回次数Gmax=5,邻域解集个数β=3ABC-WOAPopsize=100,pc=0.9,pm=0.2,lj=5
为了说明所提ABC-WOA混合算法中各改进部分的影响,开展以下数值实验。
(1)NEH启发式法初始化对比实验。对比使用NEH启发式法和不使用NEH启发式法产生的初始工件序列集的解的质量,为客观评价初始工件序列集解对算法的影响提供依据。
(2)鲸鱼优化算法对比实验。比较ABC-WOA混合算法引入鲸鱼优化算法前后的性能,为人工蜂群算法与鲸鱼优化算法的融合提供依据。
(3)不同规模算例对比实验。对比4种算法求解不同问题规模的优化结果,为评估所提算法的优化效果提供数据支持。
3.2 NEH启发式法初始化对比实验
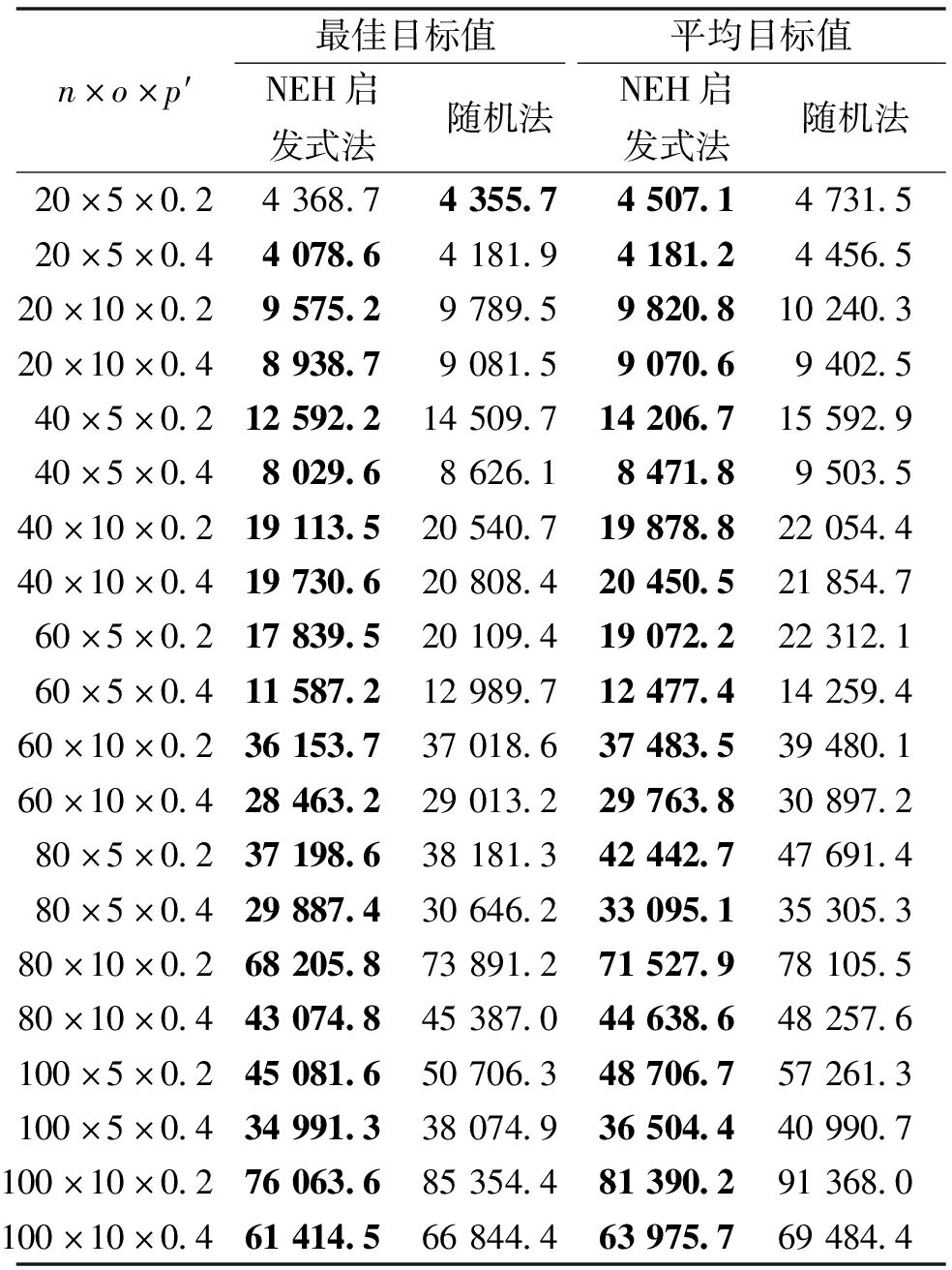
为验证NEH启发式法对改善初始工件序列集的影响,进行初始化对比实验。取n={20,40,60,80,100},o={5,10},p′={0.2,0.4},产生20种规模问题,每种规模问题随机运行10次,分别测试由NEH启发式法和随机法产生的初始工件序列集的解的质量。表2列出了NEH启发式法和随机法得到的初始工件序列集的最佳目标值和平均目标值。由表2可知,对几乎所有规模问题,NEH启发式法产生的初始解的性能均优于随机法。
表2 NEH启发式法初始化对比结果
Table 2 Comparison results of NEH heuristic initialization
n×o×p′最佳目标值平均目标值NEH启发式法随机法NEH启发式法随机法20×5×0.24368.74355.74507.14731.520×5×0.44078.64181.94181.24456.520×10×0.29575.29789.59820.810240.320×10×0.48938.79081.59070.69402.540×5×0.212592.214509.714206.715592.940×5×0.48029.68626.18471.89503.540×10×0.219113.520540.719878.822054.440×10×0.419730.620808.420450.521854.760×5×0.217839.520109.419072.222312.160×5×0.411587.212989.712477.414259.460×10×0.236153.737018.637483.539480.160×10×0.428463.229013.229763.830897.280×5×0.237198.638181.342442.747691.480×5×0.429887.430646.233095.135305.380×10×0.268205.873891.271527.978105.580×10×0.443074.845387.044638.648257.6100×5×0.245081.650706.348706.757261.3100×5×0.434991.338074.936504.440990.7100×10×0.276063.685354.481390.291368.0100×10×0.461414.566844.463975.769484.4
3.3 鲸鱼优化算法对比实验
由于人工蜂群算法与GA和邻域搜索的融合较为常见,而鲜有与鲸鱼优化算法的混合,由此本实验提出了引入鲸鱼优化算法前后的对比实验以说明鲸鱼优化算法的融合效果。
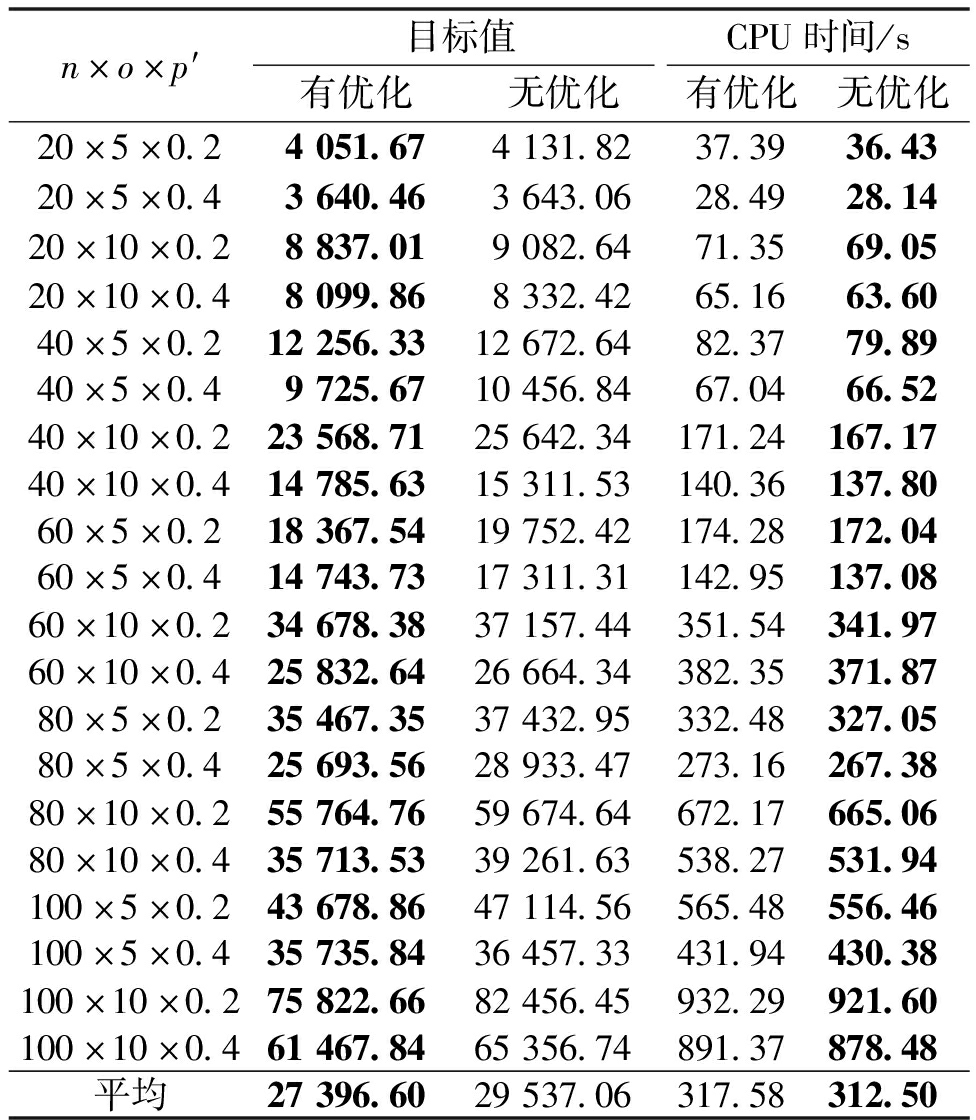
以3.2节20种规模问题为例,每个规模问题随机运行10次,以100次迭代作为停止条件分别测试引入和不引入鲸鱼优化算法的ABC-WOA混合算法,得到平均目标值以及平均CPU时间,结果见表3。由表3可知,在求解不同的规模问题时,引入鲸鱼优化算法的ABC-WOA混合算法得到的平均目标值均优于引入前。
表3 有无鲸鱼优化算法的ABC-WOA混合算法对比结果
Table 3 Comparison results of ABC-WOA hybrid algorithm with and without whale optimization algorithm
n×o×p′目标值CPU时间/s有优化无优化有优化无优化20×5×0.24051.674131.8237.3936.4320×5×0.43640.463643.0628.4928.1420×10×0.28837.019082.6471.3569.0520×10×0.48099.868332.4265.1663.6040×5×0.212256.3312672.6482.3779.8940×5×0.49725.6710456.8467.0466.5240×10×0.223568.7125642.34171.24167.1740×10×0.414785.6315311.53140.36137.8060×5×0.218367.5419752.42174.28172.0460×5×0.414743.7317311.31142.95137.0860×10×0.234678.3837157.44351.54341.9760×10×0.425832.6426664.34382.35371.8780×5×0.235467.3537432.95332.48327.0580×5×0.425693.5628933.47273.16267.3880×10×0.255764.7659674.64672.17665.0680×10×0.435713.5339261.63538.27531.94100×5×0.243678.8647114.56565.48556.46100×5×0.435735.8436457.33431.94430.38100×10×0.275822.6682456.45932.29921.60100×10×0.461467.8465356.74891.37878.48平均27396.6029537.06317.58312.50
3.4 不同规模算例对比实验
{n,o,p′}的不同组合共产生45种规模问题,每种规模问题随机进行10次,取其平均值作为测试结果。定义相对偏差百分比δc为
(16)
式中:ZABC-WOA和Zc分别为由ABC-WOA混合算法和当前算法c(c∈{ABC&GA,IGA&VNS,IDMBO})得到的平均目标值。
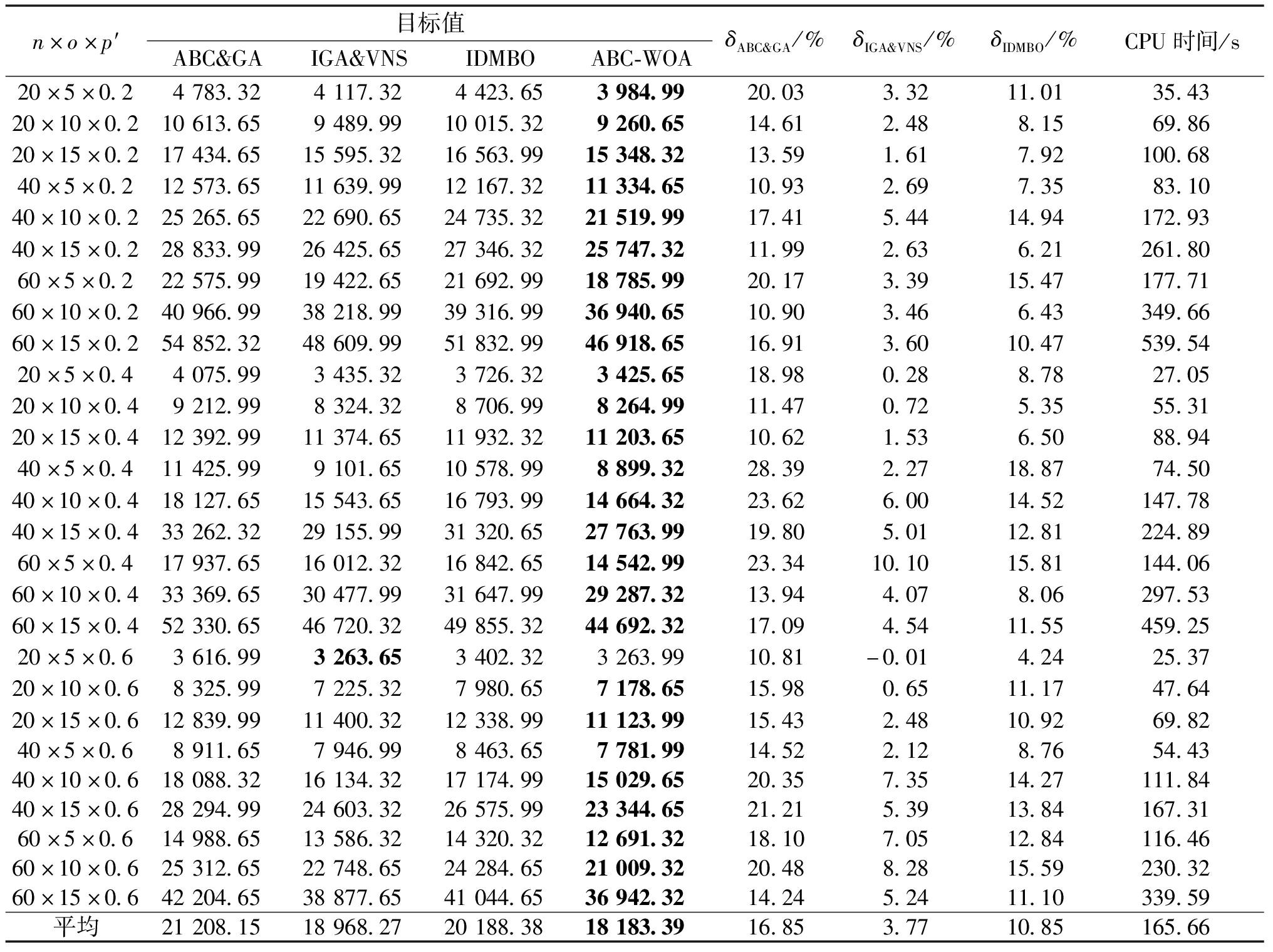
所有规模问题的测试结果见表4和表5,可知对于中小规模问题,在平均的CPU时间165.66 s内,由ABC-WOA混合算法得到的平均目标值在ABC&GA、IGA&VNS和IDMBO的基础上分别改进了16.85%,3.77%和10.85%;对于大规模问题,在平均的CPU时间695.40 s内,由ABC-WOA混合算法得到的平均目标值在ABC&GA、IGA&VNS和IDMBO的基础上分别改进了19.01%,4.53%和13.46%。在相同的CPU时间内,由ABC-WOA混合算法得到的解的质量几乎均优于其他3种算法。
表4 中小规模问题的测试结果
Table 4 Test results of small and medium-sized problems
n×o×p′目标值ABC&GAIGA&VNSIDMBOABC-WOAδABC&GA/%δIGA&VNS/%δIDMBO/%CPU时间/s20×5×0.24783.324117.324423.653984.9920.033.3211.0135.4320×10×0.210613.659489.9910015.329260.6514.612.488.1569.8620×15×0.217434.6515595.3216563.9915348.3213.591.617.92100.6840×5×0.212573.6511639.9912167.3211334.6510.932.697.3583.1040×10×0.225265.6522690.6524735.3221519.9917.415.4414.94172.9340×15×0.228833.9926425.6527346.3225747.3211.992.636.21261.8060×5×0.222575.9919422.6521692.9918785.9920.173.3915.47177.7160×10×0.240966.9938218.9939316.9936940.6510.903.466.43349.6660×15×0.254852.3248609.9951832.9946918.6516.913.6010.47539.5420×5×0.44075.993435.323726.323425.6518.980.288.7827.0520×10×0.49212.998324.328706.998264.9911.470.725.3555.3120×15×0.412392.9911374.6511932.3211203.6510.621.536.5088.9440×5×0.411425.999101.6510578.998899.3228.392.2718.8774.5040×10×0.418127.6515543.6516793.9914664.3223.626.0014.52147.7840×15×0.433262.3229155.9931320.6527763.9919.805.0112.81224.8960×5×0.417937.6516012.3216842.6514542.9923.3410.1015.81144.0660×10×0.433369.6530477.9931647.9929287.3213.944.078.06297.5360×15×0.452330.6546720.3249855.3244692.3217.094.5411.55459.2520×5×0.63616.993263.653402.323263.9910.81-0.014.2425.3720×10×0.68325.997225.327980.657178.6515.980.6511.1747.6420×15×0.612839.9911400.3212338.9911123.9915.432.4810.9269.8240×5×0.68911.657946.998463.657781.9914.522.128.7654.4340×10×0.618088.3216134.3217174.9915029.6520.357.3514.27111.8440×15×0.628294.9924603.3226575.9923344.6521.215.3913.84167.3160×5×0.614988.6513586.3214320.3212691.3218.107.0512.84116.4660×10×0.625312.6522748.6524284.6521009.3220.488.2815.59230.3260×15×0.642204.6538877.6541044.6536942.3214.245.2411.10339.59平均21208.1518968.2720188.3818183.3916.853.7710.85165.66
表5 大规模问题的测试结果
Table 5 Test results of large-scale problems
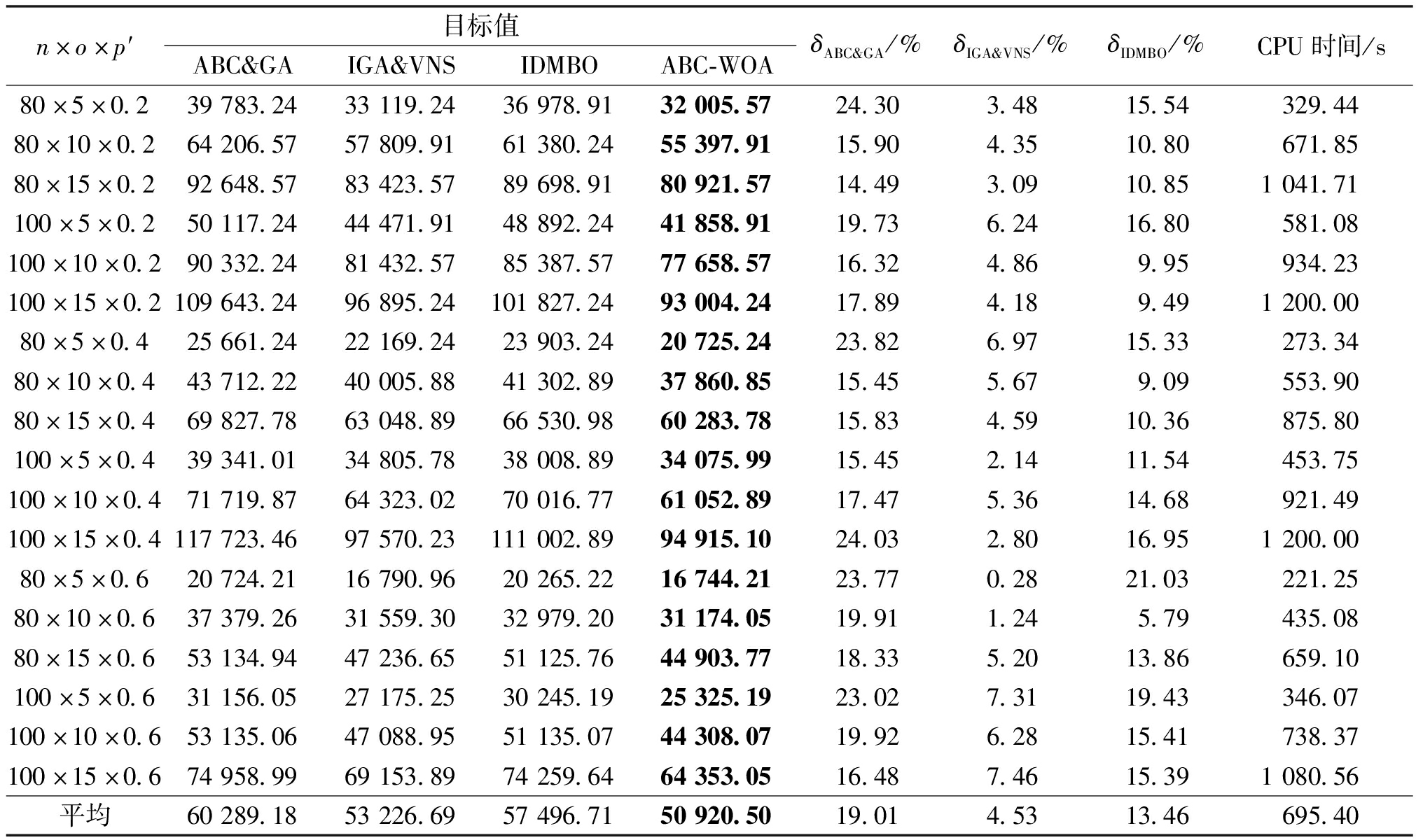
n×o×p′目标值ABC&GAIGA&VNSIDMBOABC-WOAδABC&GA/%δIGA&VNS/%δIDMBO/%CPU时间/s80×5×0.239783.2433119.2436978.9132005.5724.303.4815.54329.4480×10×0.264206.5757809.9161380.2455397.9115.904.3510.80671.8580×15×0.292648.5783423.5789698.9180921.5714.493.0910.851041.71100×5×0.250117.2444471.9148892.2441858.9119.736.2416.80581.08100×10×0.290332.2481432.5785387.5777658.5716.324.869.95934.23100×15×0.2109643.2496895.24101827.2493004.2417.894.189.491200.0080×5×0.425661.2422169.2423903.2420725.2423.826.9715.33273.3480×10×0.443712.2240005.8841302.8937860.8515.455.679.09553.9080×15×0.469827.7863048.8966530.9860283.7815.834.5910.36875.80100×5×0.439341.0134805.7838008.8934075.9915.452.1411.54453.75100×10×0.471719.8764323.0270016.7761052.8917.475.3614.68921.49100×15×0.4117723.4697570.23111002.8994915.1024.032.8016.951200.0080×5×0.620724.2116790.9620265.2216744.2123.770.2821.03221.2580×10×0.637379.2631559.3032979.2031174.0519.911.245.79435.0880×15×0.653134.9447236.6551125.7644903.7718.335.2013.86659.10100×5×0.631156.0527175.2530245.1925325.1923.027.3119.43346.07100×10×0.653135.0647088.9551135.0744308.0719.926.2815.41738.37100×15×0.674958.9969153.8974259.6464353.0516.487.4615.391080.56平均60289.1853226.6957496.7150920.5019.014.5313.46695.40
表6列出了不同p′取值下4种算法求解所有规模问题的平均测试结果。当p′=0.2时,在平均CPU时间436.60 s内,由ABC-WOA混合算法得到的平均目标值在ABC&GA、IGA&VNS和IDMBO的基础上分别改进了16.46%,3.97%和10.79%;当p′=0.4时,在平均CPU时间386.51 s内,由ABC-WOA混合算法得到的平均目标值在其他3种算法的基础上分别改进了18.76%,4.33%和12.83%;当p′=0.6时,在平均CPU时间309.55 s内,由ABC-WOA混合算法得到的平均目标值在其他3种算法的基础上分别改进了18.59%,5.37%和13.81%。随着p′的增加,工件访问的加工阶段有所减少,各算法所消耗的CPU时间随之缩短,ABC&GA、IGA&VNS和IDMBO的相对偏差百分比呈上升趋势,而所提ABC-WOA混合算法在解的质量方面的表现越有优势。
表6 不同p′取值时各算法的测试结果
Table 6 Test results of various algorithms with different values of p′

p′目标值ABC&GAIGA&VNSIDMBOABC-WOAδABC&GA/%δIGA&VNS/%δIDMBO/%CPU时间/s0.244308.7539557.5342150.6738045.8716.463.9710.79436.600.437341.4332804.6235478.0631443.8918.764.3312.83386.510.628871.4925652.7727706.4224344.9518.595.3713.81309.55
为了说明实验结果具有统计学意义,在95%的置信水平下,得出各算法在求解不同规模问题的目标值区间图如图5所示,可以看出,ABC-WOA混合算法对比3种对比算法具有显著性优势。
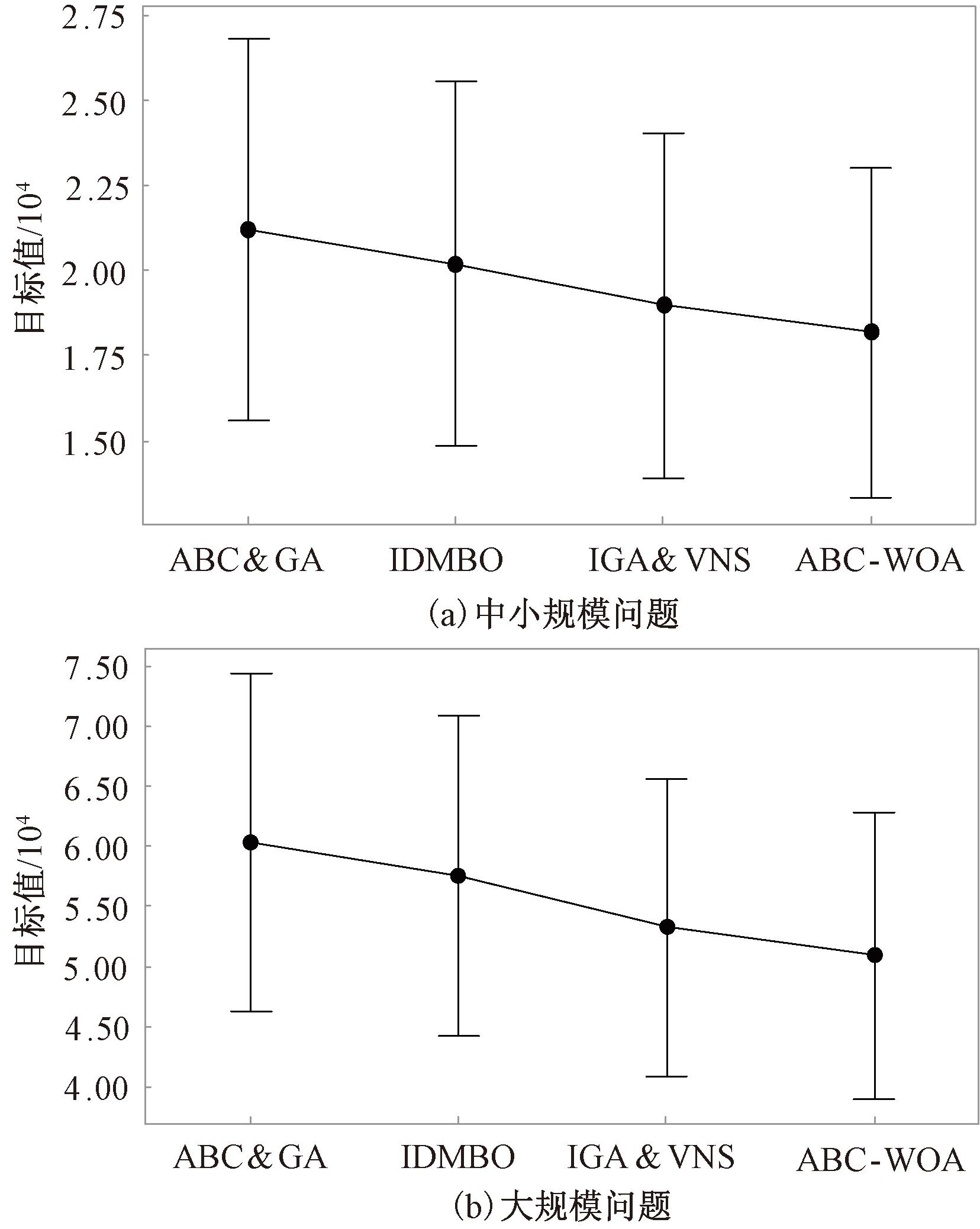
图5 目标值区间图
Figure 5 Interval graph of target values
4 结论
本文研究了考虑不相关并行机、运输时间和强制工期约束的HFFS,目标是最小化总加权完成时间。考虑到工件跳过阶段对于调度的影响,通过设置工件实际加工阶段集的方式,确定工件在所访问阶段的排序以及机器选择问题。为了使所有工件都满足强制工期约束,提出基于强制工期前移策略的两阶段动态解码方案。为了提高算法初始解的质量、局部搜索能力且防止过快收敛,在ABC算法的基础上,融入NEH启发式法、改进GA和邻域搜索策略提出了ABC-WOA混合算法。不同算法的对比实验验证了引入NEH启发式法和鲸鱼优化算法的有效性;通过不同规模问题的仿真实验,比较所提混合算法与现有算法,测试结果显示了ABC-WOA混合算法求解HFFSDC的有效性和优越性。
本文研究还存在一些局限:对于更复杂的实际生产,模型和算法的适应性需进一步增强;绿色调度是现代制造业发展的一大趋势,未来可继续深入探讨节能和经济影响在车间调度领域的应用。
[1] 轩华,耿祝新,李冰.组合缓冲约束下的多目标混合流水线节能调度[J].郑州大学学报(工学版),2025,46(1):17-25.XUAN H,GENG Z X,LI B.Multi-objective hybrid flowline energy-saving scheduling with combined buffer constraints[J].Journal of Zhengzhou University (Engineering Science),2025,46(1):17-25.
[2] OUJANA S,AMODEO L,YALAOUI F,et al.Mixed-integer linear programming,constraint programming and a novel dedicated heuristic for production scheduling in a packaging plant[J].Applied Sciences,2023,13(10):6003.
[3] LONG J Y,ZHENG Z,GAO X Q,et al.Scheduling a realistic hybrid flow shop with stage skipping and adjustable processing time in steel plants[J].Applied Soft Computing,2018,64:536-549.
[4] SCHUMACHER C,BUCHHOLZ P,FIEDLER K,et al.Local search and tabu search algorithms for machine scheduling of a hybrid flow shop under uncertainty[C]∥2020 Winter Simulation Conference (WSC).Piscataway:IEEE,2020:1456-1467.
[5] OUJANA S,YALAOUI F,AMODEO L.A linear programming approach for hybrid flexible flow shop with sequence-dependent setup times to minimise total tardiness[J].IFAC-PapersOnLine,2021,54(1):1162-1167.
[6] 轩华,赵一航,李冰.带阶段跳跃和恶化效应的炼钢-连铸调度的混合启发式算法[J].工业工程与管理,2024,29(6):82-92.XUAN H,ZHAO Y H,LI B.Hybrid heuristic algorithm for steelmaking-continuous casting scheduling with stage skipping and deterioration effect[J].Industrial Engineering and Management,2024,29(6):82-92.
[7] YU Y,PAN Q K,PANG X F,et al.An attribution feature-based memetic algorithm for hybrid flowshop scheduling problem with operation skipping[J].IEEE Transactions on Automation Science and Engineering,2025,22:99-114.
[8] 黄辉,李梦想,严永.考虑序列设置时间的混合流水车间多目标调度研究[J].运筹与管理,2020,29(12):215-221.HUANG H,LI M X,YAN Y.Research on multi-objective scheduling of hybrid flow production shop considering sequence setting time[J].Operations Research and Ma-nagement Science,2020,29(12):215-221.
[9] 李浩平,朱成彪,陈心怡,等.带忽略工序的多目标批量流混合流水车间调度[J].计算机集成制造系统,2025,31(1):89-101.LI H P,ZHU C B,CHEN X Y,et al.Research on multi-objective lot streaming hybrid flowshop scheduling with missing operations[J].Computer Integrated Manufacturing Systems,2025,31(1):89-101.
[10] CHEN W C,LI J,MA W T.Hybrid flow shop rescheduling algorithm for perishable products subject to a due date with random invalidity to the operational unit[J].The International Journal of Advanced Manufacturing Technology,2017,93(1):225-239.
[11] MARCHESANO M G,GUIZZI G,POPOLO V,et al.Dynamic scheduling of a due date constrained flow shop with deep reinforcement learning[J].IFAC-PapersOnLine,2022,55(10):2932-2937.
[12] JANAKI E,ISMAIL A M.Using the genetic algorithm to reduce tardiness by tightening the deadline date for stochastic processing[J].Soft Computing,2023:1-6.
[13] 宋存利.禁止拖期交付的无等待流水车间调度问题算法研究[J].大连交通大学学报,2018,39(6):100-105.SONG C L.Research on modeling and algorithm of no-wait flow shop scheduling problem with prohibited tardiness[J].Journal of Dalian Jiaotong University,2018,39(6):100-105.
[14] YING K C,POURHEJAZY P,SUNG C E.Two-agent proportionate flowshop scheduling with deadlines:polynomial-time optimization algorithms[J].Annals of Operations Research,2024,343(1):543-558.
[15] SHI S Y,XIONG H G,LI G F.A no-tardiness job shop scheduling problem with overtime consideration and the solution approaches[J].Computers &Industrial Engineering,2023,178:109115.
[16] 史双元,熊禾根.考虑加班的无拖期作业车间调度问题多目标金鹰优化算法研究[J].中国机械工程,2023,34(17):2077-2088.SHI S Y,XIONG H G.Research on multi-objective golden eagle optimizer for no-tardiness job shop scheduling problems with overtime consideration[J].China Mechanical Engineering,2023,34(17):2077-2088.
[17] 史双元,熊禾根.考虑外协的作业车间无拖期调度问题多目标差分进化算法[J].计算机集成制造系统,2024,30(12):4352-4368.SHI S Y,XIONG H G.Multi-objective differential evolution algorithm for no-tardiness job shop scheduling problem with outsourcing option[J].Computer Integrated Manufacturing Systems,2024,30(12):4352-4368.
[18] 崔琪,吴秀丽,余建军.变邻域改进遗传算法求解混合流水车间调度问题[J].计算机集成制造系统,2017,23(9):1917-1927.CUI Q,WU X L,YU J J.Improved genetic algorithm variable neighborhood search for solving hybrid flow shop scheduling problem[J].Computer Integrated Manufacturing Systems,2017,23(9):1917-1927.
[19] 轩华,樊银格,李冰.改进离散候鸟优化算法求解带缺失阶段的柔性流水车间问题[J].工业工程与管理,2023,28(1):98-109.XUAN H,FAN Y G,LI B.Improved discrete migrating birds optimization algorithm for flexible flowshop problem with missing stages[J].Industrial Engineering and Management,2023,28(1):98-109.
[20] 轩华,樊银格,李冰.含忽略工序和不相关机的混合流水车间调度[J].智能系统学报,2022,17(3):459-470.XUAN H,FAN Y G,LI B.Hybrid flowshop scheduling with missing operations and unrelated machines[J].CAAI Transactions on Intelligent Systems,2022,17(3):459-470.
[21] 轩华,李文婷,李冰.混合离散人工蜂群算法求解含不相关并行机的分布式柔性流水线调度[J].控制与决策,2023,38(3):779-789.XUAN H,LI W T,LI B.Hybrid discrete artificial bee colony algorithm for distributed flexible flowline scheduling with unrelated parallel machines[J].Control and Decision,2023,38(3):779-789.