随着汽车行业的快速发展和消费者对汽车安全性和稳定性要求的不断提高,车辆制动系统的性能优化成为了研究的热点之一。电子机械制动系统(electronic mechanical braking,EMB)凭借精简设计和易集成等优势,正逐渐成为汽车制动技术发展的焦点[1]。防抱死制动系统(anti-lock braking system,ABS)通过一套机电一体化的装置对制动系统的压力进行调节,使滑移率保持在一定范围(10%~20%),防止车轮抱死[2]。
在ABS控制策略中,滑移率是一个至关重要的参数,直接反映了车轮与地面之间的摩擦状态。所以如何准确估计并控制车轮的滑移率,使其保持在最优范围内,是提高ABS系统性能的关键。有很多学者对最佳滑移率的识别进行了研究,常用的方法是用递推最小二乘法对最佳滑移率进行实时准确辨识,能够快速准确地识别出不同路面的最佳滑移率[3-4]。Devadiga等[5]采用一种线性插值、递归和函数逼近相结合的方法,以改善现有的最佳参考滑移算法,改进后ABS性能得到优化。Dinçmen[6]提出了一种基于滑模的极值搜索算法,可以在线搜索最佳滑移比以便在未知路况下获得最大制动力。Kim等[7]使用超声波发射器配合深度学习卷积神经网络(D-CNN)以及反射的超声波信号来识别路面类型,从而得到最佳滑移率。Wang等[8]设计了一种模糊权重路面识别算法,利用设计的模糊推理逻辑将输入信息与模块中现有标准路面的路面附着系数滑移率曲线进行比较,得到当前路面与各标准路面的相似系数,从而估计出当前路面的最佳滑移率。
在很多的防抱死制动控制研究中,最佳滑移率的选择过程往往给定的是一个固定的经验值,而不考虑不同路面之间路面附着系数的差异,且传统的逻辑门限ABS控制方式有着控制逻辑复杂和滑移率波动大导致舒适性较差等缺点。所以本文在文献[8]的基础上,根据不同典型路面间附着系数的差异设计了一种最佳滑移率估计算法,能够比较准确地识别出典型路面间的最佳滑移率且实时计算量较少。又因为滑模控制具有响应快速、物理实现简单、鲁棒性良好等优点,是一种良好的处理非线性系统的控制方法,能够很好地实现最佳滑移率控制[9],所以ABS最佳滑移率控制方法采用积分滑模控制器控制EMB和轮毂电机协调配合,输出适当的制动力矩,保证最佳滑移率的精确跟踪。
1 汽车ABS模型建立
为了便于理解ABS的工作原理,需要搭建汽车ABS数学模型,主要包括单轮车辆动力学模型、汽车轮胎模型和EMB执行机构模型。
1.1 单轮车辆动力学模型
从图1可以看出,对车轮受力分析可以推导出车轮旋转动力学模型公式[10]为
(1)
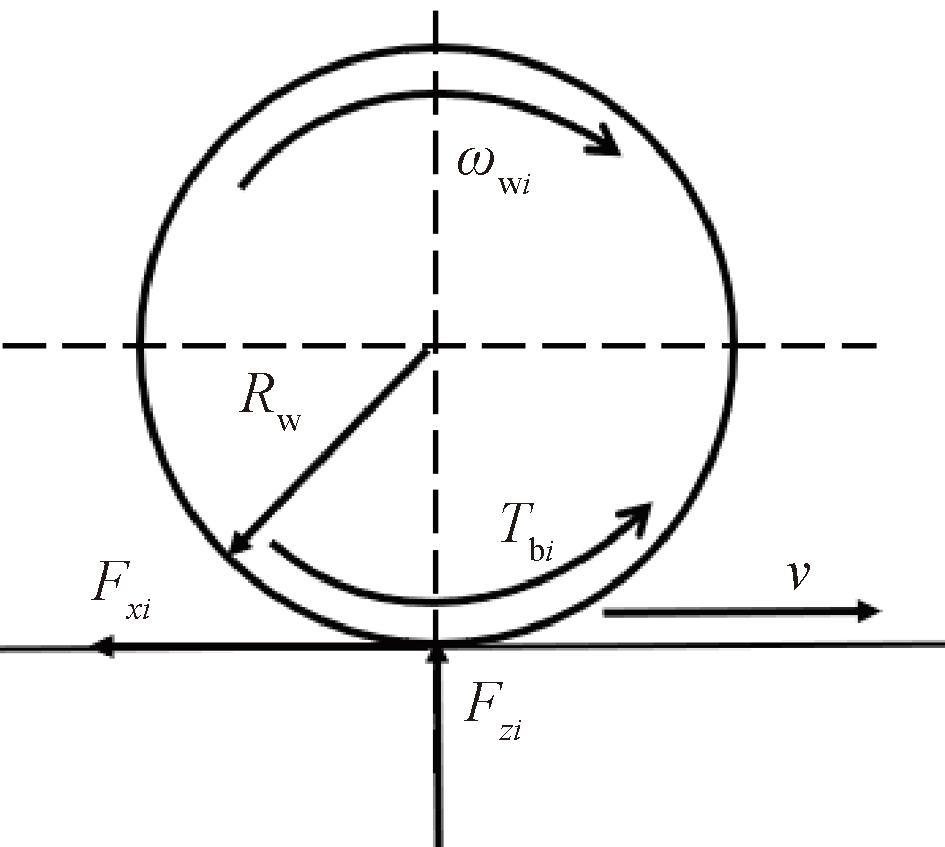
图1 单轮受力分析图
Figure 1 Single-wheel force analysis diagram
式中:Jw为车轮的转动惯量,kg·m2;ωwi为各车轮的角速度,rad/s;Tbi为各车轮的制动力矩,N·m;Fxi为各车轮受到的纵向力,N;Fzi为各车轮受到的垂向力,N;Rw为车轮的滚动半径,m;f为车轮的滚动阻力系数。
1.2 汽车轮胎模型
在制动过程中,可以用魔术轮胎公式描述轮胎纵向力与滑移率之间的关系,魔术轮胎公式[11]为
Fx=Dsin(C·arctan(Bλ-E(Bλ-arctan Bλ)));
(2)
C=a0;
(3)
(4)
(5)
(6)
式中:Fx为纵向力;Fz为车轮受到的垂向力;a0~a8为不同路面轮胎与路面间关系的经验拟合参数;λ为滑移率。
轮胎与地面的利用附着系数[12]为
(7)
式中:μ为路面利用附着系数。
由式(1)可以得到纵向力为
(8)
忽略载荷对地面与轮胎间纵向附着特性的影响,对魔术轮胎模型进行简化,可以得到路面利用附着系数与滑移率的关系式[13]:
μ=D sin(C·arctan(Bλ-E(Bλ-arctan Bλ)))。
(9)
1.3 EMB执行机构模型
EMB执行机构模型主要由电机模型、传动机构模型和负载模型组成。
1.3.1 电机模型
EMB执行机构模型中使用的电机为无刷直流力矩电机,其动态方程[14]为
(10)
(11)
式中:U为电枢电压,V;La为电枢电感,H;Ia为电枢电流,A;Ra为电枢电阻,Ω;Ke为电机反电动势系数,V/(s·rad);ωm为电机转速;J为等效转动惯量;Tf为电机摩擦转矩,N·m;TL为负载转矩;Kt为电机力矩系数,N·m/A。
1.3.2 传动机构模型
传动机构包括行星齿轮减速器模块和滚珠丝杠模块,其作用是按固定比例增大电机输出力矩并将行星齿轮减速器的转动转换为滚珠丝杠螺母轴向位移量。
(12)
式中:θm为电机转角,rad;i为行星齿轮减速器传动比;x为滚珠丝杠螺母轴向位移量,mm;Pn为滚珠丝杠导程,mm。
1.3.3 负载模型
在活塞推动制动块压紧制动盘过程中,首先要消除制动块与制动盘间的间隙,消除间隙后,进入电机堵转状态,此时,制动夹紧力与制动盘的变形量存在非线性关系。
通过对提出的制动器方案进行实验,并设计制动间隙为0.2 mm,可以得到制动夹紧力Fcl与滚珠丝杠螺母轴向位移量x之间的关系式[15]为
Fcl=1 049.2(x-0.2)3+20 161.9(x-0.2)2+
155.5(x-0.2)。
(13)
最终可以得到制动器输出的制动力矩为
Tb=2FclμbRb。
(14)
式中:Tb为输出的制动力矩,N·m;μb为制动盘的摩擦系数;Rb为制动盘的有效摩擦半径,m。
2 最佳滑移率估计算法
在积分滑模控制器的设计中,精确且快速响应的最佳滑移率估计算法至关重要。该算法需要估计车轮滑移率在最优区间,以最大化路面利用附着系数,提升车辆的制动效能。
2.1 基于EMB的ABS工作原理
在汽车制动过程中,汽车车轮中心速度即实际车速与轮速并不一定相同,一般用滑移率来定义,其公式[16]为
(15)
式中:v为车速,m/s。
传统的ABS执行器一般使用液压助力,通过液压泵、电磁阀等液压元件调节制动轮缸的压力,从而控制车轮的滑移率,响应速度较慢。而基于EMB 的ABS控制策略则是在接收到紧急制动信号后,由级联式 PI 控制策略将制动信号转变成电机信号,再由电机控制器驱动电机工作,经过传动机构将输出力矩放大并将旋转运动转变成水平运动,从而推动摩擦片移动产生制动力,实现制动力的精确调节,确保车轮滑移能够控制在最佳滑移率附近。EMB省去了液压系统中的液压管路、泵、阀等复杂元件,减少了能量传递过程中的损失和延迟,从而具有更快的响应速度和更高的控制精度。
2.2 最佳滑移率估计算法的设计
本文使用文献[17]的用来描述轮胎路面利用附着系数和滑移率关系的经验公式:
μ(λ)=C1(1-e-C2λ)-C3λ。
(16)
式中:C1、C2、C3均为路面的拟合参数。
如果已知C1、C2、C3,对式(16)求导找出导数为零的点就对应该路面的最佳滑移率λopt和峰值路面利用附着系数μopt。各典型路面的曲线如图2所示,其拟合参数、最佳滑移率和峰值路面利用附着系数如表1所示。由图2和表1可知,峰值路面利用附着系数越大,对应的最佳滑移率也越大;同时还可知,在小滑移率区[0,0.005],各曲线的路面利用附着系数的区别不大,而在其他滑移率区间[0.005,1],各曲线的路面利用附着系数区别较大,而这个特点可以作为识别路面最佳滑移率的重要特征。
表1 典型路面拟合参数
Table 1 Typical pavement fitting parameters
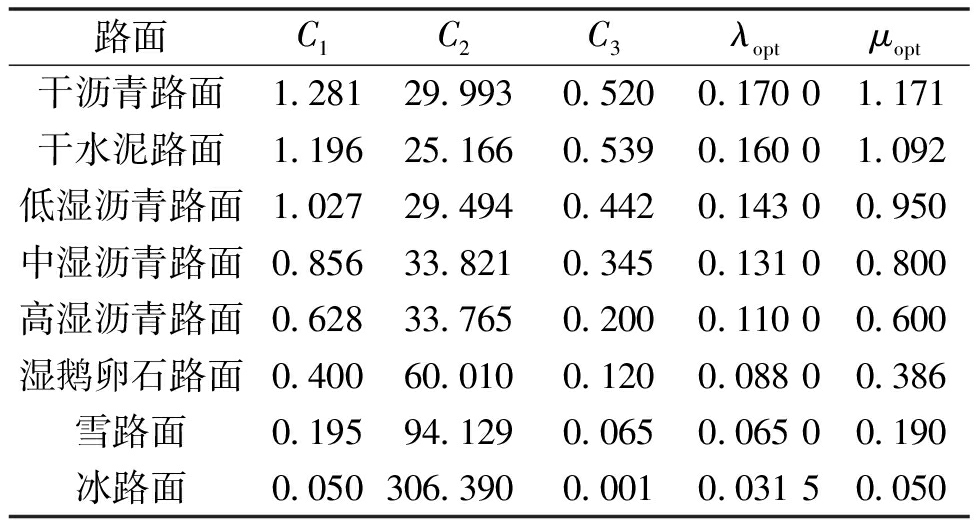
路面C1C2C3λoptμopt干沥青路面1.28129.9930.5200.17001.171干水泥路面1.19625.1660.5390.16001.092低湿沥青路面1.02729.4940.4420.14300.950中湿沥青路面0.85633.8210.3450.13100.800高湿沥青路面0.62833.7650.2000.11000.600湿鹅卵石路面0.40060.0100.1200.08800.386雪路面0.19594.1290.0650.06500.190冰路面0.050306.3900.0010.03150.050
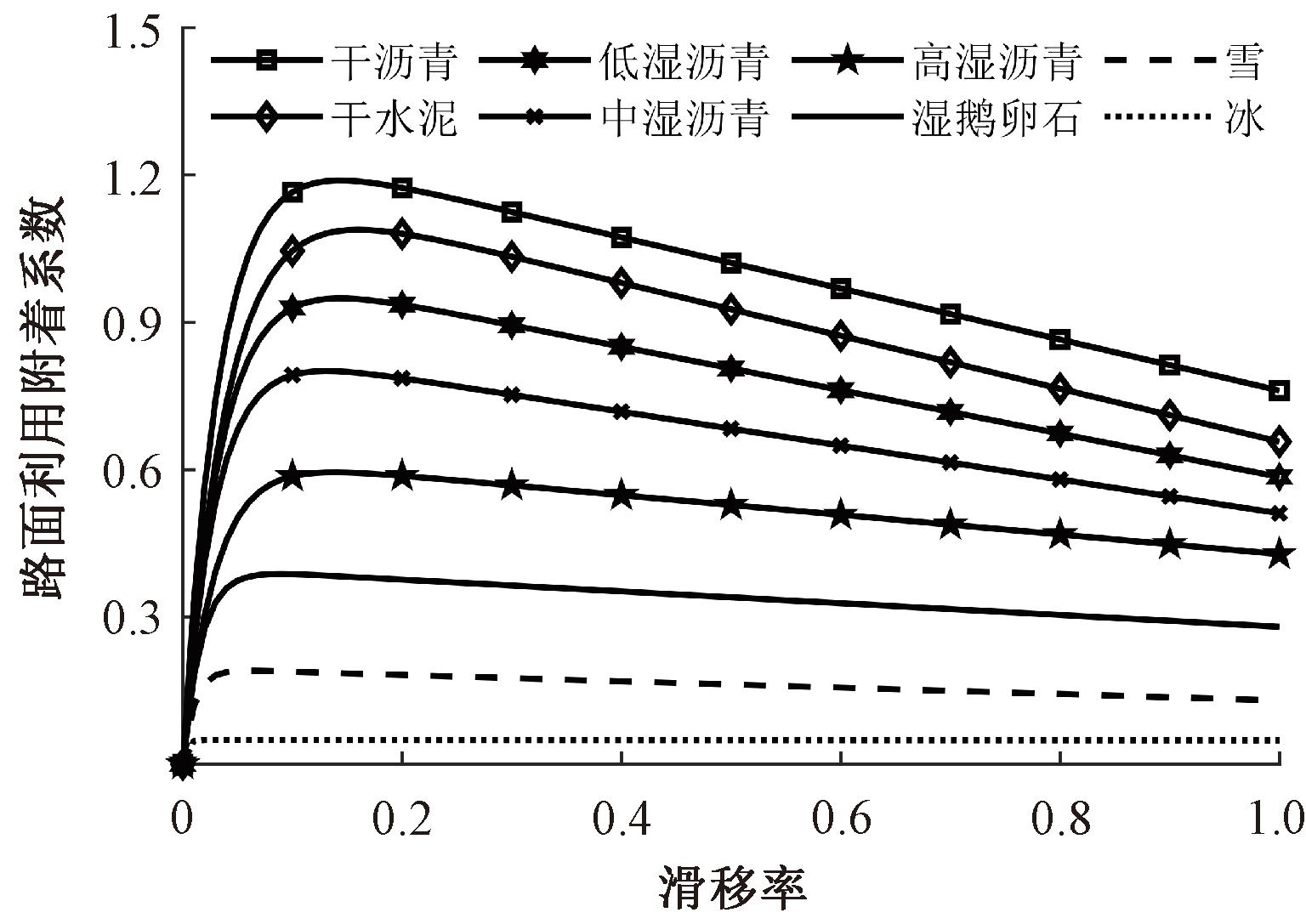
图2 典型路面μ-λ曲线图
Figure 2 Typical pavement μ-λcurve
申超[18]通过当前路面与模块中存在的典型路面的路面利用附着系数-滑移率(μ-λ)曲线进行对比,求出典型路面下的权重系数,进而获得当前路面下车轮最佳滑移率。为了减少此估计算法的计算量,可以先通过路面利用附着系数的大小确定当前路面处于哪两条典型路面之间,再通过当前路面的利用附着系数与两条典型路面的利用附着系数差值的关系去设计两条典型路面的权重,最后根据权重估计出当前路面的最佳滑移率。估算公式为
(17)
(18)
(19)
式中:x1、x2为两条相邻典型路面的权重系数;λopt、λopt1和λopt2分别为当前路面、典型路面1和典型路面2的最佳滑移率;μ、μ1和μ2分别为当前路面、典型路面1和典型路面2的路面利用附着系数;φ为一个接近于零的极小正数。
为了验证提出的最佳滑移率估计算法的准确性,首先在8条典型路面任意选择相邻的3条典型路面,之后选取这3条路面中的高附着与低附着路面为估计的参考路面,中附着路面为识别目标,识别结果如图3所示。选择估计误差e和估计平均误差![]() 作为估计准确度的评价指标[19]:
作为估计准确度的评价指标[19]:
(20)
(21)
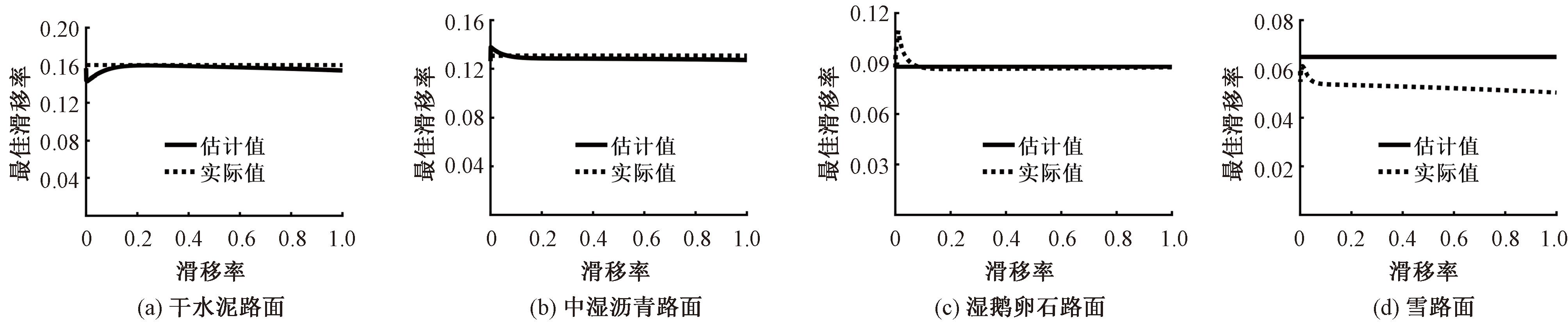
图3 典型路面估计结果
Figure 3 Typical pavement estimation results
式中:![]() 为最佳滑移率的实际值,即估计目标。
为最佳滑移率的实际值,即估计目标。
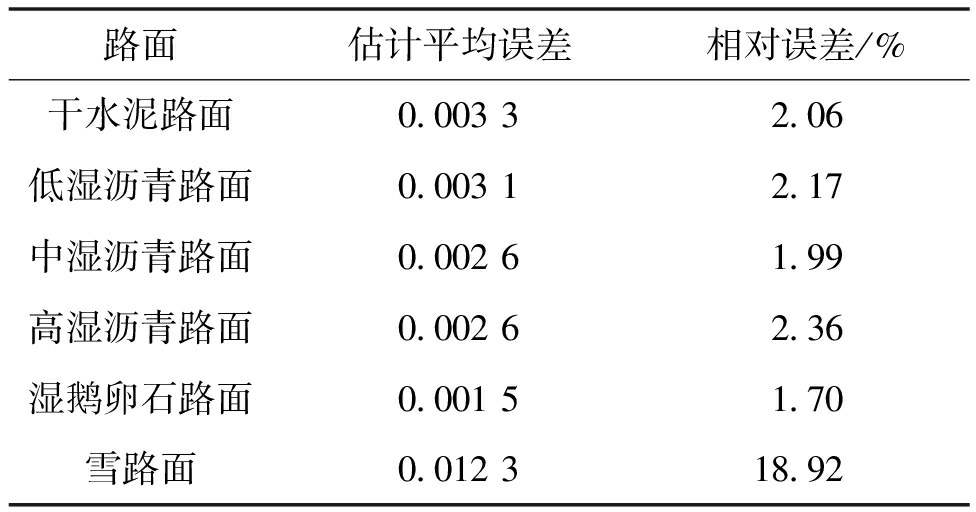
各典型路面的估计平均误差和相对误差如表2所示。
表2 估计误差
Table 2 Estimation error
路面估计平均误差相对误差/%干水泥路面0.00332.06低湿沥青路面0.00312.17中湿沥青路面0.00261.99高湿沥青路面0.00262.36湿鹅卵石路面0.00151.70雪路面0.012318.92
由图3和表2可知,除雪路面之外的各路面的估计平均误差一般在0.001~0.003 5之间,相对误差较小。但同时可知其估计的雪路面最佳滑移率的相对误差较大,达到了18.92%。考虑到雪路面本身的最佳滑移率较小,所以还是认为该估计算法具有较好的估计准确度。
综上所述,本文提出的最佳滑移率的估计算法在全滑移率范围内有着较好的估计准确度,虽然在雪路面中估计的最佳滑移率的相对误差相对较大,但还是能够比较正确地估计出相邻路面间的最佳滑移率,所以可以认为该估计算法对各典型路面的最佳滑移率的估计准确度较高,因此也可以认为该估计算法对典型路面之间的目标路面同样具备较高的估计准确度。
2.3 基于CarSim-Simulink的车辆-路面模型
本文研究对象是分布式独立驱动电动汽车,整车模型参考的是CarSim中的一款B型车,具体参数如表3所示。
表3 CarSim车辆参数
Table 3 CarSim vehicle parameters

参数数值整车质量/kg1260轴距/m2.6车轮滚动半径/m0.325车轮转动惯量/(kg·m2)1.5车轮滚动阻力系数0.0038(前轮制动转矩/制动压力)/(N·m·MPa-1)150(后轮制动转矩/制动压力)/(N·m·MPa-1)100
在2.2节估计算法用到的路面模型是Burckhardt路面模型,但在仿真过程中本文使用的模型为CarSim软件内部的模型,所以有必要对各典型路面进行仿真数据的采集以及参数拟合,便于估计算法的实现。
首先需要在CarSim中设定仿真工况,因在路面数据采集过程中需要采集各路面全滑移率的μ-λ数据,所以设定仿真工况为初始车速100 km/h,制动压力在0~5 s上升到10 MPa,并关闭车辆的ABS功能。
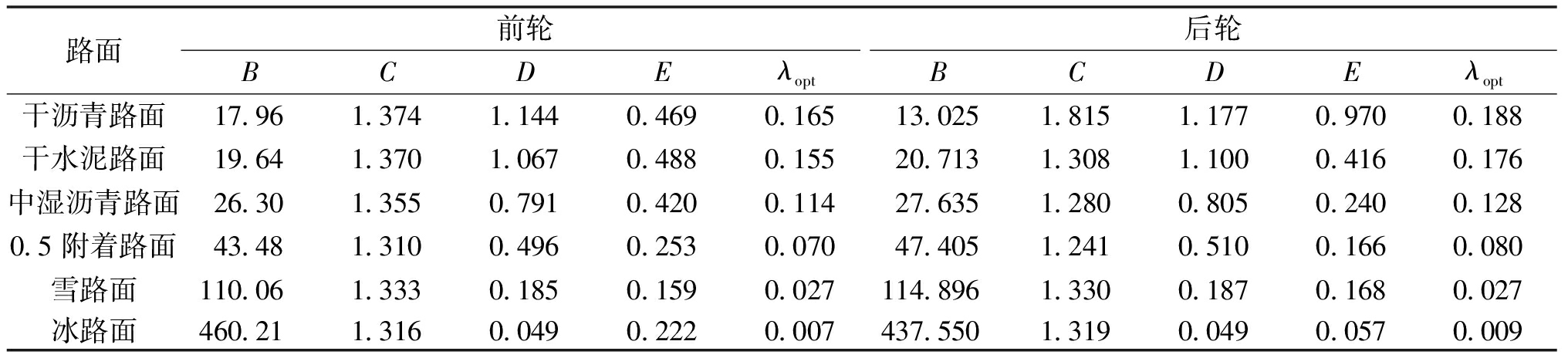
之后CarSim中的路面参数设置为选择的5种典型路面的峰值路面利用附着系数。为了进一步提高估计算法的准确度,在仿真过程中加入了一条峰值路面利用附着系数为0.5的路面,作为对5种典型路面的补充。考虑到前后两轮的最佳滑移率可能不同,所以由CarSim输出车速、左前后轮轮速、左前后轮的制动力矩、左前后轮的垂直载荷,最终得到6条路面的μ-λ曲线数据。并利用得到的数据对简化的魔术轮胎模型参数进行拟合,拟合数据如表4所示。
表4 各典型路面魔术轮胎拟合参数
Table 4 Fitting parameters for each typical road surface with magic tire
路面前轮后轮BCDEλoptBCDEλopt干沥青路面17.961.3741.1440.4690.16513.0251.8151.1770.9700.188干水泥路面19.641.3701.0670.4880.15520.7131.3081.1000.4160.176中湿沥青路面26.301.3550.7910.4200.11427.6351.2800.8050.2400.1280.5附着路面43.481.3100.4960.2530.07047.4051.2410.5100.1660.080雪路面110.061.3330.1850.1590.027114.8961.3300.1870.1680.027冰路面460.211.3160.0490.2220.007437.5501.3190.0490.0570.009
得到各典型路面的利用附着系数与滑移率的关系式后,利用式(17)~(19)就可以搭建最佳滑移率识别模块。但考虑到提出的最佳滑移率估计算法需要实时判断当前路面处于哪两条典型路面之间,运算量较大,同时考虑到在小滑移率区各曲线的路面利用附着系数区别不大,加上典型路面曲线样本数据有限,对于非典型路面条件下的目标路面,由于缺少相关路面信息,所以想要精确预估其最佳滑移率非常困难,因而对前后车轮的路面利用附着系数大于干沥青路面与小于冰路面的目标路面的最佳滑移率估计过程进行了简化,最终最佳滑移率估计公式如下所示:
λopt(λ,μ)=
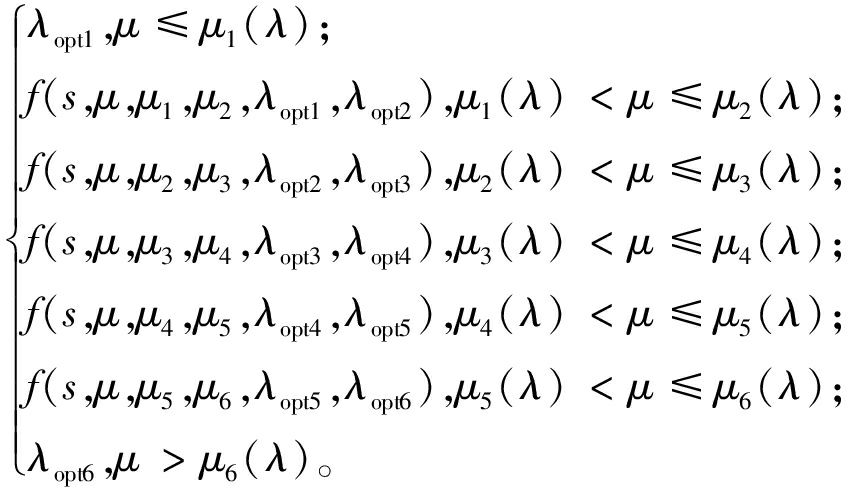
(22)
式中:下标1,2,…,6分别表示冰路面、雪路面、0.5附着路面、中湿沥青路面、干水泥路面、干沥青路面;f(·)为本文提出的最佳滑移率估计算法。
3 基于EMB的ABS控制策略设计
3.1 基于ABS的复合制动控制策略设计
复合制动即利用电动机的再生制动和EMB共同完成车辆的制动功能。电动机采用的是轮毂电机,类型为永磁同步电机,4个轮毂电机分别安装在各个车轮的轮毂内,能够实现各轮驱动转矩独立可控。在制动过程中,可以根据峰值路面利用附着系数(μopt)和制动强度Z的大小关系,将制动工况分为常规制动工况(Z≤μopt)和紧急制动工况(Z>μopt),二者有着不同的复合制动控制策略[20]。在常规制动工况,路面提供的附着力可以满足制动需求,车轮一般不会抱死,ABS一般不启动。复合制动控制策略的目标一般是在保持制动稳定性的同时尽可能提高再生制动的占比,从而提高能量回收量。而在紧急制动工况中,因为路面所能提供的附着力已经不能满足制动需求,车轮极易发生抱死,所以此时ABS启动,使滑移率能够尽可能维持在最佳滑移率附近。EMB有着响应速度快,控制精度高等优点,能够很好地与轮毂电机进行制动力的协调配合。为了在紧急制动过程中充分发挥轮毂电机的制动力矩,提高能量回收量,制动力矩优先由电机制动力矩提供,不足的部分由EMB制动力矩提供。
因为本文主要考虑的是ABS的功能,所以以紧急制动工况为研究对象,具体控制策略如图4所示。
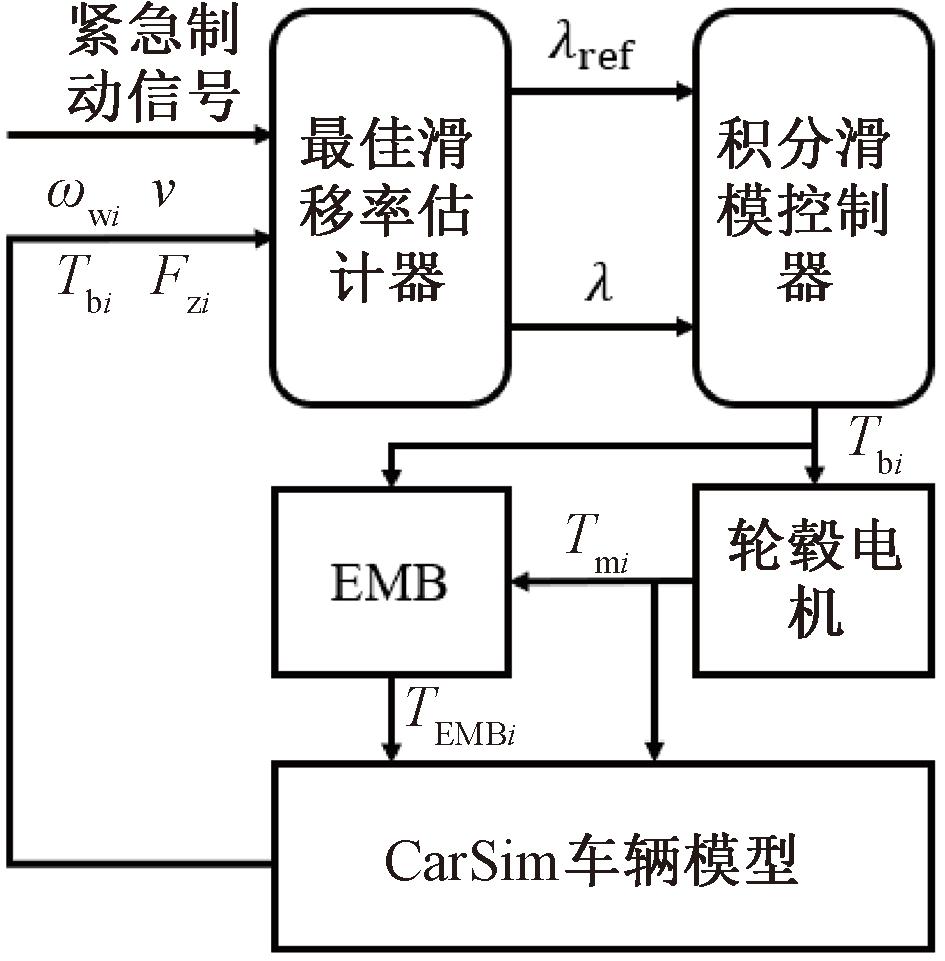
图4 CarSim-Simulink联合仿真模型
Figure 4 CarSim-Simulink co-simulation model
首先在接收到紧急制动信号后,ABS开始工作,最佳滑移率估计器是由第2节最佳滑移率估计算法搭建的估计模型,可以通过CarSim提供的车速、轮速、制动力矩、垂直载荷等信号估计出当前路面的最佳滑移率,并将实际滑移率信号和估计出的最佳滑移率信号输入到积分滑模控制器中,积分滑模控制器输出需要的单轮总制动力矩(Tbi)。当轮毂电机产生的电机制动力矩能够满足总制动力矩需求时,单轮制动力矩完全由电机制动力矩提供,EMB制动系统不工作,此时为纯电机制动;当最大电机制动力矩不能满足总制动力矩需求时,不足部分由EMB制动力矩补充。考虑到当车速过小时,再生制动的能量回收效果不好,所以车速v≤3 m/s时,电机不进行制动工作,由EMB提供制动力,且因为此时车速较低,需要关闭ABS,此时采用常规制动控制方法,将EMB输出的制动力矩都设置为10 MPa,能让车辆比较平稳地停下。
3.2 积分滑模控制器的设计
积分滑模控制器需要实现的功能是让实际滑移率能够跟踪目标滑移率,所以选择实际滑移率λ为状态变量,最佳滑移率为控制目标,设计控制器的跟踪误差为
e=λ-λref。
(23)
切换函数s设计为
(24)
式中:b1为大于零的常数。
对式(15)求导得
(25)
对切换函数求导得
(26)
将式(25)以及式(1)代入式(26)得
(27)
为了减小系统的抖振,采用一种改进的指数趋近率:
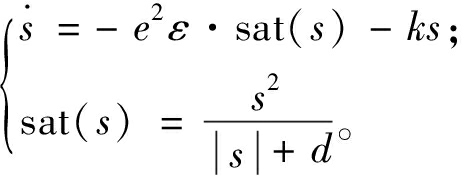
(28)
式中:ε>0; k>0; d为大于零的极小量。
所以可以得到单轮总制动力矩:
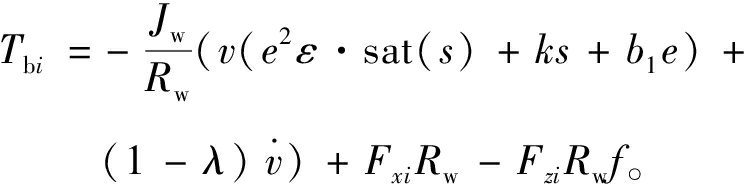
(29)
定义Lyapunov函数为
(30)
对式(30)求导得
(31)
所以定义的Lyapunov函数满足Lyapunov稳定性判据,该积分滑模控制器是渐近稳定的。
4 仿真结果分析
4.1 单一路面仿真分析
以0.6附着路面对控制策略进行验证,初始车速为60 km/h,对应的前后轮最佳滑移率分别为0.086,0.096,仿真结果如图5所示。从图5(a)和图5(b)可以看出,积分滑模控制方法在ABS工作时间内可以使前后轮的滑移率快速且准确地跟踪估计的最佳滑移率,且估计出的最佳滑移率在稳态时与实际的最佳滑移率的最大误差不超过3%。而在制动后期,由于此时车速v≤3 m/s,EMB输出的制动力矩设置为10 MPa,轮速快速降低,实际滑移率快速增大到1.0,而估计的最佳滑移率会在几种典型路面的最佳滑移率区间内,前后轮最佳滑移率的估计值不会大于干沥青路面的最佳滑移率。图5(c)为车速和轮速图,结果表明,在车速为3 m/s之前车轮未发生抱死,前后轮轮速在0.5 s前发生轻微波动,之后维持线性变化的趋势。图5(d)为本文控制策略与CarSim内部策略控制的对比图,且CarSim中开启了ABS功能。可以看出,CarSim控制策略的制动总时间为3.536 s,制动总距离为32.515 m;而本文控制策略的制动总时间为3.154 s,制动总距离为27.380 m,制动总时间缩短了10.8%,制动总距离减少了15.8%,说明本文的控制策略有着更好的制动性能,能够提高车辆的制动安全性。

图5 单一路面仿真结果
Figure 5 Single pavement simulation results
4.2 对接路面仿真分析
设置对接路面仿真工况,初始车速为100 km/h并进行紧急制动,对接路面前50 m的路面利用附着系数为0.801 3,之后驶入附着系数0.380 0的路面,直到车速为0。对应的前50 m的前后轮最佳滑移率分别为0.114 0,0.128 4;后面路程的前后轮最佳滑移率分别为0.054 0,0.055 0。仿真结果如图6所示。

图6 对接路面仿真结果
Figure 6 Docking pavement simulation result
从图6(a)和图6(b)可以看出,在前50 m处,前后轮滑移率在1 s左右到达最佳滑移率并很好地跟踪估计的最佳滑移率,在路面发生变化后,前后轮滑移率经过一定时间的波动后依然能很好地跟踪最佳滑移率,证明估计算法有较高的准确度。图6(c)为车速和轮速图,结果表明,前后轮轮速在对接处会有着一定量的波动,但之后依然维持线性变化的趋势。图6(d)为本文控制策略与CarSim内部策略控制在对接路面的制动距离的对比图,CarSim中同样开启了ABS功能。其中CarSim控制策略的制动总时间为6.865 s,制动总距离为86.660 m;而本文控制策略的制动总时间为5.632 s,制动总距离为76.460 m,制动总时间缩短了18.0%,制动总距离减少了22.2%。说明本文的控制策略在对接路面条件下依然保持了出色的制动性能与制动稳定性。
5 结论
本文在使用EMB系统的基础上,设计了基于最佳滑移率估计的ABS积分滑模控制算法。其中,在最佳滑移率估计部分,同时考虑了典型路面的峰值路面利用附着系数和最佳滑移率间的差异,且为了减少估计过程中的计算量,对估计过程进行了预先处理,平衡了估计算法实时计算量小与估计准确度高的要求。基于CarSim和Simulink的联合仿真模型验证了估计算法在典型路面间的单一路面和对接路面都有良好的准确度,并证明了ABS积分滑模控制器具有良好的控制效果,能够显著降低车辆的制动距离和制动时间,提高车辆的安全性。相比于CarSim内部基于逻辑门限值的ABS算法,本文基于最佳滑移率估计的ABS控制策略在提高汽车制动性能方面具有显著优势。
[1] 陈烨强.浅谈EMB线控制动系统控制策略研究[J].内燃机与配件,2023(17):76-78.CHEN Y Q.Research on control strategy of EMB line control system[J].Internal Combustion Engine &Parts,2023(17):76-78.
[2] 黄会茹.浅谈ABS汽车防抱死制动系统[C]∥第十三届河南省汽车工程科技学术研讨会.信阳:河南省汽车工程学会,2016:113-114.HUANG H R.A brief discussion on ABS automotive anti lock braking system[C]∥ The 13th Henan Province Automotive Engineering Technology Academic Symposium.Xinyang:Society of Automotive Engineers of Henan,2016:113-114.
[3] 孙鹏鹏.紧急制动工况下四轮轮毂电动汽车的滑移率控制策略研究[D].长春:吉林大学,2022:24-33.SUN P P.Research on slip rate control strategy of four in-wheel motors electric vehicle under emergency braking condition[D].Changchun:Jilin University,2022:24-33.
[4] KIM C S,HAHN J O,HONG K S,et al.Estimation of tire-road friction based on onboard 6-DoF acceleration measurement[J].IEEE Transactions on Vehicular Technology,2015,64(8):3368-3377.
[5] DEVADIGA S S,GAURKAR P V,VIVEKANANDAN G,et al.A computationally and data-efficient reference slip estimation algorithm for antilock brake system[C]∥2023 9th International Conference on Control,Decision and Information Technologies (CoDIT).Piscataway:IEEE,2023:471-476.
[6] DINÇMEN E.Adaptive extremum seeking scheme for ABS control[C]∥2014 13th International Workshop on Variable Structure Systems (VSS).Piscataway:IEEE,2014:1-6.
[7] KIM M H,PARK J,CHOI S.Road type identification ahead of the tire using D-CNN and reflected ultrasonic signals[J].International Journal of Automotive Technology,2021,22(1):47-54.
[8] WANG H L,WANG J N,PI D W,et al.Optimization of commercial vehicle mechatronics composite ABS braking control considering braking efficiency and energy regeneration[J].IEEE transactions on transportation electrification,2024:3421303.
[9] 尹安东,李聪聪.电动汽车ABS最优滑移率滑模控制研究[J].汽车科技,2018(2):8-14.YIN A D,LI C C.Research on optimal slip control for ABS of electric vehicle based on sliding mode control[J].Auto Sci-Tech,2018(2):8-14.
[10] 朱振华.独立驱动/制动电动汽车制动能量回收优化控制策略研究[D].长春:吉林大学,2023.ZHU Z H.Research on braking energy recovery optimal control strategy of independent drive/brake electric vehicle[D].Changchun:Jilin University,2023.
[11] 潘公宇,徐申.考虑道路识别的四驱电动汽车再生制动策略[J].江苏大学学报(自然科学版),2024,45(1):1-7.PAN G Y,XU S.Regenerative braking control strategy of four-wheel drive electric vehicle considering road identification[J].Journal of Jiangsu University (Natural Science Edition),2024,45(1):1-7.
[12] WANG J C,HE R.Varying charge voltage in the steps control method of ABS for in-wheel motors driven electric vehicles based on an improved LQG scheme[J].IEEE Access,2018,6:15039-15050.
[13] 夏利红.基于EMB的分布式复合制动系统研究[D].重庆:重庆大学,2019.XIA L H.The study on distributed hybrid braking system based on EMB[D].Chongqing:Chongqing University,2019.
[14] 潘公宇,徐豪晖,刘志强,等.汽车电子机械制动系统的ABS自抗扰控制[J].重庆理工大学学报(自然科学),2024,38(6):55-62.PAN G Y,XU H H,LIU Z Q,et al.ABS automatic disturbance rejection control of automotive electronic mechanical braking system[J].Journal of Chongqing University of Technology (Natural Science),2024,38(6):55-62.
[15] 刘志强,陈玉锦,陈林.电子机械制动器的间隙调控方法[J].兵工学报,2022,43(7):1478-1487.LIU Z Q,CHEN Y J,CHEN L.A gap control method for electromechanical brakes[J].Acta Armamentarii,2022,43(7):1478-1487.
[16] 余志生.汽车理论[M].6版.北京:机械工业出版社,2019:115-117.YU Z S.Automobile theory[M].6th ed.Beijing:China Machine Press,2019:115-117.
[17] ZHANG J H,SUN W C,JING H H.Nonlinear robust control of antilock braking systems assisted by active suspensions for automobile[J].IEEE Transactions on Control Systems Technology,2019,27(3):1352-1359.
[18] 申超.基于路面识别的四轮轮毂电机电动汽车驱动防滑控制策略研究[D].成都:电子科技大学,2016:33-36.SHEN C.Study on acceleration slip regulation control strategy of four-wheel independent drive electric vehicle based on road identification[D].Chengdu:University of Electronic Science and Technology of China,2016:33-36.
[19] 何仁,冯海鹏.基于峰值附着系数曲面的路面辨识算法[J].吉林大学学报(工学版),2020,50(4):1245-1256.HE R,FENG H P.Road surface identification algorithm based on peak adhesion coefficient surface[J].Journal of Jilin University (Engineering and Technology Edition),2020,50(4):1245-1256.
[20] 何仁,李梦琪.基于路面识别的复合制动与ABS集成控制策略[J].江苏大学学报(自然科学版),2020,41(1):20-26.HE R,LI M Q.Integrated control strategy of combined braking system and ABS based on road identification[J].Journal of Jiangsu University (Natural Science Edition),2020,41(1):20-26.