中国拥有一个庞大而复杂的配电网络,但随着分布式能源和新型电动汽车的广泛接入,配网系统的智能化进程显得有些缓慢,暴露出了管理效率较低等多个问题,尤其是缺乏对台区配变短期负荷的精确预测能力[1-2]。负荷预测是电力系统管理的关键环节,它主要包括两个层面:系统层面和配电台区层面。配电台区层面的负荷预测更专注于特定配电变压器服务的区域,可能只针对一个居民区、商业区或工业区的电力需求[3]。精确的台区负荷预测不仅能够帮助公司合理安排维护计划,还能提前发出预警,有效分配抢修资源,并调整电网运行策略[4]。这些措施共同确保了台区用户的电力供应稳定可靠,从而维护了整个电力系统的健康运行。
为了实现精确的短期电力负荷预测,国内外学者进行了广泛且深入的研究。这些研究涉及由简单到复杂、单一模型到组合模型等方法,主要可分为统计分析和机器学习两大类。在统计分析方法中,诸如自回归移动平均模型、卡方检验、傅里叶变换等技术可以利用较为有限的线性数据来构建预测模型。然而,当涉及处理负荷与众多变量之间复杂的非线性关系时,这些方法的性能通常有所不足。目前,已经有多种机器学习的方法[5-6]被提出,如Zhang等[7]采用长短期记忆网络进行用户负荷短期预测,能够很好地处理数据多、波动大、随机性较强的用户负荷时间序列,但因其门结构使得模型较复杂,易出现过拟合情况。为了克服这些缺点,Li等[8]提出了基于GRU门控单元网络的电力负荷预测模型,通过仿真实验表明相较于LSTM模型,GRU模型的平均绝对百分比误差更低、训练速度更快; Li等[9]引入了时间卷积网络(temporal convolutional network,TCN)模型,该网络通过并行处理和扩大感受野的方式,有效克服了传统模型的局限性,为序列数据建模提供了一种高效的方法,尤其适用于处理数据中的长期依赖的问题。
台区配变负荷数据通常包含多种成分,如季节性波动、趋势变化、周期性模式和随机波动等。为了将这些复杂的成分分离出来,以便单独分析它们各自的影响,Su等[10]采用了经验模态分解(empirical mode decomposition,EMD)技术,将数据集分解为4个分量和1个残差,经过仿真验证,平均绝对误差达到了0.015;Wen等[11]引入了变分模态分解(variational mode decomposition,VMD)方法,并利用中心频率法优化VMD的基本参数,进一步提高了预测准确度;为了进一步消除白噪声,Song等[12]通过逐阶向残差加入白噪声的方式构建了完全自适应噪声集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)技术对电力负荷数据进行序列分解,避免了在EMD中人为选择参数的主观性,提高了分解效率。
但是由于受到多元负荷在时间序列中的高频波动性、分解算法固有的限制以及人工调参的主观因素的影响,初次分解得到的一次分量仍然保持着较高的复杂性。这意味着时间序列中的随机性和不规则性并未被完全去除,这给台区配变短期负荷的精确预测带来了挑战。
为了解决这个问题,本文提出了一种基于二次分解和优化变分模态分解的混合模型,用于台区配变短期电力负荷预测。首先,使用最大互信息系数法(maximal information coefficient,MIC)对高维特征的负荷数据集进行了特征提取;其次,使用CEEMDAN对初始台区配变负荷数据进行一次分解;再次,使用白鲨优化算法对VMD的分解序列数K与惩罚系数α进行优化并对第一个高频分量进行分解;最后,将两次分解的子序列输入TCN模型后将得到的子序列重构得到预测结果。将郑州某台区配变负荷数据作为实验对象进行对比实验验证,证明所提模型具有高预测准确性和良好的适用性。
1 模型原理
1.1 变分模态分解
VMD用于非平稳信号的时频分析,每个模态都是独立确定的,这有效地解决了EMD中常见的递归分解所导致的模式混叠问题[13-14],从而保证了信号分解的清晰度和准确性。VMD分解性能的优劣受到分解序列数K与惩罚系数α的显著影响[15]:K的数量直接关系到信号被分解成多少个独立的模态;而α的大小则关乎模态分解的紧致性和平滑性。
1.2 完全自适应噪声集合经验模态分解
CEEMDAN是对集合经验模态分解(ensemble empirical mode decomposition,EEMD)的改进,它提供了更有效的模式混合解决方案,并在计算效率和分解稳定性方面有所提升。与传统分解方法不同,CEEMDAN并不直接在原始信号上叠加高斯白噪声,而是在经验模态分解得到的各个本征模态函数分量(intrinsic mode functions,IMF)中引入自适应的辅助噪声,从而提高了分解的稳定性并优化了信号重构质量[16]。CEEMDAN的分解过程是首先向待分解信号y(t)添加高斯白噪声:
yi(t)=y(t)+zi(t)。
(1)
接着,对叠加了白噪声的信号进行经验模态分解,得到M个固有模态分量Cm(t)(m=1,2,…,M)。为进一步提升分解结果的有效性,将这M个分量进行平均得到
其中
为第一个分量:
(2)
(3)
得到
后,剩余的信号部分即为残差h1(t):
(4)
然后,将h1(t)再次添加高斯白噪声,得到新信号p1(t),以获得第二阶固有模态分量c2和残差h2(t):
(5)
h2(t)=h1(t)-c2。
(6)
重复以上步骤,直至残差无法进一步分解,此时分解过程完成,得到最终信号为
(7)
1.3 白鲨优化算法
白鲨优化算法(white shark optimization,WSO)是Braik等[17]提出的一种新型优化算法,受到大白鲨在导航和捕食过程中展现出的卓越听觉和嗅觉能力的启发。该算法具有全面的搜索策略和有效规避局部极值的优点。白鲨依靠高度发达的感官系统,能够根据猎物移动所带来的水波振动来清楚地发现目标,并以最快速度向其靠近。白鲨的移动速度如下所示:
(8)
p1=pmax+(pmax-pmin)e-(4k/K)2;
(9)
p2=pmin+(pmax-pmin)e-(4k/K)2。
(10)
式中:i为个体数量;k为迭代步数;
和
分别为第i条白鲨在第k和k+1次迭代的速度;wk和lk分别为白鲨在第k次迭代全局所处的最佳位置和群体所处的最佳位置;
为第i条白鲨在第k次迭代的位置;p1和p2分别为wk和lk对
的影响参数;c1和c2均为[0,1]的随机数;μ为收缩速度,计算公式为
(11)
式中:τ表示加速度系数。
在锁定目标后,白鲨会围绕目标展开攻击,随后迅速调整游动路径,朝最优地点靠近并准备对目标发动进攻:
(12)
式中:
为第i条白鲨位置的调整量;r1、r2、r3均为[0,1]的随机数;sgn(r2-0.5)表示给出1或-1来改变移动的方向;Dw为目标距离白鲨的长度;ss为搜索敏感度,计算公式为
ss=|1-e(-a2k/K)|。
(13)
重复以上操作,保留最优秀的两个位置调整量,并根据这两个位置调整量选择白鲨的最优位置:
(14)
式中:rand为随机生成的小数。经过模拟以上白鲨捕食行为的过程,可以在解空间中进行渐进式搜索,扩大了搜索范围,进而适应多种优化问题,展现出非常强的全局搜索能力。
1.4 时间卷积网络
TCN通过引入扩张卷积和因果卷积,有效克服了卷积神经网络(convolutional neural network,CNN)在处理长时间序列数据时遇到的感受野受限和梯度消失等问题[18],从而更适应时序数据的特性[19]。因果扩张卷积的示意图如图1所示。这种结构确保了输出的时间序列严格遵循时间顺序,避免了未来信息的泄露,同时扩张卷积有效地增大了感受野,使得网络能够在更广泛的上下文中捕捉时间依赖性,而不需要增加额外的参数,从而在保持模型简洁的同时提高了对复杂时序数据的处理能力[20]。
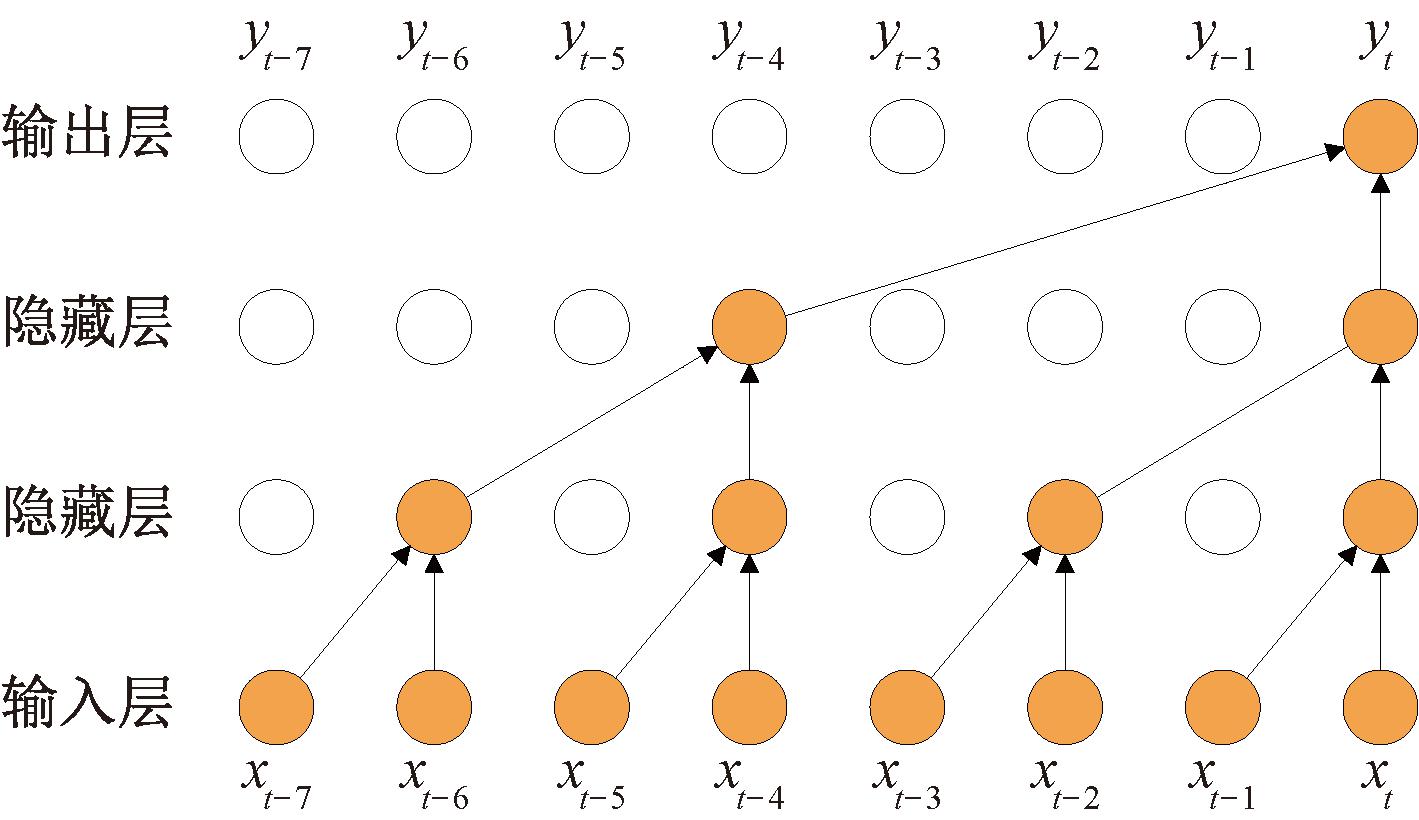
图1 因果扩张卷积
Figure 1 Causal expansion convolution
在CNN的基础上,TCN进一步引入了残差网络。如图2所示,这种连接方式有助于缓解深层网络中的梯度消失问题,并促进恒等映射的充分学习,从而使网络能够更有效地进行反向传播,增强模型对时序数据的表征能力,进而提高了网络的训练效率和稳定性。
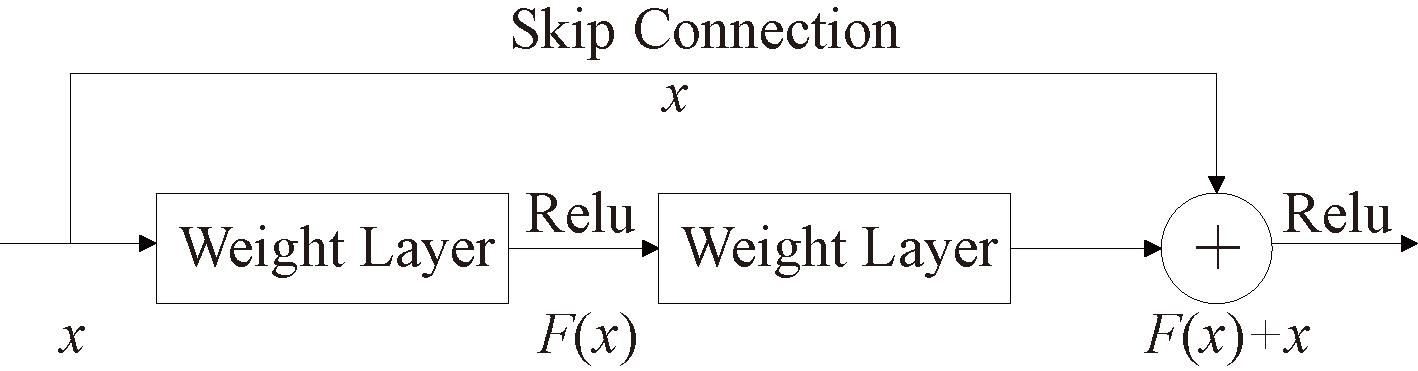
图2 TCN残差网络
Figure 2 TCN residual networks
2 基于二次分解的台区配变短期电力负荷预测模型
2.1 二次分解模型构建
本文建立了基于优化VMD二次分解的台区配变短期电力负荷预测模型,模型预测流程如图3所示,主要包括以下部分。
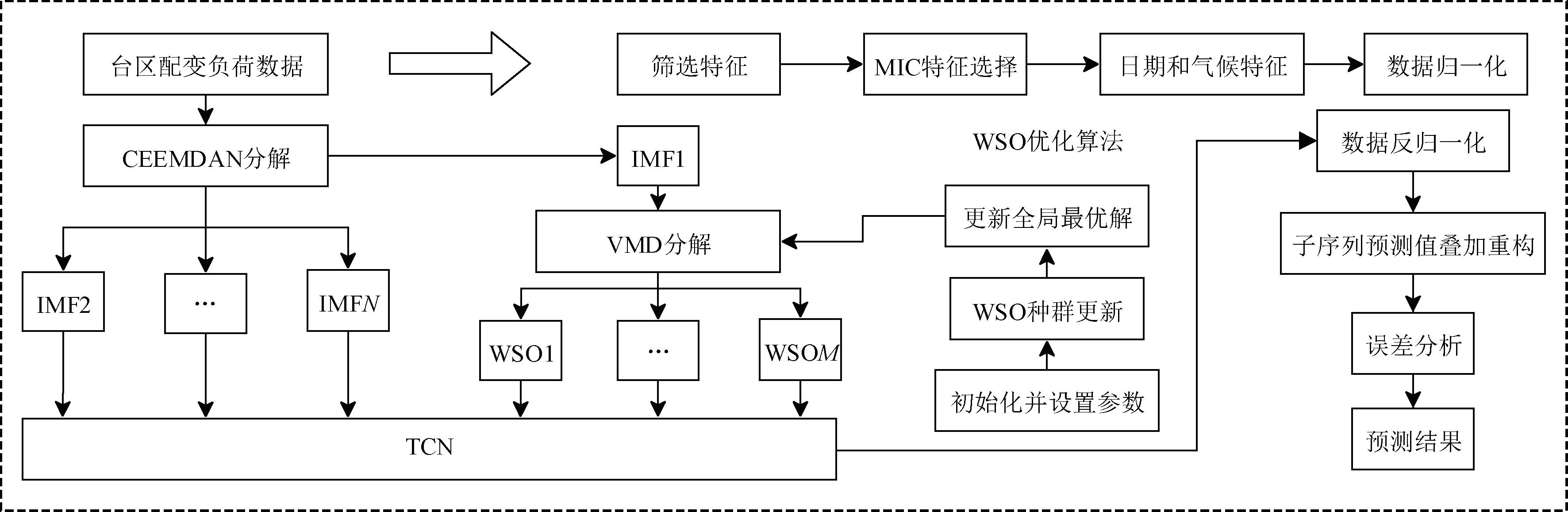
图3 预测模型整体架构
Figure 3 Overall architecture of prediction model
(1)数据预处理。短期负荷预测依赖历史数据,而这些数据的采集过程通常包括测量、记录和传输等多个环节。只要任何环节出现失误都会导致负荷数据存在异常值或缺失值,同时日常生活中的各种随机因素也会影响采集负荷数据的准确性。因此,初始数据预处理对预测精度起关键作用。
(2)MIC特征选择。计算负荷数据集所有特征与负荷之间的MIC值并进行排序,然后选择MIC值较大的特征作为输入。
(3)完全自适应噪声集合经验模态分解。通过CEEMDAN分解技术对台区配变负荷序列进行处理,将其转换为N个平稳且易于处理的子序列,充分保留原始负荷信号在时频域的局部特征。
(4)使用经WSO优化的VMD对第一个高频分量进行二次分解,得到M个WSO子序列。
(5)对一次分解和二次分解得到的子序列建立TCN预测模型并输入到TCN中进行负荷预测。
(6)台区配变短期电力负荷预测结果。在对各个子序列进行预测后,将其结果叠加以得到最终的负荷预测值。
(7)评价与分析。将预测值与实际负荷数据对比分析,并借助误差评估指标对预测结果进行分析,以检验模型的预测性能。
2.2 评价指标
为了评估所使用模型的准确性和可靠性,本文所选的评价指标为平均绝对百分比误差MAPE、平均绝对误差MAE和均方根误差RMSE:
(15)
(16)
(17)
式中:n为总数量;i为第i个特征值;yi为第i个真实值;
为第i个真实值的预测值。
3 算例分析
3.1 数据说明及数据预处理
本文数据选用郑州市某小区一个配变2022年6月1日—2022年8月31日的负荷数据,以每1 h为步长进行一次采集,单位为kW,每天共包含24个数据点,原始电力负荷数据序列如图4所示。将数据集中2022年6月1日—2022年8月30日的数据作为训练集,将最后一天的数据作为测试集。
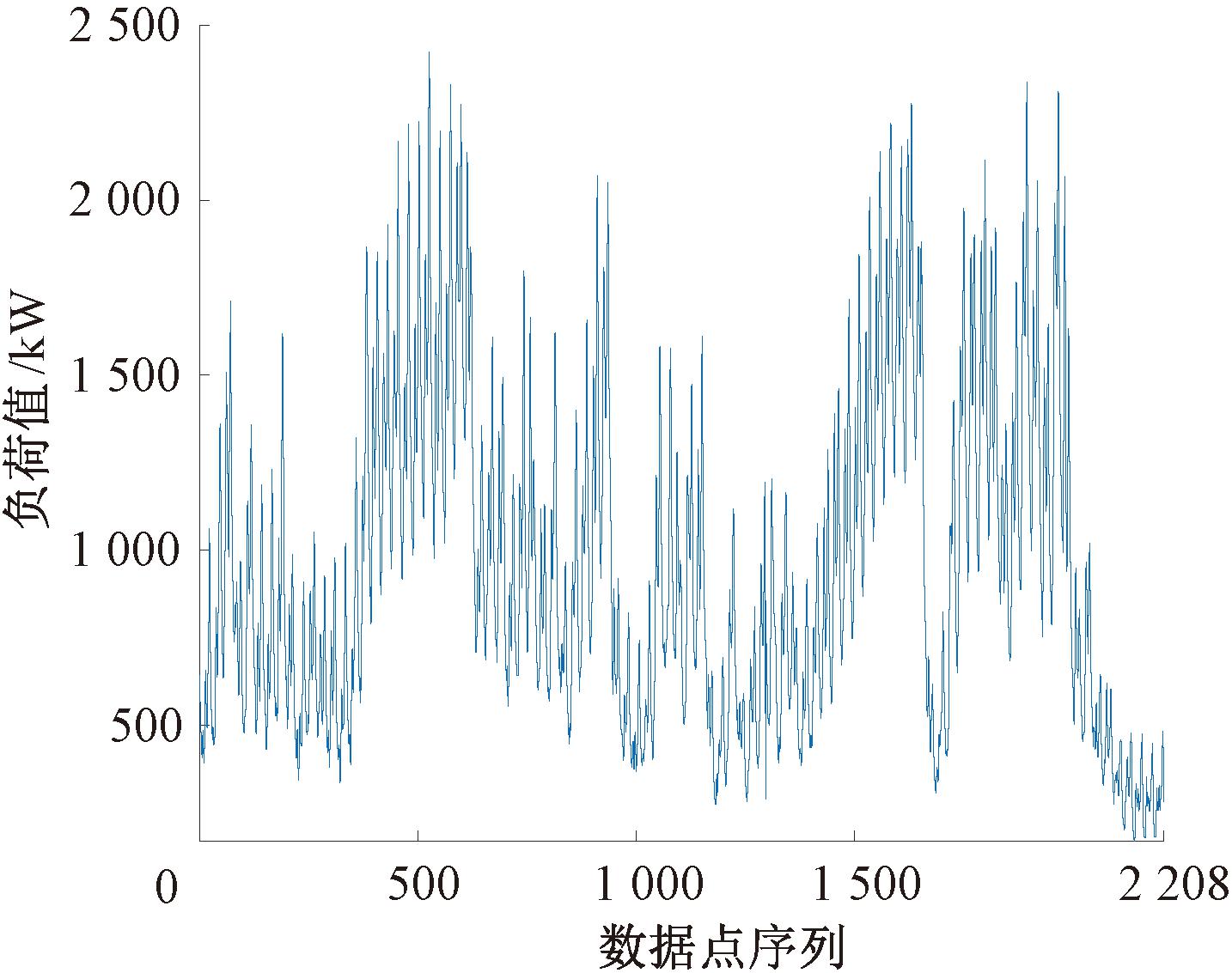
图4 原始负荷图
Figure 4 Original electric load
对预处理的数据进行最大最小值归一化处理,将数据压缩到[-1,1],使负荷预测模型能适应不同数据类型,计算公式如下所示:
(18)
式中:x为原始值;Xnorm为经过归一化处理后的值;xmax和xmin分别为数据集中的最大值和最小值。
3.2 最大互信息系数
利用MIC法得到了每个特征跟电力负荷的重要性结果,其中,温度、时间、平均风速、工作日、相对湿度、平均风向、降雨量的MIC值分别为0.77,0.64,0.60,0.53,0.52,0.35,0.29。因此,温度的最大互信息系数最大,降雨量的最大互信息系数最小。通过实验,本文决定选择温度、时间、平均风速、工作日和相对湿度作为后续配变负荷预测的输入特征。
3.3 二次分解参数选择
如图5所示,对采集到的台区配变负荷数据进行第一次CEEMDAN分解,其中IMF1～IMF9表示分解的子序列,res表示分解的残差分量。从图5可以看出,经过CEEMDAN分解,原始负荷数据的复杂度得到了降低。其中,IMF1～IMF9的频率依次降低。IMF9反映了台区配变负荷数据在低频上的整体变化趋势,过程缓慢且平缓。而IMF1则反映了台区配变负荷的瞬间波动和局部变化趋势,仍然包含一些随机噪声,并保留了原始数据中的非线性细节。因此,本文对IMF1使用VMD进行二次分解,并利用WSO算法对VMD的参数进行寻优。当VMD的分解序列数K为3、惩罚系数α为2 173时达最优,最优综合指标为2.752 7,产生了3个子序列。与IMF1分量相比,这些子序列显示出更高的规律性和平稳性,其序列复杂度显著降低。具体结果见图6。
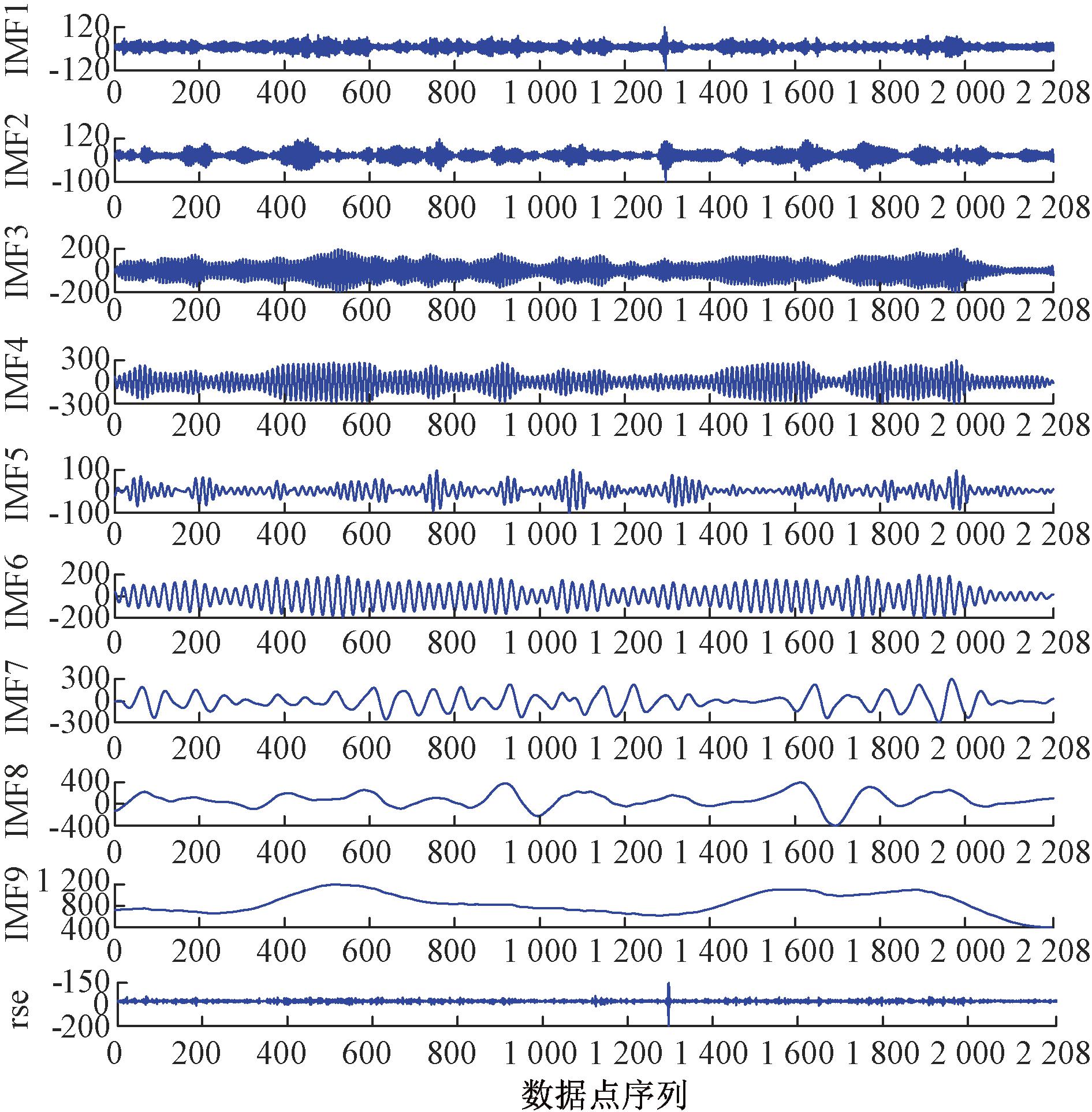
图5 一次分解序列图
Figure 5 One time decomposition sequence diagram
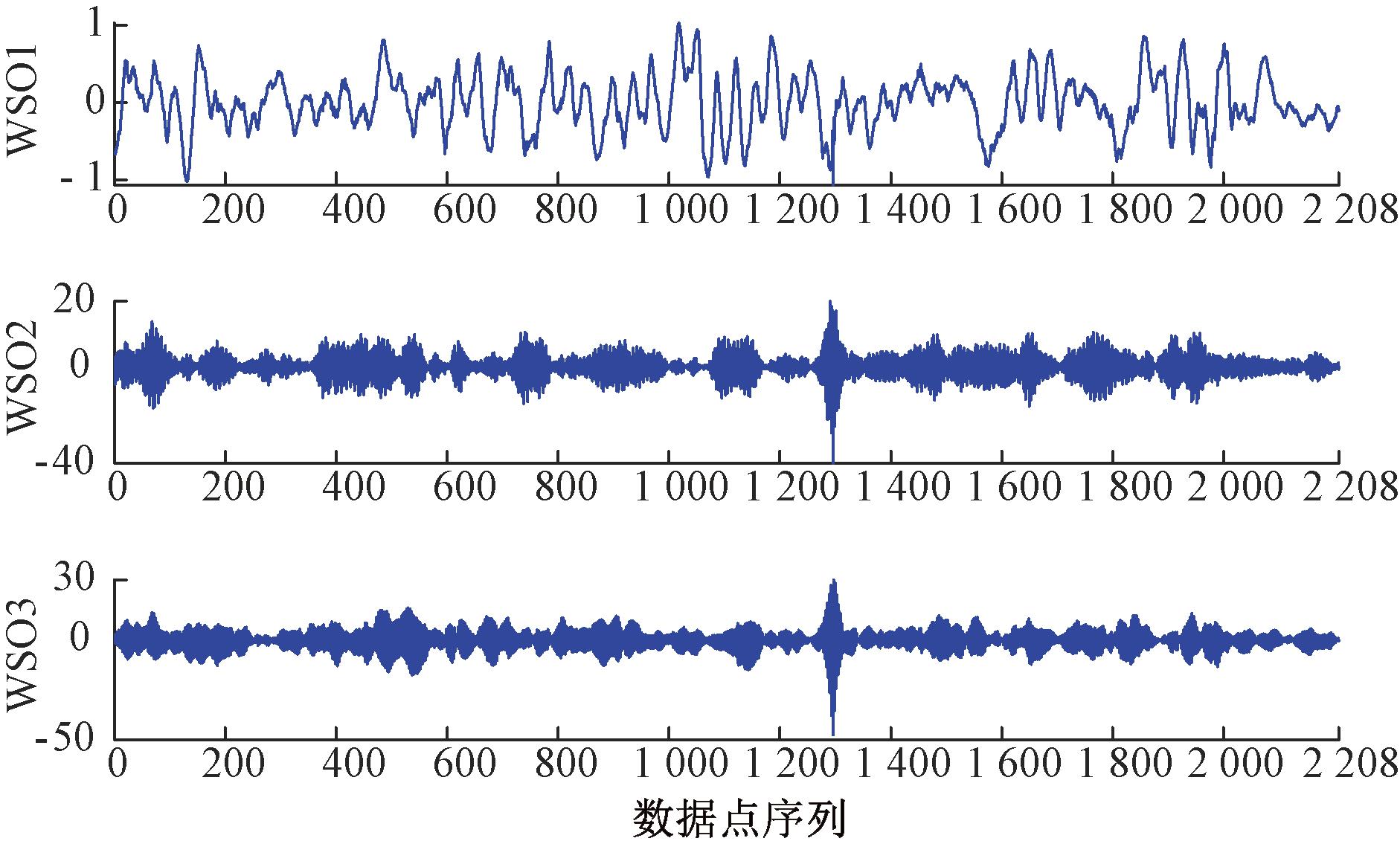
图6 IMF1分量二次分解图
Figure 6 IMF1 component secondary decomposition diagram
3.4 短期负荷预测
设置TCN网络滤波器数量为16,滤波器大小为3;激活函数是Relu;残差单元数量为2;Dropout率为0.2。如表1和图7所示,预测值与实际负荷值非常接近,最小的平均绝对百分比误差达0.88%,证明了本文的CEEMDAN-WSO-VMD-TCN预测模型对台区配变时间序列负荷有很好的预测效果。
表1 预测结果误差分析
Table 1 Error analysis of prediction results
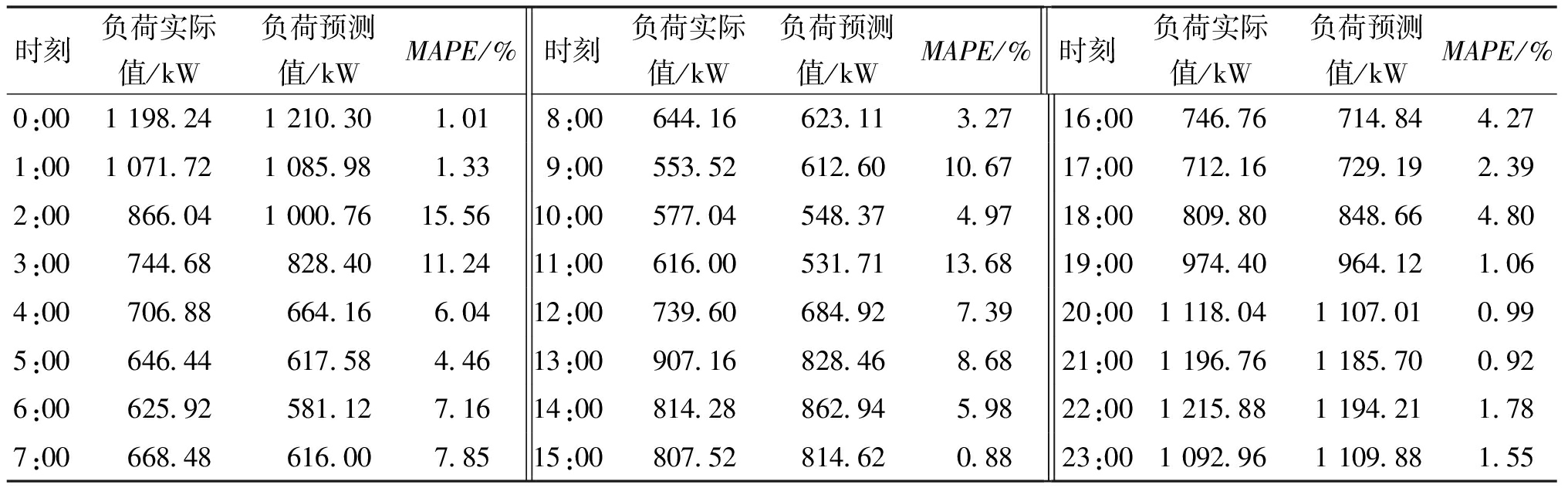
时刻负荷实际值/kW负荷预测值/kWMAPE/%时刻负荷实际值/kW负荷预测值/kWMAPE/%时刻负荷实际值/kW负荷预测值/kWMAPE/%0:001198.241210.301.018:00644.16623.113.2716:00746.76714.844.271:001071.721085.981.339:00553.52612.6010.6717:00712.16729.192.392:00866.041000.7615.5610:00577.04548.374.9718:00809.80848.664.803:00744.68828.4011.2411:00616.00531.7113.6819:00974.40964.121.064:00706.88664.166.0412:00739.60684.927.3920:001118.041107.010.995:00646.44617.584.4613:00907.16828.468.6821:001196.761185.700.926:00625.92581.127.1614:00814.28862.945.9822:001215.881194.211.787:00668.48616.007.8515:00807.52814.620.8823:001092.961109.881.55
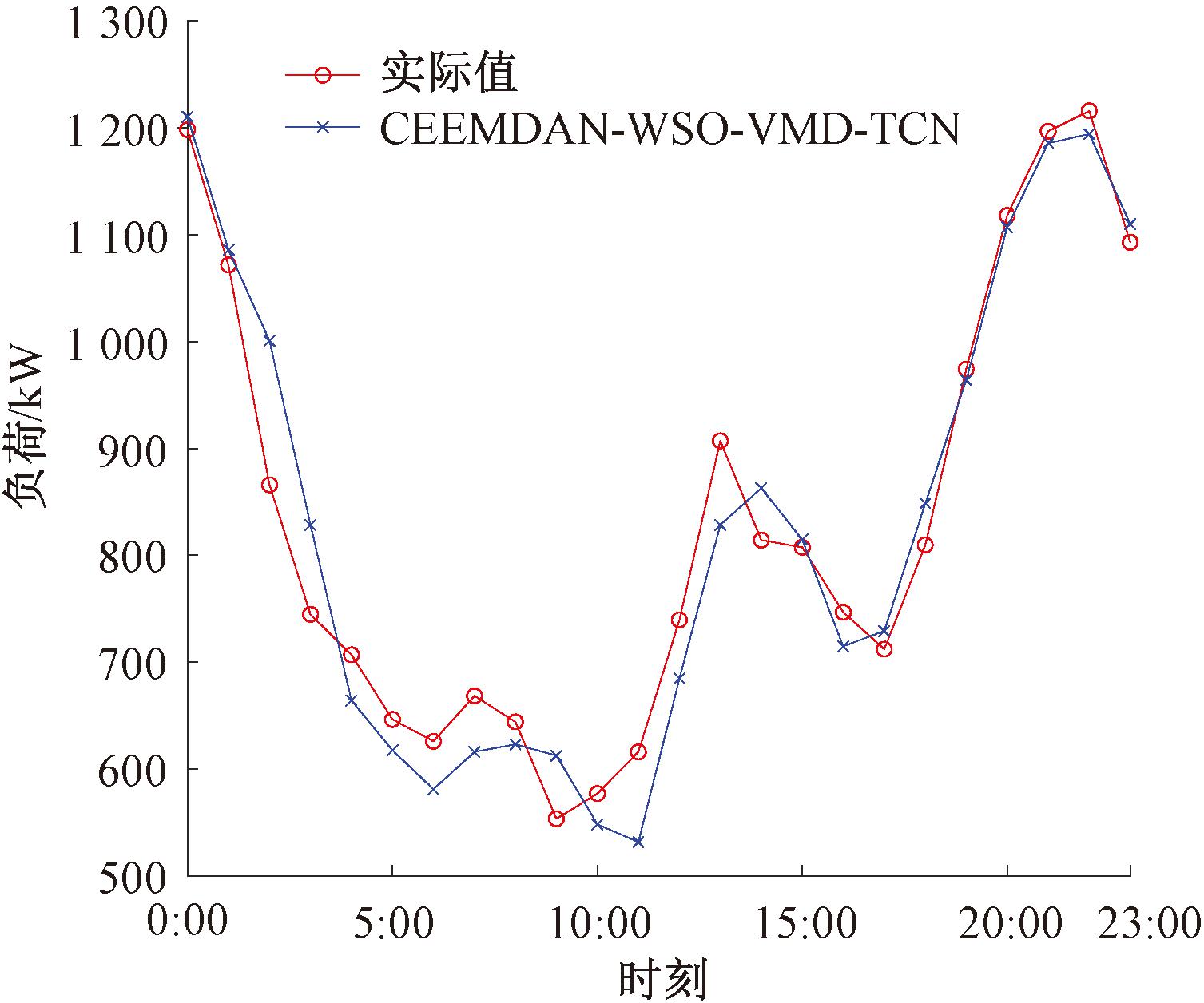
图7 CEEMDAN-WSO-VMD-TCN预测结果
Figure 7 CEEMDAN-WSO-VMD-TCN prediction results
为了验证本文所提方法的有效性,将不进行模态分解的TCN模型(模型1)、仅使用一次分解的TCN模型(模型2)和未经优化的二次分解的TCN模型(模型3)与经过优化的二次分解的TCN模型(模型4)进行对比实验。
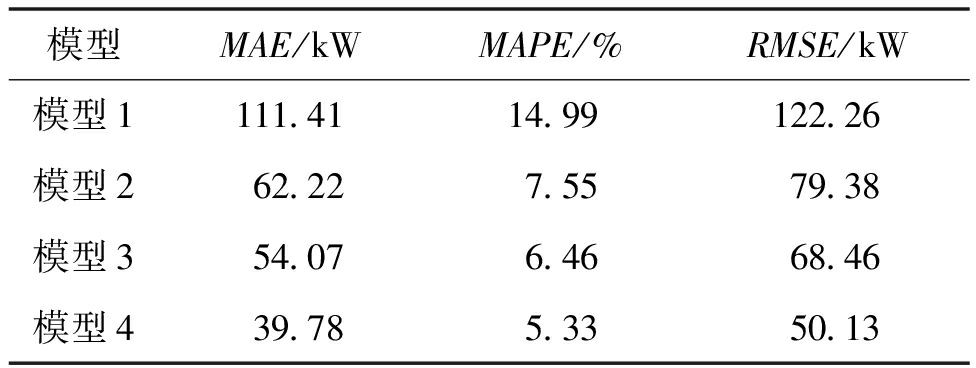
由表2和图8可知,仅使用TCN模型无法有效捕捉时间序列负荷数据的周期性特征,因此在进行预测时得到的预测曲线与实际负荷曲线存在较大偏差,其MAE、MAPE和RMSE分别为111.41 kW、14.99%和122.26 kW。相较之下,CEEMDAN-TCN模型在预测性能上有了显著的提升,MAE、MAPE和RMSE分别减少了44.15%,7.44百分点和35.07%,但在负荷的高峰和低谷时段的预测误差仍较大。通过进一步对负荷序列使用VMD二次分解后,预测误差得到进一步降低。与CEEMDAN-TCN模型相比,CEEMDAN-VMD-TCN的MAE、MAPE和RMSE分别下降了13.10%,1.09百分点和13.76%。本文提出的CEEMDAN-WSO-VMD-TCN模型在性能上表现最优,与CEEMDAN-VMD-TCN相比,其MAE、MAPE和RMSE分别减少了26.43%,1.13百分点和26.77%。特别在负荷曲线的拐点处,该模型的拟合效果最佳,预测曲线更加接近实际负荷数据曲线,从而验证了所提方法在提高台区配变负荷预测精度和模型性能方面的有效性。
表2 预测模型评价指标
Table 2 Evaluation indicators for predictive models
模型MAE/kWMAPE/%RMSE/kW模型1111.4114.99122.26模型262.227.5579.38模型354.076.4668.46模型439.785.3350.13
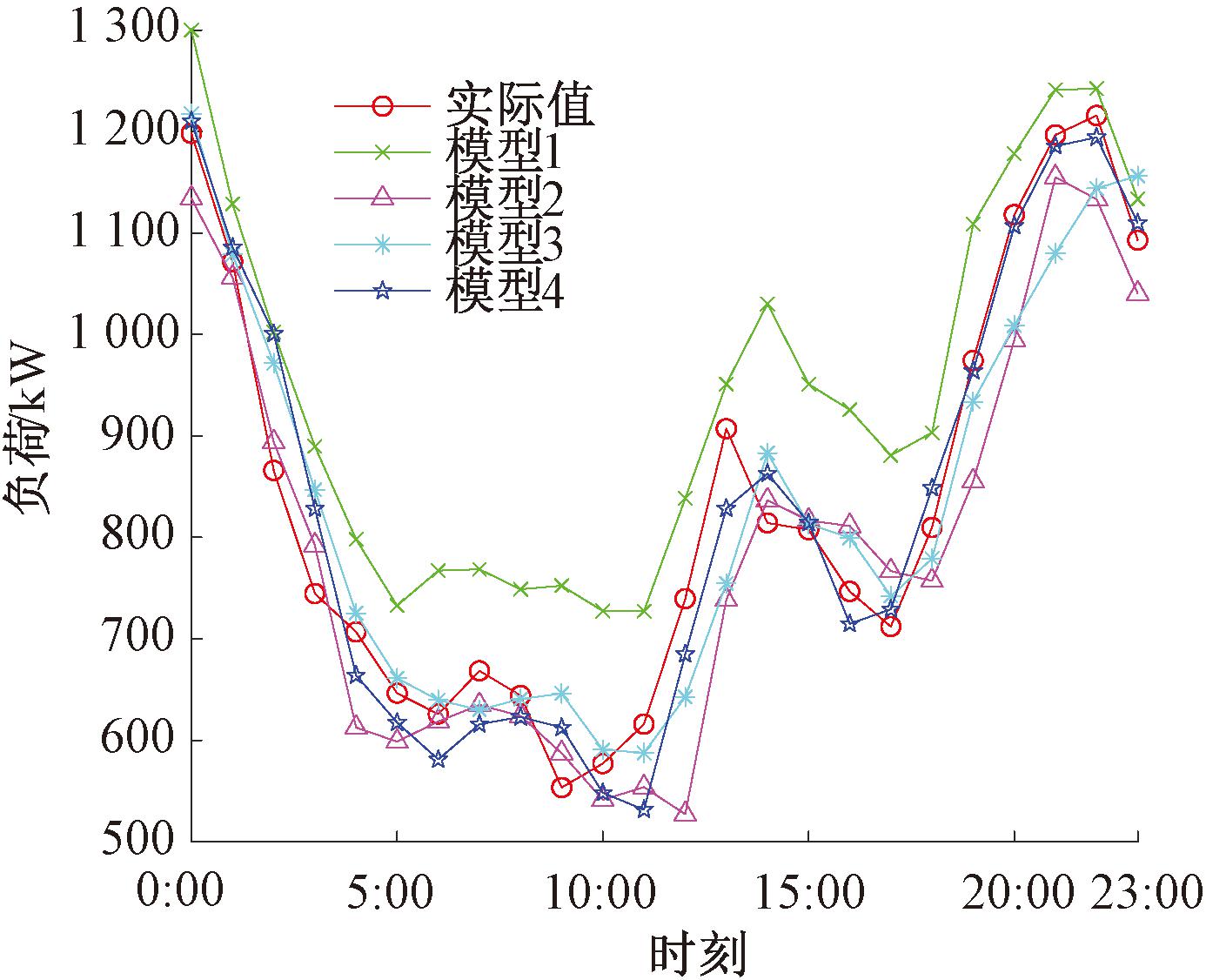
图8 预测对比图
Figure 8 Prediction comparison chart
4 结论
为了解决台区配变负荷数据中的高复杂性和强波动性问题,本文提出了一种基于优化VMD二次分解的数据处理技术。通过采用CEEMDAN和VMD进行二次分解,成功地减少了负荷数据中的噪声成分,显著增强了数据的可预测性和稳定性。此外,本文引入WSO优化算法对VMD的参数进行优化,提升了模型的预测精度。
本文提出了一种结合二次分解和时间卷积网络的负荷预测模型,充分考虑了负荷数据的非线性特性以及时间序列的依赖性。通过将分解后的多个子序列输入TCN模型进行预测,本文方法能够有效捕捉负荷数据中的复杂波动和长期变化趋势。与传统的预测模型相比,本文提出的模型在预测准确性和鲁棒性方面展现了显著优势,能够更好地应对台区配变负荷数据的复杂性。
(本文受到国网河南省电力公司科技项目(52171024000A)的资助。)
[1] 张明泽,栾文鹏,艾欣,等.基于边缘计算的台区短期负荷预测方法[J].电测与仪表,2024,61(4):93-99.ZHANG M Z,LUAN W P,AI X,et al.Short-term substation load forecasting method based on edge computing[J].Electrical Measurement &Instrumentation,2024,61(4):93-99.
[2] 李甲祎,赵兵,刘宣,等.基于DWT-Informer的台区短期负荷预测[J].电测与仪表,2024,61(3):160-166,191.LI J Y,ZHAO B,LIU X,et al.Short-term substation load forecasting based on DWT-Informer model[J].Electrical Measurement &Instrumentation,2024,61(3):160-166,191.
[3] 习伟,蔡田田,张镇,等.融合多元影响因素的配电台区BiLSTM负荷预测方法[J].天津大学学报(自然科学与工程技术版),2023,56(11):1205-1216.XI W,CAI T T,ZHANG Z,et al.BiLSTM load forecasting method for transformer districts integrated with multiple influencing factors[J].Journal of Tianjin University (Science and Technology),2023,56(11):1205-1216.
[4] 季玉琦,严亚帮,和萍,等.基于K-Medoids聚类与栅格法提取负荷曲线特征的CNN-LSTM短期负荷预测[J].电力系统保护与控制,2023,51(18):81-93.JI Y Q,YAN Y B,HE P,et al.CNN-LSTM short-term load forecasting based on the K-Medoids clustering and grid method to extract load curve features[J].Power System Protection and Control,2023,51(18):81-93.
[5] 魏骜,茅大钧,韩万里,等.基于EMD和长短期记忆网络的短期电力负荷预测研究[J].热能动力工程,2020,35(4):203-209.WEI A,MAO D J,HAN W L,et al.Short-term load forecasting based on EMD and long short-term memory neural networks[J].Journal of Engineering for Thermal Energy and Power,2020,35(4):203-209.
[6] 张建寰,吉莹,陈立东.深度学习在电力负荷预测中的应用[J].自动化仪表,2019,40(8):8-12,17.ZHANG J H,JI Y,CHEN L D.Application of deep learning in power load forecasting[J].Process Automation Instrumentation,2019,40(8):8-12,17.
[7] ZHANG S Q,ZHANG N J,ZHANG Z Q,et al.Electric power load forecasting method based on a support vector machine optimized by the improved seagull optimization algorithm[J].Energies,2022,15(23):9197.
[8] LI C,GUO Q J,SHAO L,et al.Research on short-term load forecasting based on optimized GRU neural network[J].Electronics,2022,11(22):3834.
[9] LI M X,ZHANG T Y,YANG H Z,et al.Multiple load forecasting of integrated renewable energy system based on TCN-FECAM-informer[J].Energies,2024,17(20):5181.
[10] SU Z Y,ZENG J H,LIU J,et al.A short-term power load forecasting approach based on EMD-SSA-LSTM[J].Journal of Physics:Conference Series,2024,2774(1):012005.
[11] WEN Y,PAN S,LI X X,et al.Highly fluctuating short-term load forecasting based on improved secondary decomposition and optimized VMD[J].Sustainable Energy,Grids and Networks,2024,37:101270.
[12] SONG K Y,YU Y,ZHANG T F,et al.Short-term load forecasting based on CEEMDAN and dendritic deep learning[J].Knowledge-Based Systems,2024,294:111729.
[13] 穆晨宇,薛文斌,穆羡瑛,等.基于VMD-LSTM-Attention模型的短期负荷预测研究[J].现代电子技术,2023,46(17):174-178.MU C Y,XUE W B,MU X Y,et al.Research on short-term load forecasting based on VMD-LSTM-Attention model[J].Modern Electronics Technique,2023,46(17):174-178.
[14] 贾世会,刘立夫,迟晓妮,等.基于BWO和WOA的VMD-LSTM短期风速预测[J].郑州大学学报(工学版),2025,46(3):59-66.JIA S H,LIU L F,CHI X N,et al.VMD-LSTM short-term wind speed prediction model based on BWO and WOA[J].Journal of Zhengzhou University (Engineering Science),2025,46(3):59-66.
[15] 蒋建东,张海峰,郭嘉琦.基于改进蜣螂优化算法的短期风电功率预测[J].郑州大学学报(工学版),2025,46(4):129-136.JIANG J D,ZHANG H F,GUO J Q.Short-term wind power prediction based on improved dung beetle optimization algorithm[J].Journal of Zhengzhou University (Engineering Science),2025,46(4):129-136.
[16] CHEN Z X,JIN T,ZHENG X D,et al.An innovative method-based CEEMDAN-IGWO-GRU hybrid algorithm for short-term load forecasting[J].Electrical Engineering,2022,104(5):3137-3156.
[17] BRAIK M,HAMMOURI A,ATWAN J,et al.White shark optimizer:a novel bio-inspired meta-heuristic algorithm for global optimization problems[J].Knowledge-Based Systems,2022,243:108457.
[18] LIU M P,SUN X H,WANG Q N,et al.Short-term load forecasting using EMD with feature selection and TCN-based deep learning model[J].Energies,2022,15(19):7170.
[19] ZHOU F Z,ZHOU H,LI Z Y,et al.Multi-step ahead short-term electricity load forecasting using VMD-TCN and error correction strategy[J].Energies,2022,15(15):5375.
[20] CAI C C,LI Y J,SU Z H,et al.Short-term electrical load forecasting based on VMD and GRU-TCN hybrid network[J].Applied Sciences,2022,12(13):6647.