移动群智感知(mobile crowdsensing,MCS)是一种新型的数据收集模式,广泛应用于商业和公共领域。典型的MCS系统由服务提供商、移动用户和云平台组成,服务提供商通过云平台发布任务,移动用户利用智能设备(如智能手机、平板电脑)采集数据。例如,环境监测部门通过MCS收集空气质量和噪声数据,实现实时监控;应急响应机构获取灾害现场信息支持救援;地理信息系统通过更新数据提升地图精度[1];交通管理部门收集流量信息优化交通系统,提高城市效率[2]。MCS具有大规模、实时、低成本、高效益和广泛覆盖等优势[3]。早期用户通常自愿参与感知任务,导致参与度低且数据质量难以保障。为提高参与积极性并确保数据可靠性,服务提供商引入激励机制,支付报酬吸引用户完成任务。MCS的激励机制类似反向拍卖,低报价用户更易中标。因此,激励机制设计[4-5]、隐私保护[6]和任务分配[7-8]等问题成为研究重点。
现有的MCS激励机制通常采用反向密封投标拍卖,用户需向服务提供商提交私人信息(如报价),服务提供商根据这些信息选取用户。然而,该机制存在缺陷,如缺乏透明性,用户需信任服务提供商不滥用其私人信息并严格执行规则。尽管理论上反向拍卖具有防策略性,但实际中用户常提供虚假信息,主要原因在于其防策略性难以验证,难以获得用户信任[9]。
时钟拍卖是一种多轮拍卖机制,每轮拍卖中,拍卖者向投标人提供价格,投标人可选择接受、拒绝或退出。随着轮次推进,价格逐步下降,拍卖在达到预设条件时结束,交易根据最后一轮协议完成。图1展示了基于时钟拍卖的移动群智感知服务模型。时钟拍卖具备显式防策略性、弱群体防策略性、高透明度和简单实现等优点,具有较强的实际操作性[10]。
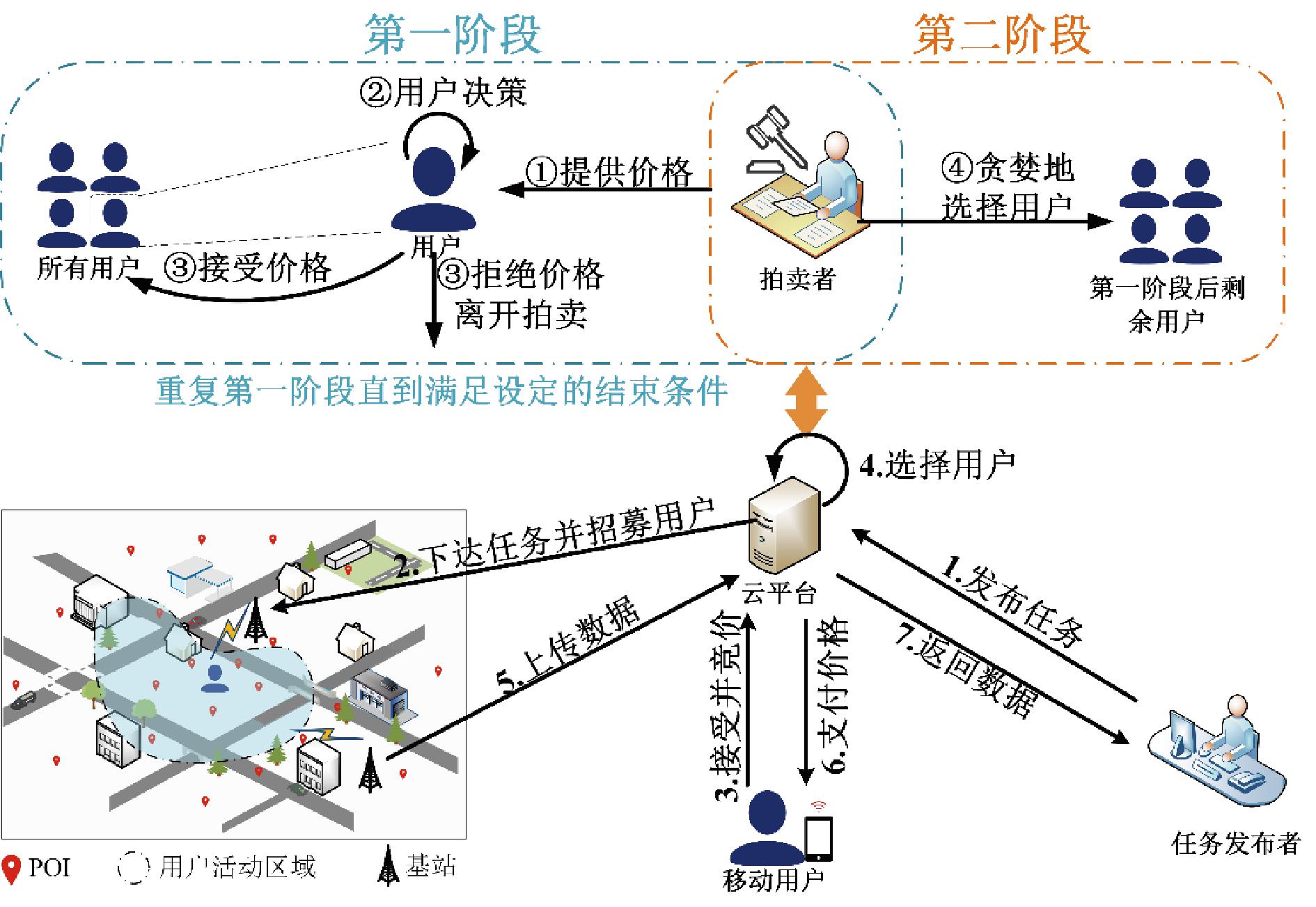
图1 基于时钟拍卖的移动群智感知服务模型
Figure 1 Clock auction-based mobile crowdsensing model
在移动群智感知中,服务提供商通常面临预算约束,用户选择需考虑任务完成后的价值收益和合理补偿。因此,预算可行性成为机制设计的关键限制。时钟拍卖的防策略性简化了机制设计,只需要解决预算约束与价值最大化问题。然而,这也带来了新挑战:如何在预算约束下,基于时钟拍卖理论合理分配数据采集任务,以实现数据价值最大化。
为应对上述挑战,本文基于时钟拍卖理论设计了一种多阶段激励机制,继承了时钟拍卖的优良特性。本文的主要贡献包括以下内容。将MCS中预算约束下的数据价值最大化问题建模为整数规划,并证明其单调次模特性;提出移动群智感知的时钟拍卖(mobile crowdsensing clock auction,MCCA)机制,实现用户分配与支付,满足真实性、个体理性和预算约束,运行时间为多项式级;实验表明,MCCA在价值收益、隐私保护和执行效率上优于现有算法。
1 相关工作
1.1 移动群智感知
当前,解决移动群智感知问题的常见方法是将问题建模为兴趣点(point of interest,POI)模型。该模型中,服务提供商在数据收集区域设置多个POI,为每个POI分配相应的数据收集任务。许多研究基于POI模型展开。Zhang等[4]探讨了在UAV-BS网络下实现DT模型效用最大化的问题,并采用逆向拍卖机制求解。Xiong等[11]提出了新的移动群智感知框架EMC3,在考虑用户隐私、最小任务分配数量和感知区域覆盖的约束条件下,减少用户执行任务时的资源损耗。Zhang等[12]则基于POI模型,研究了地震灾区的无人机数据收集问题,将其转化为整数规划模型,并设计了Max-UDC进化算法,通过迭代和变异选择最佳任务序列。这些研究表明,基于POI模型的移动群智感知服务建模已成为一种主流方法。
1.2 时钟拍卖
Milgrom等[10]证明时钟拍卖对应一种特定的后向贪婪算法,并介绍了其类别和优良属性,进一步研究了其在不同环境中的表现。Dütting等[13]提出了一种高效的时钟拍卖算法,对于背包拍卖设置(物品数量为m)实现了O(log m)的近似,对于单一目标投标者的组合拍卖设置则实现了![]() 的近似。Li[14]指出时钟拍卖属于更广泛的明显防策略(OSP)机制类,并在单一目标投标者的组合拍卖背景下进行了研究。尽管如此,包含不相交最大集合的可行性约束的实例仍然是一个挑战性问题。Balkanski等[15]在O(n2log n)时间复杂度下,为预算可行时钟拍卖实现了单调次模价值的4.75常数近似。上述研究表明,时钟拍卖已受到广泛关注,但其在移动群智感知任务分配中的应用仍较为罕见。
的近似。Li[14]指出时钟拍卖属于更广泛的明显防策略(OSP)机制类,并在单一目标投标者的组合拍卖背景下进行了研究。尽管如此,包含不相交最大集合的可行性约束的实例仍然是一个挑战性问题。Balkanski等[15]在O(n2log n)时间复杂度下,为预算可行时钟拍卖实现了单调次模价值的4.75常数近似。上述研究表明,时钟拍卖已受到广泛关注,但其在移动群智感知任务分配中的应用仍较为罕见。
2 问题及机制设计
2.1 参数定义
在有限预算B的约束下,服务提供商需要从M个POI中收集数据,并通过云平台发布任务。设POI集合为![]() ={1,2,…,M},服务提供商对不同POI的偏好各异,重要性较高的POI能够带来更高的收益。定义任意POI点为j∈
={1,2,…,M},服务提供商对不同POI的偏好各异,重要性较高的POI能够带来更高的收益。定义任意POI点为j∈![]() ,其对应的价值为vj∈R+。为了确保数据收集的完整性和有效性,POI点j可能需要多个用户参与,并且每个POI的收集次数有限,超出该限值将不再产生额外价值。进一步定义POI点j的有效数据收集次数为rj∈Z+。当数据收集任务达到或超过rj次时,服务提供商将获得价值vj;若任务次数少于rj次,则获得的价值为vj的部分。服务提供商可以根据具体需求合理设定每个POI点j的价值vj和有效次数rj。
,其对应的价值为vj∈R+。为了确保数据收集的完整性和有效性,POI点j可能需要多个用户参与,并且每个POI的收集次数有限,超出该限值将不再产生额外价值。进一步定义POI点j的有效数据收集次数为rj∈Z+。当数据收集任务达到或超过rj次时,服务提供商将获得价值vj;若任务次数少于rj次,则获得的价值为vj的部分。服务提供商可以根据具体需求合理设定每个POI点j的价值vj和有效次数rj。
此外,假设有N个用户参与数据收集服务,用户通过云平台获取服务提供商发布的数据收集任务。设用户集合为![]() ={1,2,…,N}。任意用户i是否参与POI点j的数据收集由变量aij表示,aij∈{0,1},其中1代表i参与j点收集数据,0则代表不参与。用户i在M个POI点的参与情况由向量ai=(ai1,ai2,…,aiM)表示。用户i参与任务时会产生数据收集成本ci,该成本与用户i对各POI点的参与情况,数据收集的通信成本、时间成本等因素密切相关。
={1,2,…,N}。任意用户i是否参与POI点j的数据收集由变量aij表示,aij∈{0,1},其中1代表i参与j点收集数据,0则代表不参与。用户i在M个POI点的参与情况由向量ai=(ai1,ai2,…,aiM)表示。用户i参与任务时会产生数据收集成本ci,该成本与用户i对各POI点的参与情况,数据收集的通信成本、时间成本等因素密切相关。
当服务提供商发布数据收集任务后,用户i根据任务要求和自身情况向云平台提交参与信息ai。设所有用户的参与情况为θ=(a1,a2,…,aN),服务提供商根据θ使用向量p=(p1, p2,…,pN)表示各用户的补偿。用户i参与任务后的效益ui定义为ui=pi-ci,即用户获得的补偿减去其成本。
在MCS模型中,POI点的价值来源于收集的数据,但对同一POI点的多次收集会导致边际效益迅速下降。考虑到单调次模函数的直观性,选择![]() 型函数作为价值函数,它能有效反映边际效益下降的特征。单个POI点j的价值函数为
型函数作为价值函数,它能有效反映边际效益下降的特征。单个POI点j的价值函数为
Vj(
![]()
(1)
式中: 为选中的用户集合,即
为选中的用户集合,即 ⊆
⊆![]() ;
; j为参与POI点j数据收集的用户集合,即
j为参与POI点j数据收集的用户集合,即 j⊆
j⊆ ;|
;| j|表示在j收集次数。当|
j|表示在j收集次数。当| j|≥rj时,服务提供商获得POI点j的全部价值。基于此,服务提供商在M个POI点获得的总价值可定义为
j|≥rj时,服务提供商获得POI点j的全部价值。基于此,服务提供商在M个POI点获得的总价值可定义为
V(
![]()
 )。
)。
(2)
对于任意用户集合![]() 、
、![]() ⊆
⊆![]() ,定义V(
,定义V(![]() |
|![]() )为集合
)为集合![]() 对于集合
对于集合![]() 的边际效益,V(
的边际效益,V(![]() |
|![]() )=V(
)=V(![]() ∪
∪![]() )-V(
)-V(![]() )。主要参数如表1所示。
)。主要参数如表1所示。
表1 主要参数
Table 1 Main parameters

符号 含义 选中的用户集合 B 预算 vj POI 点 j 的价值 pi 给用户 i 的补偿 ui 用户 i 的效益 Et t 轮设定的目标价值 t t 轮中选中的用户集合 POI 集合 ai 用户 i 对 POI 点的参与情况向量 rj POI 点 j 数据有效收集次数 ci 用户 i 的成本 活跃用户集合 θ 所有用户的参与情况 V({i} | t) 用户 i 对 t 产生的边际效益
2.2 问题模型
研究目标是在预算约束下选择一个用户子集 ⊆
⊆![]() ,使得该子集产生的价值最大化,可以表述为
,使得该子集产生的价值最大化,可以表述为
Maximize V(
![]()
 ),
),  ⊆
⊆![]() ;
;
(3)
![]()
(4)
pi≥ci,∀ i∈ 。
。
(5)
其中,式(4)表示总支付小于等于预算;式(5)表示补偿大于等于用户成本。
在模型中,用户i仅需要提交参数ai,不需要提交隐私数据如真实成本ci,因此不存在谎报风险。虽然ci不需提交,但确定补偿pi时通常需参考该信息。用户i的补偿策略定义为![]() 当si=ci时视为诚实;当
当si=ci时视为诚实;当![]() 时视为不诚实,通过提交虚假成本获取更高补偿。用向量S=(s1,s2,…,sN)表示所有用户策略,S-i=(s1,…,si-1,si+1,…,sN)表示除用户i外的策略。定义用户效益函数为
时视为不诚实,通过提交虚假成本获取更高补偿。用向量S=(s1,s2,…,sN)表示所有用户策略,S-i=(s1,…,si-1,si+1,…,sN)表示除用户i外的策略。定义用户效益函数为
(6)
(7)
其中,式(6)是用户i诚实时的效益;而式(7)是不诚实时的效益。
2.3 机制设计要求
为防止用户策略操纵分配结果与补偿,需设计满足以下定义的机制。
定义1 个体理性。如果一个机制满足个体理性,当且仅当用户i提交ai后,其效益满足ui({S-i,ci})≥0。即用户在诚实参与分配时,效益始终非负,不会产生损失[16]。
定义2 真实性。一个机制满足真实性,当且仅当用户i提交ai并以真实成本参与分配是其优势策略,即用户无法通过虚假报告提升效益[17]。
定义3 预算可行性。如果拍卖机制在预算上是可行,则对所有赢家的支付总额不得超过最大预算B,即![]()
定义4 计算效率。为保证计算效率,实际应用中需在多项式时间内求解一般背包问题的可行解[19],而非追求指数级时间复杂度的最优解。
2.4 单调次模属性
定义5 单调次模函数。设一个有限集![]() 和定义在
和定义在![]() 上的函数f:2
上的函数f:2![]() →R,如果该函数满足以下两个性质,则称其为单调次模函数:
→R,如果该函数满足以下两个性质,则称其为单调次模函数:
(1)单调性:对于任意集合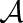 ⊆
⊆![]() ⊆
⊆![]() ,有f(
,有f(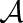 )≤f(
)≤f(![]() )。
)。
(2)次模性:对于任意集合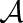 ⊆
⊆![]() ⊆
⊆![]() 和任意元素x∈
和任意元素x∈![]() \
\![]() 有
有
f( ∪{x})-f(
∪{x})-f( )≥f(
)≥f(![]() ∪{x})-f(
∪{x})-f(![]() )。
)。
(8)
引理1 Vj( )是单调次模函数。
)是单调次模函数。
证明 假设 1⊆
1⊆ 2⊆
2⊆ ,x∈
,x∈ \
\ 2,可得
2,可得
![]()
(9)
则Vj( 1∪{x})-Vj(
1∪{x})-Vj( 1)的最终结果为
1)的最终结果为
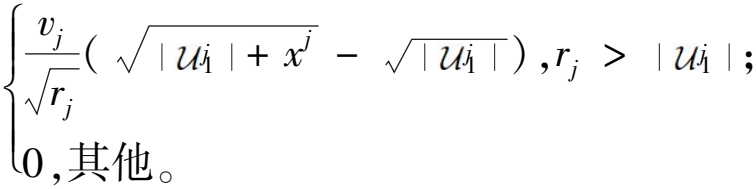
(10)
其中,xj∈{0,1}表示元素x对子价值函数Vj的贡献:0表示无贡献;1表示有贡献。
同理,Vj( 2∪{x})-Vj(
2∪{x})-Vj( 2)的最终结果为
2)的最终结果为
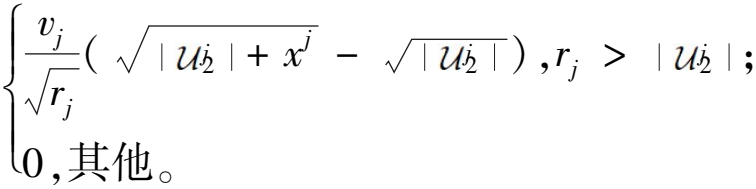
(11)
由式(10)、(11)可得
Vj( 1∪{x})-Vj(
1∪{x})-Vj( 1)≥Vj(
1)≥Vj( 2∪{x})-Vj(
2∪{x})-Vj( 2)。
2)。
(12)
所以Vj( )是单调次模函数。
)是单调次模函数。
定理1 V( )是单调次模函数。
)是单调次模函数。
证明 对于总价值函数V( ),由式(2)知:
),由式(2)知:
V( 1∪{x})-V(
1∪{x})-V( 1)=
1)=
(13)
V( 2∪{x})-V(
2∪{x})-V( 2)=
2)=
(14)
结合式(12)可得
V( 1∪{x})-V(
1∪{x})-V( 1)≥V(
1)≥V( 2∪{x})-V(
2∪{x})-V( 2)。
2)。
(15)
所以,V( )是一个单调次模函数。
)是一个单调次模函数。
3 MCCA机制设计
3.1 设计MCCA算法
受时钟拍卖机制[15]启发,提出移动群智感知的时钟拍卖机制MCCA,通过逐轮提高服务提供商最大可获价值的预估,逐步向用户提供补偿。每轮中,满足预估值的用户被搁置,未满足的用户进入下一轮,直到没有用户满足预估值,类似反向贪婪算法。初始时,所有用户为活跃用户,选择效益最大的用户i,初始估计E1设为较低的单个用户价值,所有用户获初始补偿B。每轮中,目标Et更新为前一轮的两倍,MCCA选择边际贡献最大用户i满足Et,并为新增用户提供补偿pi,其中:
(16)
若用户i接受补偿pi,则加入集合![]() t;若拒绝,则从活跃用户集合
t;若拒绝,则从活跃用户集合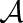 中移除。
中移除。
第一阶段后,MCCA生成用户集合![]() 和
和 以及补偿向量p,接着,基于
以及补偿向量p,接着,基于![]() 在
在 中以贪婪策略选出符合预算的最佳用户,确定赢家集合。
中以贪婪策略选出符合预算的最佳用户,确定赢家集合。
算法1 移动群智感知的时钟拍卖算法。
输入:移动用户![]() ,价值函数V,预算B,用户的投标信息θ;
,价值函数V,预算B,用户的投标信息θ;
输出:赢家集合 ,补偿向量p。
,补偿向量p。
① t←1;
② 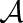 ←
←![]() ;
;
③ ![]() 0←∅;
0←∅;
④ ![]() 1←{argmaxi∈
1←{argmaxi∈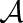 V({i})};
V({i})};
⑤ Et←V(![]() 1);
1);
⑥ for each i∈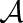 do
do
⑦ pi←B;
⑧ end for
⑨ while 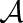 \(
\(![]() t∪
t∪![]() t-1)≠∅ do
t-1)≠∅ do
⑩ t←t+1;
 Et←2Et-1;
Et←2Et-1;

![]() t←∅;
t←∅;
 while V(
while V(![]() t)<Et and
t)<Et and 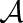 \(
\(![]() t∪
t∪![]() t-1)≠∅ do
t-1)≠∅ do
 i←argmaxi∈
i←argmaxi∈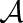 \(
\(![]() t∪
t∪![]() t-1)V({i}|
t-1)V({i}|![]() t);
t);
 if user i accepts price pi then
if user i accepts price pi then

![]() t←
t←![]() t∪{i};
t∪{i};
 else
else

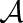 ←
←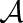 \{i};
\{i};
 end if
end if
 end while
end while
 end while
end while

![]() ←
←![]() t-1;
t-1;

 ←
←![]() t;
t;
 while
while ![]() ≠∅ do
≠∅ do
 u←argmaxi∈
u←argmaxi∈![]() (V(i|
(V(i| )/pi);
)/pi);

![]() ←
←![]() \{u};
\{u};

 ←
← ∪{u};
∪{u};
 end if
end if
 end while
end while
 return
return  ,p;
,p;
3.2 MCCA的性质
引理2 在MCCA中,当用户策略S、价值函数V、参与情况θ和预算B已知时,每轮选定的用户集合![]() t是唯一确定的。
t是唯一确定的。
证明 MCCA是一种迭代算法,每轮用户选择与支付补偿均基于上一轮结果。初始用户集合![]() 1、目标值E1和支付补偿pi已初始化且确定。在用户选择中采用argmaxi∈
1、目标值E1和支付补偿pi已初始化且确定。在用户选择中采用argmaxi∈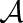 \(
\(![]() t∪
t∪![]() t-1)V({i}|
t-1)V({i}|![]() t)方式,这是一种贪婪策略,而非随机。因此,第t轮选定的用户集合
t)方式,这是一种贪婪策略,而非随机。因此,第t轮选定的用户集合![]() t是确定的。
t是确定的。
引理3 任意i∈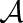 ,给i提供的补偿pi与si无关。
,给i提供的补偿pi与si无关。
证明 由MCCA机制可知,当i被选中时,给i的补偿为![]() 由i∈
由i∈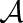 可知i接受了上一次给他的补偿,也就是min函数中的pi是已知的。
可知i接受了上一次给他的补偿,也就是min函数中的pi是已知的。![]() 结合引理2也是可以确定的。故给i的补偿pi与si无关。
结合引理2也是可以确定的。故给i的补偿pi与si无关。
定理2 MCCA机制是真实的。
证明 当用户决策为{S-i,ci}时,用户i有两种可能:i不是赢家i∉ ;i是赢家i∈
;i是赢家i∈ 。
。
(1)i∉ 。此时ui({S-i,ci})=0,只需要得到
。此时ui({S-i,ci})=0,只需要得到![]() 而i∉
而i∉ 有以下两种可能。
有以下两种可能。
i∉![]() ∪
∪ 。此时i拒绝了补偿pi,拒绝的原因是pi<ci,效益为负。并且由引理3可知,pi与si无关,而给i的补偿pi是递减的,所以不管i是否用
。此时i拒绝了补偿pi,拒绝的原因是pi<ci,效益为负。并且由引理3可知,pi与si无关,而给i的补偿pi是递减的,所以不管i是否用![]() 成为赢家,效益都不为正,即
成为赢家,效益都不为正,即![]()
i∈![]() ,但i∉
,但i∉ 。i接受最后补偿pi,如果i使用
。i接受最后补偿pi,如果i使用![]() 拒绝补偿pi(第一阶段就离开),i∉
拒绝补偿pi(第一阶段就离开),i∉![]() ∪
∪ ,此时ui({S-i,c′i})=0;当i使用si=c′i同样接受给他的最后补偿,即i∈
,此时ui({S-i,c′i})=0;当i使用si=c′i同样接受给他的最后补偿,即i∈![]() 。到第二阶段,MCCA机制在
。到第二阶段,MCCA机制在![]() 中选出赢家的方式为argmaxi∈
中选出赢家的方式为argmaxi∈![]() (V(i|
(V(i| )/pi),只与用户的补偿和对集合
)/pi),只与用户的补偿和对集合 产生的边际效益有关,与si无关,不管i使用任何策略,i都无法成为赢家,
产生的边际效益有关,与si无关,不管i使用任何策略,i都无法成为赢家,![]()
(2)i∈ 。此时ui({S-i,ci})>0,只需证明i使用si=c′i同样成为赢家,因为如果不是赢家,则此时
。此时ui({S-i,ci})>0,只需证明i使用si=c′i同样成为赢家,因为如果不是赢家,则此时![]() 成立。i∈
成立。i∈ 则一定有i∈
则一定有i∈![]() ∪
∪ ,而MCCA机制在第二阶段中选出赢家集合
,而MCCA机制在第二阶段中选出赢家集合 只与价值函数V、预算B、用户参与情况θ有关。所以此时i∈
只与价值函数V、预算B、用户参与情况θ有关。所以此时i∈ ,依然是赢家。同样由引理3可知,不管si=ci还是
,依然是赢家。同样由引理3可知,不管si=ci还是![]() 给i的最后补偿pi与si无关。所以
给i的最后补偿pi与si无关。所以![]() 综上,
综上,![]() 由定义2可知,MCCA机制是真实的。
由定义2可知,MCCA机制是真实的。
定理3 MCCA满足个体理性。
证明 如果机制满足个体理性,则有ui({S-i,ci})≥0。当用户未成为最终赢家时,其效益为 0,因此仅需关注赢家用户i的最终支付补偿pi>ci。在MCCA机制中,用户通过双向选择参与决策[20]。当用户接受补偿pi时,其选择符合个体理性,因此MCCA机制满足个体理性。
定理4 MCCA是预算可行的。
证明 如果MCCA是预算可行的,则![]() 假设第一阶段在第
假设第一阶段在第![]() 轮结束,此时
轮结束,此时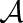
![]() 可得
可得
(17)
在![]() 轮的目标价值
轮的目标价值![]() 过高,没有更多的活跃用户可提供更低的补偿来达到目标价值
过高,没有更多的活跃用户可提供更低的补偿来达到目标价值![]() 可得
可得
(18)
![]() 是满足预算B的,因为当
是满足预算B的,因为当![]() 时,
时,![]() 结合式(17)可知:
结合式(17)可知:
(19)
(20)
根据二阶段的用户选择方式可知集合 满足预算B。
满足预算B。
定理5 MCCA满足计算效率。
证明 MCCA的执行时间主要集中在第一阶段[15]。内部循环最多执行n次,每次在至多n个用户中选出边际效益最大的用户,复杂度为O(n2)。外部循环在条件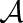
![]() 满足时终止,目标值Et从初始值E1(单用户最高价值)倍增至最多nE1,循环次数为O(log n)。第二阶段采用贪婪选择,复杂度为O(n2)。因此,MCCA的总复杂度为O(n2log n),满足计算效率要求。
满足时终止,目标值Et从初始值E1(单用户最高价值)倍增至最多nE1,循环次数为O(log n)。第二阶段采用贪婪选择,复杂度为O(n2)。因此,MCCA的总复杂度为O(n2log n),满足计算效率要求。
4 实验
本文将MCCA算法与Truthful Greedy算法[21]和CPLEX求解器的最优结果OPT进行对比。Truthful Greedy用于云服务的虚拟机分配问题,具有高效、易实现、接近最优等特点,适合作为基准。最优结果由CPLEX求解器计算,但因其为NP难问题,实际应用中不可行,且不具有真实性和个体理性,仅用于评估MCCA的价值收益。实验从用户规模、预算规模和POI规模3个维度展开,比较总价值、支付金额和执行时间等指标。
4.1 实验设置
选择POI。实验基于图2所示的实际地图(云南省昆明市呈贡区,约3 km2),在地图可达区域内选取50个POI。设置wj∈{1,2,…,10}表示POI覆盖区域的重要性,价值和覆盖次数均与wj相关,其中覆盖次数rj=「σwj⎤;价值vj=「4σrj⎤;σ为随机值,取值为[1.5, 2]。

图2 POI覆盖区域的真实地图
Figure 2 Real map of the POI coverage area
生成用户。根据实际地图的人员密集程度生成500名用户,其参与POI的情况如下:以用户为中心,半径100 m范围内的POI数量为nj,用户i的参与个数为⎣njδ」,其中δ为[0.5,1]的随机数。参与情况基于参与个数和用户位置生成。用户成本ci根据参与情况与各参与POI间的路程计算,最终乘以随机因子β∈(1.2,2)得出。
MCCA算法仅要求用户提供参与情况ai,无须上报成本。而Truthful Greedy算法要求用户同时上报参与情况ai和报价bi,其用户效益为
(21)
为适配本问题,假设用户报价bi=ci。为比较CPLEX最优结果,因其仅负责分配且无法确定补偿,设定用户补偿为成本,用户效益始终为0。然而,CPLEX面临较大的求解复杂度,例如用户数为200时解空间规模达2200。因此限制求解时间为600 s,输出求解时间内的最优解。在MCCA中,只要给用户的补偿pi>ci,用户就会接受补偿并参与任务。所有算法使用相同数据,并对每个指标进行50次测试以消除随机性影响,结果取平均值。
4.2 实验结果
4.2.1 用户规模影响
实验设置用户数量从20起,每次增加20,直至200;服务提供商预算为400元,POI数量为50。结果如图3所示。
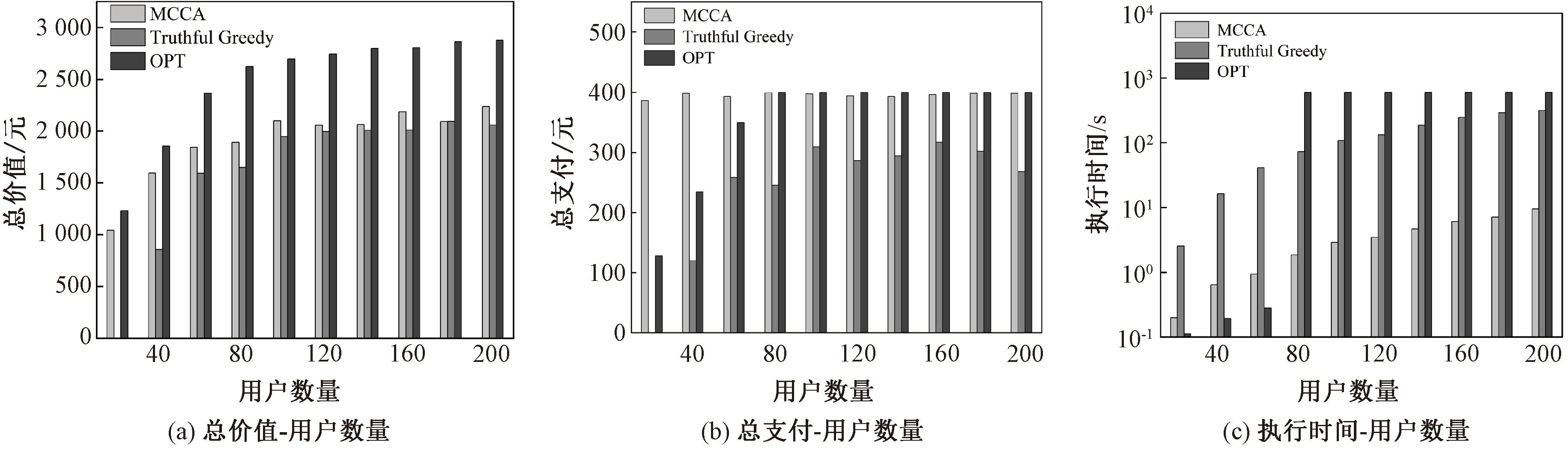
图3 用户规模的影响
Figure 3 Impact of user scale
由图3(a)可知,总价值基于式(1)和式(2)计算,呈单调次模特性。初期用户增加时,总价值快速增长,随后逐渐放缓。当用户数为20时,Truthful Greedy因采用Vickrey定价且用户过少无法替代定价,未选出赢家。而MCCA总价值略优于Truthful Greedy。尽管OPT理论最优,但不具真实性,MCCA与最优结果差距较小。由图3(b)可知,MCCA支付成本高于Truthful Greedy。MCCA支付与边际效益和预算B紧密相关,接近预算上限,第二阶段通过预算约束选出更多用户,进一步提高支付。相比之下,Truthful Greedy通过替代用户定价,通常留有部分预算。OPT支付随着用户的增加先上升后趋稳定,反映了预算限制的影响。由图3(c)可知,OPT初期执行时间较短,但随着用户增多,受限于CPLEX求解器,最终达到600 s。MCCA执行时间约为OPT和Truthful Greedy的1/10。Truthful Greedy需要多次重复分配步骤,且分配的赢家越多,重复次数越多;而MCCA通过逐步降低用户补偿、减少剩余用户,限制了时钟拍卖轮次,从而实现较低执行时间。
4.2.2 预算影响
在此实验中,服务提供商的预算从50元开始,按50元的步长增加至500元,用户数量为200,POI数量为50。实验结果如图4所示。
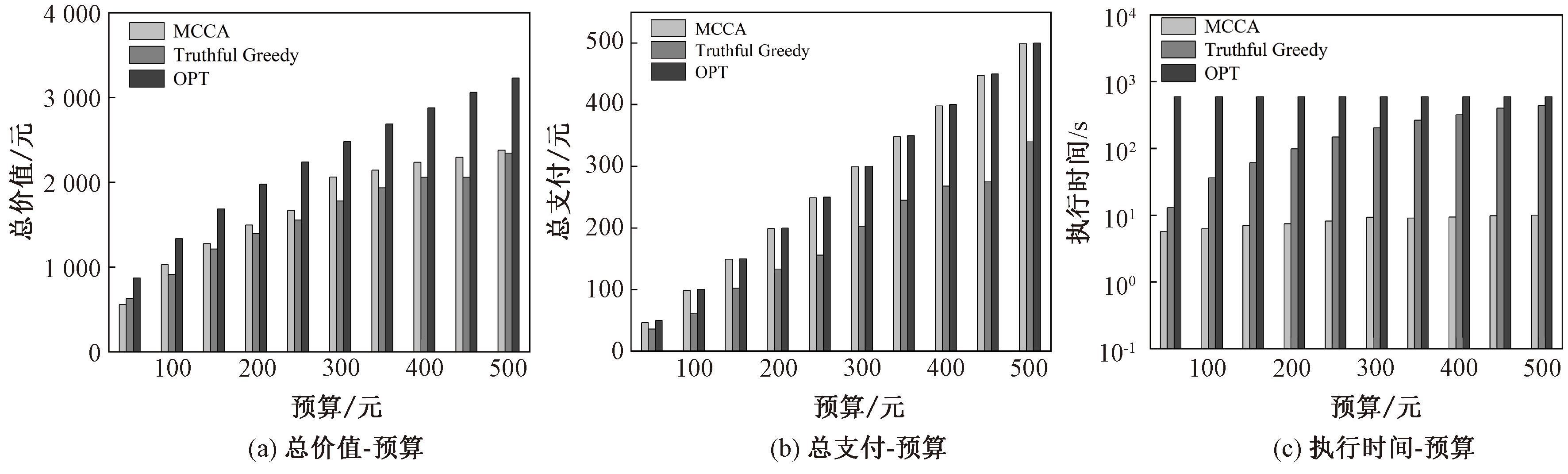
图4 预算规模的影响
Figure 4 Impact of budget scale
如图4(a)所示,随着预算增加,3种算法的总价值均上升,但由于边际效益递减,增幅逐渐减小。MCCA的总价值略高于Truthful Greedy,而OPT由于预算限制较松,达到了最大总价值。图4(b)显示,随着预算增加,赢家数和支付金额增加。MCCA支付高于Truthful Greedy,因为MCCA更充分利用预算,而Truthful Greedy则通过替代用户确定补偿。由图4(c)可知,MCCA的执行时间为OPT和Truthful Greedy的1/10,且几乎与预算无关,主要受用户规模影响。
4.2.3 POI规模影响
本实验中,POI数量从10开始,以10为步长增加至50,POI通过随机选择,用户数量为200,服务提供商预算为400元。实验结果如图5所示。
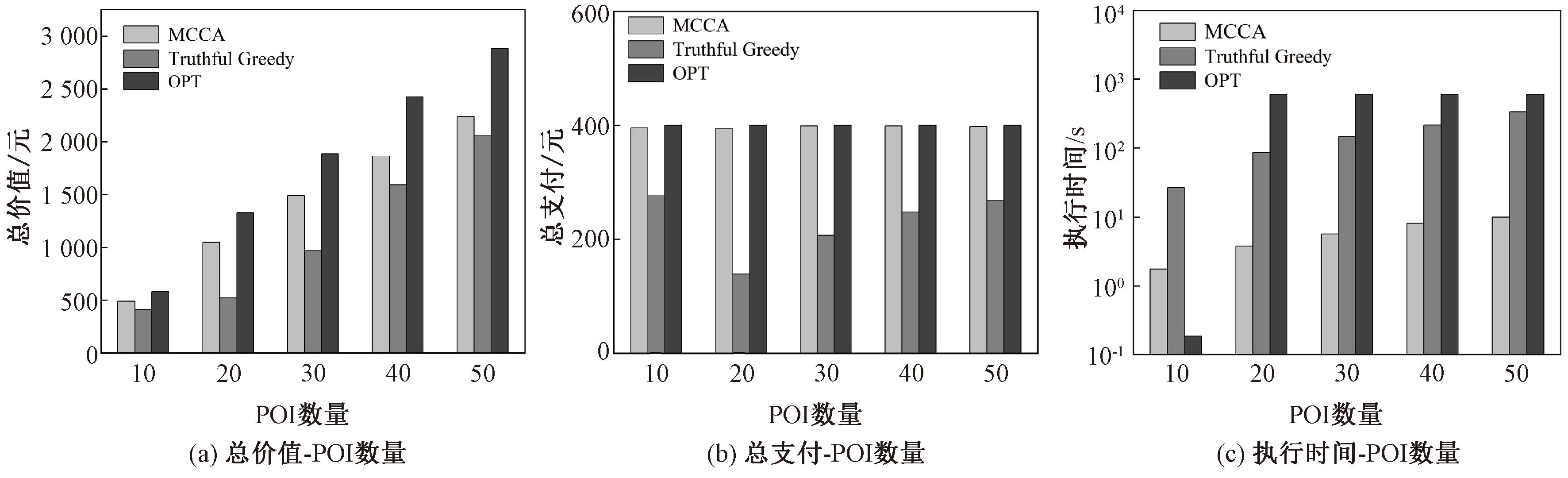
图5 POI规模的影响
Figure 5 Impact of POI scale
从图5(a)可以看出,随着POI数量的增加,总价值迅速上升,因为用户可以覆盖更多的POI点。MCCA的总价值高于Truthful Greedy,并接近OPT。由图5(b)可知,OPT和MCCA都尽可能地使用完预算B以获取更大价值;随着POI点的增多,Truthful Greedy中的V({i}|![]() t)/bi发生变化,导致选取的用户和支付发生变化。由图5(c)可以看出,MCCA的执行时间显著低于Truthful Greedy,而且随着POI数量的增加,3种算法的执行时间均有所上升,但是主要受用户规模和轮次的影响。MCCA通过argmaxi∈
t)/bi发生变化,导致选取的用户和支付发生变化。由图5(c)可以看出,MCCA的执行时间显著低于Truthful Greedy,而且随着POI数量的增加,3种算法的执行时间均有所上升,但是主要受用户规模和轮次的影响。MCCA通过argmaxi∈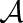 \(
\(![]() t∪
t∪![]() t-1)V({i}|
t-1)V({i}|![]() t)选择边际效益最大用户,虽然与POI数量相关,但影响较小。总体来看,MCCA在执行效率上明显优于Truthful Greedy。
t)选择边际效益最大用户,虽然与POI数量相关,但影响较小。总体来看,MCCA在执行效率上明显优于Truthful Greedy。
5 结论
本文针对移动群智感知任务分配中用户隐私暴露的问题,提出了带边际效益的数学模型,并设计了基于时钟拍卖的MCCA机制。MCCA无须用户提前暴露价值判断,从而保护隐私。仿真实验结果表明,MCCA在保护用户隐私的同时,实现了任务分配的高收益,并具备出色的执行效率。同时所设计的方案还可以用于其他的应用场景如云计算、边缘计算、算力网资源分配中,可向需要为虚拟资源进行分配及定价的场景提供理论及应用上的参考方案。
[1] WANG E, YANG Y J, WU J, et al. An efficient prediction-based user recruitment for mobile crowdsensing[J]. IEEE Transactions on Mobile Computing, 2018, 17(1): 16-28.
[2] KONG X J, LIU X T, JEDARI B, et al. Mobile crowdsourcing in smart cities: technologies, applications, and future challenges[J]. IEEE Internet of Things Journal, 2019, 6(5): 8095-8113.
[3] SUHAG D, JHA V. A comprehensive survey on mobile crowdsensing systems[J]. Journal of Systems Architecture, 2023, 142: 102952.
[4] ZHANG J X, ZONG M Y, VASILAKOS A V, et al. UAV base station network transmission-based reverse auction mechanism for digital twin utility maximization[J]. IEEE Transactions on Network and Service Management, 2024, 21(1): 324-340.
[5] SONG Y W, JIN H M. Minimizing entropy for crowdsourcing with combinatorial multi-armed bandit[C]∥IEEE INFOCOM 2021 - IEEE Conference on Computer Communications. Piscataway: IEEE, 2021: 1-10.
[6] LI Y L, XIAO H P, QIN Z, et al. Towards differentially private truth discovery for crowd sensing systems[C]∥2020 IEEE 40th International Conference on Distributed Computing Systems (ICDCS). Piscataway: IEEE, 2020: 1156-1166.
[7] HUAI M D, WANG D, MIAO C L, et al. Privacy-aware synthesizing for crowdsourced data[C]∥The 28th International Joint Conference on Artificial Intelligence. Macao: IJCAI, 2019: 2542-2548.
[8] ZHANG J X, ZHANG Y, WU H, et al. An ordered submodularity-based budget-feasible mechanism for opportunistic mobile crowdsensing task allocation and pricing[J]. IEEE Transactions on Mobile Computing, 2024, 23(2): 1278-1294.
[9] KAGEL J H, HARSTAD R M, LEVIN D. Information impact and allocation rules in auctions with affiliated private values: a laboratory study[J]. Econometrica, 1987, 55(6): 1275.
[10] MILGROM P, SEGAL I. Clock auctions and radio spectrum reallocation[J]. Journal of Political Economy, 2020, 128(1): 1-31.
[11] XIONG H Y, ZHANG D Q, WANG L Y, et al. EMC3: energy-efficient data transfer in mobile crowdsensing under full coverage constraint[J]. IEEE Transactions on Mobile Computing, 2015, 14(7): 1355-1368.
[12] ZHANG J X, WANG Z M, WU H, et al. Ordered submodularity-based value maximization of UAV data collection in earthquake areas[J]. IEEE Transactions on Network Science and Engineering, 2024, 11(5): 4886-4897.
[13] DÜTTING P, GKATZELIS V, ROUGHGARDEN T. The performance of deferred-acceptance auctions[J].Mathematics of Operations Research,2017,42(4):897-914.
[14] LI S W. Obviously strategy-proof mechanisms[J]. American Economic Review, 2017, 107(11): 3257-3287.
[15] BALKANSKI E, GARIMIDI P, GKATZELIS V, et al. Deterministic budget-feasible clock auctions[EB/OL].(2021-07-21)[2025-01-03].https://arxiv.org/abs/2107.09239.
[16] MASHAYEKHY L, NEJAD M M, GROSU D, et al. An online mechanism for resource allocation and pricing in clouds[J]. IEEE Transactions on Computers, 2016, 65(4): 1172-1184.
[17] MYERSON R B. Optimal auction design[J]. Mathematics of Operations Research, 1981, 6(1): 58-73.
[18] SINGER Y. Budget feasible mechanisms[C]∥2010 IEEE 51st Annual Symposium on Foundations of Computer Science. Piscataway: IEEE, 2010: 765-774.
[19] LUST T, TEGHEM J. The multiobjective multidimensional knapsack problem: a survey and a new approach[J]. International Transactions in Operational Research, 2012, 19(4): 495-520.
[20] FERRAIOLI D, VENTRE C. Obvious strategyproofness, bounded rationality and approximation[J]. Theory of Computing Systems, 2022, 66(3): 696-720.
[21] NEJAD M M, MASHAYEKHY L, GROSU D. Truthful greedy mechanisms for dynamic virtual machine provisioning and allocation in clouds[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26(2): 594-603.