针对不同的患者需求,康复机器人通常分为被动训练和主动训练两大类。尽管被动训练已广泛应用于临床实践,但由于缺乏患者的主动参与,恢复效果可能不理想[1]。相较之下,主动训练能够根据患者的意图和状态进行自适应调整,这对于神经恢复和功能重建尤为重要[2]。
在主动康复训练过程中,控制策略必须根据患者的运动状态进行自适应调整,因此,及时并且准确地识别出使用者的运动意图至关重要。表面肌电信号(sEMG)因其能够反映肌肉状态,且具有超前性、无创性等优点,已被用于运动意图识别和人机交互控制[3]。柏林工业大学研发的基于sEMG控制的外骨骼机器人TUPLEE,通过大腿内侧安装的电极贴片,实时预测肌力,控制膝关节的力矩,从而为患者提供助力,减少患者的运动负担[4]。筑波大学研发的HAL Lower limb下肢外骨骼机器人能检测患者在产生运动意图时的肌电信号,通过构建闭环控制,诱导患者神经进行重塑[5]。上海交通大学机器人研究所研发了一款包括sEMG的多信号融合控制的下肢康复外骨骼机器人,可以实现个性化的运动康复训练[6]。
此外,机器人应该具备一定的柔顺性,当人与机器人接触或发生碰撞与冲击时能有一定的顺应与缓冲时间,从而使得人机交互更加友好[7]。采用一些自适应控制算法主动控制外部作用力来实现柔顺性,也是许多研究的重点[8]。由于下肢外骨骼系统是一个复杂的非线性系统,不仅难以得到精确的动力学模型,而且易受干扰,因此传统线性控制方法在下肢康复外骨骼中的应用受限[9]。滑模控制因其响应速度快、鲁棒性强,被认为是非线性系统控制的理想选择。北京航空航天大学Liu等[10]设计的滑模控制器能够实现下肢外骨骼系统的轨迹跟踪控制,但当模型中存在较大的不确定部分时,系统就会出现抖振。为了解决这一问题,Rahman等[11]提出了一种引入了边界层的鲁棒滑模控制器,可以有效削减抖振。抖振会对执行器及系统机构造成损坏,因此在设计滑模控制器时,要减小抖振。
针对当前康复机器人在人机交互方面的不足,本文提出了一种基于肌电预测模型的下肢外骨骼自适应控制方法。与传统方法相比,本文提出的控制方法具备以下创新点:①通过综合分析股二头肌、股直肌和股外侧肌的表面肌电信号,准确获取患者的期望运动轨迹;②为应对系统中常见的不确定性和模型误差,设计了一种基于人体肌肉激活度的非线性自适应滑模控制器,能够动态调整滑模面系数,实现更精确的轨迹跟踪的同时,优化了控制柔顺性。
1 人机系统的建立
本文使用的外骨骼机器人是BEAR-H1,它是由深圳市MileBot机器人有限公司研制的新型双侧外骨骼机器人[12],如图1所示。整个系统由背包(内含控制模块)、腰部和双腿部分以及触摸板界面组成。所有的主动关节都由柔性执行器驱动,从结构设计上保证了系统的安全性。初始版本的下肢康复机器人采用传统的比例-积分-微分(PID)控制器进行控制,但轨迹跟踪性能不够理想。
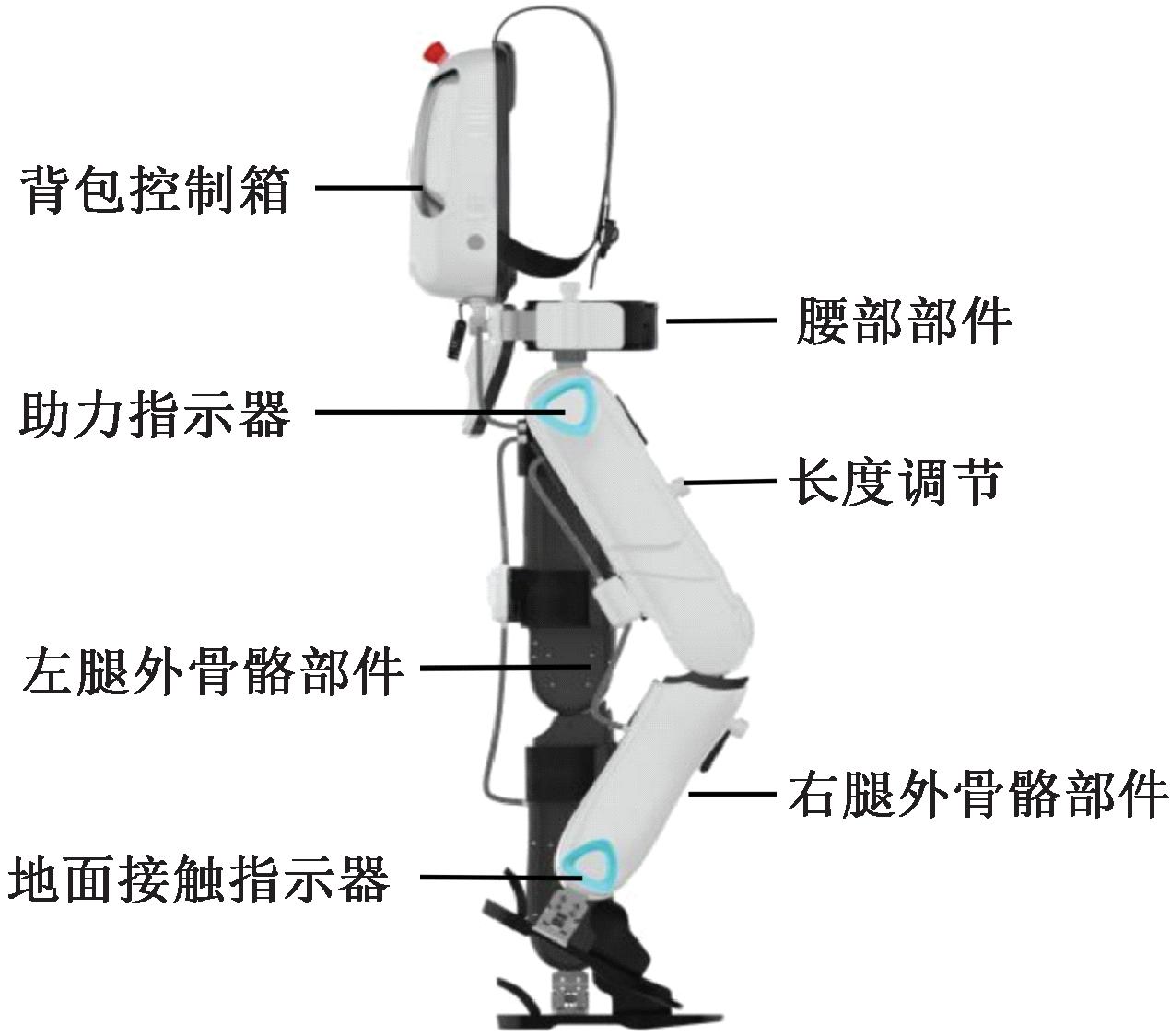
图1 下肢康复机器人
Figure 1 Lower limb rehabilitation robot
因此,本文提出了一种如图2所示的针对髋关节与膝关节的自适应控制方法来优化人-机系统的控制效果。其中,上层通过检测肌肉的表面肌电信号识别人体的运动意图,生成患者的期望轨迹。下层是期望轨迹与助力策略的融合过程,通过肌肉激活度动态调整滑模控制器的参数,对轨迹进行跟踪。
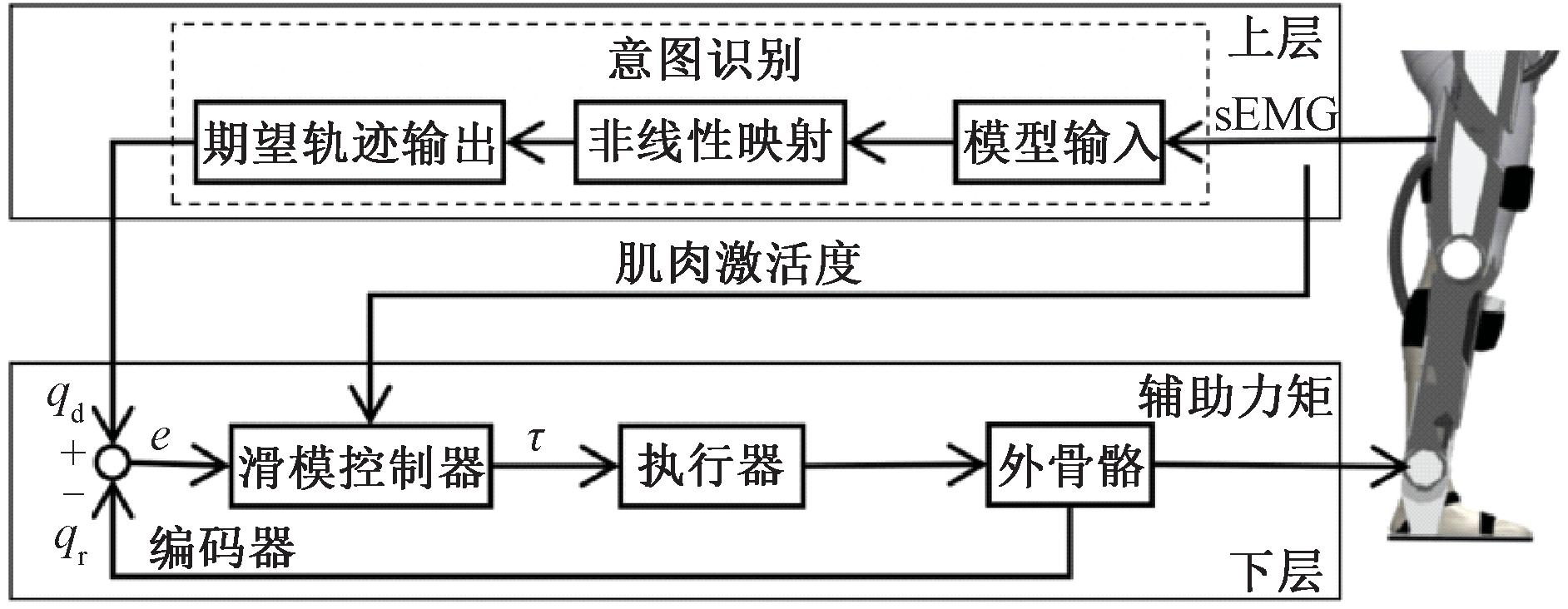
图2 基于肌电预测模型的自适应控制框图
Figure 2 Adaptive control block diagram based on myoelectric prediction model
为验证本文方法,首先建立了机器人系统模型作为研究的控制对象。为降低建模复杂度,将康复机器人简化为两连杆串联机构。以髋关节为原点建立笛卡尔坐标系,如图3所示,其中,机器人连杆参数mt=0.87 kg;lh=0.43 kg;ltg=0.2 m;It=0.011 kg·m2;ms=0.77 kg;lk=0.39 m;lsg=0.16 m;Is=0.009 8 kg·m2;g=9.8 m/s2。下肢康复机器人DH 参数如表1所示。
表1 下肢康复机器人DH参数
Table 1 DH parameters of lower limb rehabilitation robot

ψ a ψ a ′ ψ d ′ ψ θ ′ ψ 1 0 l b 0 q h 2 0 l k 0 q k
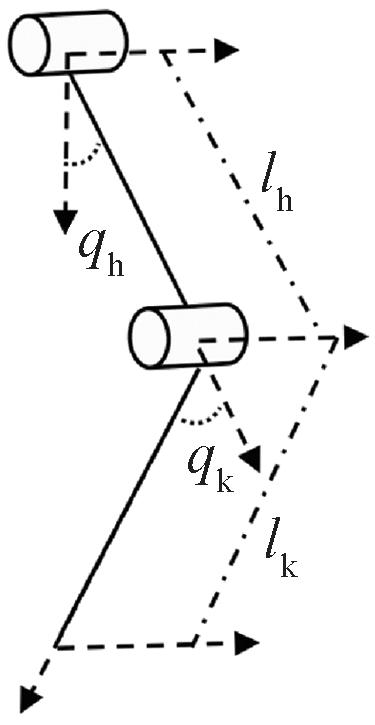
图3 下肢康复机器人连杆示意图
Figure 3 Linkage diagram of lower limb rehabilitation robot
通过运动学计算机器人摆动腿的末端位置坐标X以及角度:
(1)
式中:lh为大腿的长度,m;lk为小腿的长度,m;qh为髋关节角度,(°);qk为膝关节角度,(°)。
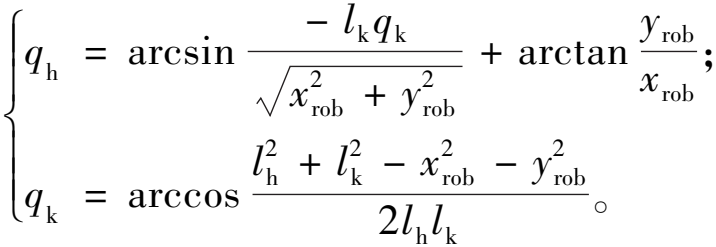
(2)
使用欧拉-拉格朗日方法对机器人进行建模,外骨骼机器人摆动腿的动力学方程可以表示为
(3)
式中:q包括髋关节角度和膝关节的角度;τ∈Rn×1为人机系统的力矩;τd∈Rn×1为系统受到的扰动。![]() 为人机系统的正定惯性矩阵,其中,
为人机系统的正定惯性矩阵,其中,
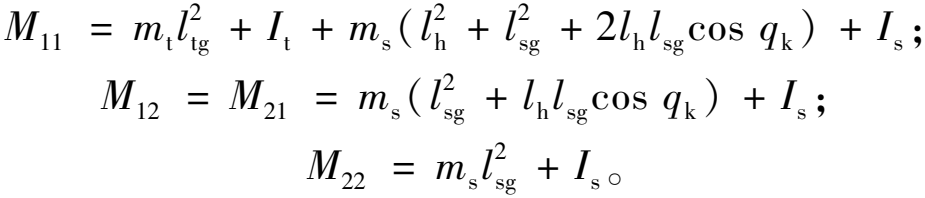
![]() 为科氏力和离心力的矩阵,其中,
为科氏力和离心力的矩阵,其中,
![]()
![]()
![]()
N22=0。
![]() 为重力矩阵,其中,
为重力矩阵,其中,
G1=(mtltg+mslh)gcos qh+mslsggcos(qh+qk);
G2=mslsggcos(qh+qk)。
2 期望轨迹生成
深度学习算法因其能够从大规模数据中获取高层次的抽象特征而被广泛应用于各种分类和回归任务中[13]。Liu等[14]提出使用CNN来预测膝关节角度,并证明了基于特征的CNN相比基于原始数据的CNN具有更高的估计精度。同时,近年来的大量研究表明,LSTM在运动意向方面表现出色[15]。因此,本文提出了一种具有自注意力机制的CNN-LSTM模型,生成期望轨迹的过程如图4所示。
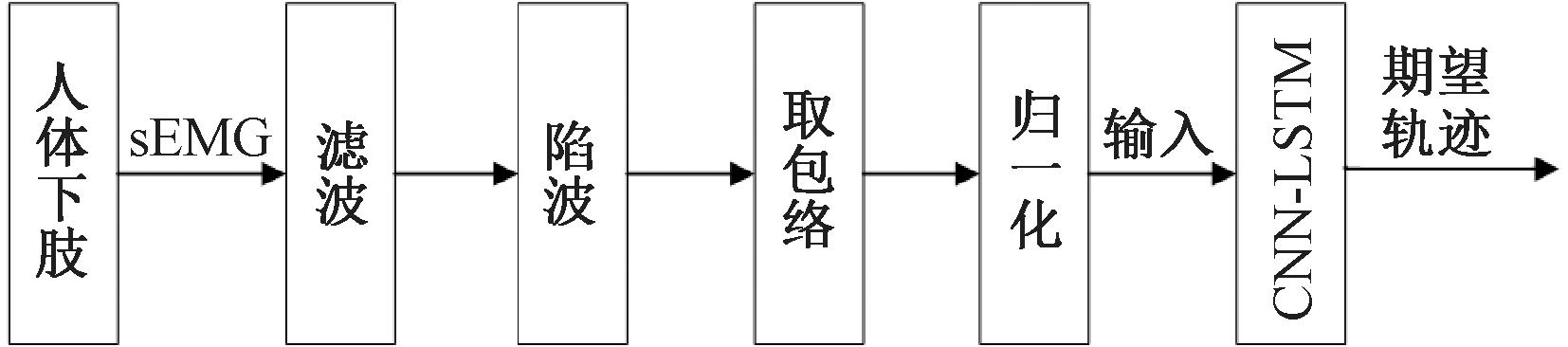
图4 生成期望轨迹
Figure 4 Generate expected trajectory
2.1 数据采集与预处理
5名健康受试者(年龄:25岁±3岁,身高:1.75 m±0.08 m,体重:70 kg±10 kg)参与了本实验的数据收集。表面肌电信号采集设备为Noraxon Ultium肌电信号系统和AgCl电极,如图5(a)所示。使用酒精湿巾擦拭肌肉表面皮肤,去除附着在皮肤表面的死皮和汗液。每个通道的电极片间隔20 mm,沿受试者双腿目标肌肉的肌纤维方向贴在肌肉腹部。受试者在跑步机上以2.0 km/h的速度行走,并采集肌电信号。每次步行3 min,中间休息1 min,以避免肌肉疲劳的影响,共进行10组。采集股外侧肌、股直肌和股二头肌的表面肌电信号,采样频率为1 200 Hz。同时,使用Noraxon myoMOTION惯性测量单元(IMU)采集下肢髋关节和膝关节的矢状面角度变化,采样频率为200 Hz,如图5(b)所示。
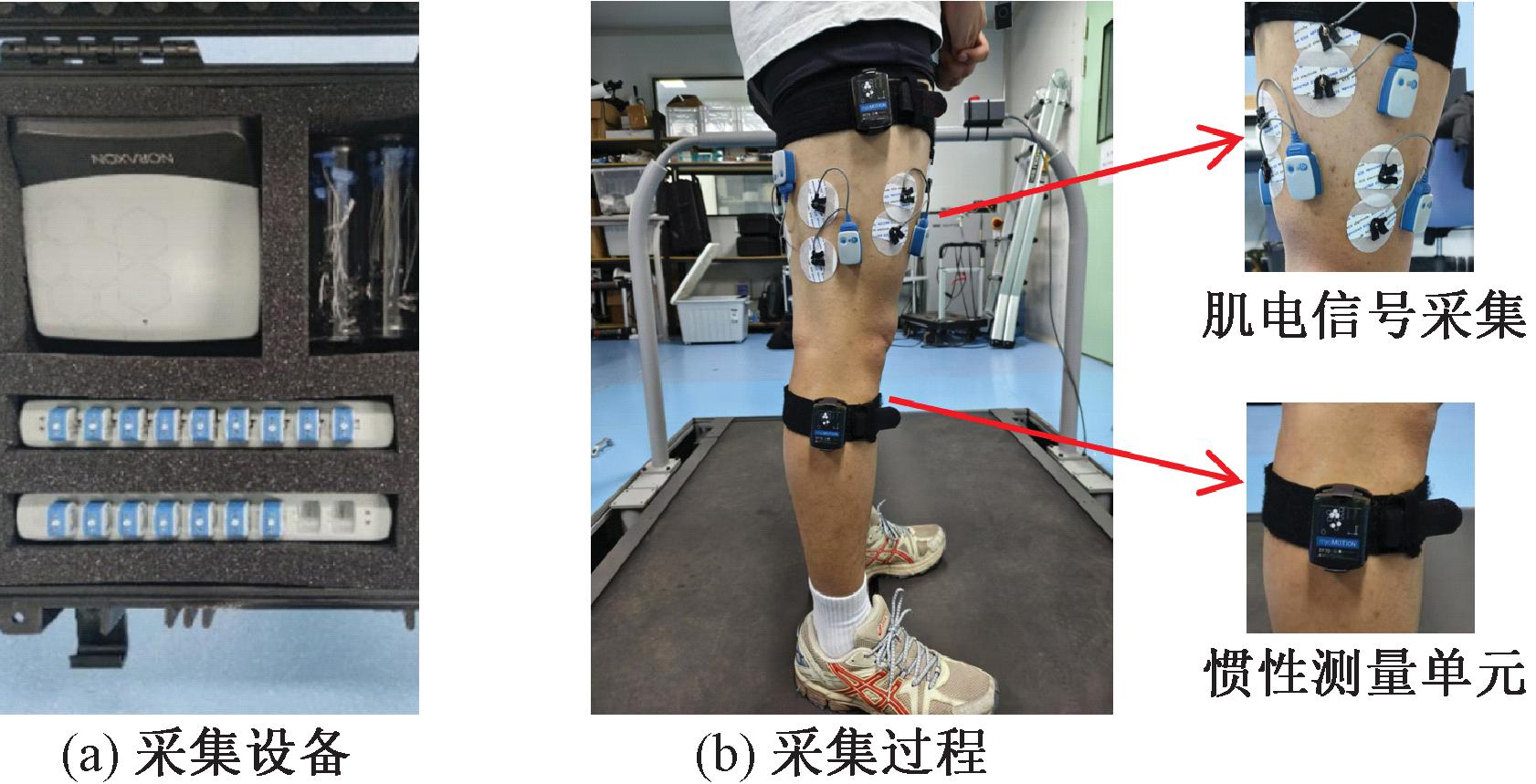
图5 肌电信号采集
Figure 5 Acquisition of sEMG signals
信号的预处理过程如图6所示。由于原始采集的表面肌电信号中含有大量的噪声信号,并且其频率为0~500 Hz。为了尽可能地保留有价值的信息,需要去除不相关的噪声。肌电信号首先用四阶500 Hz巴特沃思低通滤波器进行滤波。然后使用50 Hz陷波滤波器来消除电力线干扰,使用5 Hz的五阶低通巴特沃斯滤波器取包络。对关节角度信息进行预处理,以在时间上与sEMG对齐,并对数据进行归一化。肌电信号经过具有250 ms长度的时间窗口和200 ms的滑动窗口分割后,按照8∶2的比例划分为训练集和测试集,同时保留原始的时间顺序,用于模型训练。
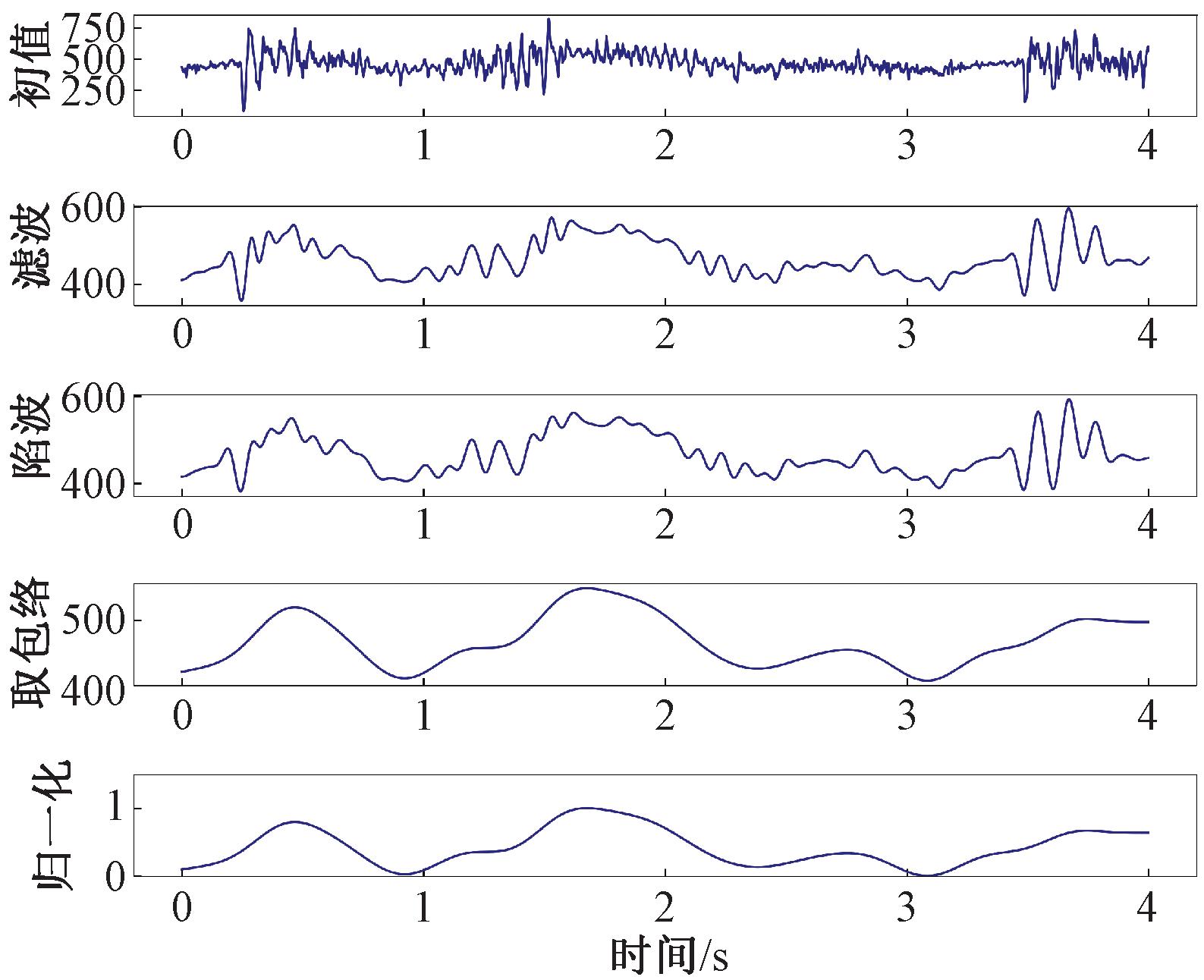
图6 信号预处理
Figure 6 Signal preprocessing
2.2 具有自注意力的CNN-LSTM网络
2.2.1 卷积神经网络
对于输入的数据,首先通过卷积层对输入向量矩阵进行卷积操作,以提取时间序列数据的局部特征[16]。特征序列生成公式为
(4)
式中:B[i+j]为输入向量在i+j处的值;ω[j]为卷积核在位置j处的权重;b为偏置;σ(·)为对卷积结果进行非线性变换的激活函数。该算法既可以通过多个卷积核的卷积运算提取特征,还可以通过滑动窗口的卷积运算获得序列数据的局部相关性。
2.2.2 LSTM神经网络
LSTM因其良好的记忆能力,常用于处理序列数据。LSTM的关键在于其门控机制,通过门来控制信息的流动和遗忘,从而更好地处理序列中的长期依赖关系。LSTM网络中最重要的组成部分是状态单元![]() 相关联的时间常数由遗忘门fi(t)控制,由Sigmoid函数将权重设置为[0,1] [17],如式(5)所示:
相关联的时间常数由遗忘门fi(t)控制,由Sigmoid函数将权重设置为[0,1] [17],如式(5)所示:
(5)
式中:![]() 为当前输入向量;
为当前输入向量;![]() 为当前隐藏层向量,包含所有LSTM细胞的输出;
为当前隐藏层向量,包含所有LSTM细胞的输出;![]() 分别为偏置、输入权重和遗忘门的循环权重。
分别为偏置、输入权重和遗忘门的循环权重。
外部输入门单元![]() 以类似遗忘门的方式更新,但有自身的参数,如式(6)所示:
以类似遗忘门的方式更新,但有自身的参数,如式(6)所示:
(6)
LSTM细胞输出![]() 也可以由输出门
也可以由输出门![]() 关闭,如式(7)和式(8)所示:
关闭,如式(7)和式(8)所示:
(7)
(8)
2.2.3 自注意力机制
自注意力机制是一种用于捕捉序列数据中不同元素之间依赖关系的机制。在处理序列数据时,每个元素的表示都会根据序列中其他所有元素的重要性重新计算。假设有一个序列X={x1,x2,…,xn},其中xi为序列中第i个元素的向量表示,对于每个输入向量xi,通过线性变换生成查询向量qi、键向量ki和值向量vi,如式(9)所示:
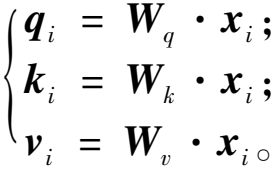
(9)
式中:Wq、Wk、Wv为可学习的权重矩阵。
每个元素的查询向量与所有元素的键向量进行点积操作,计算它们的相关性,然后通过Softmax函数转化为注意力权重,如式(10)所示:
(10)
2.2.4 CNN-LSTM网络
本文提出的CNN-LSTM预测模型集成了自注意机制,如图7所示。首先,将输入数据传入卷积层,进行初步特征提取,其次,对提取到的特征进行批量归一化,通过ReLU激活函数进行非线性映射。引入Dropout层,防止过拟合。卷积输出被传入LSTM,在时间步维度逐步计算隐藏状态。经Sigmoid函数激活,并通过自注意力机制生成权重,最后由全连接层将全局特征映射到目标输出空间,输出的特征维度为2,对应髋关节和膝关节的角度。训练过程在GPU设备上进行,损失函数为均方根误差。
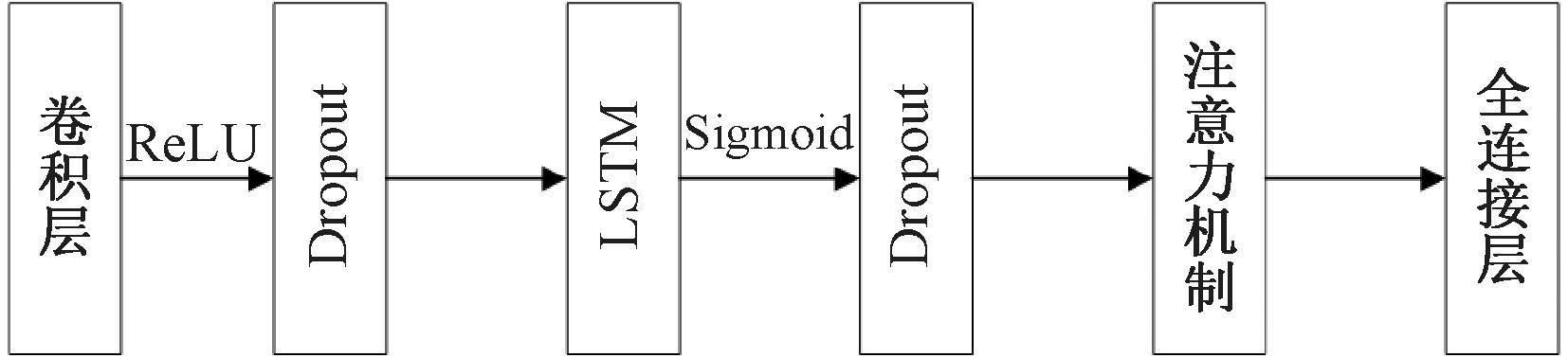
图7 具有自注意机制的CNN-LSTM网络模型
Figure 7 CNN-LSTM network model with self-attention mechanism
2.2.5 肌肉激活度
肌肉激活度直接反映了肌肉的活跃水平,通常引入一个函数表达神经信号与肌肉活跃度之间的非线性关系[18]:
(11)
式中:u(t)表示t时刻的处理后的肌电信号;A为非线性形状系数,代表神经激活强度u(t)和肌肉激活强度a(t)的非线性程度。本文在计算肌肉活跃度时,取A=-1.5。
3 人-机系统的自适应柔顺控制
滑模控制是一种简单且适用于非线性系统的控制算法,即使在模型建立不精确的情况下,该算法也能在有限时间内实现优良的运动轨迹跟踪[19]。为实现康复机器人系统的人机交互和自适应柔顺控制,提出了一种自适应滑模控制的下肢康复机器人控制方法:通过实时感知肌肉激活度,动态调整滑模面系数,使控制器能够根据人体运动能力的变化进行自适应调节,从而有效改善传统刚性控制策略在柔顺性方面的不足。
在机器人的位置控制中,将轨迹跟踪误差定义为
(12)
式中:![]() 为通过意图识别生成的髋关节和膝关节的期望角度;
为通过意图识别生成的髋关节和膝关节的期望角度;![]() 为通过IMU检测到的髋关节和膝关节的实际角度。
为通过IMU检测到的髋关节和膝关节的实际角度。
c为正定矩阵,则可以导出![]()
(13)
滑模存在条件为
(14)
滑动模态是状态沿着轨迹在滑动面上的受约束运动。滑模控制器必须保证对于任何初始状态x(0)=x(t0),状态x(t)首先在有限时间tf内到达滑动面,然后在所有t>tf>t0内保持在滑动面上。对于连续滑模控制,选择一般趋近律:
(15)
式中:sgn(s)为符号函数。
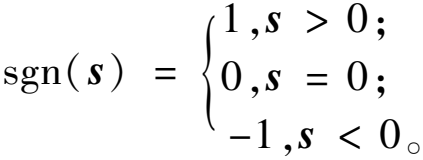
(16)
结合式(3)、(13)和(15)可得
(17)
如果初始状态不在滑模面上,或状态点偏离参数,则必须设计控制器,使其能够将系统状态驱动到滑动面。选择李雅普诺夫公式:
(18)
对式(18)求导:
(19)
代入式(17)得
(20)
系统的镇定条件为![]() 所以定义:
所以定义:
令

(21)
为了减小控制器中的抖振,可以使用饱和函数sat(s)来代替理想滑差模式中的符号函数sgn(s):
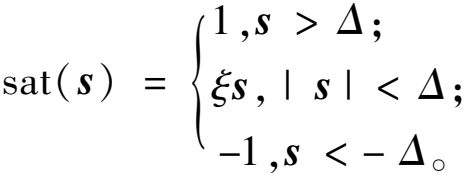
(22)
同时,ε应减小。但ε过小时也会影响系统到达滑动面的速度,因此应在减小的同时增大f(s)。于是将趋近律设计为
(23)
式中:α、β、φ均大于0。
为了提高控制器的柔顺性,在肌肉激活度较低时,应适当降低控制器的输出力矩,避免外骨骼机器人对人体动作的过度干预,使人体肌肉力量主导运动过程,保持使用者的自然步态并维持人机系统的稳定性;在肌肉激活度较高时,则应增强控制器的输出力矩,以有效减轻肌肉负担、提高动作效率,同时确保人机系统的协调性和响应能力。设置c与a(t)之间的关系为
c=c0+γ·Δa·EΔa。
(24)
式中:Δa=a(t)-a0;c0为基础增益;γ为比例因子;a0为固定值,用以区分激活度的强弱状态。根据肌肉激活度,动态调整c的值。因此,自适应滑模控制器实质上是一种变滑模控制器。
结合式(17)、式(21)~(24),得到最终控制律为
(25)
控制器经过计算后向关节电机输出控制力矩,电机通过电流环调节电流,从而执行力矩指令,带动外骨骼运动。
4 实验
4.1 实验方案
为进一步验证所提策略的可行性,选择参与肌电数据采集的5名健康受试者(S1~S5,年龄25岁±3岁)进行实验。将股外侧肌、股直肌和股二头肌作为数据收集点,为受试者粘贴Noraxon Ultium肌电信号系统并穿戴BEAR-H1。收集的sEMG信号经上位机中的肌电预测模型处理后,将预测数据下发到BEAR-H1的背包控制箱中的控制器中。跑台设置为2.0 km/h恒定速度供受试者行走。每名受试者重复进行10次测试,每次测试时长为3 min。实验设备如图8所示。
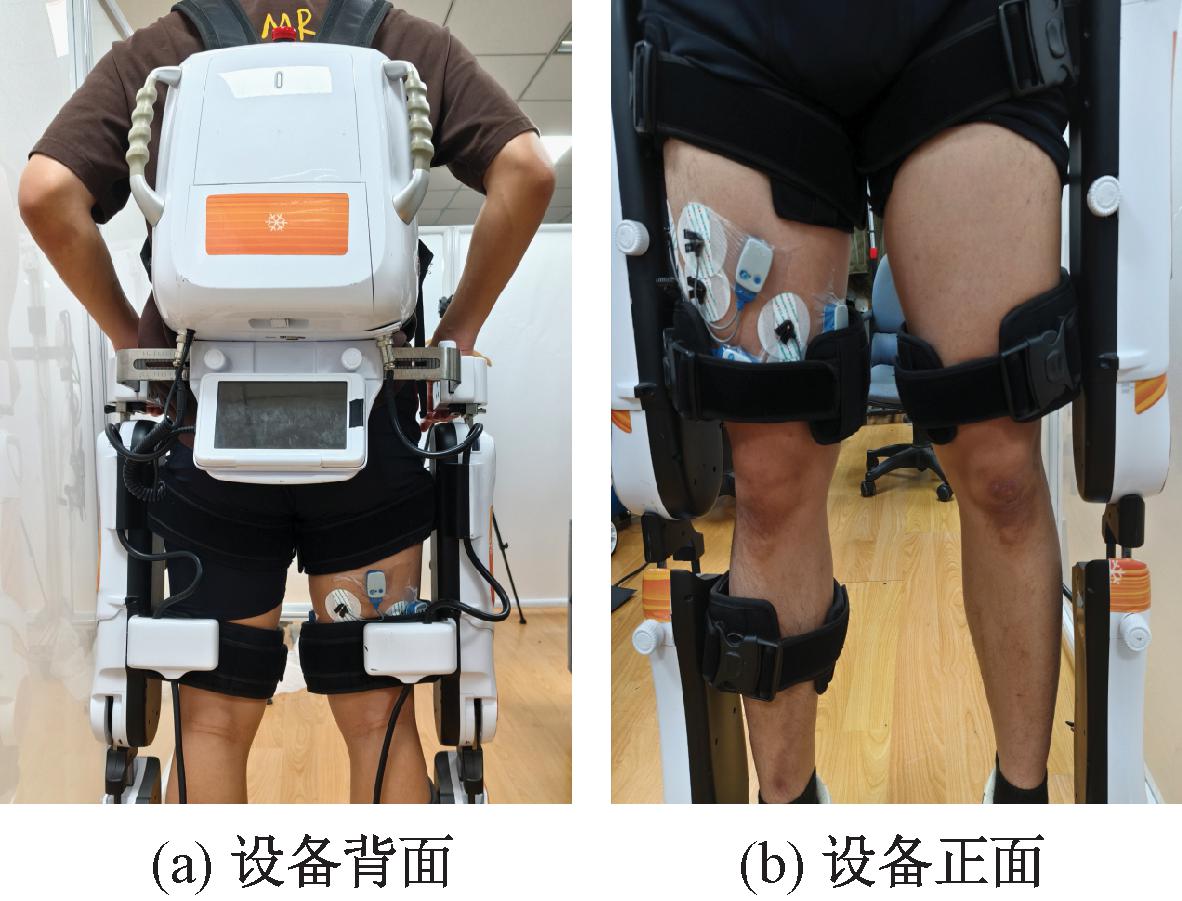
图8 实验设备
Figure 8 Experiment apparatus
4.2 结果与评估
RMSE均方根误差通常用作关节角度连续估计的回归性能的评估指标[20],它的定义如式(26)所示:

(26)
式中:n为采样序列的长度;Ei为每个时刻的误差。
采集受试者下肢行走运动时的表面肌电信号并使用CNN-LSTM模型对关节角度进行预测,实现期望轨迹的生成。表2是模型预测的RMSE结果。
表2 肌电模型的RMSE结果
Table 2 RMSE results of sEMG model

受 试 者 R MS E 髋 关 节 膝 关 节 S 1 7 . 8 3 9 . 7 3 S 2 8 . 3 6 1 0 . 0 9 S 3 7 . 1 6 8 . 8 5 S 4 7 . 5 7 8 . 7 3 S 5 8 . 8 2 9 . 1 8
图9展示了在一个训练过程中受试者S3的关节预测角度。实验结果表明,髋关节的RMSE平均值为7.94,膝关节的RMSE平均值为9.31,能够满足轨迹生成的准确性要求。该模型的主要优点是设计的网络结构可以提高自回归模型的可解释性和预测精度,还减少了冗余传感器信息引起的梯度消失或爆炸问题。然而,由于表面肌电信号具有较强的个体差异性,模型在面向不同使用者时,需要进行预训练,否则会导致准确性降低。
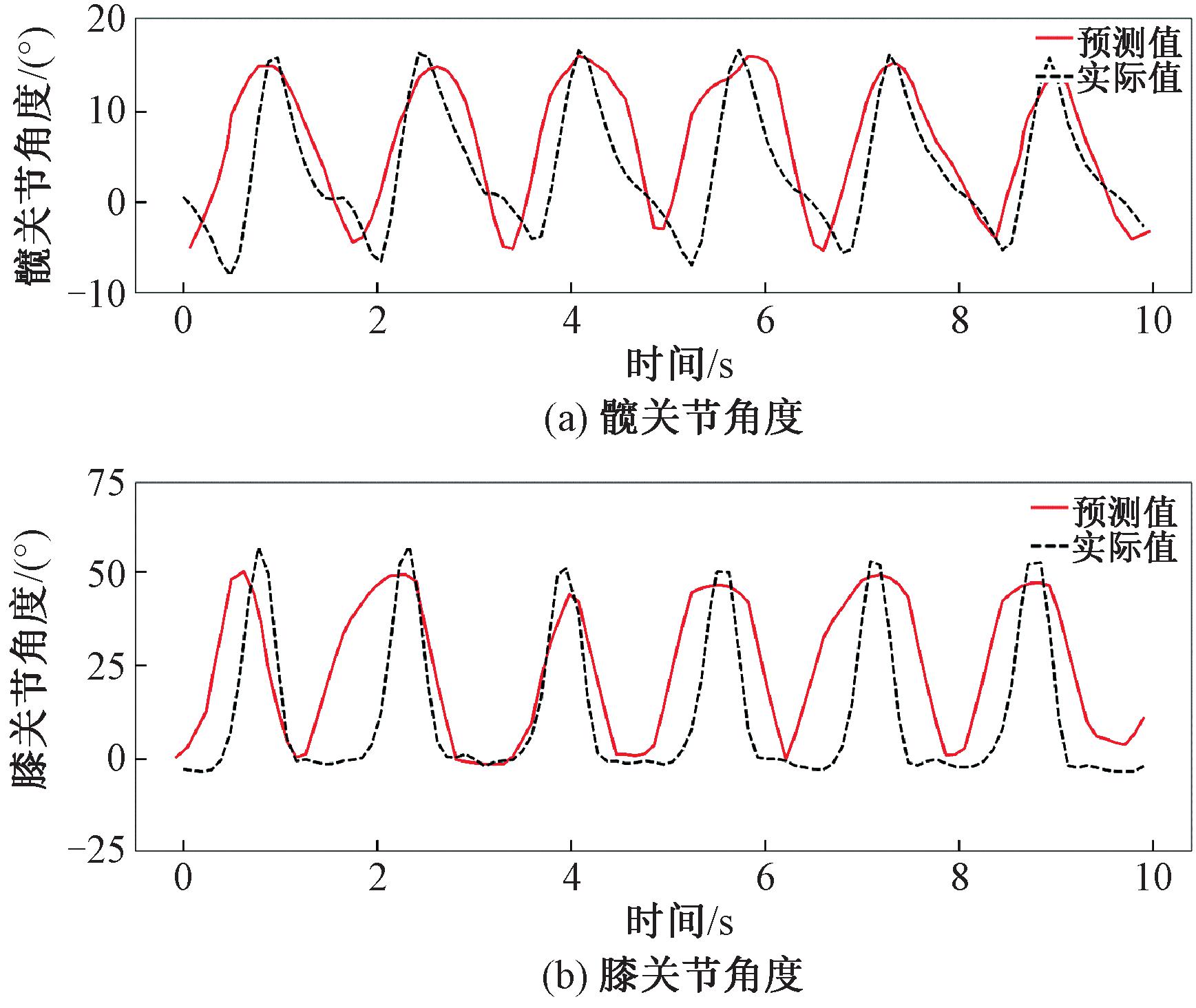
图9 肌电模型的预测效果
Figure 9 Prediction effect of sEMG model
按照式(11)计算下肢肌肉激活度与滑模面系数曲线,如图10所示。
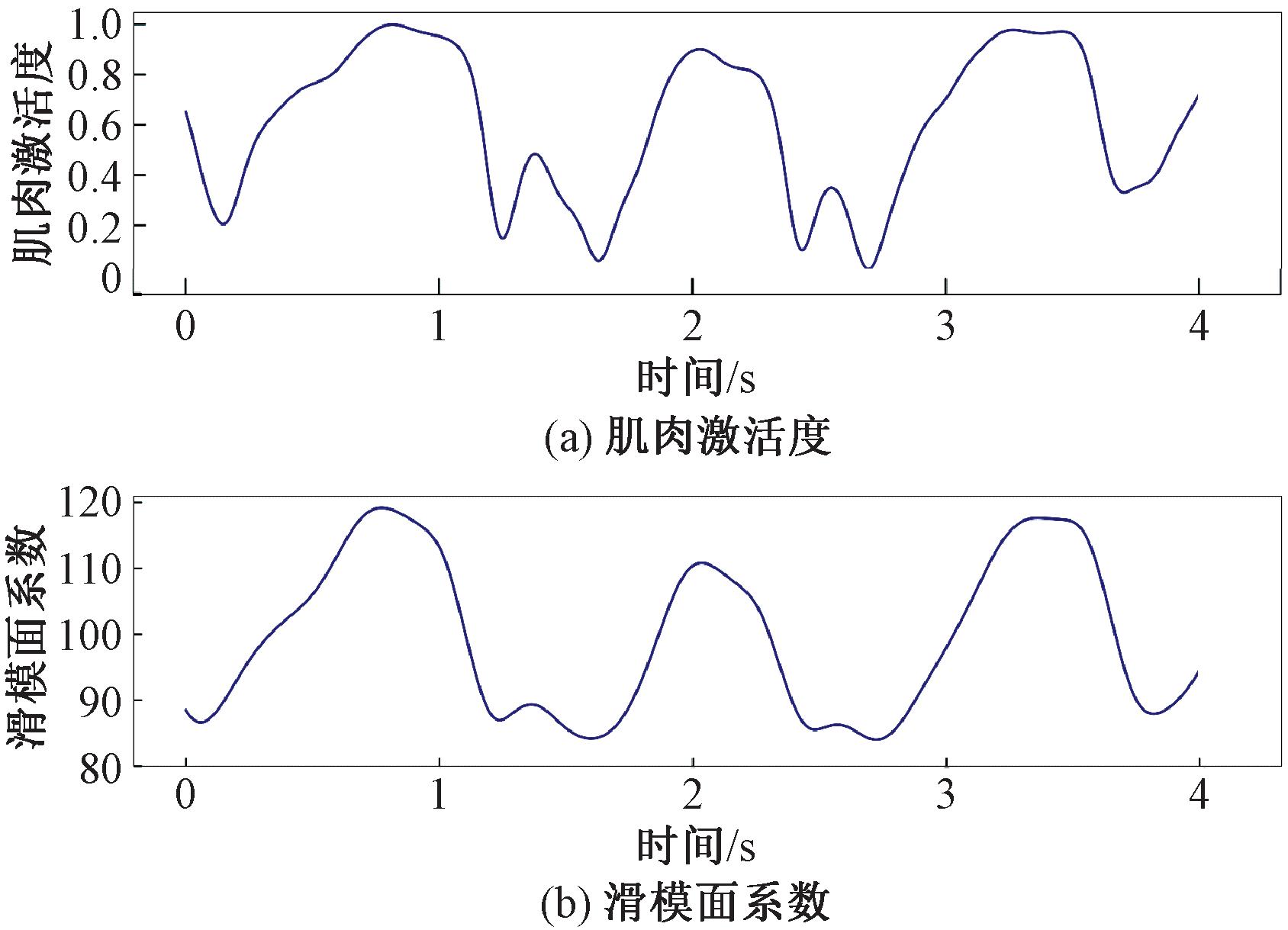
图10 肌肉激活度与滑模系数
Figure 10 Muscle activation and sliding mode coefficient
从图10可以看出,肌肉激活度曲线反映了受试者的运动状态,滑模面系数的变化趋势与下肢活动的变化趋势相似。例如在0.3 s至0.8 s的持续时间内,肌肉激活度上升,滑模面系数也在增加;在1.2 s至1.6 s的持续时间内肌肉激活度下降,滑模面系数也减小。因此,滑模面系数可以根据人体的运动来调整,用来修正实际跟踪轨迹。
随着步态的变化,控制器能够自动调整参数,从而实现下肢康复机器人稳定的末端轨迹跟踪。为了验证自适应滑模控制器校正参考轨迹的有效性,将其与定滑模控制器进行比较。设置髋关节和膝关节的定滑模面系数为c1=100,c2=90,自适应滑模面系数分别为c01=120,c02=80。关节跟踪曲线如图11所示。
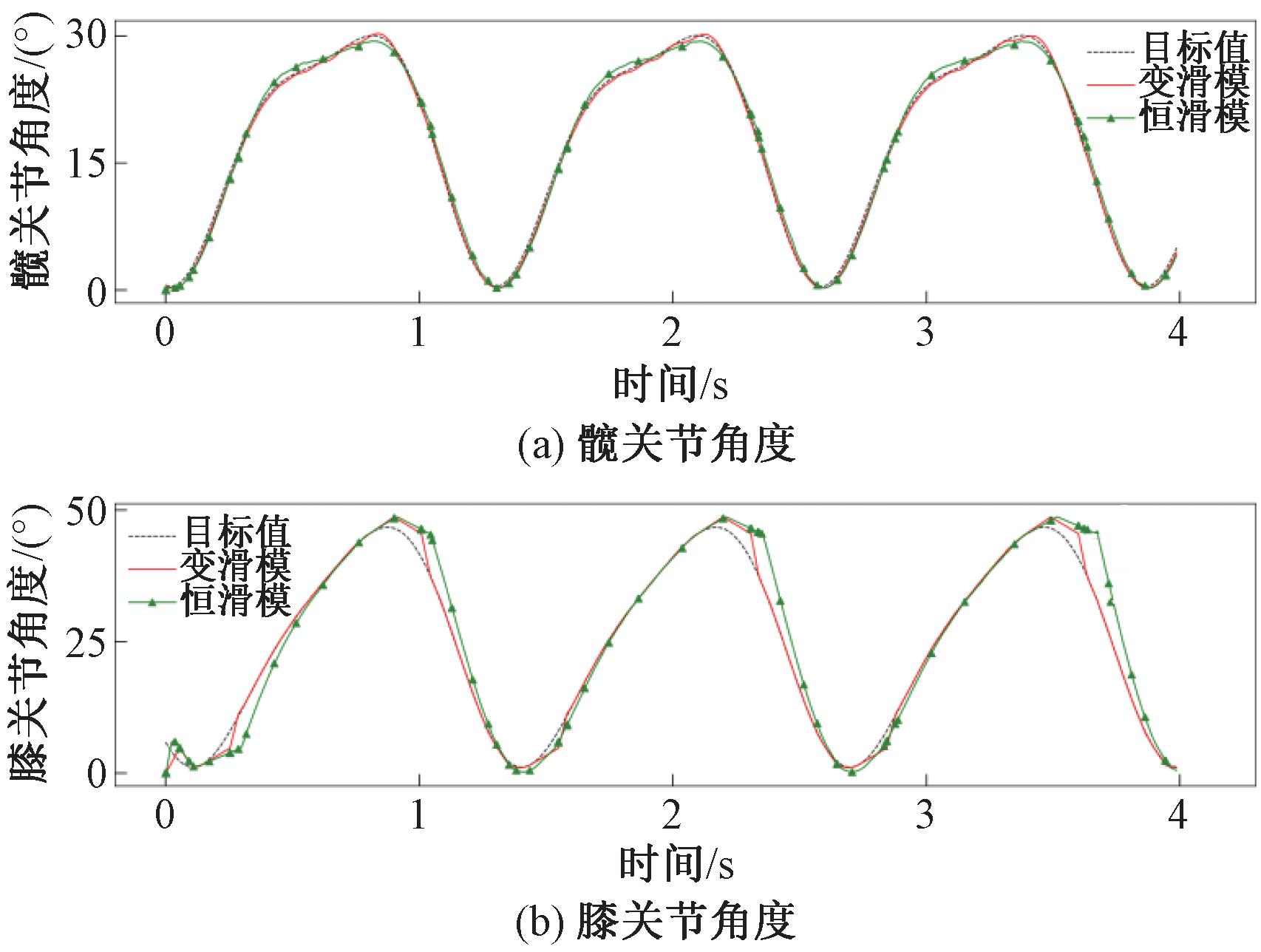
图11 关节跟踪曲线
Figure 11 Joint tracking curve
由图11可以看出,在第1 s时,受试者下肢处于由伸到屈的过渡状态,目标曲线变化较快,但因为系统中存在常见的不确定性,例如弹性关节的形变、模型的误差等,使得系统在高动态变化区域无法迅速适应,因而不能完全跟踪受试者的运动状态。但由于下肢肌肉激活度的增强,自适应滑模控制器的滑模面系数增加,控制力矩得到改善,因此自适应滑模控制器的跟踪曲线比恒滑模控制下的跟踪曲线更接近目标曲线。此后滑模面系数不断减小,在1.6 s左右与恒滑模面系数相等,跟踪效果相同。此后滑模面系数依然在减小,第2 s时,受试者下肢处于由屈到伸的过渡状态,下肢肌肉激活度最小,由人体肌肉力量主导运动过程,自适应滑模控制器的输出力矩达到最小,从而降低了人机交互的对抗性,提高了控制效果。
为了进一步验证变滑模控制的可行性,分别使用PID控制器与自适应滑模控制器对机器人的髋关节和膝关节进行跟踪,对误差进行统计分析。该误差来自5名受试者,每个受试者使用自适应滑模控制器和PID控制器训练,取平均误差后所得。图12是两种控制器在前4 s内,分别跟踪髋关节和膝关节的平均误差。
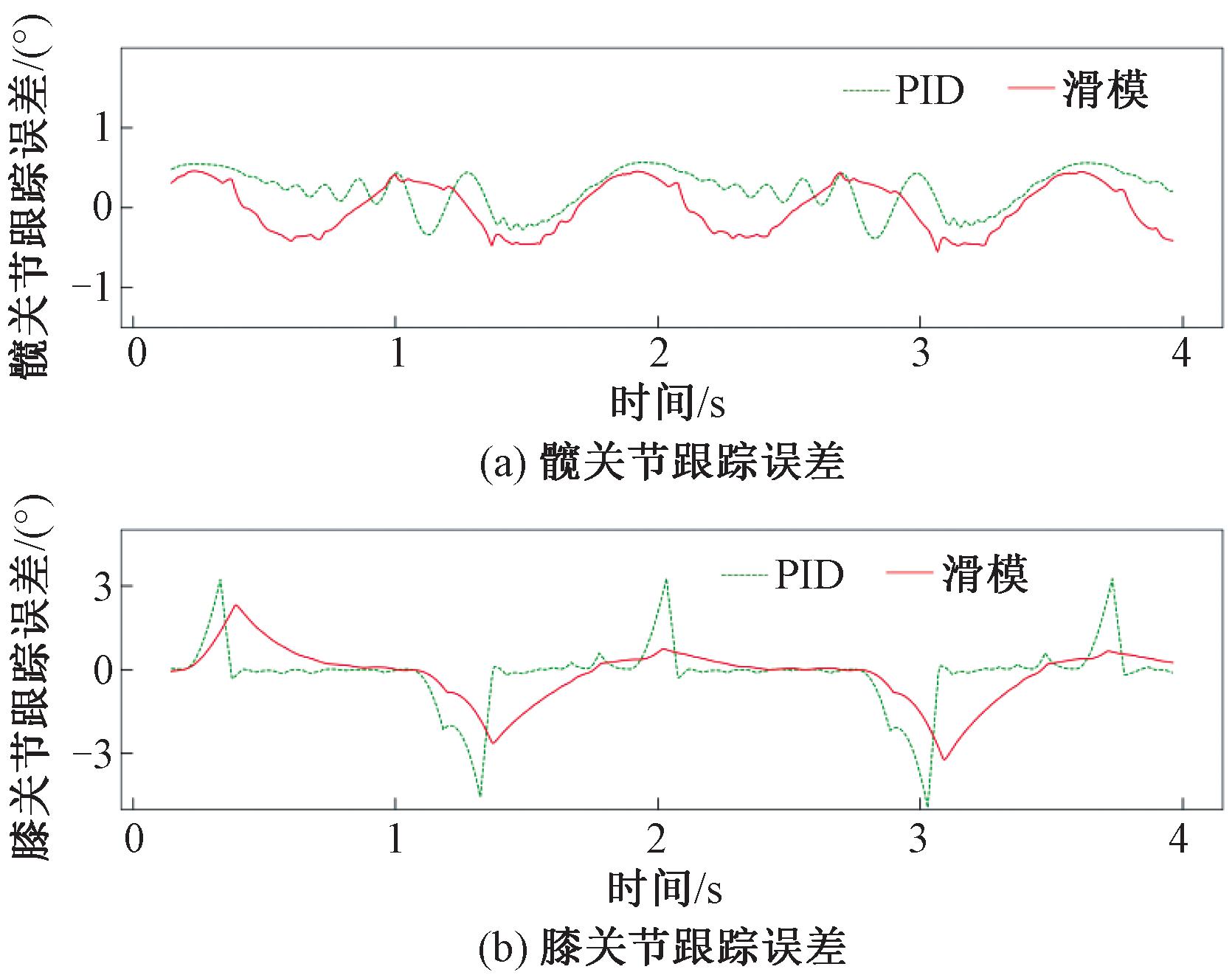
图12 跟踪误差比较
Figure 12 Tracking error comparison
从图12中可以看出,两种控制器的跟踪误差均在0处上下变化,这两种方法都可以实现末端轨迹跟踪。对于髋关节,两者的跟踪效果接近。但滑模控制器的误差波动更小且更为规律,其RMSE为0.30,而 PID 控制器的RMSE为0.35。这表明滑模控制器能降低控制过程中的振荡,从而减少机械部件的磨损,延长系统使用寿命。对于膝关节,滑模控制器表现的效果更加显著,其误差为±0.023 m,相比PID控制器的误差为±0.032 m。降低了约28%。这主要得益于滑模控制器能够动态调节控制参数,从而更好地应对膝关节动作幅度大、变化迅速的非线性特性。然而,从收敛性能来看,PID控制器表现更好,这可能是滑模控制器的自适应调参的结果。
5 结论
本文提出了一种基于肌电预测模型的下肢外骨骼自适应控制方法,针对当前康复机器人在适应性方面的不足进行了深入研究。通过综合分析股二头肌、股直肌和股外侧肌的表面肌电信号,成功构建了能够生成患者期望运动轨迹的预测模型。为应对系统中的不确定性和模型误差,设计了一种基于人体肌肉激活度的非线性自适应滑模控制器,能够根据患者的实际运动能力动态调整控制器参数。实验结果表明,肌电预测模型对髋关节和膝关节的轨迹生成误差分别为7.94和9.31,满足轨迹生成精度要求。相比传统PID控制器,自适应滑模控制器的跟踪误差降低了28%,控制过程更加平稳,减小了振荡幅度和机械磨损。此外,该方法在5名受试者的实验中表现出良好适应性。然而,肌电预测模型的准确性和自适应滑模控制器的收敛性仍有待进一步优化。
[1] GONZALEZ A, GARCIA L, KILBY J, et al. Robotic devices for paediatric rehabilitation: a review of design features[J]. Biomedical Engineering Online, 2021, 20(1): 89.
[2] ZHOU B, WANG H, HU F, et al. Accurate recognition of lower limb ambulation mode based on surface electromyography and motion data using machine learning[J]. Computer Methods and Programs in Biomedicine, 2020, 193: 105486.
[3] XIONG D Z, ZHANG D H, ZHAO X G, et al. Synergy-based neural interface for human gait tracking with deep learning[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2021, 29: 2271-2280.
[4] FLEISCHER C, WEGE A, KONDAK K, et al. Application of EMG signals for controlling exoskeleton robots[J]. Biomedizinische Technik Biomedical Engineering, 2006, 51(5/6): 314-319.
[5] SUZUKI K, MITO G, KAWAMOTO H, et al. Intention-based walking support for paraplegia patients with robot suit HAL[J]. Advanced Robotics, 2007, 21(12): 1441-1469.
[6] FAN Y J, YIN Y H. Active and progressive exoskeleton rehabilitation using multisource information fusion from EMG and force-position EPP[J]. IEEE Transactions on Bio-medical Engineering, 2013, 60(12): 3314-3321.
[7] 张弼, 姚杰, 赵新刚, 等. 一种基于肌电信号的自适应人机交互控制方法[J]. 控制理论与应用, 2020, 37(12): 2560-2570.
ZHANG B, YAO J, ZHAO X G, et al. An adaptive human-robot interaction control method based on electromyography signals[J]. Control Theory &Applications, 2020, 37(12): 2560-2570.
[8] 赵佳伟, 朱立忠, 陈万鑫, 等. 基于动态运动基元的6自由度下肢外骨骼步态轨迹规划与控制策略[J]. 信息与控制, 2024, 53(1): 33-46.
ZHAO J W, ZHU L Z, CHEN W X, et al. Gait trajectory planning and control strategy of 6-DOF lower limb exoskeleton based on dynamic movement primitives[J]. Information and Control, 2024, 53(1): 33-46.
[9] 高建设, 刘陆骐, 王杰, 等. 基于模糊控制的上肢康复机器人变导纳控制[J]. 郑州大学学报(工学版), 2024, 45(1): 12-20.
GAO J S, LIU L Q, WANG J, et al. Variable admittance control of upper limb rehabilitation robot based on fuzzy control[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(1): 12-20.
[10] LIU J M, ZHANG Y P, WANG J H, et al. Adaptive sliding mode control for a lower-limb exoskeleton rehabilitation robot[C]∥The 13th IEEE Conference on Industrial Electronics and Applications (ICIEA).Piscataway: IEEE, 2018: 1481-1486.
[11] RAHMAN M H, KITTEL-OUIMET T, SAAD M, et al. Development and control of a robotic exoskeleton for shoulder, elbow and forearm movement assistance[J]. Applied Bionics and Biomechanics, 2012, 9(3): 275-292.
[12] LI X, ZHANG X, LI X, et al. BEAR-H: an intelligent bilateral exoskeletal assistive robot for smart rehabilitation[J]. IEEE Robotics &Automation Magazine, 2022, 29(3): 34-46.
[13] 魏浩, 张道辉, 谷亚伦, 等. 基于织物的柔性可穿戴上肢运动辅助系统设计[J]. 机器人, 2024, 46(6): 692-702, 712.
WEI H, ZHANG D H, GU Y L, et al. Design of a fabric-based soft wearable upper-limb motion assistive system[J]. Robot, 2024, 46(6): 692-702, 712.
[14] LIU G, ZHANG L, HAN B, et al. sEMG-based continuous estimation of knee joint angle using deep learning with convolutional neural network[C]∥2019 IEEE 15th International Conference on Automation Science and Engineering (CASE). Piscataway: IEEE, 2019: 140-145.
[15] WANG C, GUO W Y, ZHANG H, et al. sEMG-based continuous estimation of grasp movements by long-short term memory network[J]. Biomedical Signal Processing and Control, 2020, 59: 101774.
[16] 张安琳, 张启坤, 黄道颖, 等. 基于CNN与BiGRU融合神经网络的入侵检测模型[J]. 郑州大学学报(工学版), 2022, 43(3): 37-43.
ZHANG A L, ZHANG Q K, HUANG D Y, et al. Intrusion detection model based on CNN and BiGRU fused neural network[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 37-43.
[17] 吴振龙, 莫艺鹏, 王荣花, 等. 基于LSTM和粒子群算法的多机组风电功率预测[J]. 郑州大学学报(工学版), 2024, 45(6): 114-121.
WU Z L, MO Y P, WANG R H, et al. Multi-unit wind power prediction based on long short-term memory and particle swarm optimization[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(6): 114-121.
[18] HAN J D, DING Q C, XIONG A B, et al. A state-space EMG model for the estimation of continuous joint movements[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4267-4275.
[19] ZHONG W J, FU X M, ZHANG M M. A muscle synergy-driven ANFIS approach to predict continuous knee joint movement[J]. IEEE Transactions on Fuzzy Systems, 2022, 30(6): 1553-1563.
[20] SU J H, CHENG T, TAN X W, et al. A recurrent neural network based prediction method for continuous joint angle movement[C]∥2023 IEEE 13th International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER). Piscataway:IEEE, 2023: 521-526.