路径规划是无人机完成飞行任务的关键技术之一,被应用于很多领域,如物流配送,服务巡检、突发响应等。无人机路径规划技术是寻找一条从起始点到目标点的路径,该路径必须满足避障、飞行平稳等多种约束条件[1-2]。经典的路径规划算法涵盖了人工势场法[3-4]、模拟退火法[5]等;在智能优化算法的范畴内,主要包括蚁群算法[6]、粒子群算法[7-8]、遗传算法[9-10]等。与传统的算法相比,智能优化算法借鉴了生物体的适应性、进化和群体行为等特性,能够更有效地处理传统算法难以应对的复杂性和不确定性,这为路径规划问题提供了一种更加灵活和创新的方法。然而,众多路径规划算法所生成的路径往往含有尖锐转角,致使路径不够平滑,这不符合无人机的运动学要求。因此,在路径规划的环节中,对路径进行平滑处理尤为重要。
当前,路径规划平滑处理主要采用的技术包括多项式插值曲线、贝齐尔曲线、B样条曲线[11]等。B样条曲线比贝齐尔曲线有更强的凸包性质、局部支撑性等,在实现路径的光滑性上更灵活、更具有优势,是路径平滑最常用的数学工具。Huo等[12]提出一种基于改进的蚁群算法,结合了角点约束和B样条曲线的光滑路径规划方法,规划的光滑路径满足机器人的最大曲率约束;Liu等[13]提出一种将Fibonacci球面法与B样条曲线相结合的局部避障模型,能够识别无障碍路径并生成平滑的规划轨迹,但未考虑到无人机的特性,如机动性约束和航向约束。Yan等[14]提出了一种基于改进A*算法和贝齐尔曲线融合的三维路径规划策略,根据A*算法规划的路径,使用分段贝齐尔曲线对路径进行平滑,但平滑是路径的后处理环节,未考虑可能存在的安全问题。Phung等[15]为规划出优质路径,对粒子群算法规划的满足无人机飞行约束条件的路径进行平滑处理,原路径满足无人机飞行的性能要求,但路径修改为曲线后可能存在碰撞危险。
综上,尽管一些现有路径规划方法利用了样条曲线技术实现路径的平滑处理,但没有考虑平滑后的曲线是否能避免与障碍物碰撞。针对这一问题,本文提出一种基于三次准均匀B样条曲线和粒子群算法的无人机路径规划方法,即利用 B样条曲线的几何性质构建路径规划模型,然后采用改进的粒子群算法对模型进行求解,使规划的最优路径C2连续且安全避障。
1 模型建立
1.1 环境建模与路径表示
本文采用Qi等[16]和黄书召等[17]所提的方法来构建环境模型。该方法通过三角函数和高斯函数来模拟地形特征,以此来表征地形的复杂性,为无人机路径规划提供环境模型。具体如下所示:
Z(x,y)=Z1(x,y)+Z2(x,y);
(1)
Z1(x,y)=|asin(xb)+ccos(yd)|;
(2)
(3)
式中:(x,y)为水平面坐标;Z(x,y)为对应的高度;a、b、c、d为常数,控制地势的起伏,其中a、b控制正弦函数的振幅和周期,c、d控制余弦函数的振幅和周期;m为山峰总数;hi为第i(i=1,2,…,m)座山的高度;(xi,yi)为第i座山峰顶部的水平面坐标;xsi、ysi为第i座山的坡度。
本文障碍物所在区域统一称为禁飞区,为方便处理,禁飞区用圆柱体表示,具体如下所示:
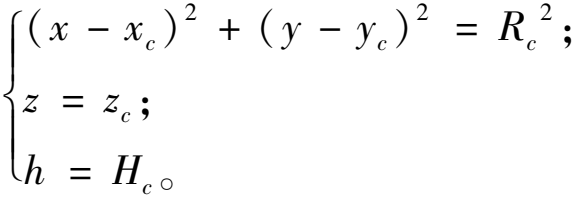
(4)
式中:(xc , yc , zc)为第c个圆柱体底部圆心的坐标;Rc、Hc分别为第c个禁飞区圆柱体所占区域底部圆的半径和圆柱体的高。
B样条曲线在形状定义与设计方面具有很大的灵活性,能兼顾路径的光滑性和避障问题。本文采用三次准均匀B样条曲线[11]表示无人机飞行路径。三次准均匀B样条定义为
(5)
式中:dj(j=0,1,…,n)为B样条曲线的控制顶点;Nj,3(u)(j=0,1,…,n)为三次B样条基函数,是由节点矢量参数u的序列U(u0≤u1≤…≤un+4,两端节点重复度为4,其余内部节点等距分布)所决定的三次分段多项式。
1.2 基于三次准均匀B样条曲线的路径优化建模
无人机的最佳飞行路径由路径长度、安全避障、飞行高度以及平稳度这4个代价函数共同确定。
1.2.1 路径长度
在路径规划中,目标是实现路径长度的最小化,为此,定义路径长度代价函数为
(6)
1.2.2 安全避障
在无人机路径规划问题中,安全避障是一个至关重要的考虑因素。路径需要避免进入禁飞区确保无人机安全飞行。在笛卡尔坐标系中,dj=(xj,yj,zj)是B样条曲线路径的控制顶点,控制顶点构成控制多边形辅助确定避障代价。设E为禁飞区的个数,将路径控制顶点和禁飞区圆柱投影至x-y平面如图1所示,其中Ce(e=1,2,…,E)为第e个圆柱投影圆心坐标;Re为圆面半径;RU为无人机半径。
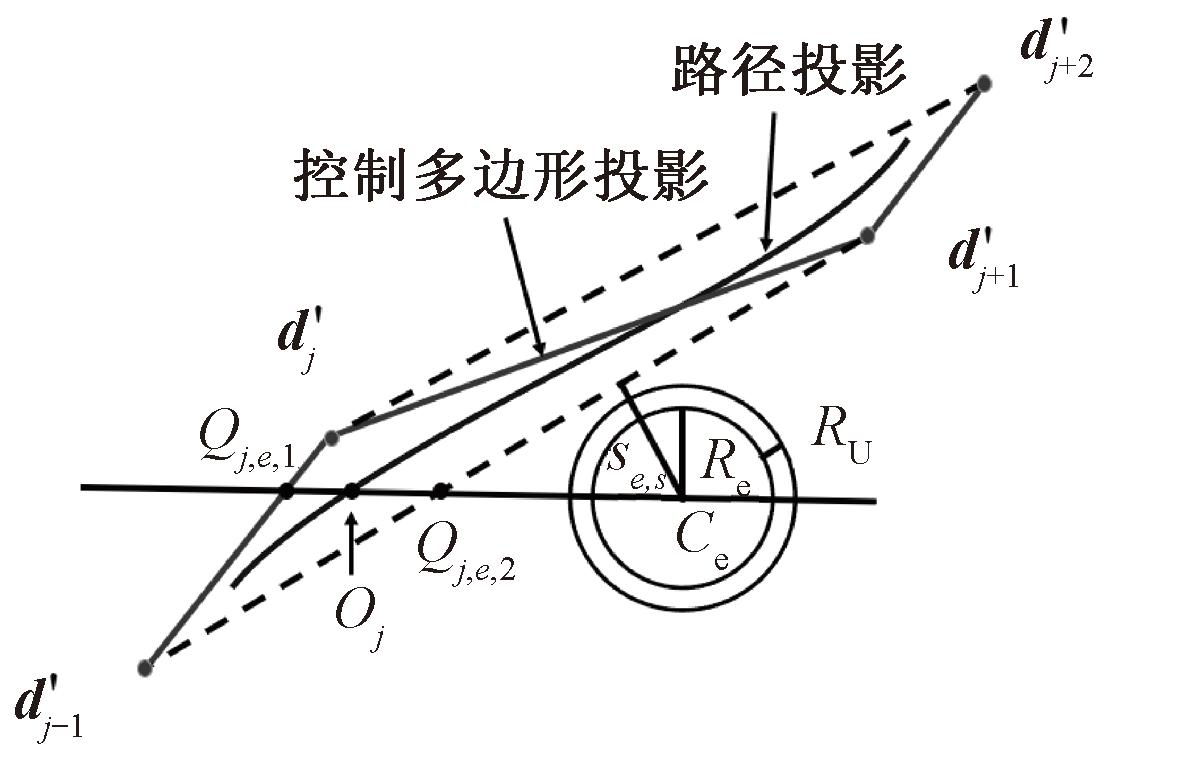
图1 安全代价确定
Figure 1 Determination of safety costs
由B样条曲线的凸包性和局部支撑性可知,顺序4个控制顶点定义三次B样条曲线的一段。三次B样条曲线的第j段由连续的4个控制顶点dj-1、dj、dj+1、dj+2定义,曲线落在这4个控制顶点形成的凸包内,记
分别为这4个控制顶点在x-y平面的4个投影点,则第j段三次B样条曲线的投影曲线落在4个投影点形成的四边形区域中。因此只要四边形区域在安全区域内则无人机便安全,为此,定义安全避障代价函数为
(7)
(8)
(9)
式中:k=3;Tj,e,s为避障条件,判断第e个障碍物与第j个四边形的第s个边是否相交;Gj,e也为避障条件,判断第e个障碍物是否在第j个四边形内;Se,s(s=1,2,3,4)为第e个禁飞区底部圆心到四边形的第s条边界的距离;Oj为协助第j段曲线计算安全代价时在四边形区域内的一个随机点;Qj,e,1、Qj,e,2为投影圆心Ce和Oj形成的直线与四边形边界的两个交点。
1.2.3 飞行高度
在无人机飞行作业中,确保与地面的相对安全距离是避免碰撞和保证飞行安全的关键措施;同时由于性能和能耗的限制,无人机不能无限升高,因此无人机的飞行高度被限制在特定的范围内。假设无人机的最低飞行高度为hmin,最高飞行高度为hmax,控制顶点dj的高度为hj,则定义飞行高度代价函数为
(10)
(11)
1.2.4 飞行平稳
为确保无人机飞行过程中保持平稳,在路径规划中,假设dj、dj+1和dj+2是相邻的3个路径控制顶点,飞行控制会考虑水平和垂直方向的偏移。水平偏转时计算方位角,即计算dj+1dj+2投影到x-y平面上的
和djdj+1投影到x-y平面的
之间的夹角φj;垂直偏转时计算仰俯角,即计算djdj+1与其在水平面上的投影
的夹角ψj。根据计算的角度,定义飞行平稳代价函数为
(12)
(13)
(14)
式中:zj为路径控制点dj的Z轴值;a1为转向惩罚系数;a2为升降惩罚系数。
综上定义,无人机路径规划总代价函数为
(15)
式中:bi为约束代价函数的权重。
2 模型求解算法设计与分析
2.1 算法设计
粒子群算法[18]是模拟自然界生物行为以及群体智慧的随机搜索策略。在优化框架内,所有粒子凭借个体在探寻过程中发掘并累积的经验,通过世代间的协作与竞争实现“进化”。假设粒子种群的规模为N,待解决搜索问题的维度为D(在本文中,D指B样条曲线的控制顶点个数,即n+1)。在搜索区域中,粒子i的当前位置记为Pi=(Pi,1,Pi,2,…,Pi,D),当前速度记为vi=(vi,1,vi,2,…,vi,D),粒子i的个体最优位置记为pi=(pi,1,pi,2,…,pi,D),整个粒子群的最优位置记为pg=(pg,1,pg,2,…,pg,D)。在迭代过程中,粒子的位置更新公式为式(16),速度更新公式为式(17)。
(16)
(17)
式中:ω为惯性权重因子;c1、c2为学习因子;
均为第t次迭代(0,1)内的随机数;
分别为粒子i在第t次迭代后速度、位置的第d维分量;
为第t次迭代后粒子i最优位置的第d维分量;
为第t次迭代后粒子群最优位置的第d维分量。
本文采用Phung等[15]提出的球形矢量编码粒子包括球坐标系中的3个分量,即位矢模长ρ、仰俯角ψ和方位角φ。则粒子i位置的第d维分量记作ui,d=(ρi,d,ψi,d,φi,d),速度的第d维分量记作Δui,d=(Δρi,d,Δψi,d,Δφi,d)。采用式(16)的更新方程,即式(16)的
用
表示,
用
表示,则粒子i的位置表示为Ωi=(ρi,1,ψi,1,φi,1,ρi,2,ψi,2,φi,2,…,ρi,D,ψi,D,φi,D),ui,d=(ρi,d,ψi,d,φi,d)映射到笛卡尔坐标系的位置Pi,d=(xi,d,yi,d,zi,d)的公式为
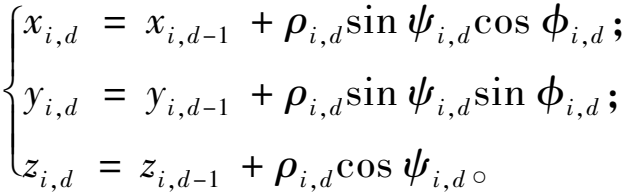
(18)
无人机B样条曲线路径的控制顶点di,d的直角坐标的Z轴值为Pi,d的Z轴值与Z(xi,d,yi,d)之和。优化粒子群算法并验证算法的有效性,依据目标函数对路径进行评估,规划出最优路径。
粒子群算法通过粒子之间的信息共享和协作,尤其擅长处理复杂且高维度的优化问题,但传统粒子群算法因收敛速度过快导致粒子在搜索空间中探索不足,算法停留在一个次优解,这种“早熟”现象限制了粒子群算法的应用效果。为克服传统粒子群算法的局限性,本文将从粒子的初始化方式、相关参数的选择以及扰动策略的制定这3个关键方面对粒子群算法进行改进。
2.1.1 粒子初始化策略
传统粒子群算法在搜索初期采用随机初始化种群的方式,但这种方式由于其初始种群的多样性不足而影响算法的全局搜索效率。粒子初始化质量对粒子群算法性能至关重要,粒子初始化聚集是导致收敛速度慢和算法性能不稳定的主要原因。Circle混沌映射[19]有随机性、均匀性和有序性等优点,因此本文使用改进的Circle混沌映射并结合反向学习策略,在混沌映射生成的种群和其对立种群中选取适应度高的粒子作为算法的初始解,增加初始粒子的多样性以此来提高初始解的质量。改进的Circle混沌映射公式为式(19),反向学习公式为式(20)。
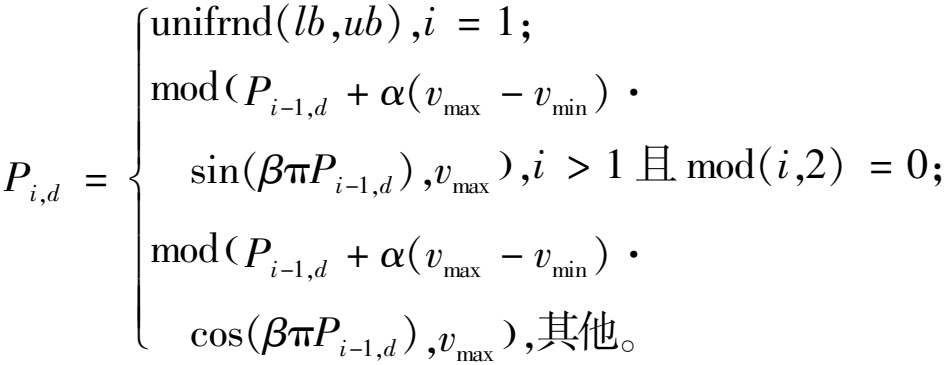
(19)
OPi,d=lb+ub-Pi,d。
(20)
式中:α、β均为控制参数,其中α=0.16、β=0.05;vmax、vmin分别为速度的最大值和最小值;OPi,d为粒子i第d维的对立位置。
算法1 粒子群初始化算法。
输入:种群数目N,维度D,位置的下界lb,上界ub,速度的最大值和最小值vmax、vmin等;
输出:种群初始解。
① 使用式(19)生成粒子初始解Pi,d;
② 使用式(20)生成粒子的反向对立解OPi,d;
③ 在初始解Pi,d和反向对立解OPi,d中选择适应度最优的前N个粒子作为初始解并输出。
2.1.2 惯性权重因子更新策略
惯性权重的作用是控制粒子在搜索空间中勘探和开采的平衡。粒子搜索过程是非线性的复杂过程,搜索初期受权重影响较大,选择较大惯性权重有助于粒子在解空间中搜索最优解,防止粒子陷入局部最优解; 搜索后期,降低权重则有利于粒子在潜在最优区域进行精细的局部搜索,进而提升搜索精度。本文采用指数衰减的方法,则权重更新为
(21)
式中:ωmin、ωmax分别为最小权重值和最大权重值;t为当前迭代次数;T为最大迭代次数。
2.1.3 学习因子更新策略
调整学习因子的数值以影响粒子的运动轨迹,在搜索初期,赋予较大的c1和较小的c2,使粒子更多地依赖其个体学习能力,而削弱其社会学习能力,能够强化算法的全局探索能力;而在搜索的后期阶段,则减小c1并增大c2,此时粒子的社会学习能力得到加强,个体学习能力相对减弱,有助于提升算法的局部搜索效率和搜索结果的精确度。本文采用线性调整学习因子c1和c2的方法 [20],更新公式如下所示:
(22)
(23)
式中:cmax、cmin分别为学习因子最大值和最小值。
2.1.4 增加粒子扰动策略
将粒子群等分为M组,选取每组适应度最高的粒子为最优粒子,对最优粒子引入电鳗觅食算法[21]的迁徙行为进行更大范围的搜索,组内其余粒子则进行粒子群算法的常规搜索。最优粒子位置更新规则为式(24),剩余粒子位置更新规则为式(16)。
(24)
(25)
(26)
(27)
(28)
(29)
(30)
式中:
均为第t次迭代(0,1)内的随机数;
为第i个粒子在第t次迭代时狩猎位置的第d维分量;
为第i个粒子在第t次迭代时休息位置的第d维分量;
为第t次迭代时种群中随机粒子位置的第d维分量;k1、k2分别为休息区系数和狩猎区系数;rand(·)为(0,1)的随机数;L为Levy飞行函数。
优化后本文算法E-PSO的具体流程如图2所示。
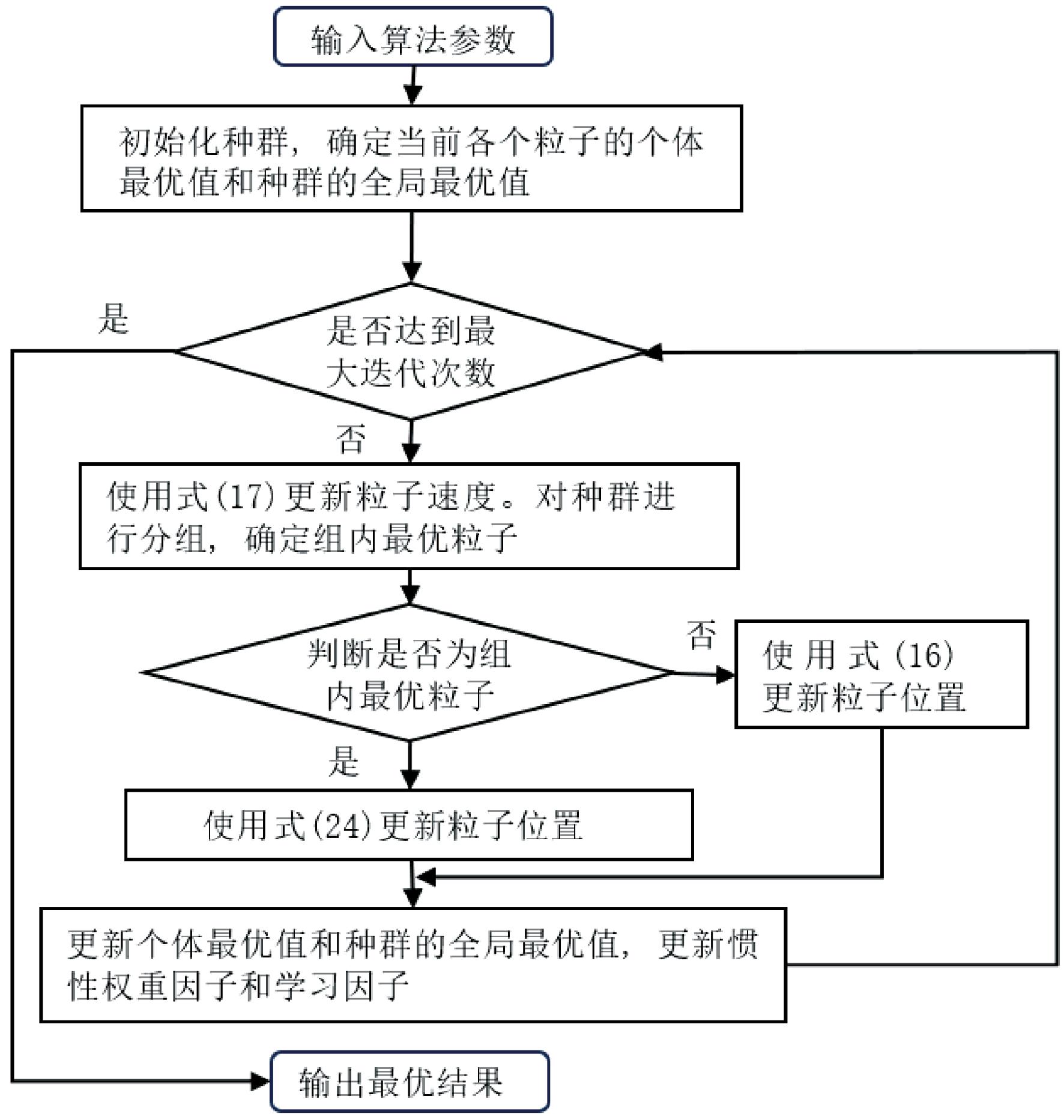
图2 E-PSO算法流程
Figure 2 E-PSO algorithm process
2.2 算法分析与验证
为验证改进粒子群算法的寻优能力,本文将它用来求解CEC2017测试集中的10个标准测试函数(本文使用的测试函数F1～F10依次为文献[18]测试函数的第1,2,4,7,10,11,12,14,15,22)。其中F1～F4为单峰测试函数,用于评估算法的精确性;F5～F7为多峰测试函数,用于检验优化算法的探索能力;F8～F10为固定维多峰测试函数,用于衡量优化算法在实际应用场景中的性能与适应性。
为验证改进算法的有效性,将E-PSO算法与对比算法在每个标准测试函数上各执行30次统计实验,并基于实验数据详细计算最优值、均值(AVG)以及标准差(STD)。均值的大小代表算法收敛的精度,标准差的大小代表算法的稳定性。对比算法选取固定惯性权重粒子群算法(PSO)[20]、融合压缩因子和异步变化学习因子的粒子群算法(IPSO)[22]和基于社会模型的改进粒子群优化算法(IPSOSM)[23]。本文算法的基本参数设定包括种群规模为500个,最大迭代次数为1 000次,其余对比算法参数的设定见表1。测试结果如表2所示。
表1 算法的相关参数
Table 1 Relevant parameters of algorithms
算法 ω ωmax ωmin c1 c2 cmax cmin 压缩因子 c3 PSO 0. 9 2. 0 1. 5 IPSO 2. 5 0. 5 4. 1 IPSOSM 0. 9 0. 4 2. 0 1. 5 0. 5 E-PSO 0. 9 0. 4 2. 0 1. 0
表2 函数优化结果
Table 2 Function optimization results
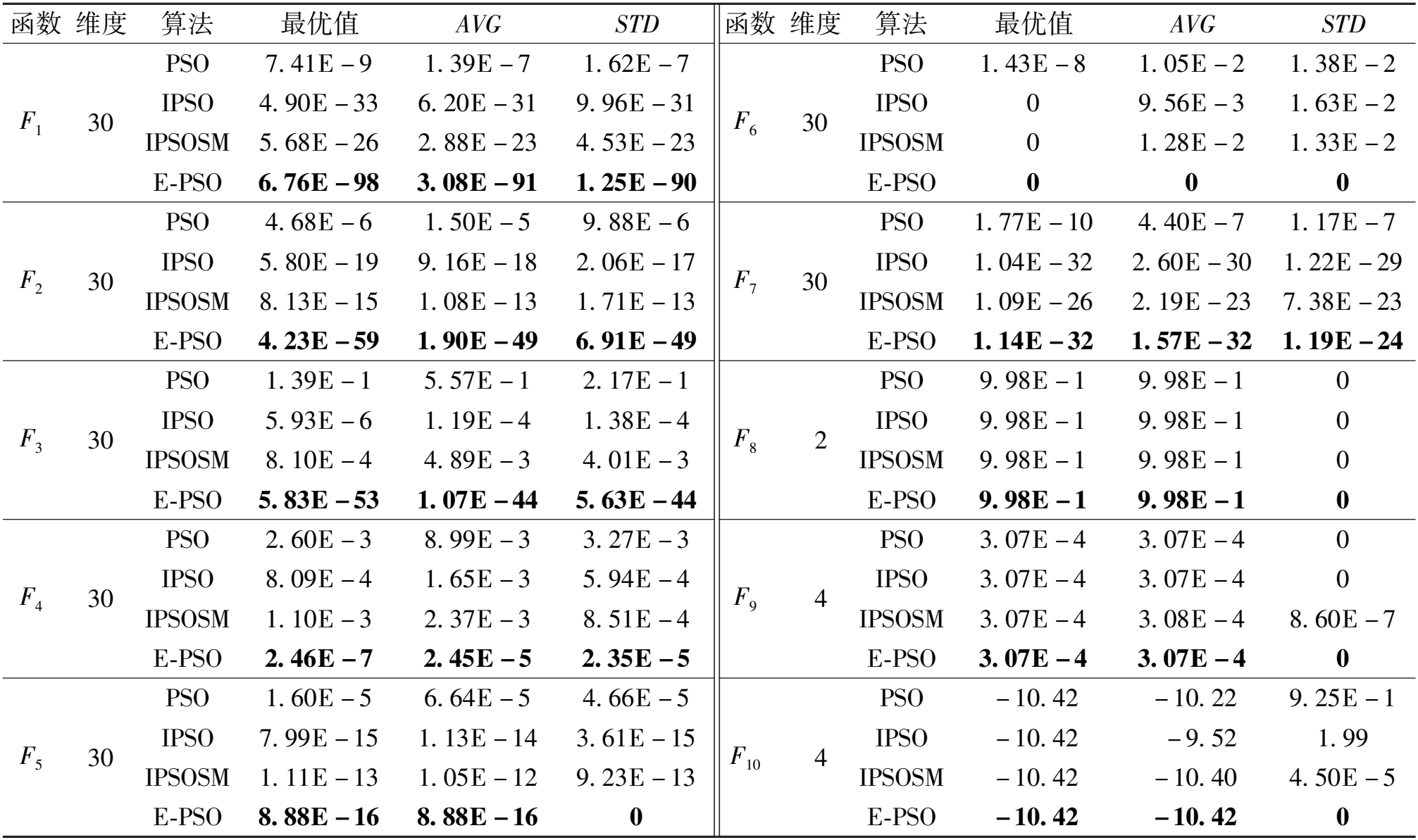
函数 维度 算法 最优值 AVG STD 函数 维度 算法 最优值 AVG STD F1 30 PSO 7. 41E - 9 1. 39E - 7 1. 62E - 7 IPSO 4. 90E - 33 6. 20E - 31 9. 96E - 31 IPSOSM 5. 68E - 26 2. 88E - 23 4. 53E - 23 E-PSO 6. 76E - 98 3. 08E - 91 1. 25E - 90 F6 30 PSO 1. 43E - 8 1. 05E - 2 1. 38E - 2 IPSO 0 9. 56E - 3 1. 63E - 2 IPSOSM 0 1. 28E - 2 1. 33E - 2 E-PSO 0 0 0 F2 30 PSO 4. 68E - 6 1. 50E - 5 9. 88E - 6 IPSO 5. 80E - 19 9. 16E - 18 2. 06E - 17 IPSOSM 8. 13E - 15 1. 08E - 13 1. 71E - 13 E-PSO 4. 23E - 59 1. 90E - 49 6. 91E - 49 F7 30 PSO 1. 77E - 10 4. 40E - 7 1. 17E - 7 IPSO 1. 04E - 32 2. 60E - 30 1. 22E - 29 IPSOSM 1. 09E - 26 2. 19E - 23 7. 38E - 23 E-PSO 1. 14E - 32 1. 57E - 32 1. 19E - 24 F3 30 PSO 1. 39E - 1 5. 57E - 1 2. 17E - 1 IPSO 5. 93E - 6 1. 19E - 4 1. 38E - 4 IPSOSM 8. 10E - 4 4. 89E - 3 4. 01E - 3 E-PSO 5. 83E - 53 1. 07E - 44 5. 63E - 44 F8 2 PSO 9. 98E - 1 9. 98E - 1 0 IPSO 9. 98E - 1 9. 98E - 1 0 IPSOSM 9. 98E - 1 9. 98E - 1 0 E-PSO 9. 98E - 1 9. 98E - 1 0 F4 30 PSO 2. 60E - 3 8. 99E - 3 3. 27E - 3 IPSO 8. 09E - 4 1. 65E - 3 5. 94E - 4 IPSOSM 1. 10E - 3 2. 37E - 3 8. 51E - 4 E-PSO 2. 46E - 7 2. 45E - 5 2. 35E - 5 F9 4 PSO 3. 07E - 4 3. 07E - 4 0 IPSO 3. 07E - 4 3. 07E - 4 0 IPSOSM 3. 07E - 4 3. 08E - 4 8. 60E - 7 E-PSO 3. 07E - 4 3. 07E - 4 0 F5 30 PSO 1. 60E - 5 6. 64E - 5 4. 66E - 5 IPSO 7. 99E - 15 1. 13E - 14 3. 61E - 15 IPSOSM 1. 11E - 13 1. 05E - 12 9. 23E - 13 E-PSO 8. 88E - 16 8. 88E - 16 0 F10 4 PSO - 10. 42 - 10. 22 9. 25E - 1 IPSO - 10. 42 - 9. 52 1. 99 IPSOSM - 10. 42 - 10. 40 4. 50E - 5 E-PSO - 10. 42 - 10. 42 0
所有仿真均在配置有Windows 10,64位操作系统,8.00 GB运行内存,Intel(R) Core(TM) i5-8265U CPU@1.60 GHz处理器的计算机上,利用MATLAB软件运行。
根据表2可知,本文提出的E-PSO算法在优化性能上表现出显著优势。无论面对单峰测试函数(F1～F4)还是多峰测试函数(F5～F7),E-PSO算法在搜索最优值的能力和算法稳定性方面均超越了其他对比算法。此外,在固定维多峰测试函数(F8～F10)测试中,尽管所有算法在平均结果上取得相似的结果,但分析标准差可以看出,E-PSO的稳定性更优。这表明E-PSO在处理复杂优化问题时,不仅能够准确找到最优值,而且稳定性表现更为出色。
3 仿真结果与分析
对E-SPSO算法在无人机路径规划问题上的性能进行仿真,对比算法选用SPSO算法[15]。基础参数配置详见表3。为验证优化算法的有效性,在2个场景中(场景1有5处禁飞区,场景2有6处禁飞区)各进行30次独立仿真。通过统计分析,计算两种算法的最优值、平均最优代价(AVG)和标准差(STD),结果如表4所示,可以看出,在两个场景中,E-SPSO算法的性能均保持优异:E-SPSO算法规划出最优路径的平均最优代价和标准差均小于SPSO 算法,路径代价可减少2%,稳定性可提高65%。这一结果表明了E-SPSO算法在提升寻优效率方面的有效性,同时也彰显了其在增强算法稳定性方面的优势。
表3 基础仿真参数
Table 3 Basic simulation parameters
参数 规模 空间范围 (1 000 × 1 000 × 500)m 最大迭代次数 300 种群规模 500 起点位置 (50,100,100)m 终点位置 (900,800,120)m D 12 ωmax 0. 9 ωmin 0. 4 cmax 2. 0 cmin 1. 0 代价权重比 10∶ 1∶ 8∶ 5
表4 两个场景中仿真统计结果
Table 4 Simulation statistics results in two scenarios
场 景 算 法 最 优 值 A VG S TD 场 景 1 S P S O 6 4 0 5 . 1 1 6 6 9 7 . 1 6 3 0 3 . 7 8 E - S P S O 6 3 9 8 . 3 1 6 5 5 6 . 3 3 5 2 . 6 9 场 景 2 S P S O 6 3 1 9 . 5 5 6 7 6 7 . 1 0 3 6 7 . 8 3 E - S P S O 6 2 7 0 . 5 9 6 5 4 8 . 5 8 1 2 7 . 4 4
图3展示了两种算法在迭代过程中最优代价的变化趋势。随着迭代次数增加,两者均明显收敛:前50次迭代中,两种算法的最优代价迅速下降,SPSO算法最优代价降低近40%,速度更快;50至150次迭代期间,E-SPSO算法表现更佳,相较第50次的最优代价降低近30%;150至300次迭代期间内,相较第150次的最优代价,降低均在5%内,且在迭代200次后两者收敛基本趋于稳定。E-SPSO算法在收敛精度上更胜一筹。进一步观察规划路径的三维路径视图(图4)和路径俯视图(图5),可以看出,两种算法均能在本文构建的模型中规划出安全且平滑的飞行路径,而相比之下,E-SPSO算法所规划的路径更为优越。
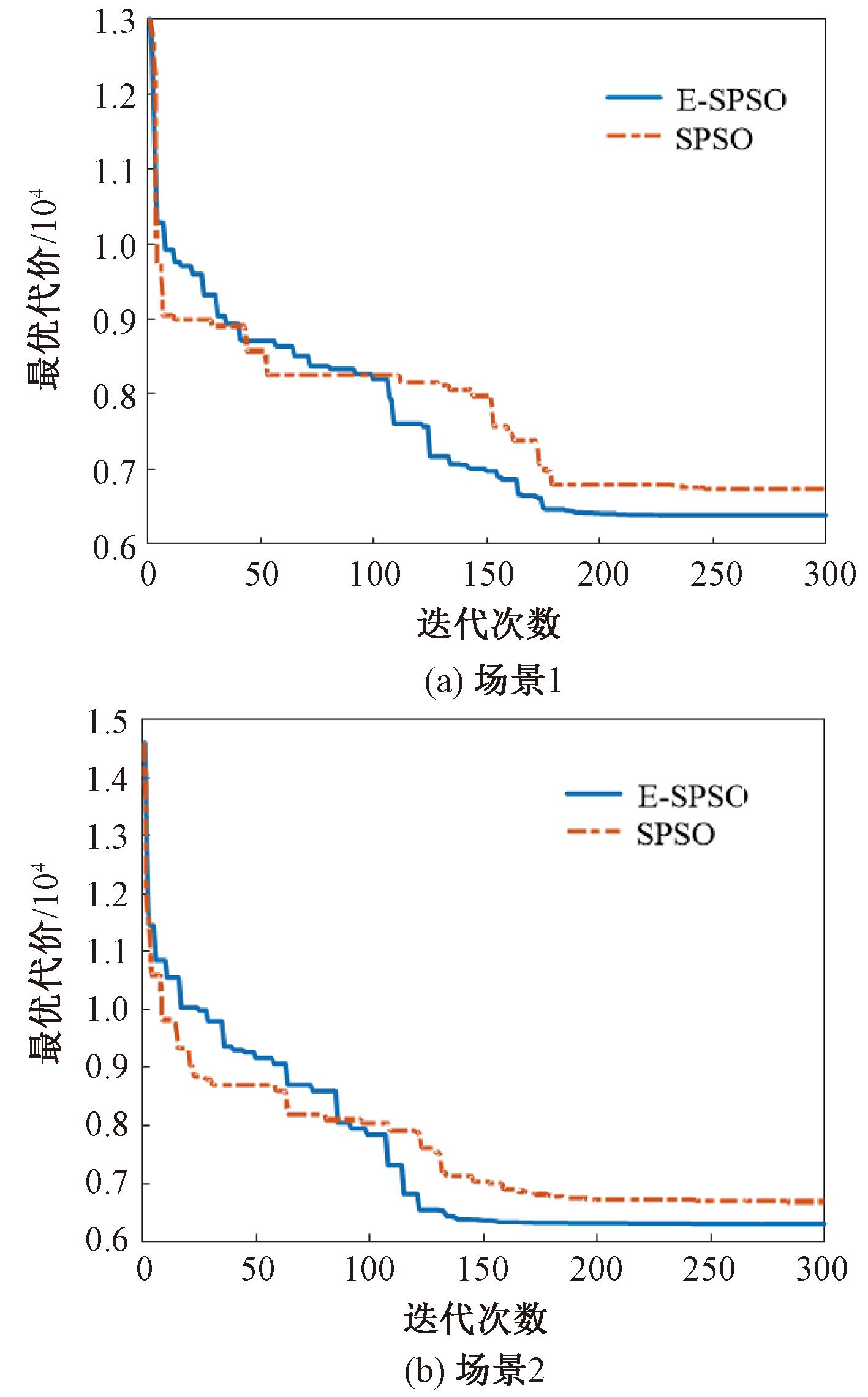
图3 最优代价随迭代对比曲线
Figure 3 Comparison curve of optimal cost with iteration
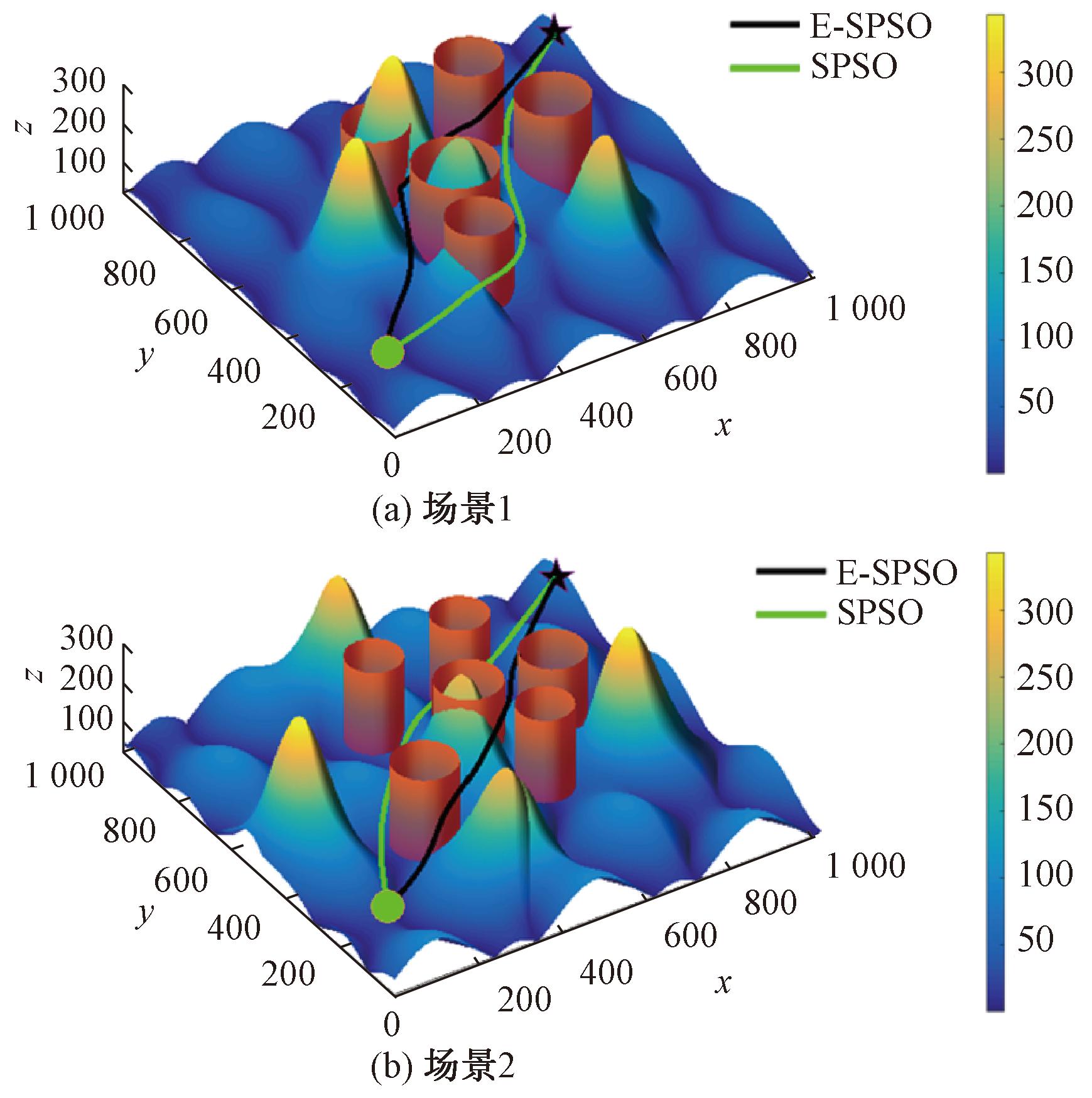
图4 3D路径视图
Figure 4 3D path view
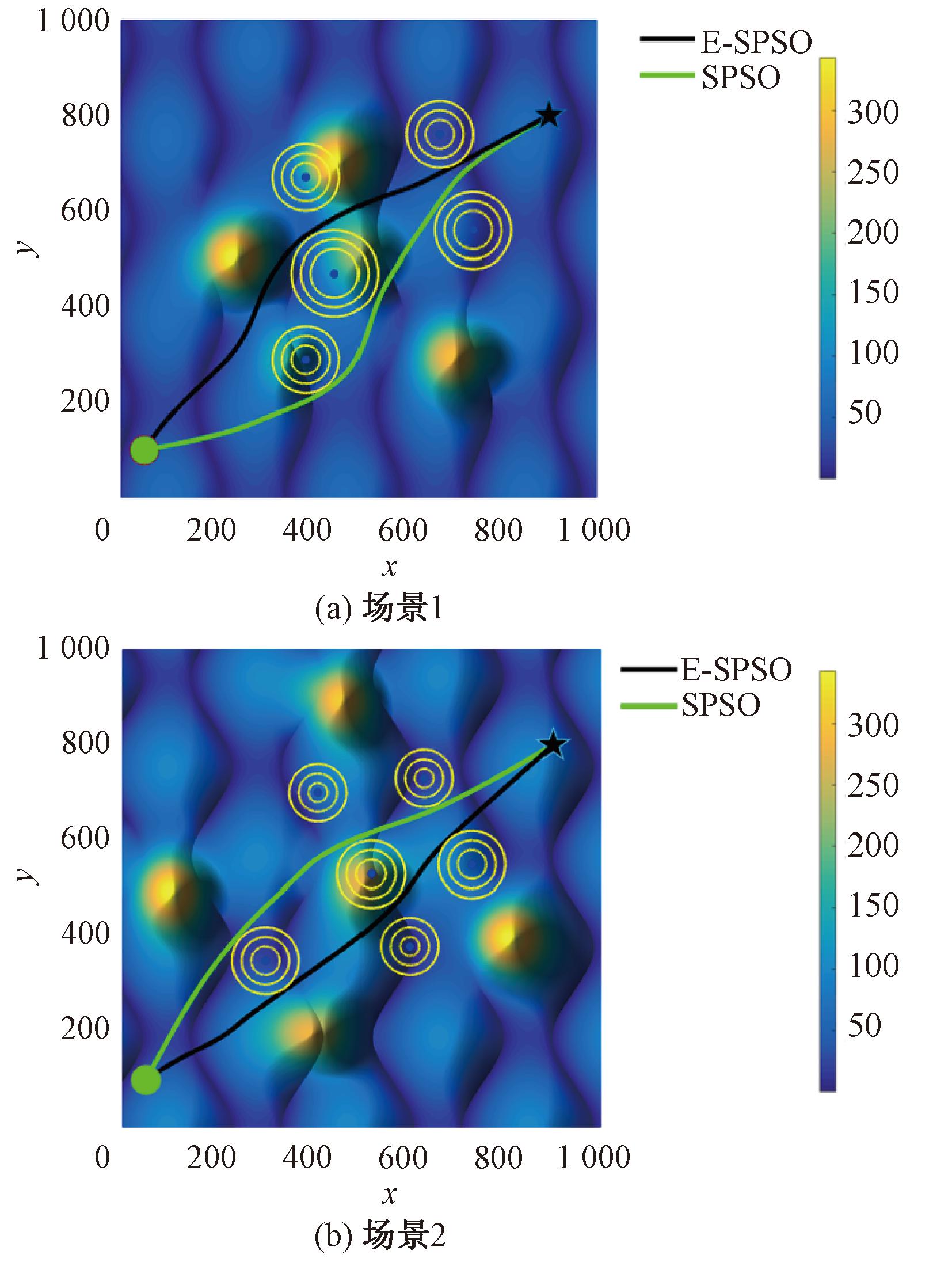
图5 路径俯视图
Figure 5 Top view of the path
4 结论
本文基于无人机飞行综合性能要求,利用B样条曲线的相关性质对飞行路径进行几何分析并建模,提出一种安全避障的无人机三维光滑路径规划方法。主要结论如下所示。
(1)利用B样条曲线的凸包性、局部支撑性等性质,对无人机飞行路径长度、安全避障、飞行高度和平稳性等性能要求进行建模,构建了以B样条曲线控制顶点为决策变量的路径规划模型。
(2)提出了一种基于改进粒子群算法的模型求解算法,并基于标准测试函数集对算法性能进行评估,评估结果表明,算法在精度(寻优能力)和稳定性方面都有更优的表现。
(3)所规划的路径在达成无人机飞行综合性能最优目标的同时,达到C2连续。
未来的工作将进一步考虑无人机动力学(如速度、加速度)约束建模和移动障碍物避障问题,使其更适应实际应用场景的需求。
[1] RADMANESH M, KUMAR M, GUENTERT P H, et al. Overview of path-planning and obstacle avoidance algorithms for UAVs： a comparative study[J]. Unmanned Systems, 2018, 6(2): 95-118.
[2] PUENTE-CASTRO A, RIVERO D, PAZOS A, et al. A review of artificial intelligence applied to path planning in UAV swarms[J]. Neural Computing and Applications, 2022, 34(1): 153-170.
[3] SUN J Y, TANG J, LAO S Y. Collision avoidance for cooperative UAVs with optimized artificial potential field algorithm[J]. IEEE Access, 2017, 5: 18382-18390.
[4] 陈江义, 殷笑勇, 王婷婷, 等. 基于改进斥力模型的人工势场局部路径规划[J]. 郑州大学学报(工学版), 2023, 44(3): 83-87, 101.
CHEN J Y, YIN X Y, WANG T T, et al. Local path planning of artificial potential field based on improved repulsive model[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(3): 83-87, 101.
[5] AIT-SAADI A, MERAIHI Y, SOUKANE A, et al. A novel hybrid chaotic Aquila optimization algorithm with simulated annealing for unmanned aerial vehicles path planning[J]. Computers and Electrical Engineering, 2022, 104: 108461.
[6] JIN Q B, TANG C N, CAI W. Research on dynamic path planning based on the fusion algorithm of improved ant colony optimization and rolling window method[J]. IEEE Access, 2021, 10: 28322-28332.
[7] XIONG T, LI H, DING K, et al. A hybrid improved symbiotic organisms search and sine-cosine particle swarm optimization method for drone 3D path planning[J]. Drones, 2023, 7(10): 633.
[8] 高岳林, 武少华. 基于自适应粒子群算法的机器人路径规划[J]. 郑州大学学报(工学版), 2020, 41(4): 46-51.
GAO Y L, WU S H. Robot path planning based on adaptive particle swarm optimization[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(4): 46-51.
[9] BAO Y Y, LIU Y, WANG J S, et al. Genetic algorithm based on grid maps for solving robot path planning problem[J]. Engineering letters, 2023, 31(4): 1635-1648.
[10] ROBERGE V, TARBOUCHI M, LABONTÉ G. Fast genetic algorithm path planner for fixed-wing military UAV using GPU[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2105-2117.
[11] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 2版. 北京: 高等教育出版社, 2013.
SHI F Z. CAGD &NURBS[M]. 2nd ed. Beijing: Higher Education Press, 2013.
[12] HUO F C, ZHU S, DONG H L, et al. A new approach to smooth path planning of Ackerman mobile robot based on improved ACO algorithm and B-spline curve[J]. Robotics and Autonomous Systems, 2024, 175: 104655.
[13] LIU M J, ZHANG H X, YANG J, et al. A path planning algorithm for three-dimensional collision avoidance based on potential field and B-spline boundary curve[J]. Aerospace Science and Technology, 2024, 144: 108763.
[14] YAN J F, DENG T, XU B H. Three dimensional path planning for flying car based on improved A* algorithm and Bezier curve fusion[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2025, 239(6): 2205-2219.
[15] PHUNG M D, HA Q P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization[J]. Applied Soft Computing, 2021, 107: 107376.
[16] QI Z, SHAO Z H, PING Y S, et al. An improved heuristic algorithm for UAV path planning in 3D environment[C]∥2010 Second International Conference on Intelligent Human-Machine Systems and Cybernetics. Piscataway: IEEE, 2010: 258-261.
[17] 黄书召, 田军委, 乔路, 等. 基于改进遗传算法的无人机路径规划[J]. 计算机应用, 2021, 41(2): 390-397.
HUANG S Z, TIAN J W, QIAO L, et al. Unmanned aerial vehicle path planning based on improved genetic algorithm[J]. Journal of Computer Applications, 2021, 41(2): 390-397.
[18] SHI Y, EBERHART R. A modified particle swarm optimizer[C]∥IEEE World Congress on Computational Intelligence. Piscataway: IEEE, 2002: 69-73.
[19] ARORA S, ANAND P. Chaotic grasshopper optimization algorithm for global optimization[J]. Neural Computing and Applications, 2019, 31(8): 4385-4405.
[20] SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]∥Congress on Evolutionary Computation. Piscataway: IEEE, 1999: 1945-1950.
[21] ZHAO W G, WANG L Y, ZHANG Z X, et al. Electric eel foraging optimization: a new bio-inspired optimizer for engineering applications[J]. Expert Systems with Applications, 2024, 238: 122200.
[22] 宋志强, 夏庆锋, 陈少博, 等. 基于改进球面向量粒子群优化的UAV航迹规划[J]. 电光与控制, 2023, 30(4): 56-60.
SONG Z Q, XIA Q F, CHEN S B, et al. UAV path planning with improved spherical vector based particle swarm optimization[J]. Electronics Optics &Control, 2023, 30(4): 56-60.
[23] 李丁, 夏露. 改进的粒子群优化算法在气动设计中的应用[J]. 航空学报, 2012, 33(10): 1809-1816.
LI D, XIA L. Application of improved particle swarm optimization algorithm to aerodynamic design[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10): 1809-1816.