锂离子电池广泛应用于电动汽车和电子产品,需具备快速充电能力。然而,高倍率充电会导致温度升高,从而加速电池老化、缩短使用寿命,并可能引发热失控风险[1]。高荷电状态下的高倍率充电易引发析锂现象,导致能量密度下降、寿命缩短,并可能引发安全问题 [2]。此外,过充可能损害电池性能,甚至导致短路或电解液分解等严重后果[3]。
常见的充电策略包括恒流恒压充电(CC-CV)策略、升压充电策略、脉冲充电策略以及多级恒流充电策略。这些策略均旨在优化充电性能并延长电池寿命。然而,这些传统策略在解决复杂问题时存在一定的局限性,因此,近年来基于电池模型的充电优化方法得到了广泛关注,这些方法普遍采用基于电池模型的等效电路模型[4]的优化方法和基于物理的电化学模型[5]的优化方法。基于等效电路模型的优化方法计算成本低,适用于实时性要求高的场景,但无法解释微观现象;基于电化学模型的方法虽然能够从本质上描述电池内部的化学反应和物理行为,但由于涉及多个偏微分方程,计算成本较高,实时应用受限[6]。基于模型优化常与遗传算法(GA)[7]、粒子群算法(PSO)[8]、动态规划(DP)算法[9]和模型预测控制(MPC)算法相结合。MPC算法预测电池未来状态,求解最优充电电流序列,并逐时更新,确保高效、安全地充电,不少研究者将其应用于充电策略中。Yang等[10]提出了一种基于无迹卡尔曼波器和模拟退火的MPC算法,该算法能够有效完成电池充满的目标,但未充分考虑析锂与过充等安全问题;Kolluri等[11]提出了一种基于伪二维(P2D)模型的非线性MPC充电策略,尽管考虑了安全约束,但由于直接使用完整的P2D模型,计算复杂度过高,难以应用于实际场景;Jia等[4]提出了一种基于MPC快速充电优化策略,然而,该策略忽略了模型随温度和荷电状态的变化以及缺乏全局预测和完善的代价函数。
综上所述,锂离子电池快充时面临温度升高、析锂、过充等问题,影响电池寿命与安全。研究者采用多种模型与优化算法改进充电策略,其中MPC算法因其优势备受关注。但现有MPC充电策略存在忽略安全问题、计算量大以及缺乏全局优化等不足,因此,本文提出了一种新的MPC充电策略,通过电池当前状态计算全局最优电流,在提升充电速度的同时限制过充和避免析锂。同时,结合等效电路模型与降阶电化学模型的优点,从微观层面减少电池损耗并降低优化过程中的计算成本,为高效、安全的锂电池快充提供了一种新的解决方案。
1 电池模型的建立
1.1 4种常用电池模型
(1)电化学模型。P2D模型控制方程[12]如下所示:
(1)
(2)
![]()
(3)
(4)
(5)
其中,式(1)为液相扩散方程;式(2)固相电势方程;式(3)为固相扩散方程;式(4)为液相电势方程;式(5)为反应动力学方程。
电化学参数命名如表1所示。
表1 电化学参数命名
Table 1 Naming of electrochemical parameters
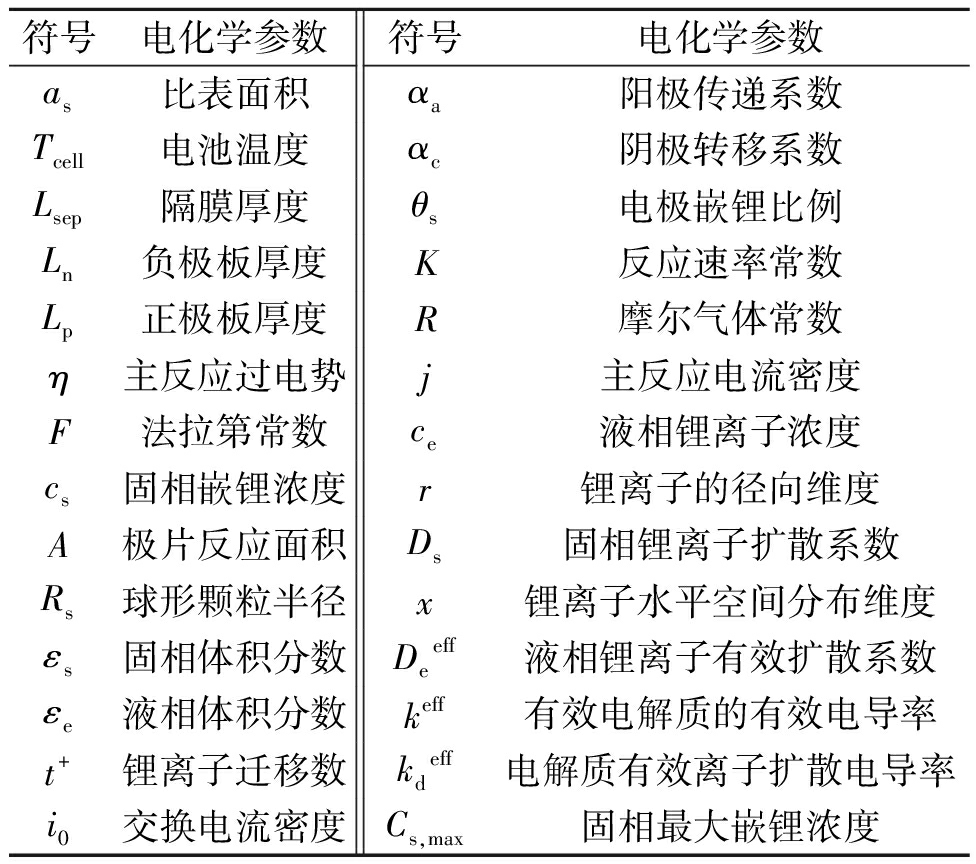
符号电化学参数符号电化学参数as比表面积αa阳极传递系数Tcell电池温度αc阴极转移系数Lsep隔膜厚度θs电极嵌锂比例Ln负极板厚度K反应速率常数Lp正极板厚度R摩尔气体常数η主反应过电势j主反应电流密度F法拉第常数ce液相锂离子浓度cs固相嵌锂浓度r锂离子的径向维度A极片反应面积Ds固相锂离子扩散系数Rs球形颗粒半径x锂离子水平空间分布维度εs固相体积分数Deeff液相锂离子有效扩散系数εe液相体积分数keff有效电解质的有效电导率t+锂离子迁移数kdeff电解质有效离子扩散电导率i0交换电流密度Cs,max固相最大嵌锂浓度
为了解决多个偏微分方程组求解的计算复杂度问题,本文引用了杨俊等[13]的研究,根据其推导的模型传递函数进行模型降阶,并应用于充电优化。
(2)二阶R-C模型。二阶R-C模型如图1所示,由开路电压UOCV、欧姆内阻R0以及极化电容电阻R1C1、R2C2并联组成[14],根据极化特性计算电池端电压U,公式如下:
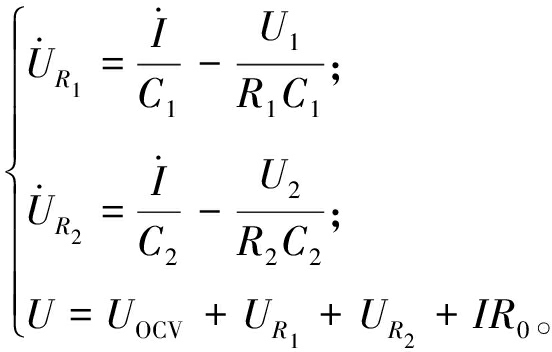
(6)
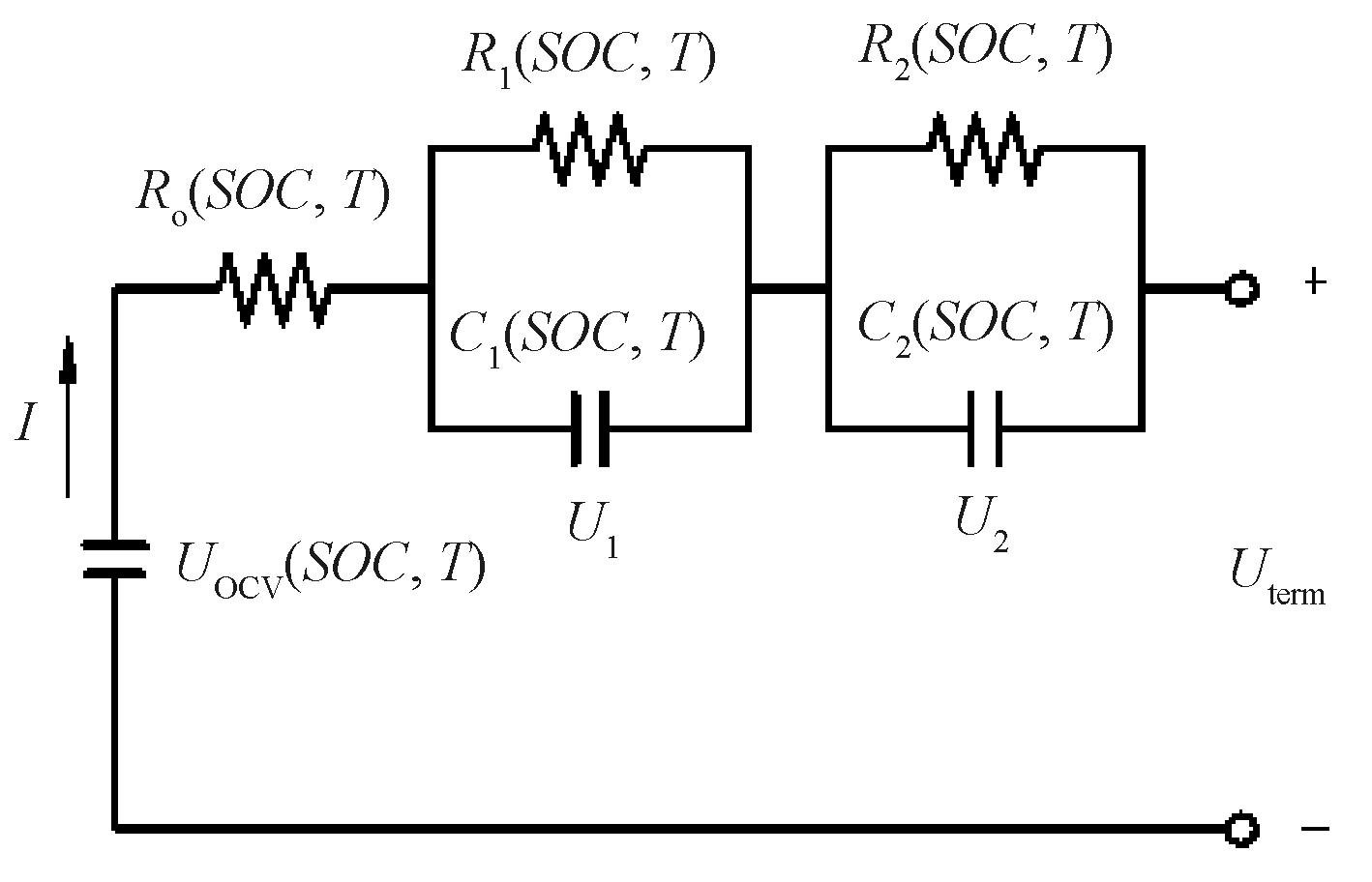
图1 二阶R-C模型
Figure 1 Second-order R-C model
式中:U为电池端电压,V;UR1、UR2分别为R1、R2两端的极化电压,V;UOCV为电池的开路电压,V;R0为欧姆内阻,Ω;R1、R2均为极化电阻,Ω;C1、C2均为极化电容,F。
(3)热模型。热交换包括电池与环境之间的热交换。电池发热量由所有支路内阻与通过电流平方的乘积之和表示(见式(7)),电池温度计算表达式由式(8)计算得到[15]。
(7)
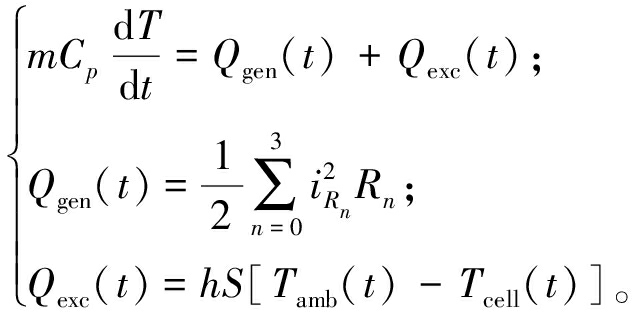
(8)
式中:Qexc(t)为t时刻电池的交换热,J;m为电池质量,kg;Cp为电池比热容,J/(kg·K);h为电池热交换系数,W/(m2.K);S为电池表面积,m2;Tamb(t)为环境温度,K;Tcell(t)为电池表面温度,K;iRn为第n个电阻流过的电流,A。
(4)老化模型。老化模型考虑了石墨阳极快速充电锂离子电池的3种主要降解机制:固体电解质界面(SEI)层生长、活性材料损失和锂电镀。SEI层在阳极颗粒表面形成,是导致容量损失的主要原因之一。其反应可表示为
S+2Li++2e-→P。
(9)
式中:S为溶剂反应物;P为形成SEI层的还原产物。SEI层形成导致的容量损失速率与副反应电流密度is(A/m2)有关,通过式(10)计算[16]。
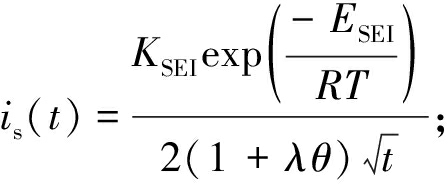
(10)
(11)
(12)
式中:ESEI为SEI形成的活化能,J/mol;KSEI为容量损失因子;![]() 分别为平衡时溶剂反应物和还原产物的体积浓度,mol/m3;Ds、Dd分别为反应物和还原产物的扩散系数,
分别为平衡时溶剂反应物和还原产物的体积浓度,mol/m3;Ds、Dd分别为反应物和还原产物的扩散系数,![]() 为副反应的平衡电位,
为副反应的平衡电位,![]() 为主反应的平衡电位,V;n=2为反应转移电子数目;λ、θ均为拟合参数。
为主反应的平衡电位,V;n=2为反应转移电子数目;λ、θ均为拟合参数。
由SEI层生长引起的总的容量损失率如式(13)[16]所示,SEI层膜的增长以及SEI膜的阻值如式(14)与式(15)所示。
QSEI=![]() isAdt;
isAdt;
(13)
(14)
(15)
式中:ΔδSEI表示沉积层厚度的增长量,![]() 表示SEI的单位摩尔体积,m3/mol;RSEI,0表示SEI膜初始阻值, Ω;kSEI表示SEI膜的电导率, S/m。
表示SEI的单位摩尔体积,m3/mol;RSEI,0表示SEI膜初始阻值, Ω;kSEI表示SEI膜的电导率, S/m。
活性材料损失是另一主要降解机制,由锂插层引起的机械应力可导致电极颗粒断裂或损坏,最终导致活性材料分离。活性材料分离引起的容量损失率QAM如式(16)所示。
(16)
式中:KAM为活性材料损失容量损失因子;EAM为容量损失反应活化能,J/mol。
在石墨阳极上镀锂反应也是导致容量快速损失的一个重要原因。沉积的锂金属与溶剂或盐反应形成不溶性产物,导致锂消耗。在充电过程中,阳极集流体与隔膜交界处的局部电位差低于镀锂反应平衡电位,触发镀锂反应[17]。局部电位ηLi的计算公式如式(17)所示[18]:
(17)
式中:φs、φe分别为固相电势和液相电势,![]() 为锂电镀平衡电位,V;RSEI为SEI电阻,Ω;j为主反应电流密度,A/m2。
为锂电镀平衡电位,V;RSEI为SEI电阻,Ω;j为主反应电流密度,A/m2。
镀锂反应的电流密度可以由局部电位求解,表达式如式(18)所示[16]:
(18)
式中:αLi为锂电镀的阴极转移系数。
镀锂反应造成容量损失QLi的表达式为
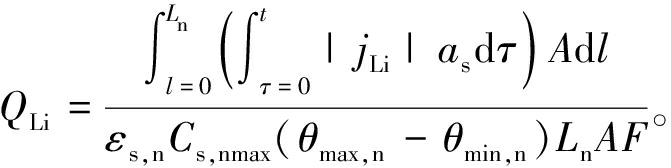
(19)
充放电循环总的容量损失Qloss的表达式为
Qloss=QSEI+QAM+QLi。
(20)
1.2 电池模型耦合
电池的性能受多种因素影响,等效电路与热模型展现了电池的宏观状态变化,如电流、电压和温度,为理解充电动态提供了基础。电化学模型与老化模型则能够深入揭示电池内部微观层面的反应机制,如SEI层的生长、活性材料的损失以及锂电镀等现象。这些内部反应是导致电池性能衰减和安全隐患的主要原因。因此,将它们纳入一个统一的耦合模型中,能够更全面、准确地描述电池在不同充电策略下的性能表现,从而找到最优的充电策略来延长电池寿命并减少安全隐患。
本文将上文提到的4个常用模型进行耦合,其中等效电路模型和热模型用于预测电池充电时电池的动态响应,即电流、电压、荷电状态SOC、温度,以及给定的电流需求。降阶电化学模型预测3种老化反应相关电位,老化模型预测电池充电时的退化过程。具体的耦合思路如下:充电电流I为所有模型的控制输入变量,初始SOC和环境温度Tamb分别为等效电路模型和热模型的输入。等效电路模型根据输入计算电池当前SOC,端电压U,欧姆电阻R0,极化电阻R1、R2,极化电容C1、C2等中间变量。将上述电性参数和充电电流输入到热模型中,更新电池温度Tcell,一方面用于更新等效电路模型电性参数,另一方面更新电化学模型中计算的析锂反应局部过电势ηLi和老化模型中KAM、KSEI两种造成容量损失的相关系数。电化学模型根据电池温度、充电电流大小来更新主反应的平衡电位UnOCP和析锂反应局部过电势ηLi,这两者与前文等效电路模型计算出的电池当前SOC以及充电电流输入老化模型估计电池老化。电池的耦合特性如图2所示。
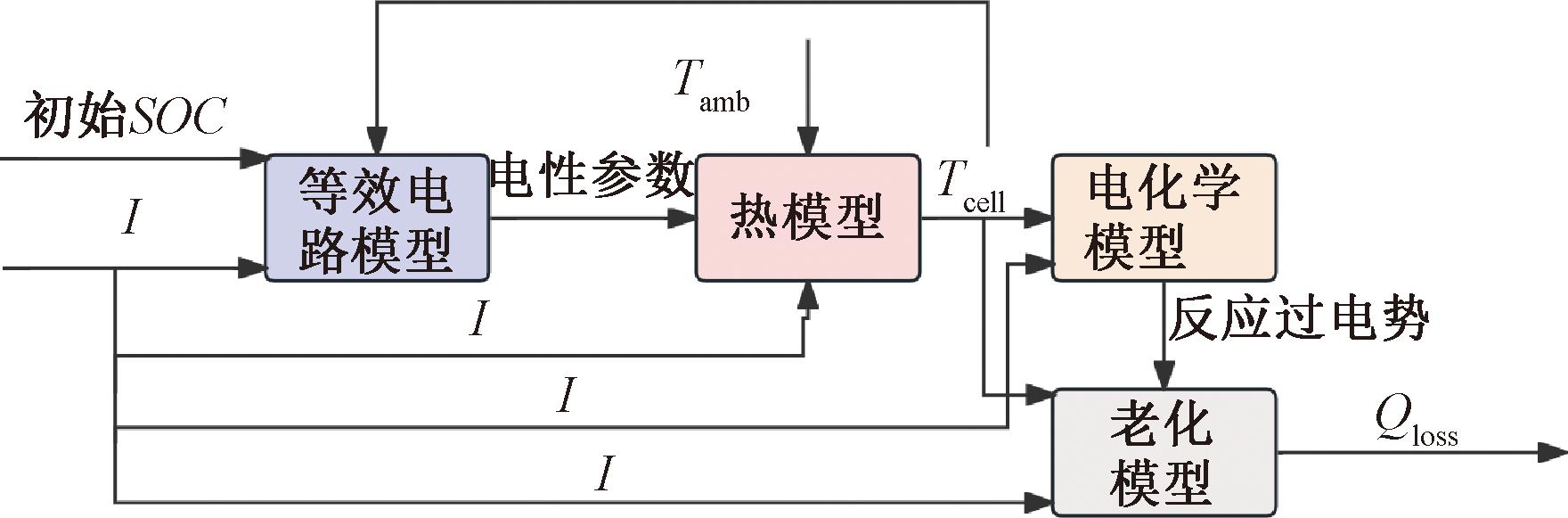
图2 电池的耦合特性
Figure 2 Coupling characteristics of the battery
2 耦合模型参数值与精度验证
本文搭建的电池实验平台如图3所示,实验电池主要参数如表2所示。

图3 LiFePO4电池实验平台
Figure 3 LiFePO4 Battery experimental platform
表2 电池主要参数
Table 2 Main parameters of the battery

参数取值标称电压/V3.2额定容量/Ah20截止电压/V2.50 ~ 3.65质量/g654 尺寸148 mm×27 mm×98 mm比热容/(J·g-1·K-1)1.06
2.1 耦合模型参数值确定
拆解电池测量物理参数,用恒流充放电和PSO算法辨识电化学参数:测正负极、隔膜厚度及面积;用0.1C(C表示电流倍率大小)放电辨识固体体积分数,0.5C充放电辨识孔隙率、颗粒半径及反应速率均通过PSO最小化误差J来确定。(式(21)~(22))。
Xi=(xi1,xi2…,xiD);i=1,2,…,N,xi∈[ximin,ximax];
(21)
(22)
式中:Xi为N×D维的矩阵;N为粒子群种群大小;D为粒子维数(即待辨识参数的数量);ximin、ximax分别表示参数的最小值和最大值,具体数值来自文献[19];Usim,t、Uref,t分别为实验测得和模型计算的端电压序列,V;SOCsim,t、SOCref,t分别为实验测得与模型计算的荷电状态序列。最终辨识得到的电化学模型参数如表3所示。
表3 电化学模型参数
Table 3 Electrochemical model parameters

参数取值参数取值Rs,p/m2e-6θmax,n0.652Rs,n/m2e-6θmin,p0.842Εs,p0.441θmin,n0.001Es,n0.548A/m20.560Kp/(m2.5/mol0.5s)3e-11 Lp/m1.01e-4Kn/(m2.5/mol0.5s)2.02e-12Lsep/m1.5e-5θmax,p0.323Ln/m7.8e-5
电-热耦合模型参数UOCV、R0、R1、R2、C1、C2和h
来自文献[20]。老化模型的参数的计算方法来自文献[17],老化模型参数如表4所示。
表4 老化模型参数
Table 4 Aging model parameters
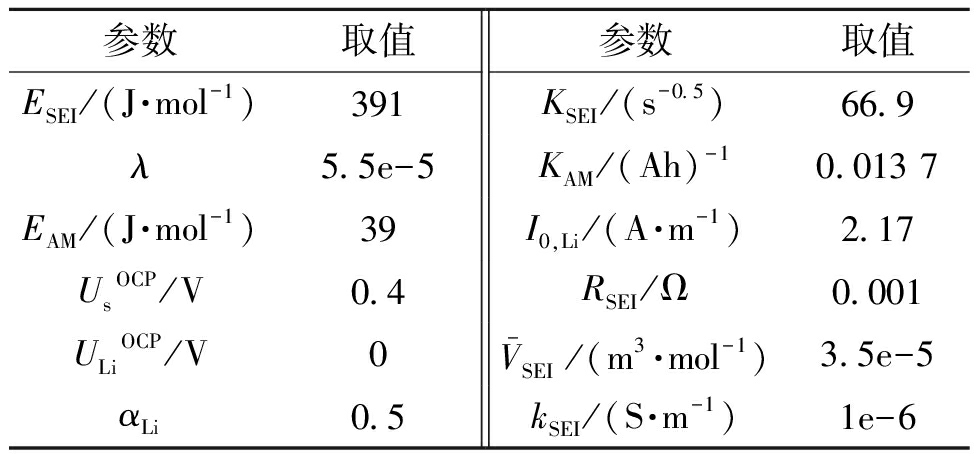
参数取值参数取值ESEI/(J·mol-1)391KSEI/(s-0.5)66.9λ5.5e-5KAM/(Ah)-10.013 7EAM/(J·mol-1)39I0,Li/(A·m-1)2.17UsOCP/V0.4RSEI/Ω0.001ULiOCP/V0 V-SEI/(m3·mol-1)3.5e-5αLi0.5kSEI/(S·m-1)1e-6
2.2 耦合模型验证
为验证模型的预测效果,进行了1C、2C、3C恒流充电实验,记录电压与温度变化并与模型进行对比。另用新电池进行10次充放电循环,记录容量衰减以验证模型。实验验证耦合模型如图4所示。耦合模型端电压与温度误差结果如表5所示。另外,经过计算模型容量衰减预测MAPE为0.54%,证明了衰减模型的准确和可靠性。
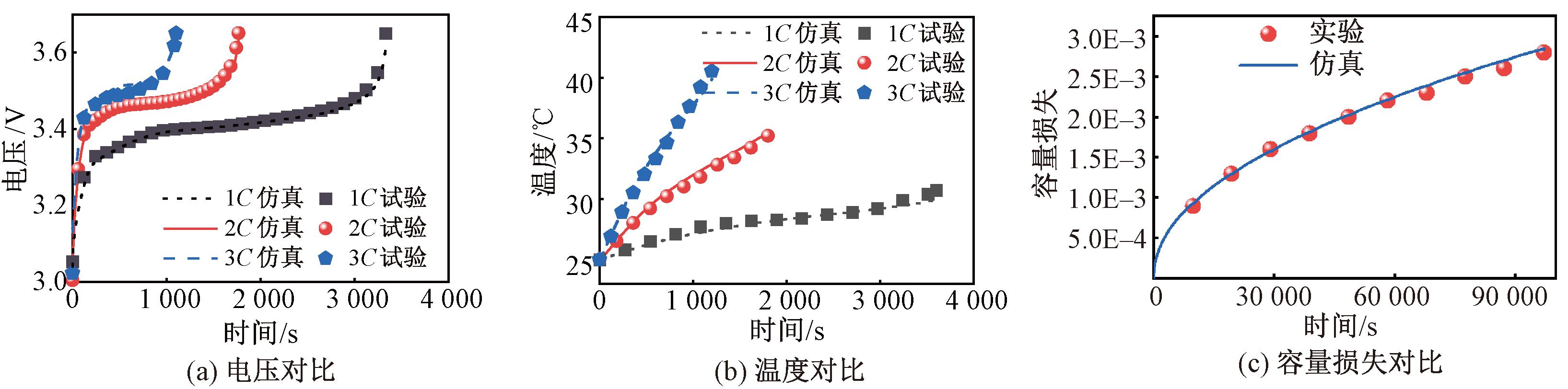
图4 实验验证耦合模型
Figure 4 Experimental verification of coupling model
表5 耦合模型端电压与温度误差结果
Table 5 Coupling model terminal voltage and temperature error results
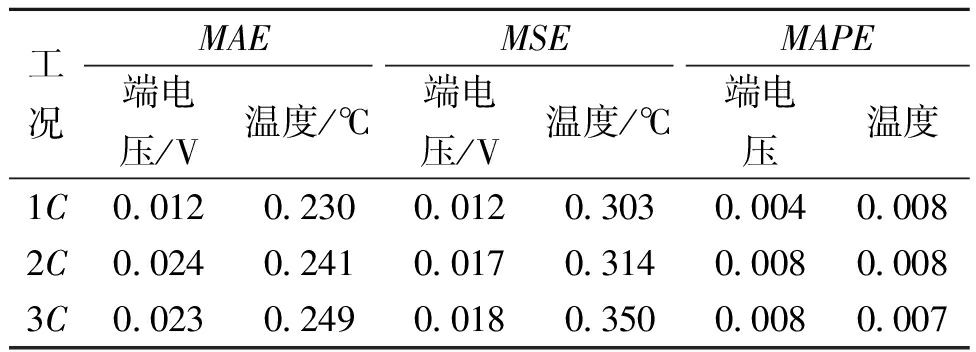
工况MAEMSEMAPE端电压/V温度/℃端电压/V温度/℃端电压温度1C0.0120.2300.0120.3030.0040.0082C0.0240.2410.0170.3140.0080.0083C0.0230.2490.0180.3500.0080.007
3 充电策略
3.1 基于MPC的充电控制策略
在电池充电的过程中,将电池的状态x=[SOC,U,Tcell,t,cs,p,φe,ηLi,Qloss]通过前文所述的电池模型计算公式进行离散化处理后,将电池完整的充电过程中的状态变化离散化为状态空间矩阵,假设其表示形式为
x(k+1)=Ax(k)+BI(k)。
(23)
假设在接下来的若干步内,每步的充电电流依次为:I=[I(k),I(k+1),I(k+2),…,I(k+N-1)],未来电池状态变量可通过式(24)迭代计算。在充电过程中,为了确保电池的安全与性能,充电电流应低于商家给定的最大充电电流60 A。为防止镀锂,阳极局部电势应始终保持在0 V以上;为了有效减缓电池的老化速度,延长其使用寿命,电池温度需维持在25~35 ℃内[21];为避免过充,电池端电压和电池荷电状态应严格控制在截止值以下。约束条件如式(25)所示。充电策略旨在综合优化充电耦合模型计算出的充电时间和容量衰减,为实现目标,构建代价函数将其转化为多目标优化问题,如式(26)所示。
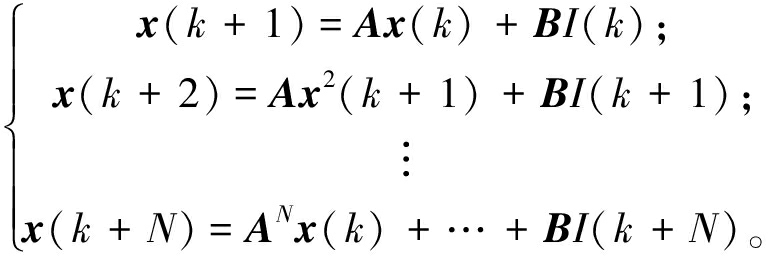
(24)
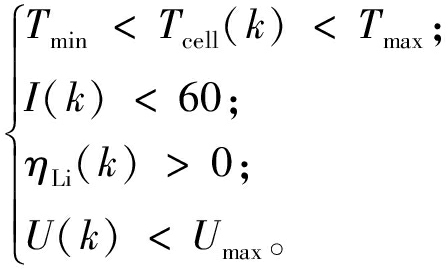
(25)
(26)
式中:![]() 为标准充电的平均损耗;tref为电池厂商标准充电模式的充电时间,s。
为标准充电的平均损耗;tref为电池厂商标准充电模式的充电时间,s。
3.2 引入改进PSO的MPC充电控制策略
为了解决多目标优化问题(式(26)),引入PSO算法,并增加约束适应度以确保可行性。约束效果根据耦合模型的相应输出进行评估。约束适应度计算方法由式(27)所示,通过gi(s)来衡量充电过程中对约束条件的遵循程度(式(28))。算法先比较约束适应度,小者优先,若相同则根据最佳适应度来进一步比较。图5为PSO-MPC算法优化流程。
(27)
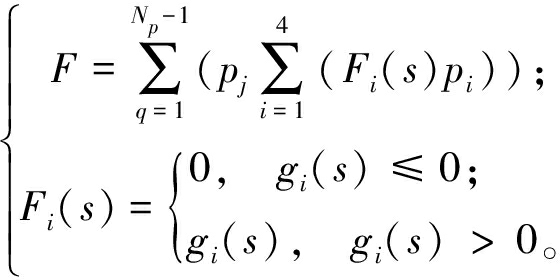
(28)
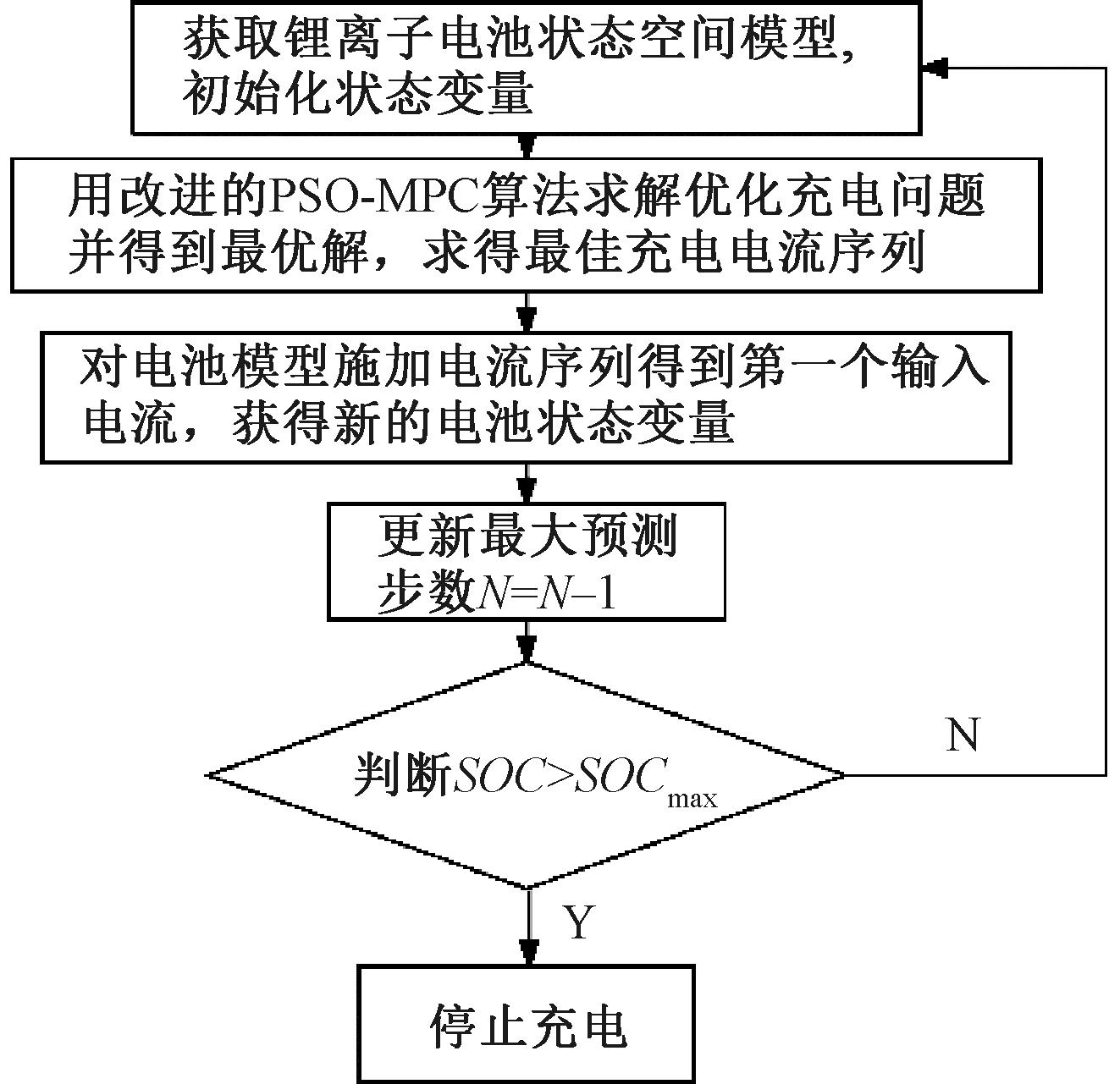
图5 PSO-MPC算法优化流程
Figure 5 PSO-MPC algorithm optimization process
式中:pj为每个约束的权重因子。
4 基于模型的充电过程优化
利用电池模型对充电策略进行了仿真模拟,以验证该策略的效果,充电策略相关参数如表6所示。
表6 充电策略相关参数
Table 6 Relevant parameters of the charging strategy

参数取值最大预测时域N100单步充电时间t/s60温度适应度权重P10.040电压适应度权重P20.274初始荷电状态SOC00
4.1 不同温度环境下电池温度约束效果
在多种环境温度((20~30 ℃,间隔2 ℃))下对充电策略进行了验证,结果如图6所示。由图6可以看出,当低于25 ℃时,电池温度先升后降,最终高于温度最低临界值。当高于25 ℃时,电池温度接近最高边界时即下降,通过调整充电电流保持在最佳温度范围内,证明了策略的有效性和广泛适用性。
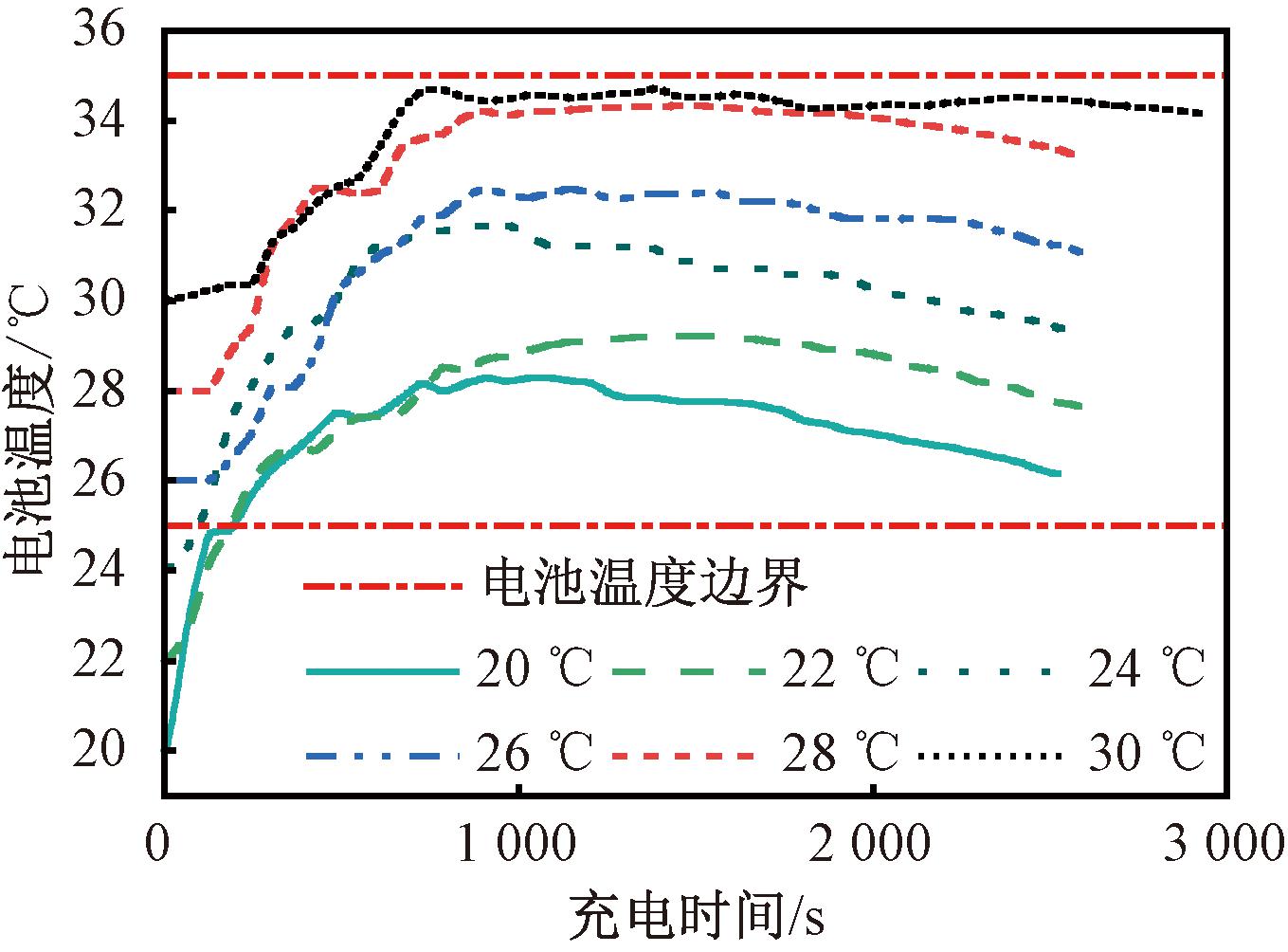
图6 宽温区电池温度变化曲线
Figure 6 Temperature variation curve of wide temperature range battery
4.2 充电过程中析锂现象和过充行为约束效果
标准室温下,验证优化电流序列对充电模型中过充和析锂的约束效果。图7展示了模型对充电过程中电池端电压和局部过电势的输出结果。由图7可以看出,充电全程电池端电压低于截止电压,负极与隔膜间电势高于镀锂平衡电势0 V,充分证明了该充电策略在限制析锂现象与避免过充行为方面的显著效果。
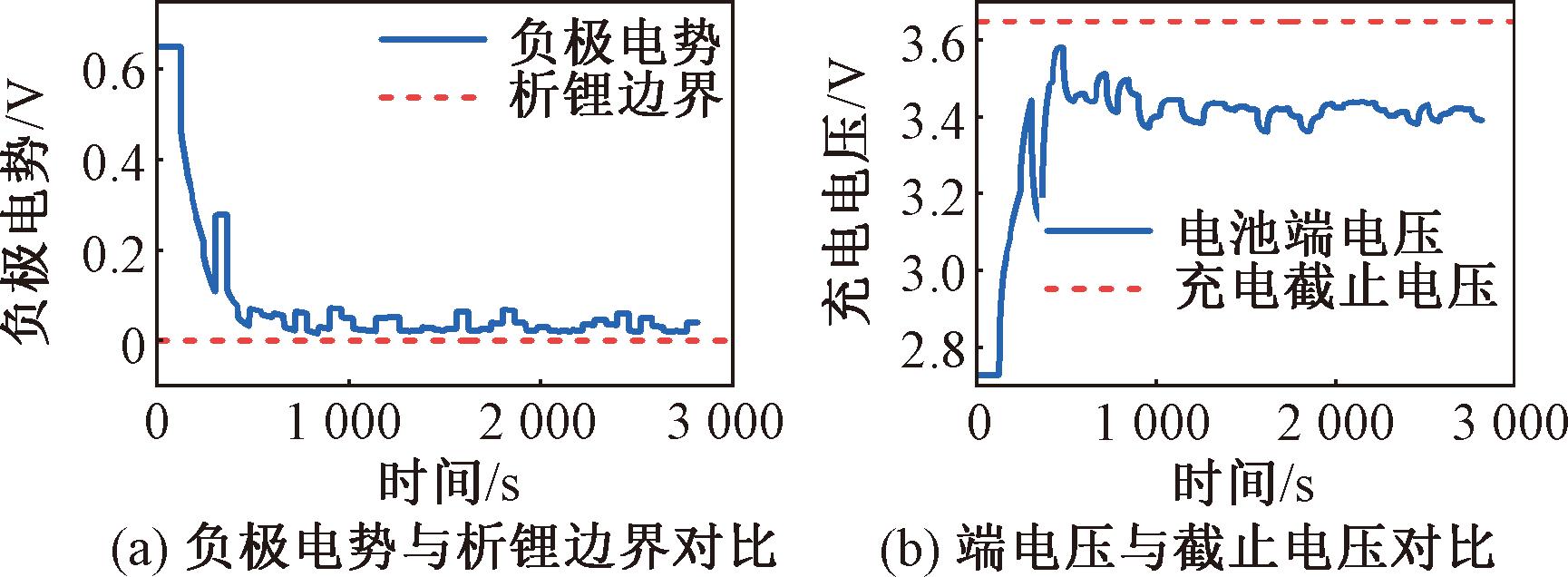
图7 析锂与过充行为约束效果验证
Figure 7 Verification of the constraint effect on lithium plating and overcharge behaviors
5 实验验证
将PSO-MPC策略与制造商提供的3种标准恒流恒压充电方案(0.5C-CV、1C-CV和1.5C-CV)进行对比。实验开始时,将4块全新的电池放置于25 ℃的恒温箱中并以0.5C倍率完全放电后,静置1 h,确保恢复热平衡状态,每块电池都重复进行10次充放电循环。实验过程中,记录了每块电池充电过程中的温度变化和电池端电压变化。
5.1 PSO-MPC策略充电安全性验证
根据上文所述锂离子电池充电时主要面临热失控、析锂和过充的风险。对比4种充电策略,图8展示了随机选择的第5次充电期间的电流、电压变化,图9则分别显示了温度和析锂过电位变化。4种充电方案的最大电压均为3.65 V,且充电结束时的SOC均不超过95%。其余方案在电压达到3.65 V后转为恒压充电以防止过充,而PSO-MPC策略则通过算法中的充电约束来预防。根据图9(b)显示,采用1.5C-CV充电的电池在1 965 s后可能发生析锂反应,影响充电安全性。相比之下,PSO-MPC、1C-CV和0.5C-CV策略最低电势均大于零,不会有安全隐患。

图8 4种充电策略下的充电电流以及对应的电压变化
Figure 8 Charging currents and corresponding voltage changes under four different charging strategies.
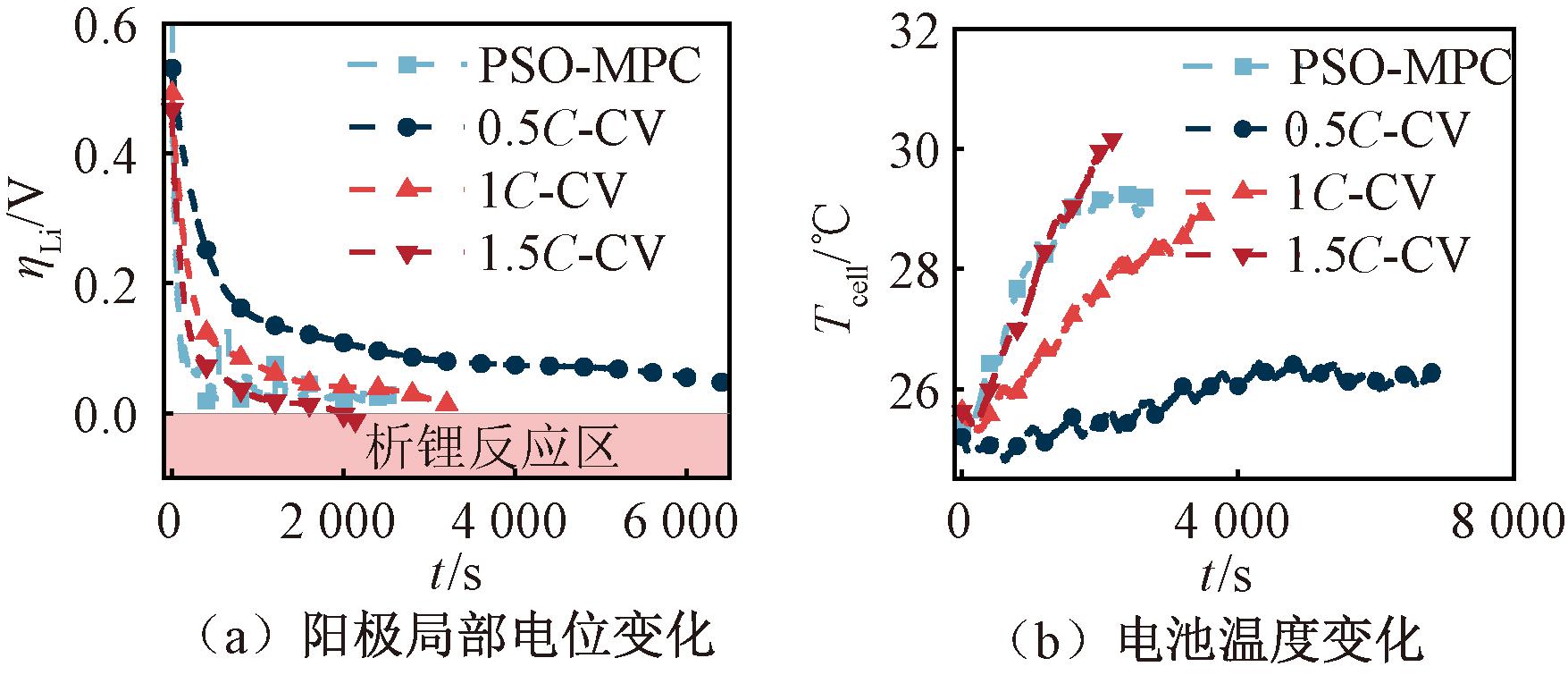
图9 4种充电策略过程中电池状态变化
Figure 9 Battery state changes during four chaxging strategies
5.2 PSO-MPC策略充电快速性验证
3种充电策略对比如图10所示。因为1.5C-CV存在充电安全问题,所以不纳入后续比较,图10(a)展示了其余3种充电策略在常温下达到关键节点SOC的平均充电时间。
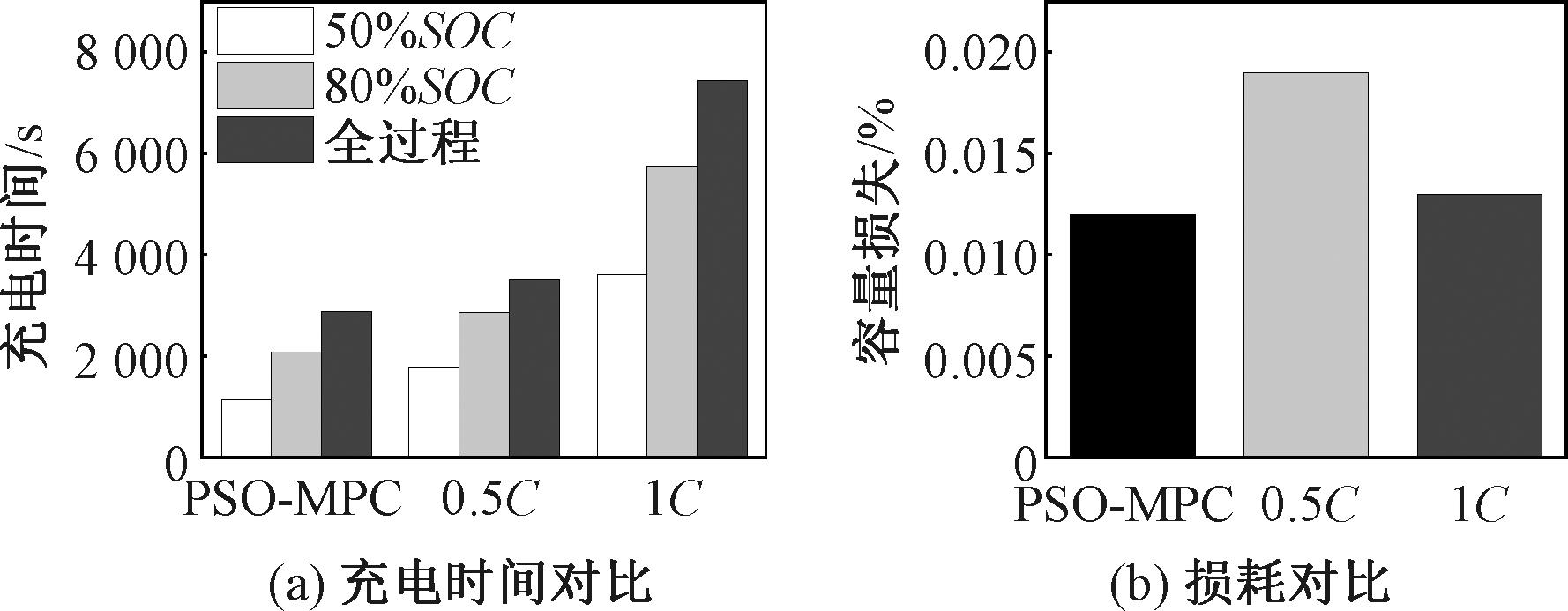
图10 3种充电策略对比
Figure 10 Comparison of three charging strategies
(1)PSO-MPC:20 min充至50%SOC,35 min充至80%SOC,全过程2 897 s。
(2)1C-CV:30 min充至50%SOC,48 min充至80%SOC,全过程3 500 s。
(3)0.5C-CV:60 min充至50%SOC,96 min充至80%SOC,全过程7 450 s。
PSO-MPC初始至50%SOC速度是0.5C-CV的3倍,是1C-CV的1.5倍,适合紧急充电。高荷电时减速以保护电池,但全局速度仍优于0.5C-CV和1C-CV,实现了快充。
5.3 降低充电损耗能力验证
在10次充电循环后测试了电池容量相对于额定容量的衰减量,结果如图10(b)所示,计算出的PSO-MPC、0.5C-CV与1C-CV每次充电的平均容量损耗分别为0.012%、0.019%与0.013%。0.5C-CV平均容量衰减最剧烈可能是充电时间过长促进了SEI的层增长导致的,而PSO-MPC可以根据电池的内部老化机理实时进行电流调节,相对两种传统充电策略分别降低了36%与7.6%的容量损失,表明其对电池健康状态的维护更为出色。
6 结论
(1)构建了时变参数电池耦合模型,深入剖析充电中的电、热、电化学及老化特性关联,结合了多种模型的优点,准确预测电压、温度变化,并揭示SEI层增长、活性材料损耗及锂电镀等老化机制。
(2)提出新的充电优化策略,引入改进PSO-MPC算法,通过控制充电时电池端电压、温度、阳极隔膜交界处电势的变化范围来避免热失控、析锂和过充等安全问题,对充电过程进行全局预测并且依据电池实时状态动态调整充电电流,实现充电过程的实时优化。
(3)提升充电综合性能,经过实验验证PSO-MPC策略较传统方案充电时间缩短17.3%~61.1%,电池容量衰减量降低7.6%~36%,在充电效率、电池寿命及安全性上均表现优异。
[1] 郭茶秀, 魏金宇. 电池排布方式对21700锂电池相变热管理系统的影响[J]. 郑州大学学报(工学版), 2023, 44(2): 91-97.
GUO C X, WEI J Y. Influence of different arrangement on phase change thermal management system of 21700 lithium battery[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(2): 91-97.
[2] HO A S, PARKINSON D Y, FINEGAN D P, et al. 3D detection of lithiation and lithium plating in graphite anodes during fast charging[J]. ACS Nano, 2021, 15(6): 10480-10487.
[3] DONG T, PENG P, JIANG F M. Numerical modeling and analysis of the thermal behavior of NCM lithium-ion batteries subjected to very high C-rate discharge/charge operations[J]. International Journal of Heat and Mass Transfer, 2018, 117: 261-272.
[4] JIA G H, CAI X. Fast charging strategy of lithium-ion batteries with thermal safety margin based on model predictive control[C]∥2022 41st Chinese Control Conference. Piscataway: IEEE, 2022: 2694-2699.
[5] XU M, WANG R, ZHAO P, et al. Fast charging optimization for lithium-ion batteries based on dynamic programming algorithm and electrochemical-thermal-capacity fade coupled model[J]. Journal of Power Sources, 2019, 438: 227015.
[6] ABASPOUR M, PATTIPATI K R, SHAHRRAVA B, et al. Robust approach to battery equivalent-circuit-model parameter extraction using electrochemical impedance spectroscopy[J]. Energies, 2022, 15(23): 9251.
[7] ZHANG C P, JIANG J C, GAO Y, et al. Charging optimization in lithium-ion batteries based on temperature rise and charge time[J]. Applied Energy, 2017, 194: 569-577.
[8] LIU K L, LI K, YANG Z L, et al. An advanced lithiumion battery optimal charging strategy based on a coupled thermoelectric model[J]. Electrochimica Acta, 2017, 225: 330-344.
[9] ZHANG S, ZHANG C N, XIONG R, et al. Study on the optimal charging strategy for lithium-ion batteries used in electric vehicles[J]. Energies, 2014, 7(10): 6783-6797.
[10] YANG S H,ZHOU X A,HUA Y, et al. High efficiency electric vehicle charging strategy based on model predictive control[C]∥ 2019 IEEE 2nd International Conference on Automation, Electronics and Electrical Engineering.Piscataway:IEEE,2019: 54-59.
[11] KOLLURI S, ADURU S V, PATHAK M, et al. Real-time nonlinear model predictive control (NMPC) strategies using physics-based models for advanced lithium-ion battery management system (BMS)[J]. Journal of the Electrochemical SOCiety, 2020, 167(6): 063505.
[12] 徐乐, 邓忠伟, 谢翌, 等. 锂离子电池电化学-热耦合模型对比研究[J]. 机械工程学报, 2022, 58(22): 304-320.
XU L, DENG Z W, XIE Y, et al. Comparative study of electrochemical-thermal models for Li-ion batteries[J]. Journal of Mechanical Engineering, 2022, 58(22): 304-320.
[13] 杨俊, 张希, 高一钊. 锂电池电化学传递函数模型建模及参数辨识[J]. 电源技术, 2019, 43(7): 1132-1135.
YANG J, ZHANG X, GAO Y Z. Modeling and parameter identification of electrochemical transfer function model for lithium battery[J]. Chinese Journal of Power Sources, 2019, 43(7): 1132-1135.
[14] 吕杰, 王敬翰, 宋文吉, 等. 储能用锂离子电池电热耦合模型研究进展[J]. 电池, 2023, 53(6): 668-672.
LYU J, WANG J H, SONG W J, et al. Advances in electro-thermal coupling models for energy storage Li-ion battery[J]. Battery Bimonthly, 2023, 53(6): 668-672.
[15] LIU Y J, HUANG Z W, HE L, et al. Temperature-aware charging strategy for lithium-ion batteries with adaptive current sequences in cold environments[J]. Applied Energy, 2023, 352: 121945.
[16] JIN X. Aging-aware optimal charging strategy for lithium-ion batteries: considering aging status and electro-thermal-aging dynamics[J]. Electrochimica Acta, 2022, 407: 139651.
[17] REN D S, SMITH K, GUO D X, et al. Investigation of lithium plating-stripping process in Li-ion batteries at low temperature using an electrochemical model[J]. Journal of the Electrochemical Society, 2018, 165(10): A2167-A2178.
[18] VON LÜDERS C, KEIL J, WEBERSBERGER M, et al. Modeling of lithium plating and lithium stripping in lithium-ion batteries[J]. Journal of Power Sources, 2019, 414: 41-47.
[19] XU L, LIN X K, XIE Y, et al. Enabling high-fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification[J]. Energy Storage Materials, 2022, 45: 952-968.
[20] 高原, 黄荣杰, 秦东晨, 等. 高倍率工况下锂离子电池的建模[J]. 电池, 2021, 51(6): 563-567.
GAO Y, HUANG R J, QIN D C, et al. Modeling of Li-ion battery at high rate condition[J]. Battery Bimonthly, 2021, 51(6): 563-567.
[21] SUN S, GUAN T, SHEN B, et al. Changes of degradation mechanisms of LiFePO4/graphite batteries cycled at different ambient temperatures[J]. Electrochimica Acta, 2017, 237: 248-258.