随着无线传感器网络和机器人技术的飞速发展,由多个移动机器人组成的集群系统引起了学术界和工业界的广泛关注[1-2]。集群中的每个机器人都具有一定的通信、决策、计算、执行及移动能力,彼此之间通过相互配合,从而完成单一机器人无法独立完成的复杂任务。由于其具有较强的鲁棒性、可扩展性、高效性和低成本等优势,被广泛地应用于物体运输[3]、搜索救援[4]等领域。
机器人集群的分组聚集问题是移动机器人路径规划和导航方向的重要研究内容之一[5-6],常见于采用大量不同类型的机器人来协同执行不同类型任务的场景。例如利用空中机器人和地面机器人组成的异构多机器人协作系统来对危险环境进行巡逻修检和自主探索[7]。又如结合无人艇和无人机集群协同航迹规划来处理海上无人集群在执行任务过程中的安全航行和通信保持问题[8]。然而,在执行任务之前或在执行过程中,隶属于不同分组的机器人往往混合在一起,需要设计导航算法将其从位置上进行分离,使隶属于同组的机器人聚集在一起执行任务。因此,实现分组聚集往往是大规模、多种群机器人联合执行任务的前提。然而,相比于实现单一集群的聚集,多组移动机器人集群的分组聚集面临聚集点多且未知、同组成员的位置分散且缺乏通信链路进行信息交互等新问题。
为解决机器人集群的分组聚集问题,现有的方法可大致分为两类:一类是确定性的方法,另一类是分散式的随机性方法。确定性的方法依赖于建立强大的通信系统来为机器人提供全局信息或维持同组成员之间的通信连接。例如,Kumar等[9]考虑了两个分组的情况,设计分组之间的虚拟人工势场不同于每个分组内部的虚拟势场,迫使两个子集群实现分离并分别实现聚集,后来,Santos等[10]将这种方法扩展到处理两组以上的机器人集群。但这种方法属于集中式的导航控制算法,要求每个机器人能随时获取并利用其他所有机器人的位置和速度信息,因而对机器人的感知和通信能力要求苛刻,不适用于感知或通信范围有限的机器人集群。在差异化人工势场的启发下,Filho等[11]、Ferreira-filho等[12]使用抽象的圆形来表示每一分组,避免了让机器人持续地获取其他机器人的信息,但仍需要间接地全局信息传递。Omotuyi等[13]利用深度学习的方法取得了与集中式控制器相近的性能,但可扩展性差。另一类确定性的方法是利用图论来描述机器人的通信关系,并利用多智能体系统的协同理论来设计分布式的控制策略,实现多个集群的状态分组的一致性[14-15]。虽然此类算法能由各机器人根据局部信息进行分布式执行,但要求每个组的所有成员之间一直存在通信链路,因而难以应用于位置不断变化的移动机器人集群中。最近,Lei等[16]为实现多个集群的分组蜂拥聚集,允许机器人之间进行多跳信息传递从而一直保持与同组成员的信息交互。这种策略对机器人的通信能力和数据存储空间的要求较高,而且受通信延时的影响较大。综上可见,确定性的分组聚集方法过于依赖机器人的通信系统,因而在集群规模变化时的可扩展性和对动态环境的适应性较弱。
相比于确定性的分组方法,随机性方法中每个机器人只利用有限范围内的感知信息和与邻近机器人的局部信息交互,避免了对全局通信范围或通信结构的依赖,因而更适用于感知和通信能力有限的大规模移动机器人集群。例如,受巴西坚果效应的启发,Gross 等[17]将每个机器人模拟为不同大小的粒子,仅依靠粒子之间的分散式交互作用力来实现机器人按照其作用力大小分别聚集。后来,Chen等[18]和Joshi等[19]对这项研究进行了扩展研究和性能评估,并进行了实验验证。Rezeck等[20]利用吉布斯随机场的方法,实现了机器人集群的分散式分组导航聚集。In
cio等[21]基于粒子群优化算法的思想,使得每个机器人通过有限邻域内其他机器人的信息来选择最有可能与同组机器人发生聚集的运动方向和速度。但现有的随机性方法的分组聚集收敛速率一般较慢[20-21]。此外,如何在探索与聚集之间进行平衡是随机性导航方法需要解决的问题。
为了提高分散式的随机性分组聚集导航方法的性能,本文借鉴启发式的灰狼优化(grey wolf optimization, GWO)算法[22]在平衡探索与开发方面的出色能力,通过将其分散化处理来解决感知和通信能力有限的机器人集群的分组聚集问题。本文还将对原始灰狼优化算法的收敛因子进行改进,通过增强机器人在前期对同组成员的探索来增加同组成员的相遇概率,从而进一步提高各分组聚集的完成速率、成功率及历次运行的稳定性。
1 问题描述
考虑在二维环境中的机器人R1,R2,…,Rn,其隶属于不同的分组,用Γ={Γ1,Γ2,…,Γm}来表示这些分组,每个Γk包含所有属于第k∈{1,2,…,m}组的机器人,且对于任意的l≠k,有Γl∩Γk=∅,即每个机器人都唯一地隶属于单一分组[21]。在初始时刻,所有机器人的位置是任意的,因而各个分组的机器人混合在一起。本文的目标是通过设计分散式的导航算法,使每个机器人根据局部感知和信息交互实现与同组机器人的聚集,即同组机器人之间的距离较近,而不同组的机器人之间的距离较远。
用Xi(t)
(xi(t),yi(t))表示机器人Ri在离散的t时刻的位置,其中xi(t)和yi(t)分别代表x和y坐标上的位置。位置的更新方程为
Xi(t+1)=Xi(t)+Vi(t)·Δt。
(1)
式中:Vi(t)为机器人在t时刻的速度;Δt为控制周期。由于感知能力有限,每个机器人只能感知到以自身为中心、λ为半径的圆内的其他机器人。邻近机器人之间可以进行通信,交互的信息内容包括各自的分组属性、位置、观测信息等。定义Ni{Rj∈Γ:‖Xj-Xi‖≤λ}为机器人Ri的邻居集合。在每一机器人的邻域中,可能存在与其同组的机器人,也可能存在来自其他分组的机器人。对于任一机器人Ri,定义其邻域内所有属于分组Γk的机器人的集合为
另外,为方便叙述,用
和
分别表示机器人Ri的邻域内所有与其同组/异组的机器人的集合。
在初始时刻,每个机器人的邻域内可能并不存在同组的任何其他机器人,即
另外,原先为邻居关系的同组机器人也可能在运动过程中丧失邻居关系。因此,在缺乏全局信息交互或中心组织者进行协调的情况下,让各机器人以分散式的导航算法来实现高效、高成功率的分组聚集具有很大的挑战性。本文以具有很强的探索和开发能力的GWO算法[22]为基础来设计每个机器人的导航速度,驱使其按照优化规则进行随机局部探索和移动,从而提高其发现同组机器人的概率并完成聚集。
2 分组聚集导航方法
本文设计的分组聚集导航算法包括两步:首先,将原始的GWO算法[22]进行分散式应用,为每个机器人求解各自的首选导航速度
然后,利用最优互惠避碰(optimal reciprocal collision avoidance,ORCA)算法[23]对首选导航速度进行修正来产生最终的导航速度Vi,避免机器人在分组聚集的运动过程中发生相互碰撞。
2.1 首选导航速度
在t时刻,每个机器人Ri下一步的首选导航速度
由三部分组成,如下所示:
(2)
其中,μ1、μ2、μ3为三部分的权重系数,设置为
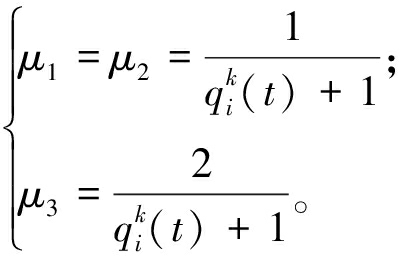
(3)
式中:
表示在t时刻机器人Ri的邻域内隶属于分组Γk的机器人的数量,这里的符号|·|表示集合中元素的数量。因此,当机器人周围的同组成员较多时,导航速度较小;反之,机器人则需以较大的速度移动来进行快速探索。其余的定义和说明如下。
式(2)等号右侧的
为机器人Ri下一时刻的第一目标位置,由后面的分散式GWO算法根据其邻居提供的与Ri同组的机器人的适应度信息来确定,目的是使机器人移动到同组机器人数量较多的位置。
式(2)等号右侧的
为第二目标位置,其定义如下:
(4)
其中,
(5)
代表机器人Ri∈Γk的每个邻居Ri′∈Ni的邻居集合
中
最大的那个机器人的标号j,而第二目标位置即为此机器人在当前时刻t的位置。这一目标位置可能处于机器人Ri∈Γk的感知范围之外,需由Ri和Rσ的共同邻居进行传递。这种信息交互方式由Incio等[21]提出,能使机器人获得来自通信范围之外的信息,从而极大地提高任务完成的速度。但是,这要求每个机器人不仅记录观测到的自己邻域内各分组机器人的数量,用向量
表示,还需预留更多的存储空间来保存和更新其每个邻居Ri′∈Ni的观测数据向量qi′(t),因而对机器人的存储和通信能力的要求较高。本文的导航算法中保留了这一部分,目的是与Incio等[21]所提出的基于粒子群优化(particle swarm optimiztion,PSO)算法公平地进行性能对比。
式(2)等号右侧的Vi(t)与当前时刻的速度有关,目的是使机器人保持移动状态,特别是当附近没有任何其他机器人时也不会因停止移动而失去探索能力。
在此指出,式(2)中的各部分组成结构与文献[21]中的相同。区别在于文献[21]中利用PSO算法来选取第一目标位置,而本文则采用GWO及其改进算法来获取更优的性能。
2.2 分散式GWO算法
GWO算法是一种启发式的群体智能优化方法[22],通过借鉴灰狼种群的等级制度和组织协调能力,能够在探索与开发之间实现平衡,在对优化问题的求解精度和求解速度方面都有优越的性能,因而被广泛应用于机器人导航与路径规划[24]、调度问题[25]。故本文采用GWO算法来计算每个机器人的第一个目标位置
2.2.1 GWO算法基本原理
将GWO算法应用于机器人集群分组聚集导航的基本原理是将机器人集群看作一个狼群,其中的每个机器人为狼群中的一匹灰狼。首先获取每匹灰狼的适应度(适应度的确定方式由下文给出),然后根据适应度构建灰狼的等级结构,即将适应度最高的3匹灰狼依次标记为α、β、δ狼(即Rα、Rβ、Rδ机器人),而其余的灰狼为ω狼。GWO的优化过程就是在每次迭代中由这3个临时最优解来指导所有灰狼的位置更新[22]。
具体地,令Xα(t)、Xβ(t)、Xδ(t)分别表示Rα、Rβ、Rδ机器人的当前位置,则每个机器人Ri下一时刻的最优目标位置的更新方式如下[22]:
X1(t+1)=Xα(t)-Aα·Dα(t);
(6)
X2(t+1)=Xβ(t)-Aβ·Dβ(t);
(7)
X3(t+1)=Xδ(t)-Aδ·Dδ(t);
(8)
(9)
其中,
D(·)(t)=|C(·)·X(·)(t)-Xi(t)|;
(10)
A(·)=2a·r1-a;
(11)
C(·)=2·r2。
(12)
式中:下标位置的符号(·)代表α、β或δ,向量的乘积运算为两个向量对应位置上的元素相乘;绝对值运算|·|也是对向量中每个元素取绝对值;向量r1和r2的每个元素在[0,1]取随机数;a为收敛因子向量,其每个元素ai的值随时间而衰减。
(13)
式中:T为运行的最大时间步数;c为正整数。原始GWO算法中一般取c=1[22],即令ai的值随时间线性地由2减小到0,从而使得随机向量A(·)的每个元素在前期具有较大的随机性以使灰狼围绕临时最优位置Xα(t)、Xβ(t)、Xδ(t)不断地探索,在后期A(·)的值则逐渐趋于固定值以对探索到的临时最优解进行开发利用。
2.2.2 分散式GWO算法
需要注意的是,上节所述的原始GWO算法在设置灰狼等级时需要全局比较种群内所有灰狼的适应度,而且所有的灰狼都需围绕相同的3个临时最优解进行迭代计算。而在将其应用于感知范围有限的机器人集群时,需要先对其进行分散化处理。本节将首先给出针对GWO的分散化处理方法,然后对原始GWO中的参数进行进一步的改进以获取更优异的性能。
令每个机器人只从自己的邻居集合中选取Rα、Rβ、Rδ机器人,然后根据这些局部临时最优位置来执行式(4)～式(12)的运算。因此,每个机器人都需各自运行一个局部GWO算法,本文称之为分散式GWO算法。另外,若在计算式(9)时,邻近范围内满足条件的机器人数量少于3个,则将其都参与计算。
原始GWO算法中每个灰狼只需有一个适应度值,而在本文所设计的分散式GWO中每个机器人Ri都有m个适应度值,定义为其邻居范围内属于分组Γk的机器人数量,即
因此,每个机器人对每一分组都有一个适应度,并不断更新。对于分组Γk中的任一机器人Ri,其需要获取邻近范围内其他机器人对其分组的适应度
以确定每一时间步的临时最优目标位置Xα(t)、Xβ(t)、Xδ(t),而其邻居机器人可能来自不同的分组。根据分组间的信息共享意愿,本文考虑各分组相互合作和相互独立两种情况。
(1)分组相互合作关系。每个机器人都会将自己感知的信息传递给异组的邻近机器人,因而任意机器人Ri∈Γk所能获取的所有适应度信息为
(2)分组相互独立关系。每个机器人只与同组的邻近机器人分享信息,因此机器人Ri∈Γk所能获得的所有适应度信息为
在相互独立的分组关系下,需将式(5)中的参数更改为
即只通过同组的邻居进行信息传递。
另外,对于初始分布比较松散的集群,某些机器人的邻近范围内其他机器人的数量可能过少,从而容易导致分组聚集失败。因此,在初始阶段增强机器人的探索能力将有利于机器人感知到更多的同组机器人。本文在收敛因子的变化律(式(13))中取c>1,因为t/T<1,则ai的衰减速度比令c=1时更慢。此时,从式(11)可知,A(·)的衰减速度也更慢,使得每个机器人围绕临时最优位置Xα(t)、Xβ(t)、Xδ(t)进行探索的范围也以更慢的速度进行收缩(式(6)～式(9)),从而增强了每个机器人的探索能力,有利于与同组的其他成员相遇。
2.3 相互避碰算法
由式(2)计算出的速度
可能会导致机器人之间发生碰撞,考虑到实际应用需求,本文采用可由机器人独立计算的ORCA算法[23]来实现机器人之间的避碰。简单来说,每个机器人将作为各自的参考速度,通过高效率的线性规划法计算出与参考速度最接近的最优避碰速度Vi(算法的原理和细节见文献[23]),并将此避碰速度作为实际的导航速度代入式(1)中执行。
综合第2.1节～2.3节的介绍,将本文所设计的基于GWO的分散式分组聚集导航算法的流程绘制在图1中。图1中只展示了分组间相互合作时的算法流程,当分组间相互独立时只需将第1步中的适应度集合替换为
即可。
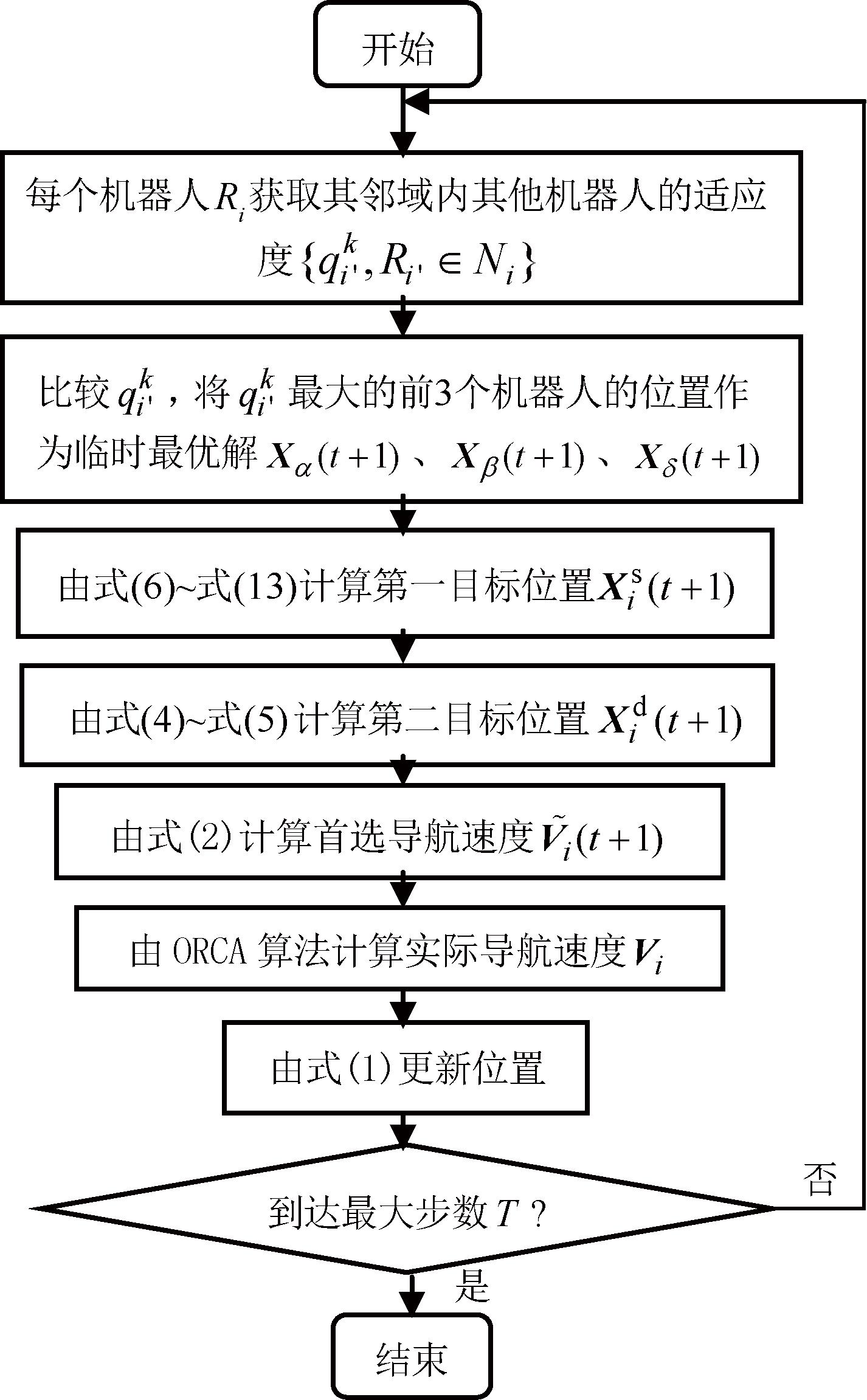
图1 基于GWO 的分组聚集导航算法流程图
Figure 1 Flowchart of the GWO-based group aggregation navigation algorithm
3 仿真与分析
本节通过一系列的仿真来评估所设计的导航方法的有效性和性能,仿真平台为搭载Ubuntu18.04操作系统的计算机,利用C++语言和Python语言在机器人操作系统(ROS)中编程,利用ROS的消息机制模拟机器人之间的信息传递。机器人集群的运动空间为一个10 m×10 m的正方形区域,所有机器人的半径统一设置为0.07 m,通信范围为0.5 m。每次仿真中,所有机器人的初始位置皆随机生成,如果同组机器人之间的相对距离小于0.3 m,则认为它们实现了聚集。仿真控制周期Δt=0.02 s,最大时间步T=20 000。
图2显示了在所设计的导航算法引导下机器人集群在不同时刻的运行结果。其中,移动机器人集群由4个不同的分组构成,用不同颜色的圆点来表示,每个分组包含30个机器人。可见,各分组的机器人由初始的混合状态逐渐实现了分组聚集。
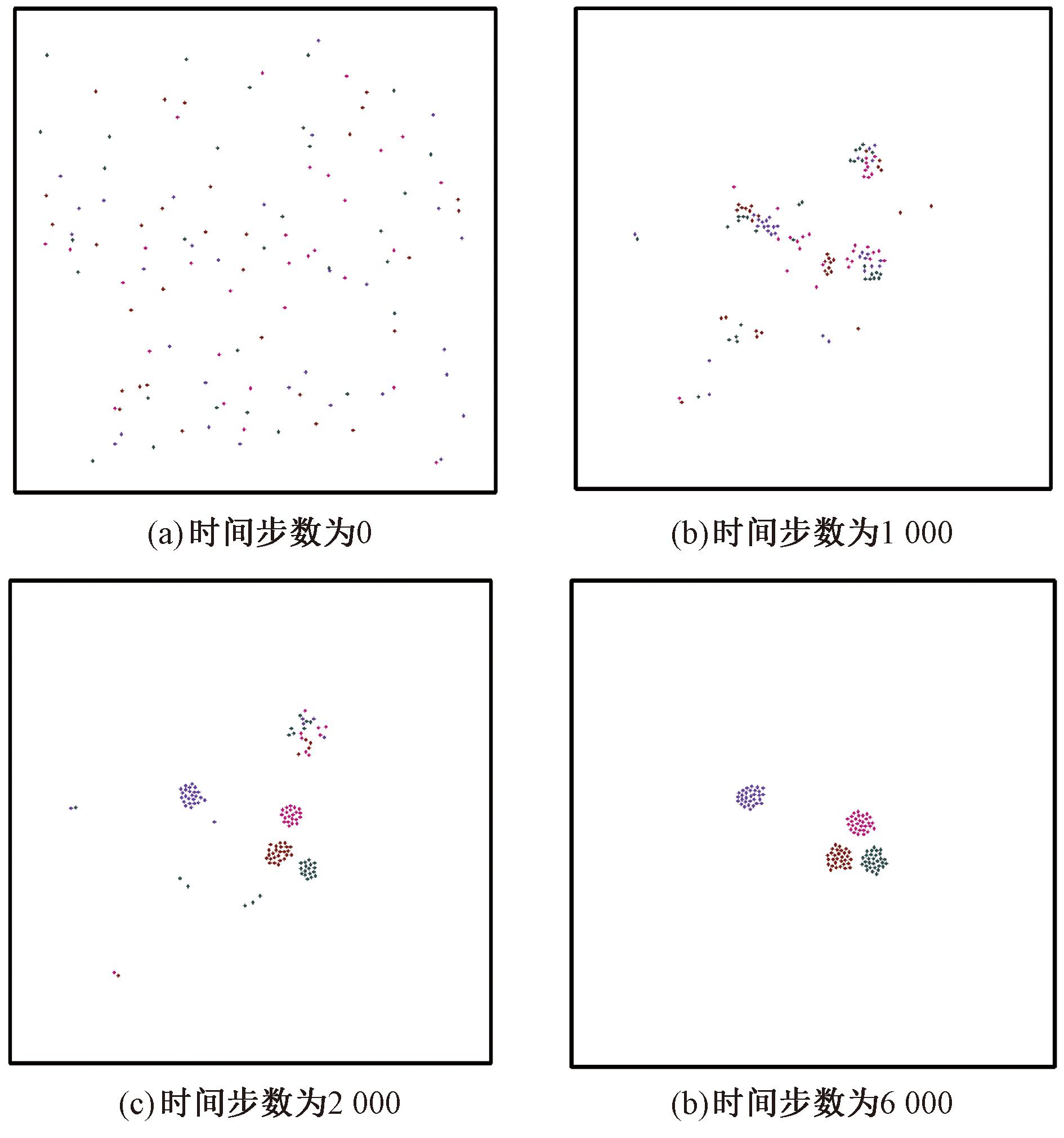
图2 机器人集群在设计的导航算法下的运行结果
Figure 2 Running results of the robots under the designed navigation algorithm
然而,由于本文的导航方法是基于机器人局部信息观测和通信的分散式方法,不能保证每个分组从任意初始位置出发都能实现聚集,即机器人最终所聚集成的组数可能会多于实际的预期分组数。为了验证算法的性能,本文在实际预期分组数量m分别为2、4、6且各分组的成员数量n分别为30、60时,进行了一系列的仿真,每种分组数量和成员数量组合的情况独立运行100次,每次运行时所有机器人的初始位置都在运动空间内随机生成。统计历次运行最终所聚集成的组数的平均值以及聚集完成所需的最小时间步数(即实际聚集成的组数不再随时间减小的时刻)的平均值,结果如图3和图4所示,其中每个图对比了3种不同类型的导航方法,包括Incio等[21]提出的基于PSO算法、本文设计的基于原始GWO算法和基于非线性收敛因子的改进GWO算法(取c=3)。
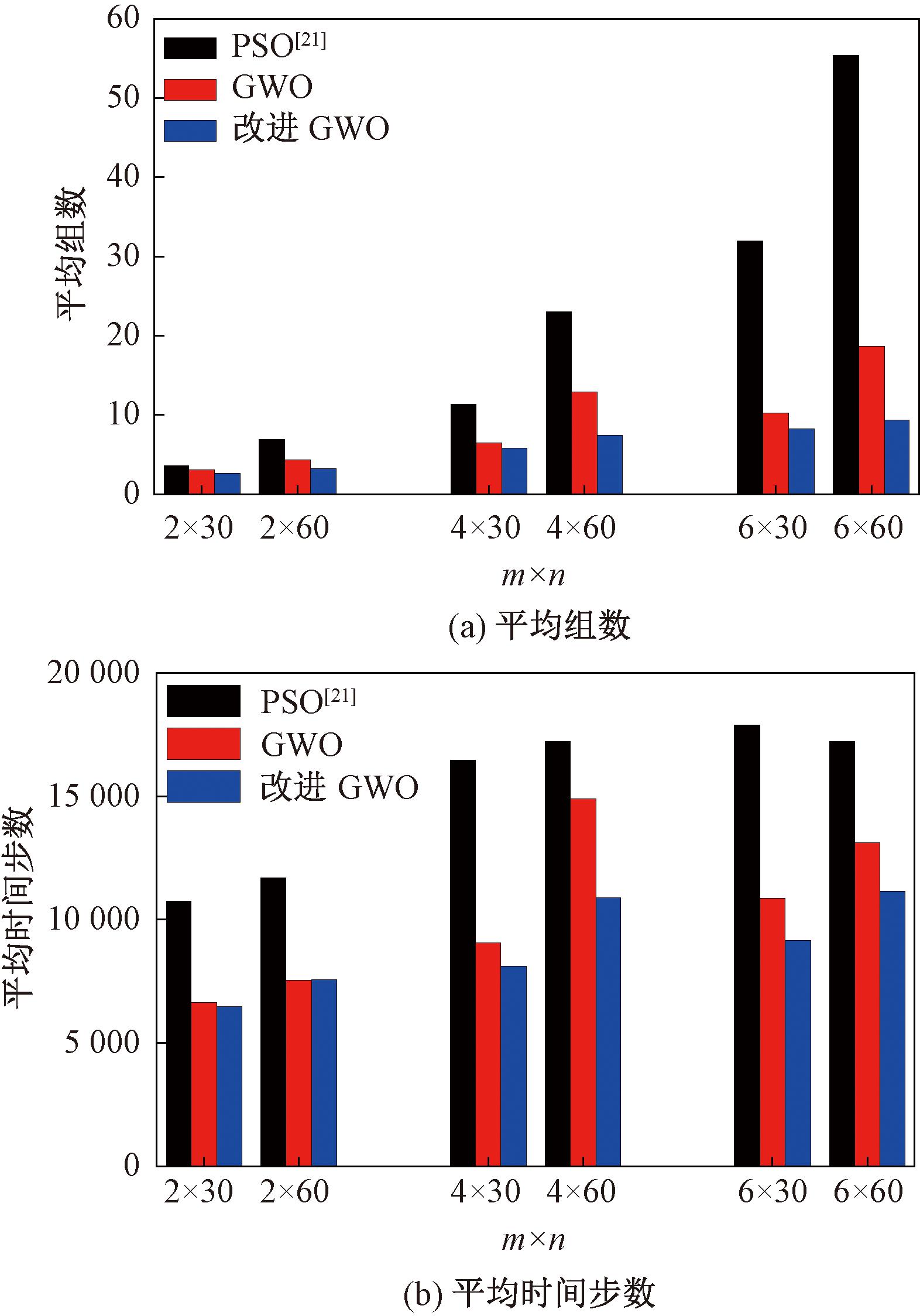
图3 各分组间相互独立时运行100次的平均结果对比
Figure 3 Comparison of the average results of 100 runs when the subgroups are independent
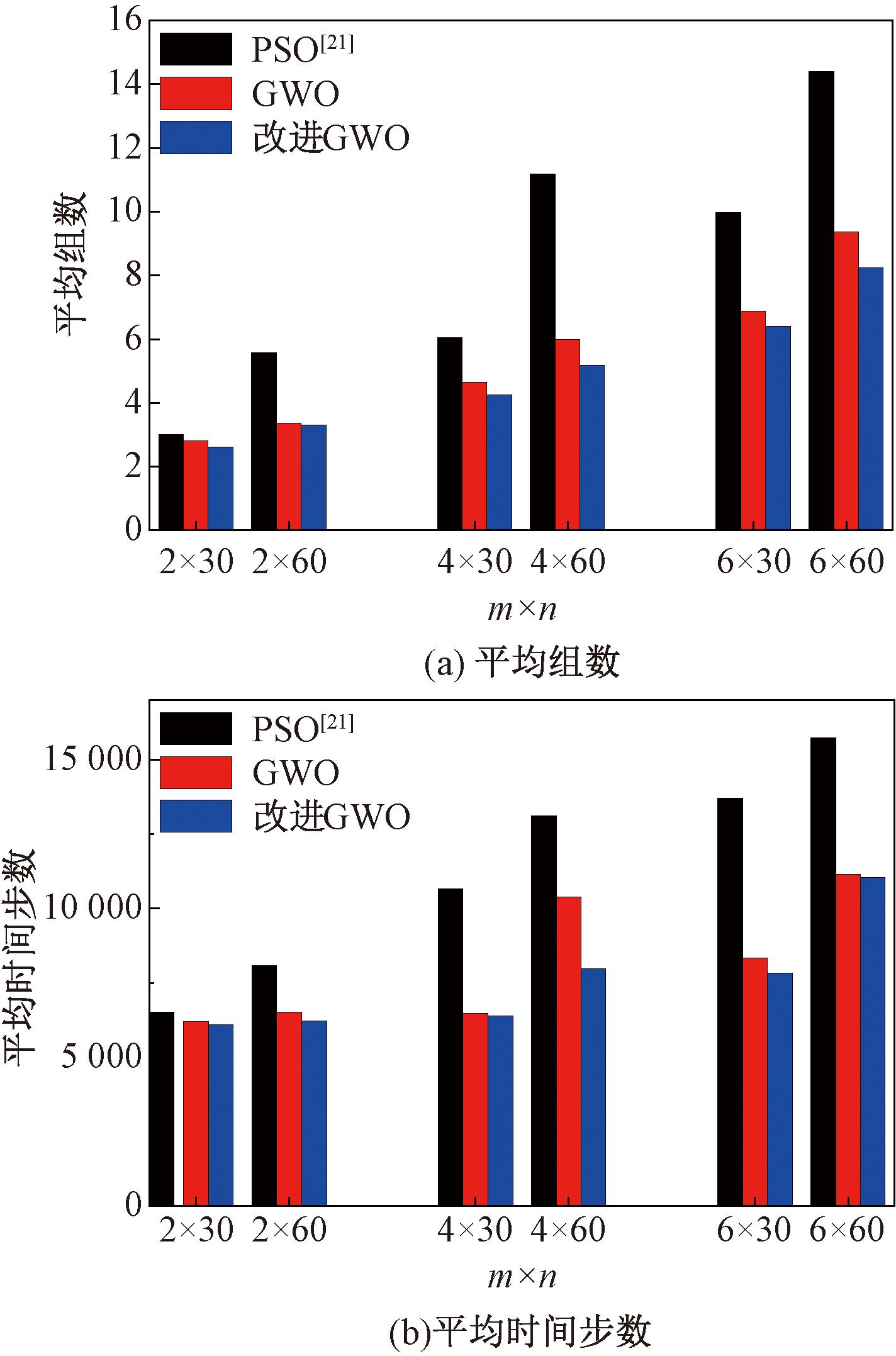
图4 各分组间相互合作时运行100次的平均结果对比
Figure 4 Comparison of the average results of 100 runs when the subgroups are all cooperative
图3展示了各分组间相互独立(只与同组成员共享数据)情况下的对比结果。图4展示了各不同分组都相互合作、共享数据情况下的对比结果。将图3和图4中的同样预期分组数量情况下的数据进行对比,可见当属于不同分组的机器人都相互合作时,最终所能聚集成的组数和运行消耗的时间都少于各组相互独立时的情况。以m×n=6×60的情况为例,各算法在分组间相互合作时比相互独立时的平均组数分别减少了75%、50%、12%,平均时间步数分别减少了8%、17%、1%。这一对比结果体现了不同分组的机器人之间进行信息共享的重要性。
对比图3和图4中不同算法下的统计数据可知,基于GWO的两种导航方法均比基于PSO的方法的性能更为优越,且采用非线性收敛因子a的改进GWO算法的性能最好。以图3中m×n=6×60的情况为例,原始GWO比PSO使所能聚集的平均组数减少了66%,而改进后的GWO比原始GWO进一步减少了17%;从所消耗的平均时间步数来看,原始GWO算法比PSO算法减少了23%,而改进后的GWO算法比原始GWO算法进一步减少了12%。两种性能指标都体现出了前期进行充分探索的优势。
为了分析机器人集群初始分布的密集程度对分组聚集效果的影响,本文在不同的正方形运动空间尺寸下进行仿真。考虑m×n=4×30的情况,各分组的机器人都相互合作(各分组相互独立时的结论类似,故省略),运动空间尺寸分别设置为6 m×6 m、10 m×10 m和14 m×14 m,其余参数如机器人尺寸、通信范围等均保持不变。统计结果如图5所示,可见机器人最终所能聚集的平均组数和所需的时间步数均随运动空间的减小而减小,且在不同算法下的结论是一致的。以10 m×10 m的运动尺寸为基准,更小的6 m×6 m的情况下所能聚集成的平均组数3种算法分别减少了4%、8%、1%,平均时间步数则分别减少了23%、5%、5%;而更大的14 m×14 m的情况下所能聚集成的平均组数3种算法分别增加了5%、8%、6%,平均时间步数分别增加了9%、16%、14%。这种结果是因为当机器人的可活动范围减小而通信范围不变时,机器人遇到同组成员的机会将会增大,因而在聚集完成速度和成功率上均有提升,且对完成速度的提升更为显著。
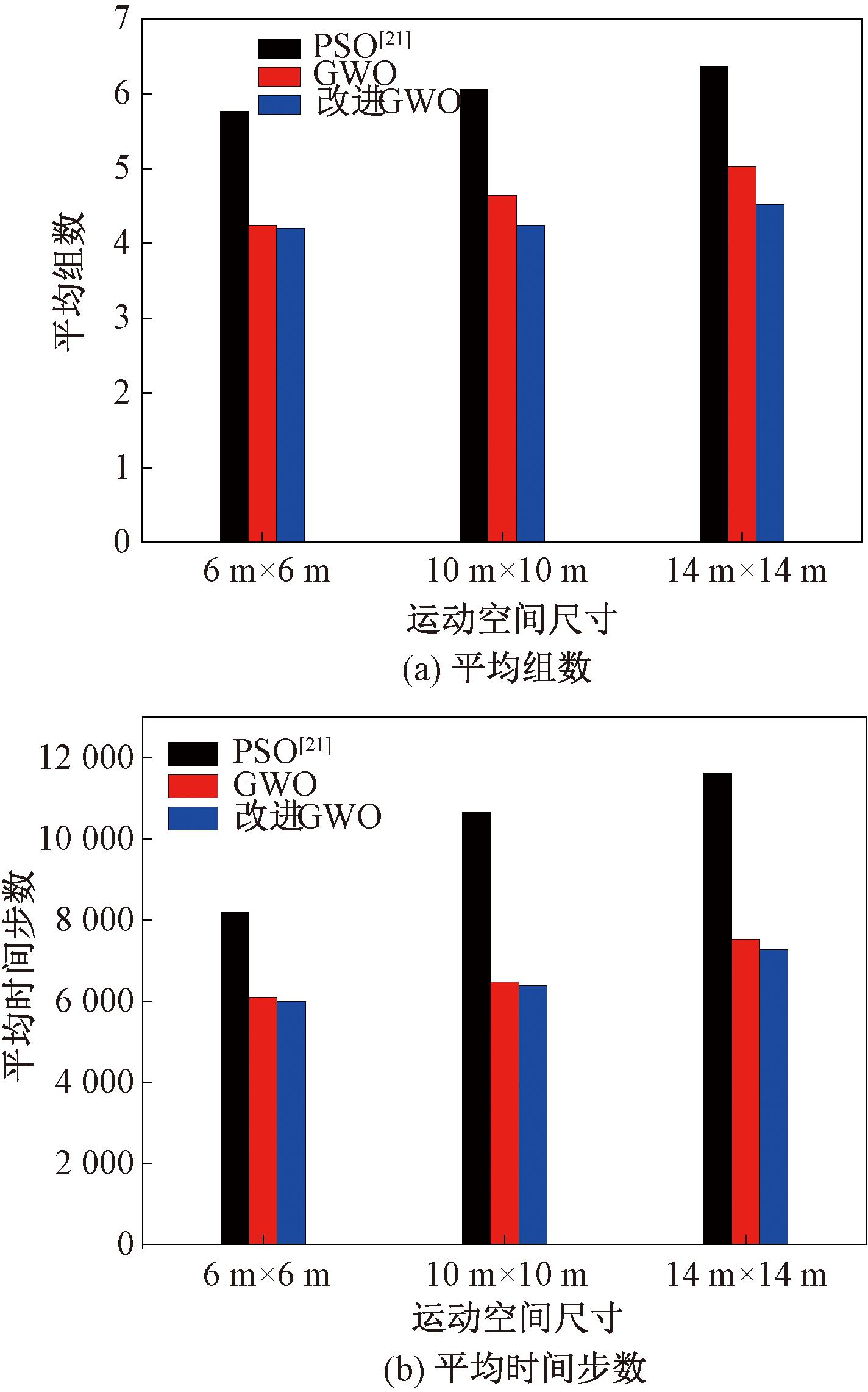
图5 不同的运动空间尺寸下运行100次的平均结果对比
Figure 5 Comparison of the average results of 100 runs with different motion areas
图6展示了采用3种导航算法各运行100次的平均聚集的组数随时间的变化曲线,其中的阴影部分为标准差。从图6可以看出,基于PSO算法的组数收敛过程比较平缓,而根据分散式GWO算法设计的两种算法在运行的早期阶段收敛速度均较慢,但随后迅速收敛到更小的值,而且在稳定阶段的波动(标准差)也比PSO的更小,这反映了基于GWO的集群分组导航方法在不同初始状态下独立多次运行时的性能更为稳定可靠。另外,由于采用了非线性的收敛因子,图6中显示改进GWO算法在初始阶段的收敛速度最慢,但是却最先收敛到更小的值,再次证明了机器人在前期进行充分探索的重要性。
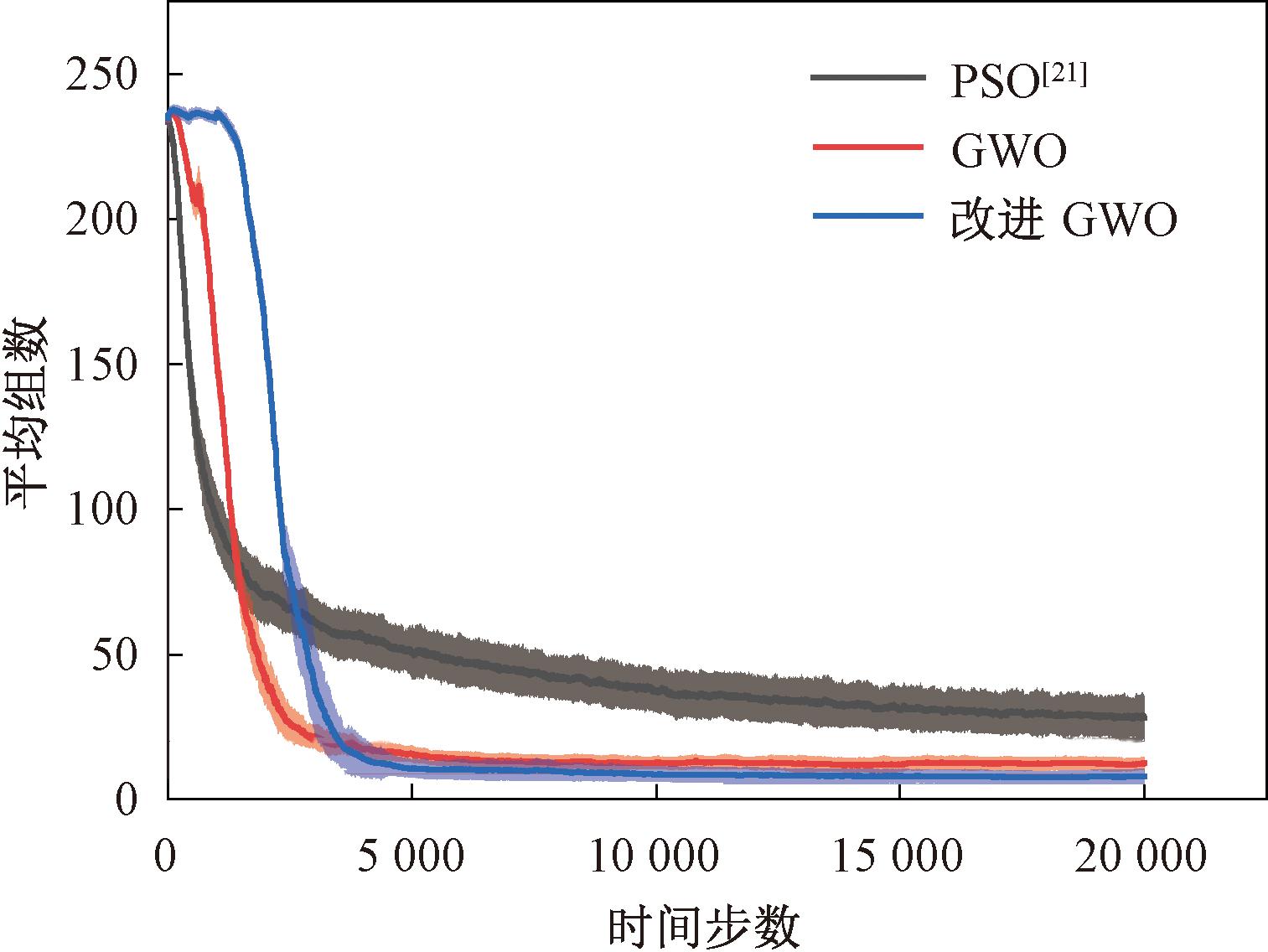
图6 3种算法平均聚集的组数随时间步数的收敛效果
Figure 6 Convergence of the average number of aggregated subgroups with three algorithms versus time steps
4 结论
本文提出了一种基于群体智能优化的分散式分组聚集导航方法,使初始混合分布的不同组机器人按照各自的分组属性分别聚集。主要根据GWO算法的思想为每个机器人设计了只利用有限感知范围内信息计算首选导航速度的方法;其次,利用ORCA算法进行修正得到最终的导航速度;最后,在ROS环境下进行仿真,展示了所设计方法的有效性和性能,且相比于现有类似方法有着更高的分组聚集成功率、更快的收敛速度及更小的波动。然而,本文的方法本质上是随机性的方法,虽然摆脱了对全局信息的依赖,但不能保证分组聚集成功的确定性。未来的研究方向是通过引入通信连接保持方法,从而提升此类方法的成功率。
[1] SHORINWA O, HALSTED T, YU J, et al. Distributed optimization methods for multi-robot systems: part 2—a survey[J]. IEEE Robotics &Automation Magazine, 2024, 31(3): 154-169.
[2] 张方方, 张文丽, 王婷婷. 基于速度补偿算法的多机器人编队控制研究[J]. 郑州大学学报(工学版), 2022, 43(2): 1-6, 14.ZHANG F F, ZHANG W L, WANG T T. Research on multi-robot formation control based on speed compensation algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(2): 1-6, 14.
[3] AN X, WU C, LIN Y F, et al. Multi-robot systems and cooperative object transport: communications, platforms, and challenges[J]. IEEE Open Journal of the Computer Society, 2023, 4: 23-36.
[4] QUERALTA J P, TAIPALMAA J, CAN PULLINEN B, et al. Collaborative multi-robot search and rescue: planning, coordination, perception, and active vision[J]. IEEE Access, 2020, 8: 191617-191643.
[5] DUBEY R, GUPTA S, CHAUDHARY S, et al. Finite-time convergence of multi-robot segregation using MPC with aperiodic motion smoothing[C]∥2024 IEEE 20th International Conference on Automation Science and Engineering (CASE). Piscataway: IEEE, 2024: 2209-2214.
[6] FERREIRA FILHO E B, PIMENTA L C A. Segregation of heterogeneous swarms of robots in curves[C]∥2020 IEEE International Conference on Robotics and Automation (ICRA). Piscataway: IEEE, 2020: 7173-7179.
[7] 郝肇铁, 郭斌, 赵凯星, 等. 从规则驱动到群智涌现: 多机器人空地协同研究综述[J]. 自动化学报, 2024, 50(10): 1877-1905.HAO Z T, GUO B, ZHAO K X, et al. From rule-driven to collective intelligence emergence: a review of research on multi-robot air-ground collaboration[J]. Acta Automatica Sinica, 2024, 50(10): 1877-1905.
[8] 侯岳奇, 陶浩, 龚俊斌, 等. 多约束条件下无人艇和无人机集群协同航迹规划[J]. 中国舰船研究, 2021, 16(1): 74-82.HOU Y Q, TAO H, GONG J B, et al. Cooperative path planning of USV and UAV swarms under multiple constraints[J]. Chinese Journal of Ship Research, 2021, 16(1): 74-82.
[9] KUMAR M, GARG D P, KUMAR V. Segregation of heterogeneous units in a swarm of robotic agents[J]. IEEE Transactions on Automatic Control, 2010, 55(3): 743-748.
[10] SANTOS V G, PIRES A G, ALITAPPEH R J, et al. Spatial segregative behaviors in robotic swarms using differential potentials[J]. Swarm Intelligence, 2020, 14(4): 259-284.
[11] FILHO E B F, PIMENTA L C A. Segregating multiple groups of heterogeneous units in robot swarms using abstractions[C]∥2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Piscataway:IEEE, 2015: 401-406.
[12] FERREIRA-FILHO E B, PIMENTA L C A. Abstraction based approach for segregation in heterogeneous robotic swarms[J]. Robotics and Autonomous Systems, 2019, 122: 103295.
[13] OMOTUYI O, KUMAR M. Learning decentralized controllers for segregation of heterogeneous robot swarms with graph neural networks[C]∥2022 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS). Piscataway: IEEE, 2022: 1-6.
[14] LIU Z C, WONG W S. Group consensus of linear multiagent systems under nonnegative directed graphs[J]. IEEE Transactions on Automatic Control, 2022, 67(11): 6098-6105.
[15] HASSAN K, TAHIR F, REHAN M, et al. On relative-output feedback approach for group consensus of clusters of multiagent systems[J]. IEEE Transactions on Cybernetics, 2023, 53(1): 55-66.
[16] LEI W Y, LIU Z C, LIU J H. Flocking control for multiple subgroups based on multi-hop communication and connectivity maintenance strategies[C]∥The 14th Asian Control Conference (ASCC).Piscataway: IEEE, 2024: 2248-2253.
[17] GROSS R, MAGNENAT S, MONDADA F. Segregation in swarms of mobile robots based on the Brazil nut effect[C]∥2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway:IEEE, 2009: 4349-4356.
[18] CHEN J, GAUCI M, PRICE M J, et al. Segregation in swarms of e-puck robots based on the Brazil nut effect[C]∥Proceedings of the 11th International Conference on Autonomous Agents and Multi-Agent Systems. Piscataway: IEEE, 2012: 163-170.
[19] JOSHI D, SHIMIZU M, HOSODA K. Segregation and flow of modules in a robot swarm utilising the Brazil nut effect[C]∥2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Piscataway:IEEE, 2019: 4080-4085.
[20] REZECK P, ASSUNÇ
O R M, CHAIMOWICZ L. Flocking-segregative swarming behaviors using Gibbs random fields[C]∥2021 IEEE International Conference on Robotics and Automation (ICRA). Piscataway:IEEE, 2021: 8757-8763.
[21] IN
CIO F R, MACHARET D G, CHAIMOWICZ L. PSO-based strategy for the segregation of heterogeneous robotic swarms[J]. Journal of Computational Science, 2019, 31: 86-94.
[22] MIRJALILI S, MIRJALILI S, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61.
[23] VAN DEN BERG J, GUY S J, LIN M, et al. Reciprocal n-body collision avoidance[C]∥The 14th International Symposium ISRR. Berlin: Springer, 2011: 3-19.
[24] 甘福宝, 王仲阳, 连寅行, 等. 基于改进灰狼优化算法的移动机器人路径规划方法[J]. 传感器与微系统, 2024, 43(8): 110-113.GAN F B, WANG Z Y, LIAN Y H, et al. Path planning method of mobile robot based on improved grey wolf optimization algorithm[J]. Transducer and Microsystem Technologies, 2024, 43(8): 110-113.
[25] 张晓凤, 王秀英. 灰狼优化算法研究综述[J]. 计算机科学, 2019, 46(3): 30-38.ZHANG X F, WANG X Y. Comprehensive review of grey wolf optimization algorithm[J]. Computer Science, 2019, 46(3): 30-38.