地应力是影响地下厂房围岩稳定性及工程设计的重要因素[1-2]。地应力反演分析旨在准确获取地下深部岩体的应力状态,反演结果的准确性将直接影响地下工程的设计,特别是对于大型水电站地下洞室群这种高构造应力场区域[3],开挖容易失稳,初始地应力的精确度将会直接影响工程安全。影响地应力场的因素众多,现场地应力测试通常只限于在选定的探洞内进行,仅能反映出围岩的部分应力状况,远离测点位置的地应力是未知的。因此,通过分析实测的地应力数据进行初始地应力场的反演分析对于全面了解围岩状态和确保工程建设的合理性与安全性是十分必要的[4-5]。
基于物理模型的经验公式和多元回归分析方法最先应用于初始地应力场反演,例如张涛等[6]用最小二乘法构建回归方程并拟合实测数据,采用三维有限元回归分析方法获得了工程区初始地应力场分布规律。但这类方法更适用于线弹性材料的问题,而许多岩体结构不满足弹性假设,将初始地应力回归简化为线性回归问题,忽略了地质环境和工程设计的复杂性带来的非线性影响,导致精度较低[7]。为提高回归精度,前人提出了有限元方法(FEM)、边界元方法(BEM)和离散元方法(DEM)等数值模拟方法,例如费万堂等[8]基于三维有限差分法进行地下厂房区域地应力场反演以及应力分析,得到和实测地应力较为符合的地应力场。但数值模拟方法解决非线性问题收敛速度较慢,处理复杂数据的能力较弱。为解决这一问题,前人融合了机器学习进行初始地应力场反演分析,例如任斌等[9]用FLAC3D建立三维模型,基于BSA-BP神经网络进行五岳抽水蓄能电站地下厂房的初始地应力场反演,为该工程建设提供指导。机器学习中的神经网络非线性拟合能力较强,提高了精度以及扩大了可能解的范围,但融入神经网络的方法计算复杂,结果受实测数据规模的影响较大。
为优化上述方法存在的问题,可以将粒子群优化算法(particle swarm optimization, PSO)[10]与有限元理论相结合,用于初始地应力场的反演分析,不仅计算简单,而且能够提高处理非线性数据的能力,并能扩大解的搜索范围,尤其适用于实测数据较少的情况,但其缺点在于随机性较强,收敛速度较慢。梯度下降法(gradient descent, GD)[11]相较于PSO算法,计算简单,能够快速收敛到最小值,且能够满足精度要求,其缺点在于可能收敛于局部最优解。故本文结合两种方法的优点,提出联合梯度下降和粒子群优化(GD-PSO)算法,提高了收敛速度和回归精度,并通过实例验证GD-PSO算法能够有效地解决实测资料较少的大型地下洞室群初始地应力场回归分析问题,得到拟合度较高的初始地应力场。
1 计算原理
1.1 基于GD-PSO算法的初始地应力场反演分析
按照地质学的观点,工程区域内的地应力可视为自重应力场和施加的构造应力场的线性叠加[12]。基于GD-PSO算法的初始地应力场反演的基本思路:根据工程现状,选取足够大的区域,建立三维有限元模型,考虑可能影响初始地应力场的主要因素(自重、构造运动),边界条件分别为不同影响因素的单位作用,利用有限元软件模拟各边界条件下测点的应力值,以测点实测地应力值为目标值。用GD-PSO算法进行回归分析,得出各边界条件的影响系数,由此计算出模型各点的初始地应力值,以此作为初始地应力场进行后续计算。
GD-PSO算法以PSO算法[10]为基础,所有粒子在解空间中运动,在求解地应力场回归系数矩阵时,每个粒子的位置可以表示地应力场反演问题的一组潜在解,即一组特定的系数,而速度决定了搜索解的方向和距离[13]。该算法扩大了回归系数矩阵的可能解的搜索范围,提高了求解精度。速度和位置的更新遵循以下公式[10]:
vi(t+1)=ωvi(t)+c1r1(pbesti-xi(t))+
c2r2(gbesti-xi(t));
(1)
xi(t+1)=xi(t)+vi(t+1)。
(2)
式中:t为时间;vi(t)为粒子i在时间t的速度;ω为惯性权重;c1和c2为学习因子;r1和r2为[0,1]的随机数,可以增加搜索的随机性;pbesti表示粒子i本身在搜索过程中的最优位置;gbesti表示整个粒子群在搜索过程中共同的最优位置;xi(t)为粒子i在时间t的位置。
GD-PSO算法先根据学习率和梯度的方向更新结果,并且以GD算法[11]回归结果初始化粒子群。相较于随机初始值,PSO能够获得较优的初始寻优位置和速度,可以加快收敛速度。GD-PSO算法应用于初始地应力场求解时,需要回归计算各边界条件影响系数,系数的更新公式为
(3)
式中:xi(i=1,2,…,k)为各边界条件的影响系数;α为学习率;![]() 为损失函数相对于系数xi的梯度。
为损失函数相对于系数xi的梯度。
GD-PSO算法结合两种不同的优化方法,综合了GD算法的定向寻优能力和PSO算法的全局寻优能力,以GD算法回归结果作为初始值,然后用PSO算法来优化这些初始估计,通过一次、二次和三次多项式回归,选择最优回归系数和回归方程。对于实测数据较少的模型,可以提高系数估计的准确性,加快收敛速度,降低随机初始值对结果的随机影响,平衡复杂性和拟合度。结合PSO算法能够在搜索空间内进行全局搜索,避免了梯度下降法可能陷入局部最小值的问题,从而找到最优解,同时进一步增强了算法处理复杂、非线性问题的能力。另外,尽管初始步骤使用梯度下降,但PSO本身不需要目标函数的梯度信息,这使得GD-PSO算法可以应用于那些梯度难以计算或不存在的问题。
综上所述,基于GD-PSO算法地应力场反演的流程如图1所示。
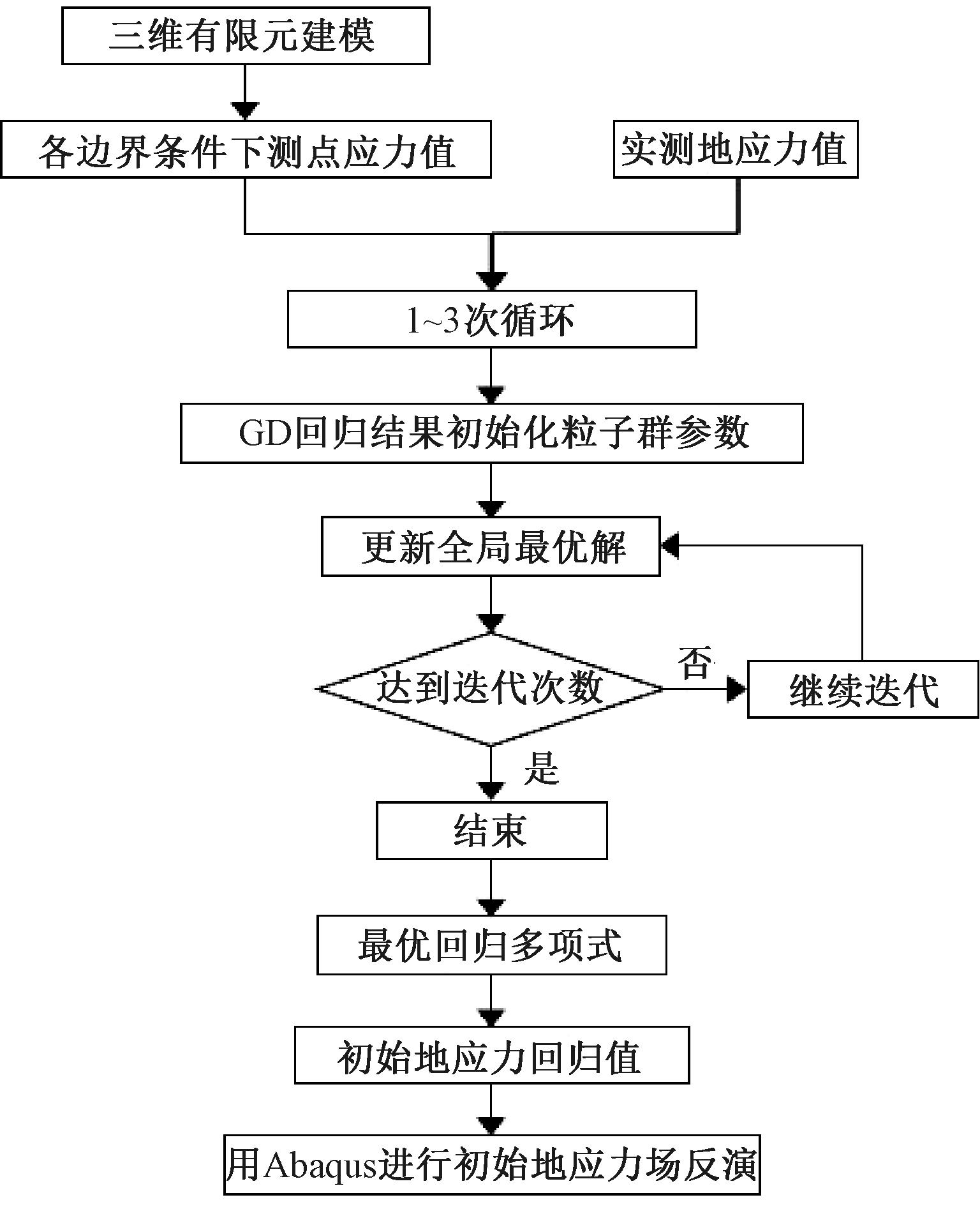
图1 基于GD-PSO算法地应力场反演流程
Figure 1 Flow of in-situ stress field inversion based on GD-PSO algorithm
1.2 参数设定
GD-PSO算法的主要参数有学习率、粒子数量、惯性权重ω、学习因子及均方误差。
(1)学习率[11]决定了初始系数在每次迭代时更新的幅度。过高的学习率可能导致模型在最优解附近振荡,甚至错过最优解;而过低的学习率会导致收敛速度降低。常用的学习率取值范围为0.001到0.100。
(2)粒子数量较少容易使回归陷入局部最优;较多可以提高收敛水平,更靠近全局最优解,但计算量也会相应增大。
(3)惯性权重ω[14]表示新一代的粒子速度受上一代的粒子速度影响的程度,在保持粒子运动惯性的同时保持搜索更大区间的趋势。较大的ω全局寻优能力强,不易陷入局部最优,提高收敛精度;而较小的ω有利于局部搜索,可以提高收敛速度。为了在搜索速度和搜索精度之间达到平衡,通常做法是使算法在前期有较高的全局搜索能力,使搜索空间快速收敛于某一区域,而在后期有较高的局部搜索能力以获得高精度的解,因此提出了动态调整惯性权重[15]的方法,即随着迭代的进行,按式(4)线性地减小ω的值。
(4)
式中:ωmax为最大惯性权重;ωmin为最小惯性权重;iter为当前迭代次数;nIterations为粒子群优化迭代次数。
(4)个体学习因子c1和社会学习因子c2分别表征个体学习能力和群体学习能力。c1表示粒子趋向个体最优位置的加速权重;c2表示粒子趋向群体最优位置的加速权重。较低的学习因子使粒子游离在目标区域外,而较高的学习因子会使粒子跳过目标区域,通常取c1=c2=2。
(5)均方误差(MSE)是预测值与真实值差异的平方求和,形式简单,且异常值影响较大,有助于模型更加关注真实数据,故选取均方误差为损失函数[16],其表达式为
(5)
式中:m为测点数量;yj为第j个测点的应力实测值;![]() 为第j个测点的应力预测值,由所求回归方程计算得到。
为第j个测点的应力预测值,由所求回归方程计算得到。
2 工程应用
2.1 工程概况及地质条件
某水电站位于福建省,主要由上水库、下水库、输水系统、地下厂房及开关站等建筑物组成。输水发电系统线路呈东北偏东方向布置,沿线山体雄厚。地下厂房位于输水线路的尾部,埋深约280~375 m,地下厂房洞室群包括主副厂房洞、主变洞、尾闸洞三大主洞室及母线洞、地下厂房排水洞等辅助洞室,三大主洞室相邻平行建造,互相影响,长度均超过百米。洞室围岩以微风化至新鲜钾长花岗岩为主,局部为辉绿岩脉、石英脉,小断层较发育,节理裂隙中等发育至较发育状态,岩体以较完整至完整岩体为主,无大的断层等不利结构面通过。地下洞室群围岩主要物理力学参数如表1所示。
表1 岩体主要物理力学参数
Table 1 Physical and mechanical parameters of rock

岩性密度/(g·cm-3)变形模量/GPa泊松比黏聚力/MPa摩擦系数钾长花岗岩2.5615~200.221.50~1.601.30~1.40辉绿岩脉2.735~100.221.20~1.301.20~1.30石英脉2.548~100.221.20~1.301.20~1.30
2.2 参数率定
根据工程地勘报告,工程实测数据较少,计算前需要将实测数据完整的所有三维测点应力值转换为计算坐标系下的应力值[17],结果如表2所示,测点位置为厂房。根据问题规模和难度,参考经验值,PSO算法和GD-PSO算法计算参数设定如表3所示。
表2 计算坐标系下测点实测应力值
Table 2 Stress at measuring points in the calculation coordinate system MPa
应力σxσyσzτxyτzxτyz取值-4.92-8.51-4.21-0.20.393.74
表3 PSO算法和GD-PSO算法计算参数设定
Table 3 Calculation parameter setting of PSO and GD-PSO
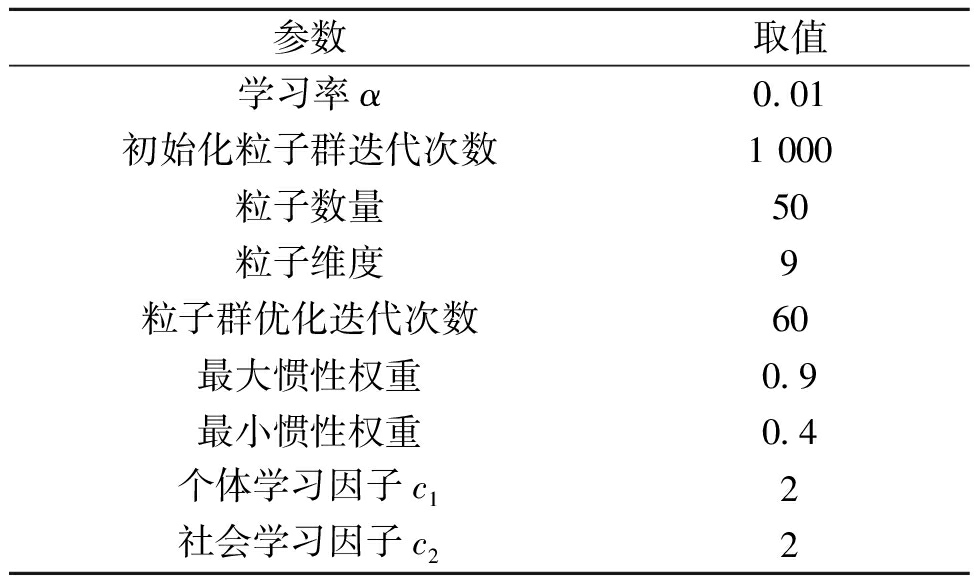
参数取值学习率α0.01初始化粒子群迭代次数1 000粒子数量50粒子维度9粒子群优化迭代次数60最大惯性权重0.9最小惯性权重0.4个体学习因子c12社会学习因子c22
2.3 初始地应力场反演及地应力平衡过程
步骤1 按照工程实际情况,选取计算区域,建立三维有限元模型,三维有限元模型及测点示意图如图2所示。为避免四周约束对地下洞室群计算结果的影响,本文以地下洞室群为中心,四周取5到6倍的主厂房宽度的区域作为地应力反演区域。整体模型单元数127 958,总节点数151 524,总体以高精度六面体单元为主,以地下厂房为中心,网格尺寸向外增大,其涵盖了地下洞室群附近所有重要地质构造和地应力测点位置,以此进行后续地应力反演计算。

图2 三维有限元模型及测点示意图
Figure 2 3D fem model and measurement point diagram
步骤2 用有限元计算各边界条件下测点的应力值。考虑重力场及5种构造应力场对初始地应力场的影响,构造应力场分别指顺河向挤压构造场、横河向挤压构造场、水平面内剪切变形构造场、横河向竖直剪切变形构造场和上下游侧面竖直剪切变形构造场[18]。为更贴合实际情况,挤压构造场由均布荷载和三角形荷载叠加模拟[19]。计算时考虑8种边界条件,分别如图3所示,计算时各边界施加单位荷载。不同作用类型下测点应力值见表4,测点位置在厂房ZKC03,高程为345 m。
表4 不同作用类型下测点应力值
Table 4 Stress values of measuring points under different action types MPa
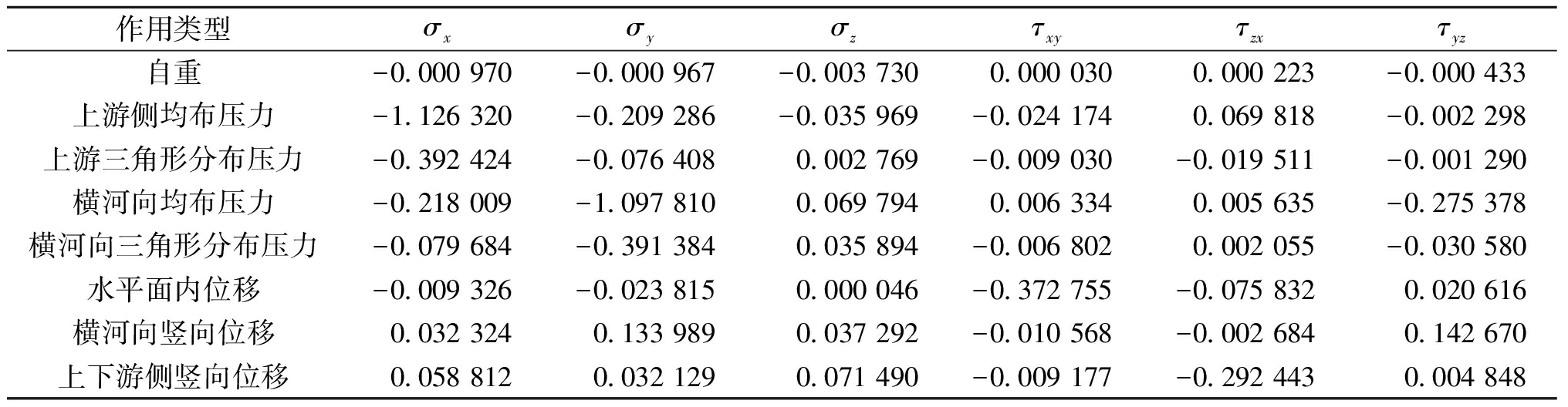
作用类型σxσyσzτxyτzxτyz自重-0.000 970 -0.000 967 -0.003 730 0.000 030 0.000 223 -0.000 433 上游侧均布压力-1.126 320 -0.209 286 -0.035 969 -0.024 174 0.069 818 -0.002 298 上游三角形分布压力-0.392 424 -0.076 408 0.002 769 -0.009 030 -0.019 511 -0.001 290 横河向均布压力-0.218 009 -1.097 810 0.069 794 0.006 334 0.005 635 -0.275 378 横河向三角形分布压力-0.079 684 -0.391 384 0.035 894 -0.006 802 0.002 055 -0.030 580 水平面内位移-0.009 326 -0.023 815 0.000 046 -0.372 755 -0.075 832 0.020 616 横河向竖向位移0.032 324 0.133 989 0.037 292 -0.010 568 -0.002 684 0.142 670 上下游侧竖向位移0.058 812 0.032 129 0.071 490 -0.009 177 -0.292 443 0.004 848
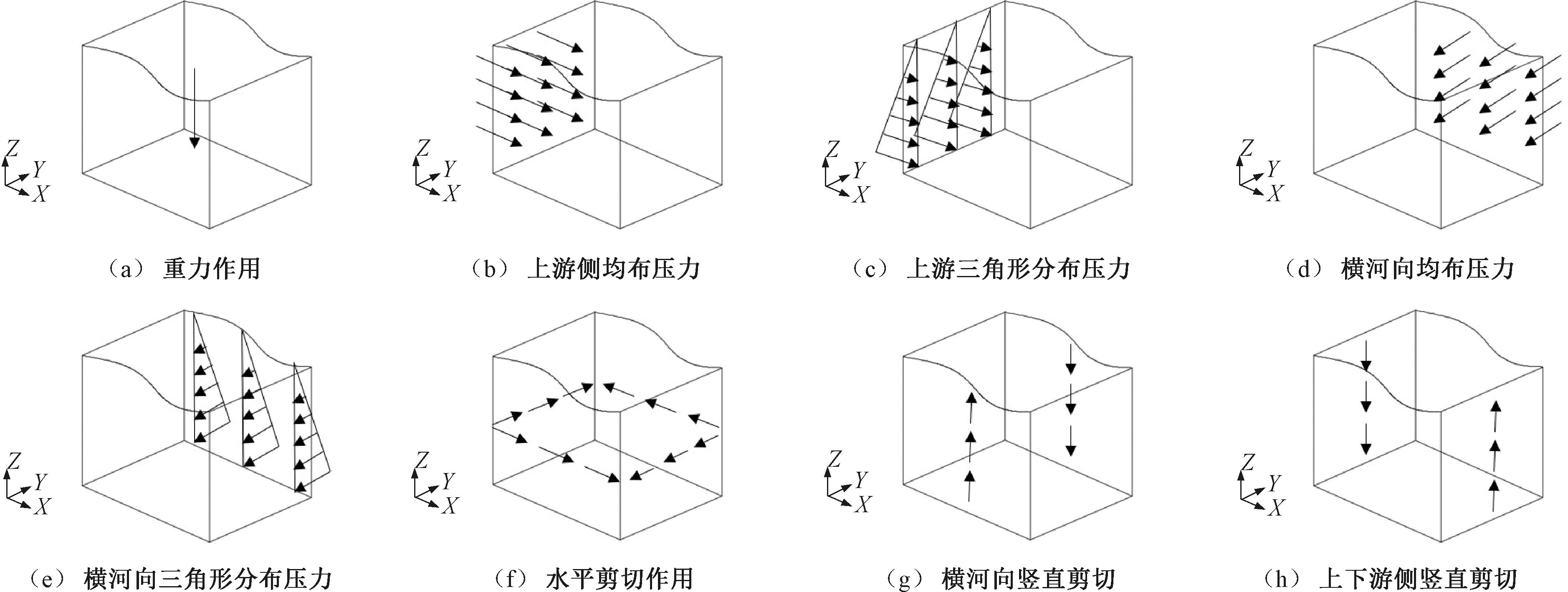
图3 边界条件施加示意图
Figure 3 Schematic diagram of boundary condition application
步骤3 以测点实测地应力值为目标值,分别用PSO算法、GD-PSO算法进行回归分析。
步骤4 计算模型各结点初始地应力值。将各边界条件下模型各点的应力值代入回归多项式,得到初始地应力场。
步骤5 将初始地应力场输入有限元模型,进行地应力平衡。
2.4 初始地应力场反演及地应力平衡结果分析
2.4.1 初始地应力场反演结果分析
为验证GD-PSO算法能够有效提高回归精度,分别用PSO算法和GD-PSO算法进行线性回归、二次多项式回归、三次多项式回归,计算过程中均方误差随迭代次数的变化曲线如图4所示。由图4可知,使用PSO算法和GD-PSO算法回归计算均为三次多项式的回归精度最高。表5为使用PSO算法和GD-PSO算法回归计算的最小MSE对比。由表5可知,最小均方误差分别为0.935和0.579,使用GD-PSO算法回归计算的结果更好,回归精度得到提高。
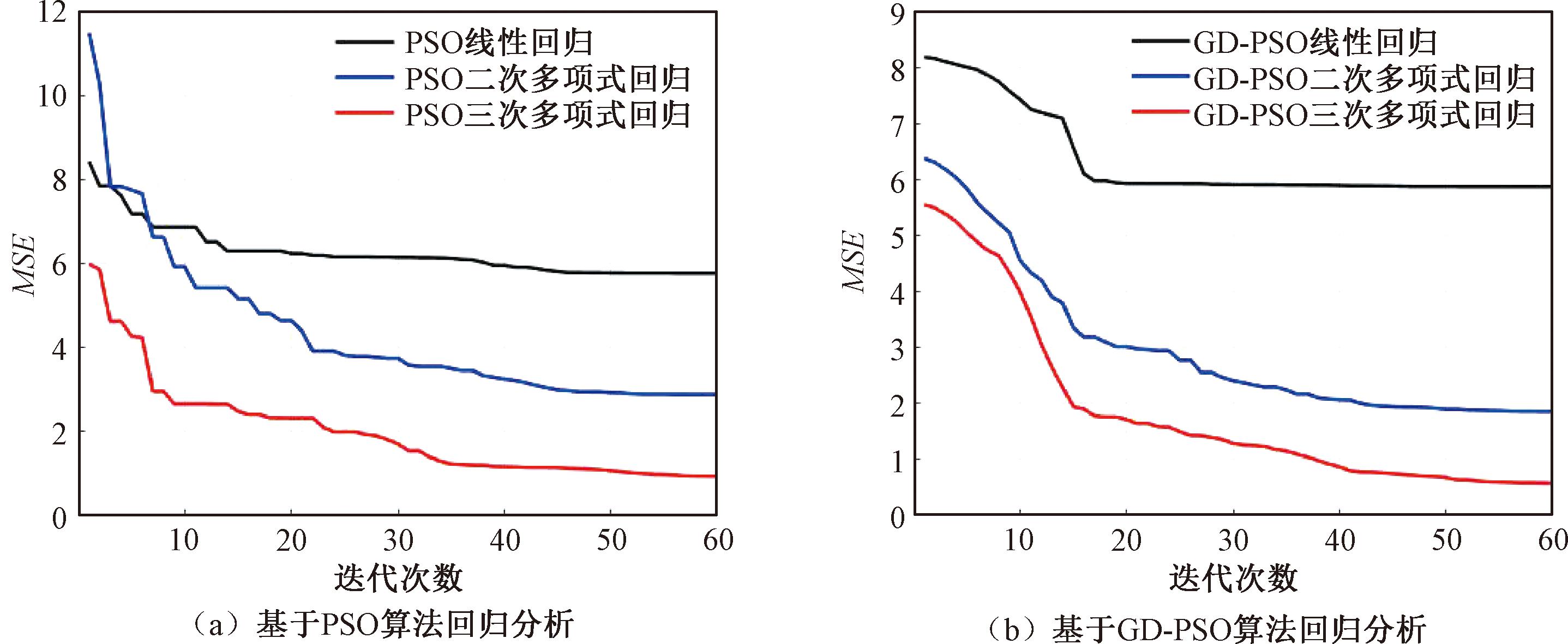
图4 均方误差与迭代次数的关系
Figure 4 Relation between mean square error and number of iterations
表5 PSO算法和GD-PSO算法最小MSE对比
Table 5 Comparison of minimum MSE between PSO and GD-PSO
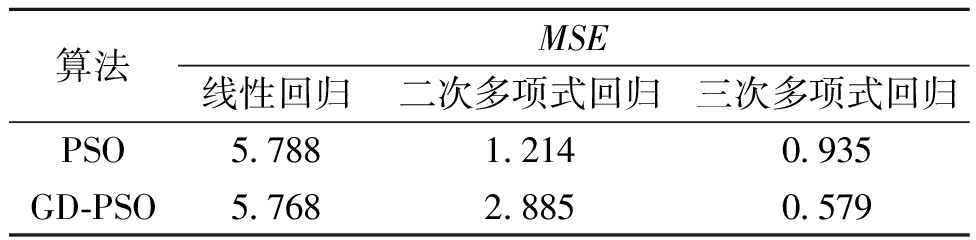
算法MSE线性回归二次多项式回归三次多项式回归PSO5.7881.2140.935GD-PSO5.7682.8850.579
根据GD-PSO回归计算结果,厂房区域最大水平主应力在7.7~14.5 MPa之间,对应的最小水平主应力在5.2~7.7 MPa之间,水平构造作用是该区域初始地应力场的主要影响因素,该部位地应力属中等偏低应力场。
2.4.2 地应力平衡结果分析
地应力平衡后测点计算值与实测值对比如表6所示。受到可用测点较少的影响,竖直方向的应力结果差值较大,大部分应力结果差值较小,可以满足计算要求。地应力平衡结果如图5所示。对于缺少实测数据的工程,地应力平衡结果较符合实际情况。模型大部分区域应力值较小,仅在局部出现应力集中较大,可能与网格质量等有关,可忽略不计。模型绝大部分位移基本为零,仅在局部出现小位移,最大值仅有5.26 mm。
表6 地应力平衡后测点计算值与实测值对比
Table 6 Comparison of calculated values and measured values at measuring points after in-situ stress balance MPa
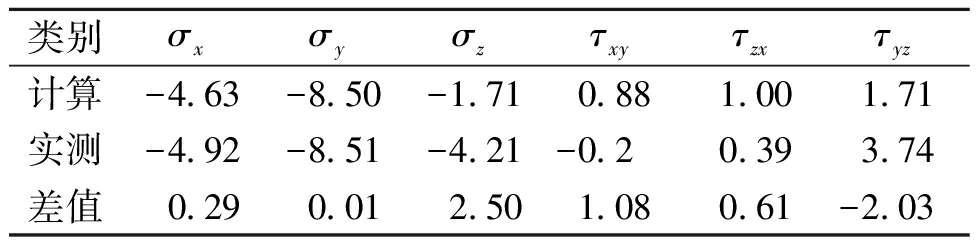
类别σxσyσzτxyτzxτyz计算-4.63-8.50-1.710.881.001.71实测-4.92-8.51-4.21-0.20.393.74差值0.290.012.501.080.61-2.03
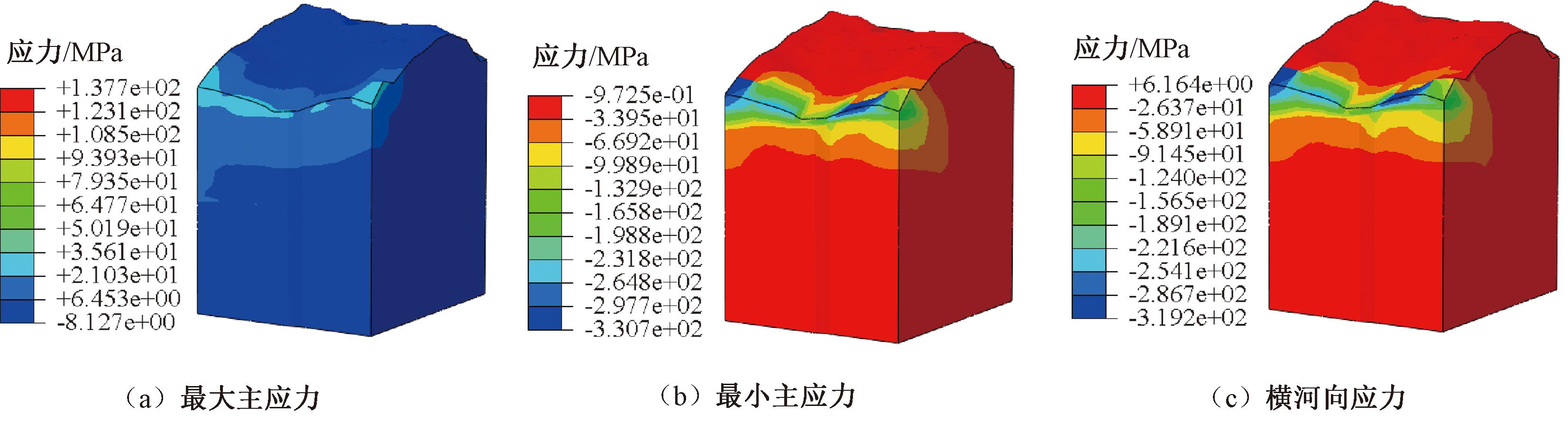
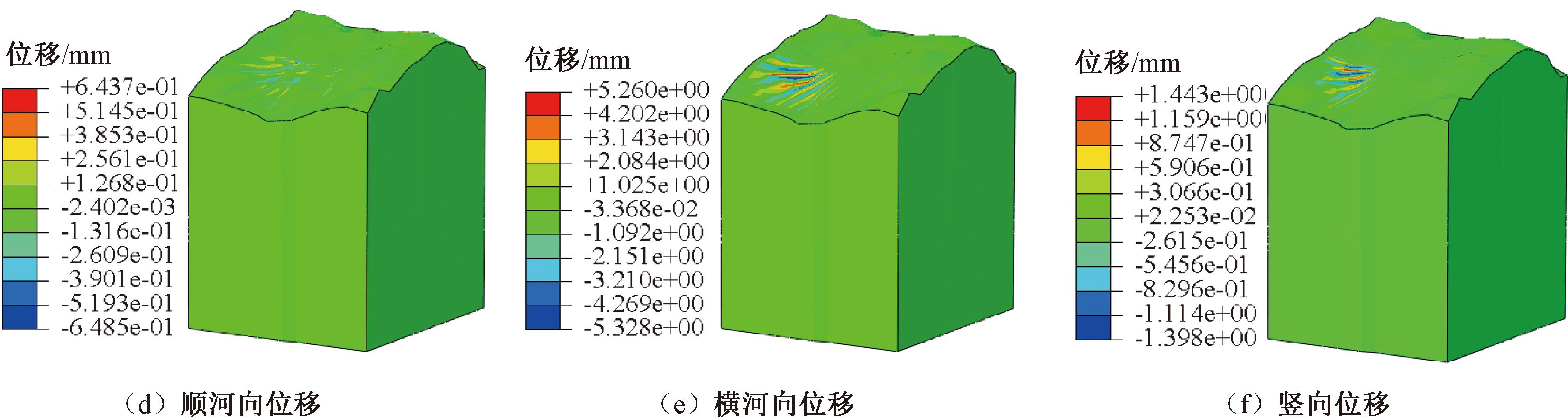
图5 地应力平衡结果
Figure 5 Results of in-situ stress balance
3 结论
本文提出了一种基于GD-PSO的大型地下洞室群初始地应力场反演分析方法,并通过实例分析得到以下结论:
(1)GD-PSO算法结合GD算法与PSO算法进行多元回归分析,扩大了最优解的搜索范围,加快了收敛速度,可以有效避免陷入局部极小值,非线性回归精度明显提高。
(2)将GD-PSO算法应用于大型地下洞室群初始地应力回归分析,计算效率高,结果误差较小,表示该方法能够很好地应用于大型地下洞室群初始地应力场反演问题。
[1] DU J J, QIN X H, ZENG Q L, et al. Estimation of the present-day stress field using in situ stress measurements in the Alxa area, Inner Mongolia for China′s HLW disposal[J]. Engineering Geology, 2017, 220: 76-84.
[2] 郑炜烽, 王乐华, 罗笙, 等. 抽水蓄能电站大型地下厂房区初始应力场反演[J]. 水电能源科学, 2023, 41(11): 143-147.
ZHENG W F, WANG L H, LUO S, et al. Inversion of initial stress field in large underground plant area of pumped storage power station[J]. Water Resources and Power, 2023, 41(11): 143-147.
[3] ZHANG S R, HU A K, WANG C. Three-dimensional inversion analysis of an in situ stress field based on a two-stage optimization algorithm[J]. Journal of Zhejiang University: Science A, 2016, 17(10): 782-802.
[4] LEE H, ONG S H. Estimation of in situ stresses with hydro-fracturing tests and a statistical method[J]. Rock Mechanics and Rock Engineering, 2018, 51(3): 779-799.
[5] 方明礼, 肖明. 三维初始地应力场反分析的变差函数法[J]. 岩石力学与工程学报, 2015, 34(8): 1594-1601.
FANG M L, XIAO M. Back analysis of 3D initial geostress field based on variogram function[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(8): 1594-1601.
[6] 张涛, 尹健民, 张新辉, 等. 尼泊尔东北部某水电站引水隧洞初始地应力场反演分析[J]. 长江科学院院报, 2021, 38(1): 108-113.
ZHANG T, YIN J M, ZHANG X H, et al. Inversion analysis of initial in-situ stress field of diversion tunnel of a hydropower station in northeastern Nepal[J]. Journal of Yangtze River Scientific Research Institute, 2021, 38(1): 108-113.
[7] 刘敬文, 白金朋, 王建, 等. 基于XGBoost的初始地应力场修正反演法[J]. 水利水电科技进展, 2022, 42(2): 101-106.
LIU J W, BAI J P, WANG J, et al. A modified inversion method of initial geo-stress field based on XGBoost algorithm[J]. Advances in Science and Technology of Water Resources, 2022, 42(2): 101-106.
[8] 费万堂, 张练, 马雨峰, 等. 丰宁抽水蓄能电站地下厂房初始地应力场反演[J]. 人民长江, 2020, 51(增刊1): 112-116.
FEI W T, ZHANG L, MA Y F, et al. Inversion of initial geostress field of underground powerhouse of Fengning Pumped Storage Power Station[J]. Yangtze River, 2020, 51(S1): 112-116.
[9] 任斌, 张帆, 李永生, 等. 五岳抽水蓄能电站地下厂房初始地应力反演及围岩稳定性分析[J]. 水电能源科学, 2023, 41(5): 117-120, 198.
REN B, ZHANG F, LI Y S, et al. Initial ground stress inversion and surrounding rock stability analysis of underground powerhouse of Wuyue pumped storage power station[J]. Water Resources and Power, 2023, 41(5): 117-120, 198.
[10] 陈婧华, 张琳娟, 卢丹, 等. 基于改进粒子群优化算法的分布式电源集群划分方法[J]. 郑州大学学报(工学版), 2023, 44(5): 77-85.
CHEN J H, ZHANG L J, LU D, et al. Cluster partition method of distributed power supply based on improved particle swarm optimization algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 77-85.
[11] 王昕. 梯度下降及优化算法研究综述[J]. 电脑知识与技术, 2022, 18(8): 71-73.
WANG X. A survey of gradient descent and optimization algorithms[J]. Computer Knowledge and Technology, 2022, 18(8): 71-73.
[12] 马健, 鄢双红, 董志宏, 等. 大型地下厂房水压致裂法地应力测量及地应力场反演分析[J]. 中国农村水利水电, 2024(6): 252-258.
MA J, YAN S H, DONG Z H, et al. In-situ stress measurement and in situ stress field inversion analysis by hydraulic fracturing in large-scale underground plants[J]. China Rural Water and Hydropower, 2024(6): 252-258.
[13] 吴振龙, 莫艺鹏, 王荣花, 等. 基于LSTM和粒子群算法的多机组风电功率预测[J]. 郑州大学学报(工学版), 2024, 45(6): 114-121.
WU Z L, MO Y P, WANG R H, et al. Multi-unit wind power prediction based on long short-term memory and particle swarm optimization[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(6): 114-121.
[14] SHI Y, EBERHART R. A modified particle swarm optimizer[C]∥1998 IEEE International Conference on Evolutionary Computation Proceedings. Piscataway:IEEE, 1998: 69-73.
[15] 张强, 李盼池, 王梅. 基于自适应进化策略的人工蜂群优化算法[J]. 电子科技大学学报, 2019, 48(4): 560-566.
ZHANG Q, LI P C, WANG M. Artificial bee colony optimization algorithm based on adaptive evolution strategy[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(4): 560-566.
[16] 李兴怡, 岳洋. 梯度下降算法研究综述[J]. 软件工程, 2020, 23(2): 1-4.
LI X Y, YUE Y. Survey of gradient descent algorithm[J]. Software Engineering, 2020, 23(2): 1-4.
[17] 蒙伟, 何川, 陈子全, 等. 岭回归在岩体初始地应力场反演中的应用[J]. 岩土力学, 2021, 42(4): 1156-1169.
MENG W, HE C, CHEN Z Q, et al. Application of ridge regression in the inversion analysis of the initial geo-stress field of rock masses[J]. Rock and Soil Mechanics, 2021, 42(4): 1156-1169.
[18] 孙港, 王军祥, 郭连军, 等. 基于IA-BP智能算法的初始地应力场反演研究[J]. 土木与环境工程学报(中英文), 2023, 45(2): 89-99.
SUN G, WANG J X, GUO L J, et al. In-situ stress field inversion via IA-BP intelligent algorithm[J]. Journal of Civil and Environmental Engineering, 2023, 45(2): 89-99.
[19] 赵雨, 白金朋. 基于FLAC3D的多元线性回归法地下厂房初始地应力场反演重构[J]. 水电能源科学, 2022, 40(3): 149-152, 185.
ZHAO Y, BAI J P. Inversion of multiple linear regression analysis of initial stress field of underground powerhouse based on FLAC3D[J]. Water Resources and Power, 2022, 40(3): 149-152, 185.