随着配电网综合能源管控和网络调控技术的发展,分布式电源(distribute generator,DG)接入配电网改变了系统的潮流分布和拓扑结构,对主动配电网的通信和控制技术提出了更高的要求[1]。
分布式控制系统凭借自身的控制能力和决策能力具有更好的容错性和鲁棒性。陈婧华等[2]采用惯性权重动态递减策略的改进粒子群优化算法,对基于综合指标体系的集群划分模型进行分布式控制。Ji等[3]采用动态事件触发一致性算法来减少各节点间的通信频率,解决智能电网受干扰下的经济调度问题。Wang等[4]提出了一种基于综合学习方法的引导突变策略,根据构建的学习样本生成突变载体,防止分布式搜索偏离全局最优值并加快收敛速度。张富强等[5]提出一种改进鲸鱼算法可以在短时间内求解有限自动引导车资源约束的智能化车间调度问题。Quan等[6]提出基于分层排序方法和多智能体理论,将机组的动态特性和最优发电调度描述为一个分层分散的多目标规划问题。通过分布式无领导一致性算法将所有机组并行配置,从而确保新型电力系统的低碳和安全运行。米阳等[7]提出一种基于功率调整项的一致性协调算法,但需要中央控制器采集临近单元信息并进行求和,增加了系统通信量和计算复杂度。张步云等[8]采用智能优化算法实现微电网集群的负荷优化分配,可有效提高分布式电源的经济性运行,该算法主要侧重于储能侧的优化控制。董璐等[9]设计一种一致性项+目标渐进项的离散型一致性算法求解电力系统能量管理优化调度问题,需要集中式处理器计算出各单元的有功出力,在应对配电网中源-荷协同的实时调度挑战时,显现出了适应性不足的问题。
针对上述研究存在的问题,本文对系统通信拓扑进行超节点选取和局部集划分,进行拓扑重构并优化节点间的数据通信路径。同时,对离散型一致性算法功率调整项进行改进,提出一种自适应全局修正系数的调频控制方法,通过调频控制来实时检测全局不平衡功率信息并调控各发电单元的有功出力,来实现能量管理分配时的快速收敛和完全分布式的实时调度目标,从而更好地适应主动配电网拓扑结构灵活变化以及“源-荷”双向不确定性场景。
1 超节点一致性算法
1.1 一致性算法
源-荷交互调度系统通过最优分配策略,能有效利用灵活性储备资源进行电力消纳,需要所有智能体单元满足“等微增率原则”[10-11]。一致性算法的本质就是将具有通信机制的智能体单元进行信息交互,使系统网络拓扑中参与协同优化控制的节点体现一致性原则,即通过不断迭代更新收敛于稳定的共同值,使各节点达到系统最优状态[12-13]。为了解决分布式电源的功率最优分配和实时优化调度问题,本研究运用离散型一致性算法来分析并描述主动配电网中供需两侧动态平衡的特性。
定义xi(k)∈X(k)表示节点i在第k次离散迭代时间序列的一致性状态信息,则其迭代过程如下:
(1)
式中:dij为状态转移矩阵D第i行第j列的元素,可以表示为
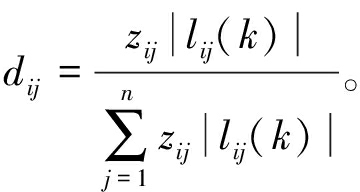
(2)
式中:zij为超节点层节点wi到节点wj进行信息交互时的增益权重;lij为拓扑图的Laplace矩阵第i行第j列的元素。
1.2 超节点选取及局部集划分
李龙斌[14]采用单跳采样法并设置图论中节点度值最大的节点作为一个超节点,本文在此基础上进行改进:以节点度值大于2的节点作为备选超节点,且其对应局部集内的节点数不小于该超节点的度值,超节点及其对应局部集的通信关系形成并行结构,优化了通信路径,减少了算法循环迭代的计算量、存储量。超节点选取流程如图1所示。
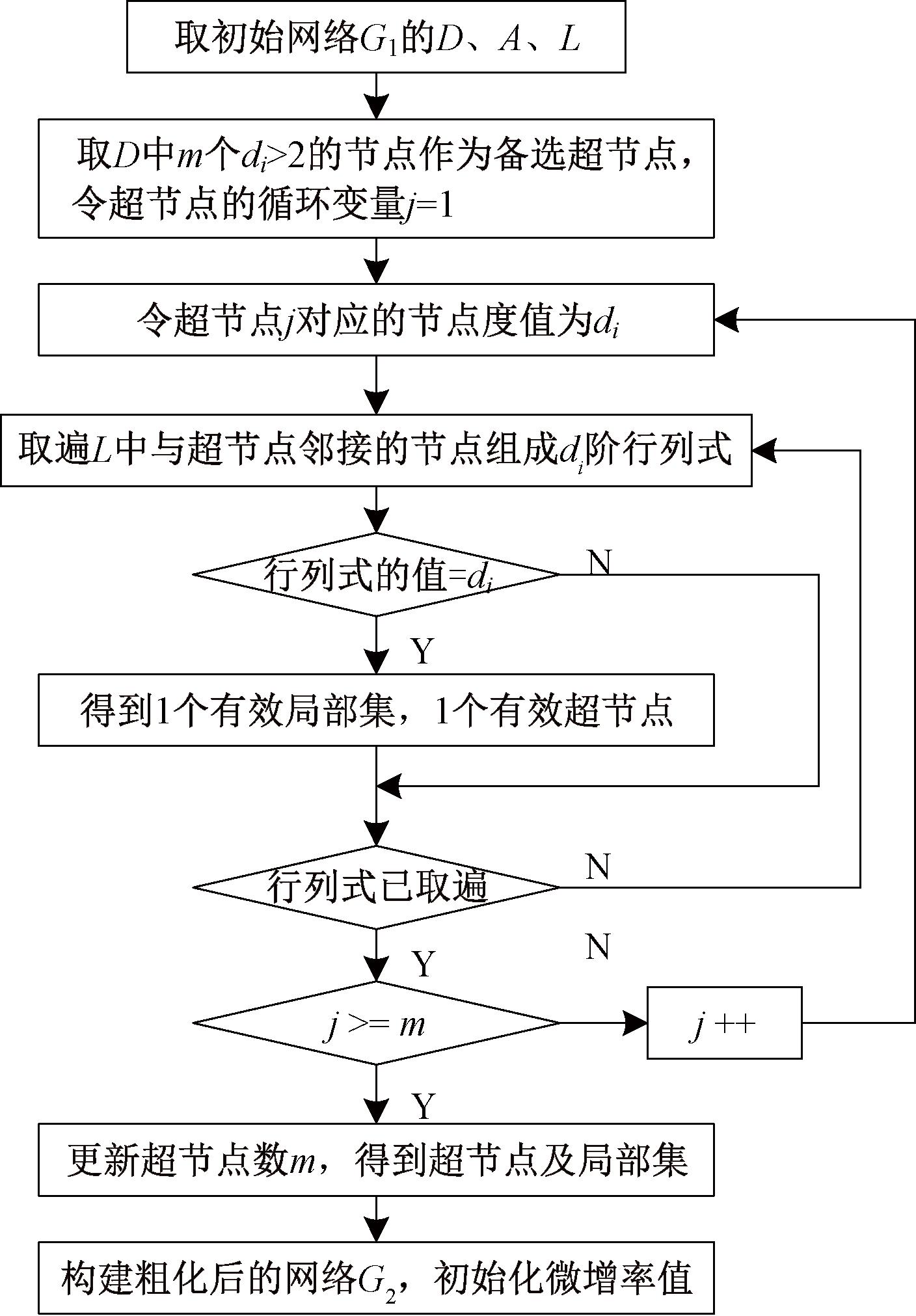
图1 超节点选取流程
Figure 1 Flow chart for supernode selection
超节点网络通信机制:首先,各超节点与上层主网调度控制层通信之后,超节点层并行获取有功功率指令,与邻居超节点进行信息交换并更新自身状态信息;其次,超节点的信号值以广播传播的方式传输给其局部集内的普通节点,普通节点根据超节点发出的控制信号进行信息交换;最后,各超节点所对应局部集内的普通节点利用图信号处理机制进行一致性协同控制。
在网络拓扑图重构过程中,各节点初始一致性变量总值与局部集内各节点初始值之和相等,即
(3)
式中:λi(0)为初始网络G1内各点的初始一致性变量,i∈(1,n);zλj(0)表示第j个超节点所对应局部集内各节点初始值,j∈(1,m)。
根据超节点层与局部集内节点一致性变量初始值之间的关系可知:
(4)
式中:![]() 为超节点层各节点的初始一致性变量;e为权重系数。
为超节点层各节点的初始一致性变量;e为权重系数。
因为网络拓扑重构前和重构后的各节点一致性变量平均值相等,所以
(5)
由式(3)~式(5)可知,通信拓扑重构后超节点的初始值为
(6)
2 目标函数
本文设计的能量管理优化目标需要在分布式电源输出功率满足配电网总负荷需求的基础上,建立负荷侧的效益最优以及源侧各常规能源和分布式光伏发电成本最小的目标函数:
(7)
负荷侧的经济效益函数表达式为
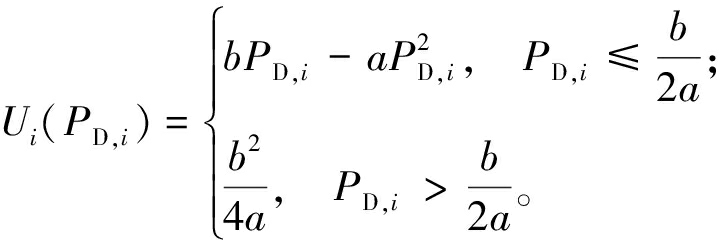
(8)
式中:a、b分别为负荷侧的经济效益系数。
包括常规能源和可再生分布式光伏发电单元的电源侧成本函数分别表示为
(9)
(10)
式中:αi、βi、γi分别为第i个常规能源的发电成本参数;αj为分布式光伏电源的发电成本参数。
同时,配电网中源-荷两侧发生突变时,仍需满足PCC功率守恒来维持系统电压和频率的稳定:
(11)
式中:PL,k为配电网总负荷需求;Pj为第j台DG的出力;PPCC,i为系统PCC跟踪调度中心的参考值。
同时,各常规发电单元和分布式光伏发电单元需在任意时刻满足有功出力的上下限约束:
(12)
3 源-荷协同调度策略
3.1 一致性增量成本计算
传统离散型一致性算法设计由一致性项+功率调整项组成迭代更新方式,根据等微增率准则,当所有DG的增量成本达成一致时,即可实现能量管理调度的最优状态[15],增量成本表达式为
(13)
(14)
式中:λ*为拉格朗日乘子;Ci(Pi)为电源侧发电成本;τ为功率调节系数;ΔPdv为全局功率偏差值。
第i个DG节点的有功功率更新方式表示为
(15)
传统能量管理调度方法需要一个中央单元集中处理发送的全局功率信息,属于集中式控制[16]。本文结合调频控制对一致性算法的功率调整项进行改进,解决系统难以实现完全分布式调度的问题。将式(14)进行改进,得到增量成本一致性迭代更新方式:
(16)
(17)
式中:ξf为静态调差系数;Δf(k)为系统频率偏差值;定义ε*为调频控制下的全局约束修正系数,表达式为
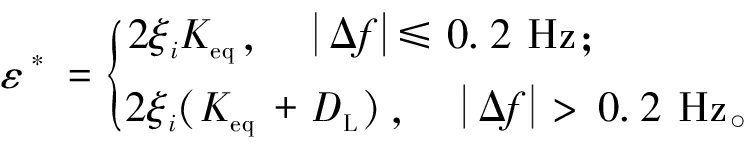
(18)
式中:Keq为电源侧的等效调节系数;DL为需求侧的调节系数。
3.2 调频控制理论
考虑到可控负荷在经济调度上的优越性[17],本文只对需求侧可控负荷进行主要研究,则整个主动配电网系统的频率偏差为
(19)
式中:ΔP为需求侧负荷的变化量;PG、PRDG分别为常规能源和分布式光伏的单位调节功率;ν为参与调频控制的光伏电源比例。
电源侧和负荷侧根据频率偏差范围共同参与系统的动态调整[18],即配电网分布式调控方式为
(20)
一致性调控策略流程如图2所示。
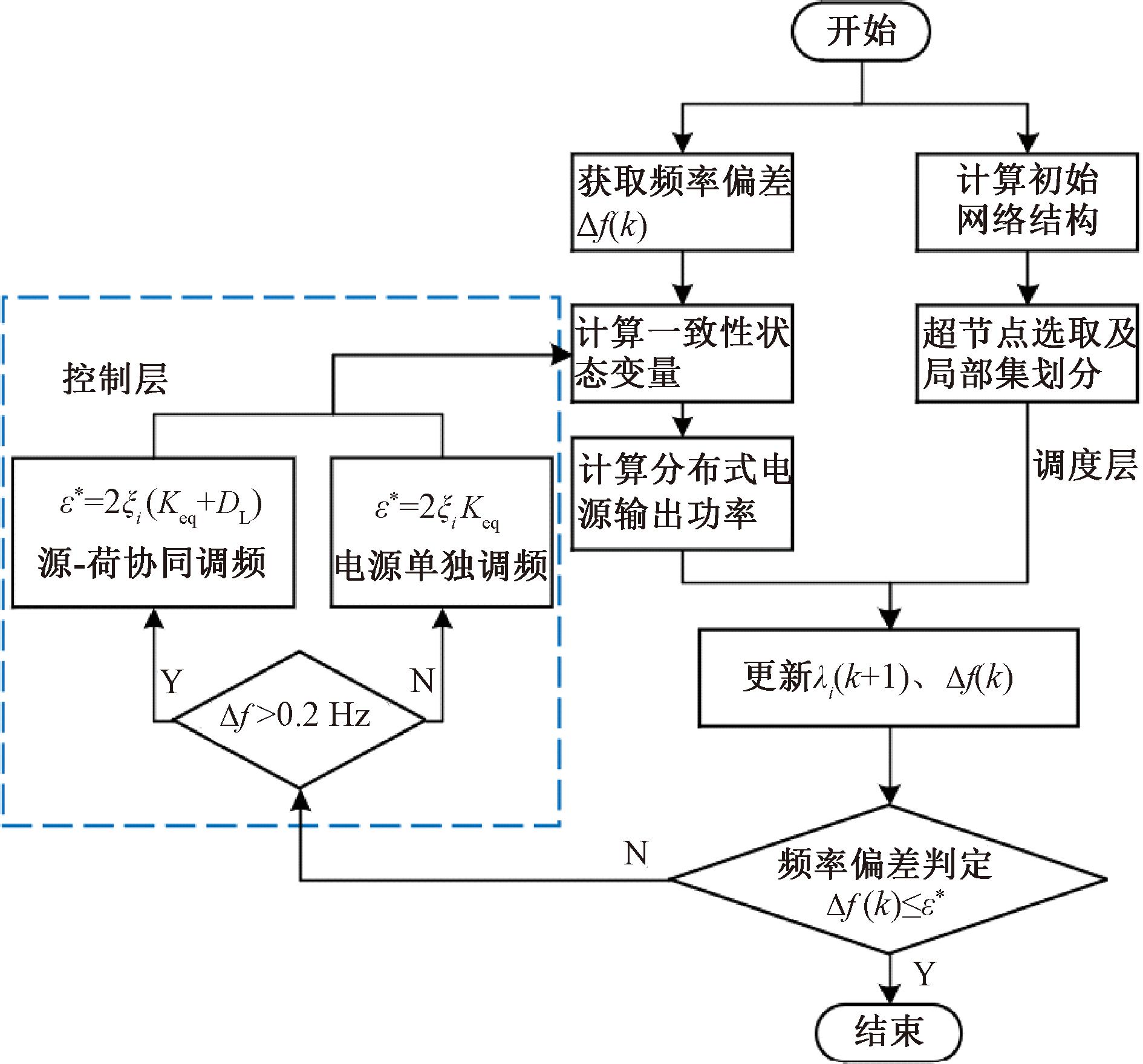
图2 一致性调控策略流程
Figure 2 Consistency regulation strategy flow
对所提一致性调控算法的收敛性及计算复杂度进行分析和验证,则关于Δλ(k)的函数表示为
(21)
当理想的一致性变量值等于实际的一致性变量值时,存在Δλ1(k)=Δλ2(k)=…=Δλn(k)=0。因此
Δλ(k)=Δλave(k)+ΔλΔ(k)=
Δλ(k)/n+ΔλΔ(k)。
(22)
式中:Δλave(k)为Δλ(k)变量的平均值;ΔλΔ(k)为平均一致性变量Δλave(k)与Δλ(k)的差值。因此
(23)
当频率偏差超过 0.2 Hz时,全局修正系数ε*由![]() 和PL共同组成,必定存在一个上限值ΔλΔmax确保
和PL共同组成,必定存在一个上限值ΔλΔmax确保![]() 收敛。此时
收敛。此时
(24)
当![]() 时
时
![]() +
+![]()
(25)
因此,![]() 越小,功率不平衡值ΔP会更快趋于零,即实现源-荷动态功率平衡。
越小,功率不平衡值ΔP会更快趋于零,即实现源-荷动态功率平衡。
4 算例仿真
4.1 仿真系统
本文搭建一个14节点小型配电网系统,8机配电系统如图3所示。
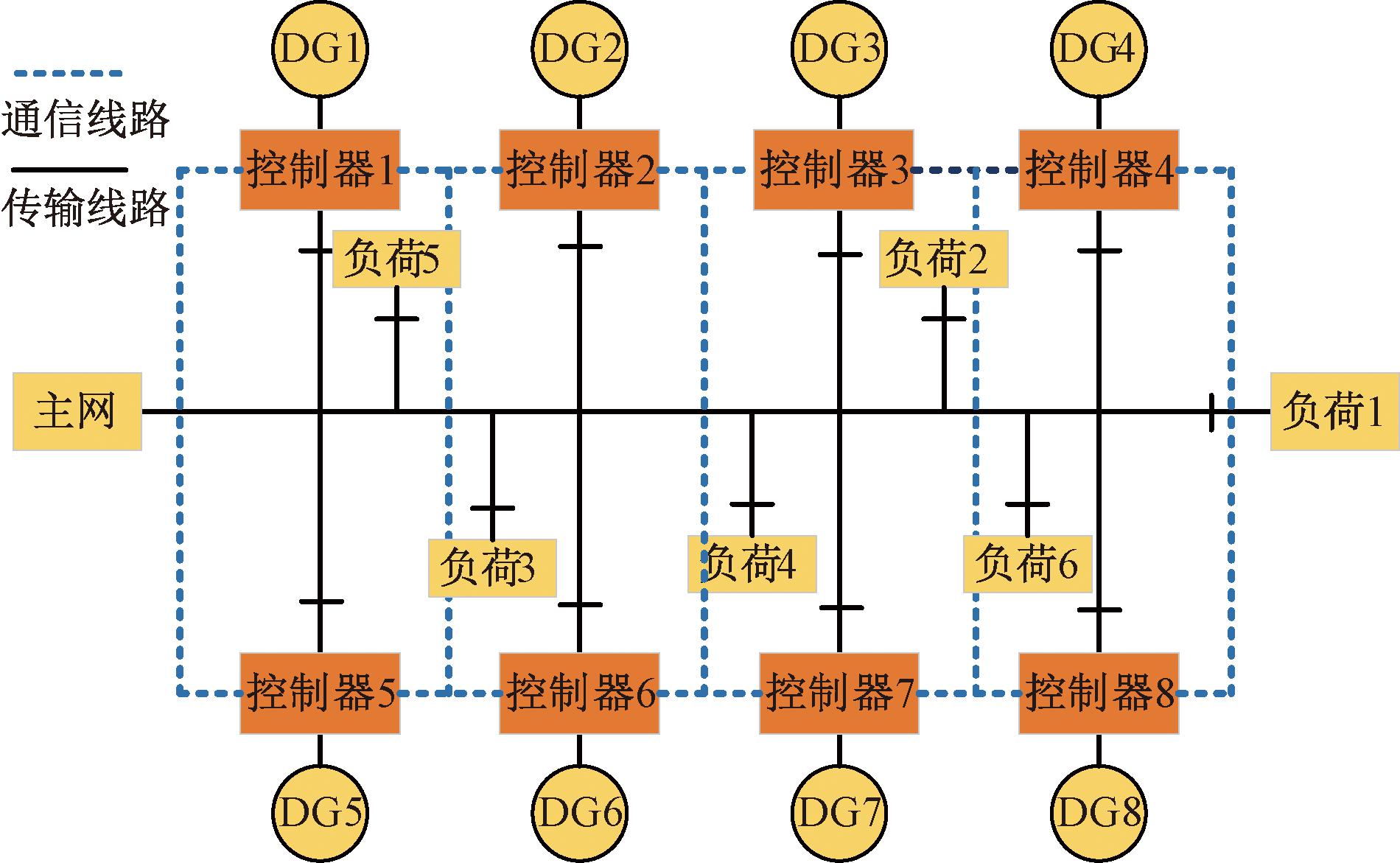
图3 8机配电网系统
Figure 3 8-generator power distribution network system
该配电网仿真调试系统配置了4个光伏电站,即DG1~DG4,DG5~DG8为可控分布式发电单元,其余节点为负荷节点。源-荷两侧详细运行成本参数由表1和表2分别给出。
表1 分布式发电单元参数表
Table 1 DG unit parameter table
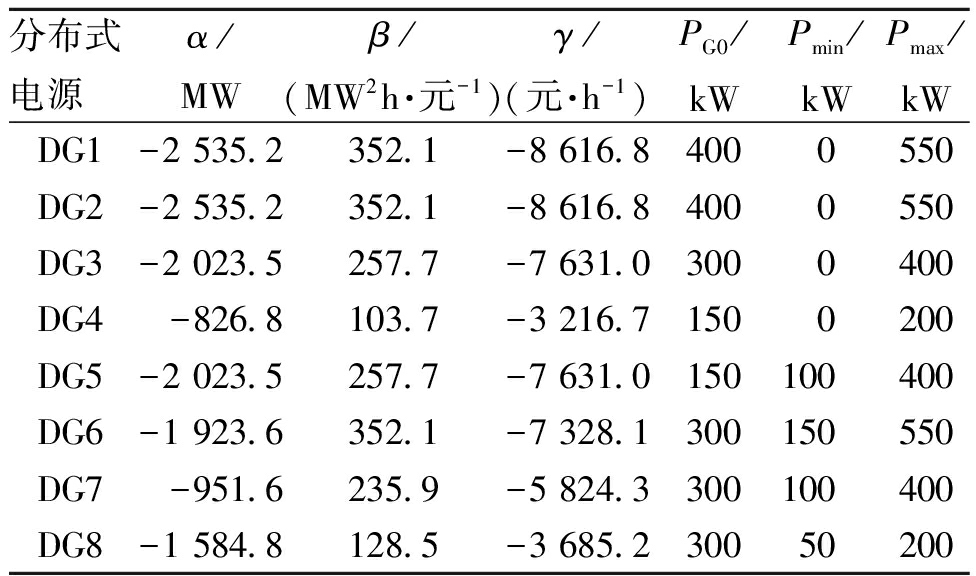
分布式电源α/MWβ/(MW2h·元-1)γ/(元·h-1)PG0/kWPmin/kWPmax/kWDG1-2 535.2352.1-8 616.84000550DG2-2 535.2352.1-8 616.84000550DG3-2 023.5257.7-7 631.03000400DG4-826.8103.7-3 216.71500200DG5-2 023.5257.7-7 631.0150100400DG6-1 923.6352.1-7 328.1300150550DG7-951.6235.9-5 824.3300100400DG8-1 584.8128.5-3 685.230050200
表2 负荷节点参数
Table 2 Load node parameter
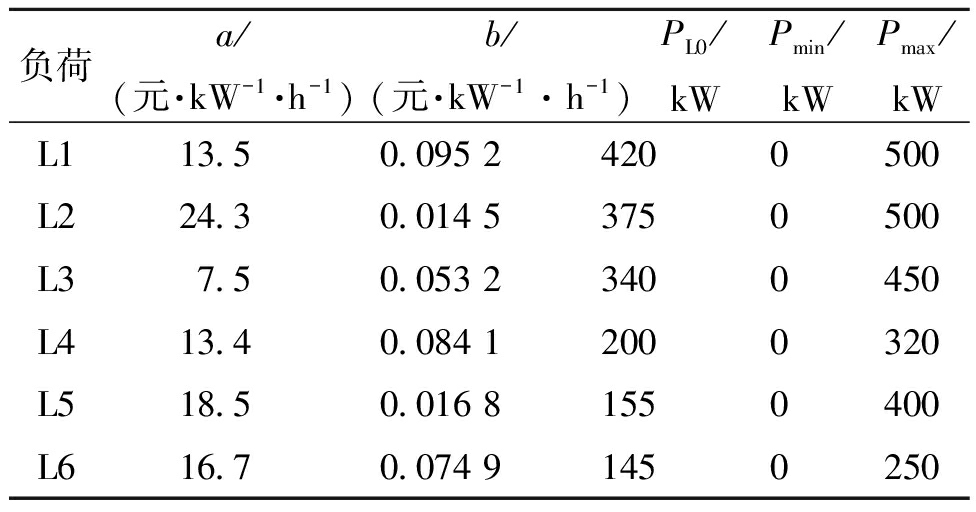
负荷a/(元·kW-1·h-1)b/(元·kW-1·h-1)PL0/kWPmin/kWPmax/kWL113.50.095 24200500L224.30.014 53750500L37.50.053 23400450L413.40.084 12000320L518.50.016 81550400L616.70.074 91450250
4.2 算法有效性测试
(1)不考虑通信时延。在不考虑通信时延时,利用上述对超节点协同一致性调度算法进行仿真,8机配电网系统改进算法有效性测试如图4所示。如图4(a)所示,当算法迭代至197次时,各发电单元的增量成本一致性变量均收敛至稳定值λ=8.76。由图4(a)可知,所提算法能够实现一致性增量成本的快速精准收敛,并始终满足系统供需平衡。图4(b)为迭代过程中采集的系统频率变化,可以看出频率偏差始终保持|Δf|≤0.2 Hz,系统在执行优化调度过程的调频控制由分布式电源单独完成,且能实现总成本最低的目标,如图4(c)所示。
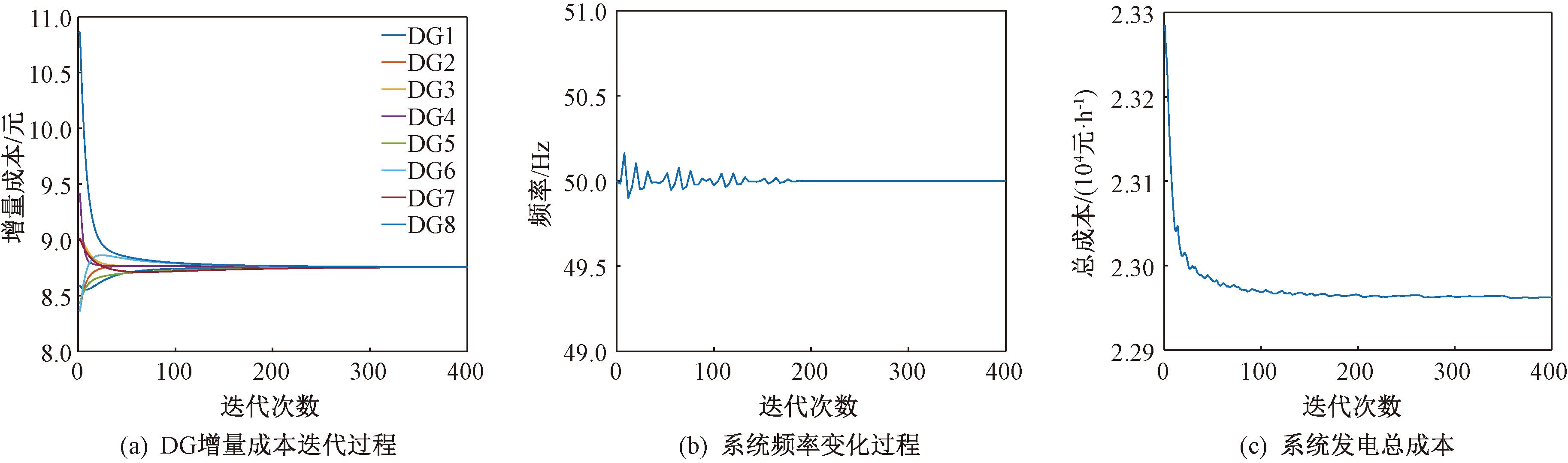
图4 8机配电网系统改进算法有效性测试
Figure 4 Improved algorithm effectiveness testing of eight machine distribution network system
(2)考虑通信时延。本文在系统初始时刻加入通信时延进行仿真验证,对比无超节点通信机制和有超节点通信机制下增量成本的迭代趋势,仿真测试结果如图5所示。图5(a)为无超节点通信机制下增量成本迭代趋势,因为存在通信延迟,所以控制信号的反馈滞后,直到k=638次迭代后各DG增量成本才收敛一致;图5(b)为超节点通信下增量成本迭代趋势图,系统仅需k=264次就可完成收敛,对比图5(a),在减少波形振荡和加快收敛速度方面均有明显改善。
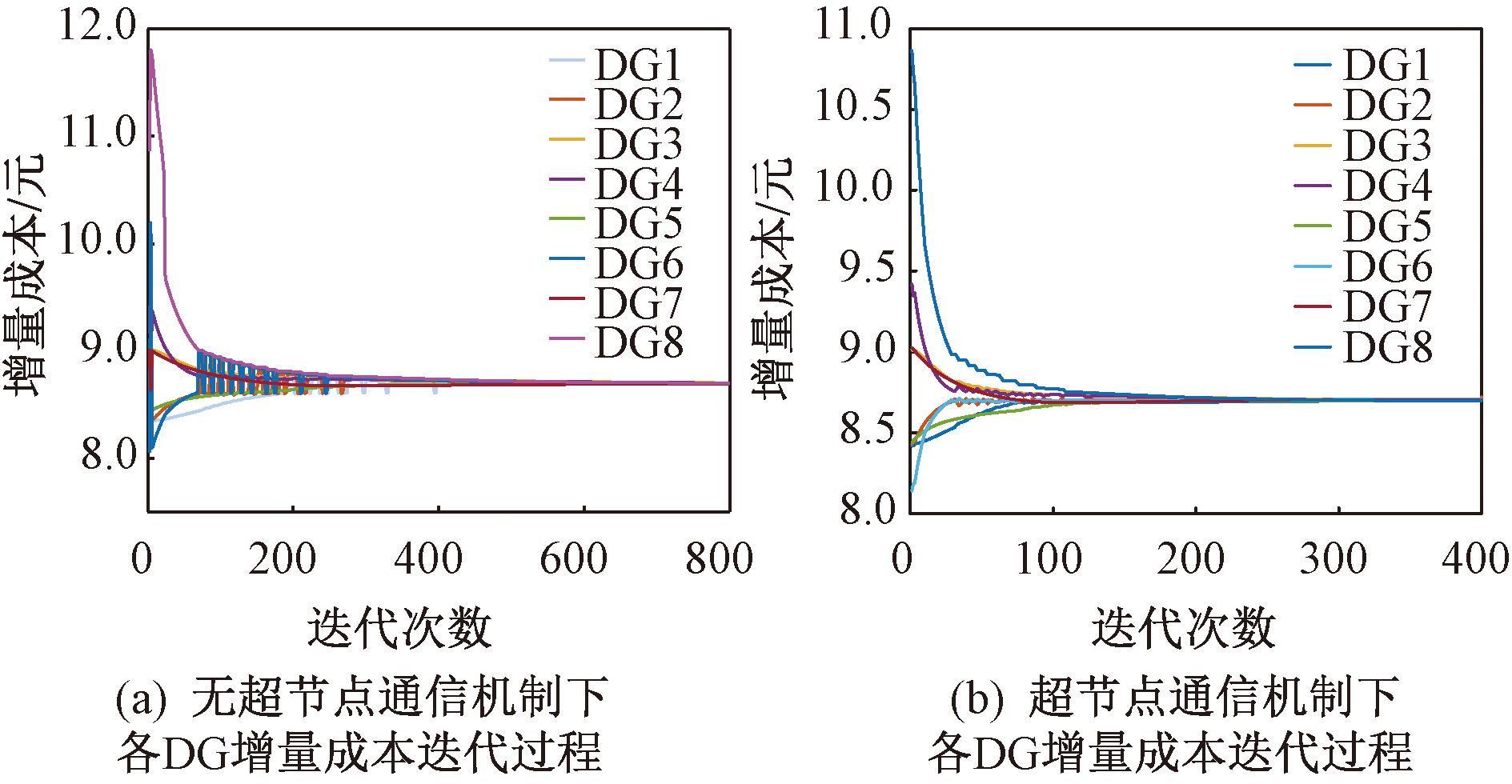
图5 系统存在通信时延仿真测试结果
Figure 5 Simulation test results of communication delay in the system
4.3 拓扑改变测试
拓扑改变测试是对所提调度方法在应对通信拓扑切换时的有效性的测试过程,即去掉L4和DG2、L4和L5、L3和DG8、L4和DG5之间的通信链路,仿真测试结果如图6所示。
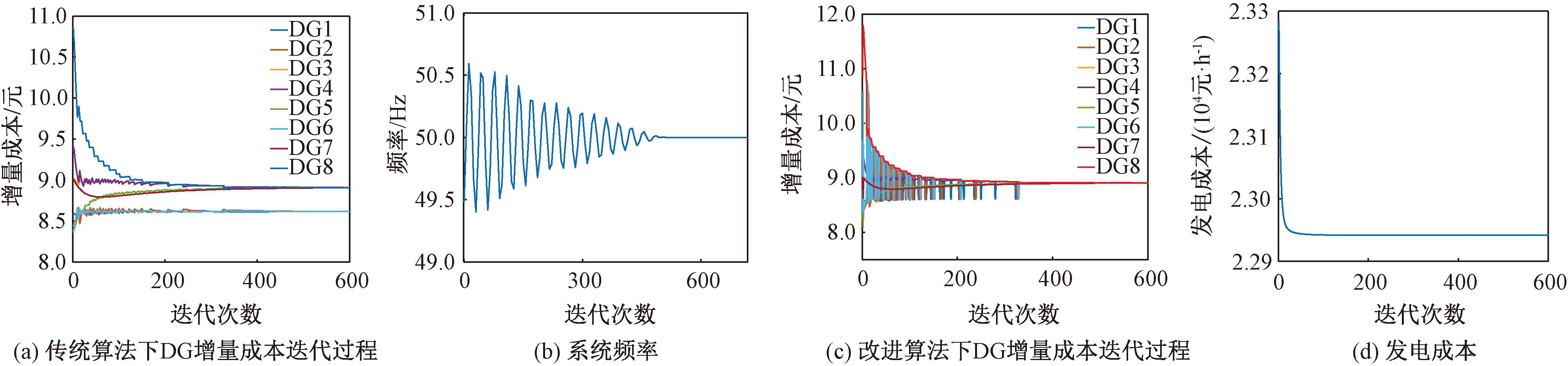
图6 拓扑结构变化仿真测试结果
Figure 6 Topology change simulation test results
图6(a)为传统一致性算法下各DG增量成本迭代过程,此时一致性变量没有趋于一致;图6(b)为改变系统拓扑后系统频率变化过程,迭代次数在0~278时,系统频率偏差|Δf|>0.2 Hz,全局修正系数ε*由电源侧+负荷侧的单位调节功率共同确定,当迭代次数在278~452次时,频率偏差|Δf|<0.2 Hz,ε*由电源侧的单位调节功率单独确定,直到k=452次时一致性增量成本收敛于稳定的共同值为λ*=8.91,此后,系统频率恢复至50 Hz,验证了所提方法在应对拓扑切换时的有效性。
4.4 源荷波动测试
设定在迭代次数k=200时,L1由420 kW变化到470 kW,L2由375 kW变化到400 kW,电源DG1出力减少30 kW。仿真结果如图7所示。
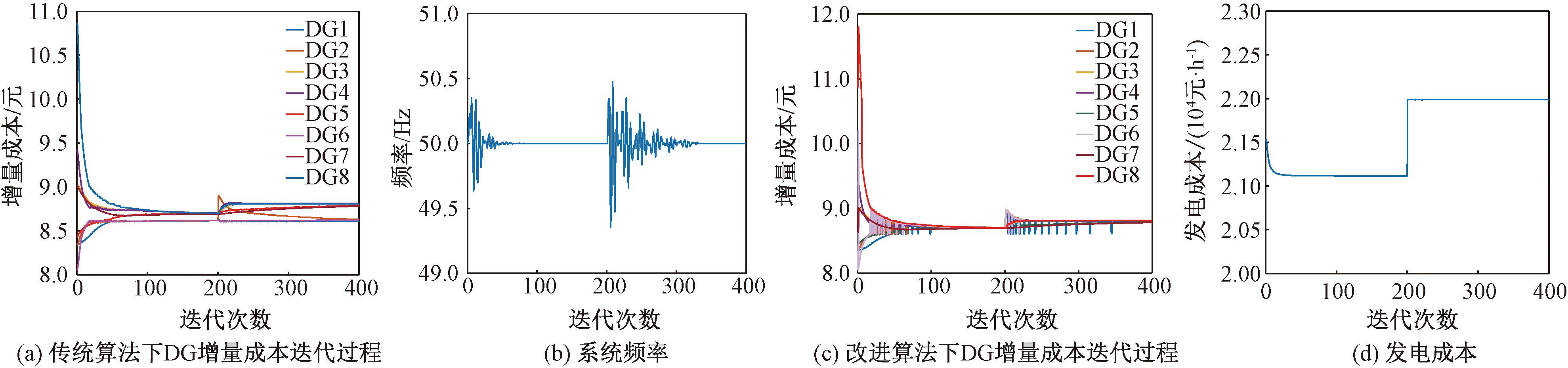
图7 源荷波动测试仿真结果
Figure 7 Simulation results of source-load fluctuation test
图7(a)为采用传统调度算法时各DG的增量成本迭代过程,打破系统初始供需平衡后一致性变量无法满足一致性要求;图7(b)为系统频率变化过程,当迭代次数为200时,负荷侧需求增大,此时系统频率偏差Δf<0,根据3.2节调频控制理论可知ΔP>0。系统需要更多的输出功率,使现有的一致性状态变量λ有所增加,一致性变量重新收敛至稳定值λ=8.796,结合式(14),计算出各分布式电源出力:P1=P2=P6=500 kW,P3=P4=P5=243 kW,P7=P8=85 kW。
5 结论
本文提出一种新型源-荷协同调度策略,通过理论与仿真验证,主要具有以下优势:
(1)对复杂网络通信拓扑结构进行超节点选取和局部集划分,降低了算法的通信量和计算复杂度。
(2)通过检测系统的频率偏差来更新功率调整项,避免了系统求解DG有功状态信息的烦琐过程。
(3)自适应全局修正系数通过决策一致性调控策略参与调频的方式,实现了一致性增量成本快速收敛至最优解和主网调控时的实时优化调度。
[1] LE J, LANG H K, WANG J, et al. The information security issues of distributed economic dispatch for new generation power systems—present situation and forecast[J]. Electronics, 2024, 13(14):2680-2680.
[2] 陈婧华,张琳娟,卢丹,等.基于改进粒子群优化算法的分布式电源集群划分方法[J].郑州大学学报(工学版), 2023, 44(5):77-85.
CHEN J H, ZHANG L J, LU D, et al. Distributed power generation cluster partitioning method based on improved particle swarm optimization algorithm [J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 77-85.
[3] JI L H , XU Z X ,YANG S S , et al. Distributed economic dispatch control in smart grid based on fixed-time dynamic event-triggered algorithm[J]. Electric Power Systems Research, 2024, 236:110933.
[4] WANG Y , XIONG G J , XU S , et al. Large-scale power system multi-area economic dispatch considering valve point effects with comprehensive learning differential evolution[J]. Swarm and Evolutionary Computation, 2024, 89101620-101620.
[5] 张富强,白筠妍,张林朋.基于生产甘特图的AGV资源约束调度方法[J].郑州大学学报(工学版),2022,43(4):23-29.
ZHANG F Q, BAI J Y, ZHANG L P. Scheduling method with AGV resource based on production gantt chart[J]. Journal of Zhengzhou University (Engineering Science), 2022,43(4):23-29.
[6] QUAN Y, XI L. Smart generation system: A decentralized multi-agent control architecture based on improved consensus algorithm for generation command dispatch of sustainable energy systems[J]. Applied Energy, 2024, 365:123209.
[7] 米阳,彭建伟,陈博洋,等.基于一致性原理和梯度下降法的微电网完全分布式优化调度[J].电力系统保护与控制, 2022, 50(15):1-10.
MI Y, PENG J W, CHEN B Y, et al. Fully distributed optimal scheduling of microgrids based on consistency principle and gradient descent method[J]. Power System Protection and Control, 2022, 50(15): 1-10.
[8] 张步云,王晋宁,梁定康,等.采用一致性算法的自治微电网群分布式储能优化控制策略[J].电网技术, 2020, 44 (5):1705-1713.
ZHANG B Y, WANG J N, LIANG D K, et al. Optimal control strategy for distributed energy storage in autonomous microgrid cluster using consistency algorithm[J]. Power System Technology, 2020, 44(5): 1705-1713.
[9] 董璐,边晓燕,周波,等.计及调频备用效益的主动配电网分层分布式协调优化调度[J].电力自动化设备, 2023, 43(1):55-63.
DONG L, BIAN X Y, ZHOU B, et al. Hierarchical distributed coordinated optimization scheduling of active distribution networks considering frequency regulation backup benefits [J]. Electric Power Automation Equipment, 2023, 43(1): 55-63.
[10] CHANG S P, WANG H, LUO X Y, et al. Distributed predefined-time economic dispatch based on event-triggered strategy for microgrids under directed graphs[J]. Neurocomputing, 2024,607:128391-128391.
[11] 乐健,周谦,赵联港,等.基于一致性算法的电力分布式经济调度方法综述[J].电力自动化设备, 2020, 40 (3):44-54.
LE J, ZHOU Q, ZHAO L G, et al. A review of power distributed economic dispatch methods based on consistency algorithm[J]. Electric Power Automation Equipment, 2020, 40(3):44- 54.
[12] 边晓燕,孙明琦,赵健等.基于一致性算法的源-荷协同分布式优化调控策略[J].中国电机工程学报, 2021, 41(4): 1334-1347,1540.
BIAN X Y, SUN M Q, ZHAO J, et al. Source-load cooperative distributed optimized regulation strategy based on consistency algorithm[J]. Proceedings of the CSEE, 2021, 41(4): 1334-1347,1540.
[13] YIN L F, CAI Z J. Multimodal multi-objective hierarchical distributed consensus method for multimodal multi objective economic dispatch of hierarchical distributed power systems[J]. Energy, 2024, 434:140130.
[14] 李龙斌.采用超节点协同的多智能体系统一致性算法[J].信息与控制, 2019, 48(6):694-699,706.
LI L B. Unified Consistency Algorithm for Multi Intelligent Systems Using Hypernode Collaboration [J]. Information and Control, 2019, 48(6): 694-699,706.
[15] 赵海祺,卢开诚,董树锋,等.考虑通信状态变化的直流微电网分布式事件驱动优化调度[J].电力系统自动化, 2023, 47(20):33-41.
ZHAO H Q, LU K C, DONG S F, et al. Distributed event-triggered optimal scheduling for DC microgrids considering communication status change[J]. Automation of Electric Power System, 2023, 47(20):33-41.
[16] SHANG L H, SUN M J, PAN C, et al. Distributed optimization scheduling consistency algorithm for smart grid and its application in cost control of power grid[J].International Journal of Advanced Computer Science and Applications (IJACSA),2024,15(4):34-42.
[17] 边晓燕,孙明琦,董璐,等.计及灵活性聚合功率的源-荷分布式协调调度[J].电力系统自动化,2021,45(17):89-98.
BIAN X Y, SUN M Q, DONG L, et al. Distributed source-load coordinated dispatching considering flexible aggregated power [J]. Automation of Electric Power System,2021,45(17):89-98.
[18] 陈燕东,李雪萍,等.孤岛微电网多虚拟同步发电机频率无差协调控制策略[J].电力系统保护与控制, 2024, 52(7):12-23.
CHEN Y D, LI X P, et al. Frequency seamless coordinated control strategy for multi virtual synchronous generators in isolated microgrids [J]. Power System Protection and Control, 2024, 52(7): 12-23.