随着自动驾驶技术的快速发展,其应用也迅速扩展到了工厂、隧道、矿区等非结构化道路的场景中[1]。路径规划作为自动驾驶技术中的一个重要研究方向,其目的是为自动驾驶装备规划出一条从起点到终点的无碰撞路径。目前常用的路径规划算法有Dijkstra算法[2]、A*算法[3]、人工势场法[4]、RRT算法[5]、蚁群算法[6]等,但上述算法在规划路径时均未考虑车辆运动学模型。
2008年,Dolgov等[7]提出了能够满足车辆运动学约束的混合A*(Hybrid A*)算法。Hybrid A*算法中节点以满足车辆运动学的方式进行扩展,同时为提升搜索效率,在搜索过程中融入了RS曲线搜索。但面对自动驾驶的实际应用需求,Hybrid A*算法仍表现出搜索效率低、路径不平滑等问题[8-9],因此,国内外学者对Hybrid A*算法的研究主要集中在搜索效率和路径质量两个方面。针对Hybrid A*算法搜索效率较低的问题,学者们通常从搜索空间[10]、搜索策略[11-13]、启发函数[14]和碰撞检测[12]等方面进行改进优化,提升算法的搜索效率。针对Hybrid A*算法路径质量不高的问题,学者们通常从二次优化[15-16]、多地图融合[17]、多算法融合[18]等方面进行改进,使规划的路径更加平滑、远离障碍物。在上述针对Hybrid A*算法搜索效率的改进算法中,节点扩展仍需不断调用A*算法或迪杰斯特拉(Dijkstra)算法计算启发值,因此,在高分辨率地图和复杂场景下仍会表现出效率低、耗时长等问题。
针对上述问题,基于Hybrid A*算法,本文提出了J-Hybrid A*算法,通过改进启发函数,在搜索过程中调用一次跳点搜索算法(jump point search,JPS)就能完成所有启发值的计算,同时将定半径RS曲线改进为变半径RS曲线,使所提J-Hybrid A*算法可以更快获得一条无碰撞路径,提升了算法的搜索效率。
1 改进Hybrid A*算法的路径规划
1.1 Hybrid A*算法
Hybrid A*算法是在A*算法的基础上改进而来,在A*算法只考虑车辆位置(x,y)的二维节点上增加代表车辆朝向的θ维度[19]。当车辆处于节点n(xn,yn,θn)时,Hybrid A*算法会根据式(1)所示的车辆运动学公式[20],计算由节点n扩展的子节点n+1的位姿信息(xn+1,yn+1,θn+1)。
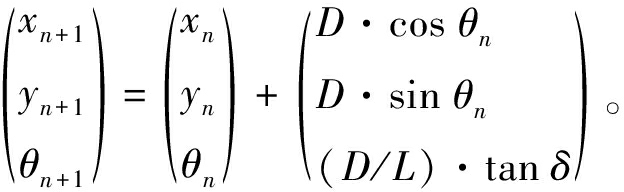
(1)
式中:L为车辆轴距;D为车辆移动距离;δ为车辆转向角。
当得到扩展节点n+1的位姿信息后,Hybrid A*算法将使用式(2)来计算该节点的代价值f(n+1)[21]。
f(n+1)=max(h1(n+1),h2(n+1))+g(n+1)。
(2)
式中:h1(n+1)为不考虑障碍物但考虑车辆运动学约束的情况下,当前节点到终点所需路径的距离,通常使用RS曲线来计算;h2(n+1)为考虑障碍物但不考虑车辆运动学约束的情况下,当前节点到终点的距离,通常使用A*算法来计算;g(n+1)为起点到当前节点的实际代价值。
在搜索过程中,Hybrid A*算法会不断使用RS曲线连接当前节点与终点,如果能获得一条无碰撞的RS路径,则搜索结束,否则继续使用上述节点扩展方式进行搜索。
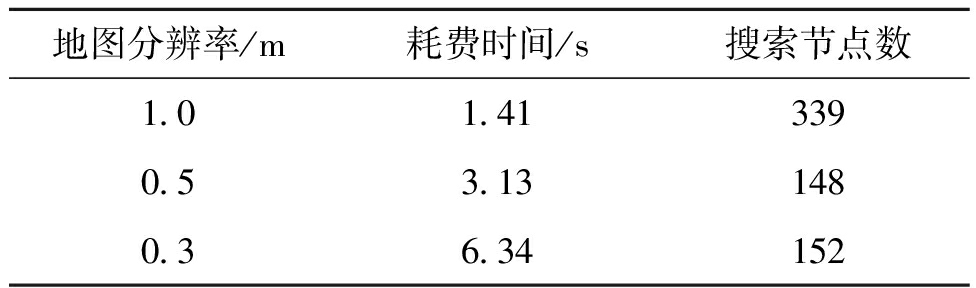
Hybrid A*算法虽然能够规划出满足车辆始末点位姿和车辆运动学约束的路径,但在使用中发现其在高分辨率地图或复杂场景下,规划效率仍然较低、耗费时间仍然较长。图1为始末点和障碍物分布图。表1为在图1所示的环境条件下,在MATLAB 中用Hybrid A*算法对不同地图分辨率进行路径规划耗费时间的结果,仿真区域大小为50 m×50 m。
表1 不同地图分辨率下Hybrid A*算法搜索结果
Table 1 Hybrid A* algorithm search time at different map resolutions
地图分辨率/m耗费时间/s搜索节点数1.01.413390.53.131480.36.34152
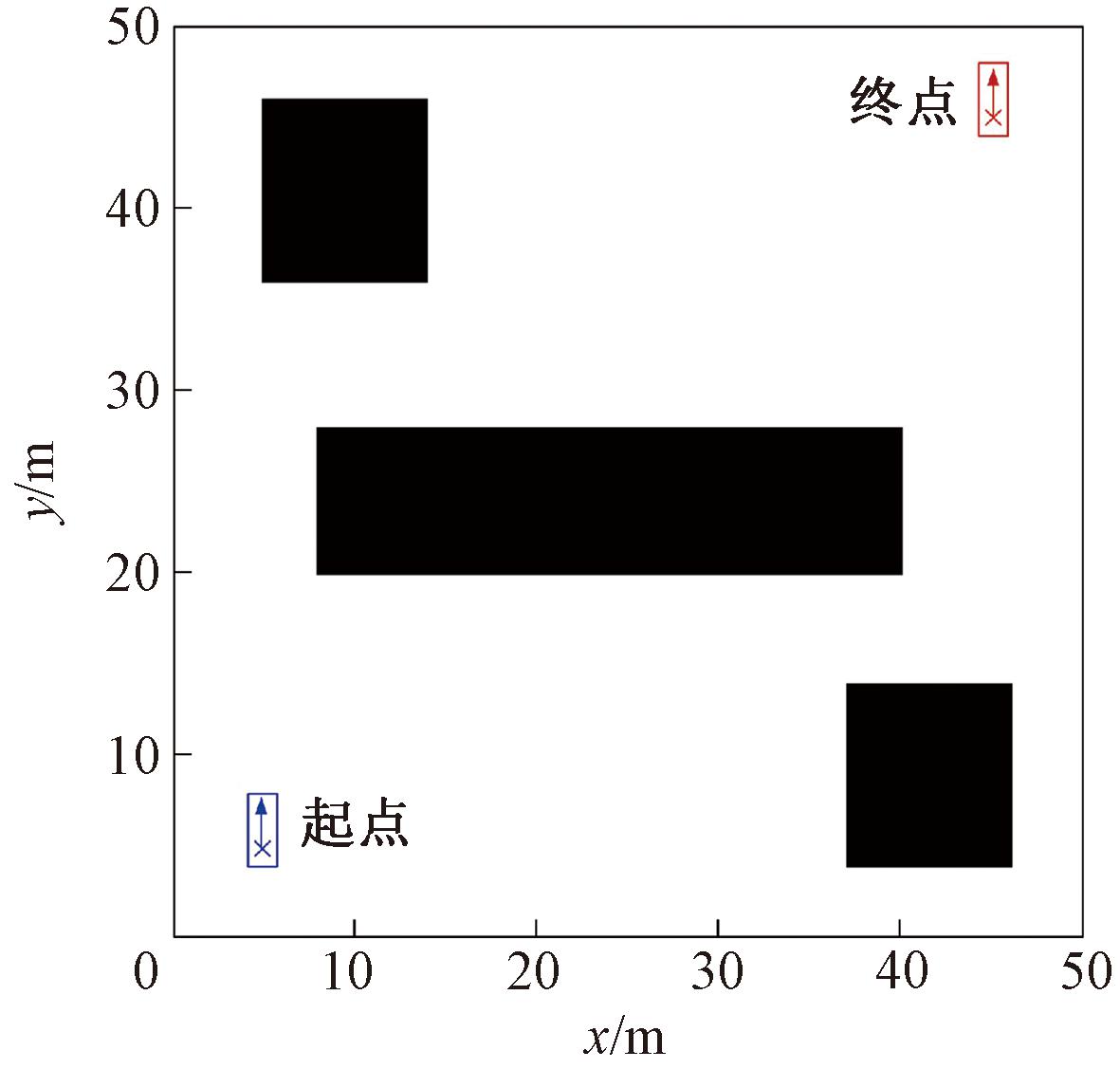
图1 始末点和障碍物分布图
Figure 1 Distribution of start and end points and obstacles
从表1可以看出,Hybrid A*算法的搜索时间会随着地图分辨率的提高大幅度增加,通过分析得出造成此现象的原因有以下两点。
(1)Hybrid A*算法需要频繁使用A*算法来计算新扩展节点的启发值。为了能够高效搜索路径,Hybrid A*算法会使用A*算法计算当前节点到终点的距离,以此作为启发值的一部分。随着地图分辨率的提高,使用A*算法的次数会随着Hybrid A*算法搜索节点数量增加而增多,A*单次搜索时间也会随着栅格数量的增加而变长,因此分辨率越高,Hybrid A*算法搜索用时将会越长。同时,A*算法搜索的路径通常靠近障碍物,这将使Hybrid A*算法在靠近障碍物的范围搜索产生大量位于障碍物内的无效节点。
(2)Hybrid A*算法的定半径RS曲线使用固定曲率曲线连接两个节点,灵活性较低,路径规划时间较长。
1.2 J-Hybrid A*算法
为了解决上述问题,提升Hybrid A*算法搜索效率,本文分别对Hybrid A*算法的启发函数h(n)、RS曲线进行改进。
1.2.1 J-Hybrid A*算法的启发函数
针对Hybrid A*算法搜索过程中需要多次调用A*算法计算启发值和搜索路径靠近障碍物的问题,本文设计了新的启发函数计算节点启发值。在获得起点、终点位姿后,首先使用JPS算法进行起点到终点的路径搜索,然后将JPS搜索路径进行拉直,最后根据栅格中心位置和拉直后的路径计算栅格地图的代价值,节点的启发值就是所处栅格的代价值,具体方法如下。
步骤1 JPS算法搜索路径。JPS算法在搜索过程中跳过了大量不感兴趣的点[22],通过减少搜索过程中遍历节点的数量,提升搜索效率。文献[22]中将JPS与其他常见路径搜索算法的效率进行比较,结果表明,JPS搜索效率明显高于其他算法,且随着地图分辨率的提高,其优势更加显著。因此本文选择使用JPS算法来获得一条从起点到终点的路径。
步骤2 JPS算法路径的拉直。在使用JPS算法规划出从起点到终点的路径后,通过剔除该路径中的无用点,将路径拉直形成一条新的无碰撞路径,路径搜索与路径拉直如图2所示,以此路径作为计算栅格地图代价值基础。
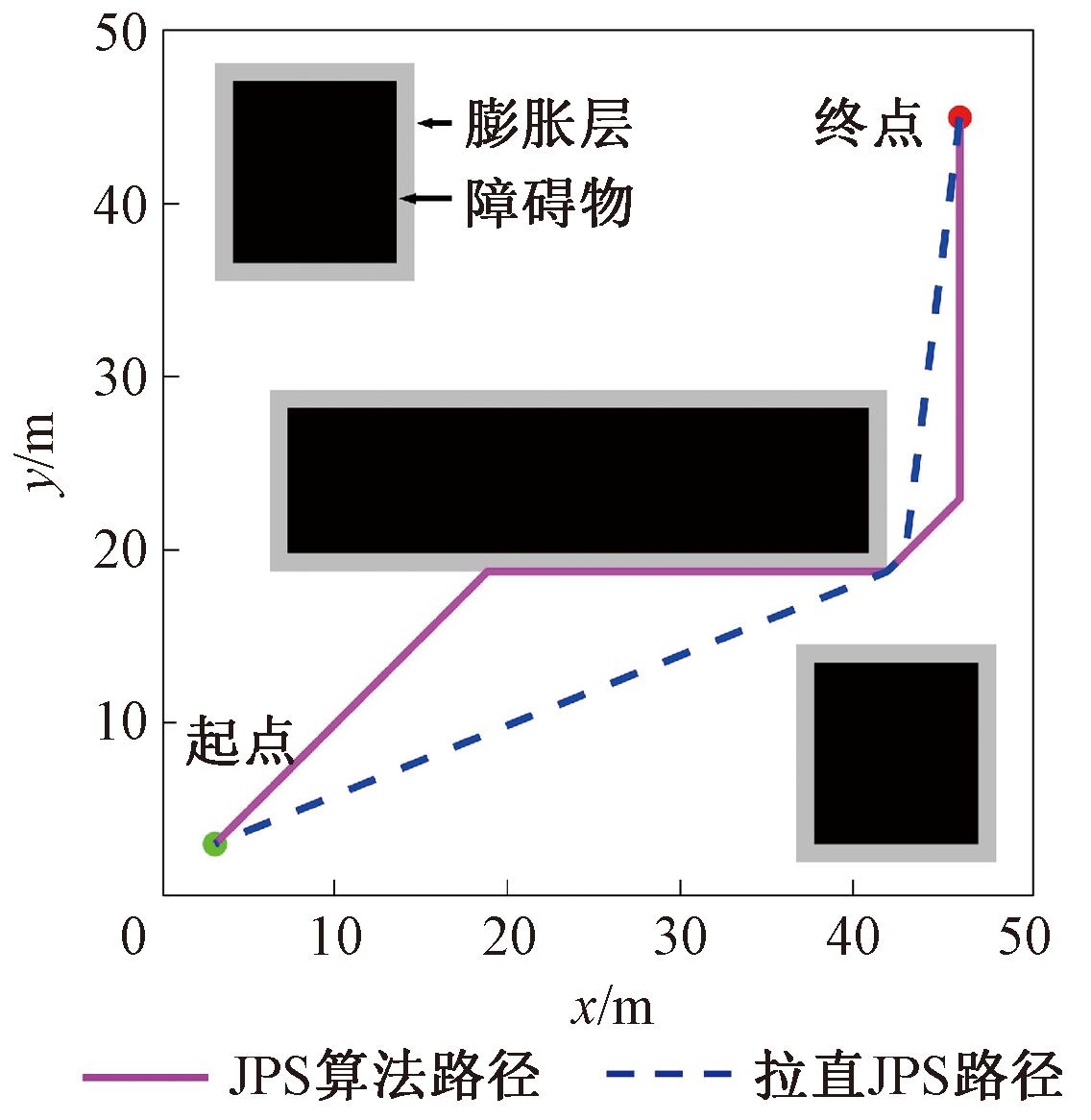
图2 路径搜索与路径拉直
Figure 2 Path search and path straightening
步骤3 启发值计算。改进后的启发函数如式(3)所示。
h(n)=k1(d(n)+FE)+k2l(n)。
(3)
式中:d(n)为当前栅格中心点n到拉直后路径的距离;FE为垂足点F沿拉直路径到终点E的折线长度;d(n)与FE二值相加可以使Hybrid A*算法在搜索时沿拉直后路径搜索;k1为该部分的权重,k1越大,则搜索结果越靠近拉直后的路径;同时,为避免Hybrid A*算法搜索时在拉直后路径两侧徘徊,再加入栅格中心点n到终点E的欧几里得距离l(n);k2为该部分的权重。
通过上述方法,可以在Hybrid A*算法搜索前得到一个代价地图,如图3所示。算法扩展时将节点所处栅格的代价值作为该节点的启发值。
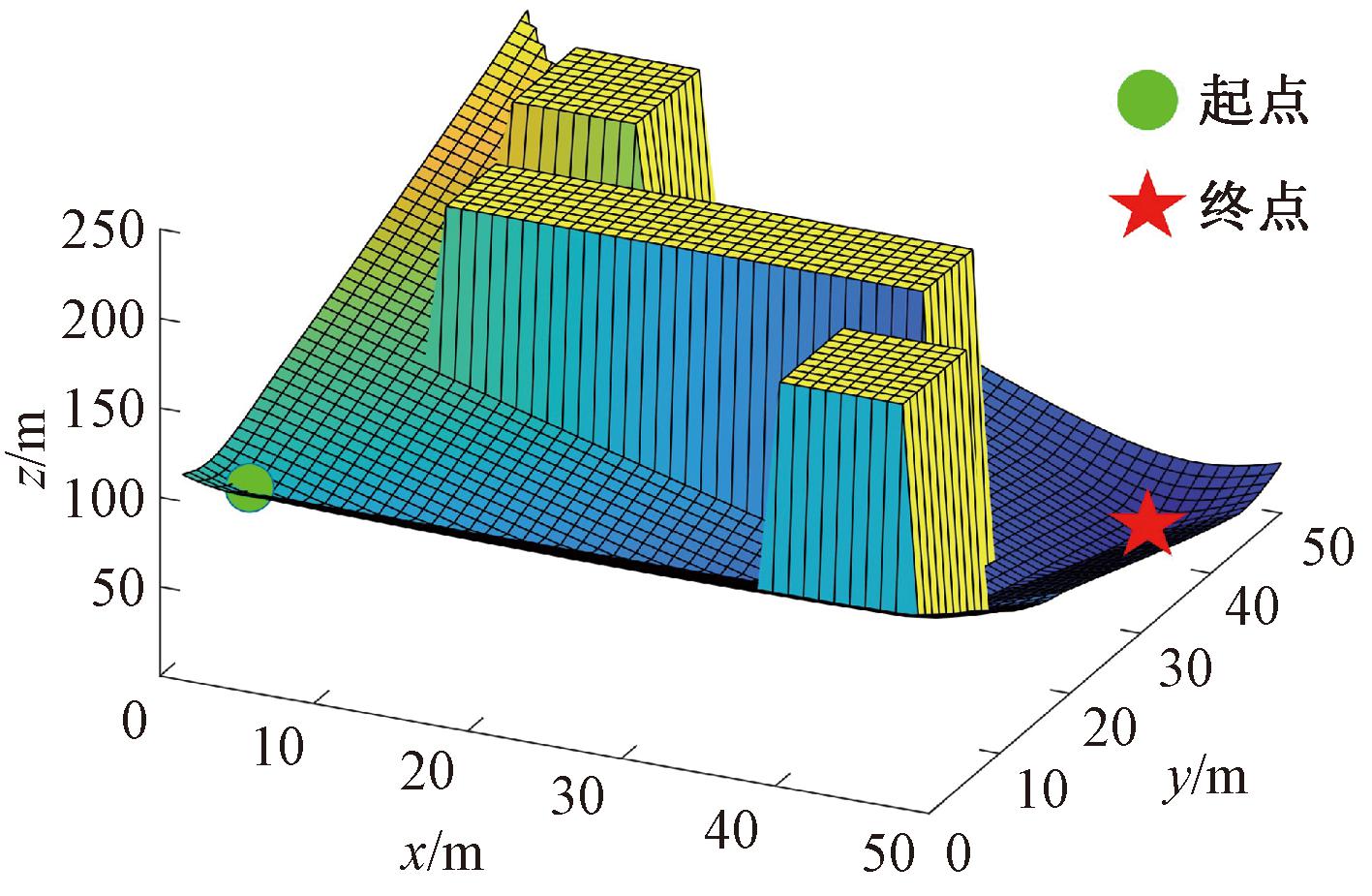
图3 改进启发函数计算的代价地图
Figure 3 Improved cost maps for heuristic function calculations
1.2.2 优化Hybrid A*算法RS曲线
RS曲线能够通过直线和圆弧的组合,再结合车辆前进和后退的运动状态[23],规划出符合车辆始末点朝向且满足车辆运动学约束的路径。在Hybrid A*算法搜索过程中,如果RS曲线能够找到当前节点到终点的无碰撞路径,则搜索提前结束。RS曲线通常以车辆最小转弯半径进行搜索,该方法有以下两个缺点。
(1)复杂环境中,获得一条无碰撞的路径难度大。只使用最小转弯半径进行搜索,则规划路径的灵活性会大幅降低,难以搜索出一条无碰撞路径。
(2)车辆平稳性难以保证。车辆行驶过程中为了保证车辆平稳、安全地过弯,很少直接使用最小转弯半径行驶。
因此本文采用了变半径RS曲线的方法,分别取最小转弯半径曲率的1倍![]() 进行RS曲线搜索,增加RS曲线搜索的多样性,以更早获得一条无碰撞的路径。图4为改进前后RS曲线搜索的对比图,图4中虚线部分为RS曲线规划的路径,可见改进后的RS曲线可以更早规划出一条无碰撞的路径。
进行RS曲线搜索,增加RS曲线搜索的多样性,以更早获得一条无碰撞的路径。图4为改进前后RS曲线搜索的对比图,图4中虚线部分为RS曲线规划的路径,可见改进后的RS曲线可以更早规划出一条无碰撞的路径。
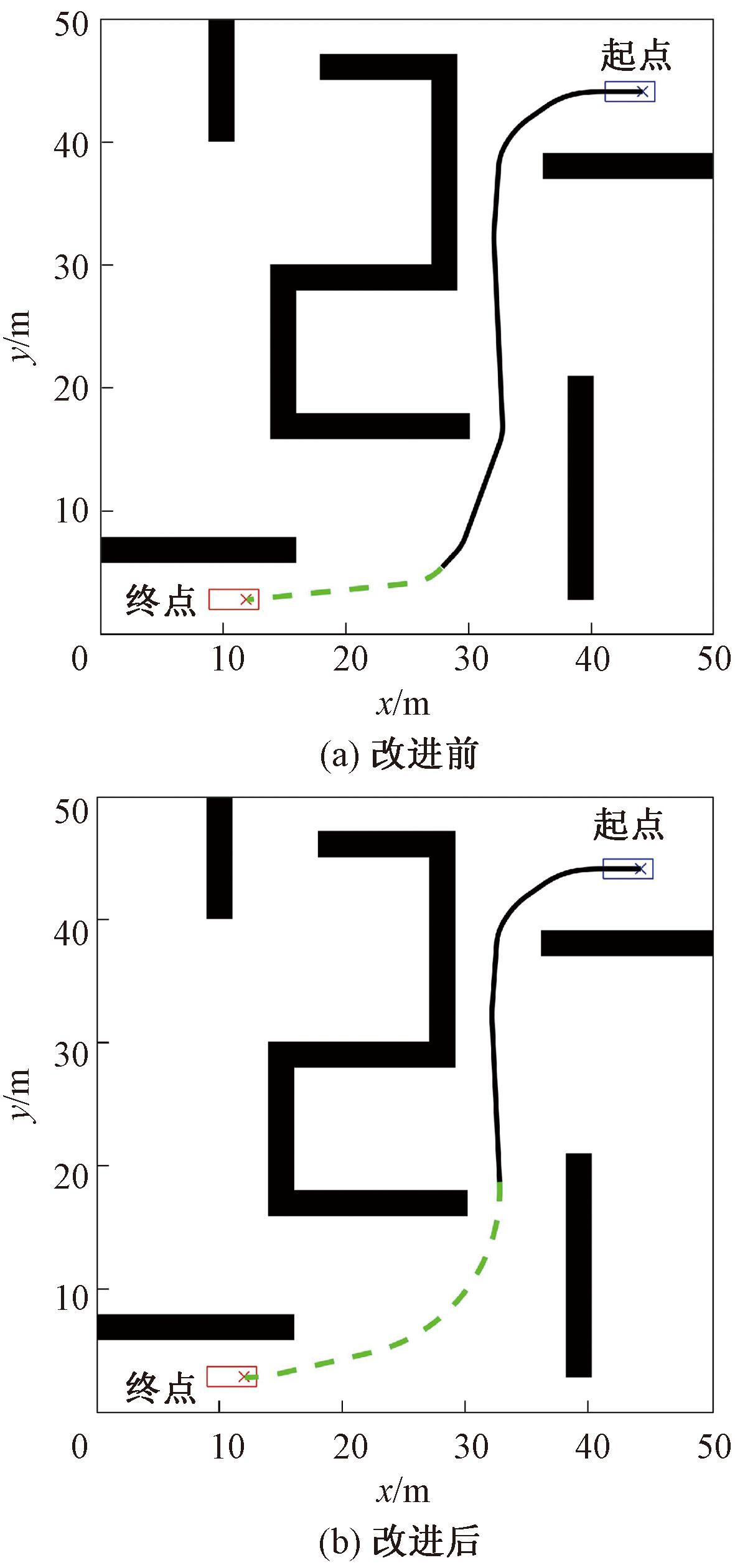
图4 改进前后RS曲线规划对比图
Figure 4 Comparison of RS curve planning before and after improvement
2 算法仿真
为验证改进算法的有效性,使用MATLAB 2022a软件进行仿真实验。仿真车辆长度4.75 m,宽度1.6 m,轴距2.75 m,前悬1 m,后悬1 m,前轮最大转角34°,仿真区域大小为50 m×50 m,障碍物分布、起点、终点、车辆朝向分别如图5、图6所示,图中左下角和右上角的方框分别为车辆在起点、终点的位姿,黑色为障碍物。根据障碍物的数量和分布情况,设置图5障碍物数量较少、分布简单的环境和图6障碍物数量多、分布较复杂的环境。通过对比传统Hybrid A*算法、文献[11]中的反向Hybrid A*算法、本文所提J-Hybrid A*算法在不同环境中的规划时间、路径长度以及不同地图分辨率下算法的搜索时间,验证所提算法的有效性。仿真算法在Windows 10、处理器Intel i5-8265U、内存16 GB的环境下运行,实验数据取20次实验平均值。
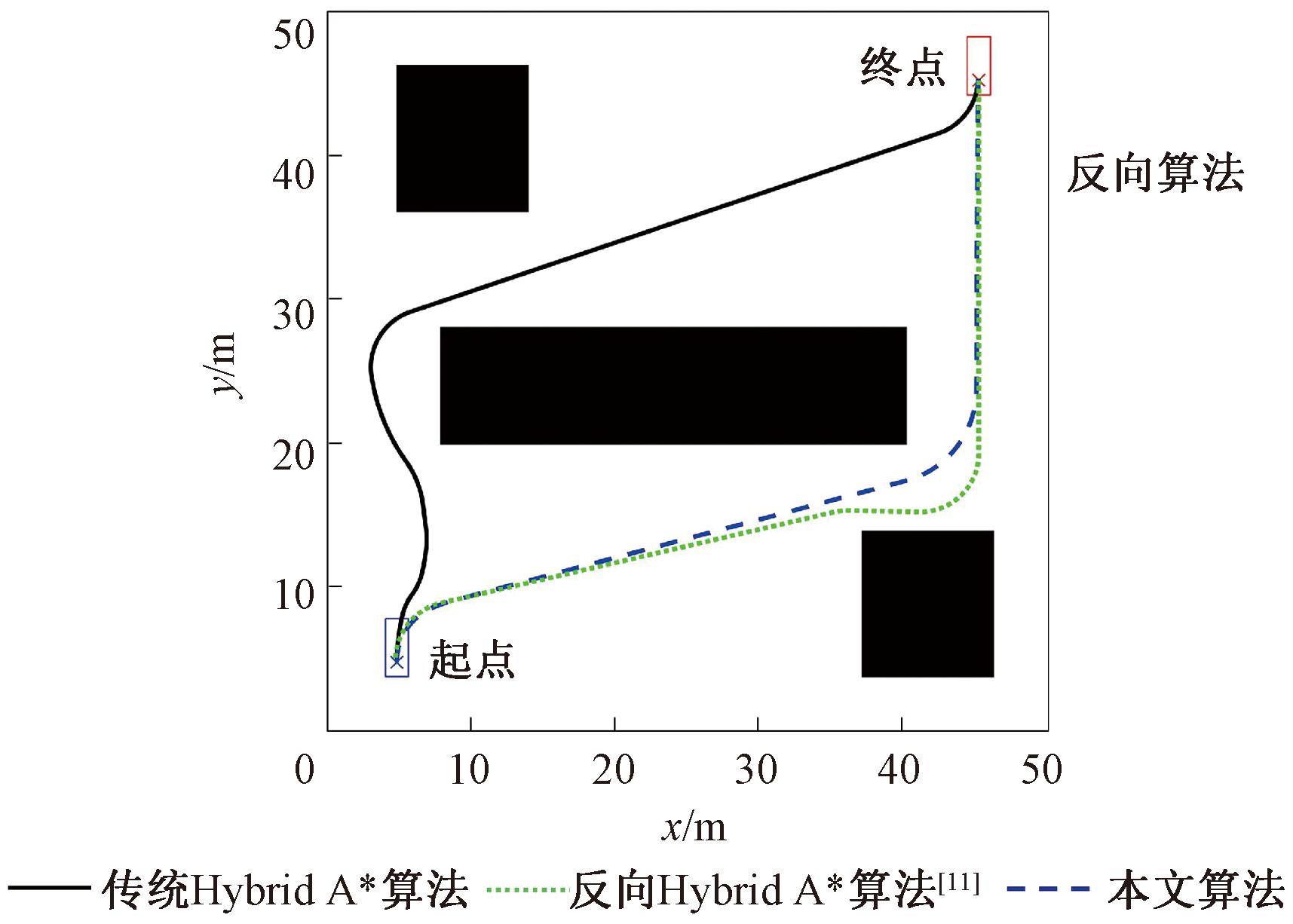
图5 简单环境下3种算法规划结果
Figure 5 Simple environment planning results for three algorithms
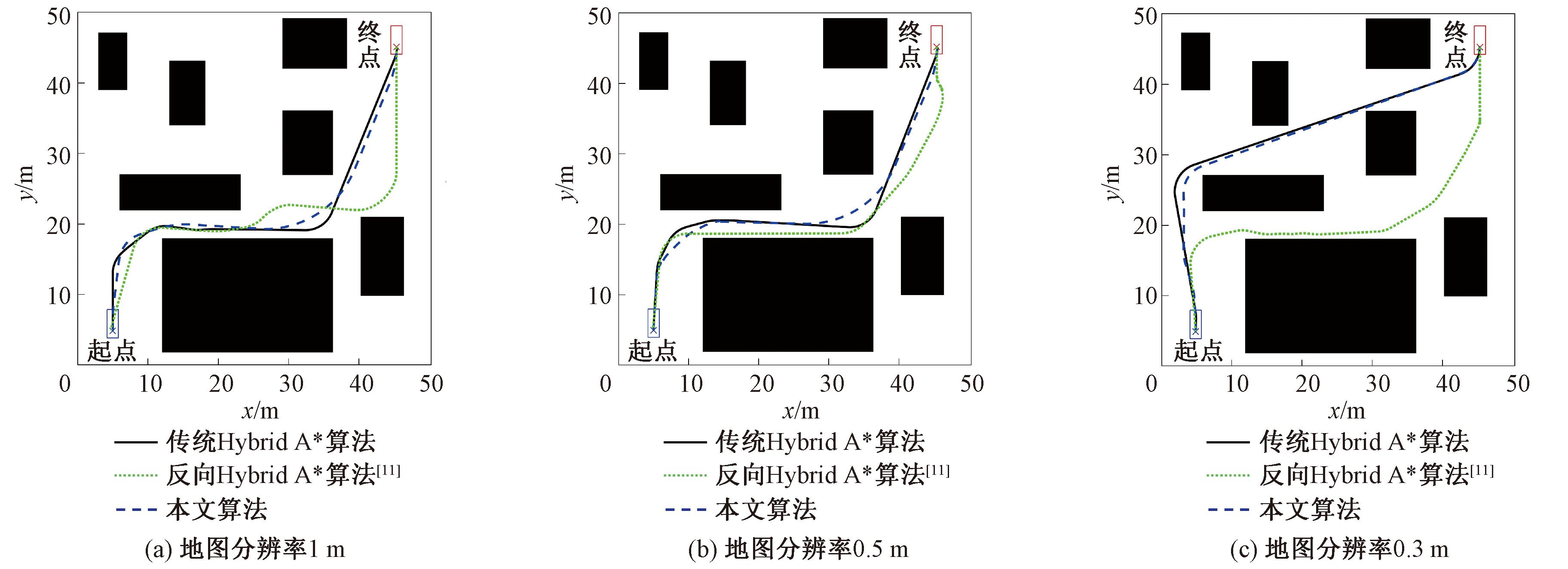
图6 复杂环境下3种算法不同地图分辨率下的规划结果
Figure 6 Complex environment planning results of three algorithms at different map resolutions
表2为3种算法在图5、图6(a)所示的简单、复杂环境中,地图分辨率为1 m时的搜索结果。从表2中可以看出,在简单环境下本文算法分别比传统Hybrid A*算法、反向Hybrid A*算法[11]搜索路径耗时减少了68%、21%,路径长度分别缩短了1%、3%。在复杂环境中,本文算法分别比传统Hybrid A*算法、反向Hybrid A*算法[11]搜索路径耗时减少了59%、27%,路径长度分别缩短了2%、7%。结果表明,在相同地图分辨率的情况下,不论简单环境还是复杂环境,本文所提J-Hybrid A*算法相较于其他两种算法都大幅度减少了搜索时间,在路径长度方面,相较于其他两种算法有小幅提升。
表2 简单环境和复杂环境下3种算法路径规划结果
Table 2 Results of three algorithms for path planning in simple and complex environments

算法简单环境复杂环境搜索节点数耗时/s路径长度/m搜索节点数耗时/s路径长度/m传统HybridA∗算法3391.4170.32571.7568.3反向HybridA∗算法[11]1990.5771.03830.9771.9本文算法2230.4568.32190.7167.2
如图6所示,地图分辨率越高,则地图进行栅格化时,划分的栅格数量也就越多,对算法效率的要求也就越高。表3为3种算法在不同地图分辨率下的规划结果。从表3可以看出,本文算法在各种分辨率的地图中搜索效率都优于其他两种算法,并随着地图分辨率的提高,效率提升明显。
表3 不同地图分辨率下3种算法规划结果
Table 3 Results of three algorithms for path planning at different map resolutions
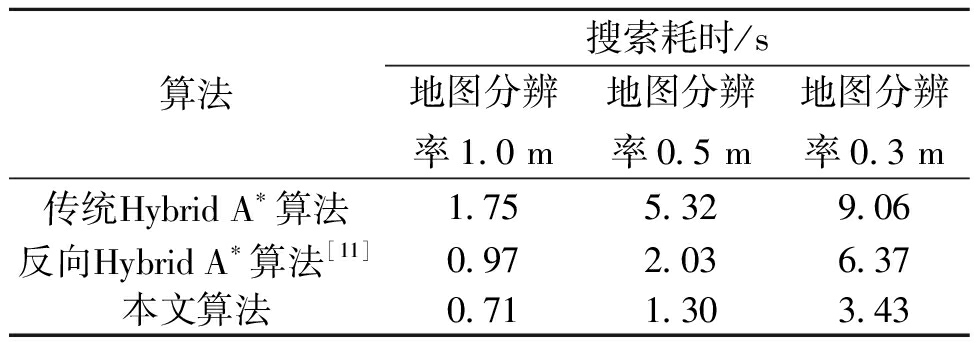
算法搜索耗时/s地图分辨率1.0 m地图分辨率0.5 m地图分辨率0.3 m传统HybridA∗算法1.755.329.06反向HybridA∗算法[11]0.972.036.37本文算法0.711.303.43
3 实车实验
为进一步验证所提J-Hybrid A*算法的有效性,使用由思岚A2激光雷达、树莓派4B、STM32F407及阿克曼小车底盘组建的ROS小车,如图7所示,进行实验验证。车辆长度0.30 m,宽度0.18 m,轴距0.20 m,前轮最大转角30°。通过在树莓派中部署ROS开源move_base导航功能包[24],完成传感器数据处理、车辆定位、路径规划等上层工作,在STM32中完成电机控制、舵机控制等下层工作,树莓派和STM32通过串口进行通信。将传统Hybrid A*算法、反向Hybrid A*算法[11]、本文算法以ROS plugin插件的形式加载到move_base框架中,替换原有Dijkstra算法进行实验。实验环境为学生实验室,如图8所示,实验室内部长15 m、宽8 m,室内摆放有桌子、凳子、电脑主机、纸箱等。

图7 自主搭建的ROS小车
Figure 7 Self-manufactured ROS car

图8 实验环境
Figure 8 Experimental environment
真实环境下3种算法实验结果如图9所示,其中栅格数量为584×584个,地图分辨率为0.05 m,小车模型为车辆起点位姿,箭头为车辆终点位姿。从图9中可以看出,3种算法都能找到一条符合车辆运动学的无碰撞路径。在搜索耗时上,传统Hybrid A*算法耗时10.68 s,反向Hybrid A*算法[11]耗时7.02 s,本文算法耗时1.21 s,改进后的算法相较于传统Hybrid A*算法效率提升了88%,相较于反向Hybrid A*算法效率提升了82%。Hybrid A*算法为启发式算法,传统Hybrid A*算法和反向Hybrid A*算法通过不断调用A*算法计算节点的启发值,占用了大量的搜索时间,而本文算法只需调用一次JPS算法就能完成启发值的计算,同时对本文算法RS曲线进行了改进,使搜索效率得到了显著提升。
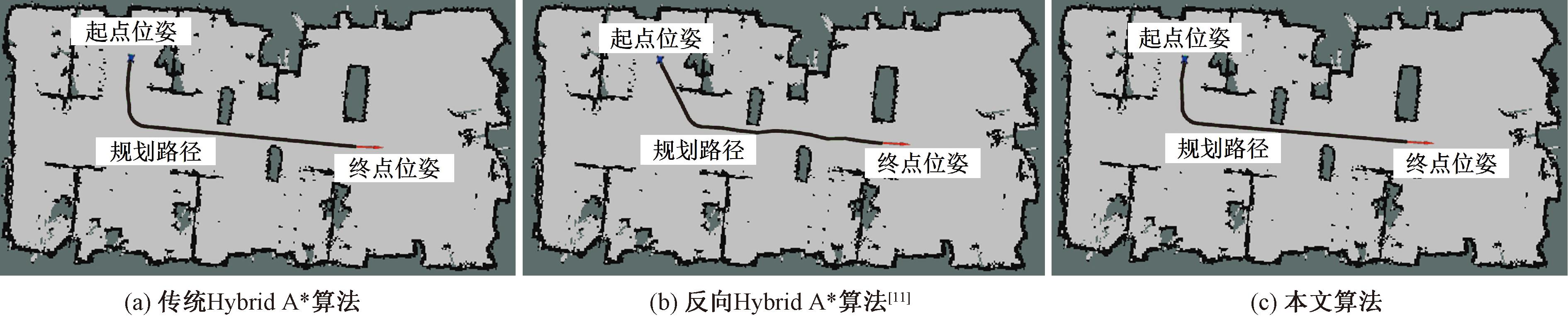
图9 真实环境下3种算法实验结果
Figure 9 Experimental results of three algorithms in a real-world environment
实车实验对本文算法在真实环境中的有效性进行了验证。结果表明,无论在本文设置的仿真环境还是在实验室真实环境中,所提J-Hybrid A*算法均能有效提升Hybrid A*算法的搜索效率,缩短路径规划所需时间。
4 结论
本文针对Hybrid A*算法规划效率低的问题,从启发函数和RS曲线两个方面对Hybrid A*算法进行了改进,提出了J-Hybrid A*算法。通过引入JPS算法、对JPS路径拉直、设计新启发函数等方法,缩短了算法计算节点启发值所用的时间。通过将RS曲线改为变半径RS曲线,使算法能够更早获得一条无碰撞的RS路径,进一步提升了算法的搜索效率。仿真实验表明,在简单环境中,J-Hybrid A*算法分别比传统Hybrid A*算法、反向Hybrid A*算法搜索用时减少68%、21%,在复杂环境中,J-Hybrid A*算法分别比传统Hybrid A*算法、反向Hybrid A*算法搜索用时减少59%、27%。ROS小车实车实验结果表明,改进后的算法分别比传统Hybrid A*算法和反向Hybrid A*算法用时减少88%、82%,进一步验证了本文所提算法的可行性和优越性。
[1] 龙邱天. 无人驾驶车辆非结构化道路检测方法研究[D]. 沈阳: 沈阳理工大学, 2023.LONG Q T. Research on unstructured road detection method for unmanned vehicles[D]. Shenyang: Shen-yang Ligong University, 2023.
[2] AKRAM M, HABIB A, ALCANTUD J C R. An optimization study based on Dijkstra algorithm for a network with trapezoidal picture fuzzy numbers[J]. Neural Computing and Applications, 2021, 33(4): 1329-1342.
[3] TANG G, TANG C Q, CLARAMUNT C, et al. Geometric A-star algorithm: an improved A-star algorithm for AGV path planning in a port environment[J]. IEEE Access, 2021, 9: 59196-59210.
[4] 陈江义, 殷笑勇, 王婷婷, 等. 基于改进斥力模型的人工势场局部路径规划[J]. 郑州大学学报(工学版), 2023, 44(3): 83-87, 101.CHEN J Y, YIN X Y, WANG T T, et al. Local path planning of artificial potential field based on improved repulsive model[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(3): 83-87, 101.
[5] YE L, WU F Y, ZOU X J, et al. Path planning for mobile robots in unstructured orchard environments: an improved kinematically constrained bi-directional RRT approach[J]. Computers and Electronics in Agriculture, 2023, 215: 108453.
[6] MIAO C W, CHEN G Z, YAN C L, et al. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm[J]. Computers &Industrial Engineering, 2021, 156: 107230.
[7] DOLGOV D, THRUN S, MONTEMERLO M, et al. Practical search techniques in path planning for autonomous driving[C]∥Proceedings of the AAAI Conference on Artifical Intelligence. Wasington DC: AAAI, 2008: 32-37.
[8] 崔高健, 陆柏霖, 贺红春, 等. 基于逆向Hybrid A*算法的自动泊车路径规划[J]. 长春工业大学学报, 2022, 43(4/5): 627-633.CUI G J, LU B L, HE H C, et al. Automatic parking path planning based on reverse Hybrid A*[J]. Journal of Changchun University of Technology, 2022, 43(4/5): 627-633.
[9] 陈翔翔.基于Hybrid A*算法的自动泊车路径规划与跟踪控制研究[D].西安:长安大学,2022.CHEN X X. Research on Hybrid A* algorithm path planning and tracking control for automatic parking[D]. Xi’an:Chang’an University, 2022.
[10] 张会丽,钱徽,陈武斌,等.基于连续状态空间的启发式路径规划算法[J]. 华中科技大学学报(自然科学版),2011,39(增刊2): 374-377,381.ZHANG H L, QIAN H, CHEN W B, et al. Heuristic path planning algorithm in continuous state spaces[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2011, 39(S2): 374-377,381.
[11] 曹彦博, 颜京才, 李旭升, 等. 基于改进混合A*算法的自动泊车系统路径搜索方法[J]. 汽车技术, 2023(6): 37-41.CAO Y B, YAN J C, LI X S, et al. A method of path search for automatic parking system based on improved Hybrid A* algorithm[J]. Automobile Technology, 2023(6): 37-41.
[12] 秦东晨, 张文灿, 王婷婷, 等. 受限泊车通道下自动驾驶平行泊车的路径规划方法[J]. 郑州大学学报(工学版), 2024, 45(5): 1-7.QIN D C, ZHANG W C, WANG T T, et al. A path planning method for parallel parking in constrained parking channels[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(5): 1-7.
[13] 陈鑫鹏, 徐彪, 胡满江, 等. 一种基于等步长分层拓展的混合A*路径规划方法[J]. 控制与信息技术, 2021(1): 17-22, 29.CHEN X P, XU B, HU M J, et al. A Hybrid A* path planning method based on equal step hierarchical expansion[J]. Control and Information Technology, 2021(1): 17-22, 29.
[14] SEDIGHI S, NGUYEN D V, KUHNERT K D. Guided Hybrid A-star path planning algorithm for valet parking applications[C]∥2019 5th International Conference on Control, Automation and Robotics (ICCAR). Piscataway: IEEE, 2019: 570-575.
[15] 邓穆坤, 刘勇, 黄佳德, 等. 基于混合A*算法的无人驾驶矿用卡车路径优化研究[J]. 控制与信息技术, 2022(5): 60-67.DENG M K, LIU Y, HUANG J D, et al. Research on Hybrid A* based path optimization of unmanned mine truck[J]. Control and Information Technology, 2022(5): 60-67.
[16] 胡智焕, 杨子恒, 张卫东. 基于混合A*搜索和贝塞尔曲线的船舶进港和靠泊路径规划算法[J]. 中国舰船研究, 2024, 19(1): 220-229.HU Z H, YANG Z H, ZHANG W D. Path planning for auto docking of underactuated ships based on Bezier curve and Hybrid A* search algorithm[J]. Chinese Journal of Ship Research, 2024, 19(1): 220-229.
[17] BONETTI A, GUIDETTI S, SABATTINI L. Improved path planning algorithms for non-holonomic autonomous vehicles in industrial environments with narrow corridors: roadmap Hybrid A* and waypoints Hybrid A*[C]∥2023 European Conference on Mobile Robots (ECMR). Piscataway: IEEE, 2023: 1-7.
[18] TANG B J, HIROTA K, WU X D, et al. Path planning based on improved Hybrid A*Algorithm[J]. Journal of Advanced Computational Intelligence and Intelligent Informatics, 2021, 25(1): 64-72.
[19] MENG T C, YANG T H, HUANG J, et al. Improved Hybrid A-star algorithm for path planning in autonomous parking system based on multi-stage dynamic optimization[J]. International Journal of Automotive Technology, 2023, 24(2): 459-468.
[20] DANG C V, AHN H, LEE D S, et al. Improved analytic expansions in Hybrid A-star path planning for non-holonomic robots[J]. Applied Sciences, 2022, 12(12): 5999.
[21] 吴梓聪. 基于改进Hybrid A*算法的移动机器人路径规划研究[D]. 广州: 华南理工大学, 2020.WU Z C. Research on path planning of mobile robot based on improved Hybrid A* algorithm[D].Guangzhou: South China University of Technology, 2020.
[22] 邱磊, 刘辉玲, 雷建龙. 跳点搜索算法的原理解释及性能分析[J]. 新疆大学学报(自然科学版), 2016, 33(1): 80-87.QIU L, LIU H L, LEI J L. Principle explanation and performance analysis of jump point search algorithm[J]. Journal of Xinjiang University (Natural Science Edition), 2016, 33(1): 80-87.
[23] 姚智龙, 张小俊, 王金刚. 改进Bi-RRT*算法的自动泊车路径规划[J]. 机械科学与技术, 2024, 43(6): 1063-1071.YAO Z L, ZHANG X J, WANG J G. Automatic parking path planning with improved Bi-RRT* algorithm[J]. Mechanical Science and Technology for Aerospace Engineering, 2024, 43(6): 1063-1071.
[24] RAJENDRAN G, UMA V, O’BRIEN B. Unified robot task and motion planning with extended planner using ROS simulator[J]. Journal of King Saud University-Computer and Information Sciences, 2022, 34(9): 7468-7481.