随着工业自动化和智能化水平的不断提升,自动引导车(automated guided vehicle,AGV)被广泛应用于工业生产中。AGV在提高生产效率、降低劳动强度以及减少物流成本等方面发挥着至关重要的作用。在AGV应用过程中,路径规划问题尤为关键,其涉及如何在有障碍物的工作环境中为AGV设计一条从起始点到目标点的无碰撞最优路径[1]。
针对AGV路径规划问题,研究者做了大量工作。常见的路径规划算法有A*算法[2-4]、Dijkstra算法[5]、快速搜索随机树算法(RRT)[6]、蚁群算法[7]以及人工势场法[8]等。在静态环境中,A*算法作为一种经典的启发式搜索算法,由于其效率和可靠性被广泛应用于路径规划中。刘生伟等[9]提出一种改进A*算法,通过融入父节点启发函数和切比雪夫距离,优化了启发函数权值,从而在大尺寸栅格地图中显著降低了AGV路径规划的时间复杂度和节点数量,同时缩减了路径长度;余震等[10]通过引入三邻域与八邻域混合搜索策略对传统A*算法进行改进,成功提升了AGV的全局路径规划效率;Jian等[11]提出了一种全局-局部耦合两阶段的路径规划(CTSP)方法,该方法通过在全局规划阶段应用改进的A*搜索算法和在局部规划阶段引入新的成本函数,实现了对机器人动态约束的有效路径规划;Xiang等[12]提出了一种结合贪婪算法的改进A*算法用于多目标路径规划,通过改进评估函数加快收敛速度,并移除不必要节点,仅保留关键转折点进行路径规划;张辉等[13]针对无人车在结构化道路场景下的路径规划问题,提出一种改进A*算法,该算法通过利用地图预览模块提取关键节点,引入基于安全距离的碰撞场模型优化代价函数,并采用准均匀三次B样条曲线平滑路径;孔慧芳等[14]提出了一种基于启发函数改进的A*算法,通过采用加权曼哈顿距离和引入转弯修正代价参数,有效减少了AGV路径规划中的节点遍历数和转弯次数,提高了路径搜索效率和平滑性,但没有考虑转弯角度过大对AGV运行时间的影响;李强等[15]针对复杂环境下A*算法在AGV路径规划中的效率和平滑度问题,提出了一种引入象限限制和时间消耗成本的改进A*算法。
除了对A*算法的改进研究,针对其他路径规划算法在AGV路径规划中的应用,不少研究者也取得了显著进展。Chen等[16]通过划分工作区域减少碰撞概率,结合改进的蚁群优化算法(ACO)和概率路网算法(PRM)进行多AGV路径规划,提高运输效率,并设定了AGV优先级和碰撞判定标准,提供了不同碰撞类型的应对方案;Zhang等[17]提出了一种双层轨迹优化方法,通过第一层的目标区域自适应快速探索随机树算法(TAA-RRT*)进行高效路径规划,以及第二层的最优控制问题求解进行轨迹优化,以实现AGV在复杂环境中的高效和平滑轨迹规划;为解决传统遗传算法在AGV路径规划中出现的早熟收敛问题,孙波等[18]通过模拟退火法优化种群选择、改进算子策略以及精英策略,并在适应度函数中综合考虑路径曲折度、繁忙度和车辆负重度等多指标,提出了一种改进的遗传算法,使规划出的路径更符合AGV实际运行。
针对传统A*算法应用于AGV路径规划时存在规划路径中障碍物较多时易陷入局部最优解,并且规划路径存在拐点多和冗余节点过多的问题,本文通过采用优化启发函数与动态邻域调整策略相结合的方法提出改进A*算法,在启发函数中引入障碍密度函数,引导算法有效规避障碍物密集区域,并引入动态邻域搜索策略提升算法运行效率,最后通过冗余节点处理策略,减少规划路径中冗余节点,以改善路径平滑度。仿真和实验结果验证了改进算法的可行性和有效性。
1 地图环境构建
在现代物流系统中,AGV路径规划是一个复杂的问题,它不仅涉及AGV的动态行为,还需要考虑其所处的环境特征。为有效进行路径规划,必须首先对AGV工作场景进行准确建模,构建一个能够反映实际环境特征的地图模型。
图1为AGV简化模型和移动方向。图2为障碍物在栅格中的处理方式。在AGV的全局路径规划方法研究中,在已知静态环境和障碍物信息的前提下,常见的地图构建方法包括栅格法和可视图法等。本文采用栅格法进行环境建模,将AGV的移动环境划分为大小均等的栅格,栅格地图在仿真环境下绘制,仿真环境依据AGV的实际应用场景进行建模。每个栅格的尺寸根据AGV的直径设定,具体为AGV直径的1倍,以确保每个栅格能够容纳整个AGV的车身,避免路径规划中因栅格过小而导致误差,并且保证栅格大小能够准确反映AGV的实际运动需求。每个栅格都融合环境信息,其中白色栅格代表可通行区域,黑色栅格代表障碍物区域,AGV在可通行区域的栅格中心连线之间进行运动,栅格长度为1,第i个栅格位置坐标描述为(xi,yi),通过对环境的栅格地图构建将AGV复杂的连续运动转换为质点在邻近栅格之间的移动。
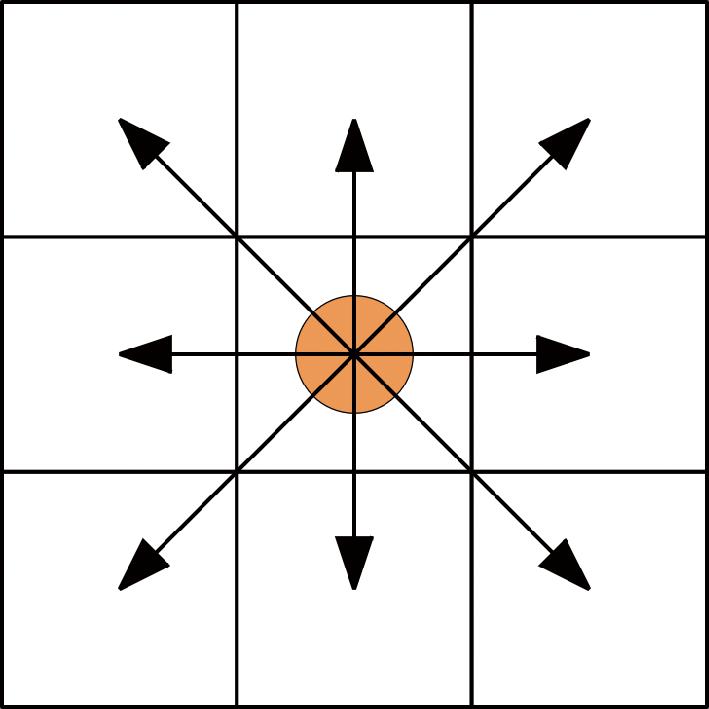
图1 AGV简化模型和移动方向
Figure 1 AGV simplified model and direction of movement
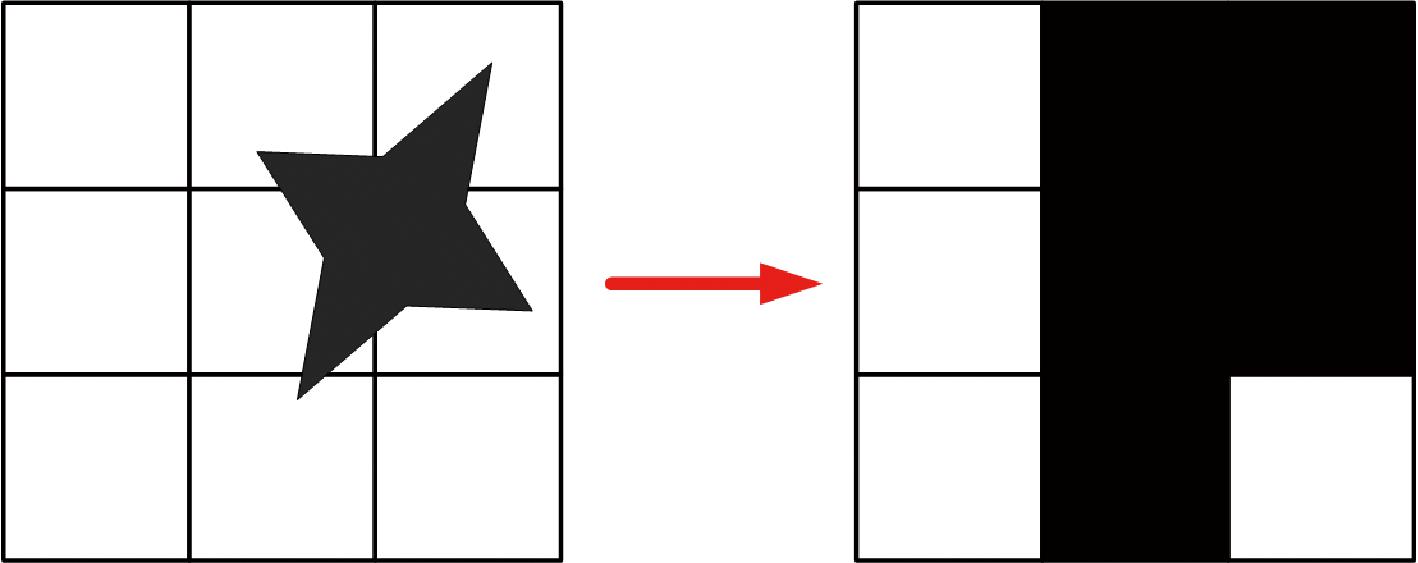
图2 障碍物简化示意图
Figure 2 Simplified schematic of obstacles
为便于开展研究和实验,本文做出以下合理假设。
(1)在进行仿真和实验阶段,将AGV的模型简化为一个圆形质点,且直径大小等于栅格边长的一半,以反映AGV的实际车身尺寸。
(2)环境中的静态障碍物位置已知,并且在AGV运动过程中,静态障碍物的状态信息恒定。
(3)AGV在栅格地图中可以分别向8个方向实现移动,如图1所示。中间圆圈所在栅格代表AGV当前位置,AGV依照箭头所指的8个方向进行移动。
(4)仿真环境对实际环境中的复杂因素进行简化建模,以便用于算法测试和性能评估,其中对于障碍物占据栅格的处理方式如图2所示[19]。
本文采用笛卡尔坐标系与索引编码的网格定位方法,各栅格均具备唯一标识及关联坐标。图3为格栅地图环境构建。如图3所示,序号从地图左下角原点起始,沿水平方向由左至右、沿垂直方向自下而上的方式进行栅格编码,坐标系横纵轴数值随右移与上移操作递增,每个栅格的坐标与其序号之间的换算关系如式(1)所示[20]:
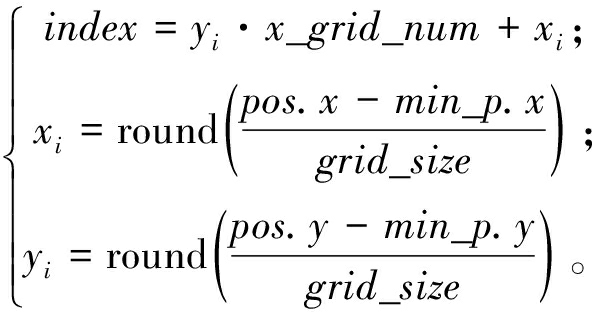
(1)
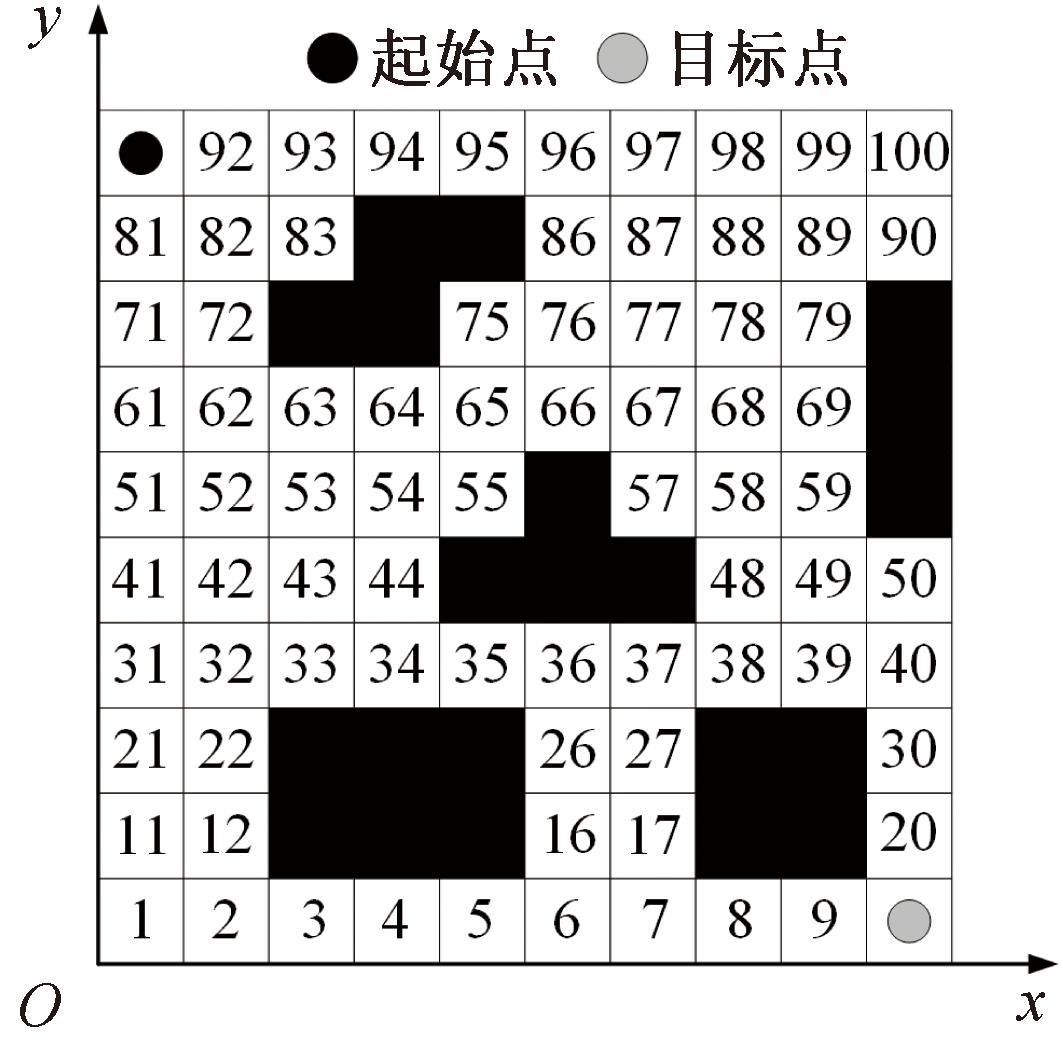
图3 栅格地图环境构建
Figure 3 Grid map environment construction
式中:index为栅格序号;xi和yi分别为栅格地图中任意栅格中心的x、y轴坐标;x_grid_num为栅格地图中x轴方向上栅格数量;pos.x和pos.y分别为实际环境中任意点的x、y轴坐标;min_p.x和min_p.y分别为实际环境中原点O的x、y轴坐标;grid_size为栅格大小;round为取整运算。
2 改进A*算法
2.1 传统A*算法
A*算法作为解决静态环境最优路径问题的直接搜索方法,广泛应用于室内机器人路径规划。该算法是在Dijkstra最短路径算法的基础上,融入广度优先搜索(BFS)策略发展而来的。作为一种启发式搜索算法,A*算法利用代价函数f(n)来评估和选择路径,以确定从起点到终点之间的最优路径解。
在A*算法中,路径寻优通过代价函数f(n)实现,该函数定义如下:
f(n)=g(n)+h(n)。
(2)
式中:f(n)为起始节点通过状态节点到达目标节点的代价估计;g(n)为真实代价函数,即从初始位置经状态转移至当前节点的真实路径累计值;h(n)为估计代价函数,即当前节点至目标节点的最优路径代价预估值,h(n)也称为启发函数。在本文中,g(n)通过欧几里得距离计算,h(n)采用曼哈顿距离进行估算。
h(n)=|xi-xG|+|yi-yG|;
(3)
(4)
式中:(xi,yi)为当前节点坐标;(xS,yS)为起始节点坐标;(xG,yG)为目标节点坐标。
在进行路径搜索时,A*搜索算法通常采用八方向邻域探索策略。该算法首先对移动机器人当前位置周围的非障碍物区域进行逐一检查,并针对每个区域计算其代价函数f(n)。通过该方式,算法能够识别出代价函数值最小区域,并将其作为下一步探索目标。整个过程会持续进行,直到成功定位到目标节点。算法流程如图4所示。由于A*算法在每一步都选择当前代价最小的节点进行扩展,因此能够确保所找到的路径在长度上为最优解。此外,如果地图中的每个栅格单元边长被定义为单位长度1,那么机器人在进行水平或垂直方向的单步移动时,其代价为1,在对角线方向上移动的代价为![]()
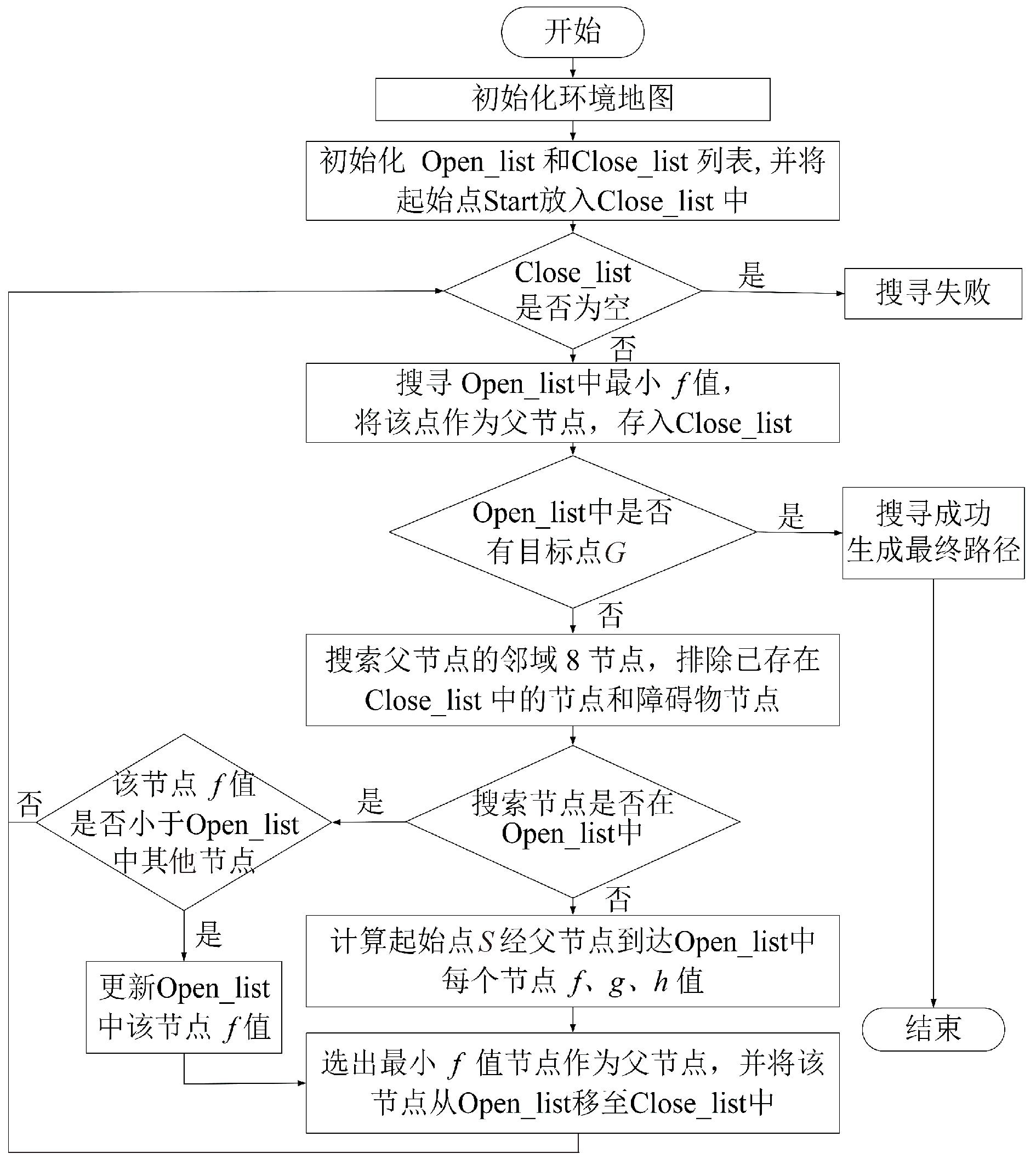
图4 A*路径搜索流程图
Figure 4 A* path search flowchart
由A*算法的基本原理可知,启发函数h(n)的选取直接决定算法的优化性能。启发函数的参数设定差异将导致路径寻优结果的显著变化。在传统A*算法中,当h(n)=0时,算法退化为Dijkstra搜索策略,虽然具备全局最优解特性,但是因遍历节点数量增加导致搜索效率显著下降;当h(n)低于真实代价时,其算法搜索域同样会出现冗余扩展,降低算法效率;若h(n)等于真实代价时,算法效率达到理论最优,即搜索域收敛效率最优与路径质量最优;而当h(n)大于真实代价时,虽然路径规划速度得以提升,但所规划路径并非最优。因此,为确保算法既能找到符合实际需求的最优路径,又能保持高效的搜索速度,选择合适的启发函数至关重要。
2.2 改进A*算法
针对AGV路径规划问题,传统A*算法在启发函数选择上需平衡最短路径与障碍物规避。为此,首先,本文提出改进A*算法,将障碍物密度函数K(n)[21]引入到启发函数h(n)优化路径选择当中,避免算法在面对障碍物数量较多时陷入局部最优解;其次,为减少引入密度函数对于算法运行效率的影响,采用动态邻域搜索策略提高算法的运行效率;最后,采用冗余节点优化处理策略降低节点数量,提升路径质量。
2.2.1 优化启发函数
传统A*算法中的启发函数h(n)并未充分考虑路径规划中障碍物分布对于路径选择的影响,随着障碍物增多,A*算法面对更多的路径选择时,会导致算法陷入局部最优解,从而显著降低搜索效率。为提高算法搜索效率,本文引入障碍物密度函数K(n),用以评估当前节点周围的障碍物分布情况,并将障碍物信息融入启发函数h(n)中,以实现算法在路径规划过程中的动态调整。选择K(n)的依据在于通过局部障碍物密度的评估,能够更快速、有效地规避路径中的局部障碍。相比于文献[21]中基于全局障碍物分布的评估方法,本文的K(n)计算相对简单,在24邻域内评估障碍物密度,不会显著增加算法的计算复杂度,且在减少搜索空间的同时,提高了算法的实时性和路径规划决策效率。
假设AGV当前节点坐标为(xi,yi),对其24邻域范围Dxiyi内进行搜索,并将该范围内的障碍物数量记为N,如图5所示。
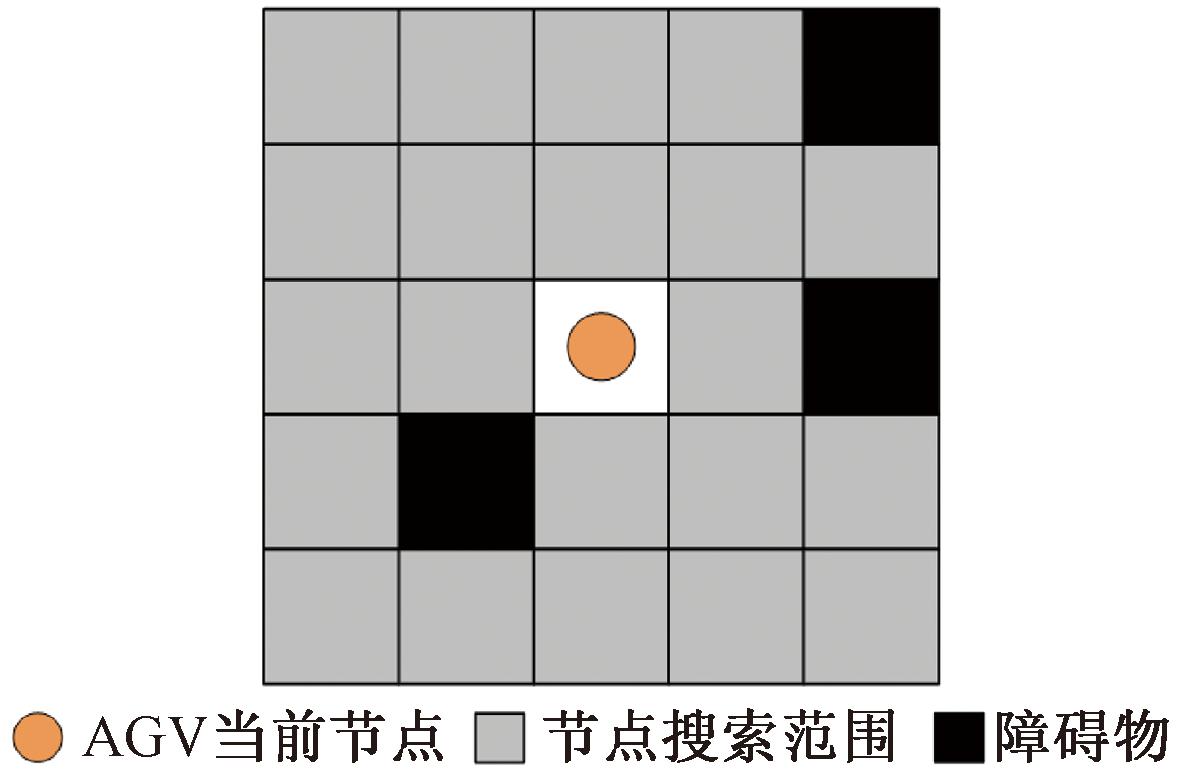
图5 障碍物密度示意图
Figure 5 Obstacle density schematic
当前节点的障碍物密度函数K(ni)可表示为
(5)
将障碍物密度函数引入到启发函数f(n)中,改变h(n)的权重,实现f(n)的自适应调整,改进后的启发函数f(n)为
(6)
改进后的启发函数在下一节点的选择上不仅考虑了直线距离,还优先评估了路径周围的环境复杂度。当节点周围障碍物密度较高时,改进后的启发函数会增加对路径的惩罚,即增加当前节点到达目标节点的预期代价,使算法更倾向于选择绕开密集障碍物区域路径,同时避免路径搜索陷入局部最优解;反之,当节点在其搜索范围内障碍物较少时,增加h(n)权重以提高搜索效率。通过改进启发函数,在确保搜索效率的同时,有效地避免选择经过密集障碍物区域路径,从而提高了路径规划的效率和准确性,启发函数改进前后对比图如图6所示。
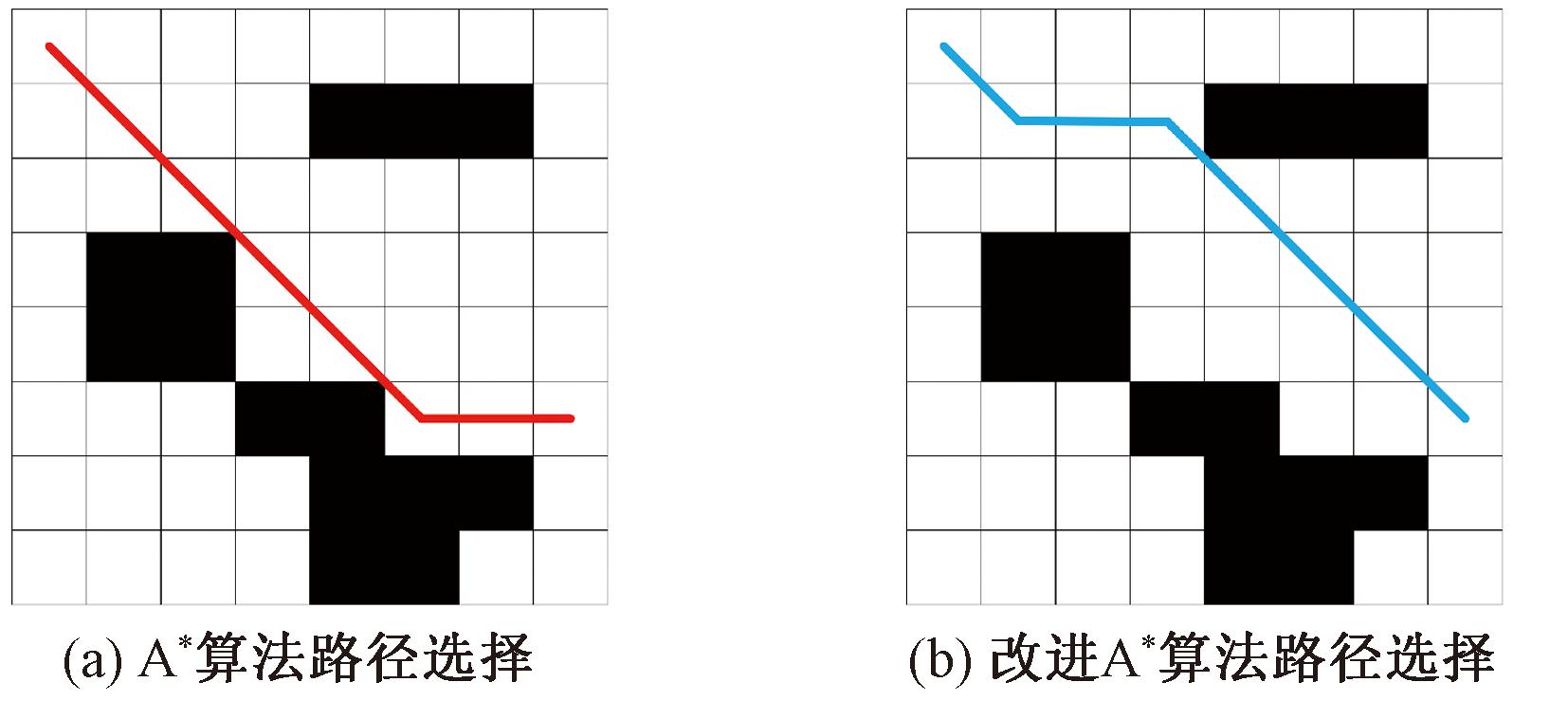
图6 启发函数改进前后对比图
Figure 6 Comparison chart before and after improvement of heuristic function
通过统计传统A*算法和优化启发函数改进算法在50×50像素和80×80像素的栅格地图中生成路径对比仿真结果如图7所示,仿真数据记录在表1中。引入K(n)的改进A*算法的障碍物数量分别平均减少了52.62%和51.11%。
表1 生成路径周围8邻域内障碍物栅格数量
Table 1 The number of obstacle grids in the 8-neighborhood area around the path
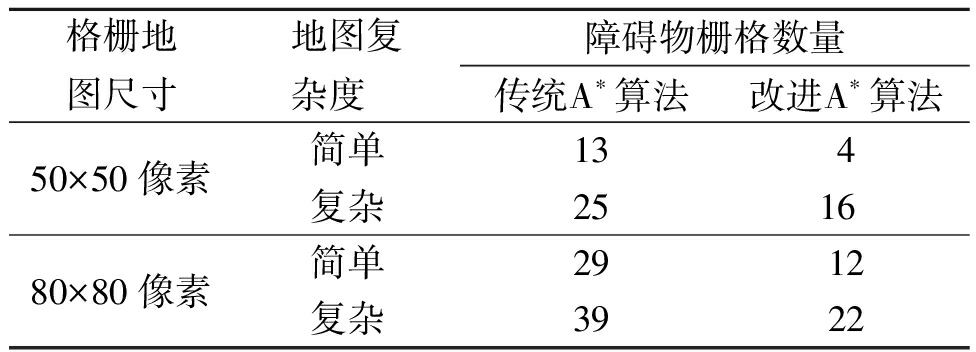
格栅地图尺寸地图复杂度 障碍物栅格数量传统A∗算法改进A∗算法50×50像素简单134复杂251680×80像素简单2912复杂3922
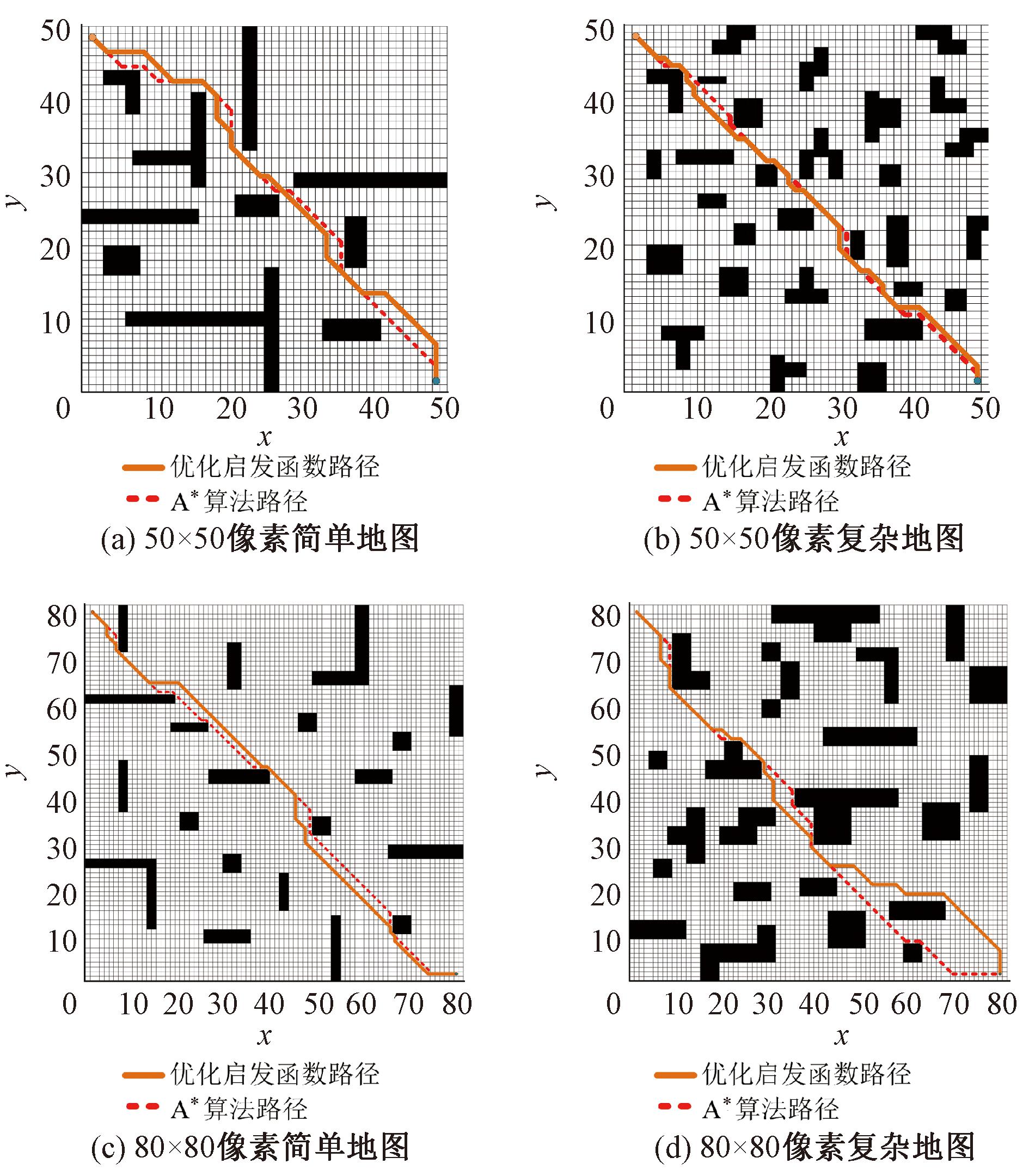
图7 优化启发函数路径和A*算法路径对比结果
Figure 7 Optimization heuristic function path and A* algorithm path comparison results
2.2.2 动态邻域搜索策略
采用上述改进启发函数的A*算法在路径选择上可以有效规避障碍物密集区域。然而,这种方法相较于传统A*算法在每个节点上的搜索范围扩大,节点融入信息更多,导致算法搜索时间增多和运行效率降低。针对上述问题,本文引入一种动态邻域搜索策略,该策略利用障碍物密度函数K(n)来动态调整邻域搜索范围。本文设定密度阈值为1/3,当节点K(n)值低于预设的密度阈值时,算法通过增加至16邻域搜索范围以加快搜索速度;当K(n)值等于或大于设定密度阈值时,算法则采用传统8邻域搜索范围以确保搜索精度。图8为8邻域和16邻域搜索示意图。
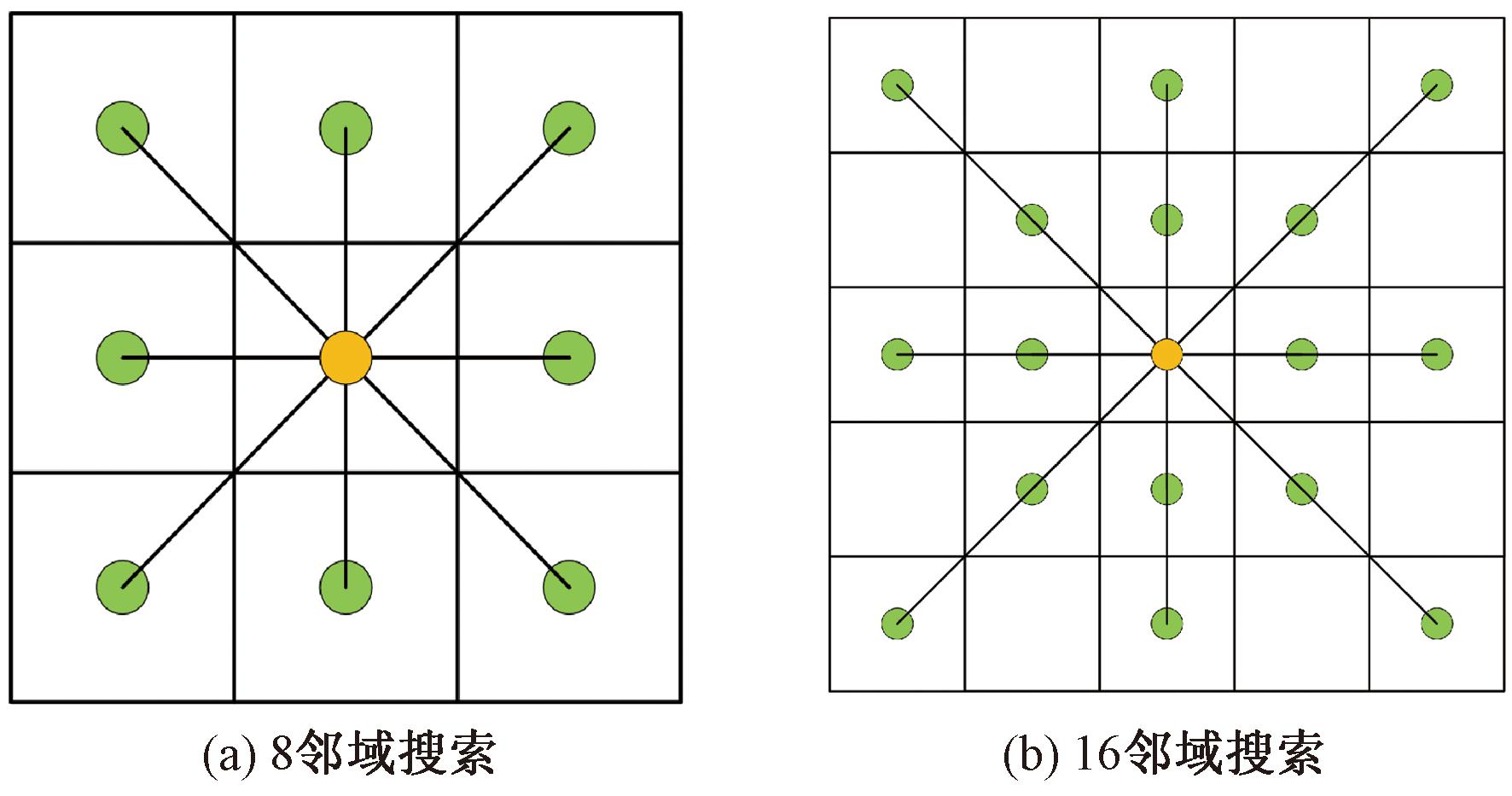
图8 两种搜索方式示意图
Figure 8 Schematic diagram of two search methods
当采用16邻域搜索方式时,算法搜索规则:第一级搜索范围为8个节点,第二级搜索视野在原有邻域基础上按照AGV移动方向再扩展8个节点。算法在搜索时可直接访问两级搜索节点,并在连接2级节点时判断当前节点与2级节点的连线间是否有障碍物,若没有障碍物则连接2级节点,否则连接其1级节点。
2.2.3 冗余节点处理
采用上述改进启发函数和动态邻域搜索的A*算法在平衡路径长度和路径周围障碍物最少问题上有显著提升,但是也会带来AGV运动过程中局部路径折弯点较多的问题,在实际场景中会影响AGV的运动平稳性。因此,本文提出一种冗余节点处理方法,以优化改进A*算法的路径规划结果,节点处理算法如下。
算法1 冗余节点处理算法。
输入:A*算法生成的路径节点集合Path={G,node1,node2,…,node7,S};
输出:优化后的路径节点集合Path。
① 初始化路径节点集合;
Path={G,node1,node2,…,node7,S};
② 初始化集合T为空集合;
③ for i=2 to length(Path)-1 do;
④ 计算![]()
⑤ 计算![]()
⑥ 计算![]()
⑦ if z ≠ 0 then:
⑧ 将当前节点nodei加入;
⑨ end if;
⑩ end for;
 if length(T)为偶数 then:
if length(T)为偶数 then:
 取T中前两个节点,记为t={G,node2};
取T中前两个节点,记为t={G,node2};
 else;
else;
 取T中前两个节点,记为t={node2,node3};
取T中前两个节点,记为t={node2,node3};
 end if;
end if;
 while nodei to nodej无障碍物时 do:
while nodei to nodej无障碍物时 do:
 将下一个节点nodei+1加入t1;
将下一个节点nodei+1加入t1;
 if 无障碍物则删除nodei;
if 无障碍物则删除nodei;
 end while;
end while;
 t2={node3,node4};
t2={node3,node4};
 t3={node5,node6};
t3={node5,node6};
 按照同样规则更新t2、t3;
按照同样规则更新t2、t3;
 将更新后的t1、t2、t3组成新的集合T={t1,t2,t3};
将更新后的t1、t2、t3组成新的集合T={t1,t2,t3};
 重复以上步骤,得到最终优化路径;
重复以上步骤,得到最终优化路径;
 return Path。
return Path。
路径冗余节点处理结果如图9所示。由图9可知,优化后的路径在折弯点数量、折弯角度和路径长度方面均显著改善,相较未优化路径,改进效果显著。
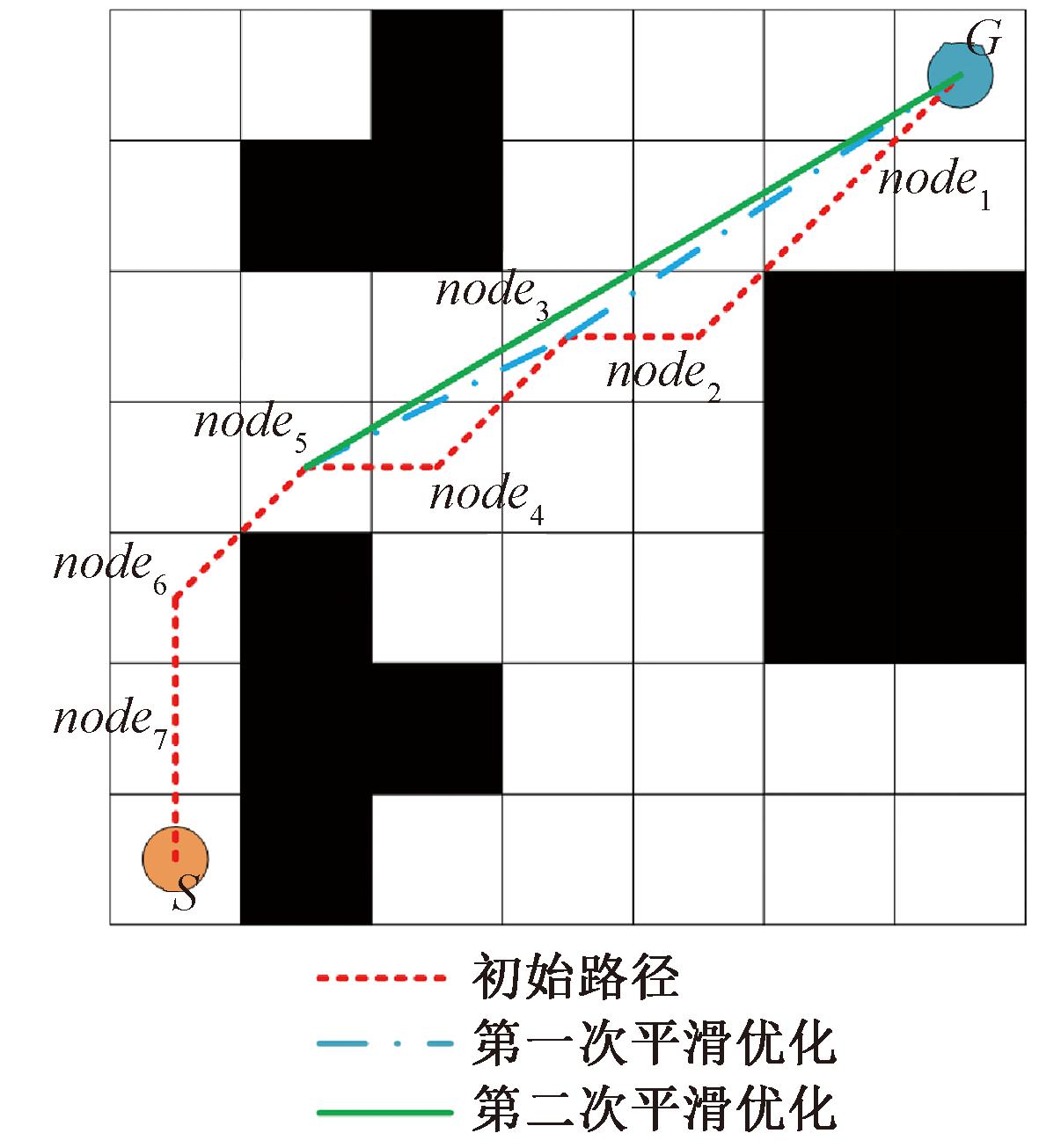
图9 冗余节点处理前后对比
Figure 9 Before and after redundant node processing
3 仿真与分析
为了有效验证本文所提出的改进A*算法在AGV路径规划中的可行性,将其与传统A*算法及文献[9]中改进A*算法,在50×50像素和80×80像素两种不同单元规模的栅格地图中进行仿真分析。并且在上述两种不同规模的栅格地图中又根据障碍物数量,障碍物形态复杂度及分布密度等,将栅格地图划分为简单和复杂地图。在上述地图中,测试算法独立运算30次,并根据路径长度、路径拐点数量和路径节点总数作为路径综合优化性能的具体量化指标。仿真实验在配置有Windows11操作系统、搭载i5-12500H处理器(3.10 GHz主频)、16 GB运行内存的计算机上进行。
3.1 简单场景下的仿真实验
在简单场景的两种不同尺寸的地图中,传统A*算法、文献[9]改进A*算法和本文改进的A*算法的路径规划结果如图10所示,地图中左上角路径开始点为起始点,右下角路径结束点为目标点(下同),并将3种算法在两类地图中的仿真数据记录在表2中。
表2 简单场景中3种算法仿真验证数据
Table 2 Three algorithms′ simulation validation data in simple scenari
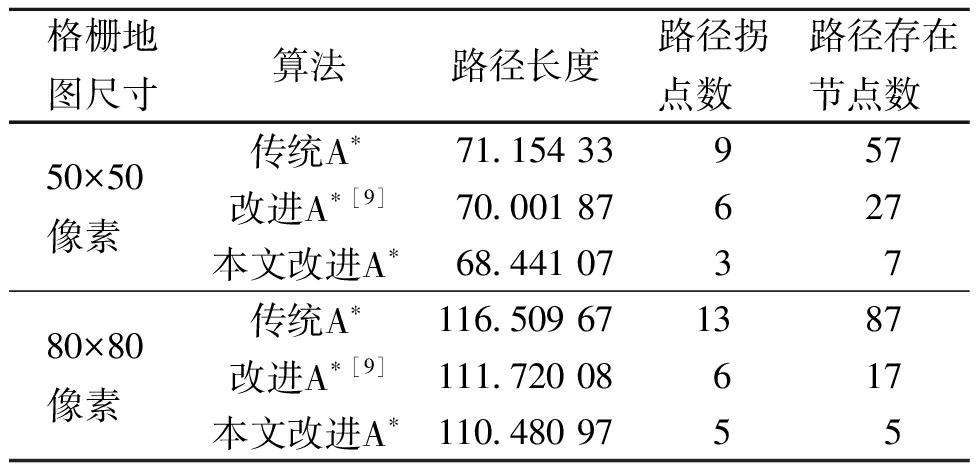
格栅地图尺寸算法路径长度路径拐点数 路径存在节点数 50×50像素传统A∗71.154 33957改进A∗[9]70.001 87627本文改进A∗68.441 073780×80像素传统A∗116.509 671387改进A∗[9]111.720 08617本文改进A∗110.480 9755
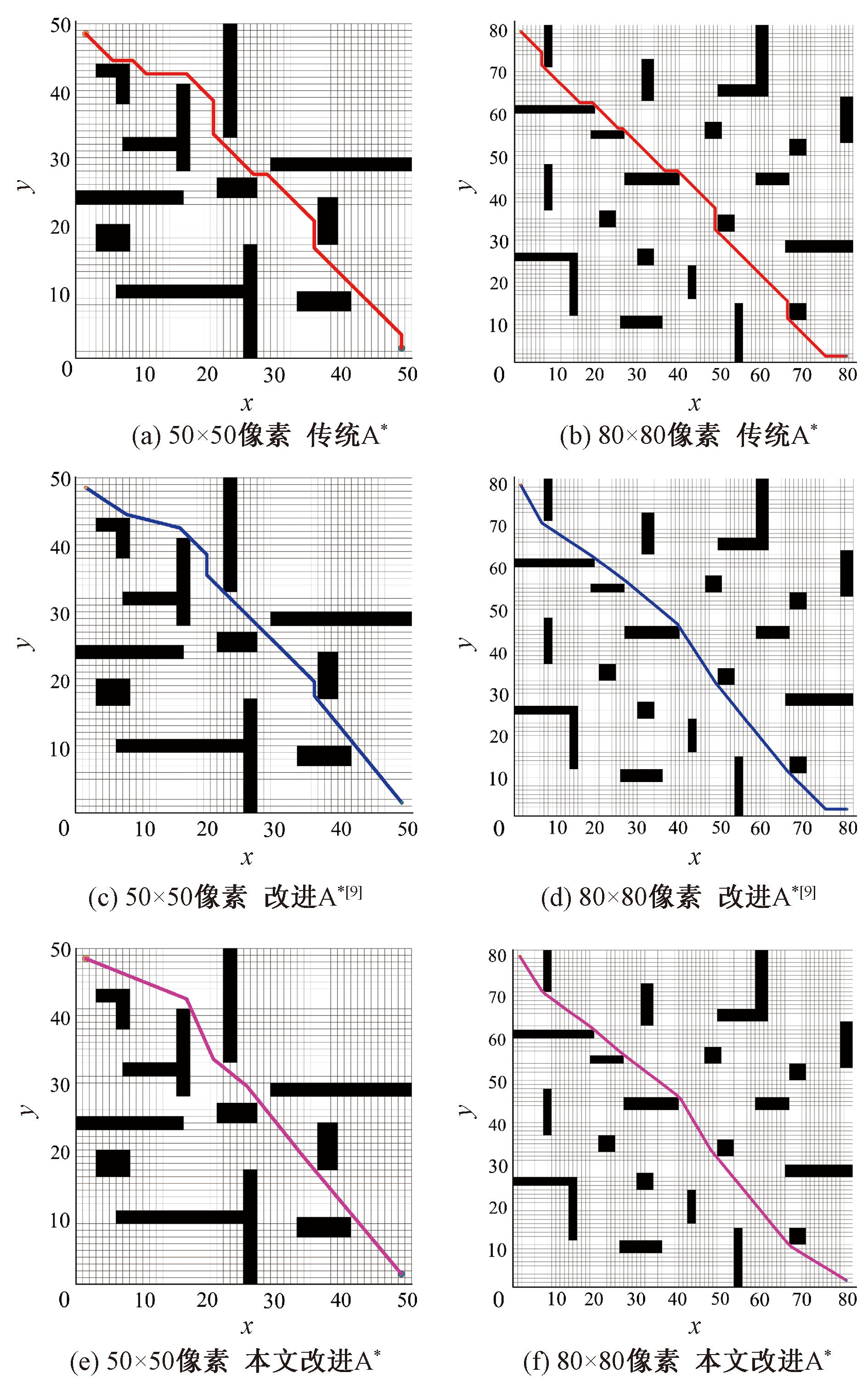
图10 简单场景中3种算法路径规划结果
Figure 10 Three algorithms′ path planning results in simple scenarios
从表2可知,在简单场景路径规划任务中,本文改进A*算法在两种不同尺寸的地图中与传统A*算法和文献[9]改进A*算法相比,在路径长度、路径拐点数和路径存在节点数上都有不同程度的优化。相比于传统A*算法,本文改进A*算法的路径长度平均减少了4.49%,路径拐点数量平均减少64.10%,在路径存在节点数方面平均减少了90.98%;与文献[9]中的改进A*算法相比,虽然在路径长度和路径拐点数量方面仅分别平均减少1.67%和33.33%,但在冗余节点的优化上,本文改进算法优势明显,路径存在节点数量平均减少72.33%,这在很大程度上降低了搜索路径所需的内存。并且,由图10中不同尺寸地图的路径规划结果可见,本文改进A*算法生成路径周围的障碍物数量较少。
3.2 复杂场景下的仿真实验
在复杂障碍物布局场景中,障碍物的形状、大小和分布具有较高的随机性和密集度,因此,在该场景下进行仿真实验更能够测试算法的避障性能。3种算法在复杂环境中的仿真路径结果如图11所示,表3为相关仿真结果的数据。
表3 复杂场景中3种算法仿真验证数据
Table 3 Three algorithms′ simulation validation data in complex scenarios
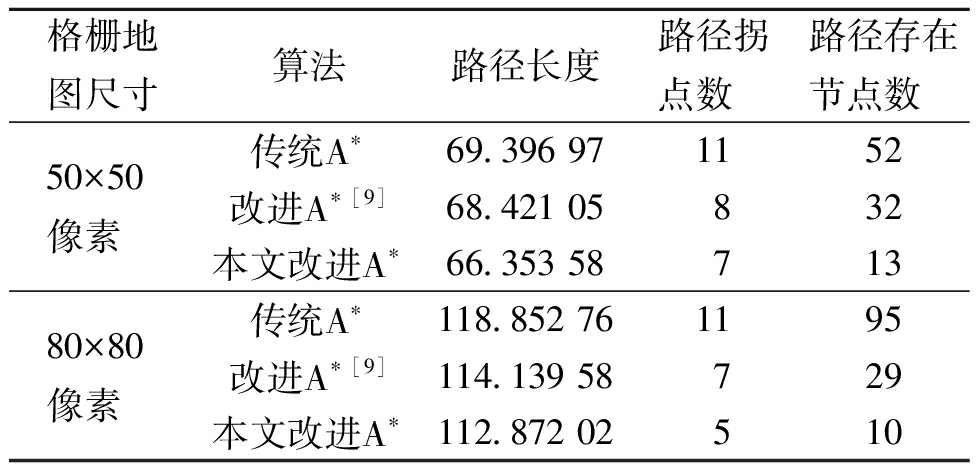
格栅地图尺寸算法路径长度路径拐点数 路径存在节点数 50×50像素传统A∗69.396 971152改进A∗[9]68.421 05832本文改进A∗66.353 5871380×80像素传统A∗118.852 761195改进A∗[9]114.139 58729本文改进A∗112.872 02510
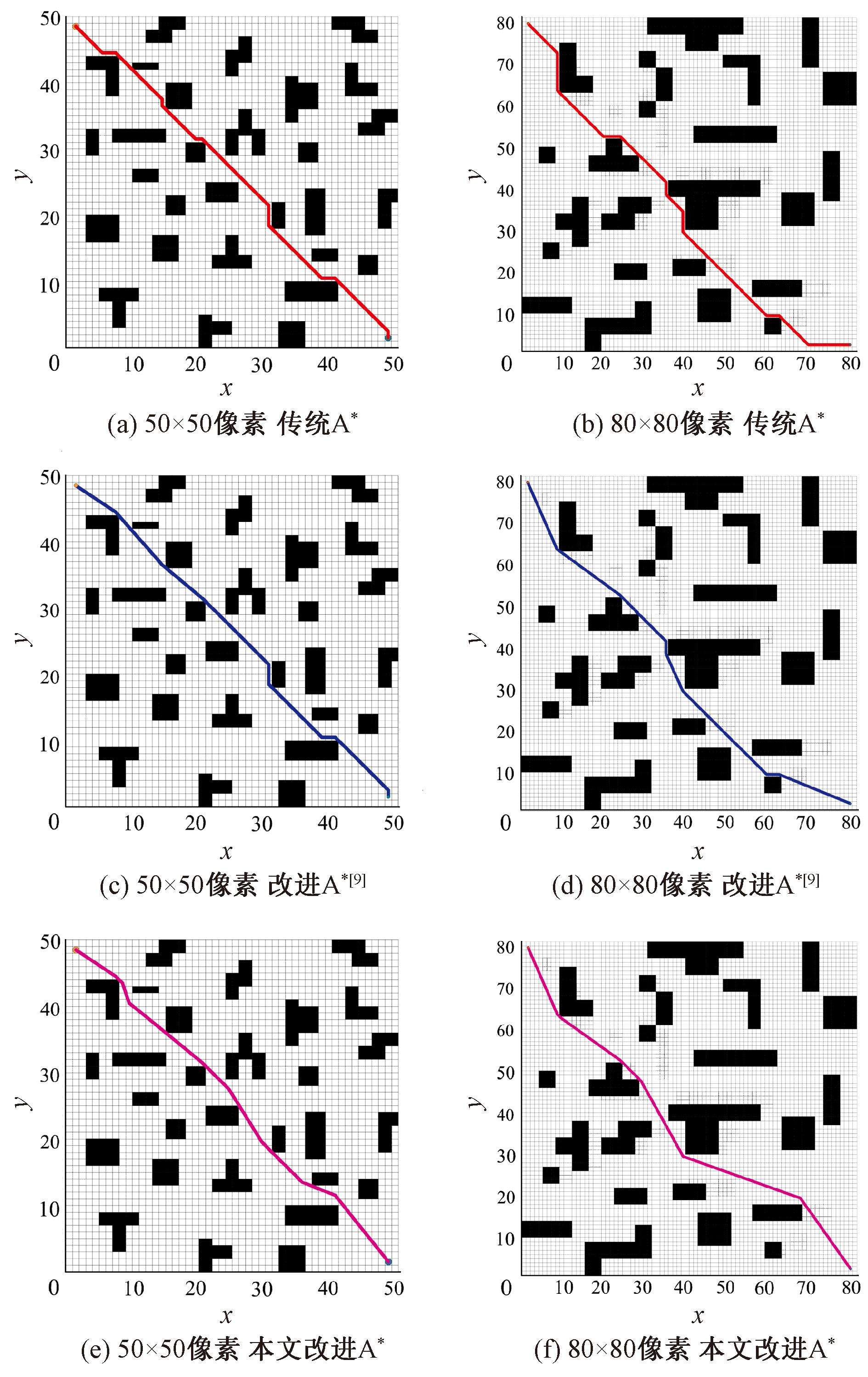
图11 复杂场景中3种算法路径规划结果
Figure 11 Three algorithms′ path planning results in complex scenarios
根据图11所示的路径规划仿真结果,在复杂场景下,传统A*算法以及文献[9]中的改进A*算法在障碍物数量增多时,所规划的全局路径并不是最优解。并且由于文献[9]中的改进A*算法仅对拐点做出优化平滑,这导致其路径优化结果并不理想。相比之下,本文提出的改进A*算法在复杂环境中,基于对路径周围障碍物分布的考虑,能够生成更优的规划路径。仿真数据表明,与传统A*算法及文献[9]中的改进A*算法相比,本文算法的路径长度平均减少4.71%和2.07%,路径拐点数量平均减少45.45%和20.54%,路径存在节点数平均减少了82.24%和62.45%。
仿真结果和数据表明,在不同尺寸的地图和障碍物复杂度条件下,本文提出的改进A*算法在路径规划中表现出显著优势。无论简单或复杂环境,相较于传统A*算法及文献[9]中的改进A*算法,本文算法均能生成更短的路径,拐点数量和冗余节点数量显著减少。这一改进不仅降低了路径搜索的内存占用,还增强了AGV在实际运行中的安全性与稳定性,进一步验证了算法在复杂环境中的适用性。
4 实验验证
为验证所提出的改进A*算法在实际应用中的效果,本文使用ROS(robot operating system)系统中的Gazebo与RViz工具进行联合仿真实验。ROS是广泛应用于机器人控制和路径规划的开放源代码系统,Gazebo提供了高保真物理仿真环境,能够模拟复杂的真实世界环境,而RViz则用于可视化机器人路径和环境感知信息。通过这两者的联合仿真,能够在仿真环境中精确测试AGV的路径性能和避障能力。
在实验中,首先使用Gazebo仿真环境构建一个包含多个障碍物的AGV工作环境和AGV简化物理模型,如图12所示,并设置AGV的初始位置和目标位置。将传统A*算法和改进的A*算法部署在ROS系统中,AGV根据路径规划避开障碍物,并实时调整运动路径。
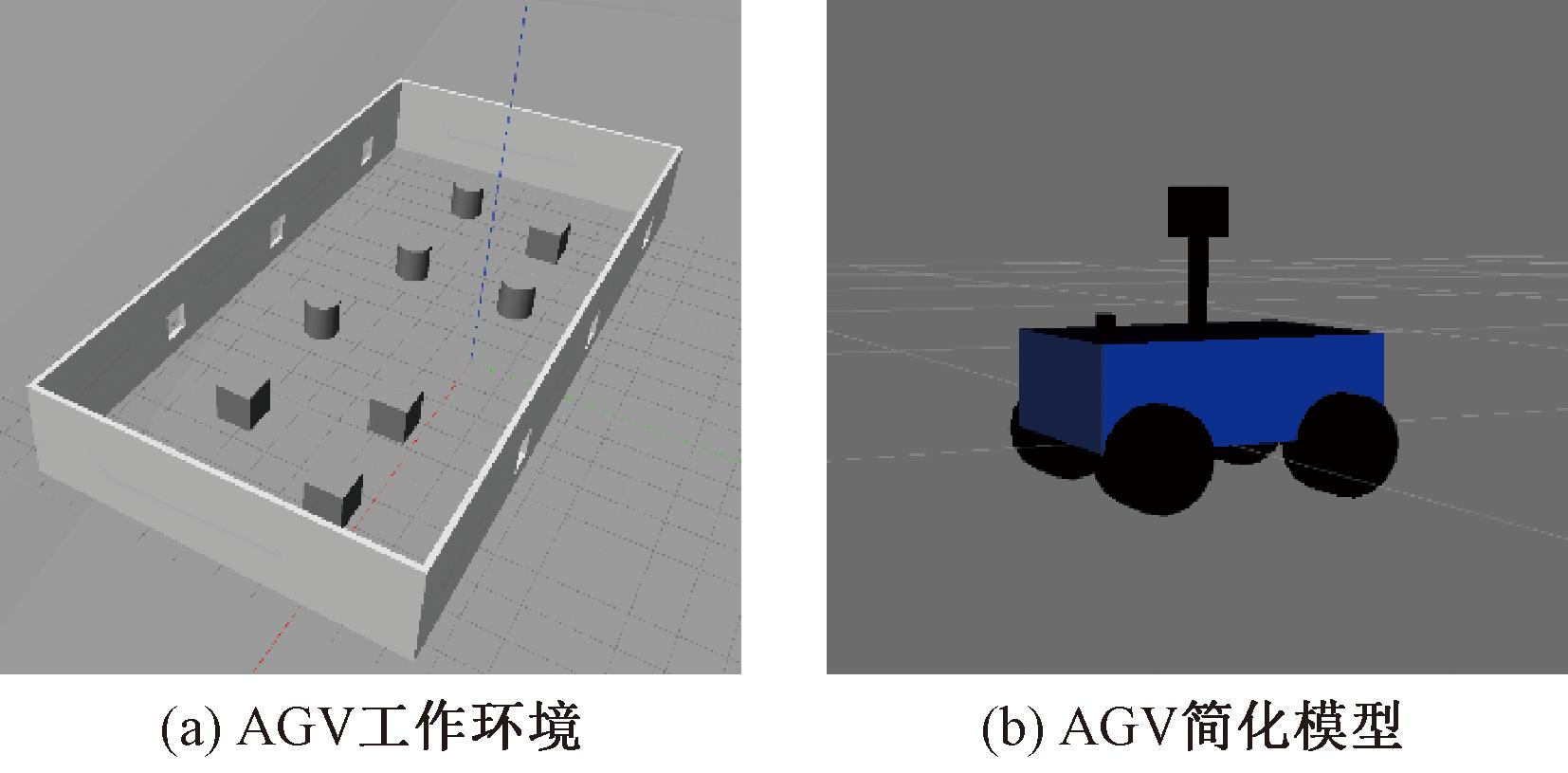
图12 物理仿真实验模型
Figure 12 Physical simulation experimental model
与传统A*算法的路径仿真对比实验结果如图13所示,实验数据见表4。相比于传统A*算法和文献[9]中的改进A*算法,本文改进的A*算法所规划的路径长度分别减少3.48%和1.60%,路径弯折次数减少了25.00%,生成路径周围的障碍物数量减少了33.33%。实验结果表明,改进后的A*算法在Gazebo仿真环境中可以有效减少路径距离、提高路径平滑度以及增强避障效果。
表4 3种算法实验路径验证数据
Table 4 Three algorithms′ experimental path validation data
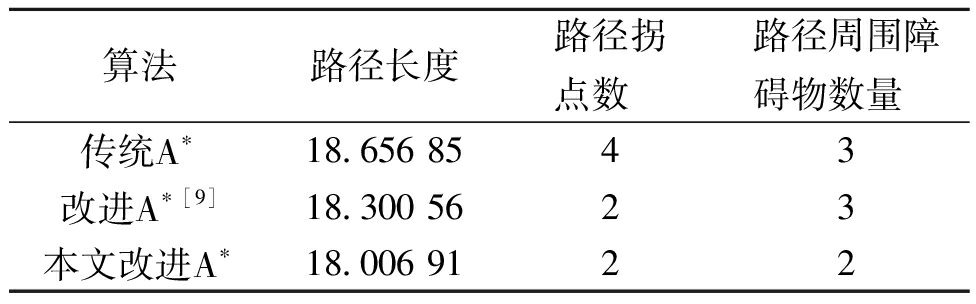
算法路径长度路径拐点数 路径周围障碍物数量 传统A∗18.656 8543改进A∗[9]18.300 5623本文改进A∗18.006 9122
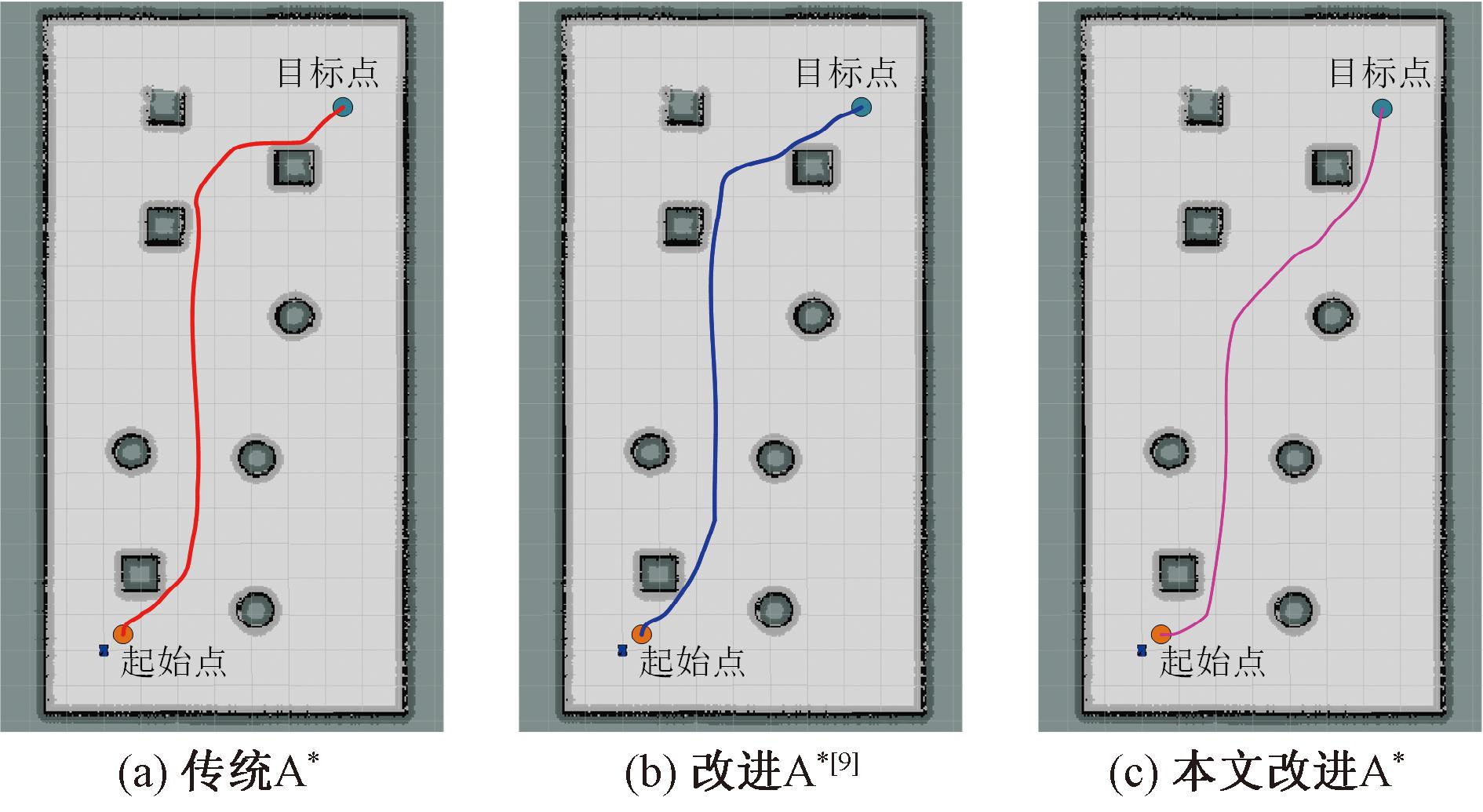
图13 3种算法路径仿真实验结果
Figure 13 Three algorithms′ path simulation experiment results
5 结论
(1)本文提出的改进A*算法通过在启发函数中引入障碍物密度函数,并结合动态邻域搜索策略和冗余节点删除策略,解决了传统A*算法在复杂环境中路径规划时易陷入局部最优解的问题。该方法不仅提升了算法搜索效率,还减少了路径中的冗余节点。
(2)在仿真实验中,改进后的A*算法在路径长度、平滑度和路径存在节点数等综合指标上均有所提升。与传统A*算法及文献中的其他改进A*算法相比,所提改进A*算法在复杂环境中的规划路径更加高效和平滑,验证了其在实际应用中的可行性。
(3)物理实验结果进一步表明,所提改进A*算法使路径长度平均缩短2.54%,路径转角次数减少25.00%,路径周围的障碍物数量减少33.33%,显著提升了路径规划的安全性和避障效果。
[1] 赵学健, 叶昊, 贾伟, 等. AGV路径规划及避障算法研究综述[J]. 小型微型计算机系统, 2024, 45(3): 529-541.ZHAO X J, YE H, JIA W, et al. Survey on AGV path planning and obstacle avoidance algorithms[J]. Journal of Chinese Computer Systems, 2024, 45(3): 529-541.
[2] 刘子豪,赵津,刘畅,等.基于改进A*算法室内移动机器人路径规划[J].计算机工程与应用, 2021, 57(2):186-190.LIU Z Y, ZHAO J, LIU C, et al. Path planning of indoor mobile robot based on improved A* algorithm[J]. Computer Engineering and Applications, 2021,57(2): 186-190.
[3] XIAO S, WU H Y, CHEN Z H. Research of mobile robot path planning based on improved A* algorithm[C]∥2020 Chinese Automation Congress (CAC). Piscataway:IEEE, 2020: 7619-7623.
[4] TANG G, TANG C Q, CLARAMUNT C, et al. Geometric A-star algorithm: an improved A-star algorithm for AGV path planning in a port environment[J]. IEEE Access, 2021, 9: 59196-59210.
[5] 姜辰凯, 李智, 盘书宝, 等. 基于改进Dijkstra算法的AGVs无碰撞路径规划[J]. 计算机科学, 2020, 47(8): 272-277.JIANG C K, LI Z, PAN S B, et al. Collision-free path planning of AGVs based on improved Dijkstra algorithm[J]. Computer Science, 2020, 47(8): 272-277.
[6] 杨炜, 谭亮, 孙雪, 等. 基于优化快速搜索随机树算法的全局路径规划[J]. 汽车技术, 2024(3): 31-36.YANG W, TAN L, SUN X, et al. The global path planning algorithm based on optimization RRT algorithm[J]. Automobile Technology, 2024(3): 31-36.
[7] 唐旭晖, 辛绍杰. 改进蚁群算法的移动机器人路径规划[J]. 计算机工程与应用, 2022, 58(5): 287-295.TANG X H, XIN S J. Improved ant colony algorithm for mobile robot path planning[J]. Computer Engineering and Applications, 2022, 58(5): 287-295.
[8] 陈江义, 殷笑勇, 王婷婷, 等. 基于改进斥力模型的人工势场局部路径规划[J]. 郑州大学学报(工学版), 2023, 44(3): 83-87, 101.CHEN J Y, YIN X Y, WANG T T, et al. Local path planning of artificial potential field based on improved repulsive model[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(3): 83-87, 101.
[9] 刘生伟, 马钺, 孟树峰, 等. 改进A*算法的AGV路径规划[J]. 计算机应用, 2019, 39(增刊2): 41-44.LIU S W, MA Y, MENG S F, et al. AGV path planning based on improved A* algorithm[J]. Journal of Computer Applications, 2019, 39(S2): 41-44.
[10] 余震,王栋,王明天,等.基于改进A*算法的AGV全局路径规划[J].武汉科技大学学报,2024,47(3):234-240.YU Z, WANG D, WANG M T, et al. Global path planning for AGV based on improved A* algorithm[J]. Journal of Wuhan University of Science and Technology,2024,47(3):234-240.
[11] JIAN Z Q, ZHANG S Y, CHEN S T, et al. A global-local coupling two-stage path planning method for mobile robots[J]. IEEE Robotics and Automation Letters, 2021, 6(3): 5349-5356.
[12] XIANG D, LIN H X, OUYANG J, et al. Combined improved A* and greedy algorithm for path planning of multi-objective mobile robot[J]. Scientific Reports, 2022, 12(1): 13273.
[13] 张辉, 张瑞亮, 许小庆, 等. 基于关键节点的改进A*无人车路径规划算法[J]. 汽车技术, 2023(3): 10-18.ZHANG H, ZHANG R L, XU X Q, et al. Key nodes-based improved A* algorithm for path planning of unmanned vehicle[J]. Automobile Technology, 2023(3): 10-18.
[14] 孔慧芳, 盛阳. 基于改进A*算法的AGV路径规划研究[J]. 现代制造工程, 2021(10): 60-64.KONG H F, SHENG Y. Research on AGV path planning based on improved A* algorithm[J]. Modern Manufacturing Engineering, 2021(10): 60-64.
[15] 李强, 于振中, 樊启高, 等. 基于改进A*算法在AGV路径规划中的应用[J]. 组合机床与自动化加工技术, 2019(5): 98-101.LI Q, YU Z Z, FAN Q G, et al. Application of improved A* algorithm for AGV path planning[J]. Modular Machine Tool &Automatic Manufacturing Technique, 2019(5): 98-101.
[16] CHEN S, ZHANG Q, HE G C, et al. Multiple-AGV path planning method for two industrial links[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2022, 36(12):2259029.
[17] ZHANG R D, CHAI R Q, CHAI S C, et al. Design and practical implementation of a high efficiency two-layer trajectory planning method for AGV[J]. IEEE Transactions on Industrial Electronics, 2024, 71(2): 1811-1822.
[18] 孙波, 姜平, 周根荣, 等. 基于改进遗传算法的AGV路径规划[J]. 计算机工程与设计, 2020, 41(2): 550-556.SUN B, JIANG P, ZHOU G R, et al. AGV optimal path planning based on improved genetic algorithm[J]. Computer Engineering and Design, 2020, 41(2): 550-556.
[19] 姚得鑫,伞红军,王雅如,等.移动机器人路径规划中A*算法的改进研究[J].系统仿真学报,2024,36(11):2684-2698.YAO D X, SAN H J, WANG Y R, et al. Research on the improvement of A* algorithm in path planning of mobile robot[J]. Journal of System Simulation,2024,36(11):2684-2698.
[20] AKKA K, KHABER F. Mobile robot path planning using an improved ant colony optimization[J]. International Journal of Advanced Robotic Systems, 2018, 15(3): 172988141877467.
[21] 刘宇庭, 郭世杰, 唐术锋, 等. 改进A*与ROA-DWA融合的机器人路径规划[J]. 浙江大学学报(工学版), 2024, 58(2): 360-369.LIU Y T, GUO S J, TANG S F, et al. Path planning based on fusion of improved A* and ROA-DWA for robot[J]. Journal of Zhejiang University (Engineering Science), 2024, 58(2): 360-369.