被动行走机器人无须复杂的控制系统,仅依赖自身重力以及内在自稳定性即可保持沿斜面向下稳定行走[1-2]。这类机构在运动中的重心转移规律以及双腿摆动轨迹与人类行走相似,其步态具有自然、高效等优点[3-5]。因此,被动行走目前已受到各领域众多学者的广泛关注,其可为双足机器人的设计及仿人行走研究提供重要的理论依据[6-7]。
被动行走理念最早由加拿大学者McGeer提出,他通过搭建直腿与带膝关节被动行走机器人,建立模型的步幅函数,研究了机器人的稳定行走步态随结构参数、斜面角度变化时的演化情况[8]。随后,Sadeghian等[9]研究了惯性、长度特性等动力学因素对被动双足机器人稳定性和倍周期级联现象的影响,分析了系统在失稳附近的能量、步幅、分岔等方面的行为;高建设等[10]研究了非平整路面环境对被动行走机器人步态演化的影响,分析了机器人步态演化过程中的分岔及混沌现象,揭示了导致机器人摔倒的双边界激变现象;彭金柱等[11]研究了并联机器人的逆运动学模型和误差模型,对引起误差的运动学参数进行了标定,并通过Adams验证了修正后逆运动学模型的准确性。目前,参数的演化对机器人行走步态的影响已被广泛研究,其中,步态吸引子的倍周期分岔已成为被动行走系统中最常见的局部分岔类型[12-13]。
然而,上述研究均将足地间的运动进行了简化,例如在点足模型中视支撑腿与地面铰接,圆弧足模型中视支撑腿与地面间的相对运动为纯滚动,即所使用的模型均忽略了由于足地接触状态的变化而发生的弹起、滑移等现象,步态切换时的足地碰撞被视为完全非弹性,且忽视足地间的摩擦。这使得上述研究结果难以全面反映机器人在实际行走环境中的步态演化。
当前,已有研究者开始尝试建立机器人的足地接触模型以探索更加真实的双足行走过程。Asano等[14]使用半圆弧足直腿模型,通过增加接触点的位置坐标实现机器人三自由度行走步态;张瑾等[15]使用圆弧足直腿模型,利用Adams软件对不同足地接触参数下的机器人行走步态进行动力学仿真;Qi等[16]通过接触刚度、阻尼和摩擦系数来表征圆弧足直腿模型的足地接触状态,探究了接触参数对行走步态的影响;郑鹏等[17]使用LuGre摩擦模型,研究了滚阻、摩擦系数改变时的行走特征演化。上述研究通过对机器人的足地接触情况进行分析,探索了接触参数中单个参数对行走步态的影响,展示了丰富的双足行走场景。但上述研究对多接触参数协同作用下的步态动力学特性研究较少,在考虑接触的情况下对机器人结构参数变化引发的步态变化缺乏进一步研究。步态变化后出现的滑动、弹跳等行为的发生扰乱了机器人的行走,使得其步态稳定性降低,此时机器人更容易跌倒[18-19],对产生这些现象的机理进行研究是解释机器人失稳行为的关键。
综上所述,本文对Qi等[16]提出的模型进行扩展,建立了含髋关节质量的圆弧足被动双足机器人。使用赫兹方程、库仑摩擦函数模拟足地接触,通过调整接触参数,对在不同路面环境下机器人步态中的滑移、弹起、摔倒等现象进行了研究。此外,探索了结构参数改变对步态演化过程的影响,分析了系统参数协同作用下的步态演化规律,并揭示了机器人的跌倒原因。本文的研究成果有助于深入理解被动行走机器人对多种路面环境的适应性,为被动行走机器人的步态变化及结构优化等方面提供了理论基础。
1 被动行走机器人建模
1.1 圆弧足被动行走机器人
本文研究的被动行走机器人模型是一种具有髋关节质量的圆弧足被动行走机器人[20],如图1所示。机器人两腿被视为完全相同的刚性直杆,质量均为m,c1与c2分别为机器人两腿的质心位置,它们到髋关节的距离为c。两腿通过光滑铰接连接在髋关节H处,并将上体质量mH集中于此关节;两足为刚性圆弧足,与腿固连,且不考虑足部质量。腿长为l,圆弧足半径为r;腿相对于质心的转动惯量为J;斜面倾角为γ;重力加速度为g。各参数取值如表1所示。
表1 系统的参数取值
Table 1 System parameter values
参 数 取 值 参 数 取 值 m/ k g 1 c / m 0 . 1 m H / k g 0 . 5 J / ( k g · m 2 ) 0 . 0 0 9 6 l / m 0 . 4 g / ( m · s - 2 ) 9 . 8 1 r/ m 0 . 0 8 γ / r a d 0 . 0 2
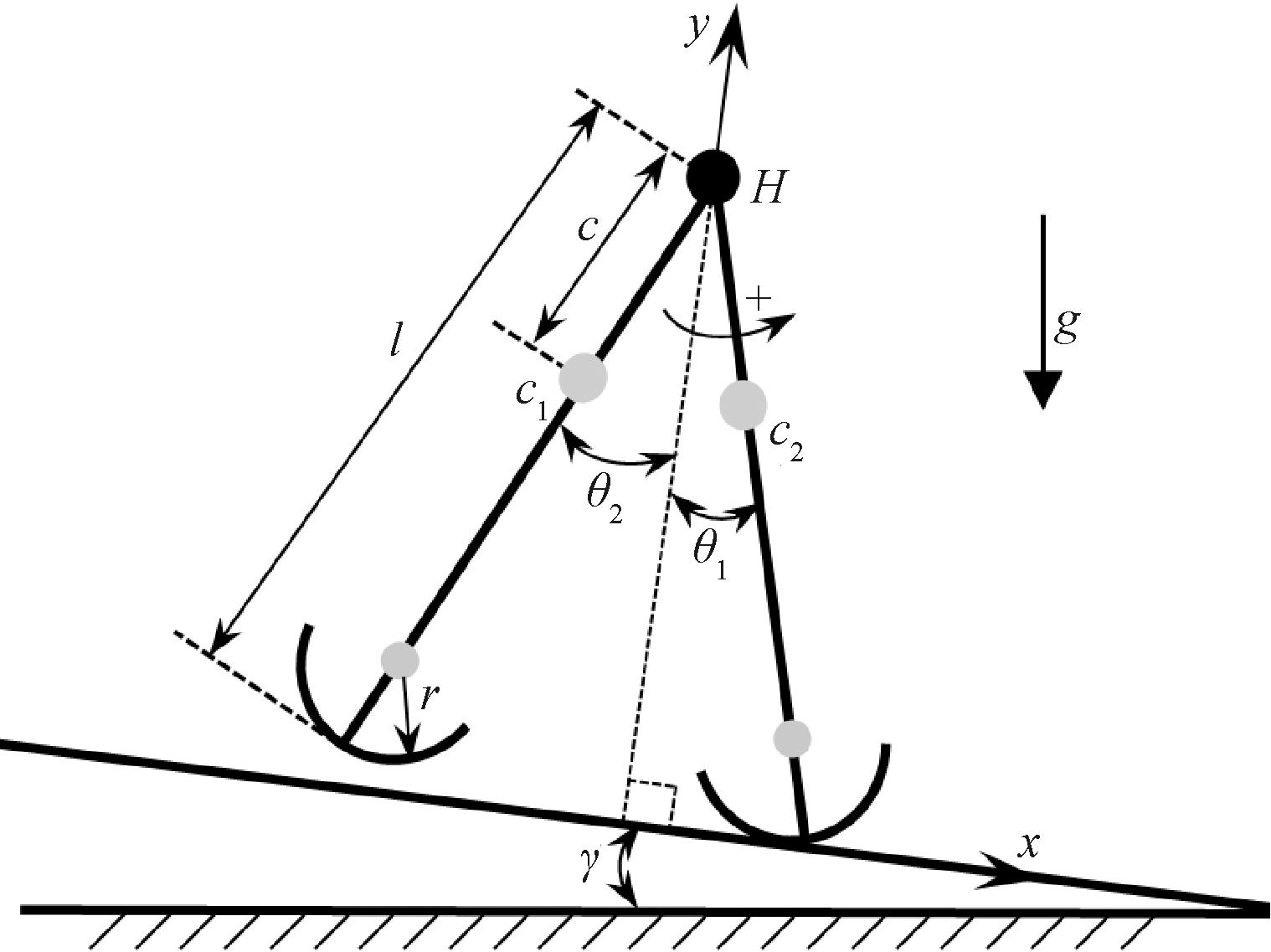
图1 被动行走机器人
Figure 1 Passive walking robot
在斜面上建立直角坐标系,x轴正方向沿斜面向下,y轴正方向垂直于斜面向上;支撑腿与y轴夹角为θ1,摆动腿与y轴夹角为θ2,均取逆时针方向为正;记髋关节坐标为(xH,yH),此时系统的广义坐标为q=(xH,yH,θ1,θ2)。
1.2 足地接触模型
引入赫兹接触模型计算法向接触力,将法向接触力Fn表示为弹性力Fc与阻尼力Fd之和[21]：
(1)
Fc=kδm;
(2)
(3)
式中:m=3/2,n=3/2,这种接触力模型适用于极弹性和极非弹性接触材料之间的情况[21];k为刚度系数,kg/(m0.5·s2);c为阻尼系数,kg/(m1.5·s);δ为两接触物体在接触点上的形变量总和,
为形变量的变化速度,m/s。在式(2)中,k取决于碰撞体的杨氏模量、泊松比、撞击处的局部表面曲率半径等,表征地面的软硬程度,数值越大,地面越坚硬。在式(3)中,c一般由实验测得,表征被动行走机器人足地接触后能量的耗散效果,数值越大,能量耗散越多。
当足与地面发生弹性碰撞时,在接触区域会产生微小形变,会有力的作用。由于足为刚性足,因此可视为在碰撞过程中只有地面发生形变。此时,将支撑腿与地面接触区域处的形变放大,如图2所示,δ为支撑腿圆弧足最低点的嵌入深度,根据几何关系,δ可表示为
δ=(l-r)cos θ1+r-yH。
(4)
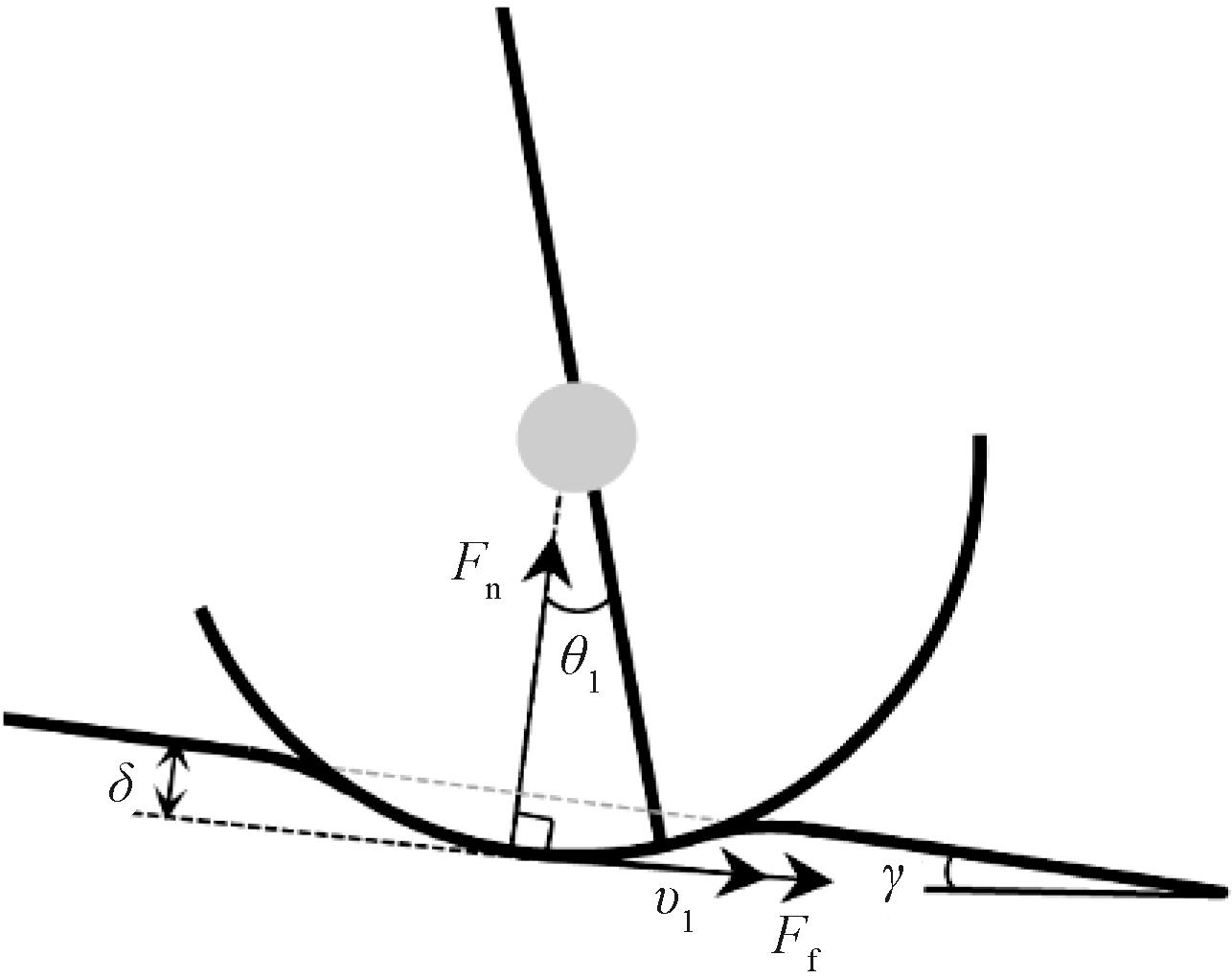
图2 接触变形区域放大图
Figure 2 Enlarged image of deformation area
根据式(4)可得圆弧足最低点与地面的切向相对速度vl为
(5)
机器人足地接触时的切向摩擦力Ff由库仑摩擦公式给出:
Ff=μFn。
(6)
式中:μ为摩擦系数;Fn为法向接触力,N。摩擦系数表征地面的粗糙程度,数值越大,地面越粗糙。在理想的库仑摩擦模型中,摩擦力在两接触物体相对静止与运动时分别被记为静摩擦力与动摩擦力,摩擦系数对应为静摩擦系数μs、动摩擦系数μd。这意味着当相对运动形式改变时,摩擦系数将发生突变,此时库仑摩擦函数曲线上存在非光滑部分,增加了计算的复杂性。为解决这一问题,常用的改进方法有拟合库仑摩擦曲线、使用LuGre摩擦模型[22]、引入线性互补问题求解[23]等,其中使用拟合库仑摩擦曲线时,无须严格限制动态摩擦参数与积分步长便可达到较高的计算精度,且计算成本低、计算过程简洁。因此,本文使用三次样条函数拟合库仑摩擦曲线[16],如图3所示,其中vs=10-4 m/s,vd=10-3 m/s。
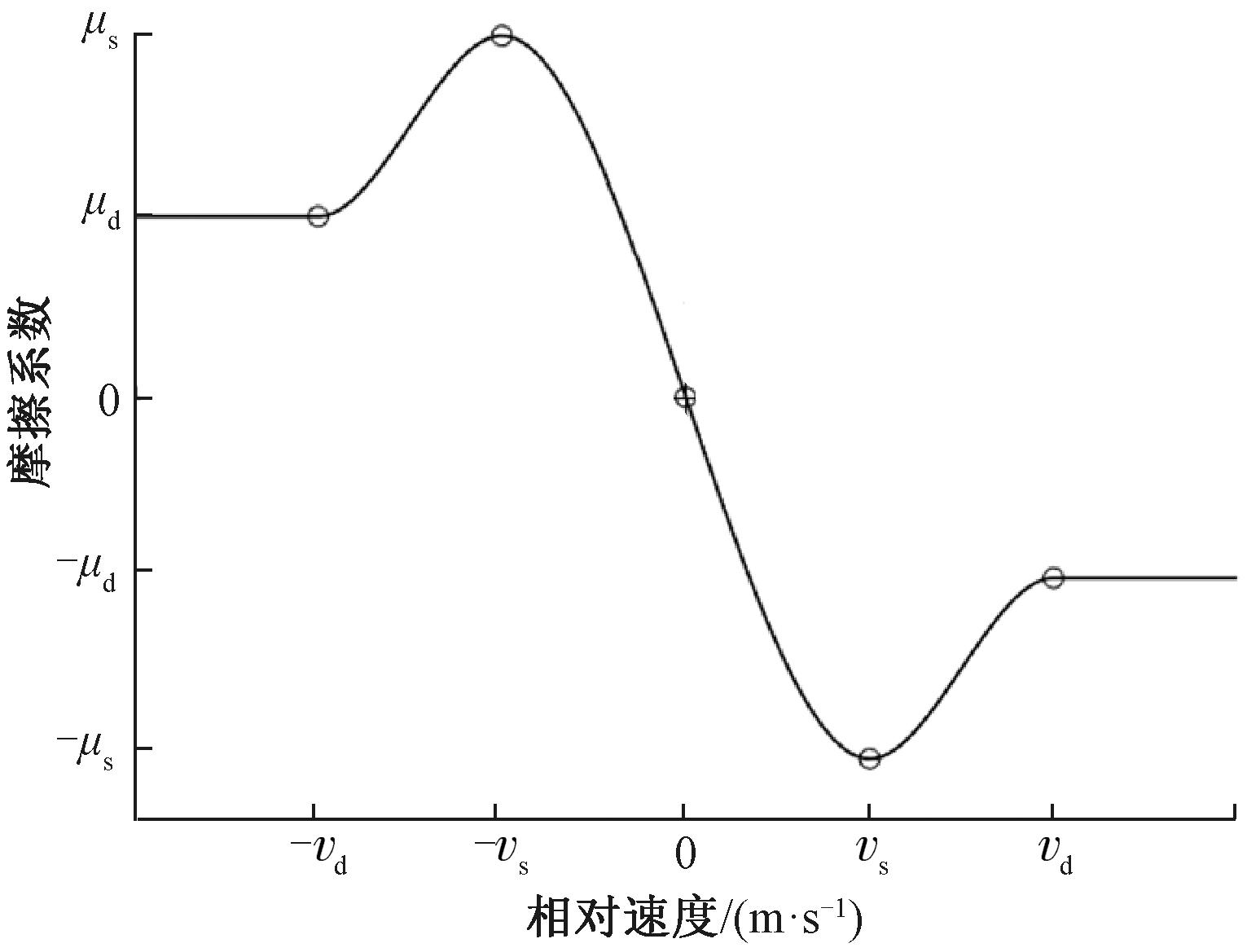
图3 库仑摩擦模型拟合曲线
Figure 3 Fitting curve of Coulomb friction model
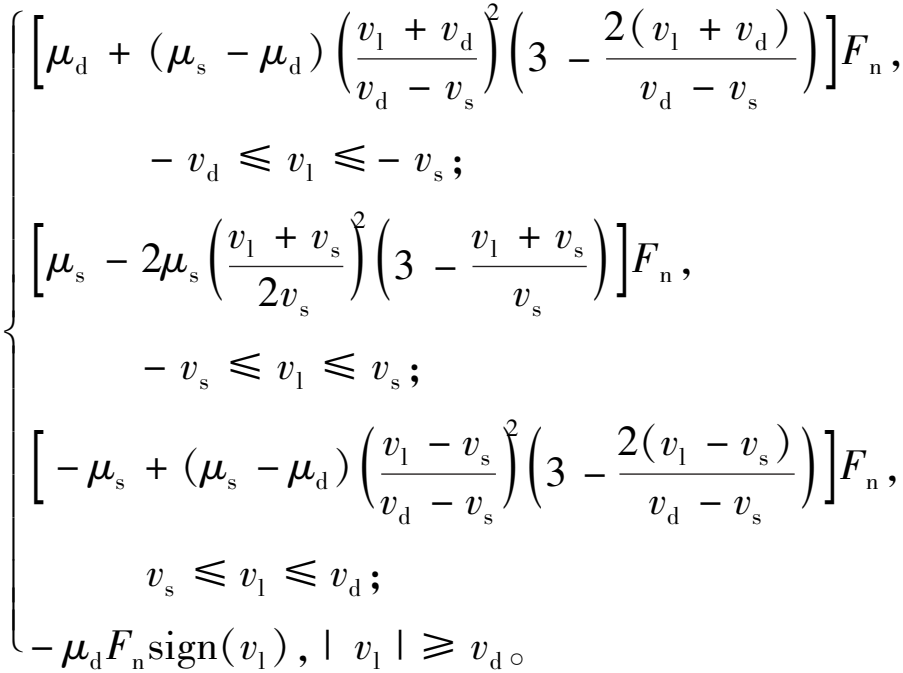
此时可对足地间相对速度较小的系统的摩擦情况进行模拟,摩擦力表达式为
Ff=
(7)
1.3 被动行走系统动力学建模
结合1.2节中式(1)和式(7)描述的接触力与摩擦力函数,本节通过第二类拉格朗日方程进一步建立被动行走机器人的动力学模型,此时机器人的运动方程为
(8)
式中:M(θ)为广义质量矩阵;
为广义加速度;
为广义惯性矩阵;QFn(θ)、QFf(θ)、Qg(θ)分别为广义支持力矩阵、广义摩擦力矩阵、广义重力矩阵。各项具体表达式如下:
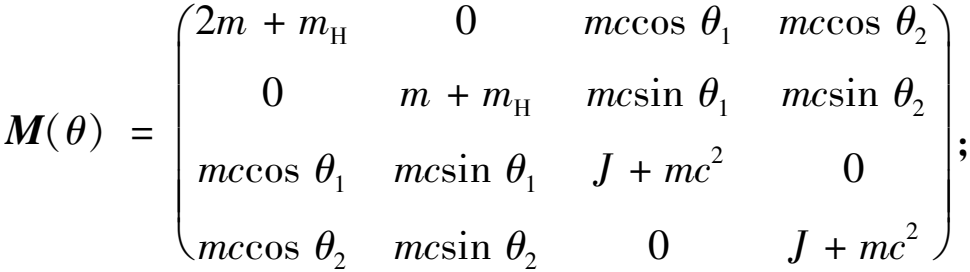
(9)
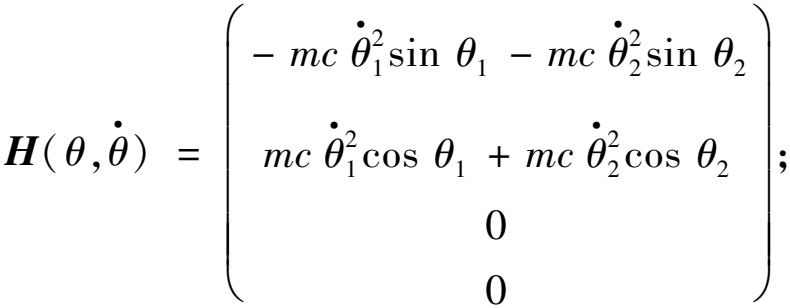
(10)
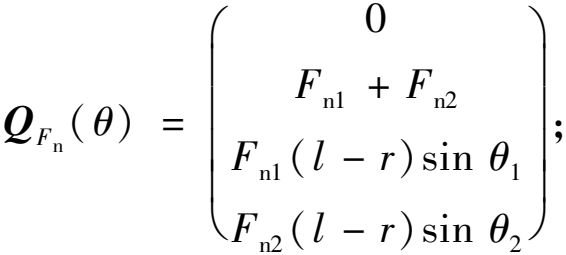
(11)
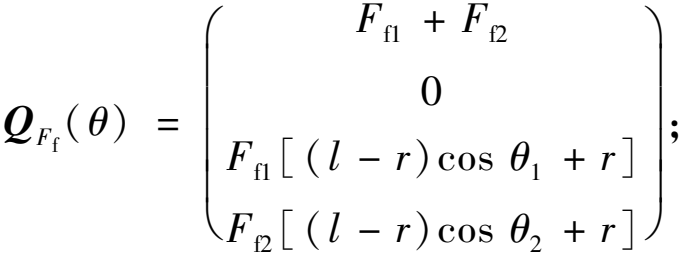
(12)
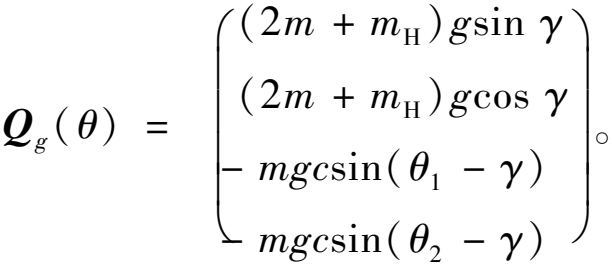
(13)
为了减少系统的参数,获得更普适的动力学方程,选取m、g、l为基本量对上式进行无量纲化处理。此时无量纲参数可依次记为
Ff/(mg),其中t为时间,s。
2 机器人的足地接触参数
2.1 接触参数对行走步态的影响
由于刚度系数、阻尼系数、动摩擦系数、静摩擦系数4个参数共同描述了被动行走机器人的路面接触环境,将它们定义为路面的接触参数。机器人在何种路面环境下具有较优的行走步态是本文关注的重点,因此需要对路面接触参数协同作用时的行走步态进行研究。
首先,对于摩擦力的计算,动摩擦系数通常为静摩擦系数的70%～80%,因此,可固定μd=0.8μs。在路面左倾(0°～20°)时,行走过程中维持前进方向平衡的摩擦系数峰值约为0.3～0.4[24]。当摩擦系数不在此范围时,会出现步态失稳,因此,本节中将μd设为 [0.2,0.5],用于保证此范围能涵盖正常行走、滑移、摔倒等多种现象。按照上述分析,此时μd∈ [0.16,0.40]。其次,对于法向力的计算,仿真结果[25]表明,当k=106 kg/(m0.5·s2),c=107 kg/(m1.5·s)时,碰撞恢复系数接近 0,即为完全非弹性碰撞;保证k值不变,c减小为106 kg/(m1.5·s)时,碰撞恢复系数约为 0.1,此时物体将发生弹跳。随着c的减小,这种弹跳现象将更加明显。因此,本节固定k=106 kg/(m0.5·s2),将阻尼系数区间限定为 [106, 107]。
图4为各接触参数协同作用下的步态变化情况,平面(μs,c)= [0.2,0.5]×[106, 107],将μs线性均分为100份,c以指数级别均分为100份,平面内共计1×104个参数点。图4中纵坐标p为阻尼系数的指数,横坐标μs表示静摩擦系数,右侧的颜色条带展示了不同的行走区域:蓝色为正常行走,紫色为足地滑移,黄色为弹起,而黑色表示机器人跌倒。这些运动形式的判断条件如下:①判定滑移,支撑腿从接触地面到与地面不发生相对滑动所用的无量纲时间大于设置的判定值0.2;②判定弹起,支撑腿离开地面(δ<0)的次数大于一次;③判定摔倒,髋关节高度yH<0。当同时满足各判定条件时,机器人的步态表现为多种运动形式的组合,然而,在图4的仿真结果中并未发现这种组合形式。
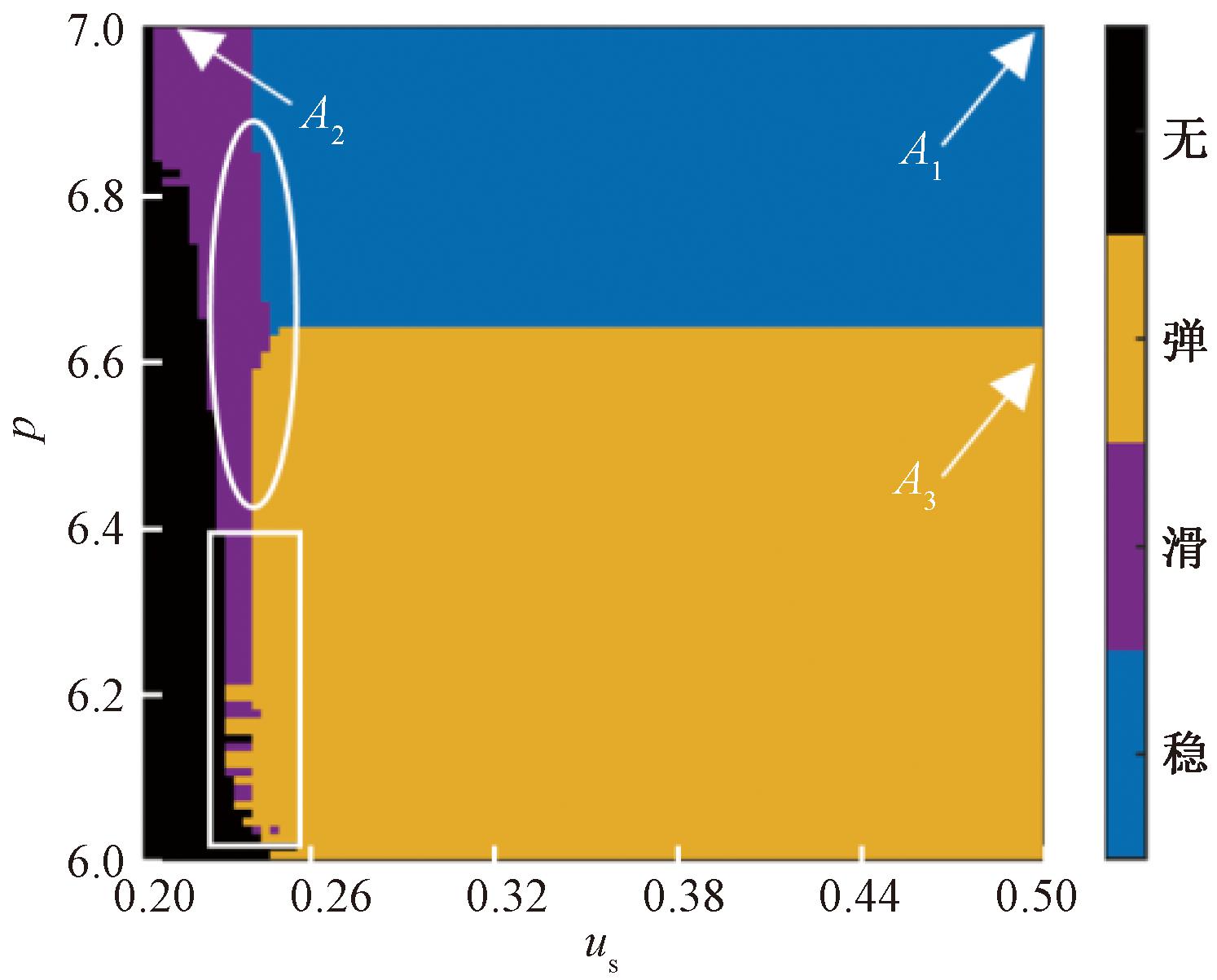
图4 不同接触参数组合下的机器人运动状态
Figure 4 Robot motion states with different contact parameter combinations
由图4可以看出,大部分参数平面被稳定行走(蓝色区域)与弹起步态(黄色区域)所占据。前者位于较大的阻尼系数与摩擦系数的组合区间内,机器人正常行走,无滑移和弹起;后者位于阻尼系数减小到4.37×106(p = 6.64)后的区域,此时摩擦系数无论如何增大,维持稳定行走都将极其困难。在图4的左侧,出现了两种颜色较窄的区域,紫色对应的滑移状态位于摩擦系数较小的区域(椭圆实线框),此位置处,阻尼系数越小,机器人实现稳定行走所需的摩擦系数越大;而在紫色区域延伸的实线方框内,原本的弹起运动状态被滑移区占据,即在较小的阻尼系数与摩擦系数下,摩擦系数对步态的影响占主导地位。而当阻尼系数与摩擦系数足够小时,几种步态的分界不再能明显区分,既可能滑移,也可能弹起或直接摔倒。
2.2 机器人的正常行走、滑移与弹起
为验证图4中数值仿真结果的正确性,在图4中依次选取3组接触参数组合,分别对机器人的行走状态进行验证,这些参数的位置如图4中的点A1～A3所示,依次对应正常行走、滑移和弹起。
2.2.1 算例1 :正常行走
此算例对应图4中点A1处的接触参数,其中k=106 kg/(m0.5·s2),c=107 kg/(m1.5·s),μs=0.5,μd=0.4。
为实现机器人稳定的正常行走步态,为机器人设置初始运动状态:
图5(a)为机器人行走时的极限环图,图5(b)为双腿角度的时间响应图,黑色为摆动阶段,红色为支撑阶段。机器人行走过程中支撑腿角速度始终为负值,即支撑腿始终围绕髋关节顺时针摆动直至脱离地面变为摆动腿;摆动腿角速度由负变为正再变为负,即支撑腿脱离地面变为摆动腿后,继续顺时针摆动再反向逆时针摆动,在碰撞前顺时针回摆一段角度后与地面发生碰撞,进入下一步。由图5可知,机器人在此算例下的行走步态为周期1。
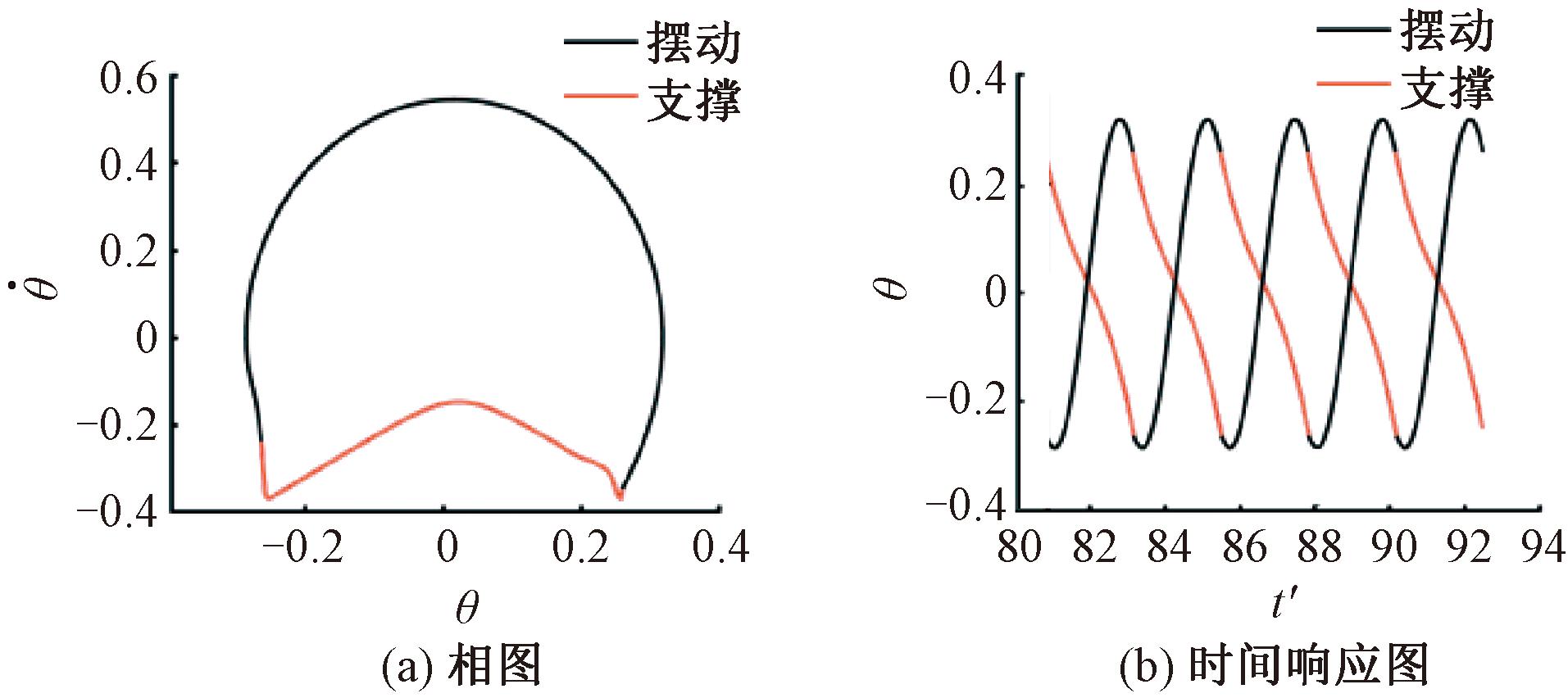
图5 算例1的极限环图及时间响应图
Figure 5 Limit cycle and time response diagrams of example 1
图6给出了此周期步态下机器人足部相对于地面的法向接触力曲线、切向摩擦力曲线以及圆弧足最低点速度曲线,依次用蓝色、浅蓝色、黄色标识。由图6可知,当圆弧足与地面接触时,法向接触力Fn激增,达到峰值12.5,是整机重量的5倍。而在足地碰撞完成后,vl的值始终为0,表明此时未发生弹起与滑移。
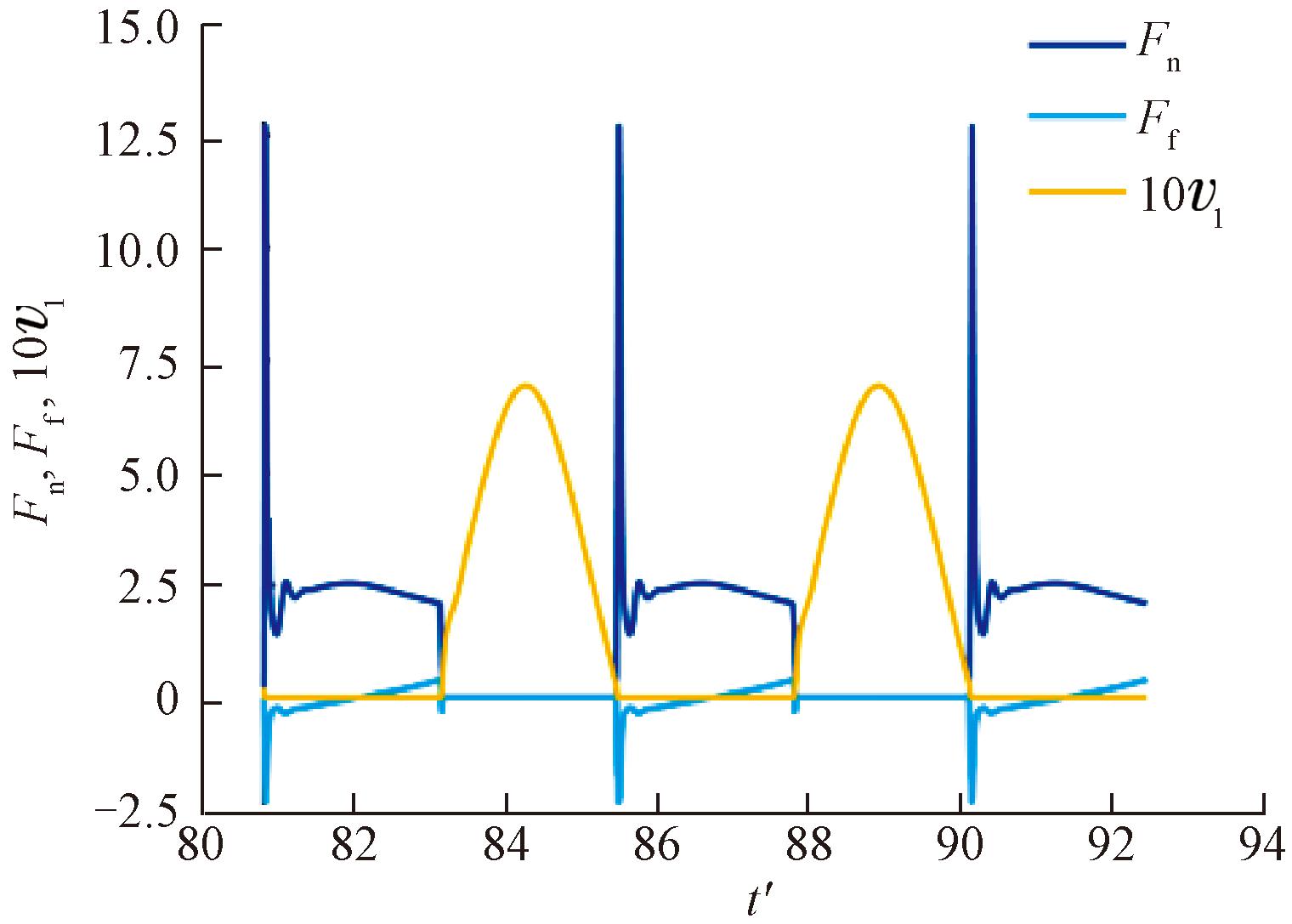
图6 算例1的Fn、Ff、vl曲线
Figure 6 The curve of Fn,Ff,vl of example 1
2.2.2 算例2 :滑移
此算例对应图4中点A2处的接触参数,其中k=106 kg/(m0.5·s2),c=107 kg/(m1.5·s),μs=0.21,μd=0.17。
机器人的运动初始状态为
图7(a)为机器人行走时的极限环图,图7(b)为双腿角度的时间响应图,黑色为摆动阶段,红色为支撑阶段。在图7(a)中,极限环存在两条闭合轨迹,一条轨迹上存在明显的滑移现象,一条轨迹表现为正常行走状态(见算例1),机器人此时行走步态为周期2。
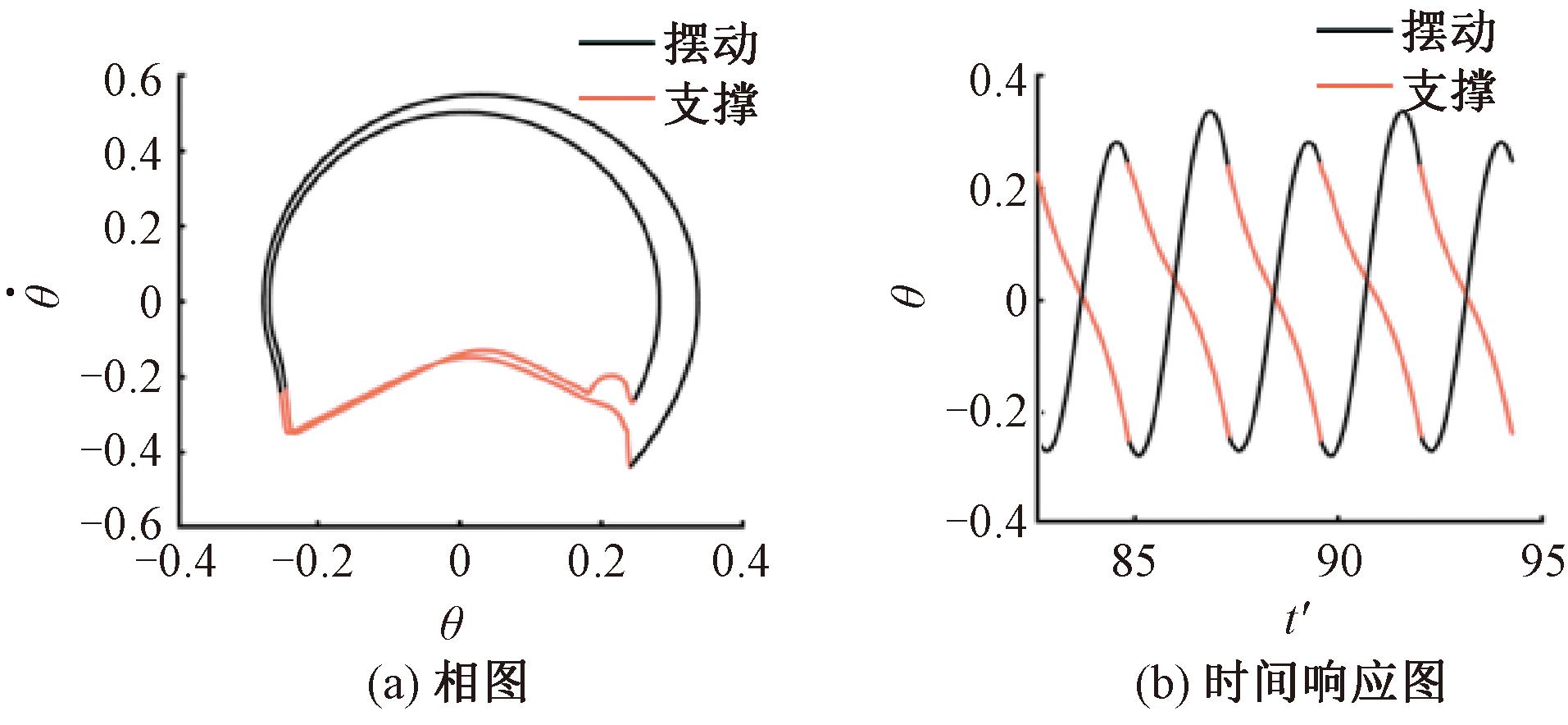
图7 算例2的极限环图及时间响应图
Figure 7 Limit cycle and time response diagrams of example 2
图8给出了存在滑移时机器人行走的Fn、Ff、vl曲线,Fn峰值为10,是整机质量的4倍,小于稳定步态,即足地碰撞时的冲击力降低。在vl曲线上也可以观察到明显的滑移现象。
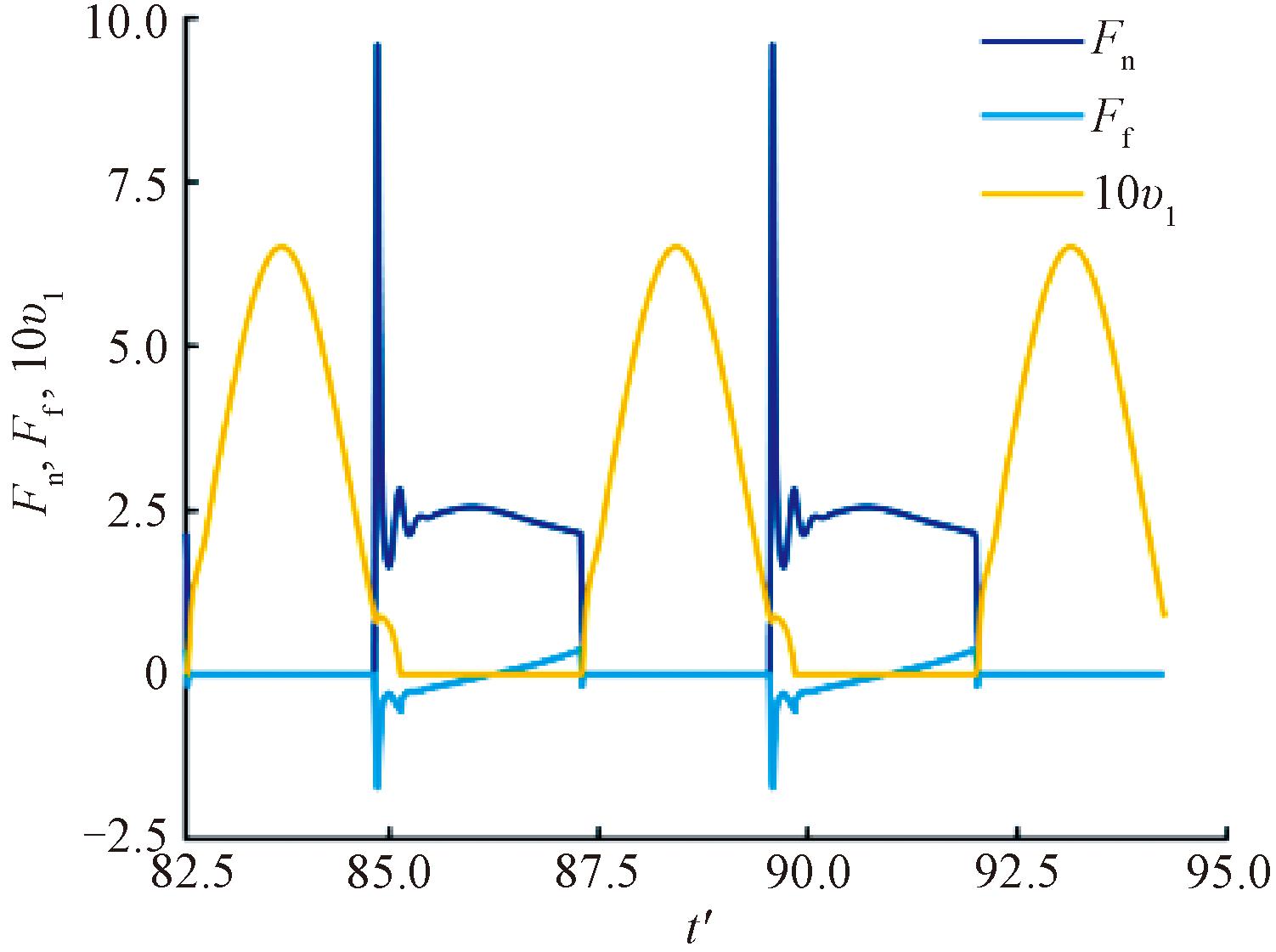
图8 算例2的Fn、Ff、vl曲线
Figure 8 The curve ofFn,Ff,vl of example 2
2.2.3 算例3:弹起
此算例对应图4中点A3处的接触参数,其中k=106 kg/(m0.5·s2),c=3.2×107 kg/(m1.5·s),μs=0.5,μd=0.4。
此时机器人的运动初始状态为
图9(a)为机器人行走时的极限环图,图9(b)为双腿角度的时间响应图,黑色为摆动阶段,红色为支撑阶段。由图9(a)可以看出,刚进入支撑阶段与摆动阶段时,极限环曲线均存在小幅度的波动,这是由于支撑腿从地面弹起或弹起的趋势造成的。Fn、Ff、vl曲线如图10所示,Fn峰值为12.2,与正常步态接近;Ff、Fn曲线上,在完成摆动腿到支撑腿的切换后均存在很长一段时间的振荡,频繁的振动会导致机器人各部件的疲劳和磨损,对机器人造成物理损坏,降低行走的稳定性。这也反映了步态中的弹起现象。
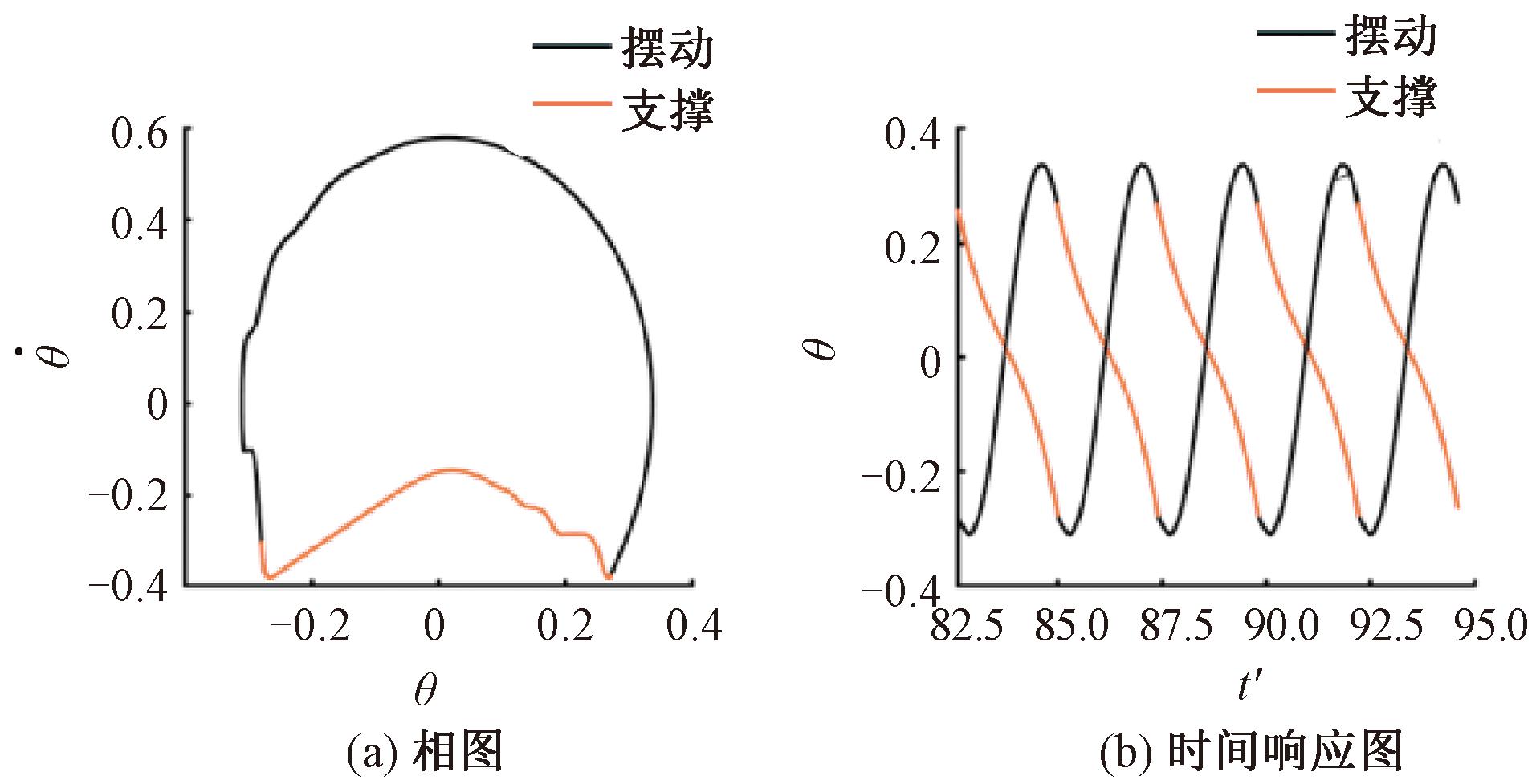
图9 算例3的极限环图及时间响应图
Figure 9 Limit cycle diagram and time response plot of example 3
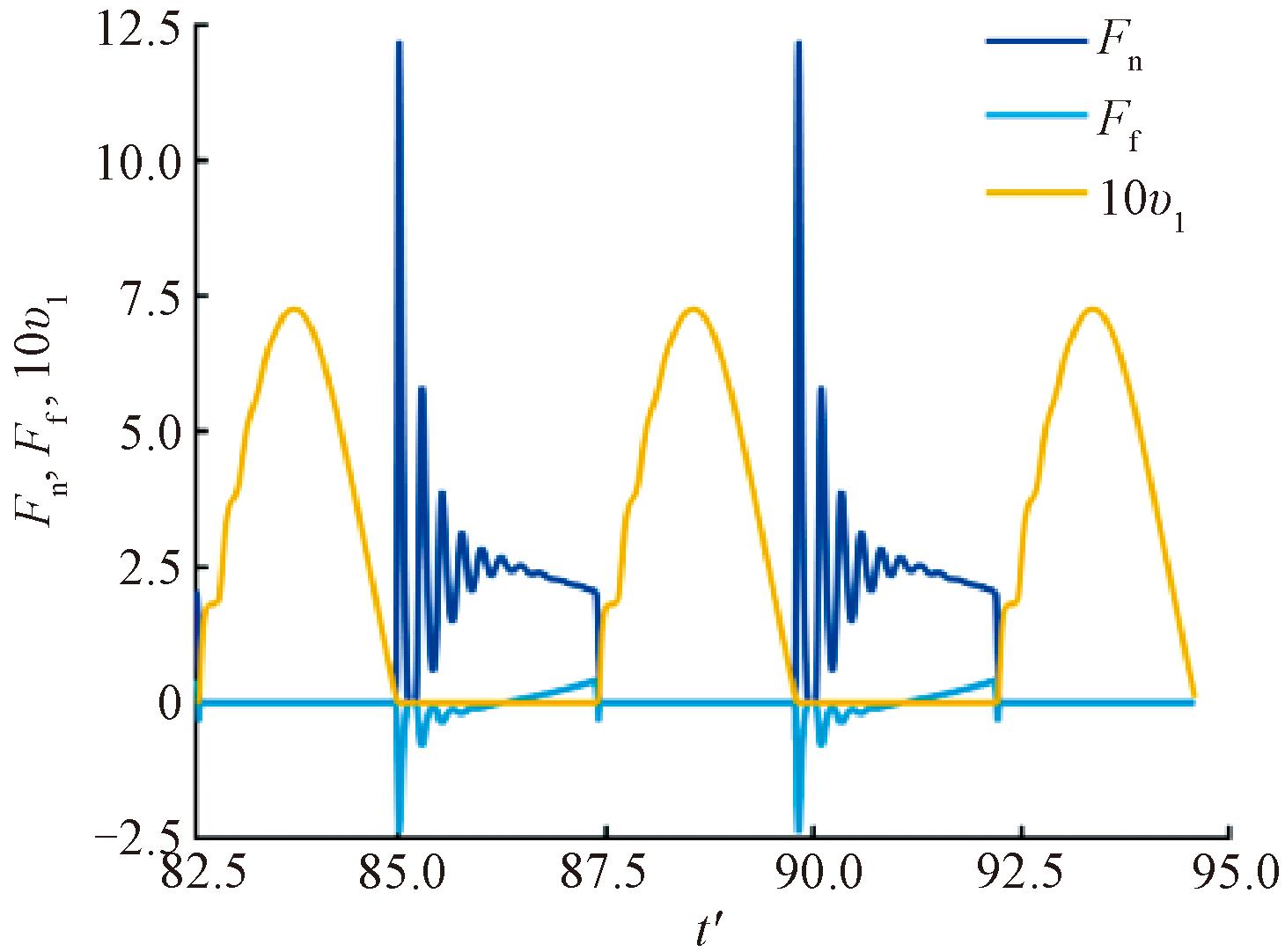
图10 算例3的Fn、Ff、vl曲线
Figure 10 The curve of Fn,Ff,vl of example 3
3 结构参数对步态的影响
探究被动行走机器人的步态随结构参数改变时的演化过程,根据探究双接触参数协同作用时的仿真结果,为机器人选取行走状态较优时的接触参数k=106 kg/(m0.5·s2),c=107 kg/(m1.5·s),μd=0.5,μc=0.4。
3.1 髋关节质量对步态的影响
将被动行走机器人的上肢质量集中在髋关节处,髋关节质量的不同反映了机器人不同的上下肢体重分布。分别取无量纲髋关节质量β1为0.2,0.5,0.8,即髋关节质量分别为腿部质量的20%,50%,80%,其他结构参数不变。随着斜面倾角的增大,被动行走机器人的步态演化过程如图11所示,此时纵坐标为机器人双腿同时着地时的支撑腿角度。由图11可以看出,机器人的行走步态由周期1经倍周期级联通向混沌。随着髋关节质量增加,相同斜面角度下机器人的支撑腿角度增大,这表明上体质量的增加将使机器人产生更大的跨距角以及步长。同时,增大髋关节质量还使分岔点提前,且机器人能行走的斜坡倾角范围更小。
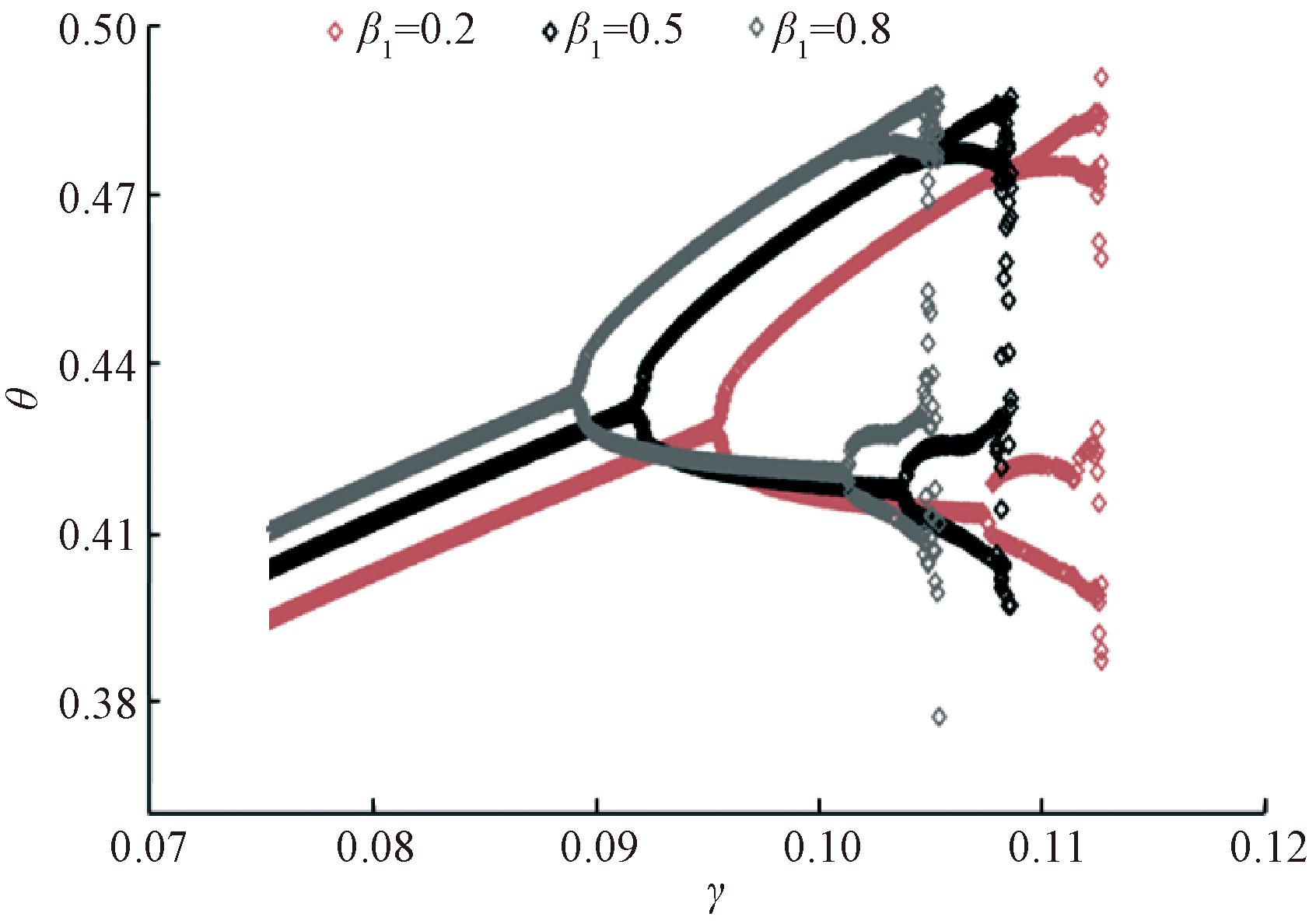
图11 不同髋关节质量对应的分岔图
Figure 11 Bifurcation diagram with different hip mass
图12给出了β1∈[0,1]时,双足机器人第1次倍周期分岔的斜面倾角与能稳定行走的最大斜面倾角,在该参数区间内进行分析可以得到髋关节质量对机器人环境适应性的影响趋势。在髋关节质量为0时,被动行走机器人演化为一种典型的模型——罗盘模型[26],此时能行走的最大斜面倾角为0.117;髋关节质量为1时,最大斜面倾角减小到0.104。在[0,1]时,髋关节质量越重,能行走的斜面范围越小。
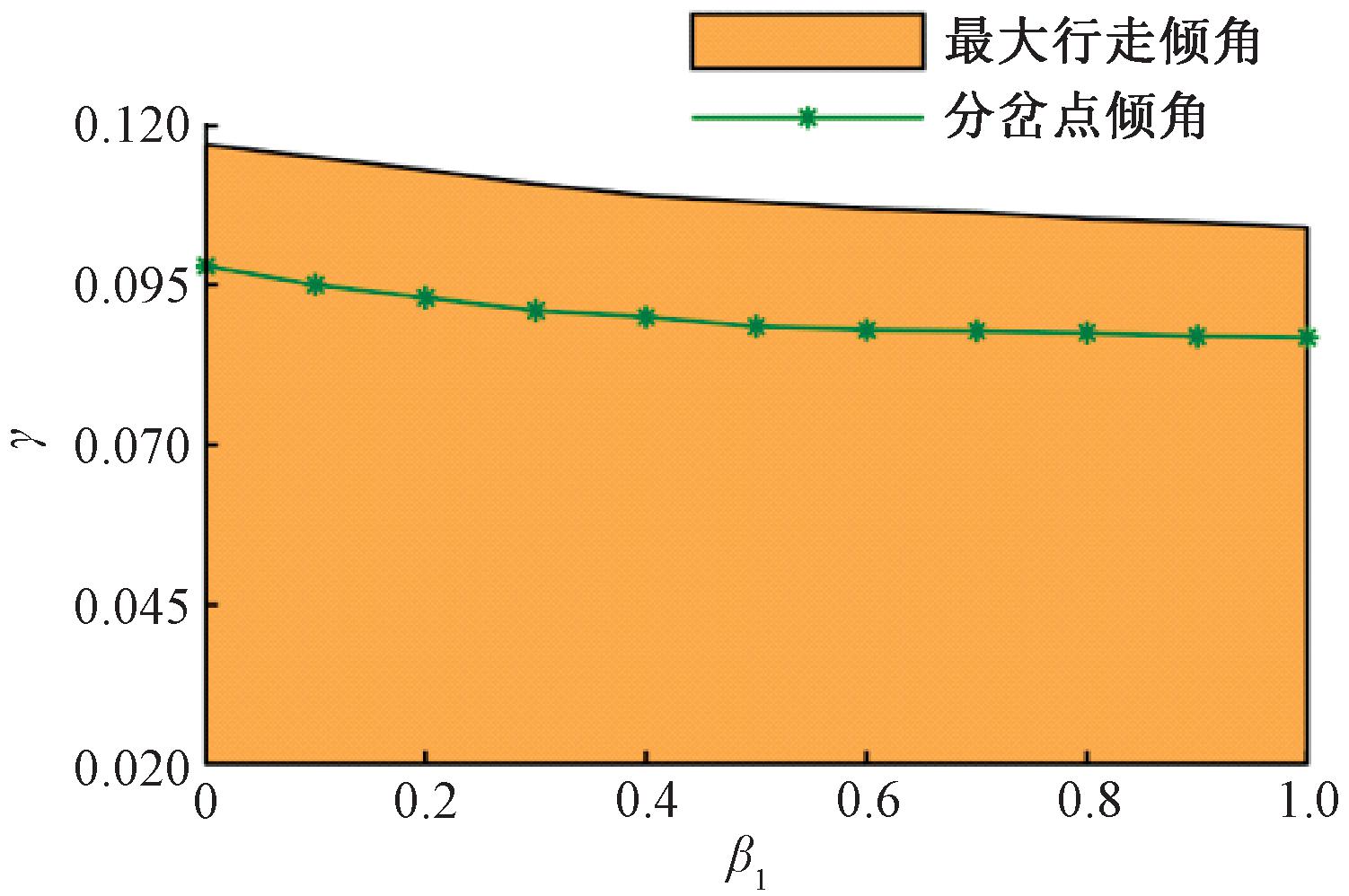
图12 倾角范围与分岔点
Figure 12 Slope range and bifurcation points
由图12可以看出,在典型的倍周期级联现象中,随斜面倾角增大,被动行走机器人步态通过倍周期分岔,经由周期1、周期2、周期4等最终通向混沌,且在一定倾角范围内继续保持混沌状态稳定行走,接着由于倾角过大而失去稳定性。但在图11中观察到混沌步态仅在极小区域内出现,由于混沌状态的消失,被动行走机器人能实现稳定行走的倾角范围减小。为探究该现象出现的原因,对机器人摔倒前的行走表现进行分析。
图13为mH=0.5时混沌行走状态消失前各状态参数的时间响应图。从图13可以看出,在跌倒前一步,圆弧足与地面接触后,最低点与地面间的切向相对速度有一段瞬时下降,接着逐渐增加,这说明摆动腿接触地面,转换为支撑腿后,与地面发生了滑移;支撑腿与摆动腿角位移都开始增大,说明双足机器人双腿都开始向后倾倒;髋关节高度迅速降低,最后摔倒在斜面上。
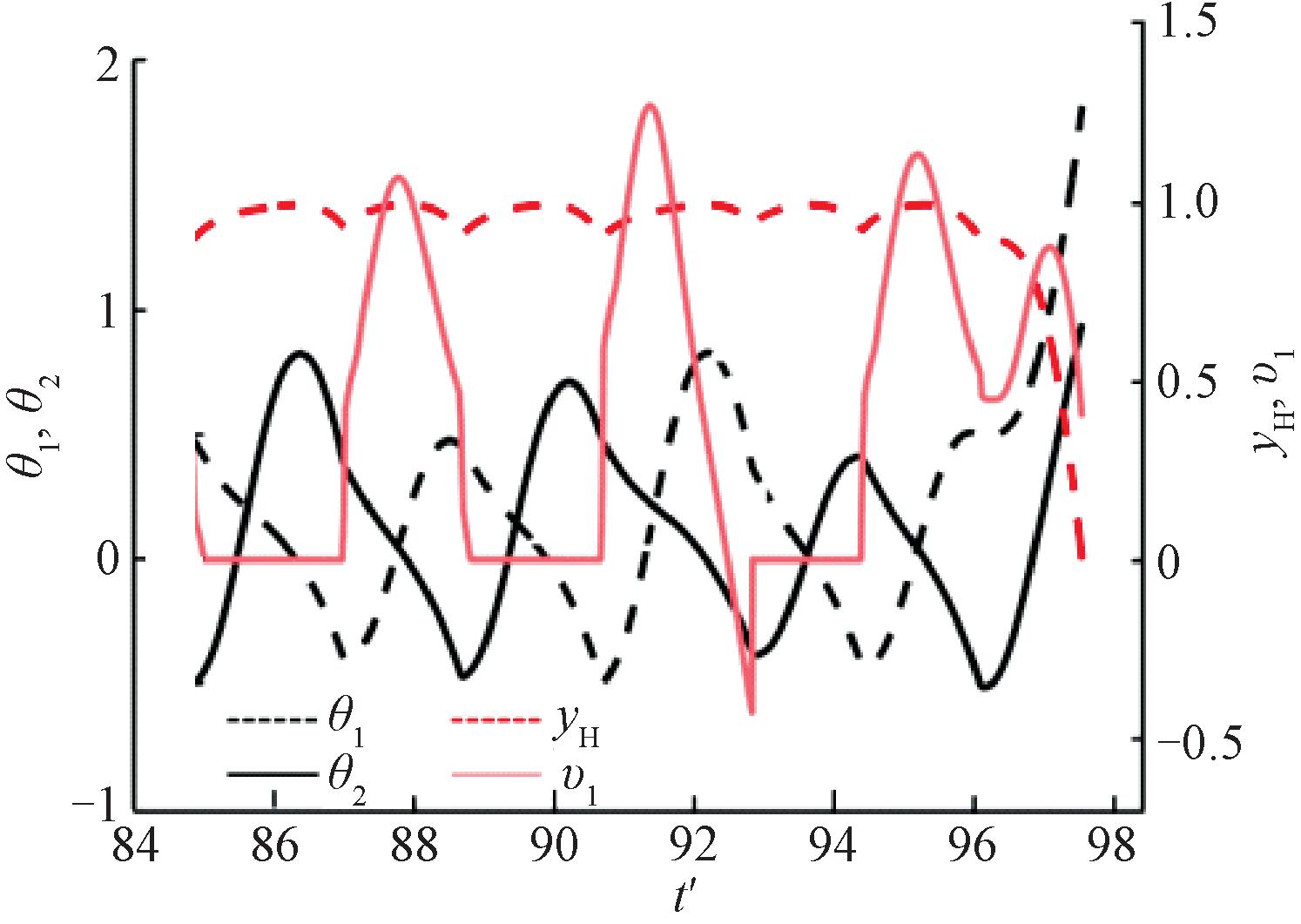
图13 摔倒发生时被动行走机器人的状态曲线
Figure 13 State curve of passive walking robot when fall occurs
机器人摔倒前的行走过程如图14所示。由于在进行数值仿真时,忽略摆动腿运动中的擦地现象,故在图14(b)和图14(c)中摆动腿不与地面发生接触而直接越过地面。上述分析表明,由于滑移现象的存在,混沌吸引子剧烈突变引发了机器人摔倒,在分岔图上表现为极窄的混沌行走步态范围。
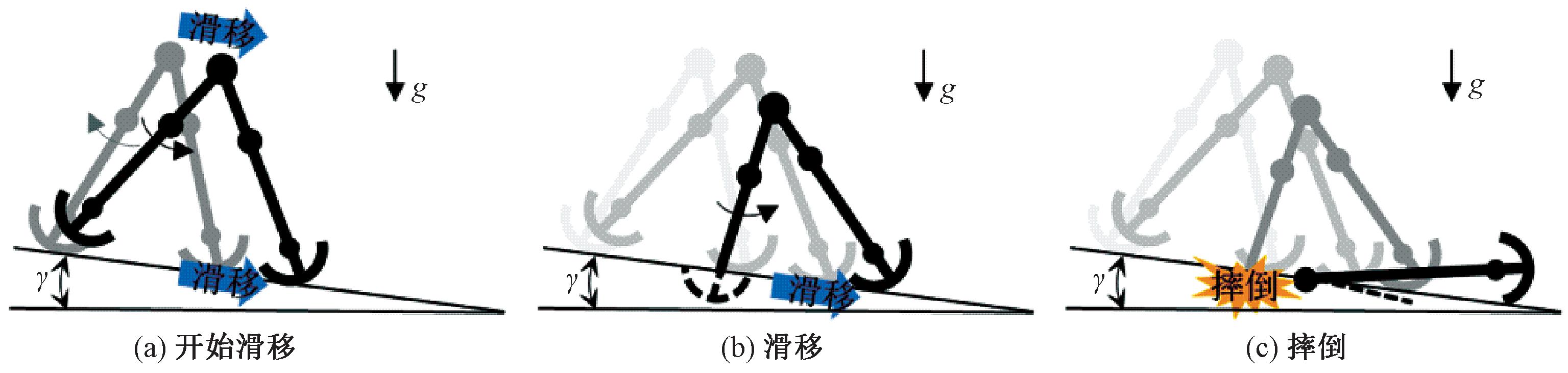
图14 机器人摔倒历程图
Figure 14 Robot falling process diagram
3.2 腿质心与髋关节距离对步态的影响
不同结构参数下的分岔图如图15所示。腿质心距髋关节的距离表征了机器人下肢的重心分布,两者间距离小则重心靠上,距离大则重心靠下。取β2= 0.125,0.250,0.375,0.500共4组数据,其步态演化过程如图15(a)所示。随着重心的下移(c逐渐增大),腿的摆动幅度逐渐减小,分岔点先后移后又前移,能行走的斜面范围先增大后减小。这说明腿质心与髋关节距离存在一个最优值,在该结构参数下,机器人能行走的斜面范围最大。
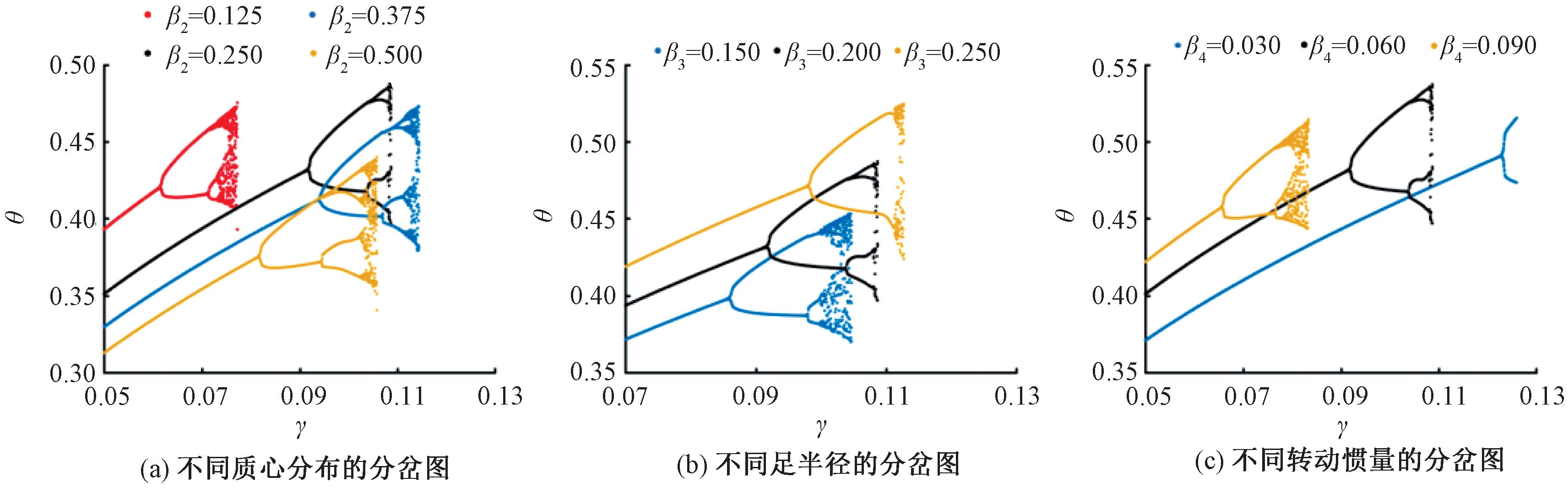
图15 不同结构参数下的分岔图
Figure 15 Bifurcation diagrams with different structural parameters
不同结构参数下的行走范围如图16所示。在图15(a)的4组数据中,能行走斜面范围最大的参数值为0.375,取包含该参数值的区间为[0.125,0.500],图16(a)给出了间隔变化更小时,双足机器人第1次倍周期分岔的斜面倾角与最大行走倾角。从图16(a)中可以得到质心距髋关节位置的最优值约为0.375。还观察到,当距离减小时,能行走的斜面范围迅速减小,这说明重心靠上的机器人结构十分不利于稳定行走。经验证,与3.1节类似,机器人在过大行走倾角下通过滑移引发了步态失稳。
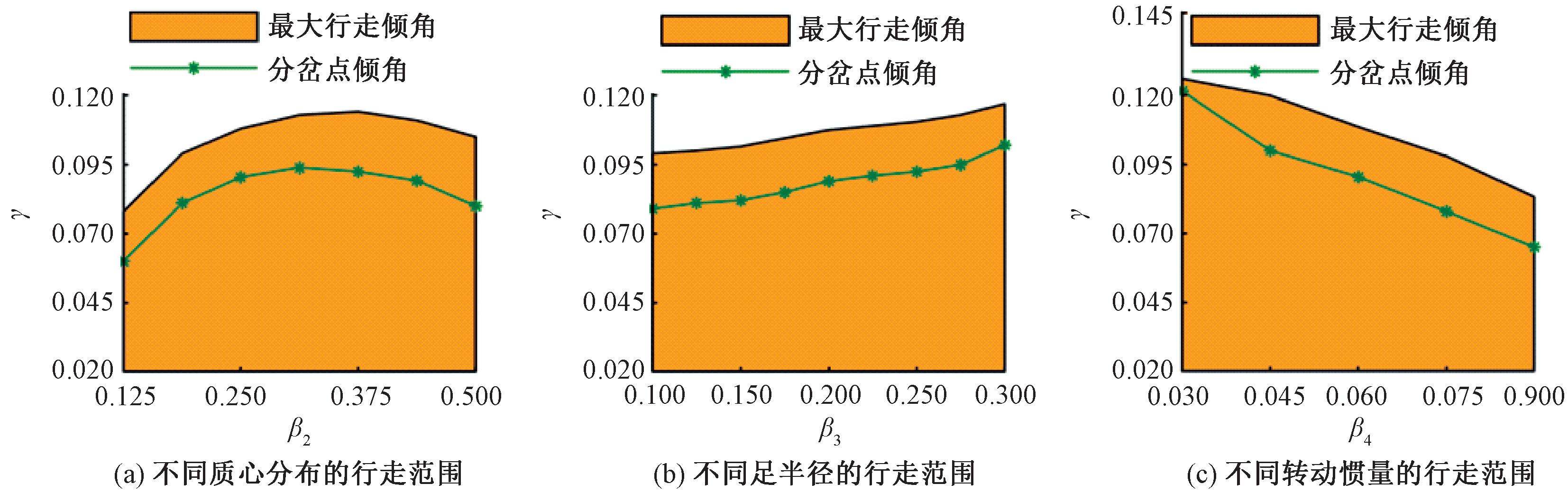
图16 不同结构参数下的行走范围
Figure 16 Walking range with different structural parameters
3.3 圆弧足半径对步态的影响
为探究足半径对步态的影响,无量纲参数β3分别取 0.150,0.200,0.250。步态演化过程如图15(b)所示。随着足半径增大,腿的摆动幅度逐渐增大,分岔点后移,能行走的斜面范围增大。图16(b)给出了参数变化区间更小时,双足机器人第1次倍周期分岔的斜坡角度与能稳定行走的斜面范围。当圆弧足半径从0.100增加到0.300,即足半径是腿长的10%～30%时,能行走的斜面范围从0.099增加到0.117,在此范围内,圆弧足半径越大,能行走的斜面范围越广。经验证,与3.1节类似,因步态中的滑移引发了机器人的跌倒。
3.4 转动惯量对步态的影响
取无量纲参数β4 =0.030,0,060,0.090,得到不同转动惯量下步态的演化过程如图15(c)所示,参数细化后得到能行走的斜坡范围与分岔点角度如图16(c)所示。图16(c)中,当β4=0.030时,与其他结构参数下的步态演化过程不同的是,被动行走机器人没有进入混沌状态,在周期2步态时摔倒在斜面上。分析仿真结果表明,这是由于此时斜面倾角过大,机器人行走步态中出现滑移导致向前摔倒。经验证,在其他结构参数下也发现了相同现象。
通过本章分析,揭示了被动行走机器人在不同结构参数下的步态演化规律,通过仿真分析探究了机器人摔倒的原因,发现了滑移现象对步态失稳的影响。
4 结论
(1)接触参数中的动、静摩擦系数与阻尼系数会影响被动行走机器人的步态,较小的摩擦系数会导致滑移现象,较小的阻尼系数会导致弹起现象。当阻尼系数与摩擦系数均较小时,摩擦系数对步态的影响占主导作用;当二者足够小时,滑移、弹起或摔倒几种步态的分界不能明显区分。
(2)被动行走机器人的结构参数会影响步态的演化。减小髋关节质量、增大圆弧足半径、减小转动惯量有利于扩大机器人能行走的斜面倾角范围,提高机器人的环境适应性。
(3)随着斜面倾角的增大,被动行走机器人的步态演化表现为倍周期级联分岔,由周期1步态经过数次分岔通向混沌,最终发生步态失稳。还发现,在本文涵盖的接触参数区间与结构参数区间组合下,斜面倾角为[0.078 2,0.126 0]时,步态中的滑移会引发步态失稳,这也造成了倍周期级联现象中混沌带变窄与混沌带消失两种特殊演化过程。
[1] JABERI MIANDOAB M, REZA HAGHJOO M, BEIGZADEH B. Toward humanlike passive dynamic walking with physical and dynamic gait resemblance[J]. IEEE Access, 2024, 12: 111060-111069.
[2] IRIBE M, HIROUJI R, URA D, et al. Experimental verification of the characteristic behaviors in passive dynamic walking[J]. Artificial Life and Robotics, 2021, 26(2): 187-194.
[3] 刘鑫宇. 双足准被动步行机器人及控制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
LIU X Y. Research on biped quasi-passive walking robot and its control strategy[D]. Harbin: Harbin Institute of Technology, 2017.
[4] MIKOLAJCZYK T, MIKO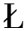
AJEWSKA E, AL-SHUKA H F N, et al. Recent advances in bipedal walking robots：review of gait, drive, sensors and control systems[J]. Sensors, 2022, 22(12): 4440.
[5] ZHOU Y N, SUN Z K, ZHAO N N, et al. Stability analysis for passive robots walking on inclined surfaces with local angles[J]. Physica Scripta, 2024, 99(10): 105245.
[6] LIU Z Y, GAO J S, RAO X B, et al. Complex dynamics of the passive biped robot with flat feet：gait bifurcation, intermittency and crisis[J]. Mechanism and Machine Theory, 2024, 191: 105500.
[7] MEMAR KOCHEH BAGH N, LIU P C. Control and gait generation of biped robots：a review[M]∥Advances in Intelligent Manufacturing and Robotics. Singapore: Springer Nature Singapore, 2024: 503-517.
[8] MCGEER T. Passive dynamic walking[J]. International Journal of Robotics Research, 1990, 9(2): 62-82.
[9] SADEGHIAN H, BARKHORDARI M. Orbital analysis of passive dynamic bipeds; the effect of model parameters and stabilizing arm[J]. International Journal of Mechanical Sciences, 2020, 178: 105616.
[10] 高建设, 暴雨萌, 赵天, 等. 非平整路面下被动行走机器人的步态动力学演化[J/OL]. 吉林大学学报(工学版), 2024: 1-10(2024-07-15)[2024-11-06]. http:∥kns.cnki.net/KCMS/detail/detail.aspx? filename=JLGY2024 0711001&dbname=CJFD&dbcode=CJFQ.
GAO J S, BAO Y M, ZHAO T, et al. Gait dynamics evolution of passive walking robot on uneven road surface[J/OL]. China Industrial Economics, 2024: 1-10(2024-07-15)[2024-11-06]. http:∥kns.cnki.net/KCMS/detail/detail.aspx? filename=JLGY20240711001 &dbname=CJFD&dbcode=CJFQ.
[11] 彭金柱, 张建新, 曾庆山. 基于改进差分进化的3-RPS机器人逆运动学参数标定[J]. 郑州大学学报(工学版), 2022, 43(5): 1-7, 38.
PENG J Z, ZHANG J X, ZENG Q S. Inverse kinematic parameters calibration of 3-RPS parallel robot based on modified differential evolution[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(5): 1-7, 38.
[12] RAO X B, GAO J S, DING S L, et al. Multistability of gaits, the basin of attraction and its external topology in the simplest passive walking model on stairs[J]. Chaos, Solitons &Fractals, 2023, 172: 113592.
[13] GRITLI H, BELGHITH S, KHRAEIF N. Intermittency and interior crisis as route to chaos in dynamic walking of two biped robots[J]. International Journal of Bifurcation and Chaos, 2012, 22(3): 1250056.
[14] ASANO F, SAKA T, HARATA Y. 3-DOF passive dynamic walking of compass-like biped robot with semicircular feet generated on slippery downhill[C]∥2016 IEEE International Conference on Robotics and Automation (ICRA). Piscataway: IEEE, 2016: 3570-3575.
[15] 张瑾, 王天舒. 考虑接触滑移的被动行走器行走步态研究[J]. 机械工程学报, 2011, 47(13): 16-22.
ZHANG J, WANG T S. Research on process of the passive walking with bouncing and slipping[J]. Journal of Mechanical Engineering, 2011, 47(13): 16-22.
[16] QI F, WANG T S, LI J F. The elastic contact influences on passive walking gaits[J]. Robotica, 2011, 29(5): 787-796.
[17] 郑鹏, 王琪, 吕敬, 等. 摩擦与滚阻对被动行走器步态影响的研究[J]. 力学学报, 2020, 52(1): 162-170.
ZHENG P, WANG Q, LYU J, et al. Study on the influence of friction and rolling resistance on the gait of passive dynamic walker[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(1): 162-170.
[18] ROELES S, ROWE P J, BRUIJN S M, et al. Gait stability in response to platform, belt, and sensory perturbations in young and older adults[J]. Medical &Biological Engineering &Computing, 2018, 56(12): 2325-2335.
[19] SAFARTOOBI M, DARDEL M, MOHAMMADI DANIALI H. Passive walking biped robot model with flexible viscoelastic legs[J]. Nonlinear Dynamics, 2022, 109(4): 2615-2636.
[20] THUILOT B, ESPIAU B,GOSWAMI A. Compass-like biped robot part I：stability and bifurcation of passive gaits[EB/OL].(1996-01-01)[2024-11-08]. http:∥fx.zzu.superlib.net/detail_38502727e7500f26d19ba 7796dcaf78bcf7b008e0e67ba611921b0a3ea2551014ccfd8 c06884d4e176114bc658cda12eb45a781c29ca01f804f04d 6b5b3b300e0ac344ecde50c20b0a3ef881b0ca39a5?.
[21] SKRINJAR L, SLAVI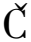
J, BOLTEŽAR M. A review of continuous contact-force models in multibody dynamics[J]. International Journal of Mechanical Sciences, 2018, 145: 171-187.
[22] COLANTONIO L, DEHOMBREUX P, HAJŽMAN M, et al. 3D projection of the LuGre friction model adapted to varying normal forces[J]. Multibody System Dynamics, 2022, 55(3): 267-291.
[23] ZHENG X D, WANG Q. LCP method for a planar passive dynamic walker based on an event-driven scheme[J]. Acta Mechanica Sinica, 2018, 34(3): 578-588.
[24] 王延昭. 横倾路面上人体足底的步进摩擦接触特性研究[D]. 洛阳: 河南科技大学, 2022.
WANG Y Z. Study on step-by-step friction contact characteristics of human plantar on cross-sloping pavement[D]. Luoyang: Henan University of Science and Technology, 2022.
[25] 祁峰. 弹性接触对被动行走多体系统动力学与稳定性的影响研究[D]. 北京: 清华大学, 2013.
QI F. Study on the influence of elastic contact on dynamics and stability of passive walking multi-body system[D]. Beijing: Tsinghua University, 2013.
[26] ADDED E, GRITLI H, BELGHITH S. Additional complex behaviors, bifurcations and chaos, in the passive walk of the compass-type bipedal robot[J]. IFAC-PapersOnLine, 2021, 54(17): 111-116.