在我国东南地区,由于软土广泛分布且水网密布,众多公路修建在河堤之上,进而形成了大量浸水路基。在我国交通需求量日益增长的背景下,为不影响一些关键路段的正常秩序并考虑到经济成本的消耗,需要对一些早期修建的旧路基进行扩建工程。这些拓宽路基在水分浸入后容易产生软化、掏蚀、冲刷等破坏[1],从而进一步加大了路基整体失稳的风险。路基失稳将会极大地危害路人及附近居民生命财产安全,而这样的案例近年来时常发生[2]。为保证路基拓宽后的长期稳定,以及方便对路基特定位置采取加固措施[3],研究水位随季节变化对浸水路基渗流特征和稳定性的影响具有重要意义。
水位变化作为影响路基土体稳定性的一个重要课题,国内外学者对其开展了多方面的讨论。张俊荣等[4]、陈龙飞等[5]将水位变化速率作为一种稳定性影响因素施加在土体边坡上,并定量评价各因素对路堤稳定性的影响效果,但缺乏水位变化后渗流场对应力场影响的深入探讨。有研究者[6-8]结合水土特征曲线和渗透系数曲线综合考虑了土体在水位变化条件下强度参数的变化,以及其对土体边坡整体稳定性的影响,但仅仅考虑了水位短期效应。刘修宇[9]对以上问题进行了综合分析,不仅建立了季节性浸水路基渗流场的有限元分析模型,还对水位变化条件下实时的土体渗流参数进行了确定。Biniyaz等[10]使用Python代码分析了水位长期波动对静水压力、非饱和抗剪强度、非饱和重度的影响,实现了对渗流影响下土体参数的更新。虽然上述两位学者所做的研究工作较为全面,但研究对象均以普通路基边坡为主,未能考虑拓宽路基渗流特征的影响。目前以拓宽路基为主体的研究大多关注其变形特性[11],较少考虑水流入渗和单侧浸水给稳定性所带来的影响。已有的路基数值模拟研究成果大多使用Geo-studio等商业软件计算得出,但其未能准确实现土体参数在渗流影响下的实时更新,或者实现的步骤较为烦琐。因此,本文基于前人研究成果,结合非饱和渗流理论和抗剪强度理论,利用FLAC3D中的FISH语言模块编写非饱和土的渗透系数和饱和度实时更新函数,在此基础上对河流动态水位下路基内部饱和非饱和渗流过程进行模拟。同时考虑水体对土体参数的影响,基于强度折减法进一步探究水位季节涨落对浸水拓宽路基渗流稳定性的影响。
1 渗流计算理论
1.1 饱和非饱和渗流计算基本方程
由于沿河路堤一侧紧邻河流,伴随着季节的更迭,河流水位也在不断改变,路基土体处在饱和与非饱和状态的变化之中。本文基于达西定律与质量守恒定律,考虑土体单元二维渗流状态,采用饱和非饱和渗流控制方程来表征流体在土体颗粒间的流动过程:
(1)
式中:H为水头高度,m;Kx和Ky分别表示x、y方向的渗透系数,m/s;θ为体积含水率;t为时间,s。
饱和渗流可以被视为非饱和渗流的一个特例,对于饱和渗流,土体中的孔隙始终充满水,单位时间内流入和流出土体中的水的质量相等,土体的体积含水量不随时间发生改变,若式(1)右边等于0,非饱和渗流控制方程随即转变为饱和渗流控制方程,因此在分析过程中可以将饱和渗流和非饱和渗流看作是统一的一个整体。
1.2 非饱和渗流计算模块的二次开发
由饱和-非饱和渗流理论可知,非饱和渗流的关键在于正确获得土体体积含水率或者饱和度与负孔隙水压力的关系,并依据渗透系数计算函数计算出非饱和土的渗透系数。在FLAC3D中进行非饱和渗流计算时饱和度与负孔隙水压力的单位时间内增量可以由流体体积改变量计算得出,而非饱和土的渗透系数在计算时则需要利用FISH语言编程以实现实时更新。
基于Van Genuchten模型的相关数学表达式,结合体积含水率与饱和度之间的关系,可得到饱和度和基质吸力的关系式:
(2)
式中:Ψ为基质吸力,kPa;s为饱和度;sr为残余饱和度;a、m、n均为拟合参数。
由于非饱和渗透系数主要受到含水量的影响,可以近似地看作是含水量的函数,由式(2)可知,含水量与基质吸力存在一个函数关系,因此非饱和渗透系数也可以表达成基质吸力的函数。为得到非饱和土的渗透系数,基于土水特征曲线数学模型进行理论推导,间接建立起非饱和渗透系数与基质吸力或者含水量之间的函数关系式,即Gardner模型:
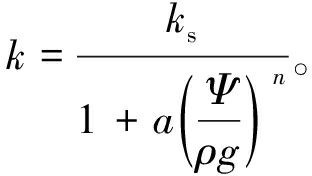
(3)
式中:k为对应基质吸力为Ψ的非饱和渗透系数,m/s;ks为饱和渗透系数,m/s;ρ为流体密度,kg/m3;g为重力加速度,m/s2;a、n为拟合参数。
基于Van Genuchten模型及文献[12]中的黏土实测数据拟合得到的饱和度与基质吸力的关系曲线如图1所示,结合Gardner模型推导得到黏土渗透系数预测曲线如图2所示。
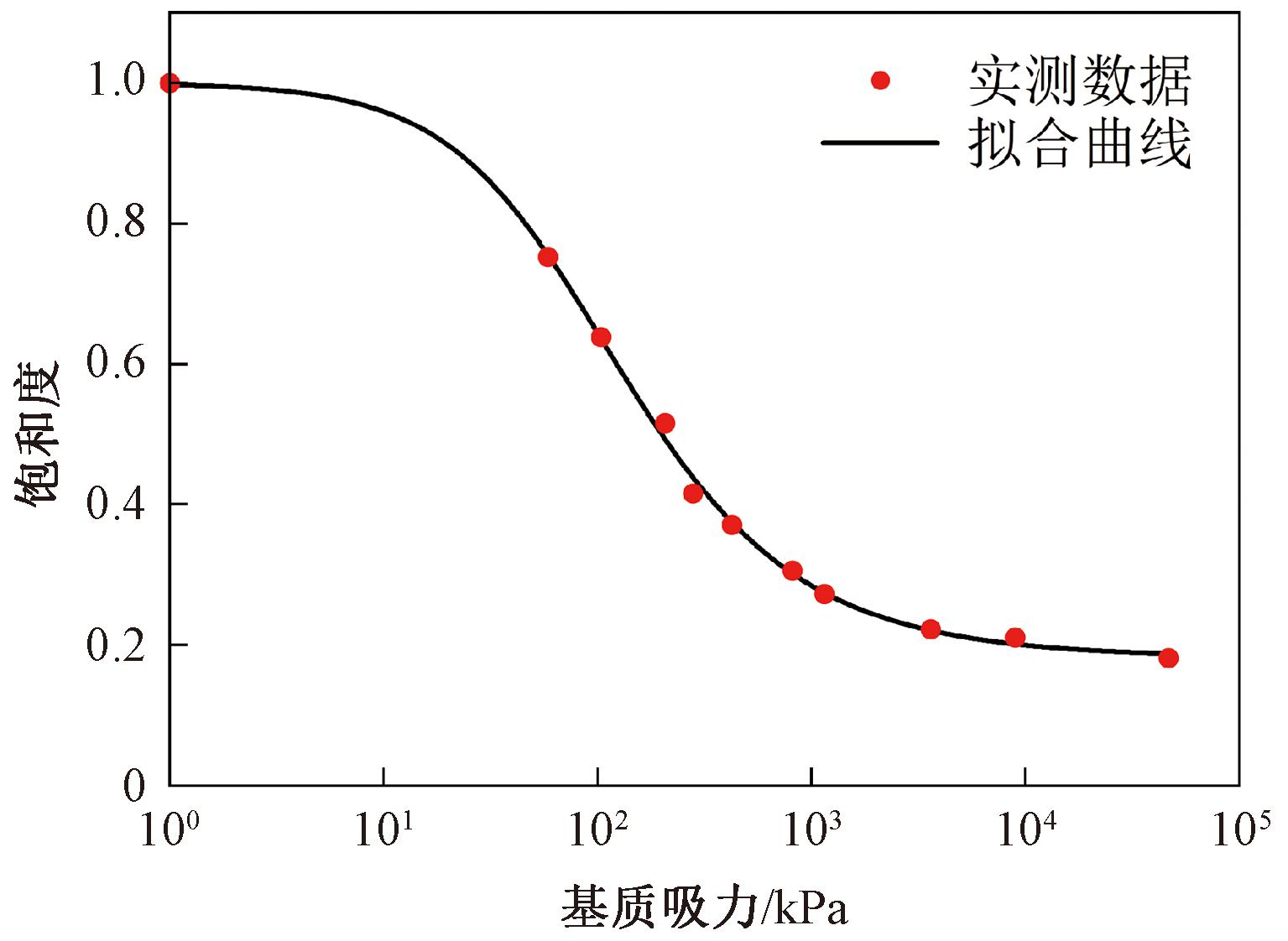
图1 黏土土水特征曲线拟合结果
Figure 1 Fitting result of clay soil-water characteristic curve
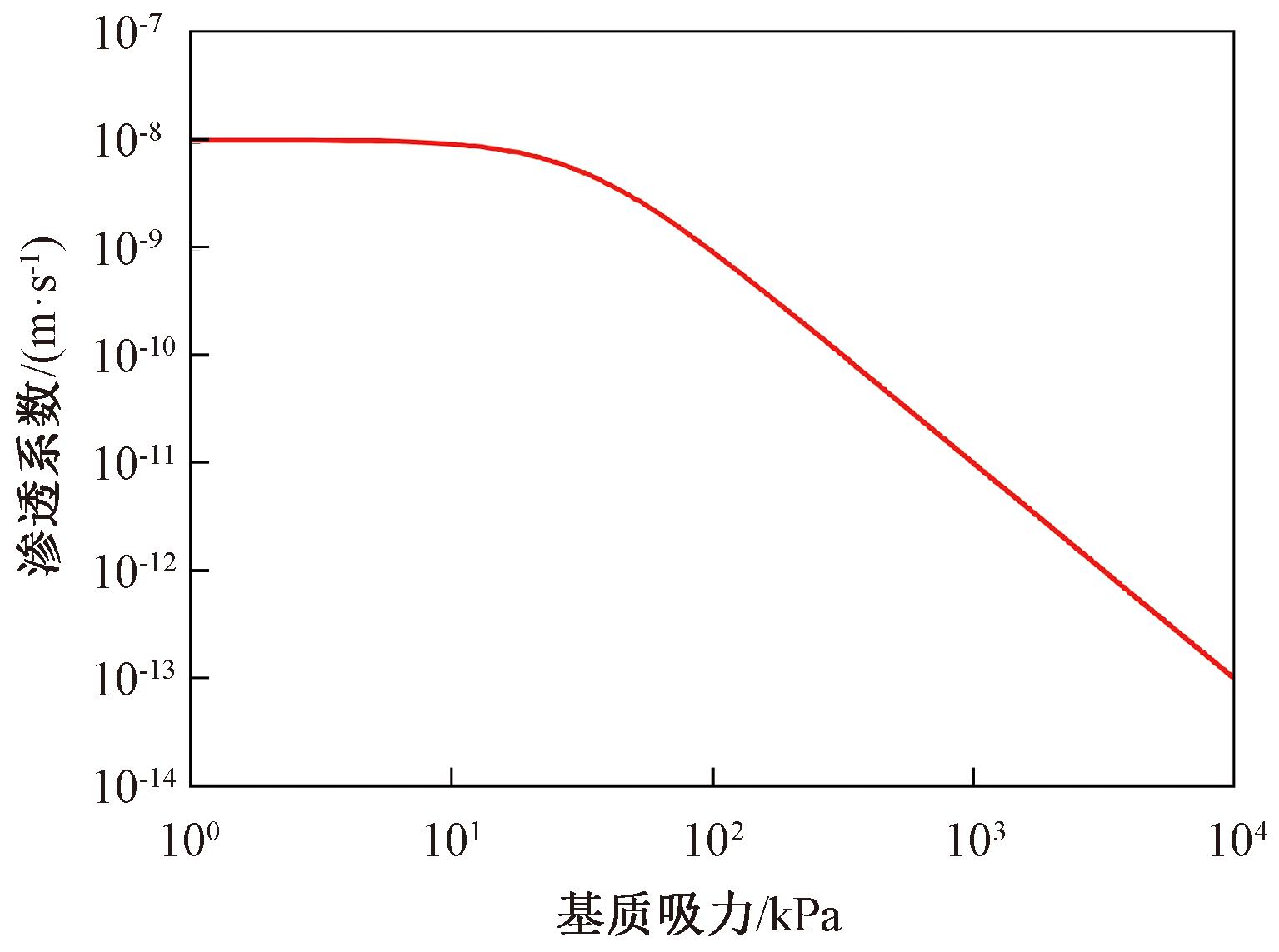
图2 黏土渗透系数曲线预测图
Figure 2 Clay permeability curve prediction diagram
利用FISH语言编程以实现非饱和土的渗透系数实时更新具体流程见图3,具体方法如下。
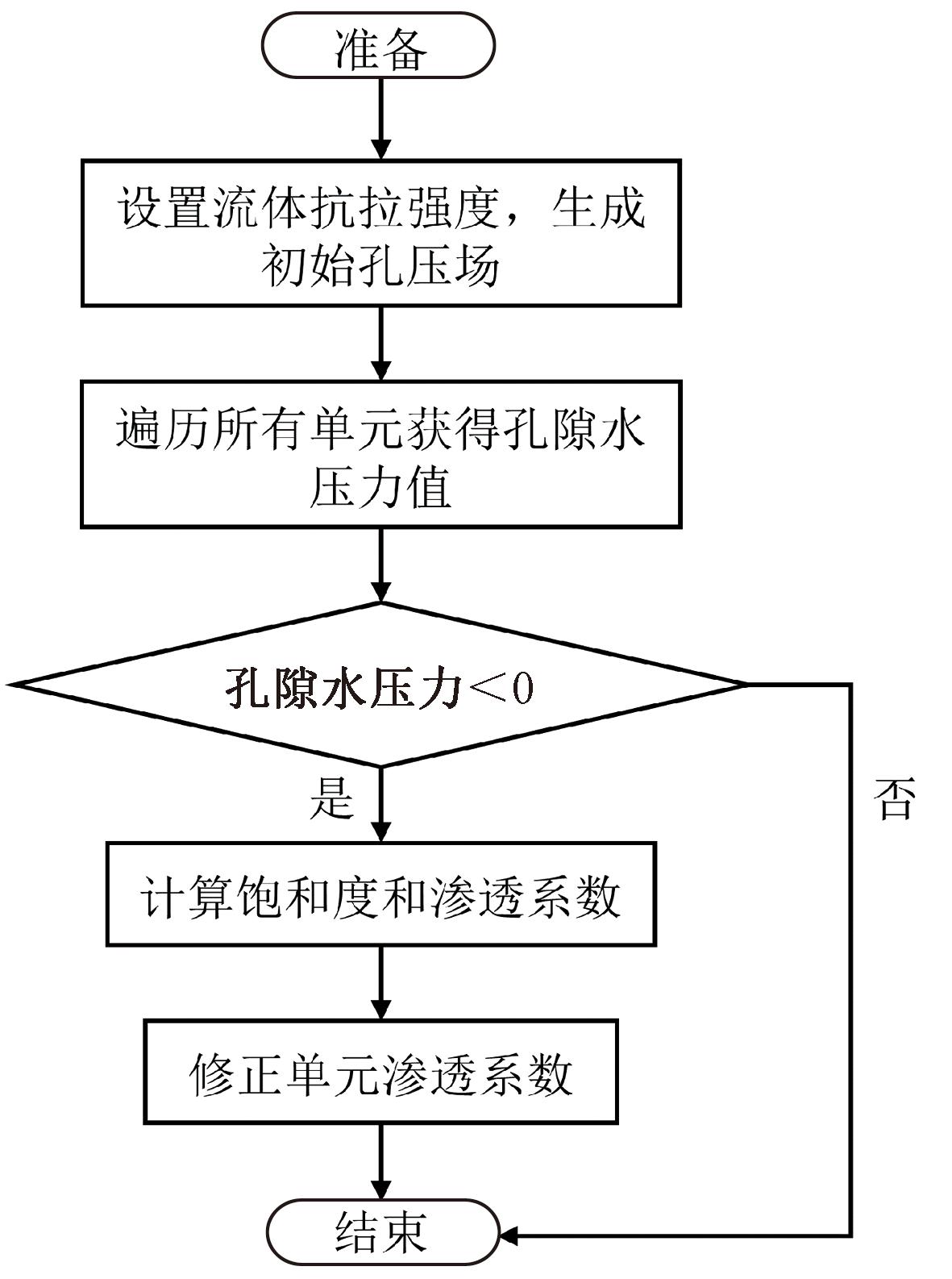
图3 非饱和土单元渗透系数修正计算流程图
Figure 3 Flow chart for calculation of permeability coefficient correction of unsaturated soil element
步骤1 将流体抗拉强度设置为合适的负值,允许在渗流过程中由于流体净流出所产生的负孔隙水压力。
步骤2 利用FISH语言中的内置变量获得非饱和区各个单元的孔隙水压力值,由孔隙水压力值的正负决定是否需要进行下一步的计算。
步骤3 根据上一步获得的负孔隙水压(基质吸力),利用土水特征曲线Van Genuchten模型和Gardner模型拟合得到的方程式计算得到各个单元的饱和度和实时渗透系数。将饱和度储存到新的存储单元中,将实时渗透系数赋值给相应单元,进而实现对非饱和土单元的渗透系数的实时修正。
步骤4 利用回调命令进行函数回调,确保在每一个计算时步都能调用函数实现对渗透系数的调整。
2 渗流特性数值计算与分析
2.1 计算模型
根据前期的模型验证工作,为研究单侧靠水的浸水拓宽路基渗流特性,本文选取某沿河软土拓宽路基为分析实例,并建立二维剖面模型,见图4。旧路基顶面宽8 m,路基高度为6 m,采用单侧拓宽的方式沿背水面侧加宽8 m,迎水面及背水面坡度均保持1∶1.5不变,路基开挖台阶尺寸为1.5 m×1.0 m,地基计算深度设为10 m,地基计算宽度设为60 m。为保证网格疏密合理,精度满足计算要求,将模型划分为7 396个单元和15 138个节点。为了方便研究水位升降过程中浸水拓宽路基内部的渗流特征及变形规律,在迎水面一侧设置了A、B、C、D、E这5个特征点以及特征截面C-C′,具体坐标为A(-15.25,1.00)、B(-13.75,2.00)、C(-12.25,3.00)、D(-10.75,4.00)、E(-9.25,5.00),河流初始水位位于地表以上3 m,与C-C′截面处在同一高程。
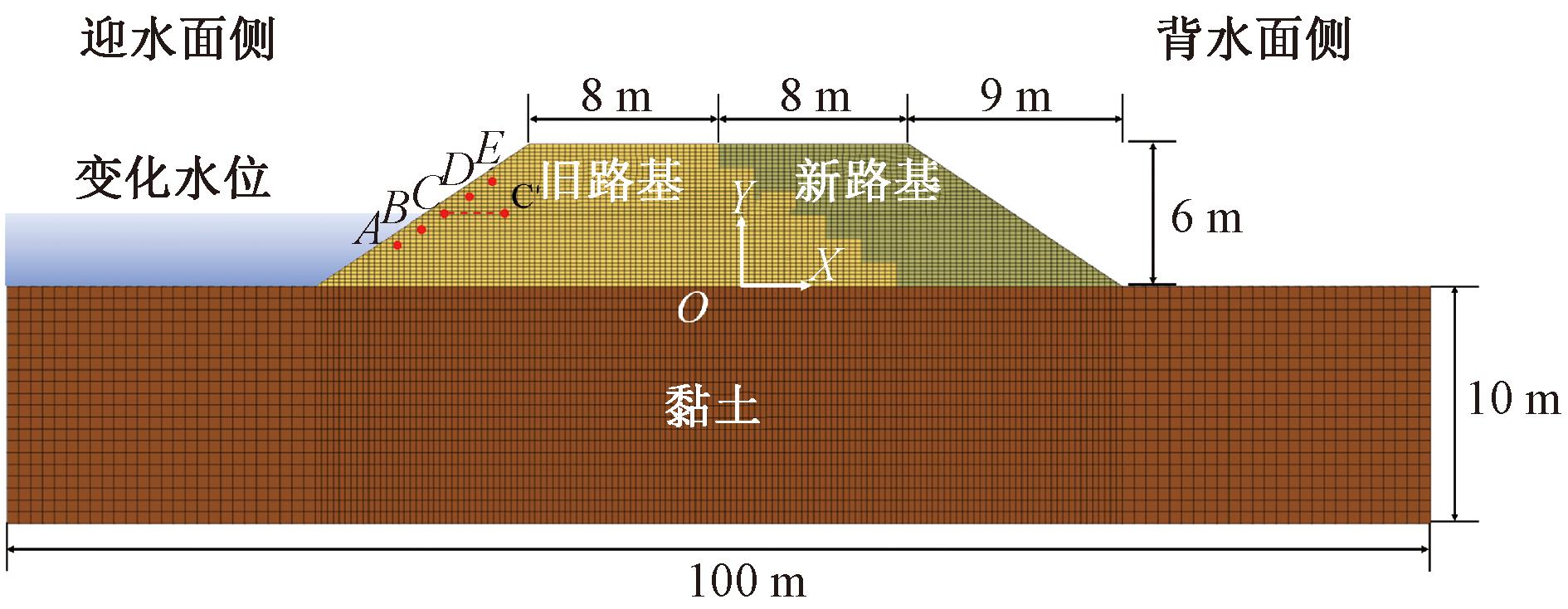
图4 浸水拓宽路基数值模型
Figure 4 Numerical model of inundated widered roadbeds
2.2 边界条件及计算参数
在水位变化过程中,由于水头差,河水从迎水面渗入路基内部,导致路基内部的渗流特征随之发生动态变化。在分析过程中模型地基左侧、右侧和底部均设为不透水边界,不与外界发生水分交换。背水面侧的地基表面设为透水边界,孔隙水压力值为0,在路基两侧水头差的作用下水分可以从该侧地基表面流出。模型底部的位移边界设为固定约束,模型两侧仅约束水平方向上的位移。
由于本文讨论重点为浸水拓宽路基在季节水位变化条件下的渗流特征及稳定性,因此在分析过程中将地基简化为单一黏土层,新旧路基均选用沿河路基工程中常见的典型黏土进行分析,具体物理力学参数如表1所示。
表1 数值模型计算参数表
Table 1 Calculation parameters of the numerical model

材料弹性模量E/MPa泊松比v重度γ/(kN·m-3)黏聚力c/kPa内摩擦角φ/(°)渗透系数k/(m·s-1)旧路基25.00.3318.020.030.01×10-8新路基10.00.3317.018.021.01×10-8淤泥质黏土3.50.3513.013.714.01×10-8
将河流初始水位设定为地表以上3 m,将计算得到的渗流场作为浸水拓宽路基的初始渗流场。根据汛期和枯水期水位变化规律,将河流水位简化为正弦函数,水位季节变动范围在2~4 m,并将其作为边界条件施加在迎水面侧,模拟分析一年时间内水位季节性涨落对浸水拓宽路基渗流特征的影响,计算总时长为360 d。水位变化曲线如图5所示。
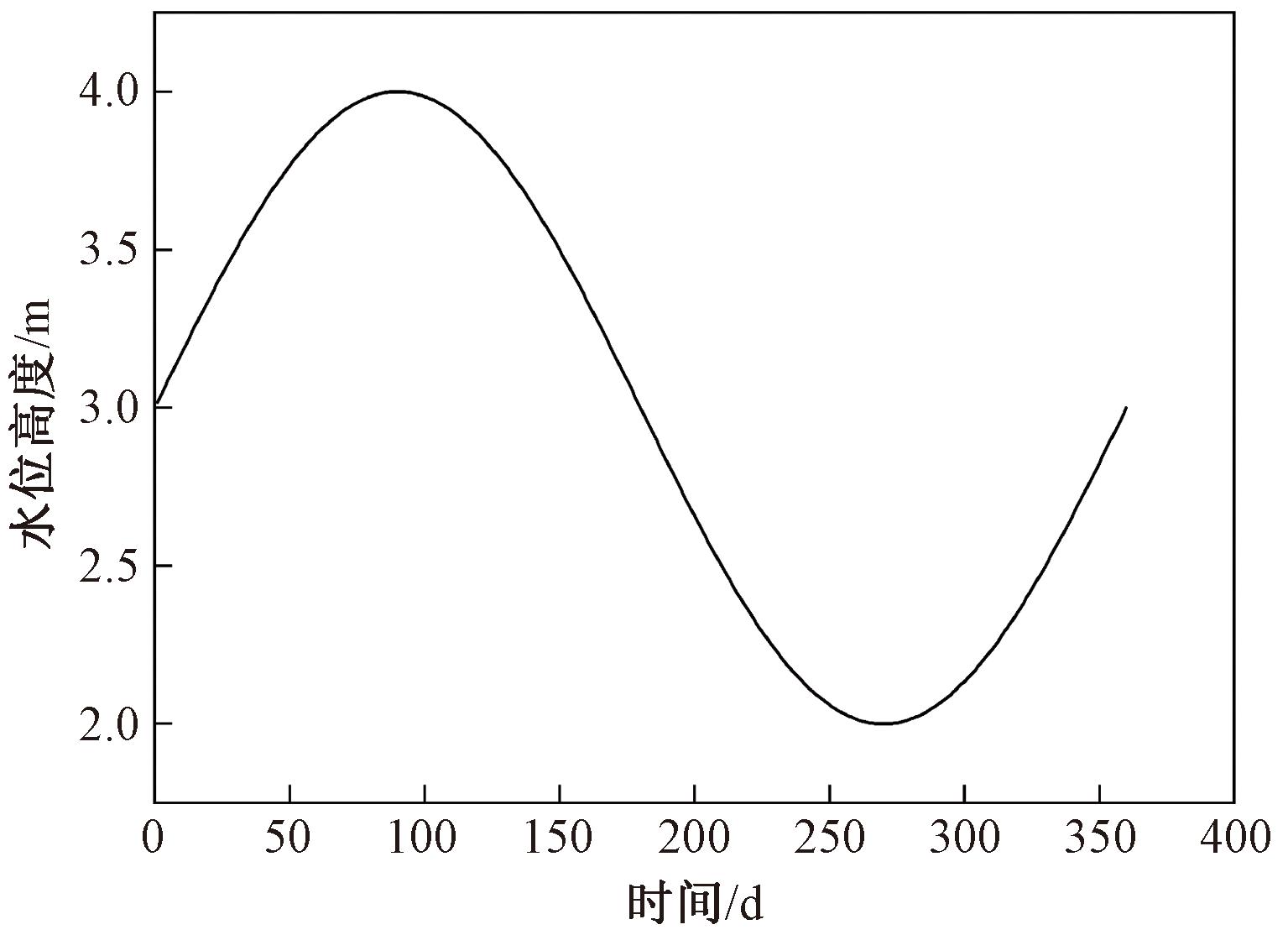
图5 水位变化曲线
Figure 5 Water level change curve
2.3 渗流特征分析
由图5可知,从初始水位开始,水位随时间经历了一个上升-下降-上升的过程。在这个变化过程中水位高度存在几个显著的特征点,分别是第90天和第270天水位的峰值和谷值,以及第180天水位回落,第360天回升了初始水位。选取初始渗流场与水位变化第90天、第180天、第270天、第360天时的浸水拓宽路基孔隙水压力及浸润线分布进行分析,如图6所示为不同时间点的路基内部孔隙水压力分布云图。
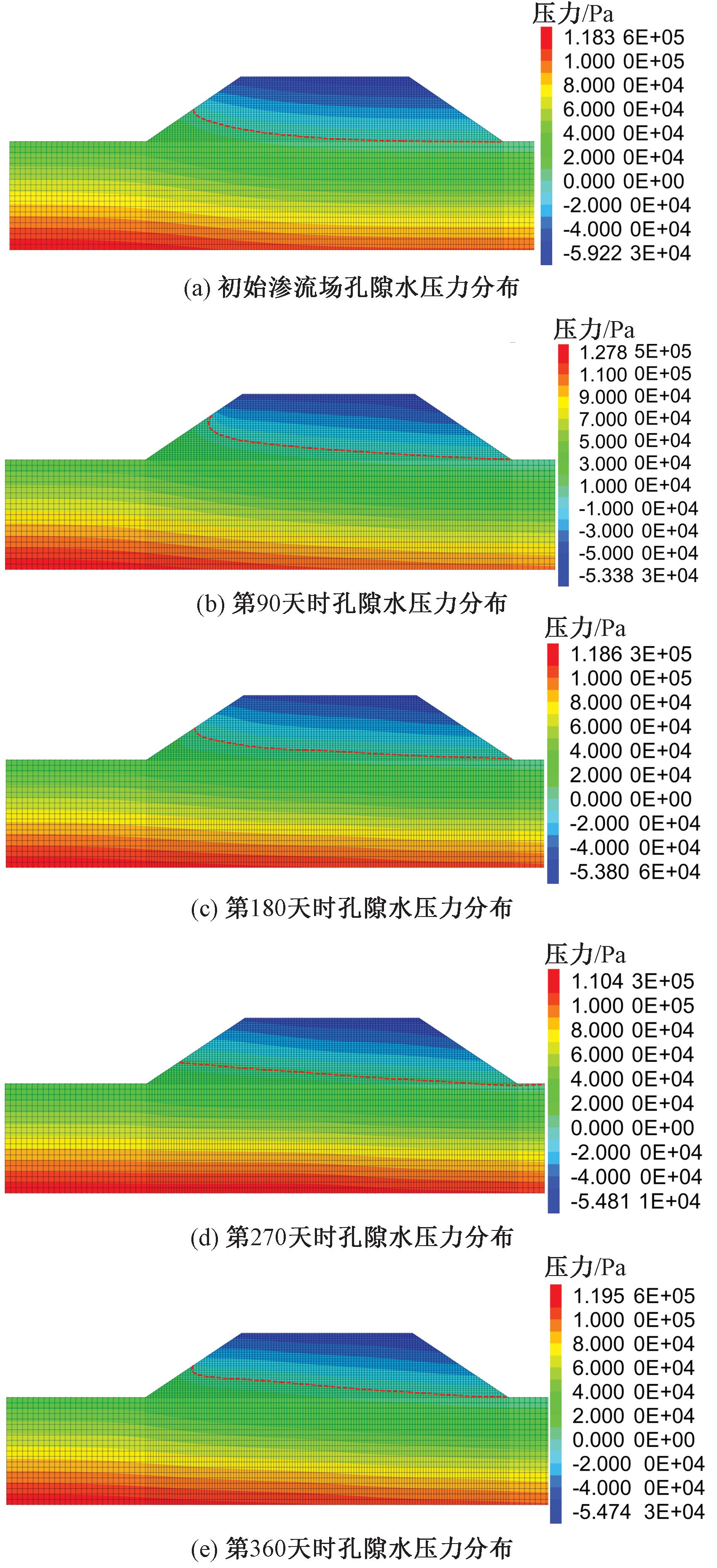
图6 水位季节性涨落下各时间点对应渗流场
Figure 6 The seasonal fluctuation of water level corresponds to the seepage field at different time points
图6中以红色虚线表示浸润线,即自由水面与路基横切面的交线。由于迎水面一侧的路基内部水位下降较快,当水分继续入渗到路基背水面一侧时,浸润线下降趋势趋于平缓,故整体呈现出向下凸的形状。对比分析各时间点与初始状态下的浸润线,可以看到迎水面一侧的浸润线变化幅度最大,靠近坡面处浸润线变化幅度与水位变化幅度基本保持一致,而路基中部的浸润线变化幅度相对较小,背水面一侧的浸润线基本保持不变,说明水位变化对靠近迎水面的土体影响更大,这是因为水分在路基内部渗流速度要远小于水位变化速度,路基内部渗流特征变化明显滞后于河流水位变化。
浸润线以下的土体处于饱和状态,随着深度的增加,孔隙水压力也在逐渐增大,最大孔隙水压力出现在模型左侧底部。浸润线以上的土体处于非饱和状态,负孔隙水压力(基质吸力)随着高度的增加而逐渐增大。进一步对比各时间点孔隙水压力大小可以发现,随着水位的升高,路基内部孔隙水压力总体呈现出上升趋势,负孔隙水压力逐渐减小,在水位下降过程中,路基内部孔隙水压力也随之减小,负孔隙水压力逐渐恢复。
为了分析水位变化下浸水拓宽路基内部孔隙水压力和饱和度随时间的具体变化情况,选取路基迎水面一侧的特征截面C-C′,选取不同时间点截面上各节点的孔隙水压力及饱和度如图7、图8所示,随着与迎水面距离的逐渐增大,路基内部土体的孔隙水压力与饱和度均呈现出逐渐减小的趋势。
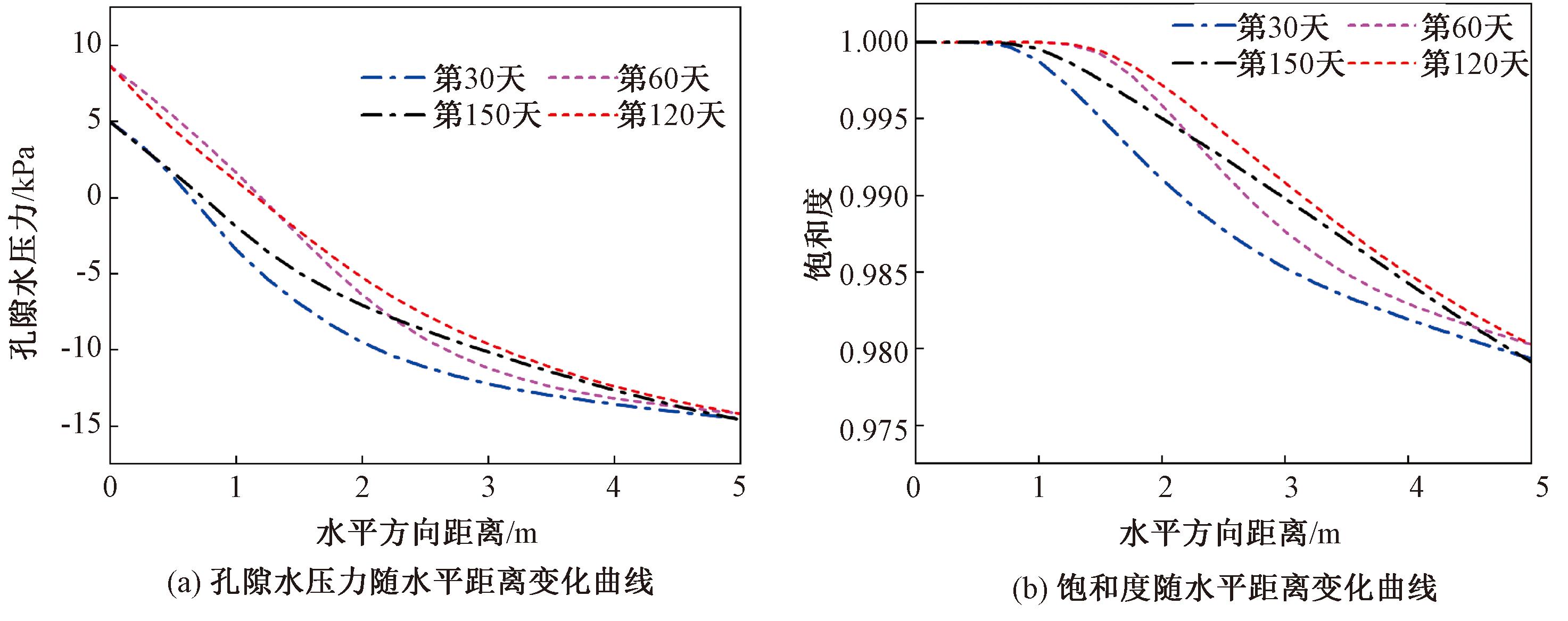
图7 高水位期不同时间点特征截面孔隙水压力及饱和度变化曲线
Figure 7 Pore water pressure and saturation change curves of characteristic cross sections at different time points during high water level period
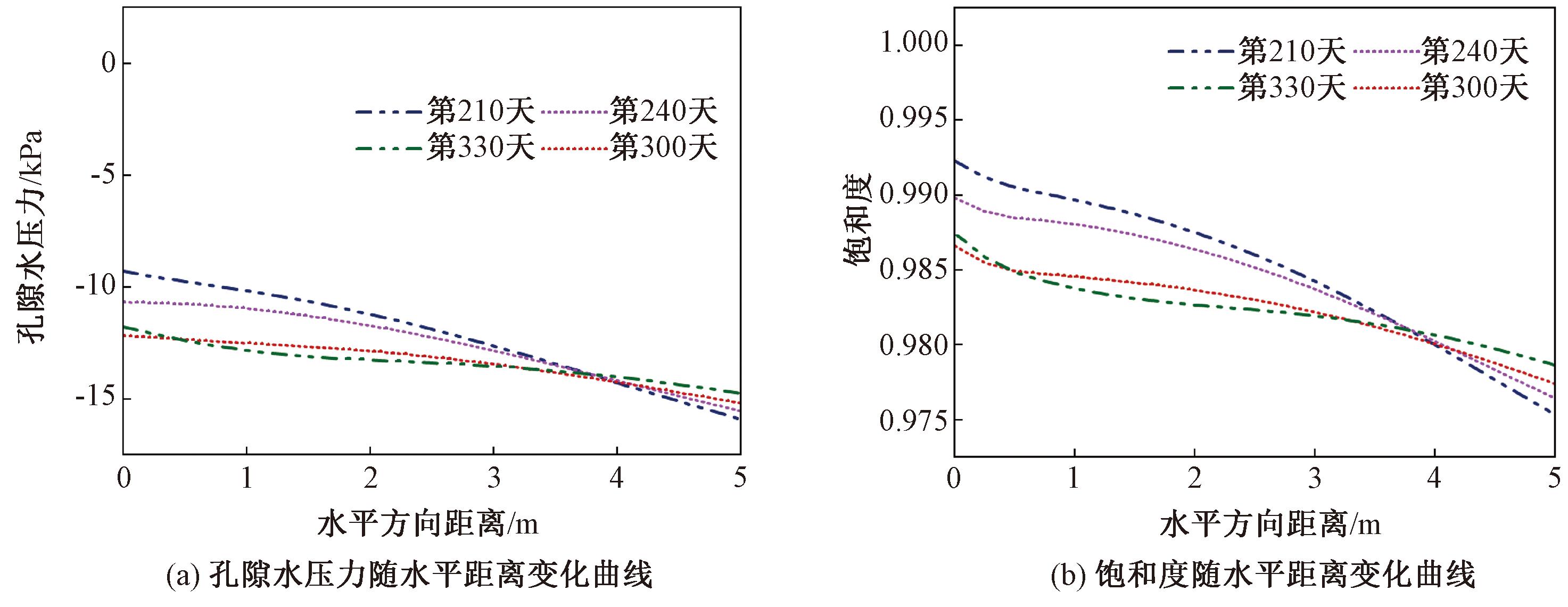
图8 低水位期不同时间点特征截面孔隙水压力及饱和度变化曲线
Figure 8 Pore water pressure and saturation change curves of characteristic cross sections at different time points during low water level period
由于水位变化近似遵循正弦函数的变化特点,以初始水位为界,河流具有较为明显的高水位期和低水位期。在不同水文期内,水位在上涨和下落的过程中会在两个不同的时间点处于同一个水位。例如高水位期的第30天和第150天、第60天和第120天,低水位期的第210天和第330天、第240天和第300天,都处于同一水位。现分别选取高低水位期不同时间点相同水位下特征截面的渗流特性进行对比研究,见图7和图8。
首先讨论水位处于高水位期时的渗流特征。当第30天和第150天的水位处于同一高程时,发现孔隙水压力随水平距离变化曲线形成了类似滞回圈的形态,并且第150天(水位下降期)的水压力显著高于第30天(水位上升期)。进一步对比这两个时间点的饱和度随水平距离变化曲线,也呈现出了类似的规律。这一现象的原因在于路基内部的水分渗流速度相较于水位的变化速度而言要慢得多,导致路基内部的渗流过程存在一定的滞后性。因此,在相同的水位条件下,脱湿过程中路基内部的孔隙水压力和饱和度始终高于吸湿过程。类似地,在对比第60 d和第120 d的数据时,也发现了这一显著特征。
当水位降低到初始水位之下,即水位在低水位期内变动时,发现负孔隙水压力与饱和度曲线随水平距离变化的幅度减缓。当第210天和第330天水位相同时,这两个时间点的孔隙水压及饱和度随水平距离变化曲线都有逐渐汇合的趋势,但与高水位期不同的是,曲线在近水区域不再交汇。第240天和第300天的曲线也出现了类似特征。这是因为在水位低于特征截面后,路基深处孔隙压力已达到一个相对稳定的水平,对水位变动的敏感度降低,而靠近水面区域则仍然存在着细微的变动。这一发现进一步验证了内部渗流的滞后性,即在水位下降后,水位的变动对路基深层内部渗流场的影响逐渐减弱。
3 路基稳定性分析
3.1 土体强度参数修正
本文基于强度折减法进行稳定性的计算。在应用FLAC3D中内置的强度折减法对浸水拓宽路基稳定性进行分析时存在两点缺陷,首先是忽略了饱和度对土体强度参数的影响;其次是在分析过程中对整体模型进行强度折减,无法准确反映边坡的真实失稳机制。
针对以上两点缺陷,借助FLAC3D内置的FISH语言通过指针调用单元饱和度函数,并根据路基典型黏土的黏聚力、内摩擦角、土体密度与饱和度的关系对单元强度参数和密度进行修正;同时在分析过程中采用局部强度折减法,将折减区域限制在上部路基中。经参数修正后的局部强度折减法可以用于准确分析浸水拓宽路基在水位变化过程中的稳定性。
3.2 水位变化对拓宽路基稳定性的影响
基于前文对水位季节变化下拓宽路基的渗流场计算结果,考虑饱和度对抗剪强度及重度的影响,采用局部强度折减法,对前述模型进行强度计算,并每30 d进行一次结果记录。剪应变增量代表了剪切应变的发展趋势,选取第90天水位最高时的最大剪应变增量分布云图进行分析,见图9。从图9(a)、图9(b)两图对比可以看出,即使处于最高水位,迎水面并未形成完整的塑性贯通区,最不利区域从迎水面坡脚水平向路基内部发展,但距离较短,且最大剪应变增量的整体数值较小。与之不同的是,背水面新旧路基交界处出现了较明显的塑性贯通区,最大剪应变出现在新路基坡脚处,潜在滑动面从坡脚逐渐向上延伸至坡顶,且剪应变增量整体大于迎水面。可见对于这类沿背水侧单侧拓宽的路基来说,背水面比迎水面更容易出现滑动失稳。
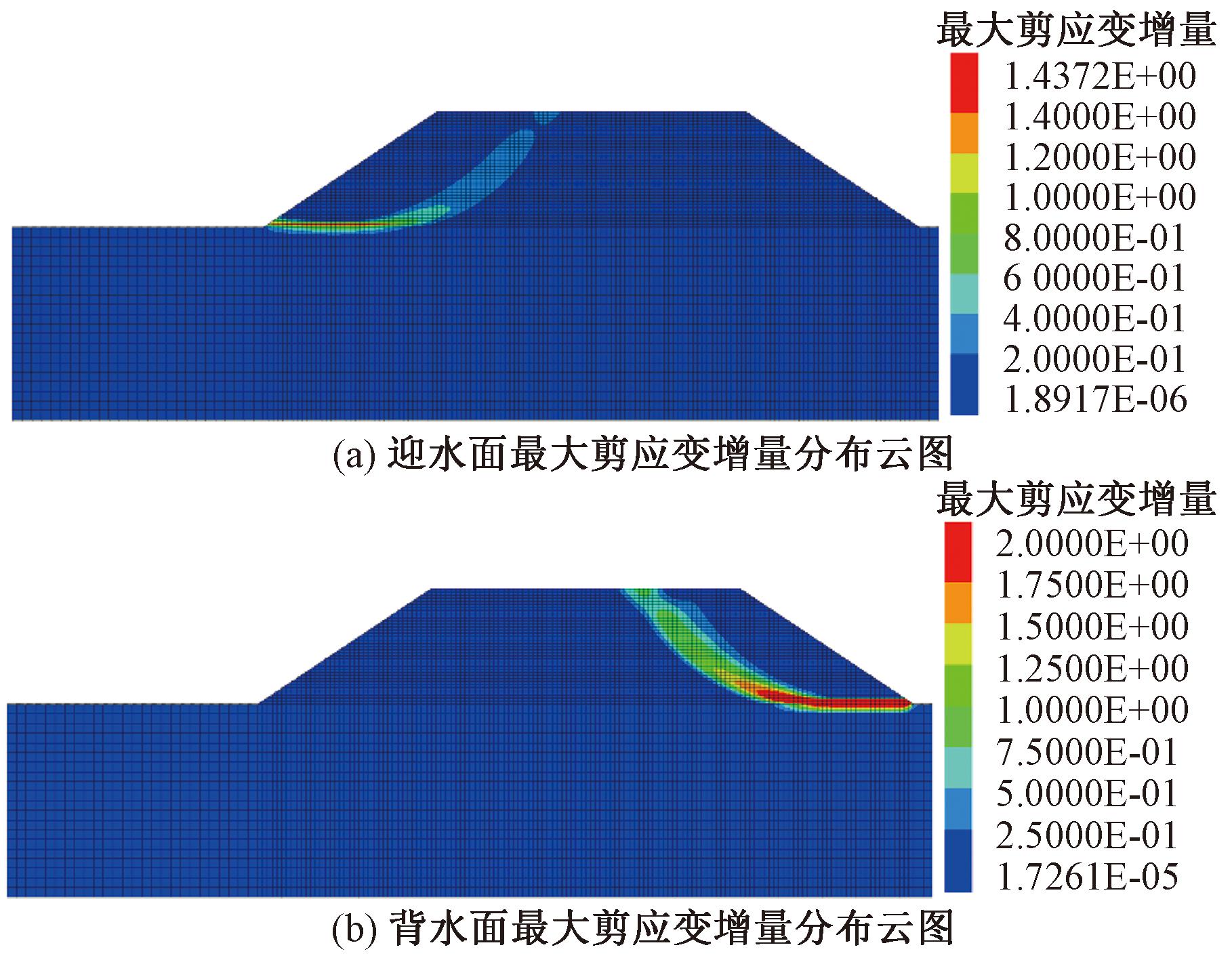
图9 第90天路基最大剪应变增量分布云图
Figure 9 Maximum shear strain increment distribution of subgrade on the 90th day
基于上述现象,进一步对各时间点路基稳定性进行计算,得到迎水面和背水面边坡安全系数随季节涨落的变化规律见图10。从图10中可以看出,在第90天时,迎水面的安全系数大于背水面。在水位季节性涨落过程中,迎水面边坡安全系数随水位上升而增大,随水位下降而减小,而背水面边坡正好与之相反。另外迎水面边坡稳定性对季节性涨落更敏感,其安全系数变化幅度最大可达22%;相比之下,背水面边坡在季节性水位涨落中的安全系数变化较为平缓,变化幅度仅为4.5%。
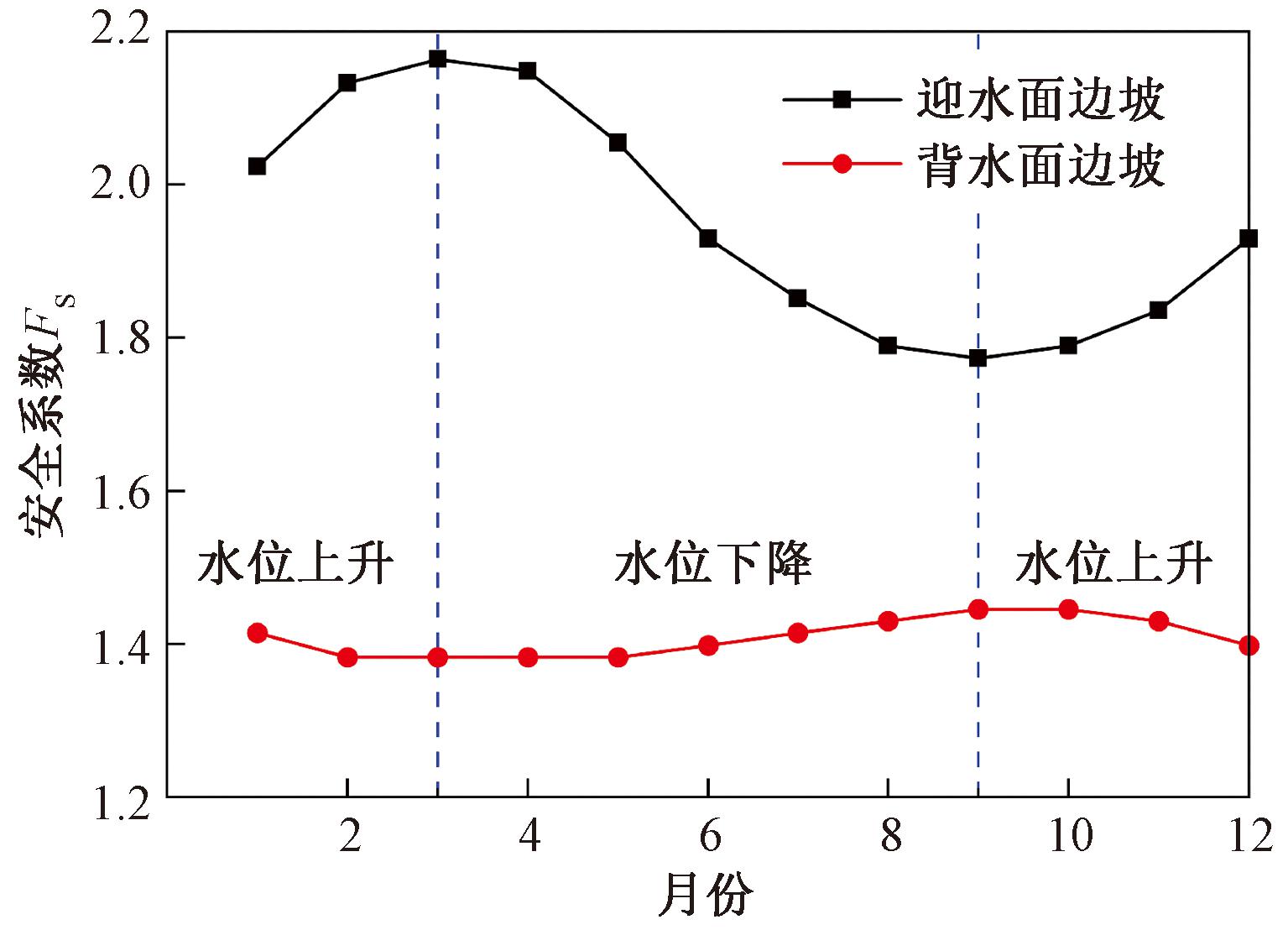
图10 安全系数随季节性涨落时间的变化曲线
Figure 10 Variation curve of safety factor with seasonal fluctuation time
由图10可观察到最小的安全系数出现在2~5月的背水面。选取最不利时间点浸水拓宽路基的最大剪应变增量云图如图11所示。从图11中可以看出,最大剪应变增量位于新路基坡脚处,剪切滑移面沿着新旧路基结合面由坡脚向坡顶发展,最终发展形成贯通的塑性区。原因是新旧路基填土抗剪强度存在明显差异,在荷载作用下新旧路基结合处容易产生应力集中,加上饱和度增加对土体抗剪强度的弱化作用,必然会导致浸水拓宽路基容易沿新旧路基结合处发生失稳破坏[13]。

图11 最不利时间点最大剪应变增量云图
Figure 11 Cloud map of the maximum shear strain increment at the most unfavorable time point
4 结论
本文利用FLAC3D构建水位季节变动下单侧拓宽路基模型,研究水位季节变化对浸水拓宽路基渗流特征和稳定性的影响,得到以下结论。
(1)路基迎水坡面深度一定范围内的渗流特性受季节性水位的影响呈现出不同的分布规律。处于高水位季节时,不同时期相同水位下的同一截面孔隙水压和饱和度随水平距离变化曲线形成类似滞回圈的形态,中间区域的孔隙水压和饱和度呈现出水位下降时间始终大于上升时间的特点。处于低水位季节时,不同时期相同水位的路基孔隙水压和饱和度在一定深度处达到一个固定值,但在近水区域水位下降期大于水位上升期。
(2)路基不同部位的稳定性受季节性水位变化的影响不同。迎水面边坡的稳定性对季节性水位涨落更为敏感,变化幅度最大可达22%。背水面边坡在季节性水位涨落中的安全系数变化较为平缓,变化幅度仅为4.5%。迎水面边坡安全系数呈现出与水位变化相一致的趋势,背水面则截然相反。
(3)拓宽路基背水面边坡比迎水面边坡更容易发生滑动失稳。水位季节性涨落过程中,最不利工况在水位最高时出现,潜在滑动面位于背水面新旧路基结合处,故在工程实际中应把浸水拓宽路基背水面新旧路基结合处作为加固重点。
[1] 郭建湖. 水塘地区高速铁路浸水路基结构优化设计研究[J]. 铁道工程学报, 2020, 37(12): 54-58, 69.GUO J H. Optimization design of soaking subgrade of high-speed railway in pond area[J]. Journal of Railway Engineering Society, 2020, 37(12): 54-58, 69.
[2] 任蓉. G5安康段水毁路基稳定性及防治技术研究[D]. 西安: 西安工业大学, 2024. REN R. Study on stability and prevention technology of subgrade damaged by water in G5 Ankang section[D]. Xi’an: Xi’an Technological University, 2024.
[3] 邓友生, 孟丽青, 蔡梦真, 等. 水泥土搅拌桩加固黄土路基稳定性研究[J]. 郑州大学学报(工学版), 2022, 43(3): 59-66.DENG Y S, MENG L Q, CAI M Z, et al. Research on stability of loess roadbed reinforced with cement-soil mixing piles[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 59-66.
[4] 张俊荣, 陈保国, 易贤龙, 等. 两侧水位变化时路堤渗流特征及稳定性分析[J]. 公路交通科技, 2017, 34(2): 35-41.ZHANG J R, CHEN B G, YI X L, et al. Analysis on seepage characteristics and stability of embankment with water level change on both sides[J]. Journal of Highway and Transportation Research and Development, 2017, 34(2): 35-41.
[5] 陈龙飞,林棋文,邓安,等.饱和-非饱和渗流作用下土质库岸路基稳定性分析[J].路基工程,2024(6):191-197.CHEN L F,LIN Q W,DENG A,et al.Stability analysis of soil reservoir bank subgrade under saturation-unsaturated seepage[J]. Subgrade Engineering,2024(6):191-197.
[6] LIU G D, ZHOU Z J, XU S Q, et al. Hysteresis of dam slope safety factor under water level fluctuations based on the LEM coupled with FEM method[J]. Computer Modeling in Engineering &Sciences, 2022, 133(2): 351-375.
[7] 何忠明, 史振宁, 付宏渊, 等. 水位下降对沿湖路堤边坡渗流特征及稳定性的影响[J]. 中南大学学报(自然科学版), 2014, 45(9): 3227-3233.HE Z M, SHI Z N, FU H Y, et al. Influence of water decline on seepage characteristic and slope stability of embankment along lake[J]. Journal of Central South University (Science and Technology), 2014, 45(9): 3227-3233.
[8] 李清华, 肖田, 邱博超, 等. 水位变化对路基边坡渗流场及稳定性影响分析[J]. 科学技术与工程, 2022, 22(13): 5403-5410.LI Q H, XIAO T, QIU B C, et al. Analysis of influence of water level change on seepage field and stability of subgrade slope[J]. Science Technology and Engineering, 2022, 22(13): 5403-5410.
[9] 刘修宇. 季节性浸水软土区路基稳定性研究[D]. 南京: 东南大学, 2018.LIU X Y. Study on stability of subgrade in seasonal immersed soft soil area[D]. Nanjing: Southeast University, 2018.
[10] BINIYAZ A, AZMOON B, LIU Z. Coupled transient saturated-unsaturated seepage and limit equilibrium analysis for slopes: influence of rapid water level changes[J]. Acta Geotechnica, 2022, 17(6): 2139-2156.
[11] 李刚, 郭艳玲. 高速公路改扩建新旧路基差异沉降影响因素分析[J]. 公路交通科技, 2021, 38(7): 22-28.LI G, GUO Y L. Analysis on influencing factors of differential settlement of new and old subgrade in expressway reconstruction and extension[J]. Journal of Highway and Transportation Research and Development, 2021, 38(7): 22-28.
[12] 吴珺华, 袁俊平, 杨松. 基于滤纸法的裂隙膨胀土土水特征曲线试验[J]. 水利水电科技进展, 2013, 33(5): 61-64.WU J H, YUAN J P, YANG S. Experimental study on SWCC of expansive soil with cracks using filter paper method[J]. Advances in Science and Technology of Water Resources, 2013, 33(5): 61-64.
[13] 袁以堂, 张杜锋, 吴春伟, 等. 高速公路改扩建软基换填拓宽段地基变形分析[J]. 公路, 2023, 68(3): 86-89.YUAN Y T, ZHANG D F, WU C W, et al. Analysis of foundation deformation in widening section of soft foundation replacement for expressway reconstruction and expansion[J]. Highway, 2023, 68(3): 86-89.