随着中国西电东送、南北互供、大区联网等一系列战略的实施,电网互联的规模与复杂度不断提升,电力系统的安全和稳定运行的控制难度也在增加[1-2]。虽然广域测量系统(wide area measurement system,WAMS)的逐步推广为实现电力系统的广域闭环控制构建了良好的基础,但是广域测量技术在利用开放式通信网络进行信息传输时不可避免地会出现信号延迟现象。已有大量研究成果表明,时滞的存在常常会引起系统控制设备失效,进而恶化电力系统的运行性能,甚至危及整个闭环系统的安全和稳定[3]。此外,实际电力系统中通常存在建模误差、外部干扰等不确定因素,导致系统出现不确定参数或未建模动态,忽略这些不确定因素将会使实际效果与理论计算仿真之间出现极大差异[4]。因此,分析计及随机时滞的不确定广域电力系统鲁棒稳定性具有重要实际意义。
目前,广大国内外学者对时滞电力系统稳定性研究已经取得了许多成果[5-12]。其中,基于Lyapunov稳定性理论的Lyapunov-Krasovskii (L-K)泛函方法应用最为广泛。该方法通过构造L-K泛函并对其进行求导得到基于线性矩阵不等式(linear matrix inequality, LMI)系统稳定的充分条件,其研究的重点和难点是如何构造恰当的L-K泛函和应用具有更小保守性的方法来处理泛函导数中的积分项。通过考虑电力系统多回路时滞的情况,李啸骢等[6]建立了含多时滞的系统模型,并在构建L-K泛函时加入二重积分项,从而降低了系统的保守性。钱伟等[7]通过构造含有时滞依赖矩阵的Lyapunov泛函,并利用新的积分不等式对时滞分割后的积分项进行处理,得到了保守性较小的变时滞电力系统稳定性判据。郭良栋等[8]分析了多时滞电力系统的稳定性问题,通过将自由矩阵代替L-K泛函中的部分正定对称矩阵,构造了新的泛函并利用Free Matrix-Based 积分不等式估计泛函导数,获得了具有更小保守性和计算复杂度的条件。郭建锋等[9]构造了一种含有多时滞积分项相互耦合的增广L-K泛函,并放松了泛函矩阵正定性的约束,从而得到了改进的稳定性准则。彭思源等[10]讨论了含有变时滞的广域电力系统稳定性,引入了关于时滞的二次函数并利用改进的不等式得到了新的判据。刘晓桂等[11]以单机无穷大系统为实例,推导出了励磁放大系数中的扰动项与时滞上界之间的变化关系,并利用自由权矩阵不等式技术获得了系统的稳定性条件。Chaibi等[12]、钱伟等[13]分析了变时滞电力系统的稳定性,但在处理泛函导数中的二次型积分项时,采用的不等式方法过于保守,导致所求的时滞上界较低。综合以上分析,上述研究对信号恒定时滞情况下广域电力系统的稳定性分析已经有了较为丰富的成果,但已有研究[14-15]表明,在实际电力系统中广域信号的时滞往往呈现出一定的随机特性并满足一定的概率分布,如果忽略了实际系统中时滞的随机特性和时滞大小的概率分布情况,将导致所得结论仍有较大保守性。因此,针对广域信号的随机时滞特性对电力系统稳定性的影响规律值得进一步的探索与研究。
基于以上讨论,本文进一步分析计及随机时滞的不确定电力系统鲁棒稳定性问题。首先,充分考虑电力系统中时滞的随机特性和不确定因素,建立具有时滞概率分布特征和参数不确定的系统模型;其次,为引入更多时滞相关的信息项,构造包含系统状态向量、随机时滞概率分布向量的增广向量和具有一重二重积分项的增广型L-K泛函,同时采用广义自由权矩阵不等式方法精确估计泛函导数,以得到保守性更小的稳定准则;最后,通过仿真结果分析验证本文所提方法的可行性和优越性。
1 时滞电力系统建模
一般来说,电力系统中的发电机动态模型可用如下微分方程组描述[7,10-13]:
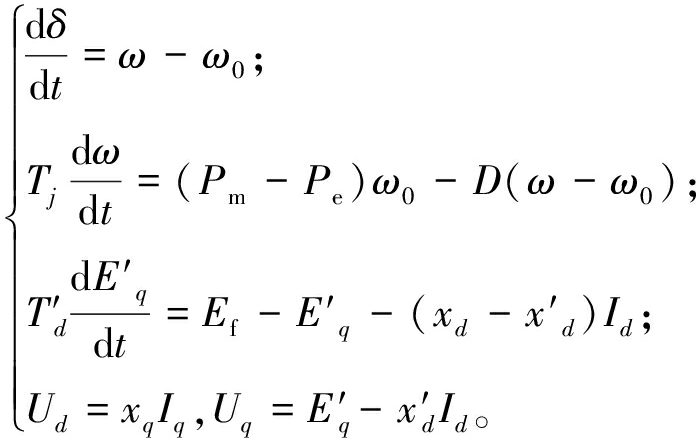
(1)
为了保障电力系统的可靠运行,运用自动电压调节励磁控制方式,考虑系统中存在的时滞现象,其动态方程可描述为[7]
(2)
综合式(1)和式(2),可以得到如下时滞电力系统的状态空间模型:
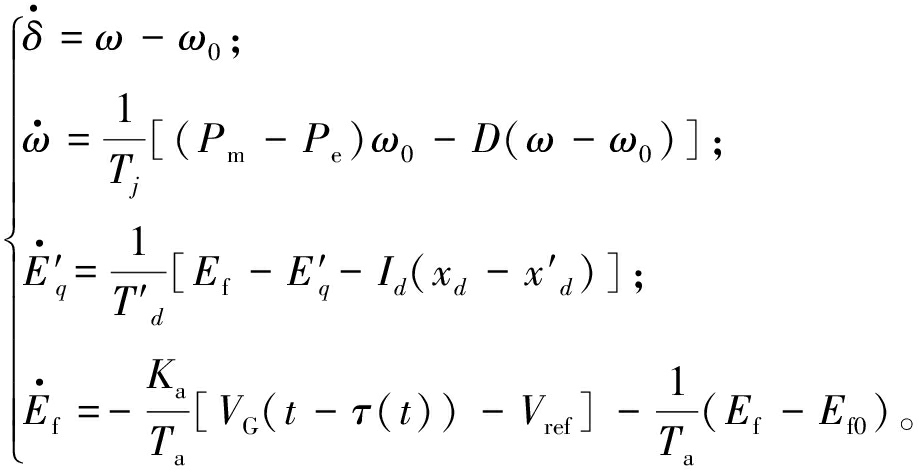
(3)
对式(3)在系统平衡点处进行线性化处理,进而推导出如下含时滞电力系统模型的一般形式[16-18]:
(4)
式中:
为系统的状态向量;φ(t)表示区间[-τ2,0]上连续可微的初始函数;τ(t)为系统区间变时滞,并满足0≤τ1≤τ(t)≤τ2,τ1和τ2为时滞的下限和上限且
为常数;A和Ad为系统状态矩阵。
根据文献[15]中对广域电力系统中TCP/IP通信网络时滞分布情况的测试,可知时滞在较小区间发生的概率较高,在较大区间内发生的概率较低,因此,本文考虑时滞的概率分布特点,将时滞区间分为两个子区间,即τ(t)∈[τ1,τ2]=[τ1,τ0)∪[τ0,τ2],
(5)
式中:
定义随机变量ρ(t),满足
假设随机变量ρ(t)服从伯努利(Bernoulli)分布,则有
(6)
式中:ρ0∈[0,1]为常量;E{ρ(t)}为随机变量ρ(t)的数学期望。
因此,将式(4)中的时滞建模为服从伯努利分布的随机时滞,可得
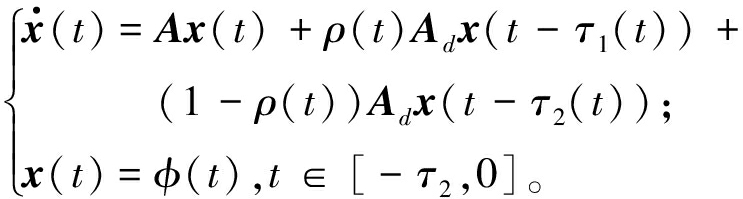
(7)
考虑实际系统在连续扰动与不断改变操作方式的状态下工作,建立如下含参数不确定性的模型:
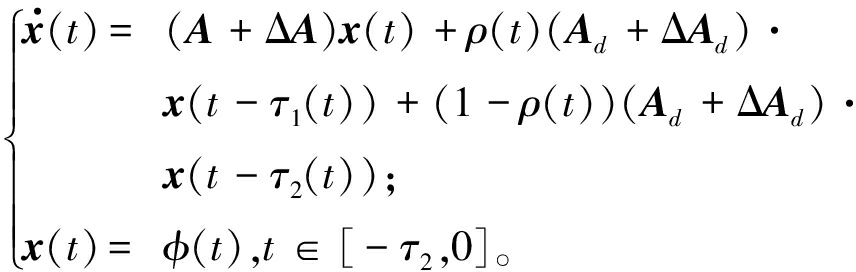
(8)
式中:ΔA和ΔAd为系统参数的不确定项,满足
其中,H、Ea和Ed分别为具有合适维数的常实数矩阵;F0为时变实矩阵,满足Lebesgue可测且
需要指出的是,相比较文献[3, 5-8],本文建立的模型(式(8))综合考虑了实际电力系统中的不确定性和时滞随机特性,此类问题的研究尚不多见。
为建立本文的主要结论,需要用到以下引理。
引理1[11] 给定适当维数对称矩阵Q、矩阵H、E和F(t),且F(t)满足FT(t)F(t)≤I,若使不等式Q+HF(t)E+(HF(t)E)T≤0成立,则充分必要条件是有∀ε>0,满足Q+ε-1HHT+εETE<0。
引理2[19] 对于任意对称矩阵G(G>0)∈Rn×n,适维矩阵L、M和标量α、β满足α<β且向量函数x∈[α,β]→Rn,那么下列积分不等式成立:
(9)
式中:φ0为任意向量,本文定义为φ0=egϑ(t),φ1=
2 随机时滞电力系统稳定性判据
本节通过构造一种新的增广向量和L-K泛函,并应用改进的泛函导数估计方法,得到随机时滞不确定式(8)的稳定性判据。为简化起见,将推导过程中出现的有关向量、矩阵定义如下:
ζ0(t)=[xT(t)
xT(s)ds
xT(s)ds
xT(s)ds]T;
ζ1(t)=[xT(t)xT(t-τ1(t))xT(t-τ2(t))xT·
(t-ρ0τ1(t))xT(t-ρ0τ1(t)-τ2(t))]T;
ϑ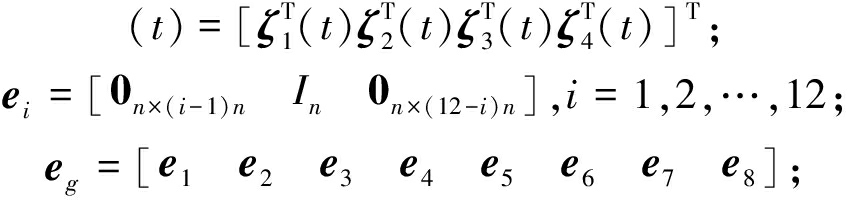
τ10=τ0-τ1;τ20=τ2-τ0。
下面给出保证式(8)均方渐近稳定的定理1。
定理1 对于任意已知标量τi(i=1,2,3)、μ、ε和0<ρ0<1,若有适维对称正定矩阵P∈R4n×4n,Qi∈Rn×n(i=1,2,3,4),Ri∈Rn×n(i=1,2,3)以及适当维数自由矩阵Lj、Mj、Nj、Xj(j=1,2),使得下列的LMI成立,则式(8)是均方渐近稳定的。
(10)
式中:
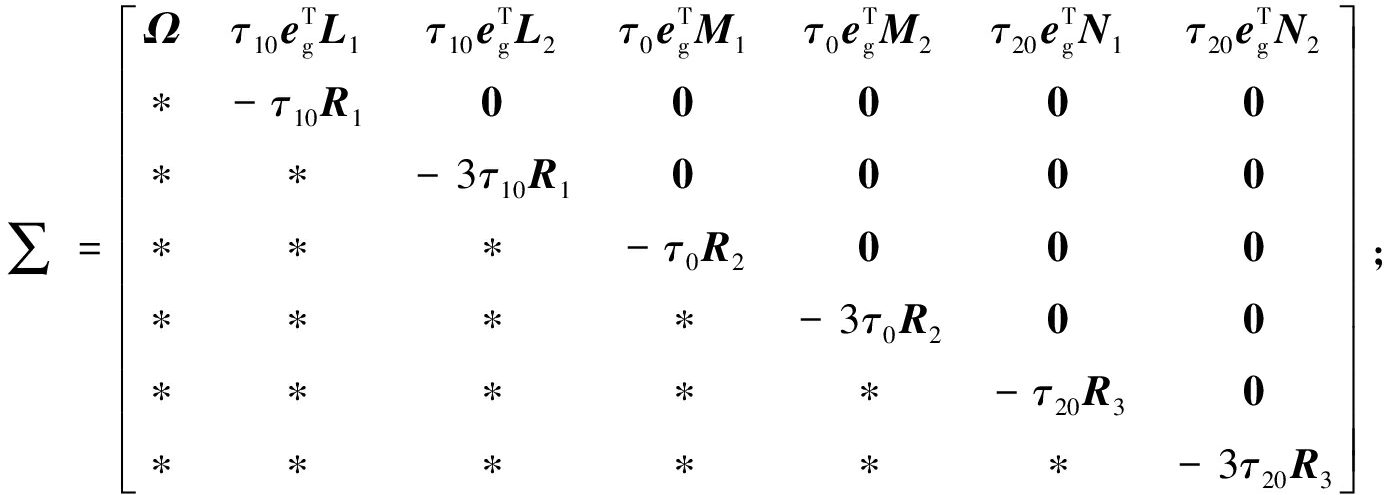
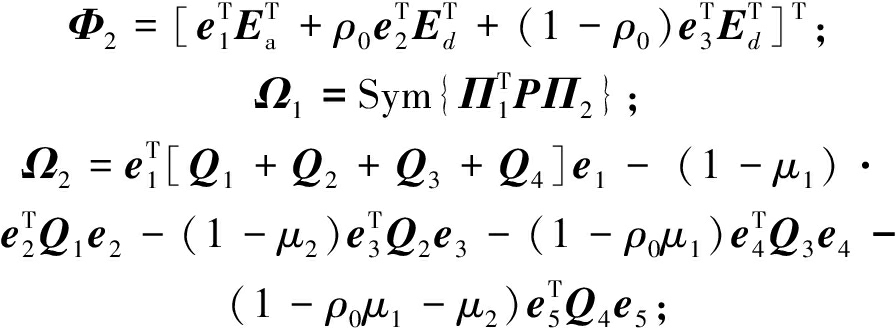
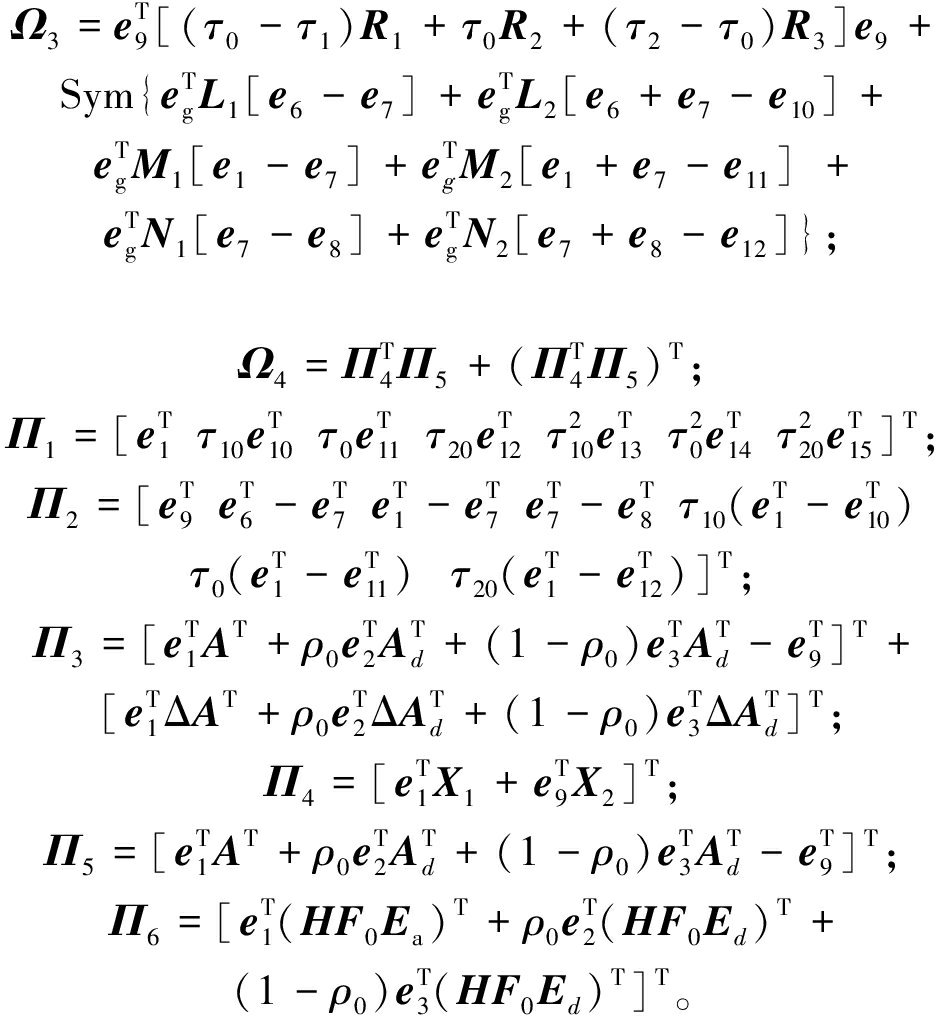
证明:对式(8)构造如下L-K泛函:
V(xt)=V1(xt)+V2(xt)+V3(xt)。
(11)
式中:
V2(xt)=
xT(s)Q1x(s)ds+
xT(s)Q2x(s)ds+
xT(s)Q3x(s)ds+
xT(s)Q4x(s)ds;
沿着系统轨迹(式(8))对V(xt)作无穷小算子可得
ϑT(t)Ω1ϑ(t)。
(12)
V2(xt)=xT(t)[Q1+Q2+Q3+Q4]x(t)-
(1-μ1)xT(t-τ1(t))Q1x(t-τ1(t))-
(1-μ2)xT(t-τ2(t))Q2x(t-τ2(t))-
(1-ρ0μ1)xT(t-ρ0τ1(t))Q3x(t-ρ0τ1(t))-
(1-ρ0μ1-μ2)xT(t-ρ0τ1(t)-τ2(t))·
Q4x(t-ρ0τ1(t)-τ2(t))=ϑT(t)Ω2ϑ(t)。
(13)
(14)
利用引理2对式(14)中的一重积分项进行估计可得
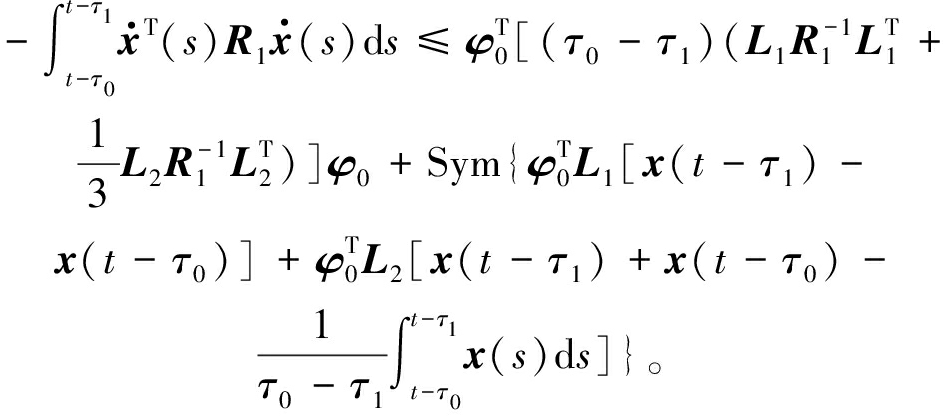
(15)
(16)
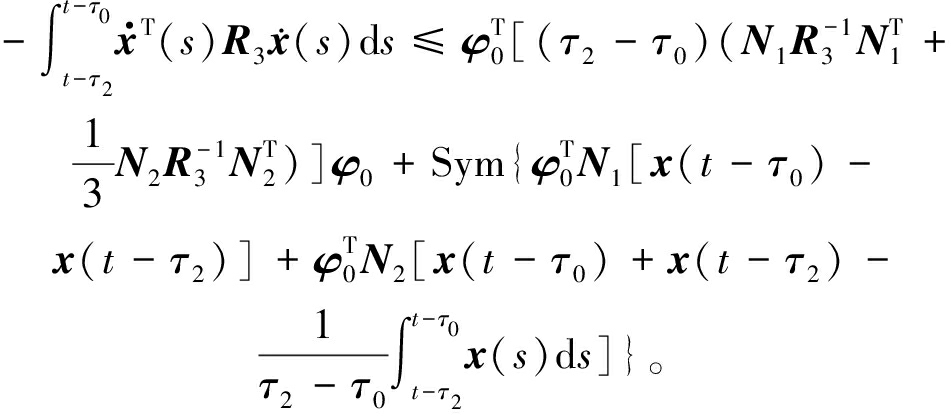
(17)
综合式(14)～(17),可得
V3(xt)=ϑT(t)Ω3ϑ(t)+Υ。
(18)
式中:
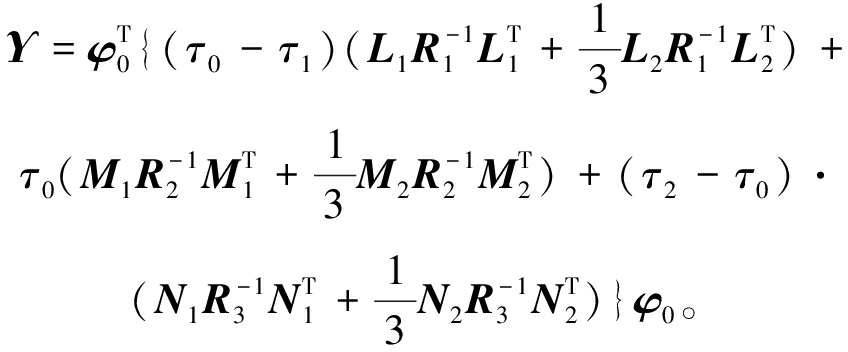
另一方面,对于任意适当维数矩阵X1和X2,由式(8)可得下列等式成立:
ρ(t)(Ad+ΔAd)x(t-τ1(t))+(1-ρ(t))·
(Ad+ΔAd)x(t-τ2(t))]=2ϑT(t)·
ϑ(t)=0。
(19)
将式(19)中的ΔA和ΔAd分别用HF0Ea和HF0Ed代替,可得
ϑ(t)=2ϑT(t)
ϑ(t)=
ϑ
ϑ(t)+
ϑ
ϑ(t)=0。
(20)
根据式(12)～(20)可以推出
V(xt)≤ϑT(t)Ω ϑ(t) 。
(21)
式中:
若
由引理1可知:
(22)
根据Schur补引理[20],推导可得式(22)等价于式(11),从而V(xt)<0,由Lyapunov稳定性理论可知,随机不确定时滞电力系统(式(8))是均方渐近稳定的,证毕。
当令式(8)中的不确定项ΔA=ΔAd=0时,在定理1的基础上,可推导出随机时滞电力系统(式(7))的均方渐近稳定判据如下。
推论1 对于任意已知标量τi(i=1,2,3)、μ和0<ρ0<1,若存在适维对称正定矩阵P∈R4n×4n,Qi∈Rn×n(i=1,2,3,4),Ri∈Rn×n(i=1,2,3)以及适当维数自由矩阵Lj、Mj、Nj、Xj(j=1,2),使得下列的LMI成立,则式(7)是均方渐近稳定的。
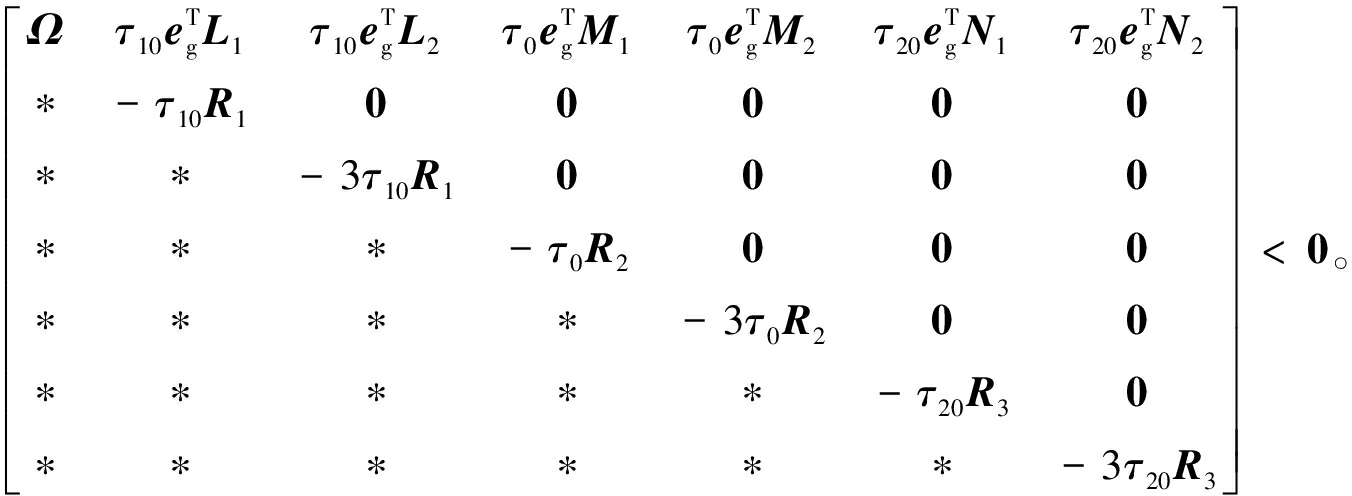
(23)
式中参数与定理1中的定义相同,这里不再列出。
3 仿真实例与结果分析
本节通过典型二阶时滞系统、单机无穷大系统和两区四机系统的模型参数进行仿真分析,说明本文所提方法的有效性和优越性。
3.1 典型二阶时滞系统
首先,通过典型二阶时滞系统验证本文所提方法的有效性,系统参数矩阵见文献[21],其中:
选取τ0=0.1,τ1=0,利用MATLAB对定理1中的LMI进行求解,可以得到给定不同μ和概率值ρ0下最大允许时滞上界τ2,如表1所示。由表1可知,相比较文献[21-23]的结果,定理1可以得到更大的时滞上界,表明定理1的保守性更小。此外,当增大时滞在[τ1,τ0]区间上的概率ρ0,时滞上界会随着概率的增大而增大,可以得到时滞发生的概率会影响系统稳定性的结论。
表1 给定不同μ和ρ0时最大允许时滞上界τ2
Table 1 Maximum allowable delay τ2 for given μ and ρ0
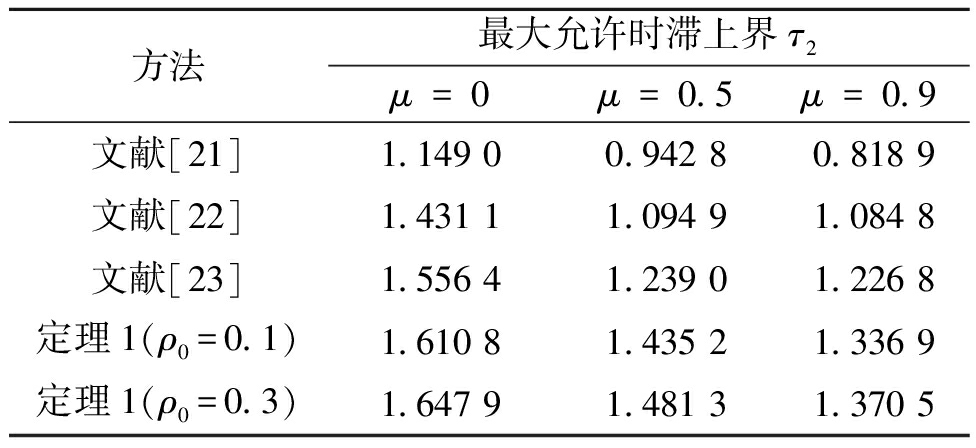
方法最大允许时滞上界τ2μ=0μ=0.5μ=0.9文献[21]1.149 00.942 80.818 9文献[22]1.431 11.094 91.084 8文献[23]1.556 41.239 01.226 8定理1(ρ0=0.1)1.610 81.435 21.336 9定理1(ρ0=0.3)1.647 91.481 31.370 5
当给定μ=0,ρ0=0.3时,由表1可知系统最大允许时滞上界为τ2=1.647 9,系统初始状态取x0=[-3,2]T,得到的状态响应曲线如图1所示。由图1可知,系统能够在较短时间内由振荡变为稳定状态,说明本文给出的稳定性判据是有效的。图2给出了时滞的分布区间。
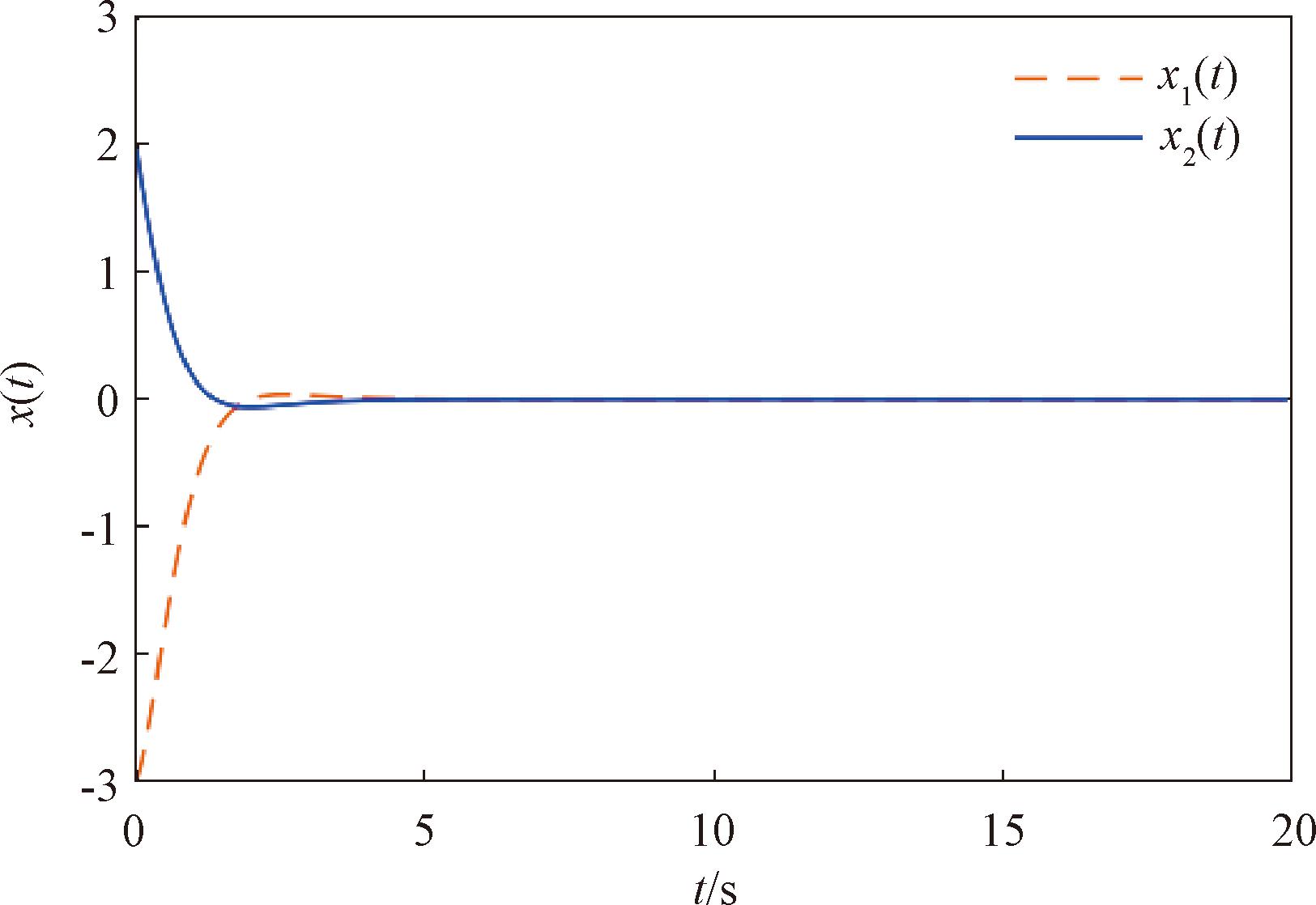
图1 系统在初始值[-3, 2]T下的状态响应曲线
Figure 1 State response of systems with initial values [-3, 2]T
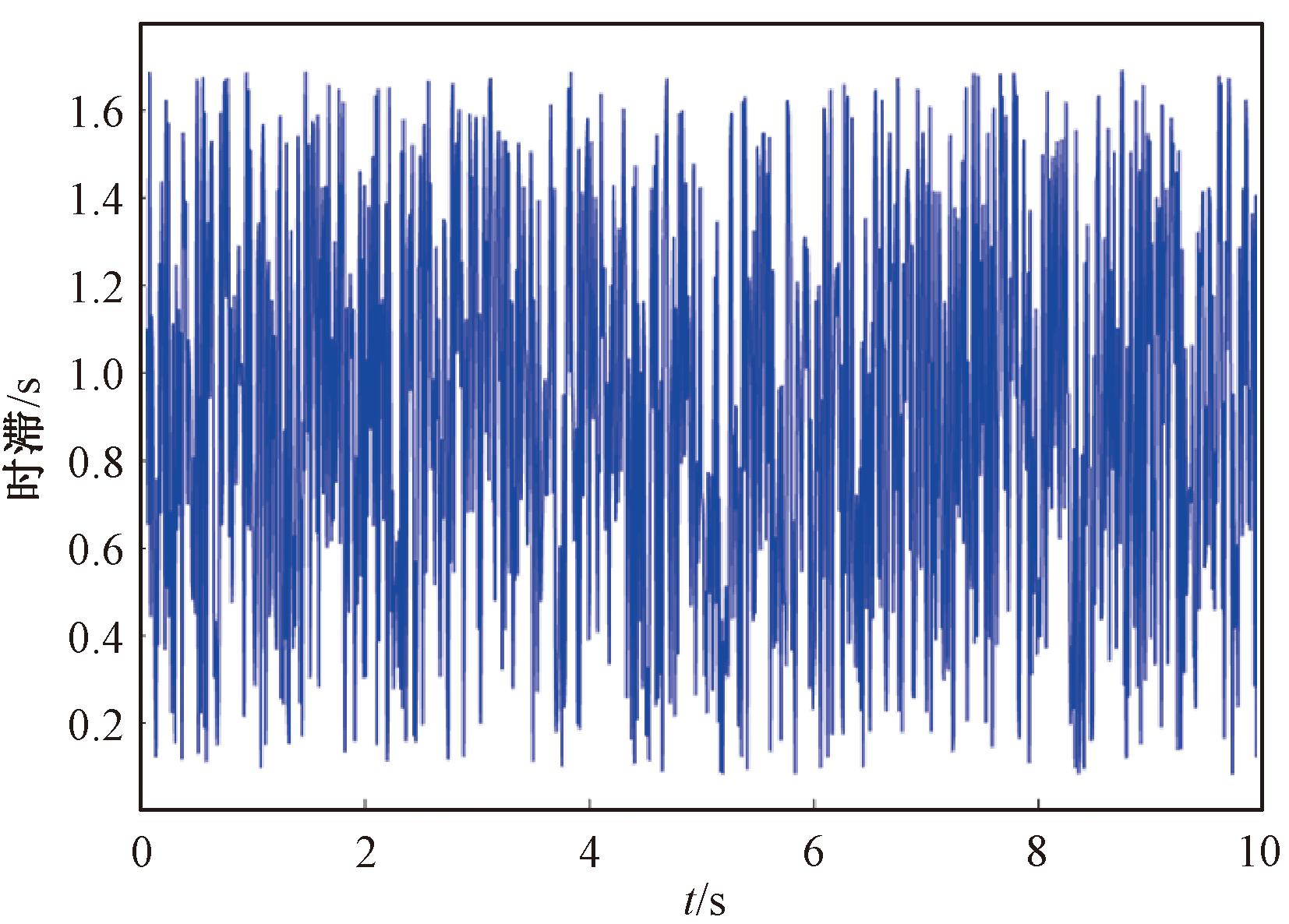
图2 时滞分布区间
Figure 2 Distribution interval of time delay
3.2 单机无穷大系统
选用单机无穷大系统验证本文方法有效性,系统具体参数见文献[16],其中矩阵A和Ad分别为
A=
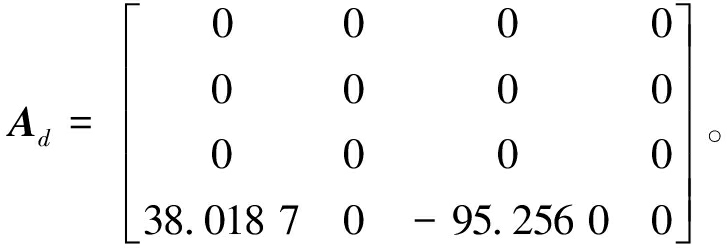
表2给出了文献 [13, 16-18]和本文方法所得到的单机无穷大系统最大允许时滞上界。由表2中的结果可知,利用本文推论1计算得到的时滞上界τ2=0.072 6 s,大于文献[13, 16-18]的结果,从而验证本文所提方法能够有效减小结论的保守性。
表2 不同方法求得的最大允许时滞上界
Table 2 Maximum allowable delay for different methods
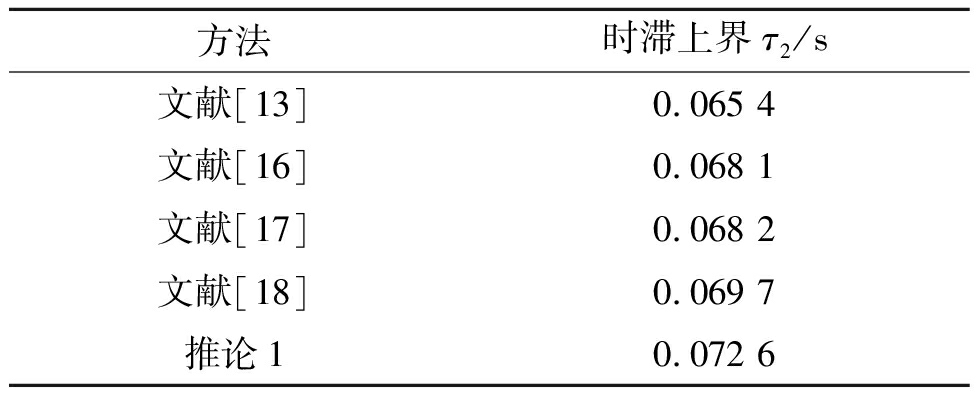
方法时滞上界τ2/s文献[13]0.065 4文献[16]0.068 1文献[17]0.068 2文献[18]0.069 7推论10.072 6
当取时滞上界τ2=0.072 s时,发电机功角响应曲线如图3所示。由图3可以看出,系统在最大允许时滞范围内是逐渐趋于稳定的,验证了本文得到的稳定性判据是有效的。然而,当时滞取0.073 s时,发电机功角响应曲线如图4所示。由图4可以看出,系统的状态是发散不稳定的。
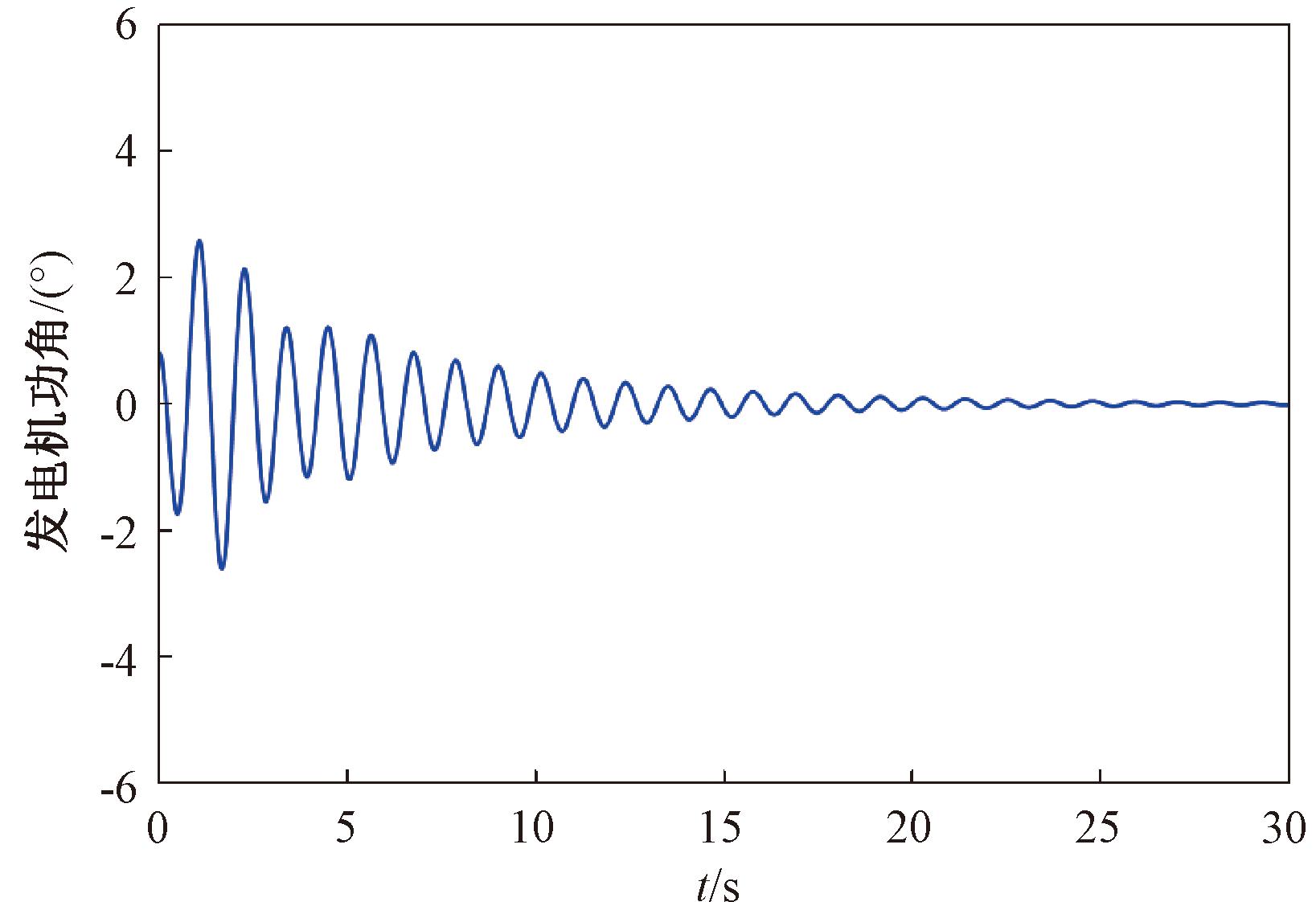
图3 τ2=0.072 s时发电机功角响应曲线
Figure 3 State response of rotor angle with τ2=0.072 s
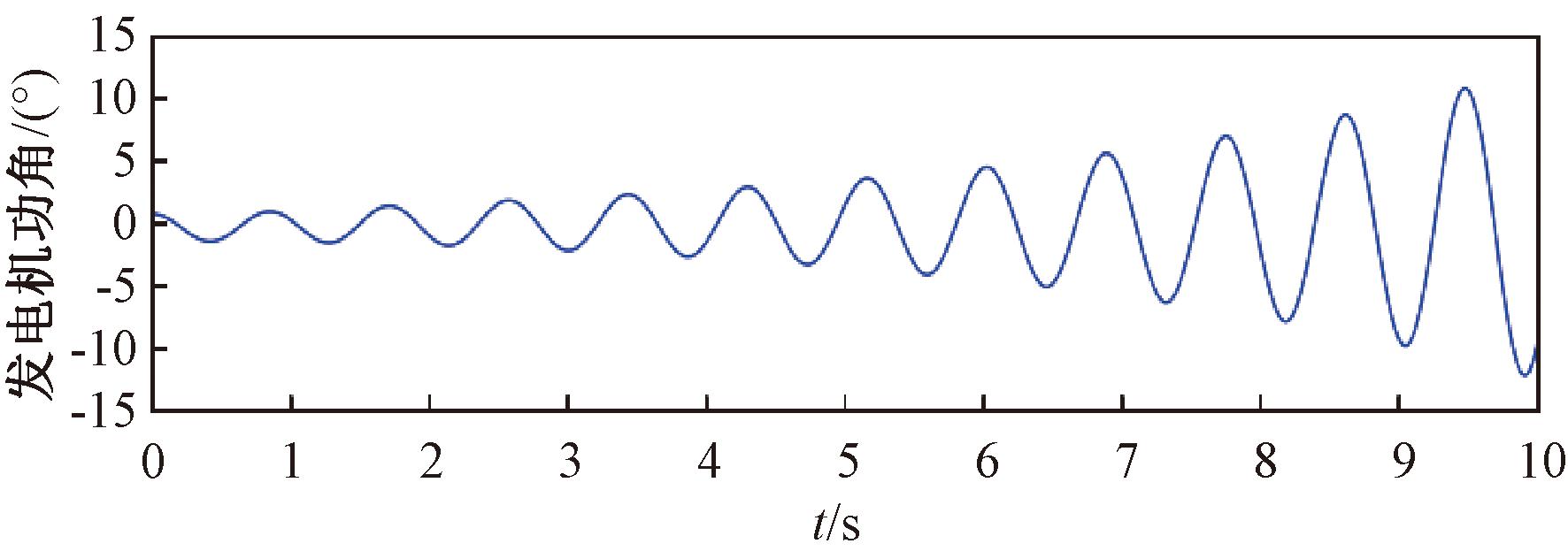
图4 τ2=0.073 s时发电机功角响应曲线
Figure 4 State response of rotor angle with τ2=0.073 s
以上为不计参数扰动的情况,现假设系统中存在励磁放大系数扰动,则放大系数实际可表示为
(24)
式中:r为扰动量。为研究扰动量r对系统稳定性的影响,令H、Ea和Ed分别为[7]
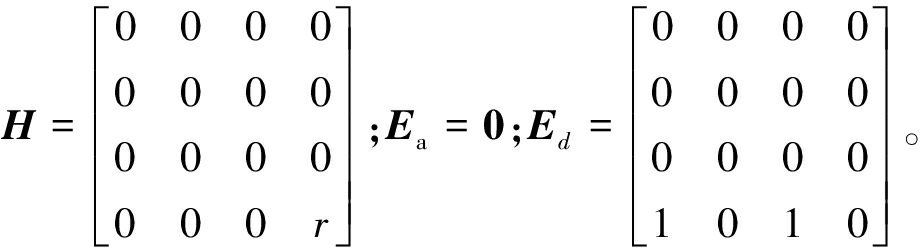
假设0≤r≤5,应用定理1可以求出r取不同值时不同方法得到的最大时滞上界,如表3所示。由表3可知,随着r的增大,系统的稳定裕度逐渐减小。相比较文献[5, 13, 16],在相同扰动下本文所得时滞上界最大,说明本文方法的鲁棒性更好。
表3 不同r求得的最大时滞上界
Table 3 Upper bounds of maximum time delay by different r
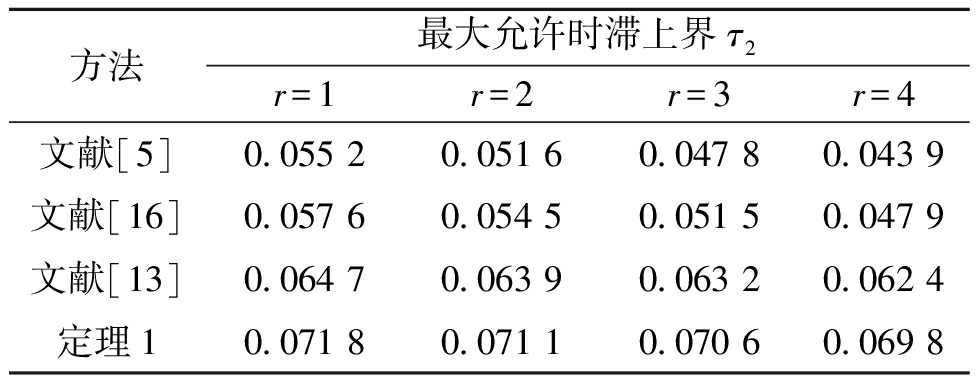
方法最大允许时滞上界τ2r=1r=2r=3r=4文献[5]0.055 20.051 60.047 80.043 9文献[16]0.057 60.054 50.051 50.047 9文献[13]0.064 70.063 90.063 20.062 4定理10.071 80.071 10.070 60.069 8
3.3 两区四机系统
为了进一步说明本文所得稳定性条件适用多机系统,本节以两区四机电力系统为研究对象,进行仿真验证,其系统模型如图5所示。
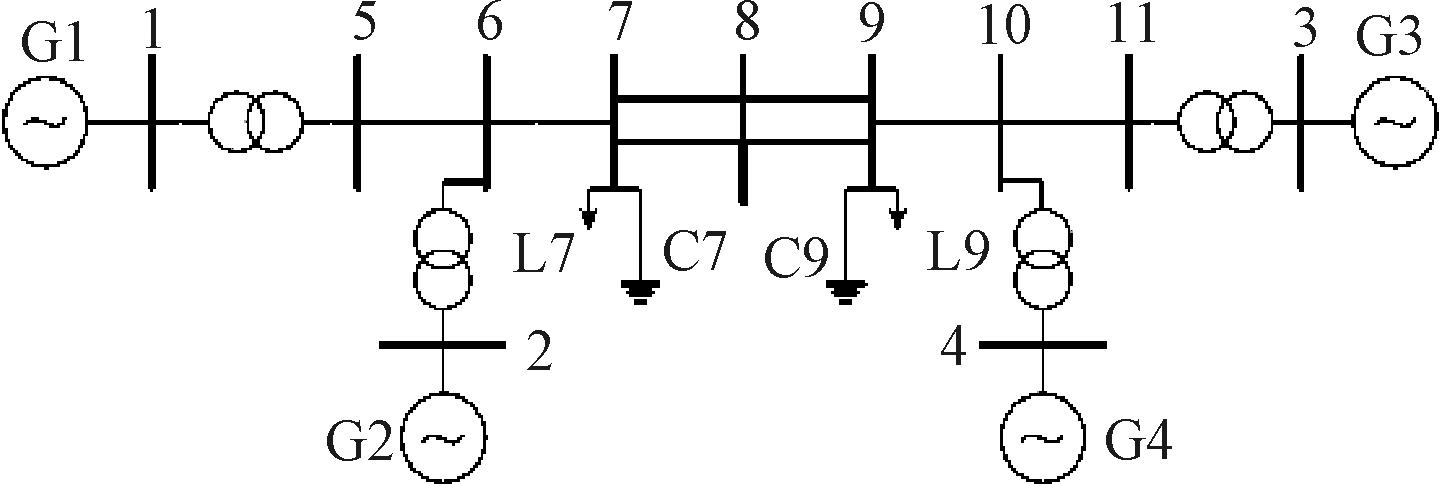
图5 两区四机电力系统模型
Figure 5 Two-zone four machine power system model
利用文献[24]中的建模分析方法,可以得到两区四机电力系统降阶后的状态矩阵A、Ad分别为
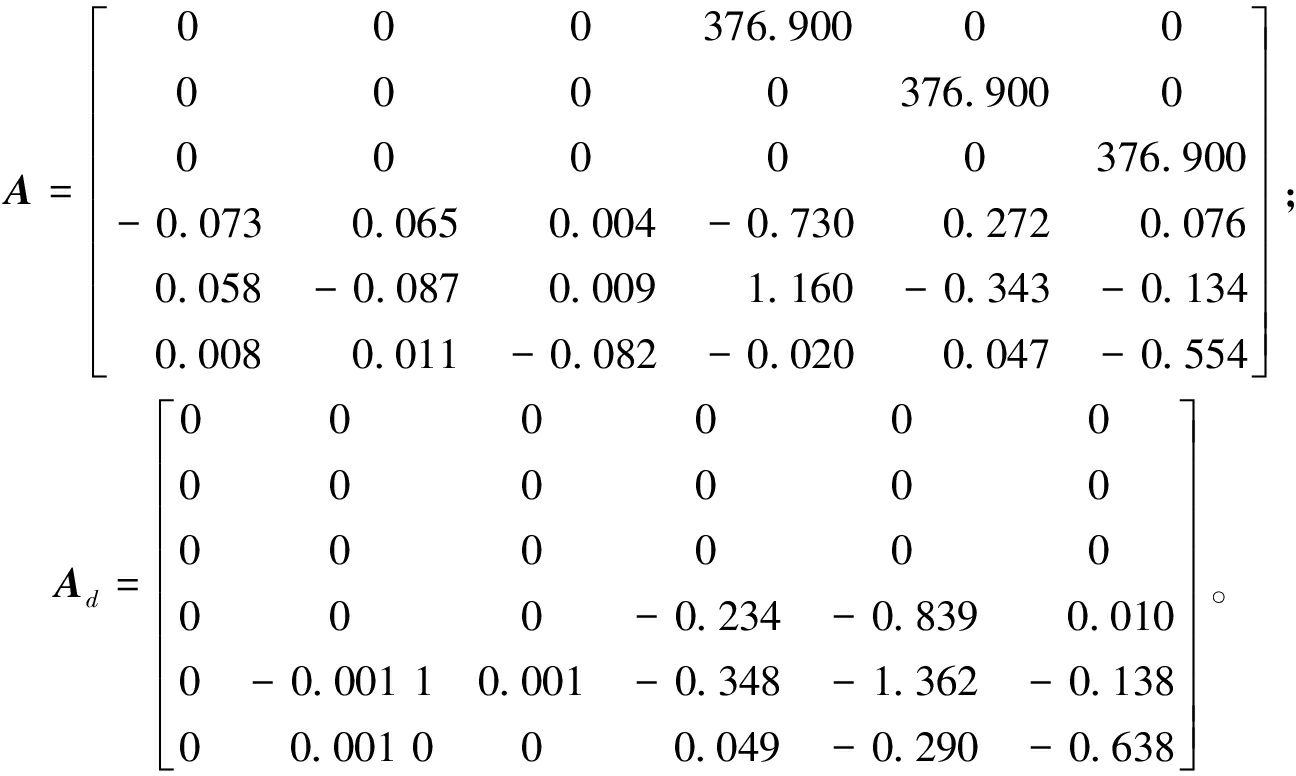
表4为不同判据得到的系统最大时滞上界对比。由表4可知,利用本文推论1求得系统的时滞上界为0.719 s,相比较文献[13, 20, 24-26]中的结果,推论1稳定性判据能够获得更大的时滞上界,表明了所提方法能够扩大两区四机系统的稳定运行区域,具有更小的保守性。此外,进一步说明了本文方法同样适用于多机电力系统稳定性分析。
表4 不同判据得到系统最大时滞上界对比
Table 4 Comparison of upper bounds of maximum time delay by different criteria
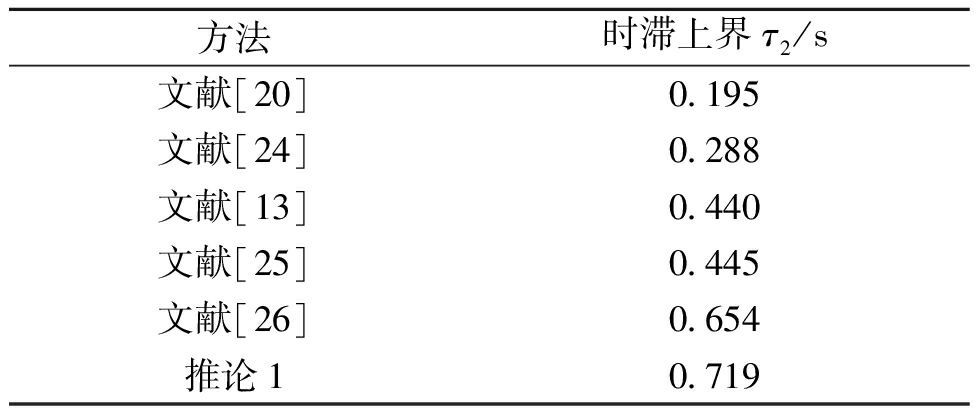
方法时滞上界τ2/s文献[20]0.195文献[24]0.288文献[13]0.440文献[25]0.445文献[26]0.654推论10.719
4 结论
针对互联电力系统中随机时滞和不确定性因素引起的稳定性问题,本文在L-K泛函方法的框架下,引入了伯努利分布描述随机时滞,构造了新的泛函并采用先进的不等式方法估计泛函导数。通过仿真实验,得出如下结论:
(1)考虑实际电力系统中时滞的随机特性和不确定性因素,建立了具有时滞概率分布和参数不确定性的随机时滞电力系统模型,和现有文献相比,建模方法更接近工程实际。
(2)构造了包括系统状态和时滞概率分布状态信息的增广向量和具有多重积分项的L-K泛函,并利用广义自由权矩阵积分不等式处理泛函导数,得到了保守性更小的稳定判据,提高了系统的时滞稳定裕度。
(3)时滞发生的概率影响结果的保守性,系统的时滞稳定裕度随着时滞发生的概率变化而变化;同时在相同参数扰动下,所提方法具有更好的鲁棒性。
[1] 王要强, 赵楷, 王义, 等. 基于平方根UPF的电力系统鲁棒预测状态估计[J]. 郑州大学学报(工学版), 2024, 45(3): 119-126,142.
WANG Y Q, ZHAO K, WANG Y, et al. Robust forecasting state estimation of power system based on square root UPF[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(3): 119-126,142.
[2] 陈中, 唐浩然, 邢强, 等. 计及随机时滞与丢包的电力系统广域信号预测补偿方法[J]. 电力系统保护与控制, 2019, 47(15): 31-39.
CHEN Z, TANG H R, XING Q, et al. A prediction compensation method considering stochastic time delay and data loss of power system wide-area signals[J]. Power System Protection and Control, 2019, 47(15): 31-39.
[3] 李宁, 孙永辉, 卫志农, 等. 基于Wirtinger不等式的电力系统延时依赖稳定判据[J]. 电力系统自动化, 2017, 41(2): 108-113.
LI N, SUN Y H, WEI Z N, et al. Delay-dependent stability criteria for power system based on wirtinger integral inequality[J]. Automation of Electric Power Systems, 2017, 41(2): 108-113.
[4] 王要强, 杨志伟, 王义, 等. 计及噪声和模型参数不确定的发电机动态状态估计[J]. 郑州大学学报(工学版), 2023, 44(6): 68-75.
WANG Y Q, YANG Z W, WANG Y, et al. Dynamic state estimation of generators considering noise and model parameter uncertainties[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(6): 68-75.
[5] 孙国强, 屠越, 孙永辉, 等. 时变时滞电力系统鲁棒稳定性的改进型判据[J]. 电力系统自动化, 2015, 39(3): 59-62.
SUN G Q, TU Y, SUN Y H, et al. An improved robust stability criterion for power systems with time-varying delay[J]. Automation of Electric Power Systems, 2015, 39(3): 59-62.
[6] 李啸骢, 王夏明. 基于积分不等式多时滞电力系统的改进稳定判据[J]. 电力系统自动化, 2020, 44(1): 59-66.
LI X C, WANG X M. Integral inequality based improved stability criterion for power system with multiple time delays[J]. Automation of Electric Power Systems, 2020, 44(1): 59-66.
[7] 钱伟, 吴嘉欣, 费树岷. 基于时滞依赖矩阵泛函的变时滞电力系统稳定性分析[J]. 电力系统自动化, 2020, 44(1): 53-58.
QIAN W, WU J X, FEI S M. Analysis on power systems stability with time-varying delay based on delay-dependent matrix functional[J]. Automation of Electric Power Systems, 2020, 44(1): 53-58.
[8] 郭良栋, 张旺. 基于积分不等式的多时滞电力系统稳定性分析[J]. 辽宁科技大学学报, 2021, 44(6): 470-476.
GUO L D, ZHANG W. Stability analysis of multiple time-delay power system based on an integral inequality[J]. Journal of University of Science and Technology Liaoning, 2021, 44(6): 470-476.
[9] 郭建锋, 钱伟, 费树岷, 等. 基于优化泛函的多时滞广域电力系统稳定性分析[J]. 电力系统保护与控制, 2023, 51(12): 47-57.
GUO J F, QIAN W, FEI S M, et al. Stability analysis for wide-area power systems with multiple time delays based on an optimized functional[J]. Power System Protection and Control, 2023, 51(12): 47-57.
[10] 彭思源, 肖会芹, 林惠潮. 时变时滞广域电力系统稳定性分析[J]. 湖南工业大学学报, 2021, 35(3): 62-67.
PENG S Y, XIAO H Q, LIN H C. Stability analysis of the wide-area power system with time-varying delay[J]. Journal of Hunan University of Technology, 2021, 35(3): 62-67.
[11] 刘晓桂, 王炜, 曾红兵, 等. 不确定时滞电力系统鲁棒稳定性分析[J]. 湖南工业大学学报, 2018, 32(4): 40-44.
LIU X G, WANG W, ZENG H B, et al. Robust stability analysis of the uncertain time-delay power system[J]. Journal of Hunan University of Technology, 2018, 32(4): 40-44.
[12] CHAIBI N, TISSIR E H. Delay dependent robust stability of singular systems with time-varying delay[J]. International Journal of Control, Automation and Systems, 2012, 10(3): 632-638.
[13] 钱伟, 蒋鹏冲, 车凯. 基于Wirtinger不等式的时变时滞电力系统稳定性分析[J]. 电力系统保护与控制, 2016, 44(23): 79-85.
QIAN W, JIANG P C, CHE K. Stability analysis for power system with time-delay based on Wirtinger inequality[J]. Power System Protection and Control, 2016, 44(23): 79-85.
[14] 罗小丽, 戴璐, 练红海, 等. 具有时滞概率分布的电力系统负荷频率稳定性分析[J]. 系统科学与数学, 2021, 41(5): 1245-1255.
LUO X L, DAI L, LIAN H H, et al. Load frequency stability analysis of power systems with probability distribution time-varying delays[J]. Journal of Systems Science and Mathematical Sciences, 2021, 41(5): 1245-1255.
[15] PENG C, ZHANG J. Delay-distribution-dependent load frequency control of power systems with probabilistic interval delays[J]. IEEE Transactions on Power Systems, 2016, 31(4): 3309-3317.
[16] 董朝宇, 贾宏杰, 姜懿郎. 含积分二次型的电力系统改进时滞稳定判据[J]. 电力系统自动化, 2015, 39(24): 35-40.
DONG C Y, JIA H J, JIANG Y L. Time-delay stability criteria for power system with integral quadratic form[J]. Automation of Electric Power Systems, 2015, 39(24): 35-40.
[17] 王蕾, 董朝宇, 贾宏杰, 等. 电力系统时滞稳定判据保守性差异量化评估方法[J]. 电力系统自动化, 2017, 41(10): 22-28.
WANG L, DONG C Y, JIA H J, et al. Diversity-based quantitative evaluation method of conservatism of time-delay stability criteria for power systems[J]. Automation of Electric Power Systems, 2017, 41(10): 22-28.
[18] 钱伟, 王晨晨, 费树岷. 区间变时滞广域电力系统稳定性分析与控制器设计[J]. 电工技术学报, 2019, 34(17): 3640-3650.
QIAN W, WANG C C, FEI S M. Stability analysis and controller design of wide-area power system with interval time-varying delay[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3640-3650.
[19] LIU H B, QIAN W, ZHAO Y J. State estimation of static neural networks with mixed delays: a new parameterized delay interval approach[J]. Journal of the Franklin Institute, 2023, 360(3): 1817-1834.
[20] YANG B, SUN Y Z. A new wide area damping controller design method considering signal transmission delay to damp interarea oscillations in power system[J]. Journal of Central South University, 2014, 21(11): 4193-4198.
[21] YAN H C, ZHANG H, MENG M Q. Delay-range-dependent robust H∞ control for uncertain systems with interval time-varying delays[J]. Neurocomputing, 2010, 73(7/8/9): 1235-1243.
[22] SUN Y H, LI N, SHEN M Q, et al. Robust H∞ control of uncertain linear system with interval time-varying delays by using Wirtinger inequality[J]. Applied Mathematics and Computation, 2018, 335: 1-11.
[23] YIN Z M, JIANG X F, WANG F. Stability criteria for systems with multiple probabilistic intervals time-varying delay[J]. International Journal of Control, Automation and Systems, 2020, 18(4): 877-885.
[24] 马静, 李俊臣, 李益楠, 等. 基于改进自由权矩阵与广义特征值的时滞稳定上限计算方法研究[J]. 电力系统保护与控制, 2014, 42(18): 1-8.
MA J, LI J C, LI Y N, et al. Research on time-delay upper-bound of power system wide-area damping controllers based on improved free-weighting matrices and generalized eigenvalue problem[J]. Power System Protection and Control, 2014, 42(18): 1-8.
[25] 汪豪, 钱伟, 郭建峰, 等. 变时滞影响下广域电力系统的H∞控制[J]. 电力系统保护与控制, 2021, 49(18): 70-80.
WANG H, QIAN W, GUO J F, et al. H∞ control for a wide-area power system with time-varying delay[J]. Power System Protection and Control, 2021, 49(18): 70-80.
[26] 钱伟, 高超. 基于凸组合方法的变时滞电力系统稳定性判据[J]. 电力系统保护与控制, 2015, 43(19): 37-42.
QIAN W, GAO C. A stability criterion for power system with time-varying delay based on convex combination[J]. Power System Protection and Control, 2015, 43(19): 37-42.