随着风电场规模的扩大和机组数量的增加,风力发电机之间的尾流干扰成为限制风电场效率提升的障碍[1]。相关研究表明,对于中大型风电场,上游风力机组的尾流干扰导致风电场的发电功率平均下降高达10%～25%[2]。主动尾流控制 (active wake control, AWC)[3]是风电场中削弱尾流效应的主要手段,该控制策略是基于某种解析尾流模型构建风电场模型,通过调整机组相关控制参数(如轴向诱导因子、转子转速、桨距角、偏航角等),来减弱上游机组的尾流效应,从而提高风电场总输出功率。
AWC策略主要分为两种:基于轴向诱导系数的风电场尾流控制方法[4]和基于尾流重定向的控制方法[5]。前者通过改变转矩和桨距角以改变轴向诱导因子,削弱下游尾流强度,提高风电场整体输出功率[6],该方法无须考虑尾流偏移量,但优化效果较为有限;后者则通过主动偏航改变上游风机后的尾流方向,提高下游风机的入流风速,从而提升风电场功率,从输出功率增长潜力来看,该方法更为直接有效[7]。
建立精确的风电场功率模型是风电场优化控制的前提。风电场功率模型主要包含风力发电机组模型和尾流模型,是一个复杂的多参数耦合非线性系统模型[8]。作为一种计算效率较高的尾流模拟方法,解析模型在风电场尾流优化控制领域具有重要的应用价值。相较于数值模拟方法,解析模型能够快速评估尾流效应对风电机组性能的影响,为风电场的智能化管理提供了可靠的理论支撑。Guo等[9]应用随机森林方法构建了风电场的数据驱动尾流模型,该模型有很好的准确性。Sun等[10]基于Jensen尾流模型,应用人工神经网络和风场实测数据构建了多台风机的尾流功率模型,用于处理风电场级的功率优化问题。焦小敏等[11]基于BP神经网络辨识出尾流交互模型,并采用粒子群算法求解风电场控制策略,以优化输出功率。Rak等[12]对风电场产量最大化挑战进行全面且一致的分析,得出基于高斯形状的Bastankhah模型风电场输出功率优化效果更好的结论。在应用AWC技术对风电场进行功率优化时,所选取的优化方法包括粒子群算法[13]、贝叶斯方法[14]、模型预测控制方法[15]等经典理论。
风电场的数值模型能有效降低计算成本,基于数据驱动的神经网络模型就是一种擅长对多输入多输出系统进行建模的工具[16]。针对风电场尾流控制与功率协调优化问题,本文提出了一种融合深度学习和群体智能的风电场偏航优化框架。首先,基于Informer网络建立风电场的输出功率等效模型;其次,采用粒子群优化算法求解以偏航角为优化变量的场级功率最大化问题;最后,利用实际风电场的布局和风况的相关数据验证所提方法的有效性。实验结果表明,基于Informer建立的等效模型相比于LSTM、GRU、RNN和Transformer有更高的建模精度,能够更好地满足后续的优化控制需求,同时,所提出的基于Informer等效模型与粒子群优化算法的优化策略可以显著降低上游风机尾流对下游机组的影响,提升风电场的整场输出功率。
1 风电场功率转换模型
1.1 风电场功率转换理论模型
本研究提出了一种基于偏航控制的尾流优化策略,通过调整上游风机的偏航角,使其尾流中心与下游风机叶轮中心产生偏移,这种方法能够有效降低尾流效应对下游风机的不利影响,减少能量损失,提升风电场的整体发电量。
在传统控制中,偏航控制使风轮偏转为正对入流风方向。但在尾流控制中,偏航以风轮不正对入流风为控制目标,使尾流方向发生偏转从而偏离下游风机,一定程度上抑制了由尾流引起的下游风速下降。风机偏航状态下的流管模型[17]如图1所示。
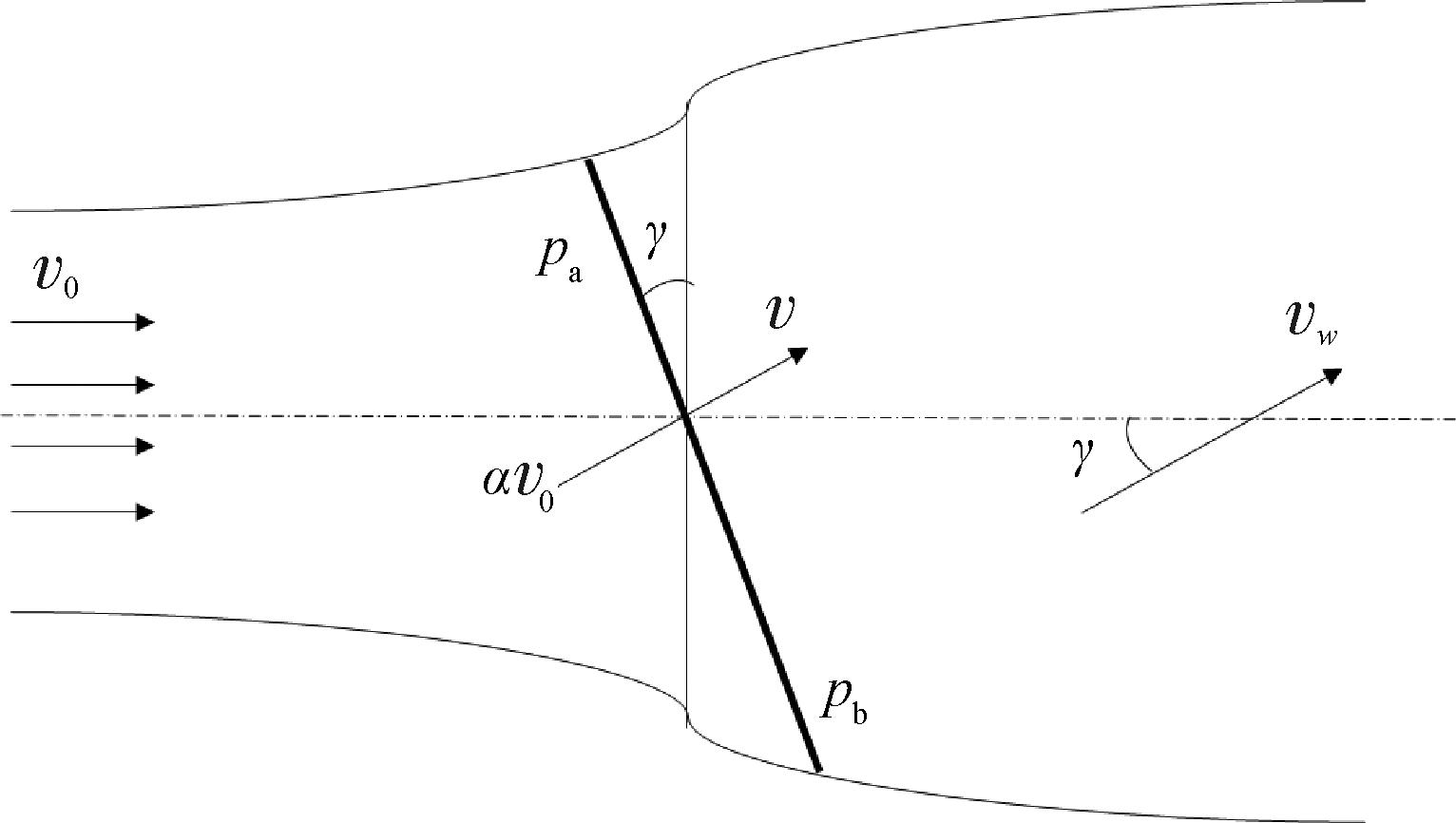
图1 风机偏航状态下的流管模型
Figure 1 Flow tube model under wind turbine yaw state
这是一个截面为圆形的气流管,风轮圆盘也称为致动盘,pa和pb分别为致动盘前后的压强;v0(t)、v(t)和vw(t)分别为无穷远处、致动盘处和尾流远端的风速;γ为致动盘固定偏转角。
根据动量守恒定理,可以得到作用在气体上的推力以及偏航状态下的风力机功率:
(1)
(2)
式中:α为诱导因子,为风机转子正后方风速的差值与自由风速之比;ρ为风电场当地的空气密度;A为风力机叶轮扫风面积。
尾流通常根据其形状和风速减小的比率来进行数学描述。常用尾流模型包括Jensen模型[18]、Bastankhah模型[19]等,其中Bastankhah模型更接近实际的尾流特征。当自由风流过风机时,在风机后方的风速可以表示为
v(d,r,α)=(1-δv(d,r,α))v0(t)。
(3)
式中:d为风机下游的轴向距离,即从风机到所研究尾流位置的纵向距离,m;r为尾流截面中的径向距离,即从尾流中心线到所研究位置的横向距离,m;δv(d,r,α)为风速损失系数。
图2显示了式(2)描述的风速曲线,其中D为风机转子直径。随着d和r的增加,风速逐渐恢复。
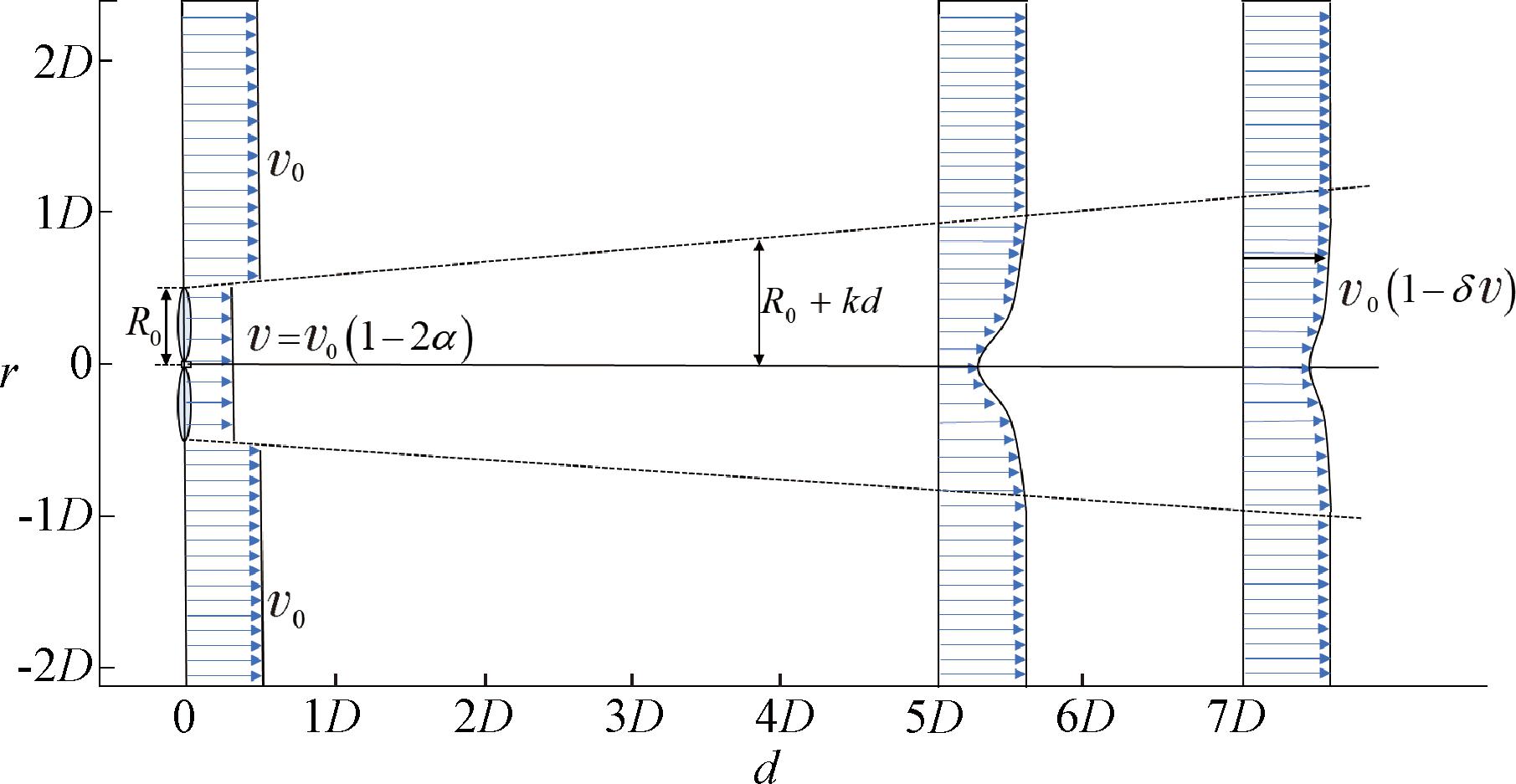
图2 Bastankhah尾流模型
Figure 2 Bastankhah wake model
由上述可知,上游风机的γ会影响风机后面的尾流强度。合并γ后,风速损失系数表示为
(4)
式中:R0为风机转子半径,m;k为尾流膨胀系数。
上游风机产生的尾流对下游风机的影响取决于尾流与下游风机转子之间的相对距离。如图3所示,上游风机j的尾流与下游风机i的转子之间的距离可以用轴向尾流间距dij和径向尾流间距rij描述[20]。
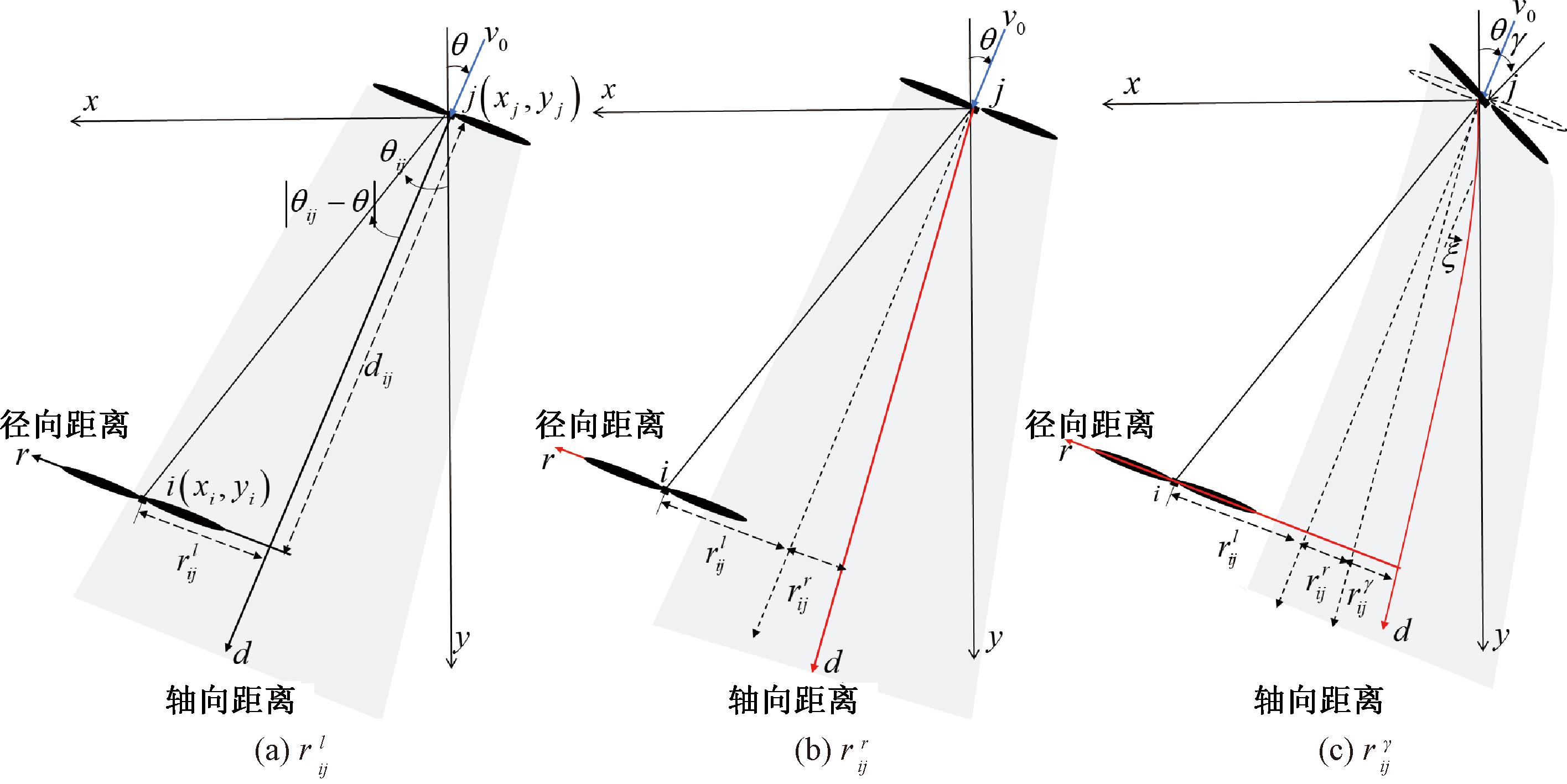
图3 偏航偏移角对尾流间距的影响
Figure 3 Influence of yaw angle on wake spacing
给定自由风向θ、风机i和j的位置i(xi,yi)和j(xj,yj),下游的轴向尾流间距dij为
(5)
将由于风机的相对位置、转子旋转和偏航角而产生的径向尾流间距分别表示为
和
径向尾流间距rij为
(6)
式中:
表示偏斜尾流轨迹的斜率;
鉴于多个上游风机形成多个尾流,风机i的风速亏损总量表示为风电场内N台风机的诱导因子矢量α=(α1,α2,…,αN)和偏航角矢量γ=(γ1,γ2,…,γN)的连续函数。在给定风力条件下,风机i转子上的风速表示为
(7)
式中:
为聚合风速亏损系数。
在尾流效应影响下,场内风机i所捕获的气动功率可以表示为α和γ的函数:
(8)
式中:α-i=α\{αi},γ-i=γ\{γi};Cp为风能利用系数。第i台风机的功率不仅受其自身偏航角和诱导因子的影响,还受其他风机的偏航角和诱导因子的影响。
由式(8)可以看出,通过控制轴向诱导因子和偏航角均可实现主动尾流控制,但控制偏航角的效果更为直接有效[7],所以本文只考虑偏航控制,风电场总输出功率可以表示为
(9)
式中:Pi为第i个机组的输出功率。
1.2 Informer神经网络原理
Informer模型[21]是一种改进的编码器-解码器结构深度神经网络模型,其整体框架如图4所示。编码器用于提取输入变量之间的依赖关系,而解码器则生成风电场总输出功率的预测结果。
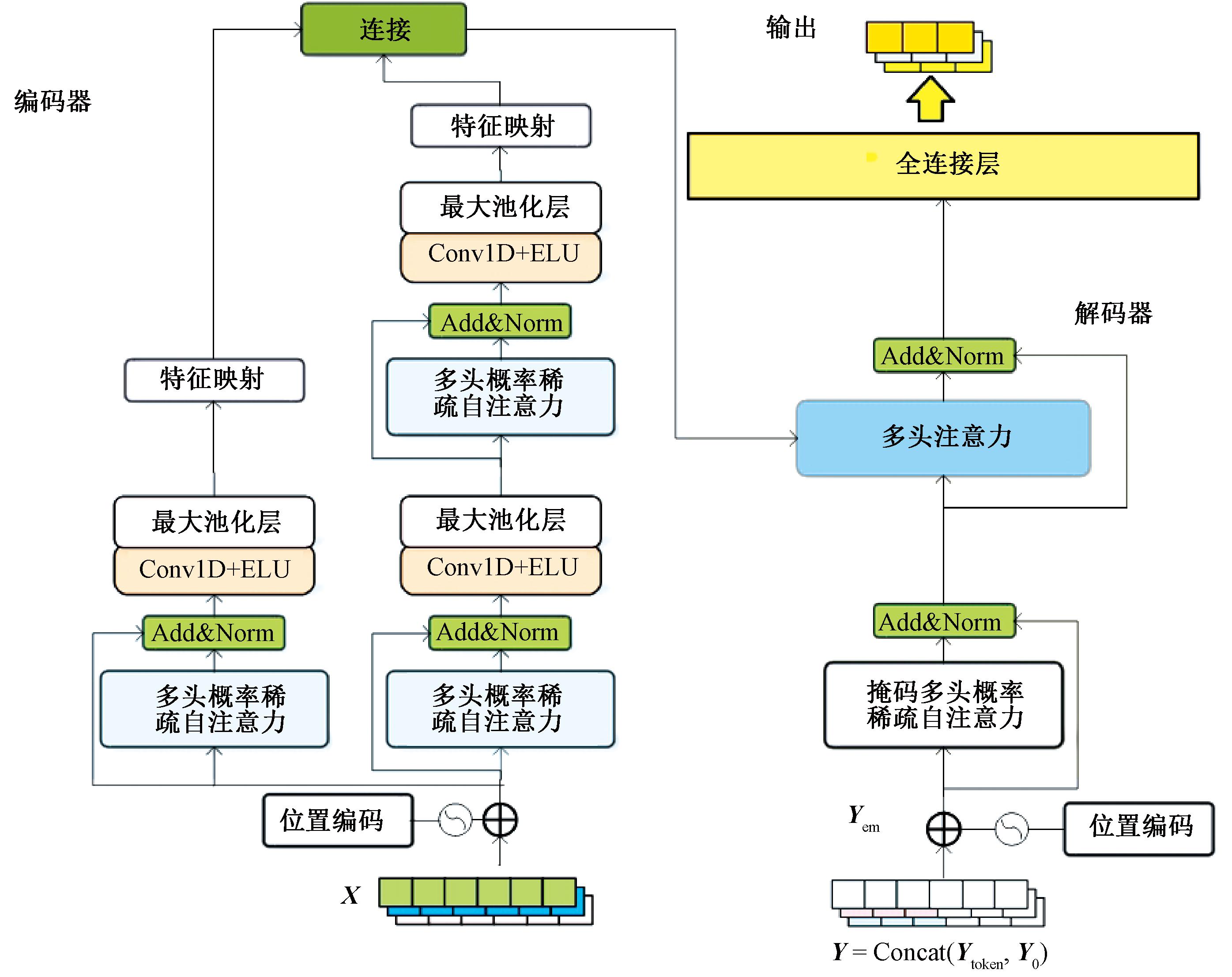
图4 Informer模型整体框架示意图
Figure 4 Schematic diagram of Informer model
1.2.1 概率稀疏自注意力模块
Informer模型中的概率稀疏自注意力模块通过对传统自注意力矩阵进行稀疏化处理, 降低了算法的计算复杂度。
与传统的 Transformer 架构相比,Informer 的自注意力机制同样接收3个关键输入矩阵:查询向量Q、键向量K以及值向量V,然后计算它们的点积,即
(10)
式中:Q∈RLQ×d,K∈RLK×d,V∈RLV×d;d′为输入维度。Softmax(·)操作是为了更好地体现查询向量q与每个键向量k之间的相关性;乘值矩阵V做加权目的是得到最终的注意力,突出与查询向量q更相关的序列部分。
用qi,ki和vi分别表示Q、K和V的第i行,那么qi的注意力系数为
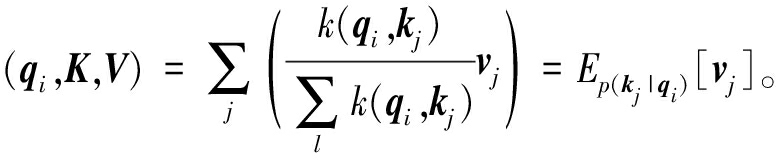
(11)
式中: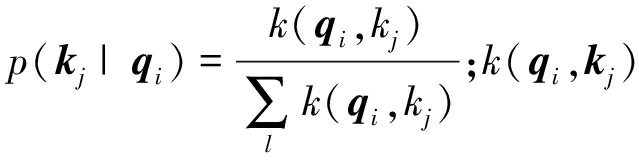
为非对称指数核函数
Transformer中的自注意力机制存在稀疏性问题,为了度量Q的稀缺性,使用KL散度(kullback-leibler divergence)计算Q的概率分布与其均匀分布的差异,其中qi的稀疏性的评价公式为
(12)
式中:公式右侧第1项是对所有键向量的LSE运算;公式右侧第2项为一个算术平均值。M(qi,K)值越大,表明qi的注意力权重分布越多样化,很可能包含了长尾分布中的主要注意力。
在计算M(qi,K)时需计算每个点积,复杂度为O(LKLQ)。采用查询向量的稀疏性评估近似得
(13)
随机筛选出
排名前u=LKln LQ个查询向量组成
得到概率稀疏自注意力的公式:
(14)
这里的概率稀疏自注意力机制对于每个键向量只需要计算O(ln LQ)次点积。
1.2.2 编码器
Informer的编码器采用注意力蒸馏机制对模型进行优化,通过将每层特征的时间维度减半,有效捕捉长序列数据间的依赖关系。Informer 模型引入蒸馏操作(Distilling)为优势特征提供更高的权重,并在一层中生成集中自注意力特征映射。具体地,从j层到j+1层的蒸馏操作为
(15)
式中:[·]AB表示多头概率稀疏自注意力及其他必要操作;Conv1D(·)为一维卷积,后面跟随ELU激活函数,然后经过MaxPool层进行下采样,将输入的长度变为原来的一半。
1.2.3 解码器
Informer的解码器由多头概率稀疏自注意力层、全注意力层、全连接层组成。历史数据和预测目标占位数据作为解码器的输入,采用掩码注意力机制进行概率稀疏自注意力的计算,避免算法自回归,再通过全注意力层生成序列特征,经过全连接层一次输出多步预测结果,提高预测效率。解码器的输入为
(16)
式中:
表示为预测序列保留的位置,
设置为0。
2 风电场偏航优化控制
2.1 风电场偏航优化问题描述
由式(1)可知,风电机组在偏航角为0°时,即其主轴线与来流风向完全对齐时,可达到最大功率输出。目前,在实际风电场中所采用的传统策略是使场内风机均正对来流方向。然而,这种传统策略忽视了尾流效应的影响,上游机组产生的尾流会显著降低下游机组的发电效率,导致整体发电量无法达到最优水平。为解决这一问题,本文提出通过主动偏航控制来优化机组运行状态。具体而言,通过调整上游机组的偏航角度,使其尾流偏离下游机组,从而实现风能资源在机组间的合理分配,最终提升风电场的整体发电量。在这一优化过程中,上游机组的偏航角为关键控制变量。
为了确定风电场中每台风机的最优偏航角,首先基于建立的风电场等效模型建立风电场整体功率最优化目标:
(17)
式中:
对于主动偏航控制,考虑偏航角的角度约束:
γmin≤γi≤γmax。
(18)
式中:γmin=-25°为偏航角最小设定值;γmax=25°为偏航角最大设定值。风机的偏航角不宜设置过大,否则风机的功率性能会明显下降,上游风机的功率损耗无法通过下游风机的功率增加来弥补[22]。
2.2 粒子群优化算法求解
粒子群优化算法[23]的核心在于对粒子位置和速度的动态调控。在该算法中,每个粒子在解空间中进行独立搜索,同时保留两个重要信息:个体历史最优解和群体全局最优解。粒子的运动方向由3个因素共同决定:当前速度方向、个体最优解方向以及群体最优解方向。算法的具体步骤如下:
步骤1 初始化规模为N的粒子群的随机位置和速度;
步骤2 计算粒子适应度值;
步骤3 比较粒子适应度值,若当前适应度present优于个体历史最优值pbest,则更新pbest; 若当前适应度优于群体全局最优值gbest,则更新gbest;
步骤4 若全局最优解gbest满足预设精度要求,终止迭代,输出最优解。否则,粒子根据式(19)和式(20)更新速度和位置,继续搜索:
v(k+1)=ωv(k)+c1r1(pbest(k)-present(k))+
c2r2(gbest(k)-present(k));
(19)
present(k+1)=present(k)+v(k+1)。
(20)
式中:ω为惯性权重;c1为自我学习因子;c2为种群学习因子。r1和r2为介于0和1之间的随机数。
3 验证与分析
为了验证所建立的等效模型的精度以及所提出的优化控制算法的有效性,基于FLORIS[24]搭建了风电场仿真模型。FLORIS软件是由美国可再生能源国家实验室研发的一款尾流特性建模工具,旨在用于风电场控制研究。
3.1 仿真设置
为验证所提出的偏航优化控制算法在实际工程中的适用性,考虑到现有风电场在设计阶段已通过优化布局降低尾流影响,本文采用真实风电场布局开展仿真实验。
Penmanshiel实际风电场由14台风机组成,其场内风电场布局如图5所示。仿真测试中所采用的风电机组型号为NREL 5 MW机组[25],功率、CT-风速如图6所示,风电机组参数见表1。
表1 NREL 5 MW风电机组参数
Table 1 NREL 5 MW wind turbine parameters
参数取值额定输出功率Pg,rated/MW5切入风速vin/(m·s-1)3额定风速vrated/(m·s-1)11.2切出风速vcut/(m·s-1)25叶片半径R/m63轮毂高度H/m90
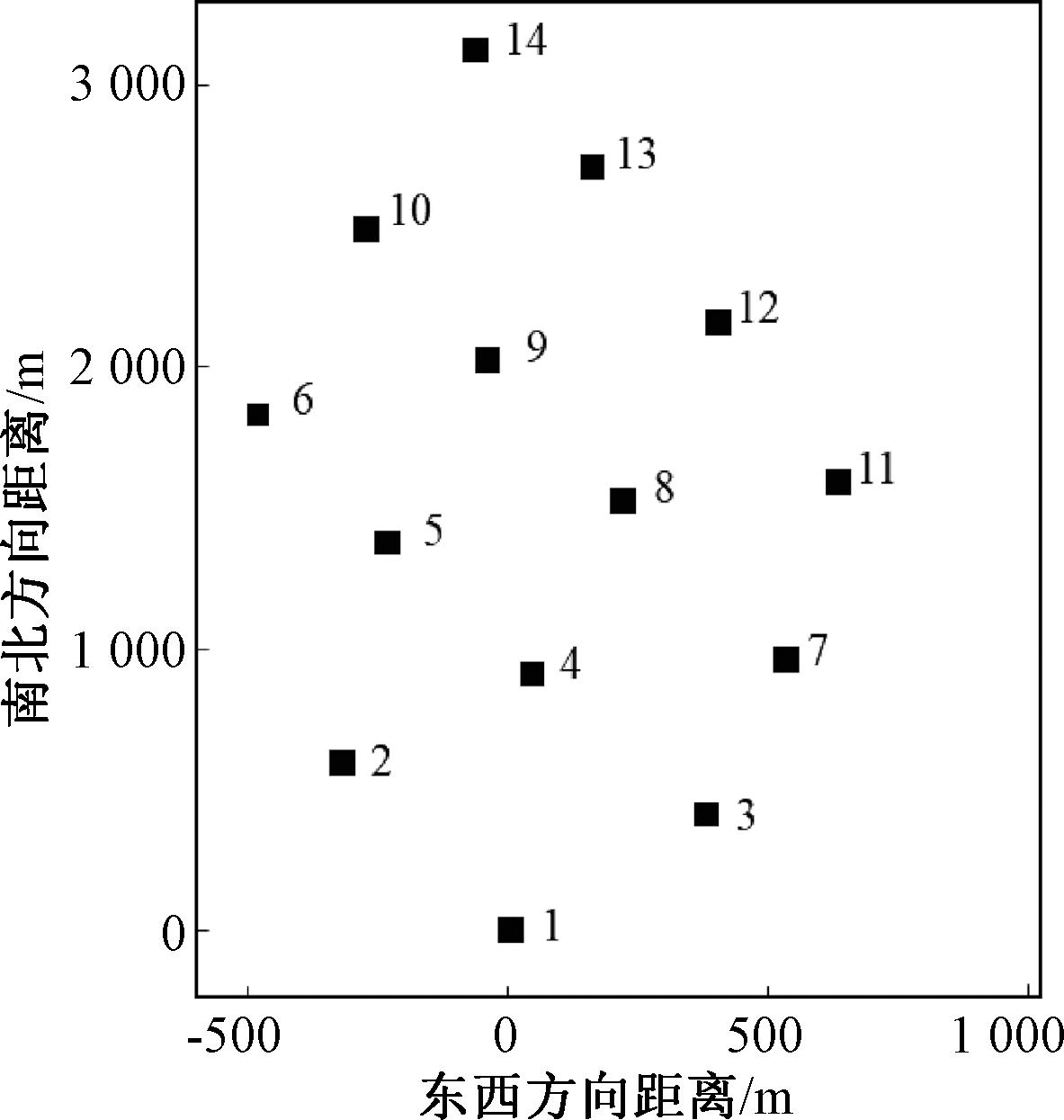
图5 Penmanshiel风电场布局示意图
Figure 5 Layout diagram of Penmanshiel wind farm
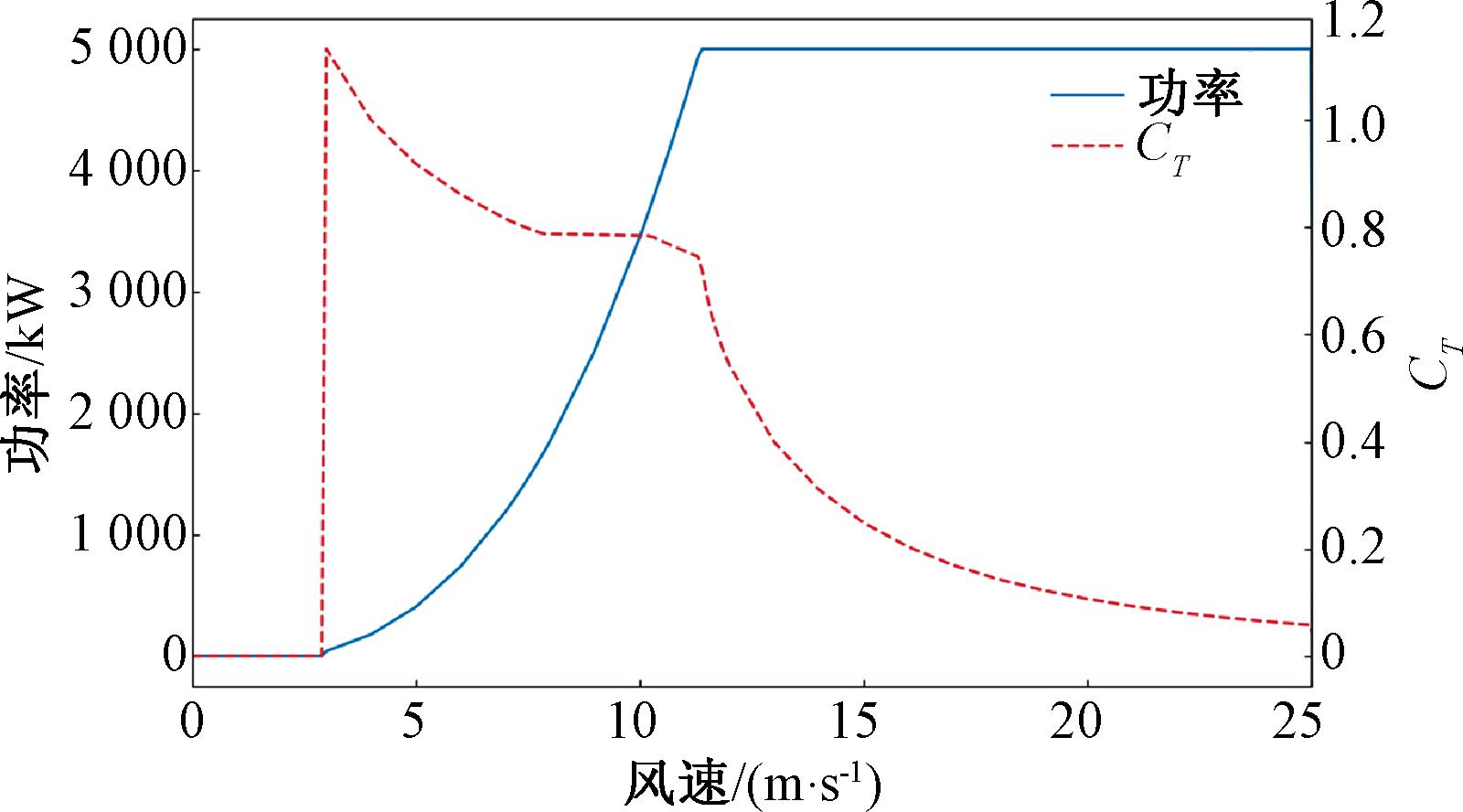
图6 NREL 5 MW风电机组特性曲线
Figure 6 NREL 5 MW wind turbine characteristic curve
3.2 基于Informer的风电场功率模型结果分析
在仿真模拟中,采用1.1节提到的Bastankhah尾流模型,将来流风速、风向及每台风机的偏航角作为特征值,将风电场总功率作为输出,随机生成场景数据,构建数据集。其中来流风速为0 m/s～25 m/s,风向为180°～360°,偏航角为-25°～25°。测试集中的风速风向数据如图7所示。
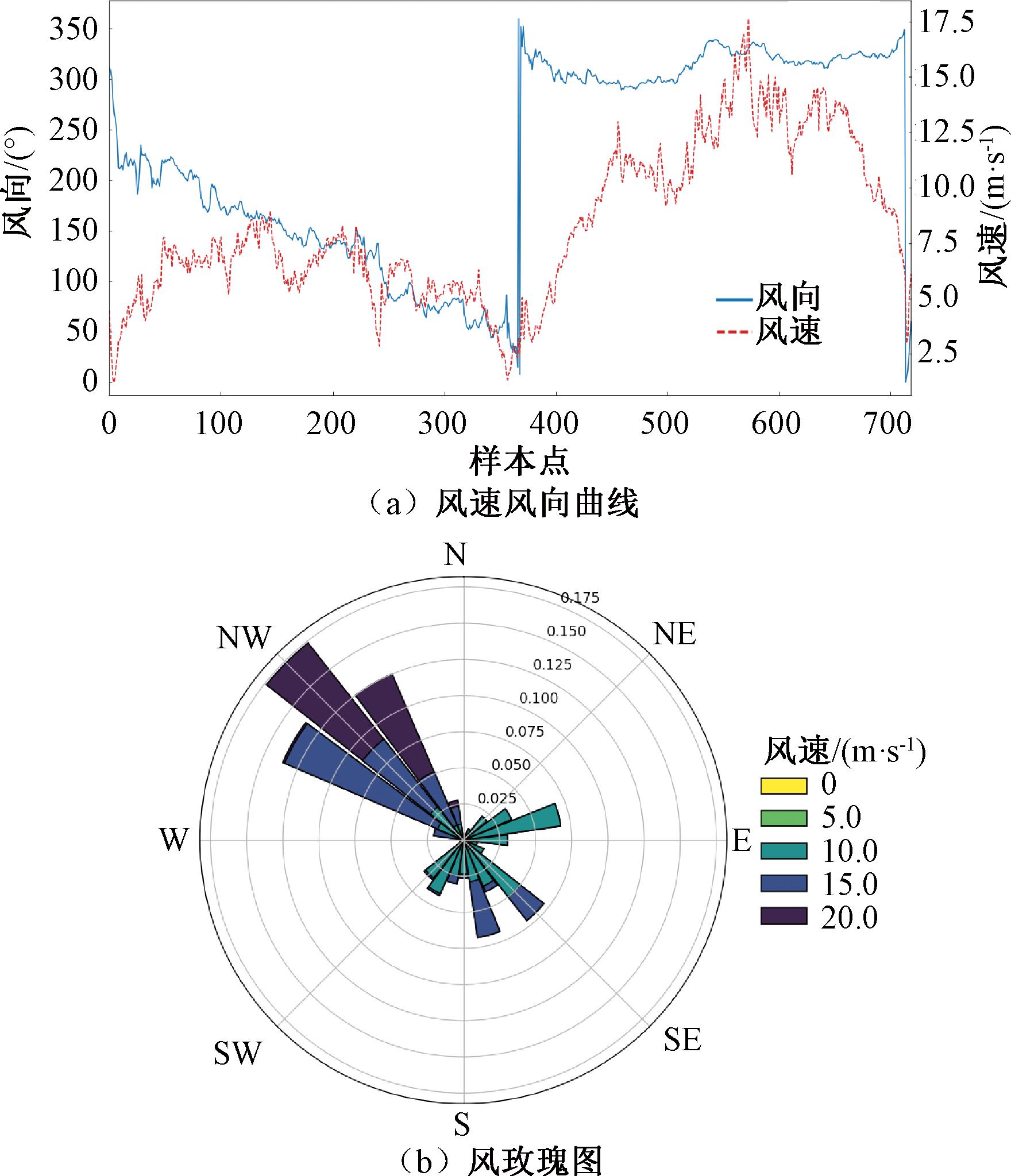
图7 测试集中的风速风向数据
Figure 7 Wind speed and direction data of the test set
为了使不同度量之间的特征具有可比性,同时不改变原始数据的分布,加快模型训练时的收敛速度,提高建模的准确度,需要对原始数据进行标准化处理:
(21)
式中:
为标准化后的数据;xi为原始数据;μ、σ分别为原始数据的均值和标准差。
本文采取均方误差(MSE)、平均绝对误差(MAE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)和决定系数(R2)作为评价指标:
(22)
(23)
(24)
(25)
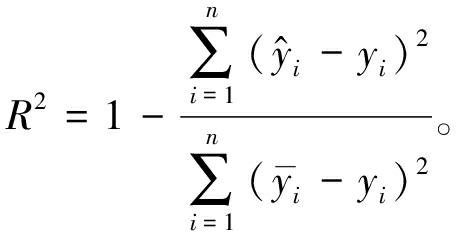
(26)
式中:n为预测总次数;
和yi分别为i时刻风电场功率的预测值和真实值。
为体现所设计的Informer风电场模型的优越性,本文选取LSTM、GRU、RNN和Transformer与Informer模型进行对比,结果如图8所示。由图8可知,Informer模型的预测值更接近真实值。
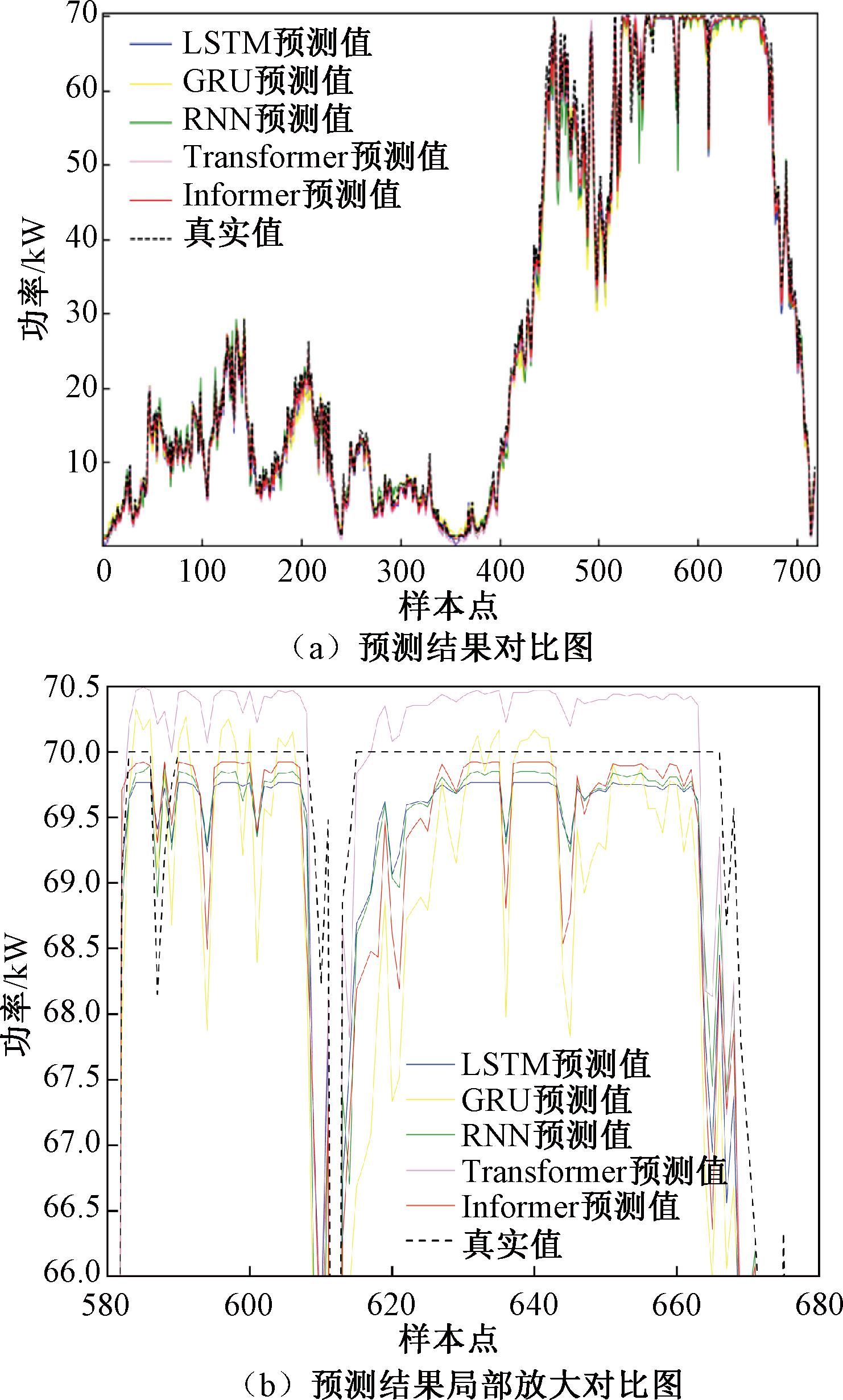
图8 风电场输出功率预测结果对比图
Figure 8 Comparison of wind farm output power forecast results
表2为风电场功率预测评价指标的对比。
表2 风电场功率预测评价指标对比
Table 2 Comparison of evaluation indicators for wind farm power prediction
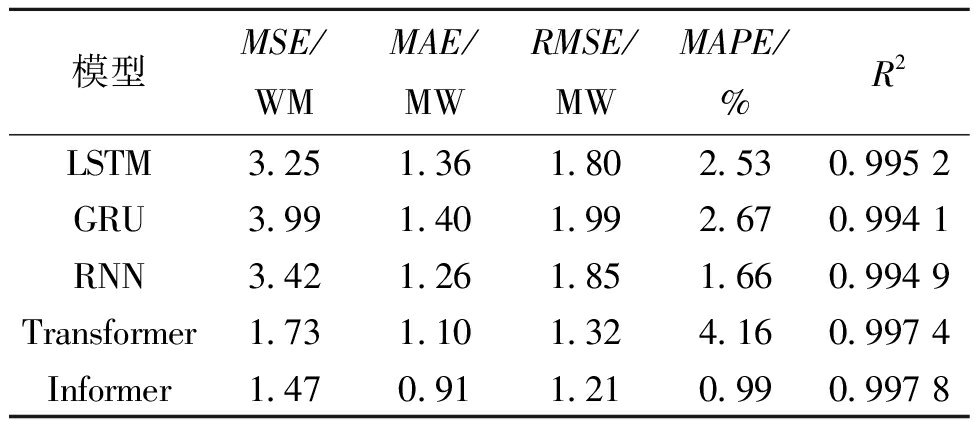
模型MSE/WMMAE/MWRMSE/MWMAPE/%R2LSTM3.251.361.802.530.995 2GRU3.991.401.992.670.994 1RNN3.421.261.851.660.994 9Transformer1.731.101.324.160.997 4Informer1.470.911.210.990.997 8
从表2可以看出,基于Informer网络的风电场功率模型的输出结果与真实值有更好的吻合性,在风电场等效建模方面有更好的精度。下文中的优化控制策略以Informer风电场模型为对象进行研究。
3.3 优化控制结果
为了测试基于Informer+PSO的优化控制策略的表现,利用所提优化算法与螳螂搜索算法(mantis search algorithm, MSA)在风速为10 m/s、风向为195°的风况下进行仿真与结果分析,风电场的偏航角设定值和优化前后的功率及其变化情况如表3所示。由表3可以看出,优化前后各机组的功率变化呈现3种不同趋势:部分机组功率提升,部分下降,还有部分基本保持不变。两种算法下风电场整体的输出功率都有提升。但相比于Informer+MSA方法,在基于Informer+PSO的优化控制策略下,风电场整场输出功率提升效果更好,增幅为1.94 MW。基于Informer+PSO优化前后的风电场尾流分布情况如图9所示。
表3 不同算法下风电场优化前后输出功率
Table 3 Output power before and after wind farm optimization with different algorithms
风机编号优化前风机功率/MWInformer+MSAInformer+PSO偏航角/(°)优化后风机功率/MW 风机功率增量/MW偏航角/(°)优化后风机功率/MW 风机功率增量/MW13.42-25.002.86-0.56-20.783.04-0.3823.42-24.362.86-0.5624.512.89-0.5333.42-25.002.86-0.56-25.002.86-0.5643.31-25.002.46-0.85-25.002.48-0.8253.00-20.211.96-1.04-25.002.83-0.1763.42-25.002.86-0.56-25.002.86-0.5671.82-25.002.470.658.462.911.0981.38-17.781.660.28-25.001.620.2491.63-25.001.740.11-19.552.290.66101.34-4.792.010.671.572.381.04112.043.161.83-0.21-5.062.140.10121.60-15.542.580.98-15.982.350.75131.627.562.610.9915.272.360.74141.209.322.511.318.041.550.35
图9 优化前后尾流分布情况
Figure 9 Wake distributions before and after optimization
结合图9和表3,位于下游的风机7,9,10,12和13在优化后功率显著增加,这主要得益于上游风机尾流的有效偏转,缓解了这些机组原先受到的严重尾流干扰。虽然上游风机1～6的功率有所下降,但是从风电场整体输出功率来看还是有很好的提升效果。
为进一步评估算法在不同风况条件下的性能,采用某风电场24 h的实测风速和风向数据进行仿真测试。风速风向数据如图10所示,其中0°代表正北方向,顺时针方向递增。本文所提优化控制算法下风电场输出功率增量如图11所示。
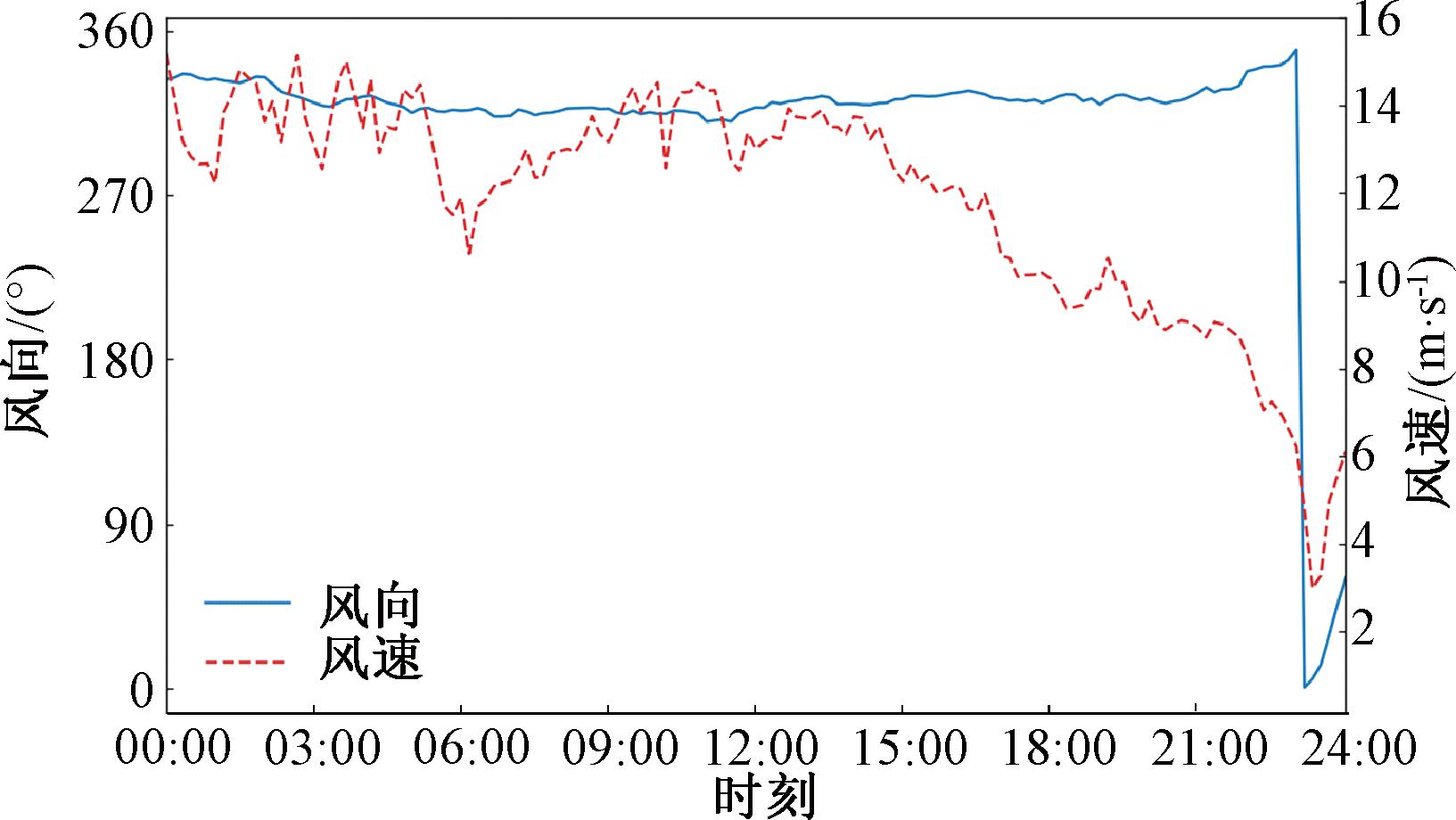
图10 某日风速风向曲线
Figure 10 Wind speed and direction curve for a day
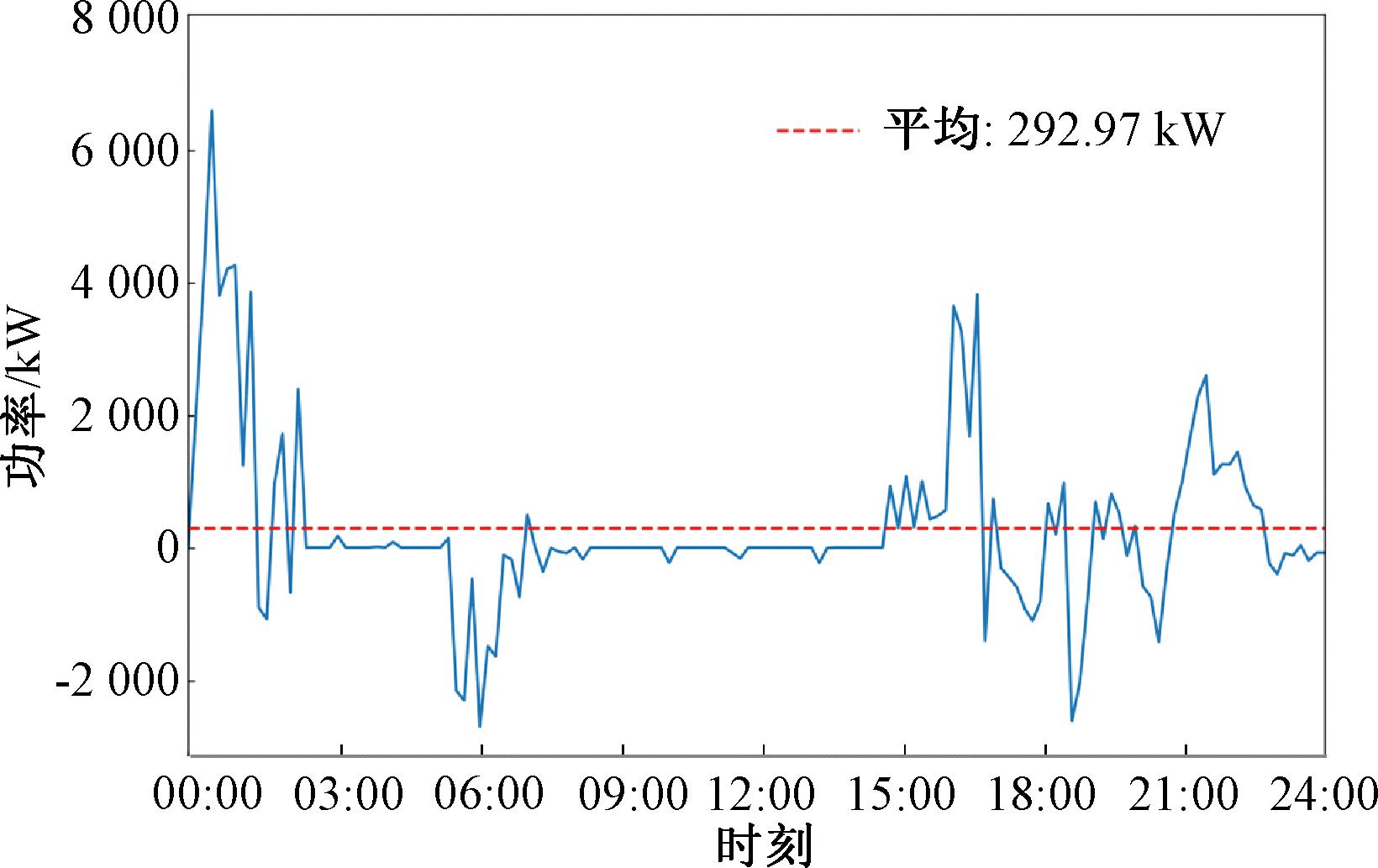
图11 所提算法对真实数据下的功率提升结果
Figure 11 The power increase results of the proposed method with real data
由图11可以看出,在实测风况下,所提优化策略使得风电场整体输出功率平均提升了292.97 kW,表明本文所提出的优化策略可以通过优化风力机的偏航角,降低场内尾流效应的影响,从而有效提升风电场整场输出功率。
4 结论
风电场内尾流效应会造成大量的风能损失。本文从场级角度出发,针对尾流效应对风电场输出功率的影响,提出了基于Informer等效模型与粒子群优化算法的优化控制策略,通过仿真对比得到以下结论。
(1)基于Informer神经网络建立的风电场等效模型有更高的建模精度,能更好适用于解决风电场的功率优化问题。
(2)所提优化控制策略能通过优化每台风机的偏航角有效缓解风电场内上游风机对下游风机的尾流影响,提高整场输出功率。
(3)在风速10 m/s、风向195°的特定风况和实测风况两种工况下,通过仿真对比,所提优化控制策略在特定风况下整场输出功率提升1.94 MW,实测风况下整场输出功率平均提升292.97 kW,优化效果更好。
[1] HOWLAND M F, LELE S K, DABIRI J O. Wind farm power optimization through wake steering[J]. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116(29): 14495-14500.
[2] BENSASON D, SIMLEY E, ROBERTS O, et al. Evaluation of the potential for wake steering for U.S. land-based wind power plants[J]. Journal of Renewable &Sustainable Energy. 2021, 13(3): 033303.
[3] 宗豪华, 孙恩博. 水平轴风力机主动尾流控制综述[J]. 空气动力学学报, 2022, 40(4): 51-68.
ZONG H H, SUN E B. Reivew of active wake control for horizontal-axis wind turbines[J]. Acta Aerodynamica Sinica, 2022, 40(4): 51-68.
[4] 邓智文, 郭苏, 许昌, 等. 海上风电场功率提升和疲劳平衡综合优化控制[J]. 太阳能学报, 2021, 42(1): 180-186.
DENG Z W, GUO S, XU C, et al. Comprehensive optimization control of power boost and fatigue balance for offshore wind farms[J]. Acta Energiae Solaris Sinica, 2021, 42(1): 180-186.
[5] 胡阳, 张冲, 房方, 等. 基于主动尾流控制的风电机群协同优化调度[J]. 动力工程学报, 2024, 44(4): 566-574.
HU Y, ZHANG C, FANG F, et al. Cooperative and optimal scheduling of wind turbine groups based on active wake control[J]. Journal of Chinese Society of Power Engineering, 2024, 44(4): 566-574.
[6] 刘一格, 赵振宙, 马远卓, 等. 基于鲸鱼优化算法的串列风力机主动尾流控制策略[J]. 中国电机工程学报, 2024, 44(9): 3702-3710.
LIU Y G, ZHAO Z Z, MA Y Z, et al. Active wake control strategy of tandem wind turbines based on whale optimization algorithm[J]. Proceedings of the CSEE, 2024, 44(9): 3702-3710.
[7] ZHANG Z Y, HUANG P, BITSUAMLAK G, et al. Analytical solutions for yawed wind-turbine wakes with application to wind-farm power optimization by active yaw control[J]. Ocean Engineering, 2024, 304: 117691.
[8] CAI W, HU Y, FANG F, et al. Wind farm power production and fatigue load optimization based on dynamic partitioning and wake redirection of wind turbines[J]. Applied Energy, 2023, 339: 121000.
[9] GUO N Z, ZHANG M M, LI B. A data-driven analytical model for wind turbine wakes using machine learning method[J]. Energy Conversion and Management, 2022, 252: 115130.
[10] SUN H Y, QIU C Y, LU L, et al. Wind turbine power modelling and optimization using artificial neural network with wind field experimental data[J]. Applied Energy, 2020, 280: 115880.
[11] 焦小敏, 耿华, 马少康, 等. 基于数据驱动的多风电机组协同控制方法[J]. 电源学报, 2020, 18(2): 24-31.
JIAO X M, GENG H, MA S K, et al. Data-driven cooperative control method for multiple wind turbines[J]. Journal of Power Supply, 2020, 18(2): 24-31.
[12] RAK B P, SANTOS PEREIRA R B. Impact of the wake deficit model on wind farm yield: a study of yaw-based control optimization[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2022, 220: 104827.
[13] SONG D R, FAN X Y, YANG J, et al. Power extraction efficiency optimization of horizontal-axis wind turbines through optimizing control parameters of yaw control systems using an intelligent method[J]. Applied Energy, 2018, 224: 267-279.
[14] PARK J, LAW K H. Bayesian ascent: a data-driven optimization scheme for real-time control with application to wind farm power maximization[J]. IEEE Transactions on Control Systems Technology, 2016, 24(5): 1655-1668.
[15] VALI M, 
V, PAO L Y, et al. Model predictive active power control for optimal structural load equalization in waked wind farms[J]. IEEE Transactions on Control Systems Technology, 2022, 30(1): 30-44.
[16] YIN X X, ZHANG W C, JIANG Z S, et al. Data-driven multi-objective predictive control of offshore wind farm based on evolutionary optimization[J]. Renewable Energy, 2020, 160: 974-986.
[17] HANSEN M O L. Aerodynamics of wind turbines[M]. 3rd ed. London: Routledge, 2015.
[18] SHAKOOR R, HASSAN M Y, RAHEEM A, et al. Wake effect modeling: a review of wind farm layout optimization using Jensen′s model[J]. Renewable and Sustainable Energy Reviews, 2016, 58: 1048-1059.
[19] BASTANKHAH M, PORTÉ-AGEL F. Experimental and theoretical study of wind turbine wakes in yawed conditions[J]. Journal of Fluid Mechanics, 2016, 806: 506-541.
[20] PARK J, LAW K H. A data-driven, cooperative wind farm control to maximize the total power production[J]. Applied Energy, 2016, 165: 151-165.
[21] ZHOU H Y, ZHANG S H, PENG J Q, et al. Informer: beyond efficient transformer for long sequence time-series forecasting[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(12): 11106-11115.
[22] NASH R, NOURI R, VASEL-BE-HAGH A. Wind turbine wake control strategies: a review and concept proposal[J]. Energy Conversion and Management, 2021, 245: 114581.
[23] 陈婧华, 张琳娟, 卢丹, 等. 基于改进粒子群优化算法的分布式电源集群划分方法[J]. 郑州大学学报(工学版), 2023, 44(5): 77-85.
CHEN J H, ZHANG L J, LU D, et al. Cluster partition method of distributed power supply based on improved particle swarm optimization algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 77-85.
[24] GEBRAAD P M O, TEEUWISSE F W, VAN WINGERDEN J W, et al. Wind plant power optimization through yaw control using a parametric model for wake effects: a CFD simulation study[J]. Wind Energy, 2016, 19(1): 95-114.
[25] JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[EB/OL]. (2009-02-01)[2024-07-03]. https:∥digital.library.unt.edu/ark:167531/metadc894033/.