深度卷积神经网络[1]在图像分类、目标检测、语义分割及自动驾驶等领域展现了卓越性能和巨大潜力。然而,近年来的研究表明卷积神经网络存在一定的脆弱性,即模型输出易受输入扰动的影响。通过向原始样本添加精心设计的微小扰动[2-3],能够有效诱使深度学习模型误判,这些经过设计的异常样本被称为对抗样本。
对抗样本最初起源于图像分类领域,但随着研究的不断深入,应用范畴已扩展至面部识别、视觉跟踪等计算机视觉任务。这些对抗样本对模型稳健性造成了严重影响,从而引起人们的重视[4]。
对抗样本在机器学习模型中普遍存在,常见的对抗攻击方法可分为白盒攻击和黑盒攻击[5]两大类。早期研究集中于白盒攻击[6-7],此场景下攻击者完全了解目标模型的内部结构,能够利用其弱点进行攻击。然而,在实际应用中,攻击者通常无法获取目标模型内部信息,因此,研究重点逐渐转向黑盒攻击。在黑盒攻击中,攻击者对目标模型内部结构一无所知,仅能查询输入输出信息,这使其在实际场景中的危害更为显著。基于迁移的攻击是典型的黑盒攻击方法,它是在白盒场景下攻击源模型生成对抗样本,并使用生成的对抗样本直接攻击目标黑盒模型。
早期的攻击方法如基本迭代方法(basic iterative method,BIM)[6]与投影梯度下降(projection grodient descent,PGD)方法[7]在黑盒模型攻击中表现出有限的可迁移性。为提高可迁移性,研究者利用模型的梯度信息,设计了动量积分[8]、输入多样化[9]和方差调整[10]等多种方法来提高黑盒攻击的可迁移性。
随着对抗攻击技术的发展,研究者发现集成方法在提升对抗样本迁移性方面优于传统的非集成方法。集成方法面临两大主要挑战:一是获取不同架构的模型并集成大量派生模型需要巨大的计算资源;二是可用于集成的模型多样性和数量受限。DGM(diverse gradient method)[11]是一种通过自蒸馏来丰富模型梯度的方法,能够在不改变模型结构的前提下,以低计算复杂度与其他方法结合,实现性能提升。它通过自蒸馏生成一系列与源模型结构相同的学生模型,使其不仅学习源模型的核心知识,还在不同程度上发展出各自的特征表现。最终,通过集成教师模型和这些学生模型进行攻击,生成迁移性更强的对抗样本。然而,单靠自蒸馏生成的学生模型多样性仍然受限。
为进一步获得更加丰富多样的学生模型群,本文提出了一种基于基因重组的自蒸馏策略,整体框架如图1所示。该策略在自蒸馏生成学生模型的同时对两个学生网络进行训练,将单个学生模型的若干结构分层视为控制相同性状的若干基因。在蒸馏过程中,通过不断对两个学生模型的等位基因进行重组,产生两个新基因组合的学生模型。历经多轮训练与重组迭代,得到高度多样化的学生模型群。最后,集成源模型与这些丰富多样的学生模型进行攻击,从而生成迁移性更优的对抗样本。

图1 基于基因重组的自蒸馏方法框架
Figure 1 Self-distillation method framework based on genetic recombination
1 相关工作
本节概述了对抗样本[12]和对抗攻击的相关研究。首先,介绍了对抗样本的定义及其生成方法;其次,讨论了基于梯度的攻击方法,并探讨了在黑盒场景下通过对抗样本进行迁移攻击的策略;最后,介绍了几种增强对抗样本迁移性和攻击效果的算法。
1.1 对抗样本
给定一个干净样本x及其真实标签ytrue、目标分类器f,如果存在一个扰动ò使得分类器f输出分类错误,并且扰动满足‖x-xadv‖∞<ò,那么这个xadv=x+ò就是一个对抗样本。
1.2 对抗攻击
对抗攻击是一种通过在干净样本上添加精心设计的微小扰动,使机器学习模型产生误判的攻击方式。这类攻击利用模型对小扰动的敏感性,通过引入细微且看似无害的变化,干扰模型的正常预测和分类。
黑盒攻击可分为基于迁移的攻击和基于查询的攻击。本文主要探讨基于迁移的黑盒攻击方法,其核心在于使用替代模型代替目标黑盒模型完成攻击。首先,在替代模型上应用白盒攻击方法生成对抗样本;其次,利用这些对抗样本的良好迁移性对目标黑盒模型实施有效攻击,从而绕过访问目标模型内部信息的限制。
1.3 基于梯度的攻击
Goodfellow等[2]提出的FGSM(fast gradient sign method)方法通过在梯度生成方向上添加扰动,增加目标模型的损失函数,从而降低模型对真实标签的预测概率,实现对目标模型的攻击。
xadv=x+ò![]()
(1)
式中:![]() 为损失函数相对于样本x的梯度。
为损失函数相对于样本x的梯度。
BIM方法是在FGSM的基础上引入步长的一种迭代攻击方法。PGD是一种迭代攻击方法,通过在干净样本上多次迭代添加扰动,并在每次迭代后将生成的对抗样本投影回预设范围内,以引导目标模型产生错误分类。
(2)
式中:projection(·)为投影函数;n为迭代次数。与FGSM相比,PGD实现了更好的攻击效果,但在黑盒攻击中的迁移性较低。
1.4 基于迁移的攻击
在黑盒场景下,由于目标模型的内部结构和参数未知,基于梯度的攻击方法无法直接应用。Goodfellow等[2]发现对抗样本具有迁移性,因此可以利用白盒模型生成对抗样本对黑盒模型实施迁移攻击。这意味着攻击者可以通过攻击替代模型来生成对抗样本,无须直接接触目标模型,从而达到攻击效果。
为进一步提高对抗样本的迁移性,动量迭代(momentum itoration,MI)方法[9]通过在每次迭代中积累梯度方向上的动量,结合Nestrov动量,更准确地估计下一步的梯度方向。
(3)
式中:μ为衰减因子。
NI方法(nesterov iterative fast gradient sign method)[13]是MI方法的改进版。PGI方法[14]通过在每次迭代中累积上一步在梯度方向上采样数据点的平均梯度,以稳定更新方向并避免陷入局部最大值。
在每次迭代中,DI方法(diverse input method)[15]通过对输入图像进行随机变换,生成不同的输入模式,以增强对抗样本的可迁移性。
(4)
式中:![]() 表示在给定概率p下应用到
表示在给定概率p下应用到![]() 的数据增强方法。
的数据增强方法。
TI方法(translation-invariant method)[16]则使用预定义的卷积核W从一组图像中获取梯度,以生成针对防御模型的可迁移对抗样本。
(5)
VT方法(variance tuning method)[10]利用前一迭代中的梯度方差来调整当前梯度,从而稳定更新方向并避免陷入局部最优。
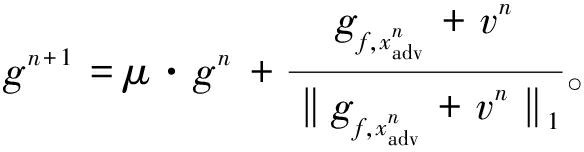
(6)
式中:![]() 表示梯度差。
表示梯度差。
2 本文方法
本节首先介绍了遗传学中的基因重组及其对生物多样性的重要性。在此基础上,提出了一种基于基因重组的蒸馏训练策略,该策略能够生成更加多样化的模型,从而提升集成攻击的效果。
2.1 基因重组
生物多样性[17]包括遗传多样性、物种多样性和生态系统多样性,它在地球生态系统中扮演着至关重要的角色。自细菌起源以来,经过几十亿年的演化,尤其是在真核生物和有性生殖机制出现后,生物多样性显著丰富。有性生殖通过基因重组创造丰富的遗传变异,加速了生物进化,并推动了多细胞生物分化和繁衍,从而形成了多样的生物群体和复杂的生态系统。
基因重组作为生物进化的重要机制,体现在3个方面:第一,它通过重组不同亲本的基因产生新的遗传组合和变异,极大丰富了生物变异多样性,为进化提供了更多选择;第二,基因重组加快了生物对环境变化的适应速度,提高了生存和繁殖成功率;第三,它对多细胞生物多样性的形成至关重要,通过细胞和组织间的基因交流促进形态和功能的多样化。这些机制共同作用增加了地球上生物种类的多样性,提升了生态系统的复杂性和稳定性。
2.2 基于基因重组知识蒸馏的对抗攻击方法
Mendel[18]通过豌豆杂交实验验证并阐述了遗传学的基本理论——分离定律与自由组合定律。在第1次实验中,Mendel将纯种高茎豌豆和纯种矮茎豌豆进行杂交,揭示了分离定律,即在减数分裂过程中,决定某一性状的等位基因独立分配至不同的配子并保持各自独立。随后,Mendel以纯种黄色圆粒豌豆与纯种绿色皱粒豌豆进行杂交实验(如图2所示),进一步验证了自由组合定律。该定律指出,在具有两对或多对相对性状的亲本杂交时,不同染色体上的等位基因分离和组合是独立的。
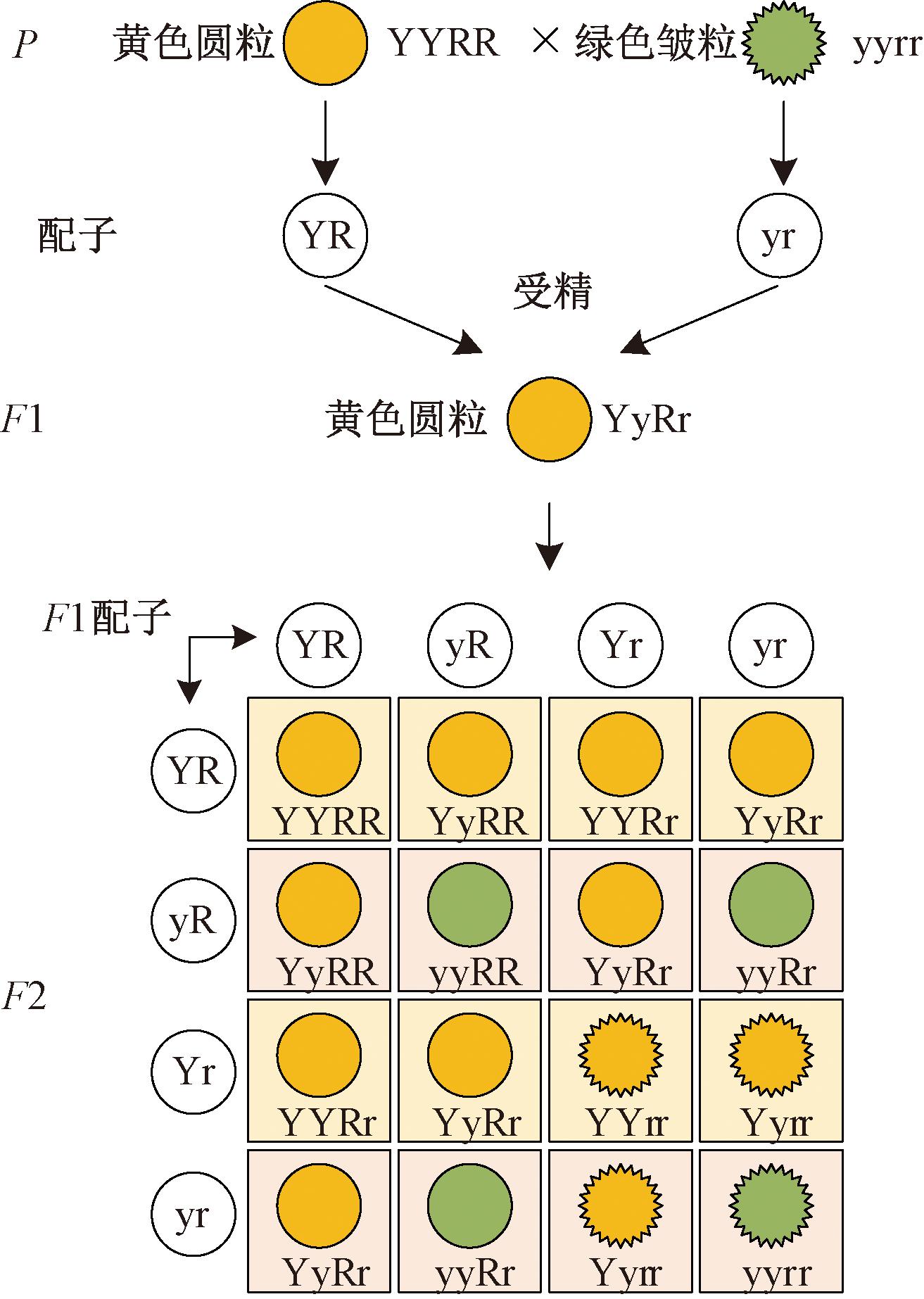
图2 黄色圆粒豌豆与绿色皱粒豌豆杂交实验图解
Figure 2 Diagram of crossbreeding experiment between yellow round pea and green wrinkled pea
2.2.1 通过基因重组自蒸馏生成多样化学生模型
将自蒸馏过程建模为遗传进化模型,其中学生模型被视为独立个体,其参数θ代表这个个体的基因。学生模型的基因初始化为θ0,然后通过学习教师的知识进化为第k代:
(7)
经过K轮进化,学生模型不断获取教师知识,逐渐进化为最终状态。通常,一个神经网络模型由包含多层的块组成。给定一个包含M块的学生模型,其参数为θ,可以将这M块视为拥有M个基因的学生个体,并将它们划分为N个等位基因:
θ=[B1,B2,…,BM]=[θ1,θ2,…,θN],1<N≤M。
(8)
第i个等位基因θi由以下基因组成:

(9)
式中:Round(·)表示舍入到最接近的整数。为确保最后的等位基因θN非空,进一步限制N的值:
(10)
给定两个初始化的学生模型的基因θinit和ϑinit,分别将它们的等位基因划分为![]() 和
和![]() 图3为基因重组示例。在图3中,设N=3,可交换的等位基因组合为[1,2,3],每次重组后可能产生3种不同的情况。最终,通过K轮的蒸馏进化和多轮基因重组操作,可以获得更加多样化的学生模型。
图3为基因重组示例。在图3中,设N=3,可交换的等位基因组合为[1,2,3],每次重组后可能产生3种不同的情况。最终,通过K轮的蒸馏进化和多轮基因重组操作,可以获得更加多样化的学生模型。
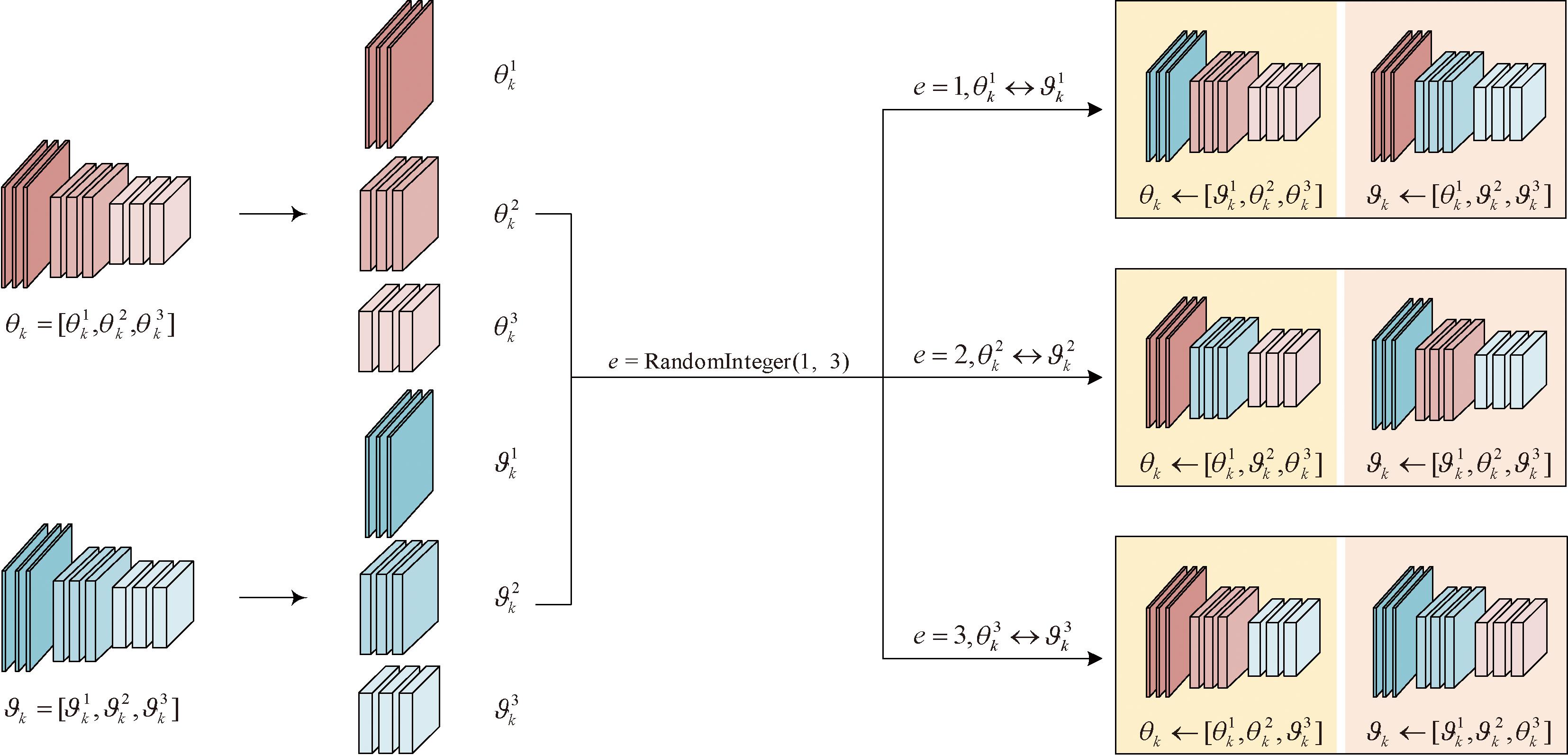
图3 2个学生模型进行基因重组的图解
Figure 3 Diagram of genetic recombination between two student models
2.2.2 多模型集成
每次使用基因重组策略进行自蒸馏时,会生成两个学生模型,始终将第1个初始化的学生模型定为s1,将获得N+1个不同的模型,包括N个多样化的学生模型fs1,fs2,…,fsN和一个教师模型ft。随后,将这N+1个模型进行集成,以获取更为多样和鲁棒的梯度信息,从而应用基于梯度的对抗攻击方法(如FGSM、BIM、PGD)生成对抗样本。为简化公式,教师模型ft视为未经过蒸馏训练的学生模型fs0,并将各种模型fs0,fs1,…,fsN的Logits进行融合,使用以下的集成策略[19]来计算集成损失:
(11)
式中:fsk(x)表示第k个模型的Logits;ωk>0为受![]() 约束的集合权值,本文实验设置
约束的集合权值,本文实验设置![]() 表示标准基向量,仅在真实标签y对应位置为1,其余为0。
表示标准基向量,仅在真实标签y对应位置为1,其余为0。
此外,集成模型![]() 集成梯度gn+1为
集成梯度gn+1为
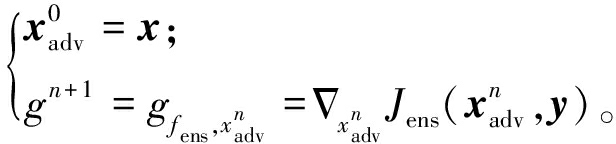
(12)
在获得集成梯度后,利用基于梯度的对抗攻击方法生成具有更优迁移性的对抗样本。
DGM方法是一种通用的对抗迁移性增强策略,能够直接与基于梯度的攻击方法结合,亦可与其他迁移性增强策略相结合,以进一步提升攻击效果。由于基于基因重组的知识蒸馏策略与模型及攻击方法无关,因此所提对抗攻击方法具有广泛的适用性。
3 实验结果与分析
3.1 数据集
从ImageNet验证集[20]中随机选择5 000张能够被正确分类的图像[21]进行训练。该子集涵盖了各个类别的图像,除极少数类别外,其余类别均包含5张合格图像。源模型能够对该子集的大部分图像进行正确分类。
3.2 使用模型
本文在不同的卷积神经网络模型上评估生成的对抗样本。评估对象包括9个未经防御训练的模型和4个防御模型,这些模型均为在ImageNet数据集上的预训练模型。未经防御训练的模型包括Res50、ResNet152(简写为Res152)、ResNet101(简写为Res101)[22-23]、DenseNet201(简写为DN201)[24]、SeNet154(简写为Se154)[25]、VGG19[26]、InceptionV3(简写为IncV3)[27]、Inception-V4(简写为IncV4)和inception-ResNet-V2(简写为IncRes)[28]。防御模型包括使用对抗训练的模型IncV3a[7]及经过集成对抗训练的模型IncV3e3、IncV3e4和IncRese[29]。
3.3 对比方法
将本文方法与多种攻击方法进行对比,包括基于梯度的一步攻击方法FGSM,多步攻击方法BIM、PGD,以及基于梯度的增强方法MI、NI、PGI、DI、TI、SI等。
3.4 实现细节
本文的实验设置与DGM方法一致,采用PGD和BIM方法作为初始基线,且L∞约束下最大约束ε=16/255。在所有多步攻击方法中,迭代次数n统一设置为10,步长设置为2(在BIM中为-1)。基准方法严格遵循相关文献中的默认参数,以确保结果的可对比性和一致性。
为保证实验的准确性和可重复性,所有实验均在相同服务器环境下进行,具体配置为Intel(R) Xeon(R) CPU E5-2697 v4 @ 2.30 GHz和NVIDIA GeForce RTX 3090 GPU 24 GB。使用PyCharm作为开发平台,以Python为开发语言,在CentOS Linux 7(Core)系统上运行。代码运行的开发环境涉及多个依赖库,advertorch版本为0.2.3、pretrainedmodels版本为0.7.4、Python版本为3.8.17、torch版本为1.9.0+cu111。
在集成攻击方法中,获得不同的集成模型的成本较高。例如,获取一个初始化参数不同的预训练模型(如Res152或DN201)需在包含120万张训练图像的ImageNet数据集上训练90个轮次,耗费大量时间和计算资源。而本文方法仅需利用ImageNet数据子集(5 000张训练图像),通过知识蒸馏在24个训练轮次内即可获得一个对攻击有正向增益的模型,耗时仅需48 min,显著降低了集成攻击获得不同集成模型所需的计算资源和时间成本。
3.5 结果分析
3.5.1 一步可迁移性
对本文方法在9个无防御模型上的一步可迁移攻击性进行评估,结果如表1所示。当源模型与目标模型相同时,结果表示白盒攻击成功率。以Res152和DN201作为源模型时,本文方法在9个目标模型上均取得最高攻击成功率。以Res152作为源模型为例,所提方法在Res101、DN201和IncV4模型上的迁移攻击成功率分别为63.36%,52.72%和33.52%,均较其他方法提高了1百分点以上。实验结果表明,本文方法在DGM基础上进一步提升了FGSM对复杂白盒模型的攻击效果。此外,与迁移方法SGM相比,本文方法显著增强了FGSM在多种黑盒模型上的可迁移攻击性能。
表1 一步可迁移攻击性对比实验结果
Table 1 Comparison experiment results of one-step attack transferability
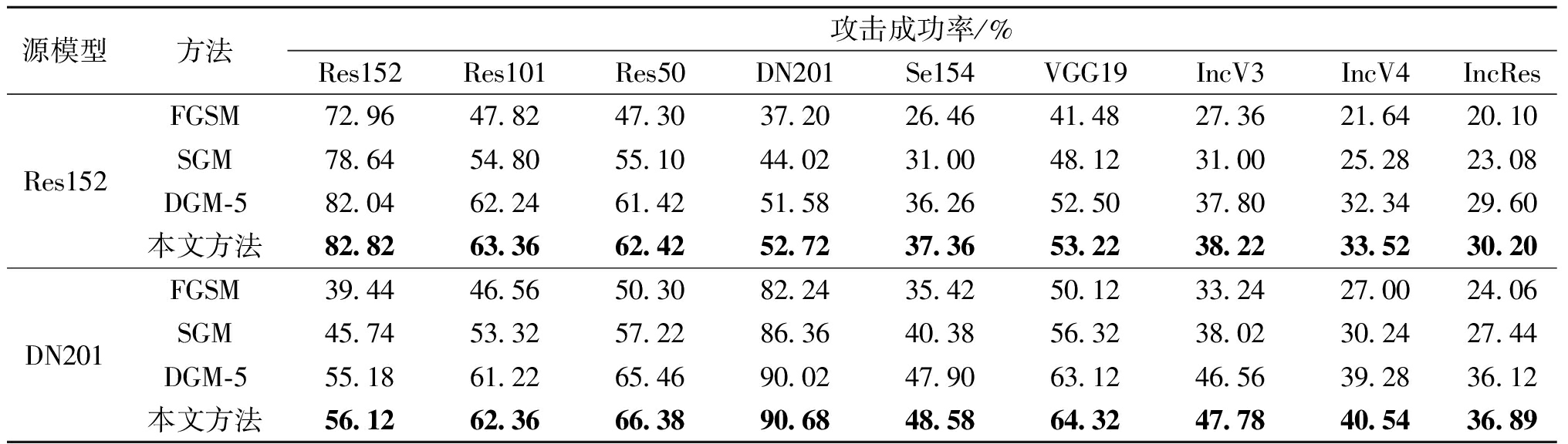
源模型方法攻击成功率/%Res152Res101Res50DN201Se154VGG19IncV3IncV4IncResFGSM72.9647.8247.3037.2026.4641.4827.3621.6420.10Res152SGM78.6454.8055.1044.0231.0048.1231.0025.2823.08DGM-582.0462.2461.4251.5836.2652.5037.8032.3429.60本文方法82.8263.3662.4252.7237.3653.2238.2233.5230.20FGSM39.4446.5650.3082.2435.4250.1233.2427.0024.06DN201SGM45.7453.3257.2286.3640.3856.3238.0230.2427.44DGM-555.1861.2265.4690.0247.9063.1246.5639.2836.12本文方法56.1262.3666.3890.6848.5864.3247.7840.5436.89
3.5.2 多步迁移性
对于多步攻击,本文在Res152和DN201源模型上,对8个无防御模型和4个防御模型进行攻击,结果如表2所示。
表2 以Res152和DN201为源模型的多步迁移性对比实验结果
Table 2 Comparison experiment results of multi-step transferability with Res152 and DN201 as the source model
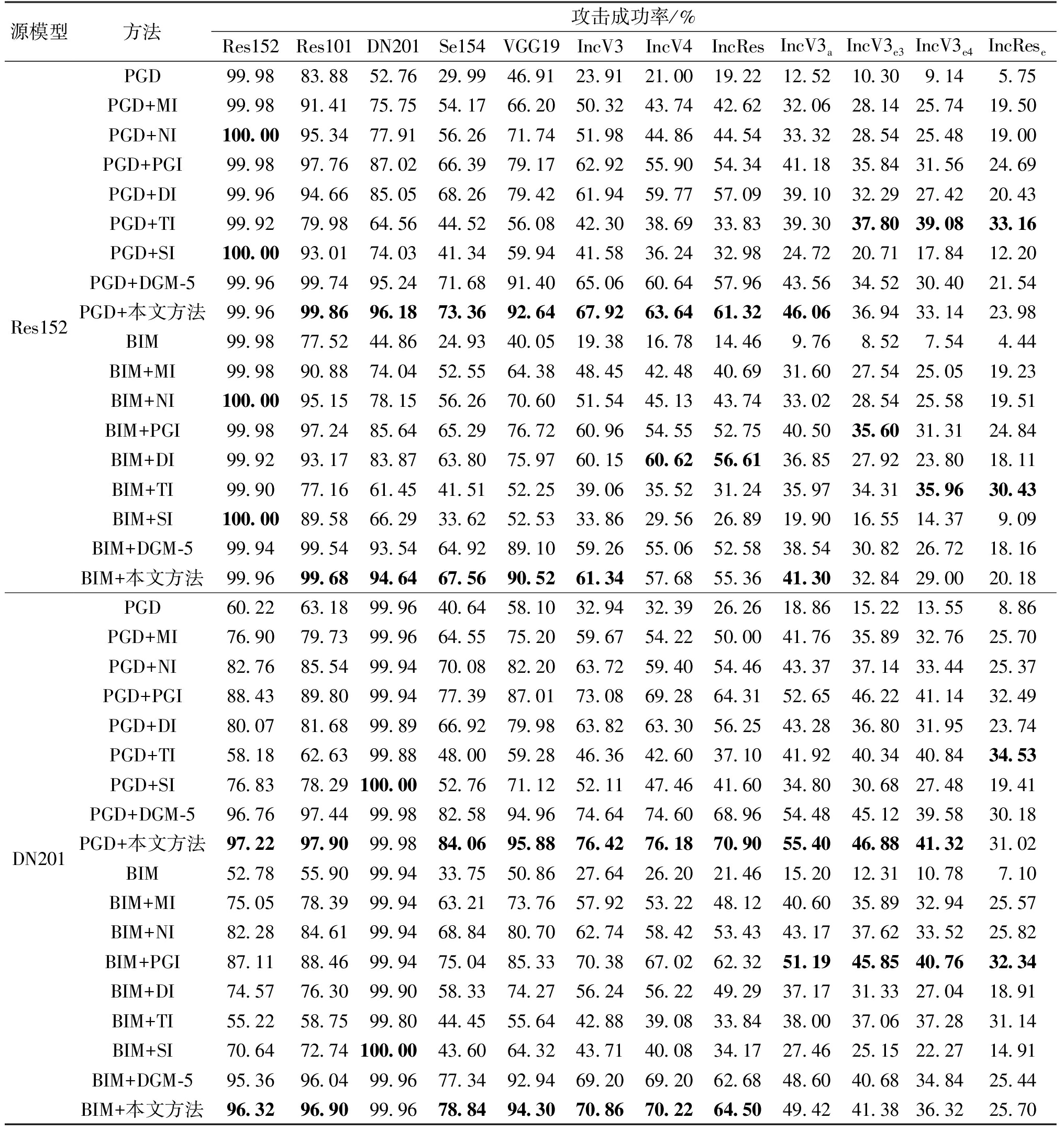
源模型方法攻击成功率/%Res152Res101DN201Se154VGG19IncV3IncV4IncResIncV3aIncV3e3IncV3e4IncReseRes152DN201PGD99.9883.8852.7629.9946.9123.9121.0019.2212.5210.309.145.75PGD+MI99.9891.4175.7554.1766.2050.3243.7442.6232.0628.1425.7419.50PGD+NI100.0095.3477.9156.2671.7451.9844.8644.5433.3228.5425.4819.00PGD+PGI99.9897.7687.0266.3979.1762.9255.9054.3441.1835.8431.5624.69PGD+DI99.9694.6685.0568.2679.4261.9459.7757.0939.1032.2927.4220.43PGD+TI99.9279.9864.5644.5256.0842.3038.6933.8339.3037.8039.0833.16PGD+SI100.0093.0174.0341.3459.9441.5836.2432.9824.7220.7117.8412.20PGD+DGM-599.9699.7495.2471.6891.4065.0660.6457.9643.5634.5230.4021.54PGD+本文方法99.9699.8696.1873.3692.6467.9263.6461.3246.0636.9433.1423.98BIM99.9877.5244.8624.9340.0519.3816.7814.469.768.527.544.44BIM+MI99.9890.8874.0452.5564.3848.4542.4840.6931.6027.5425.0519.23BIM+NI100.0095.1578.1556.2670.6051.5445.1343.7433.0228.5425.5819.51BIM+PGI99.9897.2485.6465.2976.7260.9654.5552.7540.5035.6031.3124.84BIM+DI99.9293.1783.8763.8075.9760.1560.6256.6136.8527.9223.8018.11BIM+TI99.9077.1661.4541.5152.2539.0635.5231.2435.9734.3135.9630.43BIM+SI100.0089.5866.2933.6252.5333.8629.5626.8919.9016.5514.379.09BIM+DGM-599.9499.5493.5464.9289.1059.2655.0652.5838.5430.8226.7218.16BIM+本文方法99.9699.6894.6467.5690.5261.3457.6855.3641.3032.8429.0020.18PGD60.2263.1899.9640.6458.1032.9432.3926.2618.8615.2213.558.86PGD+MI76.9079.7399.9664.5575.2059.6754.2250.0041.7635.8932.7625.70PGD+NI82.7685.5499.9470.0882.2063.7259.4054.4643.3737.1433.4425.37PGD+PGI88.4389.8099.9477.3987.0173.0869.2864.3152.6546.2241.1432.49PGD+DI80.0781.6899.8966.9279.9863.8263.3056.2543.2836.8031.9523.74PGD+TI58.1862.6399.8848.0059.2846.3642.6037.1041.9240.3440.8434.53PGD+SI76.8378.29100.0052.7671.1252.1147.4641.6034.8030.6827.4819.41PGD+DGM-596.7697.4499.9882.5894.9674.6474.6068.9654.4845.1239.5830.18PGD+本文方法97.2297.9099.9884.0695.8876.4276.1870.9055.4046.8841.3231.02BIM52.7855.9099.9433.7550.8627.6426.2021.4615.2012.3110.787.10BIM+MI75.0578.3999.9463.2173.7657.9253.2248.1240.6035.8932.9425.57BIM+NI82.2884.6199.9468.8480.7062.7458.4253.4343.1737.6233.5225.82BIM+PGI87.1188.4699.9475.0485.3370.3867.0262.3251.1945.8540.7632.34BIM+DI74.5776.3099.9058.3374.2756.2456.2249.2937.1731.3327.0418.91BIM+TI55.2258.7599.8044.4555.6442.8839.0833.8438.0037.0637.2831.14BIM+SI70.6472.74100.0043.6064.3243.7140.0834.1727.4625.1522.2714.91BIM+DGM-595.3696.0499.9677.3492.9469.2069.2062.6848.6040.6834.8425.44BIM+本文方法96.3296.9099.9678.8494.3070.8670.2264.5049.4241.3836.3225.70
由表2可知,在白盒场景中,即源模型为Res152的第2列和源模型为DN201的第4列,所列方法在攻击成功率方面表现基本一致。在这4项实验中,本文方法与表现最佳的攻击方法相比,攻击成功率的差异最大不超过0.04百分点。具体而言,以DN201作为源模型并采用BIM攻击为例,本文方法的攻击成功率达到99.96%,比BIM的99.94%高0.02百分点,仅比最优的SI方法(100.00%)低0.04百分点。
在黑盒场景中,本文方法在大多数情况下都表现出更优越的迁移性。例如,以Res152作为源模型并采用PGD攻击为例,与原始的PGD攻击相比,本文方法在11个模型上的平均攻击成功率提高了34.52百分点。而在对比方法中,提升最大的是PGI,其平均提升了29.22百分点。相比PGI,本文方法平均提升了5.30百分点。与基础的DGM-5方法相比,本文方法平均提升了2.12百分点。
在8种无防御模型上,本文方法在大多数情况下显著优于其他对比方法。以DN201作为源模型并采用PGD攻击为例,与其他增强方法相比,除对源模型进行白盒攻击时的成功率低于SI之外,本文方法在攻击其余无防御模型时均取得了最佳效果。总体上相较于基础的DGM提升了8.62百分点。在4种防御模型上,本文方法取得了第2的优异效果。
以Res152为源模型,并采用PGD对其余11个模型进行迁移攻击,本文方法对这12个模型的平均攻击成功率达到了66.25%,而DGM-5的成功率为64.30%,效果较好的TI方法仅达到了50.76%。本文方法在多个网络上的迁移攻击表现更加稳定,证明其具有较强的迁移攻击能力,这在实际应用场景尤为重要。
从实验分析可知,无论是在白盒攻击场景还是黑盒攻击场景下,本文方法相较于现有的迁移攻击和增强方法表现出显著的性能提升,并对基础的DGM方法进行了优化。由于本文方法与模型结构和攻击方式无关,因此可以与其他攻击方法有效结合,从而实现性能增益。结果表明,本文方法在增强攻击可迁移性方面取得了重要且有价值的进展。
4 结论
针对现有集成攻击面临的计算资源消耗大和可供集成的模型种类及数量有限等问题,本文提出了一种新颖的自蒸馏训练策略,旨在构建更为多样丰富的学生模型集合,以增强集成攻击的有效性和跨模型攻击的迁移能力。
具体而言,在源教师模型自蒸馏过程中,通过对学生模型进行基因重组,生成更加多样化的学生模型。随后,将源教师模型与生成的多样化学生模型进行集成,并利用基于梯度的攻击方法生成具有高度可迁移性的对抗样本。实验结果表明,本文方法显著增强了现有基于梯度的对抗攻击方法的可迁移性。此外,该策略作为一种通用的增强可迁移性的方法,能够与其他基于迁移的攻击方法有效结合。
尽管已取得上述进展,基于基因重组自蒸馏策略的潜能仍有待深入探索。未来的研究方向应聚焦于该策略的理解与优化,特别是基因交换的学生模型数量、模型结构、重组策略的细化以及系统性重组频率,以充分发挥该策略的潜在优势。通过对这些因素的深入探究,有望实现该策略的最大效益。
[1] 罗荣辉, 袁航, 钟发海, 等. 基于卷积神经网络的道路拥堵识别研究[J]. 郑州大学学报(工学版), 2019, 40(2): 18-22.
LUO R H, YUAN H, ZHONG F H, et al. Traffic jam detection based on convolutional neural network[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(2): 18-22.
[2] GOODFELLOW I J, SHLENS J, SZEGEDY C. Explaining and harnessing adversarial examples[EB/OL]. (2015-03-20)[2024-05-10]. http:∥arxiv.org/abs/1412.6572.
[3] SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks[EB/OL]. (2014-02-19)[2024-05-10]. http:∥arxiv.org/abs/1312.6199.
[4] 赵俊杰, 王金伟. 基于SmsGAN的对抗样本修复[J]. 郑州大学学报(工学版), 2021, 42(1): 50-55.
ZHAO J J, WANG J W. Recovery of adversarial examples based on SmsGAN[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(1): 50-55.
[5] YUAN X Y, HE P, ZHU Q L, et al. Adversarial examples: attacks and defenses for deep learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(9): 2805-2824.
[6] KURAKIN A, GOODFELLOW I, BENGIO S. Adversarial examples in the physical world[EB/OL]. (2017-02-11)[2024-05-10]. https:∥arxiv.org/abs/1607.02533.
[7] MADRY A, MAKELOV A, SCHMIDT L, et al. Towards deep learning models resistant to adversarial attacks[EB/OL]. (2019-09-04)[2024-05-10]. https:∥arxiv.org/abs/1706.06083.
[8] DONG Y P, LIAO F Z, PANG T Y, et al. Boosting adversarial attacks with momentum[C]∥2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 9185-9193.
[9] XIE C H, ZHANG Z S, ZHOU Y Y, et al. Improving transferability of adversarial examples with input diversity[C]∥2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2019: 2725-2734.
[10] WANG X S, HE K. Enhancing the transferability of adversarial attacks through variance tuning[C]∥2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2021: 1924-1933.
[11] CAO Y J, WANG H B, ZHU C X, et al. Improving the transferability of adversarial examples with diverse gradients[C]∥2023 International Joint Conference on Neural Networks (IJCNN). Piscataway: IEEE, 2023: 1-9.
[12] 何英哲, 胡兴波, 何锦雯, 等. 机器学习系统的隐私和安全问题综述[J]. 计算机研究与发展, 2019, 56(10): 2049-2070.
HE Y Z, HU X B, HE J W, et al. Privacy and security issues in machine learning systems: a survey[J]. Journal of Computer Research and Development, 2019, 56(10): 2049-2070.
[13] LIN J D, SONG C B, HE K, et al. Nesterov accelerated gradient and scale invariance for adversarial attacks[EB/OL]. (2020-02-03)[2024-05-10]. https:∥arxiv.org/abs/1908.06281.
[14] WANG X S, LIN J D, HU H, et al. Boosting adversarial transferability through enhanced momentum[EB/OL]. (2021-03-19)[2024-05-10]. https:∥arxiv.org/abs/2103.10609.
[15] DONG Y P, PANG T Y, SU H, et al. Evading defenses to transferable adversarial examples by translation-invariant attacks[C]∥2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2019: 4307-4316.
[16] GAO L L, ZHANG Q L, SONG J K, et al. Patch-wise attack for fooling deep neural network[C]∥European Conference on Computer Vision. Cham: Springer, 2020: 307-322.
[17] 马克平.试论生物多样性的概念[J].生物多样性,1993(1):20-22.
MA K P. Oiscussion on the concept of biodiversity[J].Chinese Biodiversity,1993(1):20-22.
[18] MENDEL G, LIBRARY B, PUNNETT R C. Versuche über Pflanzen-Hybriden[M]. Brünn: Im Verlage des Vereines, 1866.
[19] LIU Y P, CHEN X Y, LIU C, et al. Delving into transferable adversarial examples and black-box attacks[EB/OL]. (2017-06-07)[2024-05-10]. http:∥arxiv.org/abs/1611.02770.
[20] RUSSAKOVSKY O, DENG J, SU H, et al. ImageNet large scale visual recognition challenge[J]. International Journal of Computer Vision, 2015, 115(3): 211-252.
[21] WU D X, WANG Y S, XIA S T, et al. Skip connections matter: on the transferability of adversarial examples generated with ResNets[EB/OL]. (2020-02-14)[2024-05-10]. http:∥arxiv.org/abs/2002.05990.
[22] HE K M, ZHANG X Y, REN S Q, et al. Identity mappings in deep residual networks[C]∥European Conference on Computer Vision. Cham: Springer, 2016: 630-645.
[23] HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2016: 770-778.
[24] HUANG G, LIU Z, VAN DER MAATEN L, et al. Densely connected convolutional networks[C]∥2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2017: 2261-2269.
[25] HU J, SHEN L, SUN G. Squeeze-and-excitation networks[C]∥2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 7132-7141.
[26] SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL].(2015-04-10)[2024-05-10]. http:∥arxiv.org/abs/1409.1556.
[27] SZEGEDY C, VANHOUCKE V, IOFFE S, et al. Rethinking the inception architecture for computer vision[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway: IEEE, 2016: 2818-2826.
[28] SZEGEDY C, IOFFE S, VANHOUCKE V, et al. Inception-v4, inception-ResNet and the impact of residual connections on learning[EB/OL].(2016-08-23)[2024-05-10]. https:∥arxiv.org/abs/1602.07261.
[29] TRAM R F, KURAKIN A, PAPERNOT N, et al. Ensemble adversarial training: attacks and defenses[EB/OL].(2020-04-26)[2024-05-10]. http:∥arxiv.org/abs/1705.07204.
R F, KURAKIN A, PAPERNOT N, et al. Ensemble adversarial training: attacks and defenses[EB/OL].(2020-04-26)[2024-05-10]. http:∥arxiv.org/abs/1705.07204.