全断面隧道掘进机(tunnel boring machine,TBM)因施工质量好、效率高、对周围环境扰动小、安全性能好等优点,被广泛应用于各种隧道工程[1]。TBM刀盘位于掘进机的最前端,与掌子面岩体直接接触,刀盘上的盘型滚刀是破碎岩体最主要的刀具,确定滚刀在刀盘上的排列方式及选择合理的刀间距对提高TBM破岩效率具有重要意义[2]。
在试验研究方面,常用的试验方法有滚刀线性切割试验和回转切割试验。滚刀线性切割试验方面,龚秋明等[3]通过室内滚刀线性切割试验,研究了刀间距对破岩效率的影响,发现当S/P(刀间距/贯入度)为30时,比能最小,滚刀破岩效率最高;薛亚东等[4]采用离散元法建立了TBM双滚刀线性切割模型,发现S/P为20~25时,比能最小,滚刀破岩效率最高。滚刀回转切割试验方面,温森等[5]采用滚刀作用综合试验台对砂岩和花岗岩组成的复合岩体进行回转切割试验,得到了S/P约为14时,破岩效率最高;陆峰等[6]通过TBM滚刀回转切割试验研究了不同刀间距对滚刀破岩效率的影响,发现相同破岩条件下,S/P为24时滚刀间岩石完全破碎,比能最小,破岩效率最高;在相同的贯入度和刀间距下,顺次破岩的切削角度为120°时比能最小,破岩效率最高;吴峰[7]通过ABAQUS软件建立了双滚刀回转切割大理石的模型,得到S/P约为12,破岩效率最高;程永亮[8]采用Drucker-Prager本构模型进行了双滚刀回转切削软岩试验,得到当S/P约为8时,滚刀切削比能最低,破岩效率最高。
滚刀线性切割试验和回转切割试验都是目前常用的研究TBM滚刀破岩过程及效率的试验方法,但由于在两类试验中滚刀的运动方式不同,二者的试验结果存在明显差异,鲜有研究是针对两种试验结果的差异分析。张照煌等[9]通过对滚刀线性切割试验和回转切割试验结果进行总结,发现在盘型滚刀线性切割试验时岩石破碎的平均滚动力和比能均小于相同工况下回转切割试验得到的数据,但这种分析仅限于定性分析,并未将两种结果定量比较。TBM实际破岩过程中滚刀的排列方式不能仅依靠单、双滚刀的破岩过程来确定。多滚刀协同破岩可以考虑滚刀的不同位置、刀间距以及切削顺序对刀盘破岩过程和破岩效率的影响,从而确定滚刀的排列方式和最优刀间距。霍军周等[10]通过多滚刀顺次破岩的仿真模型,建立了顺次角度与岩石破碎能量之间的相关性,这种相关性能够确定刀盘上不同位置滚刀的最佳刀间距和顺次角度;刘亚迪等[11]建立了三滚刀回转破岩有限元模型,得到刀间距、相邻滚刀安装极角差和切削顺序3个主要刀盘布置参数对破岩载荷、破岩比能耗等破岩性能指标的单因素影响规律;林赉贶等[12]建立了多滚刀破岩模型,发现岩石破碎阻力随着滚刀贯入度、切削速度、刀间距和安装半径的增加而增加。上述工作大多是对双滚刀、多滚刀在单一切削顺序下的研究,简化了TBM协同破岩过程。实际工程中存在同次破岩、顺次破岩、由内向外破岩、由外向内破岩4种模式。通过不同破岩模式对破岩性能指标的影响,分析线性切割与回转切割两者之间的换算关系的相关研究较为缺乏。
综上,多滚刀协同破岩的研究对优化刀盘布局、提高TBM破岩效率、降低施工成本具有重要意义。本文采用有限元数值模拟方法,利用ABAQUS数值仿真平台,研究三滚刀协同破岩的过程;将三滚刀协同破岩划分为同次破岩、顺次破岩、由内向外破岩、由外向内破岩4种模式,研究4种模式下不同刀间距对滚刀破岩过程及破岩效率的影响;在研究三滚刀协同破岩时,进行线性切割试验和回转切割试验的对比分析,提出利用换算系数完成滚刀线性切割试验和回转切割试验预测滚刀破岩效率时相关指标的转化,为确定滚刀在刀盘上的排列方式及选择合理的刀间距提供可靠依据。
1 三滚刀线性协同破岩有限元模型
1.1 三滚刀协同破岩模型分析
刀盘破岩是在滚刀组作用下的岩石破坏过程,与单滚刀和双滚刀破岩模型相比,多滚刀破岩模型能够更准确地描述上述岩石破坏状态。在TBM破岩过程中,所有滚刀均参与破岩,并且各个滚刀之间存在协同作用。由于刀盘上的滚刀数量较多,若研究几十把滚刀协同破岩的过程,难度较大且效率低。此外,刀盘上几十把滚刀的布置形式很难进行归一化研究。因此,根据临空面的位置和数量,以及仿真结果对协同破岩模式的适用性,采用三滚刀协同破岩模型来研究多滚刀协同破岩过程,并将其归纳为4种基本破岩模式的组合,以此来提高计算效率。
TBM刀盘上,相邻滚刀以不同相位角进行安装时,滚刀将会以不同的切削顺序进行破岩。不同的切削顺序产生工作面上的高度差h会使相邻滚刀间的切削路径形成临空面,导致不同情况下滚刀力大小不同,进而发生不同的岩石破碎过程。将三滚刀协同破岩模型划分为4种破岩模式(临空面递增):同次破岩、顺次破岩、由内向外破岩和由外向内破岩,如图1所示,图1中①、②、③表示滚刀的切削顺序。
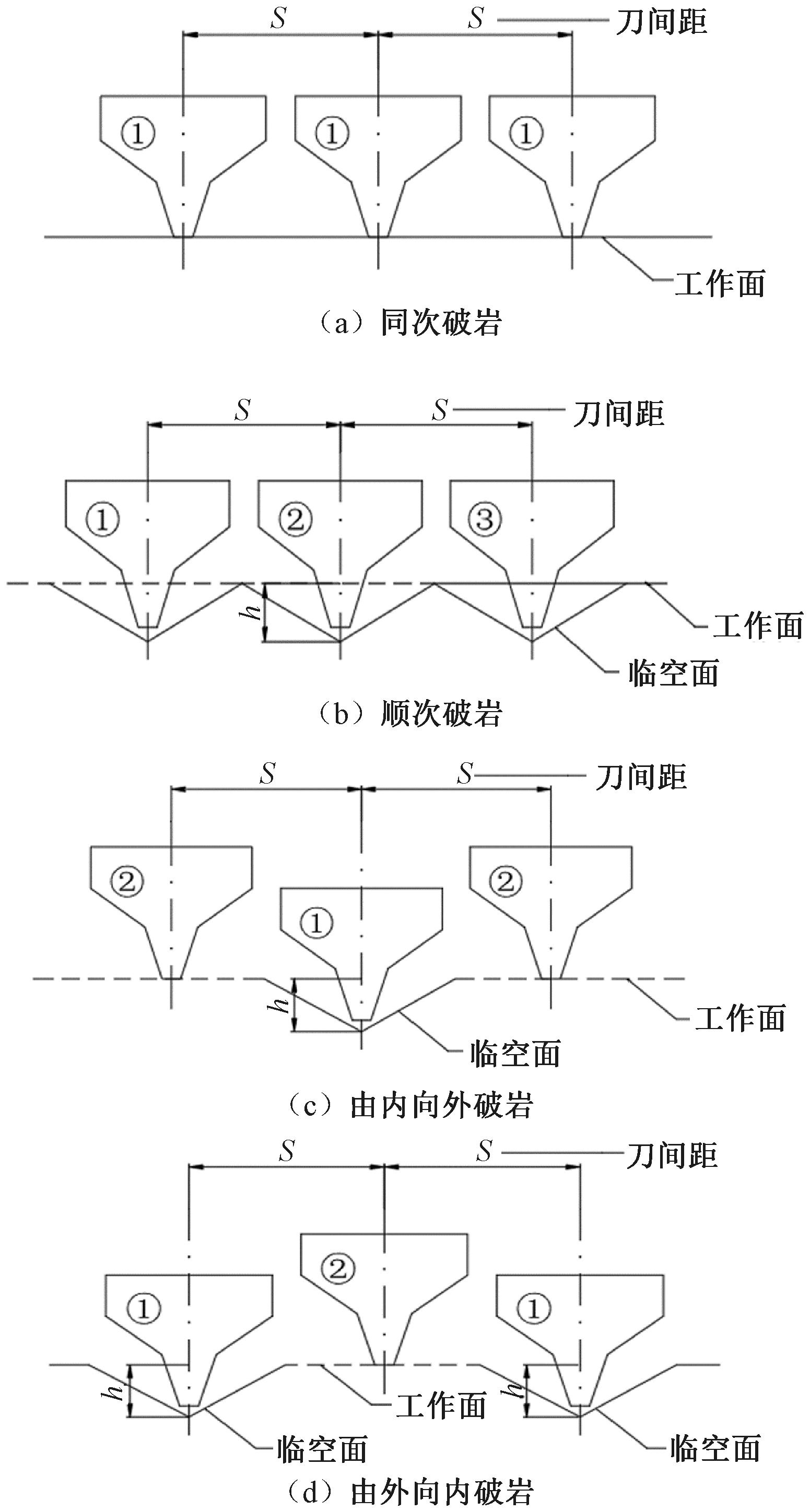
图1 破岩临空面示意图
Figure 1 Schematic diagram of the critical surface of the broken rock
1.2 岩石本构关系
ABAQUS软件基于有限元数值分析方法,包含大量的岩土力学子模型且具有强大的建模和后处理能力,能够准确反映岩石的受力变化特征,在土木工程领域使用最为广泛。由于岩石的力学性能较为复杂,本文采用适合分析岩石材料的Drucker-Prager屈服准则来模拟岩石的塑性本构关系[13-17]。
Drucker-Prager本构屈服函数表达式:
F=t-ptan β-d=0;
(1)
(2)
式中:β为材料摩擦角;d为材料凝聚力;q为Mises等效应力;r为偏应力第三不变量;k为三轴拉压强度的比值[18-20]。
本文采用花岗岩为研究材料,并假设岩石均质且各向同性,其物理力学参数如表1所示。
表1 花岗岩物理力学参数
Table 1 Physical and mechanical parameters of granite

天然密度/(g·cm-3)弹性模量/GPa泊松比抗压强度/MPa抗拉强度/MPa膨胀角/(°)2.6023.010.188105.66.40
1.3 滚刀破岩模型建立
滚刀采用432 mm常截面盘形滚刀模型,滚刀密度为7 800 kg/m3、弹性模量为206 GPa、泊松比为0.3,建立如图2所示的滚刀模型。
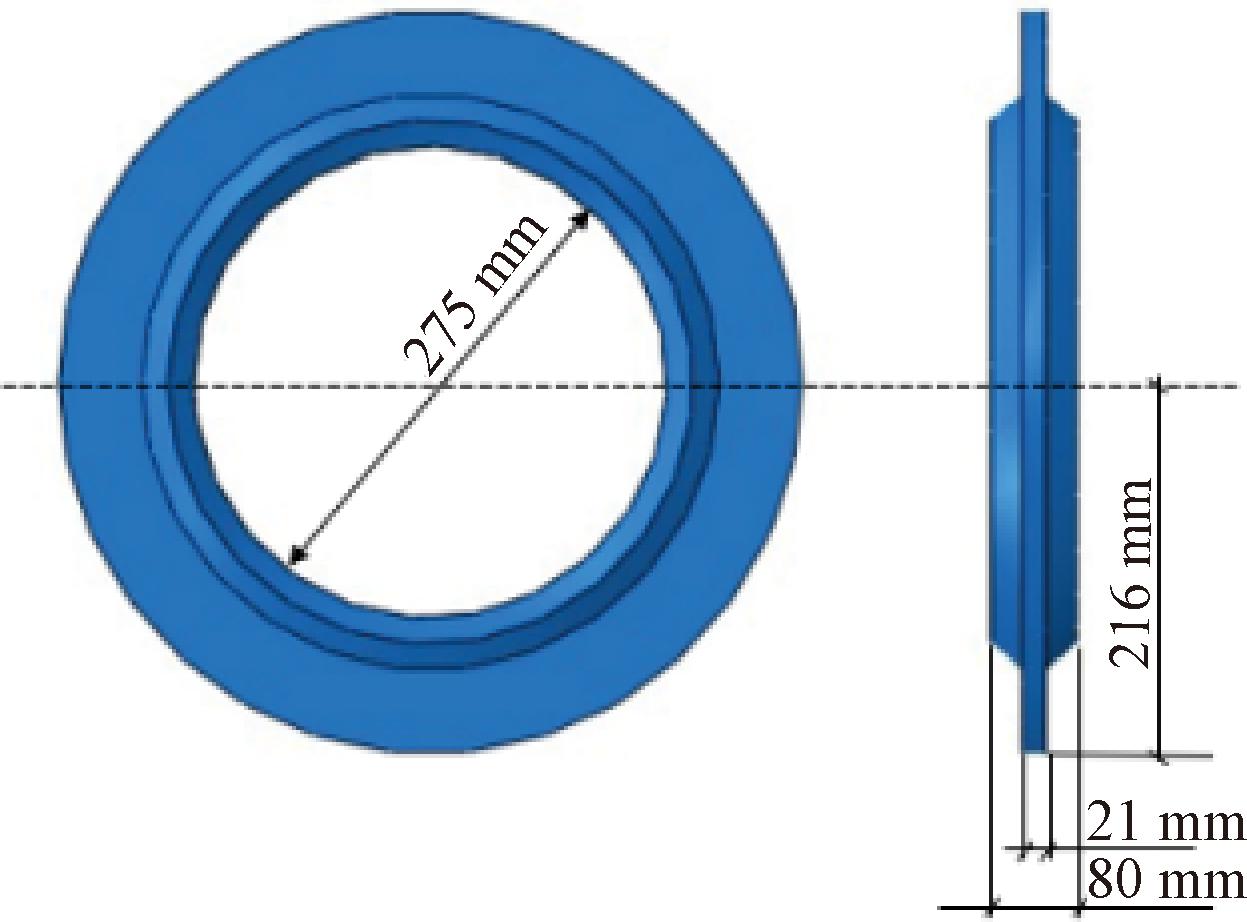
图2 滚刀模型
Figure 2 Cutter model
岩石模型尺寸:1 000 mm(长)×750 mm(宽)×400 mm(高),单元类型为C3D8R且沙漏控制。岩石模型划分单元数量为139 230个,滚刀是刚体,网格密度不影响仿真结果。对应图1的破岩临空面示意图,建立如图3所示的线性破岩模型,滚刀贯入度为2 mm,刀间距设置为60,70,80,90,100 mm。线速度为2 m/s,滚刀自转角速度为9.3 rad/s。

图3 线性破岩模型
Figure 3 Linear rock breaking model
2 4种破岩模式对滚刀线性破岩的影响
三滚刀线性切割岩石过程中,滚刀下方岩体破碎,ABAQUS软件根据单元失效原则,该处网格将会被删除。可视化模块中塑性变形(PEEQ)云图可展示出滚刀破岩的破岩路径及破岩历史,反映岩石在滚刀作用下从原始状态到破坏状态的全过程,其中PEEQ值越大,颜色越深,岩石的塑性变形就越大,则需要的破岩力就越大。同次破岩的力最大,顺次破岩和由内向外破岩的力基本一致,由外向内破岩的力最小。图4为4种模式在最佳刀间距60 mm时的线性破岩塑性变形云图。
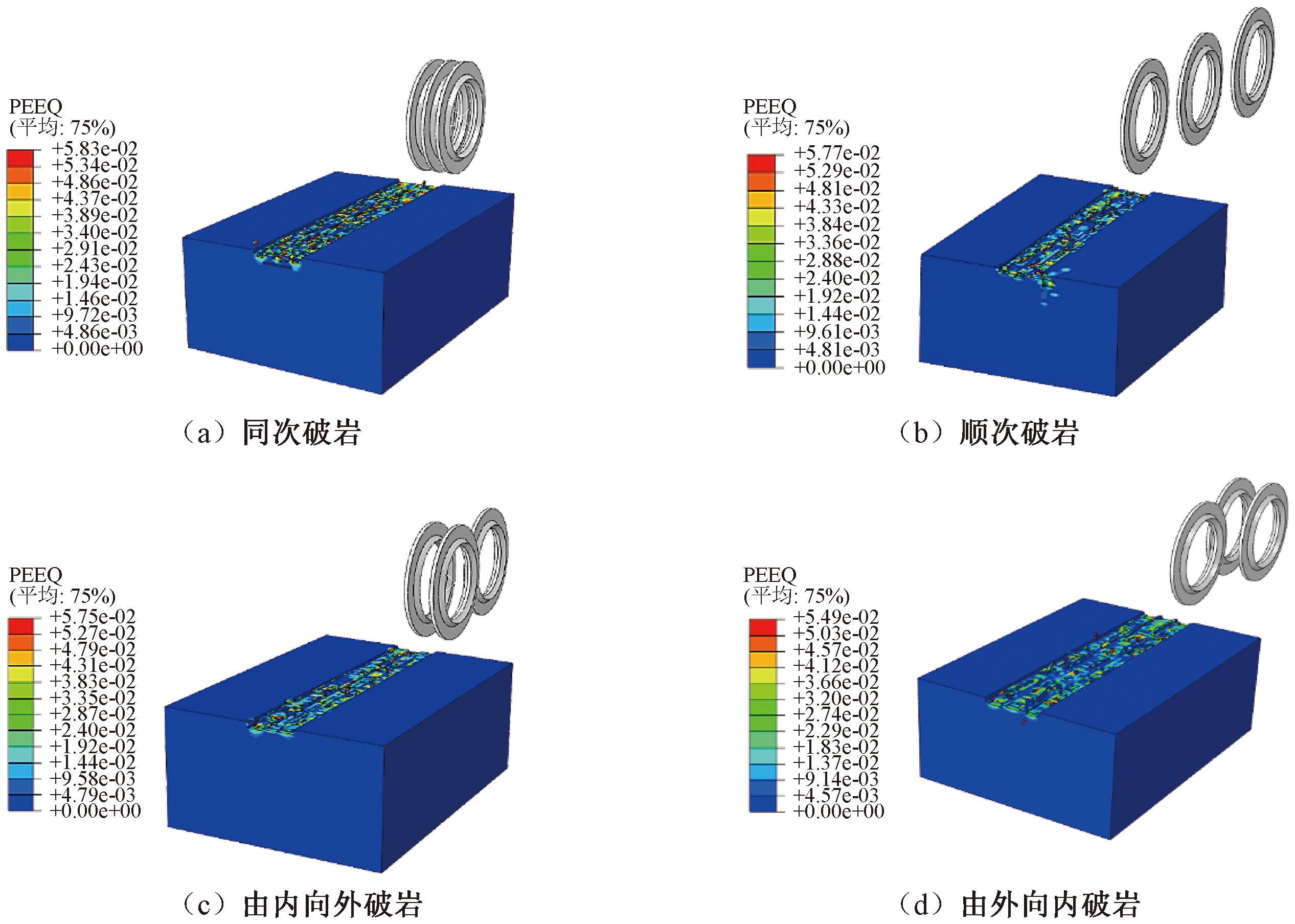
图4 刀间距为60 mm时线性破岩塑性变形云图
Figure 4 Plastic deformation cloud diagram of linear rock breakage with knife spacing of 60 mm
图5为4种模式下线性协同破岩时,不同刀间距对滚刀上的滚动力与法向力的影响。由图5可以看出,随着刀间距的增加,滚刀的滚动力和法向力均会逐渐增大,但增长速度会逐渐减缓。这是因为刀间距较小时,随着刀间距的增加,相邻滚刀之间的破岩路径间临空面增大,这使得后续滚刀更容易对岩石产生裂纹,从而促进了滚刀破岩过程及破岩效率,并导致滚动力和法向力的增长速度较快;当刀间距较大时,相邻滚刀之间的破岩路径间临空面继续增大,但相邻滚刀之间的横向贯通裂纹长度过长,导致滚刀之间的协同作用减弱,载荷的增长速度呈现出减缓的趋势。在图5中,在相同的刀间距下,线性同次破岩模式的滚动力和法向力均达到最大;由外向内破岩法向力最小,而滚动力在刀间距为60 mm时与顺次破岩接近,这可能是数值模拟存在的试验误差导致,但曲线整体增长趋势仍为最小。顺次破岩和由内向外破岩模式的滚动力和法向力曲线整体趋势处于4种破岩模式的中间水平。这主要是受临空面个数的影响,线性同次破岩模式下,在三滚刀之间没有临空面,顺次破岩和由内向外破岩在三滚刀之间均有1个临空面,而由外向内破岩在三滚刀之间有2个临空面。先行滚刀破岩后产生的临空面个数越多,后续滚刀破岩所需的力越小。
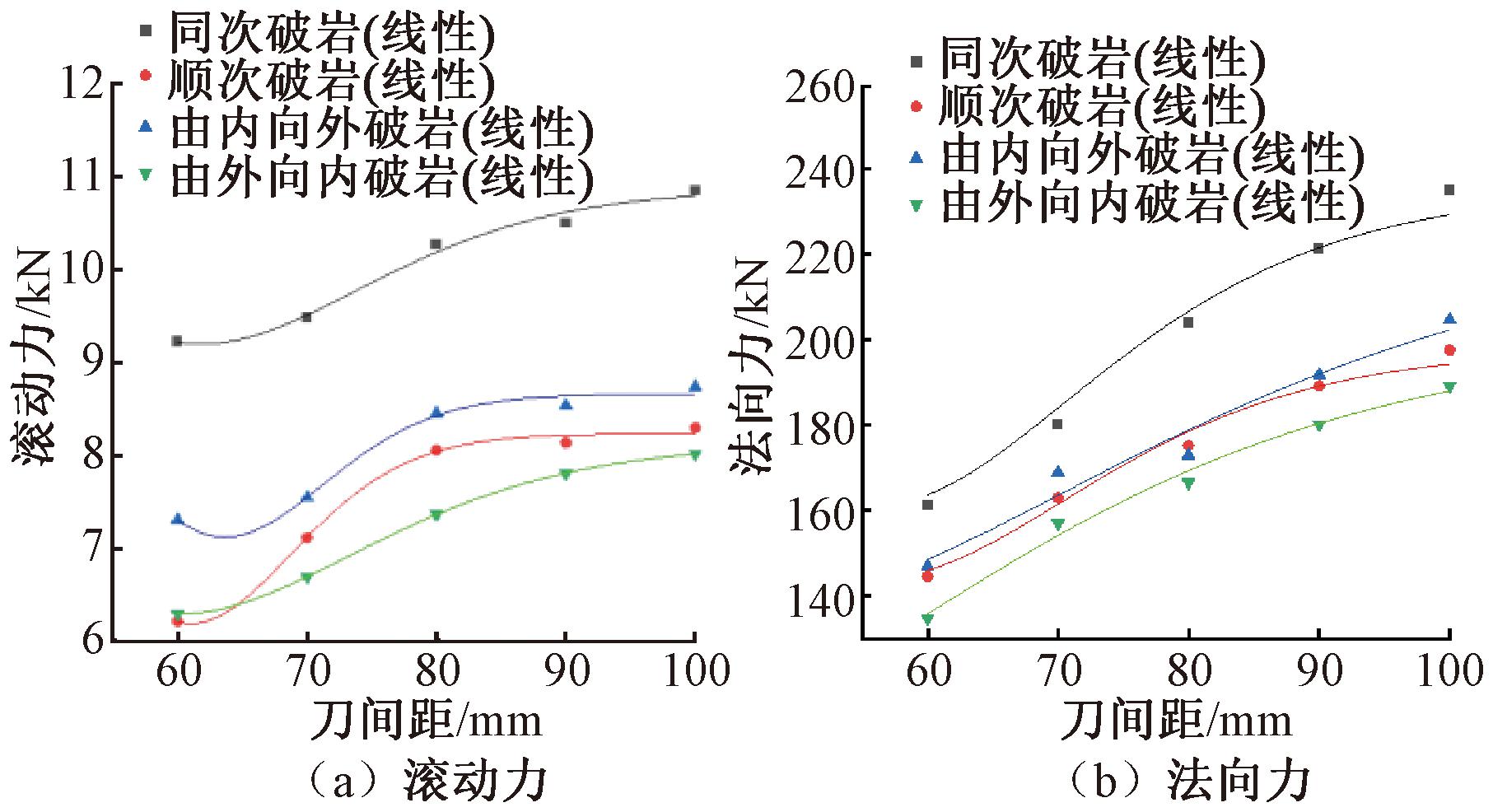
图5 线性破岩下4种模式对破岩力的影响
Figure 5 Effect of four modes on rock breaking force under linear rock breaking
比能是反映破岩效率的重要指标之一,表达式为
(3)
式中:FR为滚刀平均滚刀力,kN;L为滚刀切割岩石长度,mm;V为岩石破碎量,m3。
在滚刀破碎岩石的过程中,比能主要受刀间距和贯入度的影响。如图6所示,4种不同的破岩模式下,随着S/P的增加,比能逐渐增加。随着刀间距的增加,岩石破碎阻力也增加,导致滚刀之间的协同效应减弱,岩石破碎效率降低,比能增加。同次破岩(没有临空面)和由外向内破岩(2个临空面)受刀间距的变化影响较大,波动分别为27.12%和21.00%;而顺次破岩和由内向外破岩这2种破岩形式与线性切割试验都始终保持滚刀一侧存在临空面,受刀间距变化影响较小,波动分别为10.17%,10.24%和8.10%。
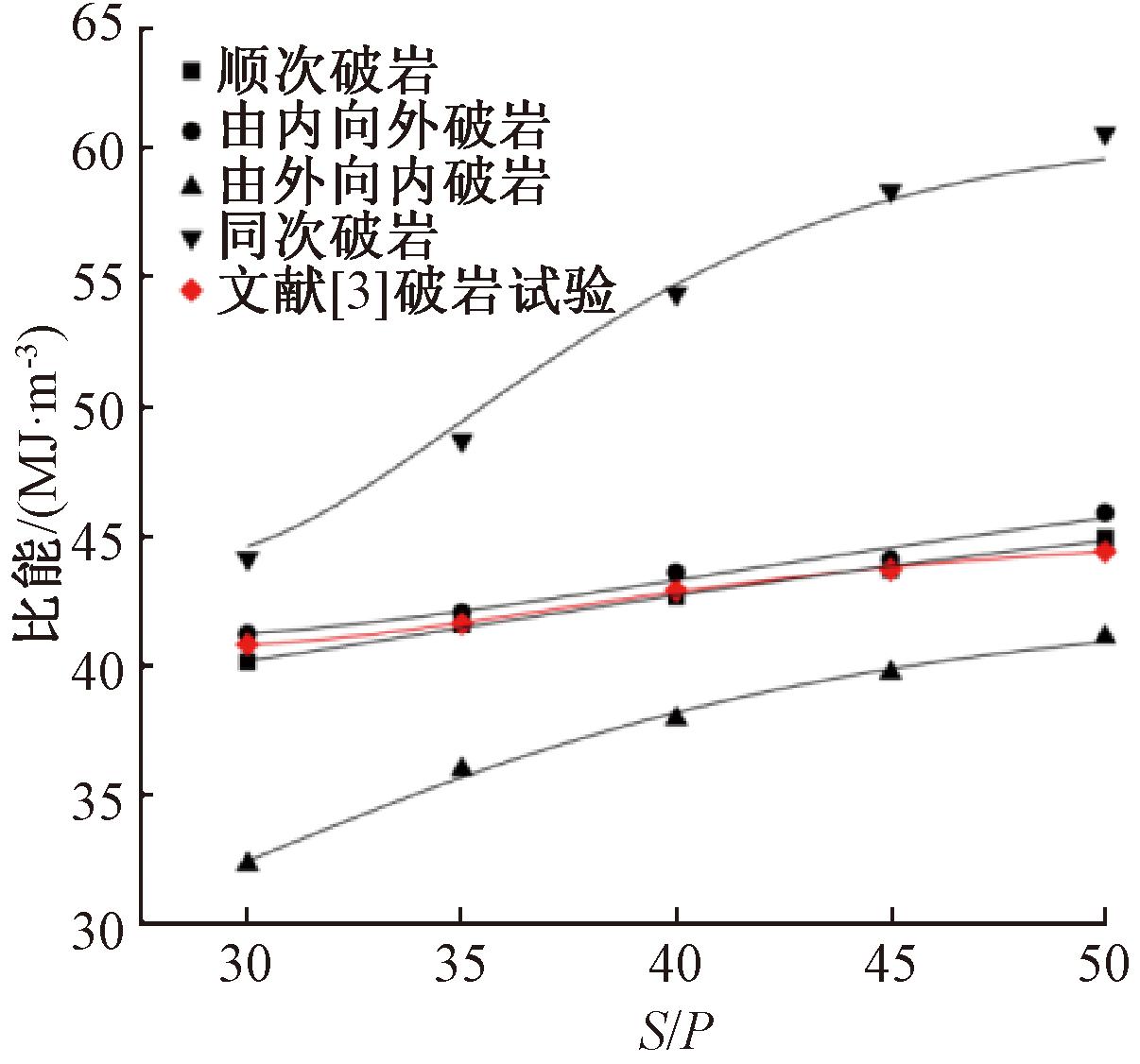
图6 不同破岩模式对破岩效率的影响
Figure 6 Effect of different rock breaking modes on rock breaking efficiency
当S/P不变时,线性同次破岩比能最大,由外向内破岩比能最小,顺次破岩和由内向外破岩时比能处于中间。因此,线性协同破岩时,不同类型的破岩模式对滚刀破岩效率有较大影响,由外向内破岩时比能最小,破岩效率最高。当S/P为30,即刀间距为60 mm时,4种破岩模式下的比能为最小值,破岩效率最高。将本文数值分析结果与北京工业大学机械破岩平台进行的TBM滚刀线性切割试验结果进行对比[3],结果基本一致,两者最大误差为2.14%,这也验证了数值仿真的可靠性。
文献[21]中基于滚刀受力与贯入度关系曲线多峰值跃进特征及双滚刀裂缝贯通为基准,得到硬岩条件下S/P在18~35时比能最低,破岩效率最高;文献[22]中设置贯入度恒定为3 mm情况下,采用不同刀间距对滚刀切割花岗岩过程进行分析,得到S/P在26~30时比能最低,破岩效率最高。对比结果见表2。
表2 试验结果对比
Table 2 Comparison of test results

方法岩石属性贯入度/mm最优刀距/mmS/P本文方法花岗岩26030文献[3]花岗岩26030文献[21]硬岩2~570~9018~35文献[22]花岗岩380~9026~30
依据上述分析可以得到,在三滚刀协同破岩过程中,当滚刀的临空面由无到有时,破岩阻力的变化值明显大于将滚刀一侧临空面转变为滚刀两侧都有临空面时破岩阻力的差值。因此,为了进一步优化刀盘的掘进性能,提高破岩效率,在进行三滚刀协同破岩时应至少需要确保滚刀一侧存在破岩临空面。
3 4种破岩模式对滚刀回转破岩的影响
3.1 模型建立
在回转协同破岩模型中,为避免滚刀360°旋转切削岩石的模拟时间过长,将岩石模型简化为扇形岩石,其尺寸为700 mm(半径)×400 mm(高)。相邻滚刀间的回转半径差分别为60,70,80,90和100 mm,贯入度为2 mm。图7为回转破岩模型。
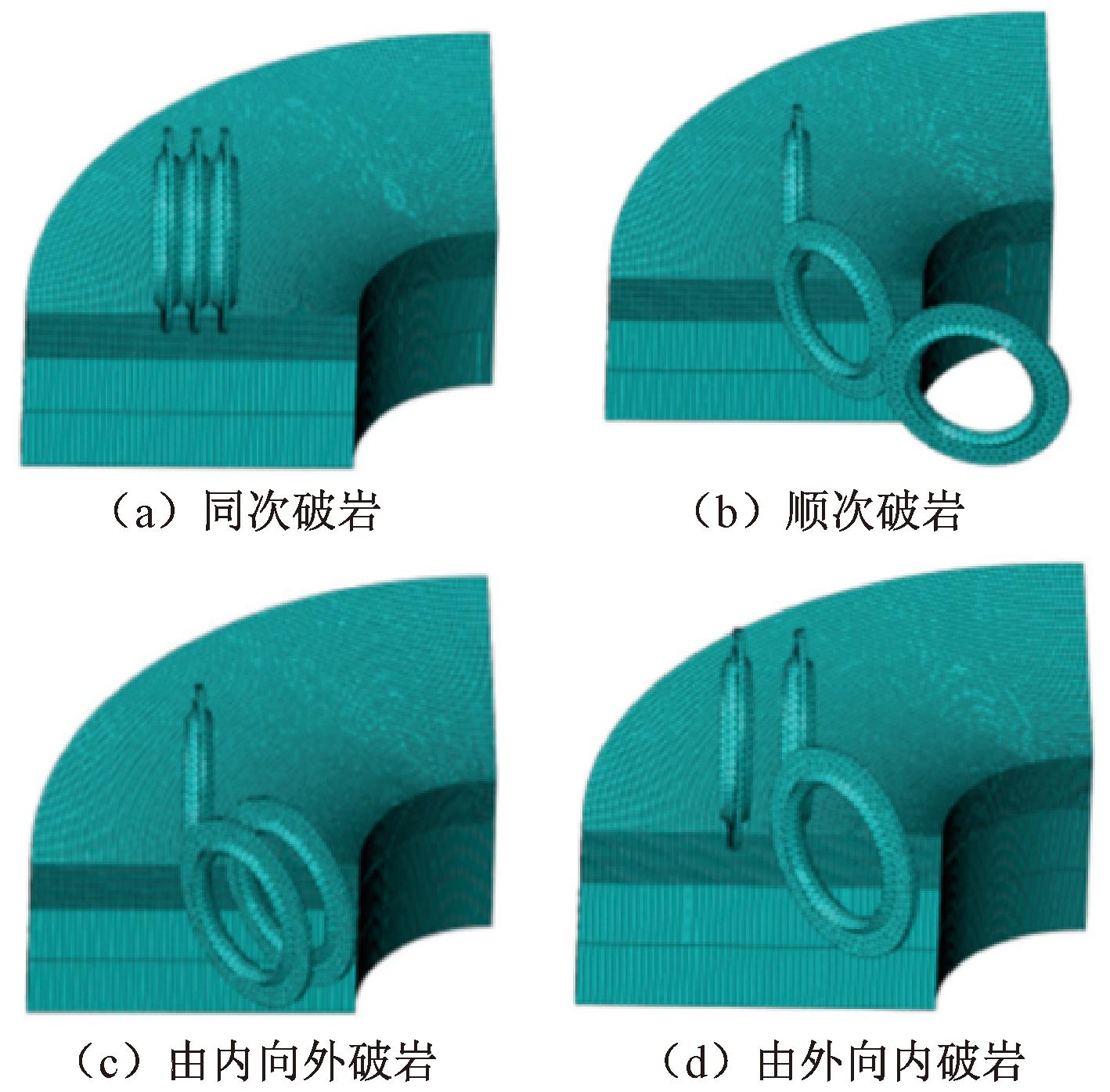
图7 回转破岩模型
Figure 7 Rotary rock breaking model
为了能够更好地模拟滚刀在回转破岩过程中的运动特性,从而使仿真结果更加符合实际情况,设置滚刀绕刀盘中心的公转和绕自身轴线的自转,即在刀盘的中心控制点和滚刀的参考点之间采用单个铰接的连接方式,该方式只允许绕轴线(X轴)进行公转。
3.2 4种破岩模式下滚刀回转破岩分析
图8为4种模式下回转协同破岩时,不同刀间距对滚刀上的滚动力与法向力的影响。由图8可以看出,随着刀间距的增加,滚刀的滚动力和法向力均会逐渐增大;相同的刀间距时,线性同次破岩的滚动力和法向力均最大,由外向内破岩的滚动力和法向力均最小;顺次破岩、由内向外破岩两种临空面数量均为1的破岩模式在刀间距为60~70 mm时,由内向外破岩滚动力高于顺次破岩;而当刀间距增加至70~90 mm时,顺次破岩滚动力高于由内向外破岩;当刀间距继续增加至90~100 mm时,由内向外破岩滚动力将会再次高于顺次破岩。因此,两种破岩在不同刀间距下表现出互有高低的现象,但整体增长趋势基本一致。顺次破岩和由内向外破岩时滚动力和法向力处于4种破岩模式的中间水平。这主要是由于先行滚刀切割岩石后,在滚刀与岩石接触区域形成新的切槽并损坏周围的岩石,为后续滚刀切割岩石创造条件;当刀间距较小时,滚刀能够更好地贯通岩石之间的裂纹,导致岩石损伤更为显著,因此法向力和滚动力较小;随着刀间距的增加,先行滚刀为后续滚刀切割岩石创造的破岩条件逐渐减弱,岩石的损伤程度也会降低,滚刀间岩石的裂缝无法很好地贯通,法向力和滚动力逐渐增加。
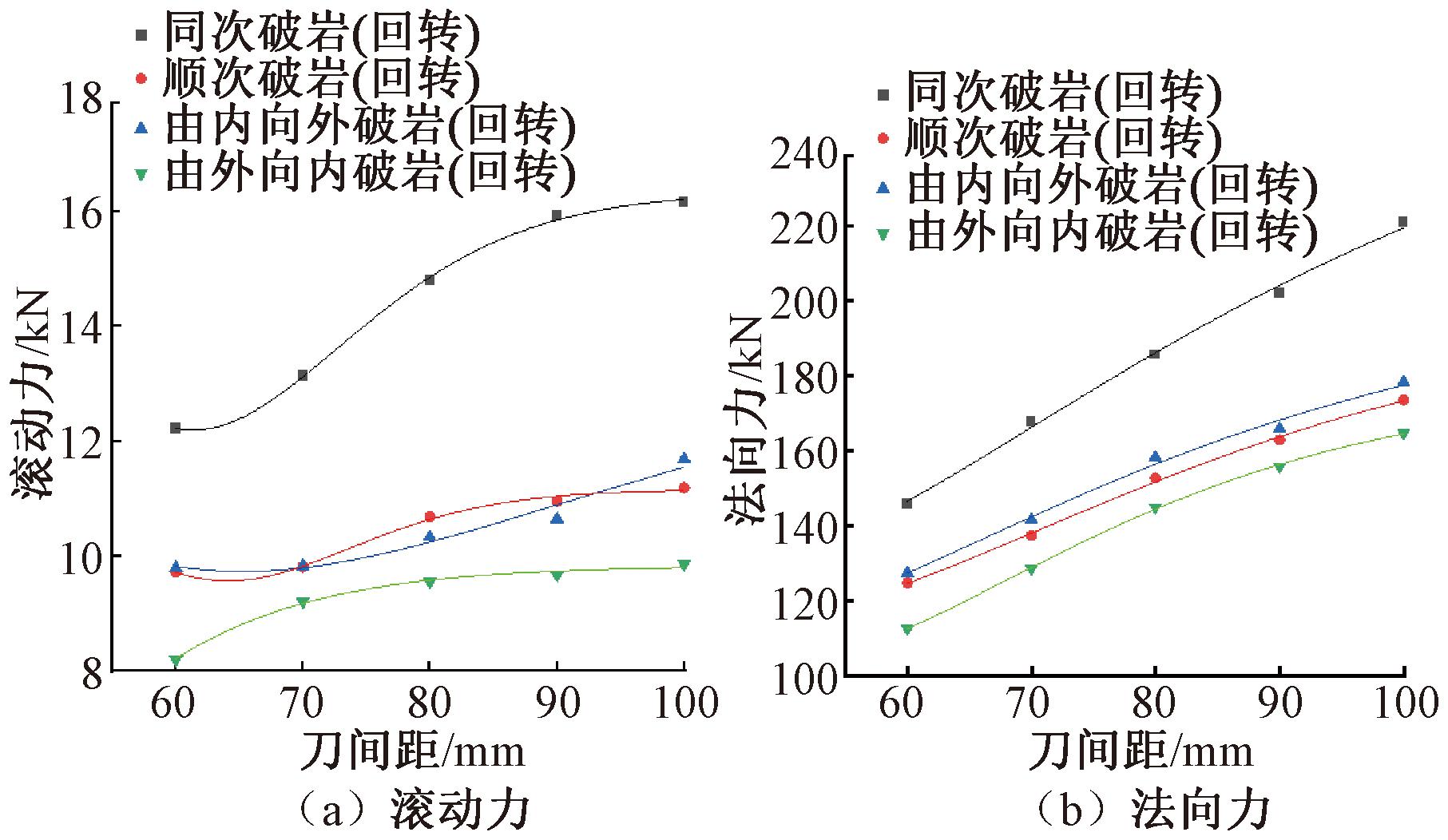
图8 回转破岩下4种模式对破岩力的影响
Figure 8 Effect of four modes on rock breaking force with rotary rock breaking
图9给出了破岩比能随着S/P的变化趋势。随着S/P的增大,同次破岩、顺次破岩、由内向外破岩和由外向内破岩的破岩比能分别增长了18.16%,20.87%,20.13%和32.36%。可见,对于只有一个临空面的破岩模式(顺次破岩、由内向外破岩),随着S/P的增加,破岩比能增幅基本相同。当S/P不变时,回转同次破岩模式下,比能最大,由外向内破岩时比能最小,顺次破岩和由内向外破岩时比能处于中间。因此,在回转协同破岩模型中由外向内破岩模式比能最小,破岩效率最高。
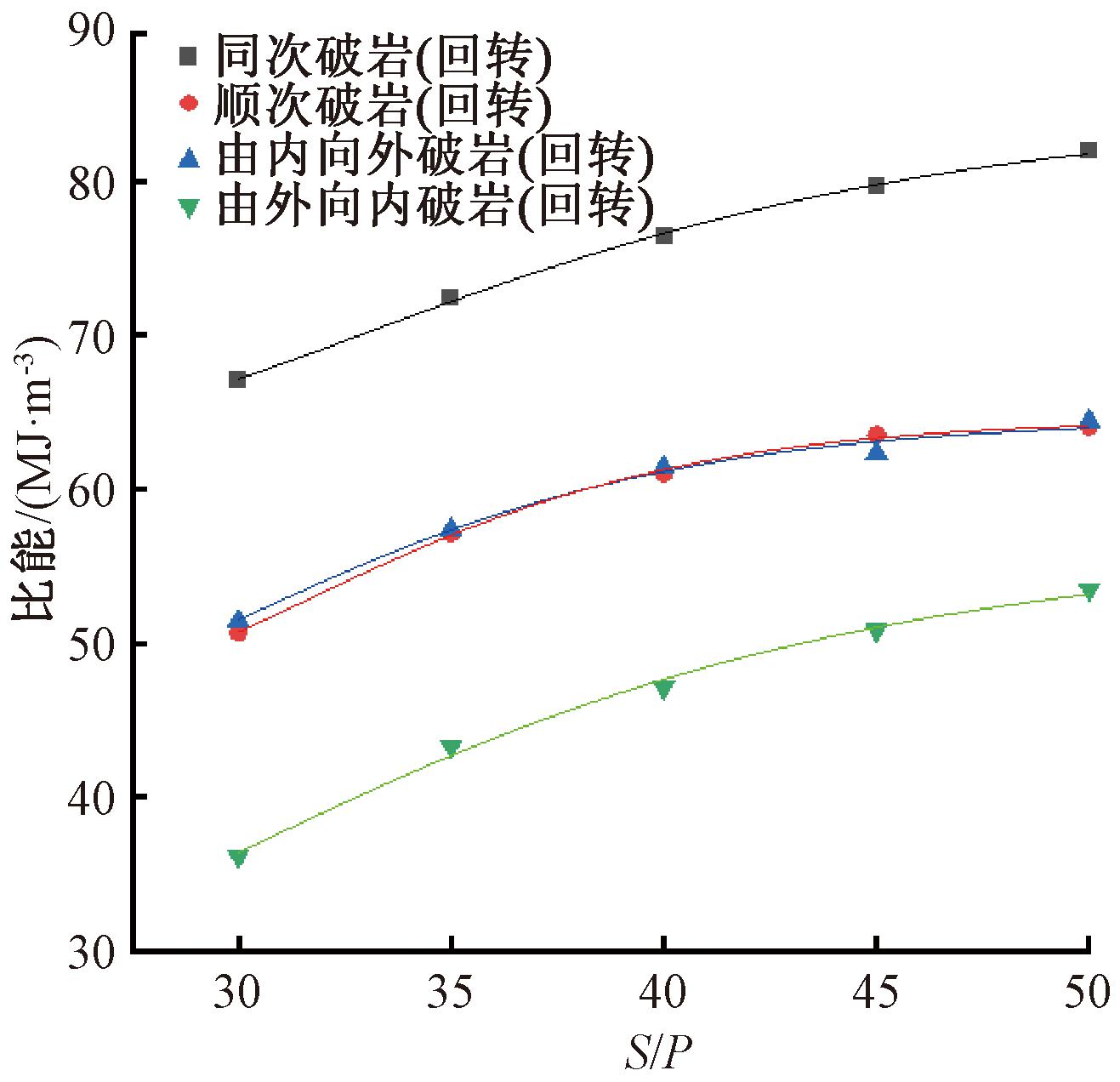
图9 回转破岩下4种模式对破岩效率的影响
Figure 9 Effect of four modes on rock breaking efficiency with rotary rock breaking
4 滚刀线性破岩与回转破岩对比
由于两种切割试验滚刀的运动方式不同,试验结果存在明显差异。图10为TBM掘进机在硬岩地层掘进时掌子面的情况,可以看出,滚刀回转破岩更符合TBM实际掘进时滚刀破岩状态。本部分主要对滚刀线性切割试验和回转切割试验研究TBM滚刀破岩效率的差异进行对比分析,利用换算系数将线性切割试验数据转化为更符合实际破岩形式的回转切割试验数据。

图10 TBM掘进硬岩地层时掌子面情况[23]
Figure 10 Palm face when TBM digging into hard rock formation[23]
4.1 破岩力对比
表3列出了4种破岩模式滚刀力的试验数据。其中,a表示线性破岩平均滚动力换算回转破岩的增加比例;b表示线性破岩平均法向力换算回转破岩的减少比例。
表3 线性破岩与回转破岩滚刀力数据对比
Table 3 Comparison of force data between linear rock breaking and rotary rock breaking cutters

切削顺序刀间距/mm平均滚动力/kN线性破岩回转破岩a/%平均法向力/kN线性破岩回转破岩b/%609.2312.2232.39161.30145.909.55709.4813.1438.61180.00167.806.78同次破岩8010.2714.8144.21204.00185.609.029010.5015.9351.71224.00202.009.8210010.8516.1749.03243.10221.109.05606.229.7256.27144.50124.7013.70707.129.8137.78163.00137.4015.71顺次破岩808.0610.6832.51175.20152.7012.84908.1410.9534.52189.20162.9013.901008.3011.1934.82199.60173.6013.03607.319.7933.93146.90127.4013.27707.559.8330.20168.90141.6016.16由内向外破岩808.4510.3322.25173.00158.308.50908.5410.6424.59191.80165.9013.501008.7411.6933.75204.70178.4012.85606.308.2030.16134.80112.5016.54706.709.2137.46157.00128.6018.09由外向内破岩807.379.5529.58166.50114.9030.99907.819.6723.82180.20155.8012.971008.029.8622.94189.20164.7012.95
由表3可以看出,在相同的刀间距下,线性破岩所需的滚动力均小于回转破岩所需要的滚动力。在破岩模式相同时,5组不同刀间距下的平均滚动力由线性破岩向回转破岩转化时的平均增长比例分别为:同次破岩43.19%、顺次破岩39.18%、由内向外破岩28.94%、由外向内破岩28.79%,其平均值为35.03%。在刀间距相同时,平均滚动力由线性协同破岩向回转协同破岩转化时的增长比例:S=60 mm时为38.19%;S=70 mm时为36.01%;S=80 mm时为32.14%;S=90 mm时为33.66%;S=100 mm时为35.14%,其平均值为35.03%,即滚动力的换算系数为1.35。
由表3可以看出,在相同的刀间距下,线性破岩所需的法向力均大于回转破岩所需要的法向力。在破岩模式相同时,5组不同刀间距下的平均法向力由线性破岩向回转破岩转化时的平均减小比例:同次破岩8.84%、顺次破岩13.84%、由内向外破岩12.86%、由外向内破岩14.82%,其平均值为12.59%。在刀间距相同时,平均法向力由线性协同破岩向回转协同破岩转化时的减小比例:S=60 mm时为13.27%;S=70 mm时为14.19%;S=80 mm时为10.83%;S=90 mm时为12.69%;S=100 mm时为11.97%,其平均值为12.59%,即法向力的换算系数为0.87。
随着刀间距的增加,线性破岩所需的法向力均大于相同刀间距下回转破岩的法向力,而线性破岩所需的滚动力均小于回转破岩所需要的滚动力。这可以用TBM掘进过程中的能量守恒来解释:破岩过程中主要考虑TBM刀盘顶部推力和扭矩实现的破岩做功,当法向力减小时,回转切割需要更大的滚动力即扭矩来维持;但在回转破岩过程中,滚刀间显著的侧向力加速了横向裂纹的发展,有利于裂纹从临空面向工作面贯通,与线性破岩相比,略微降低了回转破岩过程中的法向力。
4.2 破岩比能对比
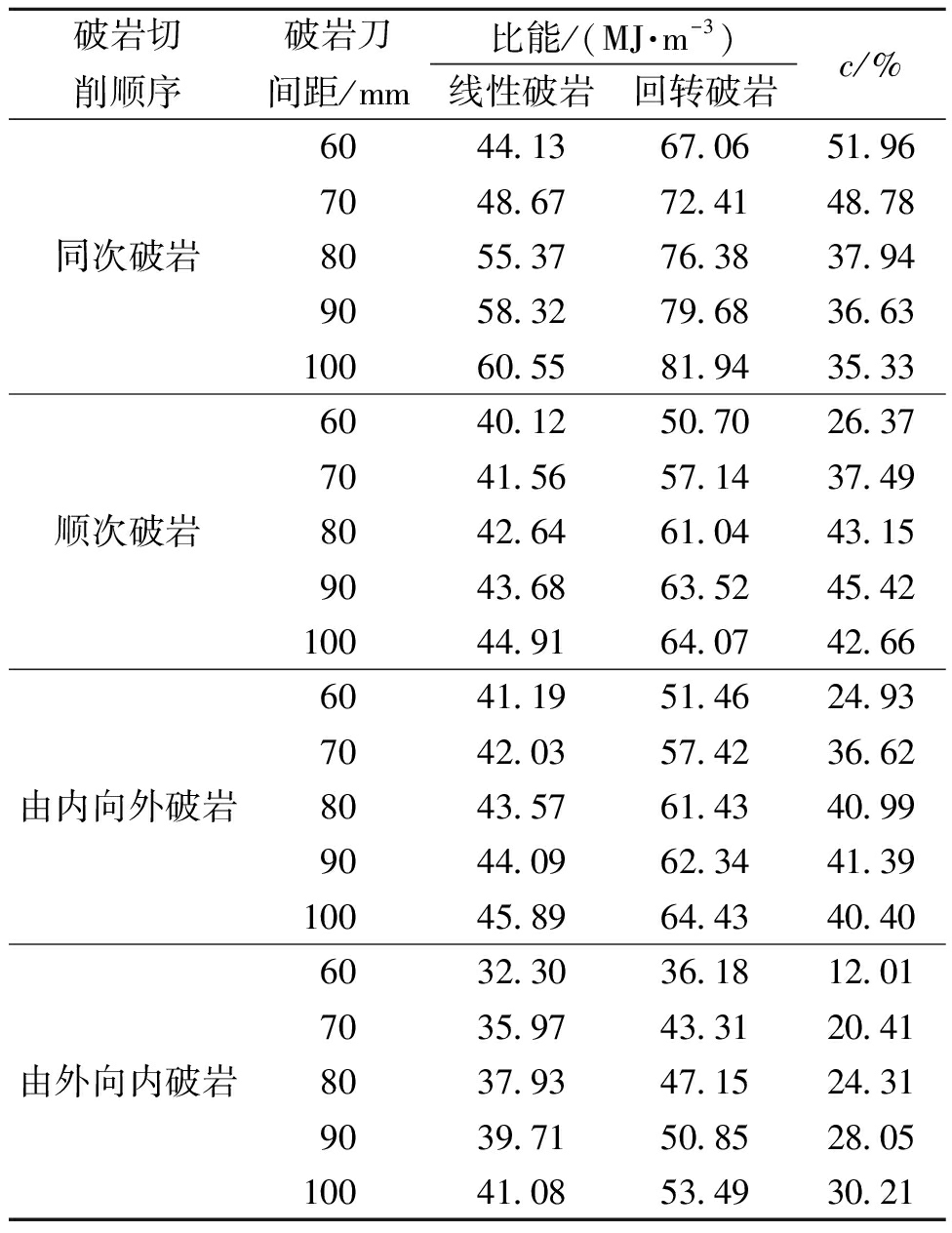
表4列出了4种破岩模式破岩比能的试验数据。其中,c表示线性破岩比能换算回转破岩的增加比例。
表4 线性破岩与回转破岩比能数据对比
Table 4 Comparison of specific energy data between linear rock breaking and rotary rock breaking
破岩切削顺序破岩刀间距/mm比能/(MJ·m-3)线性破岩回转破岩c/%6044.1367.0651.967048.6772.4148.78同次破岩8055.3776.3837.949058.3279.6836.6310060.5581.9435.336040.1250.7026.377041.5657.1437.49顺次破岩8042.6461.0443.159043.6863.5245.4210044.9164.0742.666041.1951.4624.937042.0357.4236.62由内向外破岩8043.5761.4340.999044.0962.3441.3910045.8964.4340.406032.3036.1812.017035.9743.3120.41由外向内破岩8037.9347.1524.319039.7150.8528.0510041.0853.4930.21
由表4可以看出,在破岩模式相同时,回转破岩的比能均大于线性破岩的比能。在相同的刀间距下,破岩比能由线性破岩向回转破岩转化时的增长比例:同次破岩42.13%、顺次破岩39.02%、由内向外破岩36.87%、由外向内破岩23.00%,其平均值为35.25%。在破岩模式相同时,5组不同S/P下的比能由线性破岩向回转破岩转化时的增长比例:S/P=30 mm时为28.82%;S/P=35 mm时为35.83%;S/P=40 mm时为36.60%;S/P=45 mm时为37.87%;S/P=50 mm时为37.15%,其平均值为35.25%,即比能的换算系数为1.35。
表5为本文数值模拟数据和文献[24]室内试验数据的换算系数结果对比。由表5可以看出,数值模拟结果与室内试验结果基本吻合,线性破岩向回转破岩转化的总趋势保持一致,滚动力及比能变大,法向力变小,数值模拟结果与室内试验结果存在一定的误差,误差产生的原因可能是由于模拟试验和室内试验的样本统计种类及个数不完全一致。
表5 换算系数对比
Table 5 Comparison of conversion coefficiency

方法贯入度/mm刀间距/mmS/P滚动力换算系数法向力换算系数比能换算系数本文260~10030~501.350.871.35文献[24]0.5~2.58032~1601.140.971.44
5 结论
本文针对多滚刀协同破岩问题,研究了刀盘掘进过程中相邻滚刀之间协同效应的布置参数。使用ABAQUS软件建立了同次破岩、顺次破岩、由内向外破岩、由外向内破岩4种模式的三滚刀破岩模型,分析了相邻滚刀在破岩过程中相互之间的协同作用对刀盘破岩性能的影响。
(1)在基于三滚刀协同破岩模型的数值模拟研究中,分析了刀间距和切削顺序两个重要参数对滚刀破岩载荷和破岩比能的影响规律,得到当刀间距与贯入度的比值为30时,滚刀破岩比能达到最小,破岩效率最高。
(2)在4种破岩模式中,滚刀的切削顺序不同,导致产生临空面的数量有所不同。临空面的数量对破岩过程有显著影响。临空面的数量越多,先行滚刀破岩后,后续滚刀的破岩阻力就越小。因此,在刀盘设计时,应尽量选择能使滚刀产生临空面的布置方式,以提高破岩效率。
(3)通过对比分析滚刀线性切割试验数据和回转切割试验数据,结果显示,将滚刀线性切割数据转化为更贴近实际工程的回转切割数据时的换算系数,滚动力和比能的换算系数均为1.35,而法向力的换算系数为0.87。
以上结论为TBM运行过程中操作参数的设置以及TBM刀盘上滚刀的布置设计提供了理论依据,然而本文主要研究的三滚刀协同破岩存在一些局限性,后续将研究刀盘中所有滚刀的分布形式对破岩的影响,从而更好地指导TBM刀盘上滚刀的布置设计。
[1] 翟淑芳, 杜红坤, 岳奇超, 等. 基于特征粒径的盘形滚刀破岩最优贯入度分析[J]. 现代隧道技术, 2023, 60(4): 147-152, 162.
ZHAI S F, DU H K, YUE Q C, et al. Analysis of the optimal penetration of disc cutter in rock breaking based on characteristic particle size[J]. Modern Tunnelling Technology, 2023, 60(4): 147-152, 162.
[2] 翟淑芳, 曹世豪, 冯永, 等. 断续节理岩体的TBM滚刀破岩机理研究[J]. 郑州大学学报(工学版), 2020, 41(1): 20-24.
ZHAI S F, CAO S H, FENG Y, et al. The influence of intermittent joint on rock fragmentation by TBM cutter[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(1): 20-24.
[3] 龚秋明, 何冠文, 赵晓豹, 等. 掘进机刀盘滚刀间距对北山花岗岩破岩效率的影响实验研究[J]. 岩土工程学报, 2015, 37(1): 54-60.
GONG Q M, HE G W, ZHAO X B, et al. Influence of different cutter spacings on rock fragmentation efficiency of Beishan granite by TBM[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 54-60.
[4] 薛亚东,周杰,赵丰,等.基于MatDEM的 TBM 滚刀破岩机理研究[J]岩土力学,2020,41(增刊1):337-346.
XUE Y D, ZHOU J, ZHAO F, et al. Rock breaking mechanism of TBM cutter based on MatDEM[J]. Rock and Soil Mechanics, 2020, 41(S1): 337-346.
[5] 温森, 周书宇, 盛桂琳. 复合岩层中滚刀旋转切割破岩效率试验研究[J]. 岩土力学, 2019, 40(7): 2628-2636.
WEN S, ZHOU S Y, SHENG G L. Experiments on the efficiency of rock fragment ation by rotary cutting in composite rock strata[J]. Rock and Soil Mechanics, 2019, 40(7): 2628-2636.
[6] 陆峰, 张弛, 孙健. TBM正滚刀回转切削仿真分析[J]. 制造业自动化, 2015, 37(22): 21-23.
LU F, ZHANG C, SUN J. Rotary cutting simulation analysis of TBM positive cutter[J]. Manufacturing Automation, 2015, 37(22): 21-23.
[7] 吴峰. TBM盘形滚刀贯入度与结构参数优化设计研究[D].长沙: 中南大学, 2012.
WU F. Study on penetration and structural parameters optimization design of TBM dischob[D].Changsha: Central South University,2012.
[8] 程永亮. TBM盘形滚刀破岩最优贯入度的数值模拟[J]. 中南大学学报(自然科学版), 2017, 48(4): 936-943.
CHENG Y L. Numerical simulation on optimal penetration of TBM disc cutter′s rock fragmentation[J]. Journal of Central South University (Science and Technology), 2017, 48(4): 936-943.
[9] 张照煌, 赵宏, 柴超群. 全断面岩石掘进机刀间距研究方法的发展与分析[J]. 矿山机械, 2020, 48(12): 1-9.
ZHANG Z H, ZHAO H, CHAI C Q. Development and analysis of research methods for cutter spacing of full facerock TBM[J]. Mining &Processing Equipment, 2020, 48(12): 1-9.
[10] 霍军周, 孙伟, 郭莉, 等. 多滚刀顺次作用下岩石破碎模拟及刀间距分析[J]. 哈尔滨工程大学学报, 2012, 33(1): 96-99.
HUO J Z, SUN W, GUO L,et al. Numerical simulation of the rock fracture process induced by multi-disc-cutters and cutter spacing design[J]. Journal of Harbin Engineering University, 2012, 33(1): 96-99.
[11] 刘亚迪, 齐文聪, 刘浩飞, 等. 多滚刀协同破岩过程数值模拟与滚刀布置规律研究[J]. 煤炭科学技术, 2023, 51(5): 232-244.
LIU Y D, QI W C, LIU H F, et al. Numerical simulation of cooperative breaking rock by multi-cutter and research on the layout law of disc cutter on cutterhead[J]. Coal Science and Technology, 2023, 51(5): 232-244.
[12] 林赉贶, 夏毅敏, 贾连辉, 等. 安装参数与掘进参数对滚刀破岩阻力的影响[J]. 浙江大学学报(工学版), 2018, 52(6): 1209-1215.
LIN L K, XIA Y M, JIA L H, et al. Influence of installation and tunnelling parameters on rock-breaking resistance of disc cutter[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(6): 1209-1215.
[13] 周凤玺, 李世荣. 广义Drucker-Prager强度准则[J]. 岩土力学, 2008, 29(3): 747-751.
ZHOU F X, LI S R. Generalized Drucker-Prager strength criterion[J]. Rock and Soil Mechanics, 2008, 29(3): 747-751.
[14] 周永强, 盛谦, 朱泽奇, 等. 基于修正Drucker-Prager准则的岩石次加载面模型[J]. 岩土力学, 2017, 38(2): 400-408, 418.
ZHOU Y Q, SHENG Q, ZHU Z Q, et al. Subloading surface model for rock based on modified Drucker-Prager criterion[J]. Rock and Soil Mechanics, 2017, 38(2): 400-408, 418.
[15] 黄波, 李钢. 基于经典Drucker-Prager破坏准则的岩体滑移线理论[J]. 建筑技术, 2017, 48(3): 296-298.
HUANG B, LI G. Slip-line theory for rock mass based on classical Drucker-Prager failure criterion[J]. Architecture Technology, 2017, 48(3): 296-298.
[16] 徐干成, 郑颖人. 岩石工程中屈服准则应用的研究[J]. 岩土工程学报, 1990, 12(2): 93-99.
XU G C, ZHENG Y R. Research on the application of yield criteria in roch engineering[J]. Journal of Geotechnical Engineering, 1990, 12(2): 93-99.
[17] 郭建强, 蒋建国, 刘新荣, 等. 基于弹性应变能D-P强度准则修正[J]. 土木工程学报, 2021,54(6): 110-116.
GUO J Q, JIANG J G, LIU X R, et al. Modification of Drucker-Prager strength criterion based on the elastic strain energy[J]. China Civil Engineering Journal, 2021,54(6): 110-116.
[18] 王腾跃. TBM盘型滚刀关键技术及试验装置研制[D].沈阳: 沈阳建筑大学, 2011.
WANG T Y. Development of key technology and test device for TBM dischob[D].Shenyang:Shenyang Jianzhu University,2011.
[19] 刘洪斌, 刘石头, 穆伟涛, 等. 不同贯入度下TBM盘形组合滚刀切削性能分析[J]. 中国测试, 2019, 45(2): 36-41.
LIU H B, LIU S T, MU W T, et al. Analysis of cutting performance of TBM disc shaped combined hob with different penetration[J]. China Measurement &Test, 2019, 45(2): 36-41.
[20] 李辉, 王树林, 汪加科. TBM盘形滚刀受力分析[J]. 现代隧道技术, 2012, 49(3): 193-197.
LI H, WANG S L, WANG J K. Force analysis of the disc cutter on a TBM[J]. Modern Tunnelling Technology, 2012, 49(3): 193-197.
[21] 张志强, 张洋, 张彪, 等. TBM滚刀受力及其间距优化研究[J]. 现代隧道技术, 2016, 53(6): 108-114.
ZHANG Z Q, ZHANG Y, ZHANG B, et al. Optimizationofthe force applied to cutters and the spacing of TBM cutters[J]. Modern Tunnelling Technology, 2016, 53(6): 108-114.
[22] 陆峰, 张弛, 孙健, 等. 基于TBM双滚刀破岩仿真的实验研究[J]. 工程设计学报, 2016, 23(1): 41-48.
LU F, ZHANG C, SUN J,et al. Experimental study on rock-breaking simulation of doubled isccutter of TBM[J]. Chinese Journal of Engineering Design, 2016, 23(1): 41-48.
[23] 翟淑芳. 深部复杂地层的TBM滚刀破岩机理研究[D].重庆: 重庆大学, 2017.
ZHAI S F. Study on rock breaking mechanism of TBM hob in deep complex stratum[D].Chongqing: Chongqing University,2017.
[24] 龚秋明, 董贵良, 殷丽君, 等. 线性和旋转切割方式滚刀破岩试验对比研究[J]. 施工技术, 2017, 46(11): 61-66.
GONG Q M, DONG G L, YIN L J,et al. Comparison study on therock linear and rotating cutting test by TBM cutter[J]. Construction Technology, 2017, 46(11): 61-66.