现实生活中的许多优化问题都可以用优化模型来表达[1],在工程领域和日常生活应用中,元启发式算法已被证明是一种有效且实用的算法[2],相较于梯度下降、分支界限等优化方法,元启发式算法可以避免陷入局部最优并能够更有效地得到全局最优解。
适应度地形分析是一种用于发掘问题本身信息的方法,它反映了问题的特征属性[3]。通过准确表达这些特征,有助于选择或开发更适合此类问题特征的优化算法。这些优化算法不能在每个优化问题上都优于其他单一的算法,每种算法需要考虑的主要问题是算法中探索和开发的平衡,更多的探索意味着算法需要更多资源寻找最优解,尤其是对于复杂、多峰的优化问题可以避免陷入局部最优;而更多的开发则是让算法可以更好地利用已知局部信息,提高局部搜索的精度和效率,有助于算法快速收敛于局部最优解[4]。
对于不同的问题特征,优化算法需要有不同的侧重点[5]。近年来,部分学者通过利用问题的适应度地形信息,自适应地调整算法策略与参数,以期提升优化算法的性能[6];同时,另一部分研究者致力于发掘算法本身的内在特性,并基于这些特性预测从算法组合中选择最佳算法进行下一步迭代[7-8]。然而,这些研究工作往往未能充分结合问题的地形特征与算法特性,导致其在实际应用中存在显著的局限性。
为了能够结合优化问题特征选择更合适的优化算法,本文提出了一种基于适应度地形特征的多种优化算法调度方法(meta-heuristic algorithm scheduling based on fitness landscape analysis,FL-AMAS),通过从复杂的优化问题中提取问题特征,将问题特征划分为地形复杂问题和地形简单问题。对地形复杂问题采用探索能力强的算法,对地形简单问题采用开发能力强的算法。
在众多优化算法中,差分进化(differential evolution,DE)算法[9]具有较好的探索能力,而哈里斯鹰优化(harris hawks optimization,HHO)算法[10]则具有较好的开发能力。汪慎文等[11]通过分析差分进化算法的控制参数及策略,强调该算法在处理复杂问题时具有更强的探索性能。Heidari等[10]提出的哈里斯鹰优化算法在基准问题测试中表现优秀,具有更好的开发能力与更快的收敛速度,但在处理复杂问题时容易陷入局部最优解的情况。考虑到DE和HHO各自的特性,将它们作为互补类算法,根据问题的适应度地形特征进行动态调度,以最大化发挥各自算法的优势。本文的主要贡献可总结如下:①提出了一种自适应优化算法调度方法,通过分析待解决问题的地形特征来选择更合适的优化算法,当问题的解空间相对简单时,可调度开发性较强的HHO算法;当问题的解空间结构复杂时,则调度探索性较强的DE算法进行求解。②提出了一种新的能够表征问题特征的适应度地形,即局部最优峰值簇NOPC。NOPC=1表示问题空间结构相对简单;NOPC>1表示问题空间结构较为复杂。利用NOPC为优化算法的调度提供依据。
1 相关工作
1.1 优化问题描述
对于无约束单目标数值优化问题在不失一般性的前提下,可以用式(1)进行描述:
(1)
式中:f(x)为在搜索空间Rn中定义的目标函数;x=(x1,x2,…,xD)为目标函数的解向量,求解该数值优化问题就是找到一个解向量使f(x)取最小值,D为优化问题的维度,每一维度的上下边界分别为xmin和xmax。
1.2 适应度地形
适应度地形最初是由Wright等[12]提出,用来描述问题空间的复杂程度或特征,通常是由搜索空间中个体的函数适应值来描述。
近期,适应度地形分析已经被用于指导算法策略的选择和确定问题的解决方法。王艳丽等 [13]提出了一种新的自反馈差分进化算法,通过提取各代种群的局部适应度地形特征,并结合地形中单峰和多峰的概率分布,选择最优的变异策略以自适应地解决某类型的优化问题。李亚欣等[14]在差分进化算法选择设计中利用地形特征,提出了具有适应度距离相关性的多算子DE框架,在进化过程中将更多的权重动态分配给性能最佳的算子从而产生更高质量的解决方案。
上述研究均采用适应度地形来动态选择合适的变异算子或修改权重以提高算法性能,都属于算法内部的调整。如果能够根据地形特征选择更具有优势的算法,对于提高问题解决方案更有帮助。本文通过NOPC这一指标来描述要解决问题的地形特征,并动态调度更适合的算法进行求解。
1.3 差分进化算法
DE是一种基于种群的优化算法,具有搜索能力强、优化结果稳健等特点。标准的DE结构是由突变算子、交叉概率和选择算子组成[15]。本文选择DE的主要原因在于其较强的探索性能,DE的探索性能主要受算法中变异策略的影响[16]。在DE算法中,变异操作通过对个体进行差分变异的方式生成新的候选解。具体而言,变异操作选取种群中的3个不同个体,然后通过线性组合计算差分向量,并将该差分向量与当前个体相加得到变异个体。变异操作引入了随机性和多样性,从而扩大了搜索空间,增强了算法的探索性能。变异策略中最常用的是DE/rand/1,如式(2)所示:
vi,G=xr1,G+F·(xr2,G-xr3,G)。
(2)
式中:xr1,G、xr2,G、xr3,G为从当前总体中随机选择的不同个体;F为变异中的缩放因子。
1.4 哈里斯鹰优化算法
Heidari等[10]受到哈里斯鹰觅食行为的启发,提出了哈里斯鹰优化算法。该算法基于鹰在扑食过程中不同阶段采用的策略,将扑食阶段划分为“寻觅猎物”和“捕捉猎物”两个阶段。本文选用HHO算法主要是利用其显著的开发性能,而该性能主要受算法中捕捉阶段的影响。在HHO算法中,捕捉阶段的优化涉及逃逸能量E和猎物逃脱概率随机因子r,以及软包围、硬包围、软包围与渐进快速俯冲、硬包围与渐进快速俯冲等4个策略的结合应用。这些策略使得HHO算法具有更强的开发性能,能够迅速而有效地搜索解空间以找到最优解。
1.5 随机游走算法
要获取问题的地形特征,需要对搜索空间进行采样[17]。本文采用了随机游走算法,由随机游走生成的样本通常可以覆盖整个搜索空间具有代表性的区域。相比于分层采样和基于梯度的采样,随机游走算法具有更广泛、更高效的覆盖性。
随机游走是从一个顶点出发,按照一定的概率随机移动到一个邻居节点,并将该节点作为新的当前节点,如此循环执行若干步,得到一条游走路径:
Xn=(x0,x1,…,xn)。
(3)
2 算法调度方法
算法调度方法主要包括特征提取和算法调度。特征提取阶段主要是获取待解决优化问题的地形特征,以便选择更合适的算法。地形特征利用局部最优峰簇数来描述。
2.1 特征提取
局部最优峰值簇(NOPC)反映了待解决问题的地形特征。首先,对问题的搜索空间进行随机游走采样,评估采样点的适应度值,提取排序最前列的一部分最优点。其次,通过聚类分析这些点是否位于同一峰上,从而确定峰簇数。
在随机游走采样时,随着维度的增加,搜索空间也会增大,采样的游走步数也将随之增加。考虑到时间预算,本文采用的游走步数为500D,其中D为问题维度,步长设定为单维阈值的10%。对于这些采样点,采用DBSCAN聚类方法对前2%的个体进行分类(该比例由下一节的实验确定)。由于整个搜索过程具有一定的随机性,因此对每个测试函数进行30次独立实验,然后从这30次实验结果中选择出现频率最高的两个特征值,利用轮盘赌方法从中选择一个作为最终的特征值,这个最终的特征值定义为NOPC。实验结果表明,对于简单优化问题,地形特征较为平滑,通过聚集局部最优点呈现的NOPC为1,表现为单峰结构;对于复杂优化问题,地形较为粗糙,呈现的NOPC则大于1,表现为多峰结构。
NOPC特征提取中的聚类方法采用了DBSCAN算法,该算法是基于密度的聚类方法[18],其中包含两个重要的参数:邻域半径R和核心点邻域内至少包含的样本个数minPts。本文minPts的值设定为3。
2.2 DBSCAN的半径自适应选择
DBSCAN中的邻域半径对分类结果有重要影响。尤其随着问题维度的增加,搜索空间随之增大,若保持恒定的邻域半径,将无法对提取出的最优点进行有效分类,所以DBSCAN算法中参数R(邻域半径)的选择非常重要。
本文通过不同测试函数的实验确定NOPC特征所对应的维度-半径对,并根据已知的数据对拟合出维度与半径的关系曲线,使得DBSCAN可以根据问题的维度自适应选择合适的邻域半径进行分类。通过实验得到低维空间中几个维度-半径对的具体数值,分别为(2,0.10),(4,0.40),(6,0.45),(8,0.55)。针对这些维度-半径对,分别进行线性函数拟合、指数函数拟合、对数函数拟合、幂函数拟合和多项式函数拟合实验,拟合结果如图1所示。由图1可以看出,效果最好的是线性函数拟合和幂函数拟合,再利用该拟合公式进行高维空间的实验,根据实验结果确定选用效果更好的线性拟合,如式(4)所示:
R=0.07D+0.025。
(4)
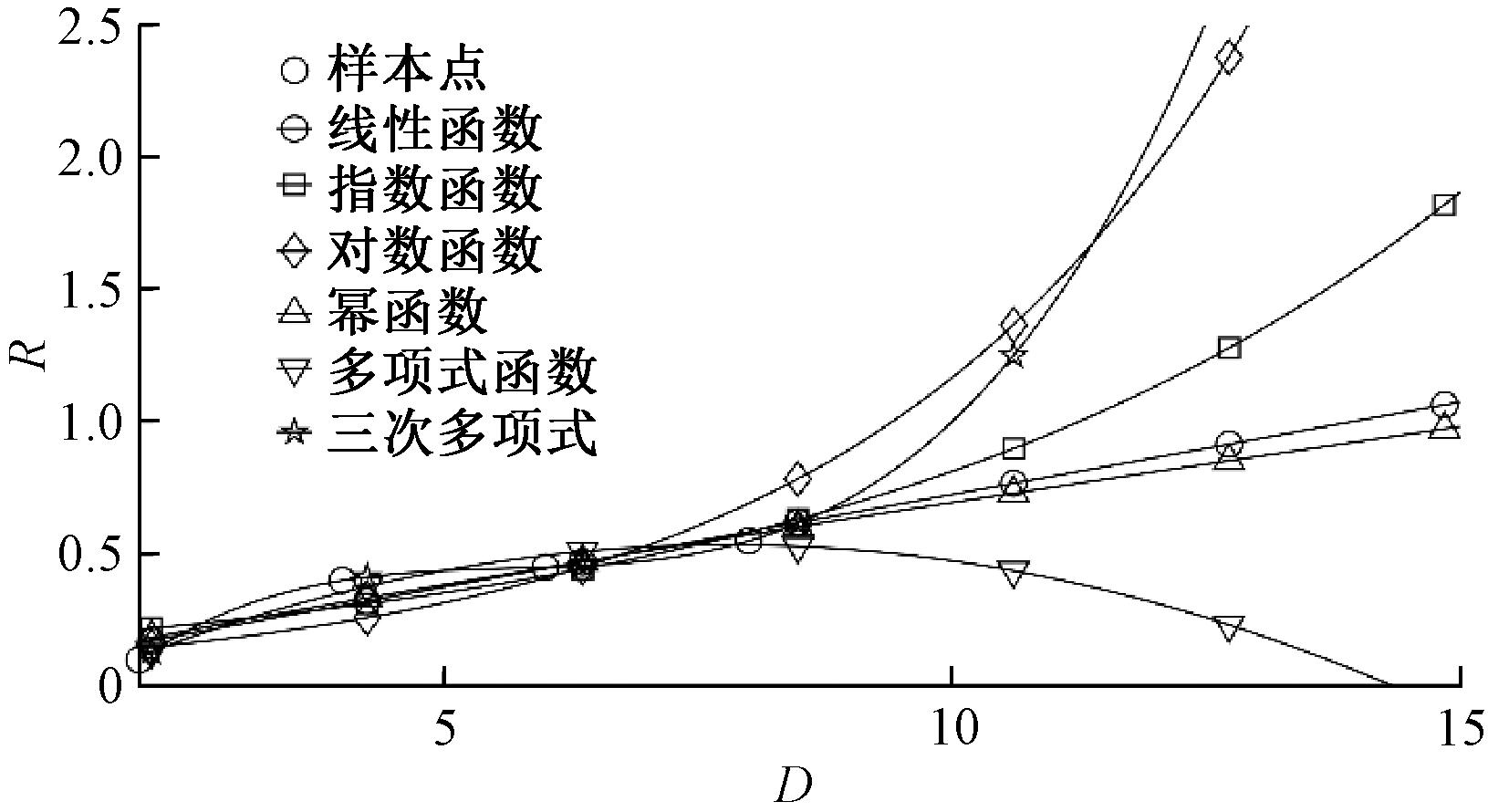
图1 自适应邻域半径预测
Figure 1 Adaptive neighborhood radius prediction
根据拟合出的公式,对于某一维度的问题空间,可以自适应地确定合适的聚类邻域半径。例如,当维度D=10时,相应的邻域半径R为0.725;当D=30时,R为2.125。由此得到的半径能够有效应用于提取适应度地形特征NOPC对问题空间进行合理分类。
2.3 自适应算法调度方法(FL-AMAS)的步骤
本文提出的自适应算法调度方法(FL-AMAS)整体流程如图2所示。首先通过特征分析得到反映地形特征的NOPC值,并根据NOPC选择哈里斯鹰优化算法或者差分进化算法,然后进行相应算法的迭代,直到满足终止条件。
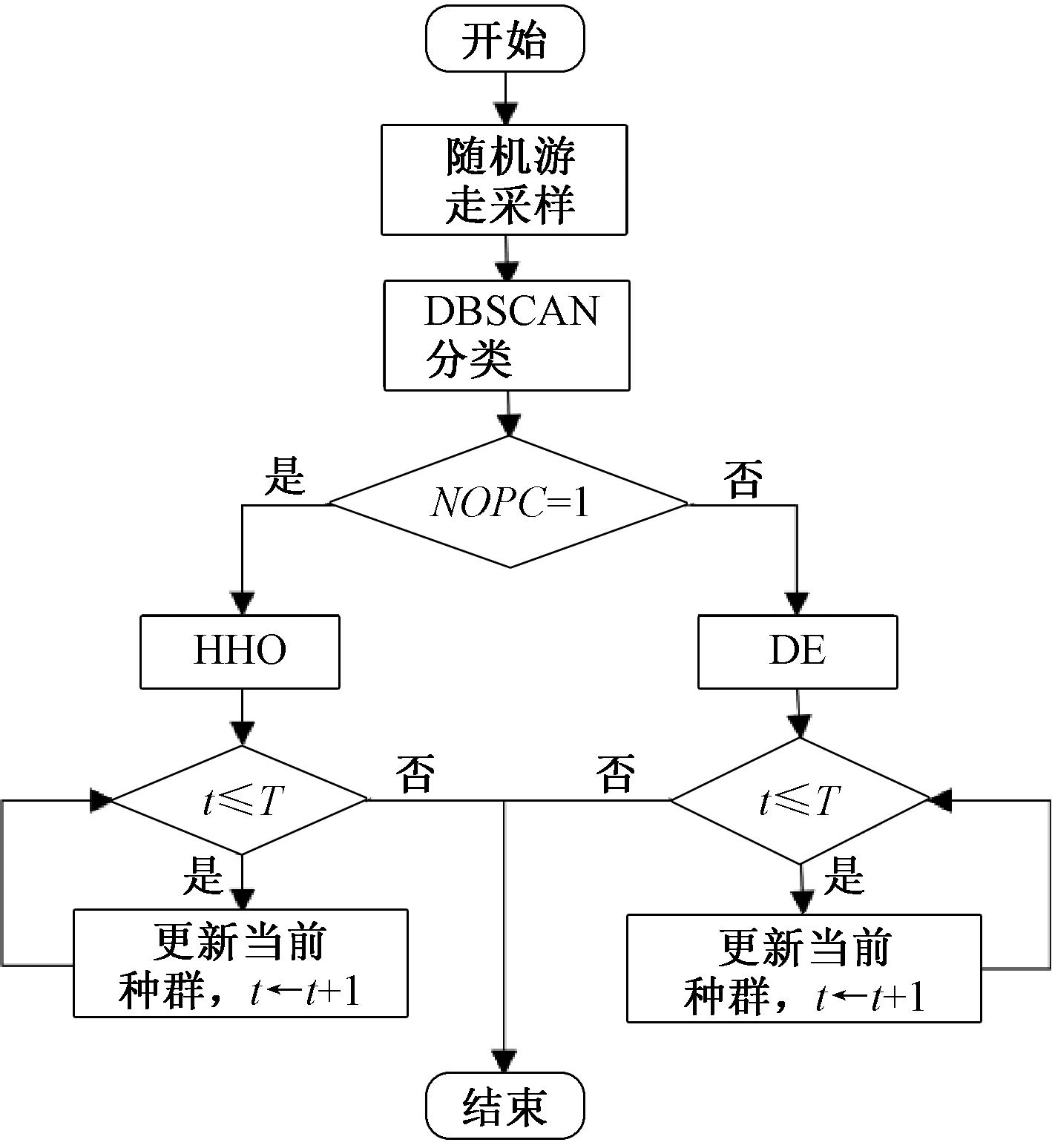
图2 自适应算法调度方法流程图
Figure 2 FL-AMAS flowchart
算法1给出了FL-AMAS的伪代码,随机游走过程中的游走步数设定为500D,对这些随机游走样本的点进行评估的计算复杂度为O(500D)。初始化种群的计算复杂度为O(NP),假设经过T次迭代完成整个种群的评估,其计算复杂度为O(T·NP),算法中其他运算符的计算复杂度为O(T)。以二维问题为例,随机游走步数计算复杂度为1 000,而T次迭代评估种群的计算复杂度T·NP为15 000,因此O(500D)≪O(T·NP)。综上所述,实现FL-AMAS总计算复杂度为O(500D)+O(NP)+O(T·NP)+O(T)=O(T·NP),与单独使用DE或HHO的复杂度同属一个量级,因此具有一定的竞争力。
算法1 FL-AMAS算法。
输入:DE和HHO,基准函数测试集,随机游走次数,最优点占比,种群数NP;
输出:种群中的最优解。
① 初始化种群NP和最大迭代次数T;
② 设置随机游走步数为500D,最优点占比为2%;
③ 计算随机游走采样个体的适应度;
④ 根据最优点占比选择最优个体;
⑤ 通过DBSCAN对最优个体分类计算NOPC;
⑥ ifNOPC=1 then
⑦ 使用HHO更新种群;
⑧ t=0;
⑨ while t≤T do
⑩ 根据HHO策略进行更新;
 t=t+1;
t=t+1;
 end while
end while
 else
else
 使用DE更新种群;
使用DE更新种群;
 t=0;
t=0;
 while t≤T do
while t≤T do
 根据DE策略进行更新;
根据DE策略进行更新;
 t=t+1;
t=t+1;
 end while
end while
 end if
end if
3 实验评估和结果
3.1 基准函数和实验验证
为了评估所提出的算法调度方法的性能,本文选择了8种不同的优化算法作为对比,在相同的一组基准测试函数上进行实验对比。基准函数选择文献中普遍使用、具有不同适应度地形的23种函数[19]。其中函数f1~f7具有单峰地形,其他为多模态函数。多模态函数中f8~f13是高维地形,f14~f23是固定维的低维地形。在维度可变的基准函数中,本文选择2维、10维和30维3个不同的维度类型,选择了f1、f4、f7、f10、f13、f16、f19、f22这8个测试函数为代表进行FL-AMAS算法的综合评估。实验中,随机游走采样步数为500D,每个优化算法在相应测试函数上的最大迭代次数设为500,并对每个测试函数重复运行30次取平均结果。实验环境为具有Intel Core 2.40 GHz CPU和8 GB的计算机,使用MATLAB R2022a软件。8种对比算法分别为HHO、DE、WOA[20]、GWO[21]、MFO[22]、MVO[23]、SSA[24]、SCA[25],表1列出了这些算法的参数取值(未在表中列出的算法则遵循其相关文献中的原始算法参数)。
表1 算法参数设置
Table 1 Algorithm parameter settings
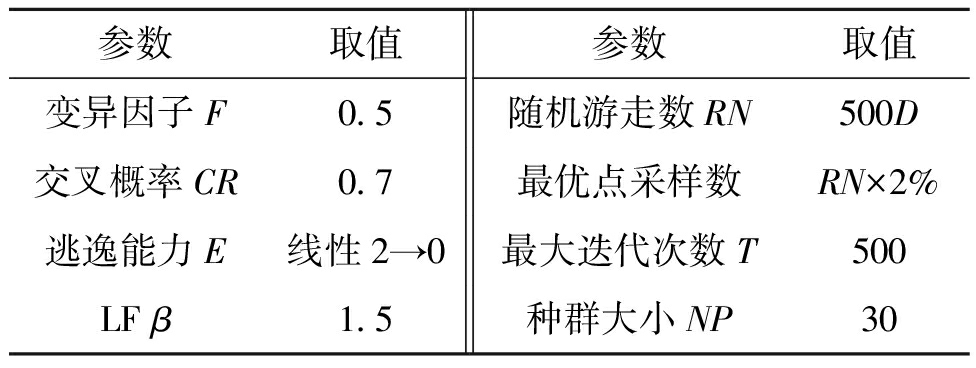
参数取值参数取值变异因子F0.5随机游走数RN500D交叉概率CR0.7最优点采样数RN×2%逃逸能力E线性2→0最大迭代次数T500LF β1.5种群大小NP30
对每种算法的性能进行统计评估。定义测试函数全局最优解的函数值误差为f(x)-f(x*),其中f(x)为优化算法得到的最优解,f(x*)为函数真实的最优解。计算误差值的均值(Mean)和标准差(Std)来衡量优化算法的准确性。此外,利用Friedman检验[26]得到了多个算法在所有函数上的排名。
3.2 实验验证
3.2.1 FL-AMAS与HHO和DE算法对比
为了验证FL-AMAS方法的有效性,在8个基准函数集上,将FL-AMAS与HHO和DE算法分别进行对比。表2给出了3种算法在2,10和30的基准函数上的实验统计结果。
表2 不同算法在测试函数f1~f23基准集上的对比
Table 2 Comparison of different algorithms on the benchmark set of test functions f1~f23
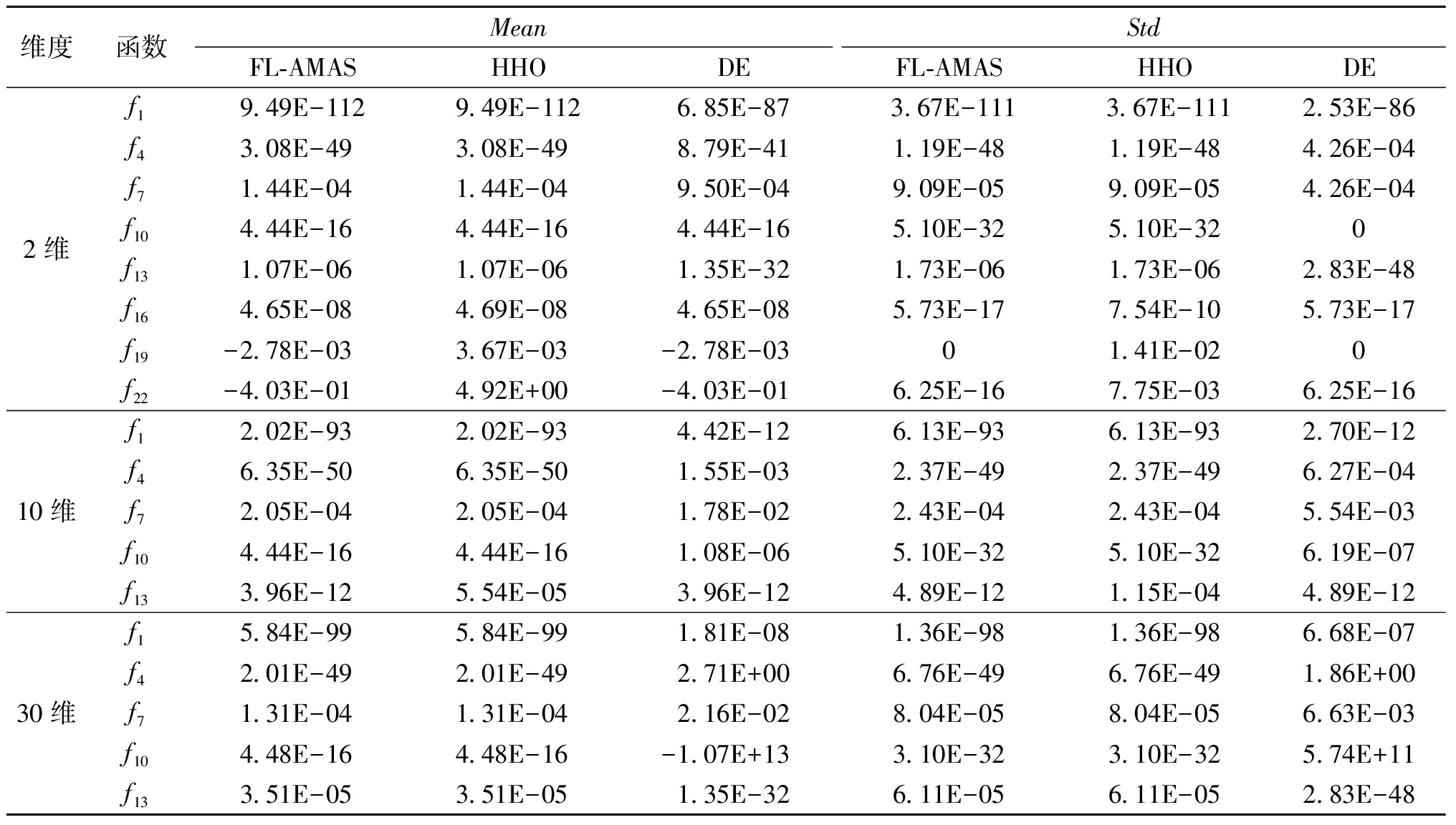
维度函数MeanStdFL-AMASHHODEFL-AMASHHODEf19.49E-1129.49E-1126.85E-873.67E-1113.67E-1112.53E-86f43.08E-493.08E-498.79E-411.19E-481.19E-484.26E-04f71.44E-041.44E-049.50E-049.09E-059.09E-054.26E-042维f104.44E-164.44E-164.44E-165.10E-325.10E-320f131.07E-061.07E-061.35E-321.73E-061.73E-062.83E-48f164.65E-084.69E-084.65E-085.73E-177.54E-105.73E-17f19-2.78E-033.67E-03-2.78E-0301.41E-020f22-4.03E-014.92E+00-4.03E-016.25E-167.75E-036.25E-16f12.02E-932.02E-934.42E-126.13E-936.13E-932.70E-12f46.35E-506.35E-501.55E-032.37E-492.37E-496.27E-0410维f72.05E-042.05E-041.78E-022.43E-042.43E-045.54E-03f104.44E-164.44E-161.08E-065.10E-325.10E-326.19E-07f133.96E-125.54E-053.96E-124.89E-121.15E-044.89E-12f15.84E-995.84E-991.81E-081.36E-981.36E-986.68E-07f42.01E-492.01E-492.71E+006.76E-496.76E-491.86E+0030维f71.31E-041.31E-042.16E-028.04E-058.04E-056.63E-03f104.48E-164.48E-16-1.07E+133.10E-323.10E-325.74E+11f133.51E-053.51E-051.35E-326.11E-056.11E-052.83E-48
表2中的f16、f19、f22为固定维测试函数,基于NOPC值,FL-AMAS在固定维基准函数上的表现均优于HHO,并且在f19、f22上获得了显著的改善效果。
对于2维函数的实验(表2),根据NOPC值,FL-AMAS较好地结合了HHO、DE算法的优点(对HHO与DE的选择),整体效果与HHO算法的性能持平,在f1、f4、f7这3个函数上优于DE,但在f13上不如DE。
在10维测试函数实验上(表2),根据NOPC值,FL-AMAS在f13上选择DE算法,在其余的函数上选择HHO算法。与HHO相比,在f13上结果得到了很大的改善,其余性能持平;与DE相比,FL-AMAS在f1、f4、f7、f10这4个函数上均优于DE,在f13上性能持平;在30维测试函数实验上(表2),根据NOPC值,FL-AMAS在f1、f4、f7、f10和f13上选择了HHO算法,因此性能与HHO持平,与DE相比,在f1、f4、f7和f10上优于DE,但在f13上不如DE。综上所述,FL-AMAS根据NOPC可以有效地利用HHO和DE算法优点,在测试函数上得到更好的结果。
3.2.2 FL-AMAS与其他算法对比
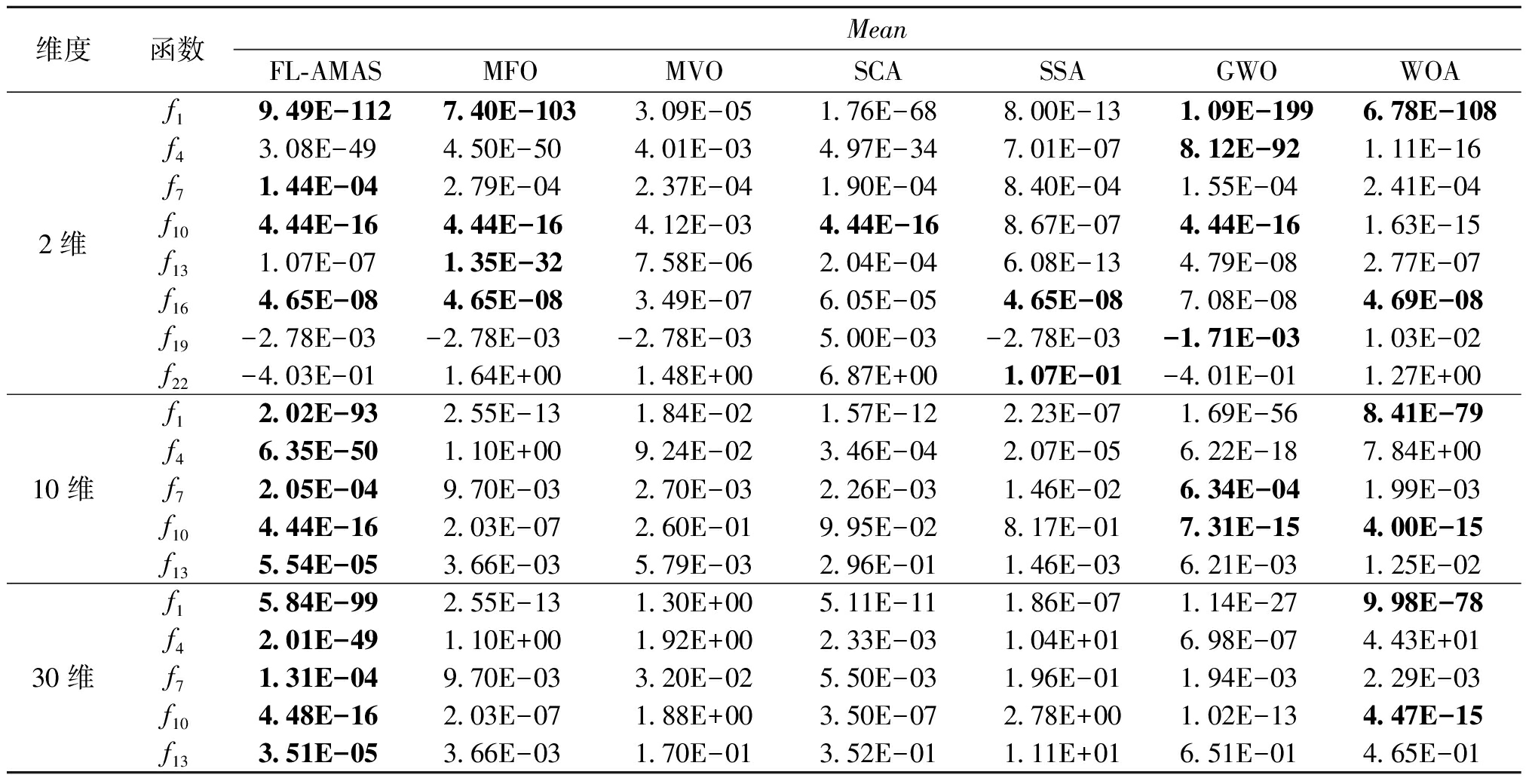
为了进一步验证FL-AMAS的有效性,将FL-AMAS与其他类型的算法进行了比较,对比结果如表3和表4所示。在2维函数(含固定维测试集)基准上,FL-AMAS在统计学结果上优于MFO、MVO、SCA、SSA、GWO、WOA,其中与GWO算法各有千秋,FL-AMAS在f7和f16上优于GWO,在f4、f13和f19上劣于GWO;在10维函数实验中,FL-AMAS在f1、f4、f7和f13函数上都优于这些先进的算法,而在f10上不如SCA、GWO、WOA,这可能是挑选机制的随机性所造成的;在30维函数实验中,FL-AMAS在f1、f4、f7、f10和f13函数上都优于对比算法。与10维函数实验相比,30维在f13上也找到了最优值,由此验证了上述说法的合理性。
表3 不同算法在测试函数f1~f23基准集上的Mean
Table 3 Mean of different algorithms on the benchmark set of test functions f1~f23
维度函数MeanFL-AMASMFOMVOSCASSAGWOWOAf19.49E-1127.40E-1033.09E-051.76E-688.00E-131.09E-1996.78E-108f43.08E-494.50E-504.01E-034.97E-347.01E-078.12E-921.11E-16f71.44E-042.79E-042.37E-041.90E-048.40E-041.55E-042.41E-042维f104.44E-164.44E-164.12E-034.44E-168.67E-074.44E-161.63E-15f131.07E-071.35E-327.58E-062.04E-046.08E-134.79E-082.77E-07f164.65E-084.65E-083.49E-076.05E-054.65E-087.08E-084.69E-08f19-2.78E-03-2.78E-03-2.78E-035.00E-03-2.78E-03-1.71E-031.03E-02f22-4.03E-011.64E+001.48E+006.87E+001.07E-01-4.01E-011.27E+00f12.02E-932.55E-131.84E-021.57E-122.23E-071.69E-568.41E-79f46.35E-501.10E+009.24E-023.46E-042.07E-056.22E-187.84E+0010维f72.05E-049.70E-032.70E-032.26E-031.46E-026.34E-041.99E-03f104.44E-162.03E-072.60E-019.95E-028.17E-017.31E-154.00E-15f135.54E-053.66E-035.79E-032.96E-011.46E-036.21E-031.25E-02f15.84E-992.55E-131.30E+005.11E-111.86E-071.14E-279.98E-78f42.01E-491.10E+001.92E+002.33E-031.04E+016.98E-074.43E+0130维f71.31E-049.70E-033.20E-025.50E-031.96E-011.94E-032.29E-03f104.48E-162.03E-071.88E+003.50E-072.78E+001.02E-134.47E-15f133.51E-053.66E-031.70E-013.52E-011.11E+016.51E-014.65E-01
表4 不同算法在测试函数f1~f23基准集上的Std
Table 4 Std of different algorithms on the benchmark set of test functions f1~f23
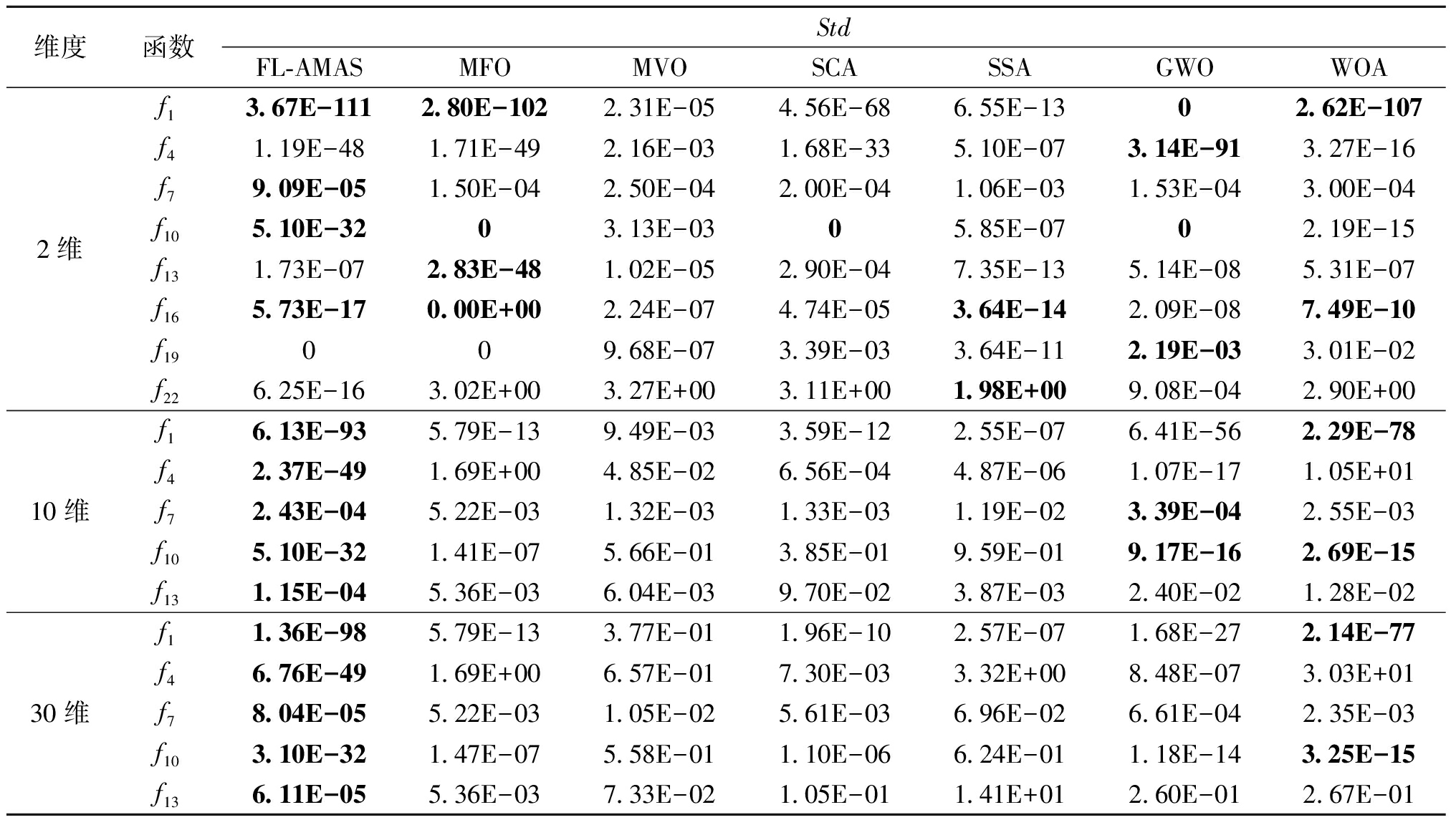
维度函数StdFL-AMASMFOMVOSCASSAGWOWOAf13.67E-1112.80E-1022.31E-054.56E-686.55E-1302.62E-107f41.19E-481.71E-492.16E-031.68E-335.10E-073.14E-913.27E-16f79.09E-051.50E-042.50E-042.00E-041.06E-031.53E-043.00E-042维f105.10E-3203.13E-0305.85E-0702.19E-15f131.73E-072.83E-481.02E-052.90E-047.35E-135.14E-085.31E-07f165.73E-170.00E+002.24E-074.74E-053.64E-142.09E-087.49E-10f19009.68E-073.39E-033.64E-112.19E-033.01E-02f226.25E-163.02E+003.27E+003.11E+001.98E+009.08E-042.90E+00f16.13E-935.79E-139.49E-033.59E-122.55E-076.41E-562.29E-78f42.37E-491.69E+004.85E-026.56E-044.87E-061.07E-171.05E+0110维f72.43E-045.22E-031.32E-031.33E-031.19E-023.39E-042.55E-03f105.10E-321.41E-075.66E-013.85E-019.59E-019.17E-162.69E-15f131.15E-045.36E-036.04E-039.70E-023.87E-032.40E-021.28E-02f11.36E-985.79E-133.77E-011.96E-102.57E-071.68E-272.14E-77f46.76E-491.69E+006.57E-017.30E-033.32E+008.48E-073.03E+0130维f78.04E-055.22E-031.05E-025.61E-036.96E-026.61E-042.35E-03f103.10E-321.47E-075.58E-011.10E-066.24E-011.18E-143.25E-15f136.11E-055.36E-037.33E-021.05E-011.41E+012.60E-012.67E-01
3.2.3 利用Friedman检验计算算法的平均排名
为了比较这些算法的性能,图3给出了不同算法通过Friedman检验的平均排名。由图3可以看出,在2维的23个测试函数(包含固定维多峰)上,FL-AMAS平均排名第一;在10维测试函数上,FL-AMAS与HHO算法的排名相似,其次是GWO、WOA、DE、SCA、SSA、MFO;在30维测试函数上,虽然FL-AMAS在这些函数上的平均排名与GWO相近,但FL-AMAS明显优于MFO、MVO、SCA、SSA、WOA,总体结果验证了FL-AMAS算法的有效性,性能优于大多数对比算法。
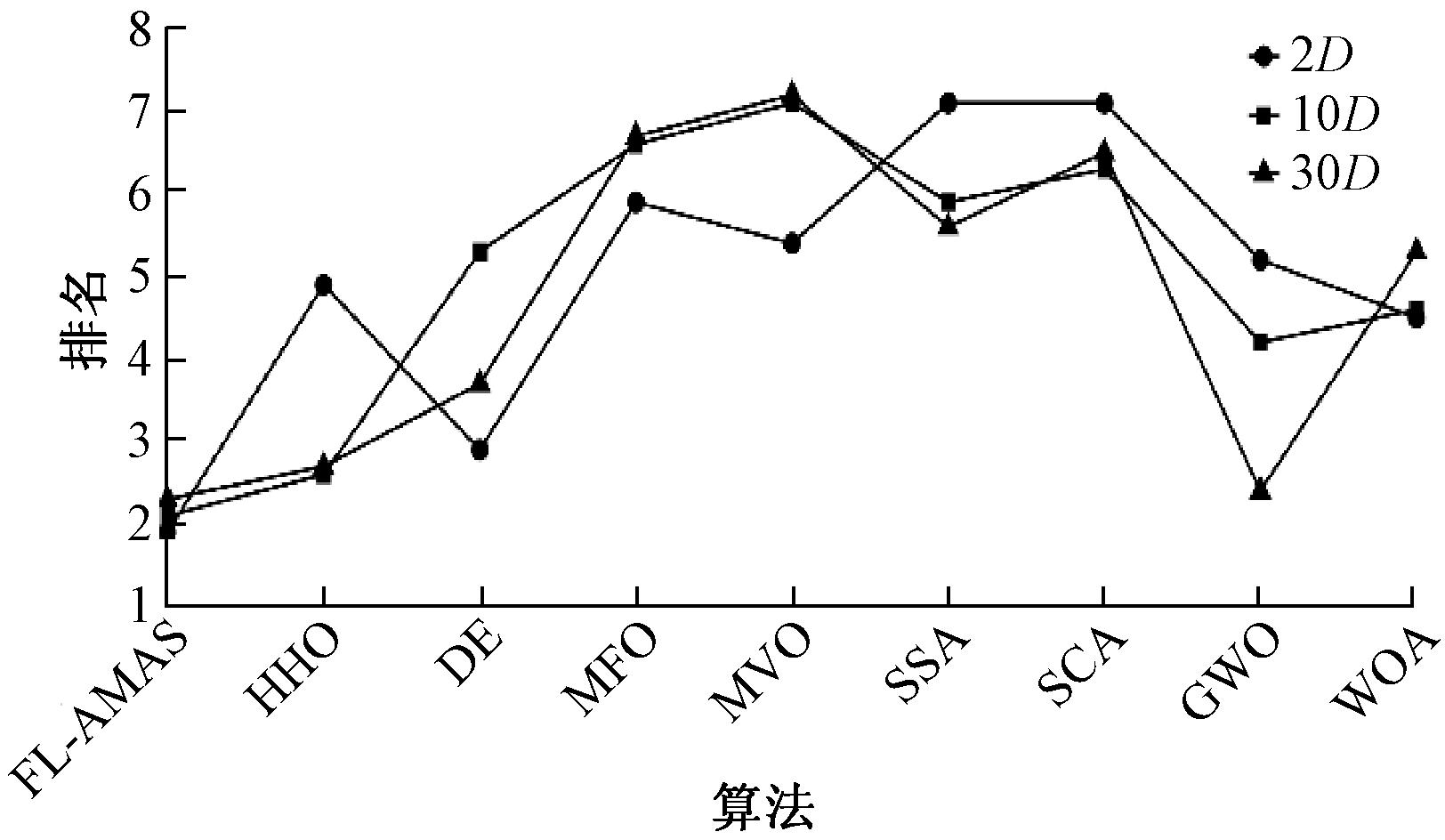
图3 不同算法在不同维度的排名
Figure 3 Ranking of different algorithmic in different dimensions
3.3 提取最优点的个数对FL-AMAS的影响
在FL-AMAS算法中,提取的最优点个数是NOPC特征中重要的一环:提取的个数太多,不仅增加计算时间,还会造成本属于两个峰簇的个体合并成一类,导致聚类结果的偏差;提取的个数太少,可能会导致一个函数本来是多峰的,但错误分类为单峰,导致不能选择更合适的算法。为此,将提取的最优点数设置为采样点总数的0.5%,1%,2%,3%,4%,5%,10%,以测试最优值点数对FL-AMAS的影响。
以30维为例,本文在基准测试函数上对采用不同采样点占比的算法进行了实验验证。通过对实验结果中收敛性和算法的计算复杂度进行归一化处理,最终将适应度值和时间复杂度的乘积作为综合评价指标(|适应度值|×|时间复杂度|),实验结果如图4所示。可以看出,综合考虑收敛精度与计算代价后,本文在FL-AMAS算法中选择的最优采样占比为2%。
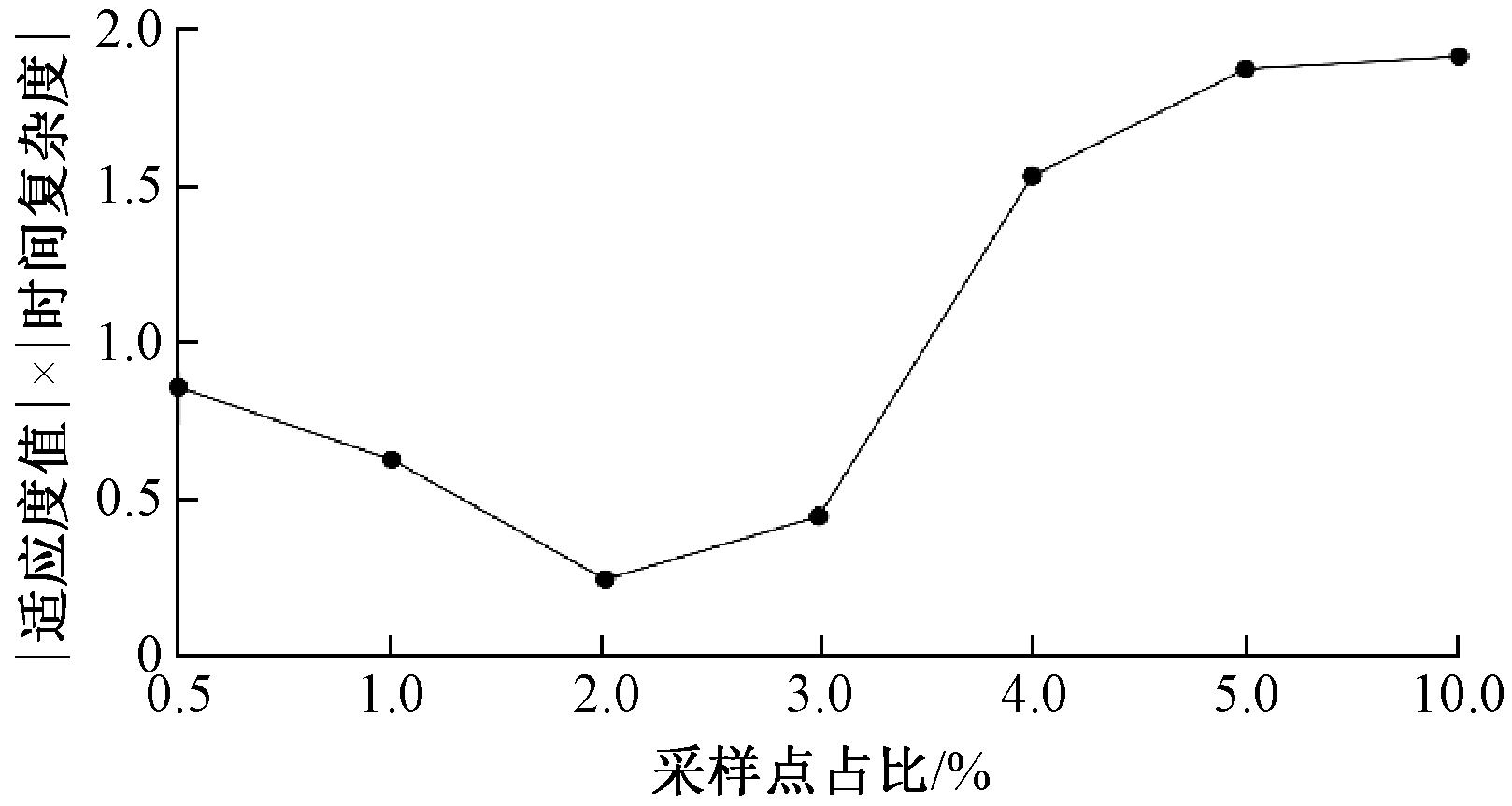
图4 不同采样数的|适应度值|×|时间复杂度|
Figure 4 Different sample numbers of |fitness value|×|time complexity|
3.4 调度方法的扩展性
本文所提出的自适应优化调度算法中所调度算法的选择也具有多样性,可以利用地形特征调度其他具有互补优势的算法。根据多数文献资料,粒子群优化算法(PSO)在解决多峰值问题也有较好的表现,而多元宇宙优化算法(MVO)则具有较好的开发性能。在使用MVO算法和PSO算法作为调度算法来验证自适应算法调度方法的扩展性时,其实验结果与本文实验结果类似:根据NOPC特征,算法调度框架结合了PSO和MVO的优点,同样产生了较好的协调作用。
4 结论
本文提出了一种自适应算法调度方法,利用有效的局部适应度地形特征自适应地为每一个优化问题调度最佳的算法进行求解。本文采用具有高开发性的哈里斯鹰优化算法和具有高探索性的差分进化算法作为调度算法。实验验证结果表明,在不增加计算量的情况下,所提算法吸纳结合每个算法的优点,使得优化结果与单个算法的结果相当或更优。此外,还将PSO和MVO作为调度算法进行了实验,实验结果也验证了所提算法调度的适用性和扩展性。
未来的工作需要在以下方面做深入研究:首先,在特征选择时,如何进一步降低适应度地形特征的计算量;其次,在算法调度后,如何根据提取的地形特征,完成所选择算法中策略或参数的自适应调整,进一步提高FL-AMAS的性能。
[1] 梁静, 刘睿, 瞿博阳, 等. 进化算法在大规模优化问题中的应用综述[J]. 郑州大学学报(工学版), 2018, 39(3): 15-21.
LIANG J, LIU R, QU B Y, et al. A survey of evolutionary algorithms for large scale optimization problem[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(3): 15-21.
[2] LU P, YE L, ZHAO Y N, et al. Review of meta-heuristic algorithms for wind power prediction: methodologies, applications and challenges[J]. Applied Energy, 2021, 301: 117446.
[3] MALAN K M. A survey of advances in landscape analysis for optimisation[J]. Algorithms, 2021, 14(2): 40.
[4] LIANG J, LI K, YU K J, et al. A novel differential evolution algorithm based on local fitness landscape information for optimization problems[J]. IEICE Transactions on Information and Systems, 2023, 106(5): 601-616.
[5] ZHENG L M, LUO S Q. Adaptive differential evolution algorithm based on fitness landscape characteristic[J]. Mathematics, 2022, 10(9): 1511.
[6] LI Y X, YU K J, LIANG J, et al. A landscape-aware particle swarm optimization for parameter identification of photovoltaic models[J]. Applied Soft Computing, 2022, 131: 109793.
[7] TANG K, LIU S C, YANG P, et al. Few-shots parallel algorithm portfolio construction via co-evolution[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(3): 595-607.
[8] YUEN S Y, CHOW C K, ZHANG X, et al. Which algorithm should I choose: an evolutionary algorithm portfolio approach[J]. Applied Soft Computing, 2016, 40: 654-673.
[9] 丁青锋, 尹晓宇. 差分进化算法综述[J]. 智能系统学报, 2017, 12(4): 431-442.
DING Q F, YIN X Y. Research survey of differential evolution algorithms[J]. CAAI Transactions on Intelligent Systems, 2017, 12(4): 431-442.
[10] HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris hawks optimization: algorithm and applications[J]. Future Generation Computer Systems, 2019, 97: 849-872.
[11] 汪慎文, 丁立新, 张文生, 等. 差分进化算法研究进展[J]. 武汉大学学报(理学版), 2014, 60(4): 283-292.
WANG S W, DING L X, ZHANG W S, et al. Survey of differential evolution[J]. Journal of Wuhan University (Natural Science Edition), 2014, 60(4): 283-292.
[12] WRIGHT S.The roles of mutation, inbreeding, crossbreeding, and selection in evolution[J]. Proceedings of the Sixth International Congress on Genetics, 1932, 1: 356-366.
[13] 王艳丽, 梁静, 薛冰, 等. 基于进化计算的特征选择方法研究概述[J]. 郑州大学学报(工学版), 2020, 41(1): 49-57.
WANG Y L, LIANG J, XUE B, et al. Research on evolutionary computation for feature selection[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(1): 49-57.
[14] 李亚欣, 梁静, 岳彩通, 等. 基于适应度地形分析的进化计算研究综述[J]. 陕西师范大学学报(自然科学版), 2021, 49(5): 39-53.
LI Y X, LIANG J, YUE C T, et al. A survey of evolutionary computing based on fitness landscape analysis[J]. Journal of Shaanxi Normal University (Natural Science Edition), 2021, 49(5): 39-53.
[15] LI Y X, LIANG J, YU K J, et al. Keenness for characterizing continuous optimization problems and predicting differential evolution algorithm performance[J]. Complex &Intelligent Systems, 2023, 9(5): 5251-5266.
[16] 廖雄鹰, 李俊, 罗阳坤, 基于自适应变异算子的差分进化算法[J]. 计算机工程与应用, 2018, 54 (06): 128-134.
LIAO X Y, LI J, LUO Y K, Differential evolution algorithm based on adaptive mutation operator[J]. Computer Engineering and Applications, 2018, 54 (6): 128-134.
[17] LANG R D, ENGELBRECHT A P. Decision space coverage of random walks[C]∥2020 IEEE Congress on Evolutionary Computation (CEC). Piscataway: IEEE, 2020: 1-8.
[18] ZUO Y Y, HU Z Q, YUAN S J, et al. Identification of convective and stratiform clouds based on the improved DBSCAN clustering algorithm[J]. Advances in Atmospheric Sciences, 2022, 39(12): 2203-2212.
[19] MEIDANI K, MIRJALILI S, BARATI FARIMANI A. Online metaheuristic algorithm selection[J]. Expert Systems with Applications, 2022, 201: 117058.
[20] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
[21] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61.
[22] MIRJALILI S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm[J]. Knowledge-Based Systems, 2015, 89: 228-249.
[23] MIRJALILI S, MIRJALILI S M, HATAMLOU A. Multi-Verse Optimizer: a nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016, 27(2): 495-513.
[24] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp Swarm Algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191.
[25] MIRJALILI S. SCA: a Sine Cosine Algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133.
[26] ALCAL -FDEZ J, S
-FDEZ J, S NCHEZ L, GARC
NCHEZ L, GARC A S, et al. KEEL: a software tool to assess evolutionary algorithms for data mining problems[J]. Soft Computing, 2009, 13(3): 307-318.
A S, et al. KEEL: a software tool to assess evolutionary algorithms for data mining problems[J]. Soft Computing, 2009, 13(3): 307-318.