21世纪以来,未知病原体引起的新发传染病频现,数次造成全球性的大流行事件,为世界各国公共卫生安全体系敲响警钟[1-2]。针对新发传染病的风险监测是制定和评估公共卫生事件预防控制策略的重要依据。如何利用多源大数据挖掘技术,结合城市人群的多场景接触模式,进而科学有效地制定新发传染病的监测策略以尽早感知疫情风险态势,是提升应急事件风险管理水平和响应能力过程中亟待解决的关键问题。
数学建模是理解和预测传染病复杂传播动态的基础方法[3],其中,高精度的混合接触网络被认为是影响疾病传播模型准确性的重要因素之一[4]。通过将多场景(家庭、学校、社区等)的接触模式映射到社会化的异质个体传播模型中,可以提高模型构建的真实性和预测能力。例如,Mistry等 [5-6]开发了一种合成接触网络构建方法,能够根据特定区域的人口普查数据,生成符合现实世界人际接触模式的接触网络,支持对新发传染病传播趋势的精确模拟,进而评估相关干预措施的有效性。
然而,高精度人际接触模式依赖于问卷调查及数字设备追踪等方法[7],在重大新发传染病发生的早期数据获取受限,通常需要消耗大量的人力物力资源。哨点监测是一种低成本、持续性的传染病监测手段[8-9],通过系统地收集和分析特定疾病的监测数据,能够及时感知疫情传播风险,为预防和控制疾病的传播与应急资源的分配提供科学依据[10]。在新发传染病传播早期,传统监测哨点系统依赖哨点医院等医卫机构,风险感知方式被动。相对地,基于人群特征的监测策略旨在识别易感且具有较高传播能力的个体,并将其布置为哨点以更早地预知疫情趋势,能够提升传染病发现及报告的准确性和及时性,将疫情控制在“萌芽之时,成灾之前”。然而,在缺少详细流行病学流调信息的情况下,基于人群异质特征的哨点监测策略难以高效实施。因此,如何结合城市多源统计数据构建人际接触网络、制定高效的传染病风险监测策略具有重要研究价值。
针对以上挑战,本文以2020年深圳市人口普查和调查数据为基础,构建具有城市人口结构特征及行为规律的接触网络。并基于以新型冠状病毒感染为例的新发传染病的早期流行病学特征,建模接触网络上的个体交互行为,以刻画多场景中的疾病传播动态。进一步,本文提出基于家庭接触模式的新发传染病风险监测策略,实现对新发传染病传播态势的风险感知与早期预警。
1 相关工作
随着智慧城市和大数据技术的迅速发展,基于人际接触模式的接触网络构建为城市新发传染病哨点监测提供了高效且可行的方案[11]。科学地构建与分析接触网络的统计特征并优化哨点监测策略,不仅能减轻传染病防控的经济负担,还能在早期感知疫情传播,实现精确防控,优化应急医疗的资源配置以阻断传染病在社区的传播[9,12]。例如,Herrera等 [13]在不同规模的社交网络中评估了最大连接个体、随机个体、熟人3种监测策略的效果,发现监测性能与网络结构和疾病的基本再生数密切相关。在基本再生数较低的情况下,选取网络中节点度较高的个体作为哨点能最早提供疫情暴发和峰值信息。然而,该研究假设接触网络的个体同质且具有相同的接触模式,并且选取的接触网络不能细致刻画特定区域的人口结构特性,因此忽略了异质个体间交互行为因素导致的疾病传播模式差异。
家庭环境等人群相对密集的室内空间是新发传染病扩散的重要场所[14],特别是对于高传染性的呼吸道传染病,即使在社区传播得到控制的情况下,家庭依然是重要的新增病例来源。当前,基于接触网络的哨点监测策略通常假设个体处于均匀同质的接触环境,而忽略了不同接触模式对监测效果的影响。此外,针对家庭接触的传染病风险监测研究多依赖于电子追踪数据,由于非公开商业数据的获取困难以及隐私保护问题,缺乏在大规模社会网络中利用城市家庭规模分布进行风险监测的有效性量化研究[15]。因此,如何基于家庭结构考虑哨点监测策略的有效性[16],成为公共卫生事件风险精准监测与应急管理面临的关键挑战。
2 基于城市接触网络的新发传染病风险监测策略
2.1 方法框架
针对城市新发传染病的早期传播风险监测的现实需求,本文利用多源城市数据,提出了基于城市接触网络的新发传染病风险监测框架,主要由3部分构成:数据驱动的城市接触网络构建、疾病传播动态模拟、风险监测策略的性能评估。本文的总体方法框架如图1所示。
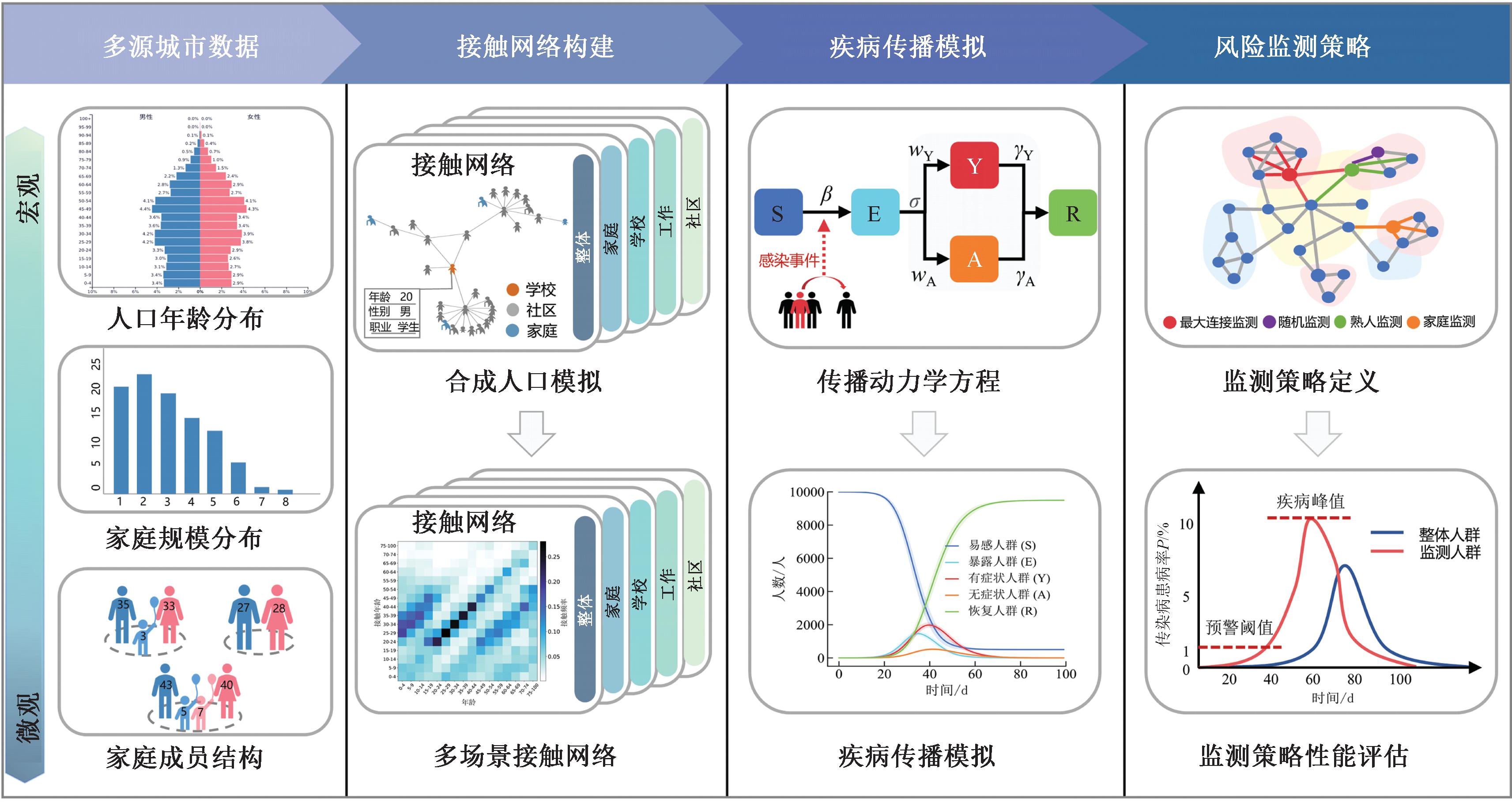
图1 基于城市接触网络的新发传染病风险监测框架
Figure 1 Framework of emerging infectious disease risk surveillance based on urban contact networks
2.2 城市接触网络的构建
由于传播事件很少能被直接观察和测量,因此大多数传播模型都基于社会接触假设[17]。利用公开的社会人口特征宏观普查数据和微观调查数据模拟具有真实世界行为模式的合成人口,是一种在无法获知流调数据情况下进行疾病传播监测的科学方法,而多源数据的分布决定了接触网络中个体属性的分配情况。本文利用数据驱动的网络构建方法SynthPops[6]刻画多场景接触模式,基于特定年龄的接触模式[7]在多层网络框架中生成个体及其预期的接触对象。
为了准确模拟特定地区的人口接触模式,本文选取深圳市作为研究对象,通过收集多源人口宏观普查数据和微观调查数据,旨在构建2020年深圳市的高精度个体接触网络。本文构建了一个反映2020年深圳市人口结构特征的多层接触网络G(Ni,Ei),其中i∈{h,s,w,c}。该接触网络包括10 000名个体(N)及123 109条边(E),网络的接触层分别为家庭层(Eh=10 823)、学校层(Es=23 633)、工作层(Ew=58 613)、社区层(Ec=30 040)。详细数据描述如表1所示。
表1 深圳市多源人口统计数据
Table 1 Multi-source demographic data of Shenzhen City
数据集 数据描述 数据来源 年龄分布 人口年龄结构分布 文献[18] 户主年龄 家庭户主年龄分布 文献[18] 家庭规模 家庭规模分布 文献[18] 学校规模 学校在校生规模分布 文献[19] 工作规模 工作场所雇员规模分布 文献[19] 入学率 各年龄组入学率分布 文献[20] 就业率 各年龄组就业率分布 文献[20] 接触模式 人口混合模式 文献[7]
图2展示了生成的接触网络在个体年龄分布及家庭规模分布的模拟结果。其中,图2(a)所示接触网络的年龄分布与普查数据高度近似(肯德尔和谐系数
=0.937,皮尔逊相关系数p-value<0.001);同样地,图2(b)中模拟网络的家庭规模分布也与普查数据高度一致(肯德尔和谐系数=0.989,皮尔逊相关系数p-value<0.001)。以上结果表明,所生成的接触网络在统计分布特征上与真实数据高度吻合,准确地反映了现实世界城市人口的年龄和家庭规模分布特性,可为传染病模拟提供接触结构基础。进一步地,本文展示了基于接触频率的家庭、学校、工作场所、社区的接触矩阵,如图3所示。
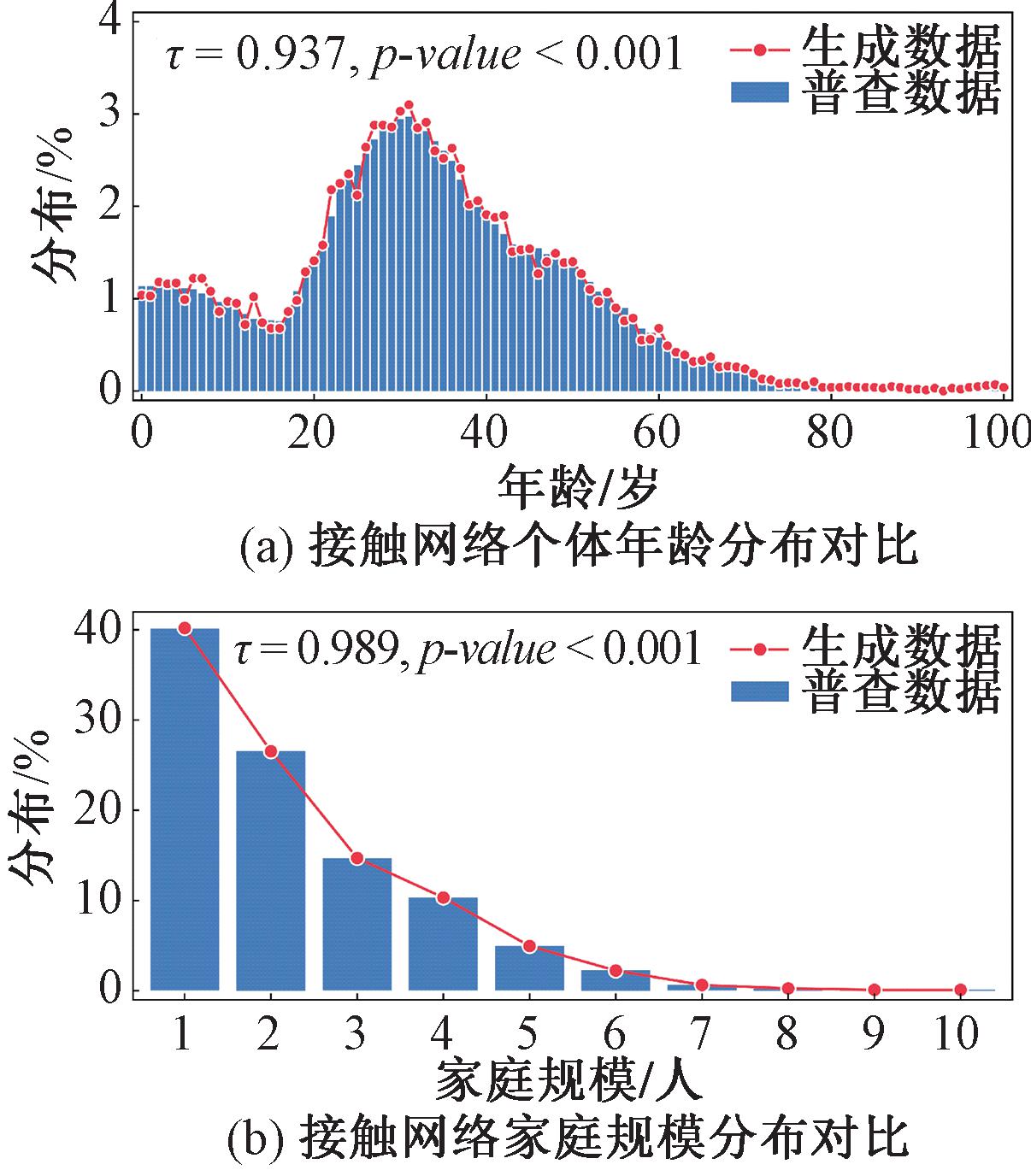
图2 生成数据与普查数据的对比
Figure 2 Comparison of generated data with census data
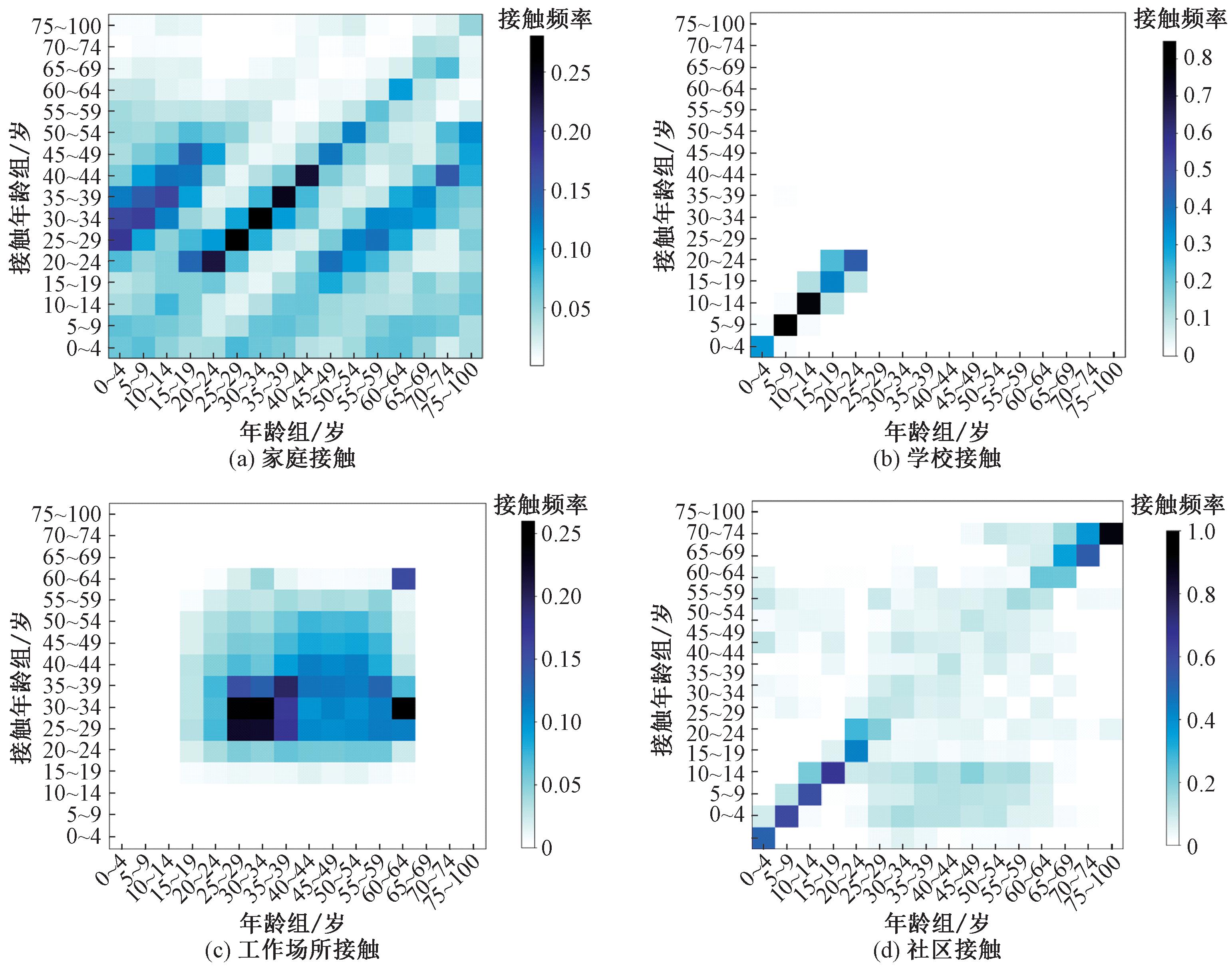
图3 多场景下的接触矩阵
Figure 3 Contact matrices in multiple scenarios
模拟生成的接触网络在不同场景下呈现出不同的年龄混合模式,这与现实世界中人们在不同场所的活动规律和社会结构相符[7],其中,家庭、学校、工作场所、社区中个体平均接触频数分别为2.16,4.72,11.93,6.05。
2.3 基于接触网络的个体传播模型构建
基于人口普查及调查数据构建的人际接触网络,可以有效模拟不同地区新发传染病的早期传播及其干预措施,并为传染病的监测提供早期预警方案。通过将接触网络的每个节点实例化,个体模型能够在简化的框架内模拟复杂的个体状态变化。本文构建了一个基于网络的个体传染病传播模型SEYAR[21],其中个体存在易感(S)、暴露(E)、有症状(Y)、无症状(A)和恢复(R)这5种状态,以描述传染病的复杂人际传播模式。本文考虑疾病在网络化人群中的传播,有症状与无症状个体具有传染性,其中个体通过在不同场景中的接触而相互连接[13],并基于接触网络中的随机链式二项式来模拟疾病在密集人群中的传播[22],个体传播模型如图4所示。
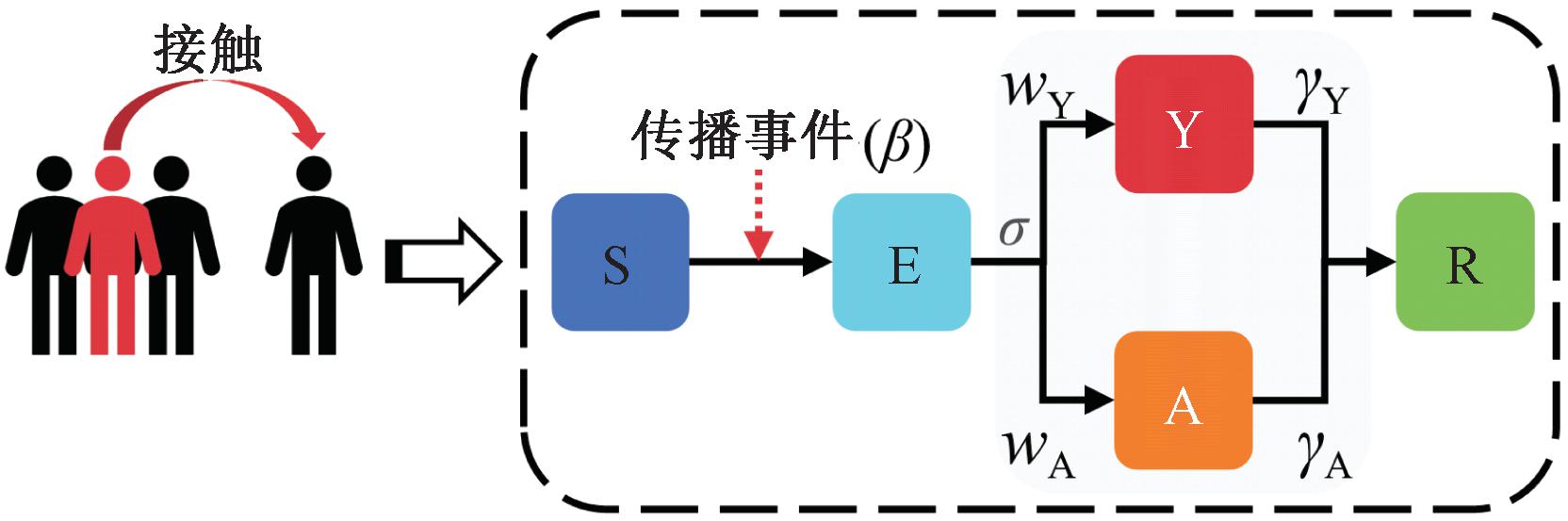
图4 个体状态转移示意图
Figure 4 Schematic diagram of individual state transition
为了深入探究新发传染病在城市人群中的传播模式,本文选取新型冠状病毒感染作为新发传染病的典型案例进行研究。为了确保模型的可靠性和有效性,本文参考了已有研究中关于早期病毒传播特征的参数分析结果,并将这些结果作为先验知识用于确定模型参数,以更准确地模拟病毒传播的动态过程。SEYAR模型的详细参数描述和具体的参数取值参见表2。
表2 个体状态参数
Table 2 Parameter description of individual status
参数 参数描述 参数取值 参数来源 R0 基本再生数 [1. 2, 1. 5, 2. 0, 3. 0] 预设 β 感染率 [0. 01, 0. 02, 0. 04, 0. 1] 预设 βh 家庭接触感染率 0. 067 文献[23] αh 家庭继发性感染率 0. 35 文献[24] σ 暴露状态的转换率 1 / 3 文献[25] wY 有症状感染者比例 0. 84 文献[26] wA 无症状感染者比例 0. 16 文献[26] ρ 无症状感染者传染性 0. 35 文献[27] γY 有症状感染者恢复率 0. 18 文献[28] γA 无症状感染者恢复率 1 / 9 文献[23] In 初始感染人数 1 预设 Δ 增长率 式(4)计算 D 传染性持续时间 式(5)计算 P 传染病患病率 式(6)计算
传染病个体传播模型中,易感个体i以
的概率被感染[28]。其中,Infi表示与易感个体i相接触的具有感染性的个体数量;
表示与其相接触个体的加权平均感染率,则
(1)
式中:
分别为家庭接触下的无症状和有症状个体,以及非家庭接触情景下的无症状和有症状个体;βh为个体在家庭中的接触感染率,家庭接触感染率的估算充分考虑了家庭成员之间的紧密接触程度,这一度量有效地反映了家庭环境作为高风险场所的特性[23],表达式为
(2)
易感个体i被感染后,将分别以wYσ与wAσ的概率由暴露状态转换为有症状状态与无症状状态,其中无症状个体相对于有症状个体的传染病传染能力为βρ。该模型中已恢复的个体不会被重复感染。
基本再生数R0反映一个病例在完全易感人群中能够产生的病例数[29],针对该模型可定义为
R0=1+ΔD;
(3)
(4)
(5)
式中:Δ为传染病发生早期的增长率;D为个体具有传染性的持续时间。在流行病的早期阶段,理论上具有传染性的个体数量会近似以指数增长[25]。本文通过计算新增病例数量从初始阶段In到达到峰值Ipeak的对数差,与对应病例数量增长时间Ti的比值来确定增长率Δ。
定义传染病患病率P为给定时间段内无症状和有症状个体总数所占整体人口的比例。新增病例数量It刻画了每个时间步内疾病传播的速度。具体地,患病率与新增病例的关系如下所示:
(6)
式中:N为接触网络的人口总数。图5分别展示了R0为1.2,1.5,2.0,3.0这4种场景下传染病的传播动态曲线,其中阴影部分表示各状态的95%置信区间。
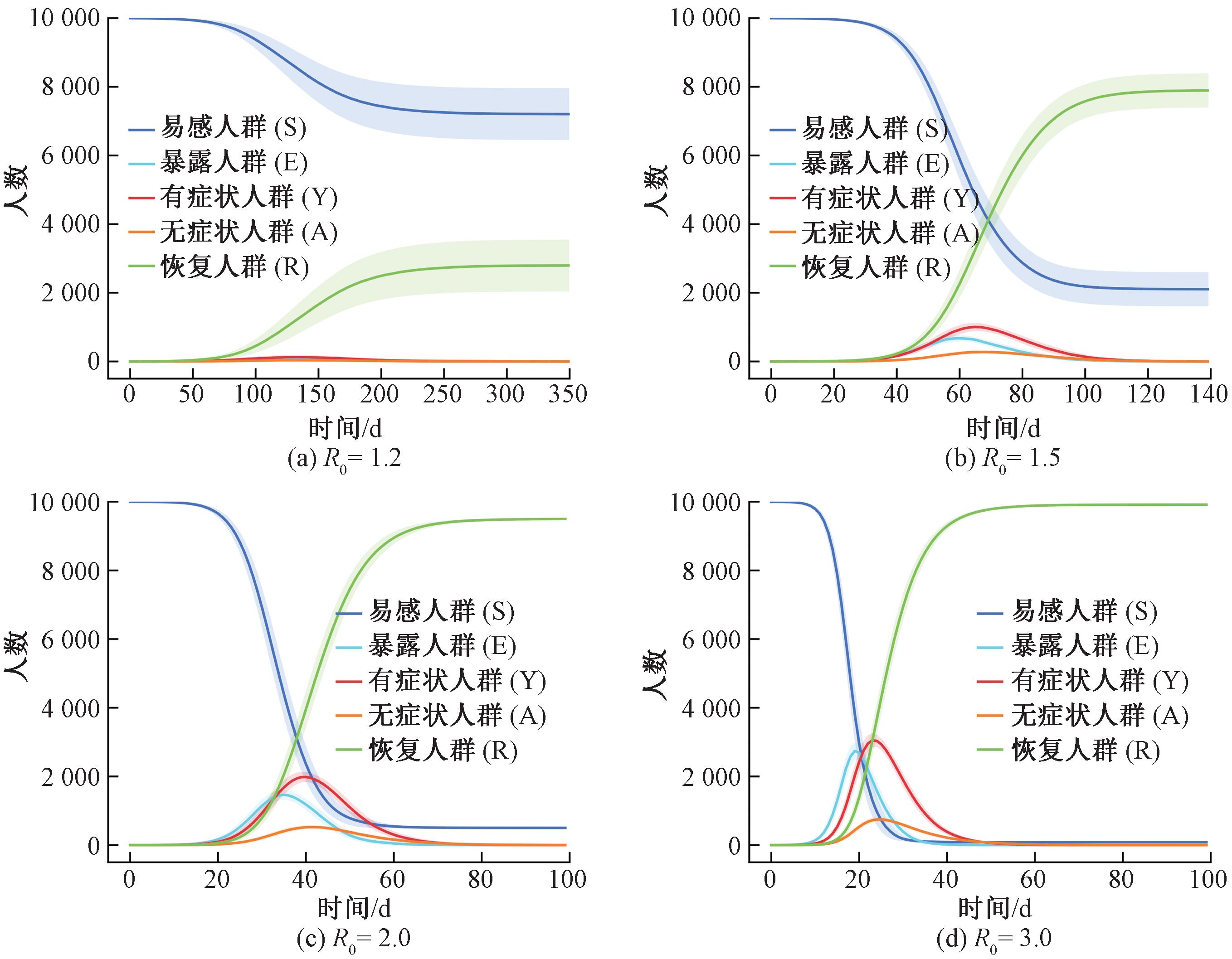
图5 不同基本再生数的传染病传播动态
Figure 5 Infectious disease transmission dynamics with different basic reproduction numbers
2.4 风险监测策略
本文关注新发传染病暴发后具有传染性的个体,通过在接触网络上模拟疾病传播过程并基于风险监测策略选择重点监测人群子集,进而实现对疾病风险的早期感知。由于城市家庭是传染病传播的密集接触场所,其规模被认为是传染病传播的影响因素之一[30]。基于此,本文结合网络的哨点风险监测研究中被广泛使用的三种监测策略[13,22],提出一种基于家庭的监测策略。图6为监测策略的示意图,监测策略定义如下。
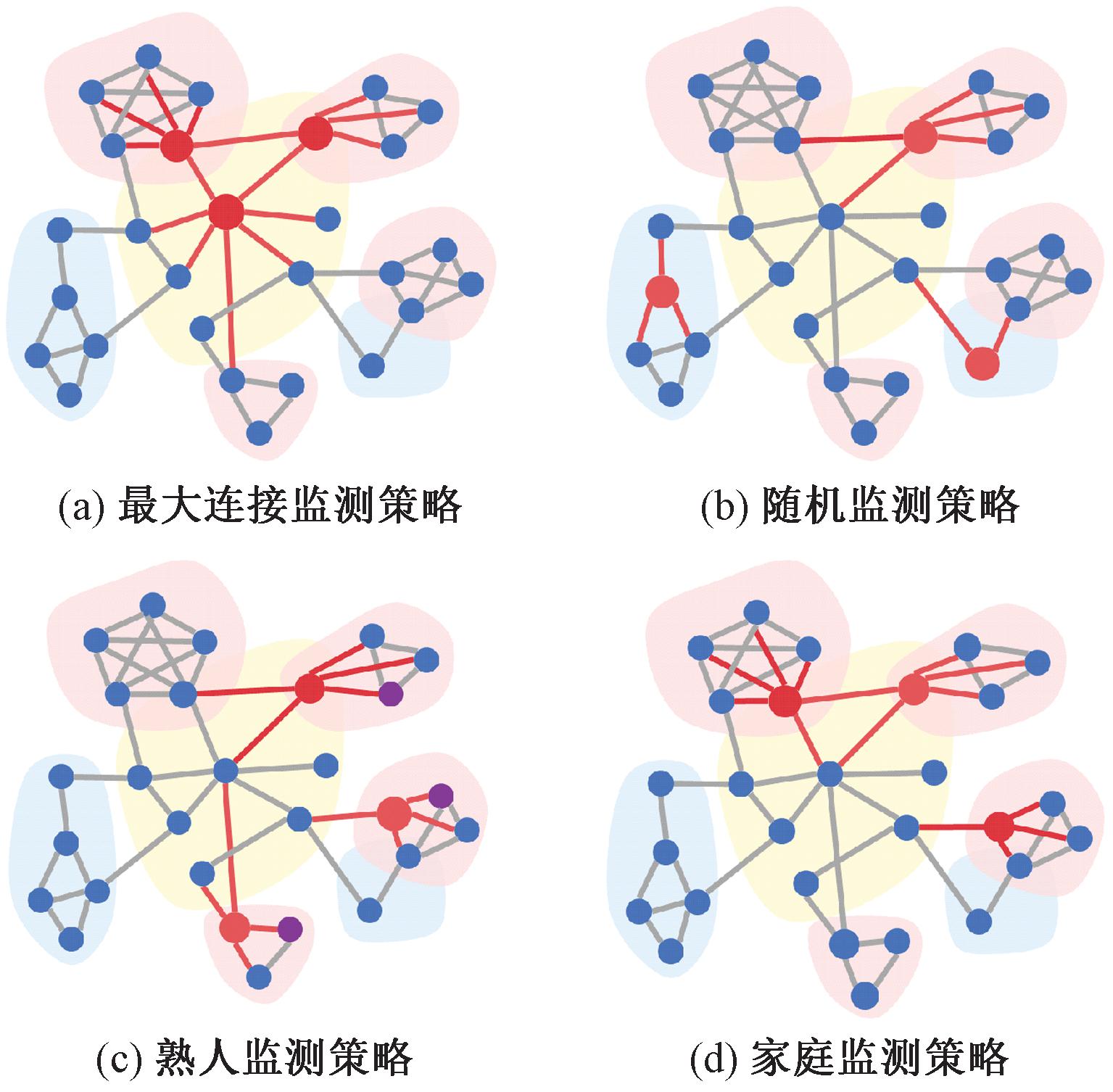
图6 风险监测策略示意图
Figure 6 Risk surveillance strategy diagram
定义1 最大连接监测策略(most connected strategy, MCs):在接触网络中选择一定量的具有最多接触的个体,将这些个体作为哨点个体,使用度中心性排名作为最大连接的节点选择标准。
定义2 随机监测策略(random strategy, RDs):在接触网络中随机选择特定比例节点作为哨点个体。
定义3 熟人监测策略(acquaintance strategy, AQs):首先在接触网络中随机选择一定量的个体,然后选择一定量的这些个体的熟人(具有最大连接)作为哨点个体。
定义4 家庭监测策略(household strategy, HHs):首先根据多层接触网络的家庭层筛选出规模较大的家庭。然后,在每个选定家庭中,选取一位年龄介于20～50岁,且拥有最多社交接触(具有最大连接)的成年个体作为监测哨点。
定义5 全民监测策略(whole population strategy, WPs):对接触网络全部个体进行监测。
在图6中,粉色、黄色和蓝色阴影分别代表家庭、学校和工作场所接触。蓝色节点表示易感个体,而红色节点则代表不同监测策略所选择的监测子集。具体而言,图6(c)中,紫色节点代表随机选择的个体,红色节点则为该节点的熟人。此外,图6(d)中家庭策略中选择的监测哨点多为网络中的桥接节点,相比于其他监测策略,这些哨点通常拥有更大的介数中心性。
3 实验结果及分析
3.1 实验设置及评估指标
本文采用动态比例缩放方法[21],利用蒙特卡罗模拟方法,模拟新发传染病在深圳市的接触网络G(N=10 000,E=123 109)上的传播趋势。首先,设定初始感染个体数量In为1并随机选择种子个体,随后根据表2中的参数分布进行随机抽样。模拟过程涵盖4种基本再生数场景,分别为1.2,1.5,2.0和3.0,对应传染病的传染性从低到高的变化。对于每种基本再生数,本文根据疾病从初始传播到完全消失所需时间周期(从模拟开始到感染状态的个体数量为0),进行100次成功的疾病传播随机模拟。
为了评估上述风险监测策略实施过程的性能表现,本文计算3种不同的风险监测目标[13],风险监测策略性能评估指标如图7所示。根据风险监测策略选择接触网络中的1%的节点作为监测子集(subset group, SG),对比监测子集与整体人群(whole population, WP)的性能指标差异,实现对提出的风险监测策略的有效性评估与分析。
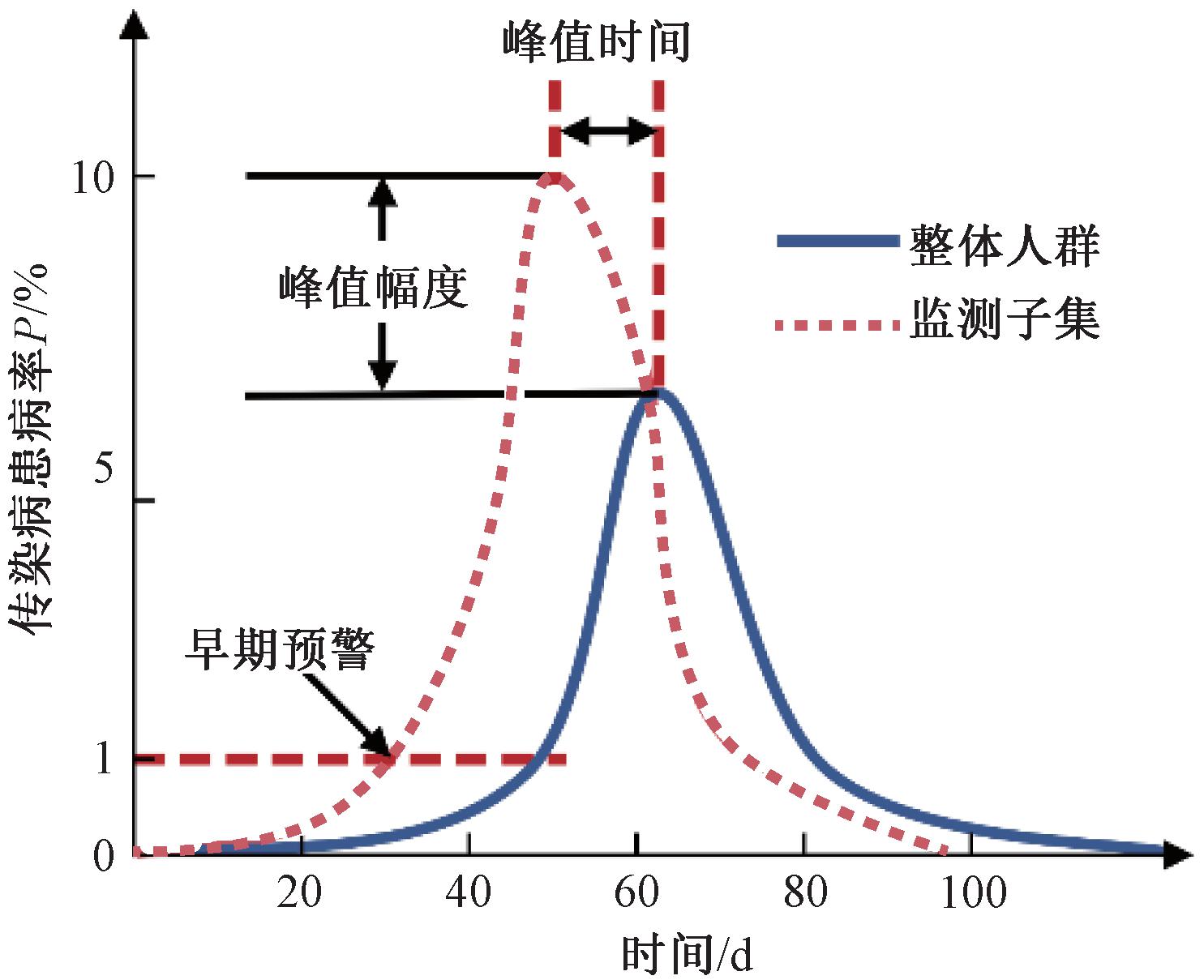
图7 风险监测策略性能评估指标
Figure 7 Performance metrics for risk surveillance strategies
定义6 早期预警(early warning)。定义
和
分别为当前R0情景下整体人群和监测子集的传染病患病率达到预警阈值(threshold, TH)的时间。本文定义早期预警阈值为人群中具有传染性的个体比例达到总体的1%,而早期预警为两者的时间差值:
(7)
定义7 峰值时间(peak timing)。定义
和
分别为当前R0情景下整体人群和监测子集的患病率达到峰值(peak)的时间,峰值时间为两者峰值的时间差值:
(8)
定义8 峰值幅度(peak magnitude)。定义
和
分别为当前R0情景下整体人群和监测子集的患病率达到峰值时的数值,峰值幅度为两者的峰值之比:
(9)
3.2 风险监测策略结果及分析
为了分析在不同传播能力条件下的风险监测策略效果,本文详细对比了4种监测策略的早期预警性能差异,结果如图8所示。
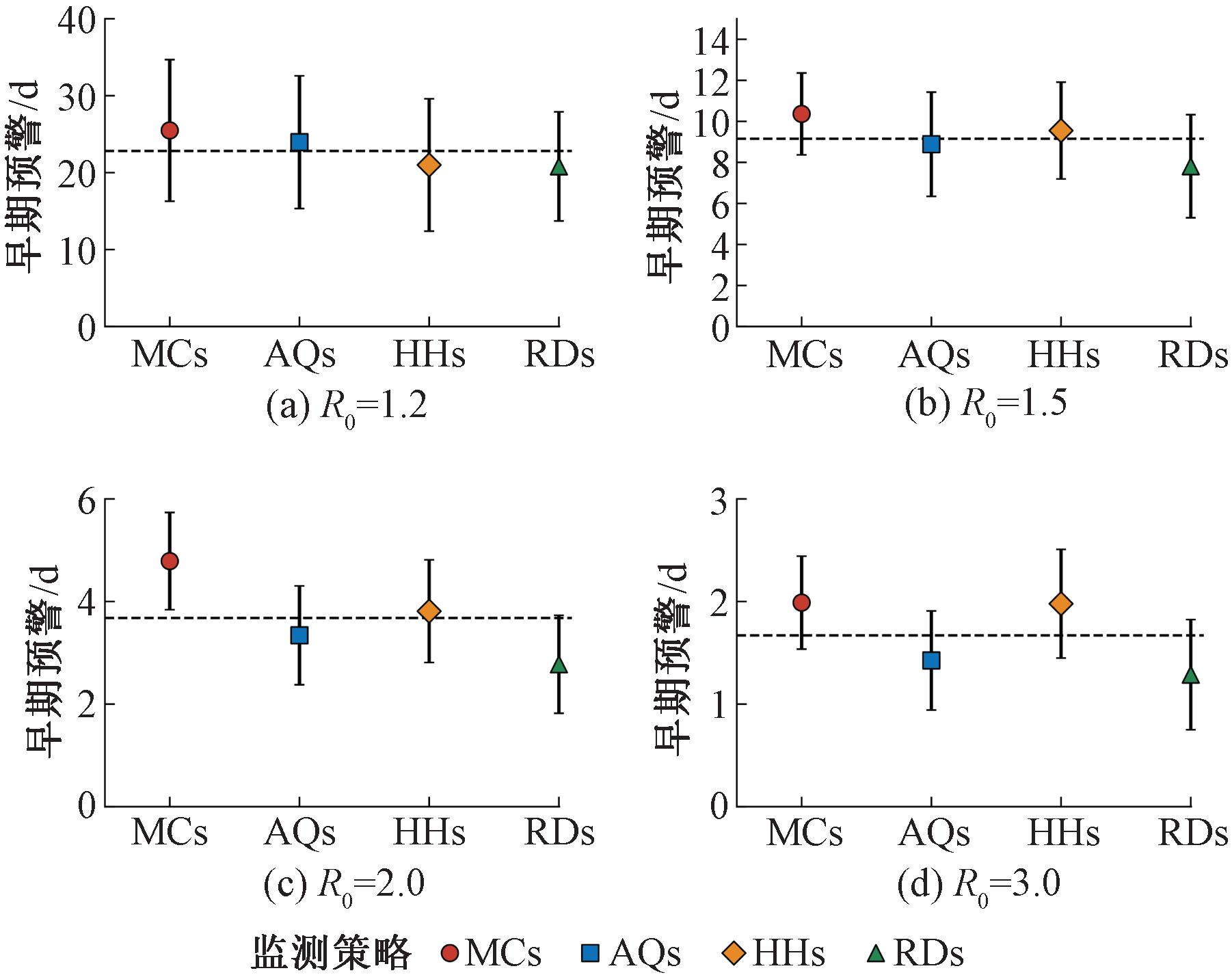
图8 不同风险监测策略的早期预警对比
Figure 8 Comparison of early warning with different risk surveillance strategies
在图8中,误差棒代表100次随机模拟的95%置信区间,虚线表示对应R0的4种监测策略的平均早期预警时间。当R0分别设置为1.2,1.5,2.0和3.0时,MCs展现了最优的监测性能,相比监测整体人群,其早期预警时间平均提前了25.49,10.36,4.78,1.99 d。由于MCs关注接触网络中具有最多接触的个体,意味着他们在群体中接触到患病个体的可能性更高,也更有可能被更早感染[13]。MCs依赖网络的全局结构特性,而现实世界中高分辨率的人际接触数据获取受限,因此MCs难以得到实际应用。当R0=1.2时,AQs监测性能仅次于MCs,说明在传播能力较低的情况下,基于熟人网络的监测策略有效,与既有研究结果相符[8]。熟人策略的优越性在于其利用了网络结构的特点,即“朋友悖论”,仅需掌握局部网络信息,便能提高选中较高连接度个体的概率,从而更有效地监测疫情。当新发传染病传播速度较慢时,HHs与RDs的性能接近,基于家庭的监测策略与随机监测策略易受网络结构对疾病传播的影响,当随机选择网络中具有弱连接的叶子节点作为哨点时,往往难以提前感知疫情的发生。相比之下,如果疾病的R0较低时,MCs和AQs利用网络结构信息,更有针对性地选择了监测对象,从而提高监测效率。
随着新发传染病的传播能力逐渐增强,HHs的早期预警性能仅次于MCs,接近了监测接触网络中最活跃的个体。在R0为1.5,2.0与3.0时,HHs达到了MCs监测性能的92.2%,80%和99.5%,相比RDs的早期预警时间分别平均提前了1.74 d(22%)、1.03 d(37%)和0.69 d(53%)。该结果表明,早期预警时间对R0高度敏感,随着传播能力的增加,不同监测策略的预警时间差异将缩小,逐渐趋于一致。基于家庭的监测策略关注于网络中的局部强连接模式(网络社团),同时家庭监测哨点呈现强中介中心性,因此在传染病传播初期,对局部的社团进行监测有助于快速发现和阻断传染病的传播[30]。此外,HHs通过一户一人的监测方式,仅依赖少量的样本即可实现近似对人群整体的全覆盖监测。
峰值时间和峰值幅度分别反映了当前监测子集与整体人群达到疾病发病率峰值的时间差值和相对比值。本文对比了上述两种评价指标的性能,结果如图9所示。
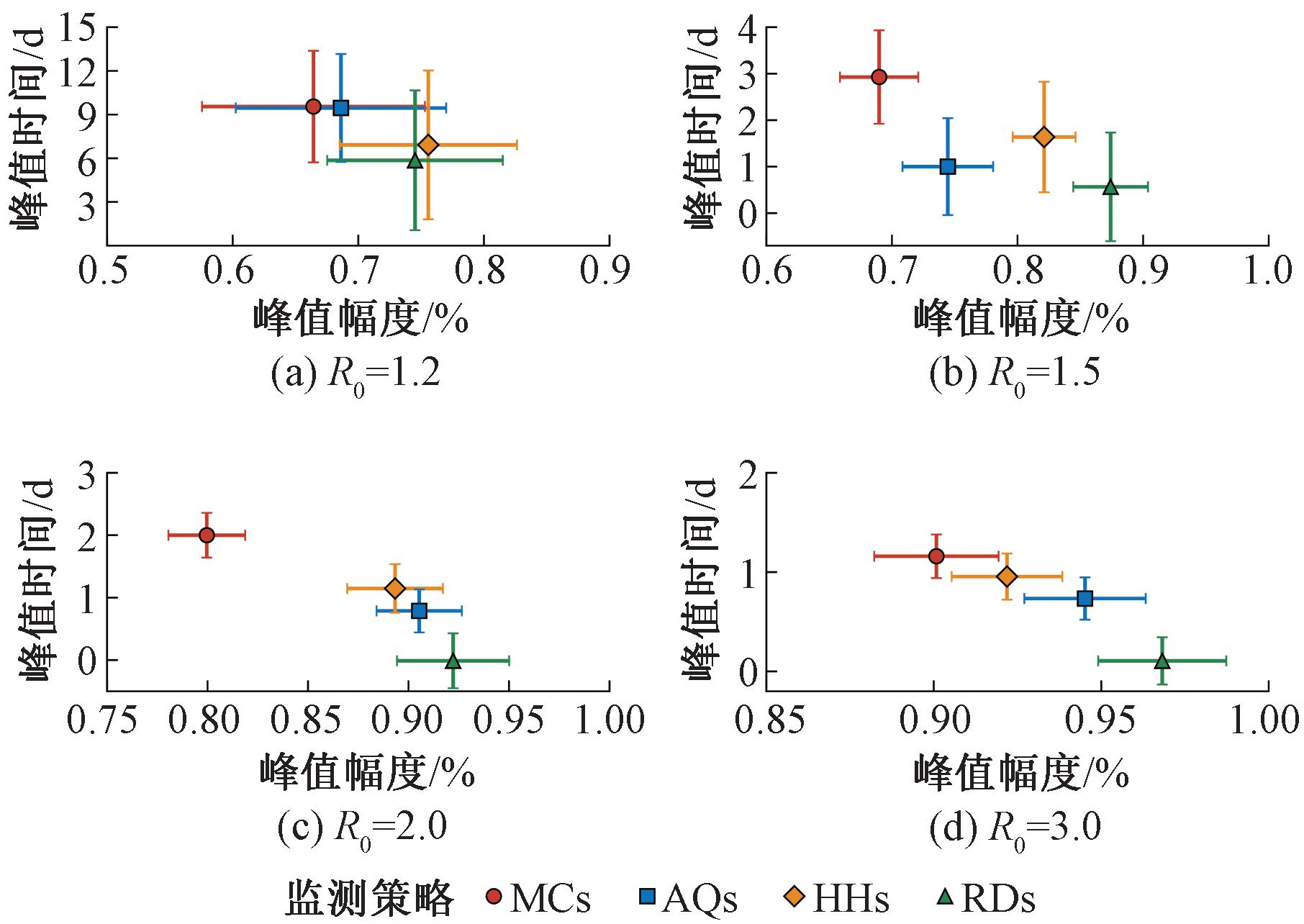
图9 不同风险监测策略的峰值幅度及峰值时间对比
Figure 9 Comparison of peak magnitude and peak timing with different risk surveillance strategies
当病毒传播能力较低(R0=1.2)时,MCs峰值时间更长且峰值幅度更小,说明相比MCs可以更早感知疾病传播峰值,能够对传染病的开始以及高峰期提供有效的态势感知,而HHs的峰值特征与RDs近似。随着传染病传染性的逐渐增加,HHs的峰值幅度以及峰值时间逐渐接近MCs,如图9中点标记所示,但相较于整体人群能够降低监测成本,可以通过筛选少数个体,在未知高精度人际接触行为和完整接触矩阵的前提下实现对新发传染病传播的风险态势感知。
4 结论
本文面向新发传染病的早期传播风险预警,将数据驱动的接触网络构建方法与传染病风险监测策略相结合,以深圳市为例,构建具有城市人口结构特征的多场景人际接触网络,并基于新发传染病的流行病学特性模拟多种接触模式下的疾病传播态势。进一步,本文提出一种基于家庭的风险监测策略,在新发传染病风险较高的场景下(基本再生数为3.0),可以在未了解个人接触行为、未获得大规模人群流调数据的情况下有效感知新发传染病的早期传播风险,能够为特定地区的新发传染病早期预警与防控提供科学的分析依据和技术支持。
本文在提出风险监测策略的同时存在相对局限性。首先,接触网络的构建依赖于统计数据的质量,由于现实世界中不同地区的数据统计能力存在差异,观测数据中固有的数据缺失、报告延迟造成建模的不确定性,因此所构建的接触网络可能存在失真以及结构异常,进而影响疾病传播模拟的准确性和可靠性。其次,现有家庭监测策略仅以日常接触人数为指标筛选监测个体,忽略了家庭成员职业和工作环境的差异性,可能低估医院等高风险场所中医疗工作者的潜在感染风险。此外,本文提出的监测策略尚未考虑疫情防控政策动态变化的影响,例如工作场所的开放程度、出行模式限制以及疫苗接种策略等因素。因此,在不同干预措施条件下,新发传染病监测策略的有效性仍需进一步研究。
未来研究将结合高质量、多类别的结构化传染病电子病历数据,研发更精准、可靠且针对性更强的新发传染病风险监测策略。此外,进一步整合政策实施、疫苗接种、工作场景等异质信息,考虑复杂的空间接触场景和人口流动模式,将能够模拟更真实的人类时空接触模式,为新发传染病风险监测策略优化提供科学见解。
[1] TEDROS A G. WHO Director-General′s speech at the world governments summit[EB/OL].(2024-02-12)[2024-09-14]. https：∥www.who.int/director-general/speeches/detail/who-director-general-s-speech-at-the-world-governments-summit---12-february-2024.
[2] JIANG S B, SHI Z L. The first disease X is caused by a highly transmissible acute respiratory syndrome coronavirus[J]. Virologica Sinica, 2020, 35(3): 263-265.
[3] HEESTERBEEK H, ANDERSON R M, ANDREASEN V, et al. Modeling infectious disease dynamics in the complex landscape of global health[J]. Science, 2015, 347(6227): 1-10.
[4] YANG B, GUO H, YANG Y, et al. Modeling and mining spatiotemporal patterns of infection risk from heterogeneous data for active surveillance planning[C]∥AAAI Conference on Artificial Intelligence. Washington DC: AAAI, 2014: 493-499.
[5] MISTRY D, LITVINOVA M, PIONTTI A P Y, et al. Inferring high-resolution human mixing patterns for disease modeling[J]. Nature Communications, 2021, 12: 323.
[6] MISTRY D, KERR C C, ABEYSURIYA R, et al. SynthPops： a generative model of human contact networks[EB/OL].(2021-07-05)[2024-09-14].https：∥docs.idmod.org/projects/synthpops/en/latest/overview.html.
[7] PREM K, COOK A R, JIT M. Projecting social contact matrices in 152 countries using contact surveys and demographic data[J]. PLoS Computational Biology, 2017, 13(9): e1005697.
[8] CHRISTAKIS N A, FOWLER J H. Social network sensors for early detection of contagious outbreaks[J]. PLoS One, 2010, 5(9): e12948.
[9] 焦敏, 高倩倩, 刘金妹, 等. 新发(重大)传染病 “全哨点” 概念界定[J]. 中国公共卫生, 2021, 37(10): 1459-1462.
JIAO M, GAO Q Q, LIU J M, et al. Defining overall sentinel surveillance on emerging (major) infectious diseases-a literature study[J]. Chinese Journal of Public Health, 2021, 37(10): 1459-1462.
[10] 欧阳聪, 关静, 杨鸣. 基于资源分配和动态分组的合作协同演化算法[J]. 郑州大学学报(工学版), 2023, 44(5): 10-16.
OUYANG C, GUAN J, YANG M. Cooperative co-evolution algorithm based on resource allocation and dynamic grouping[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 10-16.
[11] PEI S, TENG X, LEWIS P, et al. Optimizing respiratory virus surveillance networks using uncertainty propagation[J]. Nature Communications, 2021, 12: 222.
[12] MCGOWAN C R, TAKAHASHI E, ROMIG L, et al. Community-based surveillance of infectious diseases： a systematic review of drivers of success[J]. BMJ Global Health, 2022, 7(8): e009934.
[13] HERRERA J L, SRINIVASAN R, BROWNSTEIN J S, et al. Disease surveillance on complex social networks[J]. PLoS Computational Biology, 2016, 12(7): e1004928.
[14] MADEWELL Z J, YANG Y, LONGIN Jr I M, et al. Household transmission of SARS-CoV-2: a systematic review and meta-analysis of secondary attack rate[EB/OL].(2020-08-01)[2024-09-14]. https：∥www.medrxiv.org/content/10.1101/2020.07.29.20164590v1.
[15] LIU P Y, MCQUARRIE L, SONG Y X, et al. Modelling the impact of household size distribution on the transmission dynamics of COVID-19[J]. Journal of the Royal Society, Interface, 2021, 18(177): 20210036.
[16] WANG N, CHU T S, LI F R, et al. The role of an active surveillance strategy of targeting household and neighborhood contacts related to leprosy cases released from treatment in a low-endemic area of China[J]. PLoS Neglected Tropical Diseases, 2020, 14(8): e0008563.
[17] WALLINGA J, TEUNIS P, KRETZSCHMAR M. Using data on social contacts to estimate age-specific transmission parameters for respiratory-spread infectious agents[J]. American Journal of Epidemiology, 2006, 164(10): 936-944.
[18] 深圳市统计局. 深圳市第七次全国人口普查[EB/OL].(2021-05-17)[2024-09-14]. http:∥tjj.sz.gov.cn/ztzl/zt/szsdqcqgrkpc/.
Shenzhen Statistics Bureau. The seventh national population census in Shenzhen [EB/OL].(2021-05-17)[2024-09-14]. http:∥tjj.sz.gov.cn/ztzl/zt/szsdqcqgrkpc/.
[19] 深圳市统计局. 深圳统计年鉴2020[EB/OL].(2020-12-31)[2024-09-14]. http:∥tjj.sz.gov.cn/zwgk/zfxxgkml/tjsj/tjnj/content/post_8386382.html.
Shenzhen Statistics Bureau. Shenzhen statistical yearbook 2020[EB/OL].(2020-12-31)[2024-09-14]. http:∥tjj.sz.gov.cn/zwgk/zfxxgkml/tjsj/tjnj/content/post_838 6382.html.
[20] 深圳市统计局. 深圳市人口普查年鉴—2020[EB/OL].(2023-06-30)[2024-09-14]. http:∥tjj.sz.gov.cn/zwgk/zfxxgkml/tjsj/tjnj/content/post_10688160.html.
Shenzhen Statistics Bureau. Shenzhen census yearbook-2020[EB/OL].(2023-06-30)[2024-09-14]. http:∥tjj.sz.gov.cn/zwgk/zfxxgkml/tjsj/tjnj/content/post_10688160.html.
[21] KERR C C, STUART R M, MISTRY D, et al. Covasim: an agent-based model of COVID-19 dynamics and interventions[J]. PLoS Computational Biology, 2021, 17(7): e1009149.
[22] DU Z W, BAI Y, WANG L, et al. Optimizing COVID-19 surveillance using historical electronic health records of influenza infections[J]. PNAS Nexus, 2022, 1(2): pgac038.
[23] DU Z W, PANDEY A, BAI Y, et al. Comparative cost-effectiveness of SARS-CoV-2 testing strategies in the USA: a modelling study[J]. The Lancet Public Health, 2021, 6(3): e184-e191.
[24] GRIJALVA C G, ROLFES M A, ZHU Y W, et al. Transmission of SARS-COV-2 infections in households—Tennessee and Wisconsin, April-September 2020[J]. MMWR Morbidity and Mortality Weekly Report, 2020, 69(44): 1631-1634.
[25] DEL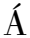 
GUILA-MEJ
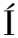A J, WALLMANN R, CALVO-MONTES J, et al. Secondary attack rate, transmission and incubation periods, and serial interval of SARS-CoV-2 Omicron variant, Spain[J]. Emerging Infectious Diseases, 2022, 28(6): 1224-1228.
[26] GARRETT N, TAPLEY A, ANDRIESEN J, et al. High asymptomatic carriage with the Omicron variant in South Africa[J]. Clinical Infectious Diseases, 2022, 75(1): e289-e292.
[27] MCEVOY D, MCALOON C, COLLINS A, et al. Relative infectiousness of asymptomatic SARS-CoV-2 infected persons compared with symptomatic individuals： a rapid scoping review[J]. BMJ Open, 2021, 11(5): e042354.
[28] MANICA M, DE BELLIS A, GUZZETTA G, et al. Intrinsic generation time of the SARS-CoV-2 Omicron variant： an observational study of household transmission[J]. The Lancet Regional Health Europe, 2022, 19: 100446.
[29] VYNNYCKY E, WHITE R G. An introduction to infectious disease modelling[M]. Oxford: Oxford University Press, 2010.
[30] HOUSE T, KEELING M J. Household structure and infectious disease transmission[J]. Epidemiology and Infection, 2009, 137(5): 654-661.