多站点选址问题是光伏电站运营过程中的主要挑战,运营者通常基于光伏发电量预测选择合适的电站地址。光伏发电量预测的方法主要分为物理模型和数据驱动模型两类。物理模型根据考虑了多种因素的数学模型来直接计算光伏功率[1]。数据驱动模型特别是机器学习(machine learning, ML)模型[2]包含两步建模过程,第一步预测天气情况[3],第二步根据天气情况预测光伏发电量。目前,一种备受瞩目的电力输出预测方法聚焦于通过精准提取深层非线性特征来预测光伏发电量[4]。集成学习技术因其独特的优势而备受推崇,它能够融合多个机器学习模型、深度学习模型以及统计方法,甚至可以将机器学习模型与统计方法巧妙结合,从而进一步提升预测的准确性和可靠性。
光伏电站选址常用的技术包括聚类、搜索和基于时空数据预测等。为了提取有价值的信息用来预测光伏发电量,通常采用聚类技术将发电数据或气象特征分组[5]。例如,Yang等[6]采用欧几里得距离聚类来得到相似日矩阵。Lai等[7]采用一种深度学习方法将辐照度时间序列数据分组到多个聚类中,以更好地识别其不规则模式。然而,聚类方法对提升站点选址效果的作用有限,搜索方法成为研究者们的重点研究对象。例如,Gao等[8]提出了一种改进的多目标优化算法来搜索最优参数。Fang等[9]提出了一种多准则决策系统来选择合适的光伏站点。这种方法结合了数学模型和决策理论,基于多个标准来评估不同地点的适宜性。地理信息系统与多准则决策的集成是改进选址和优化的另一种有效方法[10]。此外,Bawazir等[11]利用最优模型最小代价路径模型来搜索光伏电站的选址。这些选址方法有助于高效选址并进行部署决策。
近年来,数据采集技术的进步使得光伏电站选址有更多的基础数据可以应用。通过时空历史数据进行光伏发电量预测,根据预测发电量进行选址的方法逐渐受到重视,Lan等[12]利用天气数据来预测太阳辐射,重点关注时空历史数据。Jeong等[13]使用神经网络来关注时空相关性。Agoua等[14]提出了捕捉分布式光伏电站的空间和时间相关性的预测方法。多维张量表示时空数据时存在数据稀疏性的问题,张量分解可用来填充张量的零条目解决该问题。例如,Wang等[15]提出了上下文感知的Tucker张量分解来填充张量的零条目。利用残差学习框架,如深度残差网络(residual network, ResNet),可提高预测的准确性[16]。He等[17]提出一种端到端架构,命名为时空3D密度多尺度ConvLSTM Resnet网络,用于预测未来的交通流量。然而,对多站点预测问题的研究仍然有待加强。
为了解决不同背景下的多站点预测问题,Cubillos[18]采用长短期记忆(long short-term memory, LSTM)方法来捕捉时间相关性,并在考虑多个位点的情况下进行预测。在某些站点无法获得太阳辐照度数据的情况下,Gutierrez-Corea等[19]利用了邻近站点的数据,并通过附近位置的数据在没有直接测量的情况下对站点进行预测。Marzouq等[20]研究了分区情景,利用空间相关性进行预测。Persson等[21]专注于预测多个地点的光伏发电量,但没有明确时间和空间相关性,这可能导致计算密集型模型。一些研究强调了数据和模型融合在提高预测精度和捕捉不同领域的复杂相关性方面的重要性。Wang等[22]介绍了一种使用CNN处理天气数据和使用LSTM处理时间序列数据的混合模型,通过融合这两个模型,该方法可以有效地捕捉长短期相关性,进行准确预测。Zhang等[23]研究了考虑时空相关性和气象数据的融合技术。这些研究展示了用于应对多站点预测挑战的不同策略。
本文重点解决了分布式光伏电站选址中的几个关键挑战,包括保持数据连续性,利用时空相关性从非结构化文本中挖掘有价值的信息以及融合预测结果。基于此,本文提出了一种基于多站点预测模型(multi-site forecasting model, MSFM)的选址方法。本文创新点如下:
(1)提出基于时空数据的发电量预测方法,利用三维张量构建时空数据,提取时间序列趋势因素和周期因素,结合气象特征预测光伏电站发电量,提升了光伏发电量预测精度。
(2)采用山东省济南市的1 155个光伏发电站运行数据和相关气象数据训练深度网络模型,实现了分布式光伏电站多站点智能选址。
1 问题与相关概念描述
1.1 问题定义与描述
假设在R地区存在分布式光伏电站。这些光伏电站被定义为一个集合S={s1,s2,…,sM},其中M为地区R内站的数量。对于∀sm(m=1,2,…,M),有一个对应的四元组,其中lom为经度,lam为纬度,表示sm的空间位置数据。sm的装机容量为icm。Pom为发电输出的一组时间序列数据,
其中时间间隔t={1,2,…,T}。并定义了一个评估指标,用
来表示sm在时间t的装机容量日利用小时数
在本文的剩余部分中,用装机容量的日利用小时数代替了在时间t的功率输出。
1.1.1 区域分解
在R地区,现有的分布式光伏电站具有跨度大和空间分布不均匀的特点。为了实现多站点预测,首先以R为基础构建矩形区域R′,然后将R′ 除边界外平均划分为I×J个网格。网格图具体定义如下:在区域R中,存在一组站点S,S={s1,s2,…,sM}。这组站点S被绘制在地理图上。R区域的最大经度、最小经度、最大纬度和最小纬度被定义为一个矩形区域 R′。然后,将R′平均划分为除边界外I×J个的网格,其中i=1,2,…,I,j=1,2,…,J,每个网格用来表示R地区的不同位置。网格分辨率可通过I和J调整。对于网格(i,j)来说,它在t时刻的d维气象特征表示为
其中t∈{1,2,…,T}。为了表示电力输出的时空特征,进行数据建模如下。
不同时间尺度内不同网格图的功率输出表示为一个三维张量X∈RI×J×T,包含I个网格行、J个网格列及T个时间尺度。输入x(i,j,t)在网格grid (i,j)的功率输出定义为
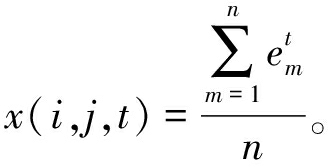
(1)
式中:n为位于网格grid(i,j)中的电站数量;
为t时刻装机容量的日利用小时数。
1.1.2 张量分解
对于光伏电站数据中的稀疏张量,可以使用塔克分解法来恢复张量的零条目。塔克分解法是找到一个非负核心张量C和非负矩阵A1,A2,…,AN,使这些分量的乘积近似于原始张量X。数学上可以表示为C×1A1×2A2…×NAN≈X,其中,×N表示N维的张量-矩阵乘积。张量分解通过将稀疏数据表示为高维张量并进行分解,有效处理数据稀疏性。塔克分解为一个优化问题,目的是最小化原始张量X与分解后重建张量之间的差值。优化问题的具体形式可表示为
C≥0,A1≥0,A2≥0,…,AN≥0。
(2)
通过对代表光伏电站数据的稀疏张量进行塔克分解,可以重建零条目并获得更完整的数据表示,这样就能更准确地分析和预测光伏发电量。
1.1.3 问题描述
根据上述定义,多站点电力输出预测可表述为给定一个时空张量X,其包含三个维度x(i,j,t),其中,i=1,2,…,I;j=1,2,…,J;t=1,2,…,T-1。T时刻的用电量
时刻的气象特征
多站点电力输出预测问题可描述为
其中,i=1,2,…,I;j=1,2,…,J;t=1,2,…,T-1。
基于多站点功率输出预测的站点选择问题可表述如下:对于任意网格grid(i,j),(i=1,2,…,I;j=1,2,…,J),计算累计值∑x(i,j,t),其中t=1,2,…,T-2,T-1,T,T+1,T+2,如果∑x(i,j,t)>α,则网格grid(i,j)适合投资新电站。
1.2 光伏发电量案例研究
本节以分布在山东省济南市的分布式光伏扶贫电站为例,分析电站之间的时间相关性、空间相关性以及气象特征的影响。
1.2.1 时间相关性
图1(a)展示了小马家光伏电站的时间相关性的邻接性。
其中x轴上的每个时间跨度代表1 d,y轴代表装机容量的日利用小时数。y值的变化相对平滑,对当前时刻,较近时间区间的发电量比远时间区间的发电量更相关,表明了时间序列具有邻接性。图1(b)展示了小马家电站时间相关性趋势,其中x轴上的每个时间跨度为一周,y轴上的值代表装机容量的日利用小时数。随着时间的推移,y值逐渐增大,表示在太阳辐射越来越强的情况下,发电量呈上升趋势。同样,在太阳辐射越来越少的时期,发电量呈下降趋势。时间相关性指发电量随着时间的变化而发生改变。主要原因在于不同时期的太阳辐射度不同,而辐射度是影响发电量的重要因素。从图2可以看出,4月至7月日发电量较高,8月之后日发电量逐渐降低。可见,发电量与太阳辐射时间高度相关。太阳辐射时长较多的春夏发电量高于辐射时长较低的秋冬发电量。将每个时间间隔内电站的发电量转换为单通道的图像矩阵。根据不同的特性将时间轴分成两个片段,表示邻接性的时间段和趋势性的时间段,其长度可根据数据特征做出选择,如邻接性数据长度可选择3,趋势数据为2,数据周期为7,则表示t-1至t-3时刻和t-7至t-14时刻的数据作为输入,然后将每个时间片段中的单通道矩阵流分别输入前两个组件中,以模拟上述两个时间属性。
表1 殷巷镇崔家光伏发电站与其他发电站的PCC值
Table 1 PCC between the station and the other stations
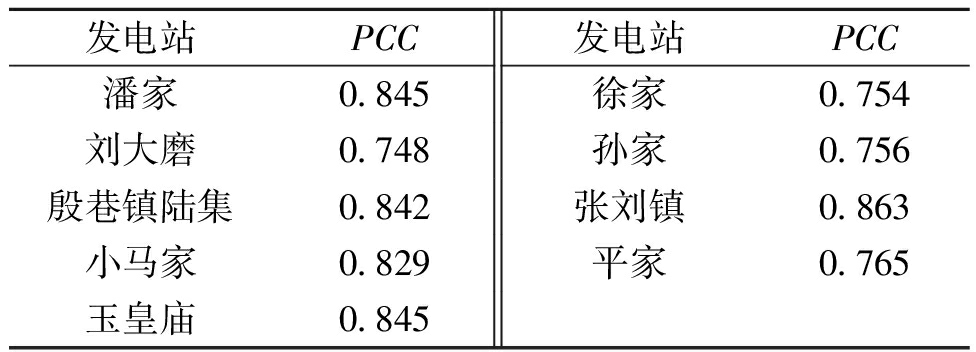
发电站PCC发电站PCC潘家0.845徐家0.754刘大磨0.748孙家0.756殷巷镇陆集0.842张刘镇0.863小马家0.829平家0.765玉皇庙0.845
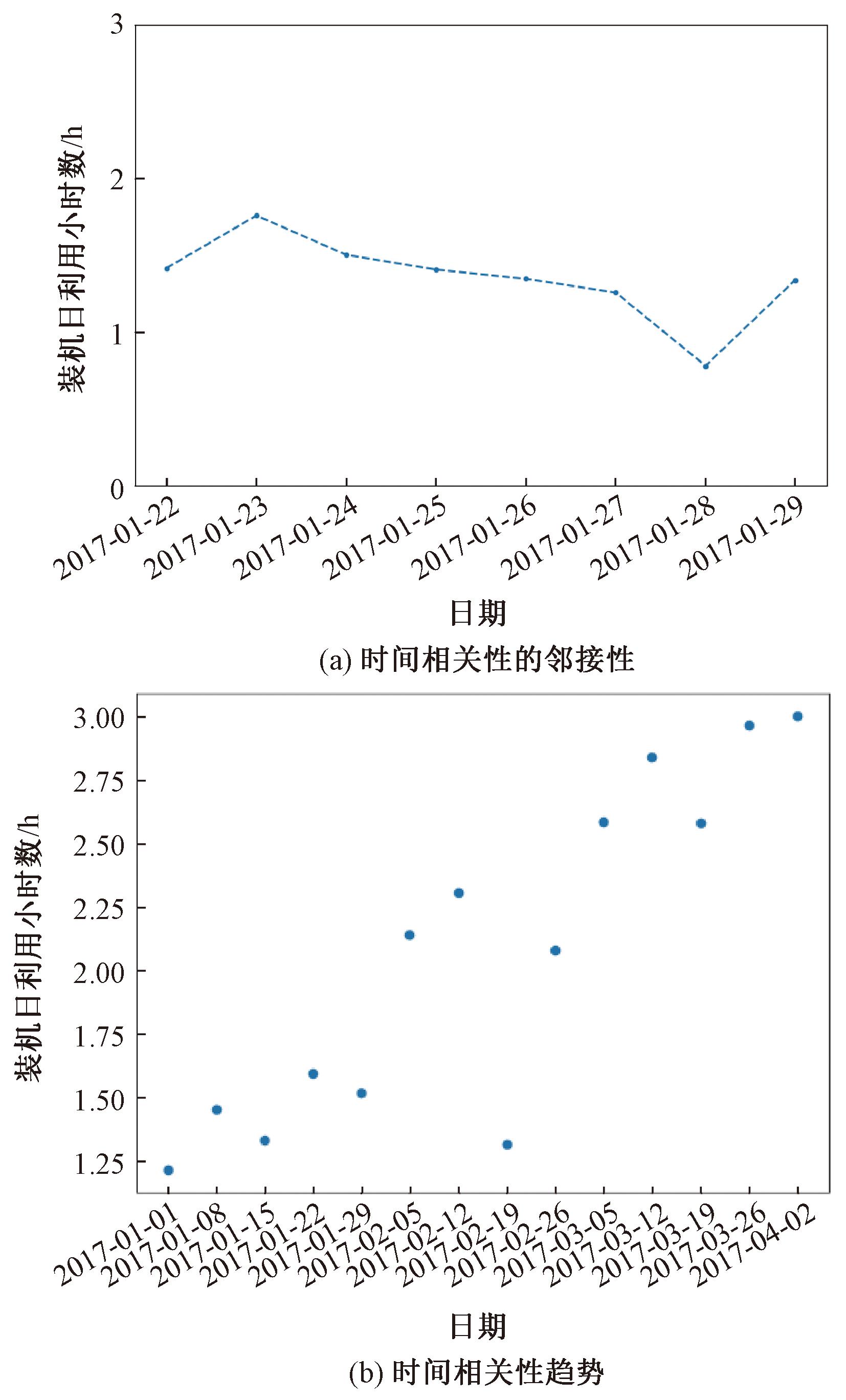
图1 光伏发电时间相关性
Figure 1 Time correlation of PV power generation
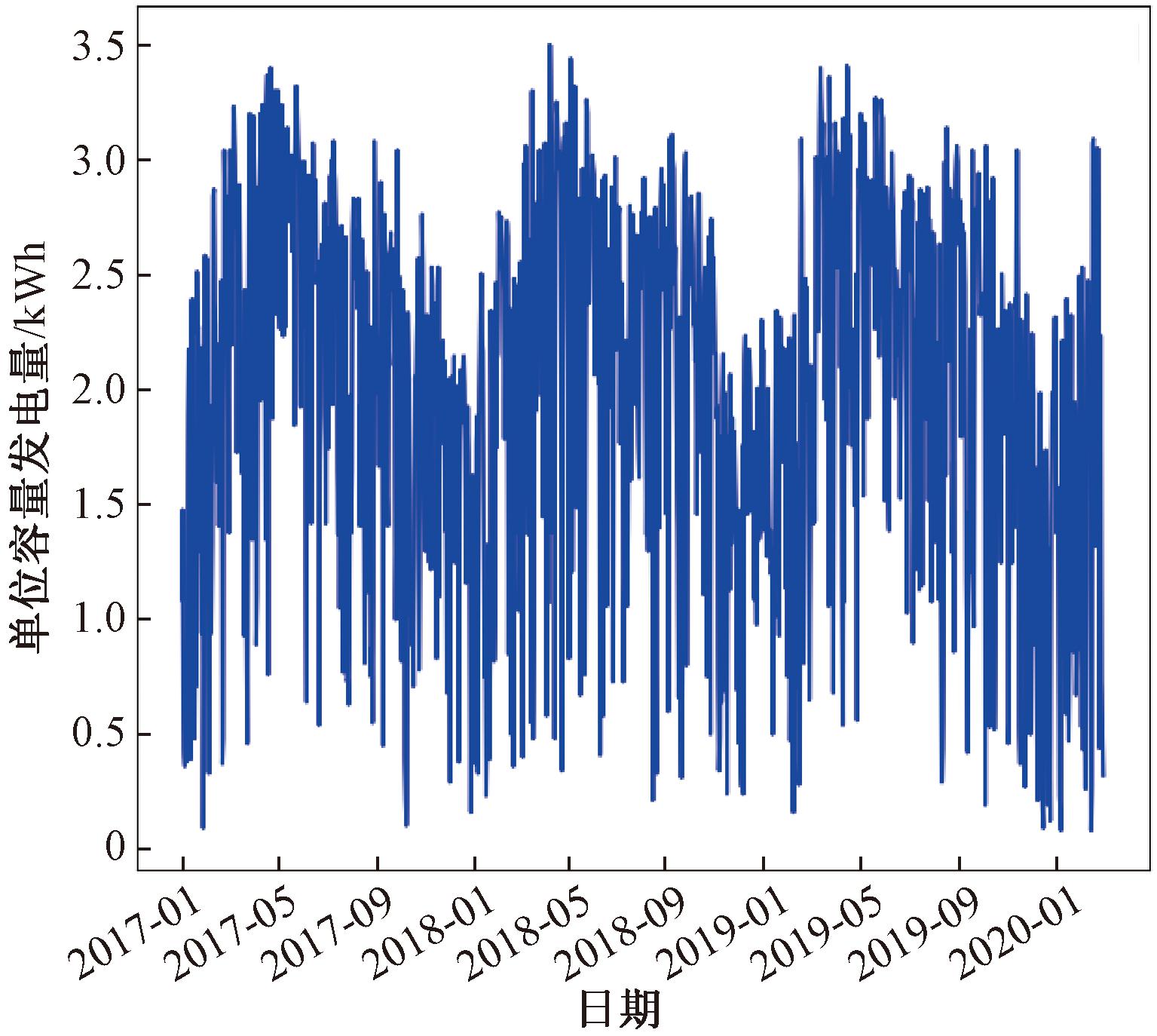
图2 济南某光伏电站日发电量
Figure 2 Daily Power generation of a PV station in Jinan
1.2.2 空间相关性
本节选择一个名为殷巷镇崔家的光伏电站来研究电站之间的空间相关性。在殷巷镇崔家周围,有6个站点离它最近,分别是潘家、刘大磨、殷巷镇陆集、小马家、玉皇庙和张刘镇。为了便于比较,还选择了距离殷巷镇崔家稍远的另外3个站点,即孙家、徐家和平家。如式(3)所示,皮尔逊相关系数PCC的取值在-1和+1之间,其表示两个站点si与sj之间的关联程度,如式(3)所示:
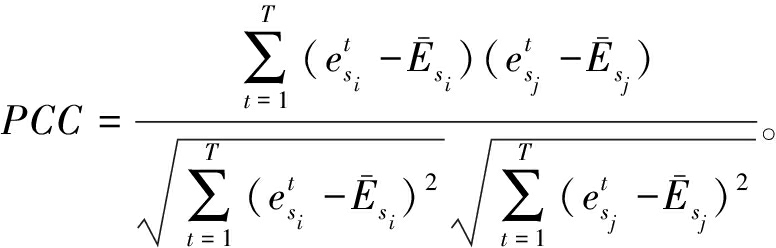
(3)
式中:
表1列出了殷巷镇崔家与其他站点在同一时间的装机容量日利用小时数的 PCC值。数据显示,殷巷镇崔家与最近的6个车站之间PCC值中的5个高于与稍远的3个站点之间PCC值。这意味着两站之间的距离与其装机容量日利用小时数在很大程度上具有一定的相关性。
1.2.3 气象相关性
气象相关性主要指气象要素如天气状况、湿度与发电量之间的相互影响和关系。图3(a)中红色折线表示晴天时的发电量,蓝色线表示雨天时的发电量。可以看出,晴天的日发电量明显大于雨天时日发电量。图3(b)中红色折线表示湿度为[80%,90%]时的日发电量,蓝色折线表示湿度为[10%,20%]时的日发电量。可以看出,湿度较低时的日发电量明显高于湿度范围高时的发电量。从而可知日发电量与气象条件高度相关,晴天、湿度较低时的发电量高于雨天、湿度较高时的发电量。
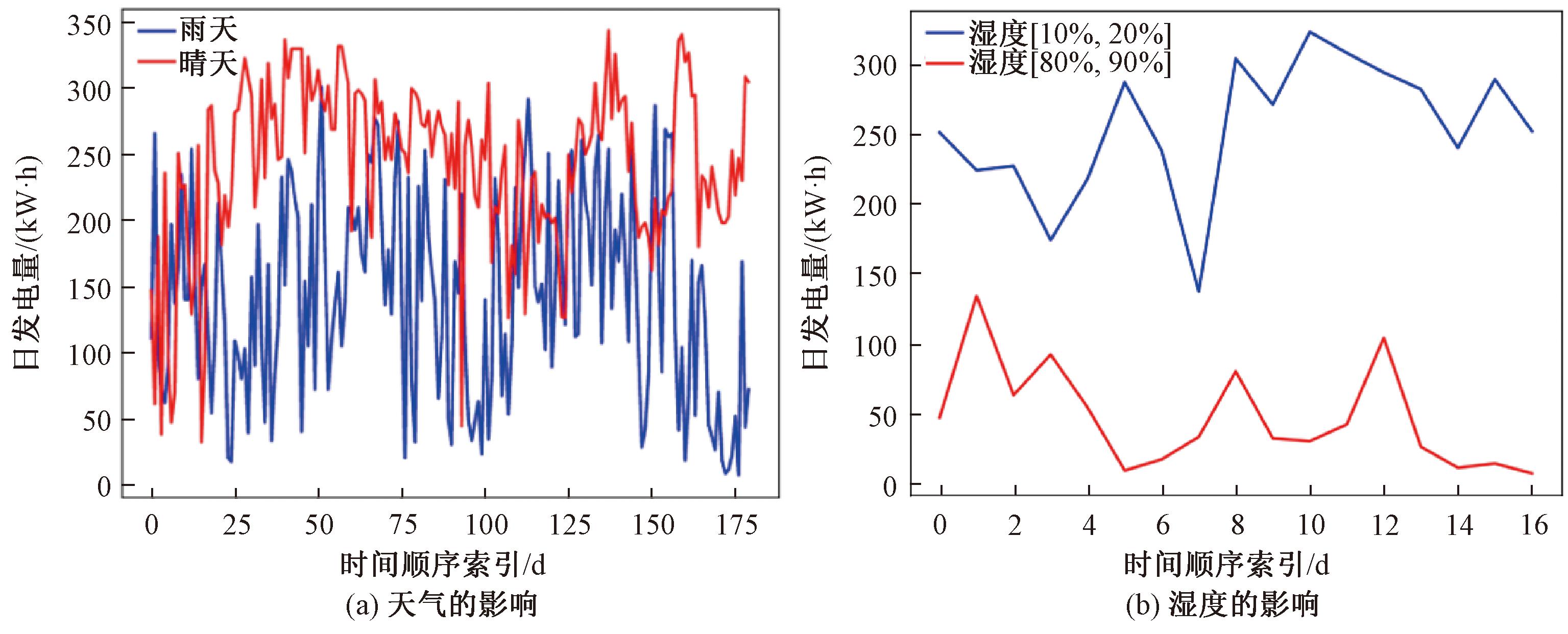
图3 天气和湿度的影响
Figure 3 Influence of weather and humidity
采用1.2.2节中的皮尔逊相关系数计算公式对气象相关性进行定量分析。空间位置上的气象数据使用温度和湿度来表达,将两类组合成数值矩阵输入到模型中。把地图划分成多个网格区域,分别填充温度和湿度数据形成张量输入到网络进行训练,使得网络获取气象特征。
2 多站点预测模型电站选址方法
智能选址问题的核心可归纳为以下两个主要部分:①数据表示。使用了一个三维张量来捕捉多站点功率输出数据的时空相关性,该张量的维度分别对应不同的站点、时间段和功率输出值。为了处理数据的稀疏性,采用了张量分解法,这样可以恢复张量中的零条目,从而获得更完整的数据表示。②预测模型和选址。首先,MSFM模型利用两个残差网络和三维张量所代表的时空数据进行预测。ResNets 是一种深度学习模型,可有效捕捉数据中的复杂模式和依赖关系,此外,全连接神经网络用于基于文本数据和气象数据的预测。其次,应用线性回归模型来融合ResNets和FC网络的预测结果,将两个模型的结果结合起来。最后,根据MSFM选择站点。
2.1 时空数据的表示
首先通过项目接口获取光伏电站的地理位置数据和时序发电量数据。如式(1)所示,区域R中的每个光伏电站都由一个四元组表示。之后将光伏发电站S映射到矩形R′,该矩形包括所有发电站。然后将R′划分为I×J个不包括边界的网格,以创建空间网格结构。其次,构建一个三维张量X∈RI×J×T,其中I和J表示网格维度。张量的每个条目表示为x(i,j,t),表示位于网格内的所有站点在T的平均功率输出。最后使用上下文感知的Tucker张量分解方法来分解和恢复张量X。这种分解方法允许恢复张量中的零条目,从而产生填充张量,提供时空数据的更完整表示。给定区域内的一组光伏电站,根据空间位置将区域平均划分为I×J网格,如图4所示。
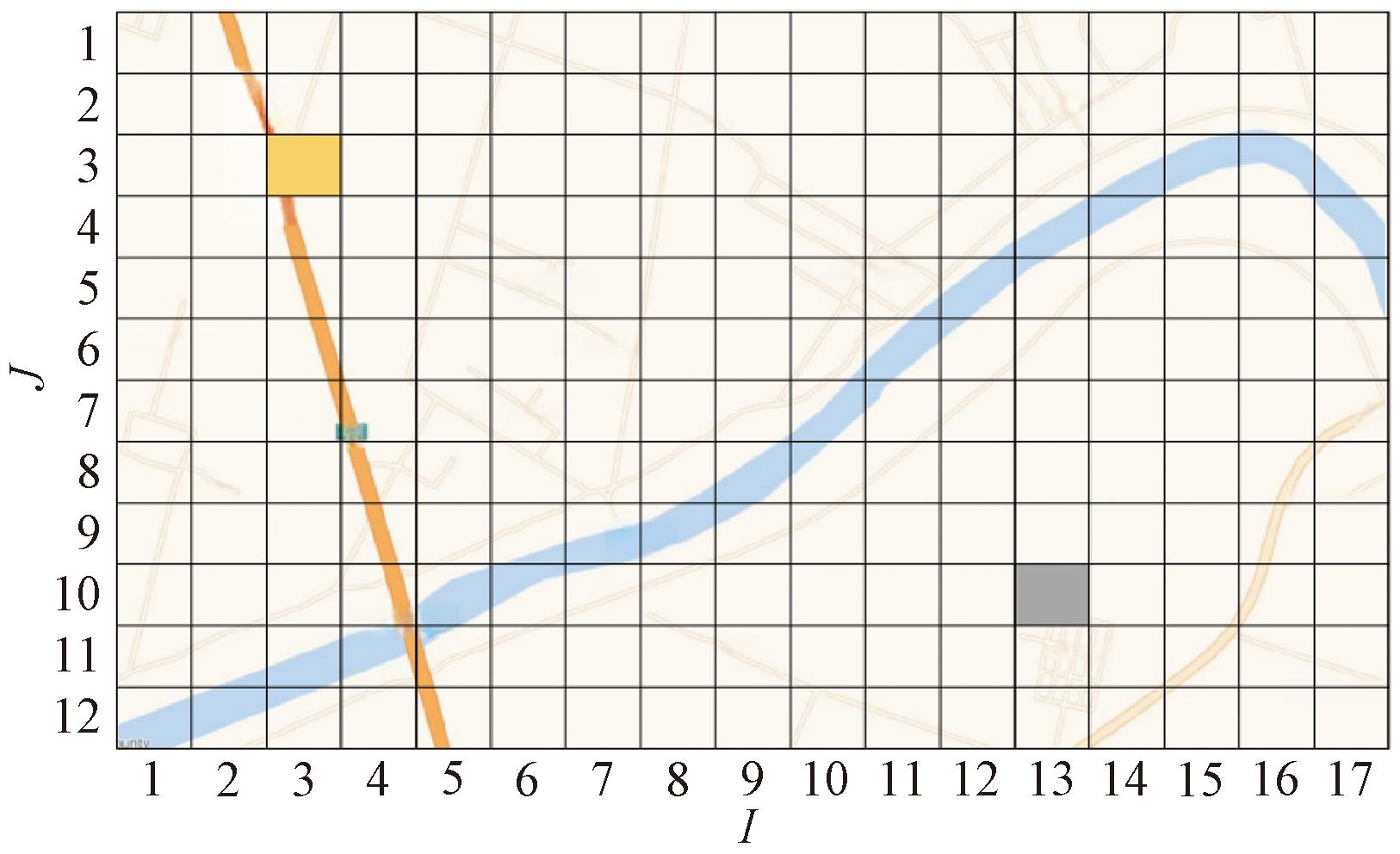
图4 基于地图分割的网格图
Figure 4 Grid graph based on map segmentation
区域被划分为12×17个网格,但是每个网格内平均光伏发电站的数量不同。例如,grid(3,3) 包含3个光伏发电站,而 grid(10,13)没有光伏发电站,这导致了空值或零条目的产生。说明光伏发电站数据张量表现出稀疏性,具有大量零条目。
2.1.1 张量构造
图5(a)表示特定时间二维(16×16)功率输出的实例。然而,二维仅反映与功率输出的空间相关性。为了解决时间序列数据的问题,构造了三维张量X∈RI×J×T,其中x(i,j,t)为输入,存储了t时刻grid (i,j)处网格中的功率输出,如图5(b)所示,用不同的颜色表示值的大小。颜色越亮表示数值越大。
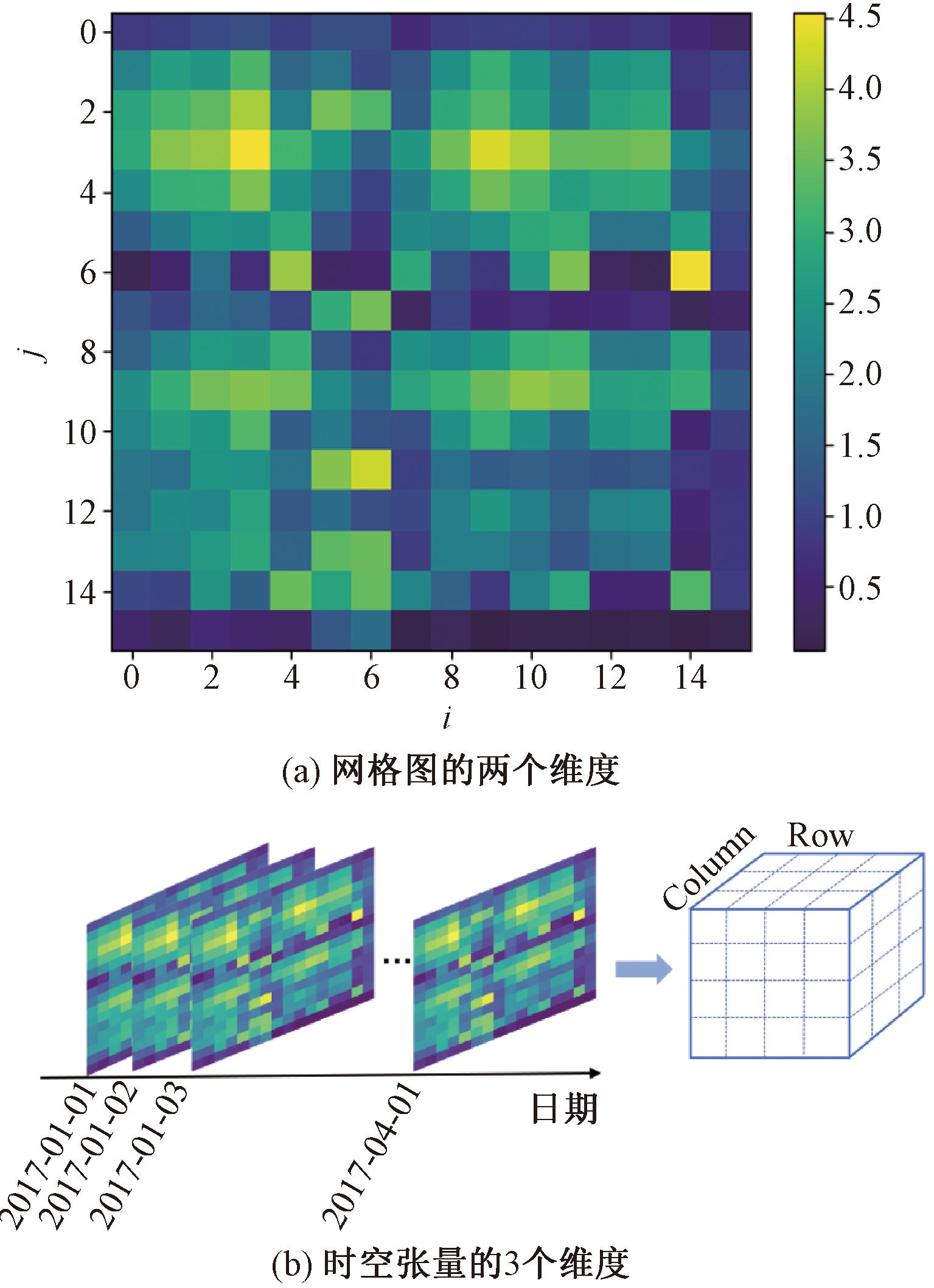
图5 时空张量图
Figure 5 Spatio-temporal tensor
2.1.2 恢复张量的零条目
为了解决数据稀疏问题,采用张量分解过程来恢复张量的零条目。利用张量分解方法可以填充缺失值并获得更完整的数据表示。首先,对稀疏数据进行归一化处理,其次,使用Tucker分解方法对张量进行分解,得到核心张量。然后,利用分解得到的核心张量来重建原始张量。将核心张量与因子矩阵分别进行模态积运算,得到近似的原始张量,对于原始张量中的零条目,使用近似原始张量的相应部分来替换其值。最后,对填充后的张量进行平滑处理以进一步改善结果,采用高斯滤波器方法平滑张量,在每个维度上创建高斯核,将高斯核与张量每个维度的切片进行卷积,直到处理完所有的维度和切片。此恢复过程有助于减轻张量的稀疏性,并能够更准确地分析和预测功率输出。
2.2 基于MSFM的预测与选址
MSFM预测阶段根据填充张量计算功率输出。该过程如图6所示。
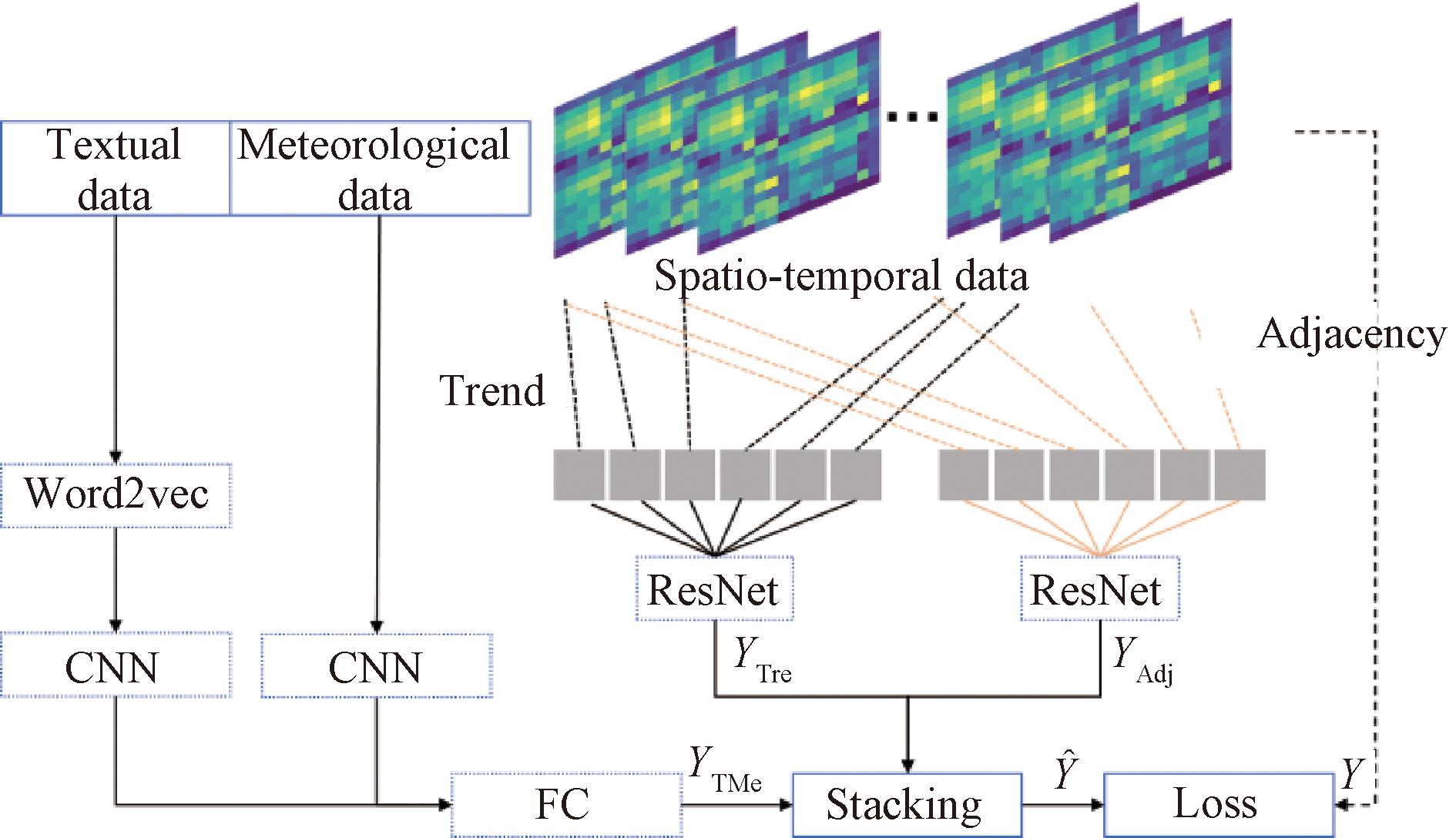
图6 多站点预测模型(MSFM)
Figure 6 Multi-site forecasting model (MSFM)
采用ResNet并通过数据的时空邻接性和趋势性来预测功率输出,这涉及捕获功率输出时间序列内的空间模式和时间趋势。将基于邻接性和趋势的ResNet的预测结果YTre和YAdj以及基于FC网络的预测结果YTMe融合在一起,得到最终的预测
在训练过程中,通过最小化均方误差L(θ)来优化模型,如式(4)所示,其中θ代表模型参数。目标是最小化功率输出的预测值YTMe和真实值YT之间的差异:
L(θ)=
。
(4)
2.2.1 CNN结构
CNN用于捕获功率输出数据中的空间和时间相关性。计算公式下:
(5)
式中:F表示卷积操作;
为i-1层的输入;
和
为层中的可学习参数。
2.2.2 残差结构
残差网络中通常使用残差单元来解决深度神经网络训练过程中的梯度消失问题。图7展示了残差单元的结构。这种结构可以有效训练深度网络并提高性能。
图7 残差单元
Figure 7 Residual unit
在MSFM中,使用两个ResNets来捕获功率输出数据的时空邻接性和趋势。ResNets模拟附近站点之间的相关性以及每个站点内的时间依赖性。两个ResNets的输出是预测结果YAdj和YTre,表示基于捕获相关性的预测功率输出。
2.2.3 全连接结构
全连接层用于学习文本和气象数据与光伏发电输出之间的映射函数。使用Word2Vec和CNN对文本数据进行建模,气象数据使用CNN进行建模,合并可能影响功率输出的附加信息,例如天气状况或与光伏电站相关的其他文本数据。
2.2.4 模型融合
MSFM 利用堆叠来集成多个回归模型。将两个ResNets的预测结果(YAdj和YTre)和FC网络的预测结果(YTMe)融合在一起以获得最终的预测结果
模型基于3方面的数据输入:邻近性、趋势性和气象数据组件。其中邻近性是以发电量数据构成一个张量作为输入,首先经过一个卷积层,然后经过6个相同的残差单元和一个卷积层得到输出;趋势性是4个趋势间隔的发电量构成一个张量作为输入,趋势时间间隔为5 d,该特性数据经过的网络层和邻近性相同。得到邻近性和趋势性的输出后,经过参数矩阵进行融合。气象数据作为张量输入,经过3个全连接层,得到与邻近性和趋势性输出相同的张量形式。最后融合3个组件的结果。
2.2.5 基于MSFM的选址
在为新的光伏电站选址时,首先,利用MSFM方法选择一个合适的区域,若区域内已有较多的光伏电站,说明这个区域具备建设光伏电站的初步条件,则选定的区域为合适区域。
其次,利用先进的地理信息系统(GIS)技术,将选定的区域划分为更小的网格,每个网格大小大于光伏电站大小,采用MSFM方法来确定这些网格单元是否适合建设光伏电站。这些粒度更细的网格单元,能够更准确地反映地形、地貌、植被、光照强度、风向风速等自然和气象因素。
最后,将网格单元中的环境因素和时空数据以张量的形式表达,利用时空数据的特性,基于2.2.4节的融合模型预测发电量,计算发电量累计值。将累计值作为选址过程中的评估标准,累计值越高说明该地址未来可能的发电量越高。因此,根据历史电力输出数据和融合模型的预测结果来确定具有较高发电潜力的地点。
3 实验
3.1 数据集和评价指标
数据集中的光伏发电站位于山东省济南市。数据来自济南的1 155个光伏发电站,时间跨度为2017年1月至2020年2月。研究中使用的数据集包括发电数据、运行和维护事件以及气象数据。发电数据包括日期、发电量和装机容量;空间特征包括电站ID、名称和经纬度;气象数据包括降水量、平均气压、气温、日照时数等信息。数据预处理包括删除异常数据和填补缺失数据。在收集的数据集中,约40%的站点有5%～20%的缺失值,30%的站点有20%～30%的缺失值,30%的站点有近50%的缺失值。为填补缺失值,利用气象条件相似的过去几天的发电量来估算缺失值。在预测模型方面,利用时空邻接性和趋势预测济南光伏发电数据集的电力输出。对于济南气象因素,利用CNN和FC模型根据天气数据预测电力输出。为了评估模型的预测性能,使用4个评估指标:MAE(平均绝对误差)、RAE(相对绝对误差)、RMSE(均方根误差)和RRSE(相对平方根误差)。
3.2 预测实验
在预测实验中,验证了MSFM的适用性和有效性。实验对象是有邻近站点的特殊站点。假设这些特殊站点并不实际存在,而是由邻近站点利用填充张量和两个 ResNets 虚拟创建的。训练数据和验证数据比例为7∶3,学习率为0.000 02,batch size为32,训练轮数为500。MSFM 由3个部分组成。相邻关系和趋势由两个ResNet模拟,而气象数据的影响则由CNN和FC模拟。
邻接性的时间跨度设定为1 d,趋势的时间跨度设定为7 d。使用Adam 优化函数训练 ResNets,并根据损失函数通过不断调整获得理想参数。图8展示了智能多站点预测系统的界面。
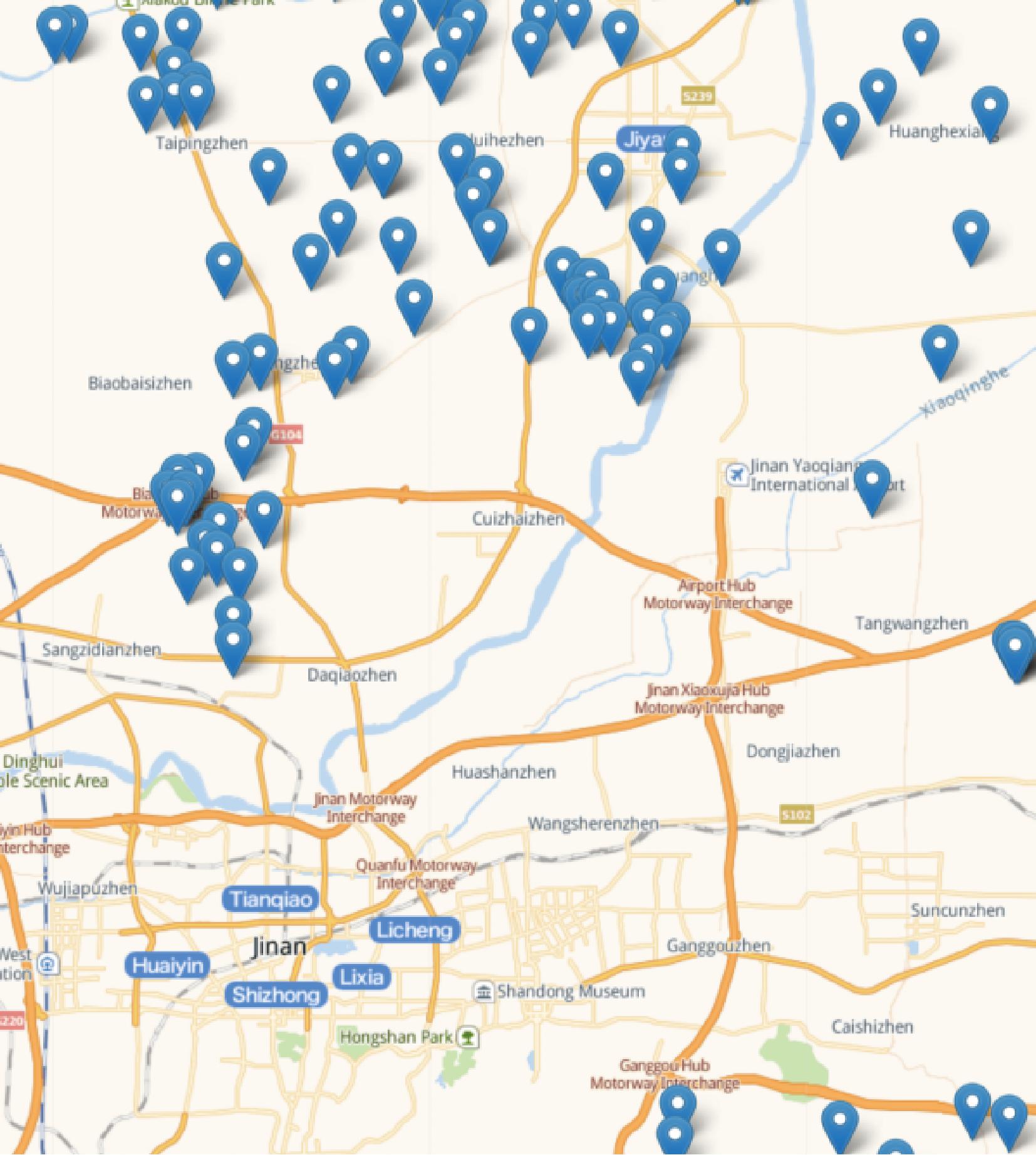
图8 智能多站点预测系统界面
Figure 8 The interface of intelligent multi-site forecast
3.3 实验结果分析
本文以基于时间序列(T)的预测结果为基准。然后加入时空邻近性(STA)、时空趋势(STT)和气象数据(M),分别进行实验,使用平均绝对误差MAE、相对绝对误差RAE、均方根误差RMSE及相对均方根误差RRSE作为确定性性能标准。使用LSTM和ResNets等深度网络框架验证了这些数据集。RMSE的收敛情况如图9所示。红线代表ResNet的RMSE,蓝线代表LSTM的RMSE。从图9中可以看出,随着训练轮次的增加,ResNets和LSTM的RMSE都在不断减小,而且ResNets的收敛速度和最终收敛结果都优于LSTM。
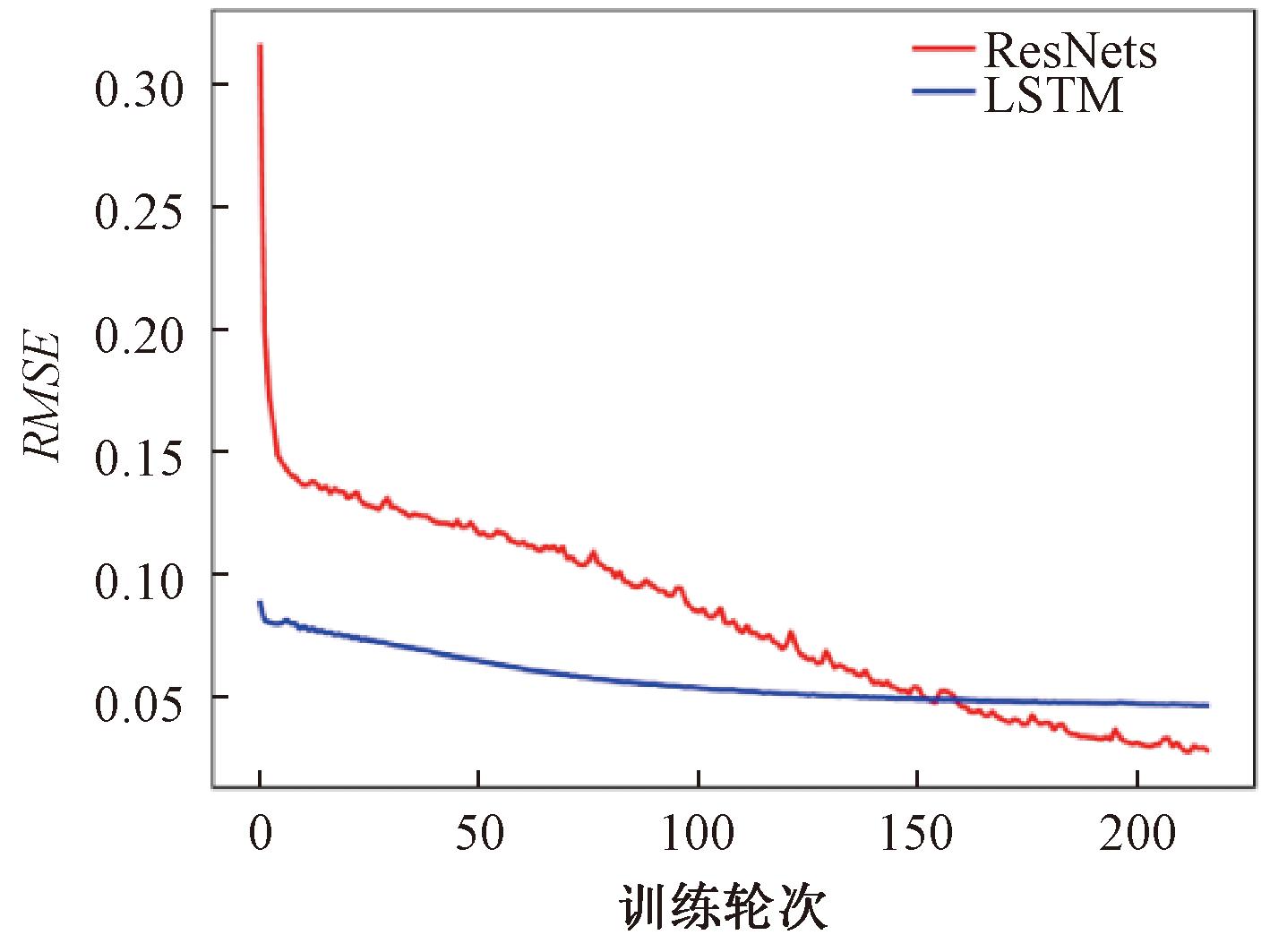
图9 ResNet 和 LSTM 的 RMSE
Figure 9 RMSE of ResNet and LSTM
3.3.1 济南光伏发电数据集的结果分析
如表2所示,济南数据集的实验结果表明,增加了时间相关性、空间相关性和气象相关性之后的融合模型预测结果的MAE、RAE、RMSE、RRSE分别为1.091、0.851、1.305、0.892,比未增加时空和气象相关性的预测模型分别降低了7.6%、5.2%、10.2%、4.2%;比仅增加时间相关性的模型分别降低了3.6%、1.5%、5.8%、3.1%;比未增加气象相关性的模型分别降低了2.3%、0.9%、2.6%、2.5%。由此可见,设计的时间相关性、空间相关性和气象相关性能够提升预测结果精度。
表2 济南数据集实验结果
Table 2 Experiment results in Jinan data set
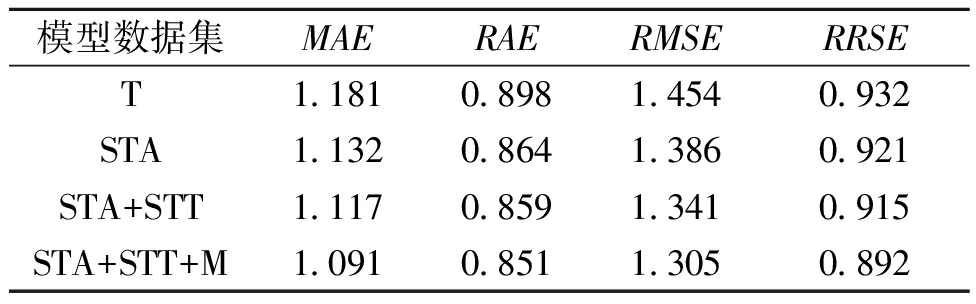
模型数据集MAERAERMSERRSET1.1810.8981.4540.932STA1.1320.8641.3860.921STA+STT1.1170.8591.3410.915STA+STT+M1.0910.8511.3050.892
3.3.2 新选址的应用
在过去两年中,MSFM已应用于新电站地址的选择。光伏发电量累计值和预测值被用作新电站选址的评估标准。利用 MSFM 成功为济南光伏扶贫项目选择了十几个新的光伏电站,例如,章丘区普集镇聘贤村1.65 MW光伏电站,官庄镇亮甲坡村55 kW光伏电站,长清区双泉镇王庄55 kW光伏电站,万德街道朱泉村55 kW光伏电站。MSFM的新颖之处在于融合了时空相关性和气象条件,能够预测网格图中的发电量,为新站点选择提供可靠的决策支持。
4 结论
光伏电站具有数量多、分布广、发电量小的特点,分布式光伏电站选址对于光伏电站运营具有重要意义。MSFM 将现有光伏电站作为参考,并利用时空相关性、气象数据和事件数据,显著提高了预测精度,为新选址决策提供了支持。具体而言,MSFM能够根据当地的气象数据预测网格图中每一个网格的电力输出。使用三维张量来捕捉多站点功率输出数据的时空相关性。利用两个残差网络根据三维张量所代表的时空数据进行预测。采用山东省济南市1 155个光伏发电站运营数据和天气数据进行实验,根据MAE、RAE、RMSE和RRSE评估预测结果,表明本文所提方法将各评价指标降低约0.9%～10.2%。与线性回归 (LR) 和 SVM 等一次只能预测一个电站的传统模型不同,MSFM 可为新电站选址提供更可靠的决策支持。
未来的工作将利用自然语言处理从运维系统中提取和挖掘语义信息,以进一步提高 MSFM 的性能,目标是将 MSFM 应用于其他城市的更多分布式光伏运维平台,为光伏场地规划和选择项目提供决策支持。
[1] DOLARA A, LEVA S, MANZOLINI G. Comparison of different physical models for PV power output prediction[J]. Solar Energy, 2015, 119: 83-99.
[2] QIU X H, ZHANG L, REN Y, et al. Ensemble deep learning for regression and time series forecasting[C]∥2014 IEEE Symposium on Computational Intelligence in Ensemble Learning (CIEL). Piscataway: IEEE, 2014: 1-6.
[3] TIAN J, OOKA R, LEE D. Multi-scale solar radiation and photovoltaic power forecasting with machine learning algorithms in urban environment: a state-of-the-art review[J]. Journal of Cleaner Production, 2023, 426: 139040.
[4] MOO E J A, DZIB J T, CANTO-ESQUIVEL J, et al. Deep learning for photovoltaic power plant forecasting[C]∥Communications in Computer and Information Science. Cham:Springer International Publishing, 2018:56-66.
[5] 李章晓, 宋微, 田野. 基于深度学习和进化计算的外汇预测与投资组合优化[J]. 郑州大学学报(工学版), 2019,40(1): 92-96.LI Z X, SONG W, TIAN Y. Exchange rate forecasting and portfolio optimization based on deep learning and evolutionary computation[J]. Journal of Zhengzhou University (Engineering Science), 2019, 40(1): 92-96.
[6] YANG X Y, XU M L, XU S C, et al. Day-ahead forecasting of photovoltaic output power with similar cloud space fusion based on incomplete historical data mining[J]. Applied Energy, 2017, 206: 683-696.
[7] LAI C S, ZHONG C K, PAN K D, et al. A deep learning based hybrid method for hourly solar radiation forecasting[J]. Expert Systems with Applications, 2021, 177: 114941.
[8] GAO Y Y, LI P, YANG H F, et al. A solar radiation intelligent forecasting framework based on feature selection and multivariable fuzzy time series[J]. Engineering Applications of Artificial Intelligence, 2023, 126: 106986.
[9] FANG H, LI J, SONG W Y. Sustainable site selection for photovoltaic power plant: an integrated approach based on prospect theory[J]. Energy Conversion and Management, 2018, 174: 755-768.
[10] ALAMI MERROUNI A, ELWALI ELALAOUI F, MEZRHAB A, et al. Large scale PV sites selection by combining GIS and analytical hierarchy process. case study: eastern Morocco[J]. Renewable Energy, 2018, 119: 863-873.
[11] BAWAZIR R O, ÇETIN N S, FADEL W. Optimum PV distributed generation based on grid and geographical area: a case study of Aden governorate, Yemen[J]. Energy Conversion and Management, 2023, 297: 117703.
[12] LAN H, YIN H, HONG Y Y, et al. Day-ahead spatio-temporal forecasting of solar irradiation along a navigation route[J]. Applied Energy, 2018, 211: 15-27.
[13] JEONG J, KIM H. Multi-site photovoltaic forecasting exploiting space-time convolutional neural network[J]. Energies, 2019, 12(23): 4490.
[14] AGOUA X G, GIRARD R, KARINIOTAKIS G. Short-term spatio-temporal forecasting of photovoltaic power production[J]. IEEE Transactions on Sustainable Energy, 2018, 9(2): 538-546.
[15] WANG Y L, ZHENG Y, XUE Y X. Travel time estimation of a path using sparse trajectories[C]∥Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York :ACM, 2014: 25-34.
[16] SHAFIQ M, GU Z Q. Deep residual learning for image recognition: a survey[J]. Applied Sciences, 2022, 12(18): 8972.
[17] HE K M, ZHANG X Y, REN S Q, et al. Identity mappings in deep residual networks[M]∥Lecture Notes in Computer Science. Cham: Springer International Publishing, 2016: 630-645.
[18] CUBILLOS M. Multi-site household waste generation forecasting using a deep learning approach[J]. Waste Management, 2020, 115: 8-14.
[19] GUTIERREZ-COREA F V, MANSO-CALLEJO M A, MORENO-REGIDOR M P, et al. Forecasting short-term solar irradiance based on artificial neural networks and data from neighboring meteorological stations[J]. Solar Energy, 2016, 134: 119-131.
[20] MARZOUQ M, ELFADILI H, ZENKOUAR K, et al. Short term solar irradiance forecasting via a novel evolutionary multi-model framework and performance assessment for sites with no solar irradiance data[J]. Renewable Energy, 2020, 157: 214-231.
[21] PERSSON C, BACHER P, SHIGA T, et al. Multi-site solar power forecasting using gradient boosted regression trees[J]. Solar Energy, 2017, 150: 423-436.
[22] WANG K J, QI X X, LIU H D. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network[J]. Applied Energy, 2019, 251: 113315.
[23] ZHANG J B, ZHENG Y, QI D K. Deep spatio-temporal residual networks for citywide crowd flows prediction[EB/OL].(2016-10-01)[2024-09-02].https:∥doi.org/10.48550/arXiv.1610.00081.