进化算法(evolutionary algorithm, EA)作为一种启发式算法,因其具有较好的全局搜索能力,多用于求解多目标优化问题(multi-objective optimization problems, MOPs)[1]。随着科学技术的发展,出现了许多与实际工程问题有关的昂贵多目标优化问题(expensive many-objective optimization problems, EMOPs)[2-4],如天线优化设计[5]、熔镁炉设计[6]、汽车侧撞试验[7]以及农用拖拉机进气通风系统设计问题等实际问题。采用计算流体动力学和昂贵的实时评估来解决农用拖拉机进气通风的设计问题。汽车侧面抗撞的性能问题用有限元分析来测试,包括车辆重量、加速时间、不同速度下的道路噪声以及车辆的空间等决策变量。然而,这些传统方法都比较费时。代理辅助进化算法(surrogate-assisted evolutionary algorithms, SAEAs)[8]即构建廉价代理模型来近似替代昂贵实验结果,再用模型管理策略选取少部分解进行有限次的真实评估,从而能够较快求解费时问题。因此SAEAs成为求解EMOPs更为有效率的一类方法。
根据代理模型的不同,SAEAs大致可分为两类:一类是采用基于回归的SAEAs,即根据历史数据信息构建代理模型来逼近真实目标函数值,模型输出为个体的预测值。K-RVEA[9]中,构建Kriging模型来近似每个目标函数,选择使用不确定性或基于角度的惩罚距离来确定需要进行真实评估的个体。在KTA2[10]中,改进了强影响点对Kriging模型的干扰,提出一种状态需求的填充采样准则。另一类是基于分类的SAEAs,即放弃构建预测精确信息的模型,考虑构建一种能够区分解是否为值得评估解的分类模型作为代理模型。一般采用径向基函数(radial basis function, RBF)、K最近邻(K-nearest neighbor, KNN)[11]和前馈神经网络(feedforward neural network,FNN)作为代理模型来判断解的类型。在CPS-MOEA[12]中,采用分类模型预测种群中解之间的支配关系,选择非支配解进行真实评估。在CSEA[13]中,采用前馈神经网络预测种群中的个体与参考点之间的支配关系,选择较优个优进行真实计算。REMO算法[14]是一种基于关系模型辅助的多目标高代价演化算法,建立面向不平衡数据的分类器,利用PBI方法的惩罚因子δ,保证正负样本相对平衡。MCEA/D[15]则是一种新的基于分类的SAEAs,利用多个局部分类器来规避问题性的过拟合,最后通过模型管理策略来增强预筛选能力。
基于回归的SAEAs求解低维问题具有高效、精度高等优点,但随着实际问题中目标空间维数和决策空间维度的增多,Kriging模型的复杂度与样本数量呈指数增长,其累积误差会影响预测结果。基于分类的SAEAs对于求解高维问题更具有竞争力,但在求解低维问题时,会存在分类器模型精度不高而导致算法性能不佳等问题。因此,本文针对分类器预测精度不高和模型管理效率低等问题,提出了一种基于自适应采样策略的模糊分类代理辅助进化算法(fuzzy classification surrogate-assisted evolutionary algorithm based on adaptive sampling strategy,FCEA-ASS),用于求解EMOPs。
本文的主要贡献点:
(1)将模糊分类器作为代理模型,保证预测模型的精度,并采用基于转移的密度估计策略提高选择压力,以此兼顾收敛性与多样性。
(2)利用分类器精度信息,设计了一种根据分类精度划分状态的自适应模型管理策略,使用模糊隶属度对具体状态进行针对性设置,能够降低误导搜索方向的可能,提高算法的运行效率。
1 相关工作
1.1 昂贵多目标优化问题
EMOPs即指在优化多目标问题的过程中,由于目标函数为黑盒,通常用耗时的数值模拟或昂贵的物理实验来评估,这会耗费较高的时间或成本。因此,一般构建廉价的代理模型来代替昂贵的物理实验。以最小化问题为例,考虑以下形式的EMOPs:
(1)
式中:x为具有d个决策变量的决策向量;X表示决策空间;fm(x)为目标向量F的第m个目标。
1.2 基于移位Pareto密度估计的多目标优化
本文使用SPEA2+SDE[16]算法作为优化器,该算法提出基于转移的密度估计策略(shift-based density estimation strategy, SDE),通过改变多样性的方式提高选择压力,同时具有更好的收敛性与分布的多样性。具体步骤:若估计个体p的密度时,SDE通过对比收敛性,p在一个目标上表现比另一个个体q好时,就将q转移到p当前目标位置上,否则q的位置不变。这种策略会将收敛性差的个体在选择过程中快速被淘汰删除,从而提高选择压力。
![]()
(2)
式中:D′(p,P)为个体p在种群P中新的密度估计;N为种群个数;dist(p,q′i)为两个体的相似度;q′i为qi转移后的点,qi为另一个对比个体,具体方法如式(3)所示。
![]()
(3)
2 基于自适应采样策略的模糊分类代理辅助进化算法
FCEA-ASS算法将多局部幂均值模糊K最近邻分类器(multi-local power means fuzzy K-nearest neighbor classifier, MLPM-FKNN)[17]作为分类代理模型,SPEA2+SDE为优化器,提出一种针对模糊分类器的自适应采样策略,具体的算法步骤如算法1所示。
算法1 FCEA-ASS算法。
输入:种群P,种群总数N,最大迭代次数Fmax;
输出:真实评估的个体Off_p。
① 初始化种群。采用随机生成种群大小为N的初始种群P,进行真实评估后放入Arc。
② 构建分类代理模型。通过帕累托支配关系筛选训练样本来构造模糊分类器。采用十折交叉验证获得分类器的分类准确率。将MLPM-FKNN预测训练样本的隶属度和标签,参与子代预选。
③ 后代生成预选。种群生成2N个后代解,排序并选择前N个较优解。然后将选定的解用作父代解继续产生新的后代解。后代生成预选为重复wmax次。
④ 填充采样准则。采用自适应采样策略,考虑当前种群的收敛性、多样性和不确定性,根据自适应采样策略,得到个体Off_p。
⑤ 环境选择机制。生成下一代的新种群。
2.1 多局部幂均值模糊K最近邻分类器
构建MLPM-FKNN的动机是希望能够克服多量样本的类会主导检验样本预测的这一缺点,这种不足可以通过使用局部平均向量来引导。
构建MLPM-FKNN过程如下。
步骤1 首先计算训练样本![]() 和检验样本Q之间的欧几里得距离,并按升序对它们进行排序。Q的K个最近邻nnK为
和检验样本Q之间的欧几里得距离,并按升序对它们进行排序。Q的K个最近邻nnK为![]() 步骤2 使用从K个最近邻中求局部幂均值子样本
步骤2 使用从K个最近邻中求局部幂均值子样本![]() 每个类的
每个类的![]()
步骤3 计算Q和![]() 之间的欧几里得距离。由式(4)和式(5)使用加权距离将隶属度分配给
之间的欧几里得距离。由式(4)和式(5)使用加权距离将隶属度分配给![]()
步骤4 将Q分类到与其具有最高隶属度的相应类ω*。
式(4)为检验样本Q在由K个最近邻表示的类中分配的隶属度,如式(4)所示:

(4)
式中:uij为训练集中第i类中第j个样本的隶属度;c为影响隶属度的模糊强度参数,c>1。
每个表示类中xj的隶属度计算如式(5)所示:
(5)
式中:nj表示属于第j类的邻居数。
幂均值也称为广义均值,是一系列均值的函数。如果x1,x2,…,xn为一组实数,z为一个参数(z∈R),则幂均值Mz可以定义为
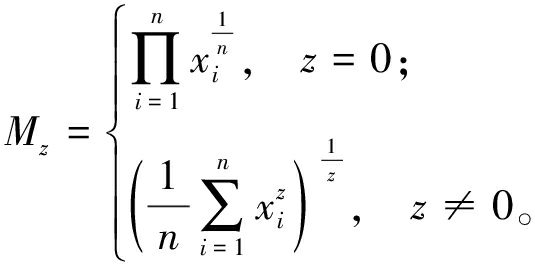
(6)
2.2 自适应采样策略
通常模型管理策略会选取少部分较优解进行有限次的真实评估,指导算法进化方向。对于SAEAs,模型管理策略是算法性能提升的关键之一。如何设计模型管理策略才能同时兼顾收敛性和多样性是值得探索的难点,这需要在选取收敛性和多样性较优解的同时,也要选取不确定性较大的解来提高代理模型的全局精度。
本文提出一种基于分类精度Accuracy评估的自适应采样策略,该策略利用模型精度划分3种度量状态,使用模糊隶属度对3种状态进行针对性设置。具体流程图如图1所示。

图1 自适应采样策略部分流程图
Figure 1 Partial flowchart of adaptive sampling strategy
将隶属度划分正负类。由于0.5在模糊隶属度中的特殊性,所以将隶属度u为0.5作为分类边界,将u≥0.5标记为正类,否则为负类。其中,在正类中u不接近0.5的解归类为不确定性较小的正解;相同地,在负类中u不接近0.5的解则归类为不确定性较小的负解。当u值接近0.5时,认为分类结果在类预测中具有较大不确定性的解。
(1)Accuracy≥75%为高精度状态。未评估的解根据隶属度值按降序排列,选取隶属度较大的解。
(2)35%≤Accuracy<75%为中精度状态。首先,正类根据隶属度值按升序排列,取隶属度接近0.5不确定性大的正解;其次,负类根据隶属度值按降序排列,取隶属度接近0.5不确定性大的负解;最后,正解与负解合并进行真实评估。其中,选取不确定性大的解是为了提高模型的准确性。
(3)Accuracy<35%为低精度状态。未评估的解随机排列,并不选取解。
在考虑划定状态的阈值时,经过大量试验证明35%与75%作为阈值是最合理的。算法在MaF1~MaF6测试集与WFG1~WFG9测试集上均独立运行20次,分别取平均值,平均精度如图2所示。由图2可知,模型优化开始时的精度较低,精度随着迭代次数的增加而提高。原因是早期训练数据集数量较小,无法反映解之间的真实关系,难以做出正确的预测。
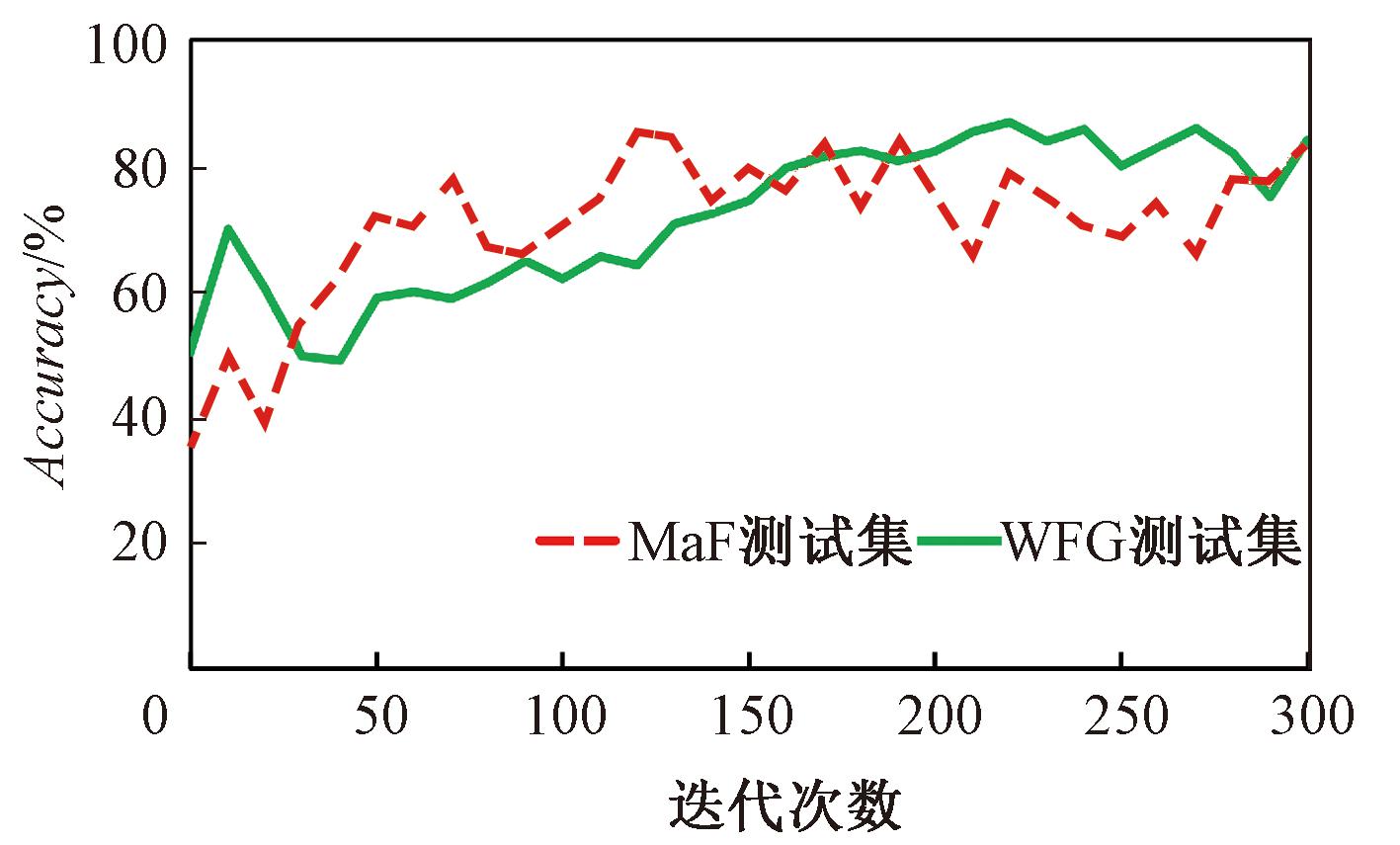
图2 在两种测试集上的分类器平均精度
Figure 2 Average classifier accuracy on two test sets
3 算法有效性实验
3.1 对比算法
(1)REMO[14]:一种基于关系模型辅助的多目标高代价演化算法,提出基于罚函数边界法的自适应种群划分策略和多目标关系模型下概率“投票-打分”策略。
(2)CPS-MOEA[12]:一种基于分类的代理辅助进化算法,使用两个归档集训练分类回归树,最后选择新的候选个体,保留正解。
(3)CSEA[13]:使用人工神经网络来预测支配关系,将不确定性与支配关系作为模型管理策略的关键。
(4)MCEA/D[15]:一种新的基于分类的SAEAs,构建基于SVM的分类器,利用多个局部分类器来规避问题的过拟合,通过模型管理策略增强预筛选能力。
3.2 MaF与WFG测试集
为了验证本文所提算法针对EMOPs的有效性,选用两个广泛应用的多目标优化问题测试集MaF和WFG。其中WFG测试问题的复杂程度更高,处理起来更具有挑战性,能够提供更有效的依据来评估优化算法在各种不同测试集上的表现性能。WFG测试集的属性包括可分性或不可分性、单峰或多峰、PF形状为凸或非凸、无偏差参数或有偏差参数。
3.3 参数设置
(1)所有算法参数设置:种群大小N=50,最大迭代次数为500。其中FCEA-ASS算法K=3,z=3,c=2,wmax=30。
(2)在MaF[18]与WFG[19]的测试集上,使用目标M为3、4、6、8,决策变量D为12、13、15、17的测试问题。利用以上测试函数来验证算法性能,如表1、表2所示。
表1 5种算法在MaF测试集上获得的IGD均值和标准差
Table 1 Average and standard deviation of IGD obtained by 5 algorithms on MaF test sets

测试集MDIGD均值(IGD标准差)REMOCPS-MOEACSEAMCEA/DFCEA-ASSMaF13121.586 8e-1 (1.07e-1)3.555 8e-1 (3.08e-2)1.334 0e-1 (1.40e-2)1.104 6e-1 (2.46e-2)1.345 7e-1 (2.90e-2)4132.106 2e-1 (3.48e-2)5.139 9e-1 (7.08e-2)2.115 8e-1 (2.61e-2)2.295 4e-1 (2.66e-2)2.056 7e-1 (3.20e-2)6153.646 5e-1 (6.63e-2)6.675 7e-1 (7.59e-2)3.139 0e-1 (5.48e-2)4.176 4e-1 (4.53e-2)3.093 2e-1 (6.45e-2)8174.839 4e-1 (7.64e-2)8.131 7e-1 (1.01e-1)4.653 1e-1 (5.38e-2)4.974 8e-1 (4.48e-2)4.638 1e-1 (5.83e-2)MaF23124.720 5e-2 (2.23e-3)1.071 4e-1 (5.26e-3)8.230 8e-2 (3.74e-3)4.117 3e-2 (2.57e-3)3.963 5e-2 (4.99e-3)4137.313 9e-2 (1.59e-3)1.740 7e-1 (4.10e-3)1.233 2e-1 (3.32e-3)8.365 3e-2 (3.76e-3)1.211 8e-1 (4.21e-3)6152.191 5e-1 (2.33e-2)2.582 5e-1 (1.63e-2)3.222 3e-1 (1.51e-2)2.235 1e-1 (2.52e-2)2.121 5e-1 (2.13e-2)8172.841 5e-1 (1.70e-2)3.611 8e-1 (2.31e-2)4.886 8e-1 (3.01e-2)2.945 4e-1 (2.56e-2)2.596 2e-1 (4.25e-2)MaF33128.235 1e+4 (6.28e+4)1.569 3e+5 (5.96e+4)2.200 6e+5 (2.76e+5)5.713 6e+4 (2.44e+4)5.687 3e+4 (4.77e+4)4131.237 7e+5 (9.99e+4)1.856 2e+5 (7.06e+4)3.628 4e+5 (4.20e+5)2.828 6e+4 (2.25e+4)1.139 1e+4 (2.35e+4)6151.986 0e+5 (1.69e+5)2.825 1e+5 (9.32e+4)6.275 3e+5 (3.26e+5)2.047 2e+4 (1.91e+4)1.464 9e+4 (5.00e+4)8172.990 6e+5 (3.26e+5)4.683 1e+5 (1.92e+5)5.836 3e+5 (3.47e+5)2.450 5e+4 (2.16e+4)1.573 5e+4 (5.89e+4)MaF43124.639 6e+2 (1.00e+2)2.883 4e+2 (4.82e+1)1.483 9e+2(3.79e+1)5.890 6e+2(2.61e+2)1.386 2e+2 (3.86e+1)4131.036 2e+3 (1.87e+2)3.877 4e+2 (6.89e+1)2.953 2e+2 (5.80e+1)7.537 6e+2 (5.17e+2)2.097 0e+2 (6.53e+1)6153.522 9e+3(5.26e+2)5.564 5e+2 (8.70e+1)2.459 6e+2(4.19e+1)2.926 4e+3 (2.40e+3)3.202 4e+2 (1.10e+2)8171.442 0e+4 (4.03e+3)7.426 0e+2 (1.16e+2)3.152 4e+2(7.64e+1)1.385 3e+4 (8.89e+3)4.422 8e+2 (1.18e+2)MaF53127.303 1e-1 (8.65e-2)6.216 0e-1 (5.32e-2)3.211 2e-1 (1.04e-1)3.157 2e+0 (1.71e+0)2.234 2e-1 (2.23e-1)4131.958 3e+0 (3.19e-1)7.269 0e-1 (4.17e-2)3.849 6e-1 (1.32e-1)6.076 1e+0 (3.06e+0)7.480 9e-1 (2.10e-1)6158.708 3e+0(1.98e+0)8.407 1e-1 (3.87e-2)4.874 7e-1 (6.81e-2)1.481 4e+1 (1.92e+0)8.196 3e-1 (8.81e-2)8173.231 3e+1 (4.55e+0)9.125 4e-1 (2.60e-2)6.194 0e-1 (4.69e-2)4.616 4e+1 (6.09e+0)5.766 3e-1 (9.88e-2)MaF63121.513 8e+0 (7.15e-1)2.022 6e+1 (5.95e+0)4.379 3e+0 (2.63e+0)5.446 9e-1 (1.94e-1)5.402 2e-1 (1.61e-1)4131.941 3e+0 (1.25e+0)2.251 2e+1 (7.40e+0)4.824 2e+0 (2.13e+0)4.554 5e-1 (1.06e-1)7.278 3e-1 (4.14e-1)6151.451 6e+0 (7.62e-1)2.216 2e+1 (6.64e+0)4.990 1e+0 (2.94e+0)4.539 1e-1 (1.31e-1)4.454 7e-1 (9.99e-1)8171.864 8e+0 (9.68e-1)3.096 3e+1 (1.00e+1)6.017 2e+0(1.92e+0)8.938 9e-1 (3.03e-1)7.174 2e+0 (7.26e+0)
表2 5种算法在WFG测试集上获得的IGD均值和标准差
Table 2 Average and standard deviation of IGD obtained by 5 algorithms on WFG test sets

测试集MDIGD均值(IGD标准差)REMOCPS-MOEACSEAMCEA/DFCEA-ASSWFG13121.508 7e+0(5.20e-2)8.501 4e-1(1.25e-2)5.972 6e-1(3.15e-2)2.024 7e+0(9.07e-2)7.364 7e-1(7.32e-2)4131.778 2e+0(7.56e-2)9.123 6e-1(1.57e-2)6.291 8e-1(3.22e-2)2.459 1e+0(6.90e-2)7.739 6e-1(5.30e-2)6152.221 0e+0(1.40e-1)9.335 5e-1(2.22e-2)6.851 5e-1(3.67e-2)2.672 5e+0(8.19e-2)6.291 5e-1(5.22e-2)8172.575 4e+0(1.24e-1)9.172 0e-1(1.86e-2)7.643 0e-1(4.87e-2)3.097 7e+0(9.17e-2)7.566 8e-1(2.94e-2)WFG23126.268 5e-1(1.78e-1)2.313 5e-1(1.59e-2)1.381 5e-1(1.68e-2)5.262 9e-1(5.73e-2)1.507 6e-1(2.01e-2)4137.516 0e-1(1.65e-1)2.622 8e-1(1.43e-2)1.660 6e-1(1.87e-2)8.462 8e-1(1.14e-1)1.501 7e-1(2.47e-2)6151.279 5e+0(4.19e-1)3.007 0e-1(2.21e-2)1.892 3e-1(2.33e-2)1.410 8e+0(2.70e-1)2.023 7e-1(2.30e-2)8171.877 6e+0(7.11e-1)3.170 2e-1(2.58e-2)2.658 2e-1(3.06e-2)2.312 4e+0(5.23e-1)2.454 8e-1(2.06e-2)WFG33124.375 5e-1(3.84e-2)2.817 2e-1(2.44e-2)2.125 0e-1(2.63e-2)4.502 3e-1(7.42e-2)2.060 0e-1(3.01e-2)4135.160 1e-1(6.29e-2)5.450 6e-1(4.92e-2)4.859 6e-1(7.32e-2)6.422 3e-1(8.92e-2)4.627 2e-1(6.80e-2)6157.353 4e-1(7.93e-2)2.384 3e+0(2.53e-1)1.468 3e+0(2.47e-1)7.607 7e-1(6.38e-2)2.272 2e+0(3.52e-2)8178.980 6e-1(1.48e-1)9.802e+0(1.62e+0)5.946 4e+0(1.43e+0)9.086 6e-1(7.88e-2)9.935 3e+0(1.27e+0)WFG43123.957 8e-1(2.59e-2)1.465 5e-1(5.14e-3)1.095 0e-1(7.41e-3)4.455 8e-1(4.56e-2)1.043 7e-1(8.90e-3)4137.405 7e-1(1.08e-1)2.231 2e-1(5.60e-3)1.861 6e-1(1.94e-2)9.947 2e-1(7.82e-2)1.675 3e-1(1.06e-2)6152.009 4e+0(2.09e-1)3.644 9e-1(1.07e-2)4.033 7e-1(2.94e-2)2.067 1e+0(8.54e-2)3.284 7e-1(2.41e-2)8174.787 6e+0(8.85e-1)4.943 9e-1(1.32e-2)5.941 5e-1(3.52e-2)3.595 3e+0(1.43e-1)4.826 6e-1(3.09e-2)WFG53124.335 9e-1(3.64e-2)1.525 3e-1(7.93e-3)1.243 0e-1(1.14e-2)3.657 1e-1(4.17e-2)1.143 3e-1(1.34e-2)4137.632 4e-1(2.44e-2)2.380 1e-1(8.82e-3)1.764 7e-1(1.16e-2)8.696 7e-1(7.18e-2)2.293 5e-1(8.11e-3)6151.852 8e+0(1.43e-1)3.799 5e-1(6.91e-3)3.504 0e-1(2.85e-2)2.097 1e+0(7.52e-2)3.448 1e-1(1.37e-2)8173.851 9e+0(2.79e-1)5.160 9e-1(1.09e-2)5.012 7e-1(1.28e-2)4.356 3e+0(2.75e-1)4.730 4e-1(1.46e-2)WFG63127.195 3e-1(3.62e-2)2.383 3e-1(7.20e-3)1.817 9e-1(1.53e-2)6.556 4e-1(9.13e-2)1.788 3e-1(1.26e-2)4139.757 6e-1(3.11e-2)3.161 3e-1(1.05e-2)2.455 3e-1(1.73e-2)1.208 3e+0(8.72e-2)2.442 7e-1(1.19e-2)6152.007 2e+0(9.41e-2)4.418 0e-1(1.32e-2)3.810 1e-1(2.20e-2)2.403 2e+0(1.49e-1)3.732 8e-1(2.25e-2)8173.799 3e+0(3.24e-1)5.653 0e-1(1.11e-2)5.293 9e-1(2.29e-2)4.573 4e+0(3.77e-1)1.154 2e-1(1.25e-2)WFG73125.356 9e-1(4.89e-2)1.786 2e-1(5.50e-3)1.495 4e-1(8.26e-3)4.797 0e-1(3.23e-2)1.353 7e-1(1.14e-2)4138.505 8e-1(8.36e-2)2.575 5e-1(6.01e-3)2.099 1e-1(1.25e-2)1.029 5e+0(1.15e-1)1.984 7e-1(9.29e-3)6151.911 3e+0(1.31e-1)4.031 0e-1(1.29e-2)3.885 9e-1(2.07e-2)2.390 0e+0(2.46e-1)3.421 9e-1(2.41e-2)8173.640 4e+0(3.05e-1)5.467 5e-1(1.85e-2)5.591 4e-1(2.74e-2)5.163 6e+0(5.43e-1)4.854 5e-1(1.67e-2)WFG83126.863 7e-1(4.00e-2)2.349 9e-1(9.25e-3)1.872 1e-1(9.20e-3)7.392 7e-1(7.15e-2)1.870 8e-1(1.08e-2)4131.090 7e+0(1.00e-1)3.308 7e-1(1.17e-2)2.828 9e-1(1.47e-2)1.326 2e+0(9.97e-2)2.709 1e-1(1.35e-2)6152.315 4e+0(1.35e-1)4.689 3e-1(9.46e-3)4.364 5e-1(1.66e-2)2.583 1e+0(2.85e-1)4.153 9e-1(1.42e-2)8174.465 6e+0(3.76e-1)6.000 1e-1(1.77e-2)5.792 e-1(1.73e-2)5.189 6e+0(6.56e-1)5.337 4e-1(1.61e-2)WFG93125.860 6e-1(7.63e-2)2.090 9e-1(1.26e-2)1.753 3e-1(2.51e-2)5.082 7e-1(8.22e-2)1.401 1e-1(1.89e-2)4139.846 4e-1(1.06e-1)3.005 2e-1(1.59e-2)2.637 1e-1(2.17e-2)1.020 1e+0(8.01e-2)2.282 7e-1(2.62e-2)6152.514 5e+0(3.68e-1)4.480 2e-1(1.30e-2)4.391 9e-1(2.23e-2)2.111 5e+0(1.05e-1)3.864 3e-1(1.65e-2)8174.453 7e+0(5.95e-1)5.965 1e-1(1.55e-2)5.843 1e-1(2.98e-2)4.146 0e+0(4.79e-1)5.177 8e-1(2.07e-2)
(3)为了保证公平性,参与实验的所有算法特定参数都严格遵循原始文献中的设置。所有仿真测试均在PlatEMO上进行。对于每个测试问题,每个算法独立执行20次,并使用反向世代距离IGD指标[20]进行综合评估,IGD值越小算法的综合性能越好。
3.4 算法有效性实验
表1为5种算法在MaF1~MaF6测试集上进行20次独立运行所获得的IGD的对比结果。由表1可以看出,FCEA-ASS算法在目标为3、4、6、8的共计24个MaF测试函数上,取得16个全局最优结果。其中FCEA-ASS算法在MaF3的各个维度上均取得了最佳结果,在MaF1和MaF3上优势最大,说明算法针对解决具有反转PF和凹型PF多模态特征问题时具有优势。
FCEA-ASS算法在求解MaF2、MaF4、MaF5、MaF6时,在每个测试集上只获得了两组最优结果,MCEA/D和CSEA算法则几乎占据了剩余维度测试问题的优势。FCEA-ASS对于具有偏好特征的问题求解效率不高,因为采用简单的帕累托支配关系筛选样本的方式优势不大,同时不能快速定位偏好区域,从而在这类问题上表现一般。
表2为5种算法在WFG1~WFG9测试集上进行20次独立运行所获得的IGD的对比结果。从表2可以看出,在测试集WFG中,算法FCEA-ASS在目标为3、4、6、8的共计36个WFG测试函数上,取得29个全局最优结果。其中FCEA-ASS在WFG4、WFG6、WFG7、WFG8、WFG9的各个维度上均取得了最佳结果。对于WFG1、WFG2和WFG3测试问题,FCEA-ASS算法仅取得6组最佳结果,CESA算法排第2位。尤其对于3和4目标的WFG1测试函数,FCEA-ASS略逊于CSEA,原因是CSEA预定义的参考向量可以帮助快速定位区域,而FCEA-ASS靠非支配关系还是很难准确定位大致前沿区域。
图3可视化了5个算法在3目标MaF2上的解集分布图。从图3可以看出,FCEA-ASS是收敛性和分布性最好的算法,该算法采用基于转移的密度估计策略,提高了选择压力,有效兼顾多样性与收敛性,并配合自适应采样策略正确引导了算法的进化方向。图4可视化了5个算法在3目标MaF4和6目标MaF5上IGD的变化趋势。从图4可以看出,只有算法FCEA-ASS的IGD最小。综上所述,能够证明该算法具有较强的优势,是所有算法中取得最佳结果次数最多的算法。
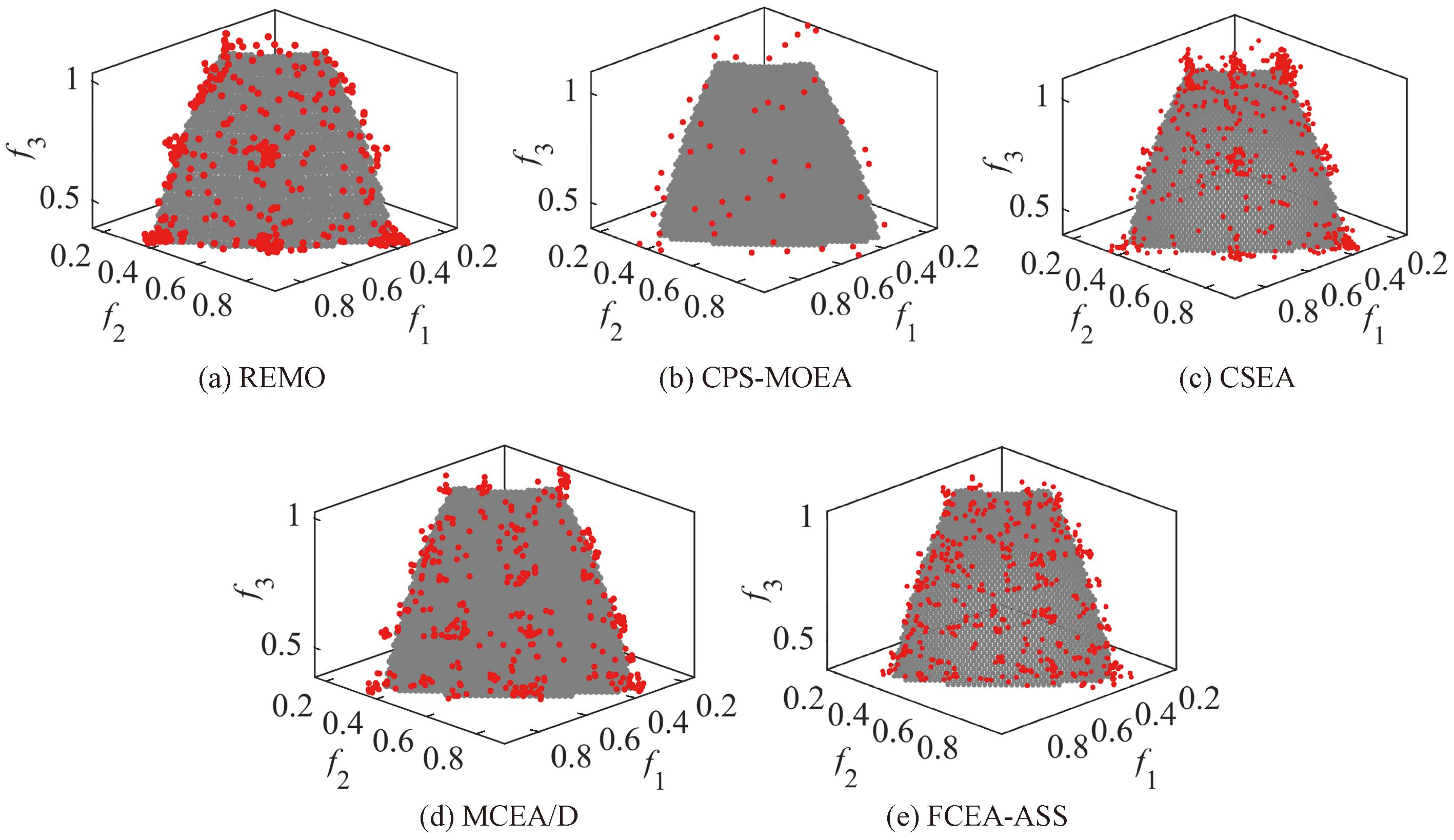
图3 5种算法在MaF2上的解集分布图
Figure 3 Distribution map of solution set for five algorithms on test function MaF2

图4 5种算法在求解MaF4和MaF5时IGD的变化
Figure 4 Variation of IGD in solving for MaF4 and MaF5 by five algorithms
WFG2问题的帕累托前沿(Pareto front,PF)是不连续的。WFG3是一个退化问题,算法在这类测试问题上表现一般,WFG4与WFG9为两类多模态问题,FCEA-ASS取得了较优的表现,这说明自适应采样策略能够提高算法的运行效率,使得算法的局部搜索能力增强。图5可视化了5种算法在3目标WFG3和8目标WFG8上IGD的变化趋势,能够明显看出FCEA-ASS的IGD为最佳。所提算法使用模糊分类器作为代理模型,采用基于转移的密度估计策略兼顾收敛性与多样性,设计自适应采样策略能够提高算法的整体性能。结合算法在两种测试集上的表现,都证明了所提算法在求解昂贵多目标优化问题时,具备较强的竞争力。
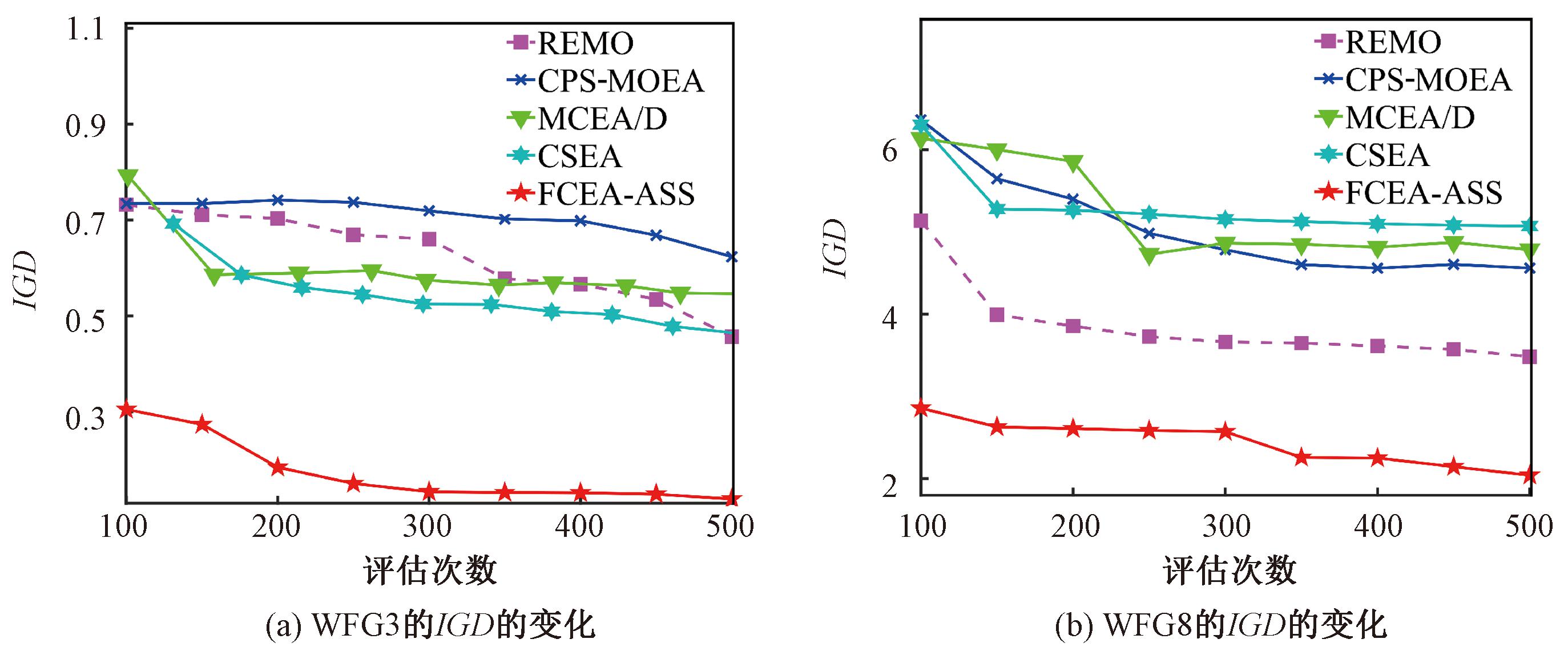
图5 5种算法在求解WFG3和WFG8时IGD的变化
Figure 5 Variation of IGD when solving WFG3 and WFG8 by five algorithms
3.5 算法时间复杂度对比分析
对算法的运行效率进行进一步分析,图6记录了5种不同算法单独运行20次求解MaF和WFG系列测试问题的平均耗时。从图6可以看出,FCEA-ASS算法比REMO和CSEA的运行时间短,但比CPS-MOEA算法运行时间长,FCEA-ASS与MCEA/D算法平均运行时间相似。但综合考虑FCEA-ASS算法在MaF、WFG测试集上均能够获得更好的优化结果,耗时都在20 s之内是可以接受的,且所提算法对于不同类型的问题的求解时间不会随着问题类型的变化而变化。综上所述,本文提出的FCEA-ASS算法时间复杂度低,具有良好、稳定的求解性能和较高的算法运行效率。

图6 5种算法在求解MaF和WFG时运行耗时
Figure 6 Running time for solving MaF and WFG by five algorithms
3.6 策略有效性分析
将MLPM-FKNN作为代理辅助模型,使用传统的模型管理策略求解问题,将其算法命名为FCEA。且FCEA算法与FCEA-ASS算法进行了对比实验,比较结果如表3所示。表3提供了两种算法在求解M=8、D=17时15个测试集的IGD均值和标准差。从表3可以看出所提FCEA-ASS算法的优势,证明了所提算法的竞争力。
表3 两种算法在15个测试集上获得的IGD均值和标准差
Table 3 Average and standard deviation of IGD obtained by two algorithms on 15 test sets

测试集IGD均值(IGD标准差)FCEAFCEA-ASSMaF15.114 6e-1 (7.10e-2)4.638 1e-1 (5.83e-2)MaF24.632 0e-1 (7.40e-2)2.596 2e-1 (4.25e-2)MaF32.689 0e+6 (8.76e+6)1.573 5e+4(5.89e+4)MaF45.342 3e+2 (1.50e+2)4.422 8e+2 (1.18e+2)MaF59.132 4e-1 (8.29e-2)5.766 3e-1 (9.88e-2)MaF61.537 5e+1 (9.81e+0)7.174 2e+0 (7.26e+0)WFG18.848 4e-1 (4.88e-2)7.566 8e-1 (2.94e-2)WFG22.872 4e-1 (4.60e-2)2.454 8e-1 (2.06e-2)WFG36.588 8e+0 (1.42e+0)9.935 3e+0 (1.27e+0)WFG46.537 8e-1 (3.29e-2)4.826 6e-1 (3.09e-2)WFG55.616 6e-1 (2.46e-2)4.730 4e-1 (1.46e-2)WFG65.720 6e-1 (2.85e-2)1.154 2e-1 (1.25e-2)WFG75.786 2e-1 (3.81e-2)4.854 5e-1 (1.67e-2)WFG86.103 3e-1 (3.01e-2)5.337 4e-1 (1.61e-2)WFG96.003 8e-1 (2.97e-2)5.177 8e-1 (2.07e-2)
3.7 实际工程优化测试
为了验证FCEA-ASS算法在实际问题中的有效性,本节在汽车侧面碰撞设计和驾驶室设计[21]案例上进行了仿真实验,并与多个经典算法进行了对比。汽车侧面碰撞设计问题为4个目标和7个决策变量。涉及最小化汽车重量、平均速度下司机所受到的冲击载荷等目标。同时驾驶室设计问题涉及9个目标和7个决策变量。包括汽车空间、燃油经济性、加速时间及不同速度下的道路噪声等。5种算法进行20次重复实验,单次500次评估后得到的IGD均值如表4所示,通过实验结果证明算法FCEA-ASS具备一定的竞争力和优势。
表4 5种算法在实际问题上的IGD均值
Table 4 The average IGD value of five algorithms in practical problems

算法IGD均值汽车侧面碰撞设计驾驶室设计REMO7.352 6e-16.148 2e+0CPS-MOEA1.125 3e+01.054 9e+1CSEA1.501 2e+08.827 3e+0MCEA/D4.921 4e-17.042 9e+0FCEA-ASS1.212 6e-12.724 9e-1
4 结论
本文提出一种自适应采样策略的模糊分类代理辅助进化算法FCEA-ASS。首先,该算法使用多局部幂均值模糊K最近邻分类器作为代理模型,利用精度信息进行模型管理,降低时间复杂度的同时保证了采样的准确度;其次,采用基于转移的密度估计策略,兼顾收敛性与多样性;最后,自适应采样策略依据隶属度标签和分类精度,针对不同状态的分类器,采取有针对性的采样策略。经过数值仿真分析表明,所提算法具有一定的竞争力,特别是在处理具有退化特征和多模态特征问题具有明显优势,在解决EMOPs上具有广阔的应用前景,同时还具有实际工程应用价值。
在未来的工作中,将算法FCEA-ASS扩展到解决具有高维约束的复杂多目标优化问题中,继续探索更有效的模型管理策略,尝试解决更多的昂贵现实问题,发挥实际应用价值。
[1] 郑金华. 多目标进化算法及其应用[M]. 北京: 科学出版社, 2007.ZHENG J H. Multi objective evolutionary algorithm and its applications [M]. Beijing: Science Press, 2007.
[2] FAN X Z, LI K, TAN K C. Surrogate assisted evolutionary algorithm based on transfer learning for dynamic expensive multi-objective optimisation problems[C]∥2020 IEEE Congress on Evolutionary Computation (CEC). Piscataway:IEEE, 2020: 1-8.
[3] 邓传义, 孙超利, 刘晓彤, 等. 惯性分组和重叠特征选择辅助的昂贵大规模优化算法[J]. 郑州大学学报(工学版), 2023, 44(5): 32-39.DENG C Y, SUN C L, LIU X T, et al. An inertial grouping and overlapping feature selection assisted algorithm for expensive large-scale optimization problems[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(5): 32-39.
[4] WANG R Y, ZHOU Y E, CHEN H N, et al. A surrogate-assisted many-objective evolutionary algorithm using multi-classification and coevolution for expensive optimization problems[J]. IEEE Access, 2021, 9: 159160-159174.
[5] 温文吉. 克里金代理模型和多目标优化算法在天线设计中的应用[D]. 镇江: 江苏科技大学, 2020.WEN W J. Application of Kriging proxy model and multi-objective optimization algorithm in antenna design[D]. Zhenjiang: Jiangsu University of Science and Technology, 2020.
[6] 郭单. 数据与模型驱动的复杂工业过程智能优化方法及应用研究[D]. 沈阳: 东北大学, 2019. GUO D. Research on intelligent optimization method and application of complex industrial process driven by data and model[D]. Shenyang: Northeastern University, 2019.
[7] DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part Ⅰ: solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601.
[8] GU Q H, WANG Q, LI X X, et al. A surrogate-assisted multi-objective particle swarm optimization of expensive constrained combinatorial optimization problems[J]. Knowledge-Based Systems, 2021, 223: 107049.
[9] CHUGH T, JIN Y C, MIETTINEN K, et al. A surrogate-assisted reference vector guided evolutionary algorithm for computationally expensive many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 129-142.
[10] SONG Z S, WANG H D, HE C, et al. A Kriging-assisted two-archive evolutionary algorithm for expensive many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(6): 1013-1027.
[11] KELLER J M, GRAY M R, GIVENS J A. A fuzzy K-nearest neighbor algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1985, SMC-15(4): 580-585.
[12] ZHANG J Y, ZHOU A M, ZHANG G X. A classification and Pareto domination based multiobjective evolutionary algorithm[C]∥2015 IEEE Congress on Evolutionary Computation (CEC). Piscataway: IEEE, 2015: 2883-2890.
[13] PAN L Q, HE C, TIAN Y, et al. A classification-based surrogate-assisted evolutionary algorithm for expensive many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2019, 23(1): 74-88.
[14] HAO H, ZHOU A M, QIAN H, et al. Expensive multiobjective optimization by relation learning and prediction[J]. IEEE Transactions on Evolutionary Computation, 2022, 26(5): 1157-1170.
[15] SONODA T, NAKATA M. Multiple classifiers-assisted evolutionary algorithm based on decomposition for high-dimensional multiobjective problems[J]. IEEE Transactions on Evolutionary Computation, 2022, 26(6): 1581-1595.
[16] LI M Q, YANG S X, LIU X H. Shift-based density estimation for Pareto-based algorithms in many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 348-365.
[17] KUMBURE M M, LUUKKA P, COLLAN M. An enhancement of fuzzy K-nearest neighbor classifier using multi-local power means[C]∥Proceedings of the 2019 Conference of the International Fuzzy Systems Association and the European Society for Fuzzy Logic and Technology (EUSFLAT 2019). Paris: Atlantis Press, 2019: 83-90.
[18] CHENG R, LI M Q, TIAN Y, et al. A benchmark test suite for evolutionary many-objective optimization[J]. Complex &Intelligent Systems, 2017, 3(1): 67-81.
[19] HUBAND S, HINGSTON P, BARONE L, et al. A review of multiobjective test problems and a scalable test problem toolkit[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(5): 477-506.
[20] ISHIBUCHI H, MASUDA H, TANIGAKI Y, et al. Modified distance calculation in generational distance and inverted generational distance[C]∥The 8th International Conference of Evolutionary Multi-criterion Optimization. Cham: Springer, 2015: 110-125.
[21] TANABE R, ISHIBUCHI H. An easy-to-use real-world multi-objective optimization problem suite[J]. Applied Soft Computing, 2020, 89: 106078.