随着我国国民经济的持续高速发展,城市的区域集群化趋势日益明显,城市区域的交通网络更加密集,但同时,交通基础设施的运营对周边环境的影响也逐渐显现,其中最引人关注的就是交通噪声导致沿线区域声环境质量的下降[1-3]。声屏障是设置在噪声源和保护区域之间的声学障板,可以衰减声音的传播,减少后侧保护区域的声污染,起到隔声降噪作用[4-6]。由于地铁引起的噪声具有中低频特性,使得现有声屏障降噪效果不够理想,因此有必要研究地铁出入线声屏障降噪效果的影响因素,选取合适的声屏障结构参数。
近年来,众多相关研究人员和工程技术人员借助数值模拟和现场实测等手段,对轨道交通领域的声屏障降噪效果进行了研究。王朝亮等[7]基于有限元法、边界元法和统计能量分析建立轮轨噪声数值预测模型,对比了新型近轨低矮声屏障和传统直立式声屏障的降噪效果;毛伟等[8]通过数值模拟,分析了轨道交通内折式声屏障辐射噪声传播规律;丁亚超[9]考虑荷载、限界、与既有桥面系连接和声屏障单元板声学性能、结构安全等因素,提出了近轨声屏障+道床吸声组合设计方案;臧传臻等[10]基于边界元理论,建立了考虑列车、声屏障、轨道的半自由场模型,确定了次级源最合理位置、消声频段、消声区界线、消声量;吴小萍等[11]建立了高速列车-声屏障流体动力学和有限元仿真模型,从列车速度、声屏障-列车距离和声屏障折板角度等研究了Y型声屏障的动态响应特性;宋立忠等[12]以某城市轨道交通高架低矮弧形声屏障为研究对象,开展了列车通过时的噪声测试;Song等[13]实测了城市轨道交通U梁直立式声屏障的降噪效果,结果表明,直立式声屏障对高频轮轨噪声具有良好的降噪效果,但对低频结构噪声降噪效果不佳;Zhang等[14]实测了高速铁路桥上半封闭声屏障的降噪效果,结果表明,半封闭声屏障比3.15 m高直立式声屏障的降噪效果提高约6 dB;He等[15]实测了城市轨道交通全封闭声屏障的降噪效果,结果表明,在距离轨道中心线7.5 m、高于轨面1.5 m处的插入损失约20.8 dB。盛峰等[16]采用传递矩阵法对高铁声屏障的多层微穿孔结构的吸声进行计算,对于给定空腔深度,适当增加具有不同声阻抗的微穿孔板可改善吸声性能。
声屏障作为常用的交通噪声控制手段,在公路、高铁和城市高架桥等领域已得到广泛应用,但截至目前,鲜有针对地铁出入线的中低频噪声开展反射型声屏障的研究探讨。本文以郑州某线路的地铁出入线为工程实例,采用Virtual Lab声学仿真软件构建了声屏障模型,分析了声源声压级、声屏障高度、声屏障与声源距离、声屏障顶端结构、受声点位置等因素对反射型声屏障降噪效果的影响,根据数值模拟分析结果,在地铁出入线靠近居民建筑一侧设置了高4 m、与双声源中心距离3 m的直立Y型反射声屏障,获得了比较理想的降噪效果,为类似工程的声屏障选型与设计提供了一定的参考依据。
1 声屏障降噪数值模型
1.1 声屏障降噪原理
郑州地铁某线路自投入运行以来,收到附近居民源源不断的投诉,为降低地铁列车运行引起的噪声污染,需要设置声屏障进行降噪处理,声屏障的降噪原理示意图如图1所示[17]。
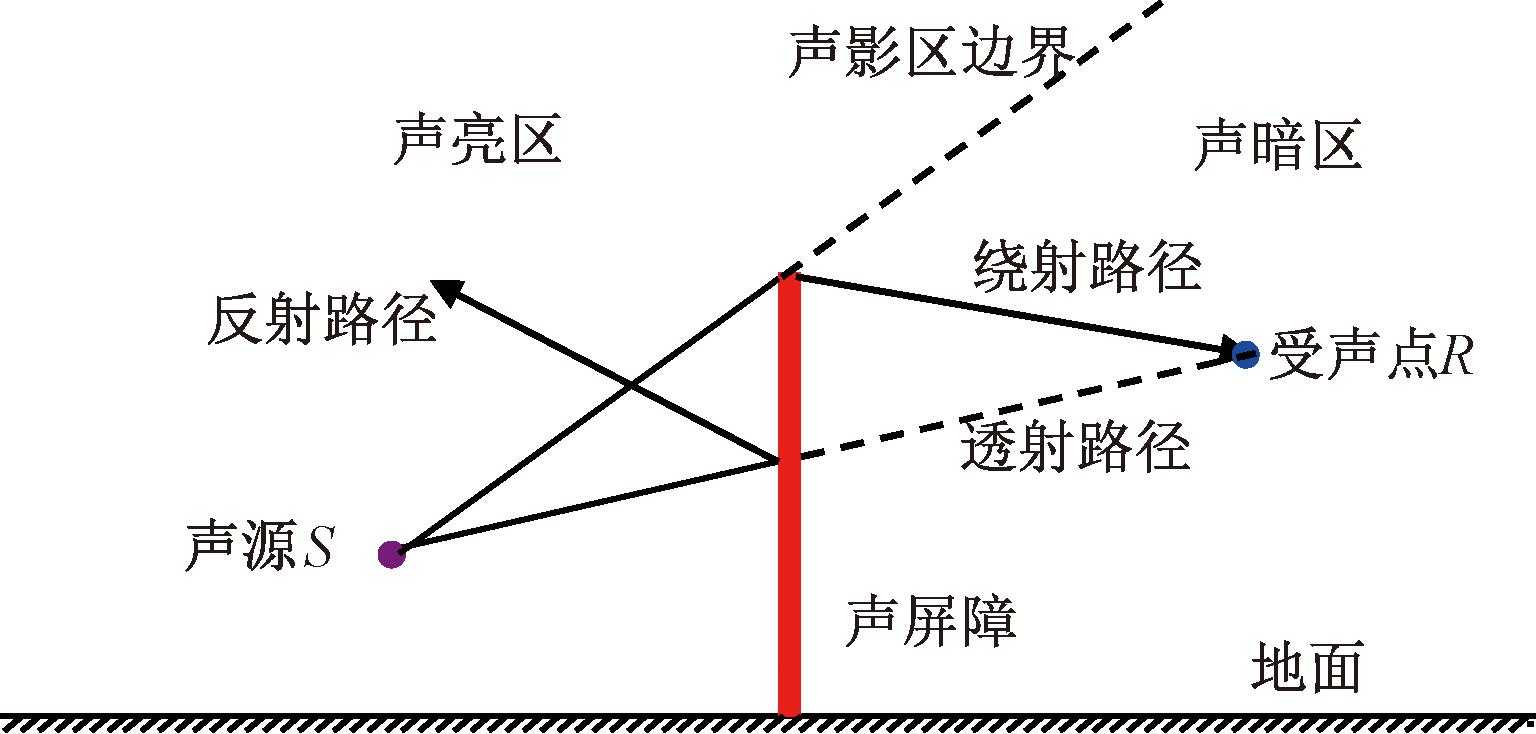
图1 声屏障降噪原理
Figure 1 Sound barrier and noise reduction principle
根据惠更斯-菲涅尔波动理论,声源发射出带有能量的声波,遇到声屏障后,会出现4条不同传播路径:接触到声屏障发生反射、穿透声屏障到达受声点、绕过声屏障顶端到达受声点和继续沿声屏障顶端直线传播,其中,声屏障反射能够阻断声波直接传到受声点,在声暗区中,声波会显著衰减。
1.2 声屏障数值模型
与列车高速通过隧道或者在隧道内交会时产生的应力波引起的噪声不同[18],地铁列车在出入线的运行速度较低,噪声主要以轮轨噪声为主[19]。在数值模拟时将其等效为双点声源,彼此间距1.435 m,地铁列车的整体辗钢车轮的直径为0.84 m,地铁出入线的轨面与空旷区域的地面基本持平,声源设置在靠近车轮中心位置处,高于地面0.5 m。声源、声屏障和测点布置横断面如图2所示。
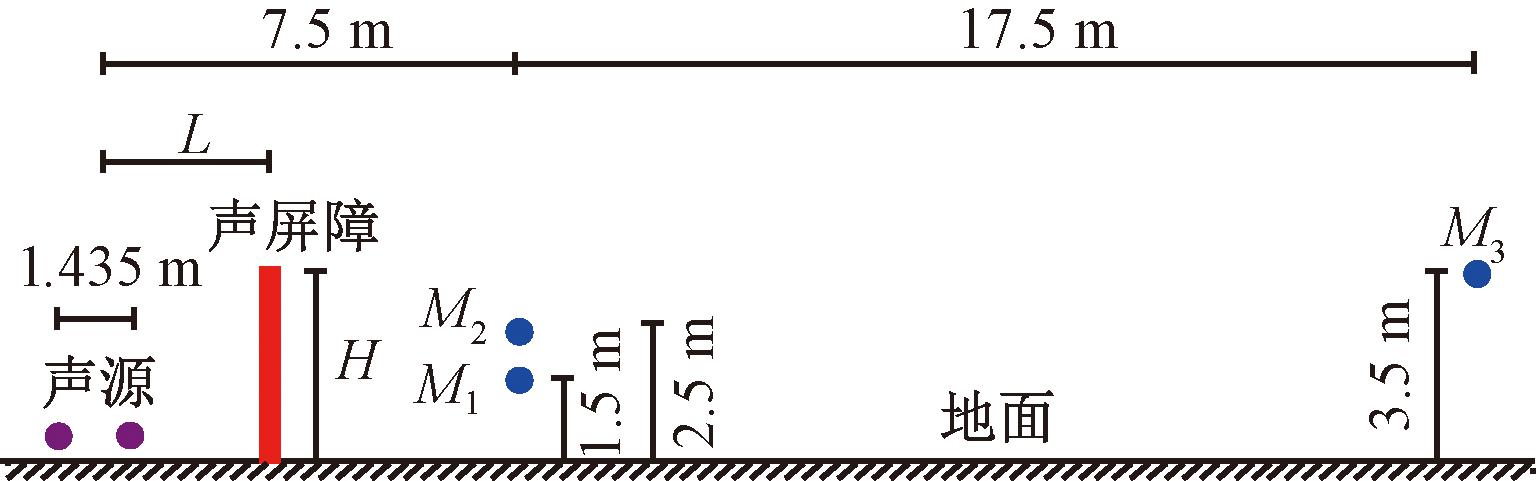
图2 声源、声屏障和测点布置横断面
Figure 2 Cross section layout of sound source, sound barrier and measuring points
声屏障的高度为H,与双声源中心的距离为L。结合HJ 453—2018《环境影响评价技术导则 城市轨道交通》[20],在声暗区内设置3个测点(受声点):测点M1和M2距轨道中心线7.5 m,分别高于地面1.5 m和2.5 m,代表地铁出入线近场噪声的特性,主要用于分析声源声压级、声屏障高度、声屏障与声源距离、声屏障顶端结构、受声点位置等因素对声屏障降噪效果的影响;测点M3距离轨道中心线25 m,高于地面3.5 m,代表远场噪声的特性,主要用于评估声屏障设置后的降噪效果。
边界元法通常用于模拟外部声场或半封闭声场,无须离散整个求解区域,仅拾取模型表面的网格就可进行声学响应计算,降低了求解的维度,缩短了计算时间,且累计误差较小,针对本文的研究环境,选择更为高效的声学边界元法进行仿真计算。
间接边界元所计算的对象是网格两侧的声场,相较于直接边界元,只需要确定网格两侧的速度差值σ和声压差值μ,或者记作单层势(single layer potential)和双层势(double layer potential),其间接边界元分别为Ωσ=Ωp和Ωμ=ΩV+Z,单元格内部的σ与μ可用边界元每个节点的单层势σi和双层势μi与全局的形函数Nσi和Nμi确定:
σ(ra)=∑Nσi(ra)σi=Nσ{σi},ra∈Ωσ;
(1)
μ(ra)=∑Nμi(ra)μi=Nμ{μi},ra∈Ωμ。
(2)
每个节点的σi和μi可由下式确定:
(3)
系数矩阵B、C和D的元素Bij、Cij、Dij表达式如下:
Bij=∬ΩσNσi(r)Nσj(ra)G(r,ra)dΩσ(r)dΩσ(ra);
(4)
(5)
(6)
系数向量fσ和fμ的元素如下:
(7)
(8)
得到间接边界元网格上单层势σ和双层势μ后,通过计算可确定声场V中任意一点的声压P(r),计算公式如下:
P(r)=[Aσi]T[σi]+[Aμi]T[μi],r∈V 且
r∈Ωa;
(9)
![]() 且
且
r∉Ωa;
(10)
r∈V 且 r∈Ωa。
(11)
基于快速多极边界元方法,采用Virtual Lab声学仿真软件,构建直立型声屏障模型,并采取以下基本假定:空气为理想状态下的气体,噪声传播速度340 m/s、空气密度1.225 kg/m3;背景噪声与地铁列车噪声的声压级差值在10 dB以上,即可等效为只存在地铁列车发出的噪声,其他背景噪声可忽略;因地面的阻抗值非常大,在声学仿真时不考虑地面吸音作用,设置Symmetry Plane障板模拟刚性全反射地面;在不考虑声屏障吸声材料吸声效果时,默认声屏障板为刚性全反射,以便分析声屏障结构与尺寸对降噪效果的影响。
在声学仿真模拟时,模型的精度受多数单元控制,因此仅放大研究区域无法提高计算精度。为了确保声学模拟的准确性,单元网格的最大边长应小于声波最小波长的1/6[21](即最大频率下的波长的1/6),地铁出入线轮轨噪声声源以中低频率为主,取20~1 000 Hz[19],经计算,单元网格的最大边长应小于56.67 mm,在满足计算精度要求的同时,还需考虑计算时间的限制,因此,设置网格尺寸为50 mm。取声屏障长40 m、厚0.1 m,声屏障的网格划分如图3所示。

图3 声屏障网格划分
Figure 3 Division of sound barrier grid
根据图2,在图3所示的声屏障的中心横截面设置地铁出入线的双声源,为研究声屏障后方不同位置处的声场分布情况,在声暗区插入高30 m、宽40 m的面场点栅格,声屏障降噪过程的整体模型如图4所示。
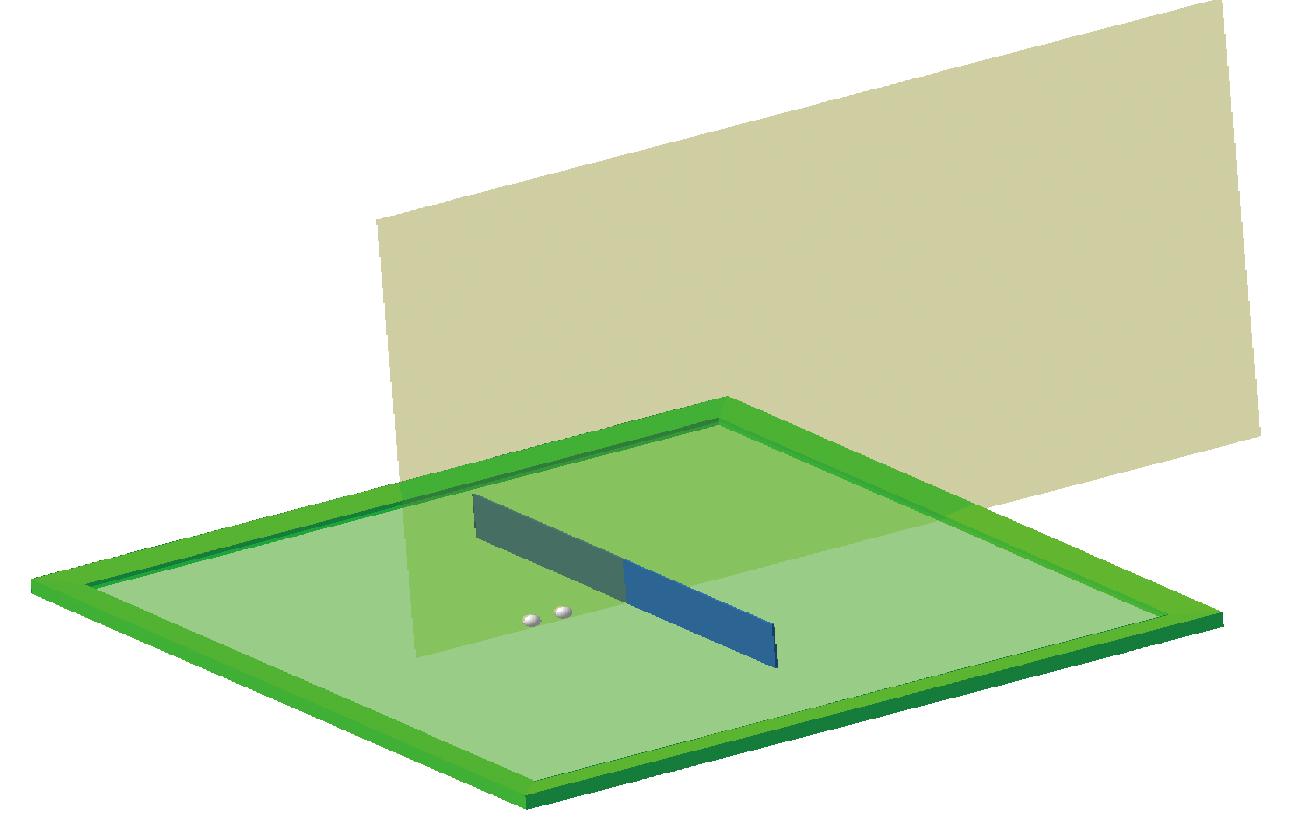
图4 声屏障仿真模型
Figure 4 Sound barrier simulation model
2 声屏障的降噪效果影响因素分析
引入插入损失评估声屏障降噪效果,插入损失是指在声源幅值及其他环境因素未改变的情况下,同一位置处的设置声屏障前后的两个声压级之间的差值,通常采用符号IL来表示:
IL=(Lref,a-Lref,b)-(Lr,a-Lr,b)。
(12)
式中:Lref,a和Lref,b为声屏障设置前后参考点位置处声压级,dB;Lr,a和Lr,b为声屏障设置前后受声点处声压级,dB。在声学仿真时,由于参考点处前后声压级保持不变,即Lref,a-Lref,b=0,因此,受声点处插入损失即为设置声屏障前后声场声压级的差值,上述插入损失计算公式可简化为
IL=Lr,b-Lr,a。
(13)
在仿真模拟时,首先,建立无声屏障声场模型,由双点声源和全反射地面组成,确定无声屏障声场中不同位置的声压级分布;其次,对不同位置、高度、吸声系数、顶端结构的声屏障进行声学仿真模拟,获得有声屏障声场声波的传播规律与各点声压级分布;最后,根据式(12)可确定声屏障的降噪效果。
2.1 声源声压级对降噪效果的影响
声屏障设置为反射直立型,双点声源中心与场屏障的距离(简称声源距离)取3 m,声屏障高度取3.5 m,双点声源的声压级分别取80,100,120和140 dB,频率取20~1 000 Hz。以测点M1为例,绘制了不同声压级声源作用下的声压级和插入损失随声源频率的变化曲线,分别如图5和图6所示。
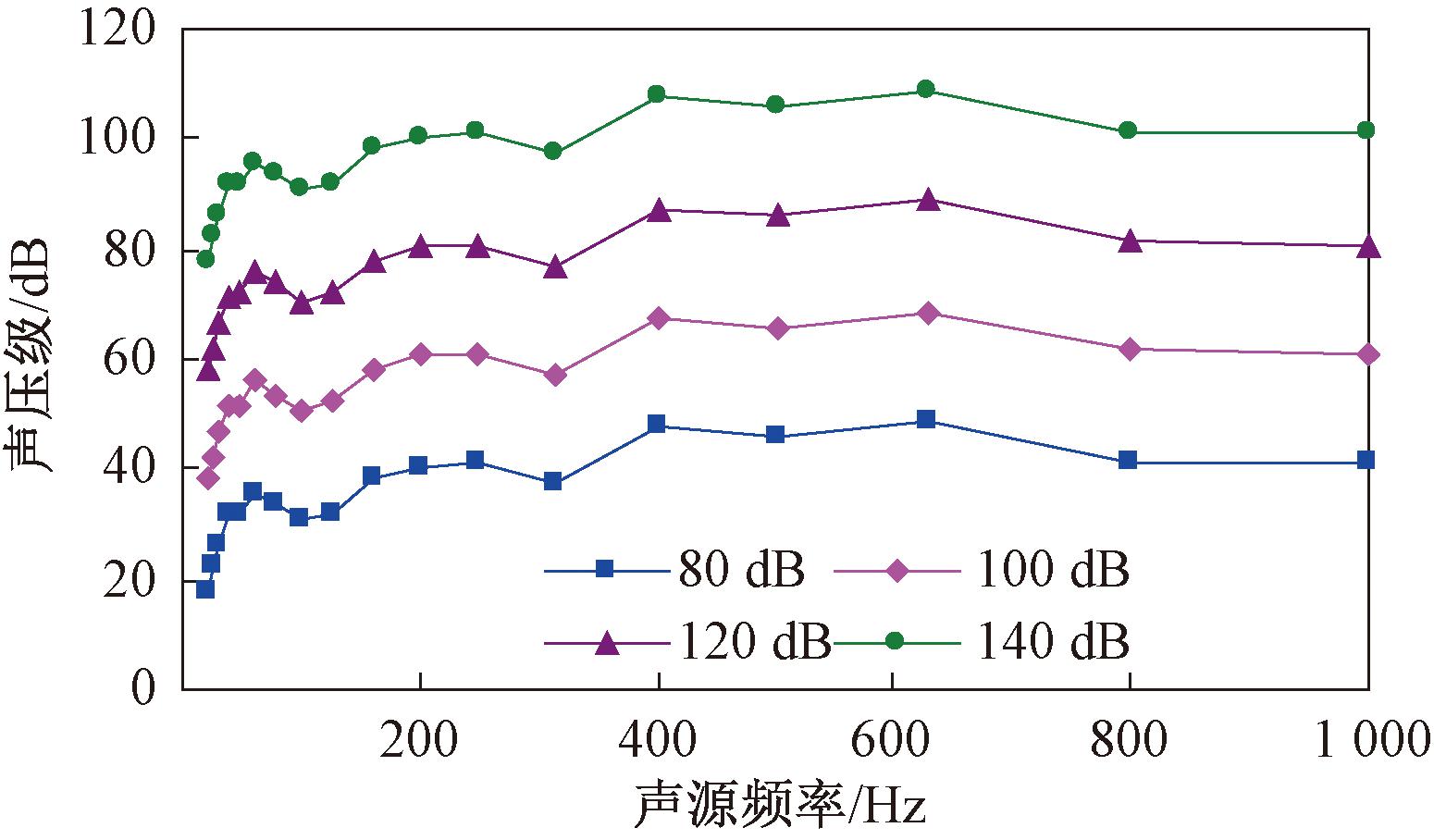
图5 不同声压级声源的声压级随声源频率的变化曲线
Figure 5 Curves of sound pressure level with different sound source pressure level changing with sound source frequency
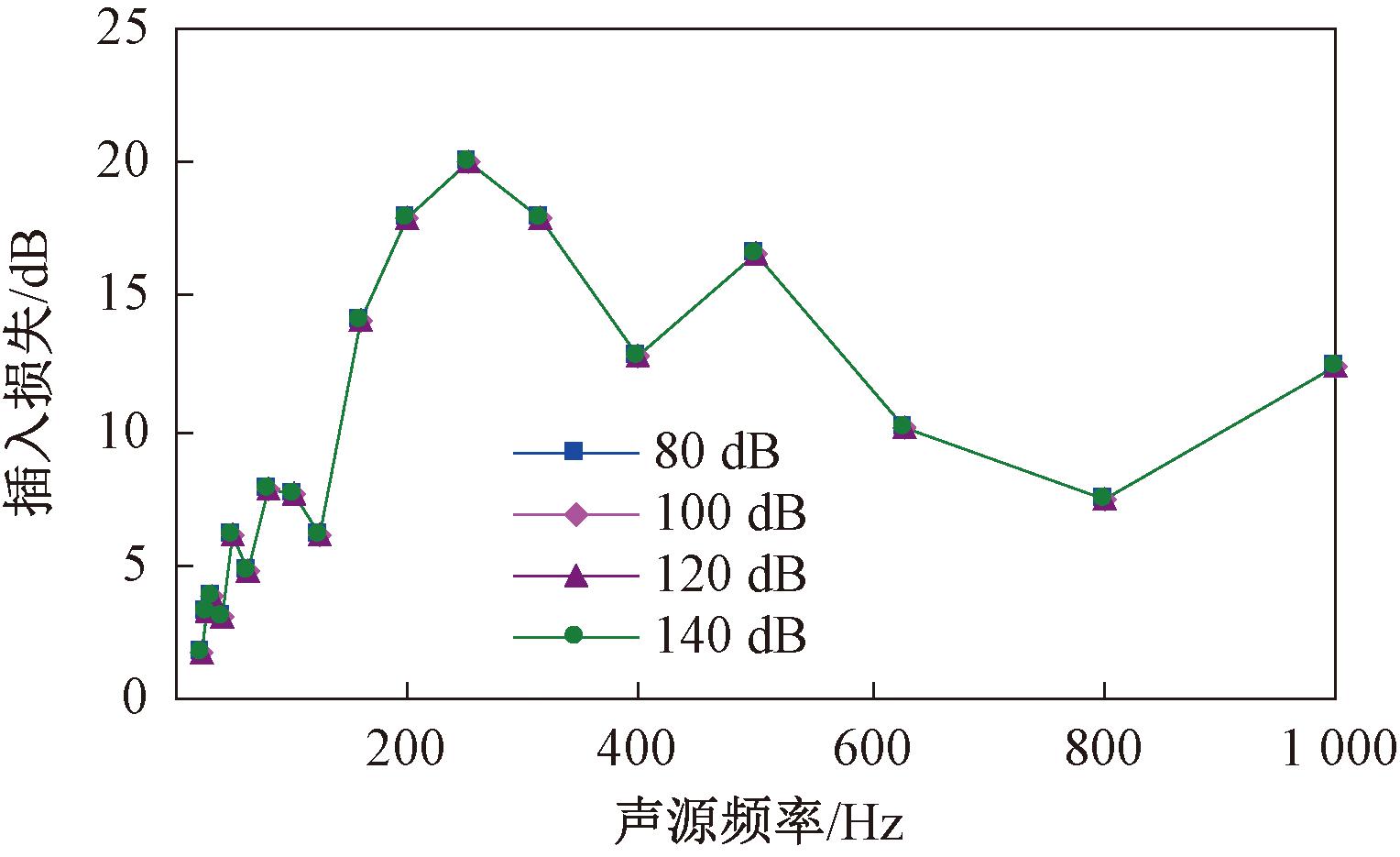
图6 不同声压级声源的插入损失随声源频率的变化曲线
Figure 6 Curves of insertion loss with different sound source pressure level changing with sound source frequency
从图5和图6可以看出,随着声源声压级的提升,测点M1的声压级曲线呈平行上升的变化趋势,而不同声源声压级下测点M1各频段插入损失则保持不变,主要是因为声源声压级的变化仅引起声场中各个位置的声压级大小变化,而无声屏障声场和有声屏障声场每个位置的声压级差值不发生改变,因此,声源声压级不影响降噪效果。而声源频率对降噪效果影响较大,在250 Hz附近的降噪效果最好,可降噪20.09 dB。
2.2 声源距离和声屏障高度对降噪效果的影响
声屏障设置为反射直立型,声源距离分别取3,4,5和6 m,双点声源的声压级和频率分别取100 dB和250 Hz,以测点M1为例,绘制了不同声源距离的插入损失随屏障高度的变化曲线,如图7所示。
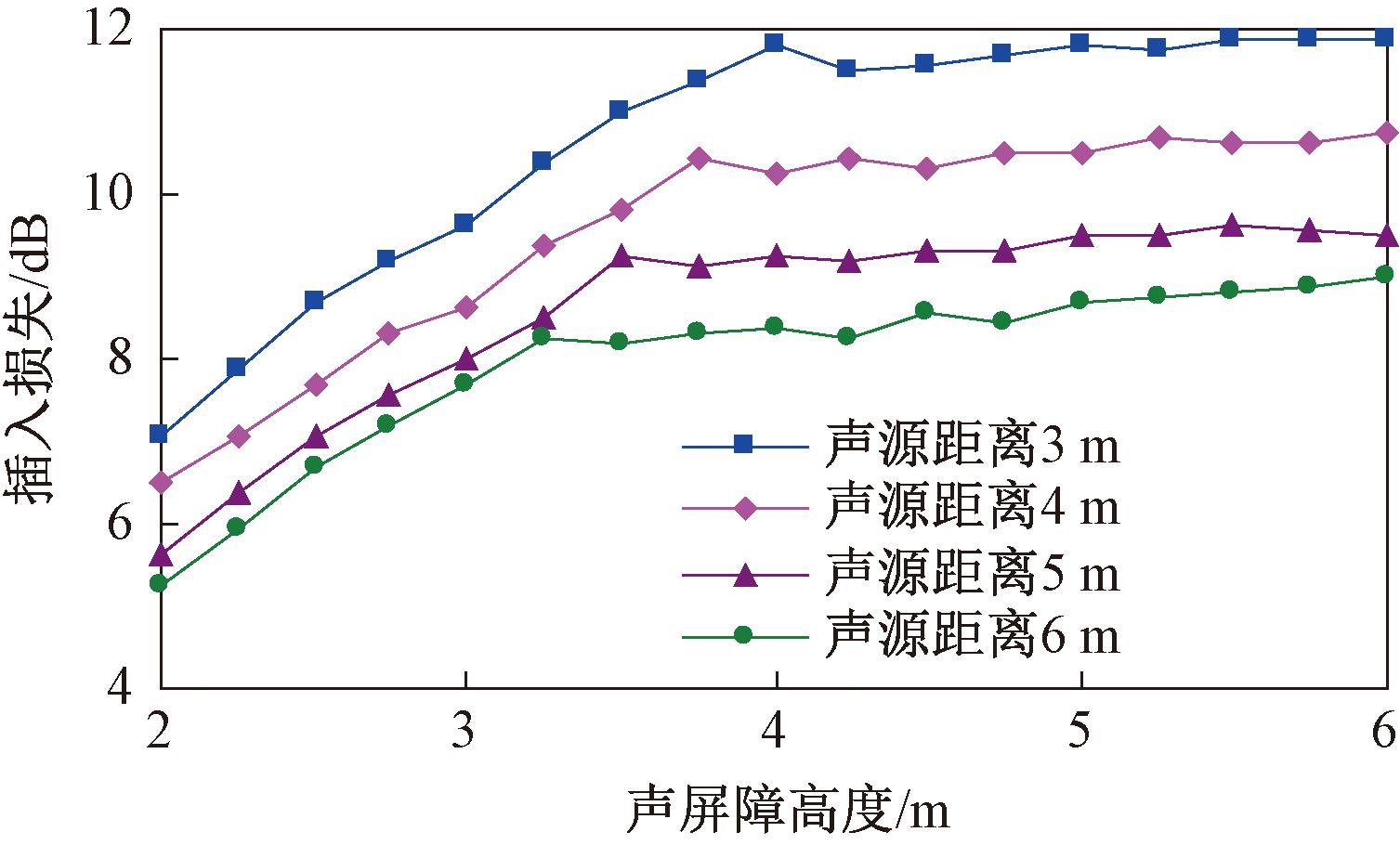
图7 不同声源距离的插入损失随声屏障高度的变化曲线
Figure 7 Curves of insertion loss with different sound source distance changing with sound barrier height
从图7可以看出,测点M1的插入损失随着声源距离的减小而增大,声屏障越靠近声源,声暗区的区域越大,声波越容易被声屏障遮挡;随着屏障高度的增大,插入损失均呈先增大、后趋于稳定的变化趋势,声源距离3,4,5和6 m对应的声屏障高度拐点分别为4.00,3.75,3.50和3.25 m,在声屏障设计时,应充分考虑降噪效果和工程成本,高度超过高度拐点后,声屏障的遮挡作用达到极限。
2.3 顶端结构对声屏障插入损失的影响分析
在保持声屏障高度相同的情况下,采用不同结构形式的顶端装置,能够进一步削弱噪声的绕射,提高降噪效果[17]。选取4种常见的单侧和双侧折壁分支的顶端结构(倒L型、折角型、T型和Y型),如图8所示。
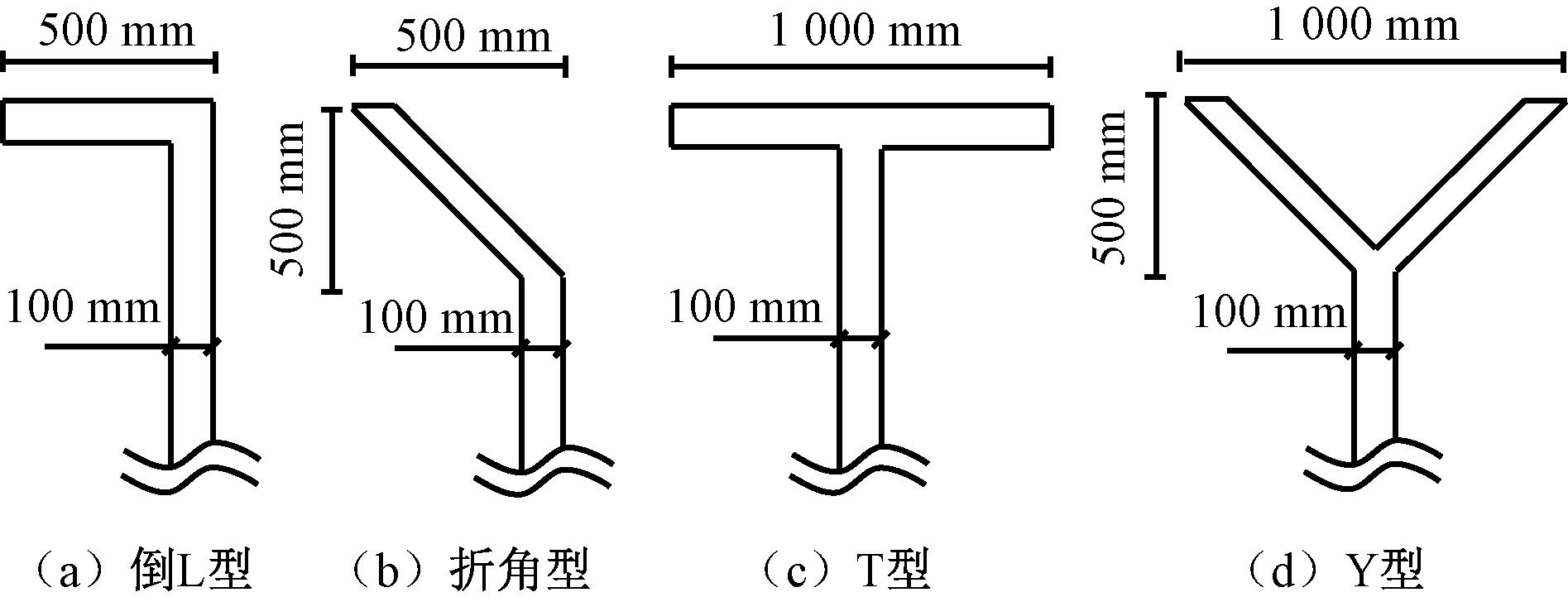
图8 声屏障型顶端结构
Figure 8 Top structures of sound screen barrier
声屏障高度取4 m,声源距离取3 m,双点声源的声压级取100 dB,以测点M1为例,绘制了5种不同顶端结构(直立型、倒L型、折角型、T型和Y型)声屏障的插入损失随声源频率的变化曲线,如图9所示。
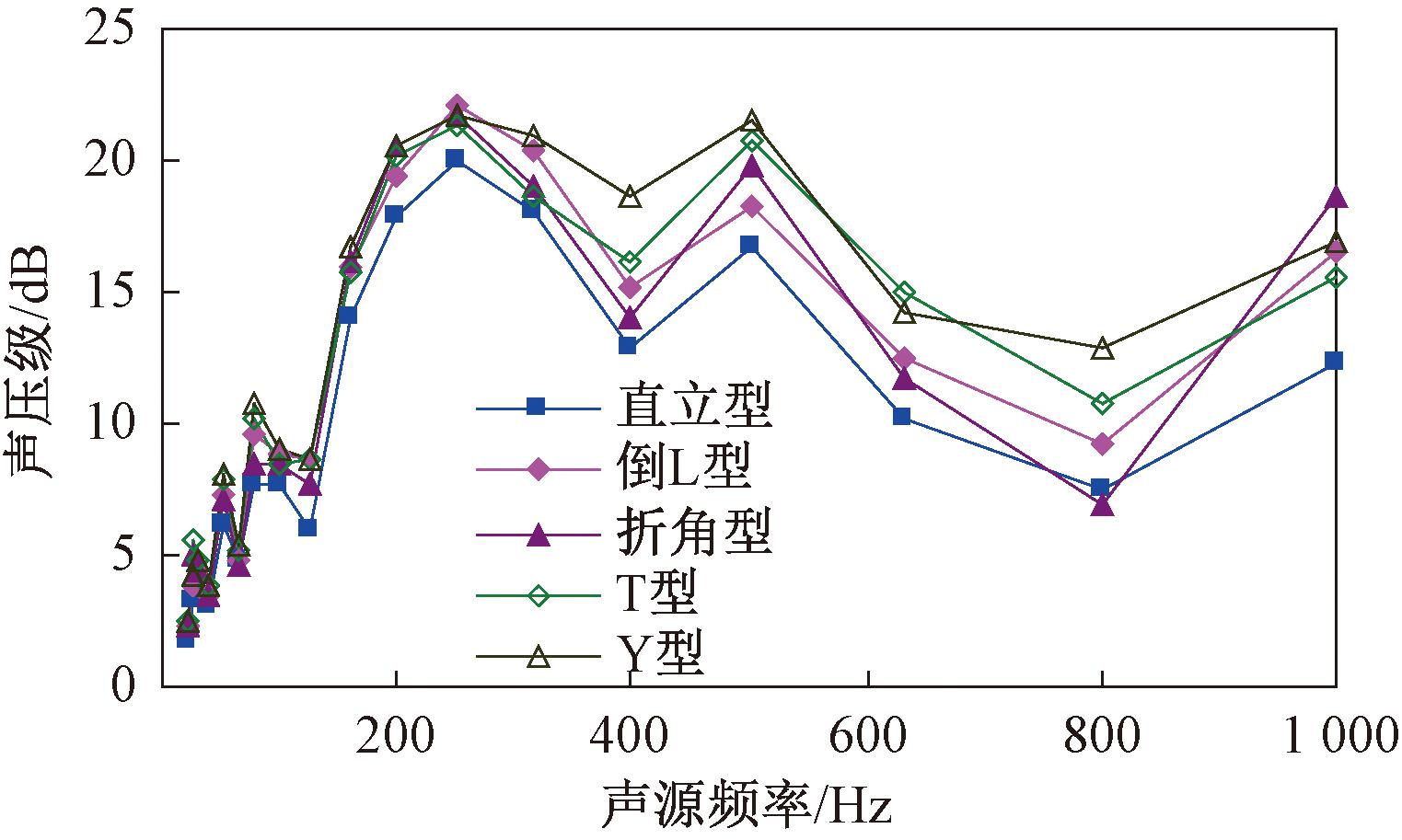
图9 不同顶端结构声屏障插入损失随声源频率的变化曲线
Figure 9 Curves of insertion loss with different top structure of sound barrier changing with sound source frequency
从图9可以看出,在20~160 Hz的低频范围内,5种不同顶端结构的插入损失基本接近,顶端结构对降噪效果的影响较小;而在160~1 000 Hz的中高频频率范围内,单侧和双侧折壁分支顶端结构声屏障的降噪效果均比直立型声屏障有所提高。
根据图9,计算得到了声源频率20~160 Hz和160~1 000 Hz的单侧和双侧反射型顶端结构声屏障的插入损失均值以及相对直立型声屏障的增幅,见表1。
表1 不同顶端结构声屏障平均插入损失均值及增幅
Table 1 Averaged and increment of insertion loss with different top structures of sound barrier dB

顶 端 结 构 2 0 ~ 1 6 0 H z 1 6 0 ~ 1 0 0 0 H z 均 值 增 幅 均 值 增 幅 直 立 型 5 . 8 4 1 4 . 4 5 倒 L 型 6 . 9 0 1 . 0 6 1 6 . 7 1 2 . 2 6 折 角 型 6 . 7 6 0 . 9 2 1 6 . 5 5 2 . 1 0 T 型 7 . 3 1 1 . 4 7 1 7 . 2 7 2 . 8 2 Y 型 7 . 4 3 1 . 5 9 1 8 . 0 2 3 . 5 7
从表1分析可知,双侧顶端结构声屏障降噪效果优于单侧顶端结构,双侧顶端结构的声屏障通过增设一侧分支,从而阻碍了中低频噪声的绕射作用,对中低频噪声的插入损失有一定提高,降噪效果从优到劣的顺序依次为Y型、T型、倒L型、折角型和直立型,因此,对以中低频噪声为主的地铁出入线的降噪设计时,应优先选择两侧均有折壁分支的双侧顶端结构。
2.4 受声点位置的降噪效果分析
声屏障设置为反射直立Y型,声屏障高度取4 m,声源距离取3 m,双点声源的声压级和频率分别取100 dB和250 Hz,绘制了0.5 m高和1.5 m高两个受声点的插入损失随声屏障距离的变化曲线,如图10所示。
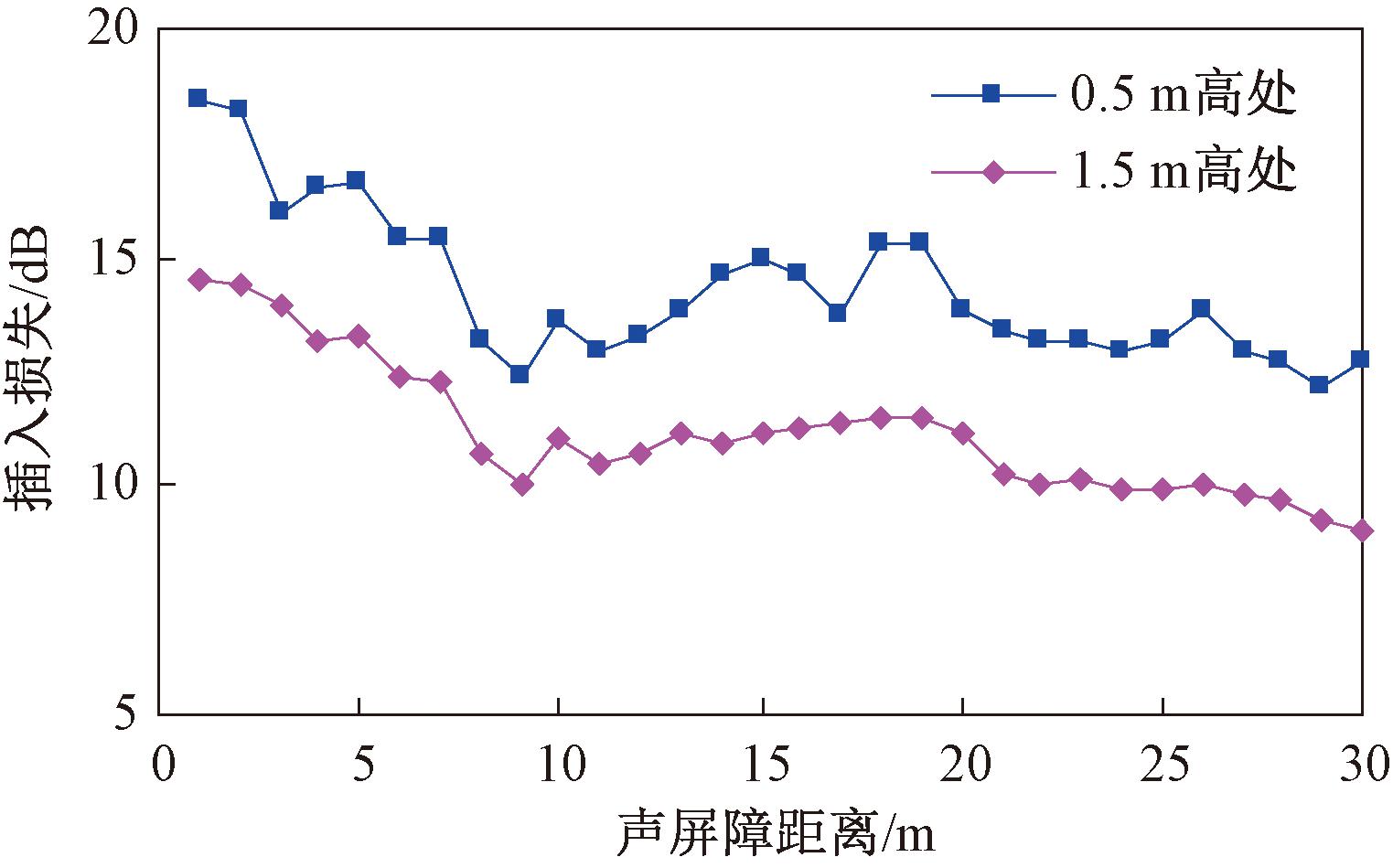
图10 不同位置处的插入损失随声屏障距离的变化曲线
Figure 10 Curves of insertion loss with different position changing with sound source distance
从图10可以看出,受声点的高度越低(越靠近地面),插入损失越大,主要是因为声波通过声屏障绕射到低处的能量越少,此外,低处受声点的插入损失具有一定的波动性,主要是因为绕射波在地面的反射导致声压级变化较为剧烈;对于同一高度的受声点,在近距离处(0~10 m),插入损失呈明显下降的变化趋势,该区域内声波被大量遮挡,仅有部分声波绕射,降噪效果较好;而在中远距离处(10~30 m),声屏障的遮挡作用达到极限,插入损失基本趋于平稳,且随着距离的增大,声波的能量衰减,插入损失有所下降。
3 地铁出入线的声屏障实测分析
根据仿真模拟结果可知,声屏障越靠近声源,降噪效果越好,声源距离3 m的屏障高度拐点为4 m,Y型声屏障的降噪效果最优。在郑州地铁某线路出入线靠近居民区一侧设置Y型全反射声屏障,相关参数如下:声屏障高4 m、厚0.5 m、与双点声源中心的距离3 m。地铁出入线轨道、声屏障布置及噪声测试照片,如图11所示。

图11 地铁出入线轨道、声屏障及现场噪声测试照片
Figure 11 Photos of metro access line tracks, sound barriers and in-situ noise measurement
采用多通道噪声采集设备在地铁列车行驶过测试断面时进行时域声波采集,时段为自列车车头到达测点所在测试断面开始,至车尾完全离开测试断面后截止,以设置声屏障的测点M1为例,选取一组实测的声压时程曲线展示,如图12所示,列车通过测点断面的速度为43 km/h。
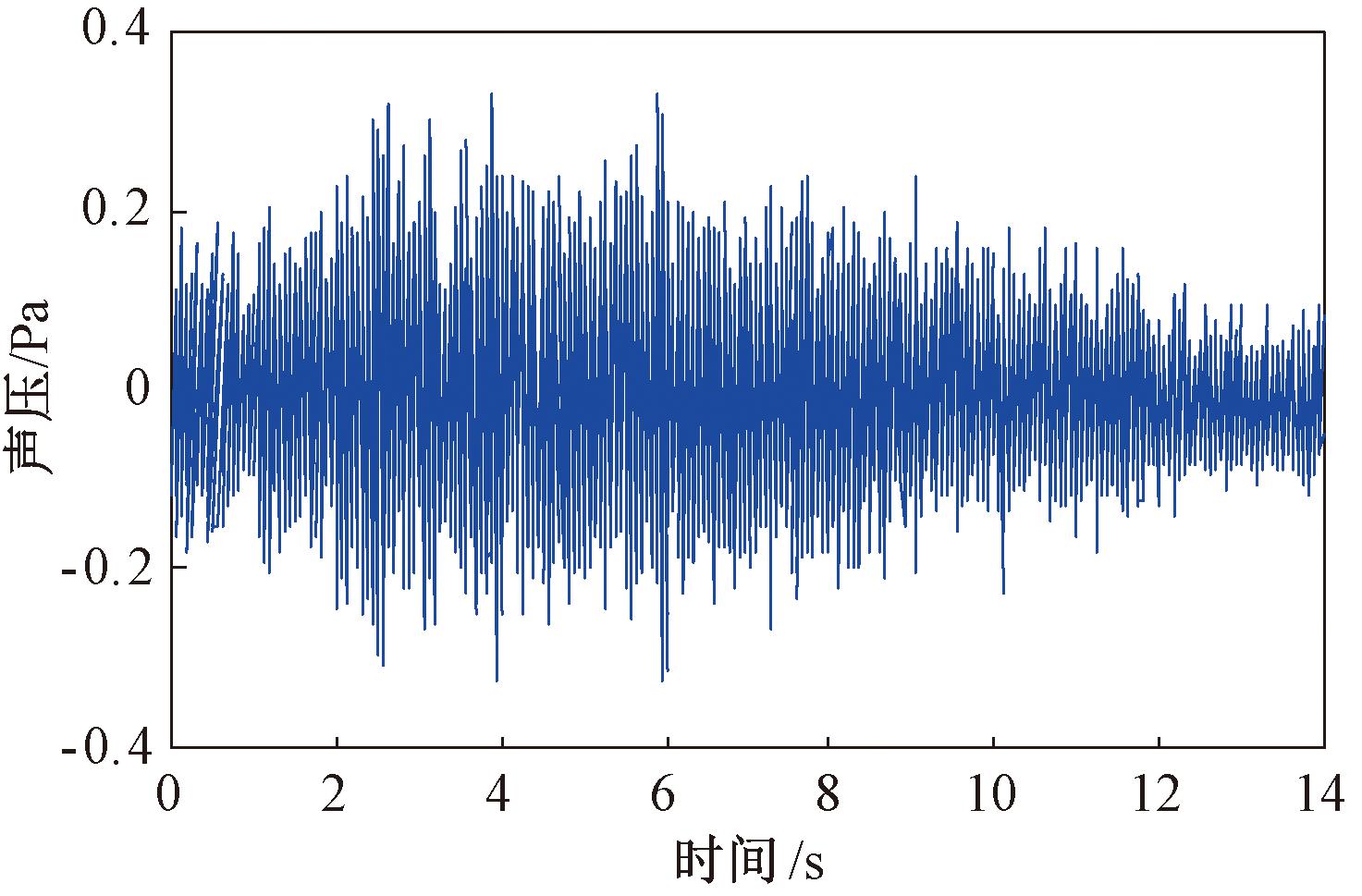
图12 有声屏障的声压时程曲线
Figure 12 Time history curve of sound pressure with sound barrier
由于现场测试影响因素较多,单组测试数据无法准确反映地铁出入线的噪声特性,为减少误差,连续测量了20趟列车,平均车速约40 km/h,并严格按照GB 14892—2006《城市轨道交通列车噪声限值和测量方法》[22]对背景噪声进行修正。
将各测点处的时域声波基于傅里叶变换转化为1/3倍频程的声压级频谱,为减少误差,频谱图中各频率相应的声压级均为20组测试数据的算术平均值。由于人耳相比于高频噪声,对低频噪声的感受不敏感,A计权声压级最贴合人耳对于噪声强度的感受,因此需将1/3倍频程声压级向A计权声压级进行修正,修正表见表2。
表2 1/3倍频程声压级向A计权声压级修正
Table 2 Correction of 1/3 octave sound pressure level to A-weighted sound pressure level

1 / 3 倍频程中心 频率/ Hz 噪声修正 值/ dB 1 / 3 倍频程中心 频率/ Hz 噪声修正 值/ dB 20 - 50. 54 160 - 13. 43 25 - 44. 68 200 - 10. 88 31. 5 - 39. 43 250 - 8. 62 40 - 34. 62 315 - 6. 61 50 - 30. 19 400 - 4. 83 63 - 26. 17 500 - 3. 24 80 - 22. 52 630 - 1. 89 100 - 19. 08 800 - 0. 77 125 - 16. 12 1 000 0
以测点M1为例,绘制了现场实测和仿真模拟的声压级随声源频率的变化曲线,如图13所示。从图13可以看出,仿真模拟与现场实测声压级随声源频率的变化曲线具有较好的吻合性,最大相对误差6.18 %,验证了声学仿真模型与计算方法的可行性。
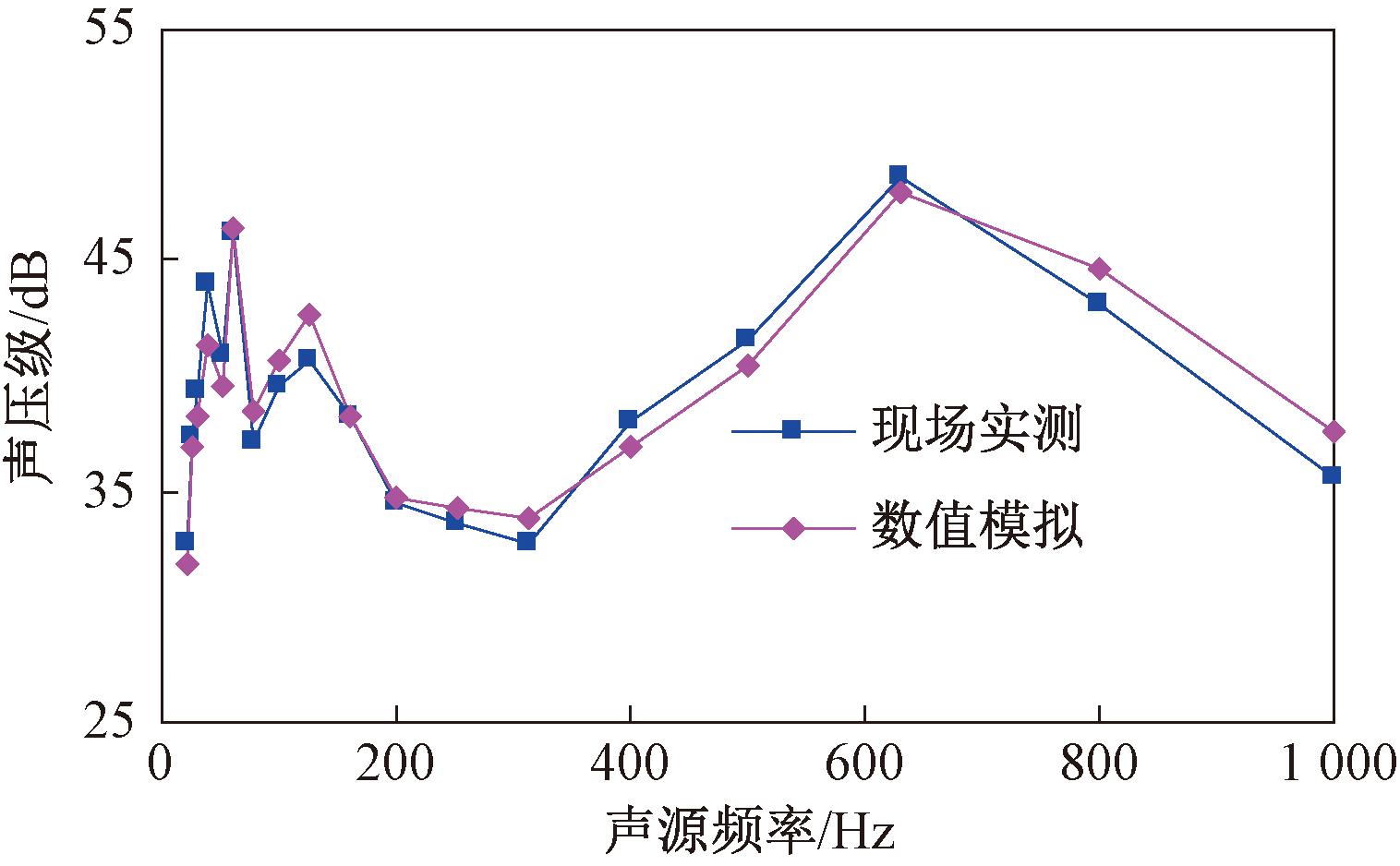
图13 现场实测与仿真模型的声压级对比曲线
Figure 13 Comparison curves of sound pressure level between on-site measurement and simulation model
GB 3096—2008《声环境质量标准》[23]规定的1类声环境功能区是指以居民住宅、医疗卫生、文化教育、科研设计、行政办公为主要功能,需要保持安静的区域。与郑州地铁某线路出入线最近距离30 m的居民小区属于1类声环境功能区,环境噪声等效声级限值为昼间(06:00~22:00)噪声55 dB和夜间(22:00~次日06:00)噪声45 dB。
设置声屏障后,根据测试结果,绘制了3个测点M1、M2和M3的实测声压级随声源频率的变化曲线,如图14所示。
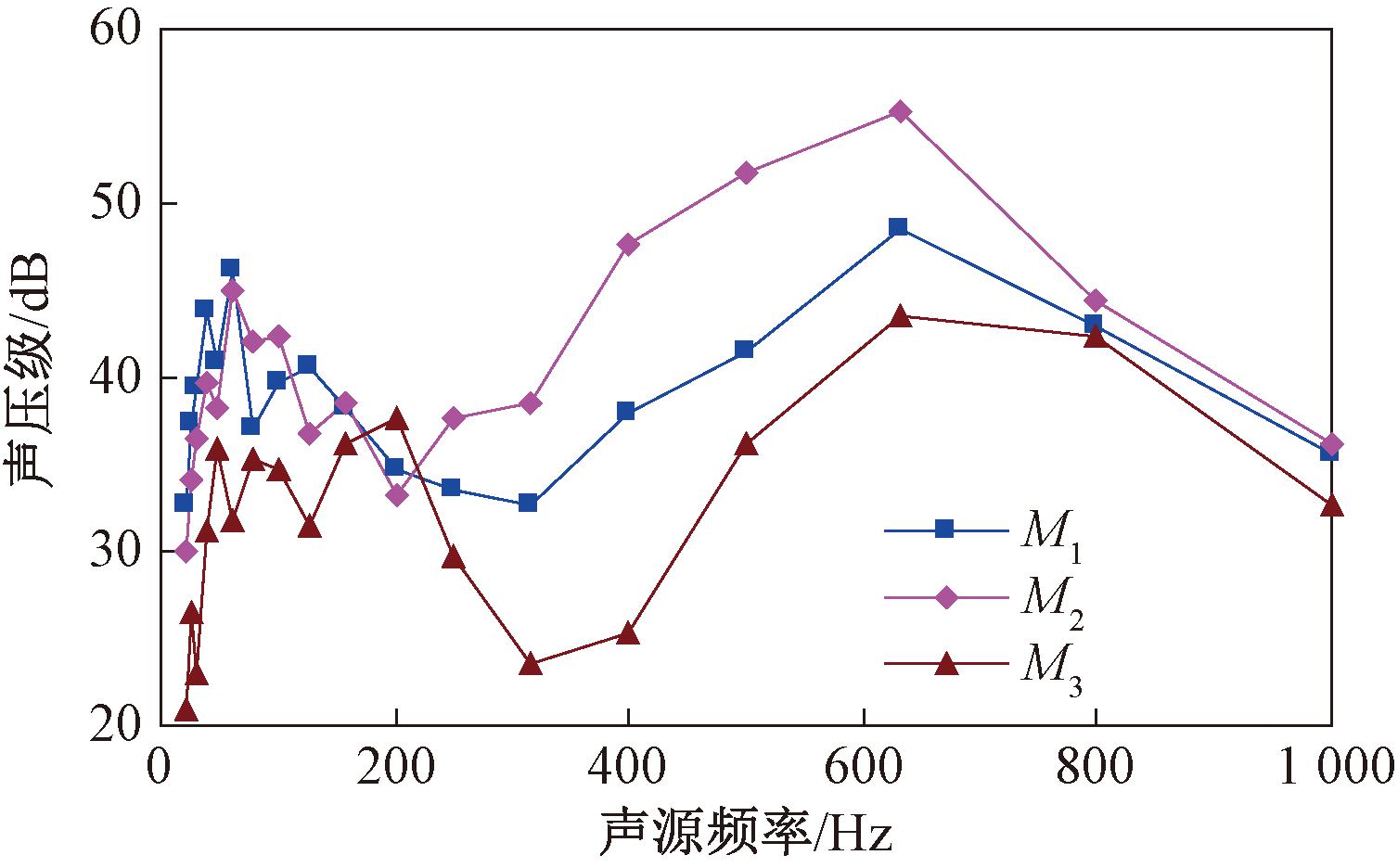
图14 设置声屏障后实测声压级随声源频率的变化曲线
Figure 14 Curves of measured sound pressure level after sound barriers changing with sound source frequency
从图14可以看出,郑州地铁某出入线设置声屏障后,近场区域(出入线轨道中心距离7.5 m处)测点M1和M2的最大声压分别为48.56 dB和55.38 dB,而远场区域(距离出入线轨道中心距离25 m)的测点M3最大声压为43.38 dB,沿线居民建筑与轨道中心的最近距离为30 m,属于远场区域,满足噪声要求较高的夜间45 dB的要求。
4 结论
以郑州某线路地铁出入线为工程实例,采用Virtual Lab声学仿真软件构建了声屏障模型,分析了声屏障降噪效果的影响因素,并确定了在出入线靠近居民区一侧的Y型全反射声屏障参数,主要结论如下。
(1)声源声压级不影响声屏障的降噪效果,而声源频率对声屏障的降噪效果影响较大。
(2)插入损失随声屏障高度提升而增加,但存在一个高度临界点,超过后插入损失增益较低;对于相同位置的受声点,声屏障越靠近声源,降噪效果越好。
(3)双侧顶端结构的声屏障通过增设一侧分支,从而阻碍了中低频噪声的绕射作用,声屏障的降噪效果从优到劣依次为:Y型、T型、倒L型、折角型和直立型。
(4)屏障后受声点的高度越低(越靠近地面),插入损失越大;随着与声屏障距离的增大,插入损失呈先明显下降,再趋于平缓的变化趋势。
(5)在地铁出入线设置了高4 m、声源距离3 m的直立Y型声屏障,现场实测了声屏障设置前后的噪声信号,获得了噪声特征参数,仿真结果与测试结果具有较好的吻合性,验证了仿真计算的合理性。地铁出入线沿线建筑与轨道中心的最近距离30 m,设置声屏障后沿线居民建筑的噪声满足相关规范要求,相关成果可为地铁出入线的降噪设计和评价提供参考。
[1] 毛东兴, 洪宗辉. 环境噪声控制工程[M]. 2版. 北京: 高等教育出版社, 2010.
MAO D X, HONG Z H. Environmental noise control engineering[M]. 2nd ed. Beijing: Higher Education Press, 2010.
[2] 张朋, 郝影, 张磊, 等. 地铁振动引起的二次辐射噪声适用标准研究[J]. 中国环境监测, 2020, 36(4): 154-159.
ZHANG P, HAO Y, ZHANG L, et al. Study on the applicable standard of secondary radiation noise caused by metro train vibration[J]. Environmental Monitoring in China, 2020, 36(4): 154-159.
[3] 赵兴征, 张秦, 高科梁, 等. 某地铁U型梁结构辐射噪声分析预测及其降噪研究[J]. 声学技术, 2024, 43(3): 394-402.
ZHAO X Z, ZHANG Q, GAO K L, et al. Analysis and prediction of radiated noise of a subway U-beam structure and its noise reduction study[J]. Technical Acoustics, 2024, 43(3): 394-402.
[4] 刘全民, 徐培培, 宋立忠, 等. 轨道交通噪声评价与控制标准探讨[J]. 噪声与振动控制, 2021, 41(6): 229-236, 243.
LIU Q M, XU P P, SONG L Z, et al. Investigation of noise assessment and control standards for rail transit[J]. Noise and Vibration Control, 2021, 41(6): 229-236, 243.
[5] 张书豪, 刘剑梅, 吴姣姣, 等. 重庆地铁各型声屏障综合降噪效果研究[J]. 噪声与振动控制, 2024, 44(4): 252-257.
ZHANG S H, LIU J M, WU J J, et al. Study on comprehensive noise reduction effect of various types of noise barriers in Chongqing metro[J]. Noise and Vibration Control, 2024, 44(4): 252-257.
[6] HU S H, ZHAO Q, JIANG B L, et al. Vibration simulation and analysis of high-speed railways sound barriers under different conditions of bolts loosening[J]. Journal of Physics:Conference Series, 2024, 2819(1): 012060.
[7] 王朝亮, 张良涛, 宋立忠, 等. 市域铁路近轨声屏障降噪效果预测分析[J]. 噪声与振动控制, 2022, 42(6): 187-191, 278.
WANG C L, ZHANG L T, SONG L Z, et al. Predication and analysis of noise reduction of near-rail sound barriers on suburban railways[J]. Noise and Vibration Control, 2022, 42(6): 187-191, 278.
[8] 毛伟, 何渝, 谢辉等. 高架轨道交通线路声屏障振动辐射噪声特性[J]. 重庆大学学报, 2022, 45(增刊1): 60-65.
MAO W, HE Y, XIE H, et al. Characteristics of radiated noise from sound barrier vibration of elevated rail transitlines[J]. Journal of Chongqing University, 2022, 45(S1): 60-65.
[9] 丁亚超. 温州市域铁路近轨声屏障设计试验研究[J]. 铁道工程学报, 2022, 39(8): 98-104.
DING Y C. Experimental study on design of near rail noise barrier for Wenzhou surburban railway[J]. Journal of Railway Engineering Society, 2022, 39(8): 98-104.
[10] 臧传臻, 魏庆朝. 有源声屏障对地铁轮轨噪声的消减性能[J]. 哈尔滨工业大学学报, 2022, 54(3): 114-121.
ZANG C Z, WEI Q C. Noise reduction performance of active noise barrier for metro wheel-rail noise[J]. Journal of Harbin Institute of Technology, 2022, 54(3): 114-121.
[11] 吴小萍, 朱烨, 鲜凌霄, 等. 高速铁路Y型声屏障动态特性数值研究[J]. 中南大学学报(自然科学版), 2022, 53(2): 737-746.
WU X P, ZHU Y, XIAN L X, et al. Numerical study on dynamic characteristics of Y-typed sound barrier in high-speed railway[J]. Journal of Central South University (Science and Technology), 2022, 53(2): 737-746.
[12] 宋立忠, 高亏, 冯青松, 等. 轨道交通桥梁低矮弧形声屏障降噪性能研究[J]. 振动与冲击, 2023, 42(24): 143-151, 168.
SONG L Z, GAO K, FENG Q S, et al. A study on noise reduction performance of low-height curved noise barriers on rail transit bridges[J]. Journal of Vibration and Shock, 2023, 42(24): 143-151, 168.
[13] SONG X D, LI Q. Numerical and experimental study on noise reduction of concrete LRT bridges[J]. The Science of the Total Environment, 2018, 643: 208-224.
[14] ZHANG X, LIU R, CAO Z Y, et al. Acoustic performance of a semi-closed noise barrier installed on a high-speed railway bridge: measurement and analysis considering actual service conditions[J]. Measurement, 2019, 138: 386-399.
[15] HE W, HE K W, ZOU C, et al. Experimental noise and vibration characteristics of elevated urban rail transit considering the effect of track structures and noise barriers[J]. Environmental Science and Pollution Research, 2021, 28(33): 45903-45919.
[16] 盛峰, 姜在秀, 贺银芝, 等. 高速铁路声屏障宽频穿孔吸声降噪结构[J]. 同济大学学报(自然科学版), 2024, 52(9): 1469-1473.
SHENG F, JIANG Z X, HE Y Z, et al. Multi-layer micro-perforated panels with broadband absorption for reduction of high-speed railway noise[J]. Journal of Tongji University (Natural Science), 2024, 52(9): 1469-1473.
[17] 侯博文, 曾钦娥, 费琳琳, 等. 城市轨道交通地下车站站台噪声评价方法[J]. 清华大学学报(自然科学版), 2021, 61(1): 57-63.
HOU B W, ZENG Q E, FEI L L, et al. Noise evaluation method for urban rail transit underground station platforms[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(1): 57-63.
[18] 尹小春, 卢耀辉, 赵宏星, 等. 隧道工况下高速列车动态气密性数值分析方法[J]. 郑州大学学报(工学版), 2022, 43(5): 52-58.
YIN X C, LU Y H, ZHAO H X, et al. Numerical analysis method for dynamic air tightness value of high-speed train[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(5): 52-58.
[19] ZHANG X Y, THOMPSON D, QUARANTA E, et al. An engineering model for the prediction of the sound radiation from a railway track[J]. Journal of Sound and Vibration, 2019, 461: 114921.
[20] 生态环境部. 环境影响评价技术导则 城市轨道交通: HJ 453—2018[S]. 北京: 中国环境科学出版社, 2018.
Ministry of Ecology and Environment of the People′s Republic of China. Technical guidelines for environmental impact assessment-urban rail transit:HJ 453—2018[S]. Beijing: China Environmental Science Press, 2018.
[21] 詹福良, 徐俊伟. Virtual.Lab Acoustics声学仿真计算从入门到精通[M]. 西安: 西北工业大学出版社, 2013.
ZHAN F L, XU J W. Virtual.Lab Acoustics acoustics acoustics simulation calculation from introduction to mastery[M]. Xi’an: Northwestern Polytechnical University Press, 2013.
[22] 国家质量监督检验检疫总局, 中国家标准化管理委员会. 城市轨道交通列车噪声限值和测量方法: GB 14892—2006[S]. 北京: 中国标准出版社, 2006.
General Administration of Quality Supervision, Inspection and Quarantine of the People′s Republic of China, Standardization Administration of the People′s Republic of China. Noise limit and measurement for train of urban rail transit:GB 14892—2006[S]. Beijing: Standards Press of China, 2006.
[23] 环境保护部. 声环境质量标准: GB 3096—2008[S]. 北京: 中国环境科学出版社, 2008.
Ministry of Environmental Protection of the People′s Republic of China. Environmental quality standards for noise: GB 3096—2008[S]. Beijing: China Environmental Science Press, 2008.