随着“双碳”目标的提出,我国电力行业正加速向可持续发展和新能源转型,太阳能等新能源在大电网中的占比迅速增长[1]。然而,太阳能发电的间歇性和波动性[2]给电力系统的频率稳定性带来了极大的挑战。一次频率调节是维持系统频率稳定性的重要手段,传统上依赖于火电机组,但在新能源大幅增加的背景下,其调频能力已显不足。因此,光伏电站参与电力系统频率调节已成为增强电网的频率安全的重要途径。
光伏发电参与电力系统频率控制时,传统控制方法有下垂控制[3]、虚拟惯性控制[4]以及将这两种控制策略结合的协调控制方法[5],这些方法依据系统频率的偏差和频率变化率线性地改变有功功率参考值来实现频率响应。为应对电力系统复杂多变的特性,引入了先进控制算法如模糊控制[6]、模型预测控制[7]、滑模控制[8]等。然而当前电力系统往往包含强非线性环节,上述控制方法大多依赖精确的系统模型,且缺乏学习记忆功能,容易陷入局部最优解的困境,而无模型或数据驱动的控制方法更能实现灵活控制。
强化学习[9]凭借其强大的搜索能力和内置的学习记忆功能,在解决非线性等复杂决策问题上展现出广泛的应用前景。经典的强化学习方法只适用于低维状态,甚至可能降低控制系统的性能,而深度学习[10]由于其强大的数据分析、预测和分类能力,在解决电力系统频率分析和控制等复杂问题上具有明显的优势,从而使得拓展出的融合深度神经网络和强化学习的深度强化学习方法(deep reinforcement learning, DRL)[11]有着对连续动作空间的适用性及在复杂系统中的出色的感知能力和决策能力,已在电力行业成为一种很有前景的频率控制方法[12]。Sun等[13]利用人工神经网络构建了一种强化学习算法并用于微电网的频率调节,有效提升了微电网的自主调频能力。杨悦等[14]借助Q学习算法的优化决策以及各调频源的控制策略,完成多源一次调频任务。Mu等[15]基于自适应学习策略提出了一种改进的滑模控制器,实现了微电网最优的自适应频率控制和更优的抗扰动性。Chen等[16]提出了一种基于深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法的非线性电力系统无模型负荷频率控制方法,对非线性电力系统具有较强的适应性。
综上可知,基于DRL的控制策略算法已被成熟地应用于电力系统的频率调节中。光伏电站参与电力系统频率调节问题需要对环境进行建模,得到下一个时刻的信息,其本质上是一个无模型DRL问题[17],其中基于动作-评价(actor-critic, AC)框架的算法综合了基于值函数采样和基于策略梯度的优点,具有效率高和适用于高维连续空间的特点。因此,本文提出了一种基于双延迟深度确定性策略梯度(twin delayed deep deterministic policy gradient, TD3)算法[18]的光伏电站参与电力系统频率控制策略。首先,基于TD3算法设计频率控制器;其次,设计其状态空间、动作空间和奖励函数;最后,施加两种不同的负荷扰动来进行仿真实验,实验结果表明,采用本文所提算法能显著提升系统快速调频能力,展现出更优越的控制性能,远远优于传统控制方法。
1 系统频率控制模型
模型的复杂性增加了研究的难度,采用简化模型来分析电网的运行原理能更方便地研究电网的运行特性和其他动态过程。光伏电站接入系统(含常规电源)的一次调频系统模型[19]如图1所示,其中带有死区、饱和非线性环节。图1中Δf为系统频率偏差;ΔPL、ΔPT、ΔPPV分别表示负荷的功率变化、火电机组输出功率变化和光伏电站输出功率变化。
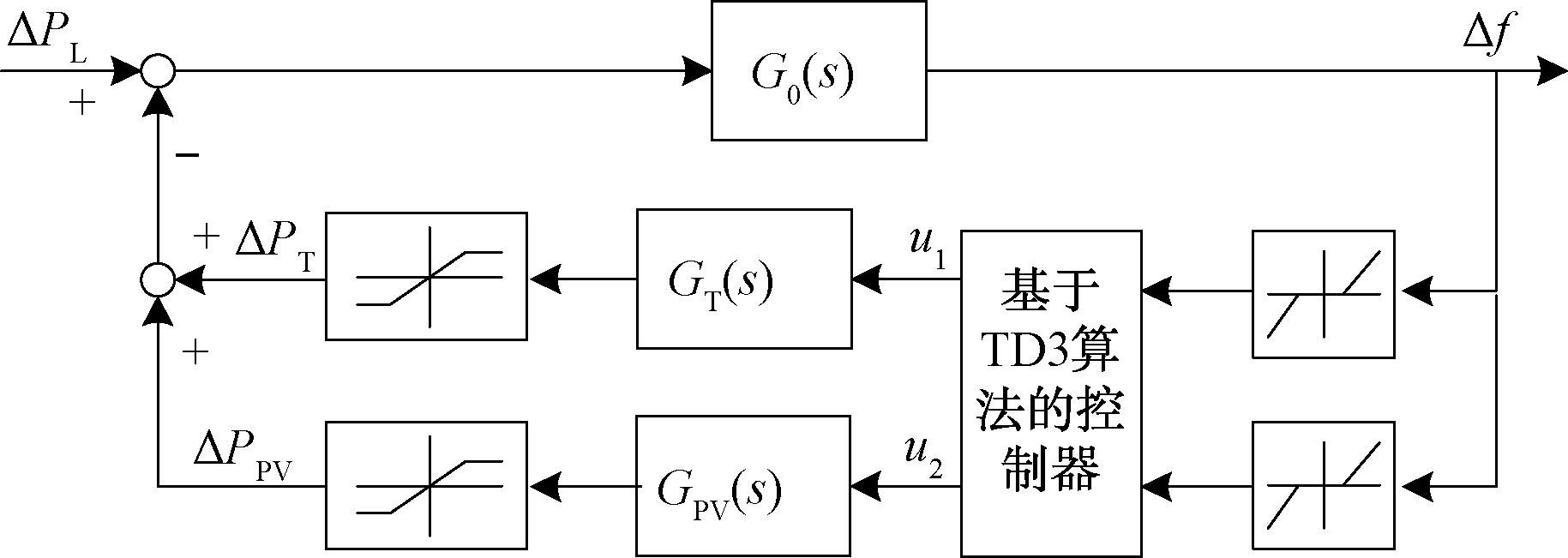
图1 光伏电站参与电力系统一次调频框图
Figure 1 Block diagram of primary frequency regulation for power system with photovoltaic plant
1.1 摆动方程
G0(s)表示发动机转子等效模型,如式(1)所示:
(1)
式中:H和D分别为发电机的等效惯性常数和等效阻尼因子。
1.2 火电机组频率特性模型
GT(s)表示火电机组等效模型,如式(2)所示:
(2)
式中:Km为光伏电站出力占所有电源出力的比例;FH、TR、TG、TC分别为再热器增益、再热器时间常数、调速器时间常数、汽轮机时间常数。
1.3 光伏电站频率特性模型
GPV(s)表示光伏电站等效模型,如式(3)所示:
(3)
式中:KMPV为光伏电站出力占所有电源出力的比例;TPV1为基于光伏电站功率控制系统的调频控制指令下发到逆变器的时间;TPV2为逆变器的执行时间。
相关参数数值设置[19]如表1所示。
表1 光伏调频研究的相关参数设置
Table 1 Relevant parameter settings for photovoltaic frequency regulation research

参 数 数 值 参 数 数 值 H 6 . 5 T C 0 . 5 D 0 . 0 1 2 TP V 1 1 . 9 F H 0 . 4 TP V 2 0 . 0 5 T R 1 4 K m 0 . 5 5 T G 0 . 3 K M P V 0 . 4 5
2 基于TD3算法的系统频率控制策略
2.1 强化学习基础
智能体的学习过程[9]如图2所示,当前时刻为t,根据智能体当前的状态st∈S,通过策略函数π(at|st)=P[a=at|s=st]选取需要执行的动作at∈a(st),执行该动作后,时间推进至下一个时刻t+1,此时智能体的状态由st转化为新的状态st+1。同时,智能体还会根据其在该时刻的行为和环境反馈获得即时奖励rt。
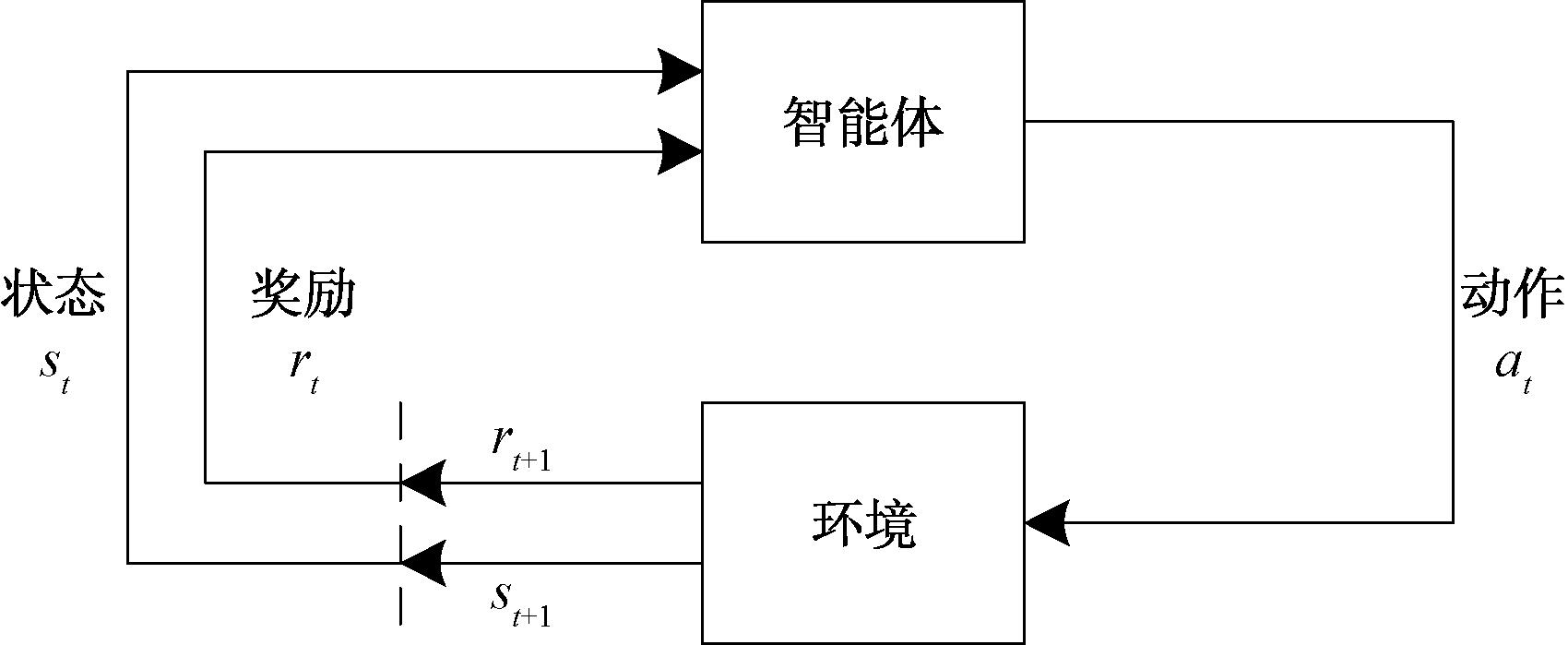
图2 强化学习的基本框架
Figure 2 The basic framework of reinforcement learning
2.2 基于TD3算法的控制器设计
2.2.1 TD3算法原理
TD3算法[18]是建立在AC框架的基础上,由DDPG算法进一步发展而来的,其独特之处在于采用了两组相同结构的AC网络,且在每一套Critic网络中都使用双网络结构以增强算法的稳定性。TD3算法的框架如图3所示,使用了6个神经网络来描述系统的非线性关系,并在连续的动作空间中进行决策。其中Actor网络由φ参数化,两个Critic网络分别由θ1和θ2参数化。为了增强学习的稳定性和鲁棒性,TD3算法引入了目标网络,包括一个由φ′参数化的目标Actor网络和两个分别由![]() 和
和![]() 参数化的目标Critic网络。
参数化的目标Critic网络。
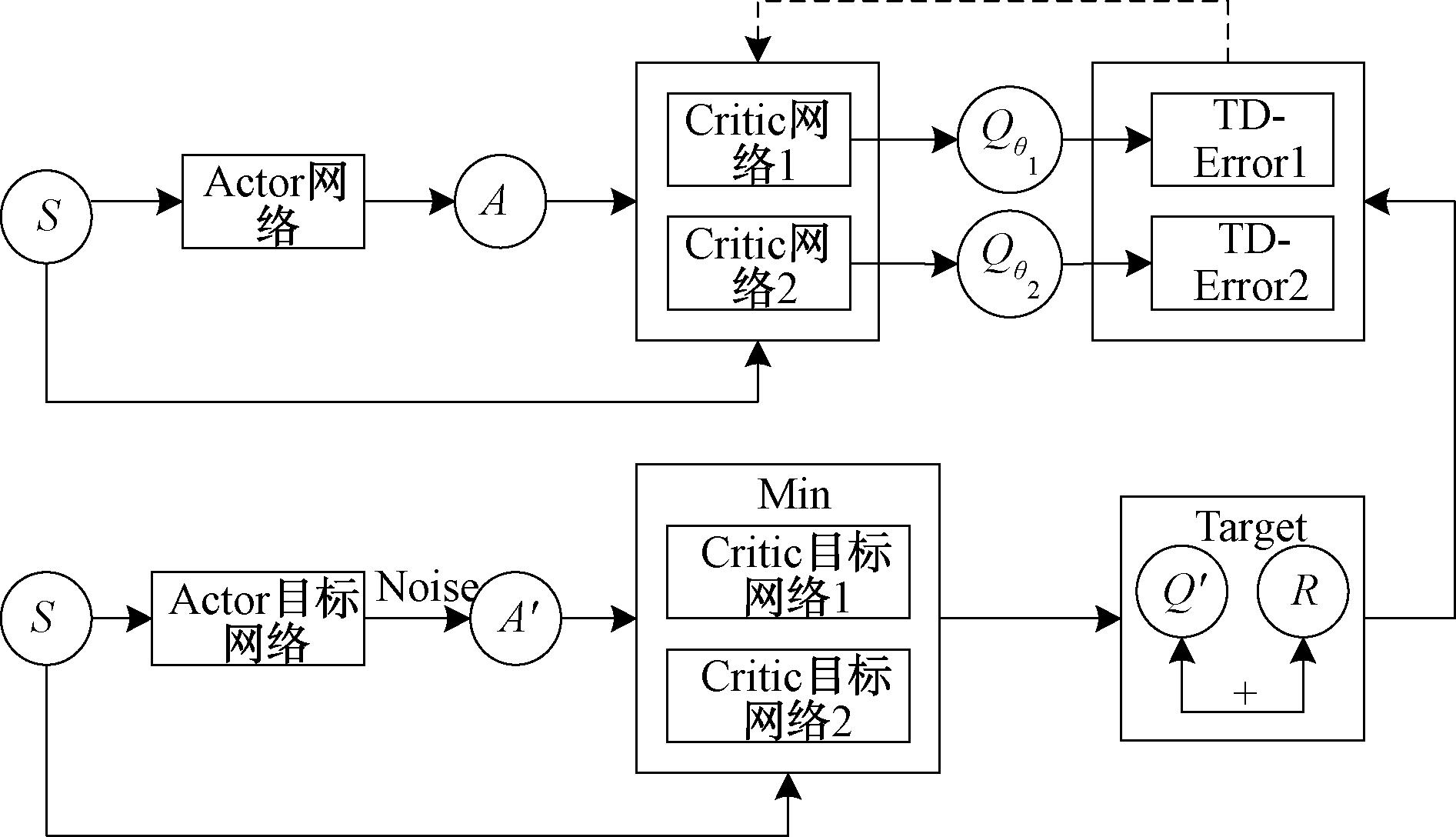
图3 TD3模型框架图
Figure 3 Framework diagram of the TD3 model
通过递归贝尔曼方程,Critic网络Qθ1与Critic网络Qθ2同时更新,具体的更新公式为
Qπ(st,at)=r(st,at)+γQπ(st+1,π(st+1))。
(4)
为了逼近最优Q函数,TD3采用均方贝尔曼误差函数来量化参数θ1和θ2满足贝尔曼方程的程度,如式(5)所示:
L(θi)=E(s,a,r,s′)~R[(Qθi(s,a)-y|(r,s′))2],
i=1,2。
(5)
两套Critic网络表示不同的Q值,将较小的Q值作为更新的目标Q值,以抑制持续过高估计。在策略网络中引入随机噪声 ε来估计目标网络,以避免在Q值的窄峰上出现过度拟合,从而产生平滑的目标策略,即目标策略平滑正则化。在TD3算法中采用高斯噪声,并通过式(6)对Critic网络进行更新:
(6)
式中:clip表示加入的噪声被截断,从而使目标保持在小范围内。
每隔一定步数,Actor网络通过期望回报的梯度上升 φJ(φ)来更新网络参数φ,如式(7)所示:
φJ(φ)来更新网络参数φ,如式(7)所示:
 φJ(φ)=Es~R[
φJ(φ)=Es~R[ aQθ1(s,a)|a=π(s)
aQθ1(s,a)|a=π(s) φπφ(s)]。
φπφ(s)]。
(7)
TD3算法中,Actor网络和Critic网络的更新频率是一个关键的平衡点。为了减少由时间差分学习造成的累积误差,应使Actor网络的更新比Critic网络慢。将延迟更新步骤值设置为2,既可以减少累积误差,又能确保训练过程的稳定性和有效性。
为了保证估计误差较小,提高算法学习过程中的稳定性和可靠性,Critic目标网络和Actor目标网络采用如式(8)所示的软更新的方式,使更新的目标不会出现变化过大的情况,从而增加训练的稳定性:
(8)
式中:τ表示软更新系数,τ≪1。
算法1 TD3算法。
输入:观测状态s,奖励函数r;
输出:动作a。
① 用随机参数θ1、θ2、φ初始化Critic当前网络Qθ1、Qθ2和Actor当前网络πφ;
② 初始化目标网络θ′1←θ1,θ′2←θ2,φ′←φ;
③ 清空经验回放池R;
④ for t=1 to T do
⑤ 由当前策略π和探索噪声选取动作a~πφ(s)+ε,ε~N(0,σ),并选取即时奖励 r 和下一个状态s′;
⑥ 将这个四元组(s,a,r,s′)存入经验回放池R;
⑦ 从经验回放池 R中取N个四元组进行训练;
⑧ ![]() ⑨
⑨![]()
⑩ 更新Critic网络参数:
θi←argminθiN-1∑(y-Qθi(s,a))2,i=1,2;
 if t mod d then
if t mod d then
 用策略梯度更新φ:
用策略梯度更新φ:
 φJ(φ)=Es~R[
φJ(φ)=Es~R[ aQθ1(s,a)|a=π(s)
aQθ1(s,a)|a=π(s) φπφ(s)];
φπφ(s)];
 更新目标网络参数:
更新目标网络参数:
θ′i←τθ+(1-τ)φθ′i,φ′←τφ+(1-τ)φ′;
 end if
end if
 end for。
end for。
2.2.2 状态、动作空间和奖励函数的设计
(1)状态设置。为了更好地描述光伏电站参与电力系统的当前状态,采用火电机组、光伏电站及负荷的功率变化量、频率偏差、频率偏差的积分及导数作为状态观测值[20]:
(9)
(2)动作设置。将动作输出设置为电力系统的频率控制信号:
A(t)=Δu(t)=[ΔuT(t),ΔuPV(t)]T。
(10)
(3)奖励函数的设置:
(11)
(12)
式(11)为一个步骤的奖励,式(12)为总奖励。其中,k1和k2为权重系数,都是常数;γ为折扣因子。式(11)的第1项考虑频率偏差,频率偏差越大,获得的负奖励越大。考虑到允许电力系统在一定频率范围内波动,而不能容忍频率阈值跨越,所以采用平方项,频率偏差较小时则忽略不计。式(11)的第2项考虑频率偏差的变化,目的是减少频率偏差较小的波动。
2.2.3 网络结构设计
由于本文研究的电力系统中含有死区等非线性环节,而深度神经网络在捕捉和表达非线性关系上有显著优势,因此可采用神经网络来预处理非线性特征并有效地提取系统的关键特征。图4展示了所设计的神经网络架构,其中输入层接收系统的当前状态与动作并作为输入数据[21]。隐藏层采用多个全连接层,并通过整流线性单元(rectified linear unit,ReLU)函数进行层间连接,以捕捉数据中的非线性关系。ReLU函数不仅加速了训练过程中的收敛速度,更使得网络对超参数的变化具有较强的鲁棒性。输出层采用双曲正切函数作为激活函数,由于其输出被限制在-1到1之间并以0为中心,这使得它能够有效地限制网络的输出范围,进而确保控制信号的合理性和稳定性。
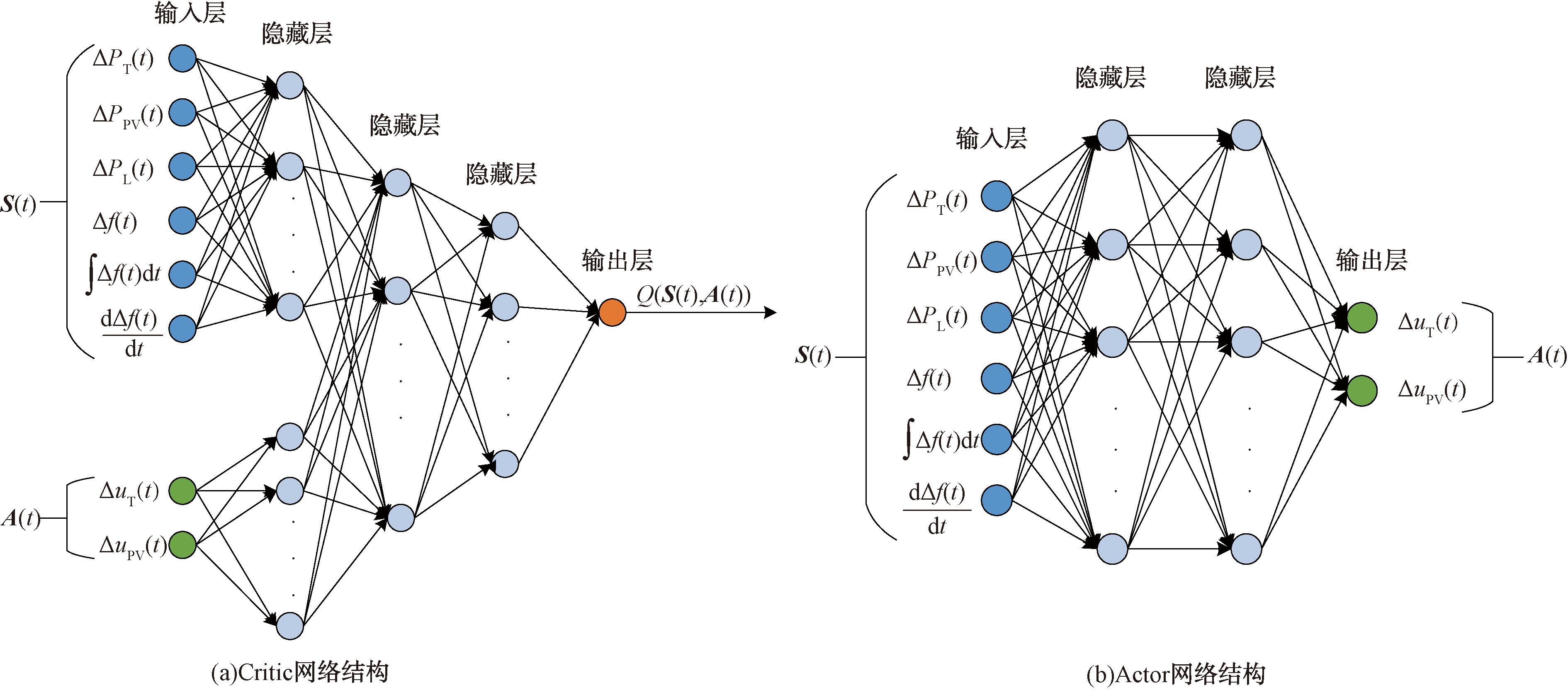
图4 神经网络结构图
Figure 4 Diagram of neural network structure
基于TD3算法的光伏电站参与电力系统频率调节的模型示意图如图5所示。该模型通过设计的状态空间、动作空间以及奖励函数,结合TD3算法中独特的神经网络架构,TD3智能体在学习过程中不断收集训练样本,并存储到一个统一的经验回收池R中。在每一轮的训练中,智能体会从经验回收池中采样一个小批量(mini-batch)的数据来训练Actor和Critic网络。该模型实现了对光伏发电系统的高效控制,优化其在电网频率调节中的表现。
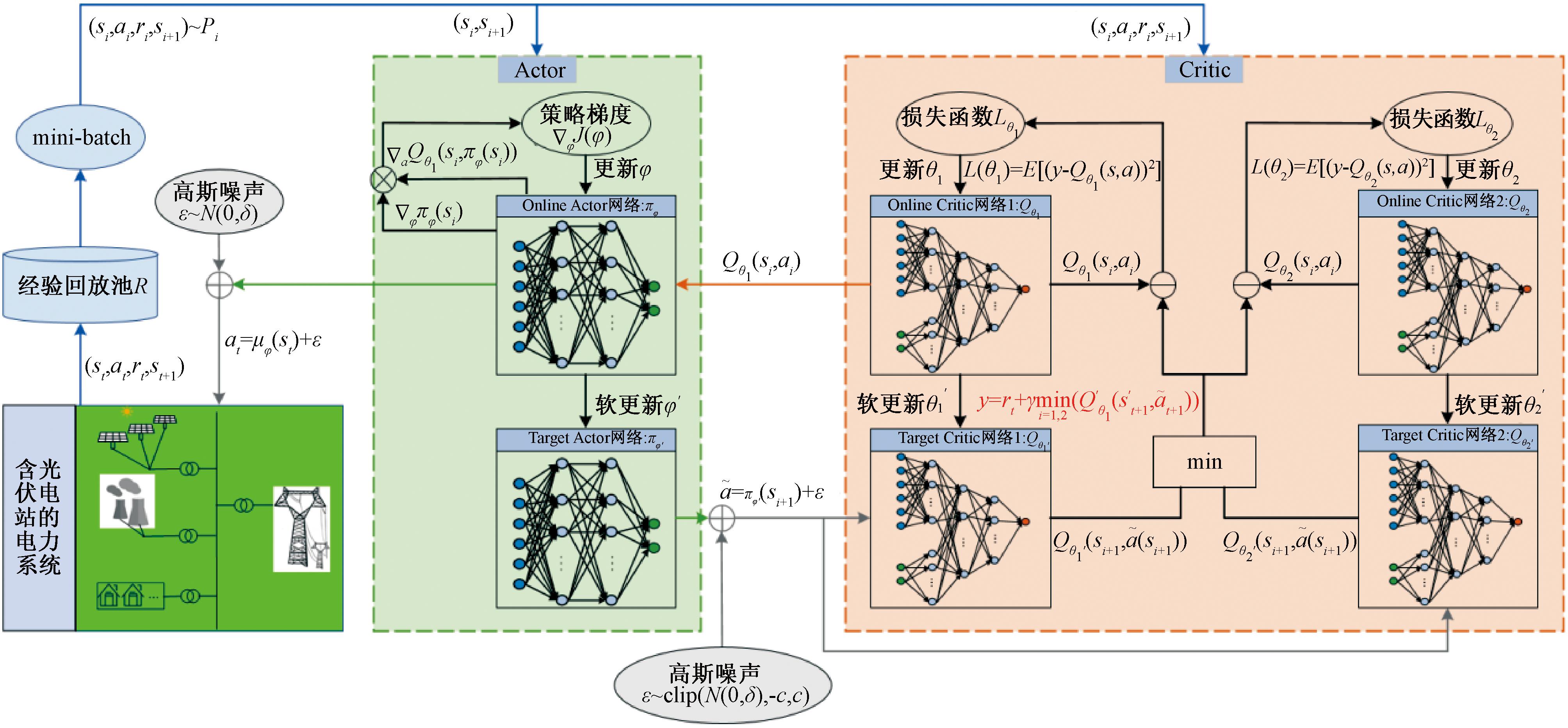
图5 TD3算法结构图
Figure 5 Structure diagram of TD3 algorithm
3 仿真分析
本文实验基于MATLAB R2022b/Simulink环境搭建了含光伏电站的电力系统模型,整个训练过程的硬件实现平台为一台配置为Intel(R) Core(TM) i7-9700 CPU @ 3.00 GHz,16 GB内存的计算机。
在基于DRL算法的训练过程中选择合适的参数对控制性能至关重要,为了高效地优化DRL算法中Actor和Critic网络的参数,本文选用自适应矩估计优化器[22],这种优化方法有助于平衡训练速度与收敛性,确保算法性能的稳定提升。在实验过程中,引入DDPG算法[23]作为对照试验,训练过程中这两种算法的各个关键参数的具体设定如表2所示。
表2 核心训练参数赋值
Table 2 Core training parameter assignments

算法 最大训练 回合数 训练 集步长 训练 批次 神经网络隐 藏单元数 Actor 网络 学习率/ 10 -4 Critic 网络 学习率 延迟更 新步骤 折扣 因子 梯度 阈度 目标平 滑因子 经验回放 池大小/ 10 6 探索噪 声方差 策略噪 声方差 DDPG 500 20 64 256 1 0. 001 0. 99 1 0. 001 1 0. 09 TD3 500 20 64 256 1 0. 001 2 0. 99 1 0. 001 1 0. 1 0. 20
3.1 场景1:负荷单次阶跃扰动
为了验证所提算法在动态条件下的性能,在t=10 s时设置加入幅值为0.1 p.u.的负荷单次阶跃扰动来模拟电网中突发的负荷变化,并与传统下垂控制、滑模控制及基于DDPG算法的控制策略进行对比。仿真得到4种控制策略下的系统频率响应、系统功率变化量、火电机组功率变化量及光伏电站功率变化量如图6所示。图6直观地展示了4种控制策略在应对负荷单次阶跃扰动时的动态性能。
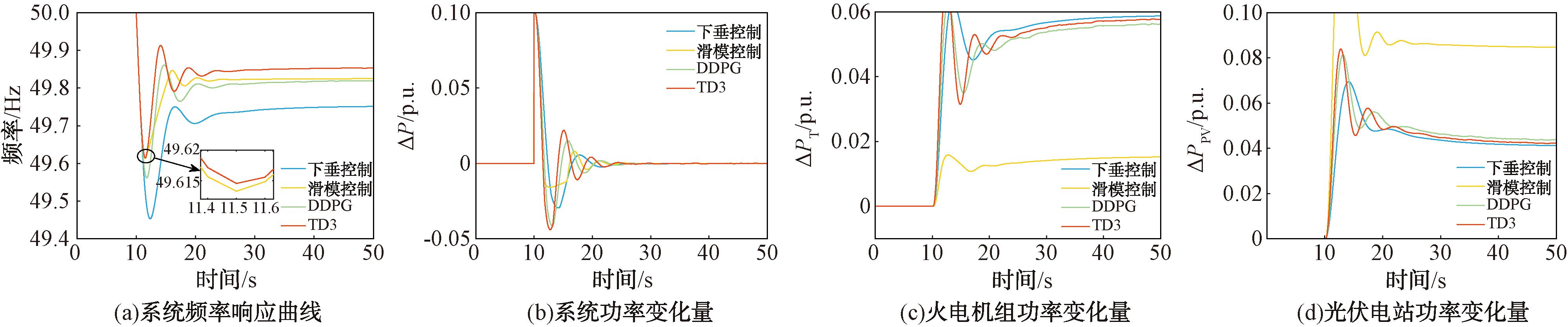
图6 负荷单次阶跃扰动下的响应曲线
Figure 6 Response curve with load single step disturbance
为了评估本文所设计的频率控制器对此类扰动的响应能力,并更准确地量化各控制策略的性能差异,引入最大频差、平均频差、稳态频差、调节时间和时间乘绝对误差积分准则ITAE等相关的动态性能指标,结果如表3所示。ITAE是一个综合评估系统动态性能和稳态性能的指标,其计算公式如式(13)所示:
ITAE=![]() t|Δf(t)|dt。
t|Δf(t)|dt。
(13)
表3 负荷单次阶跃扰动下的动态性能
Table 3 Dynamic performance with load single step disturbance

控制算法 最大频 差/ Hz 平均频 差/ Hz 稳态频 差/ Hz 调节时 间/ s ITAE 下垂控制 0. 55 0. 24 0. 25 15. 043 6. 362 0 滑模控制 0. 39 0. 15 0. 18 14. 208 4. 352 9 DDPG 0. 44 0. 16 0. 19 13. 446 4. 573 3 TD3 0. 39 0. 13 0. 15 12. 935 3. 707 1
由表3可知,TD3算法在应对负荷单次阶跃扰动时表现出较好的性能,在每个指标上均优于其他3种控制算法。TD3算法和滑模控制的最大频差均仅有0.39 Hz,这表明这两种算法在抑制扰动影响方面相对较强。TD3算法的调节时间最短,为12.935 s,显示出该算法较好的动态响应能力。TD3算法的平均频差和稳态频差都是最小的,分别为0.13 Hz和0.15 Hz,表明在整个调节过程中TD3算法都能较好地维持系统频率稳定。特别地,TD3算法的ITAE值为3.707 1,是4种算法中最小的,表明该算法整体性能最优,能明显提高系统调频质量,并且滑模控制、DDPG和下垂控制的ITAE值依次增大,进一步验证了TD3算法在应对负荷单次阶跃扰动时的优越性。
3.2 场景2:负荷连续阶跃扰动
为了模拟光伏电站在实际运行中常见的随机性和波动性,设计了如图7所示的负荷连续阶跃扰动。采用本文所设计的基于TD3算法的频率控制器进行频率调节,并与基于DDPG算法、下垂控制及滑模控制的控制策略进行对比分析,得到4种控制策略下的系统频率响应、系统功率变化量、火电机组功率变化量及光伏电站功率变化量,如图8所示。
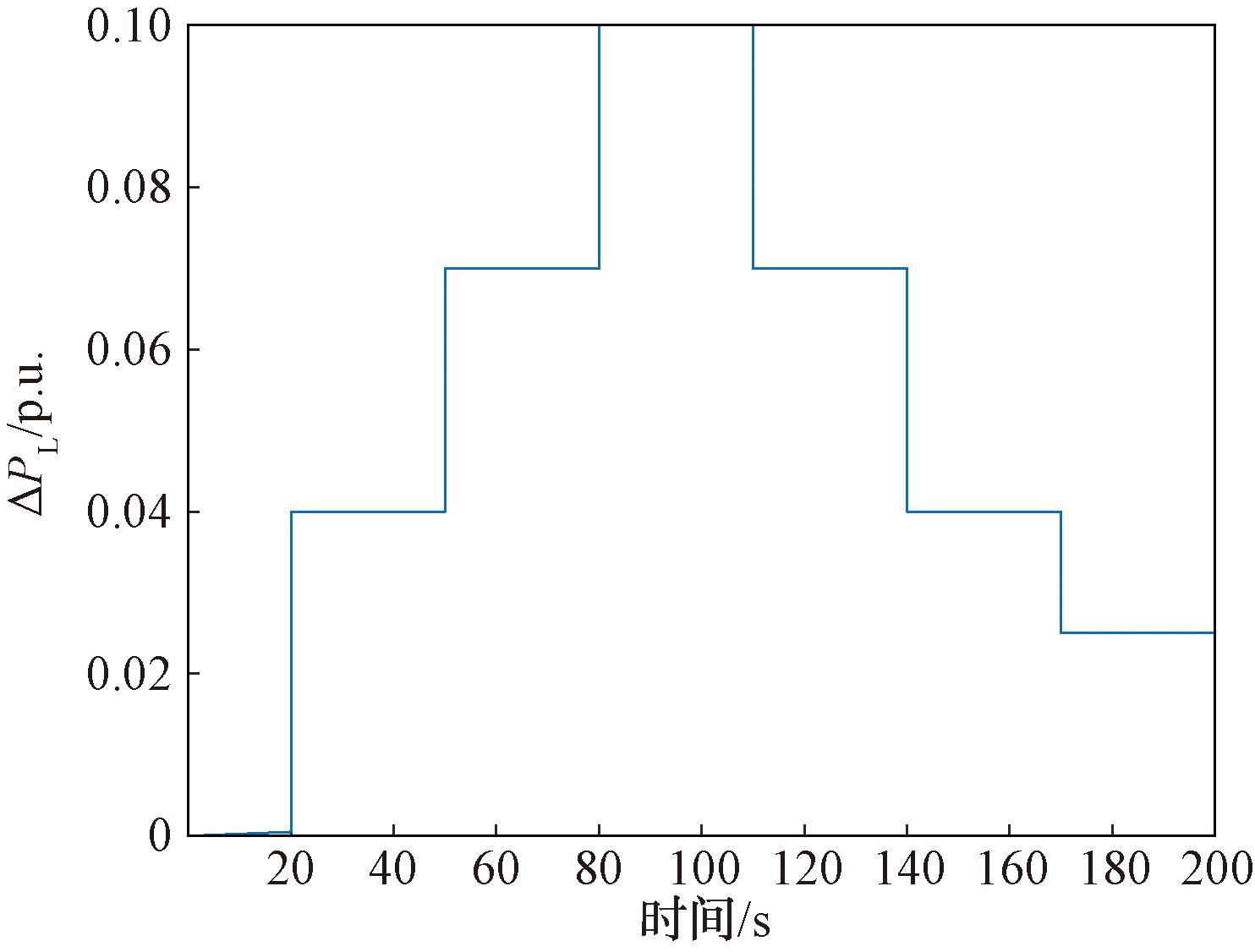
图7 负荷连续阶跃扰动
Figure 7 Load continuous step disturbances
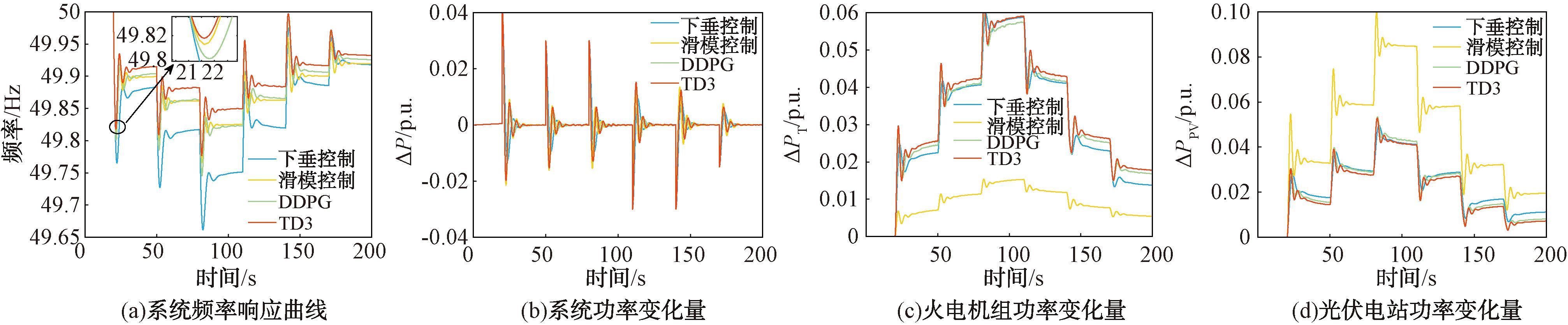
图8 负荷连续阶跃扰动下的响应曲线
Figure 8 Response curve with continuous step disturbance of load
为了评估控制系统在面对连续且不断变化的负荷扰动时的响应和调节能力,将各控制策略的最大频差、平均频差及ITAE值这3种动态性能指标汇总于表4,并进行下一步的分析和对比。
表4 负荷连续阶跃扰动下的动态性能
Table 4 Dynamic performance with continuous step disturbance of load

控制算法 最大频差/ Hz 平均频差/ Hz ITAE 下垂控制 0. 34 0. 14 55. 917 1 滑模控制 0. 23 0. 11 45. 774 4 DDPG 0. 25 0. 11 43. 636 6 TD3 0. 22 0. 09 38. 150 5
由表4可知,TD3算法在应对负荷连续阶跃扰动时表现出较好的性能,在各性能指标上都优于其他3种控制算法。TD3算法的最大频差为0.22 Hz,其次是滑模控制和DDPG算法,表明这些算法在负荷连续阶跃扰动下能够更好地维持系统频率的稳定性。TD3算法的平均频差为0.09 Hz,表现出较好的维持频率稳定的能力。仿真结果显示,当电力系统中发生负荷连续阶跃扰动时,4种算法都能在频率发生变化后快速恢复稳定,特别是TD3算法凭借其出色的快速响应特性,有效削弱了频率的波动幅度,使得系统频率偏差显著减小。TD3算法的ITAE为38.150 5,远低于其他3种算法,表明在应对连续阶跃扰动时,TD3算法在动态性能和稳态性能方面表现最优。
4 结论
针对光伏电站参与电力系统频率调节的强不确定性,本文提出了基于TD3算法的频率控制策略,旨在通过先进的深度强化学习技术提高电力系统的频率稳定性。首先详细介绍了TD3算法的原理及具体的算法流程,然后根据本文所研究的光伏发电模型,设计了基于TD3算法的频率控制器。为了全面验证该控制器的性能,在MATLAB/Simulink仿真平台上搭建仿真模型,并设置两种不同类型的负荷扰动进行仿真对比实验,由理论和仿真实验可以得出以下结论。
(1)TD3算法通过引入双重网络、目标策略平滑正则化和延迟更新等技术,能有效提高学习性能和稳定性,适用于解决电力系统的调频问题。
(2)在负荷单次阶跃扰动和负荷连续阶跃扰动两种扰动下,基于TD3算法的控制策略能够迅速反应,且能有效抑制频率的波动,确保电力系统的稳定运行,显著提高了系统的调频质量。与所设置的3种对比算法相比,所提控制策略的控制性能优于其他控制方法,表明TD3算法在频率调节方面的优越性。TD3算法优秀的控制性能不仅体现在对频率波动的有效抑制上,更在于其为电力系统的稳定运行提供了强有力的保障,对促进新能源友好并网的发展和维护电网频率稳定具有重要意义。
[1] 罗朋, 陈光浩, 杨东红, 等. 用于新能源发电的新型升降压转换器及其控制策略[J]. 郑州大学学报(工学版), 2024, 45(2): 97-105.
LUO P, CHEN G H, YANG D H, et al. A novel buck-boost converter and its control strategy for new energy power generation[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(2): 97-105.
[2] 王燕, 杨秀媛, 徐剑锋, 等. 民用可控负荷参与需求响应的控制策略[J]. 发电技术, 2020, 41(6): 638-649.
WANG Y, YANG X Y, XU J F, et al. Control strategy of civil controllable load participating in demand response[J]. Power Generation Technology, 2020, 41(6): 638-649.
[3] 王明东, 杨岙迪, 李龙好, 等. 基于VSG下垂优化控制的新能源电力系统惯性提升[J]. 郑州大学学报(工学版), 2024, 45(3): 127-133.
WANG M D, YANG A D, LI L H, et al. Inertia lifting of new energy power system based on VSG droop optimal control[J]. Journal of Zhengzhou University (Engineering Science), 2024, 45(3): 127-133.
[4] SU Y, LI H Y, CUI Y, et al. An adaptive PV frequency control strategy based on real-time inertia estimation[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 2355-2364.
[5] ZHANG J H, ZHANG B, LI Q, et al. Fast frequency regulation method for power system with two-stage photovoltaic plants[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1779-1789.
[6] RAJESH T, GUNAPRIYA B, SABARIMUTHU M, et al. Frequency control of PV-connected micro grid system using fuzzy logic controller[J]. Materials Today: Proceedings, 2021, 45: 2260-2264.
[7] VANTI S, BANA P R, D′ARCO S, et al. Single-stage grid-connected PV system with finite control set model predictive control and an improved maximum power point tracking[J]. IEEE Transactions on Sustainable Energy, 2022, 13(2): 791-802.
[8] LI Z W, CHENG Z P, SI J K, et al. Adaptive power point tracking control of PV system for primary frequency regulation of AC microgrid with high PV integration[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3129-3141.
[9] CUI W Q, JIANG Y, ZHANG B S. Reinforcement learning for optimal primary frequency control: a Lyapunov approach[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1676-1688.
[10] ZHANG Y, SHI X H, ZHANG H X, et al. Review on deep learning applications in frequency analysis and control of modern power system[J]. International Journal of Electrical Power &Energy Systems, 2022, 136: 107744.
[11] ZHANG Z D, ZHANG D X, QIU R C. Deep reinforcement learning for power system applications:an overview[J]. CSEE Journal of Power and Energy Systems, 2020, 6(1): 213-225.
[12] YAN Z M, XU Y. Data-driven load frequency control for stochastic power systems:a deep reinforcement learning method with continuous action search[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1653-1656.
[13] SUN J, ZHU Z Q, LI H Q, et al. An integrated critic-actor neural network for reinforcement learning with application of DERs control in grid frequency regulation[J]. International Journal of Electrical Power &Energy Systems, 2019, 111: 286-299.
[14] 杨悦, 王丹, 胡博, 等. 基于改进多智能体Q学习的多源最优联合调频控制策略研究[J]. 电力系统保护与控制, 2022, 50(7): 135-144.
YANG Y, WANG D, HU B, et al. Multi-source optimal joint frequency modulation control strategy based on improved multi-agent Q-learning[J]. Power System Protection and Control, 2022, 50(7): 135-144.
[15] MU C X, TANG Y F, HE H B. Improved sliding mode design for load frequency control of power system integrated an adaptive learning strategy[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6742-6751.
[16] CHEN X D, ZHANG M, WU Z G, et al. Model-free load frequency control of nonlinear power systems based on deep reinforcement learning[J]. IEEE Transactions on Industrial Informatics, 2024, 20(4): 6825-6833.
[17] 秦智慧, 李宁, 刘晓彤, 等. 无模型强化学习研究综述[J]. 计算机科学, 2021, 48(3): 180-187.
QIN Z H, LI N, LIU X T, et al. Overview of research on model-free reinforcement learning[J]. Computer Science, 2021, 48(3): 180-187.
[18] FUJIMOTO S, VAN HOOF H, MEGER D. Addressing function approximation error in actor-critic methods[EB/OL]. (2018-10-22)[2024-06-09]. http:∥arxiv.org/abs/1802.09477.
[19] 赵大伟, 马进, 钱敏慧, 等. 光伏电站参与大电网一次调频的控制增益研究[J]. 电网技术, 2019, 43(2): 425-433.
ZHAO D W, MA J, QIAN M H, et al. Research on control gain for photovoltaic power plants participating in primary frequency regulation of large power grid[J]. Power System Technology, 2019, 43(2): 425-433.
[20] KHALID J, RAMLI M A M, KHAN M S, et al. Efficient load frequency control of renewable integrated power system: a twin delayed DDPG-based deep reinforcement learning approach[J]. IEEE Access, 2022, 10: 51561-51574.
[21] TANG Y H, HU W H, CAO D, et al. Deep reinforcement learning aided variable-frequency triple-phase-shift control for dual-active-bridge converter[J]. IEEE Transactions on Industrial Electronics, 2023, 70(10): 10506-10515.
[22] KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. (2017-01-30)[2024-06-09]. https:∥arxiv.org/abs/1412.6980.
[23] LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[EB/OL]. (2019-07-05) [2024-06-09]. https:∥arxiv.org/abs/1509.02971.