基于制造执行系统(manufacturing execution system,MES)的集中计划运行模式可实现上层生产信息与下层车间之间的信息传递和资源调配,但也存在明显弊端[1]。运输资源之间缺乏必要的协作机制导致生产异常频发,难以实现实时响应和动态调度。为解决这一问题,自主移动机器人(autonomous mobile robot,AMR)作为一种具备环境感知、路径规划和避障功能的移动机器人,可以实现高效的自主协作与任务分配[2-4]。
针对传统配送模式单一固定的问题,可借鉴滴滴打车和美团外卖等软件的“抢单”配送模式,提高生产任务的灵活性以满足现代制造环境的需求[5]。“抢单”模式使配送方式从被动接受任务转变为主动参与,提高了运输效率。因此,本文主要研究AMR自主任务分配算法,多个AMR之间通过合作或竞争获取资源,快速响应任务变化并做出最佳分配决策。
关于运输任务分配,典型的研究有:刘广瑞等[6]建立了执行多目标无人机协同的多任务分配模型;Wu等[7]提出了一种用于无人系统群体的同时进行任务分配和轨迹规划的方法, 解决了任务分配和轨迹规划子问题;王俊英等[8]提出了一种任务分配概率自适应的蚁群算法,提升了算法的执行效率;吴蔚楠等[9]在多无人机执行任务的背景下,进行了任务分配的建模、算法设计和分析;鞠锴等[10]基于势博弈理论设计任务分配算法,在降低复杂度的同时,得到了近似最大化的期望全局效用的分配方案;施伟等[11]基于深度强化学习的多机协同空战决策流程的框架,针对PPO(proximal policy optimization)算法设计了4种算法增强机制,提高了智能体之间的任务分配协同程度;Motes等[12]提出了一种多机器人任务和运动集成方法,能够处理多个可分解任务中的顺序子任务依赖关系。
此外,强化学习模型的发展也为解决机器学习中各种顺序决策问题提供了新的思路。Yin等[13]提出了一种深度强化学习中考虑注意力的分散式多任务分配框架用于分配应用。Li等[14]提出了一种基于强化学习的并发任务和安全应急任务分配方法,解决了并发任务分配问题。Oroojlooy等[15]把MARL(multi-agent reinforcement learning)方法分成了5个类别(独立学习者、完全可观察的批评、价值函数分解、共识和学习沟通)用于解决多智能体合作强化学习问题。Wang等[16]基于适应度提出了一种分层强化学习方法,用于复杂地形条件下的多人机任务分配。Xiao等[17]提出了一种改进的粒子群优化算法,解决了AGV任务的多模式资源受限调度问题。
综上所述,强化学习方法因其自适应性强、可以自我调节、适用于复杂环境、能够探索未知领域和实时决策能力强等特点,在柔性生产协同决策方面具有重要的应用价值。本文基于多智能体强化学习算法,提出了一种改进多智能体强化学习算法-多智能体深度确定性策略梯度算法(multi-agent deep deterministic policy gradient,MADDPG)。
1 AMR任务分配问题的描述
柔性车间中AMR任务分配问题可描述如下:有n个工件需要在m台机器上进行加工,运输由N台AMR完成。每个工件都需要有s道工序,s≥1。每道工序都有一个对应的加工时间和加工机器集合。
根据以上描述进行假设:①在0时刻,所有机器处于空闲可用状态,所有AMR和工件材料都在装卸货点准备就绪;②不考虑机器和AMR故障等因素,AMR在各个工位的装载/卸载时间均已知,机器间运输时间固定;③每台加工机器旁边均设有一定容量的缓存区,用于存放待加工工件;④每个AMR能够实时感知和更新自身状态,还可以获取其他AMR状态;⑤AGV获得的任务下发顺序即为工件加工顺序,随着加工的不断进行,任务在不间断下发;⑥每个AGV的物料装载时间和卸载时间相同。
2 基于MADDPG算法的AMR任务分配
2.1 算法框架
在多AMR协作环境当中,每一个AMR都是独立的Agent,算法需要不断学习来达到改进策略的目的[18];基于单个AMR视角,环境从静态转变为动态。这与传统强化学习收敛的条件大不相同,在一定程度上导致无法仅仅通过改变单个Agent自身的策略来适应不稳定的环境,并且在实际应用中,传统策略梯度算法中的误差会随着Agent数量的增加而增大。而MADDPG算法基于Actor-Critic思想[19]和DDPG(deep deterministic policy gradient)[20]进行了一系列的改进,Agent通过学习每个状态下的最优策略来优化自己的策略网络(Actor网络)和价值网络(Critic网络),并考虑其他Agent的策略和行动来提高效率。
MADDPG算法采用了中心式训练和分散式执行(centralized training and decentralized execution, CTDE)[21]的框架,如图1所示。在训练阶段,每个AMR将得到的环境信息输入到自己的策略网络中,然后策略网络输出动作信息,并将这些动作应用于环境。环境的响应导致状态的变化和奖励值的产生,每个AMR不断与环境交互,不断获得新环境的状态和奖励值,最后将这些信息存储到各自的经验池中。
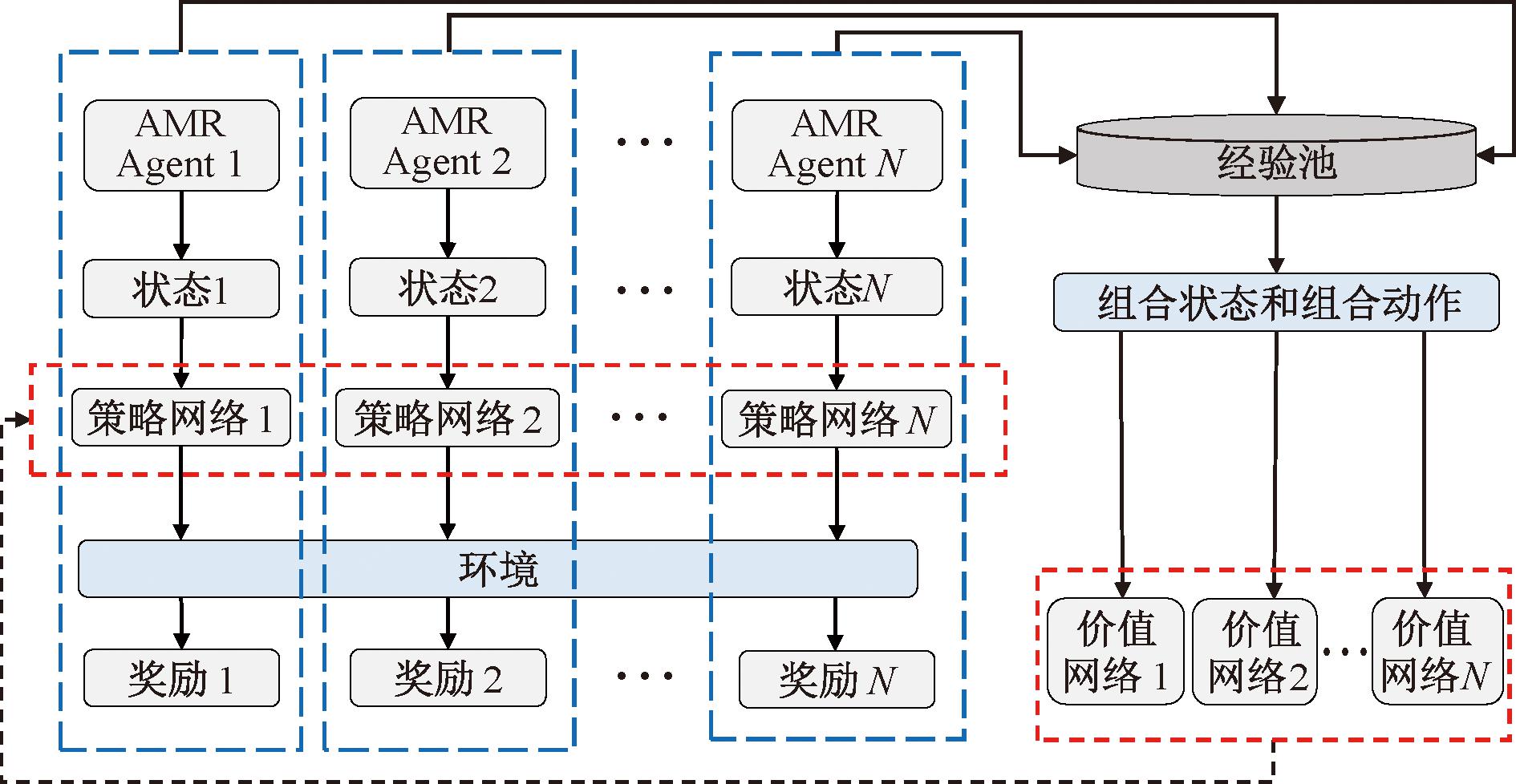
图1 MADDPG算法框架
Figure 1 MADDPG algorithm framework
2.1.1 中心式训练分散式执行框架分析
中心训练分散执行具体实现过程:每个AMR根据自身策略得到当前状态执行的动作,并与环境交互得到经验存入自身的经验缓存池。待所有AMR与环境交互后,每个AMR从经验池中随机抽取经验训练各自的神经网络。如图2所示,在训练过程中,根据现有的本地局部观察信息oi,Actor网络会采取一个动作ai,将其作为Critic网络的输入,得到一个Q值,并反馈给 Actor网络,指挥Actor网络的策略更新,因此,在训练过程中Actor网络与Critic网络都参与;而测试过程仅由Actor网络根据局部信息生成动作,无须Critic的反馈。
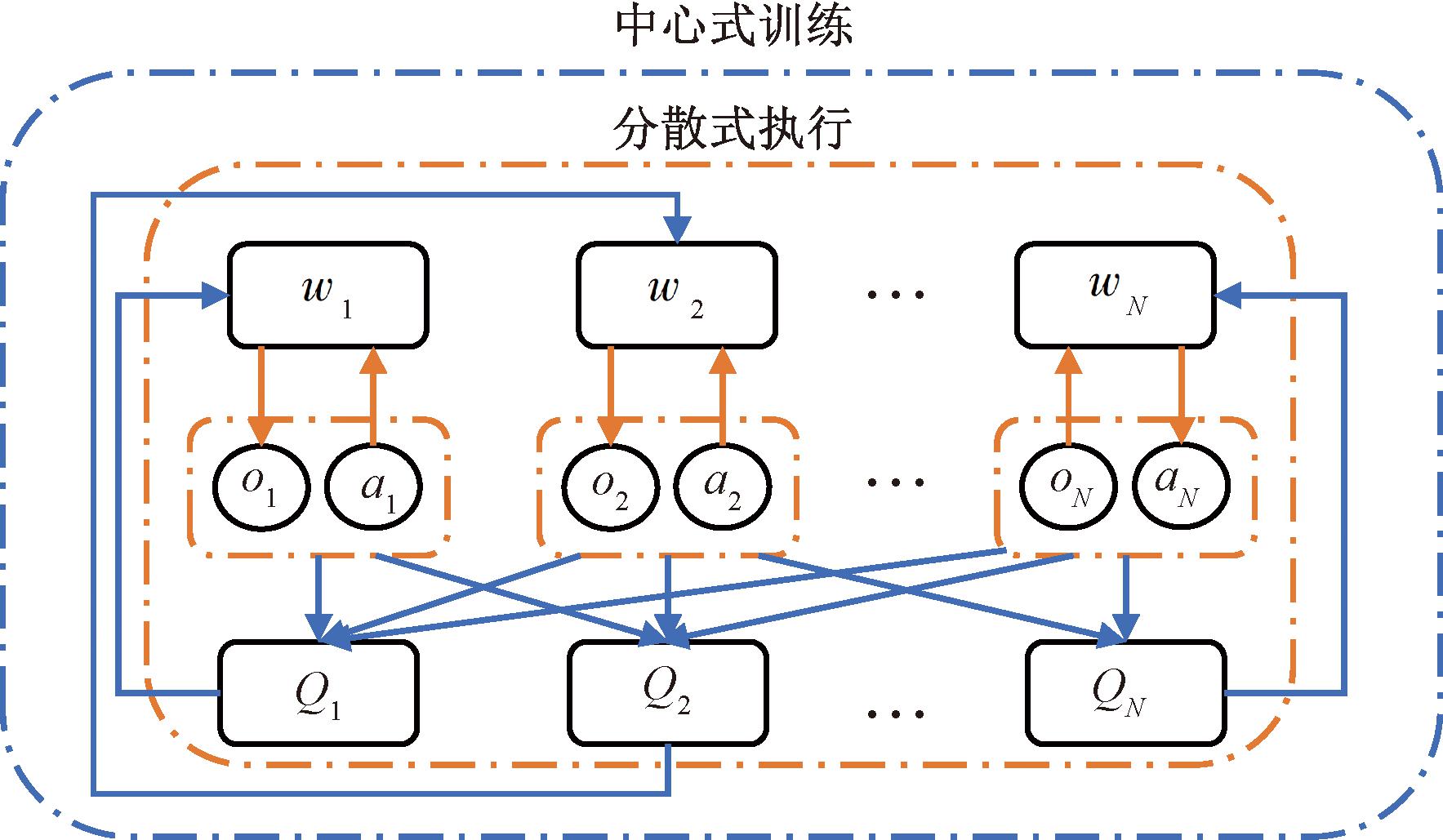
图2 中心式训练分散式执行
Figure 2 Centralized training and decentralized execution
集中训练:采用联合状态价值动作值函数对策略进行评估,同时加入其他额外信息,能够更优地评估联合策略。该模式改善了算法的收敛效果且有助于解决多智能体强化学习中的非平稳性问题。在训练阶段,AMR的Actor首先基于当前状态选择一个动作,然后Critic计算基于状态-动作对应的Q值,反馈给Actor,促使其优化动作策略。而在测试阶段,仅需要Actor来执行任务,无须Critic的反馈。
分散执行:完成强化学习的交互训练后,AMR能够根据局部观测在不同状态下做出最优决策。这种方法考虑到了实际场景中的观测限制,每个Actor都可以根据自身状态采取合适的动作,不需要其他AMR的状态或动作。
综上,集中训练和分散执行是考虑了强化学习算法训练和实际场景限制的最佳训练方式。在训练过程中充分考虑了环境和AMR的状态,在执行阶段只需AMR的局部观测即可做出决策,更符合实际场景。因此,采用集中训练分散执行的框架可确保多AMR协作环境的稳定性。
2.1.2 基于注意力机制的MADDPG算法
在神经网络的训练过程中,通过从AMR的经验池中随机抽取相同时刻的数据,构建一组经验样本(o,a,o′,r)。其中o为所有AMR的状态信息集合;a为AMR的动作集合;o′为AMR在做出动作后的环境状态信息集合;r为AMR的奖励值。最后将o′输入到Ai(第i个AMR)的目标策略网络中得到动作a′,随后将所有AMR的状态信息和动作信息组成联合状态和联合动作,输送到Aj(第j个AMR)的Critic网络中,计算下一时刻的目标Q值,计算公式为
ri=γQ′(si+1,u′(si+1|Qu′)|θQ′)。
(1)
式中:Q′为AMR的决策结果;Qu′为AMR目标策略的决策结果;ri为奖励值;γ为相关系数;si+1为第i+1个AMR的状态;u′为目标策略;θQ′为具有滞后更新的策略参数。
实际的Q值是通过一个评价网络得到的,这个评价网络会根据时间差异误差(TD-error)进行对应的更新。算法使用策略梯度来更新策略网络,策略网络与价值网络的具体结构如图3所示。
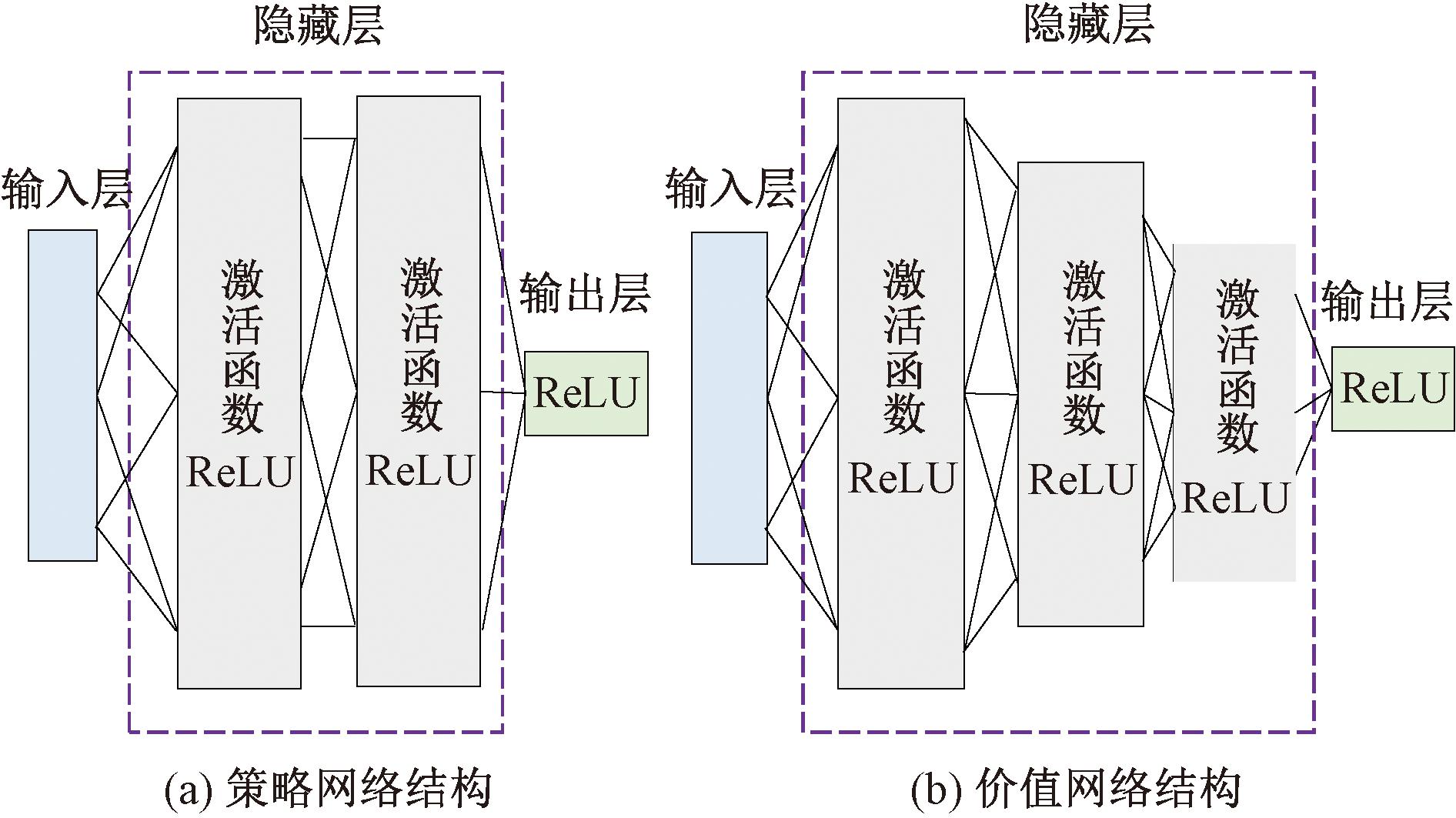
图3 网络结构
Figure 3 Network structure
环境中AMR用A表示,其策略集合为w={w1,w2,…,wN},参数集合θ={θ1,θ2,…,θN},联合动作a=(a1,a2,…,aN),联合状态o=(o1,o2,…,oN)。Ai的策略集合为wi,策略参数为θi,联合动作为ai,联合状态为oi,每一个样本数据组成为(x,x′,a1,a2,…,aN,r1,r2,…,rN),Ai的期望收益梯度为
(2)
式中:pw为状态分布;
为联合动作值函数,即集中式的状态-动作函数,每一个样本数据不仅包含了自身观测到的状态和所执行的动作,而且包含了其他AMR的动作。
针对每一个AMR建立了值函数,极大地弥补了传统强化学习算法在多Agent领域的不足。因此,每一个AMR的Critic网络不仅清楚自身AMR的变化,也知道其他所有AMR的动作策略,即使策略在不断地更新变化,环境还是稳定的。的更新公式为
(3)
MADDPG算法解决了Agent之间不可观测性的问题,但随着Agent数量的增加,问题的复杂度也随之增大。在多AMR环境中,为了应对这一挑战,引入了注意力机制,这使得每个AMR能够观察其他AMR的信息,并根据信息的重要性将其整合到自身的动作值函数估计中。这种机制允许每个AMR专注于某些信息,这些信息对于获取更大的奖励至关重要,而不是无目标地学习其他AMR提供的全部信息。在Critic模块中引入注意力机制可以实现这一目标。注意力机制的结构如图4所示。
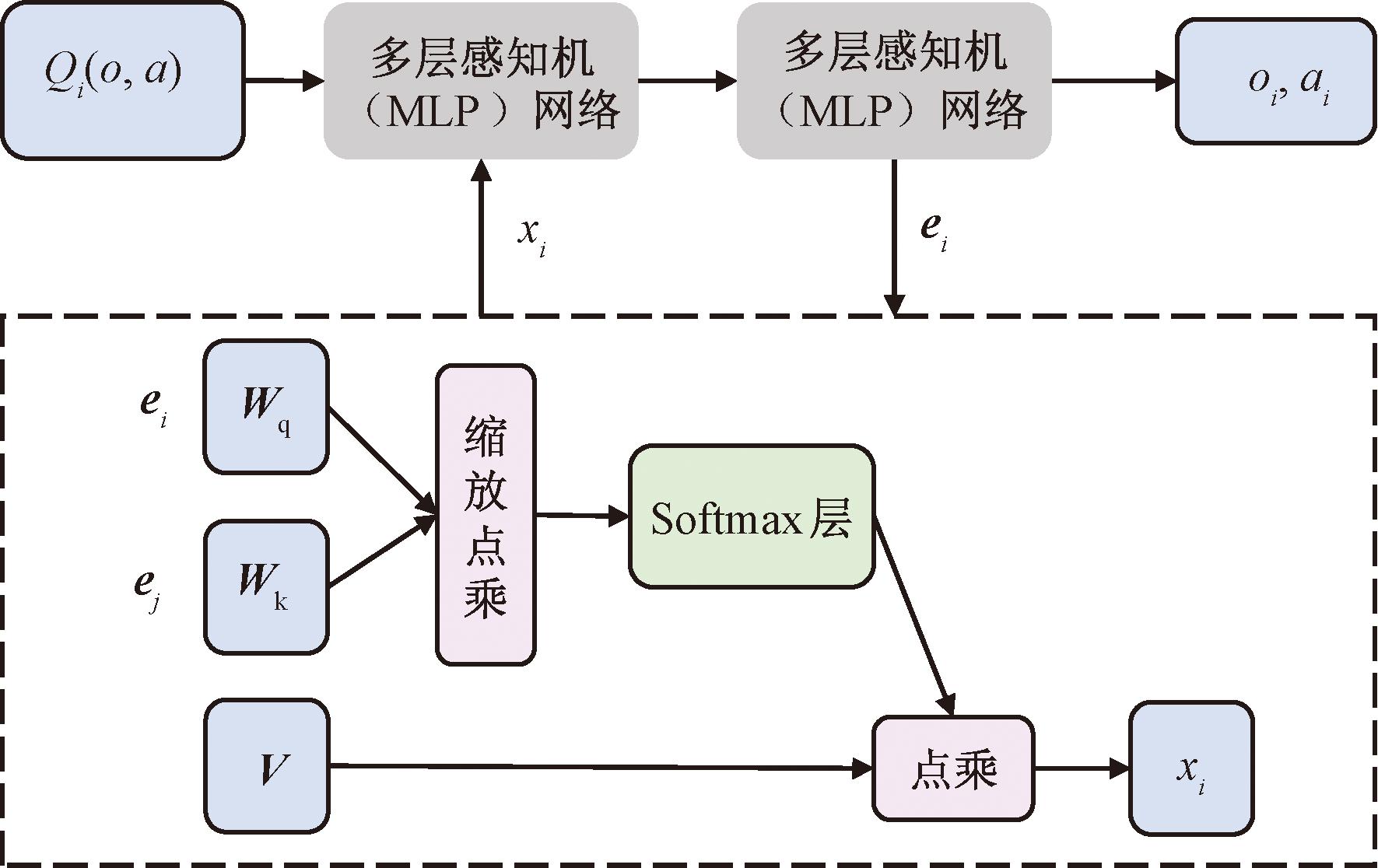
图4 注意力机制结构
Figure 4 Structure of attention mechanism
加入注意力机制后,算法发生改变,此时需要对Q值函数进行改进,Ai的Q值函数Qi(o,a)为
Qi(o,a)=fi(gi(oi,ai),xi)。
(4)
式中:ai表示策略ui与环境不断进行交互后做出的动作。多层感知机(multi-layer perception,MLP)[22-23]是由多个全连接层构成的神经网络,每个全连接层都由线性变换和非线性变换组成。式(4)中包含一个两层的MLP网络fi和一个单层MLP嵌入式网络函数gi。xi为其他AMR对Ai价值的加权和,计算式为
(5)
式中:vj为Aj的嵌入式编码函数;h(·)为ReLU激活函数;V为共享矩阵;αj为注意力权重,通过查询值-键值系统比较ej=gj(oj,aj)与ei=gi(oi,ai),将Aj和其相似值传达给Softmax网络,得到:
(6)
式中:ei和ej分别表示Ai和Aj的状态编码;Dk表示维度;Wk和Wq分别代表两个线性映射的矩阵,Wk将ej转化为键值,Wq将ei转化为查询值;每个参数 (Wq,Wk,V)都是独立的。
2.2 动作设置
AMR的动作空间是一个连续二维空间,每个AMR的速度主要包括两个方向:一个是X方向上的速度Vx,一个是Y方向上的速度Vy,将这两个方向上的速度进行矢量合成,根据t时刻的状态输入,输出一个确定速度。
表示在 X方向上t时刻所有AMR采取的接收策略;
表示在Y方向上t时刻所有AMR采取的接收策略;
为联合动作。则AMR在t+Δt时刻的位置动作为
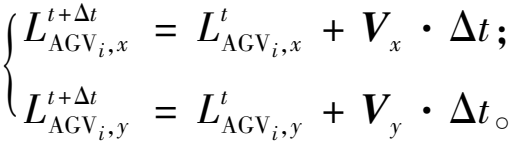
(7)
2.3 状态设置
2.3.1 工件任务状态
任务Ti在t时刻的状态用函数StateTi(t)=(posi(t),ci,calli(t),Rewardi(t))表示,其中posi(t)表示任务Ti的位置信息,posi(t)=(xi,yi);ci,1表示任务节点i对能力1的需求,ci={ci,1,ci,2,…,ci,n};calli(t)=1和calli(t)=0分别表示生产过程中t时刻Ti对AMR有任务需求和无任务需求。
2.3.2 AMR状态
在AMR自主调度过程中,AMR在时刻t的状态用函数StateAj(t)=(posj(t),cj,bj,q(t))表示。其中,posj(t)为Aj在t时刻的位置信息,posj(t)=(xj,yj);cj={cj,1,cj,2,…,cj,n},cj,1表示Aj在能力1上的取值,n为能力类型的数量;bj为Aj的速度值;q(t)为t时刻的Aj任务分配状态矩阵。qi,j(t)=1表示t时刻将目标任务Ti分配给Aj;qi,j(t)=0表示未将任务Ti分配给Aj,即Aj处于空闲状态。通过计算位置坐标,得到AMR与任务节点间的距离,见式(8),二者能力匹配值eij的计算公式见式(9),其中,cij表示能力匹配系数,所能提供的能力值与任务节点所需能力值之间差别越大,说明采用该AMR来完成该任务的效果越好。cij等于2表示AMR能力值大于该任务节点需求值,等于0.5表示AMR能力值小于任务节点需求值,见式(10)。
(8)
(9)
(10)
多AMR各自进行决策,输出的结果组成一个完整的AMR分布式协同调度方案Q={Q1,Q2,…,QA},其中,Qj表示对应Aj所获得的决策结果。
2.4 奖励函数设计
奖励函数设置如式(11)和式(12)所示,R为总奖励函数。
R=R1+R2+R3-R4;
(11)
(12)
式中:
为碰撞奖励,当两个AMR之间距离低于安全距离时,给予一个负的奖励,
表示惩罚;
为距离奖励,将AMR和任务工件距离作为奖励值,距离越近,奖励值越多,
表示t时刻任务Ti被某AMR选择执行后所能得到的奖励;
为所有AMR碰撞奖励之和;
为所有AMR距离奖励之和;R3=∑eij为各智能体与任务节点的能力匹配之和;R4为没有被分配对应的AMR的任务节点的数量。
在多AMR分布协同调度场景中,目标是车间里所有任务都被AMR自主分配,且各个AMR的能力都得到了匹配,达到群体最优。在车间AMR调度场景中将各AMR 视为多个决策Agent,“AMR Agent-配送任务”的匹配可以视为一个多智能体强化学习任务训练过程,AMR需要不断地学习来提高自己和群体的智慧。AMR的协同调度优化问题的目标函数即作为强化学习中的奖励信号,奖励函数的设计可以根据任务节点的覆盖程度以及完成效果来进行设计。
算法1 多AMR协作任务分配强化学习算法。
输入:初始化各智能体策略网络的参数θ=(θ1,θ2,…,θN),价值网络参数φ=(φ1,φ2,…,φN);
输出:训练后的最优参数θ*、φ*。
① For iep←1,2,…,max eposide do
② 重置环境,得到每个智能体的联合状态o=(o1,o2,…,oN);
③ 根据各智能体的策略网络得到各智能体的动作ai～wi(·|oi),
④ 将联合动作a=(a1,a2,…,aN)输入到环境中,得到反馈的奖励值r=(r1,r2,…,rN);
⑤ 将各智能体的数据元组(oi,ai,ri)存储到数据池datapool中,
⑥ If iep>最小参数更新间隔,
⑦ 从datapool中采样出一个批次的数据样本dataset,
⑧ for agent i=1 to N：
⑨ 计算各智能体的策略网络和价值网络的梯度值
⑩ for Agent i =1 to N：
更新各智能体的策略网络和价值网络的参数
θi←(1-δ)θi+δ·Adam(dθi)
φi←(1-δ)φi+δ·Adam(dφi)
end for。
3 仿真测试
选取某智能离散机加车间作为案例仿真场景,AMR从当前位置出发接受任务,并对相应的工位进行物料配送。在该场景中,有3个AMR参与了调度,设计了两组实验进行分析,如图5所示。在第1组实验中,任务分布情况如图5(a)所示;在第2组实验中,下发了新的随机任务,任务分布情况如图5(b)所示。实验使用基于MADDPG的任务动态分配算法与现有的DQN算法以及BicNet算法进行训练和比较。
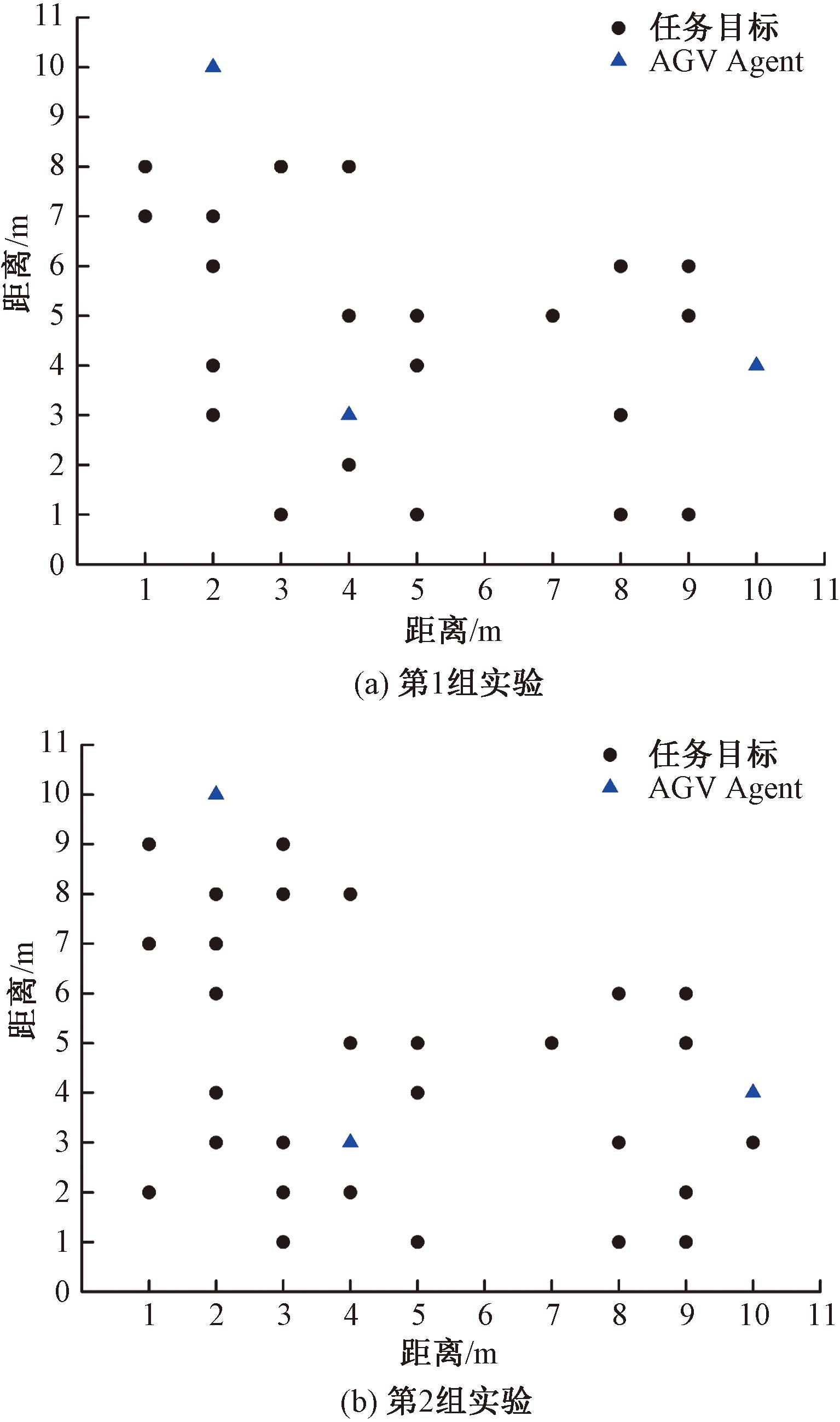
图5 实验任务布局
Figure 5 Layout of experimental tasks
3.1 参数设置
在Pycharm上进行仿真,采用的核心工具包的版本为python3.6.0、tensorflow1.8.0、numpy1.14.5、 gym0.10.5。神经网络隐藏层使用ReLU函数作为激活函数,策略和价值网络均采用了Adam Optimizer优化器进行学习,MADDPG 算法、DQN算法和BicNet算法的网络结构参数分别如表1、表2和表3所示。经过测试,模型在经过1 000次训练后基本收敛,因此训练迭代次数设定为1 000次,为平衡模型更新速度与训练性能,网络参数的批次大小被设置为64,经验池的大小为1 000 000。
表1 MADDPG 网络结构参数
Table 1 MADDPG network structure parameters
参数 取值 参数 取值 经验池大小 10 6 策略网络层数 3 隐藏层神经元 64 价值网络层数 3 更新批次大小 64 价值网络学习率 0. 01 训练次数 1 000 策略网络学习率 0. 01
表2 DQN 网络结构参数
Table 2 DQN network structure parameters
参数 取值 参数 取值 经验池大小 10 6 折扣因子 0. 9 学习率 0. 001 ε-贪心策略参数 0. 01 更新批次大小 64 目标网络更新频率 次/ (200 步) 训练次数 1 000
表3 BicNet 网络结构参数
Table 3 BicNet network structure parameters
参数 取值 参数 取值 经验池大小 10 6 ε-贪心策略参数 0. 01 学习率 0. 001 训练次数 1 000 更新批次大小 64 目标网络更新频率 次/ (200 步)
MADDPG算法的训练过程可分为两个主要阶段。第1阶段为数据收集,在每个episode中,各自的Actor网络根据当前状态选择动作并执行;然后,观察下一个状态、奖励和终止信号,并将这些经验存储到经验回放缓冲区中。第2阶段为网络更新,当经验回放缓冲区的样本数量达到一定值时,从中随机采样一批经验;对于每个AMR,根据当前状态和动作计算目标Q值,并使用这些值更新Actor网络和Critic网络的参数。
3.2 结果分析
通过MADDPG算法训练,第1组实验和第2组实验的3个AMR调度结果如图6所示,每个AMR都选择了最合适的配送任务,使得AMR的运动范围之和最小,整体完成时间达到最小。
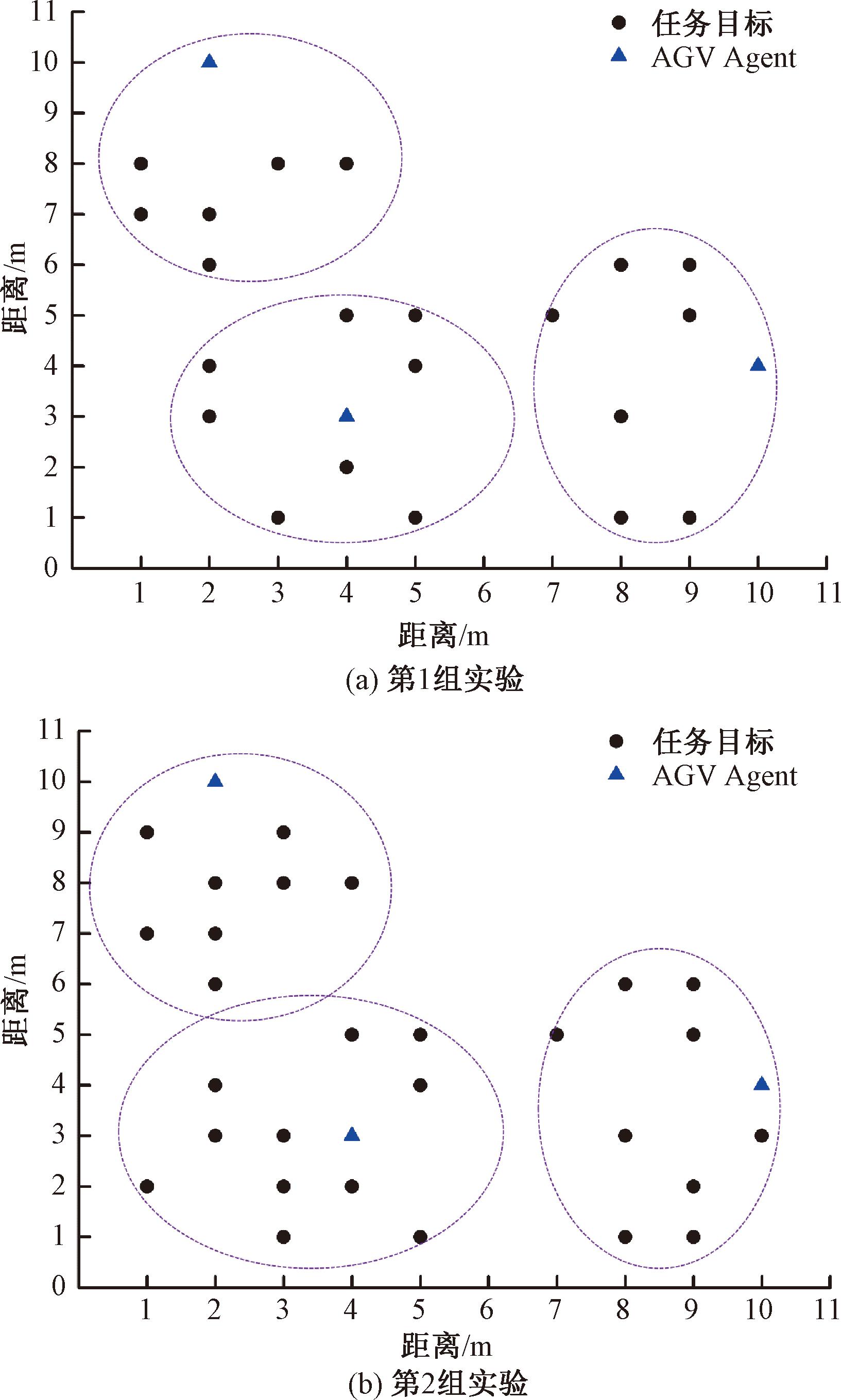
图6 AMR调度结果
Figure 6 AMR scheduling results
本案例验证算法在AMR执行任务中对任务开始时间和完成时间进行了设定,即考虑任务在一定时间约束下的完成度。
第1组实验不同算法的各个AMR的奖励曲线对比如图7所示,横坐标是训练次数,纵坐标是奖励值。每个AMR在MADDPG算法训练下的奖励值是最高的且能较快达到收敛。同时随着训练次数的增多,奖励逐渐增大,在模型训练初期,AMR由于训练刚开始,还未学会与其他AMR进行协同,没有考虑群体目标,导致任务完成效率较低,AMR获得的奖励值有限,且波动较后期有较大浮动,但随训练时间的增加,AMR不断“试错”,逐步地学会根据自身情况和外界信息与其他AMR进行分布式协同,从而完成群体任务的分配。在训练次数达到1 000次后,算法的奖励曲线都趋于平缓,呈收敛趋势。
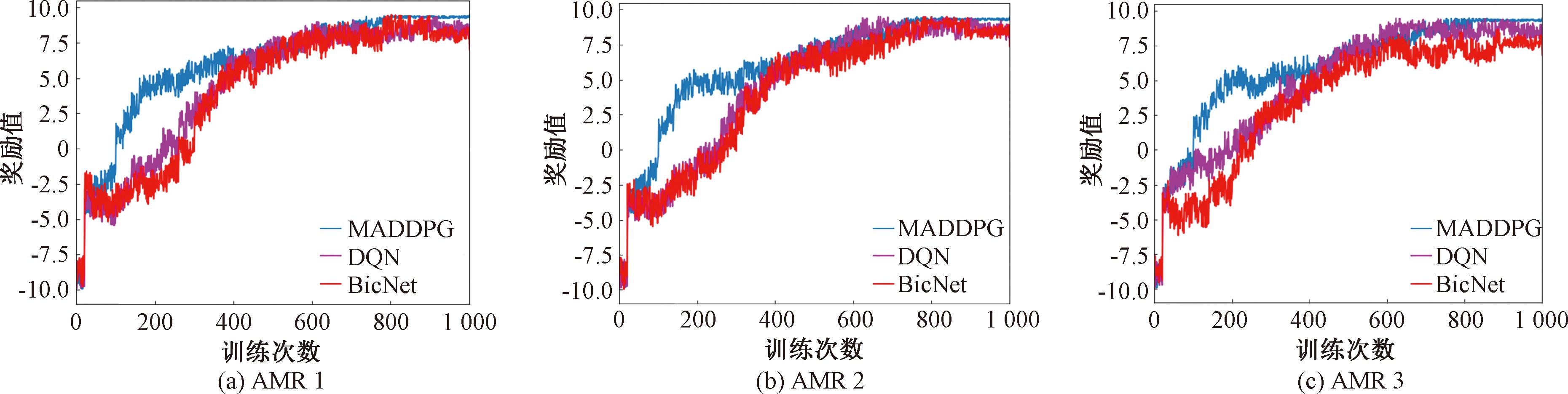
图7 第1组实验AMR的算法奖励曲线图
Figure 7 Algorithm reward curve of the first group of experiment AMR
第2组实验下系统在前期随机下发新任务后不同算法奖励值随训练次数变化的情况如图8所示。新任务刚下发时,AMR未执行过此新任务,因此奖励值变化不大,且有一定的波动,但随着训练次数的增加,整体奖励值逐渐恢复上升趋势,MADDPG算法在执行过程中展现出了更高的学习速度。相比其他算法,MADDPG算法的任务完成度位于前列,MADDPG算法的平均奖励值较其他算法增幅为3,训练次数减少了300次,学习速度更快,且能很快达到收敛。随着任务增多,时间约束更加严格。采用动态决策策略,有助于完成任务。因此,提出的MADDPG算法在下发新任务的突发情况下,能够有效地进行实时分析,实现群体决策,最终获得最优任务分配结果,提高整体任务完成效率。
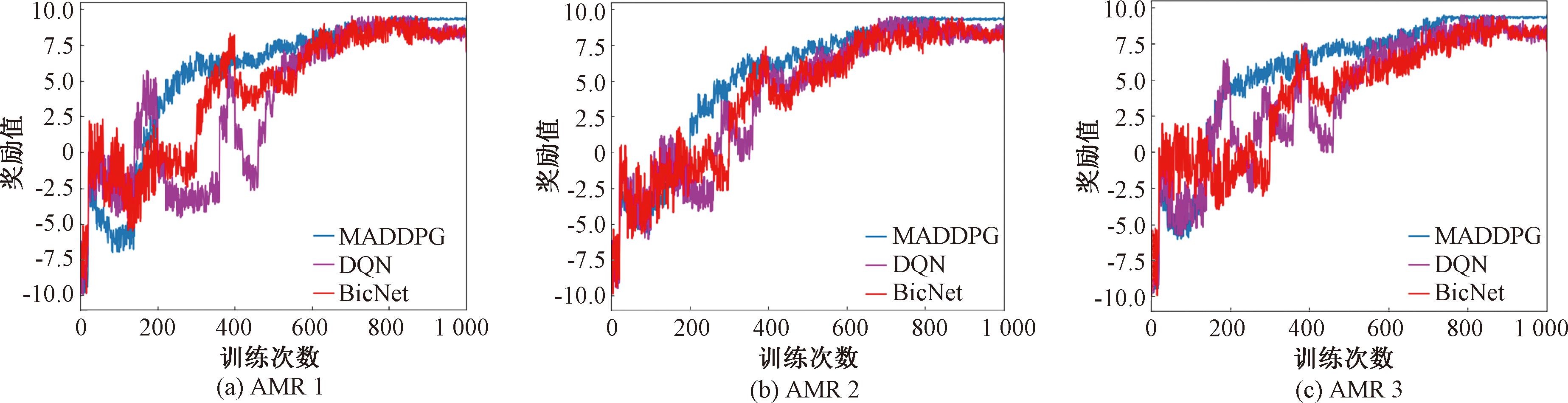
图8 第2组实验AMR的算法奖励曲线图
Figure 8 Algorithm reward curve of the second group of experiment AMR
4 结论
(1)设计MADDPG算法来实现AMR的任务分配,并引入注意力机制,对AMR的动作以及状态进行了设置,通过奖励值的大小提高了任务节点的覆盖程度以及任务的完成效果,AMR通过与环境的不断交互训练,与其余AMR信息共享,最终各自独立选择了任务,提高了AMR任务分配效率。
(2)通过仿真测试对比,MADDPG算法中的任务完成效率比DQN和BicNet算法高,MADDPG算法的平均奖励值较其他算法增幅为3,同时在下发新任务后,在同一奖励值下,MADDPG算法的训练次数比其他算法少300次。因此,MADDPG算法在保证求解任务分配完成度的基础上,具有更快的学习速度和稳定的收敛过程。
[1] SHOJAEINASAB A, CHARTER T, JALAYER M, et al. Intelligent manufacturing execution systems：a systematic review[J]. Journal of Manufacturing Systems, 2022, 62: 503-522.
[2] 李腾, 冯珊. 面向 “货到人” 拣选系统的一种随机调度策略[J]. 工业工程, 2020, 23(2): 59-66.
LI T, FENG S. A research on a random scheduling strategy of “rack to picker” picking system[J]. Industrial Engineering Journal, 2020, 23(2): 59-66.
[3] FRAGAPANE G, IVANOV D, PERON M, et al. Increasing flexibility and productivity in Industry 4.0 production networks with autonomous mobile robots and smart intralogistics[J]. Annals of Operations Research, 2022, 308(1): 125-143.
[4] HERCIK R, BYRTUS R, JAROS R, et al. Implementation of autonomous mobile robot in SmartFactory[J]. Applied Sciences, 2022, 12(17): 8912.
[5] WANG X, WANG L, WANG S Y, et al. Recommending-and-grabbing: a crowdsourcing-based order allocation pattern for on-demand food delivery[J]. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(1): 838-853.
[6] 刘广瑞, 王庆海, 姚冬艳. 基于改进人工蜂群算法的多无人机协同任务规划[J]. 郑州大学学报(工学版), 2018, 39(3): 51-55.
LIU G R, WANG Q H, YAO D Y. Multi-UAV cooperative mission planning based on improved artificial bee colony algorithm[J]. Journal of Zhengzhou University (Engineering Science), 2018, 39(3): 51-55.
[7] WU X W, XIAO B, CAO L, et al. Optimal transport and model predictive control-based simultaneous task assignment and trajectory planning for unmanned system swarm[J]. Journal of Intelligent &Robotic Systems, 2024, 110(1): 28.
[8] 王俊英, 颜芬芬, 陈鹏, 等. 基于概率自适应蚁群算法的云任务调度方法[J]. 郑州大学学报(工学版), 2017, 38(4): 51-56.
WANG J Y, YAN F F, CHEN P, et al. Task scheduling method based on probability adaptive ant colony optimization in cloud computing[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(4): 51-56.
[9] 吴蔚楠, 关英姿, 郭继峰, 等. 基于SEAD任务特性约束的协同任务分配方法[J]. 控制与决策, 2017, 32(9): 1574-1582.
WU W N, GUAN Y Z, GUO J F, et al. Research on cooperative task assignment method used to the mission SEAD with real constraints[J]. Control and Decision, 2017, 32(9): 1574-1582.
[10] 鞠锴, 冒泽慧, 姜斌, 等. 基于势博弈的异构多智能体系统任务分配和重分配[J]. 自动化学报, 2022, 48(10): 2416-2428.
JU K, MAO Z H, JIANG B, et al. Task allocation and reallocation for heterogeneous multiagent systems based on potential game[J]. Acta Automatica Sinica, 2022, 48(10): 2416-2428.
[11] 施伟, 冯旸赫, 程光权, 等. 基于深度强化学习的多机协同空战方法研究 [J]. 自动化学报, 2021, 47(7): 1610-1623.
SHI W, FENG Y H, CHENG G Q, et al. Research on multi-aircraft cooperative air combat method based on deep reinforcement learning [J]. ACTA Automatica Sinica, 2021, 47(7):1610-1623.
[12] MOTES J, SANDSTRÖM R, LEE H, et al. Multi-robot task and motion planning with subtask dependencies[J]. IEEE Robotics and Automation Letters, 2020, 5(2): 3338-3345.
[13] YIN Z Z, LIU J H, WANG D P. Multi-AGV task allocation with attention based on deep reinforcement learning[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2022, 36(9): 1-20.
[14] LI M G, MA M, WANG L, et al. Multitask-oriented collaborative crowdsensing based on reinforcement learning and blockchain for intelligent transportation system[J]. IEEE Transactions on Industrial Informatics, 2023, 19(9): 9503-9514.
[15] OROOJLOOY A, HAJINEZHAD D. A review of cooperative multi-agent deep reinforcement learning[J]. Applied Intelligence, 2023, 53(11): 13677-13722.
[16] WANG H P, LI S Q, JI H C. Fitness-based hierarchical reinforcement learning for multi-human-robot task allocation in complex terrain conditions[J]. Arabian Journal for Science and Engineering, 2023, 48(5): 7031-7041.
[17] XIAO X J, PAN Y H, LV L L, et al. Scheduling multi-mode resource-constrained tasks of automated guided vehicles with an improved particle swarm optimization algorithm[J]. IET Collaborative Intelligent Manufacturing, 2021, 3(2): 93-104.
[18] 王乐,齐尧,何滨兵,等.机器人自主探索算法综述[J].计算机应用,2023,43(A1):314-322.
WANG L, QI Y, HE B B,et al. Survey of autonomous exploration algorithms for robots[J]. Journal of Computer Applications, 2023,43(A1):314-322.
[19] VU Q T, DUONG V T, NGUYEN H H, et al. Optimization of swimming mode for elongated undulating fin using multi-agent deep deterministic policy gradient[J]. Engineering Science and Technology, an International Journal, 2024, 56: 101783.
[20] SUMIEA E H, ABDULKADIR S J, ALHUSSIAN H S, et al. Deep deterministic policy gradient algorithm: a systematic review[J]. Heliyon, 2024, 10(9): e30697.
[21] CHAI J J, LI W F, ZHU Y H, et al. UNMAS: multiagent reinforcement learning for unshaped cooperative scenarios[J]. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(4): 2093-2104.
[22] MENG X Q, JIANG J H, WANG H. AGWO: advanced GWO in multi-layer perception optimization[J]. Expert Systems with Applications, 2021, 173: 114676.
[23] 敬超,全育涛,陈艳.基于多层感知机-注意力模型的功耗预测算法[J/OL].计算机应用,2024:1-10(2024-11-13)[2024-11-15].http:∥kns.cnki.net/kcms/detail/51.1307.TP.20241112.1237.004.html.
JING C, QUAN Y T, CHEN Y. Improved multi-layer perceptron and attention model-based power consumption prediction algorithm[J/OL]. Journal of Computer Applications, 2024:1-10(2024-11-13)[2024-11-15].http:∥kns.cnki.net/kcms/detail/51.1307.TP.20241112.1237.004.html.