截至2023年底,我国60岁及以上的老年人口比重已达到21.1%[1],标志着我国已进入中度老龄化社会。老年人日常出行主要以短距离步行为主[2],信号交叉口是机动车、非机动车以及行人的重要交汇点,也是交通事故的频发地点之一。在设置交叉口交通基础设施时,对老年人过街需求考虑不足会造成老年行人在交通中的事故频发,超过50%的老年人认为危险来源于交叉口[3]。信号交叉口的各项设施设置对老年人在交叉口的安全性具有直接影响作用,行人服务水平(pedestrian level of service, PLOS)作为反映信号交叉口人行横道各项设施运行状况的重要评价体系,从使用者的角度对交叉口行人过街的情况做出评价[4],因此,研究老年人对信号交叉口行人服务水平评价方法对老年人安全出行具有重要的现实意义。
自HCM2000首次提出了行人服务水平[5]这一概念后,该领域的研究取得了显著进展。众多学者从安全性[6]、便利性[7]、舒适性[8]等多个角度丰富和完善了服务水平评价指标体系。HCM2016将行人延误及控制方案等作为信号交叉口行人服务水平评价的主要指标[9]。也有学者分析了信号交叉口的设施设置[10]、冲突情况[11]等对行人服务水平的影响。
在服务水平评价建模方法选取中,以多元线性回归分析模型应用最为广泛[12-13]。此外,为了克服多元线性回归的局限性,累积Logistic回归、模糊线性回归、岭回归等多种方法也被应用于行人服务水平评价研究[11,14-15]。
综上所述,行人服务水平评价的研究已逐渐从单一的指标评价发展成为多维度的综合评价,但鲜有考虑老年人感受的信号交叉口行人过街服务水平的评价研究。本文考虑老龄化的社会背景,综合信号交叉口的交通设施和交通流运行状况,选用多元非线性回归、多元线性回归和模糊线性回归模型构建了信号交叉口老年人对行人过街服务水平评价的模型,通过对建立的模型进行对比分析与验证,确定了各模型的精度和应用效果。
1 行人服务水平评价的影响因素
1.1 评价建模影响因素选取
考虑国内实际交通状况和相关研究[16],结合项目前期获得的老年人对过街设施设置问卷调查情况,选取各种静态及动态交通情况对过街行人服务水平评价的影响因素。图1列出了有可能影响评价建模的因素,并将其归纳为反映信号交叉口安全、便利和效率3个维度的二级指标。
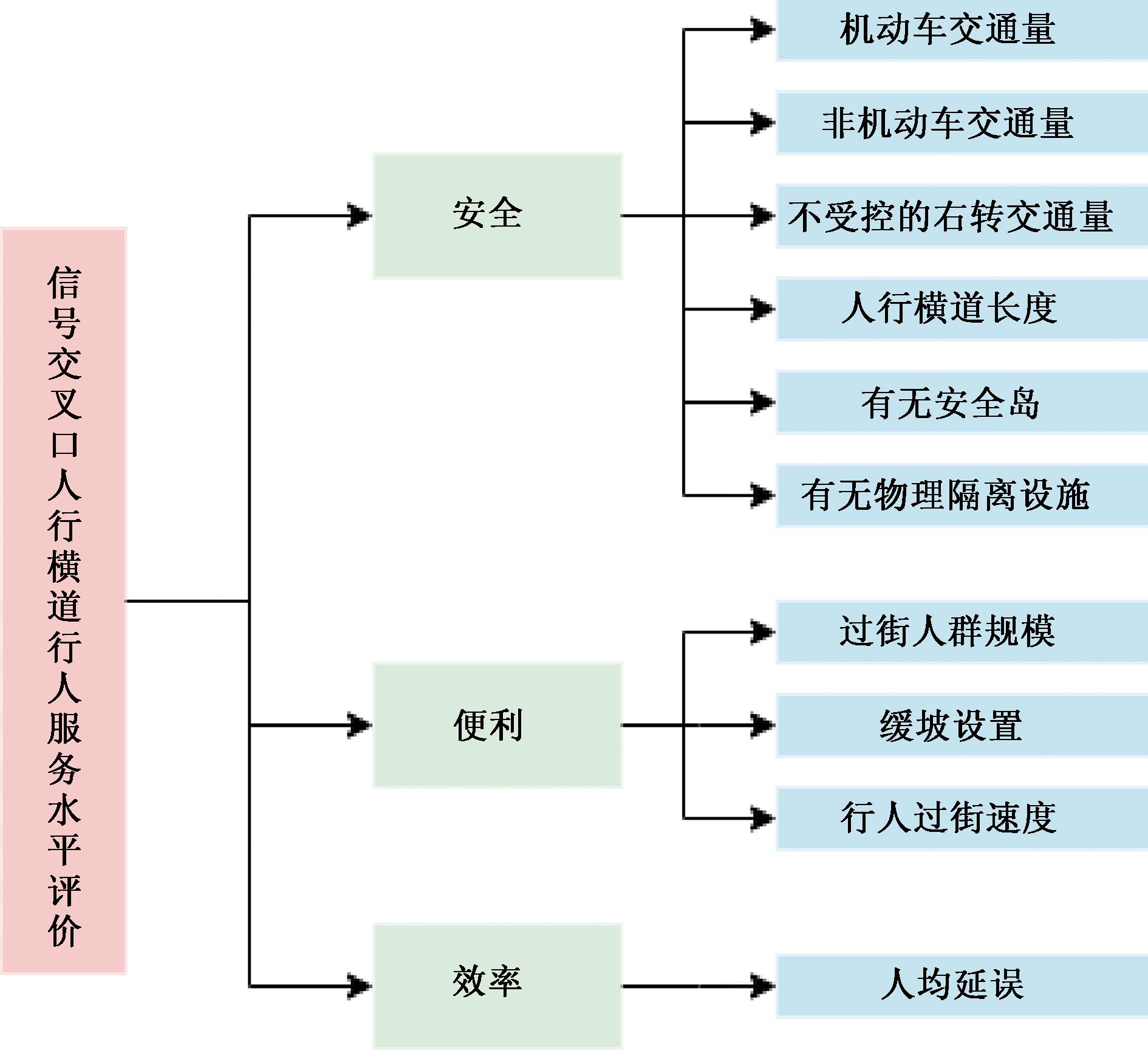
图1 过街行人服务水平评价的影响因素
Figure 1 Influencing factors in the evaluation of level of service for pedestrians crossing the street
在过街安全性方面,主要考虑交通量和交通环境特征对行人服务水平的影响,交通量主要包括机动车交通量、沿人行横道过街的非机动车交通量以及不受信号控制的右转交通量;交通环境特征考虑了人行横道的长度、过街安全岛和隔离桩等物理隔离设施的设置。在便利性方面,考虑了过街人群规模、人行横道两端是否设置缓坡以及行人过街速度。在效率方面,主要考虑信号交叉口的人均延误。
在老年人主观对交叉口服务水平评价方面,也主要从安全、便利和效率方面进行了数据采集。本次研究采用路边截断式问卷调查法同步获取过街老年人对人行横道行人服务水平的主观评价情况,为了方便参与者回答,同时确保评价更为全面,调查问卷仅包含性别、年龄等个体基本特征信息,以及行人对人行横道在过街安全、便利、效率方面的3个感知评价问题,并在问卷中通过5点正向量表(即“非常满意”的得分为5分)进行记录。
1.2 数据采集
考虑老年人的出行选择情况,本次数据采集选择天气情况较好且老年人出行时段较多的时间点,通过现场调查、视频录像和问卷调查实现数据采集。为体现研究对象的普遍性和多样性,调查地点涉及山地、平原等多种地形的信号交叉口,选取位于重庆市南岸区中心区域、重庆市秀山县、山东省济宁市兖州区、山东省淄博市张店区、四川省成都市青羊区的30条信号交叉口人行横道作为调查点。选取的调查点基本涵盖了常见的信号交叉口人行横道行人过街场景,各调查点的交通参数具有不同的参数水平且均具有一定比例的老年人通行。表1所示为各条人行横道的编号及位置信息,所有人行横道所在的交叉口均对直行和左转车辆实施信号控制。
表1 调查地点位置信息
Table 1 Survey location information
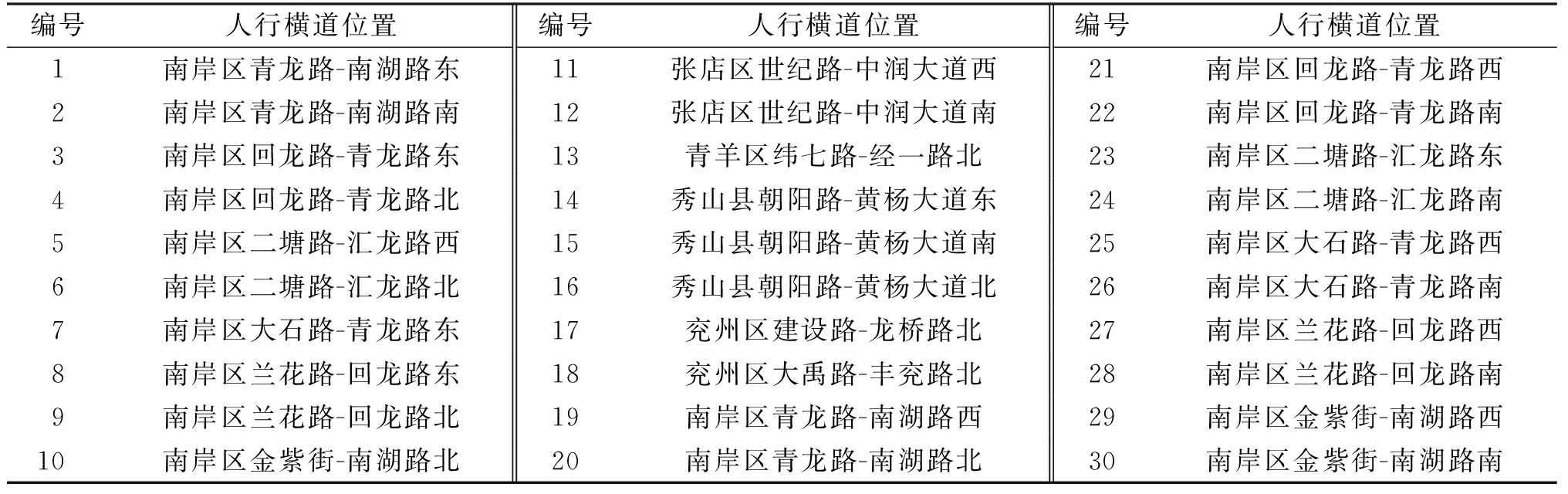
编号人行横道位置编号人行横道位置编号人行横道位置1南岸区青龙路-南湖路东11张店区世纪路-中润大道西21南岸区回龙路-青龙路西2南岸区青龙路-南湖路南12张店区世纪路-中润大道南22南岸区回龙路-青龙路南3南岸区回龙路-青龙路东13青羊区纬七路-经一路北23南岸区二塘路-汇龙路东4南岸区回龙路-青龙路北14秀山县朝阳路-黄杨大道东24南岸区二塘路-汇龙路南5南岸区二塘路-汇龙路西15秀山县朝阳路-黄杨大道南25南岸区大石路-青龙路西6南岸区二塘路-汇龙路北16秀山县朝阳路-黄杨大道北26南岸区大石路-青龙路南7南岸区大石路-青龙路东17兖州区建设路-龙桥路北27南岸区兰花路-回龙路西8南岸区兰花路-回龙路东18兖州区大禹路-丰兖路北28南岸区兰花路-回龙路南9南岸区兰花路-回龙路北19南岸区青龙路-南湖路西29南岸区金紫街-南湖路西10南岸区金紫街-南湖路北20南岸区青龙路-南湖路北30南岸区金紫街-南湖路南
对于选取的人行横道,现场记录交叉口渠化、设施设置等信息,每条人行横道均采用高清摄像机拍摄了不少于2 h的视频,并通过人工提取的方式获取机动车流量、过街行人流量、过街行人延误等动态参数。
1.3 数据描述性统计分析
1.3.1 交通数据
根据现场调查和人工提取数据的方式得到建模组30条人行横道的静态和动态交通数据,采用高清摄像机拍摄30条人行横道的行人过街特征,通过人工提取的方式得到行人交通参数,建模组人行横道的交通参数统计性描述如表2所示。
表2 建模组人行横道交通参数统计性描述
Table 2 Statistical description of crosswalk traffic parameters
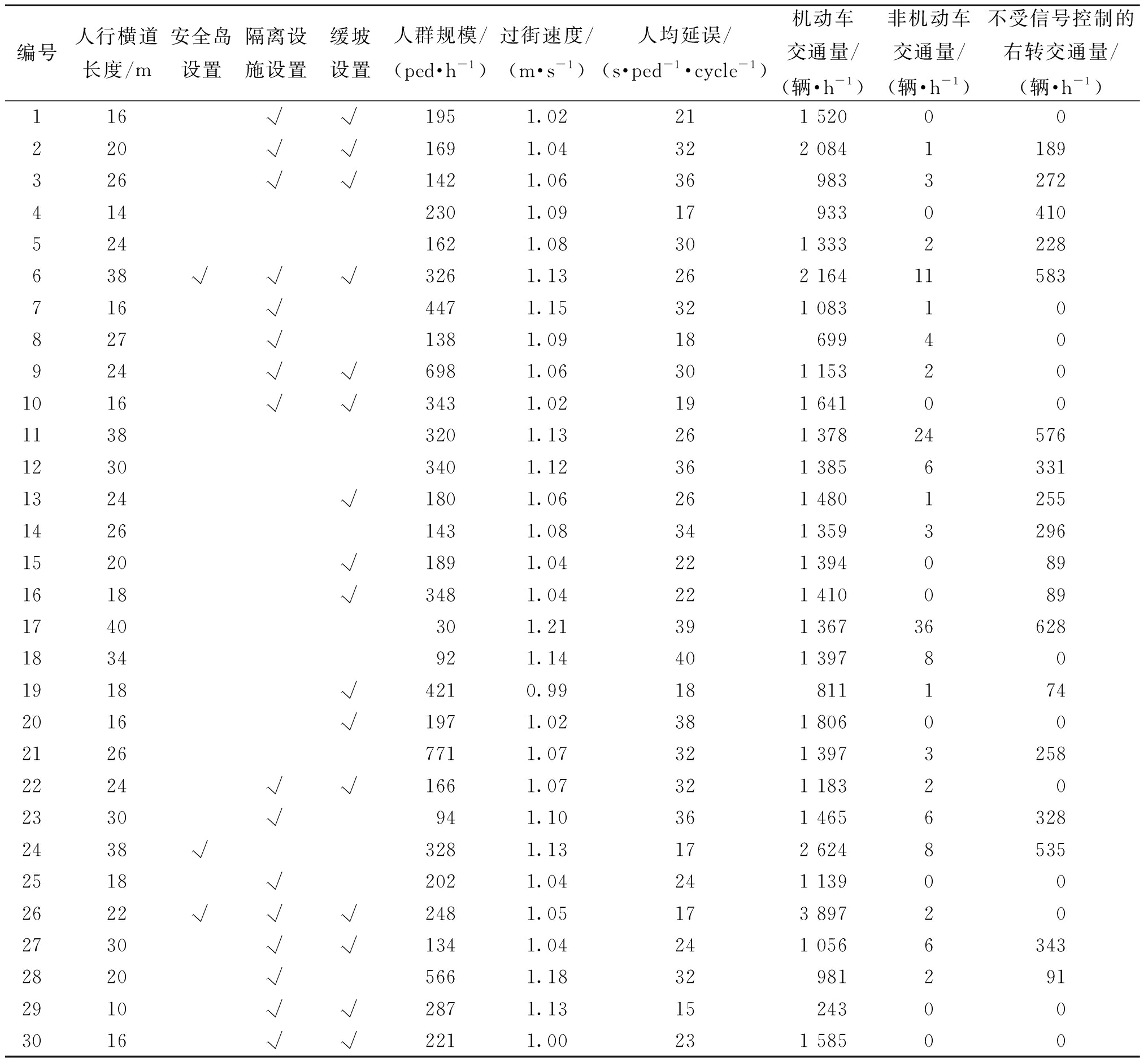
编号人行横道长度/m安全岛设置隔离设施设置缓坡设置人群规模/(ped·h-1)过街速度/(m·s-1)人均延误/(s·ped-1·cycle-1)机动车交通量/(辆·h-1)非机动车交通量/(辆·h-1)不受信号控制的右转交通量/(辆·h-1)116√√1951.02211 52000220√√1691.04322 0841189326√√1421.063698332724142301.091793304105241621.08301 3332228638√√√3261.13262 16411583716√4471.15321 08310827√1381.091869940924√√6981.06301 153201016√√3431.02191 6410011383201.13261 3782457612303401.12361 38563311324√1801.06261 480125514261431.08341 35932961520√1891.04221 3940891618√3481.04221 4100891740301.21391 367366281834921.14401 397801918√4210.99188111742016√1971.02381 8060021267711.07321 39732582224√√1661.07321 183202330√941.10361 46563282438√3281.13172 62485352518√2021.04241 139002622√√√2481.05173 897202730√√1341.04241 05663432820√5661.18329812912910√√2871.1315243003016√√2211.00231 58500
注:安全岛设置、隔离设施设置、缓坡设置3项指标为虚拟变量;√表示有该项设置;人均延误指信号周期内行人的平均等待时间。
根据现场调查数据,调查的30条人行横道中长度最短的南岸区金紫街与南湖路西进口为9 m,最长的兖州区建设路与龙桥路北进口为42 m;设置安全岛的人行横道有6条,人行横道两端设置物理隔离设施的人行横道有23条,设置缓坡的人行横道有18条,4项调查指标的不同情形在涉及的信号交叉口调查中均占有一定比例。行人过街速度均值为0.99~1.21 m/s,过街速度总体均值约为1.08 m/s;人均延误最大值为兖州区大禹路-丰兖路北进口的40 s/(ped·cycle),最小值为南岸区金紫街-南湖路西进口,仅有15 s/(ped·cycle)。建模组30条人行横道中有20条人行横道的机动车交通量为1 000~2 000 辆/h,非机动车交通量为0~36 辆/h,30条人行横道中有18条人行横道右转机动车不受信号控制。
1.3.2 样本数据
对过街老年行人开展行人服务水平感知问卷调查,30个地点共调查问卷939份,每条人行横道筛选并保留熟悉该条人行横道的30份有效问卷数据,3个维度评价值加权分别得出30条人行横道老年人服务水平评价值,行人服务水平实际评价值如表3所示。
表3 行人服务水平评价值统计性描述
Table 3 Statistical description of pedestrian service level evaluation value
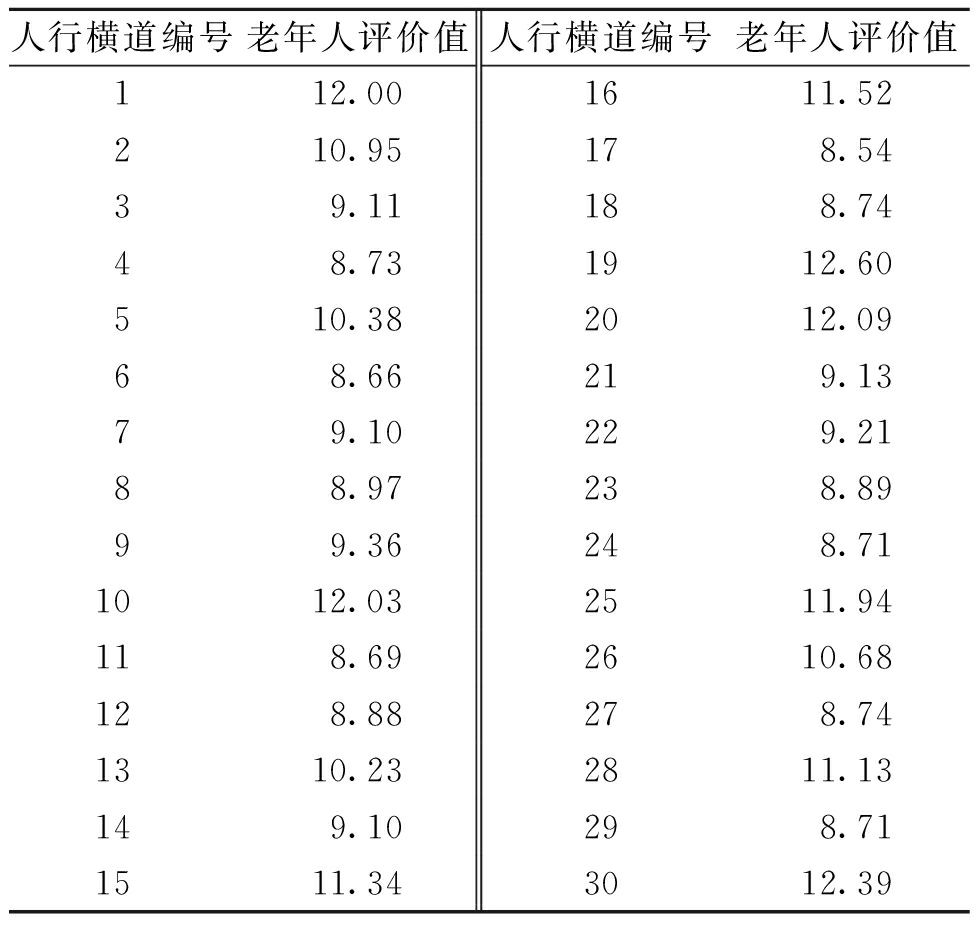
人行横道编号老年人评价值人行横道编号老年人评价值112.001611.52210.95178.5439.11188.7448.731912.60510.382012.0968.66219.1379.10229.2188.97238.8999.36248.711012.032511.94118.692610.68128.88278.741310.232811.13149.10298.711511.343012.39
由问卷调查数据可知,30条人行横道老年行人整体评价均值为10.02,各人行横道老年行人主观评价值为8.54~12.60。对行人评价数据进行独立样本T检验,检验结果表明不同人行横道的老年人对交通场景行人过街服务水平主观评价存在显著差异,问卷数据差异符合对老年人服务水平评价的研究要求。
由于调查者可能在短时间内无法完全理解问卷问题,并因此造成调查结果存在偏差,故采用克隆巴赫系数α对得到的行人评价数据进行信度分析,计算得出老年行人服务水平评价总量表的克隆巴赫系数为0.862>0.8,表明测量结果均达到了高信度水平[17]。
1.4 老年行人对服务水平评价重要变量识别
为从初选影响因素中识别出老年行人群体感知的信号交叉口行人服务水平重要影响变量,根据表2所列出的初选指标,对老年行人的综合感知评价结果与变量数据进行相关性分析。皮尔逊(Pearson)相关系数是目前使用最广泛的相关性统计量,用于测量连续变量之间的线性关系,而对于2个变量之间存在非线性关系的相关性检验,常使用斯皮尔曼(Spearman)相关系数,其不需要对2个变量的频率分布和2个变量之间的线性关系做出任何假设,也不需要在区间尺度上进行测量,具有更为广泛的适用性[18]。为分析变量与行人服务水平评价之间的线性与非线性相关性,进而解释并选取最适合的服务水平评价模型,同时采用皮尔逊相关系数与斯皮尔曼相关系数对行人服务水平评价和变量数据进行相关性检验,皮尔逊相关系数和斯皮尔曼相关系数可由以下公式计算:
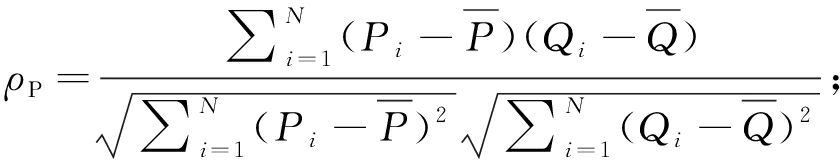
(1)
(2)
式中:ρP表示皮尔逊相关系数;ρS表示斯皮尔曼相关系数;Pi、Qi均为皮尔逊相关系数的待检验变量;![]() 为变量Pi、Qi的平均值;Ri、Si均为斯皮尔曼相关系数的待检验变量;N为数据总量。ρP、ρS取值范围均为[-1,1],其绝对值越接近1时,变量的相关性越强[19]。相关性检验结果如图2所示。
为变量Pi、Qi的平均值;Ri、Si均为斯皮尔曼相关系数的待检验变量;N为数据总量。ρP、ρS取值范围均为[-1,1],其绝对值越接近1时,变量的相关性越强[19]。相关性检验结果如图2所示。
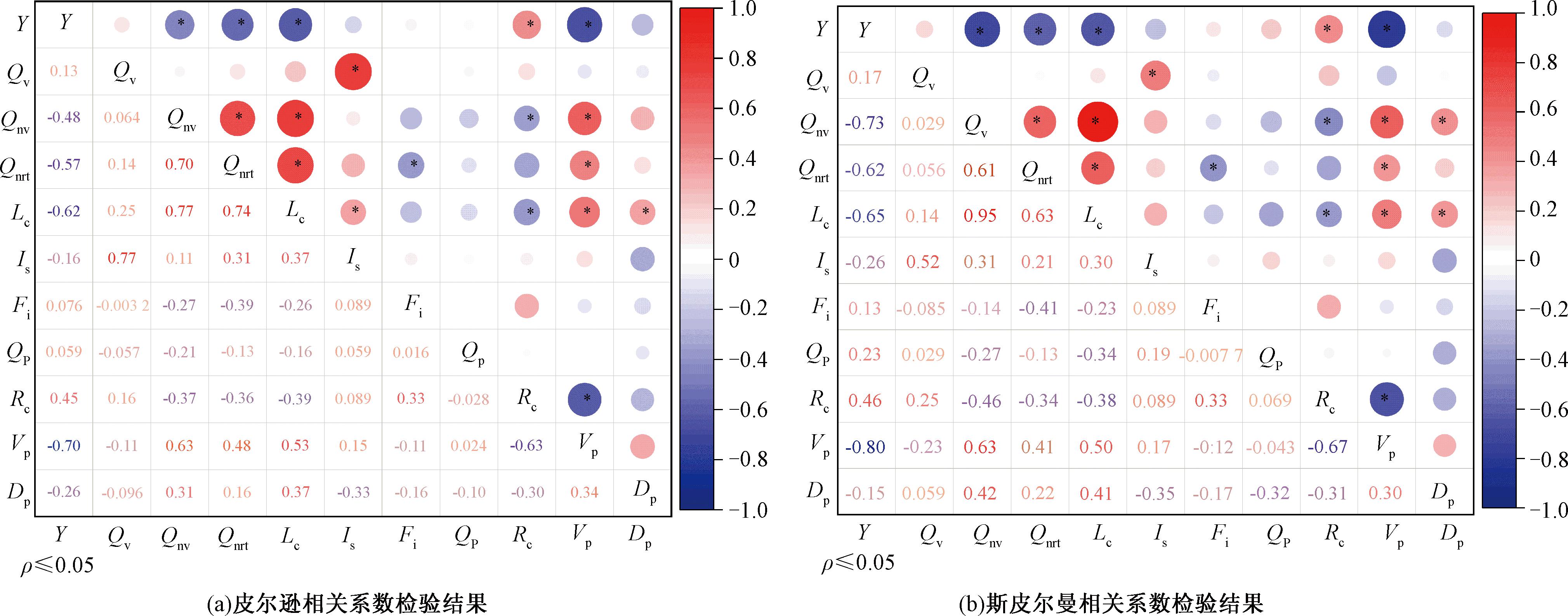
图2 老年行人服务水平评价影响因素相关性检验热图
Figure 2 Heat map of correlation test of factors influencing elderly pedestrian service level evaluation value
图2中,Y表示老年行人服务水平评价值;Qv表示机动车交通量;Qnv表示非机动车交通量;Qnrt表示不受控的右转交通量;Lc表示人行横道长度;Is表示是否设置安全岛;Fi表示人行横道两端是否设施隔离设施;Qp表示过街人群规模;Rc表示人行横道两端是否设置缓坡;Vp表示行人过街速度;Dp表示人均延误。
由相关性检验结果可知,使用皮尔逊相关系数和斯皮尔曼相关系数确定的影响老年行人服务水平评价的重要影响因素相同,老年行人服务水平评价与人行横道两端是否设置缓坡、人行横道长度、不受控的右转交通量、过街速度、非机动车交通量5项指标之间存在相关关系。使用皮尔逊相关系数和斯皮尔曼相关系数确定的重要影响因素与行人服务水平评价之间的相关程度存在差异:老年行人服务水平评价与人行横道长度、不受控的右转交通量、过街速度的相关系数均为-1.0~-0.5,且ρ≤0.05,故老年行人服务水平评价与3项指标存在强相关关系;老年行人服务水平评价与人行横道两端是否设置缓坡之间的相关系数为0.4~0.5,且ρ≤0.05,故老年行人服务水平评价与人行横道两端是否设置缓坡之间存在中等程度相关关系。通过皮尔逊相关系数确定的老年行人服务水平评价与非机动车交通量存在中等程度相关关系,使用斯皮尔曼相关系数确定的老年行人服务水平评价与非机动车交通量存在强相关关系[19]。此外,行人服务水平评价与重要变量之间的皮尔逊相关系数值均低于斯皮尔曼相关系数值,表明行人服务水平评价与重要变量之间的非线性相关程度明显强于两者之间的线性相关程度。
2 老年人对信号交叉口服务水平评价建模
2.1 老年人对信号交叉服务水平评价模型选择
2.1.1 基于非线性的评价模型建立
考虑通过调查获取的行人感知评价与信号交叉口交通参数之间可能存在的非线性关系,本文选用多元非线性回归分析方法构建信号交叉口老年行人服务水平评价模型。多元非线性回归分析(multivariate nonlinear regression analysis, MNR)是处理涉及2个或2个以上自变量非线性问题的常用手段,可用于解决变量之间可能存在非线性关系的实际问题[20]。
在求解非线性问题时,往往结合曲线估算回归分析,其目的是针对具体数据选取最优的模型以及参数初估值,从而提高收敛速度并避免模型失拟,主要适用于利用一个变量对另一个变量进行预测的情况,能够在众多回归模型中确定并建立一个简单且合适的最佳模型,用于曲线估计的主要数学模型如表4所示。
表4 曲线估计模型形式
Table 4 Form of curve estimation model

模型模型表达式二次函数 y=b0+b1x+b2x2复合函数y=b0(b1)x增长函数y=e(b0+b1x)对数函数y=b0+b1lnx三次函数y=b0+b1x+b2x2+b3x3S型曲线y=e(b0+b1/x)指数函数y=b0eb1x逆函数y=b0+b1/x幂函数y=b0xb1逻辑函数y=(1/u+b0b1x)-1
选用样本判定系数R2和F统计量检验备选曲线方程的拟合优度,拟合优度检验公式和回归方程显著性检验公式分别为
(3)
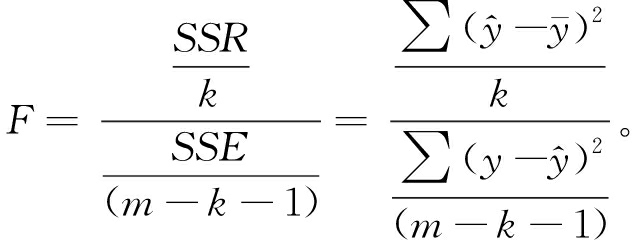
(4)
式中:SSR为回归平方和;SSE为残差平方和;SST为总离差平方和;y为样本实际值;![]() 为样本实际值均值;
为样本实际值均值;![]() 为预测值;m为样本数;k为自变量个数;F为统计量,F~(k,n-k-1)。判定系数R2是对回归模型拟合程度的综合度量,R2越大,说明模型拟合程度越高。F统计量是平均回归平方和与平均残差平方和之比,F值越大,说明自变量造成的因变量的变化越大于随机因素对因变量造成的影响,回归方程的拟合优度也越高。
为预测值;m为样本数;k为自变量个数;F为统计量,F~(k,n-k-1)。判定系数R2是对回归模型拟合程度的综合度量,R2越大,说明模型拟合程度越高。F统计量是平均回归平方和与平均残差平方和之比,F值越大,说明自变量造成的因变量的变化越大于随机因素对因变量造成的影响,回归方程的拟合优度也越高。
基于上述分析,多元非线性回归模型的一般表达式可以表示为
(5)
式中:fi(xi)为关于第i个解释变量xi的最优曲线估计模型,i=1,2,…,n,fi(xi)的具体形式由变量间的实际关系决定;α为常数截距项;ε1为不可观测的随机变量;Y为非线性回归模型中以解释变量xi表示的综合得分。
2.1.2 基于多元线性回归的模型
多元线性回归模型[21]是HCM模型中对于行人服务水平评价和因素间建模选用的方法,在行人服务水平评价研究中应用较为广泛。因此,本文基于HCM2010[12]的建模思路,建立老年人对信号交叉口行人服务水平评价的多元线性回归模型,表示为
Y′=β0+β1x1+β2x2+…+βnxn+ε2。
(6)
式中:n为解释变量即重要影响因素的数目;xi为第i个解释变量,i=1,2,…,n;βi为回归系数;ε2为不可观测的随机变量;Y′为多元线性回归模型中以解释变量xi表示的综合得分。
2.1.3 基于模型线性回归模型
由于通过问卷调查得到的老年行人服务水平感知评价数据是老年行人通过个人判断得到的主观数据,具有一定的模糊性,同时为了将定性的语义变量的表达形式进行数学上的定量描述及表达以便于对比不同模型基础下的行人服务水平评价值,因此选用基于模糊线性回归的方法构建老年行人服务水平评价模型。模糊线性回归模型(fuzzy linear regression, FLR)将回归系数看成具有某种隶属度函数的模糊数[22],其表达式为
(γ1,η1,ζ1)LRx1+…+(γn,ηn,ζn)LRxn。
(7)
式中:xn为第n个解释变量;![]() 为FLR模型中以LR-型模糊数表示的第n个解释变量的回归系数;
为FLR模型中以LR-型模糊数表示的第n个解释变量的回归系数;![]() 为模糊线性回归模型中以LR-型模糊数表示的综合得分。
为模糊线性回归模型中以LR-型模糊数表示的综合得分。
2.2 模型拟合结果
2.2.1 基于非线性回归的评价模型
根据老年行人的重要变量检验结果,分别对选定的交通场景指标与老年行人服务水平评价值进行曲线估计。结合非线性拟合函数判定指标R2和回归方程显著性检验F值,综合选取各影响因素的最佳一元非线性拟合模型,各影响因素确定的老年行人服务水平评价的最佳一元非线性拟合函数方程如表5所示。
表5 重要因素最佳一元非线性模型拟合结果
Table 5 Best unitary nonlinear model fitting results for important factors

影响因素最佳一元非线性模型最佳一元非线性拟合函数方程R2Fρ人行横道长度Lc三次函数yLc=-7.376+2.568Lc-0.111L2c+0.001L3c0.67317.8340 不受控的右转交通量Qnrt三次函数yQnrt=10.522+0.015Qnrt-0.000 95Q2nrt+1.081×10-7Q3nrt0.4466.9890.001过街速度Vp二次函数yVp=261.065-442.897Vp+194.382d2V2p0.69030.0270.010缓坡设置Rc指数函数yRc=9.304e0.122Rc0.2057.2180.012非机动车交通量Qnv三次函数yQnv=11.123-0.557Qnv+0.032Q2nv-0.001Q3nv0.5169.2320
通过上述曲线估计得到了各自变量相对于因变量的表达式,可知5项指标与老年行人服务水平评价之间均具有较强的非线性关系。以老年行人主观评价的服务水平评价值为因变量,交通场景指标为自变量,构建多元非线性回归模型:
(8)
式中:Yplos为基于非线性回归的老年行人服务水平评价值;Lc为人行横道长度;Qnrt为不受控的右转交通量;Vp为过街速度;Rc为人行横道两端是否设置缓坡;Qnv为非机动车交通量;a为常数项;b、c、d、f、g为自变量的系数。
根据最小二乘L-M算法原理[23],得到满足最小误差的模型参数解,将老年行人服务水平相关重要变量的模型系数估计值代入式(8),得到基于非线性回归的老年行人服务水平的评价模型为
(9)
2.2.2 基于线性回归的评价模型
利用建模组30条人行横道的数据,即老年行人服务水平主观评价值与交通场景中的人行横道长度、不受控的右转交通量、过街速度、人行横道两侧是否设置缓坡、非机动车交通量5项指标,对模型采用最小二乘法估算其参数,得到基于多元线性回归的老年行人服务水平评价模型的回归方程为
16.518Vp-0.164Rc+0.075Qnv。
(10)
式中:![]() 为基于多元线性回归的老年行人服务水平评价值;Lc为人行横道长度;Qnrt为不受控的右转交通量;Vp为过街速度;Rc为人行横道两端是否设置缓坡;Qnv为非机动车交通量。
为基于多元线性回归的老年行人服务水平评价值;Lc为人行横道长度;Qnrt为不受控的右转交通量;Vp为过街速度;Rc为人行横道两端是否设置缓坡;Qnv为非机动车交通量。
2.2.3 基于模糊线性回归的评价模型
应用建模组30条人行横道数据,计算FLR模型的参数估计,得到基于模糊线性回归的老年行人服务水平的评价模型为
(-0.076 7,0.017 5,-0.027 9)LRLc+
(-0.001 7,-0.000 2,0.000 3)LRQnrt+
(-16.628 7,-2.749 3,0.940 4)LRVp+
(-0.165 1,0.018 6,-0.022 9)LRRc+
(0.074 1,0.003 6,0.011 7)LRQnv。
(11)
由于行人服务水平评价值为一维数据,可利用质心法对求解结果进行解模糊:
(12)
式中:![]() 分别表示第i条人行横道老年行人服务水平评价得分的下限值、中间值和上限值。
分别表示第i条人行横道老年行人服务水平评价得分的下限值、中间值和上限值。
3 模型验证与对比
为进一步分析前文构建的老年人对行人服务水平评价模型预测的准确性和稳定性,同时验证研究结果对常见的人行横道具有广泛的适用性,本文综合考虑人行横道长度、人行横道两端是否设置缓坡等评价指标的数据参数差异性,选取了山东省济南市商河县青年路兴隆街南进口(验证组1)、山东省济南市商河县青年路兴隆街东进口(验证组2)、重庆市南岸区青龙路南湖支路东进口(验证组3)的调查数据和老年行人服务水平评价数据对老年行人服务水平评价模型进行验证。
验证组的3条人行横道中,验证组1具有人行横道长度相对较短、不受控的右转交通量相对较少且人行横道两端设置有缓坡等特征;验证组2具有人行横道长度相对较短、非机动车交通量相对较多、行人过街速度较慢且人行横道两端没有设置缓坡等特征;验证组3具有人行横道长度适中、非机动车交通量相对较少且人行横道两端设置有缓坡等特征。验证组的静态和动态交通数据如表6所示。
表6 验证组交通数据统计性描述
Table 6 Statistical description of traffic data of the verification group

验证组人行横道长度/m缓坡设置人群规模/(ped·h-1)过街速度/(m·s-1)人均延误/(s·ped-1·cycle-1)机动车交通量/(辆·h-1)非机动车交通量/(辆·h-1)不受信号控制的右转交通量/(辆·h-1)114√1871.04 21.22 51013972162761.02 42.12 66527327326√2121.11 38.79 7331276
注:√表示有该项设置。
根据表6老年行人服务水平重要影响因素数据得到基于3种模型的老年行人服务水平评价预测值,老年人对3个交叉口行人服务水平得分实际值与各模型计算得到的预测值结果对比如图3所示。

图3 验证组行人服务水平实际值与预测值对比
Figure 3 Comparison of actual and predicted pedestrian service level in the verification group
根据验证组人行横道的老年人对行人服务水平得分实测值和预测值得到误差分析,如表7所示。
表7 验证组行人服务水平预测值误差分析
Table 7 Error analysis of the predicted value of pedestrian service level in the verification group
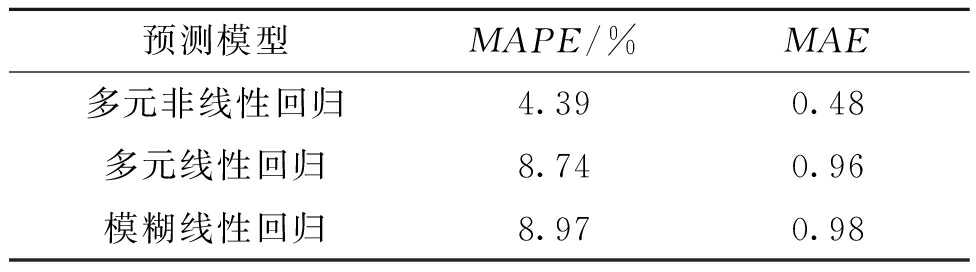
预测模型MAPE/%MAE多元非线性回归4.390.48多元线性回归8.740.96模糊线性回归8.970.98
由表7可知,多元非线性回归模型的平均绝对百分比误差(MAPE)为4.39%,多元线性回归和模糊线性回归模型的MAPE分别为8.74%和8.97%,明显低于其他2个模型。同时,多元非线性建模的MAE也比其他2个模型小,表明基于多元非线性回归的老年行人服务水平评价模型的准确度更高、误差更小,在应用于新调查地点时具有较好的适应性,能够根据较少的交通参数值较为准确地预测出老年行人对当前信号交叉口对应的交通情况下行人服务水平的感知情况。
4 结论
本文基于多元非线性回归模型对老年人在信号交叉口人行横道的过街需求进行分析,对老年人感受的信号交叉口行人服务水平进行评价建模,得出以下结论。
(1)将行人服务水平看作由多个因素共同影响的因变量,通过相关性检验,确定人行横道长度、不受控的右转交通量、行人过街速度、人行横道两侧是否设置缓坡以及非机动车交通量是影响老年行人服务水平的显著因素;同时认为老年行人服务水平与各项影响因素的非线性相关关系更强。
(2)利用采集的不同地点的30组人行横道的交通特征数据和同步调查的老年人主观评价赋值,建立了基于多元非线性、多元线性和模糊线性回归的老年人信号交叉口行人服务水平评价模型,应用该数据分别拟合了相同交通特征影响因素作用下的3种回归模型。结合验证组3条人行横道的数据,并对比3种回归模型的应用情况可知,基于多元非线性回归的老年行人服务水平评价模型在预测精度和稳定性方面效果最优。在实际应用中,通过考虑评价指标的非线性关系来建立服务水平评价模型,对研究与提升人行横道行人服务水平更具参考价值。
本文将老年行人作为主要研究对象,基于老年人的主观评分和交叉口的交通特征建立了信号交叉口老年行人服务水平评价模型,后续的研究将考虑不同年龄行人群体混行情况下信号交叉口行人服务水平评价模型,提升模型的实用化水平。
[1] 国家统计局. 中华人民共和国2023年国民经济和社会发展统计公报[EB/OL]. (2024-02-29)[2024-03-20]. https:∥www.stats.gov.cn/sj/zxfb/202402/t20240228_1947915.html.National Bureau of Statistics. Statistical bulletin of the People′s Republic of China on the 2023 national economic and social development[EB/OL]. (2024-02-29) [2024-03-20]. https:∥www.stats.gov.cn/sj/zxfb/202402/t20240228_1947915.html.
[2] 黄建中, 张芮琪, 胡刚钰. 基于时空间行为的老年人日常生活圈研究: 空间识别与特征分析[J]. 城市规划学刊, 2019(3): 87-95.HUANG J Z, ZHANG R Q, HU G Y. A research of the elderly′s daily life circle based on spatial-temporal behaviors—analysis of place recognition and spatial features[J]. Urban Planning Forum, 2019(3): 87-95.
[3] 潘义勇, 吴静婷, 施颖. 交叉口处老年人碰撞事故伤害严重程度分析[J]. 重庆交通大学学报(自然科学版), 2022, 41(9): 39-44.PAN Y Y, WU J T, SHI Y. Injury severity analysis of the elderly in collision accidents at intersections[J]. Journal of Chongqing Jiaotong University (Natural Science), 2022, 41(9): 39-44.
[4] ZHANG H L, ZHANG D K, WANG R H. Evaluation of pedestrian level of service at signalised intersections from the elderly perspective[J]. Promet-Traffic &Transportation, 2023, 35(3): 434-445.
[5] TRANSPORTATION R B. Highway capacity manual 2000[M]. Washington: Transportation Research Board,2000.
[6] 刘孟歆, 秦华, 岳晨, 等. 右转车辆与过街行人交互过程的影响因素研究[J]. 包装工程, 2023, 44(12): 118-125.LIU M X, QIN H, YUE C, et al. Influencing factors of interaction process between right-turning vehicles and pedestrians crossing the street[J]. Packaging Engineering, 2023, 44(12): 118-125.
[7] LI W F, HE J W, YU Q, et al. Using POI data to identify the demand for pedestrian crossing facilities at mid-block[J]. Sustainability, 2021, 13(23): 13256.
[8] JIA X L, FELICIANI C, MURAKAMI H, et al. Revisiting the level-of-service framework for pedestrian comfortability: velocity depicts more accurate perceived congestion than local density[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2022, 87: 403-425.
[9] TRANSPORTATION R B. Highway capacity manual 2016[M]. Washington: Transportation Research Board, 2016.
[10] AHMED T, MOEINADDINI M, ALMOSHAOGEH M, et al. A new pedestrian crossing level of service (PCLOS) method for promoting safe pedestrian crossing in urban areas[J]. International Journal of Environmental Research and Public Health, 2021, 18(16): 8813.
[11] SAHANI R, BHUYAN P K. Modelling pedestrian perspectives in evaluating satisfaction levels of urban roadway walking facilities[J]. Transportation Research Procedia, 2020, 48: 2262-2279.
[12] DIVISION T A, BOARD T R. Innovative Applications of the Highway Capacity Manual 2010[M]. Washington: Transportation Research Board, 2014.
[13] 边扬, 王炜, 陆建. 人行道行人服务水平评价方法[J]. 东南大学学报(自然科学版), 2007, 37(4): 695-699.BIAN Y, WANG W, LU J. Pedestrian level of service for sidewalks[J]. Journal of Southeast University (Natural Science Edition), 2007, 37(4): 695-699.
[14] YE X F, CHEN J, JIANG G Y, et al. Modeling pedestrian level of service at signalized intersection crosswalks under mixed traffic conditions[J]. Journal of the Transportation Research Board, 2015, 2512(1): 46-55.
[15] MARISAMYNATHAN S, VEDAGIRI P. Modeling pedestrian level of service at signalized intersection under mixed traffic conditions[J]. Journal of the Transportation Research Board, 2017, 2634(1): 86-94.
[16] RAAD N, BURKE M I. What are the most important factors for pedestrian level-of-service estimation? A systematic review of the literature[J]. Journal of the Transportation Research Board, 2018, 2672(35): 101-117.
[17] 景鹏, 王伟, 吴麟麟. 老年人对自动驾驶汽车接受度研究[J]. 中国公路学报, 2021, 34(6): 158-171.JING P, WANG W, WU L L. Acceptance of autonomous vehicles for the elderly[J]. China Journal of Highway and Transport, 2021, 34(6): 158-171.
[18] SACCENTI E, HENDRIKS M H W B, SMILDE A K. Corruption of the Pearson correlation coefficient by measurement error and its estimation, bias, and correction under different error models[J]. Scientific Reports, 2020, 10: 438.
[19] XIAO C W, YE J Q, ESTEVES R M, et al. Using Spearman′s correlation coefficients for exploratory data analysis on big dataset[J]. Concurrency and Computation: Practice and Experience, 2016, 28(14): 3866-3878.
[20] MIROSHNICHENKO V, MAIBORODA R. Asymptotic normality of modified LS estimator for mixture of nonlinear regressions[J]. Modern Stochastics: Theory and Applications, 2020: 435-448.
[21] 郝翠萍. 基于多元线性回归模型的考试评价与预测研究[J]. 电子设计工程, 2021, 29(15): 142-145.HAO C P. Research on examination evaluation and prediction based on multiple linear regression model[J]. Electronic Design Engineering, 2021, 29(15): 142-145.
[22] LI Y F, HE X X, LIU X Q. Fuzzy multiple linear least squares regression analysis[J]. Fuzzy Sets and Systems, 2023, 459: 118-143.
[23] 武继刚, 李妙君, 赵淑平. 基于低秩稀疏表达的弹性最小二乘回归学习[J]. 郑州大学学报(工学版), 2023, 44(6): 25-32.WU J G, LI M J, ZHAO S P. Low-rank sparse representation based on elastic least squares regression learning[J]. Journal of Zhengzhou University (Engineering Science), 2023, 44(6): 25-32.