土体本构模型在岩土工程研究和实践中都具有重要意义,已有大量学者进行各类土的本构模型研究。但砂土有其独特之处,砂土等颗粒材料在外荷载作用下会发生颗粒破碎,从而影响其强度和变形特性。在临界状态土力学框架内对试验数据进行分析时,发现颗粒破碎会导致e-ln p空间的临界状态线发生弯曲或者向下平移,从而改变了土体当前状态与临界状态线的距离[1-2]。对于密砂而言,其初始状态处于e-ln p空间的临界状态线下方,剪切时颗粒破碎导致的临界状态线下移会使得其在经历了较小程度的剪胀后即能达到临界状态,从而使得试验时观测到的试样剪胀程度减小;但对于松砂而言,其初始状态处于e-ln p空间的临界状态线上方,剪切时颗粒破碎导致的临界状态线下移会使得其需要经历更多的压缩后才能达到临界状态线,从而使得试验时观测到的试样剪缩程度增大。
在对涉及砂土等颗粒材料相关工程问题进行离散元或者有限元分析时,颗粒破碎是不容忽视的因素。考虑颗粒破碎的离散元模型在受剪切时剪胀会得到抑制,峰值强度会有所降低[3],模拟结果都更接近于真实试验。在进行有限元分析时,需要首先建立考虑颗粒破碎的土体本构模型,如考虑颗粒破碎的边界面模型[4]、亚塑性模型[5]、广义塑性模型[6]、分数阶塑性模型[7]等,然后对模型进行二次开发。这些模型通常可以归类为唯像模型,在不改变基本力学框架的基础上,通过引入考虑颗粒破碎的临界状态线,来进行本构建模。
考虑颗粒破碎的临界状态线通常可以分为两类[8]。第一类是直接表达,即通过将颗粒破碎指标,如Br[9]和B[10]等,直接引入到e-ln p空间的临界状态线表达式,与临界状态线参数唯像地关联;第二类是间接表达,即放弃e-ln p空间,而采用其他比例空间,如e-ln (p+pr) [11]或e-pξ[12]等,来重新构造具有线性或者其他简单函数关系的临界状态线,其中,pr和ξ为模型参数。这两种思路均可以考虑颗粒破碎所导致的临界状态线下弯。然而,鲜有学者对基于这两类临界状态线的本构模型预测效果进行深入细致的比较研究。
本文拟选取两种具有代表性的临界状态线表达式,分别直接和间接地考虑颗粒破碎对临界状态线的影响;基于这两种临界状态线,建立三轴加载条件下的SANISAND边界面模型与相应的数值算法;最后,模拟排水和不排水三轴加载条件下的砂土力学行为,并与试验结果进行对比,探究这两类临界状态线的适应性。
1 直接和间接考虑颗粒破碎的临界状态线
目前可以考虑破碎影响的临界状态线表达式众多,其中直接考虑破碎的临界状态线往往是通过将颗粒破碎率Br与e-ln p空间的临界状态参数eΓ关联来建立表达式[8]:
(1)
式中:ec为临界状态孔隙比;p为平均有效应力;f(Br)为考虑颗粒破碎的影响性函数;λ为临界状态线参数;大气压强Pa=101 kPa;当Br =0时,f(Br)=1,当Br>0时,f(Br)<1。为了建模的方便,通常可以采用f(Br)=1-Br。应力和应变的变化均会导致颗粒破碎发生,因此,Daouadji等[13]和Liu等[14]提出采用塑性功wp的变化来标定加载过程中Br的演化:
(2)
式中:a和b均为模型参数;
为有效应力张量,
为塑性应变增量张量。除此之外,借鉴边界面塑性力学概念,可提出一种新的破碎演化方法:
(3)
式中:cw为模型参数;
为塑性功增量。
间接考虑颗粒破碎的临界状态线将e-ln p空间的临界状态数据在其他尺度空间再归纳。正如Li等[12]所指出,原本在e-ln p空间中下弯的丰浦砂临界状态线,在e-pξ空间中将重新变为直线,可以采用以下方程表达:
(4)
式中:eΓ0、λ0、ξ均为模型参数。
2 修正的SANISAND模型
根据原始SANISAND模型[15],确定三轴加载条件下砂土的弹塑性本构关系如下:
(5)
(6)
(7)
(8)
(9)
式中:应变增量
应力增量
分别为体变增量、剪应变增量、平均有效应力增量、偏剪应力增量;Ce、Kp、m、n分别为弹性柔度矩阵、塑性模量、塑性加载张量、塑性流动张量。
式(6)中,G为剪切模量,K为体积模量,分别定义为
(10)
(11)
式中:G0为弹性参数;e为孔隙比;ν为泊松比。
式(7)中,α为背应力比,h、αb、s的计算公式如下:
h=G0h1exp(h2A)(e-1-ch)2(Pa/p)1/2。
(12)
αb=Mexp(-nbζ)-m。
(13)
(14)
式中:h1、h2和ch为模型参数;A为砂土各向异性标量,后文会有具体解释;m=0.01;M=6sin φc/(3-ssin φc),φc为模型参数;nb也为模型参数;应力比η=q/p;ζ为考虑砂土组构影响的修正状态参数,可定义[16]为
ζ=e-ec-eA(A-1)。
(15)
式中:eA为模型参数。
式(8)中f为屈服函数,f=(q-pα)-spm=0;mv为压缩相关的加载方向分量;ms为剪切相关的加载方向分量。
式(9)中nv为压缩相关的流动方向分量;ns为剪切相关的流动方向分量;dg为剪胀比,不同于传统SANISAND模型,这里的dg采用分数阶剪胀比[17],从而使得模型参数变少,计算式如下所示:
dg=(μM-sη)|η|αf-1。
(16)
式中:μ=ψ(2)-ψ(2-αf),ψ(·)代表digamma函数,αf=exp(ndζ),nd为模型参数。至此,修正SANISAND模型的主要元素已经构建完毕。
砂土各向异性标量A的确定方法可以诠释为
A=F:R′;
(17)
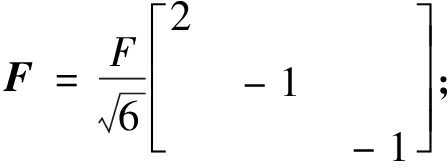
(18)
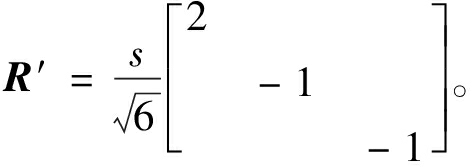
(19)
式中:F为组构张量,参考原始SANISAND模型[15],对于沉积面垂直于主应力轴方向的砂土,F初始值可以表述为式(18),其中F为组构标量,定义为
为塑性流动偏张量,参考原始SANISAND模型[15],在三轴加载条件下,R′可以定义为式(19)。F和R′两个张量仅对角线元素不为零,对角线上3个值分别代表3个主应力方向上的值。联合式(17)～(19),可得A=sF。加载过程中,F的演化可以确定为
(20)
式中:
为塑性剪应变增量;N=1;c0为模型参数。
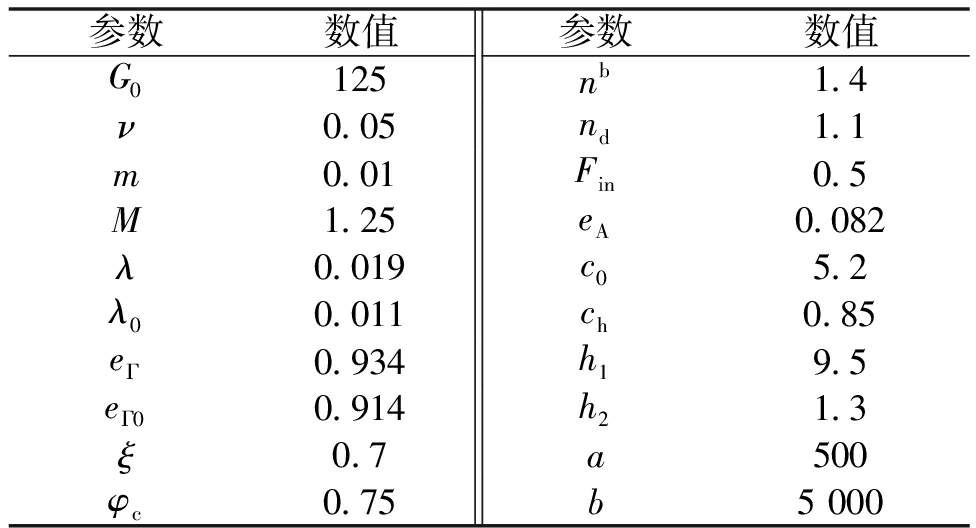
根据所选取的临界状态线,所建立的边界面本构模型有以下模型参数:eΓ、λ、a、b、eΓ0、λ0、ξ、G0、ν、h1、h2、ch、φc、nb、eA、nd、c0、Fin、m、M。所有参数均可以通过三轴试验获得,具体可以参见文献[8,18]。本文SANISAND模型借鉴文献[18]的参数来开展数值模拟,具体参见表1。由于本文采用了不同的剪胀方程表达式,因此将和体变相关的参数(nd、h1、a、b)进行了优化。
表1 模型参数
Table 1 Model parameter
参数数值参数数值G0125nb1.4ν0.05nd1.1m0.01Fin0.5M1.25eA0.082λ0.019c05.2λ00.011ch0.85eΓ0.934h19.5eΓ00.914h21.3ξ0.7a500φc0.75b5000
3 数值算法与模型验证
将基于直接和间接考虑颗粒破碎的两类临界状态线应用到修正的SANISAND模型,然后进行编译模拟,对比试验数据验证模型。本文采用基于切平面法的返回映射算法来进行数值模拟研究。具体来说,切平面法假设材料在每个时刻都处于弹塑性平衡状态。在这种方法中,首先需要确定初始状态下的应力状态和应变状态,通过施加载荷来改变材料状态,最后通过切平面法计算新的应力状态和应变状态。具体步骤如下。
步骤1 输入第n + 1增量步的应力和应变初值:
步骤2 弹性试探:
步骤3 如果f>0,则需要返回映射到屈服面上。
开始第k次迭代:
当f≤tol时,k次迭代结束,更新应力应变:
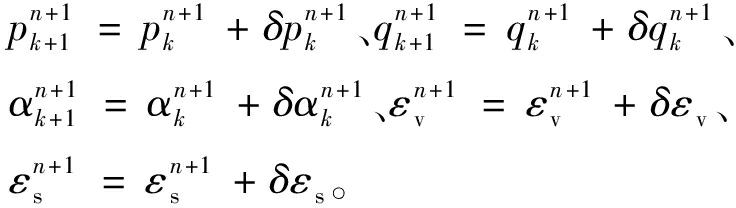
否则,继续迭代。
步骤4 如果f ≤0,则用弹性加载步更新应力应变:
步骤5 下一个增量步。
根据上述算法,采用MATLAB编辑程序,开展丰浦砂排水和不排水三轴试验的模拟,其中,丰浦砂排水和不排水试验的试验数据来源于Verdugo等[19]的砂土稳定状态研究,以及Yoshimine等[20]的一系列三轴试验。
丰浦砂排水的模拟结果如图1、2所示。分析图1可知,基于直接和间接考虑颗粒破碎的本构模型均可以较好地模拟不同初始孔隙比(e0)的丰浦砂试样在低围压(σ3=100 kPa)时的排水剪切行为,且两者模拟结果无肉眼可见的差别。具体来说,基于两种方法的模型可以较好地模拟较低孔隙比试样在排水剪切时候的剪缩、剪胀,以及相应的硬化和软化;同样,基于两种方法的模型也可以描述高孔隙比试样的剪缩和硬化特性。虽然基于两种方法的模型均可以较好地模拟低围压下丰浦砂的排水试验行为,但对于较高围压(σ3=500 kPa)下的丰浦砂试样,基于间接法的模型模拟更接近于试验值。如图2所示,基于直接法的模型模拟高估了各初始条件下砂土的剪切强度。
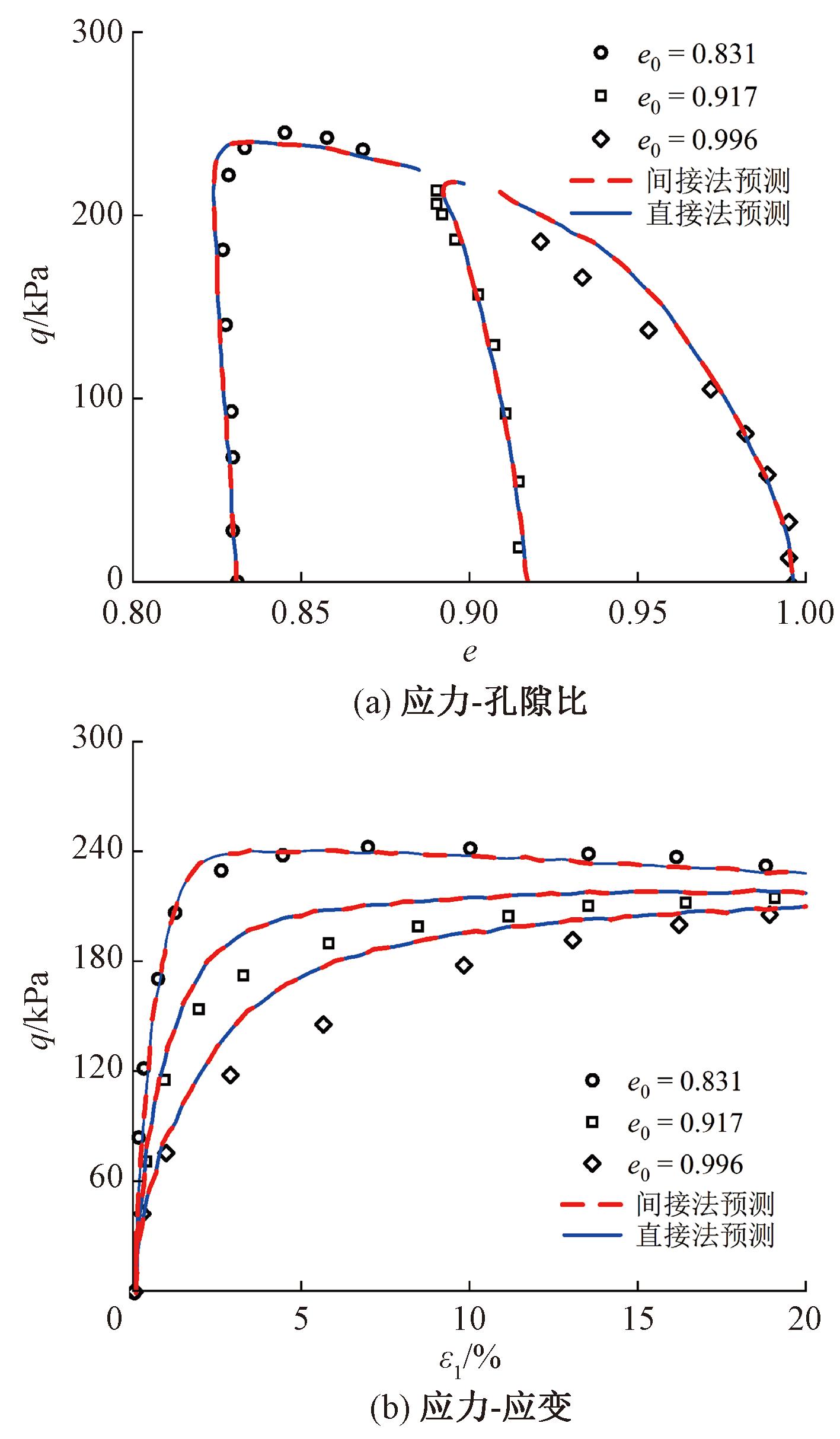
图1 100 kPa围压下丰浦砂排水试验模拟
Figure 1 Simulations of the drained tests on Toyoura sand with the confining pressure of 100 kPa
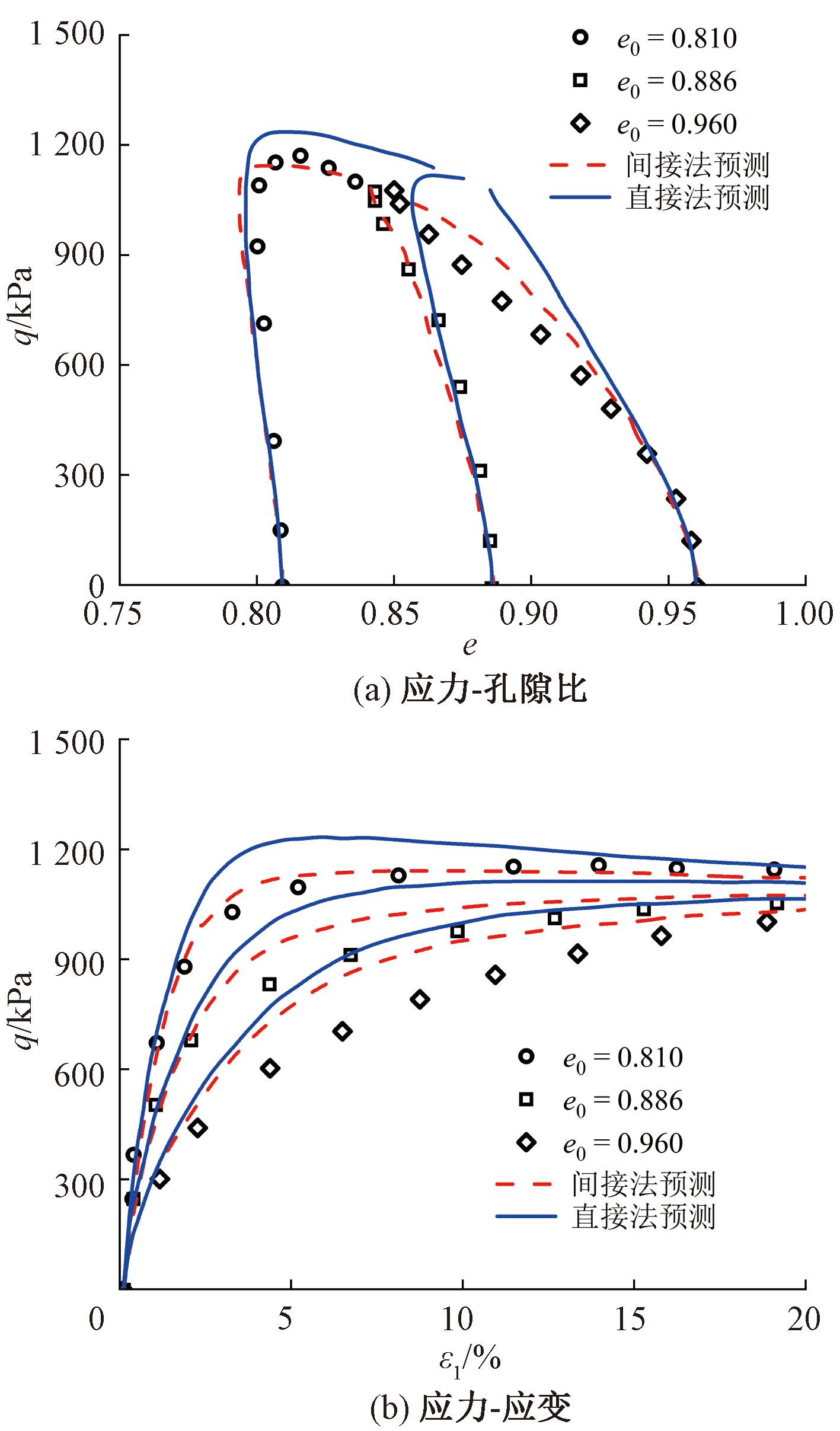
图2 500 kPa围压下丰浦砂排水试验模拟
Figure 2 Simulations of the drained tests on Toyoura sand with the confining pressure of 500 kPa
围压越高,砂土破碎程度越高是定论。图3为不同初始条件下致密丰浦砂的不排水试验模拟。分析图3可知,基于直接法和间接法的模型均可以在一定程度上刻画致密丰浦砂的不排水应力路径,但是基于间接法的模型预测更接近真实试验结果。基于直接法的模型预测无法刻画致密丰浦砂的剪切应力应变行为,加载初始,模型低估了砂土剪切应力;加载后期模型高估了砂土剪切应力。相比之下,基于间接法的模型预测可以较好地贴合试验数据。
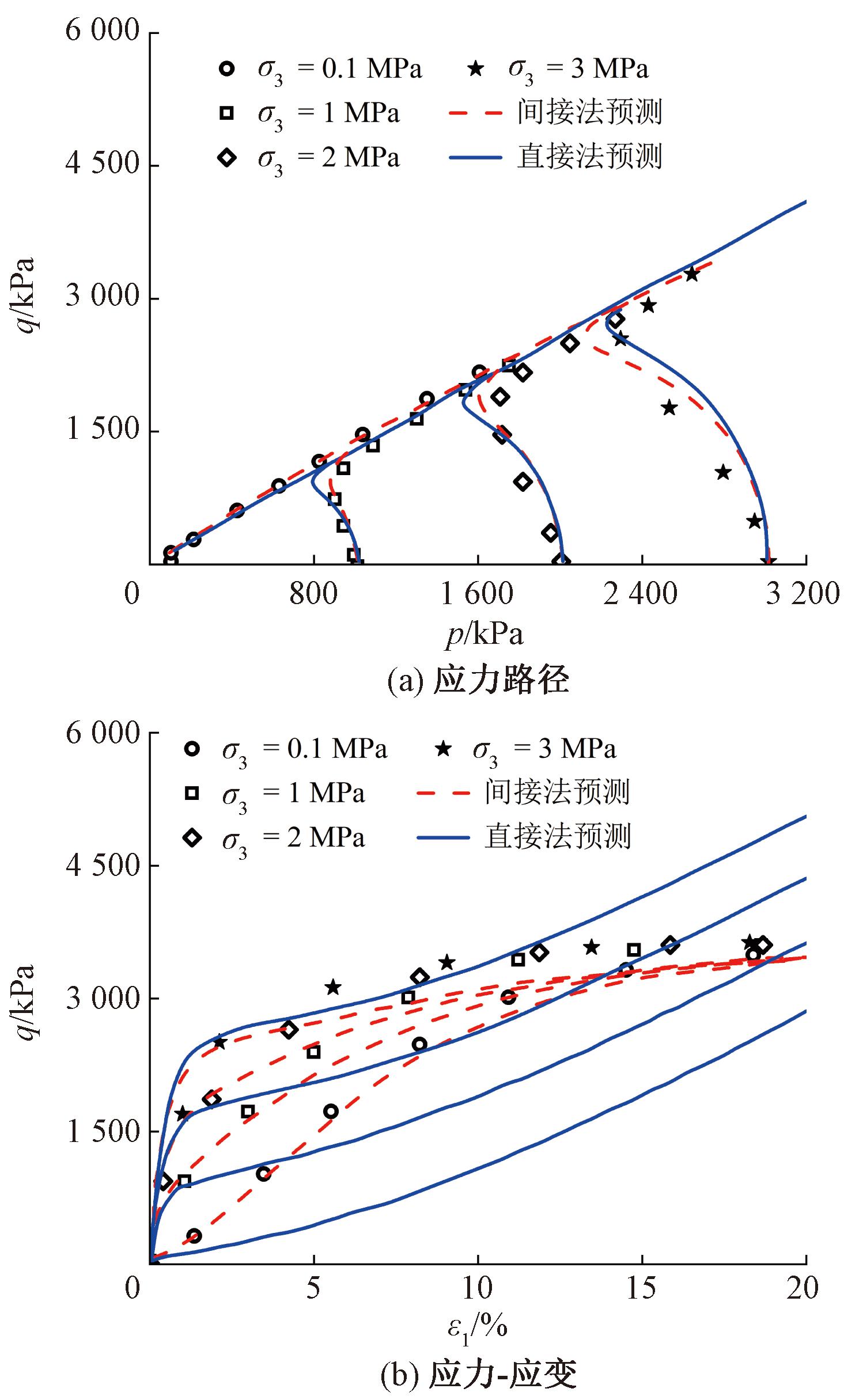
图3 致密丰浦砂不排水试验模拟
Figure 3 Simulations of the undrained tests on dense Toyoura sand
图4展示了模型对松散丰浦砂在不同初始围压下剪切行为的预测。分析可见,在低围压时,基于直接法的模型预测与基于间接法的模型预测表现相近。但随着初始围压的增加,采用直接法将高估松散砂试样在不排水剪切时的峰值强度。
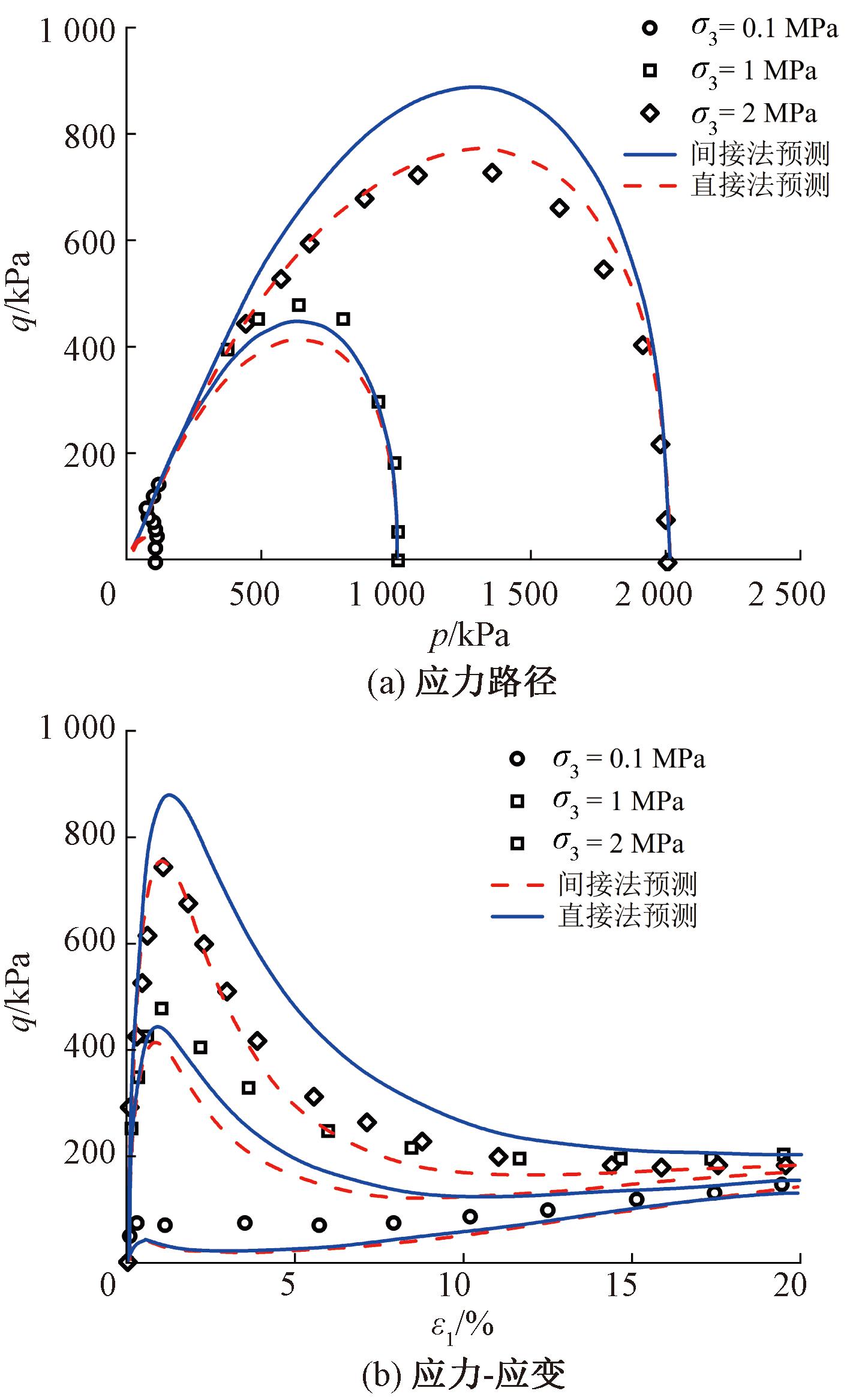
图4 松散丰浦砂不排水试验模拟
Figure 4 Simulations of the undrained tests on loose Toyoura sand
图5展示了模型对不同初始状态丰浦砂不排水压缩和拉伸剪切行为的预测。分析可见,在三轴拉伸条件下,基于两种方法的模型预测结果相近,所有砂土试样最后均达到了液化。但是,在三轴压缩条件下,基于直接法的模型预测结果在高初始围压条件下会高于实测值和基于间接法的预测值,基于间接法的模型预测值与试验实测值拟合较好。
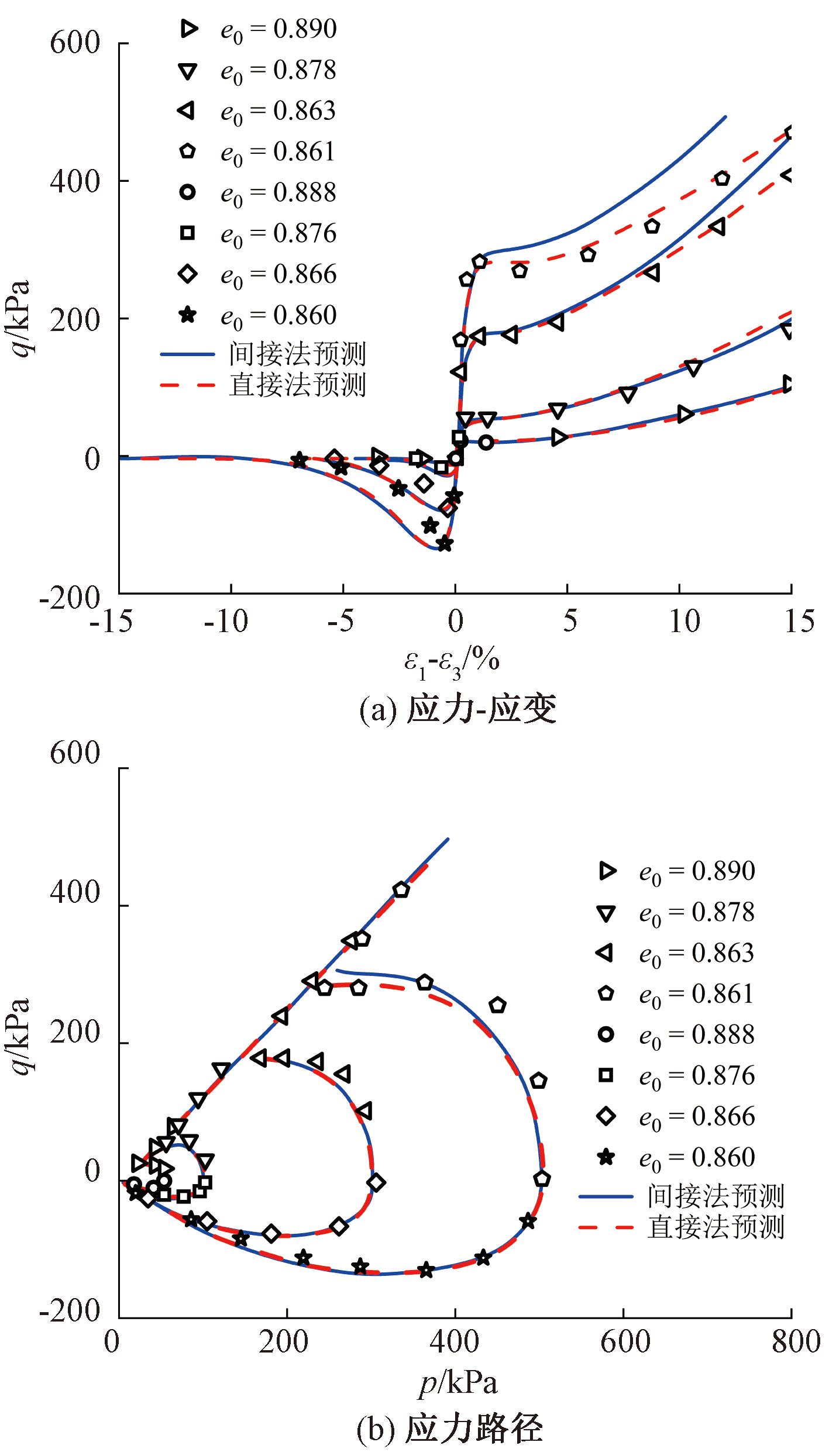
图5 丰浦砂压缩和拉伸试验模拟
Figure 5 Simulations of the compressive and tensile tests on Toyoura sand
综上可知,在对考虑颗粒破碎的砂土进行本构建模时,采用基于间接法的考虑颗粒破碎临界状态线更便捷高效。采用直接法的模型仅能适应部分初始状态的砂土力学行为预测,即初始围压或者孔隙比变化较小的试验模拟;对初始状态变化跨度较大的砂土试样,即初始围压或孔隙比变化范围较大的试验模拟,适应性较差。
4 结论
本文研究了两类不同的考虑颗粒破碎临界状态线在预测砂土排水与不排水应力应变特性时的表现,得出主要结论如下。
(1)考虑颗粒破碎的临界状态线常常可以分为两类:一类为直接将颗粒破碎率引入到e-ln p空间的临界状态线,考虑颗粒破碎率对该空间临界状态线移动的影响;另一类为间接考虑颗粒破碎对临界状态线的影响,即在其他空间重新构造关于e-p关系的简单函数。
(2)基于两类方法的临界状态线均可以较好地描述丰浦砂在低围压时候的应力应变特性,但是,基于直接法的临界状态线及其修正SANISAND本构模型较难描述高围压条件下丰浦砂的力学特性。
(3)对于初始状态变化较大的砂土,采用间接考虑颗粒破碎的临界状态线来构造本构模型,可以更好地描述其排水和不排水应力应变特性。
[1] DE BONO J P,MCDOWELL G R.Particle breakage criteria in discrete-element modelling[J].Géotechnique,2016,66(12):1014-1027.
[2] YU F W.Particle breakage and the critical state of sands[J].Géotechnique,2017,67(8):713-719.
[3] 潘洪武,王伟,张丙印.基于计算接触力学的粗颗粒土体材料细观性质模拟[J].工程力学,2020,37(7):151-158.PAN H W,WANG W,ZHANG B Y.Simulation on meso-mechanical property of coarse-grained soil materials based on computational contact method[J].Engineering Mechanics,2020,37(7):151-158.
[4] XIAO Y,LIU H L,CHEN Y M,et al.Bounding surface model for rockfill materials dependent on density and pressure under triaxial stress conditions[J].Journal of Engineering Mechanics,2015,141(7):08215001.
[5] ALAEI E,MARKS B,EINAV I.A five-parameter hydrodynamic-plastic model for crushable sand[J].International Journal of Solids and Structures,2022,254:111914.
[6] LIU H B,SONG E X,LING H I.Constitutive modeling of soil-structure interface through the concept of critical state soil mechanics[J].Mechanics Research Communications,2006,33(4):515-531.
[7] WU E L,ZHU J G,SUN Y F,et al.A general plastic model for rockfill material developed by using Caputo fractional derivative[J].Computers and Geotechnics,2022,151:104948.
[8] SHU S,YAN C,ZHAO W,et al.The role of breakage-dependent critical state lines in constitutive modelling of sand under axisymmetric drained and undrained loads:a comparative study[J].Marine Georesources &Geotech-nology,2024,42(11):1717-1727.
[9] HARDIN B O.Crushing of soil particles[J].Journal of Geotechnical Engineering,1985,111(10):1177-1192.
[10] EINAV I.Breakage mechanics:part I:theory[J].Journal of the Mechanics and Physics of Solids,2008,55(6):1274-1297.
[11] SUN Y F,SUMELKA W,GAO Y F.Bounding surface plasticity for sand using fractional flow rule and modified critical state line[J].Archive of Applied Mechanics,2020,90(11):2561-2577.
[12] LI X S,WANG Y.Linear representation of steady-state line for sand[J].Journal of Geotechnical and Geoenvironmental Engineering,1998,124(12):1215-1217.
[13] DAOUADJI A,HICHER P Y.An enhanced constitutive model for crushable granular materials[J].International Journal for Numerical and Analytical Methods in Geomechanics,2010,34(6):555-580.
[14] LIU H B,LING H I.Constitutive description of interface behavior including cyclic loading and particle breakage within the framework of critical state soil mechanics[J].International Journal for Numerical and Analytical Methods in Geomechanics,2008,32(12):1495-1514.
[15] DAFALIAS Y F,MANZARI M T.Simple plasticity sand model accounting for fabric change effects[J].Journal of Engineering Mechanics,2004,130(6):622-634.
[16] LI X S,DAFALIAS Y F.Anisotropic critical state theory:role of fabric[J].Journal of Engineering Mechanics,2012,138(3):263-275.
[17] SUN Y F,SUMELKA W,HE S H,et al.Enhanced fractional model for soil-structure interface considering 3D stress state and fabric effect[J].Journal of Engineering Mechanics,2022,148(9):1-16.
[18] PETALAS A L,DAFALIAS Y F,PAPADIMITRIOU A G.SANISAND-F:sand constitutive model with evolving fabric anisotropy[J].International Journal of Solids and Structures,2020,188-189:12-31.
[19] VERDUGO R,ISHIHARA K.The steady state of sandy soils[J].Soils and Foundations,1996,36(2):81-91.
[20] YOSHIMINE M,ISHIHARA K,VARGAS W.Effects of principal stress direction and intermediate principal stress on undrained shear behavior of sand[J].Soils and Foundations,1998,38(3):179-188.