大坝在供水、发电、防洪和灌溉等方面发挥重大作用,但由于大坝运行、极端天气多方面因素,溃坝事故时有发生。一旦发生溃坝事件,洪水将迅速穿越各种复杂地形,对下游造成严重的影响[1]。
近年来,随着关于溃坝洪水研究的增多,研究者们开始关注复杂地形下溃坝洪水的演进规律,许志发等[2]通过室内溃坝模型,探讨了不同下游坡降条件下尾砂流的演进规律。向波等[3]提出基于重力引力的动量修正单元冻结法,以便更好模拟超大坡度复杂地形下洪水演进。孙振宁等[4]研究了溃坝洪水在下游行洪过程中遇到急弯或驼峰等特殊地形的演进情况。李扬[5]利用HEC-RAS研究不同下游河道条件及溃坝条件对溃坝洪水过程的影响。Tan等[6]对比研究了陡峭地形和缓坡流域的溃坝情景。以上研究主要集中于下游复杂地形,如急弯、驼峰和陡坡等对洪水演进的影响,但缺乏对上游地形的影响研究。实际上,上游地形特征对洪水的流量、速度和传播路径有着重要影响,进而对整体洪水演进过程起着关键作用。目前缺乏一种能够同时整合上游库区和下游地形影响的综合模拟方法,这使得现有研究难以全面反映上下游地形对溃坝洪水演进的影响。
为了准确评估地形对溃坝洪水演进的影响,高精度的数字高程模型(digital elevation model,DEM)是研究的基础。尽管DEM技术发展迅速,但全球公开可用的DEM仍难以满足大多数洪水数值模拟的精度要求,尤其是水下河床高程和复杂河谷地形。为此,许多学者提出了不同的地形处理和重构方法。王昆等[7]采用无人机(unmanned aerial vehicle,UAV)遥感技术获取高分辨率地形数据。程馨玉[8]结合HEC-RAS和ArcGIS软件对研究区域地形进行处理并修正DEM。马勇勇[9]结合河流河道地貌特征,提出基于河道纵向特征和三维特征的地形重构方法。蒋芳旋等[10]利用CAD和Gambit软件建立符合实际地形的区域三维模型。辛岩[11]将处理后的实测图导入3DMine软件中建立三维模型,提取DEM数据。王扬等[12]提出一种基于TIN和NURBS软件建立三维模型,提取DEM数据的方法。以上方法操作复杂、成本高昂且技术要求高,限制了其广泛应用。因此,亟须一种简便且成本可控的地形建模方法,以提高实际应用中的效率和可操作性。
针对上述问题,以某水库工程为基础,考虑到上游库区的天然束窄断面特殊地形,本文提出了一种结合Civil 3D和HEC-RAS软件的新方法,并提出一种改进模拟方法,使用二维网格区域代替常规使用的蓄水区域模拟上游库区,同时考虑上游库区和下游地形的存在,全面反映上下游地形对溃坝洪水演进的影响。
1 工程概况
某水库于1974年建成,为狭长河道型水库。正常蓄水位474.0 m,复核后总库容为2 074万m3,设计洪水位475.5 m,校核洪水位478.0 m,属三等中型工程,主要建筑物为3级。水库大坝为混凝土单曲圆筒拱坝,坝顶高程478.3 m,最大坝高39.4 m,坝顶弧长110 m,坝顶宽2 m,坝底厚10 m。距大坝上游约1 km处的峡谷通道存在一处天然束窄断面,位置见图1(a),认为该断面将水库分为上、下库区。该断面在472 m对应河宽仅约15 m,过水面积显著减小,水位474 m时束窄断面过流面积约为上游断面的31%、下游断面的14%,虽然在水位达到474 m以后束窄断面逐渐开阔,但相对于上、下游断面仍较为狭窄。束窄断面及上下游断面如图1(b)所示。
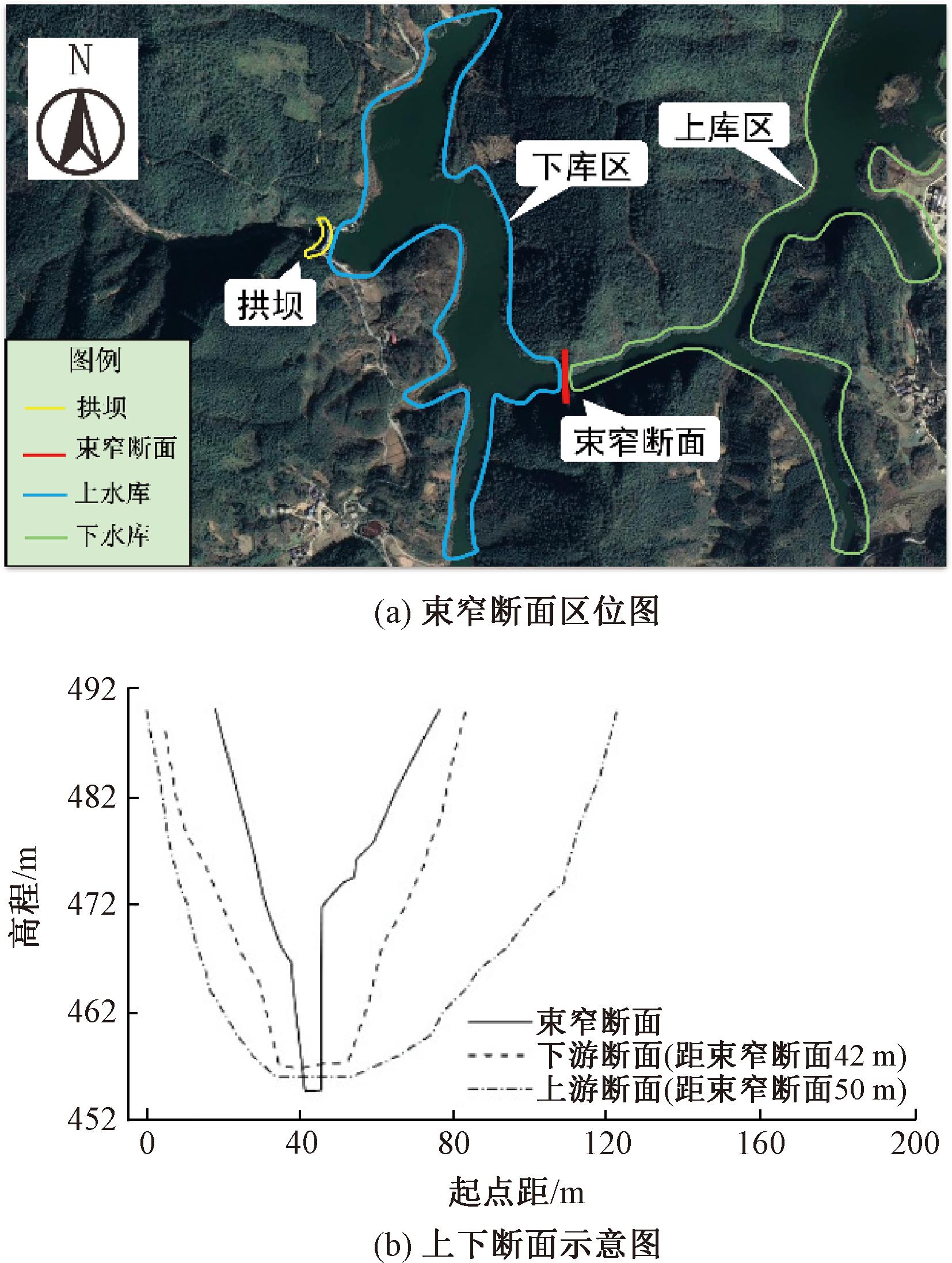
图1 束窄断面区位及上下游断面示意图
Figure 1 Schematic diagram of narrow section location and upstream and downstream sections
2 计算原理及方法
二维HEC-RAS水动力学模型采用浅水扩散波近似(DSW)方程[12],其中连续性方程如下:
(1)
式中:H为水面高程,m;t为时间,s;h为水深,m;V=(u,v)T为水流速度矢量;q为旁侧入流量,![]() 为梯度算子。
为梯度算子。
动量方程采用扩散波形式,其与连续方程组合的计算速度较完全的浅水方程快且累积误差小,适用河床坡降大的河流,该拱坝下游为峡谷段且坡降较大,较为适用。扩散波方程如下:
(2)
式中:R(H)为水力半径,m;n为糙率。
将扩散波方程代入连续性方程,可得到浅水扩散波近似(DSW)方程的经典微分形式:
(3)
式中:![]()
采用有限差分和有限体积相结合的混合离散格式对浅水扩散波近似(DSW)方程进行离散求解,并运用Newton-Raphson迭代法进行计算。
3 二维溃坝模型构建
3.1 数据获取
建立二维溃坝模型需要用到的地形、土地覆盖及水文数据如图2所示。地形数据来源于ALOS的2019版,分辨率为12.5 m×12.5 m,使用ArcGIS将数字正射影像图(DOM)叠加DEM,制作3D地形图。土地覆盖数据来源于欧空局Sentinel-2数据,分辨率为10 m×10 m。水文数据包括洪水流量过程线以及库容曲线,研究假设在洪水叠加闸门失效的情况下发生漫顶溃坝,上游入库流量选择校核洪水过程(P=0.2%)。
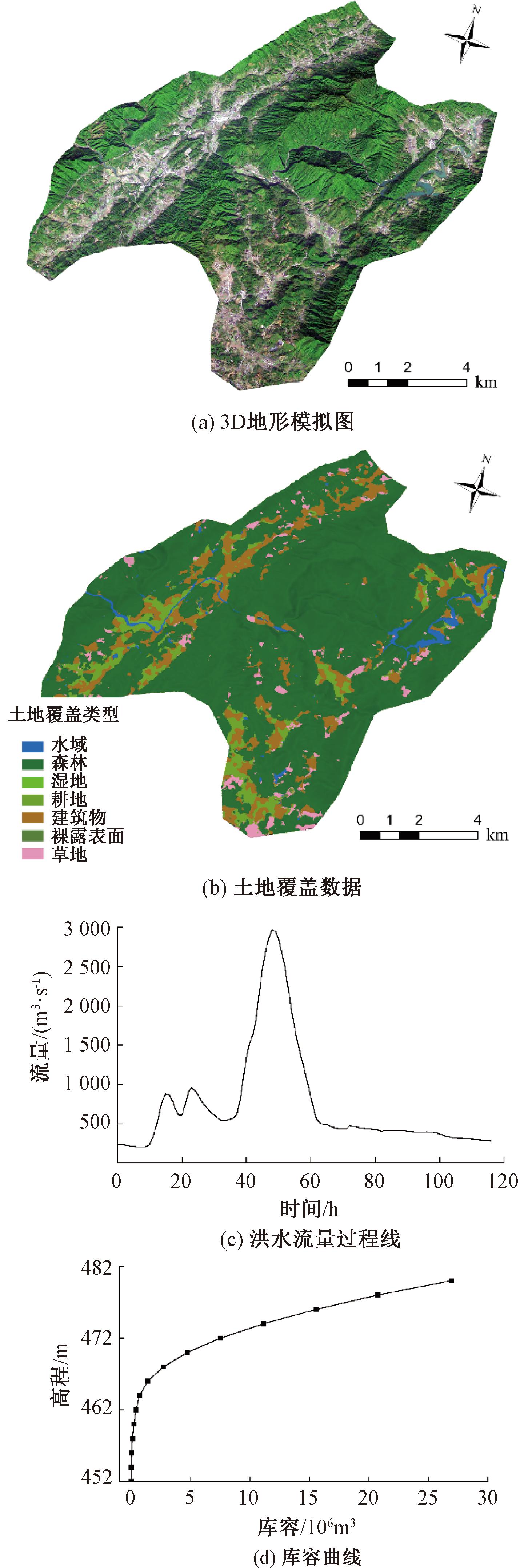
图2 模型构建数据
Figure 2 Model building data
3.2 地形处理
由于现有DEM不涵盖河道水面以下的地形,且无法准确反映束窄断面处的真实地形。本文提出一种结合Civil 3D和HEC-RAS的方法进行地形修正,Civil 3D是一款专业的工程设计与地形建模软件,主要功能包括地形建模、道路设计、管线设计以及水利工程的分析与设计,广泛应用于基础设施建设和水利工程等领域。在本文中,Civil 3D用于对上游库区的复杂地形进行精细化处理,生成高精度的DEM数据,特别是补充和修正水面以下及束窄断面处的地形,优化HEC-RAS模型的输入,具体操作流程图如图3所示。
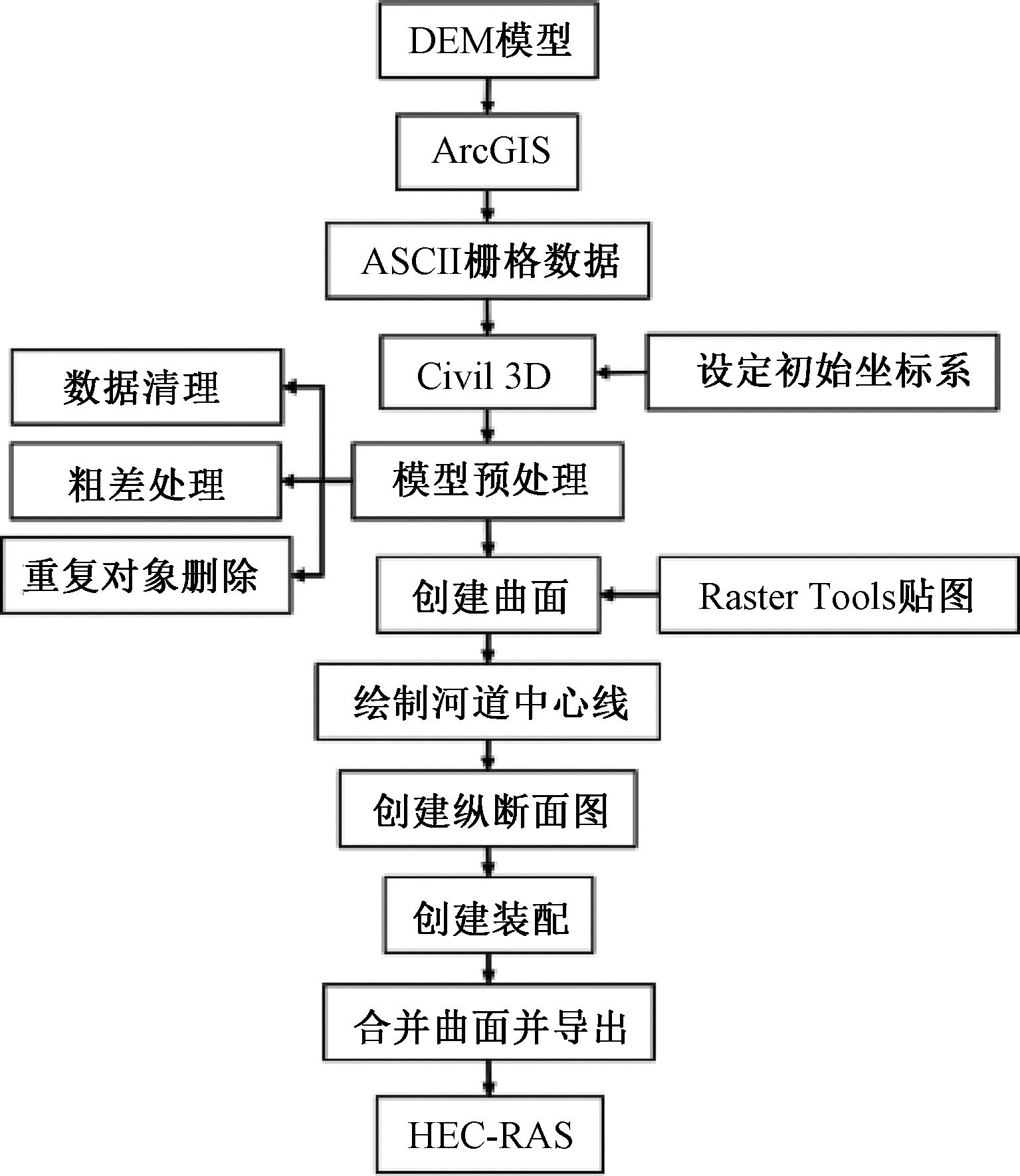
图3 地形处理流程图
Figure 3 Terrain processing flow chart
3.3 计算参数
3.3.1 网格剖分与时间步长
HEC-RAS模型采用内部正交网格与不规则多边形边界网格,综合考虑计算精度和效率,二维模拟区域网格尺寸为10 m×10 m,主河槽段网格加密为1 m×1 m。根据网格大小与库朗数,时间步长确定为5 s,使用扩散波方程计算,满足模型稳定要求。
3.3.2 溃口参数
溃口形态主要与坝型和筑坝材料有关。水库大坝为混凝土单曲圆筒拱坝,属于刚性坝,根据历史溃坝案例,此类坝型的溃决类型一般为全坝段瞬时溃决[13]。因此,本研究将溃决类型设定为瞬时溃决,并设定从溃口初现到发展至全坝段的整个过程所需时间为0.1 h。同时,由于本次是全坝段溃决,溃口将扩展至全坝段,最终达到坝顶弧长的宽度和最大坝高的深度,从而与整个坝体的几何尺寸相一致。溃口的几何形状近似梯形,宽度为坝顶弧长110 m,深度为最大坝高39.4 m。
3.3.3 糙率
在HEC-RAS建模过程中,首先,收集了研究区域的土地覆盖数据,本文采用的是来自欧空局Sentinel-2的数据源; 其次,根据这些土地覆盖数据,对研究区域进行了分类,根据相关规范中提供的各类土地覆盖类型的典型糙率值,选择了适合本研究的糙率值; 最后,通过HEC-RAS中的RAS-Mapper插件,将选定的糙率值赋予相应的土地覆盖类型,具体赋值为水域0.040、森林0.100、湿地0.070、耕地0.040、建筑物0.300、裸露表面0.030、草地0.035。
3.4 常规方法
在使用HEC-RAS进行溃坝洪水模拟时,库区通常采用蓄水区(库容曲线关系)常规方法模拟,大坝采用SA/2D连接关系,下游洪泛区采用二维网格模拟。初始条件和边界条件设置如下:上游库区采用汛前水位474 m作为初始水位,库容曲线采用2013年复测数据。上游侧向入流条件采用校核洪水过程线(P=0.02%),束窄断面位于上游库区模拟范围内,具体位置以及断面形态见图1。为模拟校核洪水叠加闸门无法开启导致的漫顶溃坝,溃坝触发水位设为坝顶高程478.3 m。其余保持系统默认值。下游边界条件取河道平均比降。
模型的具体方案见图4(a)。按照常规方法设置条件进行计算,上游库区各位置水位变化情况如图4(b)所示。溃坝发生在模拟开始后的10 h 59 min 10 s。在模拟前期阶段,上游库区各位置水位高度一致。到模拟后期阶段,由于来流量急剧下降且发生溃坝,上游库区失去蓄水能力,各位置水位降至地表高程。常规方法将库区简化为水位与库容的对应关系,适用于上游地形平坦且行洪通道顺畅无阻的情况。然而,该方法无法反映上游库区的行洪过程,也难以模拟上游束窄断面对洪水演进的具体影响。因此,需要更准确的模型来进行模拟。
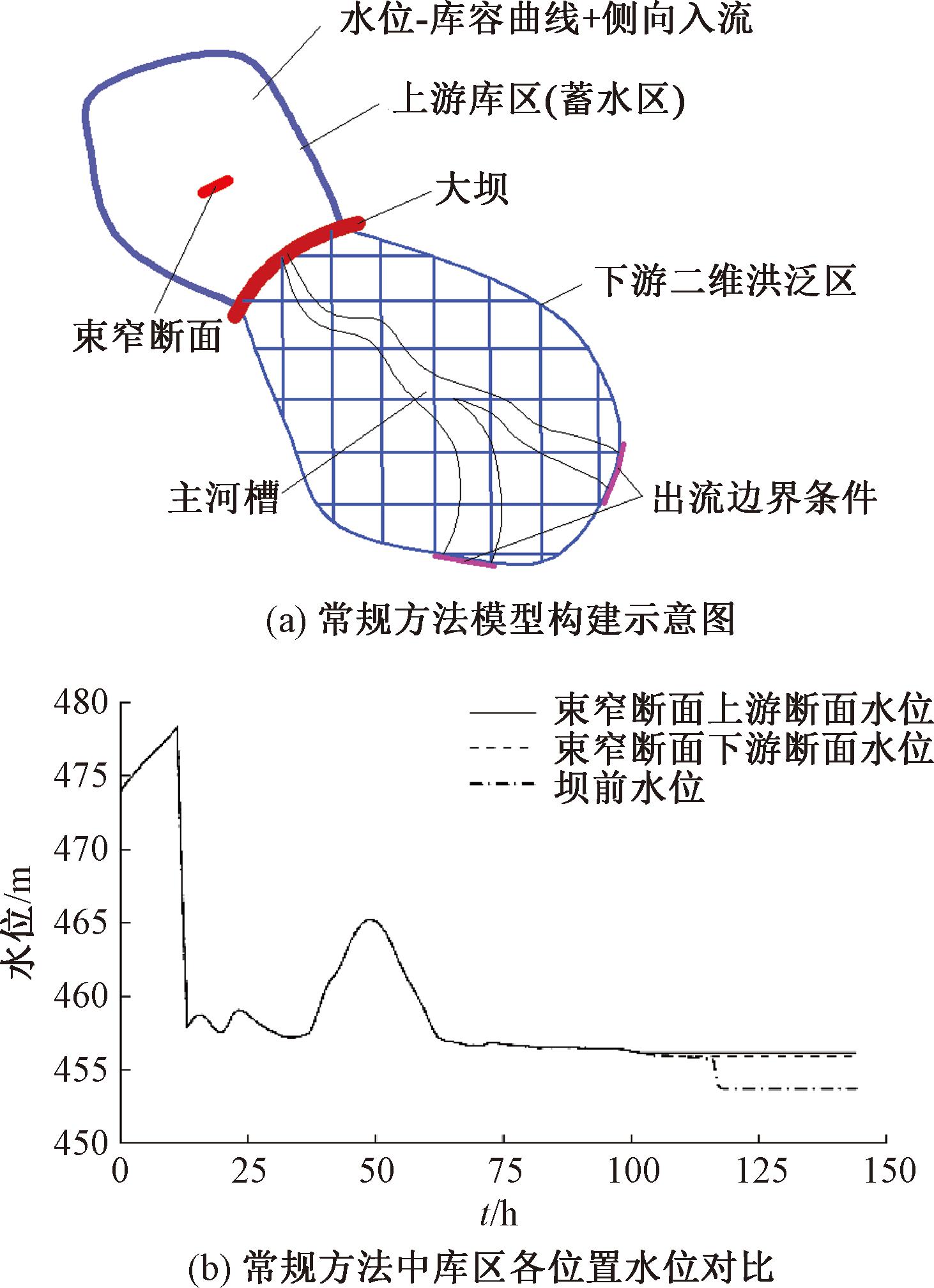
图4 常规方法计算方案与结果分析
Figure 4 Conventional method calculation scheme and result analysis
3.5 改进方法
为更准确地反映溃坝洪水的演进过程,综合考虑上下游地形特征,通过将库区改为二维网格区域(2D flow),并利用Civil 3D软件补充和修正水面以下及束窄断面处的复杂地形,生成高精度DEM数据并导入HEC-RAS中进行模拟。与常规方法相比,改进方法允许洪水在上游库区内进行二维流动,充分考虑地形的作用,特别是在束窄断面的阻水效果方面。具体方案实施细节示意图见图5(a)。按照改进方法设置条件进行计算,上游库区各位置水位变化情况如图5(b)所示。在50 h左右,水位突然上升是由于入流条件采用的洪水流量过程线在此时间段经历了主洪峰,水库中各监测点的水位迅速增加。随后,水位突然下降是因为主洪峰已过,随着溃口的泄流,水位逐渐下降。其次,在120 h左右,水位突然下降是因为模拟总时长超过了电站提供的校核洪水过程时长。为了反映退水现象,在校核洪水过程结束后,入流条件改为年径流量,由于流量较小,水位出现突然下降的现象。
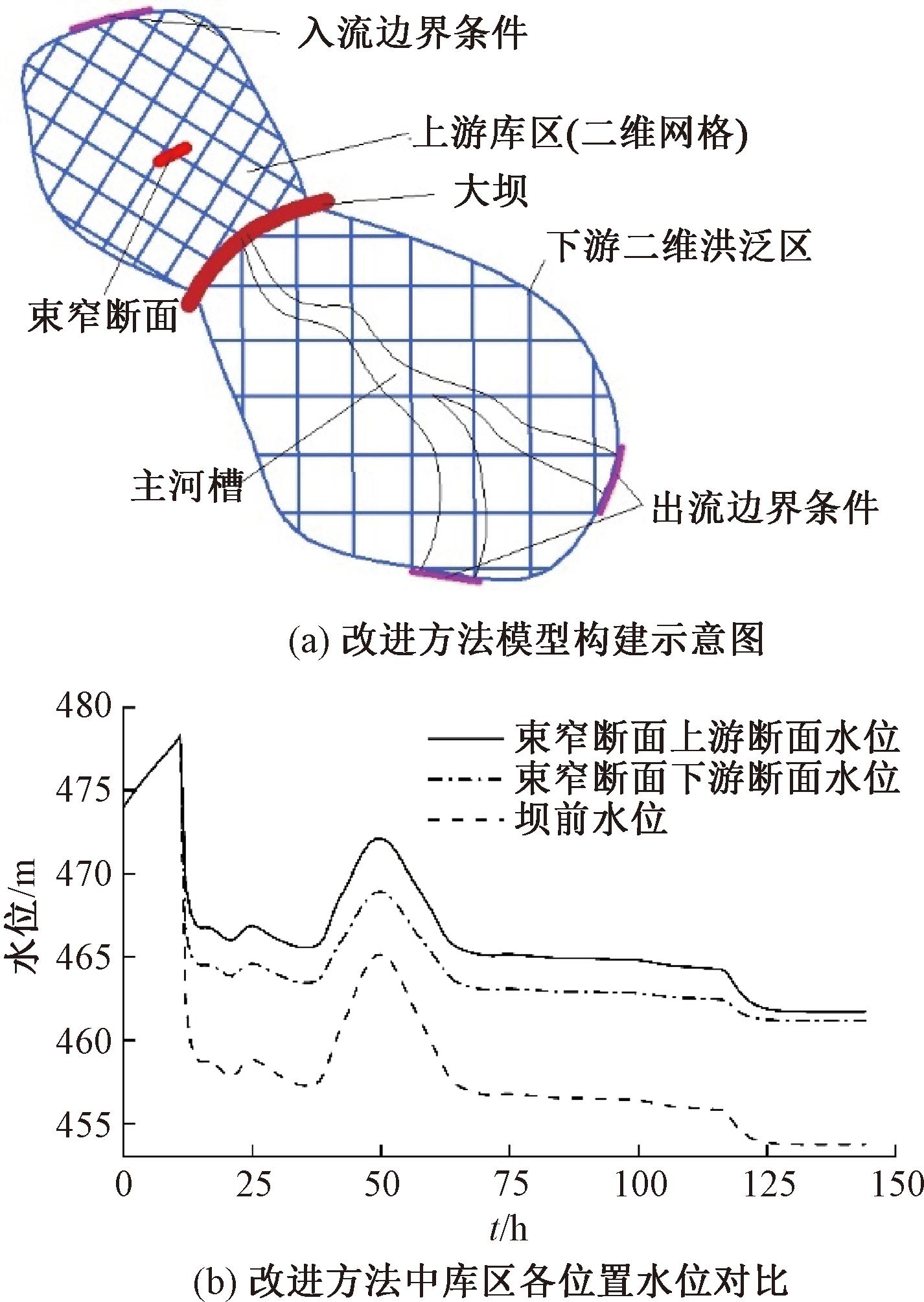
图5 改进方法计算方案与结果分析
Figure 5 Improved method calculation scheme and result analysis
比较图4(b)与图5(b),改进方法计算得到的溃坝时间为模拟开始后的11 h 5 s,比常规方法延后约1 min。在溃坝发生前,各位置水位基本保持一致,束窄断面的阻水作用可忽略不计;待溃坝发生后,在极大的流量宣泄下,各位置水位开始出现明显落差,束窄断面上下游选取测量断面(距离28.5 m)最大水位差达到3.219 m,束窄断面的雍水效果明显。故改进方法将上游库区设置为二维流动区域后,可体现束窄断面的作用,基于此方法,进一步开展束窄断面对溃坝洪水下游洪泛区演进影响的机制研究。
4 结果分析
4.1 敏感点选取
为了分析溃坝洪水对下游区域的影响及其演进规律,本文选择从峡谷段到下游大型水库之间的范围作为研究区域,如图6所示,并根据该区域的地形特征和人口分布情况选取9个敏感点,重点涵盖河道弯曲处、干支流交汇处及人口密集处等关键位置,这些点有助于全面分析洪水的演进规律和潜在风险。
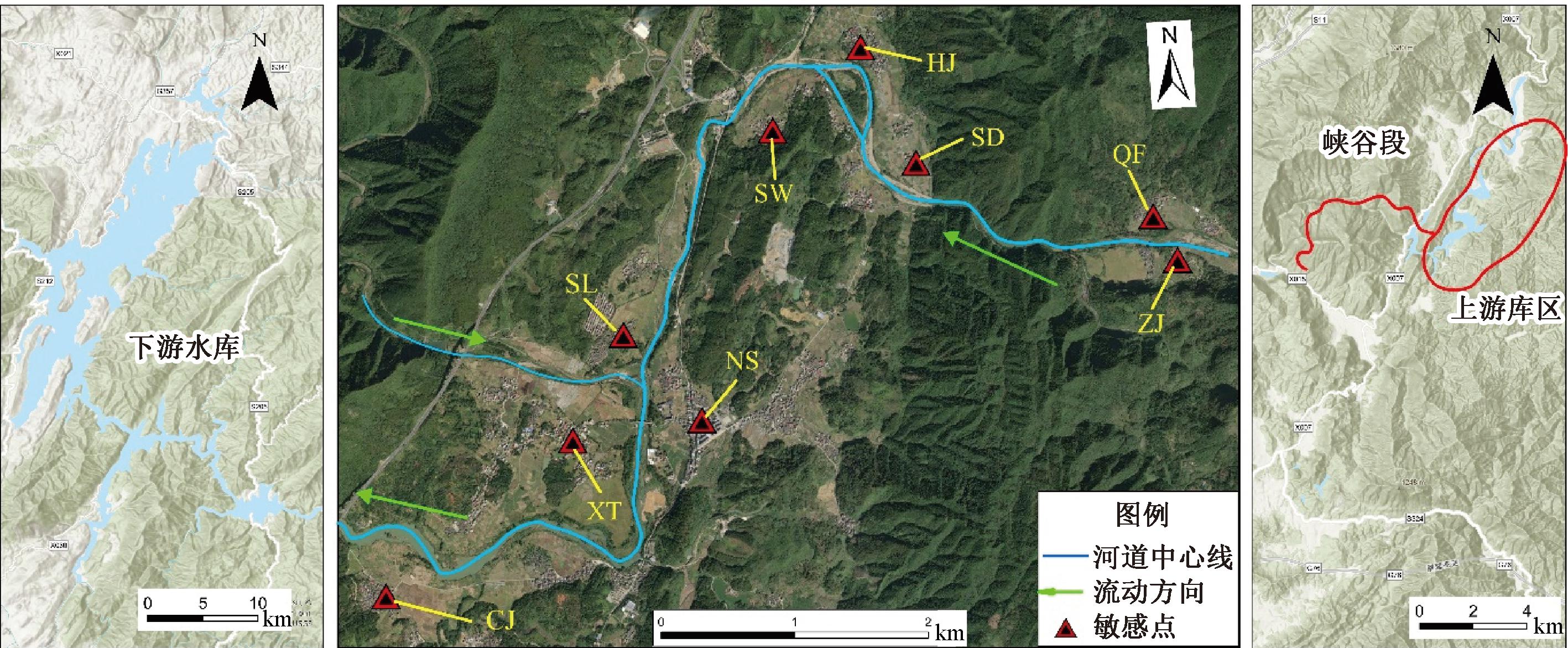
图6 研究区域敏感点分布图
Figure 6 Distribution map of sensitive points in the research area
4.2 束窄断面对溃坝洪水演进影响分析
4.2.1 淹没水深分析
基于校核洪水入库流量(P=0.2%),利用HEC-RAS进行溃坝模拟,洪水淹没范围和水深分布如图7所示,大坝溃决后洪水首先经过峡谷段,后沿河道自东北向西南淹没下游区域,敏感点均处于淹没范围内。如图8所示,溃坝后多数敏感点的水深经历了急剧抬升后又快速下降的过程,后续水深变化过程与洪水入库流量规律相似,呈现“一主峰两次峰”的趋势,尤其是靠近坝址和靠近主河道的敏感点,这一趋势更加显著。55 h左右之后所有敏感点开始出现退水现象。各敏感点的平均淹没水深为6.92 m,其中QF处最大,达到9.338 m;NS处最小,为1.552 m。以上敏感点的最大淹没水深除NS处均大于3.0 m,均属于严重危险区域。
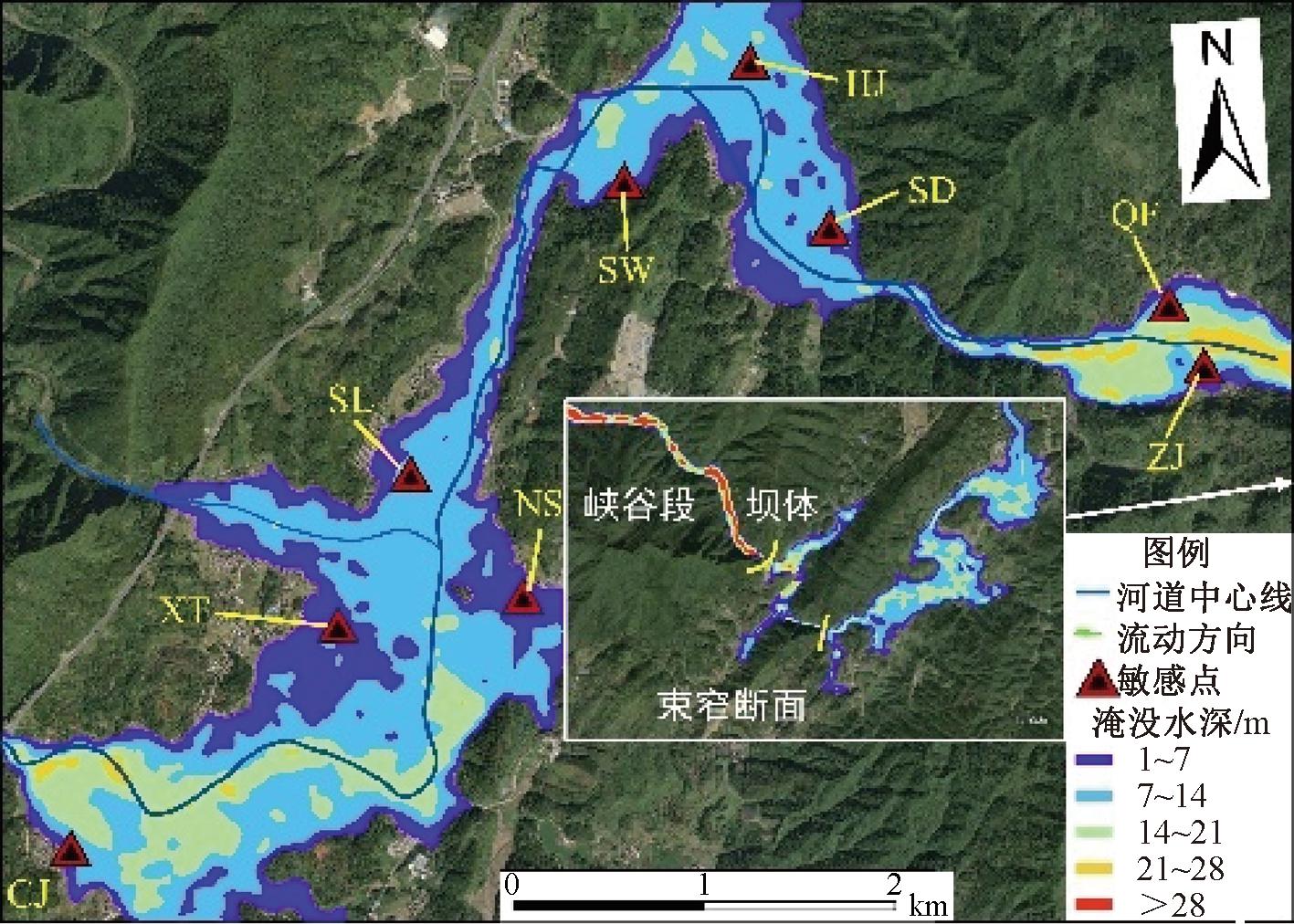
图7 最大淹没水深分布示意图
Figure 7 Schematic diagram of maximum inundation depth
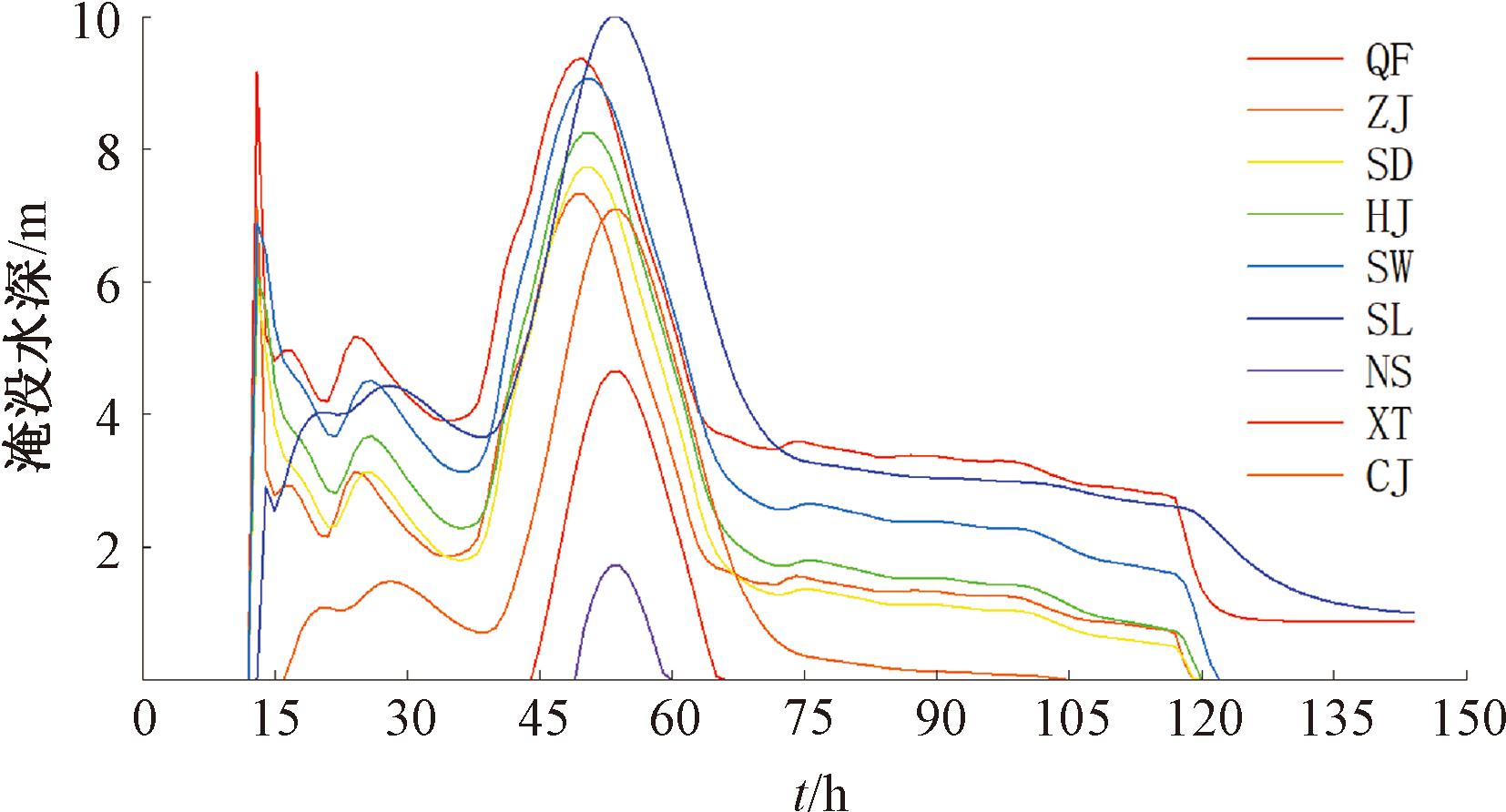
图8 各敏感点淹没水深变化过程示意图
Figure 8 Schematic diagram of changes in inundation depth at various sensitive points
为体现改进方法与常规方法在洪水演进计算结果上的差异,并研究上游束窄断面对洪水演进的影响机制,挑选具有代表性的敏感点,并对不同方法下的结果进行对比。其中,QF、ZJ点距离坝址最近,计算结果规律相似,归为第一类敏感点,选取QF点展示其水深变化;SD、HJ、SW、SL、NS、XT为河曲地形、干支流交汇处近的敏感点,归为第二类敏感点,选取SD点展示其水深变化;CJ为河道末端敏感点,距离坝址最远,归为第三类敏感点。代表性敏感点QF、SD、CJ的淹没水深对比如图9所示。
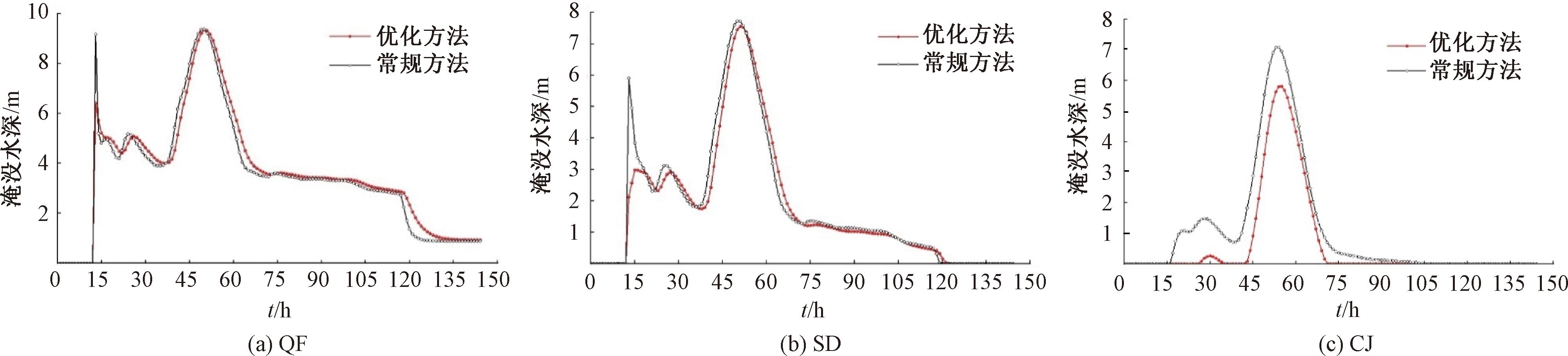
图9 改进方法与常规方法对比
Figure 9 Comparison between improved method and conventional method
根据计算结果,以QF、SD为代表的第一、二类敏感点由于离坝址较近,对溃坝洪峰具有较高的敏感性。改进方法下溃坝洪峰减弱,尤其是SD点,常规方法计算得到的溃坝洪峰淹没水深极值为5.909 m,而改进方法计算得到的为2.983 m,降幅达49.52%。其他敏感点的淹没水深也都有所降低。这表明束窄断面对洪峰具有显著的削峰作用,束窄断面的存在导致实际的过流面积减小,使得单位时间内的过流量减少。通过束窄断面的水量被限制,削弱了洪峰强度。
从图9可以看出,QF相对接近坝址,两种计算方法得到的首次淹没水位极大值发生时刻基本重合,表明溃坝发生时间基本一致。改进方法计算得到的QF点在达到最大淹没水深所需的时间比常规方法的计算值延后了约47.5 min。其他敏感点也存在类似情况,其中CJ点延迟最为显著,约59.5 min。可见束窄断面起到了显著的错峰作用,距离坝址越远,错峰效应越明显。束窄断面的存在使洪水下泄受阻,导致洪水波传播速度减慢,延迟洪峰的到达时间。此外,束窄断面短暂地储存洪水,使得洪水在断面上下游形成水位差,进一步延缓洪峰的传递。由于能量损失、水流形态变化的共同作用,错峰和削峰协同出现,两者均是由于断面突然收缩引起的复杂水动力学过程的结果,之间的关系有待于进一步研究。
4.2.2 洪水到达时间分析
溃坝事件发生后,洪水开始在下游地区出现的时间称为溃坝洪水到达时间,其对应急响应和灾害管理至关重要。根据改进方法计算结果,溃坝发生在模拟开始后的11 h 5 s。如图10所示,溃坝后1 h内洪水从库区内进入峡谷段,并在第1 h末流出峡谷段。在第1~2小时,洪水先后抵达ZJ、QF、SD,主要沿河道中心线传播,淹没范围达1.98 km2。在第2~4小时,洪水淹没HJ、SW、SL,并到达演进区域的出流边界,同时向河道两岸扩散,淹没范围扩大至4.02 km2。在第4~6小时,洪水继续向河道两岸扩散,淹没范围扩大至5.08 km2,并通过下游出流边界。在第6~10小时,洪水淹没到CJ点,淹没范围扩大至5.97 km2。10 h后,洪水淹没了XT、NS,且在此后的时间内,淹没范围达到最大8.02 km2,随后逐渐退水,各敏感点区域的退水时刻可查看图8。
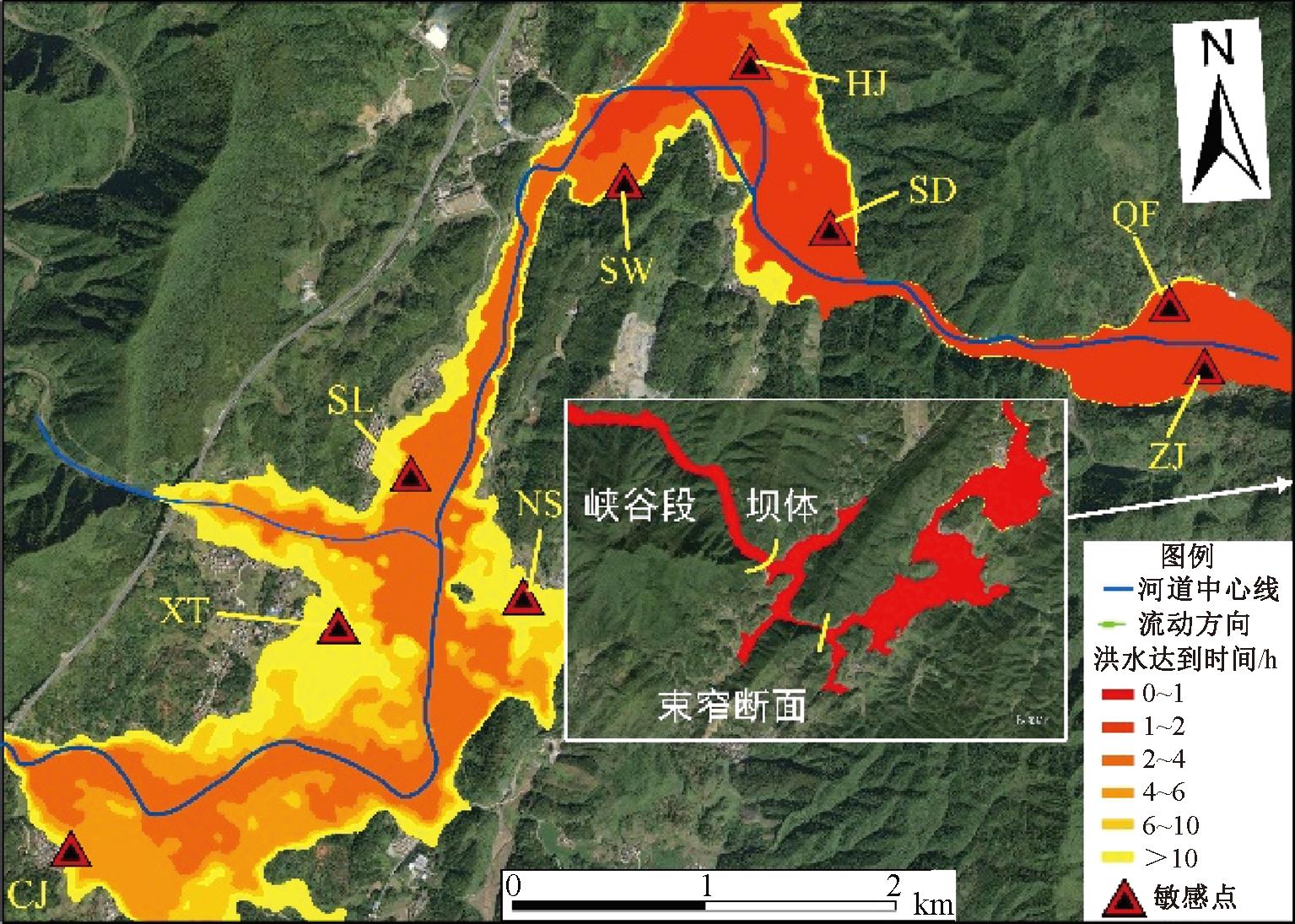
图10 溃坝洪水到达时间分布示意图
Figure 10 Schematic diagram of arrival time of flood
此外,为研究束窄断面对洪水错峰作用的影响,本文将改进方法计算得到的各敏感点的洪水到达时间与常规方法进行比较,结果见表1。由表1可知,在改进方法下,各敏感点的洪水到达时间均比常规方法要延后1 h左右,平均延后率为17.56%。其中,延后最明显的是距离坝址最远的CJ点。由此可见常规方法计算更为保守,但忽略了束窄断面等地形因素,改进方法更贴近实际情况。计算结果进一步证实了束窄断面的错峰作用,延长了下游居民的应急撤离时间。
表1 改进方法与常规方法得到的洪水到达时间对比
Table 1 Comparison of flood arrival times obtained by improved methods and conventional methods
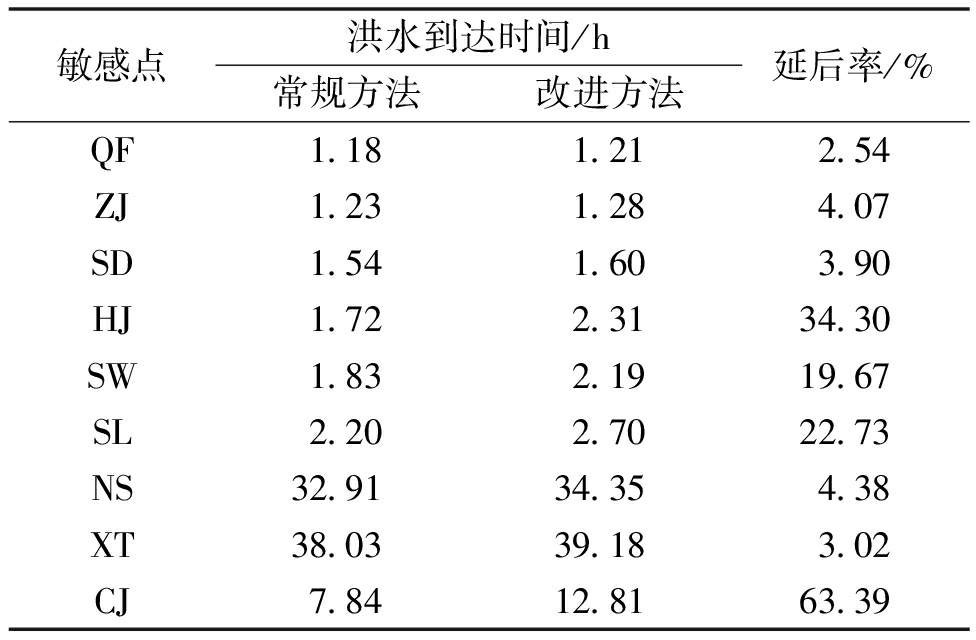
敏感点洪水到达时间/h常规方法改进方法延后率/%QF1.181.212.54ZJ1.231.284.07SD1.541.603.90HJ1.722.3134.30SW1.832.1919.67SL2.202.7022.73NS32.9134.354.38XT38.0339.183.02CJ7.8412.8163.39
综上所述,束窄断面有着显著的错峰和削峰作用,因此束窄断面的存在可显著降低淹没损失和溃坝洪水风险,表明改进方法可以更真实准确地模拟洪水演进情况,使应急撤离时间得以最大程度优化。
5 结论
本文提出一种经济高效的地形处理方法以及一种适用于复杂地形下溃坝洪水演进的改进方法,并结合实际工程案例,采用HEC-RAS二维水动力学模型进行计算,具体结论如下。
(1)提出了一种结合Civil 3D和HEC-RAS的精细化DEM地形处理方法,基于某工程上游库区的束窄断面地形,处理效果较好,可为具有复杂地形条件的相关工程提供借鉴思路。
(2)针对HEC-RAS将库区设置为蓄水区的常规方法无法模拟复杂地形的问题,本文提出一种改进方法,将上游库区类型改进为二维流动区域,允许洪水在复杂地形内流动,真实反映上游的束窄断面对洪水演进的影响作用。
(3)相比于常规方法,改进方法计算得到的溃坝洪峰淹没水深极值为2.983 m,降幅达49.52%;延后洪水到达时间平均为1 h,平均延后幅度为17.56%,可见束窄断面起到显著的错峰和削峰作用,可增加下游居民应急撤离的宝贵时间以及有效降低下游淹没风险。
(4)在复杂地形条件下,改进方法具有可行性和实用性,能够更准确地模拟洪水传播和淹没情况,为制定应急预案提供准确依据,可为其他水库防洪避险工作提供科学支持。
[1] 葛巍,焦余铁,洪辛茜,等.基于AHP-BN法的溃坝生命损失风险评价[J].郑州大学学报(工学版),2021,42(3):8-12.GE W,JIAO Y T,HONG X Q,et al.Risk assessment of life loss caused by dam breach based on AHP-BN method[J].Journal of Zhengzhou University (Engineering Science),2021,42(3):8-12.
[2] 许志发,王光进,赵怀刚,等.不同下游河道坡降尾矿库溃坝模型试验及下游影响研究[J].中国安全生产科学技术,2018,14(8):134-140.XU Z F,WANG G J,ZHAO H G,et al.Study on dam-break model tests and downstream influence of tailings pond with different downstream river slopes[J].Journal of Safety Science and Technology,2018,14(8):134-140.
[3] 向波,周杰,于普兵,等.超大坡度谷坡复杂地形守恒溃坝洪水模拟[J].水动力学研究与进展A辑,2023,38(3):363-370.XIANG B,ZHOU J,YU P B,et al.Dam break flooding conservative simulation at extreme complex topographic steep valley and slope[J].Chinese Journal of Hydrodynamics,2023,38(3):363-370.
[4] 孙振宇,周运浩,张勤旭,等.基于二维浅水方程的胖头泡蓄滞洪区洪水演进数值模拟[J].人民珠江,2024,45(6):82-91.SUN Z Y,ZHOU Y H,ZHANG Q X,et al.Numerical simulation of flood evolution in Pangtoupao flood storage area based on two-dimensional shallow water equation[J].Pearl River,2024,45(6):82-91.
[5] 李扬.山区河道土石坝溃坝洪水演进特性研究[D].重庆:重庆交通大学,2021.LI Y.Study on flood routing characteristics of earth-rock dam break in mountainous river[D].Chongqing:Chongqing Jiaotong University,2021.
[6] TAN F J,BALCERA J A A,BALUYOT G P S,et al.Dam break scenario in steep terrain watershed-the case of Ambuklao Dam in Benguet Province,Luzon Island,Philippines[J].AIP Conference Proceedings,2018,2045(1):020051.
[7] 王昆,张俊阳,杨修志,等.考虑精细地形的尾矿库溃坝外泄泥流运移规律研究[J].中国安全科学学报,2022,32(12):95-101.WANG K,ZHANG J Y,YANG X Z,et al.Research on migration law of tailings dam breach runout mud flow considering fine terrains[J].China Safety Science Journal,2022,32(12):95-101.
[8] 程馨玉.基于HEC-RAS的闸坝溃坝洪水演进数值模拟分析[D].成都:西华大学,2022.CHENG X Y.Numerical simulation analysis of flood evolution of gate dam break based on HEC-RAS[D].Chengdu:Xihua University,2022.
[9] 马勇勇.面向水动力模拟的河道地形重构及多分辨率数据融合方法研究[D].西安:西安理工大学,2023.MA Y Y.River channel terrain reconstruction method and multi-resolution data fusion method for hydrodynamic simulation[D].Xi’an:Xi’an University of Technology,2023.
[10] 蒋芳旋,付俊峰,李翰卿,等.实际地形下尾矿库溃坝对下游的冲击影响研究[J].中国水运,2022,22(4):101-103.JIANG F X,FU J F,LI H Q.Study on the impact of tailings dam collapse on downstream under actual terrain[J].China Water Transport,2022,22(4):101-103.
[11] 辛岩.云南某“头顶库” 溃坝对下游高速设施的模拟分析及影响研究[D].昆明:昆明理工大学,2023.XIN Y.Simulation analysis and influence study on downstream high-speed facilities caused by dam failure of an "overhead warehouse" in Yunnan Province[D].Kunming:Kunming University of Science and Technology,2023.
[12] 王扬,黄本胜,倪培桐,等.韩江南北堤防洪保护区溃坝洪水演进数值模拟研究[J].水资源与水工程学报,2018,29(5):175-179,185.WANG Y,HUANG B S,NI P T,et al.Numerical modeling of dam-break flood in the Hanjiang River Flood Protection Area[J].Journal of Water Resources and Water Engineering,2018,29(5):175-179,185.
[13] 杨彦龙,沈海尧,黄维.混凝土坝破坏模式及溃口几何参数探讨[J].大坝与安全,2022(3):1-9.YANG Y L,SHEN H Y,HUANG W.Discussion on failure modes of concrete dams and geometric parameters of dam break[J].Dam &Safety,2022(3):1-9.