地热能是一种潜力巨大、环境友好的可再生能源,在稳定性、因地制宜性等方面具有较大优势[1]。其中,干热岩[2](hot dry rock,HDR)温度高、储量相对较大,但利用率低。干热岩通常是指温度高、埋深数千米、内部不存在流体或仅有少量地下流体的高温岩体,需要通过水力压裂等刺激手段来提取HDR地热资源,形成增强型地热系统(enhanced geothermal system,EGS)[3-5]。水力压裂[6]是提取地热能的关键技术,也是难点技术之一,其原因是压裂液用量、注液方式[7-8]、储层岩石的物理力学特征等因素都会对水力裂缝的扩展形态产生一定影响。
目前,水力压裂过程中岩石起裂与裂缝扩展方面的研究主要有3种方法:理论方法、室内试验方法、数值模拟方法。在理论方面,Hubbert等[9]首次提出岩石起裂压力的计算公式,进一步验证了裂缝会沿着垂直于最小主应力的方向起裂并扩展。王永亮等[10]利用KGD、PKN两类等高解析模型对储层岩石剪切模量等压裂主控因素进行分析,获得了水力裂缝长度、张开度动态演化行为的量化数值。在室内试验方面,周舟等[11]基于改造的真三轴水力压裂模拟试验系统对青海共和盆地露头岩心进行压裂试验,验证了岩石起裂可以通过起裂模型预测起裂压力。Zhang等[12]利用实验室微断裂力学模拟测试系统研究了围压、注水流量和温度对岩石破裂压力的影响,明确了破裂压力随围压和注水流量的增加而增加。在数值模拟方面,Esfandiari等[13]采用扩展有限元法(XFEM)评估了地应力对水力裂缝特性的影响,检验了KGD、PKN模型解析公式的准确性。贾善坡等[14]利用ABAQUS软件对岩石三轴压缩试验进行了数值模拟,模拟结果与已有试验规律吻合较好,说明该软件用于岩石力学方面的模拟是可靠有效的。龚迪光等[15]基于ABAQUS软件实现二次编程开发,对岩石水力裂缝的扩展过程进行了数值模拟研究,为水力压裂研究提供了新方法。
解析模型中有部分简化假设,并忽略了地应力等水力和地质力学参数,导致由分析公式得到的裂缝长度、宽度和流体压力与计算结果存在差异。虽然通过室内试验能得到相对准确的岩石起裂压力,但受试验设备的限制,获取试验过程中水力裂缝的相关参数具有一定的难度。XFEM方法具有计算结果精度高和计算量小的优点,将该方法与ABAQUS软件结合,进行岩石的水力压裂模拟可对不同的储层物性参数及压裂施工参数进行分析,且裂缝形态逼真,结果准确。
考虑到解析模型和室内试验的局限性,本文以松辽盆地干热岩地热储层为研究对象,基于ABAQUS软件建立水力压裂二维数值模型,对热储花岗岩进行水力压裂参数敏感性分析。与以往假设一个结点为注入点不同,该模型在中心位置设置了射孔,尺寸与实验室的物模保持一致。通过对模型进行二次开发以提取起裂压力和裂缝宽度,对水平应力差异系数、压裂液黏度、压裂液排量、岩石抗拉强度和岩石弹性模量5个影响水力压裂特性的主要参数进行敏感性分析,定量分析不同因素对研究区花岗岩水力压裂特性的影响程度。
1 Cohesive单元法
在ABAQUS数值模拟中,选择Cohesive单元[16]来模拟二维和三维条件下的水力压裂过程。Cohesive单元是一种被假设为0厚度的特殊单元,可以通过二次开发在模型中批量嵌入,实现水压裂缝沿网格边界的任意拓展模拟。因此,本文采用全局嵌入Cohesive单元结合XFEM数值模拟方法[17]。
1.1 牵引-分离准则
模拟过程中,根据Cohesive单元的受力状态可将其力学响应分为破坏前的线弹性阶段和达到破坏条件后的渐进破坏阶段两部分[17],使用ABAQUS中自带的牵引-分离准则来描述,如图1所示。线弹性阶段内牵引力与分离量的关系如式(1)所示:
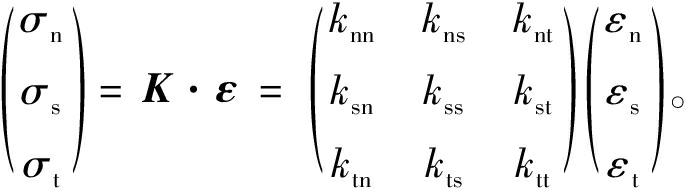
(1)
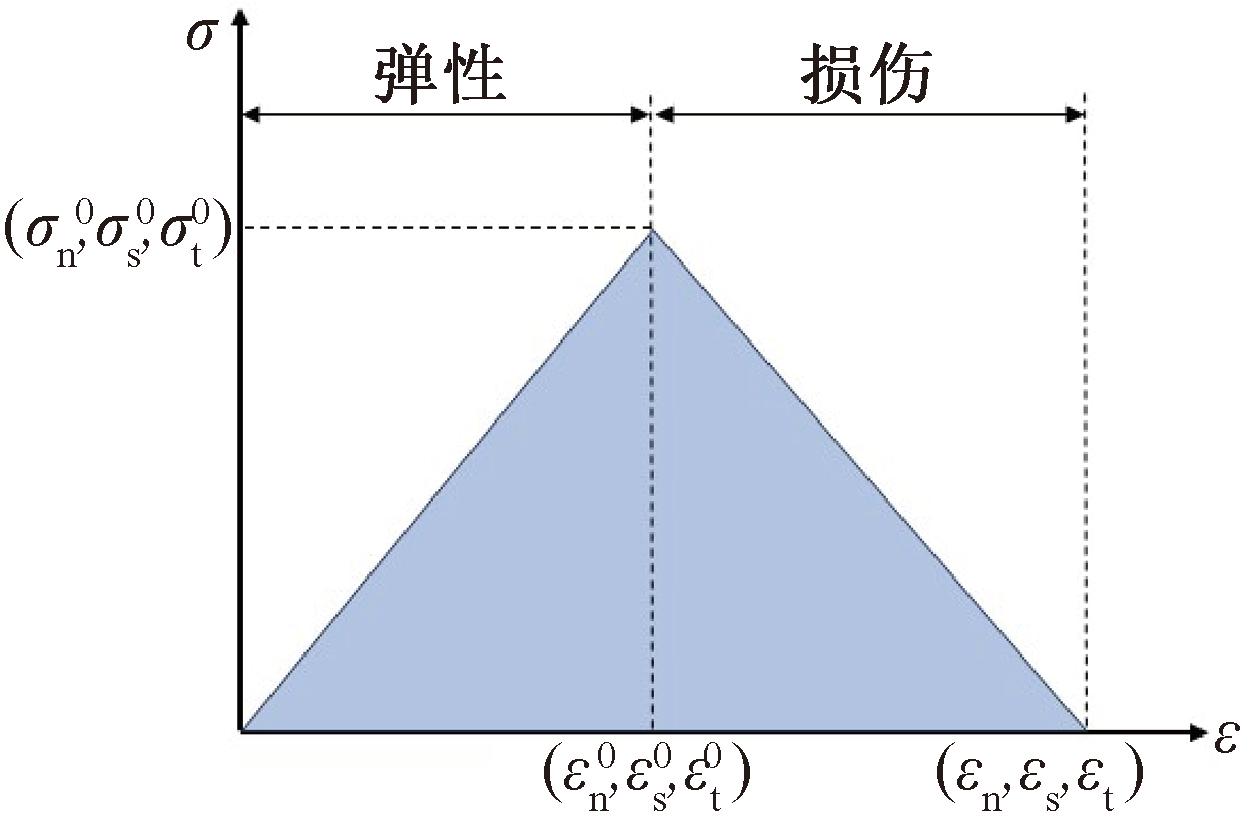
图1 牵引-分离曲线
Figure 1 Traction-separation curve
式中:σn、σs、σt分别为3个主应力方向上的牵引力,MPa;K为弹性刚度矩阵;εn、εs、εt分别为3个主应力方向上对应的应变。
1.2 裂缝初始损伤准则
目前,ABAQUS中常用的裂纹萌生准则有4种:最大名义应力损伤准则、最大名义应变损伤准则、二次应力损伤准则和二次应变损伤准则。本次模拟采用最大名义应力损伤准则来描述裂纹产生时应力之间的关系,当单元在任一方向上达到其极限应力时,单元将开始破裂,其表达如式(2)所示:
(2)
式中:![]() 分别为3个主应力方向上的极限应力,MPa;〈·〉表示Cohesive单元承受压应力时不会发生破坏。
分别为3个主应力方向上的极限应力,MPa;〈·〉表示Cohesive单元承受压应力时不会发生破坏。
1.3 裂缝损伤演化准则
引入无量纲因子D,取值为0~1。当D=0时,Cohesive单元未出现损伤;当D=1时,Cohesive单元完全破坏,产生裂纹;当0<D<1时,Cohesive单元处于渐进损伤阶段,其表达如式(3)所示:
(3)
式中:δmax为单元最大位移,![]() 为单元张开时的位移,
为单元张开时的位移,![]() 为单元开始损伤时的位移,m。
为单元开始损伤时的位移,m。
渐进损伤阶段牵引力分量大小为
(4)
(5)
(6)
式中:![]() 表示Cohesive单元为受拉状态,
表示Cohesive单元为受拉状态,![]() 表示Cohesive单元为受压状态;
表示Cohesive单元为受压状态;![]() 分别为未损伤前按牵引-分离准则计算的线弹性条件下单元的法向应力分量和两个切向应力分量,MPa。
分别为未损伤前按牵引-分离准则计算的线弹性条件下单元的法向应力分量和两个切向应力分量,MPa。
1.4 裂缝内流体运移方程
裂缝内流体压力通常为裂缝扩展提供能量,流体在Cohesive单元中的流动方向分为沿单元的径向流和滤失至常规单元的法向流,如图2所示。
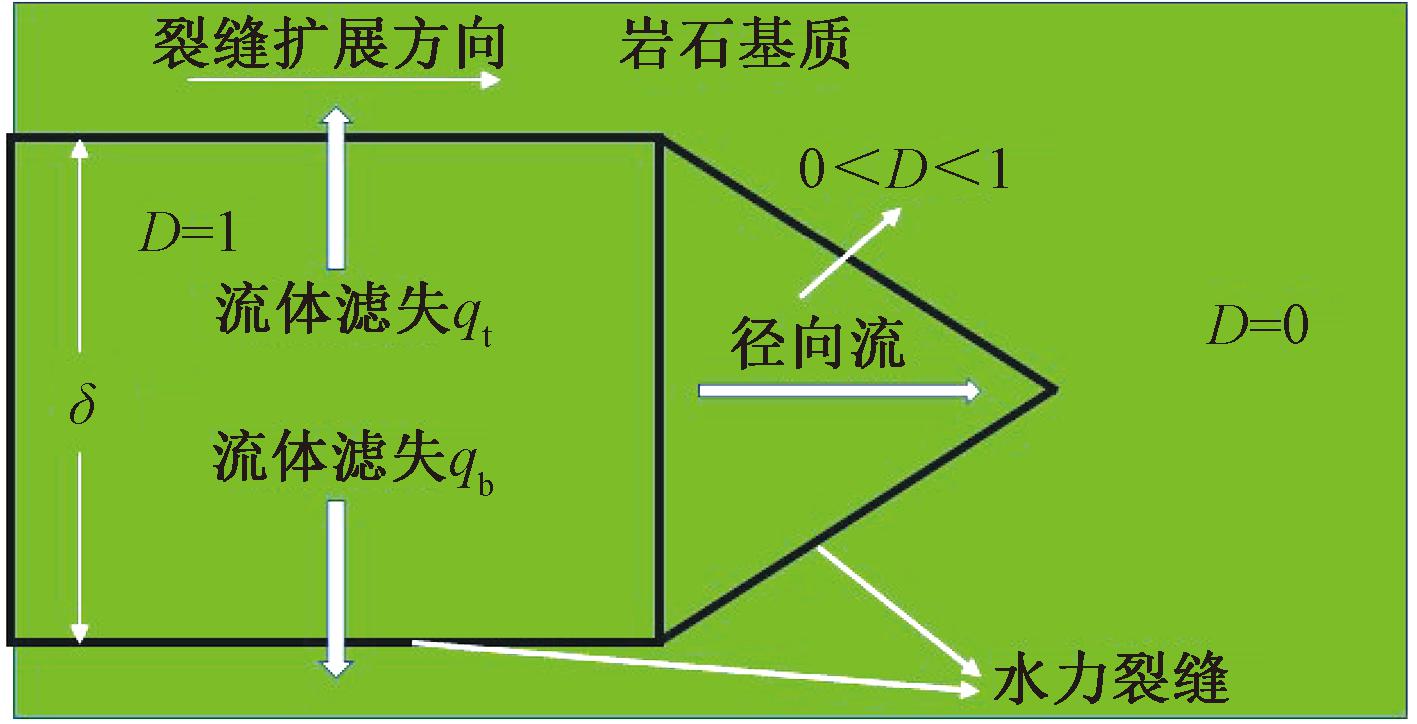
图2 流体运移示意图
Figure 2 Schematic diagram of fluid flow
径向流计算公式如式(7)所示,法向流计算公式如式(8)所示:
(7)
(8)
式中:q为缝内径向流量,m2/s;w为裂缝宽度,m;μ为压裂液黏度,![]() 为径向流体压力梯度,MPa/m;qt、qb分别为裂缝内流体流向上下表面的滤失流速,m2/s;Ct、Cb分别为裂缝上下表面的滤失系数,m2/(Pa·s);pm为裂缝内流体压力,MPa;pt、pb分别为裂缝上下表面孔隙压力,MPa。
为径向流体压力梯度,MPa/m;qt、qb分别为裂缝内流体流向上下表面的滤失流速,m2/s;Ct、Cb分别为裂缝上下表面的滤失系数,m2/(Pa·s);pm为裂缝内流体压力,MPa;pt、pb分别为裂缝上下表面孔隙压力,MPa。
2 数值模型建立与验证
2.1 模型建立
在实际的压裂工程中,有很多因素会对压裂结果造成影响,比如部分岩体的非均质性等。为方便计算,做出如下假设。
(1)假设储层岩体为各向同性的均质材料。
(2)假设压裂液不可压缩且不与岩体发生化学反应。
(3)忽略压裂过程对储层地应力的影响。
水力裂缝扩展模型的建立基于XFEM法,借助ABAQUS软件对二维模型进行网格划分,单元类型选择四边形单元,单元数量为35 731个。通过二次开发在所有实体单元间批量嵌入Cohesive单元,单元数量为23 750个。对岩石基质和内聚力单元分别赋予不同的材料属性。模型的岩石力学参数参考松辽盆地相关参数[18],模型参数见表1。依据实际数据建立的水力压裂模型见图3。
表1 水力压裂模型相关参数
Table 1 Related parameters of hydraulic fracturing model
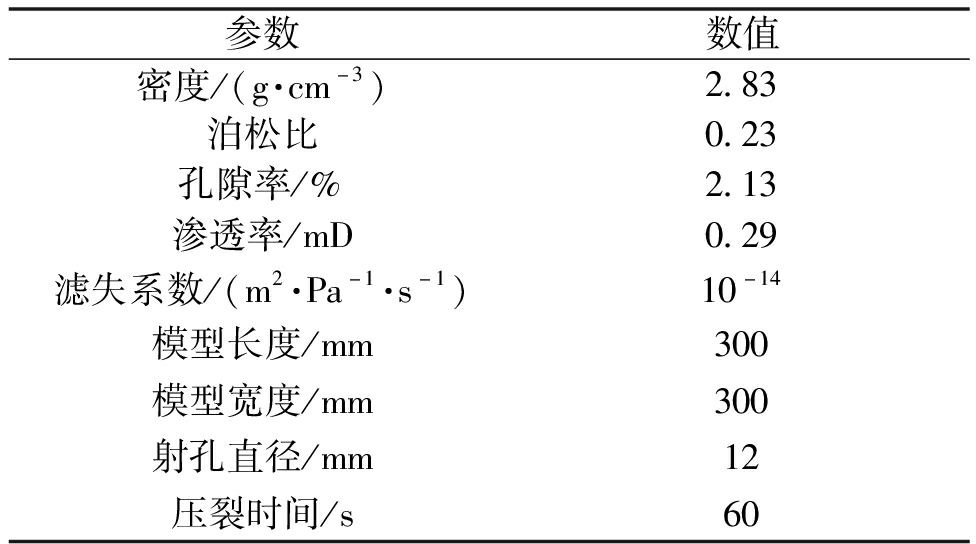
参数数值密度/(g·cm-3)2.83泊松比0.23孔隙率/%2.13渗透率/mD0.29滤失系数/(m2·Pa-1·s-1)10-14模型长度/mm300模型宽度/mm300射孔直径/mm12压裂时间/s60
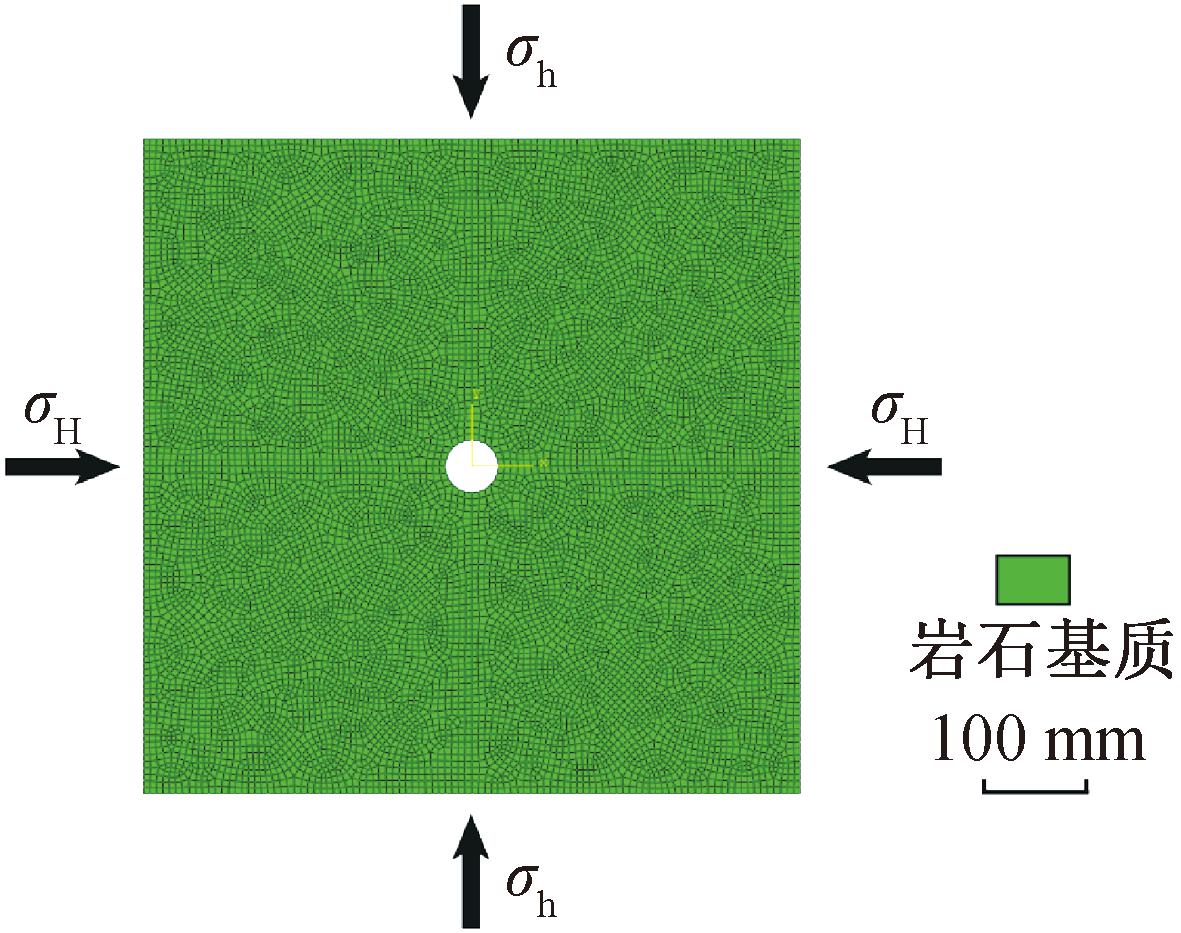
图3 水力压裂模型
Figure 3 Hydraulic fracturing model
模型整体采用有效应力和超静水压力原理,对应的孔压边界为0。约束模型在X和Y方向的节点位移为0,即UX=UY=0。
2.2 模型验证
在前人的研究中,尚未开展对松辽盆地露头花岗岩试样的水力压裂室内试验,数值模拟缺少相应的试验结果作为对照。为验证数值模型的准确性,以相同的建模方法,参考青海共和盆地花岗岩试样水力压裂室内试验[19],模型中岩石力学参数与试验保持一致,比较相同工况下二者水力裂缝扩展情况和破裂压力。数值模型尺寸与物理模型尺寸保持一致,为300 mm×300 mm,应力场σV、σH、σh分别为4,10,6 MPa,注水速率为10 mL/min。
图4展示了数值模拟结果与压裂试验结果的对比。图4(a)、4(b)分别为模拟与试验条件下的注水压力曲线变化图,可以看出,压裂变化趋势相似,模拟结果中起裂压力为22.7 MPa,试验结果中试块的起裂压力为23.3 MPa,模拟误差仅为2.6%。图4(c)、4(d)分别为模拟与试验条件下的水力裂缝扩展结果,可以看出,二者裂缝的扩展路径基本相同。以上对比说明采用本文方法进行花岗岩水力压裂模拟,结果是准确可靠的,同时也表明该建模方式更符合实际。
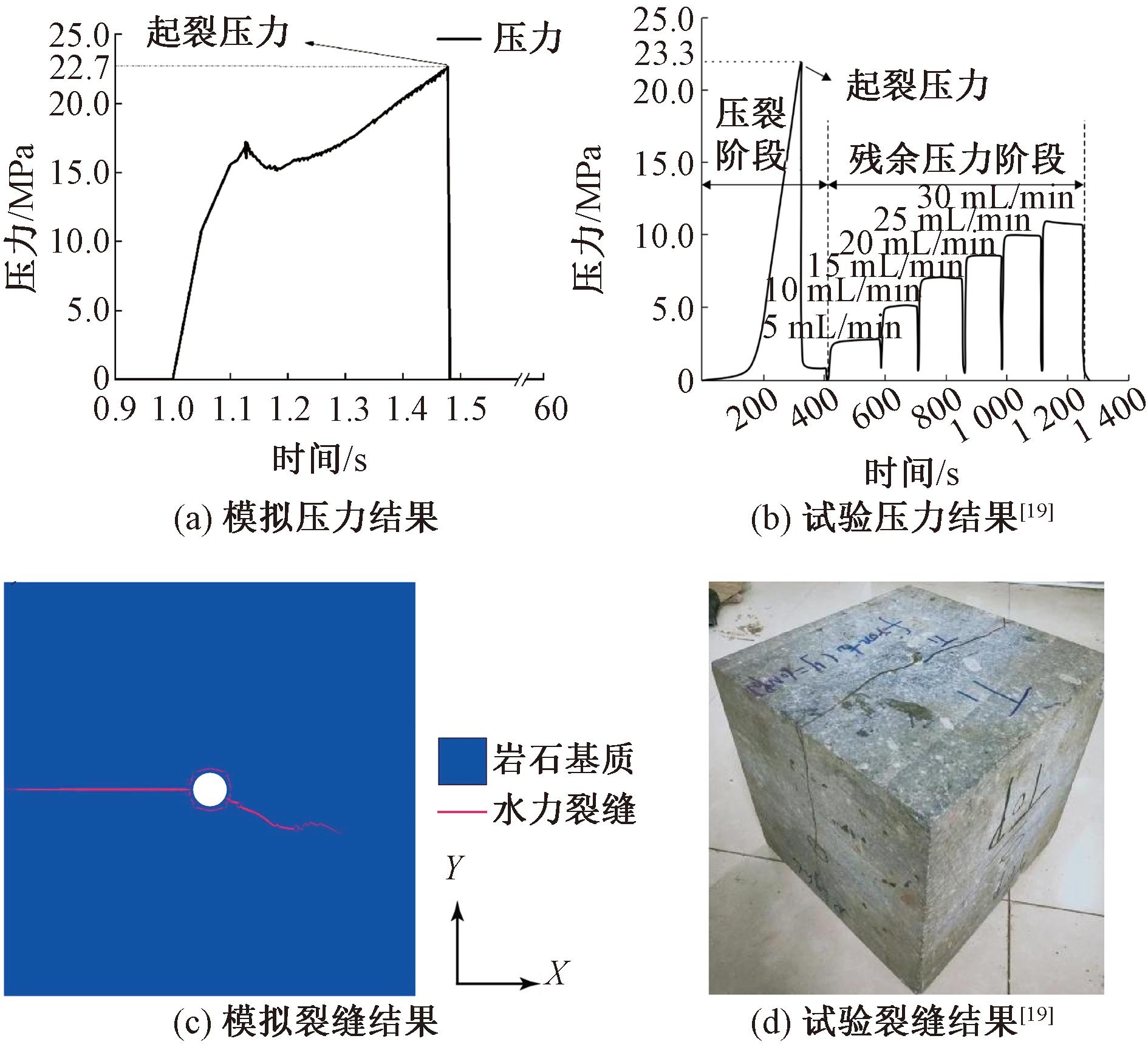
图4 数值模拟与试验结果对比
Figure 4 Comparison of numerical simulation and experimental results
3 正交试验
3.1 正交试验方法
正交试验法是使用已经设计好的正交表来安排试验并进行数据分析的一种数理统计方法,它根据正交性从全面试验中挑选出部分有代表性的点进行试验,是一种高效、快速、经济的试验设计方法。
对于试验结果的分析方法通常有极差分析法和方差分析法,极差分析法更加直观形象,故本文采用极差分析法对正交试验结果进行分析。
设X、Y、…分别为试验中的几个不同因素;t为各因素的水平数;Xi表示因素X在第i个水平的值,i=1,2,…,t;Mij表示第j个因素的第i个水平的值,i=1,2,…,t,j=X,Y,…。在Mij下进行n次试验得到n个试验结果Nk,k=1,2,…,n。计算统计参数为
(9)
式中:Kij为第j个因素在第i个水平下试验结果的平均值;Nk为第k个实验值;![]() 为所有试验结果的平均值。
为所有试验结果的平均值。
极差分析因素的敏感性程度是根据极差值进行评价的,第j个因素的极差值计算公式为
Rj=max(K1j,K2j,…,Knj)-min(K1j,K2j,…,Knj)。
(10)
极差值Rj越大,说明该因素的水平改变对试验指标的影响越大,即该因素的敏感性越大;相反,极差值Rj越小,该因素的敏感性越小。
3.2 正交试验设计
在本文中,选取水平应力差异系数(K)、压裂液黏度(μ)、压裂液排量(v)、岩石抗拉强度(Rm)和岩石弹性模量(E)这5个参数作为敏感性分析的主要指标,其中水平应力差异系数计算公式为
(11)
本文共设置4个因素水平。假定各参数之间没有相互影响,由试验因素个数和水平数,选择L16(45)正交表,将各因素及水平数对应分配到正交表中,正交试验方案如表2所示。
表2 正交试验方案
Table 2 Orthogonal test scheme
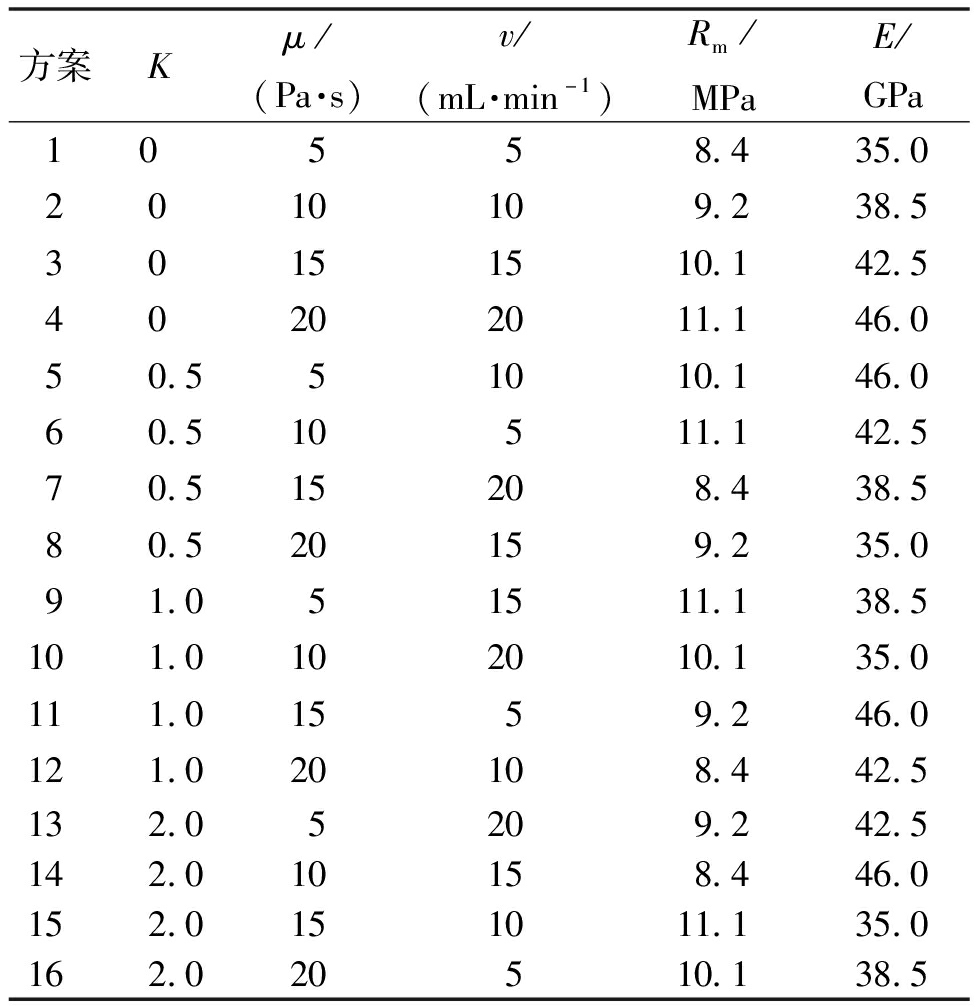
方案Kμ/(Pa·s)v/(mL·min-1)Rm/MPaE/GPa10 558.435.02010109.238.530151510.142.540202011.146.050.551010.146.060.510511.142.570.515208.438.580.520159.235.091.051511.138.5101.0102010.135.0111.01559.246.0121.020108.442.5132.05209.242.5142.010158.446.0152.0151011.135.0162.020510.138.5
在模拟过程中,保持其他物理参数不变,按照上述正交试验设计,将方案中的16组参数依次在ABAQUS中进行设置替换,可以得到不同条件下水力压裂模型的裂缝形态和注水压力随时间变化情况。
4 模拟结果与分析
4.1 裂缝扩展形态
模拟方案1~8的裂缝扩展情况如图5所示。
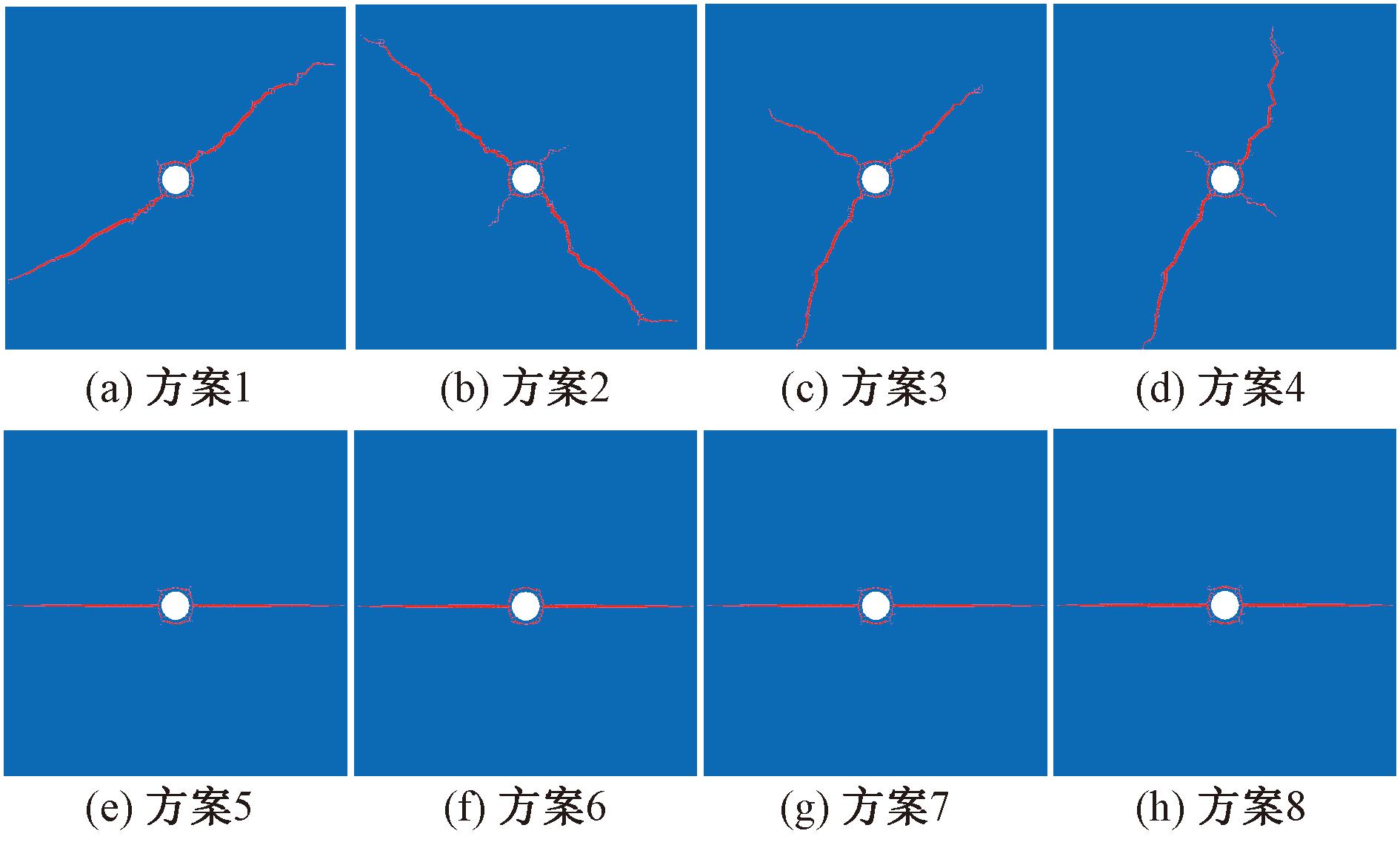
图5 不同方案下水力裂缝扩展情况
Figure 5 Hydraulic fracture propagation with different schemes
从图5(a)~5(d)可以看出,当水平应力差异系数为0,即σH=σh时,水力裂缝的起裂和扩展方向具有随机性,此时裂缝延伸受水平应力差的影响较小,容易转向和分叉,形成复杂的裂缝网络。从图5(e)~5(h)可以看出,在K=0.5,即σH>σh情况下,裂缝扩展沿着最大主应力方向,扩展产生的诱导应力对扩展方向的影响较小,水力裂缝未发生明显的转向和动态分叉,形态比较单一,难以形成复杂缝网。K=1.0,2.0时的水力裂缝形态与图5(e)~5(h)相似,这里不再一一列举。模拟结果产生该种平直裂缝的主要原因可能是用Cohesive单元模拟水力裂缝起裂与延伸时,各单元并不代表实际情况下的岩石,仅用于简化模拟岩石破裂时岩石结构间的作用力。对于模拟水力裂缝的扩展路径,只能按照预设的Cohesive单元进行裂缝的扩展延伸,且扩展过程中水力裂缝不能发生转向。总体来看,裂缝宽度随着到注水孔的距离增大而减小,在孔附近宽度达到最大。
4.2 注水压力变化
不同模拟方案下的模型注水压力随时间变化情况如图6所示,由于模拟方案较多,且各方案下的压力变化情况具有一定的规律性,故只选取方案1,2,3,4(图6(a))来讨论。从图6(a)可以看出,4个方案的压裂曲线均有5个明显的变化阶段:在压裂初期,孔眼充水过程中,孔壁几乎不承受水压力;当孔眼内完全充满水后,进入增压阶段,注水压力呈线性增加,压裂液的注入速率很大程度上决定了压力的增加速率,注入速率越大,压力增长越迅速;当注水压力达到岩石破裂压力后,岩石发生压裂破坏;岩石起裂后,裂缝在流体压力的作用下开始迅速延伸,注水压力随之降低;裂缝完全贯穿岩石试样后,压力骤减,压裂过程结束。
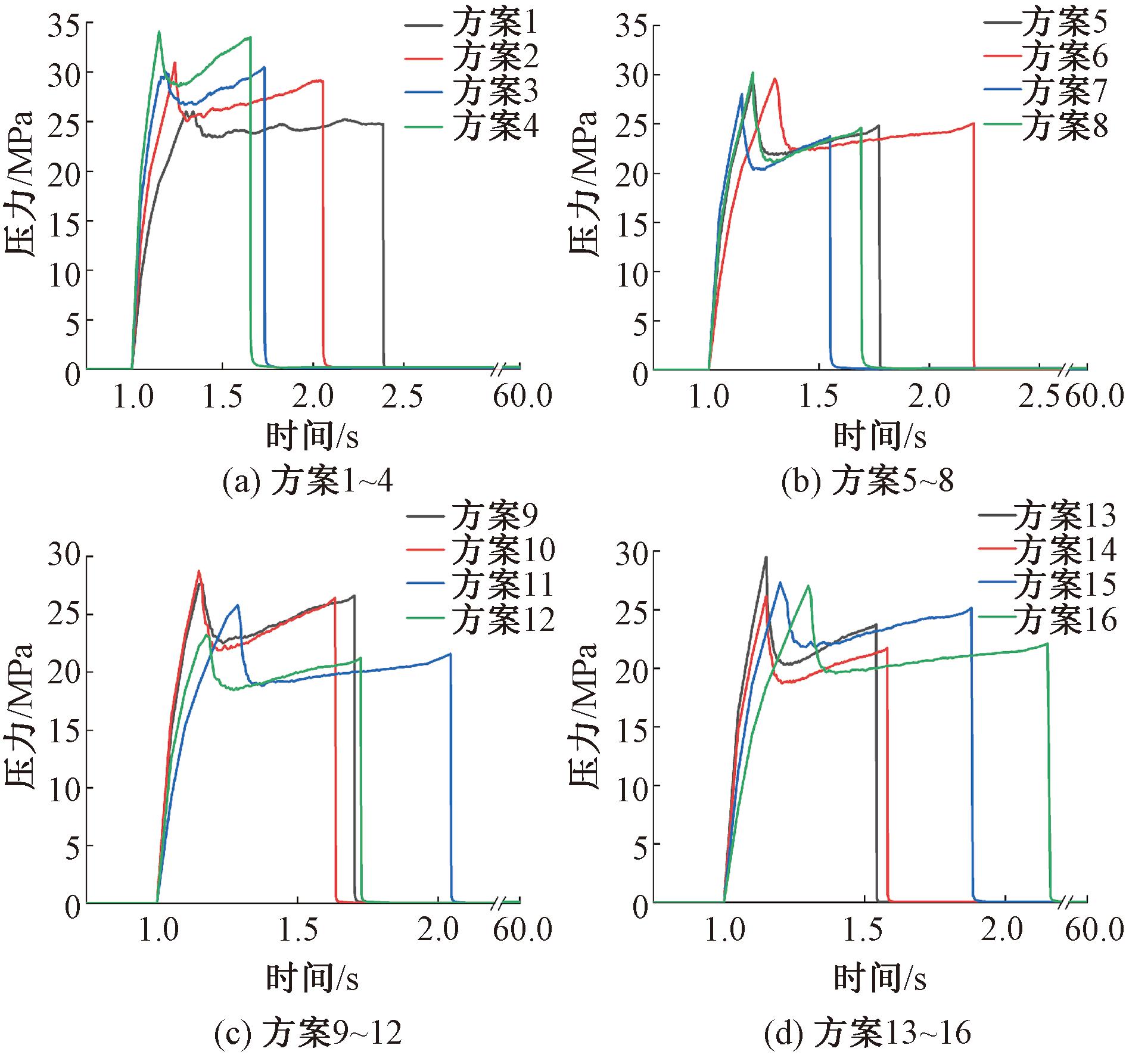
图6 不同方案下注水压力情况
Figure 6 Injection pressure situation with different schemes
4.3 敏感性分析
在ABAQUS中提取了不同正交试验方案下模拟计算的裂缝宽度和起裂压力,如表3所示。
表3 模拟结果
Table 3 Simulation results
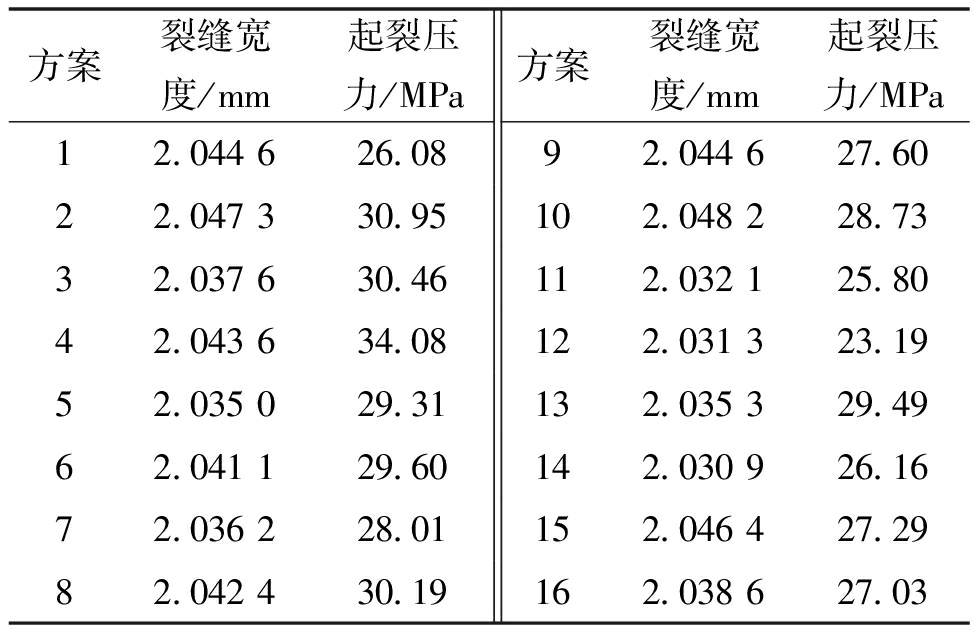
方案裂缝宽度/mm起裂压力/MPa方案裂缝宽度/mm起裂压力/MPa12.044626.0892.044627.6022.047330.95102.048228.7332.037630.46112.032125.8042.043634.08122.031323.1952.035029.31132.035329.4962.041129.60142.030926.1672.036228.01152.046427.2982.042430.19162.038627.03
对模拟计算的结果,采用极差分析法对影响压裂结果的相关参数进行敏感性分析,由其原理可以知,极差值Rj越大,该因素的敏感性越强,对结果的影响也越大。极差值的对比结果如图7所示。
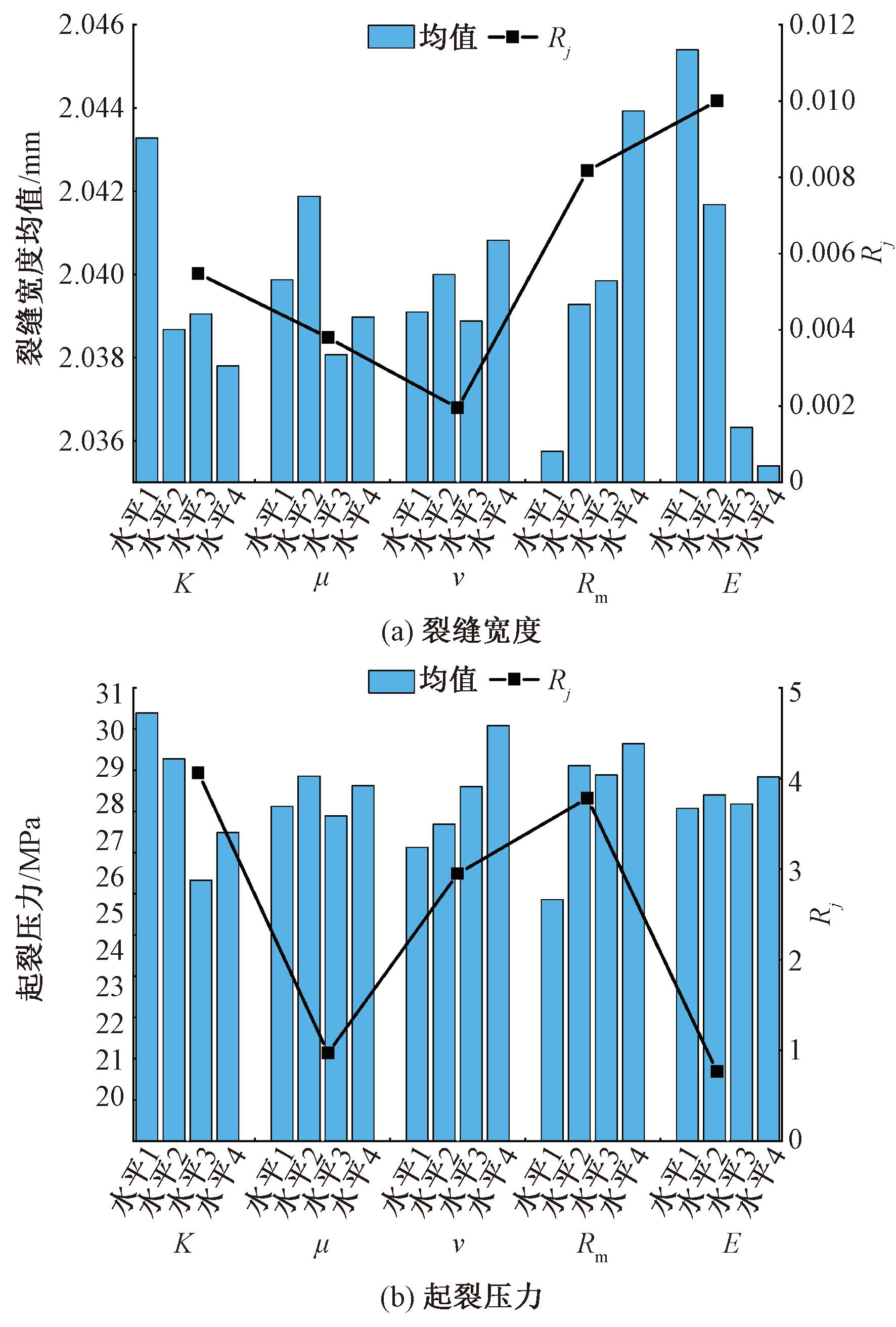
图7 不同参数敏感性对比结果
Figure 7 Comparison of sensitivity of different parameters
从图7(a)可以看出,各影响因素的极差值大小顺序为RE>RRm>RK>Rμ>Rv,说明5个因素中对水力裂缝宽度影响程度从强到弱排序为岩石弹性模量、岩石抗拉强度、水平应力差异系数、压裂液黏度、压裂液排量。比较各影响因素不同水平下的均值可知,在水平应力差异系数的作用下,水平1时裂缝宽度取得最大值。同理在压裂液黏度、压裂液排量、岩石抗拉强度和岩石弹性模量因素的作用下,最优水平分别水平2、水平4、水平4和水平1。
从图7(b)可以看出,各影响因素的极差值大小顺序为RK>RRm>Rv>Rμ>RE,说明5个因素中对岩石破裂压力影响程度从强到弱排序为水平应力差异系数、岩石抗拉强度、压裂液排量、压裂液黏度、岩石弹性模量。比较各影响因素不同水平下的均值可知,在水平应力差异系数、压裂液黏度、压裂液排量、岩石抗拉强度和岩石弹性模量因素的作用下,起裂压力分别在水平1、水平2、水平4、水平4和水平4时取得最大值。结合图6可以知,压裂液排量越大,达到起裂压力的时间越短。同时可以看出,只有水平应力差异系数、岩石抗拉强度和压裂液排量的改变会导致起裂压力发生显著变化。
5 结论
在低水平应力差下,裂缝扩展形态更加随机,且容易发生转向和分叉,形成更复杂的裂缝网络。高水平应力差下,裂缝扩展形态比较单一。比较各因素的极差值大小,对影响水力裂缝宽度的因素进行敏感性分析,按影响程度的强弱从大到小排序为岩石弹性模量、岩石抗拉强度、水平应力差异系数、压裂液黏度、压裂液排量。对起裂压力影响程度的强弱从大到小排序为水平应力差异系数、岩石抗拉强度、压裂液排量、压裂液黏度、岩石弹性模量。但只有水平应力差异系数、岩石抗拉强度和压裂液排量的改变会导致起裂压力发生显著变化,其他因素的变化对起裂压力的影响不明显。
本文利用ABAQUS软件基于扩展有限元法建立水力压裂的数值模型,并与室内试验结果进行对比,验证了该方法的准确性与可靠性;通过设计正交试验,研究了不同方案下的裂缝扩展形态与起裂压力,利用数理统计的方法分析了各因素对模拟结果的影响程度。
本文揭示了不同影响因素对水力裂缝和注水压力的影响程度大小,下一步根据敏感性分析的结果,进行场地尺度下的储层水力压裂缝网效果模拟与优化,为EGS开发提供指导。
[1] GONG F C,GUO T K,SUN W,et al.Evaluation of geothermal energy extraction in enhanced geothermal system (EGS) with multiple fracturing horizontal wells (MFHW)[J].Renewable Energy,2020,151:1339-1351.
[2] MA W W,YANG C,AHMED S F,et al.Effects of thermophysical parameters of fracturing fluid on hot dry rock damage in hydraulic fracturing[J].Geomechanics for Energy and the Environment,2022,32:100405.
[3] 李根生,武晓光,宋先知,等.干热岩地热资源开采技术现状与挑战[J].石油科学通报,2022,7(3):343-364.LI G S,WU X G,SONG X Z,et al.Status and challenges of hot dry rock geothermal resource exploitation[J].Petroleum Science Bulletin,2022,7(3):343-364.
[4] 许天福,张延军,于子望,等.干热岩水力压裂实验室模拟研究[J].科技导报,2015,33(19):35-39.XU T F,ZHANG Y J,YU Z W,et al.Laboratory study of hydraulic fracturing on hot dry rock[J].Science &Technology Review,2015,33(19):35-39.
[5] 郭亮亮.增强型地热系统水力压裂和储层损伤演化的试验及模型研究[D].长春:吉林大学,2016.GUO L L.Test and model research of hydraulic fracturing and reservoir damage evolution in enhanced geothermal system[D].Changchun:Jilin University,2016.
[6] GUO T K,HAO T,CHEN M,et al.Numerical simulation on geothermal extraction by radial well assisted hydraulic fracturing[J].Renewable Energy,2023,210:440-450.
[7] ZHUANG D D,YIN T B,LI Q,et al.Fractal fracture toughness measurements of heat-treated granite using hydraulic fracturing under different injection flow rates[J].Theoretical and Applied Fracture Mechanics,2022,119:103340.
[8] LIU Y L,XU T F,YUAN Y L,et al.A laboratory study on fracture initiation and propagation of granite under cyclic-injection hydraulic fracturing[J].Journal of Petroleum Science and Engineering,2022,212:110278.
[9] HUBBERT M K,WILLIS D G.Mechanics of hydraulic fracturing[J].Transactions of the AIME,1957,210(1):153-168.
[10] 王永亮,张辛,朱天赐,等.水力压裂解析模型裂缝扩展参数敏感性分析[J].力学季刊,2021,42(2):263-271.WANG Y L,ZHANG X,ZHU T C,et al.Sensitivity analysis for controlling parameters of fracture propagation in hydrofracturing based on analytical models[J].Chinese Quarterly of Mechanics,2021,42(2):263-271.
[11] 周舟,金衍,曾义金,等.青海共和盆地干热岩地热储层水力压裂物理模拟和裂缝起裂与扩展形态研究[J].吉林大学学报(地球科学版),2019,49(5):1425-1430.ZHOU Z,JIN Y,ZENG Y J,et al.Experimental study on hydraulic fracturing physics simulation,crack initiation and propagation in hot dry rock geothermal reservoir in Gonghe Basin,Qinghai[J].Journal of Jilin University (Earth Science Edition),2019,49(5):1425-1430.
[12] ZHANG Y J,MA Y Q,HU Z J,et al.An experimental investigation into the characteristics of hydraulic fracturing and fracture permeability after hydraulic fracturing in granite[J].Renewable Energy,2019,140:615-624.
[13] ESFANDIARI M,PAK A.XFEM modeling of the effect of in situ stresses on hydraulic fracture characteristics and comparison with KGD and PKN models[J].Journal of Petroleum Exploration and Production Technology,2023,13(1):185-201.
[14] 贾善坡,林建品,刘团辉,等.温度作用下岩石热弹塑性模型及其数值模拟[J].郑州大学学报(工学版),2015,36(2):52-56.JIA S P,LIN J P,LIU T H,et al.A thermo-elasto-plastic constitutive model of the rock under the temperature effect and its numerical implementation[J].Journal of Zhengzhou University (Engineering Science),2015,36(2):52-56.
[15] 龚迪光,曲占庆,李建雄,等.基于ABAQUS平台的水力裂缝扩展有限元模拟研究[J].岩土力学,2016,37(5):1512-1520.GONG D G,QU Z Q,LI J X,et al.Extended finite element simulation of hydraulic fracture based on ABAQUS platform[J].Rock and Soil Mechanics,2016,37(5):1512-1520.
[16] 刘金龙.基于ABAQUS平台的水力压裂裂缝扩展模拟研究[D].西安:西安石油大学,2020.LIU J L.Simulation study on fracture propagation of hydraulic fracturing based on ABAQUS platform[D].Xi’an:Xi’an Shiyou University,2020.
[17] 王小龙.扩展有限元法应用于页岩气藏水力压裂数值模拟研究[D].合肥:中国科学技术大学,2017.WANG X L.Numerical simulation of hydraulic fracturing in shale gas reservoir based on the extended finite element method[D].Hefei:University of Science and Technology of China,2017.
[18] 谢洋洋.吉林松原中深层地热供暖潜力及模型研究[D].长春:吉林大学,2019.XIE Y Y.Research on medium-deep geothermal heating potential and model assessment in Songyuan,Jilin[D].Changchun:Jilin University,2019.
[19] 雷治红.青海共和盆地干热岩储层特征及压裂试验模型研究[D].长春:吉林大学,2020.LEI Z H.Study on the characteristics of hot dry rock reservoir and fracturing test model in the Gonghe Basin,Qinghai Province[D].Changchun:Jilin University,2020.