近几年,风能作为一种无污染、安全可靠的可再生资源,得到了广泛的关注[1]。然而,风电的出力受气象因素影响较大,表现出随机性、间歇性和波动性[2],其大规模并网给电力系统的稳定运行带来了严峻的挑战[3]。因此,开发高精度的风电功率预测技术具有非常重要的现实意义[4]。
传统的风电功率预测方法可大致分为物理法和统计法[5]两大类。物理法是基于风电场的NWP(数值天气预报)时序数据、地貌等因素建立流体力学模型来获取风电场的预测功率,该方法计算模型复杂、计算效率较低,一般用来做中长期预测[6-7]。统计法是利用历史实测数据,通过寻找数据间的潜在规律,构建输入输出间的映射函数,从而实现风电功率预测的方法,主要包括自回归模型(autoregressive,AR)[8]、极限学习模型(extreme learning machine,ELM)[9]、模糊推理模型[10]、灰色相关理论[11]以及机器学习等。统计法不受物理模型复杂程度的限制,因此适用于短期风电功率预测。
现阶段,基于统计法的短期风电功率预测技术已经取得较大进展。Wang等[12]提出了CNN-LSTM模型,该模型的预测准确度明显高于单一的CNN模型和单一的LSTM模型,但无法准确提取风电序列中的时序信息。Liu等[13]采用了双向长短期记忆(BiLSTM)模型,能够有效提取风电序列中的时序信息。Li等[14]在此基础上将CNN模型与BiLSTM模型结合,构建出CNN-BiLSTM模型,该模型在预测精度上较CNN模型与BiLSTM模型有显著提升。但以上模型依旧难以有效提取波动剧烈的气象信息,在恶劣天气下,模型的预测难度大幅度增加。李润金等[15]提出了VMD-CNN-LSTM混合深度学习模型,VMD(变分模态分解)可以将非平稳的功率数据进行平稳化处理,可以有效提取风电序列中波动剧烈的气象信息,然而该模型中关于分解数K和惩罚因子α难以选取最优值,会在一定程度上影响到模型预测的精度。陈申等[16]采用天鹰优化算法对预测模型进行优化处理,取得了良好的预测结果,但是该优化算法存在全局探索能力和局部开发能力不平衡的问题,有可能陷入局部最优解。
针对上述问题,本文建立了一种改进蜣螂优化算法的短期风电功率预测模型POTDBO-VMD-CNN-BiLSTM。首先,对蜣螂优化算法进行改进,解决其全局探索能力和局部开发能力不平衡的问题。其次,用改进的蜣螂优化算法对VMD的模态分解数K和惩罚因子α进行寻优处理,提高VMD的分解性能和分解效果。然后,对非平稳的风电功率数据进行适当分解,得到不同频率的分量,将其分别输入到CNN-BiLSTM模型中,再将不同频率分量的预测结果进行序列重构得到最终预测结果。最后采用新疆某风电场和吉林某风电场的实测数据进行仿真分析,证明该方法的有效性。
1 变分模态分解
变分模态分解是一种自适应、非递归的分解方法,可以有效处理非平稳的功率数据。相比与EMD、EEMD、WD,VMD在采样和噪声方面更具有鲁棒性[17-19]。
VMD以最小化各模态分量中心频率之和构造模型,受约束变分模型为
(1)
(2)
式中:k为模态数;δ(t)为Dirac分布;ωk为中心频率;‖·‖ 为L2范数;f为原始信号。
引入拉格朗日乘子λ和二次惩罚项α,将式(1)由约束转为非约束问题:
L({uk},{ωk},λ)=
(3)
式中:⊗为卷积算子。
2 改进蜣螂优化算法
2.1 蜣螂优化算法(DBO)
蜣螂优化算法(DBO)的灵感来自蜣螂群体的生活习性,包括滚球、繁育、觅食和偷窃行为[20],DBO算法的原理[21]如下所示。
2.1.1 蜣螂滚球
(1)无障碍模式。滚球蜣螂通常会以太阳等环境因素作为参考,保证粪球在直线上滚动,位置更新公式为
Xi(t+1)=Xi(t)+akXi(t-1)+
b|Xi(t)-Xworst(t)|。
(4)
式中:Xi(t+1)为第i只蜣螂在第t+1次迭代时的位置;k为偏转系数,取值为(0,2];b取值为(0,1);a取1表示无偏差,取-1表示偏离原方向;Xworst(t)为当前种群最差位置。
(2)有障碍模式。当滚球蜣螂遇到障碍物无法前进时,会通过跳舞行为调整前进方向,位置更新定义为
Xi(t+1)=Xi(t)+|Xi(t)-Xi(t-1)|tan θ。
(5)
式中:θ∈[0,π]。
2.1.2 蜣螂繁育
雌性蜣螂会寻找产卵区域,定义为

(6)
式中:Lb*和Ub*分别为产卵区域的下限和上限;Lb和Ub分别为优化问题的下限和上限;![]() 为当前局部最优位置;Tmax为最大迭代次数。
为当前局部最优位置;Tmax为最大迭代次数。
一只雌性蜣螂在一次迭代中会在产卵区域内产下一个育雏球,育雏球的更新位置为
b2(Bi(t)-Ub*)。
(7)
式中:Bi(t+1)为第i个育雏球在第t+1次迭代的位置;b1和b2为两个1×D的独立随机向量中的元素,D为优化问题的维度。
2.1.3 蜣螂觅食
刚成年的蜣螂(也被称为小蜣螂)会从巢穴中爬出来寻找食物,觅食区域更新为
(8)
式中:X′best(t)为当前全局最优位置;Lb′和Ub′分别为最优觅食区域的下限和上限。
小蜣螂位置更新为
Xi(t+1)=X′best(t)+C1[Xi(t)-Lb′]+
C2[Xi(t)-Ub′]。
(9)
式中:C1为服从正态分布的1×D的随机向量中的元素;C2为取值(0,1)的1×D的随机向量中的元素。
2.1.4 蜣螂偷窃
在蜣螂种群中,会有一部分蜣螂偷窃其他蜣螂的粪球,偷窃蜣螂的位置更新为
(10)
式中:S为常数;g为服从正态分布的1×D的随机向量中的元素。
2.1.5 种群划分
在蜣螂优化算法中,滚球蜣螂、繁育蜣螂、小蜣螂、偷窃蜣螂的数量比例为6∶6∶7∶11。
2.2 多策略融合的改进蜣螂优化算法POTDBO
普通的DBO算法具有寻优能力强的特点,但是也存在全局探索能力和局部开发能力不平衡的问题,有可能陷入局部最优。针对以上缺点,引入以下3种策略对DBO算法进行改进。
2.2.1 采用Piecewise混沌映射
混沌映射可以增加粒子的多样性,减少粒子的寻优时间。在初始化位置更新过程中,采用Piecewise混沌映射代替DBO算法中的随机分量,表达式为

(11)
式中:P=0.4。
2.2.2 融合鱼鹰优化算法
DBO算法中,在无障碍模式下,滚球蜣螂的位置更新过于依赖当前种群的最差位置,导致全局探索能力较弱。鱼鹰优化算法[22]具有很强的全局勘探能力,可以弥补DBO算法的缺陷。采用鱼鹰算法第一阶段的全局勘探策略公式代替无障碍模式下滚球蜣螂的位置更新公式,鱼鹰算法第一阶段的全局勘探策略公式为
(12)
式中:![]() 为第i只鱼鹰在第一阶段时第j维的位置;SFi,j为鱼鹰选中的鱼;ri,j为0~1的随机数;Ii,j取0或1。
为第i只鱼鹰在第一阶段时第j维的位置;SFi,j为鱼鹰选中的鱼;ri,j为0~1的随机数;Ii,j取0或1。
2.2.3 融合自适应T分布扰动策略
采用自适应T分布策略对蜣螂个体位置进行扰动。其中,迭代前期t(iter)很小,类似柯西异变,而迭代后期t(iter)偏大,类似高斯异变,这就使得DBO算法在迭代前期具有更好的全局探索能力,在迭代后期具有更好的局部开发能力,具体的位置更新公式为
Xi_new=Xi+t(iter)Xi。
(13)
式中:Xi_new和Xi分别为变异后和变异前种群中第i个体的位置;t(iter)为以迭代次数为自由度的T分布值。
POTDBO算法流程图如图1所示。
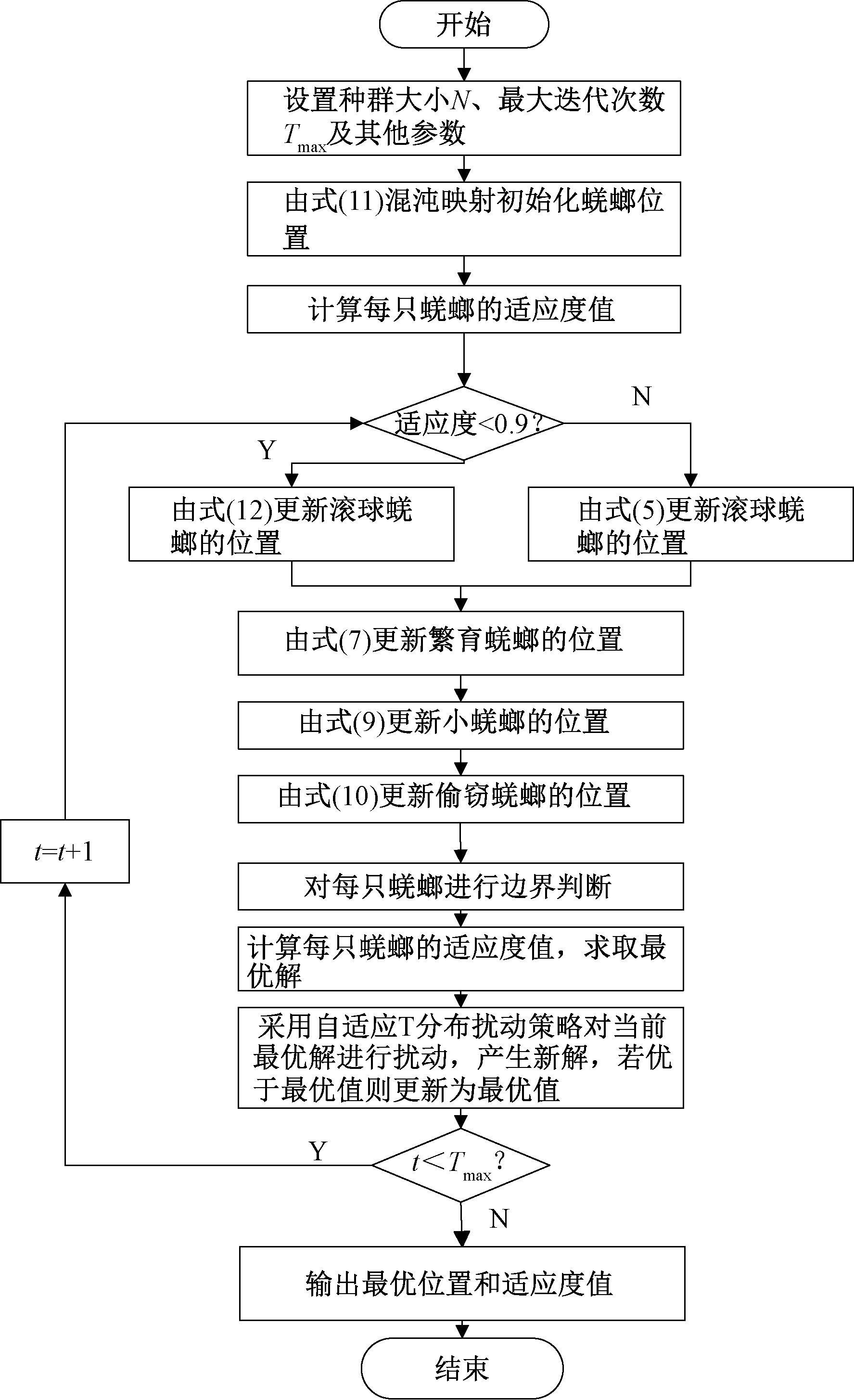
图1 POTDBO算法流程图
Figure 1 Flow chart of POTDBO algorithm
3 短期风电功率预测模型的建立
3.1 气象因素选取
风电功率预测的主要影响因素为风速、风向、温度等气象因素。本文选取新疆某风电场2018年3月份的气象数据、功率数据和吉林某风电场2019年1月份气象数据、功率数据作为研究对象。其中新疆风电场有测风塔70 m风速、风向、温度、湿度等11个气象特性,吉林风电场有测风塔轮毂处风速、风向、温度、气压等8个气象特性。本文采用最大信息系数法[23]计算每个气象因素与输出功率的相关系数,选取相关系数较大的气象因素作为风电功率预测模型的输入。新疆最终筛选的气象因素为测风塔70 m风速和测风塔70 m风向,吉林最终筛选的气象因素为测风塔轮毂处风速和风向。
3.2 数据预处理
3.2.1 异常数据清洗
四分位法可以分析数据集的分布特性,得到数据的离散程度[24]。本文采取四分位法对风电功率数据进行清洗,剔除异常值。
3.2.2 缺失数据填补
对于缺失的数据,采用线性插值法填补,计算公式为
(14)
3.2.3 数据归一化
为了统一量纲,需要对原始数据进行归一化处理:
(15)
3.3 CNN-BiLSTM模型
本文采用一种短期风电功率预测的混合深度学习模型CNN-BiLSTM[25-26]。在CNN层通过二维卷积层提取气象数据的空间特征,当原始气象数据经过二维卷积处理之后,会被降维,但其中的重要信息会被保留。卷积层提取的重要信息会被输入到池化层,该层采用最大池化算法,选出特征图中最显著的特征进行采样,经过Flatten层将二维数据转化为一维数据,将一维数据输入BiLSTM网络中。BiLSTM网络能够同时获取过去到未来的数据流向特征和未来到过去的数据流向特征,可以充分利用数据信息中的时间特征,同时引入Dropout(随机失活)技术,减少BiLSTM网络神经元之间的共适应性。最后,经过全连接层输出风电功率预测结果。
3.4 预测步骤
本文建立了POTDBO-VMD-CNN-BiLSTM短期风电功率预测模型,结构图如图2所示,步骤如下。
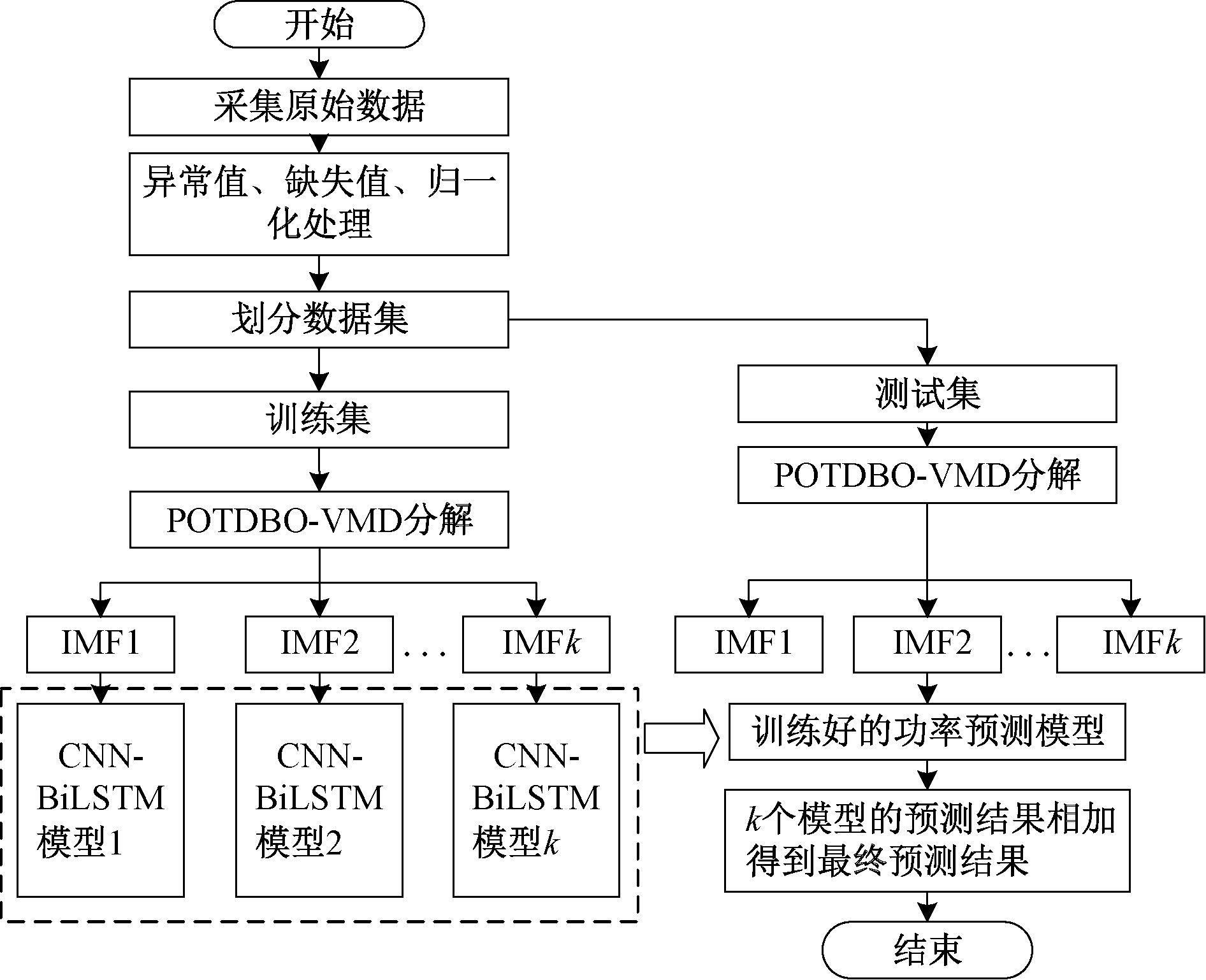
图2 POTDBO-VMD-CNN-BiLSTM模型结构
Figure 2 Model structure of POTDBO-VMD-CNN-BiLSTM
步骤1 对原始数据进行预处理,包括异常数据清洗、缺失数据填补、数据归一化等,同时将数据集划分为训练集和测试集。
步骤2 采用POTDBO-VMD将训练集和测试集的原始功率数据分解为多个固有模态分量(IMF),构造输入信号序列。
步骤3 将训练集的信号序列输入到CNN-BiLSTM网络中,得到训练好的功率预测模型;再将测试集的信号序列输入到已经训练好的功率预测模型中,得到各个模态分量的预测结果;最后将各个模态分量的预测结果叠加得到最终的功率预测值。
3.5 评价指标
本文采取均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和决定系数(R2)作为评价指标:
(16)
(17)
(18)

(19)
4 算例分析
4.1 基于变分模态法的风电功率分解结果分析
本文选择新疆某风电场2018年3月份的NWP数据、功率数据和吉林某风电场2019年1月份的NWP数据、功率数据作为变分模态分解的研究对象,数据采样间隔为15 min。
为验证POTDBO算法具有更强的寻优能力,本文选取新疆某风电场和吉林某风电场的历史功率数据,分别用DBO和POTDBO对VMD的模态分解数K和惩罚因子α进行寻优实验。其中,DBO和POTDBO的种群数量设置为10,最大迭代次数设置为20,K的搜索范围为[3,15],α的搜索范围为[100,2 500]。
收敛曲线如图3所示,可以看出,POTDBO具有更快的收敛速度,且有平衡全局探索和局部开发的能力。此时,新疆风电场数据中,VMD最优分解参数为分解数K=10、惩罚因子α=1 591;吉林风电场数据中,VMD最优分解参数为分解数K=8、惩罚因子α=1 151。
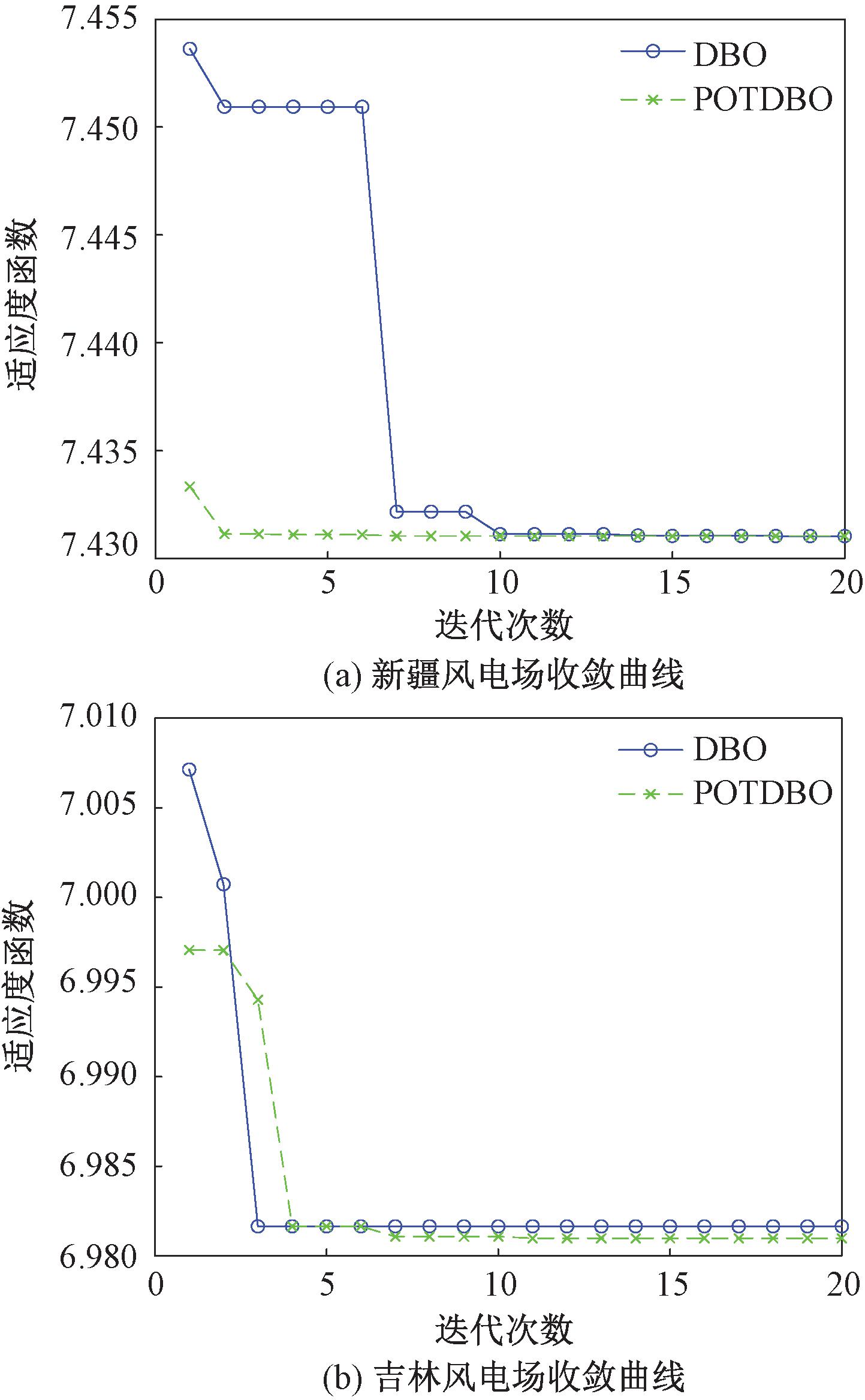
图3 DBO和POTDBO收敛曲线
Figure 3 Convergence curve of DBO and POTDBO
新疆风电场经VMD的结果如图4所示。可以看出,从IMF1到IMF10,数据的波动性依次减弱,说明存在随机因素,且会影响风电输出功率;IMF10序列的波动性最小,波形最平缓,可以反映风电输出功率的整体情况。此外,经过VMD的10个子序列与原始信号相比,数据的波动性均有一定程度的下降,且每个子序列没有出现比较明显的模态混叠现象,说明原始风电功率数据经过VMD之后,数据质量有所提升,进而提高了风电功率预测的准确度,表明VMD在提高风电功率预测准确度方面有可行性。
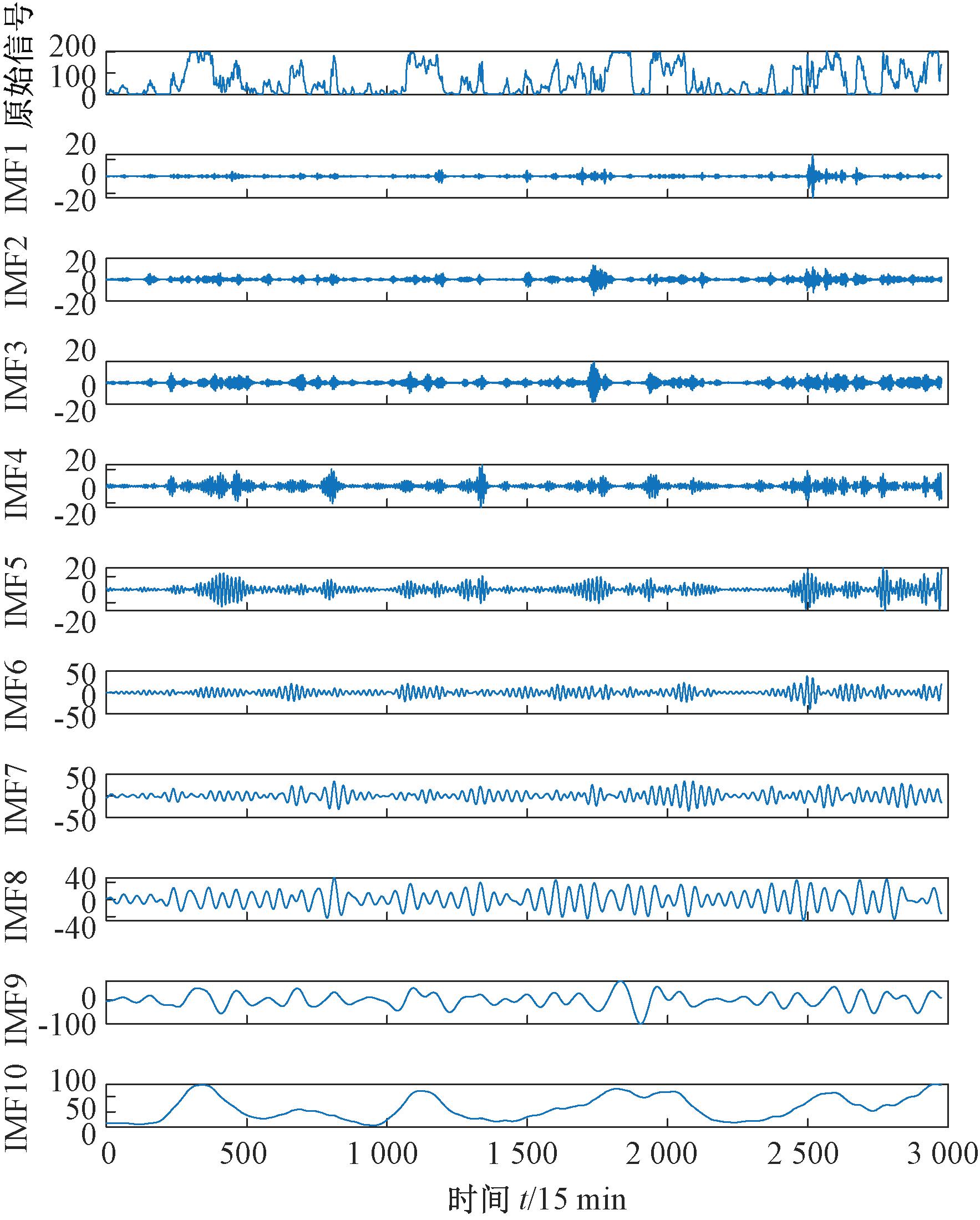
图4 新疆风电场历史功率序列VMD图
Figure 4 VMD of historical power series of Xinjiang wind farm
吉林风电场经VMD的结果如图5所示。从图5可以看出,从IMF1到IMF8,数据的波动性依次减弱;IMF8序列的波动性最小,波形最平缓。经过VMD之后,数据质量有所提升,进一步表明VMD在提高风电功率预测准确度方面有可行性。
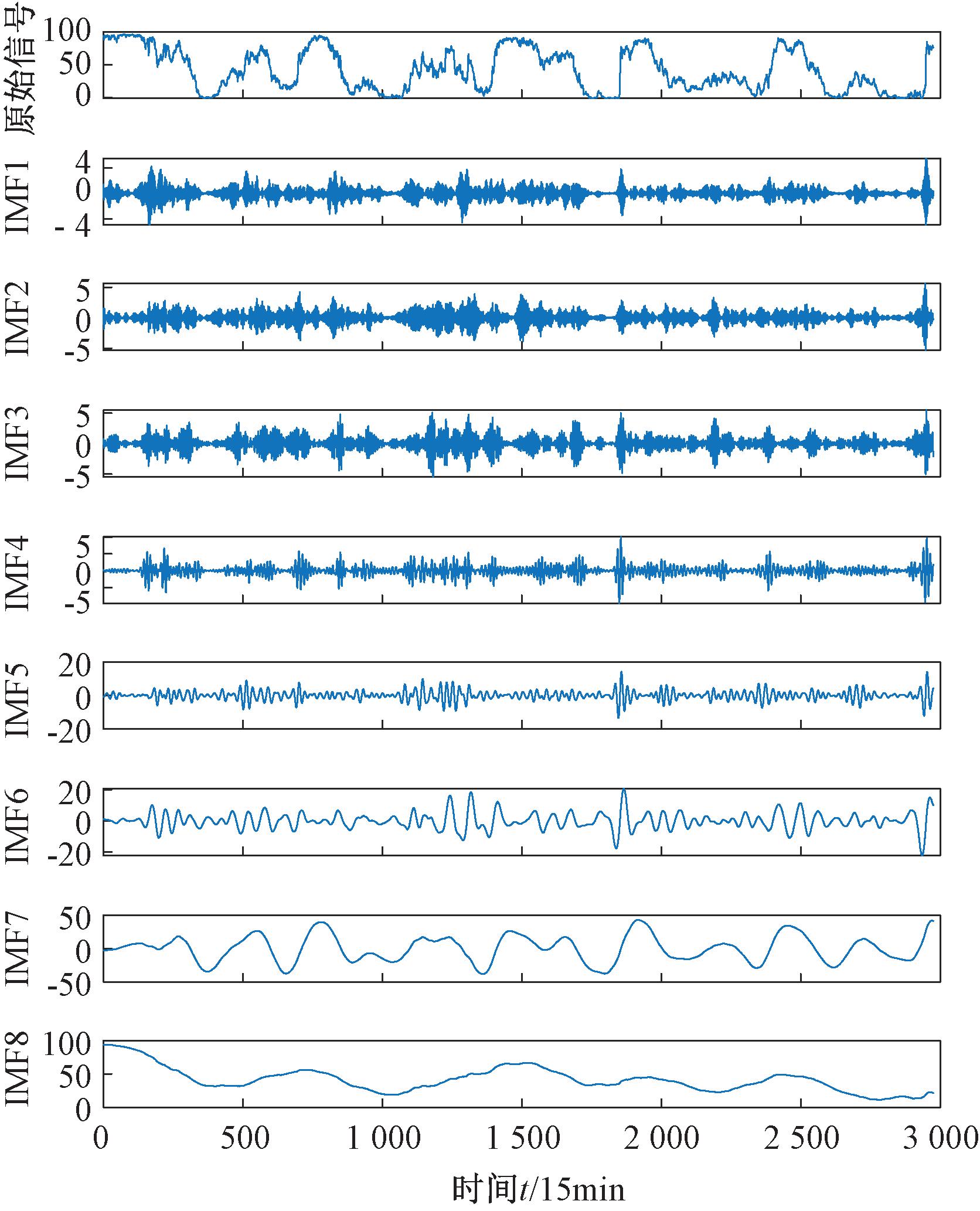
图5 吉林风电场历史功率序列VMD图
Figure 5 VMD of historical power series of Jilin wind farm
4.2 基于POTDBO-VMD-CNN-BiLSTM模型的风电功率预测结果分析
本文选择新疆某风电场2018年3月份的NWP数据、功率数据和吉林某风电场2019年1月份的NWP数据、功率数据作为变分模态分解的研究对象,数据采样间隔为15 min。新疆风电场共计2 976组数据,前2 679组数据作为训练集,后297组数据作为测试集;70 m风速、风向为功率预测模型的输入,风电功率为功率预测模型的输出。其中,VMD的模态分解数K和惩罚因子α分别为10和1 591。吉林风电场共计2 976组数据,前2 679组数据作为训练集,后297组数据作为测试集;轮毂处风速、风向为功率预测模型的输入,风电功率为功率预测模型的输出。其中,VMD的模态分解数K和惩罚因子α分别为8和1 151。
CNN层采用二维卷积层,卷积核尺寸为3×1,步长为[1,1],卷积核个数为32,池化层采用最大池化算法,激活函数采用Sigmoid;BiLSTM网络中考虑到过拟合的影响,隐含层个数并非越多越好,最终设置两层LSTM,神经元数目分别为128和32;优化器为Adam,最大训练次数为100次,初始学习率0.01,学习率调整因子0.01,全连接层激活函数为tanh。为了验证本文模型的有效性,同时选取CNN-BiLSTM模型进行对比,风电功率预测结果和误差如图6所示。
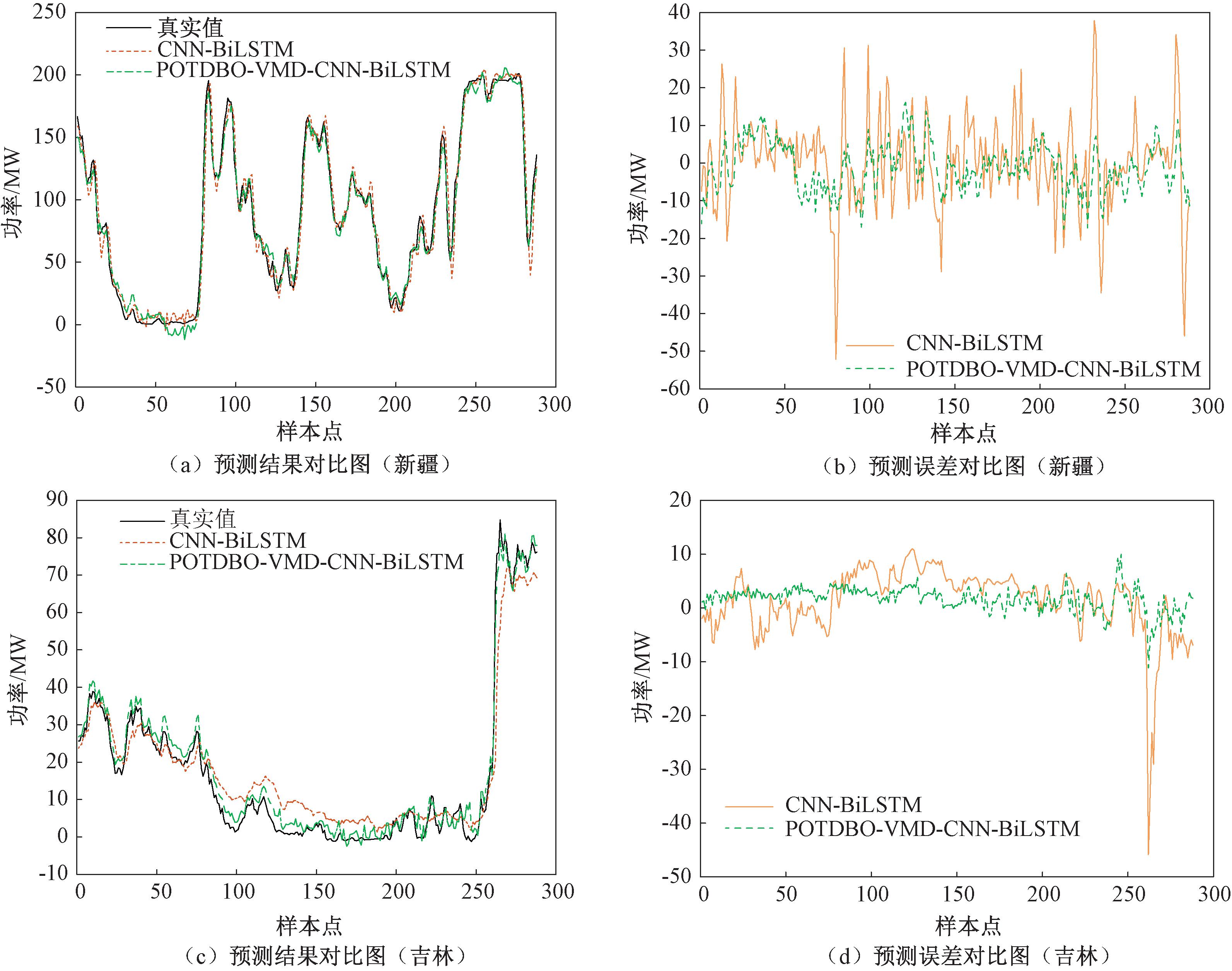
图6 风电功率预测结果和误差对比图
Figure 6 Comparison chart of wind power prediction results and errors
从表1可以看出,经过POTDBO-VMD模型分解之后,风电预测模型的准确度得到了大幅提升。在新疆风电场中,与CNN-BiLSTM模型相比,本文所提出的模型在RMSE上降低了54.03%,MAE降低了51.90%,MAPE降低了60.77%,R2提高了4.21%。在吉林风电场中,与CNN-BiLSTM模型相比,本文所提出的模型在RMSE上降低了53.13%,MAE降低了53.97%,MAPE降低了48.28%,R2提高了7.69%。结果表明,POTDBO-VMD-CNN-BiLSTM模型在短期风电功率预测方面有着更好的预测精度,证明了本文方法的有效性。
表1 风电功率预测评价指标对比
Table 1 Comparison of evaluation indicators for wind power prediction

数 据 来 源 预 测 模 型 R MS E/ M W MA E/ M W MA PE/ % R 2 新 疆 吉 林 C N N - B i L S T M 1 4 . 5 3 1 1 . 0 8 8 . 8 7 0 . 9 4 9 本 文 方 法 6 . 6 8 5 . 3 3 3 . 4 8 0 . 9 8 9 C N N - B i L S T M 6 . 5 5 4 . 7 8 1 3 . 9 2 0 . 9 1 0 本 文 方 法 3 . 0 7 2 . 2 0 7 . 2 0 0 . 9 8 0
5 结论
本文建立了POTDBO-VMD-CNN-BiLSTM的短期风电功率预测模型,得到以下结论。
(1)改进蜣螂优化算法(POTDBO)具有更快的收敛速度,且有平衡全局探索和局部开发的能力。
(2)采用POTDBO算法对VMD的参数K和α进行寻优处理,可以避免因K和α选择不适而造成虚假模态或模态混叠现象,进一步提高VMD的分解效果。
(3)针对气象信息波动剧烈、难以有效提取的情况,采用POTDBO-VMD模型对非平稳的风电功率数据进行处理。实验数据表明,本文建立的改进蜣螂优化算法的短期风电功率预测模型具有更好的泛化能力。
[1] 韩自奋, 景乾明, 张彦凯, 等. 风电预测方法与新趋势综述[J]. 电力系统保护与控制, 2019, 47(24): 178-187.
HAN Z F, JING Q M, ZHANG Y K, et al. Review of wind power forecasting methods and new trends[J]. Power System Protection and Control, 2019, 47(24): 178-187.
[2] GONG M J, YAN C C, XU W, et al. Short-term wind power forecasting model based on temporal convolutional network and Informer[J]. Energy, 2023, 283: 129171.
[3] 涂思嘉, 杨悦荣, 林舜江, 等. 考虑风电不确定性的交直流混联电网静态电压稳定优化控制方法[J]. 电力科学与技术学报, 2023, 38(3): 94-104.
TU S J, YANG Y R, LIN S J, et al. An optimal control method for static voltage stability of AC/DC hybrid power grid considering the uncertainty of wind power[J]. Journal of Electric Power Science and Technology, 2023, 38(3): 94-104.
[4] 张颖超, 成金杰, 邓华, 等. 基于相似日和特征提取的短期风电功率预测[J]. 郑州大学学报(工学版), 2020, 41(5): 44-49.
ZHANG Y C, CHENG J J, DENG H, et al. Short-term wind power prediction based on similar day and feature extraction[J]. Journal of Zhengzhou University (Engineering Science), 2020, 41(5): 44-49.
[5] 蒋建东, 孙书凯, 董存, 等. 风电中长期电量预测研究现状[J]. 高电压技术, 2022, 48(2): 409-419.
JIANG J D, SUN S K, DONG C, et al. Research status of mid-long term wind power generation forecasting[J]. High Voltage Engineering, 2022, 48(2): 409-419.
[6] ANTONANZAS J, OSORIO N, ESCOBAR R, et al. Review of photovoltaic power forecasting[J]. Solar Energy, 2016, 136: 78-111.
[7] AHMED R, SREERAM V, MISHRA Y, et al. A review and evaluation of the state-of-the-art in PV solar power forecasting: techniques and optimization[J]. Renewable and Sustainable Energy Reviews, 2020, 124: 109792.
[8] SOUBDHAN T, NDONG J, OULD-BABA H, et al. A robust forecasting framework based on the Kalman filtering approach with a two-fold parameter tuning procedure: application to solar and photovoltaic prediction[J]. Solar Energy, 2016, 131: 246-259.
[9] DE ALENCAR D B, DE MATTOS AFFONSO C, DE OLIVEIRA R C L, et al. Different models for forecasting wind power generation: case study[J]. Energies, 2017, 10(12): 1976.
[10] YANG D Z. Making reference solar forecasts with climatology, persistence, and their optimal convex combination[J]. Solar Energy, 2019, 193: 981-985.
[11] HU W B, YANG C Z. Grey model of direct solar radiation intensity on the horizontal plane for cooling loads calculation[J]. Building and Environment, 2000, 35(7): 587-593.
[12] WANG S, LI B, LI G Z, et al. Short-term wind power prediction based on multidimensional data cleaning and feature reconfiguration[J]. Applied Energy, 2021, 292: 116851.
[13] LIU W, LIU Y M, FU L, et al. Wind power forecasting method based on bidirectional long short-term memory neural network and error correction[J]. Electric Power Components and Systems, 2021, 49(13/14): 1169-1180.
[14] LI Z, XU R S, LUO X R, et al. Short-term wind power prediction based on modal reconstruction and CNN-BiLSTM[J]. Energy Reports, 2023, 9: 6449-6460.
[15] 李润金, 李丽霞. 基于VMD-CNN-LSTM模型的短期风电功率预测[J]. 沈阳工程学院学报(自然科学版), 2024, 20(1): 6-13.
LI R J, LI L X. Short-term wind power prediction based on VMD-CNN-LSTM model[J]. Journal of Shenyang Institute of Engineering (Natural Science), 2024, 20(1): 6-13.
[16] 陈申, 叶小岭, 熊雄, 等. 基于天鹰优化算法的短期风电功率区间预测[J]. 重庆理工大学学报(自然科学), 2023, 37(4): 304-314.
CHEN S, YE X L, XIONG X, et al. Short-term wind power interval prediction based on Aquila optimization algorithm[J]. Journal of Chongqing University of Technology (Natural Science), 2023, 37(4): 304-314.
[17] 欧阳资生, 唐伯聪. 基于VMD-BiLSTM-ATT预测模型的碳中和指数量化投资研究[J]. 金融经济, 2023(10): 75-90.
OUYANG Z S, TANG B C. Quantifying carbon neutrality investment research based on VMD-BiLSTM-ATT forecasting model[J]. Finance Economy, 2023(10): 75-90.
[18] 肖烈禧, 张玉, 周辉, 等. 基于IAOA-VMD-LSTM的超短期风电功率预测[J]. 太阳能学报, 2023, 44(11): 239-246.
XIAO L X, ZHANG Y, ZHOU H, et al. Ultra short trem wind power prediction based on IAOA-VMD-LSTM[J]. Acta Energiae Solaris Sinica, 2023, 44(11): 239-246.
[19] 李飞宏, 肖迎群. 基于VMD-GRU-EC的短期电力负荷预测方法[J]. 中国测试, 2023, 49(10): 120-127.
LI F H, XIAO Y Q. Short-term power load forecasting method based on VMD-GRU-EC[J]. China Measurement &Test, 2023, 49(10): 120-127.
[20] XUE J K, SHEN B. Dung beetle optimizer: a new meta-heuristic algorithm for global optimization[J]. The Journal of Supercomputing, 2023, 79(7): 7305-7336.
[21] 郭琴, 郑巧仙. 多策略改进的蜣螂优化算法及其应用[J]. 计算机科学与探索, 2024, 18(4): 930-946.
GUO Q, ZHENG Q X. Multi-strategy improved dung beetle optimizer and its application[J]. Journal of Frontiers of Computer Science and Technology, 2024, 18(4): 930-946.
[22] DEHGHANI M, TROJOVSKY P. Osprey optimization algorithm: a new bio-inspired metaheuristic algorithm for solving engineering optimization problems[J]. Frontiers in Mechanical Engineering, 2023, 8: 1126450.
[23] 李津, 史加荣, 张琰妮, 等. 基于最大信息系数的短期太阳辐射协同估计[J]. 太阳能学报, 2023, 44(9): 286-294.
LI J, SHI J R, ZHANG Y N, et al. Short-term solar radiation synergy estimation based on maximum information coefficient[J]. Acta Energiae Solaris Sinica, 2023, 44(9): 286-294.
[24] 杨锡运, 刘玉奇, 李建林. 基于四分位法的含储能光伏电站可靠性置信区间计算方法[J]. 电工技术学报, 2017, 32(15): 136-144.
YANG X Y, LIU Y Q, LI J L. Reliability confidence interval calculation method for photovoltaic power station with energy storage based on quartile method[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 136-144.
[25] 杨子民, 彭小圣, 熊予涵, 等. 计及邻近风电场信息与CNN-BiLSTM的短期风电功率预测[J]. 南方电网技术, 2023, 17(2): 47-56.
YANG Z M, PENG X S, XIONG Y H, et al. Short-term wind power prediction based on information in neighboring wind farms and CNN-BiLSTM[J]. Southern Power System Technology, 2023, 17(2): 47-56.
[26] 辛征, 王琦, 刘兴然. 短期风电功率预测的深度学习模型[J]. 计算机时代, 2023(2): 33-36, 41.
XIN Z, WANG Q, LIU X R. Deep learning model for short-term wind power prediction[J]. Computer Era, 2023(2): 33-36, 41.