闸门是水工建筑物引水和排水的重要设备,平面闸门结构简单、布置紧凑,应用广泛。使用平面闸门时,需在闸墩上设置门槽以传递闸门上的荷载及引导闸门启闭。在闸门推力作用下,门槽可能发生3种破坏:闸墩颈部受拉破坏、二期混凝土局部受压破坏和门槽结构受剪破坏。对颈部受拉破坏和混凝土局部受压破坏已有成熟设计方法[1-4];对于受剪破坏,《水工混凝土结构设计规范》[3-4]要求每延米门槽承受闸门推力大于2 000 kN时,应进行下游墩墙受剪承载力复核,但由于国内外尚无系统研究,未能给出具体的方法。因此,规范修订时对门槽结构的受剪承载力进行了专题研究。
水工建筑中平面闸门常不止一道,不同位置的闸门门槽受力状态不同。对位于最下游的闸门门槽而言,其受力状态与闸墩下游末端以及闸墩外侧面是否受约束有关,因此对不同位置、不同约束条件的门槽应分别进行研究。张涛等[5]和喻君等[6]通过试验和数值方法研究了非最下游门槽的受剪承载力并提出了计算公式。也有学者对最下游门槽的承载力进行了专门研究。杨静安等[7]以某实际工程为例,对导流隧洞平面闸门门槽结构设计进行了探讨,建议按照偏压构件进行斜截面承载力计算。需要指出的是,按照偏压构件计算的斜截面承载力是用于抵抗闸墩所受的横流向水压力,而非顺流向的闸门推力,因此该建议不适用于门槽结构的受剪。吴松峰[8]和Han等[9]采用12个竖直立于地面的试件对最下游平面闸门门槽进行了试验研究,基于抛物线莫尔-库伦准则推导了门槽斜截面承载力计算公式。王建等[10]采用塑性损伤模型分析了某大坝工作闸门门槽的破坏模式和承载力,计算时约束了下游墩墙末端的法向位移,破坏形态与文献[8-9]相同,未发生受剪破坏。需说明的是,文献[8-10]均约束了下游墩墙端面,对应下游末端受约束的事故门槽,其受力状态、破坏模式更接近局部受压破坏,而非受剪破坏。孙斌等[11]对某实际工程无约束事故闸门中墩门槽结构进行了有限元分析,验算二期混凝土局部受压承载力满足要求后,假定二期混凝土发生斜向滑动破坏,按重力坝混凝土层面抗滑稳定条件复核了该工程的斜截面承载力,但未说明关于门槽受剪破坏形态的假定的理论依据,也未讨论其他破坏形态的可能性。蔡睿恒等[12]对最下游平面闸门门槽进行了小比例试件的试验研究和有限元计算,对门槽受剪机理和破坏模式进行了有益的探索,提出了发生颈部受拉破坏与下游墩墙受剪破坏的尺寸界限,并给出了受剪承载力的计算公式,但该文献试件的颈部纵向钢筋伸入下游墩墙长度远大于实际工程,影响了下游墩墙斜裂缝的走向,且试件数量有限,尚不能反映实际门槽结构的受剪承载力。可见,针对最下游闸门门槽承载力的研究尚不多见,其中,对闸墩末端无约束时发生的研究相当少见。
本文为NB/T 11011—2022《水工混凝土结构设计规范》[2]修订专项研究,以拉西瓦水电站进水口中事故闸门门槽为原型,对侧边和下游末端自由的最下游边墩平面闸门门槽进行受剪承载力试验研究,确定其破坏形态,给出门槽结构受剪承载力计算公式。末端自由的中墩门槽仅受到一侧闸门推力作用时,也适用本文研究成果。
1 门槽结构试验方案
1.1 门槽结构设计
本文以拉西瓦水电站进水口闸门门槽为原型,浇筑小型门槽结构开展平面试验研究。
试验研究分批次进行。第一批试验共4个门槽结构,编号TSP1~TSP4,用于研究门槽的破坏模式和横向钢筋用量对门槽受剪承载力的影响。门槽厚度取300 mm,一期和二期混凝土强度等级分别为C25和C30。基准门槽TSP1的结构形式和配筋率与拉西瓦电站事故闸门门槽相同,见图1,其中①、②、③号钢筋分别为纵向、横向和斜向钢筋。下游墩墙内横向钢筋和斜向钢筋各取2Φ14,颈部加强钢筋(④号)为2Φ12。颈部纵向钢筋为3Φ18,限于结构尺寸,钢筋锚固长度不满足《水工混凝土结构设计规范》[3-4]要求,故将TSP1~TSP3中纵向钢筋通过端部焊板锚固,仅TSP4为直线锚固。
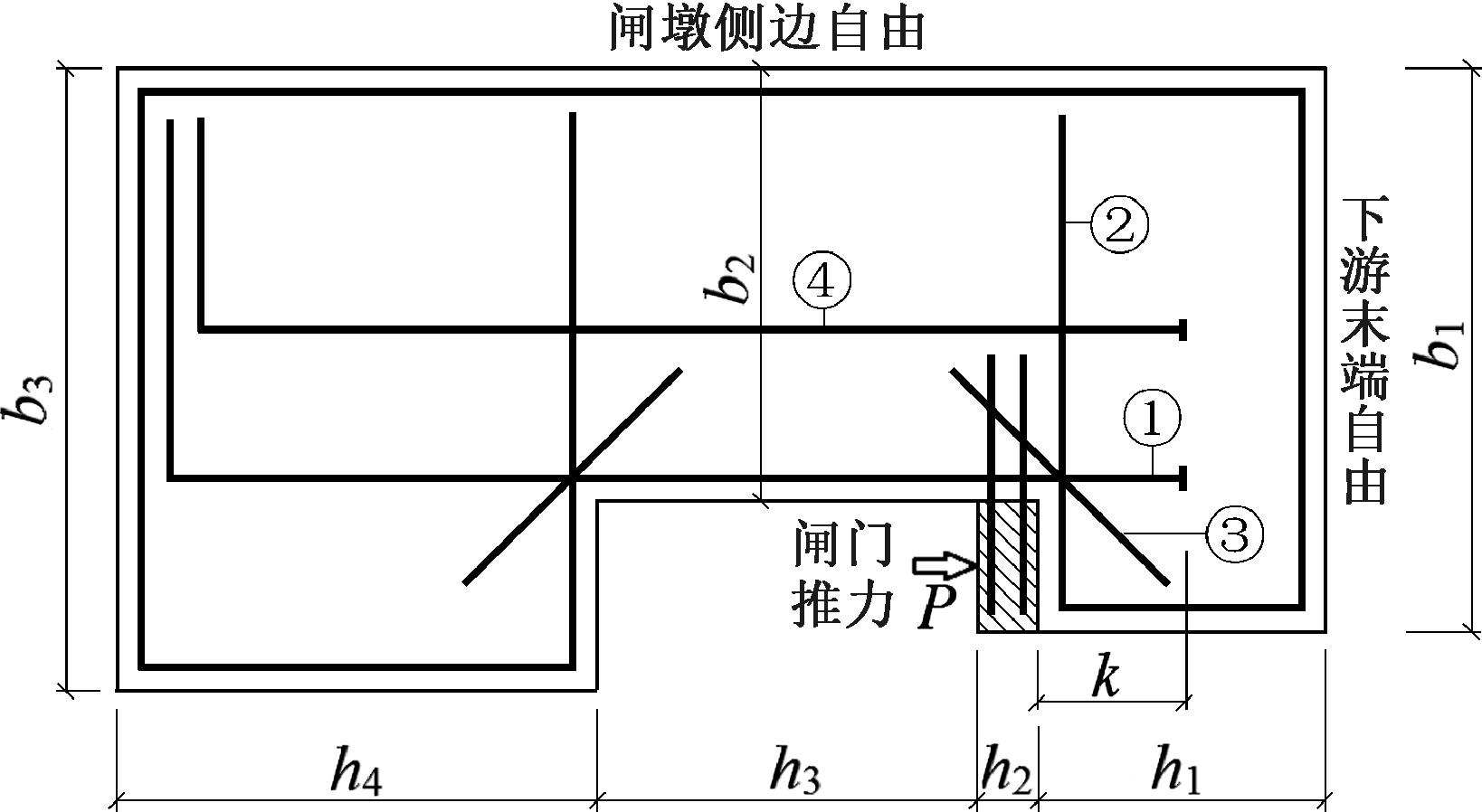
图1 门槽结构示意图
Figure 1 Gate slot structure
一期混凝土养护7 d后拆模,界面凿毛后浇筑二期混凝土(图1中阴影部分)。二期混凝土厚(h2)100 mm,内部配置预埋件,顶面布置有钢板和钢条以模拟闸门滑块轨道。二期混凝土内预埋薄钢板以防止局部受压破坏;颈部粘贴碳纤维布以防止发生颈部受拉破坏。各门槽结构详情见表1。
表1 门槽结构基本参数
Table 1 Essential parameters of gate slots
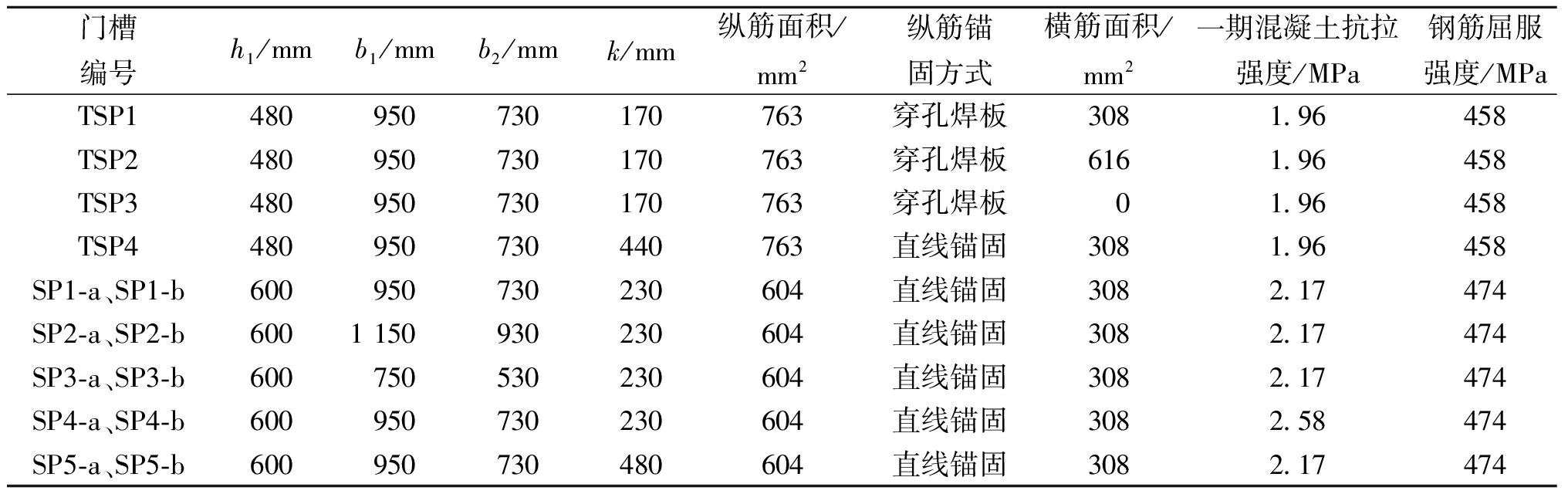
门槽编号h1/mmb1/mmb2/mmk/mm纵筋面积/mm2纵筋锚固方式横筋面积/mm2一期混凝土抗拉强度/MPa钢筋屈服强度/MPaTSP1480950730170763穿孔焊板3081.96458TSP2480950730170763穿孔焊板6161.96458TSP3480950730170763穿孔焊板01.96458TSP4480950730440763直线锚固3081.96458SP1-a、SP1-b600950730230604直线锚固3082.17474SP2-a、SP2-b6001 150930230604直线锚固3082.17474SP3-a、SP3-b600750530230604直线锚固3082.17474SP4-a、SP4-b600950730230604直线锚固3082.58474SP5-a、SP5-b600950730480604直线锚固3082.17474
第一批门槽结构均发生受剪破坏,验证了试验方案的可行性。在此基础上,为减小纵向钢筋末端锚板对裂缝形态的影响,设计了第二批5组共10个门槽结构,组编号为SP1~SP5,组编号末尾加字母a或b区分同组的门槽结构。结构尺寸、混凝土强度等基本参数也列于表1中。第二批门槽结构中,纵向钢筋采用12Φ8,按钢筋屈服前不被拔动、尽可能符合比例的原则确定纵筋锚固长度,以反映实际结构纵筋锚固段对受剪承载力的影响。SP1组为基准门槽,其余为对照组,分别研究下游墩墙宽度b1、一期混凝土强度等级、纵筋锚固长度对门槽受剪的影响。所有门槽结构厚度仍为300 mm,除颈部纵筋外,其他钢筋与第一批门槽结构的基准门槽相同。
1.2 加载与测量方案
将门槽结构平置于地面,与地面之间布置3根外径10 mm的钢管以消除摩擦。采用1 000 kN千斤顶自平衡加载,加载装置及方案见图2。先预加载至20 kN,观察加载装置可靠,确定加载装置和测量仪器正常后正式加载。试验采用单调分级加载,裂缝出现前每级荷载增量为10 kN,裂缝出现后为15 kN,每级持荷3 min。当裂缝迅速开展且荷载下降时,认定门槽失效并停止加载。图3展示了钢筋应变片和位移测点的布置。
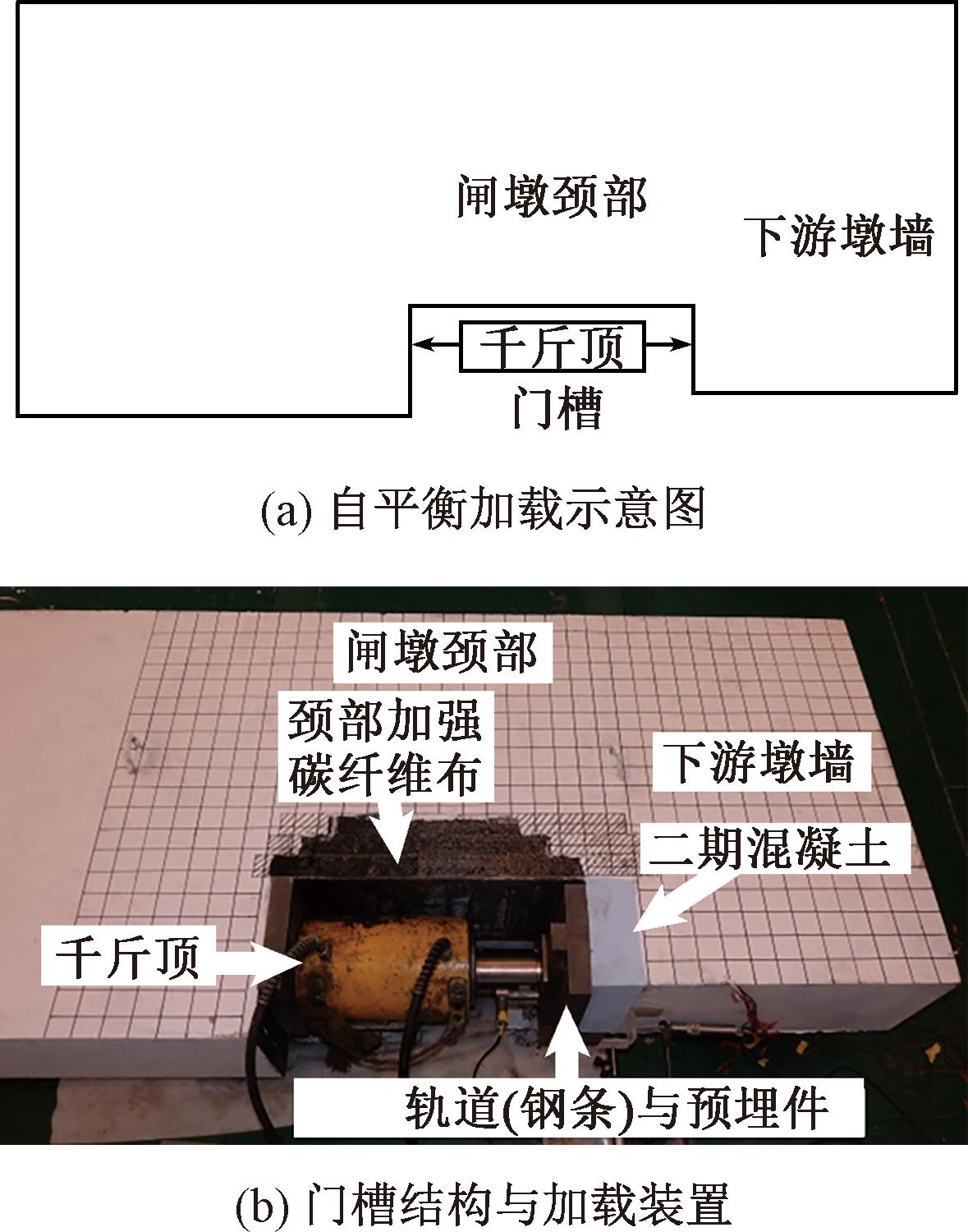
图2 门槽结构加载方式
Figure 2 Loading method for the gate slots
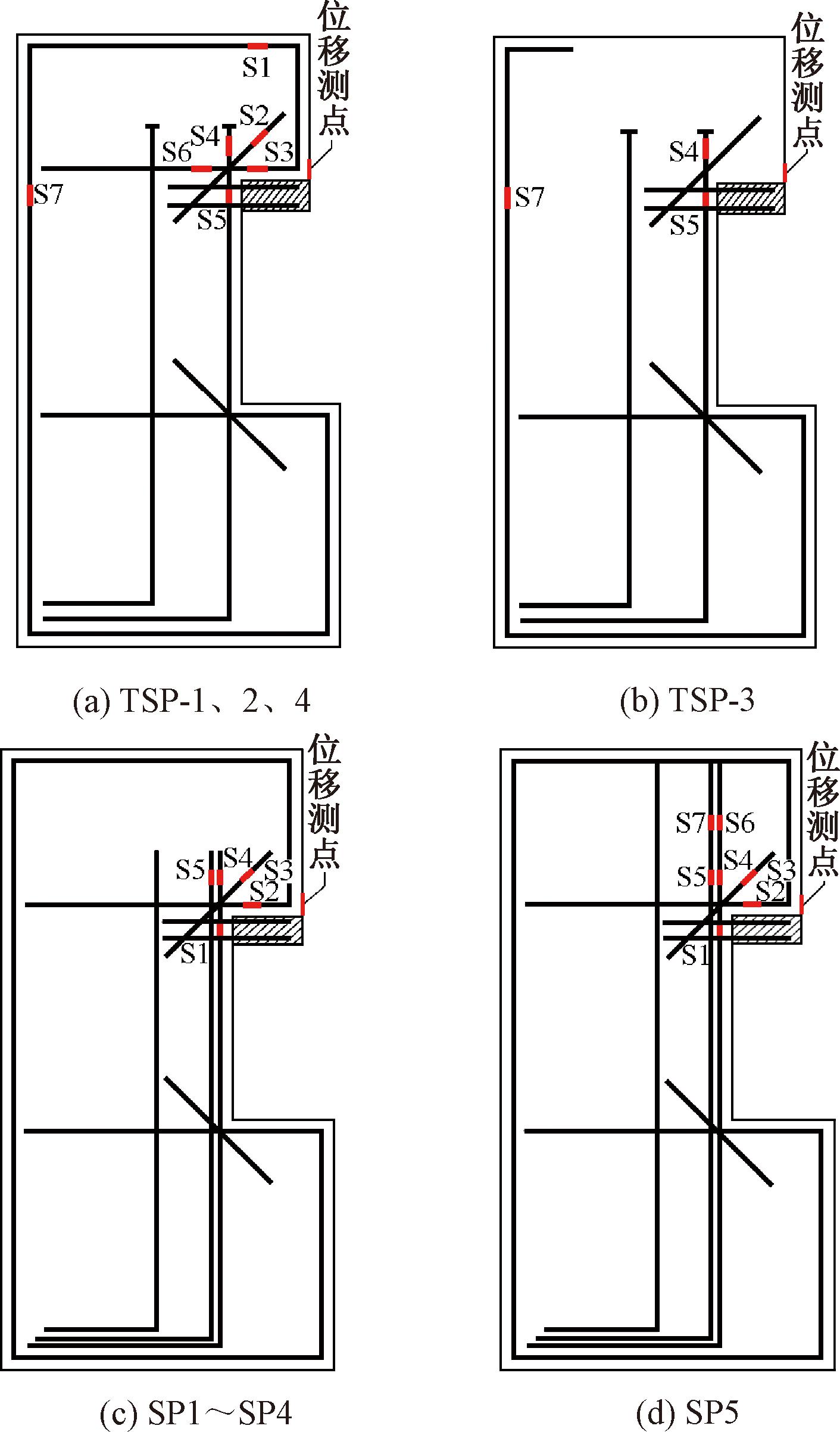
图3 应变片及位移测点布置
Figure 3 Positions of strain gages and displacement gauge
2 试验结果
2.1 第1批试验结果
各门槽结构破坏时裂缝分布与破坏形态见图4,图4中左侧均为实物照片,右侧均为局部详图,详图中带圈数字为裂缝出现顺序,不带圈数字为裂缝出现时的荷载值,单位为kN。限于篇幅,仅列出了荷载达到Pu时的裂缝形态。
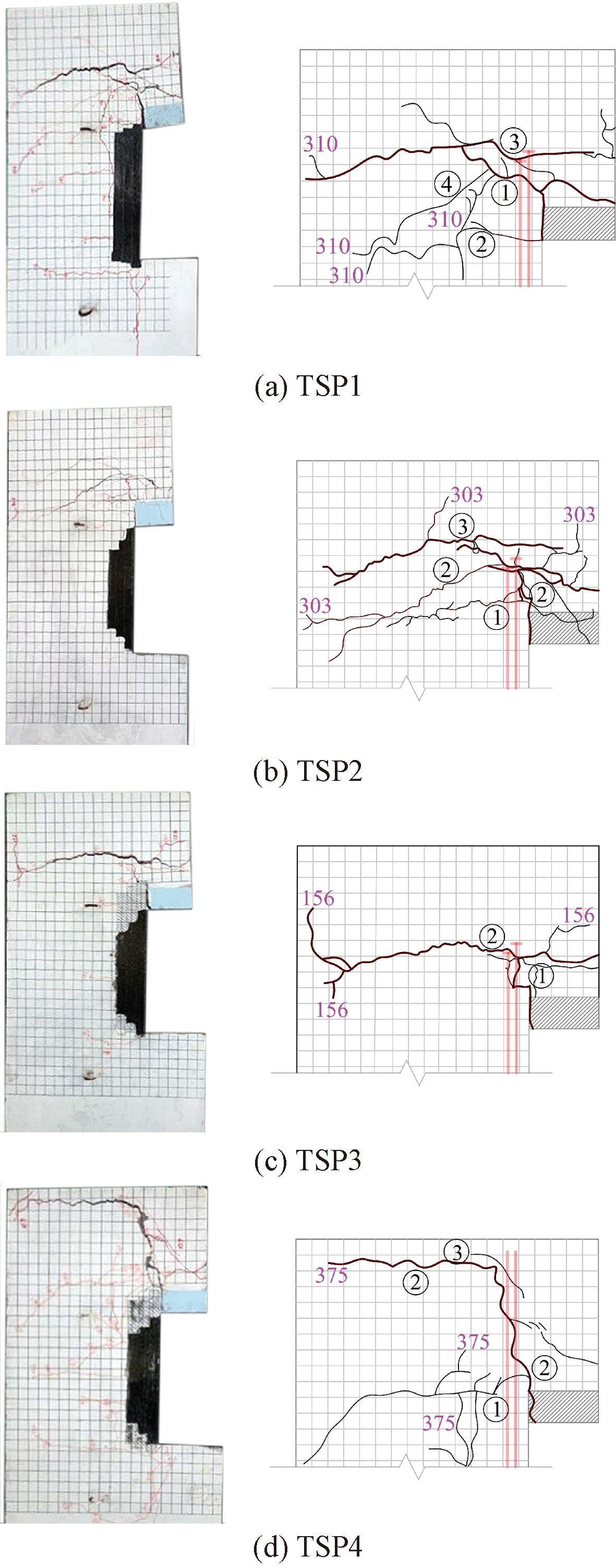
图4 第1批门槽裂缝分布与破坏形态
Figure 4 Cracks and failure of the first batch gate slots
TSP1的首条裂缝①出现于二期混凝土内侧,开裂荷载(Pcr)为116 kN。加载至135 kN时,闸墩颈部出现细小裂缝②。裂缝①向下游延伸,荷载达到224 kN时,裂缝①开始向内侧斜向发展形成斜裂缝,随荷载增大,横水流方向余留宽度(裂缝①尖端至闸墩外侧边的宽度)逐渐减小。荷载达到260 kN时,纵筋端部附近出现裂缝③。裂缝③基本沿横水流向延伸,在加载至Pu=310 kN时与裂缝①贯通,余留截面不足以承担荷载,裂缝①与裂缝③的宽度迅速增加,荷载突然下降,门槽破坏。破坏时,裂缝①还分岔出了指向颈部的裂缝④。
TSP2和TSP3的横向钢筋用量与TSP1不同,裂缝发展过程和最终破坏形态均与TSP1基本相同。TSP4纵向钢筋由锚板锚固变为直锚并增加了锚固长度,破坏过程与破坏形态不变,但余留截面相应向下游移动,大致与纵筋末端平齐。
第1批门槽结构钢筋平均屈服应变为2 290×10-6,各门槽钢筋应变随荷载的变化如图5所示。可以看出,对侧边自由且下游端无约束的门槽,其颈部受到偏心推力作用,因而靠近推力一侧纵筋受拉,远离推力一侧纵筋受压。与斜裂缝相交处受拉纵筋应力较小,即纵筋对受剪承载力贡献较小。横向钢筋全程受拉,应力值较大,但未达屈服强度,即横向钢筋对斜截面承载力有较大贡献,但有上限。与斜筋相交处裂缝宽度较小,斜筋应力较低。因而斜裂缝附近钢筋均未屈服,门槽受剪破坏为脆性破坏。
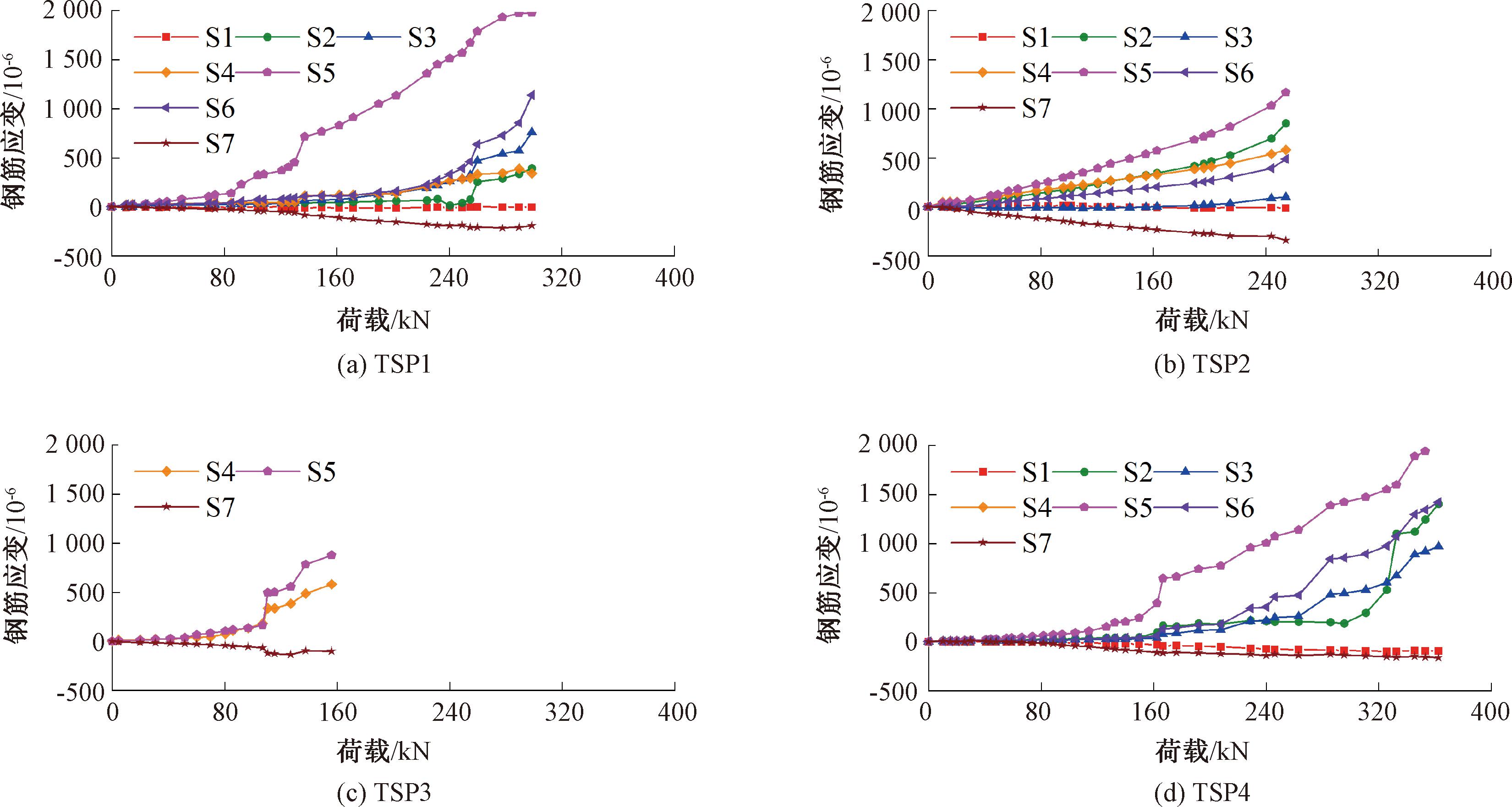
图5 第一批门槽钢筋应变-荷载关系
Figure 5 Reinforcement strain-loading curves of the first batch gate slots
2.2 第2批试验结果
SP2~SP4这3组门槽结构发生受剪破坏,破坏时裂缝分布与破坏形态见图6,图6中数字含义同前。限于篇幅,图6仅列出各组中的门槽a,门槽b的裂缝分布和破坏形态基本相同。SP1和SP5两组门槽结构未发生受剪破坏,本文不列出其破坏形态,也不统计、分析其承载力。

图6 第二批门槽裂缝分布与破坏形态
Figure 6 Cracks and failure of the second batch gate slots
(1)SP2门槽组。荷载达到Pcr=212 kN时,二期混凝土角部出现首条裂缝①并向闸墩颈部延伸,荷载达225 kN时二期混凝土角部出现裂缝②并倾斜向下游延伸。随荷载增大,与纵筋端部平齐处出现横向裂缝③。加载至Pu=257 kN时,随一、二期混凝土交界面撕裂,裂缝②和裂缝③贯通,余留截面混凝土破坏,荷载突然下降,门槽破坏。
(2)SP3门槽组。SP3门槽组较SP2门槽组的差别为闸墩颈部宽度减小了400 mm,其他参数相同。荷载为Pcr=200 kN时,二期混凝土角部出现裂缝①和裂缝②,裂缝①向颈部横向延伸,裂缝②倾斜延伸入下游墩墙。荷载增大至212 kN时,下游墩墙内与纵筋端部平齐处出现裂缝③,继续加载至Pu=239 kN时,门槽下缘中部出现裂缝④并与裂缝②和裂缝③贯通。随一、二期混凝土交界面撕裂,裂缝②、③、④显著增大,余留截面混凝土不足以承担荷载,门槽破坏。
(3)SP4门槽组。SP4门槽组较SP2门槽组的差别为一期混凝土的强度等级提高了两级、闸墩颈部宽度增大200 mm,其他参数相同,裂缝发展过程、破坏时裂缝分布、破坏形态均与SP2一致,区别为承载能力不同,开裂荷载和破坏荷载分别为Pcr=130 kN和Pu=285 kN。
第2批门槽结构钢筋平均屈服应变为2 300×10-6,受剪破坏的门槽内各钢筋应变随荷载的变化如图7所示。由图7可知,混凝土开裂后,钢筋应变出现陡增。由于测点S1接近初始裂缝,其应变陡增明显早于其他测点。随下游墩墙尺寸的增大,更多混凝土参与了受拉,除S1之外的其他测点应变陡增对应的荷载均有所增大。由于纵向钢筋用量较少,颈部纵向钢筋受拉屈服。发生受剪破坏时,横向钢筋应力较大,表明横向钢筋对门槽受剪承载力贡献相对较大,但横向钢筋未屈服表明横向钢筋的有利作用是有限的。与第1批门槽相同,破坏时裂缝附近钢筋均未屈服,表明门槽受剪破坏为脆性破坏。
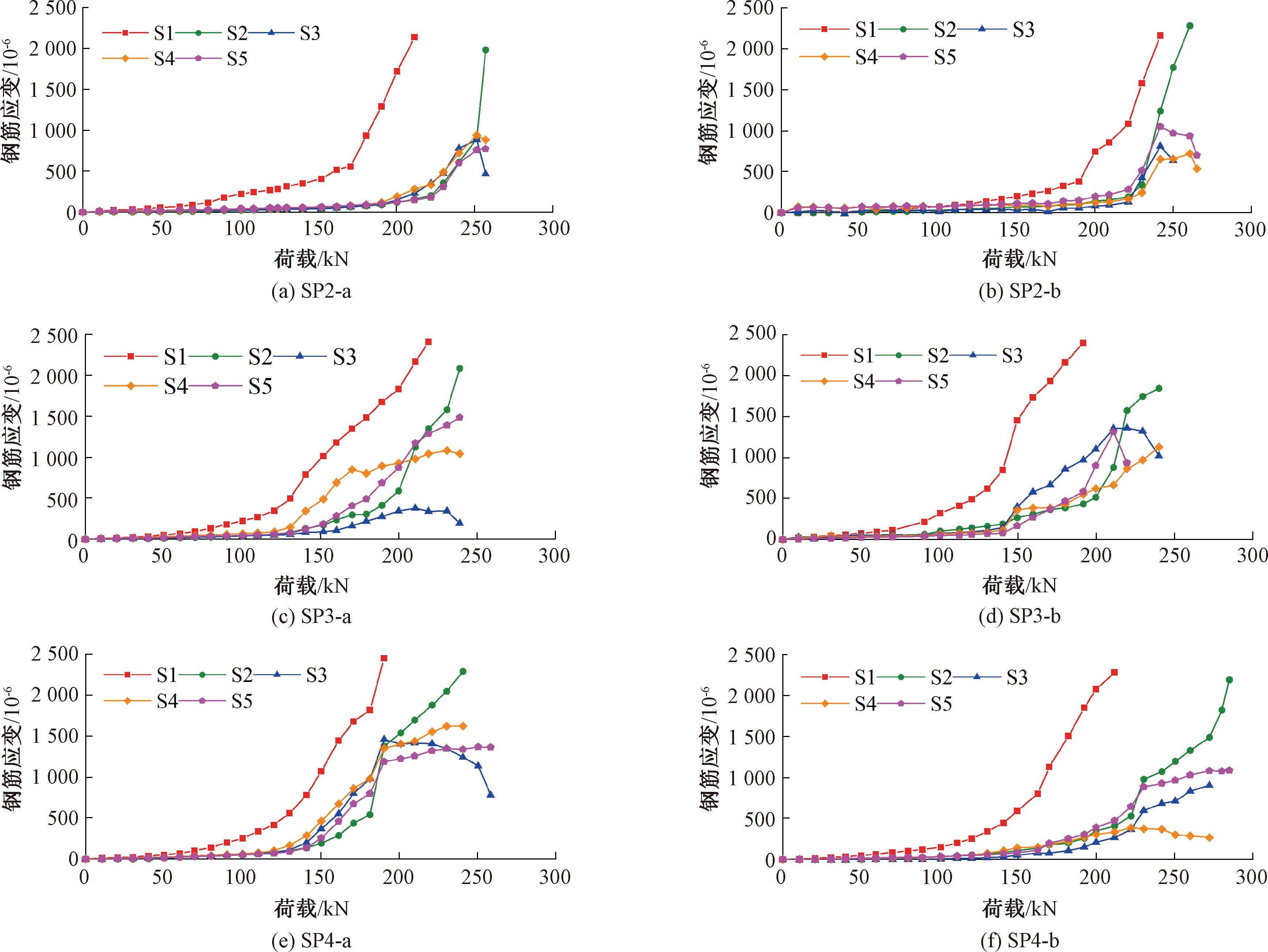
图7 第2批门槽钢筋应变-荷载关系
Figure 7 Reinforcement strain-loading curves of the second batch gate slots
2.3 受剪破坏形态
如图8所示,各门槽受剪破坏的形态相似,可归纳为首条裂缝出现于一期混凝土角部附近并向颈部横向延伸,但发展较为缓慢。破坏裂缝则起始于一期混凝土角部,随荷载增大斜向延伸(图8中红色实线),当斜裂缝的尖端与纵向钢筋末端大致平齐时,余留混凝土(发生斜向裂缝后,下游墩墙内余留未裂通的部分,即图8中红色虚线)不足承担闸门推力而发生破坏。由此,门槽受剪破坏截面(破坏裂缝)可简化为由倾斜段和横向段组合而成,斜裂缝段和余留截面混凝土、钢筋共同承担闸门推力。
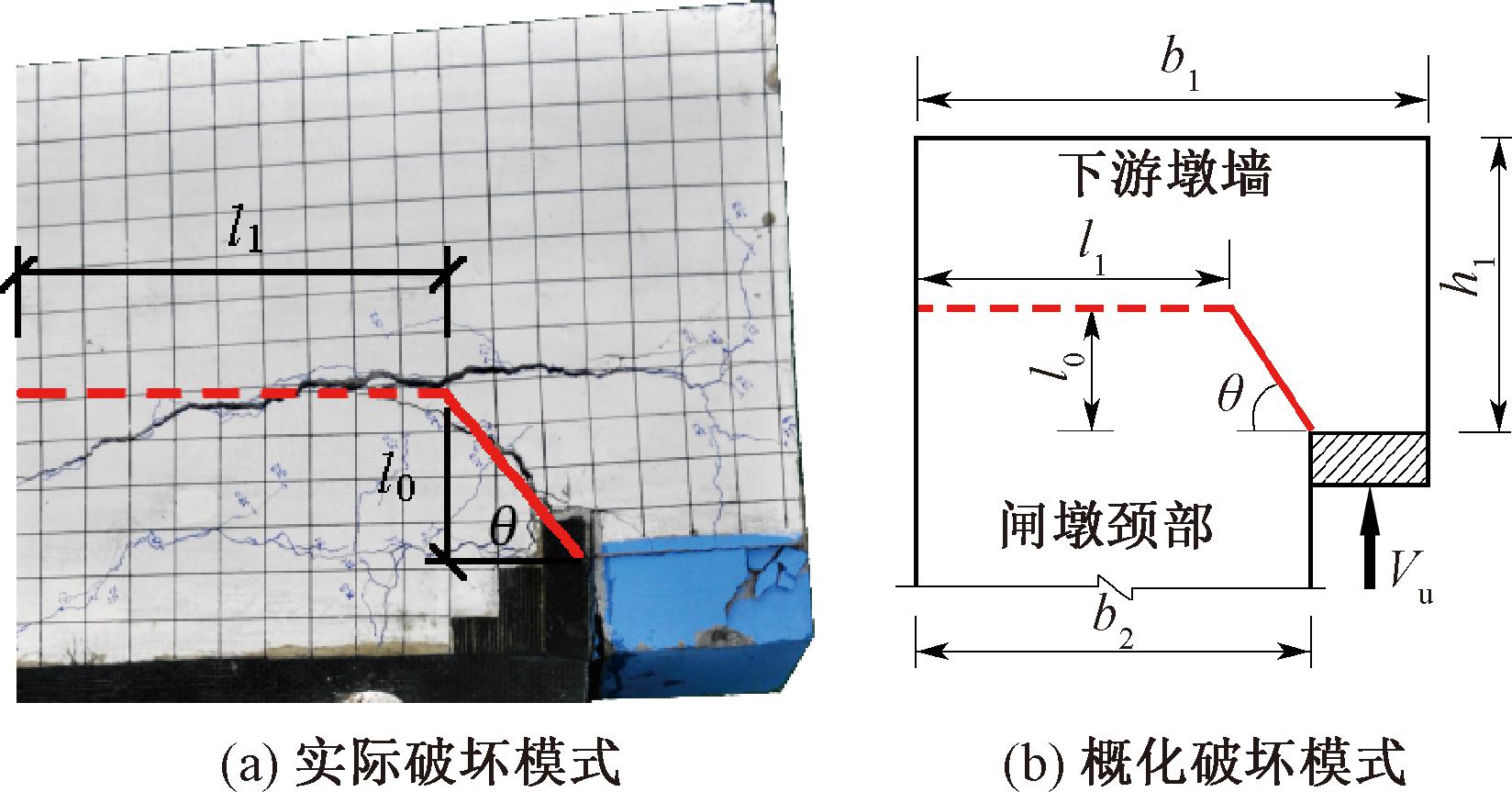
图8 下游边墩门槽受剪破坏模式
Figure 8 Shearing failure pattern of gate slot of downstream side pier
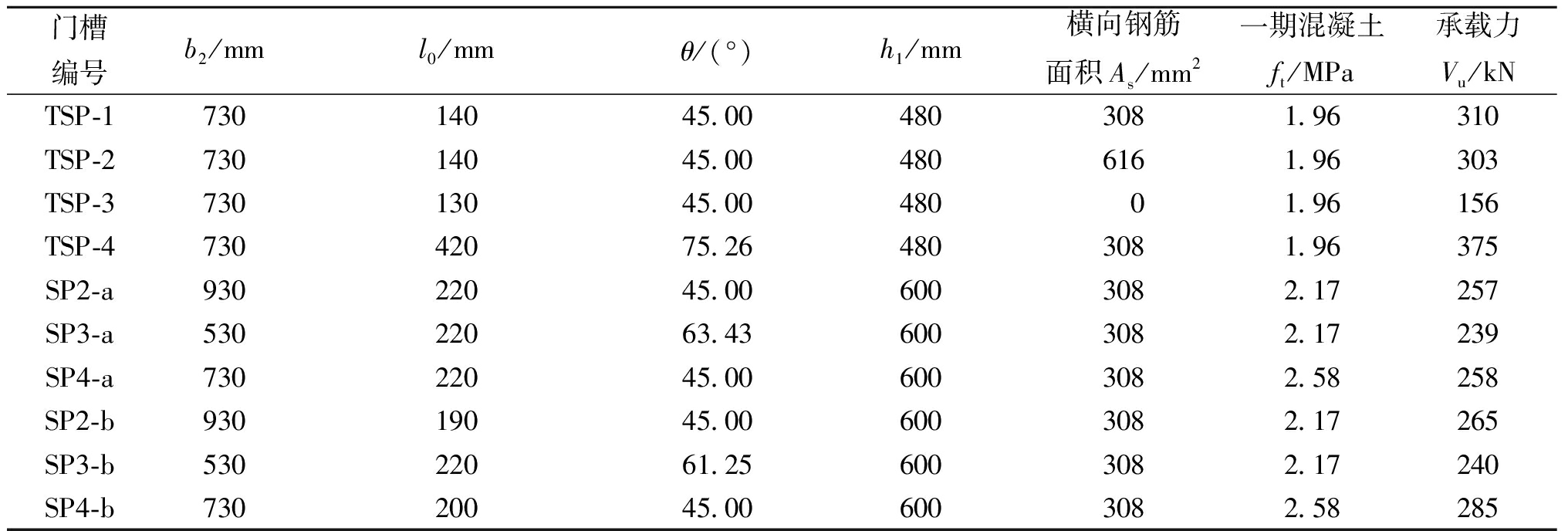
为描述破坏截面,需确定斜裂缝倾角θ及向下游方向的延伸长度l0和余留截面长度l1,其中l1可根据闸墩颈部宽度b2和l0、θ求得。两批试验发生受剪破坏门槽的b2、l0和θ列于表2。
表2 破坏截面参数与门槽承载力
Table 2 Details of failure section and bearing capacity of gate slots
门槽编号b2/mml0/mmθ/(°)h1/mm横向钢筋面积As/mm2一期混凝土ft/MPa承载力Vu/kNTSP-173014045.004803081.96310TSP-273014045.004806161.96303TSP-373013045.0048001.96156TSP-473042075.264803081.96375SP2-a93022045.006003082.17257SP3-a53022063.436003082.17239SP4-a73022045.006003082.58258SP2-b93019045.006003082.17265SP3-b53022061.256003082.17240SP4-b73020045.006003082.58285
2.4 受剪承载力
发生受剪破坏的各门槽的承载力也列于表2。由表2可见,TSP3未配置横向钢筋,破坏荷载约为TSP1破坏荷载的50%,表明横向钢筋可提高门槽受剪承载力,同时,TSP2的横向钢筋用量为TSP1的2倍,二者的破坏荷载相当,即横向钢筋的贡献有上限;TSP4纵筋锚固长度比TSP1长270 mm,破坏荷载增加了21.0%,表明增大纵筋锚固长度可提高门槽受剪承载力;门槽组SP2颈部宽度较门槽组SP3增大400 mm,其破坏荷载明显提高,表明受剪承载力随下游闸墩颈部宽度的增大而增大;对比门槽组SP4和门槽组SP2及门槽组SP3,一期混凝土抗拉强度越高,门槽受剪承载力越高。
3 承载力计算
3.1 受力分析
沿图8中破坏面取下游墩墙为脱离体,其受力见图9,其中Vc为即将破坏时余留混凝土(图9中虚线)承担的拉力,Va为斜向裂缝面两侧混凝土的骨料咬合力,Vd为横向钢筋的销栓力,T1和T2分别为纵向钢筋和横向钢筋的拉力。纵向钢筋承受的拉力T1较小且不可靠,将其并入Vd,可列出水流方向平衡方程为
Vu=Vc+Vasin θ+Vd。
(1)
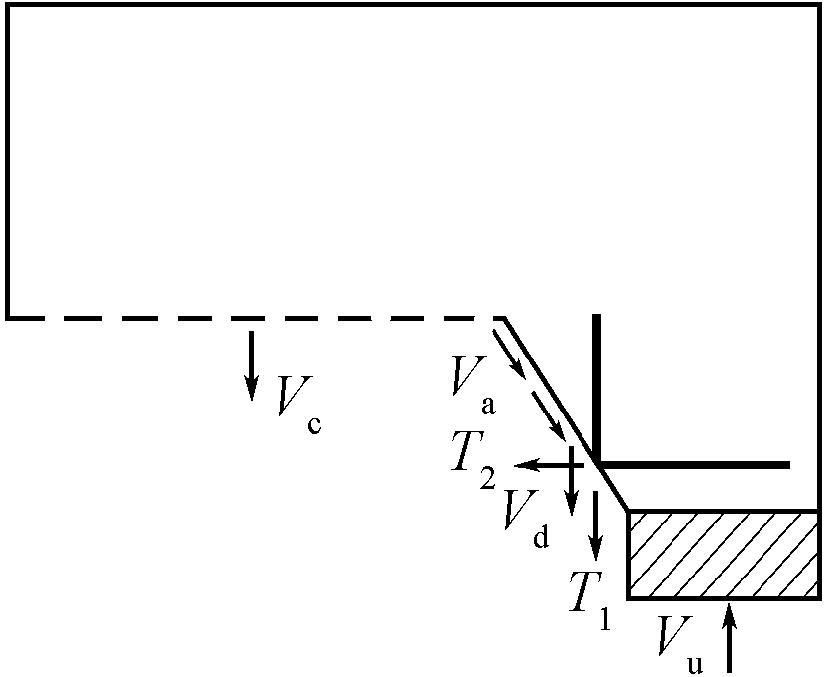
图9 破坏截面受力分析
Figure 9 Forces on failure section
令Vc=αftbl1、Vasin θ=βftbl2sin θ=βftbl0、Vd=γfyAs,并注意到l1=b2-l0cot θ,式(1)可写为
Vu=αftb(b2-l0cot θ)+βftdl0+γfyAs。
(2)
式中:Vu为门槽结构的受剪承载力,N;ft为一期混凝土抗拉强度,MPa;fy为横向钢筋屈服强度,MPa;As为横向钢筋截面面积,mm2;b为平面门槽结构的厚度,mm;α、β和γ均为系数;b2、l0和θ含义如图8所示。
3.2 计算公式
若由各门槽试验实测数据拟合出l0和θ的计算公式,进而由表2所列Vu回归得到式(2)中的α、β和γ,即可得到门槽受剪承载力计算公式。整理实测数据发现,l0与k为线性关系,θ与各参数均函数关系不明显,无法拟合其计算公式。但由材料力学可知,闸墩颈部宽度b2影响下游墩墙内正应力大小,下游墩墙长度h1影响剪应力大小,二者共同影响拉主应力方向,故θ与b2和h1有关。
由3.1节已知,门槽受剪承载力来自余留截面混凝土、斜裂缝及钢筋,借鉴中国混凝土结构设计规范中梁、柱等构件的斜截面受剪承载力计算公式,本文认为门槽受剪承载力可表达为混凝土项和钢筋项之和。混凝土可承受的剪力主要与一期混凝土抗拉强度ft、平面门槽结构厚度b、闸墩颈部宽度b2和下游墩墙长度h1有关,钢筋可承受的剪力主要来源于横向钢筋的销栓力,与横向钢筋的强度fy及截面面积As有关。
考虑到计算公式简便,将以上承载力影响参数转化为无量纲形式![]() 和
和![]() 其中,b0为闸墩颈部有效宽度,b0=b2-as1,as1为颈部最外层纵向钢筋合力点至闸墩边缘的距离。用两个无量纲值表达的试验数据绘于图10,可见试验结果较为离散,其线性拟合公式如式(3)所示。参照我国混凝土结构设计规范受剪承载力计算公式的做法,偏实测点下限拟合受剪承载力计算公式并取整,得到门槽受剪承载力计算公式如式(4)所示。
其中,b0为闸墩颈部有效宽度,b0=b2-as1,as1为颈部最外层纵向钢筋合力点至闸墩边缘的距离。用两个无量纲值表达的试验数据绘于图10,可见试验结果较为离散,其线性拟合公式如式(3)所示。参照我国混凝土结构设计规范受剪承载力计算公式的做法,偏实测点下限拟合受剪承载力计算公式并取整,得到门槽受剪承载力计算公式如式(4)所示。
Vu=0.183ftb(b0+h1)+0.396fyAs;
(3)
Vu=0.125ftb(b0+h1)+0.35fyAs。
(4)

图10 受剪承载力公式拟合
Figure 10 Fitting of shearing capacity formulation
式中,Vu为门槽结构的受剪承载力,N;ft为一期混凝土抗拉强度,MPa;b为计算高度,可取1 000 mm;b0为闸墩颈部有效宽度,mm;h1为下游墩墙长度,mm;fy为横向钢筋屈服强度,MPa;As为横向钢筋截面面积,mm2。结构设计时,为保证可靠度,材料强度应采用设计值。
如第2节所述,边墩门槽发生受剪破坏时,横向钢筋没有屈服,可认为横向钢筋的主要作用为限制斜裂缝开展,提高混凝土骨料咬合力。根据试验结果,该作用是有限的,横向钢筋承担的剪力不超过混凝土承担的剪力,即0.35fyAs的计算取值不应超过0.125ftb(b0+h1)。代入式(4)并考虑可靠度,可得门槽结构尺寸和混凝土强度的下限为
V≤[0.25ftb(b0+h1)]/γd。
(5)
式中:V为门槽承受剪力的设计值;γd为结构系数,对钢筋混凝土结构,取1.20;其余符号意义同前。
需说明的是,门槽结构为三维受力结构,其受剪面(图11中阴影面)所受剪力及脱离体上、下断面剪力共同与闸门推力平衡。将门槽视为二维结构,忽略了上、下断面的剪力,认为闸门推力全由门槽受剪面承担,使设计结果偏于保守。若按二维问题计算受剪承载力不足,可通过有限元分析确定门槽受剪面上的剪应力,对其积分得到门槽结构实际承受的剪力V,再复核门槽受剪承载力。
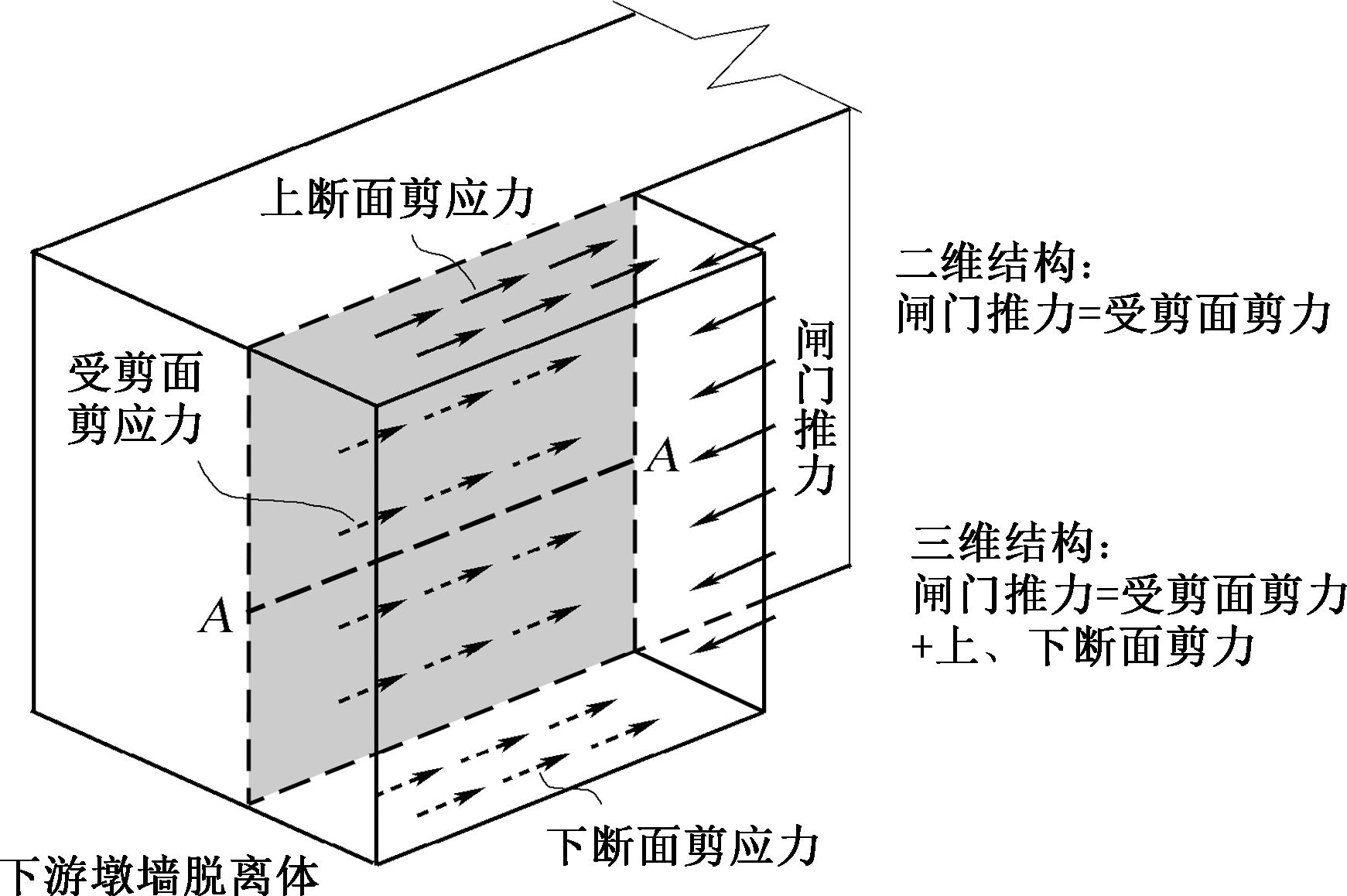
图11 门槽受剪空间效应
Figure 11 Spatial effect of shearing of gate slots
4 工程实例应用
里底水电站为澜沧江上游河段梯级开发规划的第三级电站,拦河重力坝最大坝高74.0 m,左岸布置两孔溢洪道,右岸布置三孔泄洪底孔,河床布置3台轴流式水轮发电机组,电站装机容量420 MW。
进水口建筑物级别为2级,事故门孔口尺寸为5.30 m×15.80 m。每米高度单侧闸门推力设计值为V=1 576.0 kN。如图12所示(尺寸单位为cm),中墩宽2.50 m,门槽深度0.60 m,颈部宽度为1.30 m,门槽下游墩墙长h1=10.25 m。一期混凝土抗拉强度设计值 ft=1.27 N/mm2;门槽横向钢筋为双层Φ28@200(6 158 mm2/m,fy=360 N/mm2)。
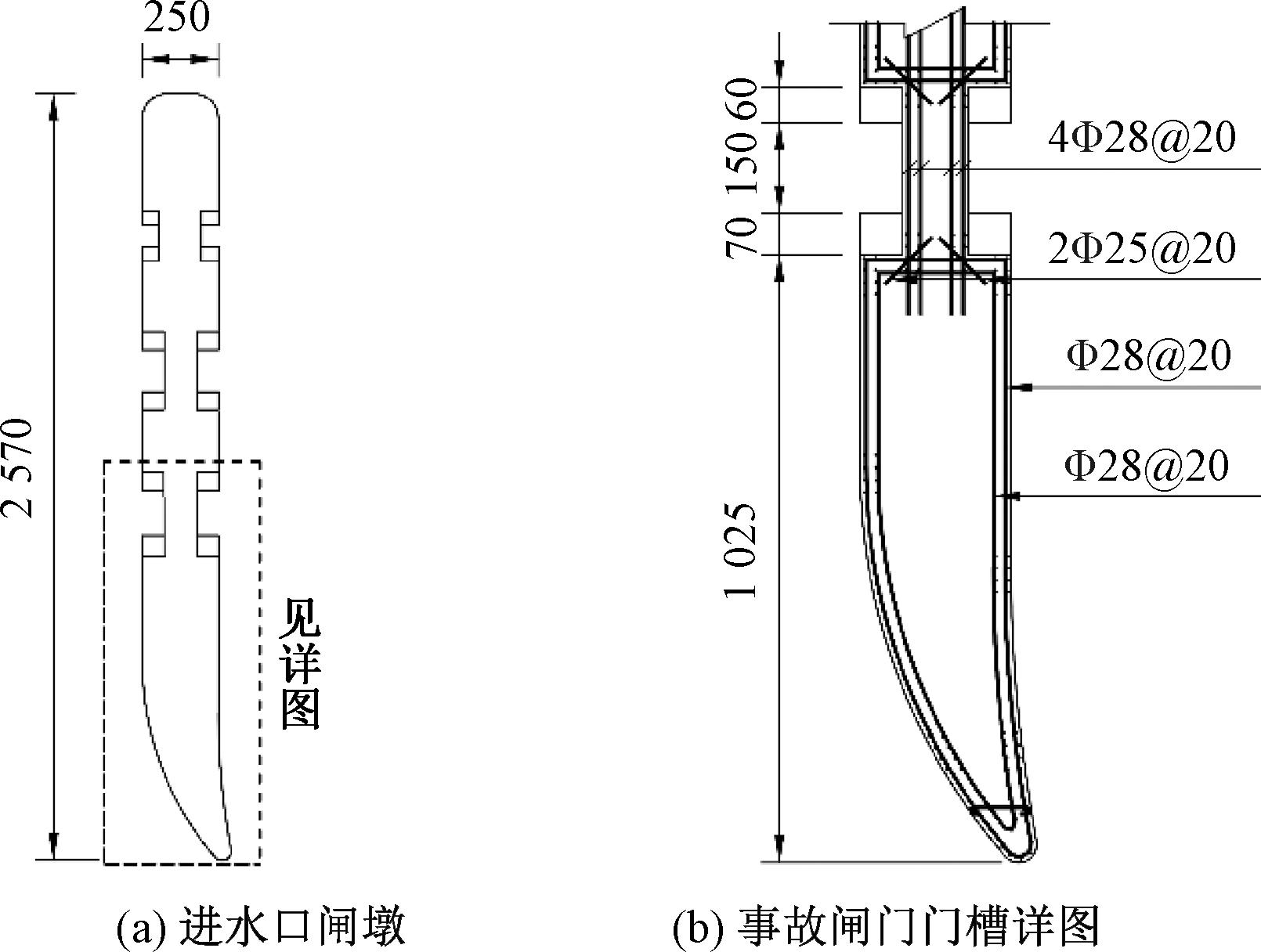
图12 里底水电站事故闸门门槽
Figure 12 Emergency gate slot of Lidi hydropower station
门槽结构的结构安全级别为Ⅱ级,重要性系数γ0=1.0;持久状况,设计状况系数ψ=1.0。
单侧闸门挡水时,可将中墩门槽视为侧边自由的边墩门槽,可按本文式(4)计算受剪承载力,此时,颈部有效宽度为b0=b2-as1=1 235 mm。
由式(5)可得V<[0.25ftb(b0+h1)]/γd=3 039 kN。截面尺寸和混凝土强度满足要求。
由式(4)可得门槽结构受剪承载力为Vu=0.125ftb(b0+h1)+0.35fyAs=2 599 kN。因而有V<Vu/γd。门槽结构受剪承载力满足要求。
建立此闸墩的有限元模型,采用ABAQUS软件进行非线性分析。钢筋本构采用弹塑性模型,混凝土采用塑性损伤本构模型,弹性阶段极限应力取0.4倍混凝土轴心抗压强度。混凝土与钢筋强度均取标准值。混凝土材料单轴应力应变关系按NB/T 11011—2022《水工混凝土结构设计规范》[2]的规定确定,模型其他相关参数按ABAQUS推荐或工程习惯取值为:膨胀角(dilation angle)ψ=30°,流动势偏心率(eccentricity)ε=0.1,双轴与单轴抗压强度比值σb0/σc0=1.16,偏平面受拉与受压等效应力比值K=2/3,黏性系数(viscosity parameter)μ=0.000 5。
里底水电站事故闸门门槽计算结果见图13(为节省篇幅,仅绘出了事故闸门门槽及下游墩墙)。计算结果表明,闸门推力作用下,裂缝始发于门槽角点,倾斜向下游墩墙内侧延伸,当余留混凝土不足以承担闸门推力时,结构破坏,计算发散不能收敛,此时拉损伤分布与图8中红色实线一致。
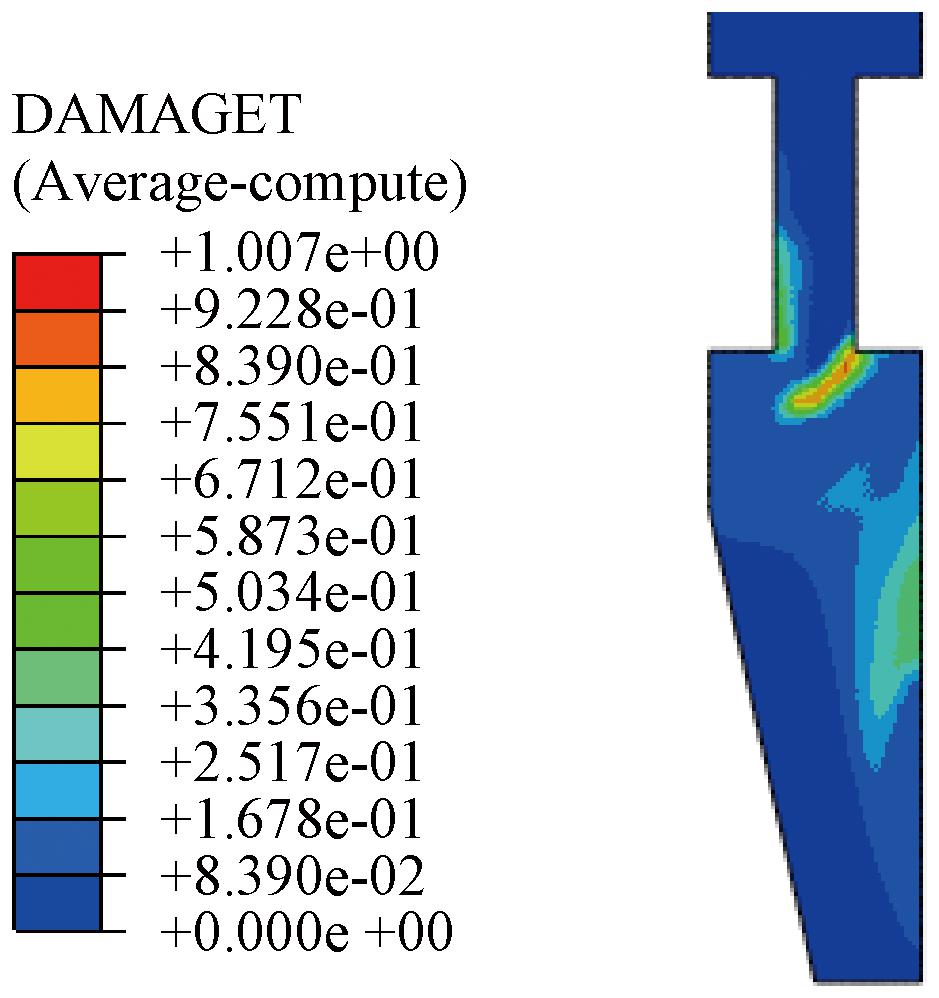
图13 非线性计算里底门槽破坏模式
Figure 13 Nonlinear numerical failure of Lidi gate slot
计算得到门槽可承受的极限闸门推力标准值为2 127 kN/m,按规范规定的γd、γ0、γc和ψ等分项系数换算得设计值为Vu=3 674 kN/m;由式(3)得Vu=3 556 kN/m;由式(4)得Vu=2 599 kN/m。可见,非线性分析结果处于试验数据点分布范围之内,与式(3)结果相差3.32%,可认为相互吻合良好;按式(4)设计结果较式(3)结果偏低26.91%,大幅提高了门槽结构受剪的可靠度,与规范为脆性破坏结构设置较高的目标可靠指标的做法一致。
5 结论
本文以拉西瓦水电站进水口事故闸门门槽为原型,分两个批次共进行了14个门槽结构的受剪承载力试验,提出了侧边和末端自由最下游门槽的受剪承载力计算公式。本文主要成果和结论如下。
(1)各门槽结构受剪破坏过程和破坏形态一致:闸门推力作用下,裂缝首先出现于一期混凝土角部附近。随荷载增大,裂缝缓慢向颈部横向延伸,同时也倾斜向下游墩墙内部延伸。当斜裂缝的尖端与纵向钢筋末端大致平齐时,余留截面混凝土不足以承担闸门推力,门槽结构发生受剪破坏。最终破坏面由倾斜裂缝和横向余留截面构成。
(2)破坏面附近横向钢筋均不屈服,门槽结构受剪破坏为脆性破坏。
(3)门槽受剪承载力可表达为混凝土的贡献和横向钢筋贡献之和,与一期混凝土抗拉强度、闸墩颈部宽度、下游墩墙长度正相关,横向钢筋用量对门槽受剪承载力也有提高作用,但提高幅度有上限,不超过混凝土可承担的剪力。
(4)由试验结果,参考混凝土结构设计规范斜截面受剪承载力计算公式的形式,按试验数据下限并取整,拟合了门槽结构受剪承载力计算公式,并给出了门槽结构尺寸和混凝土强度的下限要求。
(5)中墩门槽仅一侧承受闸门推力时,适用本文计算公式。实际工程验证了本文公式的适用性和合理性。
[1] 李子青, 李子春. 条形荷载下高强度混凝土局部承压试验研究[J]. 西安公路交通大学学报, 1998(3): 29-33.
LI Z Q, LI Z C. The local bearing strength of the high-strength concrete under the stripe load[J]. Journal of Xi’an Highway University, 1998(3): 29-33.
[2] 国家能源局. 水工混凝土结构设计规范: NB/T 11011—2022[S]. 北京: 中国水利水电出版社, 2023.
National Energy Administration. Code for design of hydraulic concrete structures: NB/T 11011—2022[S]. Beijing: China Water &Power Press, 2023.
[3] 中华人民共和国国家能源局. 水工混凝土结构设计规范: DL/T 5057—2009[S]. 北京: 中国电力出版社, 2009.
National Energy Administration of the People′s Republic of China. Design specification for hydraulic concrete structures: DL/T 5057—2009[S]. Beijing: China Electric Power Press, 2009.
[4] 中华人民共和国水利部. 水工混凝土结构设计规范: SL 191—2008[S]. 北京: 中国水利水电出版社, 2009.
Ministry of Water Resources of the People′s Republic of China. Design code for hydraulic concrete structures: SL 191—2008[S]. Beijing: China Water &Power Press, 2009.
[5] 张涛, 喻君, 汪基伟. 检修闸门门槽承载力性能及破坏模式[J]. 水利水电科技进展, 2019, 39(6): 88-94.
ZHANG T, YU J, WANG J W. Bearing capacity performance and failure modes of a maintenance gate slot[J]. Advances in Science and Technology of Water Resources, 2019, 39(6): 88-94.
[6] 喻君, 陈祖鹏, 张涛, 等. 检修闸门门槽受剪承载力研究[J]. 土木工程学报, 2023, 56(5): 134-148.
YU J, CHEN Z P, ZHANG T, et al. Study on ultimate shear capacity of overhaul gate slots[J]. China Civil Engineering Journal, 2023, 56(5): 134-148.
[7] 杨静安, 杨鑫平, 杜永. 导流洞平面闸门门槽结构计算分析[J]. 西北水电, 2015(6): 49-53.
YANG J A, YANG X P, DU Y. Calculation an analysis of slot structure of plane gate for diversion tunnel[J]. Northwest Hydropower, 2015(6): 49-53.
[8] 吴松锋. 闸门门槽受剪切性能试验研究[D]. 郑州: 郑州大学, 2009.
WU S F. Experimental study on the performance of the shear capacity of gate slot[D]. Zhengzhou: Zhengzhou University, 2009.
[9] HAN J H, WU S F, LIU W L. Experimental study on the shear failurelaw of gate slot[J]. Advanced Materials Research, 2010(163/164/165/166/167): 1891-1894.
[10] 王建, 彭泽豹, 张鹏, 等. 基于混凝土损伤塑性模型的闸门槽抗剪稳定研究[J]. 人民长江, 2018, 49(9): 67-70, 90.
WANG J, PENG Z B, ZHANG P, et al. Study on shear stability of sluice gate slot based on concrete damage plasticity model[J]. Yangtze River, 2018, 49(9): 67-70, 90.
[11] 孙斌, 彭睿哲, 贺智安. 某导流洞闸室门槽结构截面承载力分析[J]. 西北水电, 2015(5): 36-38.
SUN B, PENG R Z, HE Z A. Analysis on bearing capacity of slot structural section of gate chamber of diversion tunnel[J]. Northwest Hydropower, 2015(5): 36-38.
[12] 蔡睿恒, 喻君, 汪基伟. 门槽结构受剪破坏界限条件试验研究[J]. 河海大学学报(自然科学版), 2019, 47(2): 144-150.
CAI R H, YU J, WANG J W. Experimental study on the limit conditions of shear failure of gate slot[J]. Journal of Hohai University (Natural Sciences), 2019, 47(2): 144-150.