与传统的地面通信网络和卫星通信网络相比,无人机(unmanned aerial vehicle,UAV)辅助通信网络具有成本低、部署能力强、可控性高等优点。UAV辅助通信是6 G移动通信网络中不可或缺的潜在技术之一[1-2]。在UAV中继通信系统设计中,除飞行控制方面的能耗外,UAV作为中继还会额外增加信号传输和数据处理方面的能耗,这对UAV的续航时间提出了挑战[3]。同时,由于UAV机载能量有限且在恶劣的天气条件等复杂无线环境因素下UAV通信的可靠性难以保证,使得UAV在执行长期通信、复杂计算任务等方面具有挑战性[4]。虽然UAV中继通信系统面临上述挑战,但有望通过使用可重构智能表面(reconfigurable intelligent surface,RIS)技术来应对,从而进一步促进6 G网络的发展。
将RIS集成到UAV(RIS-UAV)作为中继,可以改善信号传播环境、增强信号强度,并且UAV的高机动性为RIS部署带来了灵活性[5]。与传统的UAV中继通信系统相比,RIS-UAV中继通信系统具有更低的功耗和更高的频谱效率。Long等[6]研究了RIS-UAV作为中继辅助上行无线通信系统的能效最大化问题,仿真表明,与无RIS的传统方案相比,所提设计可提高38%的能效。
目前,对于RIS-UAV中继通信系统的联合主被动波束赋形优化问题的研究主要分为两类:一类是基于深度学习,另一类是基于传统优化算法。基于深度学习算法的联合主被动波束赋形相关研究主要有Peng等[7]提出了一种RIS-UAV辅助系统的能量收集方案,该方案通过在几何空间上分割RIS无源反射阵列,并采用基于深度强化学习的鲁棒算法实现信息传输和能量收集的同步操作。Sun等[8]研究了RIS-UAV辅助车载通信系统,在无人机预测车辆位置的情况下,利用深度强化学习算法进行UAV轨迹和RIS被动波束赋形的联合优化,以最大化系统通信速率。基于深度学习的优化算法虽然在固定场景下表现出色,但对UAV的内存和功耗施加了额外限制。此外,由于训练复杂度高,这类算法也难以在实际应用中灵活适应各种变化。基于传统优化算法的联合主被动波束赋形相关研究主要有Cui等[9]研究了RIS辅助的安全无线通信系统,提出了一种基于交替优化和半定松弛方法(semidefinite relaxation,SDR)来联合优化主被动波束赋形,旨在最大限度地提高合法通信链路的保密率,当RIS单元个数较多时,SDR算法复杂度也较高。Elmossallamy等[10]采用流形优化算法优化RIS被动波束赋形,使恒模约束下的总干扰最小,所提算法与广泛使用的处理恒模约束的SDR算法进行比较,结果表明流形优化方法大大优于SDR算法,该算法的复杂度主要取决于梯度计算,复杂度较高。Guo等[11]首先通过分式规划(fractional programming,FP)算法将问题化简,然后结合基于线性块坐标下降更新规则和连续凸近似(successive convex approximation,SCA)算法,联合优化主被动波束赋形,用以最大化系统WSR,将所提算法与流形优化算法进行比较,结果表明优化问题经FP算法化简后再使用SCA算法具有较低复杂度。Shang等[12]研究了UAV群支持的空中RIS辅助下行链路通信系统用户设备(user equipment,UE)加权和速率最大化问题,作者首先通过FP算法中的二次变换法(quadratic transform,QT)将问题化简进而推导出基站(base station,BS)主动波束赋形和RIS被动波束赋形闭式解。然而文献[11-12]在主被动波束赋形交替迭代中只对FP算法引入的辅助变量更新一次,使得优化被动波束赋形时辅助变量并未随主动波束赋形变量更新,导致收敛速度慢。本文设计了基于FP的流形优化的交替优化(alternating optimization,AO)双重循环算法,采用双重循环结构更新FP算法引入的辅助变量,简化了优化问题,降低求解梯度复杂度的同时提高了算法收敛速度。
1 系统模型及问题描述
本文构建了城市复杂通信场景下的RIS-UAV辅助窄带下行链路通信模型,如图1所示。系统中BS配备M根天线,UAV集成含有R个反射单元的RIS服务于K个单天线UE,假设K个单天线UE均匀分布在以c为半径的圆内,且UE与BS处于同一高度。考虑RIS-UAV有固定飞行高度H和飞行轨迹L,飞行轨迹L由BS端上方直线飞行到UE区域中心上方。
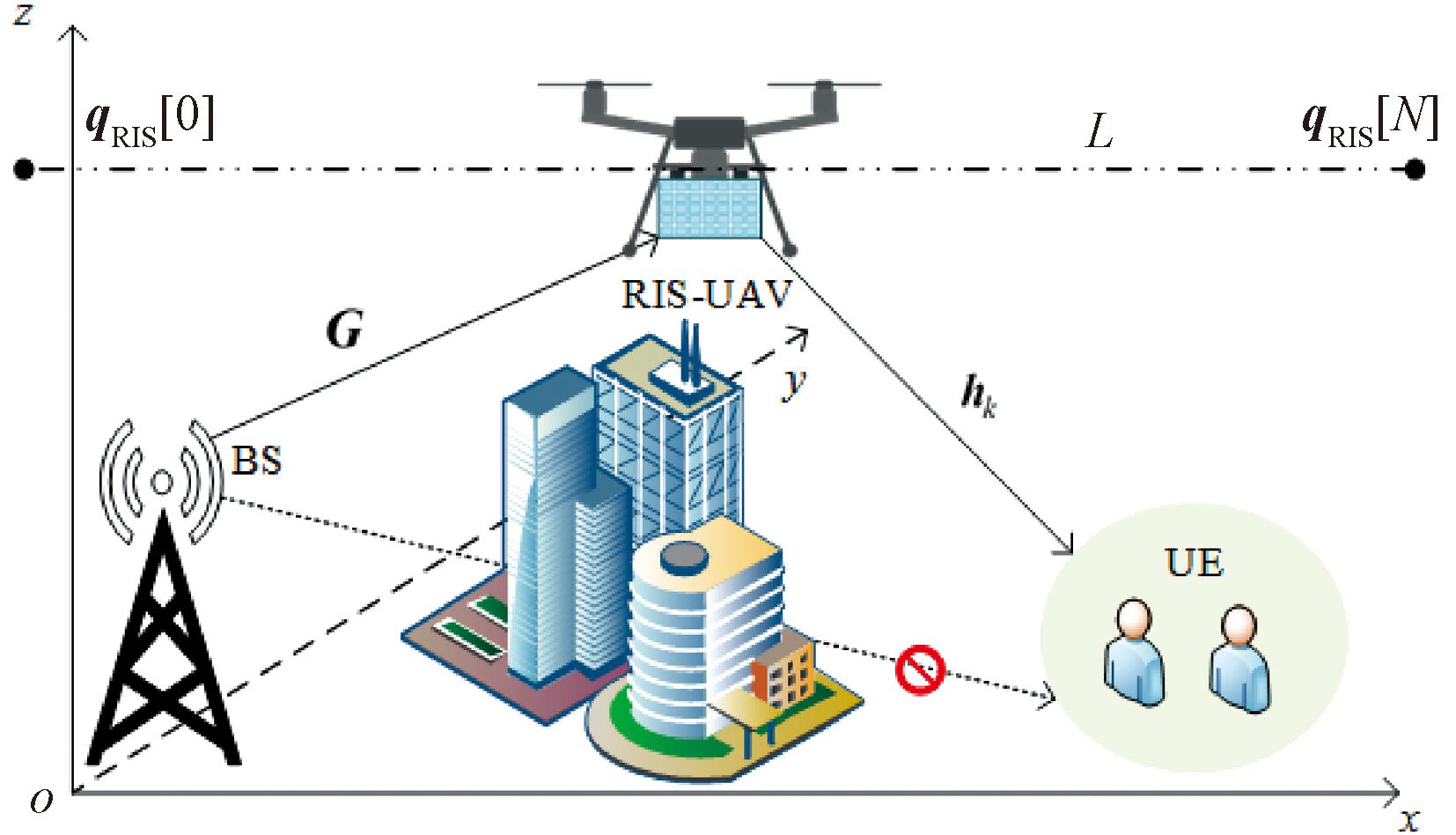
图1 RIS-UAV辅助多UE通信系统
Figure 1 RIS-UAV assisted multi-UE communication system
RIS-UAV以Vavg匀速飞行且飞行周期T被分为N个时隙,每个时隙长度为▽t。qRIS[n]=[xRIS[n],yRIS[n]]为RIS-UAV在第n时隙的水平坐标,n={0,1,…,N},因此RIS-UAV的轨迹应满足以下条件[13]:
(1)
(2)
式中:qRIS[0]和qRIS[N]分别表示RIS-UAV初始位置水平坐标与最终位置水平坐标;lUE=[xUE,yUE]为UE区域中心水平坐标,则第k个UE的水平坐标为lUE,k=[xUE,k,yUE,k],k={0,1,…,K};lBS=[xBS,yBS]为BS的水平坐标。
假设研究系统所涉及的信道状态信息(channel state information,CSI)在BS处是完全已知的,BS天线和RIS反射元件的排列采用均匀线性阵列,BS与RIS之间的链路(B-R链路)以及RIS与UE之间的链路(R-U链路)中含有视距分量。第n时隙,BS到RIS-UAV、RIS-UAV到第k个UE的基带等效信道分别表示为[14]
(3)
(4)
式中:
为第n时隙BS到RIS-UAV距离;
为第n时隙RIS-UAV到第k个UE距离;
和
表示非视距分量,其元素服从均值为0方差为1的循环对称复高斯分布[14];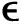
为单位距离信道功率增益;κ和τ分别为B-R和R-U链路的路径损耗指数;ε为莱斯衰落因子。
BS的发送阵列响应矢量和RIS的接收阵列响应矢量表示为[14]
(5)
(6)
式中:ω[n]=(xRIS[n]-xBS)/dBR[n]为第n时隙BS的离开角余弦值;ψ[n]=(xBS-xRIS[n])/dBR[n]为第n时隙RIS-UAV的到达角余弦值;d表示天线间距;Г表示载波波长。
RIS的发送阵列响应矢量表示为
(7)
式中:νk[n]=(xUE,k-xRIS[n])/dRU,k[n]为第n时隙RIS-UAV到第k个UE的离开角余弦值[14]。
第n时隙BS的复基带传输信号可以表示为
(8)
式中:sk[n]表示第n时隙第k个UE的传输数据;P[n]=[p1[n],…,pK[n]]表示第n时隙波束赋形矩阵;pk[n]∈CM×1表示第n时隙第k个UE的波束赋形向量,则第n时隙BS端总发射功率约束为
相移矩阵可表示为Φ[n]=diag{φ1[n],φ2[n],…,φR[n]}∈CR×R,φr[n]=ejθr[n],第r个RIS单元的相移可表示为θr[n]∈[0,2π),r={1,2,…,R}[15]。
第n时隙第k个UE的可达速率表示为
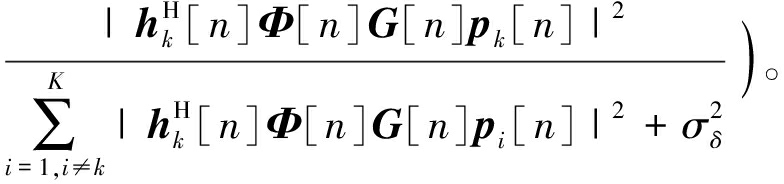
(9)
式中:
表示噪声功率。
本文以BS发射功率和RIS相移为约束,以RIS-UAV沿着轨迹L飞行时每时隙所有UE和速率最大化为优化目标,联合优化BS主动波束赋形和RIS被动波束赋形。由于构建的优化问题在每时隙具有相同数学表达形式,因此省略时隙n。每时隙所有UE的和速率最大化优化问题(10)构建如下。
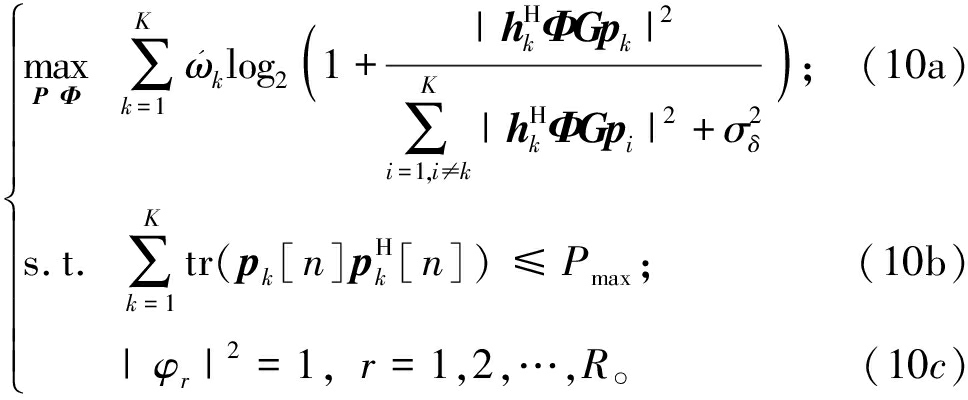
式中:
表示第k个用户的数据权重;约束(10b)表示BS发射功率约束;约束(10c)表示RIS相移约束。
2 优化问题转换及求解
在本节设计一种AO算法,将问题(10)分解为分别对BS主动波束赋形和RIS被动波束赋形进行优化的两个子问题。当给定Φ时,首先通过应用拉格朗日对偶变换法[16]将对数问题转换为FP问题,然后利用QT法[17]将FP问题转换为凸问题,最后采用拉格朗日乘子法对P进行优化;当给定P时,提出了一种基于FP的流形优化算法对Φ进行优化。所设计的AO算法采用内外双重循环结构,外循环交替优化关于P和Φ两个子问题,内循环解决每个子问题并更新辅助变量,迭代优化目标函数并逐步接近全局最优解。
2.1 BS主动波束赋形优化
当给定优化变量Φ时,问题(10)转化为
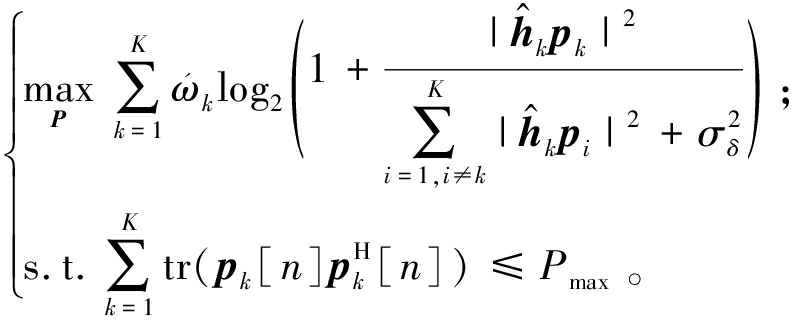
(11)
式中:
使用拉格朗日对偶变换法,同时引入辅助变量X=[X1,…,XK]T,问题(11)可以等价为[16]
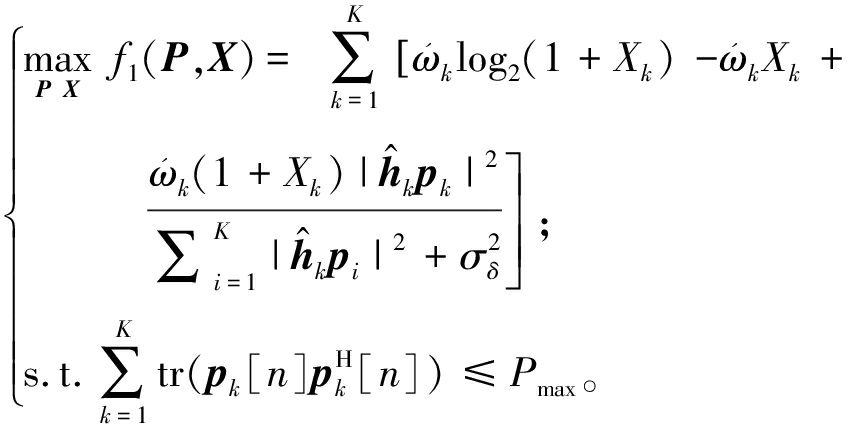
(12)
当给定优化变量P时,问题(12)关于Xk是可微的且在Xk≥0时函数有最大值。令∂f1/∂Xk=0,则最优的Xk可由下式更新得到
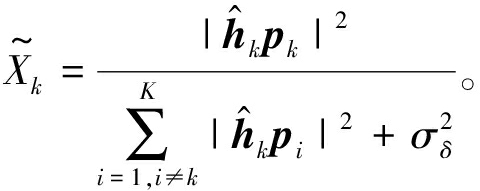
(13)
当给定X时,问题(12)可以表示为
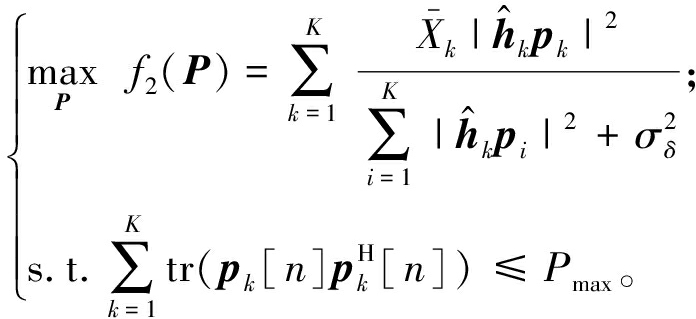
(14)
式中:
接着使用QT算法将问题(14)进一步转换。利用QT算法,同时引入辅助变量ρ=[ρ1,ρ2,…,ρK]T,问题(14)可以等价为[17]
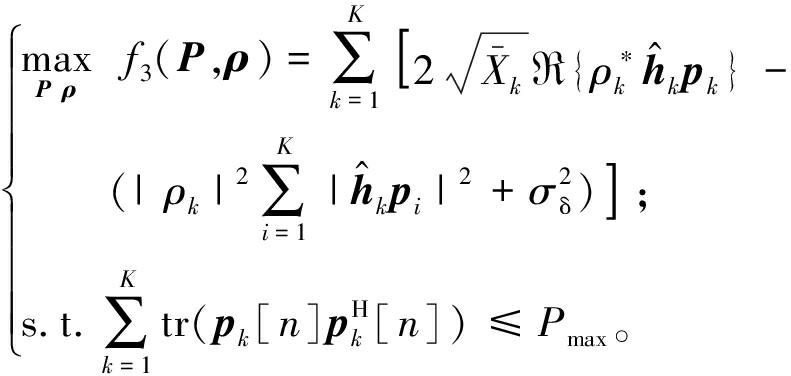
(15)
式中:
表示取
的实部。
对于问题(15),当给定P时,最优的ρk为
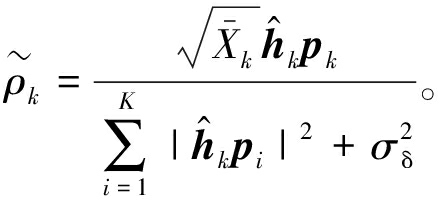
(16)
当给定ρ时,得到关于变量P的优化问题为
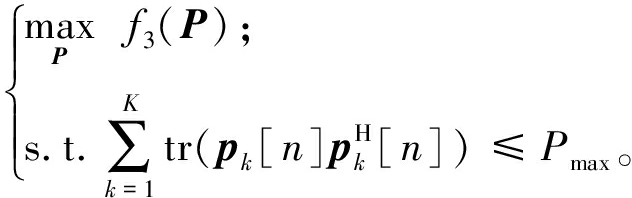
(17)
式中:目标函数f3(P)是关于pk的凹函数,约束(10b)所形成的可行域是一个凸集,问题(17)为凸优化问题,利用拉格朗日乘子法来求解问题(17),拉格朗日函数表示为
(18)
式中:λ≥0为功率约束(10b)的拉格朗日乘子。当给定拉格朗日乘子λ时,令∂F/∂pk=0,则最优的pk可由下式更新:
(19)
式中:IM代表M维单位矩阵;λ可由Prox线性更新规则[11]得到。
2.2 RIS被动波束赋形优化
优化完BS主动波束赋形变量P后,接着求解RIS被动波束赋形变量Φ。令φ=[φ1,φ2,…,φR]H,则BS到第k个UE的级联信道可以表示为
(20)
当给定优化变量P时,问题(10)转化为
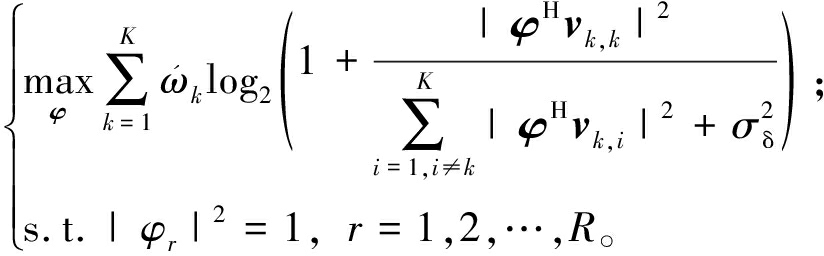
(21)
式中:
问题(21)为非凸优化问题,本文提出基于FP-流形优化算法来解决该问题。具体来说,首先通过拉格朗日对偶变换法,同时引入辅助变量o=[o1,o2,…,oK]T,将问题(21)进行等价转换,该过程与问题(11)的等价转换过程相似,等价问题可以表示为
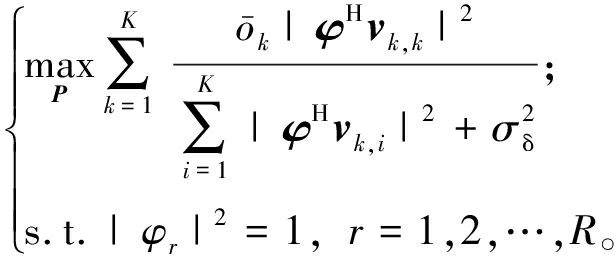
(22)
式中:
最优的ok可由式(3)更新得到:
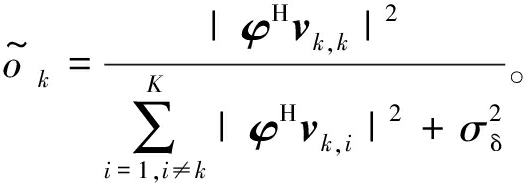
(23)
将问题(22)经过QT算法转换得到下式:
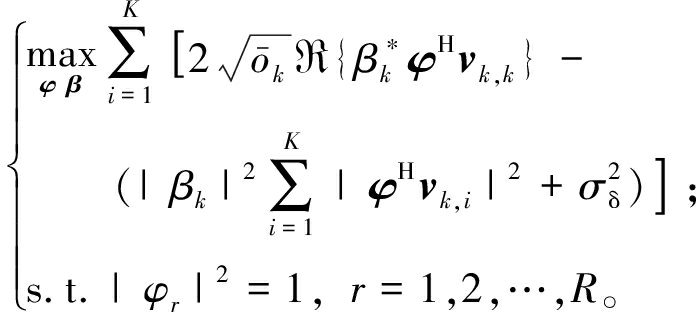
(24)
式中:β=[β1,β2,…,βK]T为QT法引入的辅助变量。
当给定φ时,最优的βk为
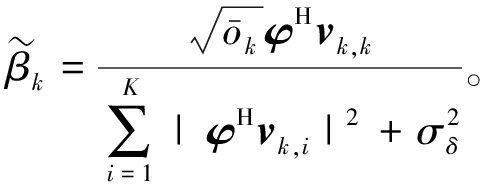
(25)
当给定β时,令
问题(24)可以表示为
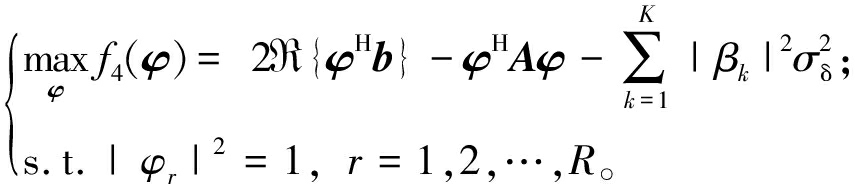
(26)
式中:R{φHb}表示取φHb的实部。
因为RIS相移约束(10c)是非凸约束,所以问题(26)仍为非凸优化问题。RIS相移约束可以在几何意义上解释为变量φ属于定义域CR的光滑黎曼流形上。每个优化变量φr都存在于一个由复圆S所给出的连续搜索空间中,
复圆S是光滑黎曼子流形,所以RIS被动波束赋形可行集为R个复圆S的笛卡尔积,这个乘积是CR的光滑黎曼流形,称为复圆流形[18]。
SR={φ∈CR:|φ1|2=…=|φR|2=1}。
(27)
因此RIS被动波束赋形的优化问题(26)可以表示为复圆流形SR表面上的无约束优化问题:
(28)
通过RCG算法能够获得f5(φ)的稳态解,下降方向取Polak-Ribiére共轭梯度方向[19]。下面给出在SR流形上某一点φm的第m+1次RCG迭代求解步骤[10]。
步骤1 计算黎曼梯度。黎曼梯度是欧几里得梯度▽f5(φm)在切空间C上的正交投影,点φm的切空间定义为包含在点φm处的所有切向量的空间:
(29)
式中:⊙为逐元素乘法;▽f5(φm)为欧几里得梯度,即
▽f5(φm)=Aφ-b。
(30)
步骤2 确定搜索方向dm。
(31)
式中:
为共轭梯度Polak-Ribiére的更新参数。
步骤3 确定步长μ,更新φ并回缩。采用著名的Armijo回溯线搜索算法选择步长μ,通过下式迭代更新φm+1直到目标函数(21)值收敛。
(32)
2.3 算法分析
本文设计的一种基于AO的联合主被动波束赋形优化算法如算法1所示。
算法1 基于AO的联合主被动波束赋形优化算法。
输入:
输出:P,Φ。
① 初始化P(0),Φ(0);
② 外循环:
③ 迭代计数t=0;
④ 由式(13)和(16)更新X(t)和ρ(t);
⑤ 由式(19)更新P(t+1);
⑥ 内循环:迭代计数m=0;
⑦ 由式(23)和(25)更新o(t)和β(t);
⑧ 由式(30)得到
⑨ 由式(31)得到黎曼梯度
⑩ 由式(32)更新
m=m+1;
直到问题(21)的函数值收敛;
更新
t=t+1;
直到问题(10)的函数值收敛;
得到P=P(t)、Φ=Φ(t)。
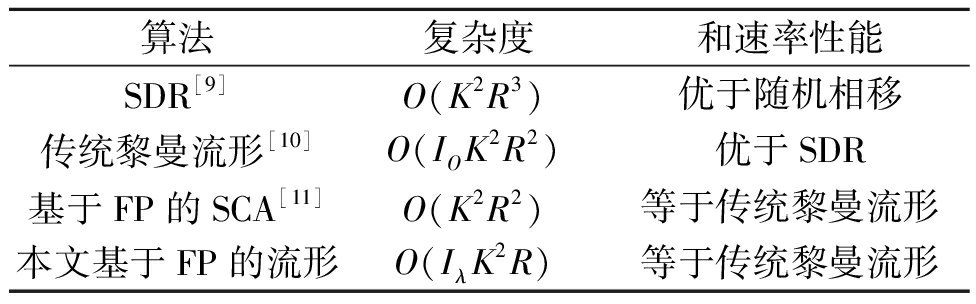
将算法1中的步骤③～替换为SDR算法[9]、传统黎曼流形优化算法[10]及基于FP的SCA算法[11]。下面将分析比较这4种算法的复杂度。在4种RIS被动波束赋形算法中,本文所提算法复杂度主要是计算f5(φ)的欧几里得梯度,因此复杂度为O(IλK2R);基于FP的SCA算法复杂度为O(K2R2)[11];传统黎曼流形优化算法复杂度主要是计算式(22)的欧几里得梯度,因此复杂度为O(IOK2R2);SDR算法复杂度为O(K2R3)[9]。其中搜索步长迭代次数Iλ和IO的数量级小于RIS单元数R的数量级。表1为所提RIS被动波束赋形算法与其他RIS被动波束赋形算法的比较结果。算法复杂度由低到高依次为:本文基于FP的流形、基于FP的SCA、传统黎曼流形、SDR算法。
表1 不同算法对比
Table 1 Comparison of different algorithms
算法复杂度和速率性能SDR[9]O(K2R3)优于随机相移传统黎曼流形[10]O(IOK2R2)优于SDR基于FP的SCA[11]O(K2R2)等于传统黎曼流形本文基于FP的流形O(IλK2R)等于传统黎曼流形
3 数值仿真及分析
3.1 模拟场景
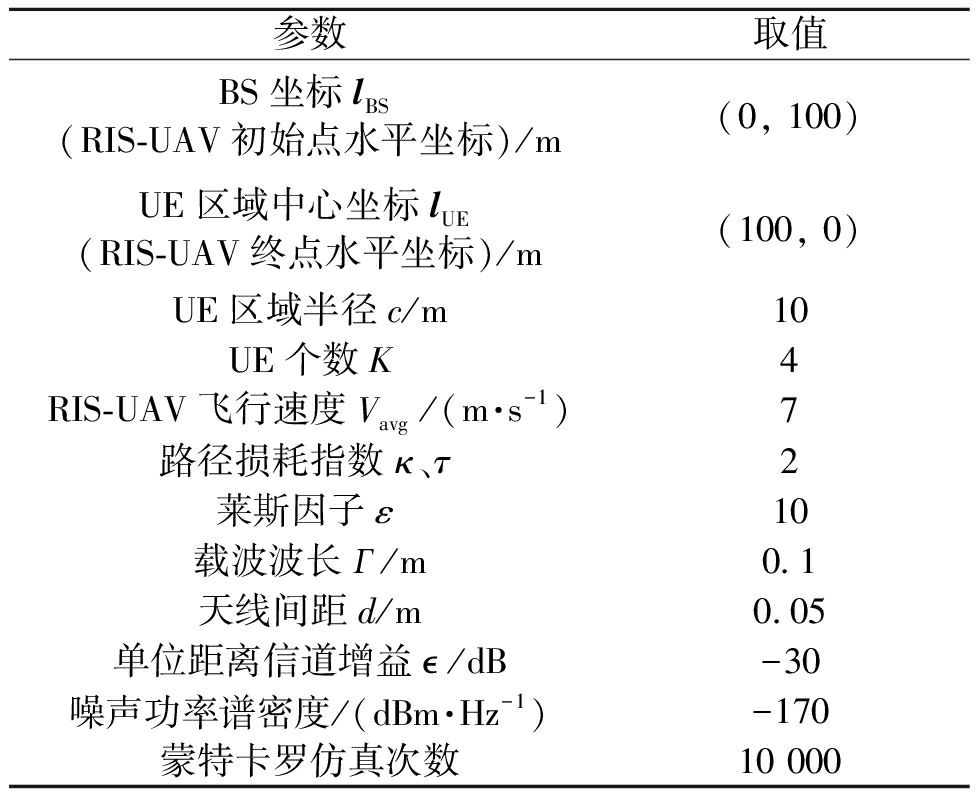
RIS-UAV辅助BS与多UE下行通信场景的笛卡尔坐标系如图2所示。UAV轨迹固定由(0, 100)沿着路径L直线飞往(100, 0)。本节通用的仿真参数如表2所示,在没有特别说明的情况下,其他仿真参数取值如下:RIS-UAV高度L=40 m、RIS单元数R=100、BS天线数M=20、BS最大发射功率Pmax=30 dBm,同时假设RIS-UAV位于初始点。
表2 仿真参数
Table 2 Simulation parameters
参数取值BS坐标lBS(RIS-UAV初始点水平坐标)/m(0, 100)UE区域中心坐标lUE(RIS-UAV终点水平坐标)/m(100, 0)UE区域半径c/m10UE个数K4RIS-UAV飞行速度Vavg/(m·s-1)7 路径损耗指数κ、τ2莱斯因子ε10载波波长Г/m0.1天线间距d/m0.05单位距离信道增益 /dB-30噪声功率谱密度/(dBm·Hz-1)-170蒙特卡罗仿真次数10 000
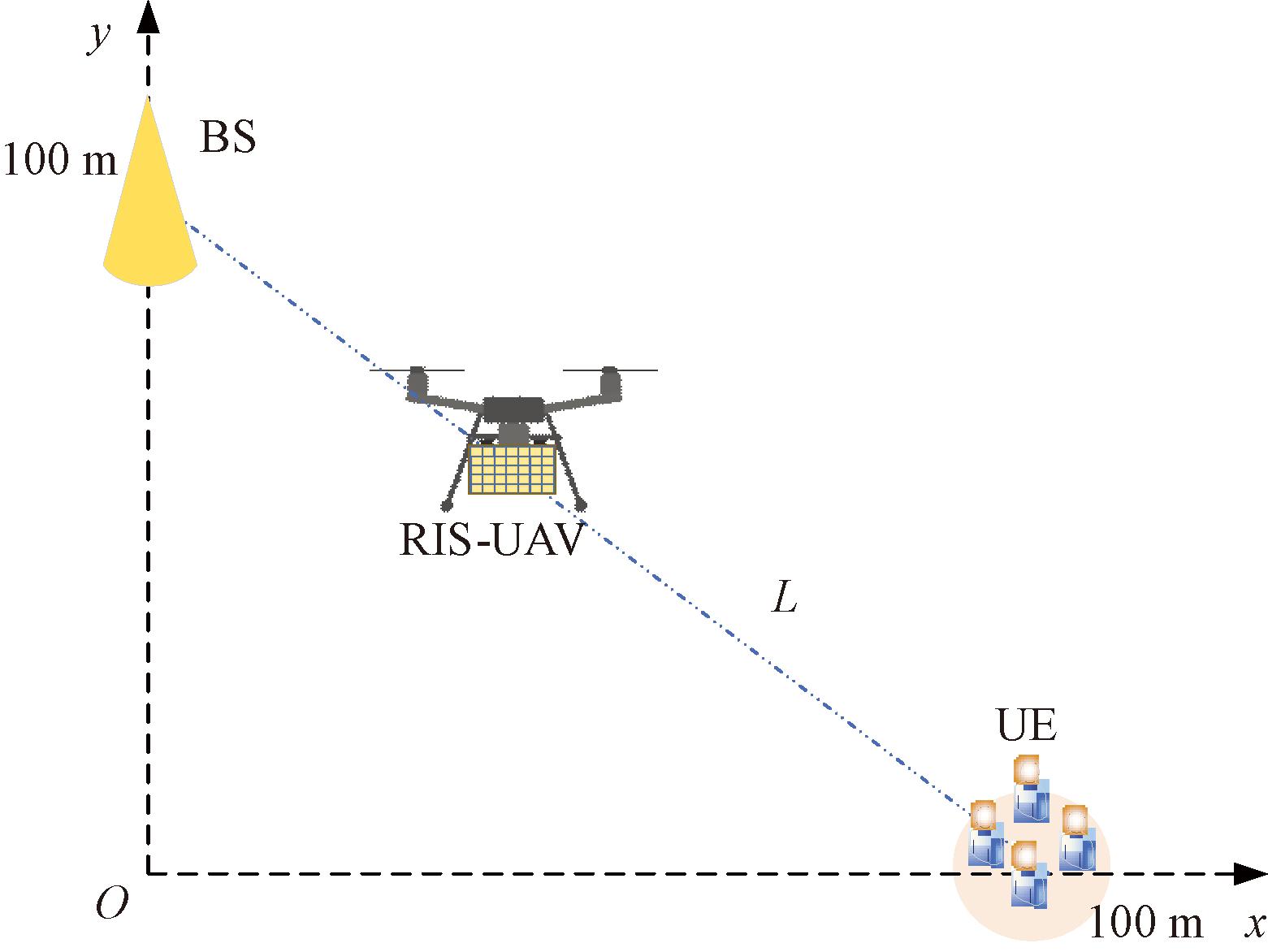
图2 RIS-UAV辅助BS与多UE下行通信模拟场景
Figure 2 Simulation scenario of RIS-UAV assisted BS and multi-UE downlink communication
图3为BS、UE坐标和UAV-RIS轨迹。RIS-UAV沿着定轨迹L从BS上方处初始点飞往UE区域上方处终点。根据RIS-UAV飞行轨迹L和飞行速度Vavg,飞行周期T被分为20个时隙,每个时隙长度为▽t=1 s,对应一个等效位置点,如图3中飞行轨迹L上20个时隙分别等效20个位置点。
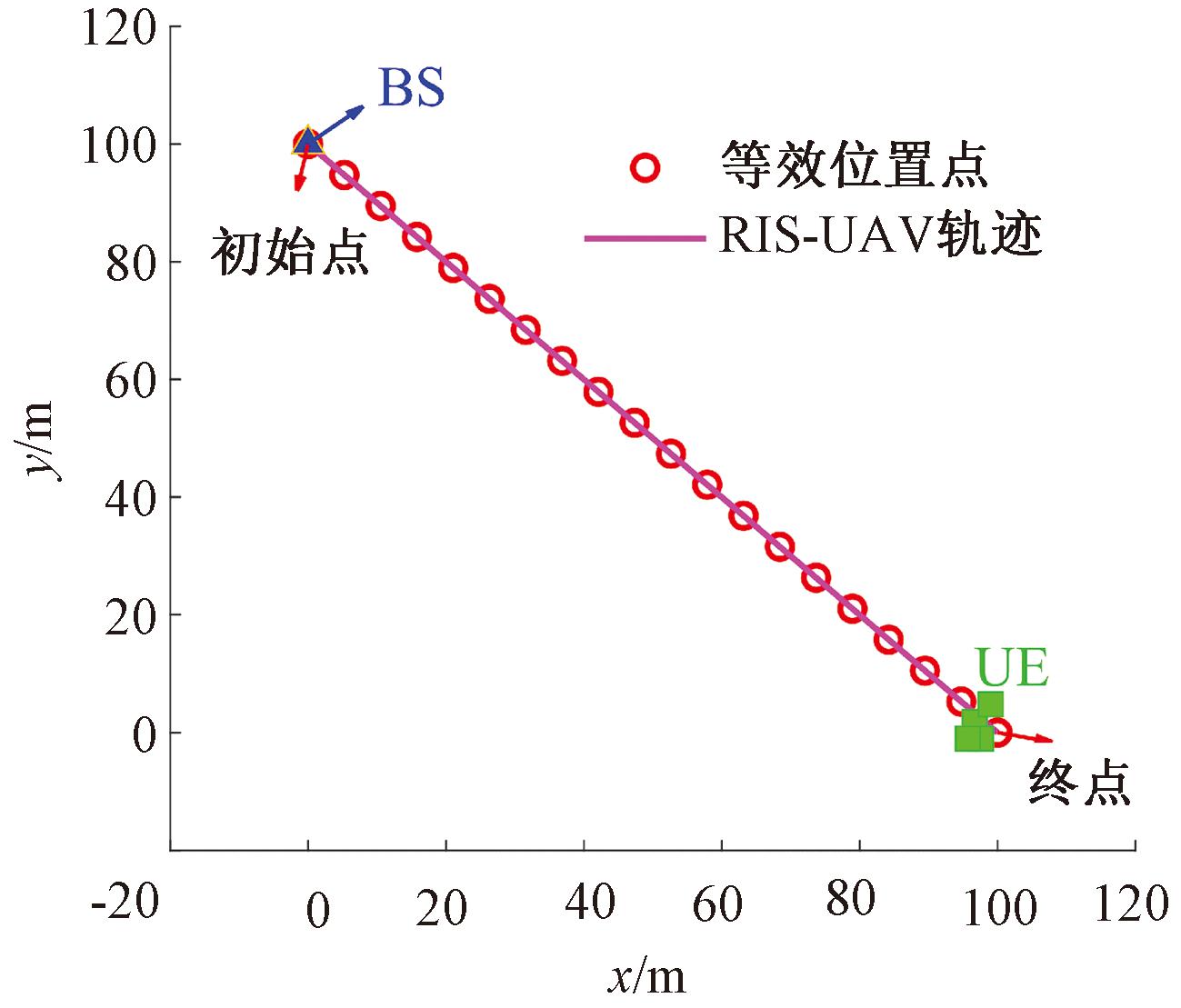
图3 BS、UE坐标和UAV-RIS轨迹
Figure 3 BS, UE coordinates and UAV-RIS trajectory
3.2 仿真结果分析
图4给出使用不同算法优化RIS被动波束赋形时系统和速率随着AO迭代次数变化的收敛情况。由图4可以看出,基于FP的SCA算法在迭代10次左右达到收敛,传统黎曼流形算法在迭代11次左右达到收敛,本文所提基于FP的流形优化算法在迭代11次左右达到收敛。3种优化算法收敛值近似且收敛次数相差不大,本文所提算法可以收敛到一个稳定值。
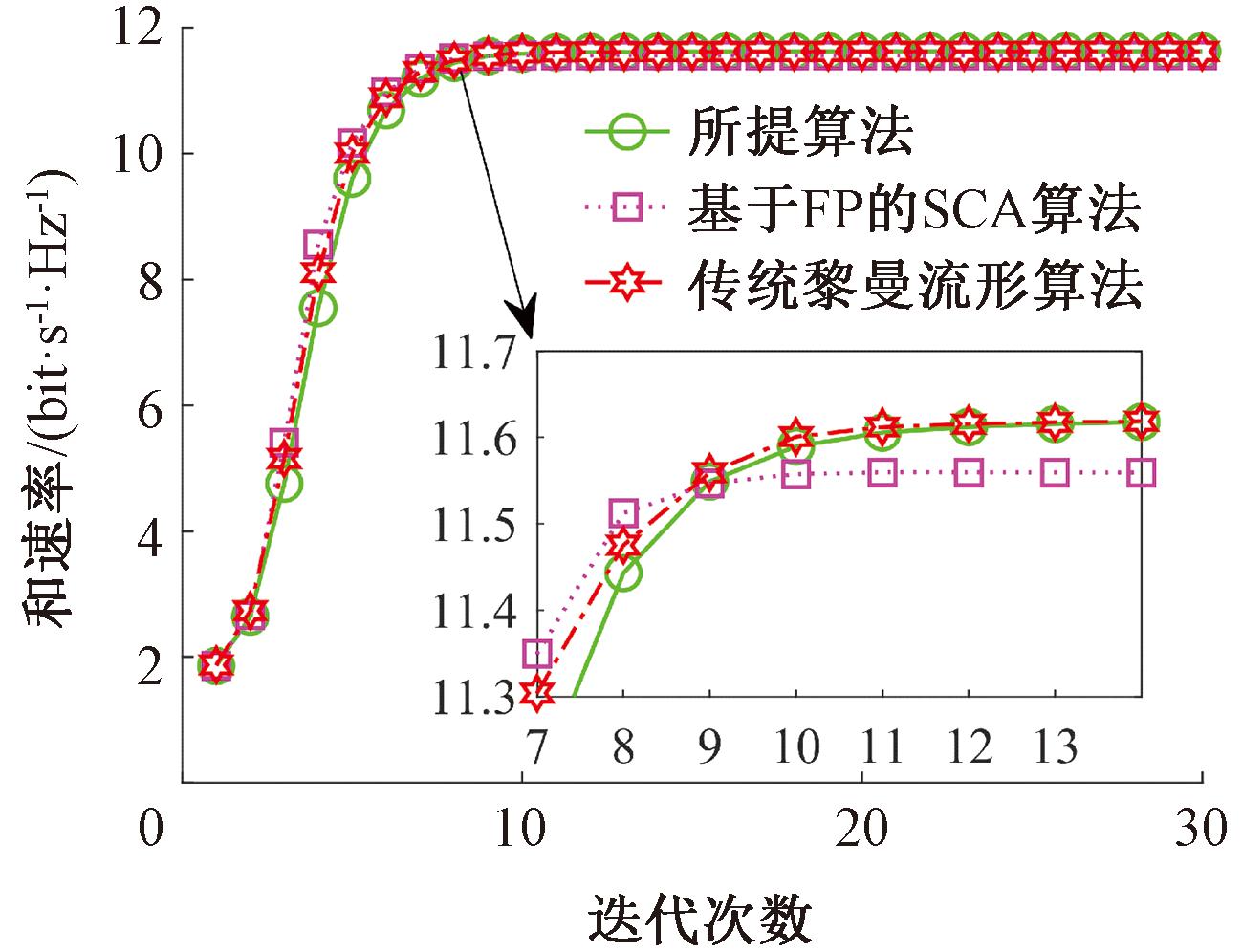
图4 不同算法的收敛情况
Figure 4 Convergence of different algorithm
图5给出了使用不同算法优化RIS被动波束赋形时30次AO迭代所需要的时间与RIS单元数R的关系。由图5可以看出,本文所提算法运算时间最少,所提算法复杂度分别低于传统黎曼流形算法复杂度和基于FP的SCA算法复杂度,与2.3节算法复杂度分析结论一致。
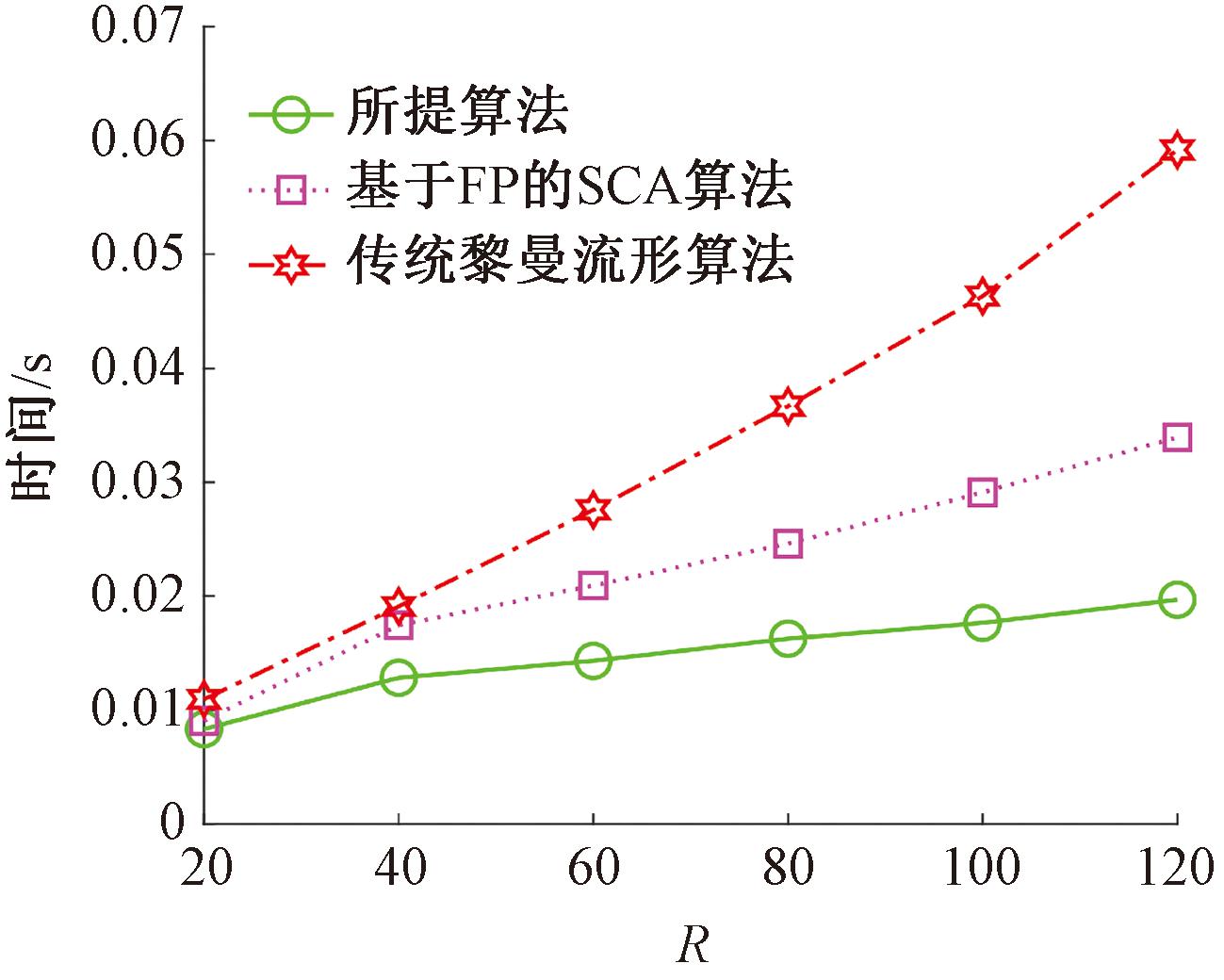
图5 不同算法30次迭代时间与R关系
Figure 5 Relationship between the time of 30 iterations of different algorithms and R
由于硬件限制,在实践中RIS实现连续相移具有挑战性,因此本文考虑RIS每个单元的相移采用有限数量的离散值。令bt代表相移电平D的比特数,其中D=2bt,bt=1代表RIS采用1 bit离散相移。假设这种离散相移值通过均匀量化区间[0,2π]获得,因此,每个RIS单元的离散相移值由Q={0,Δθ,…,(D-1)Δθ}给出,其中Δθ=2π/D[15]。图6给出了RIS采取不同相移情况时,BS最大发射功率Pmax与和速率的关系,同时与基于FP的SCA算法和随机相移方案做对比。从图6可以看出,本文所提算法和速率在RIS采用不同离散相移情况下均随BS最大发射功率增加而增大,并且与基于FP的SCA算法性能曲线基本重合。与随机相移对比,本文所提算法在RIS采用连续相移且Pmax=20 dBm时,和速率可以实现大约6 dB的增益。此外,随着离散相移比特数增加,和速率与连续相移时的差距逐渐减小且趋于零,当离散相移采用3 bit时即可达到与连续相移近似的性能。
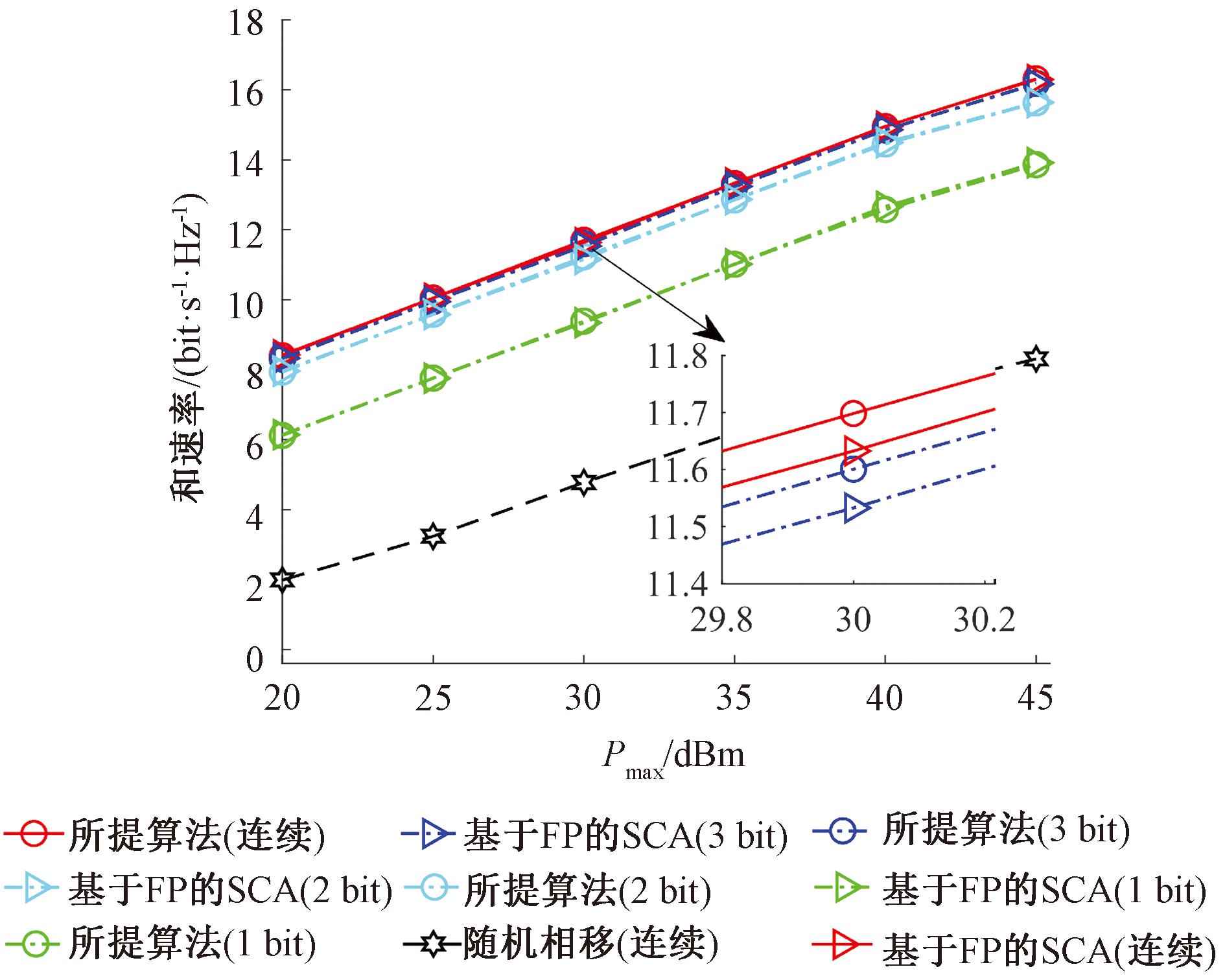
图6 不同相移下的和速率与Pmax关系
Figure 6 Relationship between sum_rate and Pmax with different phase shifts
图7给出了本文所提算法和基于FP的SCA算法在RIS采取不同相移情况时,RIS单元数R和BS天线数M与和速率之间的关系。当RIS单元数R从20增加到120以及BS天线数M从10增加到60时,所提算法在和速率方面均优于随机相移方法,并且与基于FP的SCA算法性能相当。由于BS发射功率有限,随着R和M的增加,和速率增长均趋于平缓。此外,从图7还可以看出,当RIS采用1 bit离散相移时和速率性能优于随机相移方法,当采用2 bit离散相移时和速率性能接近随机相移的性能。
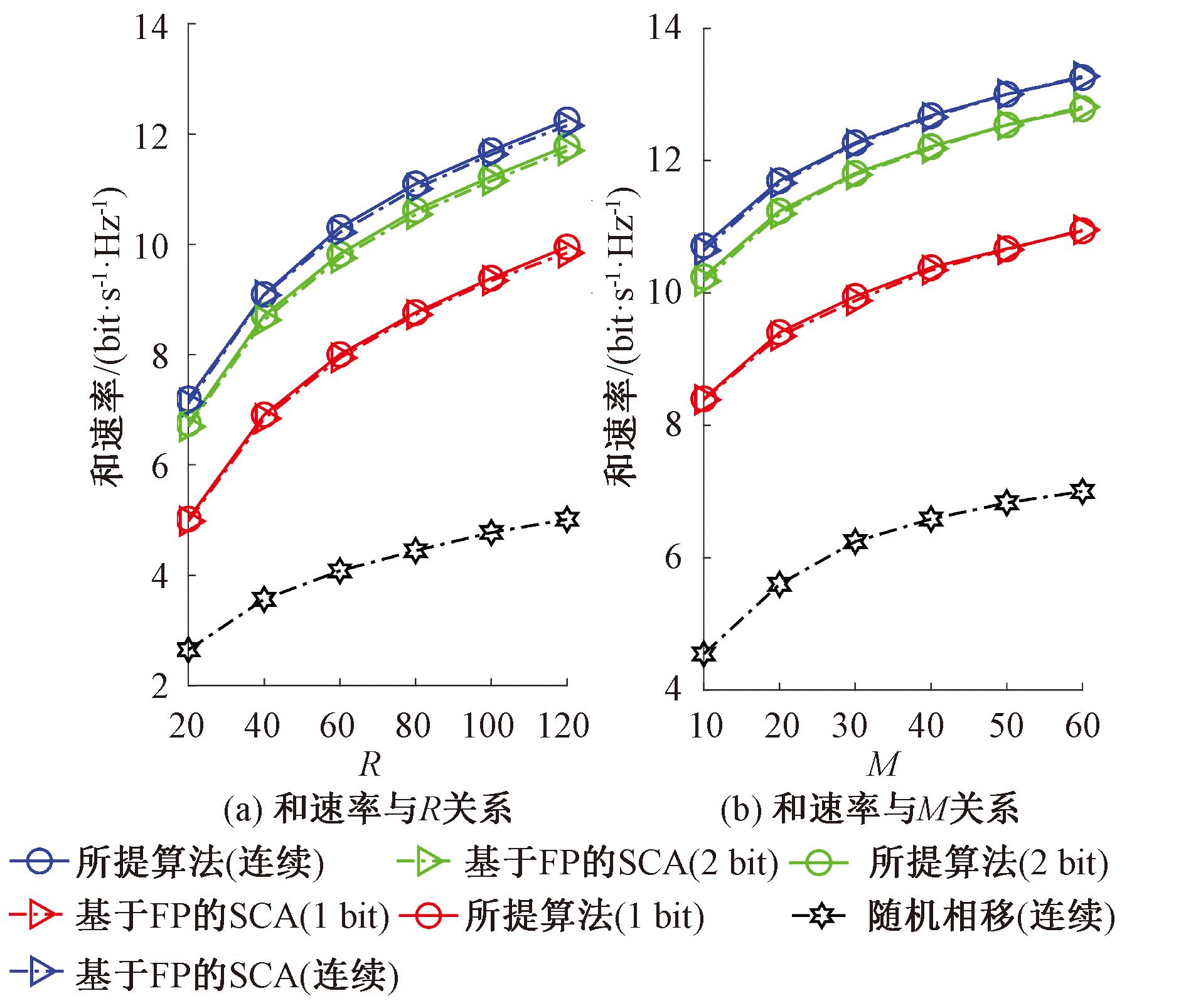
图7 不同相移下和速率与R(或M)关系
Figure 7 Relationships between sum rate and R (or M) with different phase shifts
图8给出了和速率与RIS-UAV位置之间的关系。从图8可以看出,随着RIS-UAV位置的改变,和速率的值也在改变,这种改变存在极值,当RIS-UAV飞行高度低于60 m时,和速率峰值靠近BS上方和UE端上方。当RIS-UAV飞行高度大约高于60 m时,和速率峰值在BS和UE两者中间。原因是RIS辅助通信形成了级联信道,路径损耗为两段信道路径损耗的乘积,和速率取最大时即RIS-UAV最佳位置与RIS-UAV高度和BS到UE之间的距离有关[20]。
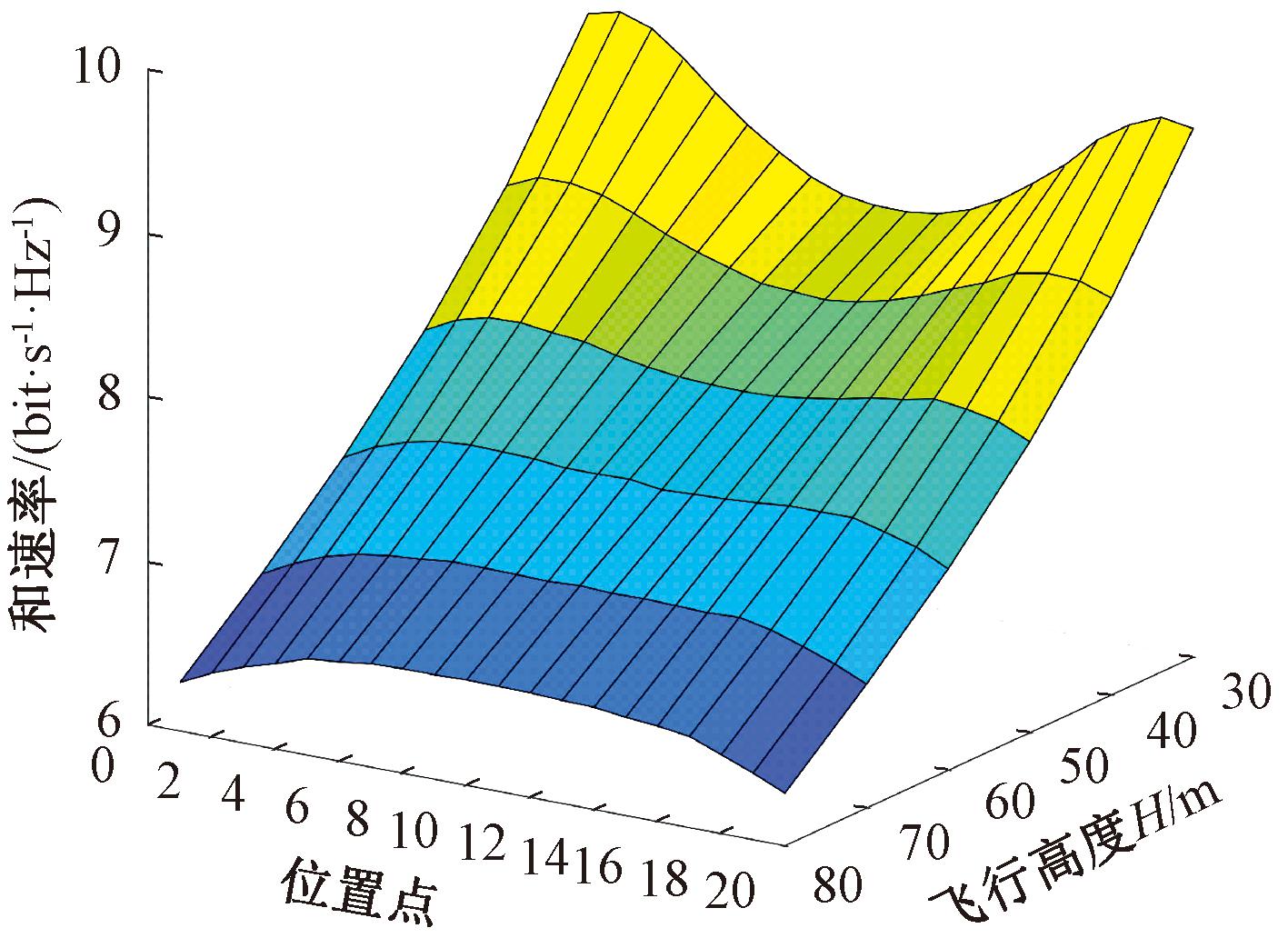
图8 和速率与RIS-UAV位置关系仿真图
Figure 8 Simulation diagram of the relationship between sum rate and RIS-UAV position
4 结论
本文建立了RIS-UAV定轨迹通信系统模型,其中RIS-UAV作为无源中继在BS和UE之间进行协作通信。以RIS-UAV系统每时隙所有UE和速率最大化为优化目标,设计了一种基于FP的流形优化低复杂度的内外双重循环AO算法。仿真结果证明了本文所提算法具有较好的收敛性,并且与经典算法相比具有较低的复杂度,且所提算法在RIS实现3 bit离散相移时即可达到与连续相移近似的性能。此外,研究了RIS-UAV的最佳位置与RIS-UAV高度和BS到UE之间的距离有关。
[1] CHEN X Y, SHENG M, LI B, et al. Survey on unmanned aerial vehicle communications for 6G[J]. Journal of Electronics &Information Technology, 2022, 44(3): 781-789.
[2] 陈新颖, 盛敏, 李博, 等. 面向6G的无人机通信综述[J]. 电子与信息学报, 2022, 44(3): 781-789.CHEN X Y, SHENG M, LI B, et al. Survey on unmanned aerial vehicle communications for 6G[J]. Journal of Electronics &Information Technology, 2022, 44(3): 781-789.
[3] 樊娇, 雷涛, 韩伟, 等. 无人机航迹规划技术研究综述[J]. 郑州大学学报(工学版), 2021, 42(3): 39-46.FAN J, LEI T, HAN W, et al. A survey of UAV path planning[J]. Journal of Zhengzhou University (Engineering Science), 2021, 42(3): 39-46.
[4] PANG X W, SHENG M, ZHAO N, et al. When UAV meets IRS: expanding air-ground networks via passive reflection[J]. IEEE Wireless Communications, 2021, 28(5): 164-170.
[5] RAHMATOV N, BAEK H. RIS-carried UAV communication: current research, challenges, and future trends[J]. ICT Express, 2023, 9(5): 961-973.
[6] LONG H, CHEN M, YANG Z H, et al. Joint trajectory and passive beamforming design for secure UAV networks with RIS[C]∥2020 IEEE Globecom Workshops (GC Wkshps. Piscataway: IEEE, 2020: 1-6.
[7] PENG H R, WANG L C. Energy harvesting reconfigurable intelligent surface for UAV based on robust deep reinforcement learning[J]. IEEE Transactions on Wireless Communications, 2023, 22(10): 6826-6838.
[8] SUN W X, XU Z R, ZHU M K, et al. Achievable rate maximization for RIS-UAV assisted vehicular communication network[C]∥The 24th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC). Piscataway: IEEE, 2023: 306-310.
[9] CUI M, ZHANG G C, ZHANG R. Secure wireless communication via intelligent reflecting surface[J]. IEEE Wireless Communications Letters, 2019, 8(5): 1410-1414.
[10] ELMOSSALLAMY M A, SEDDIK K G, CHEN W, et al. RIS optimization on the complex circle manifold for interference mitigation in interference channels[J]. IEEE Transactions on Vehicular Technology, 2021, 70(6): 6184-6189.
[11] GUO H Y, LIANG Y C, CHEN J, et al. Weighted sum-rate maximization for reconfigurable intelligent surface aided wireless networks[J]. IEEE Transactions on Wireless Communications, 2020, 19(5): 3064-3076.
[12] SHANG B D, BENTLEY E S, LIU L J. UAV swarm-enabled aerial reconfigurable intelligent surface: modeling, analysis, and optimization[J]. IEEE Transactions on Communications, 2023, 71(6): 3621-3636.
[13] 刘志新, 赵松晗, 杨毅, 等. 智能反射面辅助的无人机无线携能通信网络吞吐量最大化算法研究[J]. 电子与信息学报, 2022, 44(7): 2325-2331.LIU Z X, ZHAO S H, YANG Y, et al. Throughput maximization algorithm for intelligent reflecting surface-aided unmanned aerial vehicle communication networks with wireless energy transfer[J]. Journal of Electronics &Information Technology, 2022, 44(7): 2325-2331.
[14] LI S, DU H Q, ZHANG D Y, et al. Joint UAV trajectory and beamforming designs for RIS-assisted MIMO system[J]. IEEE Transactions on Vehicular Technology, 2024, 73(4): 5378-5392.
[15] WU Q Q, ZHANG R. Beamforming optimization for wireless network aided by intelligent reflecting surface with discrete phase shifts[J]. IEEE Transactions on Communications, 2020, 68(3): 1838-1851.
[16] SHEN K M, YU W. Fractional programming for communication systems—part Ⅱ: uplink scheduling via matching[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2631-2644.
[17] SHEN K M, YU W. Fractional programming for communication systems—part Ⅰ: power control and beamforming[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2616-2630.
[18] 戈忠义, 岳殿武, 李光辉, 等. 智能反射面辅助的毫米波MIMO系统波束成形设计[J]. 电讯技术, 2023, 63(1): 7-13.GE Z Y, YUE D W, LI G H, et al. Beamforming design of millimeter wave MIMO system assisted by intelligent reflecting surface[J]. Telecommunication Engineering, 2023, 63(1): 7-13.
[19] ABSIL P A, MAHONY R, SEPULCHRE R. Optimization algorithms on matrix manifolds[M]. Princeton: Princeton University Press, 2008.
[20] REN Y Q, ZHOU R Y, TENG X K, et al. On deployment position of RIS in wireless communication systems: analysis and experimental results[J]. IEEE Wireless Communications Letters, 2023, 12(10): 1756-1760.