在城市交通网络中,级联失效是拥堵在路网中动态传播的过程。当路网中的部分交叉口(路段)发生故障,其承担的流量需要分配给正常工作的交叉口(路段)。但交叉口的剩余容量小于其负载时,可能会导致正常工作的交叉口拥堵,直到不再产生新的拥堵交叉口或交通网络崩溃为止[1]。
当前对城市交通网络级联失效的研究主要集中在级联失效模型和系统性能两个方面。在级联失效模型方面,国内外学者提出了一系列级联失效模型,如沙堆模型[2]、耦合映像格子模型[3]、CASCAD模型[4]等。其中,最常用的是Motter等[5]提出的负载-容量模型,模型假设网络中节点(边)的初始容量和初始负载服从线性关系,由于外部干扰或者自身故障,部分节点(边)失效,导致其负载分配至剩余正常节点,直至网络趋于稳定。詹斌等[6]构建线性负载-容量模型分析武汉市轨道交通网络特征。但是,部分学者认为城市道路交通网络容量与负载之间存在非线性的关系[7]。朱玉洁等[8]基于非线性负载-容量模型分析极端气象灾害对城市公共交通系统级联失效的影响。
在系统性能方面,Chen等[9]从弹性角度量化交通网络运行状态,并基于渗流理论计算交通网络的性能下限和临界拥堵阈值。Hamedmoghadam等[10]基于智能卡数据和渗流理论,提出了一种用于识别交通网络性能瓶颈的方法。潘恒彦等[11]探究公交-地铁加权复合网络在不同攻击方式下鲁棒性的变化情况。
上述研究大多忽略了节点的现实特征。在真实情况中,路网中的负载和容量不会无限制增长,拥堵传播会以非线性的方式影响节点状态,直至路网到达运行能力下限。因此,本文在传统的非线性负载-容量模型[12]中引入时空相关性来描述节点容量变化的动态特征。此外,节点状态的改变必然影响起讫点(OD)需求的改变。这是因为出行者较难获取全部交通信息,当交叉口状态改变时,出行者会选择相邻路段绕行,导致流量从前一个拥堵交叉口转移到相邻交叉口。基于可调负载重分配原则[13],本文提出了一种混合负载重分配策略,将失效负载分配到故障节点的相邻节点和次相邻节点。
为弥补当前研究的不足,本文的主要贡献如下:①构建加权双层城市交通网络模型评估级联失效过程中不同攻击方式对网络可靠性的影响;②建立可变容量的非线性负载-容量模型,并引入临界失效阈值表征节点实时状态;③考虑到节点规模和连边阻抗对失效负载的影响,提出了一种混合负载重分配策略。
1 加权复合网络构建
为了研究网络结构与交通需求的变化对城市交通网络可靠性的影响,本文建立OD-Road双层加权网络G={GOD,GR},如图1所示。上层无向无权网络设置为OD需求网络,分析级联失效过程中网络性能的变化。下层无向有权网络为道路交通网络,用来研究上层需求变化对下层流量分配的影响[14]。
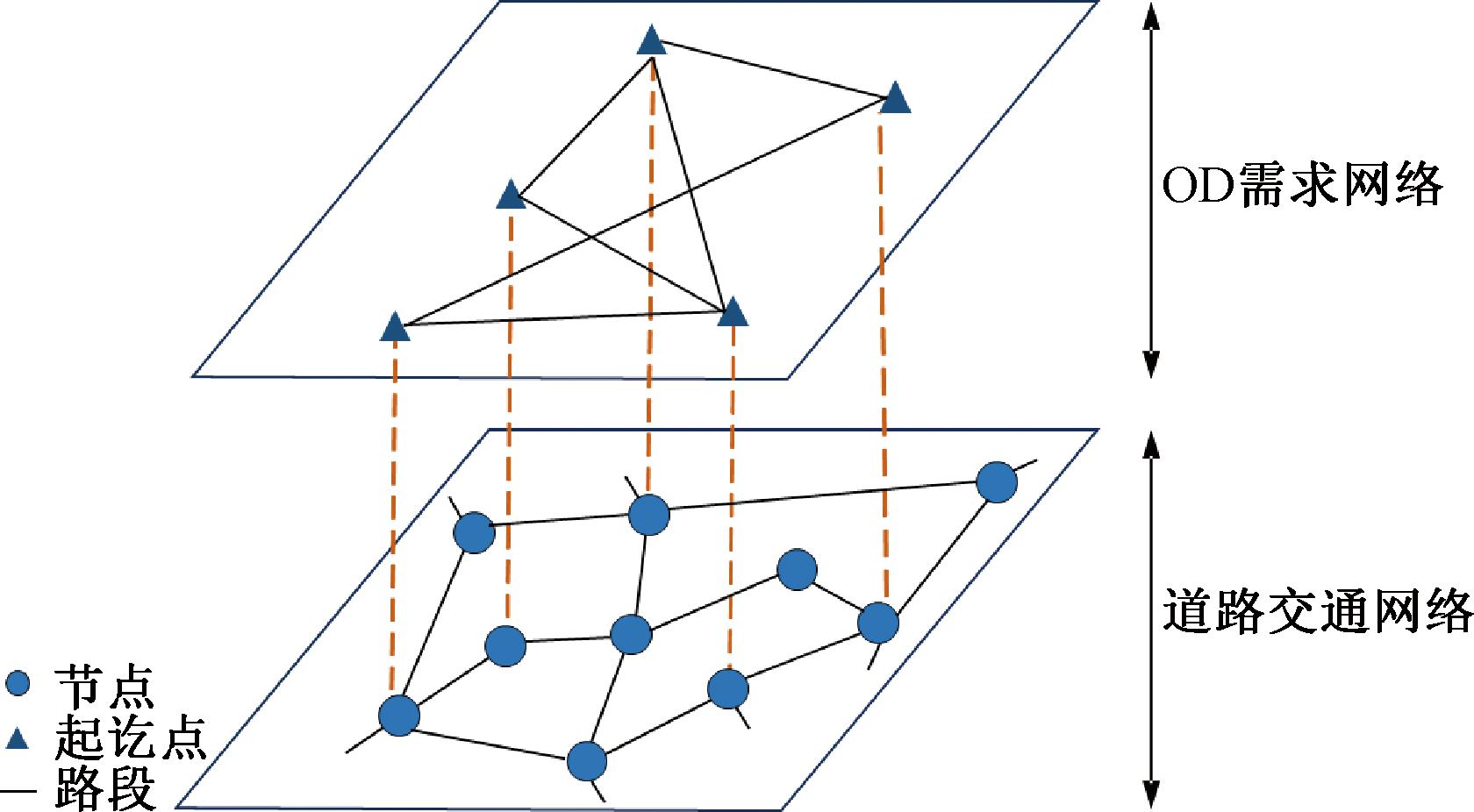
图1 OD-Road双层加权网络
Figure 1 OD-Road double-layer weighted network
双层加权网络模型包括:
(1)网络。假设城市交通网络G={GOD,GR}由上层OD需求网络GOD={VOD,EOD}和下层道路交通网络GR={VR,ER,NR,ΓR}构成。
(2)节点。
表示上层网络OD需求点的集合,
和
分别表示下层网络节点的集合和节点权重的集合。
(3)连边。采用Space-L方法构建网络的连边,若任意两个相邻站点之间存在一条线路,则构建一条连边。
表示上层网络起讫点之间连边的集合,
和
分别表示下层网络路段集合和路段权重的集合。
2 级联失效模型
2.1 非线性负载-容量模型
现有研究证明非线性负载-容量模型比线性负载-容量模型更加灵活可控,能够更好地反映城市交通网络中节点的状态[15]。本次研究假定初始阶段(t=0时),节点(边)的容量与其负载呈非线性关系。
(1)
式中:I表示下层网络中的节点
或边
表示节点(边)I的初始容量;
表示节点(边)I的初始负载;λ和μ为初始阶段节点(边)的强度参数,表示该节点(边)容量的承载能力,强度参数对城市交通网络可靠性的影响暂不讨论,令λ=0.3,μ=0.8。
现实交通网络中节点(边)的容量不仅与前一时刻该节点(边)存在时间相关性,还与前一时刻其他节点(边)存在空间相关性[16],如图2所示。考虑到节点(边)之间的时空相关性,本文基于非线性负载-容量模型,提出一种随时间动态变化的容量更新方法。节点(边)I在t+1阶段的容量
定义为
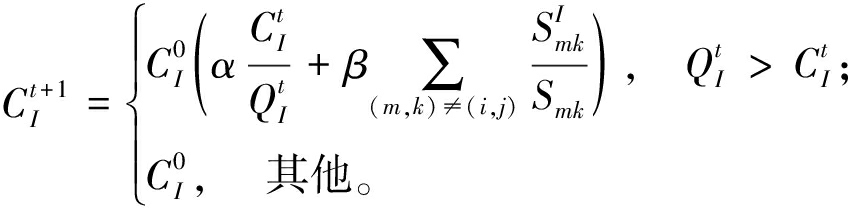
(2)
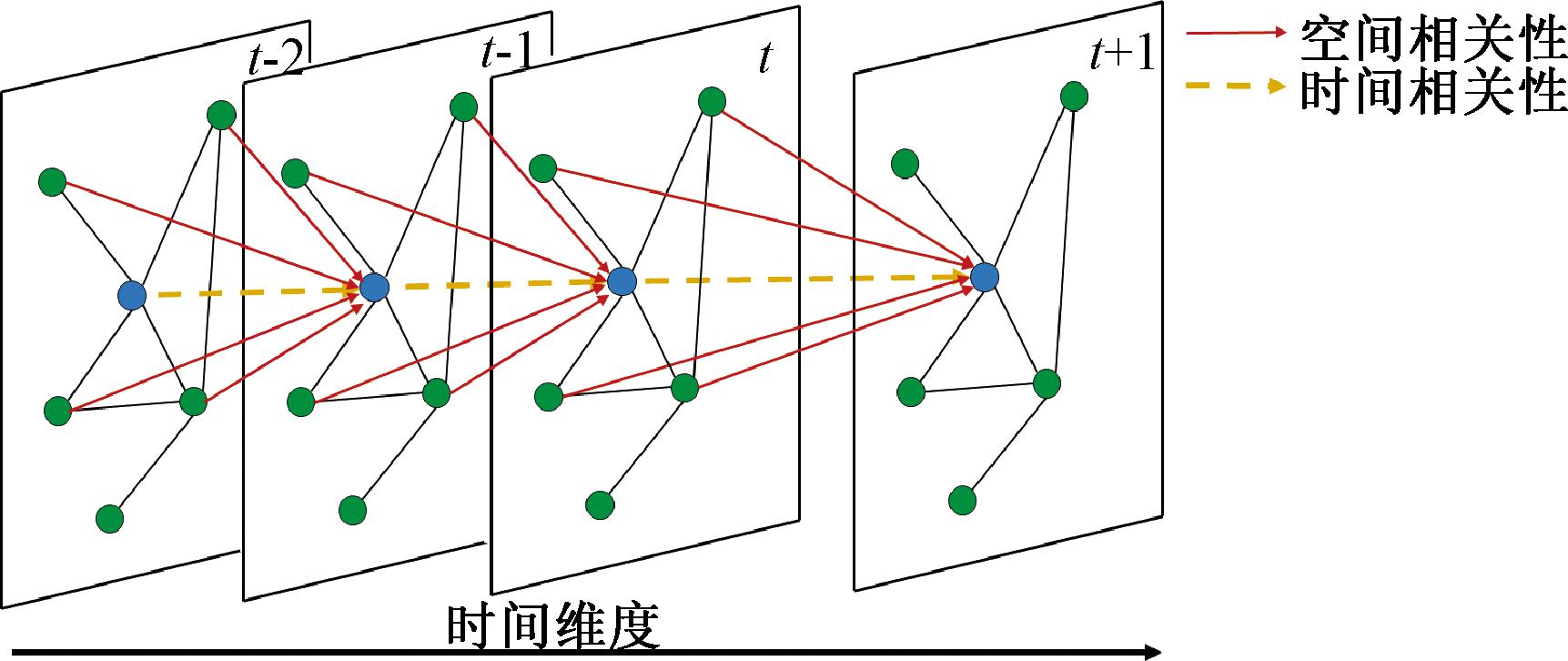
图2 节点(边)容量的时空相关性
Figure 2 Relationship between time and space of node
式中:
表示连接节点m和节点k且经过节点(边)I的最短路径条数;Smk表示连接节点m和节点k的最短路径条数;α、β为时间相关性和空间相关性的权重,α、β∈[0,1]且α+β=1。
2.2 状态更新策略
本文为描述级联失效过程中节点(边)的运行状态,引入临界失效阈值δ(δ>1)将节点(边)I分为正常、失效和拥堵3种状态,分别用0、1、2来表示。在阶段t+1时节点(边)I的状态
定义为
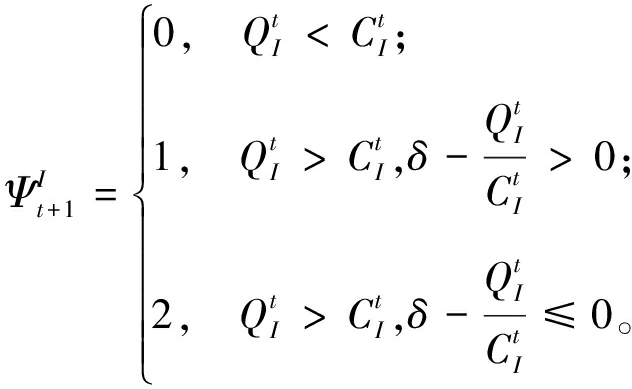
(3)
式中:δ(δ>1)为该网络中节点(边)的临界失效阈值,取值与网络中节点(边)的自恢复能力以及交通管控水平呈正相关。
2.3 负载重分配策略
根据上层网络的OD需求对下层网络进行负载分配时,考虑下层路网阻抗对出行偏好的影响,本文采用经典BPR函数计算得到的阻抗作为网络的权重,上层OD需求网络的最短路径是选择权重和最小的路径。为避免经典BPR函数不适用于混合交通的情况,假设同种类型的小汽车在路网上运行[17]。路网连边阻抗计算如下:
(4)
式中:a和b通常取值为0.15和
为阶段t时车辆在边I上的车辆行驶时间;
为初始阶段车辆在边I上的自由行驶时间,当车辆处于自由行驶状态时,可近似认为节点(边)I上阻抗干扰为0,即
为阶段t时边I上的负载。
为引入负载重分配策略,首先介绍失效负载在节点和边之间转移的过程。图3为边和节点的负载转移过程。如图3(a)所示,当边
失效时,边上的负载转移到相邻节点的连边上;如图3(b)所示,当节点失效时,节点的连边同时失效,两者的失效负载转移到相邻节点及其连边。拥堵节点(边)的负载转移方式与失效负载相同。其次,本文假设拥堵由交叉口向路段传播,所以下文重点解释初始失效节点负载的重分配原则。
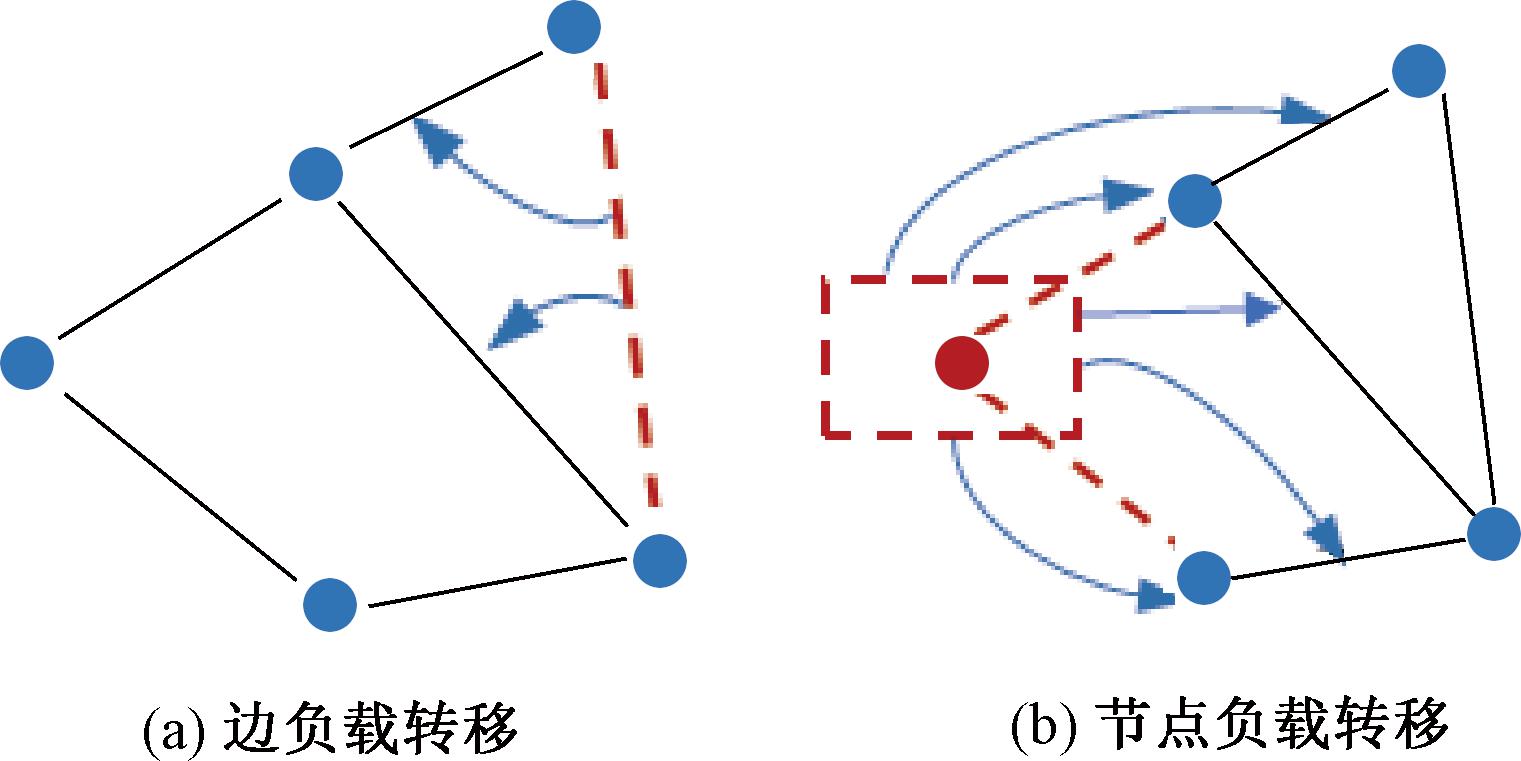
图3 边和节点的负载转移
Figure 3 Load transfer of edges and nodes
在大多数交通网络的研究中,通常将失效节点的负载分配给网络中所有正常工作的节点(全局分配原则[18]);或者将失效节点的负载按重要性指标分配至邻居节点(最近邻分配原则[19])。
上述两种分配原则过度关注网络的全局或局部信息。相比之下,本文提出的混合负载重分配策略不仅考虑故障节点的相邻节点,还将负载分配给次相邻节点,两者承担负载的比例计算如下。
(1)在阶段t时,节点vi失效或拥堵(下文用故障节点代替),节点vi相连接的边同时失效,计算故障节点及其连边的全部负载
(2)采用高斯分配,将
分成两个部分,如式(5)所示。将每部分负载分别分配至故障节点vi的相邻节点和次相邻节点。
(3)若故障节点vi的相邻节点vj也属于故障节点,vi、vj及边eij被看作整体计算其总负载再进行负载重分配,如图4所示。
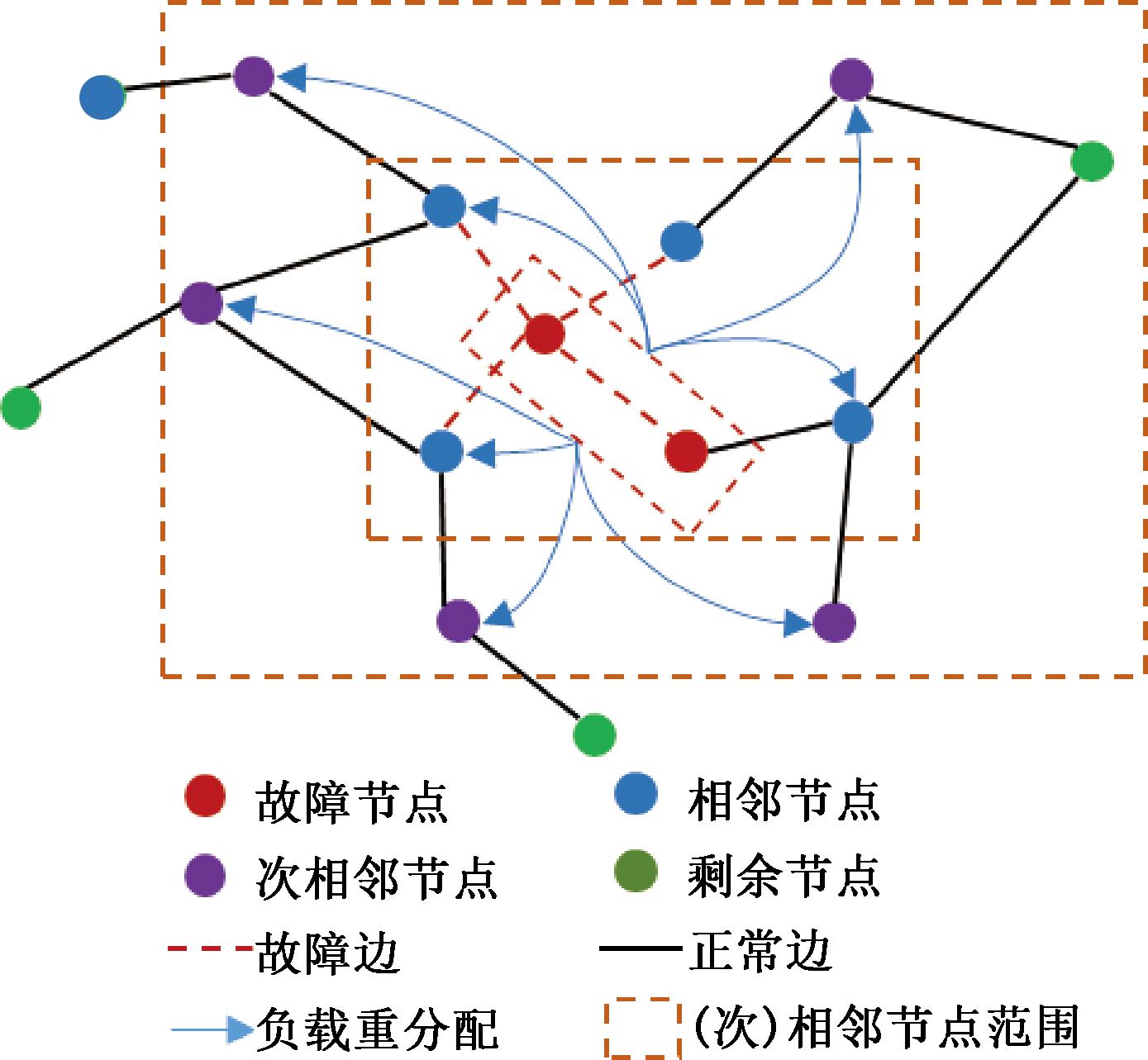
图4 负载重分配示意图
Figure 4 Load redistribution strategy
(4)相邻节点和次相邻节点分配到的负载受两种因素影响。①节点规模:故障节点与相邻节点或次相邻节点之间的距离;②连边阻抗:相邻节点或次相邻节点之间的阻抗,具体计算见式(6)。
(5)
(6)
式中:r=1,2分别表示故障节点vi的相邻节点和次相邻节点;表示故障节点vi及其连边的全部负载,
表示故障节点vi的所有相邻节点或次相邻节点所承担的负载;
表示相邻节点或次相邻节点vj分配到的负载;
为故障节点vi与相邻节点或次相邻节点vj之间的阻抗;
为故障节点vi与相邻节点或次相邻节点vj之间的距离;w1和w2分别表示节点规模和连边阻抗的权重。
(5)根据状态更新策略计算所有节点和边的状态,若出现新的故障节点,则按照上述步骤继续分配故障负载,级联失效的具体流程见2.5节。
2.4 评价指标
本文将网络可靠性定义为城市交通网络在遭受攻击时,能正常运行并疏散故障负载的能力。现有研究中常使用网络效率、节点度、平均路径长度等指标评估网络性能的变化情况[20-21]。
本文从网络拓扑结构和节点运行质量两个方面评估级联失效对城市道路交通网络可靠性的影响,选取网络平均效率、阻塞程度及网络通行质量3个指标对可靠性进行评价。
(1) 网络平均效率 E。网络平均效率是评价网络高效运行的重要指标之一,其值与两节点之间的最短路径(本文用节点间的最小阻抗代替)的倒数成正比。节点间的阻抗越小,网络平均效率越高,级联失效程度越低,网络的可靠性越高。
(7)
式中:E(t)为阶段t时的网络平均效率;
为阶段t时节点vi和节点vj间的最小阻抗;N为网络节点总数。
(2)阻塞程度J。阻塞程度反映路网运行质量。本文考虑了交叉口延误和通行能力的影响,采用改进的阻塞程度作为网络可靠性的衡量指标之一。
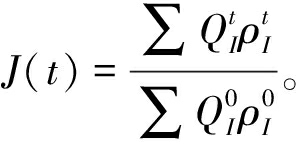
(8)
式中:J(t)为阶段t时的网络的阻塞程度;
为阶段t时节点I的负载。
(3)网络通行质量Z。网络通行质量表示所有OD对在阶段t的平均行程时间。该指标与可靠性成反比。网络通行质量越高,起讫点之间的阻抗越高,可靠性越低。
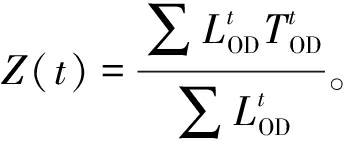
(9)
式中:Z(t)为阶段t时的网络的通行质量;
为阶段t时OD间的需求;
为阶段t时OD间的行程时间。
2.5 仿真流程
城市交通网络级联失效模型的算法流程如下。
Step1 构建网络。建立OD-Road双层加权网络。
Step2 初始化网络。根据式(1)计算节点(边)的初始容量
和初始负载
根据BPR函数设置初始阻抗
Step3 分配OD需求。利用Floyd算法计算OD间最短路径,将OD需求分配到OD间的最短路径上。
Step4 更新网络。在初始阶段(t=0),利用随机和蓄意攻击策略选择初始失效节点,并更新节点状态
Step5 负载重分配。计算故障节点及其连边的全部负载
根据负载重分配原则计算故障节点的相邻节点和次相邻节点承担的负载
Step6 模拟级联失效。检查节点状态若存在失效或拥堵节点,节点状态
或2,更新故障节点的实时容量和负载
并再次分配故障负载。否则,跳到Step7。
Step7 评价网络质量。计算网络平均效率、阻塞程度和网络通行质量。
Step8 重复Step3～Step8直至OD需求全部加载且路网不再发生级联失效现象。
级联失效算法流程图如图5所示。
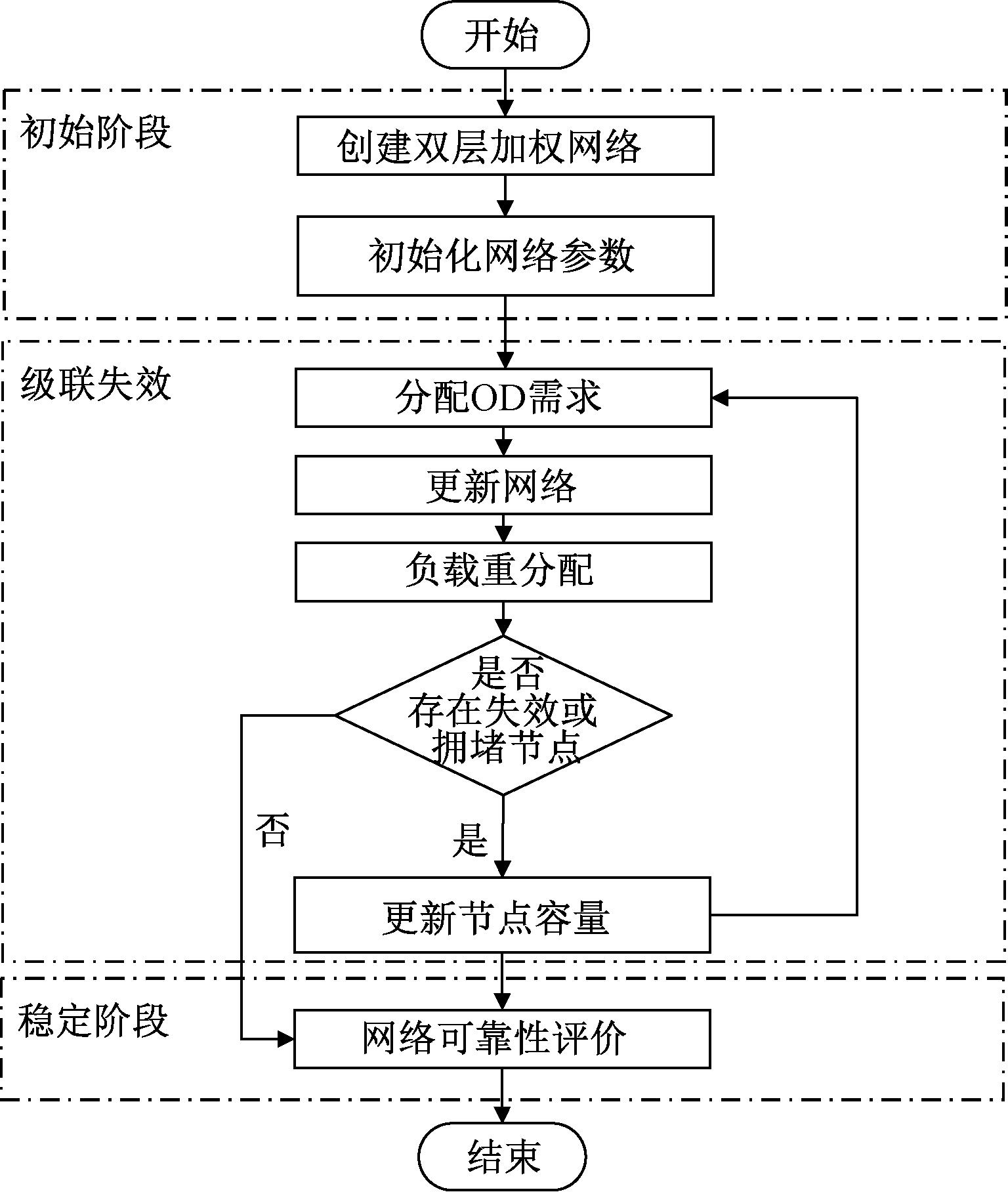
图5 级联失效算法流程图
Figure 5 Flow chart of cascading failure
3 仿真分析
3.1 道路交通网络模型构建
本文选取南京市某区域作为研究对象,构建道路交通网络,该网络包含96个节点、155条连边,并按照道路等级初始化网络节点和边的流量、容量、速度及阻抗等数据。具体构建流程如下。
Step1 利用百度开发者平台生成该区域路网。该区域中主要交叉口和路段分别简化为网络中的节点和连边,并忽略部分次要道路,如图6所示。
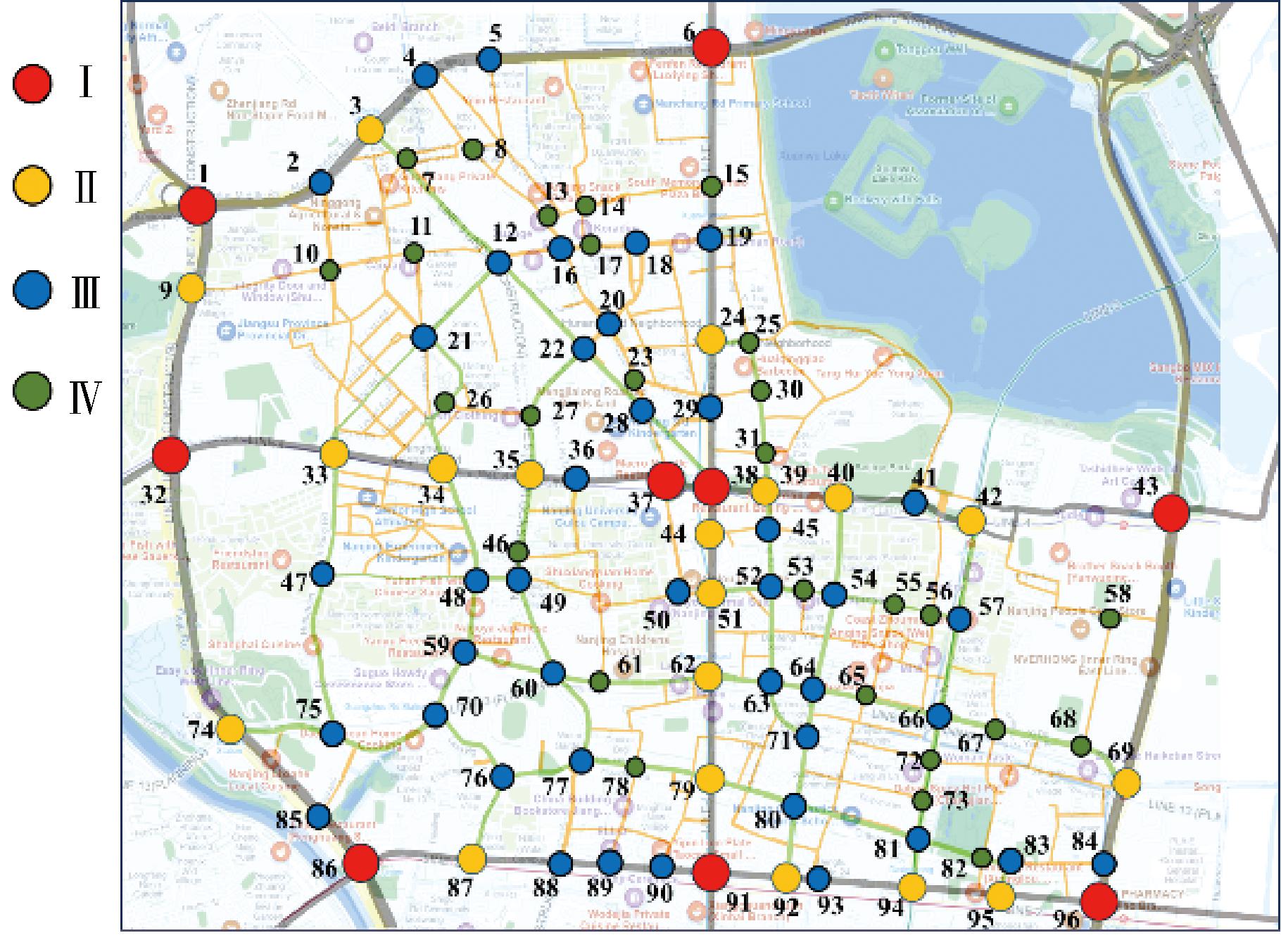
图6 城市道路交通网络模型
Figure 6 The model of urban road traffic network
Step2 利用ArcGIS提取交叉口内部间距和道路长度,即节点内部和节点之间的物理距离。根据物理距离将该区域路网分为4个等级,设定不同等级道路初始流量和初始阻抗
如表1、表2所示。
表1 不同等级路段初始阶段参数(t=0)
Table 1 Initial parameters of different levels of links
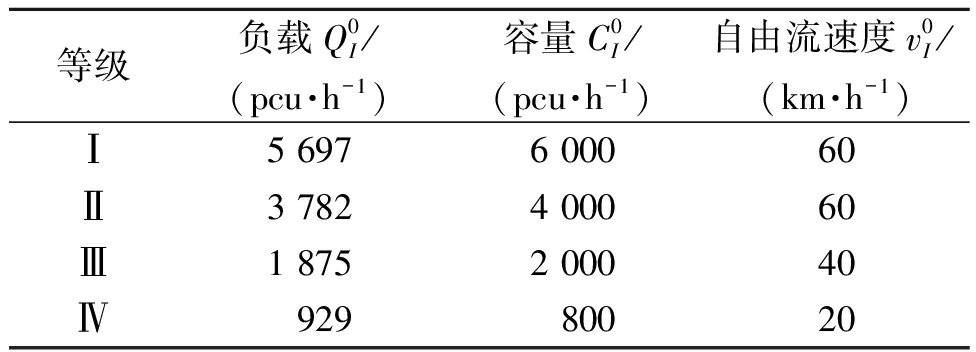
等级负载Q0I/ (pcu·h-1)容量C0I/ (pcu·h-1)自由流速度v0I/ (km·h-1)Ⅰ5 6976 00060Ⅱ3 7824 00060Ⅲ1 8752 00040Ⅳ92980020
表2 不同等级交叉口初始阶段参数(t=0)
Table 2 Initial parameters of different levels of nodes(t=0)
等级负载Q0I/(pcu·h-1)容量C0I/ (pcu·h-1)间距l0I/m阻抗ρ0I/sⅠ2733005030Ⅱ1261403520Ⅲ44502515Ⅳ1012155
Step3 依据道路交通数据以及实地调查问卷,选取13、33、28、78、55、69为交通需求的起讫点,根据网络拓扑结构和OD需求生成复合网络模型。网络中节点(边)初始阶段参数,如表3所示。
表3 部分不同等级路段的初始数据
Table 3 Part datas of different levels of links
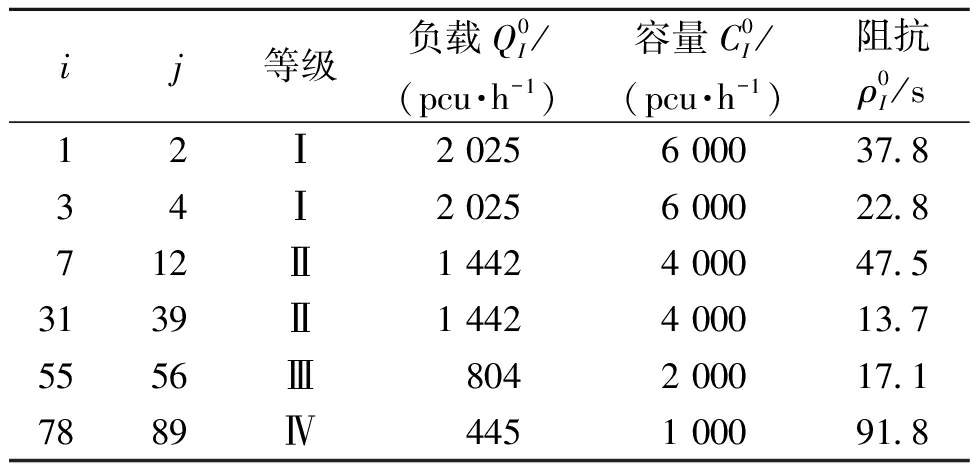
ij等级负载Q0I/(pcu·h-1)容量C0I/(pcu·h-1)阻抗ρ0I/s12Ⅰ2 0256 00037.834Ⅰ2 0256 00022.8712Ⅱ1 4424 00047.53139Ⅱ1 4424 00013.75556Ⅲ8042 00017.17889Ⅳ4451 00091.8
Step4 为模拟级联失效现象,假定每组OD之间需求为1 000 pcu/h(共15组OD,不考虑重复OD),采用用户均衡(UE)分配方式将交通流量加载到上述构建的道路交通网络中,迭代次数为100次[22]。
3.2 仿真结果分析
为了探究不同攻击方式对城市交通网络可靠性的影响,本文采用随机攻击和蓄意攻击两种策略模拟研究区域级联失效传播过程。
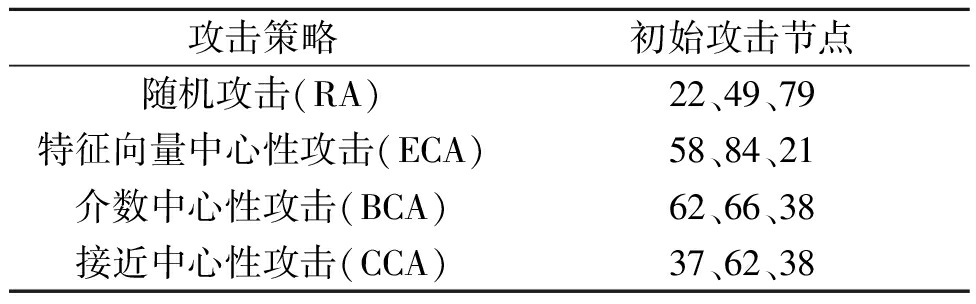
蓄意攻击的核心原则是攻击网络中的关键节点,现有研究经常从网络结构角度识别关键节点[23]。因此,本文选取特征向量中心性、介数中心性和接近中心性3个指标来识别研究区域的关键节点,如表4所示。对于蓄意攻击,计算网络中所有节点的特征向量中心性、介数中心性及接近中心性,按降序排列;选择排名前3的节点作为初始攻击节点。对于随机攻击,随机选取3个节点作为初始攻击节点。
表4 不同攻击策略下的初始攻击节点
Table 4 Initial attack nodes with different attack strategies
攻击策略初始攻击节点随机攻击(RA)22、49、79特征向量中心性攻击(ECA)58、84、21介数中心性攻击(BCA)62、66、38接近中心性攻击(CCA)37、62、38
对不同的攻击策略设置相同的失效阈值(δ=1.6),如图7(a)、图8(a)、图9(a)所示。
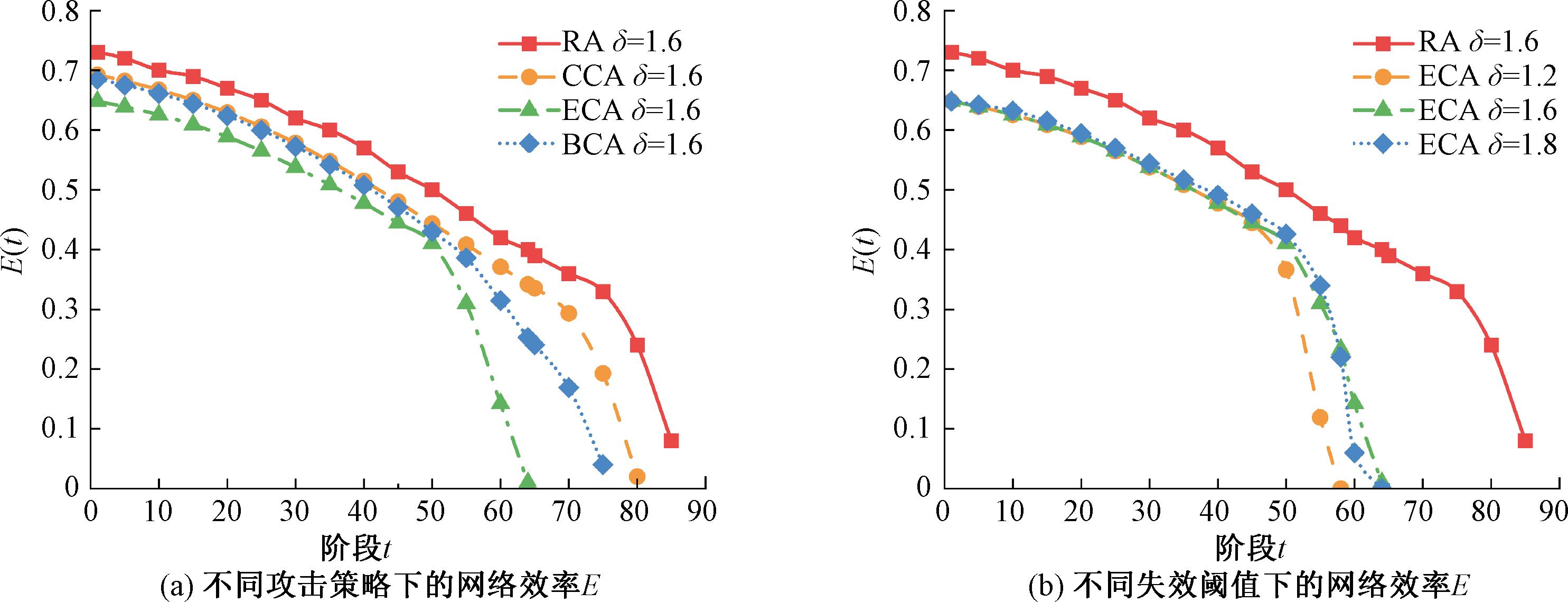
图7 不同攻击方式和失效阈值下的网络效率E
Figure 7 The network efficiency with different attack strategies and failure thresholds
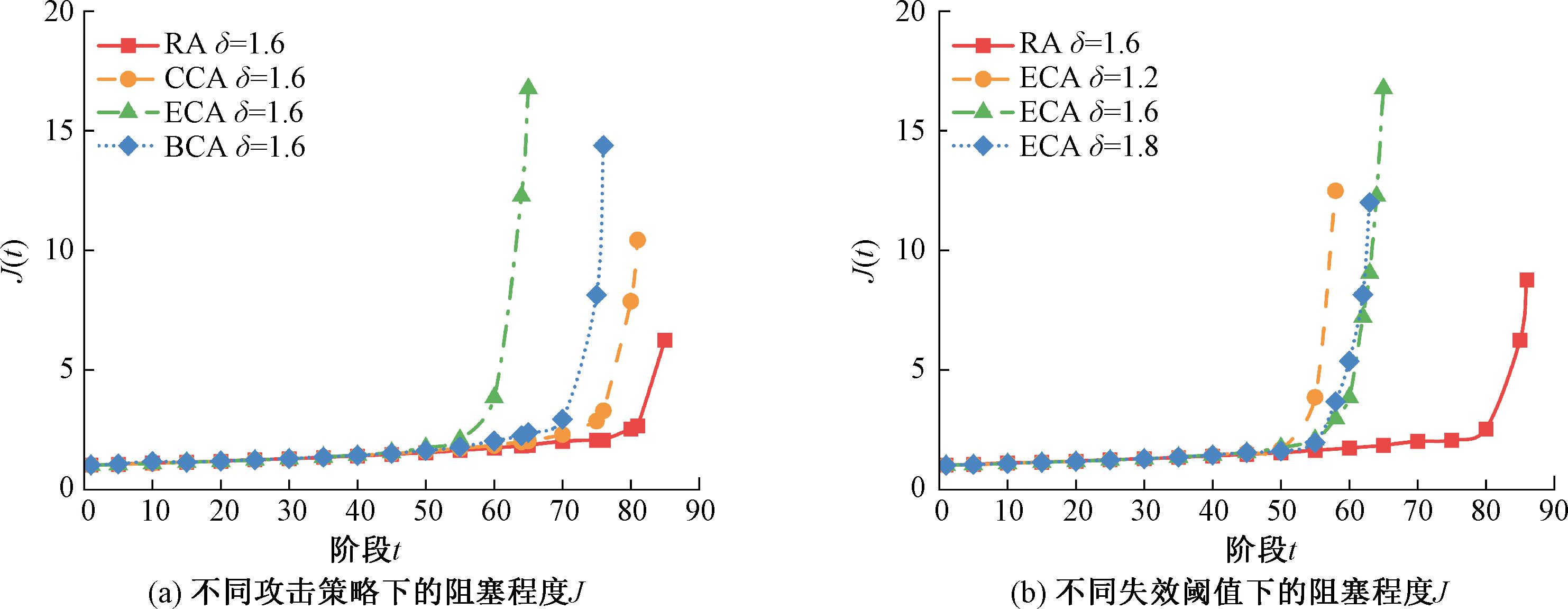
图8 不同攻击方式和失效阈值下的阻塞程度J
Figure 8 The congestion degree with different attack strategies and failure thresholds
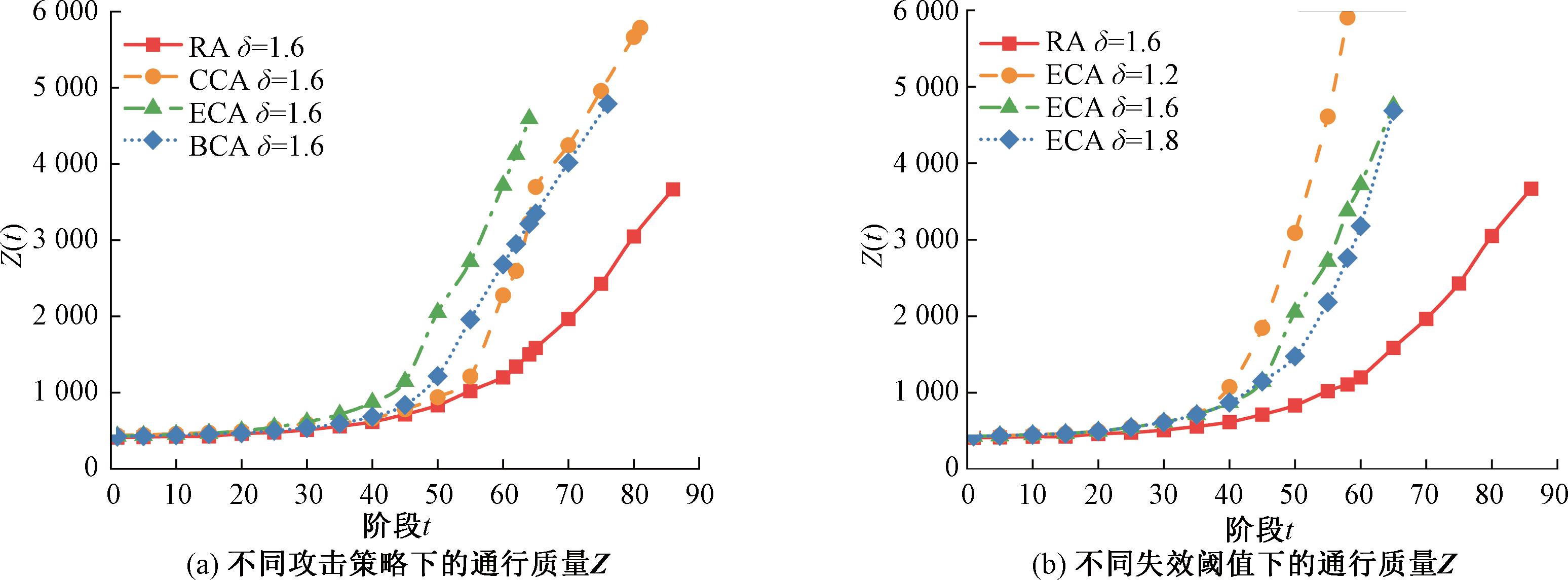
图9 不同攻击策略和失效阈值下的通行质量Z
Figure 9 The traffic quality with different attack strategies and failure thresholds
从图8(a)、图9(a)可知,在不同攻击策略下,通行质量Z(t)和阻塞程度J(t)在级联失效初期上升缓慢,随后急剧增加直到网络崩溃。通过RA仿真可知,阻塞程度J在t=81后才出现明显的上升趋势。这表明网络具备抵抗风险的能力,小规模的节点和边失效不会对网络可靠性造成较大影响。在拥堵扩散时,采取适当的疏散策略能有效缓解交通拥堵现象。
从图7(a)、图8(a)可知,不同攻击策略下的网络效率E(t)和阻塞程度J(t)显示,RA对网络可靠性影响最小,其次是CCA、BCA,影响最大的是ECA。对于ECA策略,网络在发生级联失效后的15个时间步内彻底崩溃(t=50～65),同样的情况也出现在网络效率E(t)和通行质量Q(t)上,这证明攻击EC指标较大的节点会给网络造成更为明显的级联失效现象。因为EC指标较高的节点故障会导致相邻节点和次相邻节点承担故障负载,增加了相邻节点和次相邻节点故障的可能性,即重要节点故障会加速网络崩溃。
从图9(a)可知,CCA的通行质量Z(t)在t=65之后,发生大幅度上升,并超越BCA。由此得知t=65是CCA的临界时间点,在这之后,网络发生大规模失效,导致道路阻抗变大,平均行驶时间增加。
对最不利的攻击方式ECA设置不同的失效阈值(δ=1.2、1.6、1.8)如图7(b)、图8(b)、图9(b)所示。
比较δ=1.2和δ=1.6可知,在级联失效初期,网络效率E(t)和通行质量Z(t)上升缓慢,如图7(b)、图9(b)所示。在t=50～63,失效阈值δ越大,网络效率E(t)越小。同样的情况可以从通行质量Z(t)图9(b)中的t=40～65中看到,这表明在拥堵传播初期,增大失效阈值能在一定程度上延缓级联失效扩散,说明除了网络自身抵抗风险的能力外,交通管理水平的提高也可以延缓拥堵扩散。保持适当的交通管理水平,能够在很大程度上减缓级联效应的影响,提高网络的可靠性。
失效阈值δ的从1.6增加到1.8可以提高节点的容量从而延缓拥堵扩散,但在级联失效后期,如图7(b)、图9(b)所示,网络效率E(t)和通行质量Z(t)之间相差较小。从阻塞程度J(t)可以更明显看出这一现象,在t=58之后,更大的失效阈值δ已经不能缓解拥堵,相反,更大的失效阈值δ引发了更严重的拥堵现象(δ=1.6相较于δ=1.8)。这表明失效阈值较大的节点故障后,其相邻节点和次相邻节点将承担更多的故障负载,导致网络更容易崩溃。此外,级联失效初期失效阈值δ的增加能减少拥堵带来的损失,但这种增益不会无限制增大。这一结论与现实相符,交通管理水平的提高可以缓解拥堵但不会彻底解决该问题。
4 结论
本文利用复杂网络理论建立了双层加权城市交通网络模型,分析了不同攻击方式和失效阈值对城市交通网络可靠性的影响。仿真结果表明,城市交通网络具有抵御拥堵传播的能力。小规模节点和边的失效不会对网络可靠性产生较大影响。对于仿真区域而言,攻击特征向量中心性较高的节点,会导致网络级联失效现象更明显。其次,失效阈值只能在一定程度上抑制级联失效,这表明交通管理对缓解拥堵的效果有限。
[1] 刘伟, 陈科全, 刘玉印, 等. 前景理论下道路网络的级联失效演变[J]. 交通运输系统工程与信息, 2018, 18(1): 145-151.LIU W, CHEN K Q, LIU Y Y, et al. Cascading failure simulation of road network based on prospect theory[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(1): 145-151.
[2] BAK P, TANG C, WIESENFELD K. Self-organized criticality: an explanation of the 1/f noise[J]. Physical Review Letters, 1987, 59(4): 381-384.
[3] SUN L S, HUANG Y C, CHEN Y Y, et al. Vulnerability assessment of urban rail transit based on multi-static weighted method in Beijing, China[J]. Transportation Research Part A: Policy and Practice, 2018, 108: 12-24.
[4] DONG H, CUI L R. System reliability under cascading failure models[J]. IEEE Transactions on Reliability, 2016, 65(2): 929-940.
[5] MOTTER A E, LAI Y C. Cascade-based attacks on complex networks[EB/OL]. (2003-01-08)[2024-08-12].https:∥doi.org/10.1103/PhysRevE.66.065102.
[6] 詹斌, 袁野, 杨世武, 等. 基于加权网络的城市轨道交通网络特性与级联失效分析[J]. 武汉理工大学学报(信息与管理工程版), 2022, 44(6): 917-923, 929.ZHAN B, YUAN Y, YANG S W, et al. Analysis of the structural characteristics and cascading failure of urban rail transit network based on weighted network model[J]. Journal of Wuhan University of Technology (Information &Management Engineering), 2022, 44(6): 917-923, 929.
[7] MA F, SHI W J, YUEN K F, et al. Exploring the robustness of public transportation for sustainable cities: a double-layered network perspective[J]. Journal of Cleaner Production, 2020, 265: 121747.
[8] 朱玉洁. 极端气象灾害下城市公交-地铁双层网络韧性研究[D]. 西安: 长安大学, 2023.ZHU Y J. The resilience of bus-subway urban transport network under the extreme meteorological disasters[D].Xi’an: Changan University, 2023.
[9] CHEN H R, ZHOU R Y, CHEN H, et al. A resilience-oriented evaluation and identification of critical thresholds for traffic congestion diffusion[J]. Physica A: Statistical Mechanics and Its Applications, 2022, 600: 127592.
[10] HAMEDMOGHADAM H, JALILI M, VU H L, et al. Percolation of heterogeneous flows uncovers the bottlenecks of infrastructure networks[J]. Nature Communications, 2021, 12: 1254.
[11] 潘恒彦, 张文会, 胡宝雨, 等. 城市公交-地铁加权复合网络构建及鲁棒性分析[J]. 吉林大学学报(工学版), 2022, 52(11): 2582-2591.PAN H Y, ZHANG W H, HU B Y, et al. Construction and robustness analysis of urban weighted subway-bus composite network[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(11): 2582-2591.
[12] DOU B L, WANG X G, ZHANG S Y. Robustness of networks against cascading failures[J]. Physica A: Statistical Mechanics and Its Applications, 2010, 389(11): 2310-2317.
[13] 段东立, 吴俊, 邓宏钟, 等. 基于可调负载重分配的复杂网络级联失效模型[J]. 系统工程理论与实践, 2013, 33(1): 203-208.DUAN D L, WU J, DENG H Z, et al. Cascading failure model of complex networks based on tunable load redistribution[J]. Systems Engineering-Theory &Practice, 2013, 33(1): 203-208.
[14] DUAN J X, LI D Q, HUANG H J. Reliability of the traffic network against cascading failures with individuals acting independently or collectively[J]. Transportation Research Part C: Emerging Technologies, 2023, 147: 104017.
[15] LIU Z Z, CHEN H, LIU E Z, et al. Exploring the resilience assessment framework of urban road network for sustainable cities[J]. Physica A: Statistical Mechanics and its Applications,2022.
[16] 苏飞, 董宏辉, 贾利民, 等. 基于时空相关性的城市交通路网关键路段识别[J]. 交通运输系统工程与信息, 2017, 17(3): 213-221.SU F, DONG H H, JIA L M, et al. Identification of critical section in urban traffic road network based on space-time correlation[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(3): 213-221.
[17] ZHAO F, FU L P, ZHONG M, et al. Development and validation of improved impedance functions for roads with mixed traffic using taxi GPS trajectory data and simulation[J]. Journal of Advanced Transportation, 2020, 2020: 7523423.
[18] 段东立, 战仁军. 基于相继故障信息的网络节点重要度演化机理分析[J]. 物理学报, 2014, 63(6): 385-393.DUAN D L, ZHAN R J. Evolution mechanism of node importance based on the information about cascading failures in complex networks[J]. Acta Physica Sinica, 2014, 63(6): 385-393.
[19] WANG W X, CHEN G R. Universal robustness characteristic of weighted networks against cascading failure[EB/OL]. (2008-02-01)[2024-08-12].https:∥doi.org/10.1103/PhysRevE.77.026101.
[20] XING R R, YANG Q F, ZHENG L L. Research on cascading failure model of urban regional traffic network under random attacks[J]. Discrete Dynamics in Nature and Society, 2018, 2018: 1915695.
[21] YANG S H, CHEN W R, ZHANG X X, et al. A graph-based method for vulnerability analysis of renewable energy integrated power systems to cascading failures[J]. Reliability Engineering &System Safety, 2021, 207: 107354.
[22] 王杰. 城市道路交通网络级联失效及控制研究[D]. 长沙: 长沙理工大学, 2014.WANG J. The research on cascading failure and control methods in urban road traffic networks[D].Changsha: Changsha University of Science &Technology, 2014.
[23] FANG X Y, LU L J, LI Y, et al. A driver-pressure-state-impact-response study for urban transport resilience under extreme rainfall-flood conditions[J]. Transportation Research Part D: Transport and Environment, 2023, 121: 103819.