串级系统因其拥有两个控制回路,系统的调节性能和抗干扰能力都有了很大的提升,在众多控制系统中占据着重要地位[1]。近年来,对于串级系统评价的研究愈发深入,也取得了不少研究成果。在高斯噪声情况下,最小方差控制(minimum variance control, MVC)方法往往会导致控制动作过多,鲁棒性差。因此,Tan等[2]提出了基于LQG基准的串级控制系统性能评估方法,有效改善了MVC方法过于保守的问题,同时兼顾控制工作量和输出性能。但在实际生产时,噪声更多服从非高斯分布。为了解决最小方差基准在评估非高斯扰动系统时不准确的问题,Jia等[3]将最小熵与输出均值相结合提出了新的基准,并得出结论,在非高斯干扰下,使用最小熵的性能评估方法更合适。刘阳等[4]则对另一种较为特殊的并行串级系统(parallel cascade control,PCC)进行了噪声估计和性能评价,得出了同样的结论。
在评价指标方面,前人已经验证了最小方差指标有着运算简单、适用于简单工程的优点,但对于处在复杂工况的系统,最小方差控制律具有增益高、带宽宽、控制信号偏差大等缺点。虽然熵指标能有效克服这些缺点,但仍有缺陷,其中最主要的是具有平移不变性的缺陷,即熵的大小仅由其分布的形状决定。为此不少学者提出了改进方法,比如Zhang等[5]提出了将均值与Renyi熵基准结合的新的基准,保留了熵指标是对整个输出序列的统计特征的特点,同时加入了均值的限定,改善熵指标平移不变性造成的影响。同时,给出了一种改进的分布估计(estimation of distribution algorithm,EDA)算法用于对串级系统进行辨识,提高了搜索速度,但仍然存在运算时间长、效率差等缺点。
为了更好地对系统模型进行辨识,不少学者提出了改进算法,如黄国豆[6]结合摸石头过河算法(wading across stream algorithm,WSA)思想,对EDA算法进行改进,提出了一种改进的混合EDA算法,与传统EDA算法相比拥有更快的迭代速度与搜索能力。Zhang等[7]利用定点最小误差熵算法可以准确、快速地估计参数值的特点,与EDA算法结合起来,提出最小化双误差熵(double error entropy minimization,DEEM)算法,算法所提不仅可以提高参数识别的准确性,还可以提高估计噪声概率密度函数的准确性。Zhang等[8]则是在EDA算法的迭代过程中,选取优秀个体的中心与最优解交叉,以充分保留最优个体的信息,提高算法速度和精度,同时提出了广义相关熵(generalized correntropy,GC)指标来改善熵指标的平移不变性。
综上所述,近几年对串级非高斯系统的研究主要集中在指标的改进和系统辨识算法的创新上。针对熵指标的平移不变性,本文进行学科的交叉引用,借鉴图像处理指标[9],提出了SI指标,该指标能有效地克服熵指标的平移不变性。将其与熵指标混合后形成混合性能评价指标,能更加全面地对系统进行评价。此外,为了快速准确地获取系统参数,本文提出了一种改进的混合麻雀搜索算法(hybrid sparrow search algorithm,HSSA),改进的算法具有寻优速度快、不易陷入局部最优等特点。最后通过仿真实验验证混合指标和改进算法的有效性。
1 串级控制系统评价方法
以图1所示串级控制系统为例,取设定值r=0的情况,图1中GL1和GL2表示扰动通道,y1(k)和y2(k)为主副回路的输出,其表达式如下:
(1)
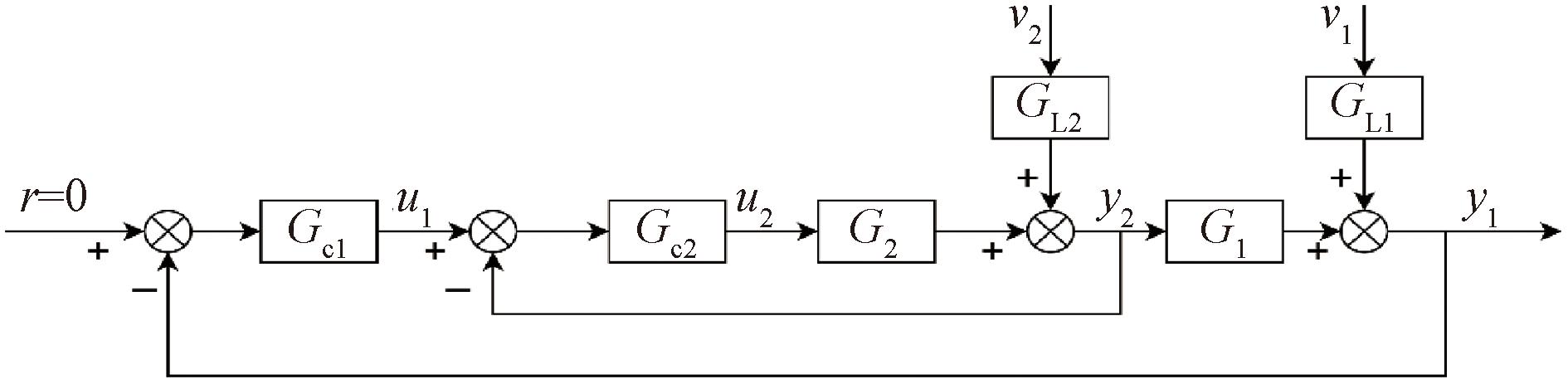
图1 串级控制系统结构图
Figure 1 Cascade control system structure diagram
式中:v1(k)和v2(k)表示系统的未知噪声;u1(k)和u2(k)为主副控制器的输出;主回路被控对象表达式为![]() 表示无延迟的对象模型,d1为延迟时间;副回路被控对象表达式为
表示无延迟的对象模型,d1为延迟时间;副回路被控对象表达式为![]()
根据梅森公式推导得出主回路表达式为
(2)
GL1(z)和GL2(z)用丢番图方程分解,得
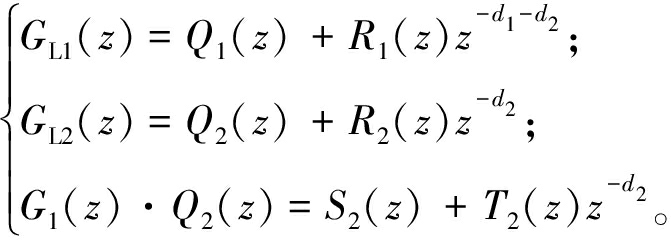
(3)
式中:Q1(z)、Q2(z)、S2(z)均为关于z的多项式,阶次分别为d1+d2-1、d2-1、d2-1;其余为余项表达式。
将Q1(z)、S2(z)展开可得
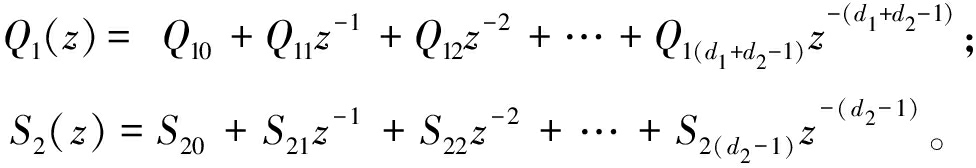
将式(3)代入式(2)可得
y1(k)=Q1(z)v1(k)+S2(z)z-d1v2(k)+[T1v1(k)+T2v2(k)]z-d1-d2。
(4)
其中,式(4)右侧前两项为反馈不变量;式(4)右侧第3项为反馈相关量。
将单回路计算最小方差性能指标的方法推广到串级系统,将系统的主回路输出并进行分解,分为反馈不变量部分和反馈相关量部分,系统性能评估的关键是反馈不变量部分。通过调节主副回路控制器Gc1(z)和Gc2(z)的参数使T1=T2=0,此时反馈相关量部分为0,系统的主回路输出方差只和反馈不变量有关,得到系统输出基准yb,对应的Harris最小方差指标[3]为
(5)
式中:varmin(y1)表示系统的最小方差;var(yt)表示系统实际输出的方差。
在本文中使用MATLAB仿真平台进行数据的模拟采集。同理得到最小有理熵指标[3]如下:
(6)
式中:H(yt)表示系统实际输出的熵值。
2 混合性能评价指标
2.1 结构相似性指标
结构相似性(structural similarity,SSIM)指标最早由德州大学奥斯丁分校的图像和视频工程实验室提出,该指标常用于图像结构相似性比较,是衡量图像质量的指标之一。对于图像x和y,SSIM[9]可以定义为
(7)
式中:μx为x的平均值;μy为y的平均值;![]() 为x的方差;
为x的方差;![]() 为y的方差;σxy为x和y的协方差;c1=(K1L)2,c2=(K2L)2,c1和c2均为常数,L=255,K1=0.01,K2=0.03。
为y的方差;σxy为x和y的协方差;c1=(K1L)2,c2=(K2L)2,c1和c2均为常数,L=255,K1=0.01,K2=0.03。
SSIM指标主要用于图像处理领域,它综合考虑了3个方面的相似性:亮度相似性、对比度相似性以及结构相似性。本文借鉴SSIM指标提出用于性能评估的SI指标,SI指标可以有效反映两个概率密度函数( probability density function,PDF)的差距。SI指标的计算原理如下,以PDF(p(x))和PDF(q(x))为例。
(1)亮度相似性可以通过均值来衡量,反映整体位置的相似程度:
(8)
(2)对比度相似性可通过标准差衡量,反映分布宽度的相似程度:
(9)
(3)结构相似性可通过协方差衡量,反映形状和结构的相似程度:
(10)
(4)为避免分母为零的情况,并使其适用于PDF的比较,常数设定如下:
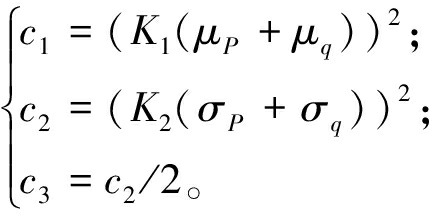
(11)
式中:K1=0.01,K2=0.03。
因此,用于性能评价的SI指标计算方式为式(8)~(10)的乘积:
![]()
(12)
通过上述描述可知,SI指标能有效地应用于PDF的比较。将SI指标用于PDF的比较,是一种学科交叉引用和思路的扩展不同于常规的PDF比较方法(如KL散度、JS散度[10])。而对表达式进行分析可知,该指标拥有对称性、归一性及最大值唯一性,可以很好地作为控制系统的评价指标。其值在[0,1]内,值越大说明其相似程度越高。
将此指标与系统性能评价结合,系统性能评价可以看作是用来比较实际输出PDF与基准PDF的相似程度[6]。将实际输出PDF与基准PDF按同一离散尺度离散后得到两个数组,计算这两个数组的均值、方差和协方差,代入式(12)进行计算,即可得到SI指标性能评价结果。SI指标可以较好地反映两个数组的相似程度,进一步反映两个概率密度函数的相似程度。在本文中,离散尺度选择[-10∶0.1∶10],此时能准确反映所选系统的PDF形状特征。
2.2 熵指标
熵指标在系统性能评估领域已经有了广泛的运用,主要有renyi熵、有理熵、香农熵等。其中有理熵[11]定义式如下:
(13)
式中:γ(x)为随机变量x概率密度函数,在MATLAB中可以使用核密度估计函数来进行近似估计;R为随机变量x的取值范围。
2.3 混合性能指标
SI指标虽然对平移不变性有显著的改善,但对于形状的敏感程度还是不够。因此,提出了对输出PDF形状敏感的有理熵指标,将两者进行一个动态加权的组合,得到一个更为综合的SI混合指标。SI混合指标计算方式如下:
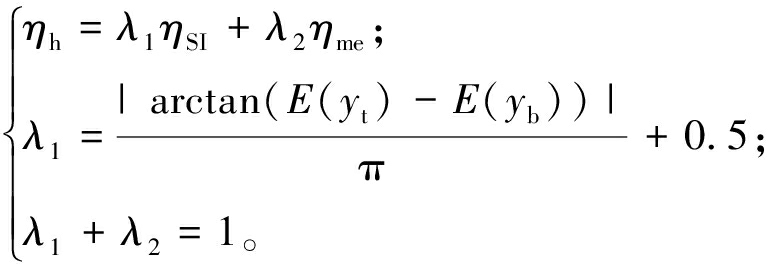
(14)
式中:ηh为混合性能指标;ηSI为SI系数指标;ηSI表示最小有理熵指标;λ1、λ2为动态权值系数;E(yt)和E(yb)分别为实际输出的均值和基准输出的均值。
当实际输出与基准输出之间的均值相差较大时,提高SI指标占比来克服平移不变性;当两者差值较小时,提高熵指标的占比,从而提高对PDF的形状变化的敏感程度;同时为了确保SI指标的主体地位,使其指标占比始终在0.5以上。
3 基于HSSA的参数辨识
3.1 搭建模型
在对系统进行评价之前需要先进行系统的参数辨识。辨识方法有多种,在综合考虑辨识的速度与辨识的准确性之后,选择采取HSSA来进行参数辨识,选择二阶renyi熵作为适应度函数。
以CARMA模型来表示串级系统:
(15)
(16)
式中:![]() 表示需要辨识的模型参数;n1、n2、m1、m2、h1、h2表示模型阶次。
表示需要辨识的模型参数;n1、n2、m1、m2、h1、h2表示模型阶次。
3.2 混合麻雀算法
麻雀搜索算法(sparrow search algorithm,SSA)是群体智能优化算法[12]的一种,其思路是对自然界麻雀种群的捕食行为及反捕食行为进行模仿,种群中的麻雀分为发现者、追随者和随机产生的警觉者[13]。为了克服麻雀搜索算法在后期搜寻能力相对较弱的问题,本文结合正余弦算法提出了HSSA,从而增强局部搜索能力,避免陷入局部最优,混合麻雀搜索算法具体流程如图2所示。
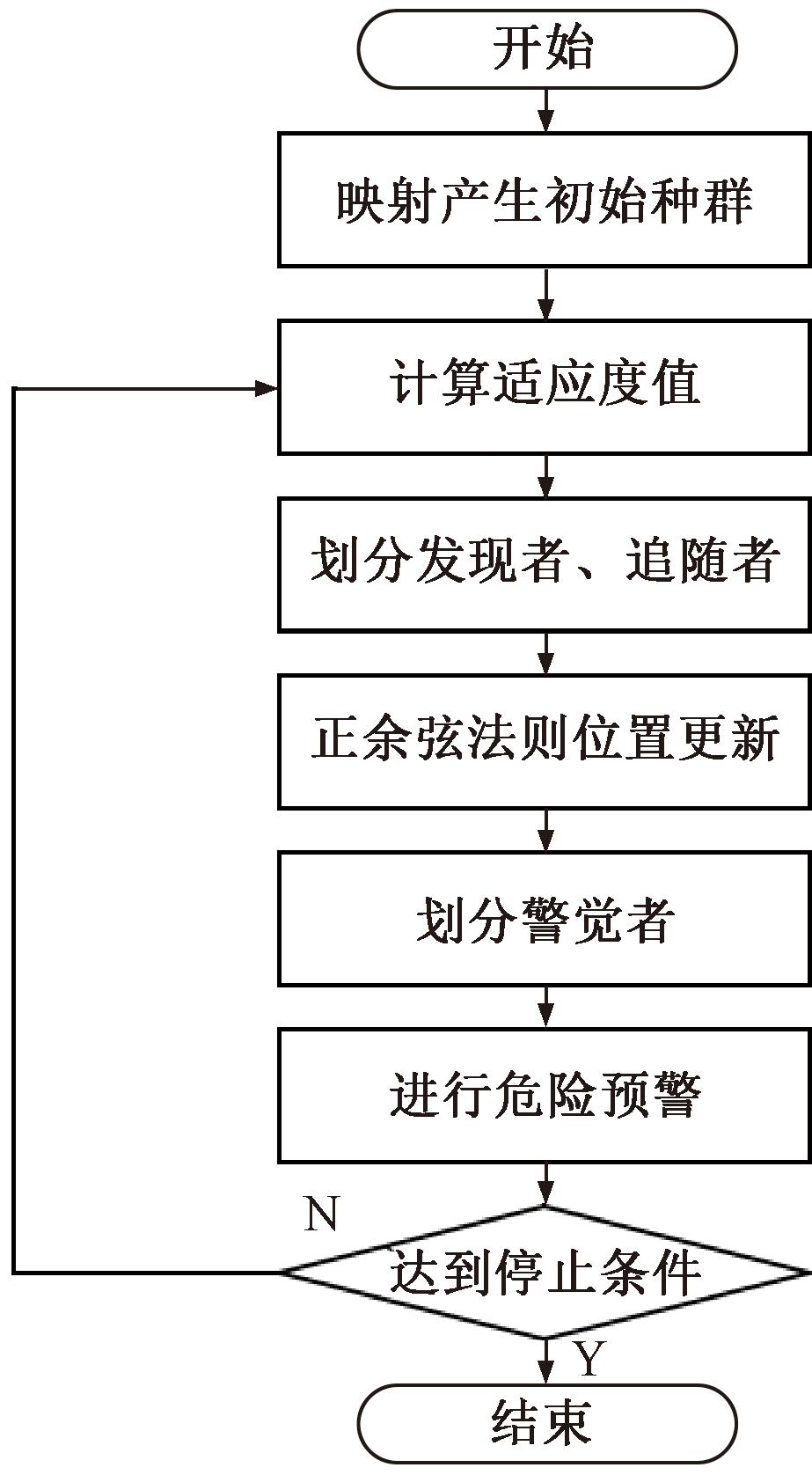
图2 混合麻雀搜索算法流程图
Figure 2 Flowchart of the hybrid sparrow search algorithm
将原有算法中发现者的迭代方式进行更改,改为性能更优的正余弦算法(sinecosine algorithm,SCA)[14-15]迭代方式。正余弦算法原理式如下:
(17)
式中:r1=1为步长搜索因子,负责调整种群的收敛或扩张速度;r2为[0,2π]的随机数;r3为目标值的随机权重,设置大于1则强调目标值的作用,小于1则减弱目标值影响;Xbest为本次迭代的全局最优;R4为[0,1]的随机数;迭代时随机选择正弦函数或余弦函数。
为了兼顾算法的前期探索和后期开发能力,与原正余弦算法取定值的做法不同的是步长搜索因子r1采用了以下的表达式:
(18)
式中:a=1;η为调节系数,η≥1;t为当前迭代次数;Itermax为迭代总数。分析表达式可知,r1的值从1先缓后急地收缩到 0,这种变化合理地兼顾了算法的全局搜索和局部寻优能力。
为了改善初始种群的质量,在种群的初始化阶段引入Circle混沌映射,映射的公式如下:
(19)
式中:bmod表示取模运算。
SSA产生初始种群时,利用上下限进行种群的随机生成,这样生成的种群分布不均匀,可能会错过最优解的位置因而影响算法搜索速度。因此采用circle混沌映射进行初始化,使种群较为均匀地分布在解空间内,提高初始种群质量。
4 仿真验证
选取如下串级回路:
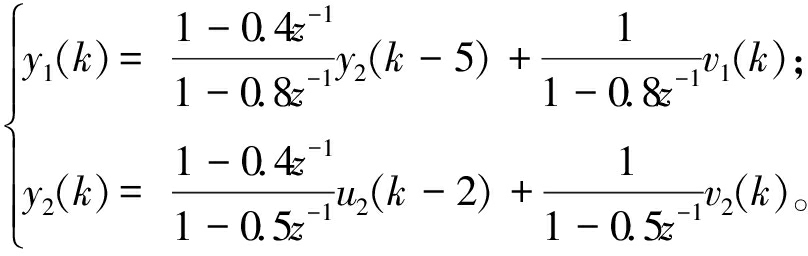
(20)
式中:![]() 和
和![]() 分别为主回路和副回路被控对象;
分别为主回路和副回路被控对象;![]() 和
和![]() 分别为主回路和副回路扰动通道。
分别为主回路和副回路扰动通道。
根据式(15)和式(16)可得主回路待辨识参数为(-0.8,1,-0.4,0),副回路待辨识的参数为(-0.5,1,-0.1,0)。此时将系统假设为一个黑箱模型,使用系统输入输出数据对系统进行参数估计,用估计得到的参数与系统真实参数进行比较,来验证辨识算法的准确性。
联立式(3)、式(4)可得系统输出反馈不变量为
yb(k)=Q1(z)v1(k)+S2(z)z-d1v2(k)=(1+0.8z-1+…+0.86z-6)v1(k)+(1+0.9z-1)z-5v2(k)。
(21)
式中:yb(k)代表反馈不变量;v1(k)和v2(k)分别表示主回路和副回路的噪声扰动。系统实际输出数据由MATLAB仿真平台采集得到。再根据式(5)、式(6)、式(12)、式(14)分别计算得到系统的最小方差指标、最小有理熵指标、SI系数指标、SI混合指标。
在仿真时,因最优控制器表达式过于复杂,所以根据经验法选择结构更简单的控制器。其中主副回路分别选取PI和P控制器,其表达式如下:
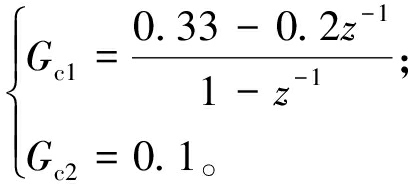
(22)
4.1 高斯扰动
首先选择主副噪声为高斯噪声的情况进行模拟,主回路噪声选择v1~N(0,0.255),副回路噪声选择v2~N(0,0.255)。分别使用HSSA算法和原SSA算法对串级系统进行分步辨识,得到系统主副回路的估计参数如表1所示。
表1 系统参数寻优结果
Table 1 System parameter optimization results

参数参数寻优结果 运行时间/s真实值[-0.800 1.000 -0.400 0 -0.500 1.000 -0.100 0]HSSA估计值[-0.814 0.997 -0.390 -0.021 -0.483 1.006 -0.094 -0.020]15.680SSA估计值[-0.741 0.984 -0.352 -0.114 0.532 0.654 0.076 0.254]17.815
由表1可知,改进算法有着更高的辨识精度,误差都在0.05以内,而原算法某些数值产生了较大偏差,如最后一位数0辨识为0.25;再观察运行时间,改进后的算法速度提升了11.98%,说明了算法改进的有效性。
图3为高斯扰动下系统主回路输出对比。图3中y1表示的是系统实际输出PDF,y2和y3分别代表系统的估计基准输出PDF和理论基准输出PDF。y2曲线和y3曲线接近,说明辨识算法估计的较为准确。得到各项性能指标如表2所示,从表2的数据来看,SI指标及其混合指标和熵指标的数值都接近1,表明在高斯噪声影响下的SI指标及其混合指标与最小熵指标评价效果相近。此时最小方差指标为0.9左右,说明高斯噪声下的方差指标能对系统进行正确评价。
表2 高斯扰动下的性能评估结果
Table 2 Performance evaluation results under Gaussian perturbations
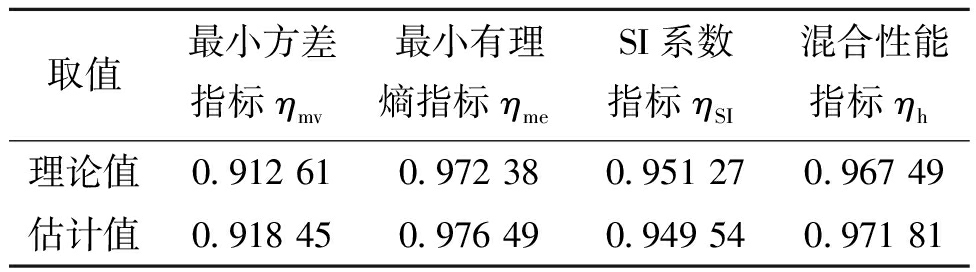
取值最小方差指标ηmv最小有理熵指标ηmeSI系数指标ηSI混合性能指标ηh理论值0.912 610.972 380.951 270.967 49估计值0.918 450.976 490.949 540.971 81
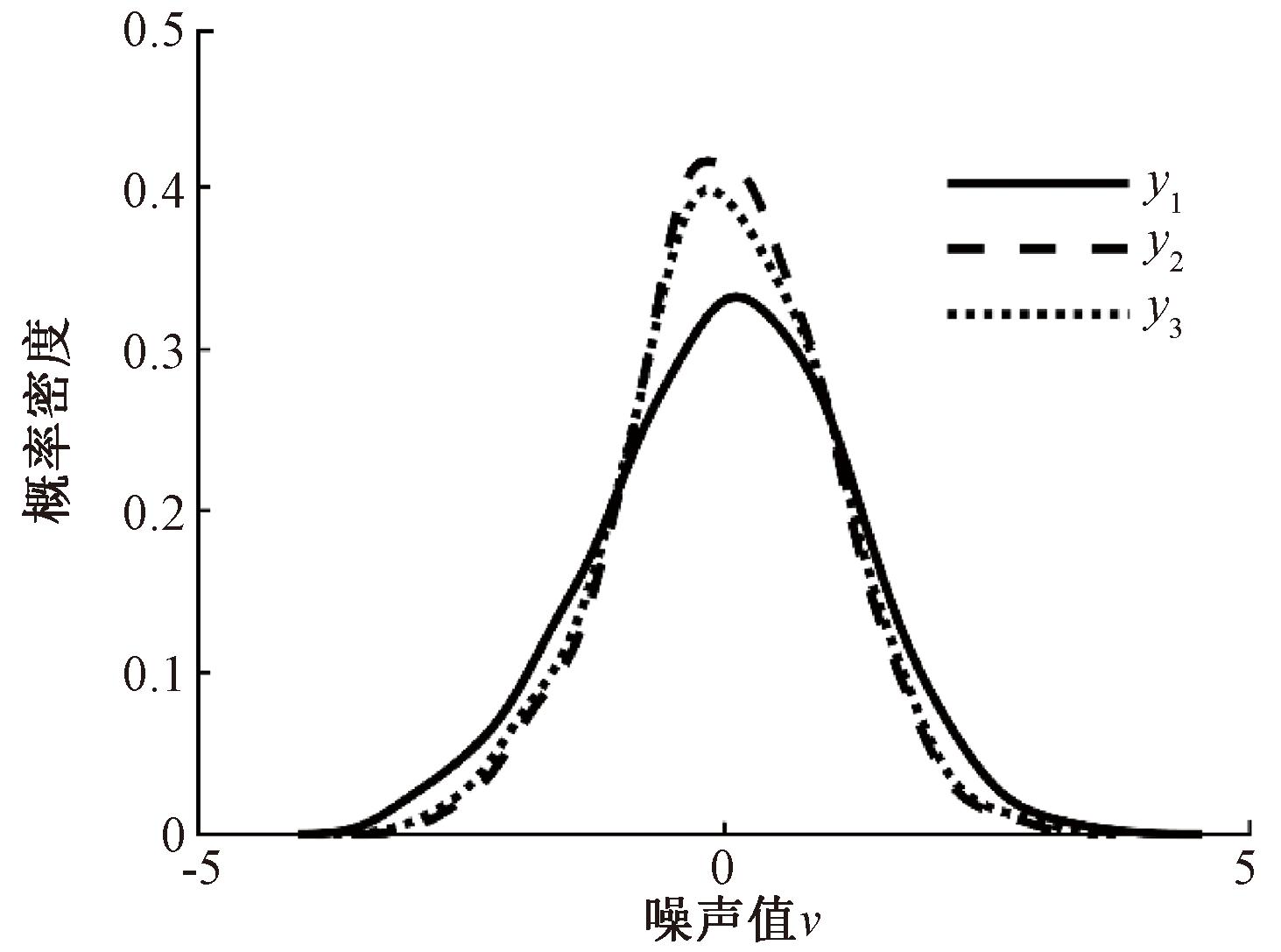
图3 高斯扰动下系统主回路输出
Figure 3 Main loop output with Gaussian perturbations
4.2 非高斯扰动
对主回路施加指数噪声v1~E(0.8),副回路施加指数噪声v2~E(0.5),得到系统性评价结果如表3所示,系统主回路输出如图4所示。
表3 指数扰动下的性能评估结果
Table 3 Performance evaluation results with exponential perturbations
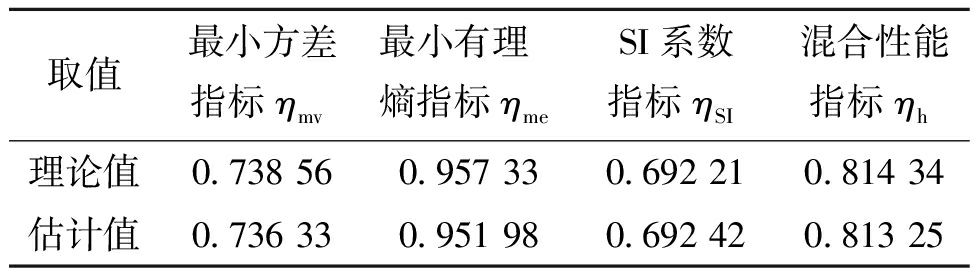
取值最小方差指标ηmv最小有理熵指标ηmeSI系数指标ηSI混合性能指标ηh理论值0.738 560.957 330.692 210.814 34估计值0.736 330.951 980.692 420.813 25
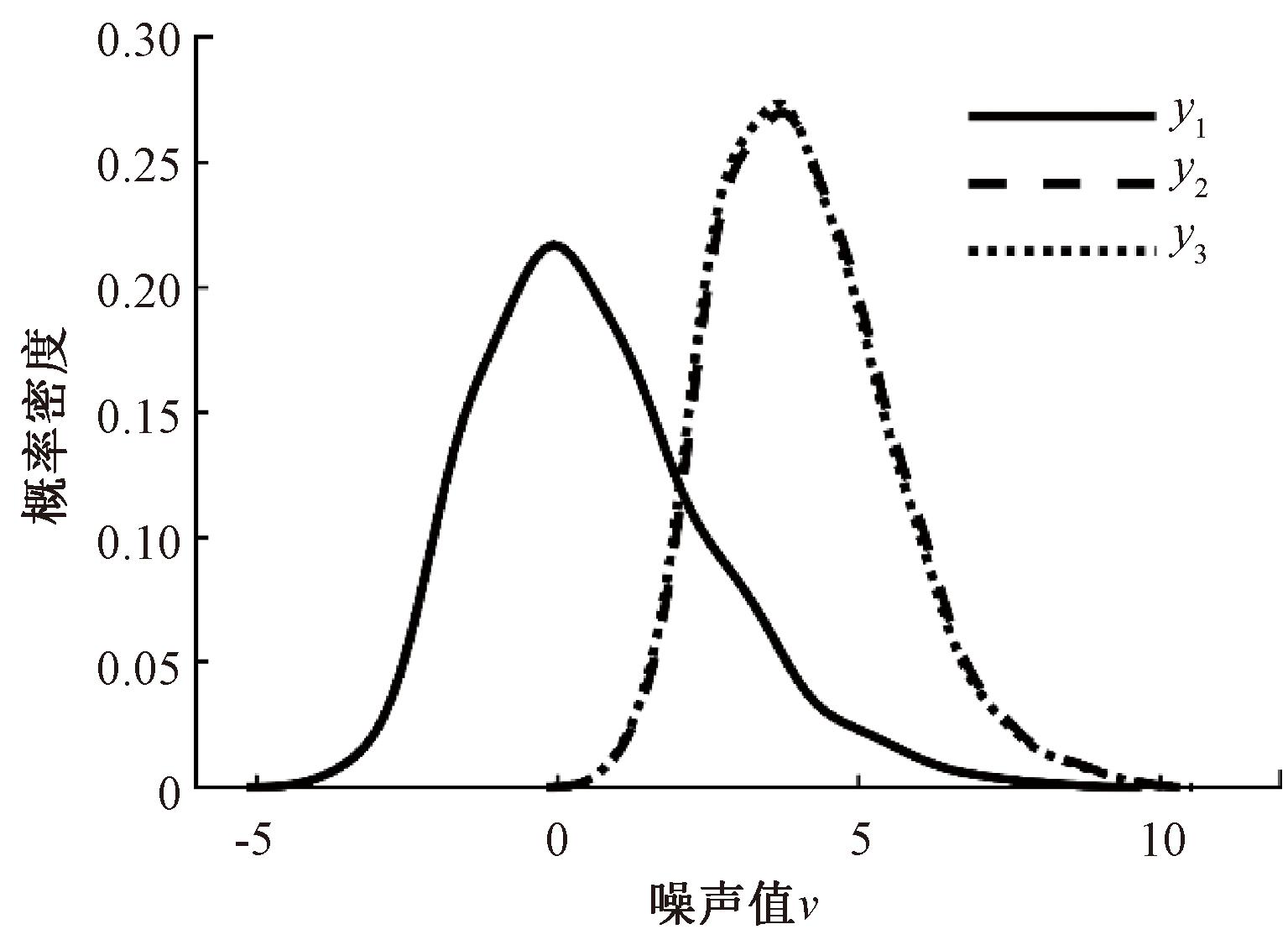
图4 指数扰动下系统主回路输出
Figure 4 Main loop output with exponential perturbations
观察图4指数扰动下的系统输出可知,系统的实际输出y2与理论基准输出y3发生了偏移现象,此时系统性能指标应该下降,而表3中最小有理熵指标仍然维持在0.95左右,与高斯情况下对比,没有反映出PDF的位移情况。反观SI指标和SI混合指标分别下降了0.269 06和0.153 15,下降幅度明显,反映了PDF发生位移,因此证明SI指标和混合指标可以有效克服熵指标的平移不变性。此时最小方差指标也有所下降,说明最小方差指标对简单的非高斯噪声仍然有一定的评价能力。
接下来给系统施加更为复杂的双峰噪声。令主回路为指数分布v1~E(0.8),副回路服从如下双峰分布:
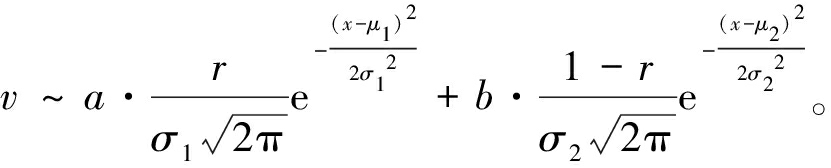
(23)
式中:μ1=-3;μ2=3;σ1=1;σ2=0.4;r=0.5。仿真结果如表4和图5所示。
表4 双峰扰动下的性能评估结果
Table 4 Performance evaluation results with bimodal perturbations
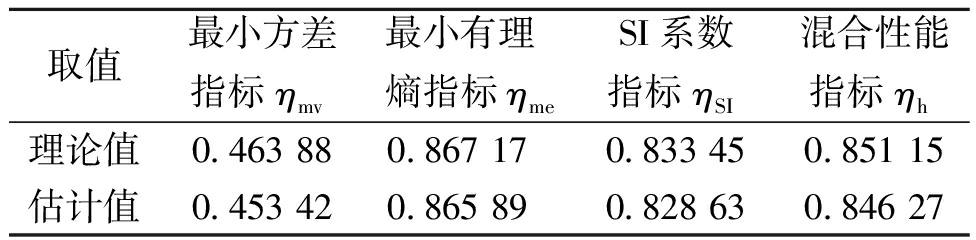
取值最小方差指标ηmv最小有理熵指标ηmeSI系数指标ηSI混合性能指标ηh理论值0.463 880.867 170.833 450.851 15估计值0.453 420.865 890.828 630.846 27
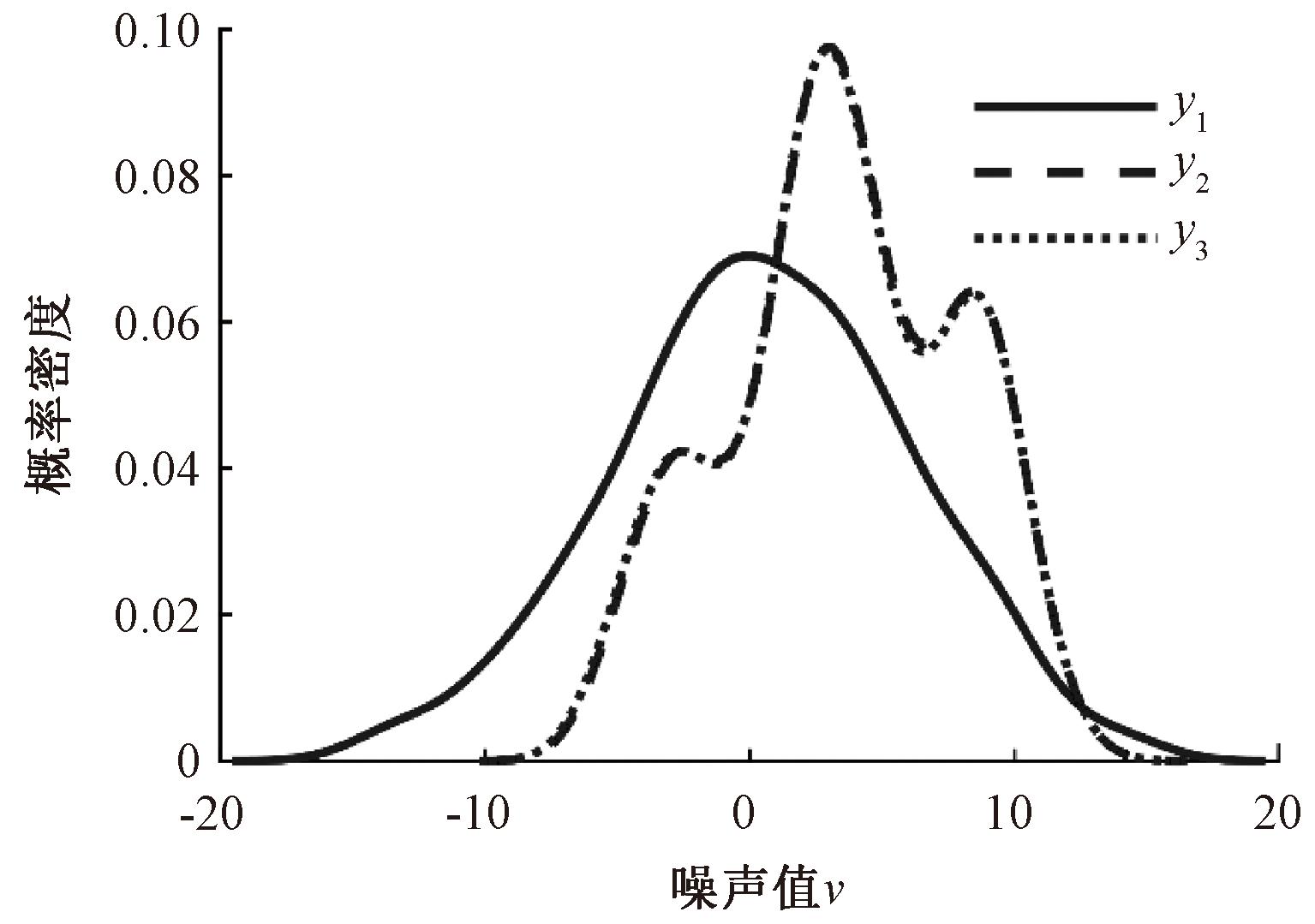
图5 双峰扰动下系统主回路输出
Figure 5 Main loop output with bimodal perturbations
在双峰噪声的干扰下,最小方差指标数值急剧减小,此时可以认为最小方差指标已经无法正常评价系统的性能。反观其余指标数值都在0.85左右,仍能正确评价系统。说明熵类指标在复杂噪声条件下对系统的评价具有优越性。
通过仿真实验可知,在串级系统中,最小方差指标能对高斯噪声或者简单的非高斯噪声做出正确评价,但对于复杂的噪声无法评价。而熵类指标对简单噪声或者复杂噪声都能做出正确评价,在加入SI指标之后更能适用于各种情况,优越性进一步增强。
5 结论
本文对非高斯系统性能评估相关问题进行了研究。为了克服传统熵指标平移不变性的缺陷,结合图像质量评价指标SSIM提出了SI指标。实验证实了该指标在噪声平移情况下能比熵指标更准确地评价系统性能,同时针对SI指标对于输出PDF的形状变化不够敏感的情况提出了以SI指标为主体的混合指标,能对系统进行更加全面的评价。
对于性能评价基准的获取,利用正余弦策略局部搜索能力强的优点,提出一种麻雀算法和正余弦算法相结合的混合麻雀算法。实验结果证明了所提算法与原麻雀算法相比有着更优的全局寻优能力和收敛速度。
[1] PIMENTEL M R, MUNARO C J. Performance monitoring and retuning for cascaded control loops[C]∥The 15th IEEE International Conference on Industry Applications (INDUSCON). Piscataway: IEEE, 2023: 647-654.
[2] TAN S B, YU X, WANG H H, et al. Performance assessment of cascade control systems based on LQG benchmark[C]∥2016 Chinese Control and Decision Conference (CCDC). Piscataway:IEEE, 2016: 49-52.
[3] JIA Y, ZHOU J L, LI D Z. Performance assessment of cascade control loops with non-Gaussian disturbances[C]∥2018 Chinese Automation Congress (CAC). Piscataway:IEEE, 2018: 2451-2456.
[4] 刘阳, 王亚刚. 最小熵基准的并行串级控制系统的性能评估[J]. 控制工程, 2019, 26(10): 1899-1904.LIU Y, WANG Y G. Performance assessment of parallel cascade control system based on minimum entropy[J]. Control Engineering of China, 2019, 26(10): 1899-1904.
[5] ZHANG Q, WANG Y G, LEE F F, et al. Improved renyi entropy benchmark for performance assessment of common cascade control system[J]. IEEE Access, 1074, 7: 6796-6803.
[6] 黄国豆. 非高斯随机系统控制回路性能评估方法的研究[D]. 北京: 华北电力大学, 2022.HUANG G D. Research on performance evaluation method of control loop of non-Gaussian stochastic system[D]. Beijing: North China Electric Power University, 2022.
[7] ZHANG H, ZHOU J L, WANG J. Performance assessment of non-Gaussian systems based on double error entropy minimization[C]∥The IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS). Piscataway:IEEE, 2019: 1177-1182.
[8] ZHANG J F, HUANG G D, ZHANG L. Generalized correntropy criterion-based performance assessment for non-Gaussian stochastic systems[J]. Entropy, 2021, 23(6): 764.
[9] HORÉ A, ZIOU D. Image quality metrics: PSNR vs. SSIM[C]∥The 20th International Conference on Pattern Recognition. Piscataway:IEEE, 2010: 2366-2369.
[10] 胡文, 景玉海. 基于KL散度与JS散度相似度融合推荐算法[J]. 哈尔滨商业大学学报(自然科学版), 2020, 36(1): 48-53.HU W, JING Y H. Recommendation algorithm based on fusion of KL divergence and JS divergence similarity[J]. Journal of Harbin University of Commerce (Natural Sciences Edition), 2020, 36(1): 48-53.
[11] JIANG H X, ZHOU J L, FAN S Y, et al. Analysis on control performance assessment based on minimum entropy[C]∥2018 IEEE 4th International Conference on Computer and Communications (ICCC). Piscataway:IEEE, 2018: 2731-2735.
[12] 高岳林, 杨钦文, 王晓峰, 等. 新型群体智能优化算法综述[J]. 郑州大学学报(工学版), 2022, 43(3): 21-30.GAO Y L, YANG Q W, WANG X F, et al. Overview of new swarm intelligent optimization algorithms[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(3): 21-30.
[13] 薛涛, 张安杰. 多策略改进的麻雀搜索算法及应用[J]. 西安工程大学学报, 2023, 37(2): 96-104.XUE T, ZHANG A J. Improved sparrow search algorithm based on multiple strategies and its application[J]. Journal of Xi’an Polytechnic University, 2023, 37(2): 96-104.
[14] MIRJALILI S. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133.
[15] ZHANG J, WANG J S. Improved salp swarm algorithm based on Levy flight and sine cosine operator[J]. IEEE Access, 2020, 8: 99740-99771.